Abstract
Deep models trained in supervised mode have achieved remarkable success on a variety of tasks. When labeled samples are limited, self-supervised learning (SSL) is emerging as a new paradigm for making use of large amounts of unlabeled samples. SSL has achieved promising performance on natural language and image learning tasks. Recently, there is a trend to extend such success to graph data using graph neural networks (GNNs). In this survey, we provide a unified review of different ways of training GNNs using SSL. Specifically, we categorize SSL methods into contrastive and predictive models. In either category, we provide a unified framework for methods as well as how these methods differ in each component under the framework. Our unified treatment of SSL methods for GNNs sheds light on the similarities and differences of various methods, setting the stage for developing new methods and algorithms. We also summarize different SSL settings and the corresponding datasets used in each setting. To facilitate methodological development and empirical comparison, we develop a standardized testbed for SSL in GNNs, including implementations of common baseline methods, datasets, and evaluation metrics.
Keywords: Self-supervised learning, graph neural networks, deep learning, unsupervised learning, graph analysis, survey, review
1. Introduction
A Deep model takes some data as its inputs and is trained to output desired predictions. A common way to train a deep model is to use the supervised mode in which a sufficient amount of input data and label pairs are given. However, since a large number of labels are required, the supervised training becomes inapplicable in many real-world scenarios, where labels are expensive, limited, imbalanced [1], or even unavailable. In such cases, self-supervised learning (SSL) enables the training of deep models on unlabeled data, removing the need of excessive annotated labels. When no labeled data is available, SSL serves as an approach to learn representations from unlabeled data itself. When a limited number of labeled data is available, SSL from unlabeled data can be used either as a pre-training process after which labeled data are used to fine-tune the pre-trained deep models for downstream tasks, or as an auxiliary training task that contributes to the performance of main tasks.
Recently, SSL has shown its promising capability in data restoration tasks, such as image super-resolution [2], image denoising [3, 4, 5], and single-cell analysis [6]. It has also achieved remarkable progress in representation learning for different data types, including language sequences [7, 8, 9], images [10, 11, 12, 13], and graphs with sequence models [14, 15] or spectral models [16]. The key idea of these methods is to define pretext training tasks to capture and use the dependencies among different dimensions of the input data, e.g., the spatial, temporal, or channel dimensions, with robustness and smoothness. Taking the image domain as an example, Doersch et al. [17], Noroozi and Favaro [18], and He et al. [19] design different pretext tasks to train convolutional neural networks (CNNs) to capture relationships between different crops from an image. Chen et al. [11] and Grill et al. [20] train CNNs to capture dependencies between different augmentations of an image.
Based on how the pretext training tasks are designed, SSL methods can be divided into two categories; namely contrastive models and predictive models. The major difference between the two categories is that contrastive models require data-data pairs for training, while predictive models require data-label pairs, where the labels are self-generated from the data, as illustrated in Figure 1. Contrastive models usually utilize self-supervision to learn data representation or perform pre-training for downstream tasks. Given the data-data pairs, contrastive models perform discrimination between positive pairs and negative pairs. On the other hand, predictive models are trained in a supervised fashion, where the labels are generated based on certain properties of the input data or by selecting certain parts of the data. Predictive models usually consist of an encoder and one or more prediction heads. When applied as a representation learning or pre-training method, the prediction heads of a predictive model are removed in the downstream task.
Fig. 1.
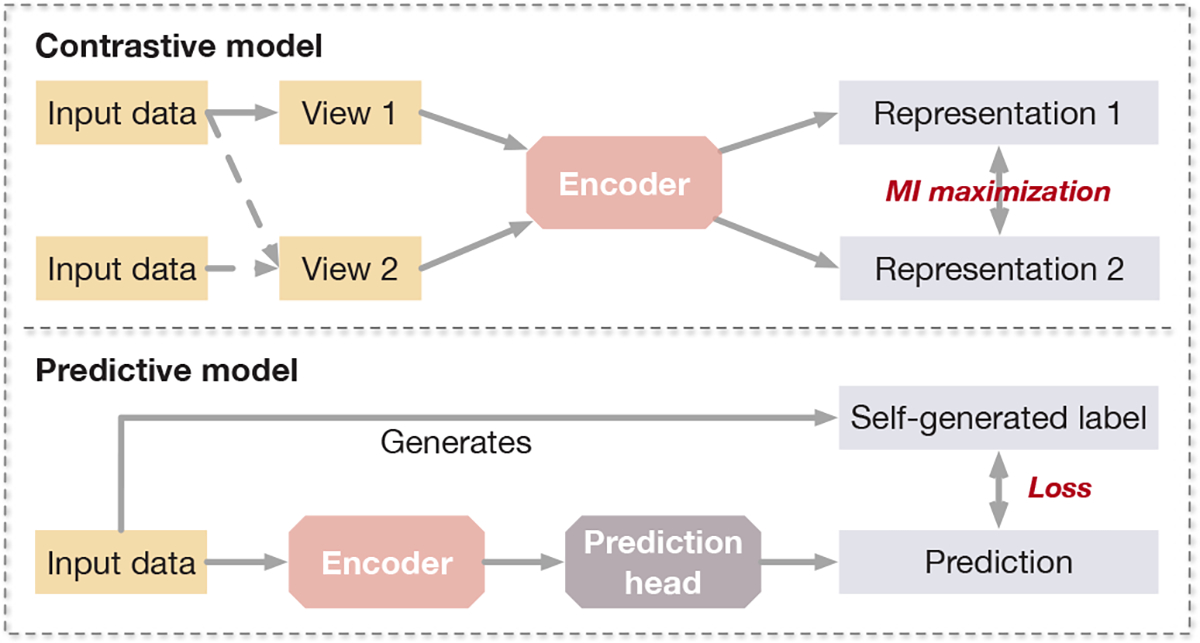
A comparison between the contrastive model and the predictive model in general.
In graph data analysis, SSL can potentially be of great importance to make use of a massive amount of unlabeled graphs such as molecular graphs [21, 22]. With the rapid development of graph neural networks (GNNs) [23, 24, 25, 26, 27, 28, 29], basic components of GNNs [30, 31, 32, 33, 34, 35] and other related fields [36, 37] have been well studied and made substantial progress. In comparison, applying SSL on GNNs is still an emerging field. Due to the similarity in data structure, many SSL methods for GNNs are inspired by methods in the image domain, such as DGI [38] and graph autoencoders [39]. However, there are several key challenges in applying SSL on GNNs due to the uniqueness of the graph-structured data. To obtain good representations of graphs and perform effective pre-training, self-supervised models are supposed to capture essential information from both nodes attributes and structural topology of graphs [40]. For contrastive models, as the GPU memory issue of performing self-supervised learning is not a major concern for graphs, the key challenge lies in how to obtain good views of graphs and the selection of graph encoder for different models and datasets. For predictive models, it becomes essential that what labels should be generated so that the non-trivial representations are learned to capture information in both node attributes and graph structures.
To foster methodological development and facilitate empirical comparison, we review SSL methods of GNNs and provide unified views for both contrastive and predictive methods. Our unified treatment of this topic may shed light on the similarities and differences among current methods and inspire new methods. We also provide a standardized testbed as a convenient and flexible open-source platform for performing empirical comparisons. We summarize the contributions of this survey as follows:
We provide thorough and up-to-date reviews on SSL methods for graph neural networks. To the best of our knowledge, our survey presents the first review of SSL specifically on graph data.
We unify existing contrastive learning methods for GNNs with a general framework. Specifically, we unify the contrastive objectives from the perspective of mutual information. From this fresh view, different ways to perform contrastive learning can be considered as performing three transformations to obtain views. We review theoretical and empirical studies and provide insights to guide the choice of each component in the framework.
We categorize and unify SSL methods with self-generated labels as predictive learning methods, and elucidate their connections and differences by different ways of obtaining labels.
We summarize common settings of SSL tasks and commonly used datasets of various categories under different settings, setting the stage for developments of future methods.
We develop a standardized testbed for applying SSL on GNNs, including implementations of common baseline methods and benchmarks, enabling convenient and flexible customization for future methods.
An overview of self-supervised learning methods of different categories is given in Figure 2.
Fig. 2.
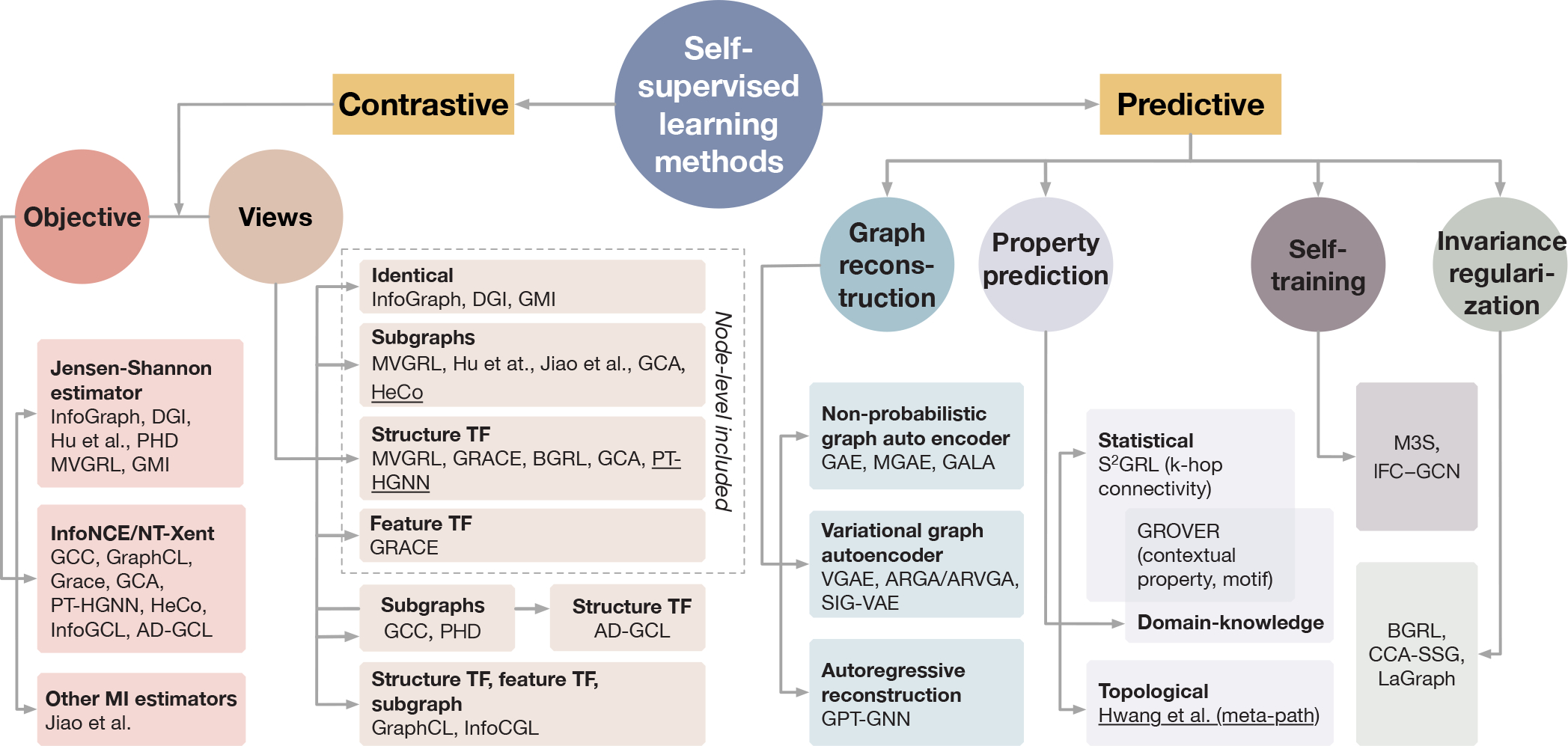
An overview of self-supervised learning methods. We categorize self-supervised learning methods into two branches: contrastive methods and predictive methods. For contrastive methods, we further divide them regarding either views generation or objective. From the aspect of views generation, Infograph [41], DGI [38] and GMI [42] contrast views between nodes and graph; Hu et al. [43] and Jiao et al. [44] contrast views between nodes and subgraph; MVGRL [10] and GCA [45] contrast views between nodes and subgraph or structurally transformed graph; GRACE [46] and BGRL [47] contrast views between nodes and structurally transformed graph or featurally transformed graph. Above methods include node-level representation to generate local/global contrastive pairs. Dissimilarly, following methods use global representation only to generate global/global contrastive pairs. GCC [48] contrasts views between subgraphs; GraphCL [49] contrasts views of subgraphs and randomly transformed graphs. From aspect of objective, Infograph [41], DGI [38], Hu et al. [43], MVGRL [10] and GMI [42] employ Jensen-Shannon estimator; GCC [48], GraphCL [49], GRACE [46] and GCA [45] employ InfoNCE (NT-Xent); Jiao et al. [44] use other MI estimators. For the predictive methods, we further divide them into graph reconstruction, property prediction, self-training, and invariance regularization methods. Under graph reconstruction, GAE [39], MGAE [50], and GALA [51] utilize the non-probabilistic graph autoencoder; VGAE [39], ARGA/ARVGA [52], and SIG-VAE [53] utilize variational graph autoencoder; GPT-GNN [54] applies autoregressive reconstruction. Under property prediction, S2GRL [55] performs the prediction of k-hop connectivity as a statistical property; GROVER [56] performs predictions of a statistical contextual property and a domain-knowledge involved property; Hwang et al. [57] predict a topological property, meta-path. M3S [58] and ICF-GCN [59] employs self-training and node clustering to provide self-supervision. BGRL [47], CCA-SSG [60], and LaGraph [61] derive self-supervised objectives involving invariance regularization without requiring negative pairs. SSL methods for heterogeneous graphs are marked with underlines. We discuss and summarize SSL methods for heterogeneous graphs and dynamic graphs in Appendix A. We further discuss and compare contrastive and predictive methods in Appendix B.
A recent work [62] provides thorough and general literature reviews on self-supervised learning for vision, natural language processing, and graph mining tasks. While both [62] and our work review SSL methods as contrastive ones and non-contrastive ones, we distinguish our reviews from [62] by the following distinct differences.
Liu et al. [62] and our paper propose different taxonomies for SSL methods from different aspects of view. Specifically, [62] categorizes contrastive methods by the levels of contrast such as instance-instance and context-instance, where mutual-information is considered as one specific subcategory at the context-instance level. In contrast, our taxonomy provides a more unified view and framework from the theoretical grounding of the methods. Specifically, in our work, all contrastive methods are theoretically grounded by mutual information maximization, and the contrastive objectives are different upper bounds or estimators of mutual information. In our framework, different levels of contrast are determined by how views are selected or generated. We believe that the more unified view enables a more clear comparison and insightful understanding of commons and differences among SSL methods.
Though adapted to graphs, the taxonomy proposed by [62] is mostly oriented by SSL methods for images. While SSL for graphs and images share some connections and similarities, there are remarkable differences between specific methods for the two types of data and some categorizations of images do not apply to graphs. For example, the relative position and the cluster discrimination methods categorized by [62] are image-specific contrastive methods and do not apply to graphs whereas view generation approaches for graphs and graph-specific predictive tasks are not discussed in [62]. Therefore, graph-specific SSL reviews such as ours are important and necessary for a better understanding of existing methods and benefit future studies.
Recently, another concurrent survey [63] provides reviews on SSL methods for GNNs. The work proposes a taxonomy with more subdivided categories including generation-based, auxiliary property-based, contrastive-based, and hybrid methods. While [63] aims to provide better coverage on existing SSL methods for review, our work focuses on providing a more timely and unified review under comparable frameworks and provide insights into future SSL studies.
2. Problem Formulation
2.1. Notations
We consider an attributed undirected graph G = (V, E, α), where V = {v1, ·· ··,v|V|} denotes the set of its nodes, E = {e1 · · ·,e|E|} denotes the set of its edges and denotes the mapping from a node to its attributes of d dimensions. We denote the adjacency matrix of G by , where for 1 ≤ i, j ≤ |V|, and denote the feature matrix of G by , where the i-th row Xi = α(vi) for 1 ≤ i ≤ |V|. A heterogeneous graph additionally includes elements ϕ: V → Tn that maps a node to a node type in Tn and ψ : E → Te that maps an edge to an edge type in Te.
Given the graph data (A, X) from the input space , we are interested in the representation of the graph at either node-level or graph-level for any downstream prediction tasks. In general, we want to learn an encoder f such that the representation H = f(A, X) can achieve desired performance on a downstream prediction task. For node-level prediction tasks, we learn a node-level encoder that takes the graph data (A, X) as inputs and computes the representations for all nodes . For graph-level prediction tasks, we learn a graph-level encoder that computes a single vector as the representation of the given graph. Practically, graph-level encoders are usually constructed as a node-level encoder followed by a readout function. In many cases, a model for node-level representation learning may also be utilized to compute graph-level representations by adding an appropriate readout function, and vice versa (by removing the readout function).
We let denote the distribution of unlabeled graphs over the input space . Given a training dataset, the distribution can be simply constructed as the uniform distribution over samples in the dataset. The self-supervision can contribute to the learning of graph encoders f by utilizing information from and minimizing a self-supervised loss determined by a specifically designed self-supervised learning task.
2.2. Paradigms for Self-Supervised Learning
Typical training paradigms to apply the self-supervision include unsupervised representation learning, unsupervised pretraining, and auxiliary learning.
In unsupervised representation learning, only the distribution of unlabeled graphs is available for the entire training process. The problem of learning the representation of a given graph data is formulated as
| (1) |
| (2) |
The learned representations H* are then used in further downstream tasks such as linear classification and clustering.
The unsupervised pretraining, also dubbed the decoupled training by Wang et al. [64], is usually performed as a two-stage training [65]. It first trains the encoder f with unlabeled graphs. The pre-trained encoder finit is then used as the initialization of the encoder in a supervised fine-tuning stage. Formally, in addition to the distribution , the learner further gains access to a distribution of labeled, graphs over , where denotes the label space. Again, given the labeled training dataset, can be simply constructed as the uniform distribution over labeled samples in the dataset. The pretrained encoder finit is then fine-tuned on , together with a prediction head h s.t. and a supervised loss , i.e.,
| (3) |
with initialization
| (4) |
The unsupervised pretraining and supervised finetuning paradigm is considered as the most strategy to perform semi-supervised learning and transfer learning. For semi-supervised learning, the labeled graphs in the finetuning dataset is a portion of the pretraining dataset. For transfer learning, the pretraining and finetuning datasets are from different domains. Note that a similar learning setting called unsupervised domain adaptation has also been studied generally [66] or specifically in the image domain [67], where the encoder is pre-trained on labeled data but finetuned on unlabeled data under self-supervision. Since the paradigm is not specifically studied in the graph domain, we do not discuss the learning setting in detail in this survey.
The auxiliary learning, also known as joint training [65], aims to improve the performance of a supervised primary learning task by including an auxiliary task under self-supervision. Formally, we let denote the joint distribution of graph data and labels for the primary learning task and denote the marginal of graph data. We want to learn both the decoder f and the prediction head h, where h is trained under supervision on and f is trained under both supervision and self-supervision on . The learning problem is formulated as
| (5) |
where λ is a positive scalar weight that balances the two terms in the loss.
3. Contrastive Learning
The study of contrastive learning has made significant progress in natural language processing and computer vision. Inspired by the success of contrastive learning in images, recent studies propose similar contrastive frameworks to enable self-supervised training on graph data. Given training graphs, contrastive learning aims to learn one or more encoders such that representations of similar graph instances agree with each other, and that representations of dissimilar graph instances disagree with each other. We unify existing approaches to constructing contrastive learning tasks into a general framework that learns to discriminate jointly sampled view pairs (e.g. two views belonging to the same instance) from independently sampled view pairs (e.g. views belonging to different instances). In particular, we obtain multiple views from each graph in the training dataset by applying different transformations. Two views generated from the same instance are usually considered as a positive pair and two views generated from different instances are considered as a negative pair. The agreement is usually measured by metrics related to the mutual information between two representations.
One major difference among graph contrastive learning methods lies in (a) the objective for discrimination task given view representations. In addition, due to the unique data structure of graphs, graph contrastive learning methods also differ in (b) approaches that views are obtained, and (c) graph encoders that compute the representations of views. A graph contrastive learning method can be determined by specifying its components (a)–(c). In this section, we summarize graph contrastive learning methods in a unified framework and then introduce (a) and (b) individually used in existing studies. In Appendix C, we introduce graph neural networks specifically adopted in contrastive learning as graph encoders and provide further comparisons and discussions on their effects in contrastive learning. Moreover, we summarize all contrastive methods being reviewed by this survey in Supplementary Table 1 for more clear comparisons.
3.1. Overview of Contrastive Learning Framework
In general, key components that specify a contrastive learning framework include transformations that compute multiple views from each given graph, encoders that compute the representation for each view, and the learning objective to optimize parameters in encoders. An overview of the framework is shown in Figure 4. Concretely, given a graph (A, X) as a random variable distributed from , multiple transformations are applied to obtain different views w1, ···, wk of the graph. Then, a set of encoding networks f1, ···, fk take corresponding views as their inputs and output the representations h1, ···, hk of the graph from each views. Formally, we have
| (6) |
| (7) |
We assume in this survey since existing contrastive methods consider their views as graphs. However, note that not all views wi are necessarily graphs or sub-graphs in a general sense. In addition, certain encoders can be identical to each other or share their weights.
Fig. 4.
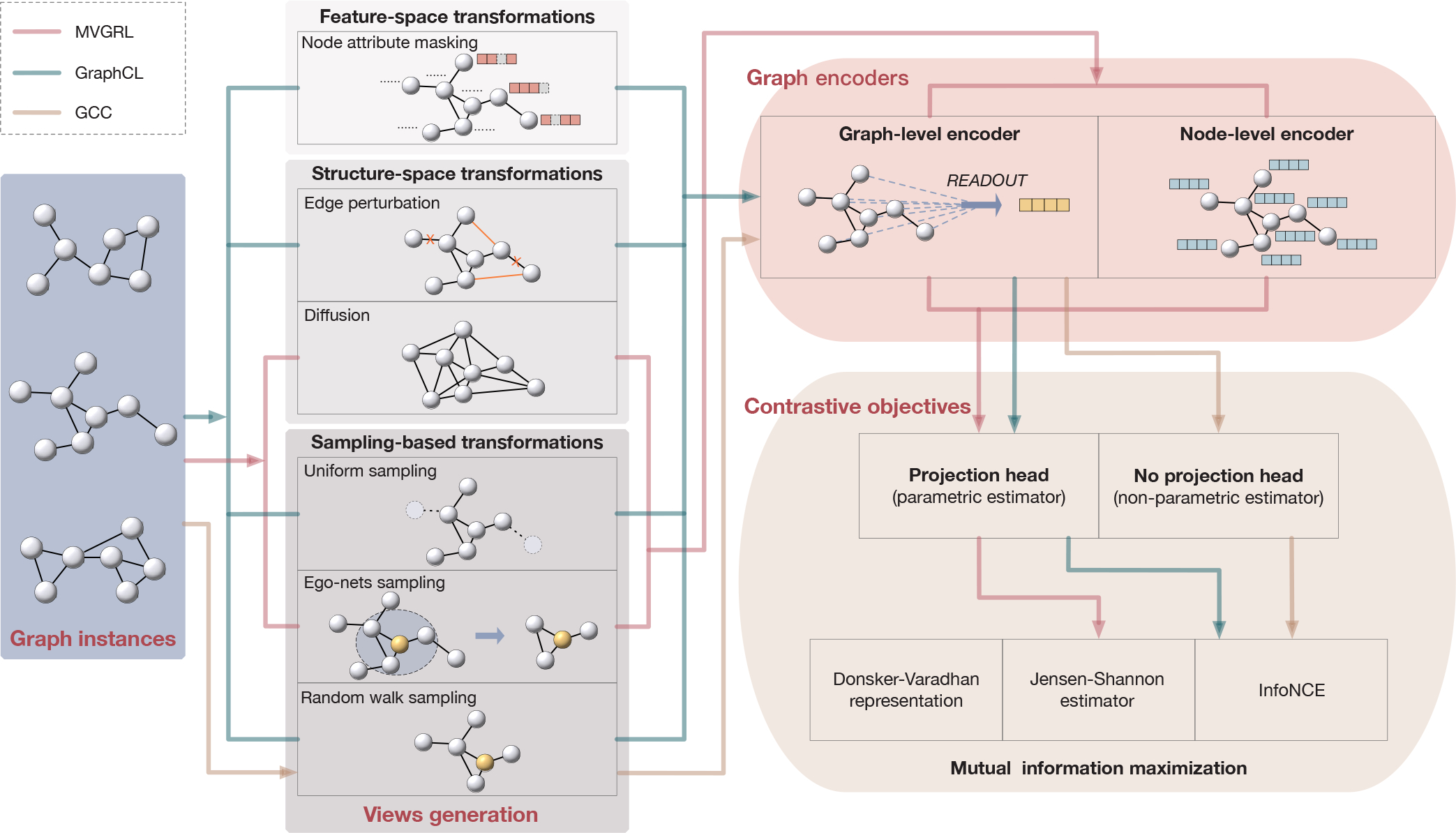
The general framework of contrastive methods. A contrastive method can be determined by defining its views generation, encoders, and objective. Different views can be generated by a single or a combination of instantiations of three types of transformations. Commonly employed transformations include node attribute masking as feature transformation, edge perturbation and diffusion as structure transformations, and uniform sampling, ego-nets sampling, and random walk sampling as sample-based transformations. Note that we consider a node representation in node-graph contrast [13, 38, 41] as a graph view with ego-nets sampling followed by a node-level encoder. For graph encoders, most methods employ graph-level encoders and node-level encoders are usually used in node-graph contrast. Common contrastive objectives include Donsker-Varadhan representation, Jensen-Shannon estimator, InfoNCE, and other non-bound objectives. An estimator is parametric if projection heads are employed, and is non-parametric otherwise. Examples of three specific contrastive learning methods are illustrated in the figure. Red lines connect options used in MVGRL [10]; green lines connect options adopted in GraphCL [49]; yellow lines connect options taken in GCC [48].
During training, the contrastive objective aims to train encoders to maximize the agreement between view representations computed from the same graph instance. The agreement is usually measured by the mutual information between a pair of representations hi and hj. We formalize the contrastive objective as
| (8) |
Where σij ∈ {0, 1}, and σij = 1 if the mutual information is computed between hi and hj, and σij = 0 otherwise, and hi and hj are considered as two random variables belonging to either a joint distribution or the product of two marginals. To enable efficient computation of the mutual information, certain estimators of the mutual information are usually used instead as the learning objective. Note that some contrastive methods apply projection heads [10, 49] to the representations. For the sake of uniformity, we consider such projection heads as parts of the computation in the mutual information estimation.
During inference, one can either use a single trained encoder to compute the representation or a combination of multiple view representations such as the linear combination or the concatenation as the final representation of a given graph. Three examples of using encoders in different ways during inference are illustrated in Figure 5.
Fig. 5.
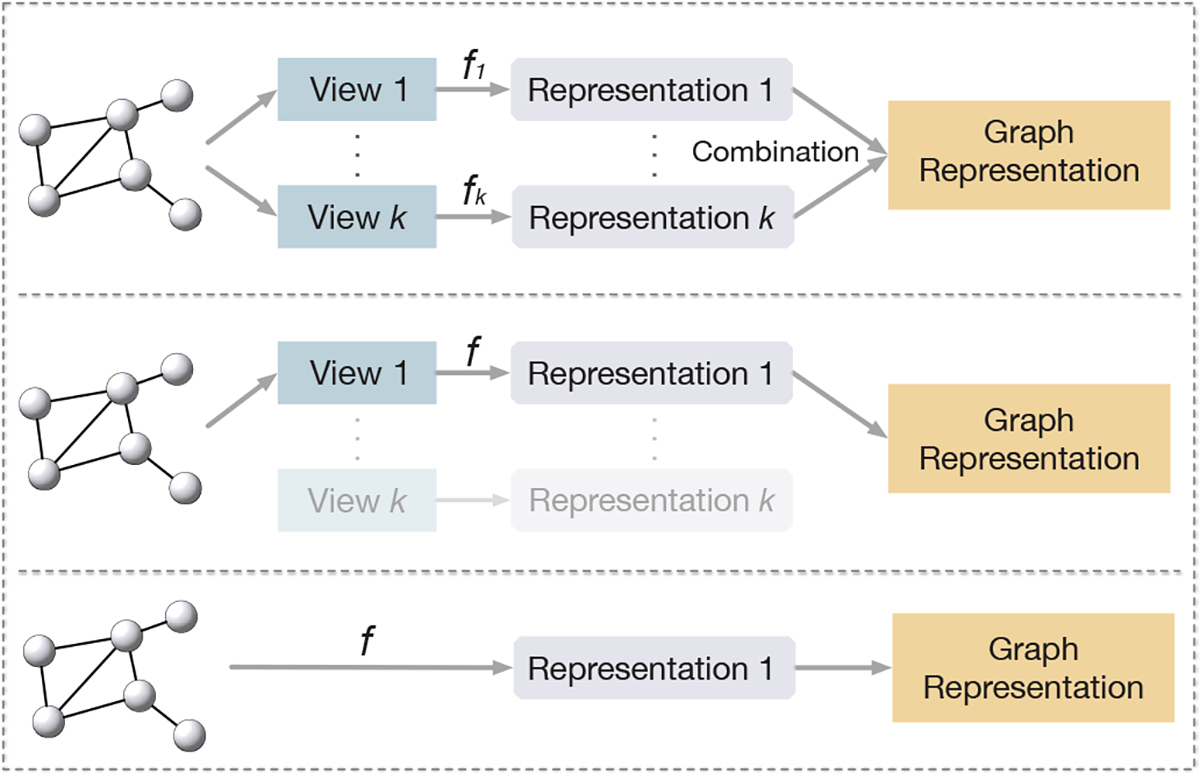
Different ways of using encoders during inference. Top: encoders for multiple views are used and output representations are merged by combinations such as summation [10] or concatenation. Middle: only the main encoder [47] and the corresponding view are used during inference. Bottom: the given graph is directly input to the only encoder [48, 49] shared by all views to compute its representation.
3.2. Contrastive Objectives based on MI Estimations
Given a pair of random variables (x, y), the mutual information measures the information that x and y share, given by
| (9) |
| (10) |
where DKL denotes the Kullback-Leibler (KL) divergence. The contrastive learning seeks to maximize the mutual information between two views as two random variables. In particular, it trains the encoders to be contrastive between representations of a positive pair of views that comes from the joint distribution p(vi, vj) and representations of a negative pair of views that comes from the product of marginals p(vi)p(vj).
In order to computationally estimate and maximize the mutual information in the contrastive learning, three typical lower-bounds to the mutual information are derived [68], namely, the Donsker-Varadhan representation [69, 70], the Jensen-Shannon estimator [71] and the noise-contrastive estimation (InfoNCE) [12, 72]. Among the three lower-bounds, and are commonly used as objectives [10, 38, 41, 49] in the contrastive learning in graphs.
A mutual information estimation is usually computed based on a discriminator that maps the representations of two views to an agreement score between the two representations. The discriminator can be either parametric or non-parametric. For example, the discriminator can optionally apply a set of projection heads [10, 49] to the representations h1, ···, hk before computing the pairwise similarity. We formalize the optional projection heads as g1, ···, gk such that
| (11) |
where gi can be an identical mapping, a linear projection or an MLP. Parameterized gi are optimized simultaneously with the encoders fi in Eqn. (8), given by
| (12) |
In following subsections, we introduce the three lower bounds as specific estimations of mutual information and a non-bound estimation of mutual information. We further compare and discuss the effect of different MI estimations in contrastive learning in Appendix D.
3.2.1. Donsker-Varadhan Estimator
The Donsker-Varadhan (DV) estimator, also knwon as the DV representation of the KL divergence, is a lower-bound to the mutual information and hence can be applied to maximize the mutual information. Given hi and hj, the lower-bound is computed as
| (13) |
where p(hi, hj) denotes the joint distribution of the two representations hi, hj and p(hi)p(hj) denotes the product of marginals. For simplicity and to include the graph data distribution , we assume transformations to be deterministic and encoders fi to be injective, and have We hence re-write Eqn. (13) as
| (14) |
where hi and hj in the first term are computed from (A, X) distributed from , hi and in the second term are computed from (A, X) and (A′, X′) identically and independently distributed from , respectively. In following formulations, we use the later notation includes .
3.2.2. Jensen-Shannon Estimator
Compared to the Donsker-Varadhan estimator, the Jensen-Shannon (JS) estimator enables more efficient estimation and optimization of the mutual information by computing the JS-divergence between the joint distribution and the product of marginals.
Given two representations hi and hj computed from the random variable (A, X) and a discriminator , DGI [38], InfoGraph [41], Hu et al. [43] and MVGRL [10] computes the JS estimator
| (15) |
where hi, hj in the first term are computed from (A, X) distributed from , hi and in the second term are computed from (A, X) and (A′, X′) identically and independently distributed from the distribution . To further include edge features, Peng et al. [42] derives the graphic mutual information (GMI) based on MI decomposition and optimizes GMI via JS estimator. Note that [41] and [10] depict a softplus version of the JS estimator,
| (16) |
where sp(x) = log(1 + ex). We consider the JS estimators in Eqn. (15) and Eqn. (16) to be equivalent by letting .
For the the negative pairs of graphs in particular, DGI [38] samples one graph (A, X) from the training dataset and applies a stochastic corruption to obtain . For node-level tasks, MVGRL [10] follows DGI to obtain negative samples by corrupting given graphs. InfoGraph [41] independently samples two graphs from the training dataset as a negative pair, which is followed by MVGRL for graph-level tasks. Discriminators in JS estimators usually compute the agreement score between two vectors by their inner product with sigmoid, i.e., .
3.2.3. InfoNCE
InfoNCE is another lower-bound to the mutual information . It is shown by You et al. [49] that maximizing InfoNCE it equivalent to maximizing the Donsker-Varadhan estimator. Given the representations hi and hj of two views of random variable (A, X), the discriminator , and the number of negative samples N, the InfoNCE is formalized as
| (17) |
where K consists of N random variables identically and independently distributed from , hi, hj are the representations of the i-th and j-th views of (A, X), and is the representation of the j-th view of (A′, X′)
In practice, we compute the InfoNCE on mini-batches of size N + 1. For each sample x in a mini-batch B, we consider the set of the rest N samples as a sample of K. We then discard the constant term log N in Eqn. (17) and minimize the loss
| (18) |
Intuitively, the optimization of InfoNCE loss aims to score the agreement between hi and hj of views from the same instance x higher than between hi and from the rest N negative samples B \ {x}. GraphCL [49] and GRACE [46] include additional contrast among the same view of different instances (i.e., hi and ) or different nodes in the same view (intra-view contrast [46]), leading to the optimization of lower bounds of InfoNCE, which are still lower bounds of MI.
Discriminators in typical InfoNCE compute the agreement score between two vectors by their inner product, i.e., . A specific type of the InfoNCE loss, known as the NT-Xent [73] loss, includes normalization and a preset temperature parameter τ in the computation of discriminator in the InfoNCE loss, i.e., . The discriminator in You et al. [49] computes the agreement score between vectors with normalizations, i.e., , where ‖·‖denotes the ℓ2-norm.
3.2.4. Other Mutual Information Estimators
There are other objectives that have been used in some studies, and optimizing these objectives can also encourage higher mutual information. Although the objectives differ from the above upper bound MI estimators
However, these objectives may not be provable lower-bounds to the mutual information, and optimizing these objectives does not guarantee the maximization of the mutual information.
For example, Jiao et al. [44] proposes to minimize the triplet margin loss [74], which is commonly used in deep metric learning [75]. Given representations hi, hj and the discriminator , the triplet margin loss is formalized as
| (19) |
where is computed as sigmoid or based on the Euclidean distance ‖hi − hj‖ and ϵ is the margin value. While the triplet loss differs from previous MI-based objectives in formulations, Khosla et al. [76] show that the triplet loss is a special case of the InfoNCE (NT-Xent) loss when there is only one negative sample where the margin value ϵ corresponds to the temperature parameter τ in NT-Xent. Moreover, the Bayesian Personalized Ranking (BPR) loss [77] used in Jiao et al. [44] is also equivalent to the InfoNCE loss when letting N = 1 and .
3.2.5. Projection Heads: Parametric MI Estimation
Many contrastive learning studies [10, 41, 49] propose to include projection heads gi when computing the MI estimations. For example, Hassani and Khasahmadi [10], Sun et al. [41] use 3-layer MLPs, You et al. [49] use 2-layer MLPs as the projection heads and Sun et al. [41] applies a linear projection to the graph-level representation. The projection heads are shown to significantly improve the contrastive learning performance [11]. For contrastive learning on heterogeneous graphs, it is common to apply individual projections to representations of different type of nodes. For example, Jiang et al. [78] adopt for nodes u and v with types ϕ(v) and ϕ(v) connected by the relationship R, where .
We consider MI estimators that include projection heads as parametric estimators and those without projection heads as non-parametric estimators. Then a reasonable explanation to the observation that the contrastive methods with projection heads usually achieve better performance is that parametric estimators provide better estimation to the mutual information.
3.3. Graph View Generation
To generate views from a graph sample distributed from , one usually applies different types of graph transformations (or augmentations) . Here, we only consider cases where still outputs the graph-structured data. We summarize the existing transformations applied to graph data in three categories, feature transformations, structure transformations and sampling-based transformations. Feature transformations can be formalized as
| (20) |
where performs the transformation on the feature matrix X. Structure transformations can be formalized as
| (21) |
where performs the transformation on the adjacency matrix A. And the sampling-based transformations are in the form
| (22) |
where S ⊆ V denotes a subset of nodes and [·] selects certain rows (and columns) from a matrix based on indices of nodes in S. We consider the transformations applied in the existing contrastive learning methods to generate different views as a single or a combination of instantiations of the three types of transformations above. Note that when node-level representations are of interest, the node-level contrasts are usually included. We consider nodes representations to be computed from views generated by ego-nets sampling from given graphs.
3.3.1. Feature Transformations
Given an input graph (A, X), a feature transformation only performs transformation to the attribute matrix X, i.e., .
Node attribute masking [49] is one of the most common way to apply the feature transformations. The node attribute masking randomly masks a small portion of attributes of all node with constant or random values. Concretely, given the input attribute matrix X, we specify for the node attribute masking as
| (23) |
where * denotes the element-wise multiplication, M denotes a matrix with masking values and 1m denotes the masking location indicator matrix. Given the masking ratio r, elements in 1m are set to 1 individually with a probability r and 0 with a probability 1 − r. To employ adaptive masking, Zhu et al. [45] propose to sample 1m with centrality-based probabilities, including degree centrality, eigenvector centrality, and PageRank centrality. The values in M specifies different masking strategies. For example, M = 0 applies a constant masking, M ~ N(0, Σ) replaces the original values by Gaussian noise and M ~ N(X, Σ) adds Gaussian noise to the original values.
In addition to contrastive models such as [49], attributes masking is also commonly applied in predictive models [3, 6] for regularized reconstruction. The node attribute masking forces the encoders to captures better dependencies between the masked attributes and unmasked context attributes and recover the masked value from its context during encoding.
3.3.2. Structure Transformations
Given an input graph (A, X), a structure transformation only performs transformation to the adjacency matrix A and remains X to be the same, i.e., . Existing contrastive methods apply two types of structure transformations, edge perturbation that randomly adds or drops edges between pairs of nodes and graph diffusion that creates new edges based on the accessibility from one node to another.
Edge perturbation [48, 49] randomly adds or drops edges in a given graph. Similarly to the node attribute masking, it applies masks to the adjacency matrix A. In particular, we have
| (24) |
where * denotes the element-wise multiplication and 1p denotes the perturbation location indicator matrix. Given the perturbation ratio r, elements in 1p are set to 1 individually with a probability r and 0 with a probability 1 − r. In addition, 1p is a symmetric matrix.
Diffusion [10] creates new connections between nodes based on random walks, aiming at generating a global view (S, X) of the graph in contrast to the local view (A, X). Two instantiations of diffusion transformations are proposed to use in [10], namely, the heat kernel and the Personalized PageRank , formulated as follows.
| (25) |
| (26) |
where is a diagonal degree matrix, α denotes the teleport probability in a random walk and t denotes the diffusion time.
Centrality-based edge removal [45] randomly removes edges based on pre-computed probabilities determined by the centrality score of each edge. Centrality-based probabilities for edge removal reflects the importance of each edge, where less important edges are more likely to be removed. In particular, the centrality score of an edge (u, v) ∈ E is computed as wuv = (ϕc(u) + ϕc(u))/2, where ϕc(u) and ϕc(v) are the centrality of nodes u and v connected by the edge and a higher centrality score leads to lower probability puv of edge removal.
3.3.3. Sampling-Based Transformations
We consider sampling-based transformations that sample node-induced sub-graphs from a given graph (A, X), i.e., with S ⊆ V Note that more generalized sub-graph sampling methods that sample both nodes from V and edges from E can be considered as a combination of the node-induced sub-graph sampling and the edge perturbation. As different sampling-based transformations are determined by the set S of sampled nodes from the node-set V, we categorize the sampling-based transformations by how the set S is obtained. Existing contrastive methods apply three approaches to obtain the node subset S, uniform sampling, random walk sampling, and ego-nets sampling.
Uniform sampling and nodes dropping can be considered as the two simplest sampling-based transformation approaches. The transformation in [10] samples sub-graphs by uniformly sampling a given number of nodes S from V and edges of the sampled nodes. In addition, transformation methods in [49] include node dropping as one of the graph transformations, where each node has a certain probability to be dropped from the graph. We denote the set of dropped nodes by D and we have S = V \ D.
Ego-nets sampling can be considered as a sampling-based transformation to unify the contrast performed between graph-level representation and node-level representations in the general contrastive learning framework, such as in DGI [38], InfoGraph [41] and MVGRL [10]. In other words, we consider that node-level representations are computed by node-level encoders from certain views, namely, ego-nets, of a given graph. Given a typical graph encoder with L layers, the computation of the representation of each node vi only depends on its L-hop neighborhood, also known as the L-ego-net of node vi. We hence consider the computing of node-level representations as performing L-ego-net sampling and a node-level encoder with L layers. In particular, for each node vi in a given graph, the transformation , samples the L-ego net surrounding node vi as the view wi computed as
| (27) |
| (28) |
where L denotes the number of layers in the node-level encoder fi, d denotes the shortest distance between two nodes and (A[·;·],X[·]) selects a sub-graph from (A, X).
Random walk sampling is proposed in GCC [48] to sample sub-graphs based on random walks starting from a given node. The subset of nodes S ∈ V is collected iteratively. At each iteration, the walk has a probability pij to travel from node vi to node vj and has a probability of pr = 0.8 to return to the start node. GCC considers the random walk sampling with restart as a further transformation of the r-ego-net centered at the start node. Given the center (start) node, the random walk sampling can be hence considered as a stronger sampling-based transformation than the ego-nets sampling.
Network Schema and Meta-path views are proposed in HeCo [79] as two specific views for the contrastive learning of heterogeneous graphs. Given a target node of type t, the network schema view is a special case of 1-ego-nets consisting of neighbor nodes whose types are connected to the target node type in the network schema, and excluding nodes with the same type t. When computing the representation for a network schema view, aggregations are computed individually for each node type. The meta-path view consists of all meta-paths between the target node and other nodes of the same type. When computing the representation for a meta-path view, nodes of other types are masked and the information is aggregated along individual meta-paths.
3.3.4. Discussions of Graph View Generation
Currently, there is no theoretical analysis guiding the generation of the view for graphs. However, Tian et al. [80] theoretically and empirically analyze the problem in a general view and image domain, considering the generation of the view from the aspect of mutual information. In particular, a good view generation should minimize the MI between two views I(v1, v2), subject to I(v1, y) = I(v2, y) = I(x, y). Intuitively, to guarantee that contrastive learning works, the generated views vi should not affect the information that determines the prediction for the downstream task, under which restriction, stronger disagreement between views leads to better learning results. Following the above idea, AD-GCL [81] proposes to generate views of graphs that achieve the above minimum under constraints by parameterizing the above types of transformations and propose learnable transformations. In particular, the transformations are learned in an adversarial manner - the transformation (views generator) is trained to minimize I(v1, v2) subject to I(v1, y) = I(v2, y) = I(x, y), whereas the encoder is trained to maximize I(v1, v2). Following a similar principle, InfoGCL [82] proposes to discretely select optimal views from a list of candidate views based on the mutual information with downstream tasks.
From the manifold point of view, a recent analytic study [83] proposes the expansion assumption and explains the data augmentation as to prompt the continuity in the neighborhood for each instance. It indicates similar requirements for the view generating by augmentation, i.e., an ideal augmentation should satisfy the following two conditions, 1) the (augmentation) neighborhood of an instance does not intersect the neighborhood of instances that belong to the other class in the downstream task, 2) the neighborhood of an instance should be as large as possible, subject to 1.
To this end, the learning on datasets with different downstream tasks may benefit from different types of transformations. For example, the property of a social network to be predicted in a downstream task may be more tolerant of minor changes in node attributes, for which the feature transformations can be more suitable. On the other hand, the property of a molecule usually depends on bonds in some functional groups, for which the edge perturbation may harm the learning while the sub-graph sampling could help. Empirically, You et al. [49] observes similar results. For example, edge perturbation is found contributory to the performance on social network datasets but harmful to some molecule data.
4. Predictive Learning
Compared with contrastive learning methods, predictive learning methods train the graph encoder f together with a prediction head g under the supervision of informative labels self-generated for free. We use the term “predictive” instead of “generative” categorized by Liu et al. [62] to avoid confusion, as not all methods introduced in this section are necessarily generative models. Categorized by how the prediction targets are obtained, we summarize predictive learning frameworks for graphs into (1) graph reconstruction that learns to reconstruct certain parts of given graphs, (2) invariance regularization that aims to directly learn robust and informative representations, (3) graph property prediction that learns to model non-trivial properties of given graphs, and (4) multi-stage self-training with pseudo-labels. In this section, we let denote the desired node-level representation and hi denote the representation of node vi. The general frameworks of three types of predictive learning methods are shown in Figure 6. We summary all predictive methods being reviewed by this survey in Supplementary Table 2 for a more clear comparison.
Fig. 6.
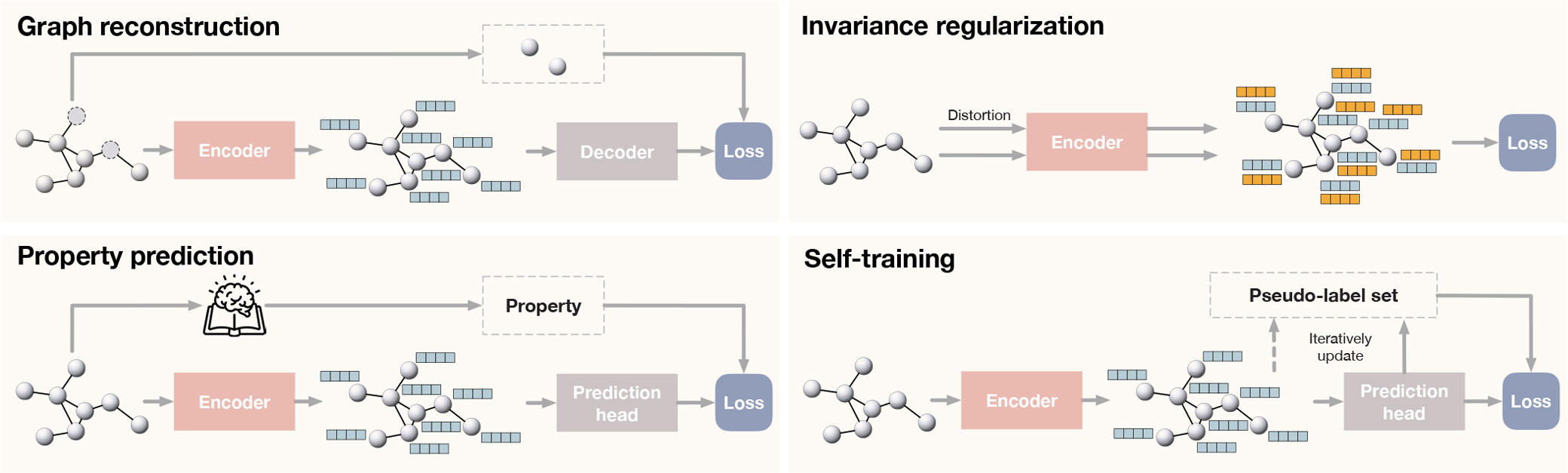
Illustrations of three predictive learning frameworks. For predictive learning methods, self-generated labels provide self-supervision to train the encoder together with prediction heads (or the decoder). We conclude predictive learning methods into three categories by how the prediction targets are obtained. Top left: the prediction targets in graph reconstruction are certain parts of given graphs. For example, GAE [39] performs reconstruction on the adjacency matrix, and MGAE [50] performs reconstruction on randomly corrupted node attributes. Top right: the supervision comes from the invariance regularization and additional constraints that are derived based on different theoretical frameworks and promote the learning of informative representations. Bottom left: the prediction targets in property prediction models are implicit and informative properties of given graphs. For example, S2GRL [55] predicts k-hop connectivity between two given nodes. Moreover, GROVER [56] utilizes motifs (functional groups) of molecules based on domain-knowledge as prediction targets. Bottom right: the prediction targets in self-training are pseudo-labels. In M3S [58], the graph neural network is trained iteratively on a pseudo-label set initialized as the set of given ground-truth labels. Clustering and prediction are conducted to update the pseudo-label set based on which a fresh graph neural network is then trained. Such operations are performed multiple times as multi-stage.
4.1. Graph Reconstruction
Graph reconstruction provides a natural self-supervision for the training of graph neural networks. The prediction targets in graph reconstruction are certain parts of the given graphs such as the attribute of a subset of nodes or the existence of edge between a pair of nodes. In graph reconstruction tasks, the prediction head g is usually called the decoder which reconstructs a graph from its representation.
4.1.1. Non-Probabilistic Graph Autoencoders
The autoencoders, firstly proposed in [84], have been widely applied for the learning of data representations. Given the success in the image domain and natural language modeling, various variations of graph autoencoder [85] are proposed to learn graph representations. Aiming at learning the graph encoder f, graph autoencoders are trained to reconstruct certain parts of an input graph, given restricted access to the graph or under certain regularization to avoid identical mapping.
GAE [39] represents the simplest version of the graph autoencoders. It performs the reconstruction on the adjacency matrix A from the input graph (A, X). Formally, it computes the reconstructed adjacency matrix by
| (29) |
| (30) |
and is optimized by the binary cross-entropy loss between and A. As GAE is originally proposed to learn node-level representations for link prediction problem, it assumes two linked nodes should have similar representations. GraphSAGE [86] introduces a similar framework with the self-supervision of the adjacency matrix based on a different objective including negative sampling. In addition, a recent work SuperGAT [87] includes the GAE objective as a self-supervised auxiliary loss during training a graph attention network to guide the learning of more expressive attention operators. Similarly, SimP-GCN [88] applies node-pair similarity as a substitute of the adjacency matrix to construct a self-supervised auxiliary task.
MGAE [50] follows the idea of denoising autoencoder [89]. Given a graph (A, X), MGAE performs reconstructions on multiple randomly corrupted feature matrices with a single-layer autoencoder fθ and the objective
| (31) |
where θ denotes the weights in the single-layer encoder, λ denotes the hyper-parameter for l2-regularization, and is considered as the reconstructed representation. To enable non-linearity, [50] proposes to stack multiple single-layer autoencoders. Formally, given the reconstructed representation H(ℓ−1) at the (ℓ−1) layer, the ℓ layer is trained by optimizing
| (32) |
| (33) |
where denotes the corrupted representation from (ℓ−1)-th layer. The reconstructed representation at the last layer is then considered as the representation for downstream tasks.
GALA [51] introduces a multi-layer autoencoder with symmetric encoder and decoder, unlike GAE and MGAE. Motivated by the Laplacian smoothing [90] effect of GCN encoders, GALA designs the decoder by performing Laplacian sharpening [90], which prompts the decoded representation of each node to be dissimilar to the centroid of its neighbors. A Laplacian sharpening layer in the decoder g in computed by
| (34) |
where and denote the decoded representation and D denotes the degree matrix. GALA reconstructs the feature matrix by optimizing the mean squared error with
| (35) |
Attribute masking [43], also referred to as graph completion [91], is another strategy to pre-train graph encoder f under the graph autoencoder framework by reconstructing masked node attributes. The encoder f computes the node-level representations H given the graph with its node attributes randomly masked. And a linear projection is applied to H as the decoder g to reconstruct the masked attributes. When the edge attributes are also available, one can also perform reconstruction on the masked edge attributes. Although the attribute masking is not explicitly named as graph autoencoders, we categorize it as graph autoencoders since the encoders are trained by performing reconstruction on the entire or certain parts of the input graph.
4.1.2. Variational Graph Autoencoders
Although sharing a similar encoder-decoder structure with standard autoencoders, variational autoencoders as generative models are built upon a different mathematical foundation assuming an existing prior distribution of latent representation that generates the observed data. Primarily targeted in learning the generation of the observed data, variational graph autoencoders also shown promising performance in learning good graph representations.
VGAE [39] introduces the simplest version of variational graph autoencoders. VGAE performs reconstruction on the adjacency matrix and is composed a inference model (encoder) parameterized by graph neural networks μ, Σ and a generative model (decoder) p(A|H) modeled by the inner product of latent variables. VGAE optimizes the variational lower bound
| (36) |
where KL(·) denotes the KL-divergence and p(H) denotes the prior given by the Gaussian distribution.
ARGA/ARVGA [52] propose to regularize the autoencoder with an adversarial network [92] which enforces the distribution of the latent variable to match the Gaussian prior. In addition to the encoder and decoder, a discriminator is trained to distinguish fake data generated by the encoder and the real data sampled from the Gaussian distribution. As the adversarial regularization is provably an equivalence of the JS-divergence between the distribution of the latent variable and the Gaussian prior, ARGA/ARVGA can achieve a similar effect to VGAE but with stronger regularization.
SIG-VAE [53] replace the inference model in the variational graph autoencoder a hierarchy of multiple stochastic layers to enable more flexible model of the latent variable. In particular, the inference model is given by p(H|A, X) = p(H|A, X, μ, Σ), where μ and Σ are considered as random variables computed by stacked stochastic layers with noise injected to each layer. The marginalized p(H|A, X) is hence not necessarily a Gaussian distribution and enabled higher flexibility and expressivity.
There exist other variations of the variational graph autoencoders such as JTVAE [93] and DGVAE [94]. However, those variational graph autoencoders focus on the generation of graphs. As we mainly consider the learning of representations, we omit the introduction to those methods.
4.1.3. Autoregressive Reconstruction
Following the idea of GPT [95] for the generative pretraining of language models, GPT-GNN [54] proposes a autoregressive framework to perform reconstruction on given graphs. Ash both variational autoencoders and the autoregressive models are generative and based on reconstruction, graph autoregressive models differ from that they perform reconstruction iteratively. In particular, GPT-GNN consists of a graph encoder f, decoders gn and ge for node generation and edge generation, respectively. Given a graph with its nodes and edges randomly masked, GPT-GNN generates one masked node and its edges at a time and optimizes the likelihood of the node and edges generated in the current iteration. GPT-GNN iteratively generates nodes and edges until all masked nodes are generated.
4.2. Representation Invariance Regularization
Adopting predictive objectives based on invariance regularization is recently trending for both image and graph domains. Methods adopting invariance regularization directly computes losses on representations and usually follows a similar framework to contrastive learning, i.e., to obtain two augmented graphs of the given graph, and compute the representations of the two graphs, but their objective does not include any contrast nor requires paired or negative samples. Hence they are categorized as predictive approaches. In particular, the objective seeks to minimize the difference between representation of two distorted graphs, encouraging representations of the graphs to be invariant to random distortions. Certain approaches are introduced to enable the learning informative representations, preventing trivial solutions to be learned.
Inspired by BYOL [20] in the image domain, BGRL [47] proposes a variation of contrastive learning framework, which eliminates the need of negative samples. Given a mini-batch of graphs B, it compute node representations Hx,a and Hx,b of two augmented graphs from each x in B and minimize the following invariance-based loss with a parametric predictor pθ
| (37) |
As no negative sample is included, certain mechanisms and restrictions, such as updating an offline encoder with exponential moving average [20] and batch normalization, are required in the framework to prevent degenerate solutions and achieve similar effect of optimizing MI bound objectives. BGRL and BYOL are commonly acknowledged as variations of contrastive methods. While the framework of BGRL follows the typical contrastive framework, the computation of the above invariance-based objective does not require paired samples or negative samples.
CCA-SSG [60] proposes an invariance-based objective inspired by a well-studied idea of canonical correlation analysis [96, 97]. The proposed objective consists of an invariance term minimizing the difference between two representations and a decorrelation term minimizing the correlation among dimensions of the representations, fomulated as
| (38) |
where Ha and Hb are batched node representations of graphs with two augmentations a and b. Similarly to Barlow-Twins [98], CCA-SSG uses batched representations to estimate the correlations among different dimensions. Both CCA-SSG and Barlow-Twins encourage the learning of imformative representation by reducing the correlation or redundancies among dimensions.
LaGraph [61] proposes another invariance-based objective based on the assumption that all observed graph data have their latent counterparts, analogically to inaccessible clean counterparts of observed noisy data such as images. The proposed objective is derived as an self-supervised upper bound to the supervised latent graph prediction loss, formulated as
| (39) |
where is a decoder network, J is a random subset of node indices, H is the node representation matrix of the given graph, H′ is the representation of the graph whose nodes in J are masked, and means the invariance is computed on the masked nodes only. Different from the above two methods, LaGraph computes the representations for the original graph and its masked version, instead of two randomly augmented graphs, and only computes the invariance on masked nodes. The characteristics come from the derivation of the objective.
One intuition behind the invariance regularization-based methods is that the learned representation are expected to contain enough information of the given data but be invariance to distortions on the data. Both CCA-SSG and LaGraph discuss the relationships between invariance-based method and the Information Bottleneck principle [99] indicating the above intuition. Moreover, LaGraph further discusses its relationship with denoising autoencoder and mutual information-based methods.
4.3. Graph Property Prediction
In addition to the reconstruction, an efficient way to perform self-supervised predictive learning is to design the prediction tasks based on informative graph properties that are not explicitly provided in the graph data. Commonly applied properties for self-supervised training include topology properties, statistical properties, and domain-knowledge involved properties.
S2GRL [55] generalizes the adjacency matrix reconstruction task to a k-hop connectivity prediction task between two given nodes, motivated by that the interaction between two nodes is not limited to their direct connection. In particular, given encoded representations of any pair of nodes, the prediction head performs classification on the absolute difference between the representations. S2GRL then trains the encoder and prediction head to classify the hop counts between the pair of nodes.
Meta-path prediction [57] provides a self-supervision for heterogeneous graphs, such as molecules, which include multiple types of nodes and edges. A meta-path of length ℓ is defined as a sequence (t1, ···, tℓ) where ti denotes the type of the i-th edge in the path. Given two nodes in a heterogeneous graph and K meta-paths, the encoder f and prediction heads gi (i = 1, ···, K) are trained to predict if the two nodes are connected by each of the meta-paths as a binary classification task. In [57], the predictions of the K meta-paths are included as K auxiliary learning tasks in addition to the main learning task.
GROVER [56] performs self-supervised learning on molecular graph data with two predictive learning tasks. In contextual property prediction, the encoder and prediction head is trained to predict the “atom-bond-count” relationship within the k-hop neighborhood of a given node (atom), e.g. “O-double bond-2” if there are two atoms “O” connected to the given atom with double bonds. In addition, a graph-level motif prediction task is applied to involve the self-supervision of domain knowledge. For molecular graphs, the motifs are instantiated by the functional groups in molecules. Given a list of motifs, the graph-level prediction head predicts the existence of each motif, as a multi-label classification task.
4.4. Self-Training with Pseudo-Labels
Instead of the labels obtained from input graphs, the prediction targets in self-training methods are pseudo-labels obtained from the prediction in a previous stage utilizing a small portion of labeled data [1] or even randomly initialized. The self-trained graph neural networks can be either applied under a semi-supervised setting or further finetuned for downstream tasks. We consider the node-level classification for an instance.
Under the node-level semi-supervised setting, the multi-stage self-training [100] is proposed to utilize the labeled nodes to guide the training on unlabeled nodes. Concretely, given both the labeled node set and unlabeled node set, the graph neural network is first trained on the labeled set. After the training, it performs prediction on the unlabeled set and the predicted labels with high confidence are considered as the pseudo-labels and moved to the labeled node set. Then a fresh graph neural network is trained on the updated labeled set and the above operations are performed multiple times.
M3S [58] applies DeepCluster [101] and an aligning mechanism to generate pseudo-labels on the basis of multi-stage self-training. In particular, a K-mean cluster is performed on node-level representations at each stage and the labels obtained from clustering are then aligned with the given true labels. A node with clustered pseudo-label is added to the labeled set for self-training in the next stage only if it matches the prediction of the classifier in the current stage. Compared to the basic multi-stage self-training, M3S considers the DeepCluster and the aligning mechanism as a self-checking mechanism and hence provides stronger self-supervision.
ICF-GCN [59] proposes to optimize the GCN model and pseudo-labels for nodes simultaneously in an Expectation-Maximization (EM) manner. In particular, the E-step updates the GCN based on the given pseudo-labels whereas the M-step updates the pseudo-labels based on the GCN predictions. Similarly to M3S, ICF-GCN performs clustering on hidden representations to obtain GCN predicted classes. To avoid the alignment issue, both pseudo-labels and the clustered node classes are represented in relational matrix of shape |V| × |V|, where an element value 1 indicates two nodes belong to the same class and 0 indicates different classes.
A recent study [? ] provides the theoretical justification for the self-training with pseudo-labels based on an assumption of the expansion property and generalizes the self-training methods from semi-supervised settings into the unsupervised setting. Intuitively, the examples with correct pseudo-labels will be utilized to denoise the incorrectly pseudo-labeled examples and high accuracy can be achieved due to the expansion assumption. Under the unsupervised setting, it theoretically shows that a classifier trained with arbitrarily assigned pseudo-labels can still achieve good accuracy for some permutation of the classes.
5. Summary of Learning Tasks and Datasets
The self-supervised learning methods are usually applied to and evaluated on two common types of graph-related learning tasks, the graph-level inductive learning and the node-level transductive learning. The graph-level inductive learning aims to learn models predicting graph-level properties, and the models are trained and perform prediction on different sets of graphs. On the other hand, the node-level transductive learning aims to learn models performs node-level property prediction, trained and performing prediction on the same sets of large graphs. In this section, we summarize datasets under the two types of learning tasks. The statistics of common datasets are shown in Table 5.
5.1. Graph-Level Inductive Learning
Graph-level learning tasks are performed as inductive learning tasks on multiple graphs [38]. Commonly used datasets for graph-level learning tasks can be divided into three types, chemical molecule datasets, protein datasets, and social network datasets.
Chemical Molecular Property Prediction.
In a molecular graph, each node represents an atom in a molecule where the atom index is indicated by the node attribute and each edge represents a bond in the molecule. Datasets for chemical molecular property prediction are also categorized as small molecule datasets in TUDataset [102]. Traditional molecule classification datasets such as NCI1 [103] and MUTAG [104] are the most commonly used datasets for unsupervised graph representation learning in self-supervision related studies [10, 49]. In addition, the molecule property prediction models can be also trained in a self-supervised pre-training and finetuning fashion for semi-supervised learning and transfer learning. Recent works [43, 49, 56] build their pre-training molecule dataset by sampling unlabeled molecules from the ZINC15 [105] database containing 750 million molecules. MoleculeNet [21] also provides a collection of molecular graph datasets for molecule property prediction, which is suitable for downstream graph classification. Among all the datasets in MoleculeNet, the classification datasets such as BBBP, Tox21, and HIV are used for the evaluation of several self-supervised learning methods [43, 49, 56].
Protein Biological Function Prediction.
The protein is a particular type of molecule but is represented differently by graph data. In a protein graph, nodes represent amino acids and an edge indicates the two connected nodes are less than 6 Angstroms apart. Datasets for chemical molecular property prediction are also categorized as bioinfomatics datasets in TUDataset. Similar to the chemical molecule datasets, protein datasets can be used in both unsupervised representation learning, such as PROTEINS [106] and DD [107], and in the two-stage training.
Social Network Property Prediction.
A social network graph dataset considers each entity (e.g. a user or an author) as a node and their social connections as edges. As social networks in different datasets represent differently, social network graph datasets are not typically used for transfer learning. Social network graph datasets used in recent self-supervised studies [48, 49] are typical datasets for graph classification [108] such as COLLAB, REDDIT-B and IMDB-B.
5.2. Node-Level Transductive Learning
Node-level learning tasks can be performed as transductive learning tasks on large graphs [38], where are nodes and the complete graph structure, together with labels of a portion of nodes, are available for training. The citation network datasets [109], including CORA [110], CITESEER [111] and PUBMED [112] are commonly used for node-level transductive learning. There are three typical ways to use the citation network datasets. Contrastive learning methods [10, 38, 41] are usually evaluated on the social network datasets by performing unsupervised representation learning followed by a linear classification with fixed representations, whereas predictive learning studies usually perform unsupervised representation learning followed by clustering [50, 51] or semi-supervised link prediction [39, 55] on the social network datasets.
Motivated by the concern that current GNN evaluations becomes saturated on above citation network datasets, Shchur et al. [113] construct four additional node-level datasets, Coauthor-CS, Coauthor-Physics from the Microsoft Academic Graph [114], Amazon-Photos, and Amazon-Computers from the Amazon Co-purchase Graph [115]. The four datasets contain larger graphs with more nodes and edges. And their learning tasks are hence more challenging compared to the citation network datasets.
5.3. Node-Level Inductive Learning
Node-level inductive learning performs training and testing on separate subsets. There are two typical ways to split the nodes for training and testing. First, in cases that all nodes are from the same large graph, a random subset of nodes are selected for testing and is masked out together with their edges during training, in contrast to the transductive learning where all nodes and the complete graph structure are used during training. Two commonly used node-level inductive learning datasets in the first case are Reddit [86] and Flickr [116]. Each node in Reddit represents a post and posts are connected by edges if they are commented by the same user. The node classification task is to predict which community the post belongs to. For the Flickr dataset, each node represents an image uploaded to Flickr and an edge between nodes indicates that they share common properties such as the same geographic location or commented by the same user. The task is to predict the class (based on tags) each image belongs to.
In cases that all nodes belong to separate graphs, the training and testing nodes are split by graphs. Zitnik and Leskovec [117] build a inductive learning dataset in the second case containing 395K unlabeled protein obtained from protein–protein interaction (PPI) networks and perform finetuning on PPI networks consisting of 88K proteins labeled with 40 fine-grained biological functions, obtained from Zitnik et al. [118]. Each node in a graph represents a protein and an edge indicates the existance of interaction between the proteins. The task of PPI is to predict the gene ontology sets a protein belongs to.
6. An Open-Source Library
We develop an open-source library DIG: Dive into Graphs [119]1, which includes a module, known as sslgraph, for self-supervised learning of GNNs. DIG-sslgraph is based on Pytorch [120] and Pytorch Geometric [121] and aims at easy implementation and standardized evaluation of SSL methods for graph neural networks. In particular, we provide a unified and highly customizable framework for contrastive learning methods, standardized data interface, and evaluation tools that are compatible for evaluating both contrastive methods and predictive methods. The overview of the library is shown in Supplementary Figure 1.
Given the developed unified contrastive framework as a base class, particular contrastive learning methods can be easily implemented by specifying their objective, functions for view generation, and their encoders. We also pre-implement four state-of-the-art contrastive methods for either node-level or graph-level tasks based on the unified framework, including InfoGraph [41], GRACE [46], MVGRL [58], and GraphCL [49]. The provided data interface includes datasets from TUDataset [102] and the citation network dataset [109]. Other datasets from Pytorch Geometric and new datasets processed by Pytorch Geometric are also supported by our data interface. The provided evaluation tools and data interface allow standardized evaluations of SSL methods and fair comparisons with existing SSL methods under common evaluation settings, including unsupervised graph-level representation learning, semi-supervised graph classification (or transfer learning, depending on the datasets), and unsupervised node-level representation learning. Altogether, our open-source library provides a complete and extensible framework for developing and evaluating SSL methods for GNNs. To show the efficiency and effectiveness of the DIG-sslgraph library, we compare the training time, memory consumption, and downstream accuracy of four SSL methods on multiple datasets between the original implementations and DIG counterparts. The results are shown and discussed in Appendix G.
7. Challenges and Future Directions
While existing SSL approaches have shown promising effectiveness on learning from graph data, there still exist several challenges due to the more complicated structure and more diverse tasks of graphs. In this section, we discuss the remaining challenges as well as potential directions for future studies on Graph self-supervised learning.
The optimal views generation w.r.t specific downstream tasks are still unclear for contrastive methods.
The performance of the learned representation or pre-trained model on downstream tasks heavily depends on the selection of transformations to generate views. The optimal view generation also depends on specific downstream tasks. However, there is still no way to obtain the optimal view for each downstream task even the task is available. Several studies have explored approaches to utilizing better views for contrast based on adversarial learning [81] or searching [82], but views generated by the two approaches are still not optimal due to their limited search space for graph transformations. In particular, Xu et al. [82] only considers a finite set of graph transformations whose search space is also limited. In addition, Suresh et al. [81] only considers parameterized structural transformations, and more complicated learnable view generation involving feature-space, structure-space, and sampling-based transformation are still challenging and are limited by the development of graph generation studies [122, 123, 124, 125]. Moreover, the above methods require available downstream tasks at the pretraining stage. They become inapplicable when downstream tasks are unavailable or in the unsupervised representation learning setting. Hence it is also desired to study universally optimal views under the downstream task-agnostic setting.
There is no unified theory or theoretical framework for predictive methods.
Unlike contrastive methods grounded by the problem of mutual information maximization, the predictive methods, especially the graph property prediction and invariance regularization-based methods, utilize different pretext learning tasks motivated by individual hypotheses and based on empirical studies. However, they lack guidance from unified theoretical frameworks to design specific pretext tasks for different downstream tasks. The information bottleneck principle may be used to interpret the effectiveness of several predictive methods but further study and investigation are desired.
Richer domain knowledge can be better utilized as self-supervision.
For graph machine learning tasks oriented by other research areas such as biomedical researches and quantum physics, existing constraints and rules from domain knowledge naturally contain rich supervision benefiting the learning of downstream tasks. Including domain knowledge has shown to be effective for both contrastive methods [126] and predictive methods [56]. Currently, only simple domain knowledge-based tasks such as the motif prediction [56] are adopted. Future studies on designing novel tasks better utilizing domain knowledge such as functional groups and quantum mechanisms are promising directions.
Scaling-up and efficiency issues are to be addressed.
Many existing SSL approaches suffer from memory issues and computing efficiency issues in terms of time consumption when scaled up to larger graphs. For contrastive methods, the scaling-up issue becomes more critical as their performance usually relies on a larger number of samples in a mini-batch. In addition, as the contrastive framework requires computing representations of multiple views, their memory consumption is times higher than predictive approaches. When the computing of view generation for contrastive methods or the graph properties computation for predictive methods is heavy, the computation time may increase sharply as the graph scales up. The above issues prevent the application of existing methods to extremely large graphs in industrial scenarios or other research areas (e.g., protein networks and particles in materials). Currently, studies addressing the scaling-up issue for SSL methods are still lacking and less explored.
Explainability of SSL for GNN requires further studies.
The explainability for GNNs is critical in multiple application scenarios to assure the reliability and security of GNN models. For example, in drug discovery, it is important to understand which functional group in a molecular graph leads to the GNN decision for a property prediction. A survey work [127] provides a thorough introduction to existing explanation methods for GNNs. However, existing SOTA studies focus on the explanation under supervised setting and require downstream tasks to perform explanation, and only limited methods, such as gradient-based methods, can be adapted to explain pre-trained GNN encoders without given the downstream prediction head. A recent work [128] proposes the task-agnostic explanation framework to enable high-quality GNN explanations without downstream tasks. The task-agnostic framework can be utilized to explain GNNs trained through SSL. More studies and investigations are desired in this direction.
8. Conclusion
Despite recent successes in natural language processing and computer vision, the self-supervised learning applied to graph data is still an emerging field and has significant challenges to be addressed. Existing methods employ self-supervision to graph neural networks through either contrastive learning or predictive learning. We summarize current self-supervised learning methods and provide unified reviews for the two approaches. We unify existing contrastive learning methods for GNNs with a general contrastive framework, which performs mutual information maximization on different views of given graphs with appropriate MI estimators. We demonstrate that any existing method can be realized by determinating its MI estimator, views generation, and graph encoder. We further provide detailed descriptions of existing options for the components and discussions to guide the choice of those components. For predictive learning, we categorize existing methods into graph reconstruction, property prediction, and self-training based on how labels are generated from the data. A thorough review is provided for methods in all three types of predictive learning. Finally, we summarize common graph datasets of different domains and introduce what learning tasks the datasets are involved in to provide a clear view to conduct future evaluation experiments. Altogether, our unified treatment of SSL in GNNs in terms of methodologies, datasets, evaluations, and open-source software is anticipated to foster methodological developments and facilitate empirical comparisons.
Supplementary Material
Fig. 3.
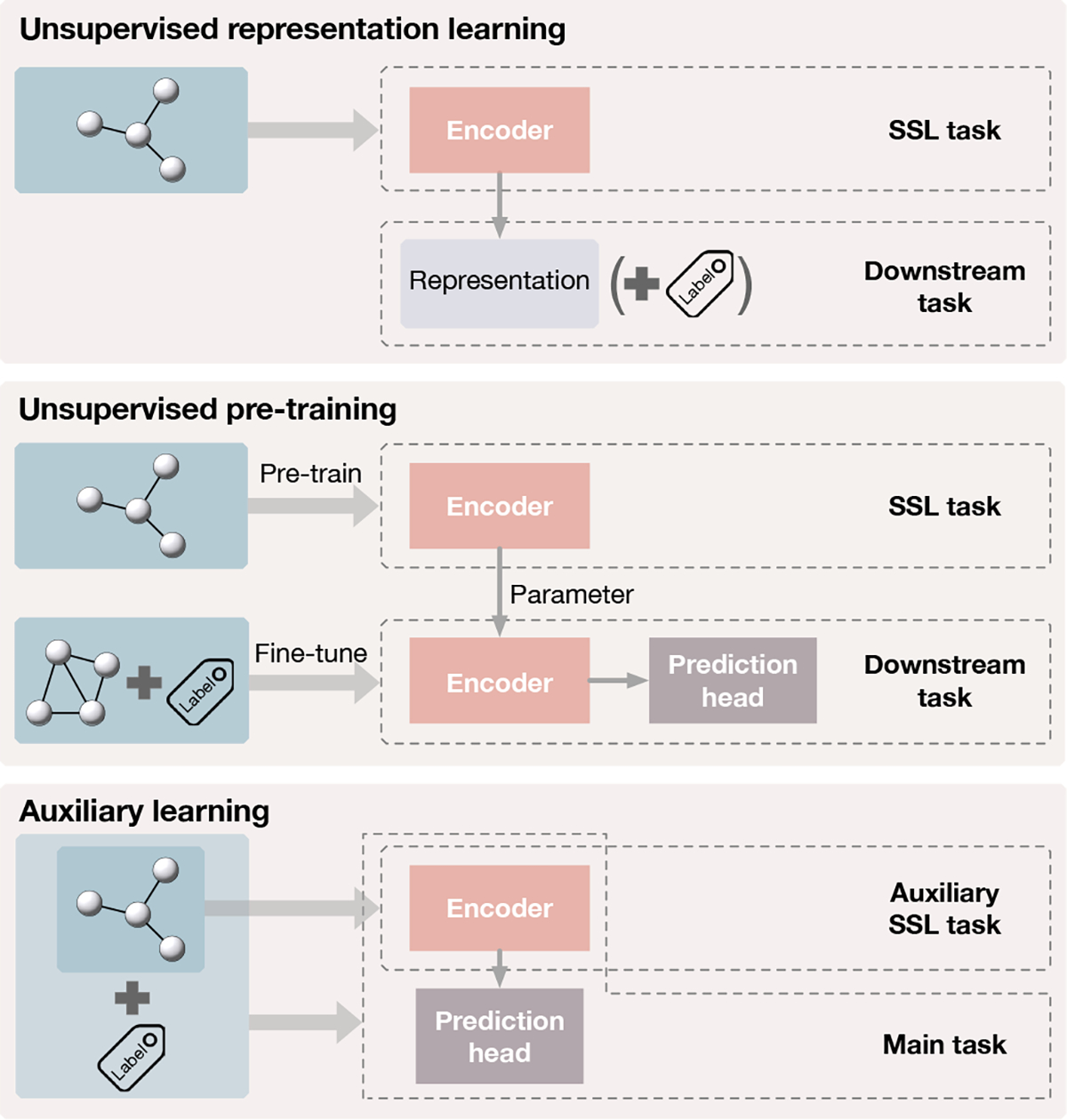
Paradigms for self-supervised learning. Top:in unsupervised representation learning, graphs only are used to train the encoder through the self-supervised task. The learned representations are fixed and used in downstream tasks such as linear classification and clustering. Middle: unsupervised pre-training trains the encoder with unlabeled graphs by the self-supervised task. The pre-trained encoder’s parameters are then used as the initialization of the encoder used in supervised fine-tuning for downstream tasks. Bottom: in auxiliary learning, an auxiliary task with self-supervision is included to help learn the supervised main task. The encoder is trained through both the main task and the auxiliary task simultaneously.
TABLE 1.
Summary and statistics of common graph datasets for self-supervised learning. Unsupervised classification refers to performing unsupervised representation learning followed by linear classification.
| Datasets | Learning tasks | Task level | Category | # graphs | Avg. nodes | Avg. edges | # classes |
|---|---|---|---|---|---|---|---|
|
| |||||||
| NCI1 | Unsupervised or semi-supervised classification | Graph | Small molecules | 4110 | 29.87 | 32.30 | 2 |
| MUTAG | Small molecules | 1113 | 17.93 | 19.79 | 2 | ||
| PTC-MR | Small molecules | 344 | 14.29 | 14.69 | 2 | ||
| PROTEINS | Bioinformatics (proteins) | 1178 | 39.06 | 72.82 | 2 | ||
| DD | Bioinformatics (proteins) | 188 | 284.32 | 715.66 | 2 | ||
| COLLAB | Social networks | 5000 | 74.49 | 2457.78 | 2 | ||
| RDT-B | Social networks | 2000 | 429.63 | 497.75 | 2 | ||
| RDT-M5K | Social networks | 4999 | 508.52 | 594.87 | 5 | ||
| IMDB-B | Social networks | 1000 | 19.77 | 96.53 | 2 | ||
|
| |||||||
| BBBP | Unsupervised transfer learning for classification | Graph | Small molecules | 2039 | 24.05 | 25.94 | 2 |
| Tox21 | Small molecules | 7831 | 18.51 | 25.94 | 12 (multi-label) | ||
| ToxCast | Small molecules | 8575 | 18.78 | 19.26 | 167 (multi-label) | ||
| SIDER | Small molecules | 1427 | 33.64 | 35.36 | 27 (multi-label) | ||
| ClinTox | Small molecules | 1478 | 26.13 | 27.86 | 2 | ||
| MUV | Small molecules | 93087 | 24.23 | 26.28 | 17 (multi-label) | ||
| HIV | Small molecules | 41127 | 25.53 | 27.48 | 2 | ||
| BACE | Small molecules | 1513 | 34.12 | 36.89 | 2 | ||
|
| |||||||
| CORA | Unsupervised or semi-supervised classification (transductive) | Node/Link | Citation network | 1 | 2,708 | 5,429 | 7 |
| CITESEER | Citation network | 1 | 3,327 | 4,732 | 6 | ||
| PUBMED | Citation network | 1 | 19,717 | 44,338 | 3 | ||
|
|
|||||||
| Coauthor CS | Node | Citation network | 1 | 18,333 | 81,894 | 15 | |
| Coauthor Phy. | Citation network | 1 | 34,493 | 247,962 | 5 | ||
| Amazon Photos | E-commerce network | 1 | 7,650 | 119,081 | 8 | ||
| Amazon Comp. | E-commerce network | 1 | 13,752 | 245,861 | 10 | ||
|
| |||||||
| PPI | Unsupervised classification (inductive) | Node | Bioinformatics (proteins) | 24 | 56,944 | 818,716 | 121 (multi-label) |
| Flickr | Social network | 1 | 89,250 | 899,765 | 7 | ||
| Social network | 1 | 232,965 | 11,606,919 | 50 | |||
ACKNOWLEDGMENTS
This work was supported in part by National Science Foundation grants IIS-2006861 and DBI-2028361, and National Institutes of Health grant 1R21NS102828. We thank the scientific community for providing valuable feedback and comments, which lead to improvements of this work.
Biographies

Yaochen Xie received the B.S. degree in Statistics from University of Science and Technology of China, Hefei, China, in 2018. Currently, he is working towards the Ph.D. degree in the Department of Computer Science and Engineering, Texas A&M University, College Station, Texas. His research interests include machine learning, deep learning, and graph data mining.

Zhao Xu received the MS degree in Biomedical Engineering from University of Michigan, Ann Arbor, Michigan, in 2017. Currently, she is working toward the PhD degree in the Department of Computer Science and Engineering, Texas A&M University, College Station, Texas. Her research interests include machine learning, deep learning and data mining.

Jingtun Zhang received the BSc degree in computer science and technology from University of Science and Technology of China, Hefei, China, in 2020. Currently, he is working toward the MCS degree in the Department of Computer Science and Engineering, Texas A&M University, College Station, Texas. His research interests include machine learning, software engineering, and data mining.

Zhengyang Wang is currently an applied scientist at Amazon.com LLC. He received his PhD degree in computer science from Texas A&M University, College Station, Texas, in 2020. And he received the MSc degree in mathematics and computer science from New York University, New York City, New York, in 2015. His research interests include machine learning, deep learning, and data mining.

Shuiwang Ji received the PhD degree in computer science from Arizona State University, Tempe, Arizona, in 2010. Currently, he is a Professor and Presidential Impact Fellow in the Department of Computer Science and Engineering, Texas A&M University, College Station, Texas. His research interests include machine learning, deep learning, graph and image analysis, and quantum systems. He received the National Science Foundation CAREER Award in 2014. He is currently an Associate Editor for IEEE Transactions on Pattern Analysis and Machine Intelligence, ACM Transactions on Knowledge Discovery from Data, and ACM Computing Surveys. He regularly serves as an Area Chair or equivalent roles for data mining and machine learning conferences, including AAAI, ICLR, ICML, IJCAI, KDD, and NeurIPS. He is a senior member of IEEE.
Footnotes
The open-source library is now publicly available at the URL: https://github.com/divelab/DIG/
Contributor Information
Yaochen Xie, Department of Computer Science & Engineering, Texas A&M University, College Station, TX 77843.
Zhao Xu, Department of Computer Science & Engineering, Texas A&M University, College Station, TX 77843.
Jingtun Zhang, Department of Computer Science & Engineering, Texas A&M University, College Station, TX 77843.
Zhengyang Wang, Amazon.com Services LLC, Seattle, WA 98109.
Shuiwang Ji, Department of Computer Science & Engineering, Texas A&M University, College Station, TX 77843.
REFERENCES
- [1].Yang Y and Xu Z, “Rethinking the value of labels for improving class-imbalanced learning,” in Advances in Neural Information Processing Systems, 2020. [Google Scholar]
- [2].Ulyanov D, Vedaldi A, and Lempitsky V, “Deep image prior,” in Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, 2018. [Google Scholar]
- [3].Xie Y, Wang Z, and Ji S, “Noise2Same: Optimizing a self-supervised bound for image denoising,” in Advances in Neural Information Processing Systems, vol. 33, 2020, pp. 20 320–20 330. [Google Scholar]
- [4].Laine S, Karras T, Lehtinen J, and Aila T, “High-quality self-supervised deep image denoising,” Advances in Neural Information Processing Systems, vol. 32, pp. 6970–6980, 2019. [Google Scholar]
- [5].Krull A, Buchholz T-O, and Jug F, “Noise2Voidlearning denoising from single noisy images,” in Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, 2019, pp. 2129–2137. [Google Scholar]
- [6].Batson J and Royer L, “Noise2Self: Blind denoising by self-supervision,” in Proceedings of the 36th International Conference on Machine Learning, vol. 97, 2019, pp. 524–533. [Google Scholar]
- [7].Devlin J, Chang M, Lee K, and Toutanova K, “BERT: pre-training of deep bidirectional transformers for language understanding,” in Proceedings of the 2019 Conference of the North American Chapter of the Association for Computational Linguistics: Human Language Technologies, 2019, pp. 4171–4186. [Google Scholar]
- [8].Wu J, Wang X, and Wang WY, “Self-supervised dialogue learning,” in Proceedings of the 57th Annual Meeting of the Association for Computational Linguistics, 2019, pp. 3857–3867. [Google Scholar]
- [9].Wang H, Wang X, Xiong W, Yu M, Guo X, Chang S, and Wang WY, “Self-supervised learning for contextualized extractive summarization,” in Proceedings of the 57th Annual Meeting of the Association for Computational Linguistics, 2019, pp. 2221–2227. [Google Scholar]
- [10].Hassani K and Khasahmadi AH, “Contrastive multi-view representation learning on graphs,” in Proceedings of the 37th International Conference on Machine Learning, 2020. [Google Scholar]
- [11].Chen T, Kornblith S, Norouzi M, and Hinton G, “A simple framework for contrastive learning of visual representations,” in Proceedings of the International Conference on Machine Learning, 2020. [Google Scholar]
- [12].Oord A. v. d., Li Y, and Vinyals O, “Representation learning with contrastive predictive coding,” arXiv preprint arXiv:1807.03748, 2018. [Google Scholar]
- [13].Tian Y, Krishnan D, and Isola P, “Contrastive multi-view coding,” arXiv preprint arXiv:1906.05849, 2019. [Google Scholar]
- [14].Perozzi B, Al-Rfou R, and Skiena S, “Deepwalk: Online learning of social representations,” in Proceedings of the 20th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, 2014, pp. 701–710. [Google Scholar]
- [15].Narayanan A, Chandramohan M, Venkatesan R, Chen L, Liu Y, and Jaiswal S, “graph2vec: Learning distributed representations of graphs,” arXiv preprint arXiv:1707.05005, 2017. [Google Scholar]
- [16].Tsitsulin A, Mottin D, Karras P, Bronstein A, and Muller E, “SGR: Self-supervised spectral graph representation learning,” arXiv preprint arXiv:1811.06237, 2018. [Google Scholar]
- [17].Doersch C, Gupta A, and Efros AA, “Unsupervised visual representation learning by context prediction,” in Proceedings of the IEEE international conference on computer vision, 2015, pp. 1422–1430. [Google Scholar]
- [18].Noroozi M and Favaro P, “Unsupervised learning of visual representations by solving jigsaw puzzles,” in European conference on computer vision. Springer, 2016, pp. 69–84. [Google Scholar]
- [19].He K, Fan H, Wu Y, Xie S, and Girshick R, “Momentum contrast for unsupervised visual representation learning,” in Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, 2020. [Google Scholar]
- [20].Grill J-B, Strub F, Altche F, Tallec C, Richemond P, Buchatskaya E, Doersch C, Avila Pires B, Guo Z, Gheshlaghi Azar M, Piot B, kavukcuoglu k., Munos R, and Valko M, “Bootstrap your own latent - a new approach to self-supervised learning,” in Advances in Neural Information Processing Systems, vol. 33, 2020, pp. 21 271–21 284. [Google Scholar]
- [21].Wu Z, Ramsundar B, Feinberg EN, Gomes J, Geniesse C, Pappu AS, Leswing K, and Pande V, “Moleculenet: a benchmark for molecular machine learning,” Chemical Science, vol. 9, no. 2, pp. 513–530, 2018. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [22].Wang Z, Liu M, Luo Y, Xu Z, Xie Y, Wang L, Cai L, and Ji S, “Advanced graph and sequence neural networks for molecular property prediction and drug discovery,” arXiv preprint arXiv:2012.01981, 2020. [DOI] [PubMed] [Google Scholar]
- [23].Kipf TN and Welling M, “Semi-supervised classification with graph convolutional networks,” in International Conference on Learning Representations, 2017. [Google Scholar]
- [24].Xu K, Hu W, Leskovec J, and Jegelka S, “How powerful are graph neural networks?” in International Conference on Learning Representations, 2019. [Google Scholar]
- [25].Gao H and Ji S, “Graph U-Nets,” in Proceedings of the 36th International Conference on Machine Learning, 2019, pp. 2083–2092. [Google Scholar]
- [26].Liu M, Wang Z, and Ji S, “Non-local graph neural networks,” arXiv preprint arXiv:2005.14612, 2020. [Google Scholar]
- [27].Cai L, Li J, Wang J, and Ji S, “Line graph neural networks for link prediction,” arXiv preprint arXiv:2010.10046, 2020. [DOI] [PubMed] [Google Scholar]
- [28].Liu M, Gao H, and Ji S, “Towards deeper graph neural networks,” in Proceedings of the 26th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, 2020, pp. 338–348. [Google Scholar]
- [29].Cai L and Ji S, “A multi-scale approach for graph link prediction,” in Proceedings of the 34th AAAI Conference on Artificial Intelligence, 2020, pp. 3308–3315. [Google Scholar]
- [30].Gao H, Wang Z, and Ji S, “Large-scale learnable graph convolutional networks,” in Proceedings of the 24th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, 2018, pp. 1416–1424. [Google Scholar]
- [31].Gao H, Chen Y, and Ji S, “Learning graph pooling and hybrid convolutional operations for text representations,” in Proceedings of the Web Conference, 2019, pp. 2743–2749. [Google Scholar]
- [32].Gao H, Liu Y, and Ji S, “Topology-aware graph pooling networks,” IEEE Transactions on Pattern Analysis and Machine Intelligence, vol. 43, no. 12, pp. 4512–4518, 2021. [DOI] [PubMed] [Google Scholar]
- [33].Wang Z and Ji S, “Second-order pooling for graph neural networks,” IEEE Transactions on Pattern Analysis and Machine Intelligence, 2020. [DOI] [PubMed] [Google Scholar]
- [34].Yuan H and Ji S, “StructPool: Structured graph pooling via conditional random fields,” in Proceedings of the 8th International Conference on Learning Representations, 2020. [Google Scholar]
- [35].Gao H and Ji S, “Graph representation learning via hard and channel-wise attention networks,” in Proceedings of the 25th ACM SIGKDD International Conference on Knowledge Discovery & Data Mining. ACM, 2019, pp. 741–749. [Google Scholar]
- [36].Yuan H, Tang J, Hu X, and Ji S, “XGNN: Towards model-level explanations of graph neural networks,” in Proceedings of the 26th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, 2020, pp. 430–438. [Google Scholar]
- [37].Liu Y, Yuan H, Cai L, and Ji S, “Deep learning of high-order interactions for protein interface prediction,” in Proceedings of the 26th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, 2020, pp. 679–687. [Google Scholar]
- [38].Veličković P, Fedus W, Hamilton WL, Liò P, Bengio Y, and Hjelm D, “Deep graph infomax,” in International Conference on Learning Representations, 2019. [Google Scholar]
- [39].Kipf TN and Welling M, “Variational graph autoencoders,” arXiv preprint arXiv:1611.07308, 2016. [Google Scholar]
- [40].Ma Y and Tang J, Deep Learning on Graphs. Cambridge University Press, 2020. [Google Scholar]
- [41].Sun F-Y, Hoffman J, Verma V, and Tang J, “Infograph: Unsupervised and semi-supervised graph-level representation learning via mutual information maximization,” in International Conference on Learning Representations, 2019. [Google Scholar]
- [42].Peng Z, Huang W, Luo M, Zheng Q, Rong Y, Xu T, and Huang J, “Graph representation learning via graphical mutual information maximization,” in Proceedings of The Web Conference 2020, 2020, pp. 259–270. [Google Scholar]
- [43].Hu W, Liu B, Gomes J, Zitnik M, Liang P, Pande V, and Leskovec J, “Strategies for pre-training graph neural networks,” in International Conference on Learning Representations, 2020. [Google Scholar]
- [44].Jiao Y, Xiong Y, Zhang J, Zhang Y, Zhang T, and Zhu Y, “Sub-graph contrast for scalable self-supervised graph representation learning,” in IEEE International Conference on Data Mining. IEEE, 2020, pp. 222–231. [Google Scholar]
- [45].Zhu Y, Xu Y, Yu F, Liu Q, Wu S, and Wang L, “Graph contrastive learning with adaptive augmentation,” in Proceedings of The Web Conference 2021, 2021. [Google Scholar]
- [46].—, “Deep graph contrastive representation learning,” in ICML Workshop on Graph Representation Learning and Beyond, 2020. [Google Scholar]
- [47].Thakoor S, Tallec C, Azar MG, Munos R, Veličković P, and Valko M, “Large-scale representation learning on graphs via bootstrapping,” arXiv preprint arXiv:2102.06514, 2021. [Google Scholar]
- [48].Qiu J, Chen Q, Dong Y, Zhang J, Yang H, Ding M, Wang K, and Tang J, “GCC: Graph contrastive coding for graph neural network pre-training,” in Proceedings of the 26th ACM SIGKDD International Conference on Knowledge Discovery & Data Mining, 2020, pp. 1150–1160. [Google Scholar]
- [49].You Y, Chen T, Sui Y, Chen T, Wang Z, and Shen Y, “Graph contrastive learning with augmentations,” in Advances in Neural Information Processing Systems, vol. 33, 2020, pp. 5812–5823. [Google Scholar]
- [50].Wang C, Pan S, Long G, Zhu X, and Jiang J, “Mgae: Marginalized graph autoencoder for graph clustering,” in Proceedings of the 2017 ACM on Conference on Information and Knowledge Management, 2017, pp. 889–898. [Google Scholar]
- [51].Park J, Lee M, Chang HJ, Lee K, and Choi JY, “Symmetric graph convolutional autoencoder for unsupervised graph representation learning,” in Proceedings of the IEEE/CVF International Conference on Computer Vision, 2019, pp. 6519–6528. [Google Scholar]
- [52].Pan S, Hu R, Long G, Jiang J, Yao L, and Zhang C, “Adversarially regularized graph autoencoder for graph embedding,” in Proceedings of the 27th International Joint Conference on Artificial Intelligence, 2018, pp. 2609–2615. [Google Scholar]
- [53].Hasanzadeh A, Hajiramezanali E, Narayanan K, Duffield N, Zhou M, and Qian X, “Semi-implicit graph variational auto-encoders,” in Advances in Neural Information Processing Systems, vol. 32, 2019, pp. 10 712–10 723. [Google Scholar]
- [54].Hu Z, Dong Y, Wang K, Chang K-W, and Sun Y, “GPT-GNN: Generative pre-training of graph neural networks,” in Proceedings of the 26th ACM SIGKDD International Conference on Knowledge Discovery & Data Mining, 2020, pp. 1857–1867. [Google Scholar]
- [55].Peng Z, Dong Y, Luo M, Wu X-M, and Zheng Q, “Self-supervised graph representation learning via global context prediction,” arXiv preprint arXiv:2003.01604, 2020. [Google Scholar]
- [56].Rong Y, Bian Y, Xu T, Xie W, Wei Y, Huang W, and Huang J, “Self-supervised graph transformer on large-scale molecular data,” in Advances in Neural Information Processing Systems, 2020. [Google Scholar]
- [57].Hwang D, Park J, Kwon S, Kim K-M, Ha J-W, and Kim HJ, “Self-supervised auxiliary learning with meta-paths for heterogeneous graphs,” arXiv preprint arXiv:2007.08294, 2020. [Google Scholar]
- [58].Sun K, Lin Z, and Zhu Z, “Multi-Stage self-supervised learning for graph convolutional networks on graphs with few labeled nodes,” in Proceedings of the AAAI Conference on Artificial Intelligence, vol. 34, no. 04, 2020, pp. 5892–5899. [Google Scholar]
- [59].Hu Z, Kou G, Zhang H, Li N, Yang K, and Liu L, “Rectifying pseudo labels: Iterative feature clustering for graph representation learning,” in Proceedings of the 30th ACM International Conference on Information & Knowledge Management, 2021, p. 720–729. [Google Scholar]
- [60].Zhang H, Wu Q, Yan J, Wipf D, and Philip SY, “From canonical correlation analysis to self-supervised graph neural networks,” in Advances in Neural Information Processing Systems, 2021. [Google Scholar]
- [61].Xie Y, Xu Z, and Ji S, “Self-supervised representation learning via latent graph prediction,” arXiv preprint arXiv:2202.08333, 2022. [Google Scholar]
- [62].Liu X, Zhang F, Hou Z, Wang Z, Mian L, Zhang J, and Tang J, “Self-supervised learning: Generative or contrastive,” arXiv preprint arXiv:2006.08218, 2020. [Google Scholar]
- [63].Liu Y, Pan S, Jin M, Zhou C, Xia F, and Yu PS, “Graph self-supervised learning: A survey,” arXiv preprint arXiv:2103.00111, 2021. [Google Scholar]
- [64].Wang Y, Zhang J, Guo S, Yin H, Li C, and Chen H, “Decoupling representation learning and classification for gnn-based anomaly detection,” in Proceedings of the 44th International ACM SIGIR Conference on Research and Development in Information Retrieval, 2021, p. 1239–1248. [Google Scholar]
- [65].Jin W, Derr T, Liu H, Wang Y, Wang S, Liu Z, and Tang J, “Self-supervised learning on graphs: Deep insights and new direction,” arXiv preprint arXiv:2006.10141, 2020. [Google Scholar]
- [66].Ganin Y and Lempitsky V, “Unsupervised domain adaptation by backpropagation,” in International Conference on Machine Learning. PMLR, 2015, pp. 1180–1189. [Google Scholar]
- [67].Sun Y, Tzeng E, Darrell T, and Efros AA, “Unsupervised domain adaptation through self-supervision,” arXiv preprint arXiv:1909.11825, 2019. [Google Scholar]
- [68].Hjelm RD, Fedorov A, Lavoie-Marchildon S, Grewal K, Bachman P, Trischler A, and Bengio Y, “Learning deep representations by mutual information estimation and maximization,” in International Conference on Learning Representations, 2019. [Google Scholar]
- [69].Donsker MD and Varadhan SRS, “Asymptotic evaluation of certain markov process expectations for large time. iv,” Communications on Pure and Applied Mathematics, vol. 36, pp. 183–212, 1983. [Google Scholar]
- [70].Belghazi MI, Baratin A, Rajeshwar S, Ozair S, Bengio Y, Courville A, and Hjelm D, “Mutual information neural estimation,” in Proceedings of the 35th International Conference on Machine Learning, vol. 80. PMLR, 2018, pp. 531–540. [Google Scholar]
- [71].Nowozin S, Cseke B, and Tomioka R, “f-gan: Training generative neural samplers using variational divergence minimization,” in Advances in Neural Information Processing Systems, 2016, pp. 271–279. [Google Scholar]
- [72].Gutmann M and Hyvärinen A, “Noise-contrastive estimation: A new estimation principle for unnormalized statistical models,” in Proceedings of the Thirteenth International Conference on Artificial Intelligence and Statistics, 2010, pp. 297–304. [Google Scholar]
- [73].Sohn K, “Improved deep metric learning with multi-class n-pair loss objective,” in Advances in Neural Information Processing Systems, vol. 29, 2016, pp. 1857–1865. [Google Scholar]
- [74].Schroff F, Kalenichenko D, and Philbin J, “Facenet: A unified embedding for face recognition and clustering,” in Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, 2015, pp. 815–823. [Google Scholar]
- [75].Hoffer E and Ailon N, “Deep metric learning using triplet network,” in International workshop on similarity-based pattern recognition. Springer, 2015, pp. 84–92. [Google Scholar]
- [76].Khosla P, Teterwak P, Wang C, Sarna A, Tian Y, Isola P, Maschinot A, Liu C, and Krishnan D,“Supervised contrastive learning,” Advances in Neural Information Processing Systems, vol. 33, 2020. [Google Scholar]
- [77].Rendle S, Freudenthaler C, Gantner Z, and Schmidt-Thieme L, “Bpr: Bayesian personalized ranking from implicit feedback,” in Proceedings of the Twenty-Fifth Conference on Uncertainty in Artificial Intelligence, 2009, p. 452–461. [Google Scholar]
- [78].Jiang X, Jia T, Fang Y, Shi C, Lin Z, and Wang H, “Pre-training on large-scale heterogeneous graph,” in Proceedings of the 27th ACM SIGKDD Conference on Knowledge Discovery and Data Mining, 2021, pp. 756–766. [Google Scholar]
- [79].Wang X, Liu N, Han H, and Shi C, “Self-supervised heterogeneous graph neural network with co-contrastive learning,” in Proceedings of the 27th ACM SIGKDD Conference on Knowledge Discovery and Data Mining, 2021, pp. 1726–1736. [Google Scholar]
- [80].Tian Y, Sun C, Poole B, Krishnan D, Schmid C, and Isola P, “What makes for good views for contrastive learning?” arXiv preprint arXiv:2005.10243, 2020. [Google Scholar]
- [81].Suresh S, Li P, Hao C, and Neville J, “Adversarial graph augmentation to improve graph contrastive learning,” Advances in Neural Information Processing Systems, vol. 34, 2021. [Google Scholar]
- [82].Xu D, Cheng W, Luo D, Chen H, and Zhang X, “Infogcl: Information-aware graph contrastive learning,” Advances in Neural Information Processing Systems, vol. 34, 2021. [Google Scholar]
- [83].Wei C, Shen K, Chen Y, and Ma T, “Theoretical analysis of self-training with deep networks on unlabeled data,” in International Conference on Learning Representations, 2021. [Google Scholar]
- [84].Kramer MA, “Nonlinear principal component analysis using autoassociative neural networks,” AIChE journal, vol. 37, no. 2, pp. 233–243, 1991. [Google Scholar]
- [85].Hamilton WL, “Graph representation learning,” Synthesis Lectures on Artificial Intelligence and Machine Learning, vol. 14, no. 3, pp. 1–159, 2020. [Google Scholar]
- [86].Hamilton W, Ying Z, and Leskovec J, “Inductive representation learning on large graphs,” in Advances in Neural Information Processing Systems, 2017, pp. 1024–1034. [Google Scholar]
- [87].Kim D and Oh A, “How to find your friendly neighborhood: Graph attention design with self-supervision,” in International Conference on Learning Representations, 2021. [Google Scholar]
- [88].Jin W, Derr T, Wang Y, Ma Y, Liu Z, and Tang J, “Node similarity preserving graph convolutional networks,” in Proceedings of the 14th ACM International Conference on Web Search and Data Mining. ACM, 2021. [Google Scholar]
- [89].Vincent P, Larochelle H, Lajoie I, Bengio Y, Manzagol P-A, and Bottou L, “Stacked denoising autoencoders: Learning useful representations in a deep network with a local denoising criterion.” Journal of Machine Learning Research, vol. 11, no. 12, 2010. [Google Scholar]
- [90].Taubin G, “A signal processing approach to fair surface design,” in Proceedings of the 22nd annual conference on Computer graphics and interactive techniques, 1995, pp. 351–358. [Google Scholar]
- [91].You Y, Chen T, Wang Z, and Shen Y, “When does self-supervision help graph convolutional networks?” in International Conference on Machine Learning. PMLR, 2020, pp. 10 871–10 880. [PMC free article] [PubMed] [Google Scholar]
- [92].Goodfellow I, Pouget-Abadie J, Mirza M, Xu B, Warde-Farley D, Ozair S, Courville A, and Bengio Y, “Generative adversarial nets,” in Advances in Neural Information Processing Systems, vol. 27, 2014, pp. 2672–2680. [Google Scholar]
- [93].Jin W, Barzilay R, and Jaakkola T, “Junction tree variational autoencoder for molecular graph generation,” in International Conference on Machine Learning. PMLR, 2018, pp. 2323–2332. [Google Scholar]
- [94].Li J, Li TYJ, Zhang H, Zhao K, Rong Y, and Cheng H, “Dirichlet graph variational autoencoder,” in Advances in Neural Information Processing Systems, 2020. [Google Scholar]
- [95].Radford A, Wu J, Child R, Luan D, Amodei D, and Sutskever I, “Language models are unsupervised multitask learners,” OpenAI blog, vol. 1, no. 8, p. 9, 2019. [Google Scholar]
- [96].Hotelling H, “Relations between two sets of variates,” in Breakthroughs in statistics. Springer, 1992, pp. 162–190. [Google Scholar]
- [97].Hardoon DR, Szedmak S, and Shawe-Taylor J, “Canonical correlation analysis: An overview with application to learning methods,” Neural computation, vol. 16, no. 12, pp. 2639–2664, 2004. [DOI] [PubMed] [Google Scholar]
- [98].Zbontar J, Jing L, Misra I, LeCun Y, and Deny S, “Barlow twins: Self-supervised learning via redundancy reduction,” in International Conference on Machine Learning. PMLR, 2021, pp. 12 310–12 320. [Google Scholar]
- [99].Tishby N, Pereira FC, and Bialek W, “The information bottleneck method,” in Proceedings of the 37-th Annual Allerton Conference on Communication, Control and Computing, 1999, pp. 368–377. [Google Scholar]
- [100].Li Q, Han Z, and Wu X-M, “Deeper insights into graph convolutional networks for semi-supervised learning,” in Proceedings of the AAAI Conference on Artificial Intelligence, vol. 32, no. 1, 2018. [Google Scholar]
- [101].Caron M, Bojanowski P, Joulin A, and Douze M, “Deep clustering for unsupervised learning of visual features,” in Proceedings of the European Conference on Computer Vision, 2018, pp. 132–149. [Google Scholar]
- [102].Morris C, Kriege NM, Bause F, Kersting K, Mutzel P, and Neumann M, “Tudataset: A collection of benchmark datasets for learning with graphs,” in ICML 2020 Workshop on Graph Representation Learning and Beyond, 2020. [Google Scholar]
- [103].Wale N and Karypis G, “Comparison of descriptor spaces for chemical compound retrieval and classification,” in Sixth International Conference on Data Mining, 2006, pp. 678–689. [Google Scholar]
- [104].Debnath AK, Lopez de Compadre RL, Debnath G, Shusterman AJ, and Hansch C, “Structure-activity relationship of mutagenic aromatic and heteroaromatic nitro compounds correlation with molecular orbital energies and hydrophobicity,” Journal of Medicinal Chemistry, vol. 34, no. 2, pp. 786–797, 1991. [DOI] [PubMed] [Google Scholar]
- [105].Sterling T and Irwin JJ, “Zinc 15–ligand discovery for everyone,” Journal of Chemical Information and Modeling, vol. 55, no. 11, pp. 2324–2337, 2015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [106].Borgwardt KM, Ong CS, Schönauer S, Vishwanathan SVN, Smola AJ, and Kriegel H-P, “Protein function prediction via graph kernels,” Bioinformatics, vol. 21, pp. i47–i56, 2005. [DOI] [PubMed] [Google Scholar]
- [107].Dobson PD and Doig AJ, “Distinguishing enzyme structures from non-enzymes without alignments,” Journal of Molecular Biology, vol. 330, no. 4, pp. 771–783, 2003. [DOI] [PubMed] [Google Scholar]
- [108].Yanardag P and Vishwanathan S, “Deep graph kernels,” in Proceedings of the 21th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, 2015, p. 1365–1374. [Google Scholar]
- [109].Yang Z, Cohen W, and Salakhudinov R, “Revisiting semi-supervised learning with graph embeddings,” in International conference on machine learning. PMLR, 2016, pp. 40–48. [Google Scholar]
- [110].McCallum AK, Nigam K, Rennie J, and Seymore K, “Automating the construction of internet portals with machine learning,” Information Retrieval, vol. 3, no. 2, pp. 127–163, 2000. [Google Scholar]
- [111].Giles CL, Bollacker KD, and Lawrence S, “Citeseer: An automatic citation indexing system,” in Proceedings of the Third ACM Conference on Digital Libraries. Association for Computing Machinery, 1998, p. 89–98. [Google Scholar]
- [112].Sen P, Namata G, Bilgic M, Getoor L, Galligher B, and Eliassi-Rad T, “Collective classification in network data,” AI magazine, vol. 29, no. 3, pp. 93–93, 2008. [Google Scholar]
- [113].Shchur O, Mumme M, Bojchevski A, and Günnemann S, “Pitfalls of graph neural network evaluation,” arXiv preprint arXiv:1811.05868, 2018. [Google Scholar]
- [114].Sinha A, Shen Z, Song Y, Ma H, Eide D, Hsu B-J, and Wang K, “An overview of microsoft academic service (MAS) and applications,” in Proceedings of the 24th international conference on world wide web, 2015, pp. 243–246. [Google Scholar]
- [115].McAuley J, Targett C, Shi Q, and Van Den Hengel A, “Image-based recommendations on styles and substitutes,” in Proceedings of the 38th international ACM SIGIR conference on research and development in information retrieval, 2015, pp. 43–52. [Google Scholar]
- [116].Zeng H, Zhou H, Srivastava A, Kannan R, and Prasanna V, “GraphSAINT: Graph sampling based inductive learning method,” in International Conference on Learning Representations, 2020. [Google Scholar]
- [117].Zitnik M and Leskovec J, “Predicting multicellular function through multi-layer tissue networks,” Bioinformatics, vol. 33, no. 14, pp. i190–i198, 2017. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [118].Zitnik M, Feldman MW, Leskovec J et al. , “Evolution of resilience in protein interactomes across the tree of life,” Proceedings of the National Academy of Sciences, vol. 116, no. 10, pp. 4426–4433, 2019. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [119].Liu M, Luo Y, Wang L, Xie Y, Yuan H, Gui S, Yu H, Xu Z, Zhang J, Liu Y, Yan K, Liu H, Fu C, Oztekin BM, Zhang X, and Ji S, “DIG: A turnkey library for diving into graph deep learning research,” Journal of Machine Learning Research, vol. 22, no. 240, pp. 1–9, 2021. [Google Scholar]
- [120].Paszke A, Gross S, Massa F, Lerer A, Bradbury J, Chanan G, Killeen T, Lin Z, Gimelshein N, Antiga L, Desmaison A, Kopf A, Yang E, DeVito Z, Raison M, Tejani A, Chilamkurthy S, Steiner B, Fang L, Bai J, and Chintala S, “Pytorch: An imperative style, high-performance deep learning library,” in Advances in Neural Information Processing Systems 32, 2019, pp. 8024–8035. [Google Scholar]
- [121].Fey M and Lenssen JE, “Fast graph representation learning with PyTorch Geometric,” in ICLR Workshop on Representation Learning on Graphs and Manifolds, 2019. [Google Scholar]
- [122].You J, Ying R, Ren X, Hamilton W, and Leskovec J, “GraphRNN: Generating realistic graphs with deep auto-regressive models,” in Proceedings of the 35th International Conference on Machine Learning, vol. 80. PMLR, 2018, pp. 5708–5717. [Google Scholar]
- [123].Shi C*, Xu M*, Zhu Z, Zhang W, Zhang M, and Tang J, “Graphaf: a flow-based autoregressive model for molecular graph generation,” in International Conference on Learning Representations, 2020. [Google Scholar]
- [124].Zang C and Wang F, “Moflow: An invertible flow model for generating molecular graphs,” in Proceedings of the 26th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, 2020, p. 617–626. [Google Scholar]
- [125].Luo Y, Yan K, and Ji S, “Graphdf: A discrete flow model for molecular graph generation,” in Proceedings of the 38th International Conference on Machine Learning, vol. 139. PMLR, 2021, pp. 7192–7203. [Google Scholar]
- [126].Li P, Wang J, Li Z, Qiao Y, Liu X, Ma F, Gao P, Song S, and Xie G, “Pairwise half-graph discrimination: A simple graph-level self-supervised strategy for pre-training graph neural networks,” in Proceedings of the Thirtieth International Joint Conference on Artificial Intelligence, 2021, pp. 2694–2700. [Google Scholar]
- [127].Yuan H, Yu H, Gui S, and Ji S, “Explainability in graph neural networks: A taxonomic survey,” arXiv preprint arXiv:2012.15445, 2020. [DOI] [PubMed] [Google Scholar]
- [128].Xie Y, Katariya S, Tang X, Huang E, Rao N, Subbian K, and Ji S, “Task-agnostic graph explanations,” arXiv preprint arXiv:2202.08335, 2022. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


