Thermodynamic determination of RNA duplex stability in magnesium solutions

Abstract

The prediction of RNA secondary structure and thermodynamics from sequence relies on free energy minimization and nearest neighbor parameters. Currently, algorithms used to make these predictions are based on parameters from optical melting studies performed in 1 M NaCl. However, many physiological and biochemical buffers containing RNA include much lower concentrations of monovalent cations and the presence of divalent cations. In order to improve these algorithms, thermodynamic data was previously collected for RNA duplexes in solutions containing 71, 121, 221, and 621 mM Na⁺. From this data, correction factors for free energy (ΔG^°₃₇) and melting temperature (T_m) were derived. Despite these newly derived correction factors for sodium, the stabilizing effects of magnesium have been ignored. Here, the same RNA duplexes were melted in solutions containing 0.5, 1.5, 3.0, and 10.0 mM Mg²⁺ in the absence of monovalent cations. Correction factors for T_m and ΔG^°₃₇ were derived to scale the current parameters to a range of magnesium concentrations. The T_m correction factor predicts the melting temperature within 1.2°C, and the ΔG^°₃₇ correction factor predicts the free energy within 0.30 $\frac{\mathrm{k}\mathrm{c}\mathrm{a}\mathrm{l}}{\mathrm{m}\mathrm{o}\mathrm{l}}$. These newly derived magnesium correction factors can be incorporated into algorithms that predict RNA secondary structure and stability from sequence.

Significance

RNA secondary structure prediction guides a variety of experimental methods involving RNA. Nearest neighbor parameters derived from RNA solutions in 1 M NaCl can be used to predict RNA secondary structure; however, these conditions are far from native cellular conditions. Here, we scale melting temperature (T_m) and free energy (ΔG^°₃₇) predictive algorithms (derived from nearest neighbor parameters) to a concentration range of magnesium that is within those found in cellular environments and in many buffers designed to mimic cellular conditions. These new predictive algorithms can be used to more accurately predict RNA secondary structure from sequence in magnesium-containing solutions that mimic cell-like conditions.

Introduction

Ribonucleic acid (RNA) has the ability to participate in a variety of cellular functions in addition to protein synthesis (1,2,3). Due to its single-stranded nature, RNA can often fold back onto itself to form complex tertiary structures that allow for unique functions (4,5). These findings have deepened the desire to understand RNA tertiary structure and how these structures can impact RNA function. Because methods for solving RNA tertiary structure, such as nuclear magnetic resonance (NMR), x-ray crystallography, and cryogenic electron microscopy (cryo-EM), are difficult, time-intensive, and resource-heavy, research working toward accurate prediction of RNA 3D structure from sequence is ongoing (6,7,8). Although predicting 3D structure from sequence can be difficult, a promising intermediate step is predicting secondary structure from sequence. The development of accurate secondary structure predictive algorithms in various environmental conditions can serve as a strong scaffold to build upon for prediction of RNA 3D structures. This is especially true if environmental conditions mimic those found in a cell.

One of the most common methods used to predict secondary structure from sequence uses free energy minimization with the nearest neighbor model (9,10). The nearest neighbor model was derived from optical melting studies of short RNA duplexes in 1.0 M NaCl, 10 or 20 mM sodium cacodylate, and 0.5 mM Na₂EDTA (10). However, intracellular [Na⁺] is much lower than the 1 M NaCl buffer used in the optical melting studies to develop the nearest neighbor model. Also, molecular biology techniques, such as PCR, often use buffers containing 20–100 mM monovalent cations (11,12). Optical melting studies to determine the thermodynamic parameters of short RNA duplexes in more biologically relevant [Na⁺] (71, 121, 221, and 621 mM) were conducted to derive Na⁺ correction factors (13). These correction factors can be incorporated into prediction algorithms to more accurately predict RNA secondary structure in varying [Na⁺].

Although these newly derived parameters for Na⁺ are more useful for modern biological techniques, they still neglect the stabilizing effects of divalent cations, such as Mg²⁺, which are essential for intracellular enzymatic reactions and modern physiological buffers. Like monovalent cations, divalent cations are responsible for binding to nucleic acids and affecting their physical properties as well as stabilizing nucleic acid duplexes and facilitating secondary and tertiary folding (14,15). Chelated and free divalent metal ions, such as Mg²⁺, also participate in more than just RNA folding interactions (16). For example, chelation of Mg²⁺ can assist with RNA catalysis, protection, and stabilization (16). Many studies have also shown Mg²⁺ to participate in an in-line attack, catalyzing RNA cleavage events (17,18,19). The free [Mg²⁺] in a cell varies depending on the organism. Free Mg²⁺ concentrations of 0.2–1.3 mM and 2.0–3.0 mM have been reported for eukaryotic and bacterial cells, respectively (16,20).

Foundational studies investigating the effects that Na⁺ (21) and Mg²⁺ (22) have on nucleic acid thermodynamics have shown similarities between the 1.0 M NaCl buffered conditions and 150 mM NaCl with 10.0 mM MgCl₂ (22). Additional studies have investigated how different monovalent and divalent cations of varying concentrations influence nucleic acid stability (23,24,25,26,27,28). However, these studies either only investigated monovalent cations (24), used a conceptual model of a single nucleotide sequence as a case study (25), or the environment containing the cations contained both divalent and monovalent cations either in the same solution (23,26,28) or in the presence of crowding agents (27). Single-molecule studies have measured DNA stability in Mg²⁺ and Na⁺ (29), measured RNA stability in Na⁺ (30), and identified RNA binding sites for Mg²⁺ and Na⁺ ions (31). To our knowledge, no studies have been conducted that focus exclusively on the stability of short RNA duplexes in the presence of biologically relevant [Mg²⁺] and no monovalent cations ([Mon⁺]).

It has been shown that monovalent and divalent cations compete for interaction with nucleic acids (32,33,34). In order to determine how Na⁺ and Mg²⁺ compete to stabilize DNA, Owczarzy et al. first studied the contributions of Na⁺ alone (35) and Mg²⁺ alone (11) on duplex stability. Next, they used information from the studies completed with Na⁺ alone and Mg²⁺ alone to help understand the thermodynamics of DNA in mixtures of monovalent and divalent cations (11). Although this study was performed with DNA, it is likely that RNA in solutions containing both Mg²⁺ and Mon⁺ may act in a similar manner. Systematic thermodynamic data for RNA oligonucleotides with different ratios of [Mg²⁺] and [Mon⁺] are needed. As mentioned previously, the effect of Mg²⁺ alone (in the absence of monovalent salt cations), which is required to understand how mixtures of Mg²⁺ and Mon⁺ affect RNA stability, has not been investigated for short RNA duplexes.

To that end, the thermodynamic data from optical melting studies are reported for a set of 17 RNA duplexes. Each duplex was melted with a range of [Mg²⁺] (0.5, 1.5, 3.0, and 10.0 mM). Using the RNA Na⁺ correction factors of Chen and Znosko (13) and the DNA Mg²⁺ correction factors of Owczarzy et al. (11) as a guide, T_m and ΔG^°₃₇ correction factors are reported here to adjust the standard 1 M NaCl RNA nearest neighbor predictions to account for the presence of Mg²⁺. Similar to the previously mentioned Na⁺ correction factors, these can be incorporated into prediction algorithms that predict RNA secondary structure and stability from sequence. Building on the knowledge of how Na⁺ alone affects RNA stability, the understanding of how Mg²⁺ alone affects RNA stability will guide future studies to determine how mixtures of Mg²⁺ and Mon⁺ affect RNA stability.

Materials and methods

RNA oligonucleotide preparation

All sequences studied here were also used by Xia et al. (10) to derive the RNA nearest neighbor parameters in 1 M NaCl and by Chen and Znosko (13) to derive a correction factor for varying [Na⁺]. All oligonucleotides were synthesized by Integrated DNA Technologies (Coralville, IA) and purified using standard procedures (36,37,38).

Optical melting studies

A melting scheme was developed to ensure that each duplex was melted at least nine times at different oligonucleotide concentrations. A Beckman-Coulter DU800 spectrophotometer was equipped with a high-performance temperature controller, allowing for variability in temperature during absorbance measurements. A heating rate of 1°C/min was used to obtain absorbance versus temperature melting curves between 15°C and 95°C at 280 nm for purely G-C duplexes and 8°C and 85°C at 260 nm for all other duplexes. MeltWin v3.5 (39) was used to analyze the absorbance versus temperature curves and produce T_m⁻¹ versus ln C_T plots to determine the thermodynamic parameters of each duplex.

All optical melting studies used to derive correction factors were conducted in the presence of 0.5, 1.5, 3.0, or 10.0 mM MgCl₂ in buffer containing 2 mM Tris at pH 8.3. This range of [Mg²⁺] represents the range of free Mg²⁺ in various cells (20,40,41,42,43). No monovalent cations were added to the buffer to determine the effect of Mg²⁺ alone on RNA duplex stability.

pH effects on RNA stability

Tris buffer was used in this study to prevent competition between the divalent cations studied here and monovalent cations. The concentration of monovalent cations in phosphate, cacodylate, and citrate buffers is higher than the trace amounts found in Tris. In addition, Tris buffers are usually employed in modern biological applications, such as PCR (11,12). However, the pH of Tris buffer is temperature dependent, leading to a decrease in pH of approximately 0.029 per 1°C increase. To verify that a change in pH of the Tris buffer over the temperature range of a typical optical melting experiment would not affect duplex thermodynamics, pH effects on T_m were determined for the RNA duplexes (5′-CGCGCG-3′)₂ and (5′-ACUUAAGU-3′)₂ as previously described by Owczarzy et al. with DNA (11). Five different buffers with pH values of 6.5, 7.0, 7.6, 8.3, and 12.1 were prepared. The buffers at pH 6.5, 7.0, and 7.6 contained 1.5 mM MgCl₂, 50 mM NaCl, and 10 mM sodium cacodylate. The buffer at pH 8.3 contained 10 mM 3-(N-morpholino)propanesulfonic acid (MOPS) instead of sodium cacodylate. The buffer at pH 12.1 contained 10 mM N-cyclohexyl-2-aminoethanesulfonic acid (CHES) instead of sodium cacodylate or MOPS.

UV monitoring of RNA cleavage and degradation

To verify that cleavage was not occurring during the optical melting experiments, forward (heating the duplex by 1°C/min) followed by reverse melting (cooling the single strands by 1°C/min) experiments were conducted with the duplexes (5′-CGCGCG-3′)₂ and (5′-ACUUAAGU-3′)₂ in both 10.0 mM MgCl₂ in Tris and standard 1 M NaCl optical melting buffer (containing 1.0 M NaCl, 20 mM sodium cacodylate, and 0.5 mM Na₂EDTA at pH 7.0). No reports of cleavage events for short RNA oligonucleotides in standard optical melting buffer during optical melting experiments exist, so the oligonucleotides in the standard optical melting buffer served as a reference. Cooling of the samples occurred directly after reaching the end temperature in the forward melting experiment. The samples remained at the end temperature for 1 min before beginning the reverse melt. These two oligonucleotides were chosen because they varied in length and fraction of G-C basepairs (f_GC). In addition, the U-A step in (5′-ACUUAAGU-3′)₂ is a known cleavage site when in the presence of Mg²⁺ (17). These oligonucleotides also represented the two extremes in terms of ΔG^°₃₇ and T_m for this study. One can assume that all oligonucleotides that fall within, or close to, these two extremes should behave in a similar manner. More specifically, if the ΔG^°₃₇ and T_m do not vary significantly for these two duplexes during the forward and reverse melting experiments while in solutions containing Mg²⁺ at high temperatures, all other duplexes should not vary significantly as well.

To further verify that cleavage was not occurring during the melting experiments and that using serial dilutions of previously melted duplexes was a valid approach, the (5′-CGCGCG-3′)₂ and (5′-ACUUAAGU-3′)₂ duplexes were melted in the 10.0 mM MgCl₂ buffer using fresh, never before melted oligonucleotide for each of the concentrations in the T_m⁻¹ versus ln C_T plot. A total of nine concentrations were used in the melt scheme. The same absorbance wavelengths and heating rates were used as previously mentioned. The results of using fresh, never before melted oligonucleotide for each of the concentrations were compared with the results of using serial dilutions of previously melted samples.

HPLC monitoring of RNA cleavage and degradation

In addition to reverse melts and using fresh oligonucleotide in a melt scheme, high-performance liquid chromatography (HPLC) was also used to verify that no cleavage and minimal degradation occurred during the melting experiments. The duplexes (5′-CGCGCG-3′)₂ and (5′-ACUUAAGU-3′)₂ were analyzed by HPLC before and after optical melting experiments in 10.0 mM MgCl₂ with 2.0 mM Tris buffer and in standard 1 M NaCl optical melting buffer. Before column injection, before and after melt samples were diluted to 200 ppm with autoclaved nanopure water. The melt buffers alone and the samples in the diluted melt buffers were analyzed on a Shimadzu LCMS-2010EV, with the MS function disconnected. UV detection wavelengths of 260 and 280 nm were used. A C18 reverse phase column was used with a flow rate of 0.25 mL/min. The pH of the sample and Mg²⁺-containing buffer was adjusted below 7.0 to prevent degradation of the C-18 column before injection. HPLC-grade 100% acetonitrile and 50 mM ammonium acetate were chosen as the solvents. An isocratic method was used, starting at 0% acetonitrile. From 4 to 24 min, the percent acetonitrile increased from 5% to 15%. The percent acetonitrile then increased to 30% for 2 min and 80% for an additional 8 min.

Predicting T_m

The RNA data collected here in varying [Mg²⁺] were tested against six DNA correction factors for [Na⁺] (44,45,46,47,48,49,50), two RNA correction factors for [Na⁺] (13), four DNA correction factors for [Mg²⁺] (11,51,52), and one RNA correction factor for [Mg²⁺] (53,54). All existing correction factors were tested using the experimental 1 M NaCl T_m values, and these values were corrected to predict T_m values at 0.5, 1.5, 3.0, and 10.0 mM Mg²⁺. The average deviation of the models was determined by comparing 68 experimental melting temperatures (17 duplexes at four different [Mg²⁺]) to the corresponding predicted melting temperatures using |ΔT_m|_ave:

$${\left|{\Delta T}_{\mathrm{m}}\right|}_{\mathrm{a}\mathrm{v}\mathrm{e}}=\frac{\sum _{j=1}^{j=n}\left|T_{\mathrm{m}}\left(j,\mathrm{p}\mathrm{r}\mathrm{e}\mathrm{d}\mathrm{i}\mathrm{c}\mathrm{t}\mathrm{i}\mathrm{o}\mathrm{n}\right)-T_{\mathrm{m}}\left(j,\mathrm{e}\mathrm{x}\mathrm{p}\mathrm{e}\mathrm{r}\mathrm{i}\mathrm{m}\mathrm{e}\mathrm{n}\mathrm{t}\right)\right|}{\mathrm{N}}$$ (1)

To improve the average deviation, the coefficients for nine of the 13 models mentioned above were updated. This was conducted using all the data reported here and the LINEST function (linear regression) in Microsoft Excel. For the linear regression, the numerical coefficients in the previously published models were set as the variables, and the melting temperatures were set as the constants, allowing for the derivation of revised coefficients based on the data reported here. These updated models were then tested using Eq. 1.

Predicting ΔG°₃₇

Similar to what was described above for T_m, previously published correction factors for ΔG^°₃₇, one for DNA in [Na⁺] (50), four for RNA in [Na⁺] (13), and one for DNA in [Mg²⁺], were tested for average deviation (11). The average deviation of the models was determined by comparing the 68 experimental ΔG^°₃₇ values to the corresponding predicted ΔG^°₃₇ values using |ΔΔG^°₃₇|_ave:

$${\left|{\Delta \Delta G°}_{37}\right|}_{\mathrm{a}\mathrm{v}\mathrm{e}}=\frac{\sum _{j=1}^{j=n}\left|{\Delta G°}_{37}\left(j,\mathrm{p}\mathrm{r}\mathrm{e}\mathrm{d}\mathrm{i}\mathrm{c}\mathrm{t}\mathrm{i}\mathrm{o}\mathrm{n}\right)-{\Delta G°}_{37}\left(j,\mathrm{e}\mathrm{x}\mathrm{p}\mathrm{e}\mathrm{r}\mathrm{i}\mathrm{m}\mathrm{e}\mathrm{n}\mathrm{t}\right)\right|}{\mathrm{N}}$$ (2)

Again, based on the RNA data reported here, the coefficients for five of the six models tested were updated in the same manner as the T_m correction factors and evaluated for average deviation using Eq. 2.

Leave-one-out analysis

To ensure the recommended correction factors and updated coefficients are predictive as well as postdictive, a comprehensive leave-one-out analysis was conducted for the recommended correction factors (see discussion). For this analysis, the data for an entire oligonucleotide sequence (experimental thermodynamic parameters for 0.5, 1.5, 3.0, and 10.0 mM Mg²⁺) were excluded in the linear regression analysis used to determine the coefficients, leaving 64 unique data points and generating new coefficients for the recommended correction factors. The process was repeated 17 times, each time leaving out one of the 17 oligonucleotides studied here. The coefficients resulting from each regression were used to predict the T_m and ΔG^°₃₇ of the oligonucleotide that was left out in each of the Mg²⁺ buffers. Both the updated coefficients and predicted parameters were compared with the original model proposed and the experimental values, respectively. The $|{{\Delta T}_{\mathrm{m}}|}_{\mathrm{a}\mathrm{v}\mathrm{e}}$ and $|{{\Delta \Delta G°}_{37}|}_{\mathrm{a}\mathrm{v}\mathrm{e}}$ were calculated for each of the 17 new models both for the oligonucleotides used in the fitting of the model and the one oligonucleotide that was left out. Predictions from the leave-one-out analysis were compared with predictions from the recommended correction factors. The average of each coefficient was also calculated across the 17 new models.

Results

Effects of buffer pH on melting temperature

RNA contains a phosphate backbone and nitrogenous bases that are capable of deprotonation and protonation at high and low pH, respectively. Deprotonation and protonation can influence hydrogen bonding interactions between bases, ultimately affecting duplex formation. The pK_a value(s) of adenosine is 3.5, guanosine are 1.6 and 9.2, uridine is 9.2, and cytidine is 4.2 (55). Therefore, at pH 7, all bases are likely to exist as neutral species with no charged groups. Hydrolysis of the RNA backbone is possible in a pH range above 8.0 (56). The presence of divalent metal ions in solution can stabilize the transition state in general acid-base-catalyzed cleavage of the RNA backbone (19). The pH of Tris buffer is temperature dependent, exhibiting a decrease in pH with an increase in temperature. An investigation into the effects of buffer pH on melting temperature was necessary.

The melting temperatures for two RNA self-complementary duplexes, (5′-CGCGCG-3′)₂ and (5′-ACUUAAGU-3′)₂, in the pH range of 6.5–12.1 were measured (Fig. S1). Melting temperatures in the pH range of 6.5–8.3 varied only slightly for each oligonucleotide (0.6°C and 0.9°C, respectively). When the pH was increased to 12.1, significant changes were evident. In theory, at this pH, all bases should be deprotonated at positions involved in hydrogen bonding, decreasing the overall stability of the duplex. Degradation and cleavage of the phosphodiester backbone would also theoretically occur at a pH of 12.1. At this pH, the melting temperature of (5′CGCGCG-3′)₂ decreased by 9.8°C. For (5′-ACUUAAGU-3′)₂ at pH 12.1, the interactions between the bases were disrupted to the point where a duplex did not form, cleavage events likely took place, and no melting temperature was obtained due to the inability to fit the melt curves to an assumed two-state model. The results found here for RNA duplexes in the pH range of 6.5–8.3 compare to the optical melting results obtained for DNA duplex oligomers with a pH range of 6.5–8.3 (11), a DNA hairpin with a pH range of 5.0–8.0 (57), T₂ phage DNA with pH ranges of 3.5–5.4 and 7.0 to 9.6 (58), and calf thymus DNA with a pH range of 3–12 (59), where melting temperatures did not change significantly between pH 6.5 and pH 8.3. Studies investigating the stability of RNA internal loops reported average differences in ΔG^°₃₇ and T_m at pH 7.5 and 5.5 of <0.4 $\frac{\mathrm{k}\mathrm{c}\mathrm{a}\mathrm{l}}{\mathrm{m}\mathrm{o}\mathrm{l}}$ and <3.0°C in the presence of Mg²⁺, respectively (28). The same study reported differences in ΔG^°₃₇ and T_m at pH 7.5 and 5.5 for an RNA helix of <0.2 $\frac{\mathrm{k}\mathrm{c}\mathrm{a}\mathrm{l}}{\mathrm{m}\mathrm{o}\mathrm{l}}$ and <1.1°C, respectively (28). Because these pH ranges had no significant effect on melting temperatures and represent a range where no deprotonation or protonation of the bases should occur, the Tris buffer used for further optical melting experiments was set at a pH of 8.3. Any decrease in pH with increasing temperature should remain in the tested range of 6.5–8.3 as demonstrated by Owczarzy et al. (11).

Monitoring of RNA cleavage and degradation

Forward optical melting experiments immediately followed by reverse optical melting experiments of the (5′-CGCGCG-3′)₂ and (5′-ACUUAAGU-3′)₂ duplexes in the 10.0 mM Mg²⁺ buffer and in standard 1 M NaCl buffer (1.0 M NaCl, 20 mM sodium cacodylate, and 0.5 mM Na₂EDTA at pH 7.0) showed minimal variation in the thermodynamic parameters acquired. The (5′-CGCGCG-3′)₂ duplex showed a ΔΔG^°₃₇ from the T_m⁻¹ versus ln C_T plot between the forward and reverse melt in 10.0 mM Mg²⁺ and in standard 1 M NaCl buffer of −0.01 $\frac{\mathrm{k}\mathrm{c}\mathrm{a}\mathrm{l}}{\mathrm{m}\mathrm{o}\mathrm{l}}$ and −0.10 $\frac{\mathrm{k}\mathrm{c}\mathrm{a}\mathrm{l}}{\mathrm{m}\mathrm{o}\mathrm{l}}$ respectively, with a ΔT_m of 0.4°C and −0.6°C, respectively (Table S1). The ΔΔG^°₃₇ for the (5′-ACUUAAGU-3′)₂ duplex in 10.0 mM Mg²⁺ and in standard 1 M NaCl buffer was −0.05 $\frac{\mathrm{k}\mathrm{c}\mathrm{a}\mathrm{l}}{\mathrm{m}\mathrm{o}\mathrm{l}}$ and 0.01 $\frac{\mathrm{k}\mathrm{c}\mathrm{a}\mathrm{l}}{\mathrm{m}\mathrm{o}\mathrm{l}}$ respectively, with no change in melting temperature for both environmental conditions (Table S1). For both duplexes studied, the ΔΔG^°₃₇ and the ΔT_m in Mg²⁺-containing buffers were relatively small and comparable to Na⁺-containing buffers. This suggested no cleavage or significant degradation occurred in Mg²⁺-containing buffers after heating to a high temperature (>80°C). If cleavage or significant degradation were to occur, one would have expected a large ΔΔG^°₃₇ and ΔT_m between the forward and reverse melts in the presence of Mg²⁺. It is important to note, a forward melting experiment immediately followed by a reverse melting experiment subjected the duplexes to high temperatures for twice the length of time compared with traditional, one-way melting experiments. Additionally, both the forward and reverse melt curves exhibited a single inflection point with a characteristic sigmoidal shape (data not shown), suggesting that there is a single species in solution, and no cleavage was taking place.

In comparison to the data collected while using serial dilutions to obtain the different concentrations of RNA duplex, using fresh oligonucleotide in Mg²⁺-containing buffers for each of the concentrations in the melt scheme also showed little variation in the thermodynamic parameters acquired. For the (5′-CGCGCG-3′)₂ duplex, there was no change in ΔG^°₃₇ and a 1.1°C difference in T_m (Table S2). For the (5′-ACUUAAGU-3′)₂ duplex, there was a −0.09 $\frac{\mathrm{k}\mathrm{c}\mathrm{a}\mathrm{l}}{\mathrm{m}\mathrm{o}\mathrm{l}}$ difference in ΔG^°₃₇ and a 0.2°C difference in T_m (Table S2). All values were within experimental error. These findings validated our method of serial diluting the RNA sample in Mg²⁺-containing buffers during the melt scheme. No significant differences between the fresh oligonucleotide and the reused oligonucleotide melt schemes were observed, again suggesting no cleavage or significant degradation occurred during our analysis.

Although there was no evidence of RNA cleavage in the UV spectrum while in the presence of Mg²⁺ during the optical melting experiments, HPLC was used to analyze two RNA oligonucleotides before and after melting to verify that no cleavage had occurred. The HPLC chromatograms were identical before and after melting the RNA sample in both 10.0 mM Mg²⁺ and standard 1 M NaCl buffer for (5′-CGCGCG-3′)₂ (Fig. S2) and (5′-ACUUAAGU-3′)₂ (Fig. S3). This indicated that the addition of heat and Mg²⁺ did not result in cleavage of the RNA duplexes. These findings were despite the presence of a U-A step in the (5′-ACUUAAGU-3′)₂ sequence, a cleavage site found in the env22 twister ribozyme that is catalyzed by Mg²⁺ (17).

RNA thermodynamic parameters

Experimental T_m, ΔG^°₃₇, ΔH^°, and ΔS^° values for all 17 duplexes in four different [Mg²⁺] are available in Table S3. The experimental T_m and ΔG^°₃₇ values from the T_m⁻¹ versus ln C_T plots for all duplexes in all [Mg²⁺] are presented in Tables 1 and 2, respectively. Duplexes melted in 0.5, 1.5, 3.0, and 10.0 mM Mg²⁺ had average T_m values that were 5.2°C lower, 2.1°C lower, 0.4°C lower, and 1.6°C higher, respectively, than that of the same duplexes melted in 1 M NaCl. Likewise, the average ΔG^°₃₇ values for the duplexes melted in the same [Mg²⁺] were 0.85 $\frac{\mathrm{k}\mathrm{c}\mathrm{a}\mathrm{l}}{\mathrm{m}\mathrm{o}\mathrm{l}}$ less, 0.30 $\frac{\mathrm{k}\mathrm{c}\mathrm{a}\mathrm{l}}{\mathrm{m}\mathrm{o}\mathrm{l}}$ less, 0.03 $\frac{\mathrm{k}\mathrm{c}\mathrm{a}\mathrm{l}}{\mathrm{m}\mathrm{o}\mathrm{l}}$ more, and 0.41 $\frac{\mathrm{k}\mathrm{c}\mathrm{a}\mathrm{l}}{\mathrm{m}\mathrm{o}\mathrm{l}}$ more stable, respectively, than the same duplexes in 1 M NaCl. Based on this data, 3.0 mM Mg²⁺ stabilizes RNA comparably to 1 M NaCl.

Table 1.

Experimental melting temperatures for self-complementary RNA duplexes in solutions of varying magnesium concentrations and in 1 M sodium chloride with no magnesium

RNA sequence (5′ to 3′)a	fGCb	Tmc (°C)
		0.5 mM Mg2+	1.5 mM Mg2+	3.0 mM Mg2+	10.0 mM Mg2+	1 M NaCld
CGCGCG	1.00	53.3	57.1	58.3	60.3	57.8
CGGCCG	1.00	58.2	61.2	63.6	64.9	63.2
GCGCGC	1.00	56.9	59.4	61.0	62.3	62.5
ACCGGU	0.67	52.3	55.6	56.8	58.4	53.9
AGCGCU	0.67	43.3	47.0	49.2	51.7	52.0
CACGUG	0.67	38.7	41.7	43.2	44.9	42.8
CAGCUG	0.67	37.9	40.8	42.4	44.7	43.1
CCAUGG	0.67	43.9	46.3	47.9	50.1	46.4
CCUAGG	0.67	48.4	51.4	52.3	54.2	50.0
CUGCAG	0.67	40.5	42.8	44.2	46.9	45.3
GACGUC	0.67	41.6	45.2	45.8	48.4	46.2
GAGCUC	0.67	41.4	44.5	46.7	48.5	48.7
GCAUGC	0.67	40.1	43.3	45.0	47.2	45.7
ACUUAAGU	0.25	32.1	35.9	38.5	40.0	40.3
AACUAGUU	0.25	38.8	42.0	43.4	45.8	45.7
ACUAUAGU	0.25	38.1	41.0	43.1	44.7	44.0
AGAUAUCU	0.25	34.9	37.8	40.0	43.1	41.4

^aAll oligonucleotides are forming self-complementary duplexes in solution.

^bf_GC is the fraction of G-C basepairs in the duplex.

^cCalculated for 0.1 mM oligonucleotide concentration based on the T_m⁻¹ versus ln C_T plots. Errors are typically ∼1.0°C for melting temperature measurements.

^dAll 1 M NaCl data are from Xia et al. (10), except for GCGCGC, which is from Chen and Znosko (13).

Table 2.

Experimental ΔG^°₃₇ values for self-complementary RNA duplexes in solutions of varying magnesium concentrations and in 1 M sodium chloride with no magnesium

RNA sequence (5′ to 3′)a	fGCb	ΔG°37 (kcal/mol)c
		0.5 mM Mg2+	1.5 mM Mg2+	3.0 mM Mg2+	10.0 mM Mg2+	1 M NaCld
CGCGCG	1.00	−8.78	−9.35	−9.40	−9.86	−9.12
CGGCCG	1.00	−9.37	−9.77	−10.07	−10.25	−9.90
GCGCGC	1.00	−9.34	−9.70	−10.13	−10.22	−10.56
ACCGGU	0.67	−8.50	−8.83	−9.21	−9.74	−8.51
AGCGCU	0.67	−6.65	−7.33	−7.61	−8.13	−7.99
CACGUG	0.67	−5.96	−6.46	−6.78	−7.05	−6.59
CAGCUG	0.67	−5.83	−6.32	−6.61	−6.99	−6.68
CCAUGG	0.67	−7.02	−7.48	−7.88	−8.26	−7.30
CCUAGG	0.67	−7.86	−8.31	−8.61	−8.84	−7.80
CUGCAG	0.67	−6.27	−6.76	−7.18	−7.53	−7.11
GACGUC	0.67	−6.51	−7.24	−7.48	−7.96	−7.35
GAGCUC	0.67	−6.45	−7.14	−7.53	−7.87	−7.98
GCAUGC	0.67	−6.23	−6.85	−7.15	−7.52	−7.38
ACUUAAGU	0.25	−4.85	−5.47	−5.97	−6.34	−6.16
AACUAGUU	0.25	−6.00	−6.69	−6.86	−7.36	−7.16
ACUAUAGU	0.25	−5.89	−6.51	−6.89	−7.35	−6.98
AGAUAUCU	0.25	−5.27	−5.83	−6.29	−6.78	−6.58

^aAll oligonucleotides are forming self-complementary duplexes in solution.

^bf_GC is the fraction of G-C basepairs in the duplex.

^cCalculated based on the T_m^-1 versus ln C_T plots. Errors are typically <0.5 kcal/mol for ΔG°₃₇ values.

^dAll 1 M NaCl data are from Xia et al. (10), except for GCGCGC, which is from Chen and Znosko (13).

T_m correction factors

It is evident that short RNA duplexes in buffers containing Mg²⁺ melt at temperatures that are different than those for RNA duplexes in varying amounts of Na⁺. Although there are T_m correction factors for RNA duplexes in varying amounts of Na⁺, T_m correction factors are needed for RNA in Mg²⁺-containing solutions for accurate predictions. There have been numerous previously published correction factors for DNA and RNA in Na⁺ and a few for DNA in Mg²⁺ that were tested using the RNA data reported here. These can be found in Table S4 (with Eqs. S1–S19 therein) with the corresponding average deviations of those models calculated as described in materials and methods. Not surprisingly, the correction factors for DNA in Mg²⁺ provided smaller deviations, |ΔT_m|_ave ≤5.0°C, than did those for DNA and RNA in Na⁺, with |ΔT_m|_ave ≥18.8°C. Nevertheless, a wide range of correction factors were updated based on the data reported here to improve the average deviations of the models (Table 3 and Eqs. 3–9 therein). With new coefficients, all models, with the exception of Eq. 8, improved, resulting in |ΔT_m|_ave values ≤ 2.7°C. Eq. 7 and Eq. 9 both had average deviations of 1.2°C. Because Eq. 7 is simpler than Eq. 9, it is the recommended T_m correction factor to be used for RNA in [Mg²⁺] ≤10.0 mM. Eq. 7 also works well predicting T_m across the entire magnesium concentration range studied here. Comparing the experimental T_m to the predicted T_m calculated using Eq. 7 resulted in an average |ΔT_m| of 1.4°C, 1.4°C, 1.1°C, and 1.1°C in the 0.5 mM, 1.5 mM, 3.0 mM, and 10.0 mM Mg²⁺ solutions, respectively.

Table 3.

Newly derived RNA correction factors

Eq no.	Name	Equation	Average deviationa
RNA Tm correction factorsb
3	Modified Schildkraut-Lifson and Tm and 12.5log[Na+] equation	$T_{\mathrm{m}}\left(2\right)=T_{\mathrm{m}}\left(1\right)+0.72\log \frac{\left[{\mathrm{M}\mathrm{g}}^{2+}\right]}{\left[{\mathrm{N}\mathrm{a}}^{+}\right]}$	2.3°C
4	Modified Wetmur equation	$T_{\mathrm{m}}\left(2\right)=T_{\mathrm{m}}\left(1\right)+0.80\log \frac{\left[{\mathrm{M}\mathrm{g}}^{2+}\right]\left(1+0.7\left[{\mathrm{N}\mathrm{a}}^{+}\right]\right)}{\left[{\mathrm{N}\mathrm{a}}^{+}\right]\left(1+0.7\left[{\mathrm{M}\mathrm{g}}^{2+}\right]\right)}$	2.2°C
5	Modified Marmur-Schildkraut-Doty and Frank-Kamenetskii Tm equation	$T_{\mathrm{m}}\left(2\right)=T_{\mathrm{m}}\left(1\right)+\left(0.012-0.008f\mathrm{G}\mathrm{C}\right)\ln \frac{\left[{\mathrm{M}\mathrm{g}}^{2+}\right]}{\left[{\mathrm{N}\mathrm{a}}^{+}\right]}$	2.7°C
6	Modified SantaLucia equationc,d	$\frac{1}{T_{\mathrm{m}}\left(2\right)}=\frac{1}{T_{\mathrm{m}}\left(1\right)}+\frac{0.0358\left(N_{\mathrm{b}\mathrm{p}}-1\right)}{\Delta H°}\ln \frac{\left[{\mathrm{M}\mathrm{g}}^{2+}\right]}{\left[{\mathrm{N}\mathrm{a}}^{+}\right]}$	2.2°C
7	Modified Chen Tm quadratic equation	$T_{\mathrm{m}}\left(2\right)=T_{\mathrm{m}}\left(1\right)+\left(-1.663-0.385f\mathrm{G}\mathrm{C}\right)\ln \frac{\left[{\mathrm{M}\mathrm{g}}^{2+}\right]}{\left[{\mathrm{N}\mathrm{a}}^{+}\right]}-0.342\left({\ln }^2\left[{\mathrm{M}\mathrm{g}}^{2+}\right]-{\ln }^2\left[{\mathrm{N}\mathrm{a}}^{+}\right]\right)$	1.2°C
8	Modified Chen 1/Tm quadratic equationc	$\frac{1}{T_{\mathrm{m}}\left(2\right)}=\frac{1}{T_{\mathrm{m}}\left(1\right)}+\left(0.432f\mathrm{G}\mathrm{C}-1.588\right)\times {10}^{-5}\ln \frac{\left[{\mathrm{M}\mathrm{g}}^{2+}\right]}{\left[{\mathrm{N}\mathrm{a}}^{+}\right]}+3.348\times {10}^{-6}\left({\ln }^2\left[{\mathrm{M}\mathrm{g}}^{2+}\right]-{\ln }^2\left[{\mathrm{N}\mathrm{a}}^{+}\right]\right)$	18.8°C
9	Modified Owczarzy magnesium Tm correction factor equationc	$\frac{1}{T_{\mathrm{m}}\left({\mathrm{M}\mathrm{g}}^{2+}\right)}=\frac{1}{T_{\mathrm{m}}\left(1\mathrm{M}{\mathrm{N}\mathrm{a}}^{+}\right)}-8.41\times {10}^{-5}-2.72\times {10}^{-6}\ln \left[{\mathrm{M}\mathrm{g}}^{2+}\right]+f\mathrm{G}\mathrm{C}\left(6.00\times {10}^{-5}+8.56\times {10}^{-6}\ln \left[{\mathrm{M}\mathrm{g}}^{2+}\right]\right)+\frac{1}{2\left(N_{\mathrm{b}\mathrm{p}}-1\right)}[4.01\times {10}^{-4}+4.04\times {10}^{-4}\ln \left[{\mathrm{M}\mathrm{g}}^{2+}\right]+3.37\times {10}^{-5}\left({\ln }^2\left[{\mathrm{M}\mathrm{g}}^{2+}\right]\right)]$	1.2°C
RNA ΔG°37 Correction factorsb
10	Modified SantaLucia ΔG°37 equation	$\Delta G_{37}^{°}\left(2\right)=\Delta G_{37}^{°}\left(1\right)-0.00796\times \left(N_{\mathrm{b}\mathrm{p}}-1\right)\ln \frac{\left[{\mathrm{M}\mathrm{g}}^{2+}\right]}{\left[{\mathrm{N}\mathrm{a}}^{+}\right]}$	0.48 kcal/mol
11	Modified Chen ΔG°37 linear equation	$\Delta G_{37}^{°}\left(2\right)=\Delta G_{37}^{°}\left(1\right)+\left(0.0782f\mathrm{G}\mathrm{C}-0.0898\right)\ln \frac{\left[{\mathrm{M}\mathrm{g}}^{2+}\right]}{\left[{\mathrm{N}\mathrm{a}}^{+}\right]}$	0.47 kcal/mol
12	Modified Chen ΔG°37 quadratic equation	$\Delta G_{37}^{°}\left(2\right)=\Delta G_{37}^{°}\left(1\right)+\left(0.078f\mathrm{G}\mathrm{C}+0.337\right)\ln \frac{\left[{\mathrm{M}\mathrm{g}}^{2+}\right]}{\left[{\mathrm{N}\mathrm{a}}^{+}\right]}+0.066\left({\ln }^2\left[{\mathrm{M}\mathrm{g}}^{2+}\right]-{\ln }^2\left[{\mathrm{N}\mathrm{a}}^{+}\right]\right)$	0.30 kcal/mol
13	Modified Chen 1/ΔG°37 quadratic equation	$\frac{1}{\Delta G_{37}^{°}\left(2\right)}=\frac{1}{\Delta G_{37}^{°}\left(1\right)}+\left(-572.34-283.99f\mathrm{G}\mathrm{C}\right)\times {10}^{-5}\ln \frac{\left[{\mathrm{M}\mathrm{g}}^{2+}\right]}{\left[{\mathrm{N}\mathrm{a}}^{+}\right]}-0.0013\left({\ln }^2\left[{\mathrm{M}\mathrm{g}}^{2+}\right]-{\ln }^2\left[{\mathrm{N}\mathrm{a}}^{+}\right]\right)$	0.36 kcal/mol
14	Modified Owczarzy magnesium ΔG°37 correction factor equationd	$\Delta G_{37}^{°}\left({\mathrm{M}\mathrm{g}}^{2+}\right)=\Delta G_{37}^{°}\left(1\mathrm{M}{\mathrm{N}\mathrm{a}}^{+}\right)-310.15\Delta H°\times \left\{\begin{array}{c}2.98\times {10}^{-5}+1.96\times {10}^{-5}\ln \left[{\mathrm{M}\mathrm{g}}^{2+}\right]+f\mathrm{G}\mathrm{C}\left(-1.34\times {10}^{-4}-1.91\times {10}^{-5}\ln \left[{\mathrm{M}\mathrm{g}}^{2+}\right]\right)+\\ \frac{1}{2\left(N_{\mathrm{b}\mathrm{p}}-1\right)}[8.45\times {10}^{-4}-2.24\times {10}^{-4}\ln \left[{\mathrm{M}\mathrm{g}}^{2+}\right]-3.20\times {10}^{-5}\left({\ln }^2\left[{\mathrm{M}\mathrm{g}}^{2+}\right]\right)\end{array}\right\}$	0.88 kcal/mol

^aAs stated in materials and methods, |ΔT_m|ave is used to evaluate the average deviation of the T_m correction factors, and |ΔΔG°₃₇|ave is used to evaluate the average deviation of the ΔG°₃₇ correction factors.

^b1 M NaCl melting temperatures and free energy values were used as the starting point for all correction factors tested. Original correction factors with their respective references can be found in Table S4.

^cIn this equation, T_m should be in units of K.

^dIn this equation, ΔH^° is in cal/mol, and the experimental ΔH^° value from the T_m⁻¹ versus ln C_T plot was used.

The leave-one-out analysis for assessing the updated coefficients for Eq. 7 showed minimal variation in each of the coefficients upon excluding each of the 17 sequences from the linear regression (Fig. S4). Taking the differences in predicted T_m using the coefficients in the leave-one-out analysis and the coefficient proposed in Eq. 7 yielded an average difference of 0.1°C (Table S5). The average coefficient from the leave-one-out analysis was equal to the proposed coefficients in Eq. 7, validating the use of the proposed coefficients in Eq. 7.

ΔG°₃₇ correction factors

Despite the many models available for predicting T_m values, there are only a few models available for predicting changes in ΔG^°₃₇ values as a function of salt concentration. Those available were tested with the RNA data reported here and are presented in Table S4 with the corresponding average deviations of those models. Similar to the T_m correction factors, the one available for DNA in Mg²⁺ resulted in smaller deviations, |ΔΔG^°₃₇|_ave = 0.59 $\frac{\mathrm{k}\mathrm{c}\mathrm{a}\mathrm{l}}{\mathrm{m}\mathrm{o}\mathrm{l}}$, than did those for DNA and RNA in Na⁺. Again, a wide range of these correction factors were updated with new coefficients based on the data reported here to improve the average deviations of the models (Table 3 and Eqs. 10–14 therein). With the exception of Eq. 14, all newly derived ΔG^°₃₇ correction factors for RNA in Mg²⁺ had |ΔΔG^°₃₇|_ave values ≤ 0.48 $\frac{\mathrm{k}\mathrm{c}\mathrm{a}\mathrm{l}}{\mathrm{m}\mathrm{o}\mathrm{l}}$. However, due to its average deviation, |ΔΔG^°₃₇|_ave = 0.30 $\frac{\mathrm{k}\mathrm{c}\mathrm{a}\mathrm{l}}{\mathrm{m}\mathrm{o}\mathrm{l}}$, and consistency with the T_m correction factor discussed above, Eq. 12 is the recommended ΔG^°₃₇ correction factor to be used for RNA in [Mg²⁺] ≤10.0 mM. Eq. 12 also works well predicting ΔG^°₃₇ values across the entire magnesium concentration range studied here. Comparing the experimental ΔG^°₃₇ values to the predicted ΔG^°₃₇ calculated using Eq. 12 resulted in an average |ΔΔG^°₃₇| of 0.32 $\frac{\mathrm{k}\mathrm{c}\mathrm{a}\mathrm{l}}{\mathrm{m}\mathrm{o}\mathrm{l}}$, 0.31 $\frac{\mathrm{k}\mathrm{c}\mathrm{a}\mathrm{l}}{\mathrm{m}\mathrm{o}\mathrm{l}}$, 0.27 $\frac{\mathrm{k}\mathrm{c}\mathrm{a}\mathrm{l}}{\mathrm{m}\mathrm{o}\mathrm{l}}$, and 0.29 $\frac{\mathrm{k}\mathrm{c}\mathrm{a}\mathrm{l}}{\mathrm{m}\mathrm{o}\mathrm{l}}$ in the 0.5 mM, 1.5 mM, 3.0 mM, and 10.0 mM Mg²⁺ solutions, respectively.

The leave-one-out analysis for assessing the updated coefficients, similar to Eq. 7, showed minimal variation in each of the coefficients upon excluding each of the 17 sequences from the linear regression (Fig. S4). Taking the differences in predicted ΔG^°₃₇ using the coefficients in the leave-one-out analysis and the coefficient proposed in Eq. 7 yielded an average difference of 0.04 $\frac{\mathrm{k}\mathrm{c}\mathrm{a}\mathrm{l}}{\mathrm{m}\mathrm{o}\mathrm{l}}$ (Table S6). The average coefficient from the leave-one-out analysis was equal to the proposed coefficients in Eq. 12, validating the use of the proposed coefficients in Eq. 12.

Discussion

RNA cleavage and degradation

It has been reported previously that if RNA solutions containing Mg²⁺ are heated, it can lead to RNA cleavage (60,61,62,63). These studies were performed on large RNA molecules, and extensive RNA cleavage was reported when [Mg²⁺] ≥50 mM (60,61,63). Additionally, the likelihood of RNA cleavage increased at pH levels ≥8.0 and at temperatures ≥37°C, especially when the temperature was elevated over an extended period of time (60,62,63). It has also been reported that cleavage of RNA is significantly reduced when [Mg²⁺] is <40 mM (60). Other thermodynamic studies indicate that the introduction of Mg²⁺ and heat does not always induce RNA cleavage (64). In this work, the highest [Mg²⁺] studied was 10.0 mM, and RNA duplexes were not incubated at elevated temperatures for extended periods of time. Nonetheless, we wanted to confirm that the RNA duplexes studied here were not cleaved during the melting experiments in the presence of low [Mg²⁺].

The results from four different experiments suggested that there is no cleavage of short RNA oligonucleotides during the optical melting experiments conducted here. First, most optical melting experiments were completed as a series of dilutions. The results of the melting experiments after each dilution were consistent with one another, suggesting that none of the short RNA duplexes studied here under these conditions were cleaved during melting experiments. Additionally, each melt curve collected here was a single, sharp sigmoidal curve. If cleavage did occur during the melting experiment, we would expect the samples resulting from serial dilutions to consist of multiple species in solution. This would likely have resulted in melt curves with multiple transitions or very broad transitions.

A forward and then a reverse melt was also conducted on two RNA duplexes, (5′-CGCGCG-3′)₂ and (5′-ACUUAAGU-3′)₂, at the highest [Mg²⁺] of 10.0 mM and in standard 1 M NaCl buffer. During the forward and reverse melting experiments, the RNA duplexes were at higher temperatures for twice the amount of time compared with standard optical melting experiments. The high temperature should theoretically increase the reaction rate for a Mg²⁺ catalyzed cleavage event of the phosphodiester backbone. If a cleavage event of the RNA backbone were to occur, the event would likely occur at high temperatures. These conditions were prolonged during the forward and reverse melting experiments. The data from the forward and reverse melts of the two duplexes were identical in both conditions (Table S1), suggesting that no cleavage and no significant degradation occurred. If cleavage did occur in the Mg²⁺-containing samples, we would expect to see large differences between the forward and reverse melting data. The sample in standard 1 M NaCl buffer sample served as a reference since there are no reported instances of RNA being cleaved when suspended in this buffer. Therefore, we assume that if the before and after optical melting data in the Mg²⁺ buffer was similar to the before and after optical melting data in the NaCl buffer, there was no significant cleavage or degradation of RNA in the Mg²⁺ buffer. Because no large differences were seen, and the differences in the Mg²⁺ data were similar to that in standard 1 M NaCl buffer, we assumed no cleavage or significant degradation of the RNA samples occurred.

Additionally, instead of using serial dilutions, fresh oligonucleotide was used for each concentration in a series of melts in the 10.0 mM MgCl₂ buffer for the (5′-CGCGCG-3′)₂ and (5′-ACUUAAGU-3′)₂ duplexes. No significant differences in the acquired thermodynamic parameters were seen when compared with the data acquired from the standard melt scheme that dilutes previously melted samples (Table S2). Both experiments utilized the same concentration range and utilized nine different concentrations of oligonucleotide in the experiment. These similarities in values gave validity to the optical melting scheme used in this work and provided additional evidence for the lack of RNA cleavage in this study.

Finally, the same two RNA duplexes were monitored by HPLC before and after optical melting experiments in 10.0 mM Mg²⁺ and standard 1 M NaCl buffer. The chromatograms before and after optical melting experiments were identical (Figs. S2 and S3), further suggesting that RNA was not cleaved during optical melting experiments. As mentioned, these oligonucleotides represented the two extremes for ΔG^°₃₇ and T_m. These two oligonucleotides appeared relatively unaltered in Mg²⁺ solutions at high temperatures before and after melting. This was further validated when comparing the Mg²⁺ sample to the standard NaCl sample. We, therefore, assumed all other oligonucleotides should behave in a similar manner. The lack of evidence of cleavage during the serial dilutions, during the forward and reverse optical melting experiments, during the fresh oligonucleotide melt scheme, and by monitoring before and after melting experiments with HPLC indicates that short RNA duplexes heated to 80°C at an increment of 1°C/min are not cleaved or significantly degraded in the presence of 10.0 mM Mg²⁺. Due to these findings, we assumed that short RNA duplexes in the presence of [Mg²⁺] <10.0 mM would also not exhibit any cleavage.

Magnesium effects on RNA duplex stability and T_m

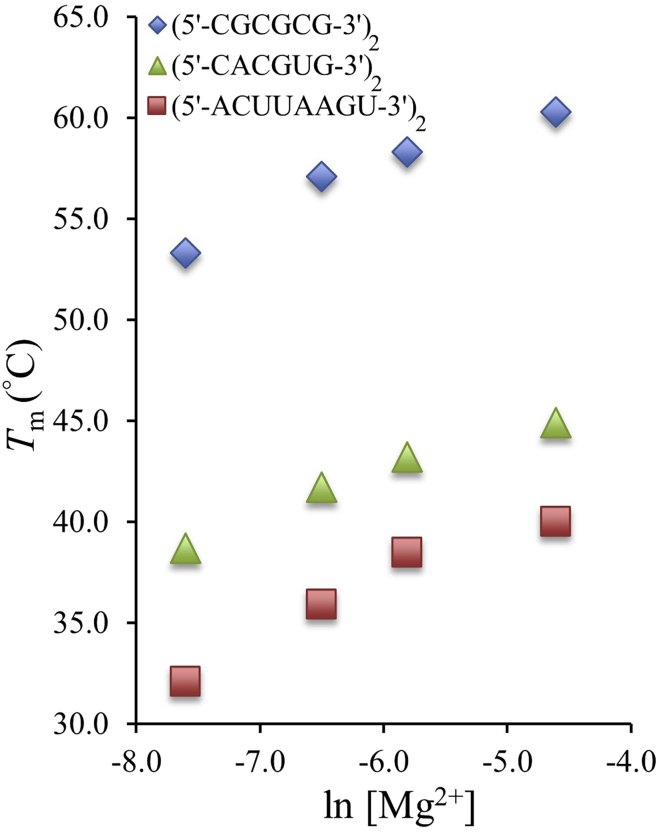
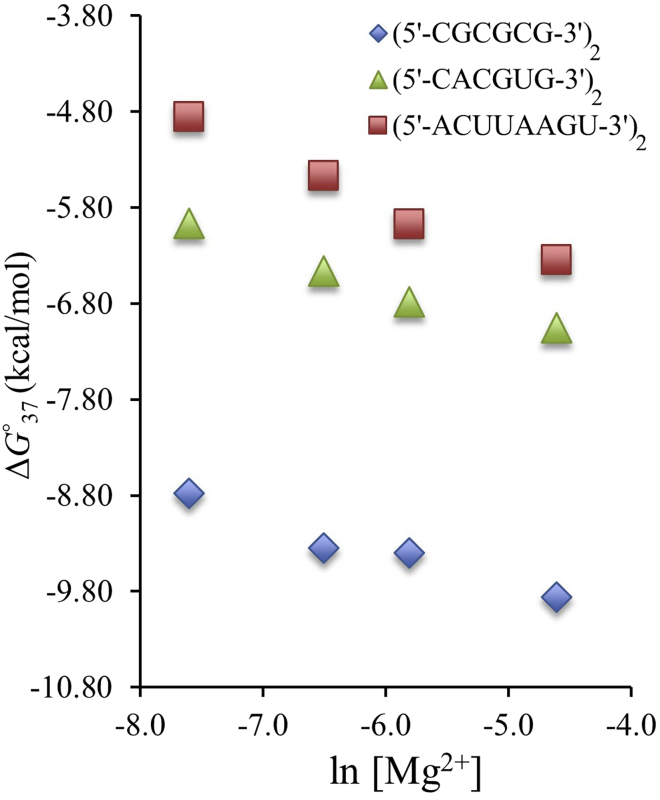
As the [Mg²⁺] was increased from 0.5 mM to 10.0 mM, the ΔG^°₃₇ values became more negative, and the T_m values increased as expected (Tables 1 and 2 and Figs. 1 and 2). These trends were consistent with what has been shown with DNA in Mg²⁺ across a larger concentration range (11). Previous studies have reported on the effects of Na⁺ on RNA duplex stability and have found that stability increases until a certain saturation point is reached (35,54,65). Although it appears as if the changes in ΔG^°₃₇ and T_m are in the process of leveling out as [Mg²⁺] approaches 10.0 mM, the range of [Mg²⁺] studied here does not allow for the determination of the exact saturation point, which is likely to occur above 10.0 mM. Figs. 1 and 2 demonstrate the relationship between T_m versus ln [Mg²⁺] and ΔG^°₃₇ versus ln [Mg²⁺] for a few RNA sequences that vary in f_GC. The shape of these curves resembles the shape of the same curves constructed for RNA in the presence of [Na⁺] in the range of 71 mM to 1.02 M (13). Also, when deriving correction factors for Na⁺, it was determined that DNA correction factors for Na⁺ were a good starting point for RNA Na⁺ correction factors (13,35). As a result, correction factors for DNA and RNA in Na⁺ and DNA in Mg²⁺ were used as starting points to derive correction factors for RNA in Mg²⁺.

Figure 1.

The relationship between melting temperatures and ln [Mg²⁺] for RNA duplexes with varying G-C content. (5′-CGCGCG-3′)₂ is 100% G-C, (5′-CACGUG-3′)₂ is 67% G-C, and (5′-ACUUAAGU-3′)₂ is 25% G-C. Errors in T_m are ∼ ±1°C. To see this figure in color, go online.

Figure 2.

The relationship between ΔG^°₃₇ and ln [Mg²⁺] for RNA duplexes with varying G-C content. (5′-CGCGCG-3′)₂ is 100% G-C, (5′-CACGUG-3′)₂ is 67% G-C, and (5′-ACUUAAGU-3′)₂ is 25% G-C. To see this figure in color, go online.

T_m correction factors

There are several previously published T_m correction factors for DNA and RNA in Na⁺ and DNA and RNA in Mg²⁺. Generally, the correction factors fell within one of three categories: those dependent exclusively on the relationship between T_m and ln (or log) [Mg²⁺], those that not only depend on the relationship between T_m and ln (or log) [Mg²⁺] but include the additional parameters N_bp-1 and ΔH^°, or those that depend on the relationship between T_m and ln (or log) [Mg²⁺] and f_GC. The previously published T_m correction factors for DNA and RNA in Na⁺ and DNA and RNA in Mg²⁺ were compared with the experimental RNA data reported here, with deviations ranging from 2.6°C to 42.8°C (Table S4). Each of the correction factors were updated to reflect the data collected here, resulting in improved average deviations ranging from 1.2°C to 18.8°C (Table 3). Eq. S7 and Eq. S13 improved to the best average deviation of 1.2°C (Eq. 7 and Eq. 9), so it was determined that the addition of the new parameter f_GC was beneficial in accurately predicting melting temperature. Fig. 1 compares f_GC and the relationship between melting temperature and ln [Mg²⁺]. However, because of simplicity and the consistency with the ΔG^°₃₇ correction factor (discussed below), the recommended T_m correction factor is Eq. 7.

In order to test this correction factor, a sample calculation using the recommended T_m correction factor with an RNA duplex used in the derivation here is illustrated below. The sample sequence is (5′-AACUAGUU-3′)₂ measured in 0.5 mM Mg²⁺ and 2 mM Tris. The experimental T_m in 1 M NaCl is 45.7°C and was used to predict the T_m at 0.5 mM Mg²⁺ in the correction calculation shown below:

$$T_{\mathrm{m}}\left(0.5\mathrm{m}\mathrm{M}{\mathrm{M}\mathrm{g}}^{2+}\right)=T_{\mathrm{m}}\left(1\mathrm{M}\mathrm{N}\mathrm{a}\mathrm{C}\mathrm{l}\right)+\left(-1.663–0.385f_{\mathrm{G}\mathrm{C}}\right)\ln \frac{\left[{\mathrm{M}\mathrm{g}}^{2+}\right]}{\left[{\mathrm{N}\mathrm{a}}^{+}\right]}–0.342\left({\ln }^2\left[{\mathrm{M}\mathrm{g}}^{2+}\right]–{\ln }^2\left[{\mathrm{N}\mathrm{a}}^{+}\right]\right)$$ (15)

$$T_{\mathrm{m}}\left(0.5\mathrm{m}\mathrm{M}{\mathrm{M}\mathrm{g}}^{2+}\right)=45.7°\mathrm{C}+\left(-1.663–0.385\ast 0.25\right)\ln \frac{\left[0.0005\mathrm{M}\right]}{\left[1.021\mathrm{M}\right]}–0.342\left({\ln }^2\left[0.0005\mathrm{M}\right]–{\ln }^2\left[1.021\mathrm{M}\right]\right)$$ (16)

$$T_{\mathrm{m}}\left(0.5\mathrm{m}\mathrm{M}{\mathrm{M}\mathrm{g}}^{2+}\right)=39.3°\mathrm{C}$$ (17)

The experimental T_m reported here for this duplex is 38.8°C, which is a difference of 0.5°C between the experimental and predicted values. Thus, this value fell within the average deviation value reported for this correction factor. If, however, the experimental T_m values are not available in 1 M NaCl, predicted values based on the nearest neighbor model are typically sufficient for prediction in Mg²⁺ (data not shown).

ΔG°₃₇ correction factors

Despite the numerous T_m correction factors available in the literature for DNA and RNA in Na⁺, there is only one DNA ΔG^°₃₇ correction factor (Eq. S14) and four RNA ΔG^°₃₇ correction factors (Eqs. S15–S18) available. In addition to these, Eq. S19 was developed for DNA in Mg²⁺. These correction factors rely on the relationship between ΔG^°₃₇ and ln (or log) [Mg²⁺] and some include other parameters such as N_bp-1 and f_GC to accurately predict ΔG^°₃₇. Like melting temperatures, Fig. 2 compares f_GC and the relationship between ΔG^°₃₇ and ln [Mg²⁺]. The previously published ΔG^°₃₇ correction factors for DNA and RNA in Na⁺ and DNA and RNA in Mg²⁺ were compared with the experimental RNA data reported here, with deviations ranging from 0.59 $\frac{\mathrm{k}\mathrm{c}\mathrm{a}\mathrm{l}}{\mathrm{m}\mathrm{o}\mathrm{l}}$ to 6.78 $\frac{\mathrm{k}\mathrm{c}\mathrm{a}\mathrm{l}}{\mathrm{m}\mathrm{o}\mathrm{l}}$ (Table S4). These correction factors were updated using data reported here, resulting in improved average deviations ranging from 0.30 $\frac{\mathrm{k}\mathrm{c}\mathrm{a}\mathrm{l}}{\mathrm{m}\mathrm{o}\mathrm{l}}$ to 0.88 $\frac{\mathrm{k}\mathrm{c}\mathrm{a}\mathrm{l}}{\mathrm{m}\mathrm{o}\mathrm{l}}$. Because Eq. S17 produced an updated correction factor (Eq. 12) with the best deviation and is consistent with the T_m correction factor recommended above, Eq. 12 is the correction factor recommended to predict ΔG^°₃₇ values for RNA in [Mg²⁺] between 0.5 and 10.0 mM.

To validate the accuracy of this model, the same oligonucleotide used in the sample T_m correction factor calculation above was used to predict ΔG^°₃₇ at 0.5 mM Mg²⁺. The experimental ΔG^°₃₇ value in 1 M NaCl is −7.16 $\frac{\mathrm{k}\mathrm{c}\mathrm{a}\mathrm{l}}{\mathrm{m}\mathrm{o}\mathrm{l}}$ and was used in the correction calculation shown below:

$${\Delta G}_{37}^{°}\left(0.5\mathrm{m}\mathrm{M}{\mathrm{M}\mathrm{g}}^{2+}\right)=\Delta G_{37}^{°}\left(1\mathrm{M}\mathrm{N}\mathrm{a}\mathrm{C}\mathrm{l}\right)+\left(0.078f_{\mathrm{G}\mathrm{C}}+0.337\right)\ln \frac{\left[{\mathrm{M}\mathrm{g}}^{2+}\right]}{\left[{\mathrm{N}\mathrm{a}}^{+}\right]}+0.066\left({\ln }^2\left[{\mathrm{M}\mathrm{g}}^{2+}\right]–{\ln }^2\left[{\mathrm{N}\mathrm{a}}^{+}\right]\right)$$ (18)

$${\Delta G}_{37}^{°}\left(0.5\mathrm{m}\mathrm{M}{\mathrm{M}\mathrm{g}}^{2+}\right)=-7.16\frac{\mathrm{k}\mathrm{c}\mathrm{a}\mathrm{l}}{\mathrm{m}\mathrm{o}\mathrm{l}}+\left(0.078\ast 0.25+0.337\right)\ln \frac{\left[0.0005\mathrm{M}\right]}{\left[1.021\mathrm{M}\right]}+0.066\left({\ln }^2\left[0.0005\mathrm{M}\right]–{\ln }^2\left[1.021\mathrm{M}\right]\right)$$ (19)

$${\Delta G}_{37}^{°}\left(0.5\mathrm{m}\mathrm{M}{\mathrm{M}\mathrm{g}}^{2+}\right)=-6.06\frac{\mathrm{k}\mathrm{c}\mathrm{a}\mathrm{l}}{\mathrm{m}\mathrm{o}\mathrm{l}}$$ (20)

The experimental ΔG^°₃₇ reported here for this duplex is −6.00 $\frac{\mathrm{k}\mathrm{c}\mathrm{a}\mathrm{l}}{\mathrm{m}\mathrm{o}\mathrm{l}}$, which is a difference of 0.06 $\frac{\mathrm{k}\mathrm{c}\mathrm{a}\mathrm{l}}{\mathrm{m}\mathrm{o}\mathrm{l}}$ between the experimental and predicted temperatures. Thus, this value fell within the average deviation value reported for this model. Again, if the experimental ΔG^°₃₇ values are not available in 1 M NaCl, predicted values are typically sufficient for prediction in Mg²⁺ (data not shown).

Oligomer length and sequence

It is apparent that different studies employed different parameters to account for duplex length and sequence composition on the stability of DNA or RNA in varying Na⁺ concentrations. Some correction factors utilized N_bp-1, which accounts for the effect of length on stability, whereas others included f_GC, which is a sequence composition parameter. After updating the majority of the previously published correction factors of both types, it was determined that the correction factor incorporating f_GC works best for the RNA duplexes studied here in Mg²⁺. Owczarzy et al. (35) stated that their correction factor developed for DNA in Na⁺ utilizing f_GC could be used for duplexes ranging in length from six to at least 60 basepairs. Although our new correction factor is based upon the same model they proposed but for RNA in Mg²⁺, it would be necessary to test the accuracy of our model as length increased. Due to experimental constraints, melting shorter or longer duplexes was not possible for this study.

Magnesium concentrations viable for correction factors

The Mg²⁺ range used here to derive the correction factors to accurately predict T_m and ΔG^°₃₇ values is 0.5–10.0 mM Mg²⁺. Thus, the correction factors can be used for RNA duplexes within this range. Conveniently, this range of [Mg²⁺] is representative of the free Mg²⁺ in cells and the concentration employed in modern physiological buffers. However, there may exist cases that include Mg²⁺ concentrations higher than what was tested here or include both Mg²⁺ and Na⁺ in concentrations that are competing. Further studies need to be conducted to validate the accuracy of our model on RNA duplexes in solutions with higher [Mg²⁺] than studied here and solutions containing both Mg²⁺ and Na⁺.

In summary, stability in Mg²⁺ solutions was studied for short RNA duplexes. Previously published T_m correction factors for DNA and RNA in Na⁺ and DNA and RNA in Mg²⁺ were updated with the RNA data reported here to derive new correction factors with better accuracies. Eq. 7, which is a modified version of Eq. S7, produced the best average deviation, 1.2°C, for the data reported here and is the recommended T_m correction factor for RNA duplexes in Mg²⁺. Likewise, previously published ΔG^°₃₇ correction factors for DNA and RNA in Na⁺ and DNA in Mg²⁺ were updated to derive new correction factors. The modification of Eq. S17 to Eq. 12 with new coefficients had the best average deviation, 0.30 $\frac{\mathrm{k}\mathrm{c}\mathrm{a}\mathrm{l}}{\mathrm{m}\mathrm{o}\mathrm{l}}$, and is the recommended ΔG^°₃₇ correction factor. These recommended correction factors can be incorporated into RNA secondary structure prediction algorithms to accurately predict the stability of RNA duplexes in [Mg²⁺] ranging from 0.5 to 10.0 mM.

Author contributions

B.M.Z., N.L.M., KE.R., S.H., and S.J.A. designed the studies. B.M.Z. supervised the project. N.L.M., K.E.R., S.H., and S.J.A. performed experiments and analyzed the data. N.L.M., M.S.A., S.J.A., and B.M.Z. wrote and edited the manuscript.

Editor: Jason Kahn.