Significance tests for R² of out-of-sample prediction using polygenic scores

Summary

The coefficient of determination (R²) is a well-established measure to indicate the predictive ability of polygenic scores (PGSs). However, the sampling variance of R² is rarely considered so that 95% confidence intervals (CI) are not usually reported. Moreover, when comparisons are made between PGSs based on different discovery samples, the sampling covariance of R² is required to test the difference between them. Here, we show how to estimate the variance and covariance of R² values to assess the 95% CI and p value of the R² difference. We apply this approach to real data calculating PGSs in 28,880 European participants derived from UK Biobank (UKBB) and Biobank Japan (BBJ) GWAS summary statistics for cholesterol and BMI. We quantify the significantly higher predictive ability of UKBB PGSs compared to BBJ PGSs (p value 7.6e−31 for cholesterol and 1.4e−50 for BMI). A joint model of UKBB and BBJ PGSs significantly improves the predictive ability, compared to a model of UKBB PGS only (p value 3.5e−05 for cholesterol and 1.3e−28 for BMI). We also show that the predictive ability of regulatory SNPs is significantly enriched over non-regulatory SNPs for cholesterol (p value 8.9e−26 for UKBB and 3.8e−17 for BBJ). We suggest that the proposed approach (available in R package r2redux) should be used to test the statistical significance of difference between pairs of PGSs, which may help to draw a correct conclusion about the comparative predictive ability of PGSs.

R² is a well-established measure for the reliability of polygenic score models although its significance test is rarely considered in this context. We release an R package r2redux that allows formal statistical comparison of two polygenic score models, providing the 95% confidence interval and significance of R² difference.

Introduction

Complex traits are affected by many risk factors including polygenic effects.^1,2,3 Genetic profile analysis can quantify how polygenic effects are associated with future disease risk at the individual and population levels.^4,5 Genetic profiling has potential benefits that can help people make informed decisions when they manage their health and medical care.^6,7,8

Genome-wide association studies (GWASs) have provided an opportunity to estimate genetic profile or polygenic scores (PGSs) that represent individual risk predictions from genetic data.^{4,9,10,11,12,13,14} Typically, the effects of genome-wide single-nucleotide polymorphisms (SNPs) associated with complex traits are estimated in a discovery dataset, which are projected in an independent target dataset. Then, for each individual in the target samples the weighted genotypic coefficients according to the projected SNP effects (i.e., PGSs) are derived and correlated with outcome (trait including affected/unaffected for disease) to quantify the prediction accuracy. The squared correlation or coefficient of determination (R²) is a useful measure to quantify the reliability of the PGS. Note that R² is equivalent to the squared regression coefficient if the dependent and explanatory variables are column standardized.¹⁵

Previously, we introduced a measure of R² on the liability scale that can be comparable across different models and scales¹⁶ when using disease traits or ascertained case-control data. Choi et al.¹² reported that this R² measure on the liability scale outperforms the widely used Nagelkerke pseudo R² in controlling for bias due to ascertained case-control samples. Nagelkerke pseudo R² estimates depend on the proportion of affected individuals in the sample. In contrast, R² on the liability scale does not depend on the proportion of cases in the sample but does require an estimate of the lifetime population prevalence of the disease.

Wand et al.¹¹ suggested that any PGS study should report R² as an indicator of the predictive ability. Choi et al.¹² concluded that R² is a useful metric to measure association and goodness of fit in the interpretation of PGS predictions. Many studies have demonstrated the predictive ability of PGSs, using R².^12,13,17,18 However, the variance of R²¹⁵ has been rarely studied especially in the context of PGSs although it is the crucial parameter for estimation of confidence intervals (CI) of R². Furthermore, estimates of the covariance between a pair of R² values (e.g., from two sets of PGSs) are necessary to assess whether they are significantly different from each other, or if the ratio of two R² values significantly deviates from the expectation. This significance test for the difference or ratio is important when comparing two or multiple sets of PGSs that are derived from different sets of SNPs, e.g., genomic partitioning, genome-wide association p value thresholds (p_T) analysis, or PGSs based on pathway subsets.^19,20

In this study, we use R² measures and their variance-covariance matrix to assess whether the predictive abilities of PGSs based on different sources are significantly different from each other. We derive the variance and covariance of R² values to generate estimates of its 95% CI and p value of the R² difference, considering two sets of dependent or independent PGSs. We also derive the variance and covariance matrix (i.e., information matrix) of squared regression coefficients in a multiple regression model, testing whether the proportion of the squared regression coefficient attributable to SNPs in the regulatory region is significantly higher than expected (i.e., PGS-based genomic partitioning method). We apply this approach to real data to compare PGSs calculated in 28,880 European individuals using UK Biobank (UKBB) and Biobank Japan (BBJ) GWAS summary statistics for cholesterol and BMI.

Material and methods

We used data from the UK Biobank (https://www.ukbiobank.ac.uk), the scientific protocol of which has been reviewed and approved by the Northwest Multi-center Research Ethics Committee, National Information Governance Board for Health & Social Care, and Community Health Index Advisory Group. UK Biobank has obtained informed consent from all participants. Our access to the UK Biobank data was under the reference number 14575.

Publicly available GWAS summary statistics of Biobank Japan (BBJ)^21,22 were used, following BBJ’s guidelines (http://jenger.riken.jp/en/result). The research ethics approval of this study has been obtained from the University of South Australia Human Research Ethics Committee.

PGS models

We use a linear model that regresses the observed phenotypes on a single or multiple sets of PGSs. It is assumed that the phenotypes are already adjusted for other non-genetic and environmental factors (e.g., demographic variables, ancestry principal components), and PGSs are already calculated based on GWAS summary statistics.

A PGS model can be written as

$$\mathbf{y}=\mathbf{X}\mathbf{\beta }+\mathbf{e}$$ (Equation 1)

where y is the vector of standardized phenotypes of trait, X is a column-standardized N × M matrix including M sets of PGS, β is the vector of regression coefficients of X (i.e., PGS), and e is the vector of residuals. For example, with two sets of PGSs (M = 2), X and $\hat{\mathbf{\beta }}$ can be expressed as

$$\mathbf{X}=\left[{\mathbf{x}}_{\mathbf{1}},{\mathbf{x}}_{\mathbf{2}}\right]$$

$$\hat{\mathbf{\beta }}=\left[\begin{array}{c}{\hat{\beta }}_1\\ {\hat{\beta }}_2\end{array}\right]={\left({\mathbf{X}}^{\prime }\mathbf{X}\right)}^{-\mathbf{1}}{\mathbf{X}}^{\prime }\mathbf{y}={\mathbf{\Sigma }}_{\mathbf{22}}^{-\mathbf{1}}{\mathbf{\Sigma }}_{\mathbf{21}}\text{,}$$ (Equation 2)

$$\mathbf{\Sigma }=\left[\begin{array}{cc}\left({\mathbf{\Sigma }}_{\mathbf{11}}\right)& \left({\mathbf{\Sigma }}_{\mathbf{12}}\right)\\ \left({\mathbf{\Sigma }}_{\mathbf{21}}\right)& \left({\mathbf{\Sigma }}_{\mathbf{22}}\right)\end{array}\right]=\left[\begin{array}{cc}\left(\mathbf{1}\right)& \left(\begin{array}{cc}{r}_{y,x_1}& r_{y,x_2}\end{array}\right)\\ \left(\begin{array}{c}{r}_{y,x_1}\\ r_{y,x_2}\end{array}\right)& \left(\begin{array}{cc}\mathbf{1}& r_{x_1,x_2}\\ r_{x_1,x_2}& \mathbf{1}\end{array}\right)\end{array}\right]$$ (Equation 3)

where $r_{y,x_1},r_{y,x_2},\mathrm{a}\mathrm{n}\mathrm{d}{r}_{x_1,x_2}$ are correlations between y and the first PGS (x₁), y and the second PGS (x₂), and between the two PGSs (x₁ and x₂), respectively, in the sample. Using $\hat{\mathbf{\beta }}$ that are estimated in the multiple regression (Equation 2), the predicted phenotypes ($\hat{\mathbf{y}}$) can be obtained as

$$\hat{\mathbf{y}}=\mathbf{X}\hat{\mathbf{\beta }}\text{.}$$

The coefficient of determination for this multiple regression model with $\mathbf{X}=\left[{\mathbf{x}}_{\mathbf{1}},{\mathbf{x}}_{\mathbf{2}}\right]$ in Equation 1 can be written as

$$r_{y,\left(x_1,x_2\right)}^2=1-\frac{\sum _{i=1}^N{\left(y_i-{\hat{y}}_i\right)}^2}{\sum _{i=1}^N{y}_i^2}=\frac{\sum _{i=1}^N{\hat{y}}_i^2}{N}={\hat{\beta }}_1^2+{\hat{\beta }}_2^2+2r_{x_1,x_2}{\hat{\beta }}_1{\hat{\beta }}_2\text{.}$$ (Equation 4)

With a single set of PGSs, i.e., M = 1 and $\mathbf{X}=\left[{\mathbf{x}}_{\mathbf{1}}\right]$ or $\left[{\mathbf{x}}_{\mathbf{2}}\right]$ in Equation 1, the expression of R² can be reduced as

$$r_{y,x_1}^2=\frac{\sum _{i=1}^N{\hat{y}}_i^2}{N}={\hat{\beta }}_1^2\mathrm{w}\mathrm{i}\mathrm{t}\mathrm{h}\mathbf{X}=\left[{\mathbf{x}}_{\mathbf{1}}\right]$$

or

$$r_{y,x_2}^2=\frac{\sum _{i=1}^N{\hat{y}}_i^2}{N}={\hat{\beta }}_2^2\mathrm{w}\mathrm{i}\mathrm{t}\mathrm{h}\mathbf{X}=\left[{\mathbf{x}}_{\mathbf{2}}\right]\text{.}$$

It is noted that $r_{y,\left(x_1,x_2\right)}^2$, $r_{y,x_1}^2$, or $r_{y,x_2}^2$ is an estimate of parameter ${\rho }_{y,(x_1,x_2)}^2,{\rho }_{y,x_1}^2,or{\rho }_{y,x_2}^2$, and each estimate has a sampling variance.

Variance of R²

The distribution of R² can be transformed to a non-central ${\chi }^2$ distribution with mean = M+ $\lambda$ and variance = $2\times (M+2\lambda$) where $\lambda =\frac{N\times R^2}{{\left(1-R^2\right)}^2}$ is the non-centrality parameter. For example, the variance of the transformed value for $r_{y,x_1}^2$ is

$$var\left[{\left(\frac{{\hat{\beta }}_1}{sd\left({\hat{\beta }}_1\right)}\right)}^2\right]=\frac{1}{{var\left({\hat{\beta }}_1\right)}^2}var\left({\hat{\beta }}_1^2\right)=2\left(M+2\lambda \right)\text{.}$$

Therefore,

$$var\left(r_{y,x_1}^2\right)=var\left({\hat{\beta }}_1^2\right)=2{var\left({\hat{\beta }}_1\right)}^2\left(M+2\lambda \right)$$ (Equation 5)

where $var\left({\hat{\beta }}_1\right)=1/N·{\left(1-{\rho }_{y,x_1}^2\right)}^2$, M = 1, and ${\rho }_{y,x_1}^2$ is the squared correlation in the population and can be approximated as ${\rho }_{y,x_1}^2\approx r_{y,x_1}^2$.^23,24

In a similar manner, Equation 5 can be extended to multiple explanatory variables as

$$var\left(r_{y,\left(x_1,x_2,\dots ,x_M\right)}^2\right)\approx 2{\left[\frac{1}{N}·{\left(1-r_{y,\left(x_1,x_2,\dots ,x_M\right)}^2\right)}^2\right]}^2\left(M+2\lambda \right)\text{,}$$ (Equation 6)

that is, Equation 6 is a generalized form of Equation 5.

Wishart²⁵ introduced a formula to obtain the variance of R² (also see Stuart and Ord²⁶ and Olkin and Finn¹⁵) as

$$Var\left(R^2\right)=\frac{\left[4\times R^2\times {\left(1-R^2\right)}^2\times {\left\{N-\left(M+1\right)\right\}}^2\right]}{\left[\left(N^2-1\right)\times \left(N+3\right)\right]}$$

which provides an equivalent estimate as in Equation 6. Wishart²⁵ derived his formula of the variance of R² based on the hypergeometric series that has been used in the literature including Olkin and Finn.¹⁵ We introduce Equation 6 derived based on the transformation of a non-central ${\chi }^2$ distribution. Both Equation 6 and Wishart equation provide identical estimates of the variance of R² (Figure S1). The s.e. of R² estimate is the square root of $var\left(R^2\right)\text{.}$

Variance of the difference between two R² values

Following Olkin and Finn,¹⁵ we use the delta method to estimate the variance of the difference between R² values based on two sets of PGS (x₁ and x₂). Assuming that the difference of R² values can be formulated as a function of the correlations, i.e., $f\left(r_{y,x_1},r_{y,x_2},r_{x_1,x_2}\right)$, the delta method approximates the variance of the difference as

$$var\left(f\right)={\mathbf{\theta }}^{\prime }\mathbf{\Omega }\mathbf{\theta }$$ (Equation 7)

where

$${\mathbf{\theta }}^{\prime }=\left(\frac{\partial f}{\partial r_{y,x_1}},\frac{\partial f}{\partial r_{y,x_2}},\frac{\partial f}{\partial r_{x_1,x_2}}\right)$$ (Equation 8)

is the derivatives of f with respect to the correlations and

$$\mathbf{\Omega }=\left[\begin{array}{ccc}var\left(r_{y,x_1}\right)& cov\left(r_{y,x_1},r_{y,x_2}\right)& cov\left(r_{y,x_1},r_{x_1,x_2}\right)\\ cov\left(r_{y,x_1},r_{y,x_2}\right)& var\left(r_{y,x_2}\right)& cov\left(r_{y,x_2},r_{x_1,x_2}\right)\\ cov\left(r_{y,x_1},r_{x_1,x_2}\right)& cov\left(r_{y,x_2},r_{x_1,x_2}\right)& var\left(r_{x_1,x_2}\right)\end{array}\right]$$

Each element of $\mathbf{\Omega }$ is shown in Olkin and Finn¹⁵ (also see Supplemental Note A).

From Equation 7, the following variances of differences can be estimated and used in our PGS analyses.

R² difference when using different discovery samples to generate the PGS

The variance of R² difference can be written as

$$var\left(r_{y,x_1}^2-r_{y,x_2}^2\right)\mathrm{w}\mathrm{i}\mathrm{t}\mathrm{h}f\left(r_{y,x_1},r_{y,x_2},r_{x_1,x_2}\right)=r_{y,x_1}^2-r_{y,x_2}^2\text{,}$$ (Equation 9)

which allows us to compare two PGS models that are not nested to each other (see R2 difference when using different information sources in results section), for which the conventional log likelihood ratio test cannot be applied.

In Equation 9, the values of $r_{y,x_1}^2-r_{y,x_2}^2$ from random samples in the population are normally distributed when the sample size is sufficient.¹⁵ Assuming that our PGS analysis is sufficiently powered (n > 25,000), the p value for the significance test of the difference can be derived from

$$\frac{{\left(r_{y,x_1}^2-r_{y,x_2}^2\right)}^2}{var\left(r_{y,x_1}^2-r_{y,x_2}^2\right)}\sim {\chi }_1^2$$

and the 95% confidence interval is

$$\left[\left(r_{y,x_1}^2-r_{y,x_2}^2\right)-1.96\sqrt{var\left(r_{y,x_1}^2-r_{y,x_2}^2\right)},\left(r_{y,x_1}^2-r_{y,x_2}^2\right)+1.96\sqrt{var\left(r_{y,x_1}^2-r_{y,x_2}^2\right)}\right]$$ (Equation 10)

When comparisons are made between R² values based on two sets of PGSs (x₁ and x₂), the sampling covariance of R² is required, which is explicitly used in Equations 7 and 9. If the sampling covariance ignored, the test statistics can be biased (Figures S2 and S3).

R² difference when using nested models

When using nested models, the variance of R² difference can be written as

$$var\left(r_{y,\left(x_1,x_2\right)}^2-r_{y,x_2}^2\right)\mathrm{w}\mathrm{i}\mathrm{t}\mathrm{h}f\left(r_{y,x_1},r_{y,x_2},r_{x_1,x_2}\right)=r_{y,\left(x_1,x_2\right)}^2-r_{y,x_2}^2={\hat{\beta }}_1^2+{\hat{\beta }}_2^2+2r_{x_1,x_2}{\hat{\beta }}_1{\hat{\beta }}_2-r_{y,x_2}^2$$ (Equation 11)

where ${\hat{\beta }}_1$ and ${\hat{\beta }}_2$ are the estimated regression coefficients from a multiple regression (Equation 2), calculated from $\mathbf{\Sigma }$ (see Equations 2, 3, and 4). Again, the derivative with respect to each of the correlations can be obtained for this function (Equation 8). Note that the comparison between $r_{y,\left(x_1,x_2\right)}^2$ and $r_{y,x_2}^2$ is equivalent to the log likelihood ratio test (i.e., $\mathbf{y}={\mathbf{x}}_{\mathbf{1}}{\beta }_1+{\mathbf{x}}_{\mathbf{2}}{\beta }_2+\mathbf{e}$ vs. $\mathbf{y}={\mathbf{x}}_{\mathbf{2}}{\beta }_2+\mathbf{e}$).¹⁵

The values of $r_{y,\left(x_1,x_2\right)}^2-r_{y,x_2}^2$ in Equation 11 from random samples in the population follows a non-central chi-squared distribution with a non-centrality parameter $=N\times \frac{r_{y,\left(x_1,x_2\right)}^2-r_{y,x_2}^2}{{\left(1-r_{y,\left(x_1,x_2\right)}^2-r_{y,x_2}^2\right)}^2}$ . The p value for the significance test of the difference can be derived from

$$\lambda \sim {\chi }_1^2$$

and the 95% confidence interval is

$$\left[\left(r_{y,\left(x_1,x_2\right)}^2-r_{y,x_2}^2\right)+\sqrt{var\left(r_{y,\left(x_1,x_2\right)}^2-r_{y,x_2}^2\right)}\frac{{\xi }_{97.5\%}-\lambda -1}{\sqrt{2\left(1+2\lambda \right)}},\left(r_{y,\left(x_1,x_2\right)}^2-r_{y,x_2}^2\right)+\sqrt{var\left(r_{y,\left(x_1,x_2\right)}^2-r_{y,x_2}^2\right)}\frac{{\xi }_{2.5\%}-\lambda -1}{\sqrt{2\left(1+2\lambda \right)}}\right]$$ (Equation 12)

where ${\xi }_{\%}$ is the value at the percentile of the inverse of non-central chi-squared cumulative distribution function with mean = $\lambda +1$ and d.f. = 1.

When the sample size is large, the values of $r_{y,\left(x_1,x_2\right)}^2-r_{y,x_2}^2$ from random samples in the population are normally distributed,¹⁵ and the 95% confidence interval is

$$\left[\left(r_{y,\left(x_1,x_2\right)}^2-r_{y,x_2}^2\right)-1.96\sqrt{var\left(r_{y,\left(x_1,x_2\right)}^2-r_{y,x_2}^2\right)},\left(r_{y,\left(x_1,x_2\right)}^2-r_{y,x_2}^2\right)+1.96\sqrt{var\left(r_{y,\left(x_1,x_2\right)}^2-r_{y,x_2}^2\right)}\right]$$ (Equation 13)

Note that Equations 12 and 13 are equivalent when the sample size is sufficient.¹⁵

R² difference when using two independent sets of PGSs

In this case, there is no correlation structure between two independent sets of PGSs ($r_{x_1,x_2}=0$, e.g., PGSs in male and female individuals), so the variance of R² difference is simply the sum of the variances of each R² value, which can be obtained from Equation 5. For example, assuming $r_{x_1,x_2}=0$, the variance of R² difference can be written as

$$var\left(r_{y_1,x_1}^2-r_{y_2,x_2}^2\right)=2{\left[\frac{1}{N_1}·{\left(1-r_{y_1,\left(x_1\right)}^2\right)}^2\right]}^2\left(1+2{\lambda }_1\right)+2{\left[\frac{1}{N_2}·{\left(1-r_{y_2,\left(x_1\right)}^2\right)}^2\right]}^2\left(1+2{\lambda }_2\right)$$ (Equation 14)

where y₁ and y₂ are the vectors of standardized phenotypes and N₁ and N₂ are the sample sizes for the two independent sets of PGSs. The non-centrality parameters (${\lambda }_1$ and ${\lambda }_2$) for two independent PGSs can be written as

$${\lambda }_1=\frac{N_1\times r_{y_1,x_1}^2}{{\left(1-r_{y_1,x_1}^2\right)}^2}\mathrm{a}\mathrm{n}\mathrm{d}{\lambda }_2=\frac{N_2\times r_{y_2,x_2}^2}{{\left(1-r_{y_2,x_2}^2\right)}^2}\text{.}$$

The p value for the significance test of the difference can be derived from

$$\frac{{\left(r_{y_1,x_1}^2-r_{y_2,x_2}^2\right)}^2}{var\left(r_{y_1,x_1}^2-r_{y_2,x_2}^2\right)}\sim {\chi }_1^2$$

and the 95% confidence interval¹⁵ is

$$\left[\left(r_{y_1,x_1}^2-r_{y_2,x_2}^2\right)-1.96\sqrt{var\left(r_{y_1,x_1}^2-r_{y_2,x_2}^2\right)},\left(r_{y_1,x_1}^2-r_{y_2,x_2}^2\right)+1.96\sqrt{var\left(r_{y_1,x_1}^2-r_{y_2,x_2}^2\right)}\right]$$ (Equation 15)

PGS-based genomic partitioning analysis

It is of interest to test whether a set of PGSs based on a genomic region of interest (or a pathway-based SNP subset) can better predict the phenotypes, compared to the rest of genomic regions. The proportion of the coefficient of determination explained by x₁ can be estimated as ${\hat{\beta }}_1^2/r_{y,\left(x_1,x_2\right)}^2$ from a multiple regression, $y=x_1+x_2+e$, where x₁ is the PGS of a genomic region of interest and x₂ is the PGS of the rest of genomic regions. The expected proportion of the coefficient of determination explained by x₁ can be calculated from prior information, referred to as p_exp = # SNPs used for PGS1/total # SNPs. We are interested in testing whether the value of ${\hat{\beta }}_1^2/r_{y,\left(x_1,x_2\right)}^2$ is significantly different from its expectation, p_exp, which requires to estimate the sampling variance of ${\hat{\beta }}_1^2/r_{y,\left(x_1,x_2\right)}^2$, using Equation 7. The variance of the proportion can be written as

$$var\left({\hat{\beta }}_1^2/r_{y,\left(x_1,x_2\right)}^2\right)\mathrm{w}\mathrm{i}\mathrm{t}\mathrm{h}f\left(r_{y,x_1},r_{y,x_2},r_{x_1,x_2}\right)={\hat{\beta }}_1^2/r_{y,\left(x_1,x_2\right)}^2$$ (Equation 16)

where ${\hat{\beta }}_1$ is the estimated regression coefficient of x₁, calculated from $\mathbf{\Sigma }$ (Equation 3), and $r_{y,\left(x_1,x_2\right)}^2={\hat{\beta }}_1^2+{\hat{\beta }}_2^2+2r_{x_1,x_2}{\hat{\beta }}_1{\hat{\beta }}_2$ is the coefficient of determination. Therefore, it is possible to get the derivative with respect to each of the correlations, $r_{y,x_1},r_{y,x_2},\mathrm{a}\mathrm{n}\mathrm{d}{r}_{x_1,x_2}$ in Equation 8. This variance can be used to obtain the significance and 95 CI of the observed proportion of the coefficient of determination.

Analogous to Equation 9, the values of $\frac{{\hat{\beta }}_1^2}{r_{y,\left(x_1,x_2\right)}^2}-p_{\mathit{exp}}$ with random samples in the population are asymptotically normal.¹⁵ Using a Wald test, the p value for the significance test of the difference can be derived from

$$\frac{{\left[\left(\frac{{\hat{\beta }}_1^2}{r_{y,\left(x_1,x_2\right)}^2}-p_{\mathit{exp}}\right)\right]}^2}{var\left(\frac{{\hat{\beta }}_1^2}{r_{y,\left(x_1,x_2\right)}^2}-p_{\mathit{exp}}\right)}\sim {\chi }_1^2$$

The 95% confidence interval of the ratio is

$$\left[\left(\frac{{\hat{\beta }}_1^2}{r_{y,\left(x_1,x_2\right)}^2}-p_{\mathit{exp}}\right)-1.96\sqrt{var\left(\frac{{\hat{\beta }}_1^2}{r_{y,\left(x_1,x_2\right)}^2}-p_{\mathit{exp}}\right)},\left(\frac{{\hat{\beta }}_1^2}{r_{y,\left(x_1,x_2\right)}^2}-p_{\mathit{exp}}\right)+1.96\sqrt{var\left(\frac{{\hat{\beta }}_1^2}{r_{y,\left(x_1,x_2\right)}^2}-p_{\mathit{exp}}\right)}\right]$$ (Equation 17)

In addition, the package, r2redux, can provide $var\left({\hat{\beta }}_1^2\right)$, $var\left({\hat{\beta }}_2^2\right)$, and $var\left({\hat{\beta }}_1^2-{\hat{\beta }}_2^2\right)$, i.e., the information matrix of the squared regression coefficients (see Supplemental Note B) that is useful when comparing the actual values of ${\hat{\beta }}_1^2$ and ${\hat{\beta }}_2^2$.

It is noted that the delta method employed in this study is a well-established approach to derive the distribution of a function of an asymptotically normal variable.²⁷ Following Olkin and Finn,¹⁵ we used the delta method to derive the variances of R² and their difference as a function of regression coefficients (Equations 7, 8, 9, 11, and 16). We explicitly checked that the regression coefficients are asymptotically normal, using a realistic correlation structure among variables (Figures S4–S6).

Data

The UK Biobank is a large-scale biomedical database that comprises 0.5 million individuals who had been recruited between 2006 and 2010; their age ranged between 40 and 69 years.^28,29 The data consist of health-related information for samples who are genotyped for genome-wide SNPs. A stringent quality control (QC) process was applied to UKBB data that excludes individuals with non-white British ancestries, mismatched sex between reported and inferred from genotypic information, genotype call rate < 0.95, or putative sex chromosome aneuploidy. The SNP QC criteria filtered out SNPs with an imputation reliability <0.6, missingness >0.05, minor allele frequency (MAF) < 0.01, or Hardy-Weinberg equilibrium p value <10⁻⁷. We also applied a relatedness cut-off QC (>0.05) so that there was no high pairwise relatedness among individuals. After QC, 288,792 individuals and 7,701,772 SNPs were retained.

Discovery GWAS data

Ninety percent of the individuals from the 288,792 QCed individuals were randomly selected as discovery samples (n = 259,912 to generate GWAS summary statistics (UKBB hereafter) for the 7,701,772 SNPs.. For the GWAS with the 259,912 UKBB discovery samples, we used BMI and cholesterol that were adjusted for age, sex, birth year, Townsend Deprivation Index (TDI), education, genotype measurement batch, assessment center, and the first 10 ancestry principal components using a linear regression.

We also have access to Japanese Biobank (BBJ) (http://jenger.riken.jp/en/result) GWAS summary statistics (BBJ hereafter) for BMI²¹ (n = 158,284) and cholesterol²² (n = 128,305) for 5,961,601 SNPs.

Target data

Ten percent of the individuals from the 288,792 QCed individuals were randomly selected as an independent target dataset (n = 28,880) that were non-overlapping and unrelated with the UKBB and BBJ discovery samples. In the PGS analyses, we used only 4,113,630 SNPs that were common between UKBB and BBJ GWAS data after excluding ambiguous SNPs and SNPs with any strand issue.

In the target dataset (n = 28,880), the phenotypes of each trait were adjusted for age, sex, birth year, TDI, education, genotype batch, assessment center, and the first 10 principal components using a linear regression. The pre-adjusted phenotypes were correlated with PGSs estimated in the following step. For each trait, we used the UKBB and BBJ GWAS summary statistics to estimate two sets of PGSs (UKBB PGSs vs. BBJ PGSs for the 28,880 target individuals ), using PLINK2 (https://www.cog-genomics.org/plink/2.0/) with the score function.³⁰ Then, we estimated the correlation between the PGS and pre-adjusted phenotypes to obtain R² values in the PGS analyses.

Functional annotation of the genome

We annotated the genome using pre-defined functional categories (regulatory vs. non-regulatory genomic regions).³¹ Regulatory region includes SNPs from coding regions, untranslated regions (UTRs), and promotors. Non-regulatory region includes all the other regions except the regulatory region. The number of SNPs belong to regulatory and non-regulatory is 158,653 and 3,954,947 (i.e., 4% of the total SNPs are located in the regulatory region).

Simulation of dependent and explanatory variables

For a quantitative trait, we simulated dependent variable (y) and PGSs (x₁ and x₂), varying the correlation structure of $\left[\begin{array}{ccc}1& r_{y,x_1}& r_{y,x_2}\\ r_{y,x_1}& 1& r_{x_1,x_2}\\ r_{y,x_2}& r_{x_1,x_2}& 1\end{array}\right]$ and the sample size (detailed simulation parameters are shown in Figures S7–S15). For a disease trait, the same simulation procedure was used, and the simulated quantitative phenotypes were transformed to binary responses using a liability threshold model with a population prevalence of k = 0.05. For example, case-control status was assigned to individuals according to their standardized quantitative phenotypes (i.e., liability), i.e., cases have liability greater than a threshold such that the proportion of cases is k = 0.05. The empirical variances of $r_{y,x_1}^2$, $r_{y,x_1}^2-r_{y,x_2}^2$, $r_{y,\left(x_1,x_2\right)}^2-r_{y,x_2}^2$, and $\frac{{\hat{\beta }}_1^2}{r_{y,\left(x_1,x_2\right)}^2}-p_{\mathit{exp}}$ were obtained over 10,000 replicates, which were compared to the theoretical variances estimated using Equations 6, 9, 11, and 17, respectively.

Results

Simulation verification

The theory of the proposed method has been explicitly verified using simulations, varying sample size, and values of $r_{y,x_1}^2$, $r_{y,x_1}^2-r_{y,x_2}^2$, $r_{y,\left(x_1,x_2\right)}^2-r_{y,x_2}^2$, and $\frac{{\hat{\beta }}_1^2}{r_{y,\left(x_1,x_2\right)}^2}-p_{\mathit{exp}}$ (Figures S7–S15). The empirical variances obtained from 10,000 simulated replicates are almost perfectly correlated with the theoretical variance for the values of $r_{y,x_1}^2$, $r_{y,x_1}^2-r_{y,x_2}^2$, $r_{y,\left(x_1,x_2\right)}^2-r_{y,x_2}^2$, $\frac{{\hat{\beta }}_1^2}{r_{y,\left(x_1,x_2\right)}^2}-p_{\mathit{exp}}$ when varying the sample size (Figures S7–S10) and when varying R² values (Figures S11–S14). When considering two independent PGSs, the theoretical and empirical variances are also agreed well (Figure S15).

R² difference when using different information sources: UKBB vs. BBJ

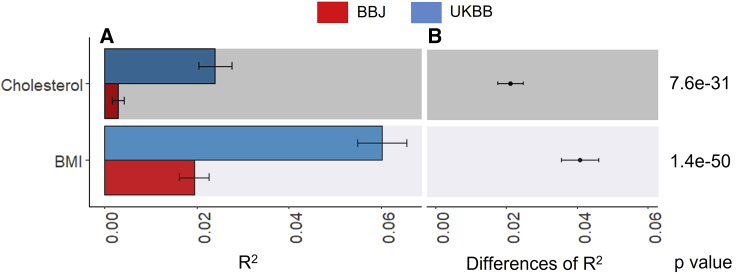
It is of interest to determine whether different information sources (e.g., ancestries) have significantly different predictive abilities in PGS analyses, which can be assessed using Equations 9 and 10. Figure 1 illustrates that when predicting the 28,880 European target samples, the coefficient of determinations (R²) with the UKBB and BBJ PGSs were 0.024 (95% CI = 0.021–0.028) and 0.003 (95% CI = 0.002–0.004), respectively, for cholesterol. However, these R² values and CIs cannot be used to assess their difference because the two sets of PGSs are not independent. Furthermore, the two PGS models with UKBB and BBJ are not nested to each other, so the likelihood ratio test could not be used either. For this problem, we used Equations 9 and 10 to obtain the variance, 95% CI (0.0175–0.0247), and p value (7.6e−31) of the R² difference, accounting for the dependency between UKBB and BBJ PGSs, for cholesterol (Figure 1). Similarly, the test statistics of the R² difference was obtained for BMI, 0.035–0.046 for 95% CI and p value = 1.4e−50 (Figure 1).

Figure 1.

The predictive ability (R²) of PGSs when predicting 28,880 European individuals using UKBB or BBJ discovery GWAS dataset

(A) The main bars represent R² values and error bars correspond 95% confidence intervals. Two sets of GWAS summary statistics were obtained from UKBB and BBJ discovery GWAS datasets to estimate two sets of PGSs.

(B) Dot points represent the differences of R² values between UKBB and BBJ PGS models, and error bars indicate 95% confidence intervals of the difference.

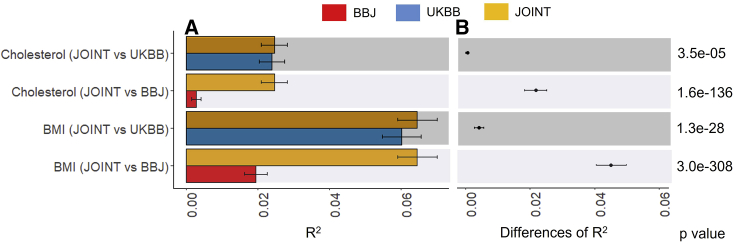
It is also interesting to whether BBJ PGSs provides a significant improvement in the predictive ability, in addition to UKBB PGSs, when predicting the 28,880 European target samples. Figure 2 compares R² value with each UKBB or BBJ PGSs to R² value from a joint model fitting UKBB and BBJ PGSs simultaneously. Using Equations 11 and 12, we acquired the variance, 95% CI (0.0001–0.001), and p value (3.5e−05) of R² difference when comparing the joint model with a single model with UKBB, indicating that BBJ PGSs contributed to a significant improvement for cholesterol. Similarly, BBJ PGSs improved the predictive ability significantly (p value = 1.3e−28) for BMI. As expected, excluding UKBB PGSs from the joint model substantially decreased the prediction accuracy (p value = 1.6e−136 for cholesterol and 3.0e−308 for BMI).

Figure 2.

The predictive ability (R²) of a PGS model based on UKBB or BBJ discovery dataset, compared to the joint model of both UKBB and BBJ when predicting 28,880 European individuals

(A) The main bars represent R² values and error bars correspond 95% confidence intervals. Two sets of GWAS summary statistics were obtained from UKBB and BBJ discovery GWAS datasets to estimate two sets of PGSs, i.e., UKBB and BBJ PGSs. In addition, a joint model fitting both UKBB and BBJ PGSs was compared.

(B) Dot points represent the differences of R² values between the joint model and UKBB or BBJ PGS model, and error bars indicate 95% confidence intervals of the difference.

R² difference when using two independent sets of PGSs: male vs. female

We were also interested in testing whether the PGSs could predict the adjusted phenotypes of the target individuals equally well for males and females. In this case, there is no correlation structure between male and female PGSs, so the variance of R² difference is simply the sum of the variances of each R² value, which can be obtained from Equation 5 or 6. Figure S16 shows that there was no significant difference between male and female PGSs in their predictive ability for cholesterol and BMI whether using UKBB or BBJ discovery GWAS dataset.

PGSs with genome-wide association p value thresholds (p_T)

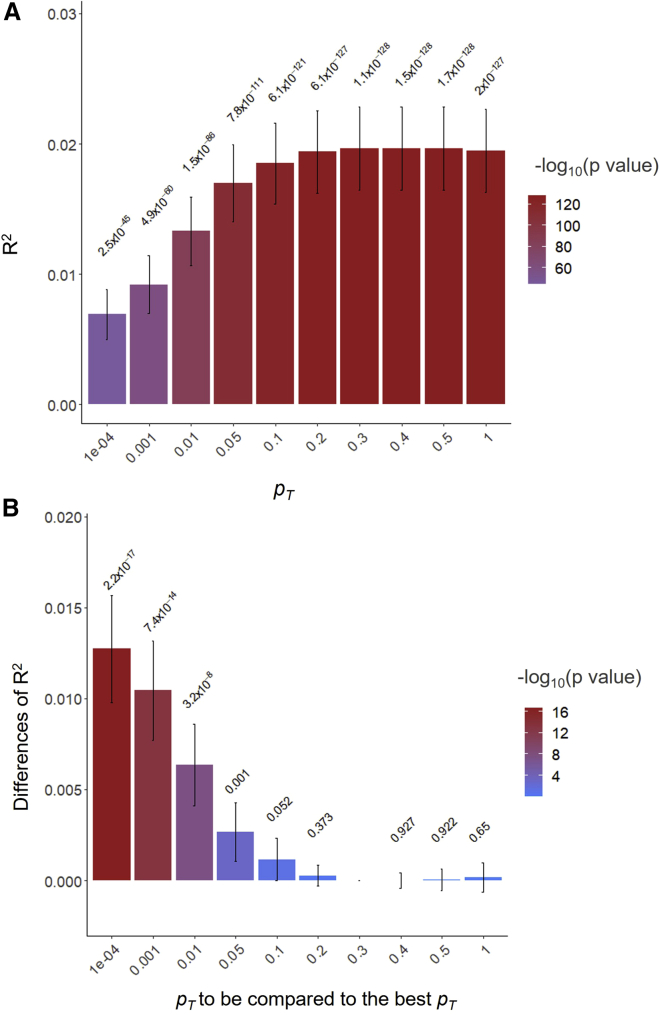
PGSs also have been widely used to determine which p_T provides the highest prediction accuracy, for example, using PGS software such as PLINK.^30,32 However, there is a lack of test statistics that can assess whether the predictive ability of the best-performing p_T is significantly different from the other p_T. Figure 3A illustrates that R² value is the highest at p_T = 0.3 when predicting 28,880 European individuals in the target dataset, using BBJ discovery GWAS dataset (BMI). However, it is not clear if the predictive ability at p_T = 0.3 is significantly higher than the adjacent p_T (e.g., p_T = 0.2 or 0.4), and it may be important to report p_T of which the predictive ability is not statistically different from the best-performing p_T. Using Equations 9 and 10, we assessed the significance of difference between the best-performing p_T and each of the other p_T (Figure 3B). From this analysis, we found that the best-performing p_T was not significantly different from p_T ranging between 0.1 and 1, but significantly different from p_T < 0.05 (Figure 3B). When using the UKBB discovery GWAS dataset to predict the 28,880 European individuals, the highest R² value at the p_T of 1 was significantly different from all the other p_T (Figure S17B).

Figure 3.

The predictive ability (R²) of PGSs estimated based on SNPs below p_T when predicting BMI in 28,880 European samples using BBJ discovery samples (GWAS summary statistics)

(A) The main bars represent R² values and error bars correspond 95% confidence intervals. The values above 95% CIs are p values indicating that R² values are not different from zero.

(B) The main bars represent the difference of R² values between the corresponding p_T and the best-performing p_T and error bars indicate 95% confidence intervals. The values above 95% CIs are p values indicating the significance of the difference between the pairs of R² values.

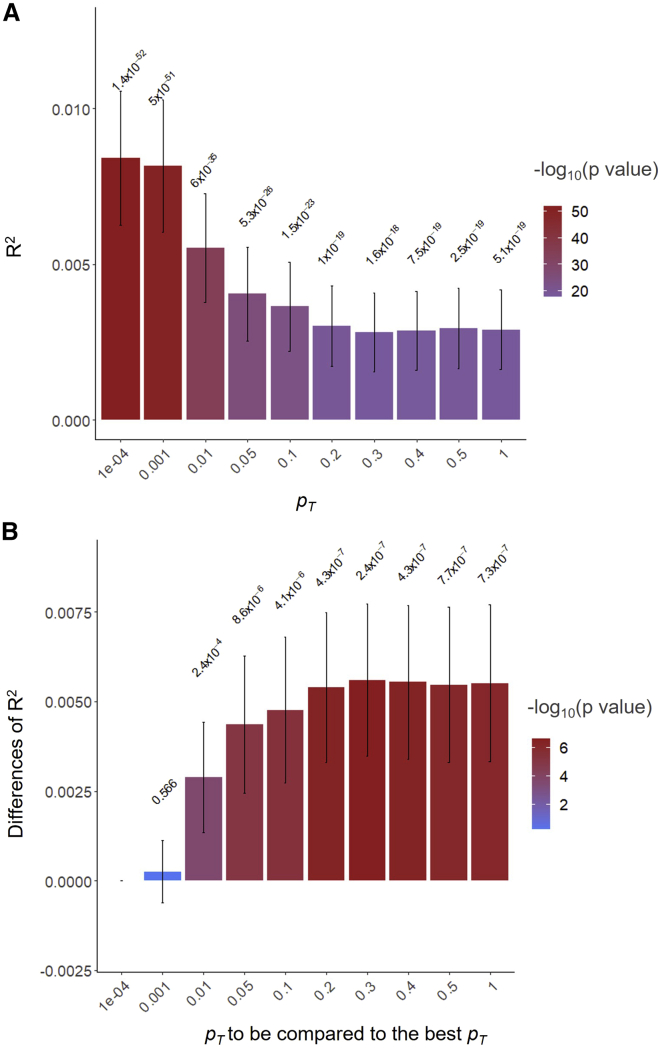
Interestingly, the highest R² value was found at p_T = 1e−04 (Figure 4A) when predicting the European target samples using BBJ discovery GWAS dataset for cholesterol, which was not statistically different from p_T = 0.001 but was significantly higher than the other p_T (Figure 4B). For the same target samples and trait, the best R² value was obtained from p_T = 0.01 when using the UKBB discovery GWAS dataset (Figure S18A). Except for p_T = 0.01, 0.05, and 0.1, R² values at the other p_T were significantly different from the best R² values (Figure S18B).

Figure 4.

The predictive ability (R²) of PGSs estimated based on SNPs below the p_T when predicting cholesterol in 28,880 European samples using BBJ discovery samples (GWAS summary statistics)

(A) The main bars represent R² values and error bars correspond 95% confidence intervals. The values above 95% CIs are p values indicating that R² values are not different from zero.

(B) The main bars represent the difference of R² values between the corresponding p_T and the best-performing p_T and error bars indicate 95% confidence intervals. The values above 95% CIs are p values indicating the significance of the difference between the pairs of R² values.

PGS-based genomic partitioning analyses

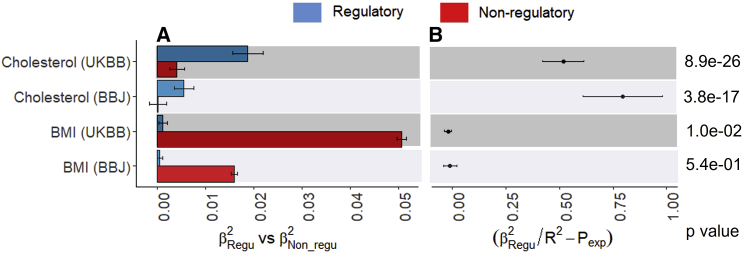
Genomic partitioning analyses have been widely applied.^31,33,34,35 Such analysis could be useful in the PGS context. Using Equation 16, we can estimate the variance of the $\frac{{\hat{\beta }}_{regu}^2}{R^2}$ where ${\hat{\beta }}_{regu}$ is the estimated regression coefficient from a multiple regression (Equation 2), and assess whether the observed proportion ($\frac{{\hat{\beta }}_{regu}^2}{R^2}$ ) is significant different from p_exp (i.e., the coverage of the SNPs belonged to the category). For example, we partitioned the genome-wide SNPs into the regulatory (158,653) and non-regulatory (3,954,947) regions, following Gusev et al.,³¹ resulting p_exp = 4% of SNP coverage for the regulatory region as the expectation. We simultaneously fit two sets of PGSs from regulatory and non-regulatory regions to get ${\hat{\beta }}_{regu}^2$ and ${\hat{\beta }}_{non-regu}^2$, using a multiple regression, then assess whether the value of $\frac{{\hat{\beta }}_{regu}^2}{R^2}-p_{\mathit{exp}}$ is significantly different from zero (Equation 17). Figure 5 shows that the predictive ability of regulatory SNPs was significantly higher than the expectation (p value = 8.9e−26 for UKBB and 3.8e−17 for BBJ) for cholesterol. In contrast, the predictive ability of regulatory SNPs was not better than the expectation for BMI (Figure 5).

Figure 5.

PGS-based genomic partitioning method to assess whether the predictive ability is enriched in the regulatory region for cholesterol and BMI

Here p_exp = 0.04 is the expectation for the regulatory SNPs based on the proportion of SNPs allocated to this annotation.

(A) The main bars represent squared regression coefficients attributable to SNPs in the regulatory region (${\hat{\beta }}_{regu}^2$) and non-regulatory region (${\hat{\beta }}_{non-regu}^2$), and error bars correspond to 95% confidence intervals when predicting 28,880 European samples using UKBB or BBJ GWAS summary statistics.

(B) Dot points represent the difference between the observed and expected proportions ($\frac{{\hat{\beta }}_{regu}^2}{R^2}-p_{\mathit{exp}}$) and error bars indicate 95% confidence intervals of the difference.

Application to binary responses and ascertained case-control data

The proposed method is also explicitly verified using simulation for binary or case-control data, varying sample size and values of $r_{y,x_1}^2$, $r_{y,x_1}^2-r_{y,x_2}^2$, $r_{y,\left(x_1,x_2\right)}^2-r_{y,x_2}^2$, and $\frac{{\hat{\beta }}_1^2}{R^2}-p_{\mathit{exp}}$ (Figures S19–S26). The empirical variances obtained from 10,000 simulated replicates are almost identical with the theoretical variances for the values of $r_{y,x_1}^2$, $r_{y,x_1}^2-r_{y,x_2}^2$, $r_{y,\left(x_1,x_2\right)}^2-r_{y,x_2}^2$, and $\frac{{\hat{\beta }}_1^2}{R^2}-p_{\mathit{exp}}$ when varying the sample size (Figures S19–S22) and when varying R² values (Figures S23–S26). In the case of ascertained case-control, a similar pattern is shown, i.e., the empirically observed variances obtained from 10,000 simulated replicates are agreed well with the theoretical variances for the values (Figures S27–S30). This finding shows that the proposed method can be applied to test the significance of difference between predictive abilities of PGSs for binary traits and ascertained case-control traits when R² is not very high (<0.1). Note that the empirical and theoretical variances diverge when R² values on the observed scale are more than 0.1 for binary responses and ascertained case control (Figures S31 and S32). Although R² value > 0.1 is not frequently observed in the current PGS studies (Table S2), a careful interpretation is required for the variance of such high R², and we would not recommend using the theoretical approximation.

Discussion

R² has been widely used to measure the predictive ability of PGSs.¹³ However, the confidence interval of R² has rarely been reported, and the test statistic for the difference of two R² values has not been well documented. Here, we show how to get the variance of each estimated R² value and covariance between two R² estimates (from two sets of PGSs) that can be used to assess whether they are significantly different from each other.

Martin et al.¹⁸ reported that the PGS prediction accuracy is higher when discovery and target samples are from the same ancestry background, compared to when the samples are from different ancestries. However, they did not formally assess the statistical significance of the increase (no p value provided). More importantly, they did not consider the correlation structure between predictors when they compared two PGSs. We applied the proposed approach and found that the predictive ability of PGSs based on UKBB discovery GWASs is significantly higher than that of PGSs based on BBJ discovery GWASs, by formally deriving the 95% CI and p value of the R² difference.

Many studies evaluating PGSs use the p_T method¹² and report the p_T that maximizes performance. This provides useful information when inferring the genetic architecture of the trait of interest and when fine-tuning p_T as a hyper-parameter in PGS methods.^32,36,37,38 For such cases, it may be crucial to determine if the best-performing p_T is genuinely better than other (adjacent) p_T or if it occurs just by random chance (i.e., sampling error). For example, in Figure 3, the best-performing p_T is 0.3 (the set of SNPs with p_T ≤ 0.3), which is, however, not statistically different from p_T ≤ 0.2 or ≤ 0.1. Note that the set of SNPs with p_T ≤ 0.1 is nested within SNPs with p_T ≤ 0.3, meaning that the additional SNPs in the latter would not significantly improve the prediction accuracy. Therefore, p_T ≤ 0.1 should be used instead of the p_T ≤ 0.3 as the former is a more parsimonious model than the latter. Our proposed approach can formally assess statistical difference among p_T, providing 95% CI of the difference with a significance p value.

We also derived an information matrix of squared regression coefficients in a multiple regression model, establishing a PGS-based genomic partitioning method that could test whether the ratio of two squared regression coefficients is significantly deviated from its expectation given the proportion of SNPs allocated to each partition. This is analogous to the existing genomic partitioning approaches using GREML or LDSC^31,33,34,35 that may have an overfitting issue because SNP effects and genomic partitioning are estimated in the same samples.

In conclusion, we show how to estimate the variance and covariance of R² estimates to quantify the 95% CI and p value of the difference and ratio when comparing two PGSs, which is available in R package r2redux (see Supplemental Note B). We suggest that the proposed approach should be used to test the statistical significance of difference and ratio between pairs of PGSs, which may help to draw a correct conclusion about the predictive ability of PGSs.

Published: January 25, 2023

Data and code availability

The genotype and phenotype data of the UK Biobank can be accessed through procedures described on its webpage (https://www.ukbiobank.ac.uk/) and summary statistics of BMI and cholesterol from Japanese Biobank (BBJ) can be obtained from its website (http://jenger.riken.jp/en/). r2redux can be downloaded from (https://github.com/mommy003/r2redux) or from CRAN [install.packages("r2redux") in R] (also see Supplemental Note B).