Fast, accurate local ancestry inference with FLARE

Summary

Local ancestry is the source ancestry at each point in the genome of an admixed individual. Inferred local ancestry is used for admixture mapping and population genetic analyses. We present FLARE (fast local ancestry estimation), a method for local ancestry inference. FLARE achieves high accuracy through the use of an extended Li and Stephens model, and it achieves exceptional computational performance through incorporation of computational techniques developed for genotype imputation. Memory requirements are reduced through on-the-fly compression of reference haplotypes and stored checkpoints. Computation time is reduced through the use of composite reference haplotypes. These techniques allow FLARE to scale to datasets with hundreds of thousands of sequenced individuals and to provide superior accuracy on large-scale data. FLARE is open source and available at https://github.com/browning-lab/flare.

Local ancestry is the ancestral origin at each point in the genome of an admixed individual. FLARE (fast local ancestry estimation) is a program for local ancestry inference that is highly accurate and computationally efficient. FLARE can analyze array and sequence data and can utilize large reference panels.

Introduction

All humans are admixtures of various historical source populations.¹ This admixture has occurred across a range of timescales, from the recent intercontinental admixture in African Americans and Hispanics^2,3,4 to the ancient admixture with Neanderthals that occurred when modern humans migrated out of Africa around 50,000 years ago.^5,6

Local ancestry is the source ancestry of an individual’s chromosomes at each point in the genome. Local ancestry can be inferred on cross-continental admixtures for recently admixed groups, such as admixed populations in the Americas which have admixed ancestry deriving from indigenous Americans, West Africans, and Western Europeans. With sensitive methods and appropriate reference panels, local ancestry of recent within-continental admixtures with less genetic divergence can also be inferred.⁷ Indeed, some consumer genetics companies now report sub-continental level ancestry.⁸

Inferred local ancestry is required for admixture mapping. Admixture mapping tests for association between local ancestry and phenotype and provides a complementary approach to genome-wide association testing in admixed populations.^9,10 Local ancestry can act as a proxy for a genetic variant that is not well captured by the available SNP-array or sequencing data, such as a structural variant that is difficult to genotype accurately.

Once a variant is found to be associated with a phenotype, local ancestry can be used to investigate the ancestral origin of an allele. For example, an Amerindian-specific variant of ACTN1 is associated with platelet count in US-based Hispanics,¹¹ and an Amerindian-specific variant of BCL2L11 is associated with urine albumin-to-creatinine ratio.¹² In African Americans, two African-specific variants in APOL1 are associated with kidney disease.¹³ Identification of the ancestry of disease-associated variants is helpful for understanding and addressing disparities in disease rates.¹⁴

Local ancestry is also useful for population genetics analyses. Local ancestry segments are used to infer demographic history, including the timing of admixture,¹⁵ the identity of source populations,^15,16 and the effective size of ancestral populations.^17,18 Local ancestry can be used for recombination rate inference^19,20 because changes in ancestry along an individual’s genome represent crossovers that have occurred since admixture. Genomic regions with local ancestry proportions that deviate from the genome-wide average can signal post-admixture selection.^21,22

Increasing amounts of high-coverage whole-genome sequence data are available from diverse and admixed populations.^23,24,25 This presents opportunities, because substantially increasing the number of reference individuals increases the accuracy of local ancestry inference, particularly in resolving ancestries that are less genetically diverged. However, larger reference panels also increase the computational burden.

Given these opportunities and challenges, we developed FLARE, which is based on the Li and Stephens model for haplotype frequencies²⁶ and follows in the footsteps of the HAPMIX and MOSAIC local ancestry inference methods.^7,27 The Li and Stephens model has been widely used for genotype phasing and imputation^{28,29,30,31,32} because it provides high accuracy and it can be combined with powerful computational optimizations.^{28,29,30,31,32,33,34} Its computation time is linear in the number of genetic markers, and after optimization its computation time is approximately linear in the number of individuals.^29,32 Extending this model to incorporate ancestry extends these advantages to local ancestry inference.

HAPMIX pioneered the application of the Li and Stephens model to local ancestry inference. However, we do not compare FLARE with HAPMIX because HAPMIX is limited to two ancestries. Instead, we compare FLARE with MOSAIC, which is a recent method based on the Li and Stephens model that allows for an arbitrary number of ancestries and unknown relationships between reference panels and ancestry. We show that FLARE has better computational performance than MOSAIC and similar accuracy in our simulation scenarios.

Other frameworks for inferring local ancestry are possible. One of the most popular alternative methods for local ancestry inference is RFMix. Rather than utilizing a generative model of haplotype frequencies, RFMix is discriminative and employs a conditional random field.³⁵ We compare our method to RFMix and show that FLARE has better computational performance than RFMix and has superior accuracy in our simulation scenarios.

FLARE incorporates several computational techniques which allow it to scale to enormous datasets while maintaining high accuracy. FLARE performs on-the-fly compression of reference haplotypes and stores checkpoints when calculating probabilities to reduce memory requirements. FLARE constructs composite reference haplotypes to reduce computation time. These techniques are described in subjects and methods.

FLARE is designed to analyze both SNP-array and whole-genome sequence data. Most existing local ancestry inference methods were designed only for SNP-array data. For example, the MOSAIC method was tested using only SNP-array data, and we found that modifications to the program parameters were necessary when analyzing sequence data. FLARE can perform local ancestry inference on sequence data without the information loss that would result from substantial marker thinning.

Subjects and methods

Hidden markov model

FLARE uses a hidden Markov model (HMM). The input data are phased reference haplotypes and phased admixed haplotypes. We use the reference haplotypes to infer local ancestry in one admixed haplotype at a time. Each target admixed haplotype is modeled as an imperfect mosaic of reference haplotypes.^26,27 For a target haplotype, the unobserved state S_m = (i, h) at marker m is comprised of the target haplotype’s ancestry, i, at that position and the donor reference haplotype, h, whose allele is being copied at that position.

We assume that there are A ancestries contributing to the admixed genomes and that these ancestries are represented by the reference haplotypes. The reference data consist of J panels. In our analyses each reference panel is associated with a single ancestry and A = J. Our algorithm for estimating model parameters (see Method S3) assumes this one-to-one matching, but the remainder of the methodology does not require a one-to-one matching of reference panels and ancestries, and one could have J < A, J = A, or J > A. As an example of a case where J < A, one might have two (or more) reference panels representing a single ancestry, such as British and Italian reference panels for European ancestry; keeping these reference panels separate rather than combining them into one allows for different parameters for each of them. The case of J < A could occur if there is no reference panel available for one of the ancestries; in this case it may be possible to choose parameters that would encourage the algorithm to infer that missing ancestry in regions where there is no good match to any of the reference panels, although accuracy may not be overly high in such a scenario.

The number of haplotypes in the j^th reference panel is denoted n_j. The total number of reference haplotypes is $N=\sum _j{n}_j$. We write p_ij for the probability that the donor haplotype is from reference panel j when the target haplotype is from ancestry i.

State transitions between two adjacent marker positions can occur due to crossover events. Crossover events that occur after admixture can change both the ancestry state, i, and the reference haplotype h. Crossover events that occur prior to admixture do not change the ancestry state but can change the reference haplotype h. We model this second class of crossover events using an ancestry-specific switch rate ${\rho }_i$. Ancestry-specific switch rates allow each ancestry to have a different effective population size and a different number of reference haplotypes.

The parameter $\mathit{\mu }$ is a vector of length A giving the overall ancestry proportions of the admixed samples. The component ${\mu }_i$ is the prior probability that an arbitrary position in the genome is derived from ancestry i. Ancestry probabilities sum to one, i.e. ${\sum }_i{\mu }_i=1$. It is assumed that all admixed samples included in the same analysis have similar ancestry proportions. If there are subgroups of admixed individuals with differing demographic histories, each subgroup can be analyzed separately.

Given a target haplotype, the prior probability for the state at any position is defined as follows. First the ancestry i is selected according to the probabilities ${\mu }_i$. Then the reference panel j is chosen according to the probabilities p_ij. Finally, the donor haplotype is chosen randomly from the reference haplotypes for panel j. If h is from panel j, we write q_ih = p_ij/n_j for the probability that the reference haplotype is h when the ancestry is i. Thus, the prior probability that the state is (i,h) is $\pi \left(i,h\right)={\mu }_i{q}_{ih}$.

The parameter T is the number of generations since admixture. The distances between consecutive pairs of crossovers arising in the last T generations are exponentially distributed with mean 1/T Morgans (100/T centiMorgans [cM]).

Any crossover in the past T generations may change the ancestry state. Consider two markers indexed by m − 1 and m and separated by an interval of d_m Morgans. The probability of at least one such crossover occurring in this interval is $1-e^{-d_{m}T}$. When a crossover occurs, a new ancestry is chosen according to the global ancestry probability vector $\mathit{\mu }$. The probability of a transition from ancestry state i to ancestry state i′ is thus ${\mu }_{i^{\prime }}\left(1-e^{-d_{m}T}\right)$ for $i\ne i^{\prime }$.

Changes in the donor reference haplotype h can occur regardless of whether there is a change in the ancestry. If there is no change in ancestry between the two markers, selection of a new donor reference haplotype occurs with probability $1-e^{-d_m{\rho }_i}$, where ${\rho }_i$ is a population-specific switch rate and i is the ancestry state at both markers. If there is a change to ancestry i′ between the two positions, a new donor reference haplotype h is always selected. In either case, the donor reference haplotype in the new state (i′, h′) is selected according to the probabilities $q_{i^{\prime }{h}^{\prime }}$.

The resulting probability $P\left(S_m=\left(i\text{'},h\text{'}\right)|S_{m-1}=\left(i,h\right)\right)$ of transitioning from state (i, h) to state (i′, h′) is given in Method S1.

If the target haplotype’s ancestry is i and the donor haplotype is from reference panel j, the emitted allele is the donor haplotype’s allele with probability $1-{\theta }_{ij}$, and is a different allele otherwise. The ${\theta }_{ij}$ are mismatch rates which model recent mutation, genotype error, and gene conversion.

Let I_m(h) = 1 if the allele at marker m on haplotype h matches the observed allele on the admixed haplotype, and let I_m(h) = 0 otherwise. The emission probability $e_m\left(i,h\right)$ (probability of the data given the HMM state) for the allele at marker m on the admixed haplotype when the state is (i, h) and the reference haplotype h is from reference panel j is

$$e_m\left(i,h\right)={\theta }_{ij}^{1-I_m\left(h\right)}{\left(1-{\theta }_{ij}\right)}^{I_m\left(h\right)}\text{.}$$

Given the parameter values and genetic data, we calculate the posterior probability of ancestry at each marker using hidden Markov model methods, which are described in Method S2. The assigned ancestry is the ancestry with the highest posterior probability.

Estimating parameter values

A user can optionally specify parameter values. If not specified, values for the reference panel probabilities p_ij and the within-ancestry switch rate ${\rho }_i$ are estimated from the reference panels and other parameters are assigned default values as described in Method S3. If the expectation maximization (EM) option is turned on (the default), the values of $\mathit{\mu }$ and T will be updated based on several iterations of the estimation scheme described in Method S3. In the analyses presented in this paper, we use the default initial parameter values and perform EM updating.

If the user wishes to parallelize their analyses by chromosome, we recommend that the user run one autosomal chromosome first, and then use the output model file to specify the analysis parameters for other autosomes. This will reduce computing time and ensures consistency across chromosomes.

Computational techniques

Many computational techniques have been developed that substantially reduce the computation time and memory requirements for genotype imputation. We incorporate several of these techniques in our local ancestry inference method. These techniques include a compressed representation for reference haplotypes in memory,^31,36 the use of a small custom panel of composite reference haplotypes for each admixed haplotype,^30,32,33 and checkpointing of HMM backward probabilities.^37,38

The accuracy of local ancestry inference increases significantly with reference panel size (Figure 1), but large reference panels also increase the computational burden. In genotype imputation the use of a small, custom subset of reference haplotypes for each individual can reduce computation time by one or more orders of magnitude with no loss in accuracy.³³ We have developed a fast method for generating a custom chromosome-length reference panel composed of composite reference haplotypes.³³ Each composite reference haplotype is a mosaic of reference haplotype segments that incorporates long identity-by-descent segments between the reference haplotypes and a target haplotype. We create a custom set of composite reference haplotypes for each target haplotype, and we record the source reference panel for each reference haplotype segment so that the appropriate transition and emission probabilities can be used.

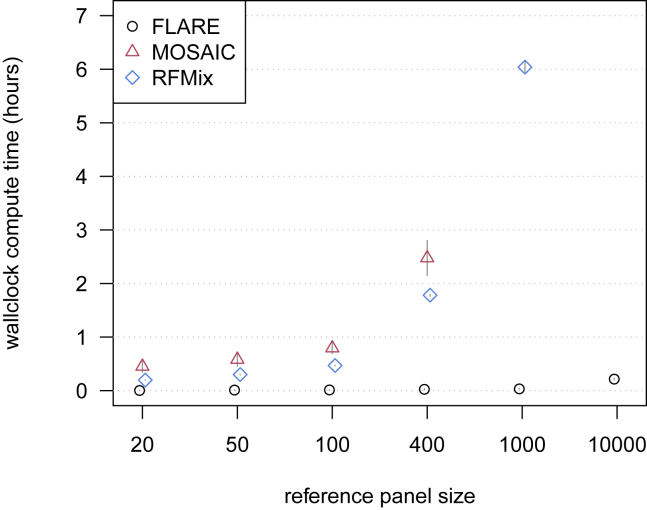
Figure 1.

Computation time for simulated sequence data with three-way admixture

Wallclock computation time in hours is shown on the y axis. Reference panel size for each of the three ancestries is shown on the x axis. Each analysis includes 100 admixed individuals, and results are averaged over four replicate simulations. Error bars (±2 standard errors) are shown as gray lines. Analyses of a simulated chromosome modeled on human chromosome 20 were run with 20 compute threads. MOSAIC could not analyze the data with 1,000 or more individuals per reference panel within the available 384 GB of computer memory. RFMix could not analyze the data with 10,000 individuals per reference panel within 48 h.

We accommodate extremely large reference panels by compressing and storing the phased input data in bref3 format during program execution.³³ This format compresses data for rare variants by storing the indices of haplotypes that carry each rare variant, and it compresses data for other variants by storing the distinct allele sequences in a genomic interval together with an array that maps each haplotype index to its allele sequence.³³ The bref3 format enables an entire chromosome of reference and target haplotypes to be stored in memory and permits rapid lookup of haplotype alleles.

Checkpointing reduces the memory for HMM calculations for M markers from O(M) to $O\left(\sqrt{M}\right)$ by storing forward probabilities at $\sqrt{M}$ checkpoints and re-calculating backward probabilities from the nearest preceding checkpoint when required.^37,38 Since there can be more than a million markers on a chromosome, checkpointing can produce a 1,000-fold reduction in the memory required for HMM calculations, at the cost of a 2-fold increase in computation time.

Marker filtering

FLARE removes the lowest frequency variants before applying the methodology described below. FLARE applies a minimum minor allele frequency (MAF) threshold of 0.005 across the reference individuals. We found that this filter reduces run time without loss of accuracy, particularly for very large datasets. For sequence data, FLARE also imposes a minimum minor allele count threshold of 50, again calculated using the reference individuals. For analyses with small reference panels, this filter effectively reduces the density of the markers, resulting in better model fit and improved accuracy. The minor allele count threshold is not applied to SNP array data because such data already have reduced marker density relative to sequence data.

Simulated data

We simulated genetic data from human out-of-Africa demographic models for three-way and four-way admixture, using modified versions of the AmericanAdmixture_4B11 and OutOfAfrica_4J17 demographic models implemented in stdpopsim v.0.1.2.³⁹ We also simulated two-way admixture for populations with various levels of divergence.

The three-way model¹⁸ extends a model of African, European, and Asian demographic history⁴⁰ to include admixture occurring 12 generations ago. The new admixed population has 1/6 African, 1/3 European, and 1/2 Asian ancestry, an initial size of 30,000, and a growth rate of 5% per generation. We added population growth in the 10 most recent generations to the unadmixed populations, at rates of 19.3% (African population), 10.8% (European population), and 7.8% (Asian population), so that each population grows to approximately 100,000 individuals in order to permit sampling of large reference panels from these populations. We sampled up to 50,000 individuals from each of the three reference ancestries and up to 10,000 admixed individuals (see below for details).

The four-way model extends the demographic history of African, European, Han Chinese, and Japanese populations inferred by Jouganous et al.⁴¹ As above, we added an admixed population occurring 12 generations ago with 15% African, 15% European, 30% Chinese, and 40% Japanese ancestry, an initial size of 30,000, and a growth rate of 5% per generation. In the four-way admixture analyses, we sampled 400 individuals from each of the four reference ancestries and 100 admixed individuals.

The two-way admixture models have an ancestral population of size 10,000 that split a specified number of generations ago (100, 200, 400, 800, 1,600, or 3,200) into two isolated populations of 10,000 each. These split durations lead to F_ST values in the approximate range 0.005–0.15. An admixed population with 30:70 admixture was formed 12 generations ago. We sampled 200 individuals from each of the two reference ancestries and 100 admixed individuals.

We used SLiM⁴² (v.3.7.1) for forward simulation of the most recent 10 × N_e generations, followed by simulation of earlier generations with msprime⁴³ (v.1.1.1) to ensure full coalescence.⁴⁴ We used the HapMap II chromosome 20 recombination map⁴⁵ to simulate data with characteristics similar to human chromosome 20, and we used this map for analysis as well as for simulating the data. For the very largest dataset (three reference panels of 50,000 individuals each and 10,000 admixed individuals), we simulated only the first 40 cM (approx. 17 Mb) of chromosome 20, due to the size of the simulation. We added mutations at a rate of 1.44 × 10⁻⁸ per base pair per generation.⁴¹ During forward simulation, gene conversion was added at a rate of twice the local recombination rate and with a mean tract length of 300 bp.

We constructed multiple datasets with a varying number of sampled individuals and different marker ascertainment schemes. The genetic data for each analysis were generated in three steps: (1) simulation of full demographic history and admixture, (2) site ascertainment, and (3) analysis-specific sampling and site filtering. In the first step, the genotype data were simulated as described above. In the second step, two distinct ascertainment schemes were applied to produce simulated sequence data and simulated array data. For the array data, we removed all sites with mean MAF less than 0.05 in the combined reference populations. For the sequence data, we removed all singletons. In the third step, the datasets were further reduced. After selecting individuals for a specific analysis, variants that were now singletons were removed. If array data had more than 20,000 sites, 20,000 randomly selected sites were retained. Next, we added genotype error to variable sites at a rate of $\epsilon =0.0002$, except at sites with MAF $<2\epsilon$ where the error rate was set to MAF/2 in order to ensure that the error-added data still contain very low frequency variants. Finally, all individuals (reference and admixed) were phased together with BEAGLE 5.4.

For each demographic history, we conducted four independent simulations and applied array and sequence ascertainment to each. This allowed four fully independent replicate analyses for each scenario, with no overlapping individuals or sites.

We inferred local ancestry with FLARE (v.0.3.0), RFMix (v.2.03-r0), and MOSAIC (v.1.3.9). All programs were supplied with the same phased genotype data, genetic map, and reference panels. Parameters affecting the statistical analyses of the programs were kept at default values, except as noted. FLARE was run with posterior probabilities turned on (probs = true) since these were used to assess accuracy and calibration, and analyses of the array data were performed with array = true. For RFMix, 5 EM iterations were requested (-e). For MOSAIC, the number of grid points per cM (-GpcM) was set to the product of 0.0012 and the number of sites in the analysis. We found that this setting greatly improved the accuracy of MOSAIC for sequence data. If a program didn’t report local ancestry at a site, the local ancestry of the closest preceding site was used.

The accuracy of each method was assessed with Pearson’s r² by comparing the inferred and true local ancestry dose. True local ancestry was defined to be the population of residence of the ancestral chromosome segment 20 generations prior to sampling (8 generations prior to admixture). For each ancestry, we summed the local ancestry posterior probabilities for the two haplotypes to obtain an estimated diploid ancestry dose at each site, and we counted the number of copies of the ancestry in the true local ancestry (0, 1, or 2) to obtain the true diploid ancestry dose. We calculated the squared Pearson correlation of the estimated and true diploid ancestry dose across all individuals and sites. Separate r² values were calculated for each ancestry and overall reported values are the unweighted mean r² across all ancestries.

Each method reports posterior probabilities, which may be more or less well calibrated. For example, ideally, 90% of sites assigned 90% posterior probability of having ancestry 1 should actually be ancestry 1 and 10% should be another ancestry. Since the simulated data are statistically phased before inferring local ancestry, we cannot check calibration at the haplotype level, but must instead work at the diplotype level. Ideally, the average true ancestry dose for sites with an estimated diploid ancestry dose of 1.8 should be 1.8. To assess the calibration, we divide the range of possible estimated diploid ancestry doses into bins and obtain the average true dose for each bin.

All analyses were run on a 24 core 2.2 GHz server with 384 GB memory and all local ancestry analyses were multi-threaded across 20 threads. We provide a repository containing all code for the generation and analysis of the simulated data presented here (see web resources).

1000 Genomes and Human Genome Diversity Project data

We downloaded high-coverage sequence data for chromosome 1 from the Human Genome Diversity Project (HGDP) and from the 1000 Genomes Project (see web resources).^24,46 We merged the two datasets and excluded variants that were not bi-allelic SNPs with <1% missingness and at least 5 copies of the minor allele in the combined data. After filtering, 2,021,066 SNPs remain on chromosome 1. We phased the data using Beagle 5.2 with the HapMap GRCh38 map (see web resources).³²

We used the HGDP data for reference panels, assigning panels using the regional labels provided by the HGDP but omitting Oceania due to its smaller size and lack of relevance for the 1000 Genomes data. The panels range in size from 61 (America) to 223 (East Asia). We used FLARE with default settings to infer local ancestry in the 26 populations of the 1000 Genomes project, using a separate analysis for each of these populations. Ancestry proportions were obtained by averaging ancestry calls across sites and individuals.

Results

Simulated data

FLARE has much faster computation times than MOSAIC or RFMix (Figure 1). Compute times for FLARE are relatively insensitive to the reference panel size due to its use of composite reference haplotypes (see subjects and methods). FLARE’s analyses of 100 admixed individuals in the three-way admixture setting with sequence data take less than 2 min on average for reference panel sizes of up to 1,000 per ancestry and an average of 13 min for 10,000 individuals in each of the three reference panels. FLARE’s analysis of 40 cM of data from 10,000 admixed individuals with 50,000 individuals in each of the three reference panels took an average of 35 min.

For the four-way admixture with sequence data, 100 admixed individuals, and 400 individuals in each of the four reference panels, FLARE took an average of 4 min, while RFMix took an average of 273 min. Compute times are expected to scale approximately linearly in the number of admixed individuals for each of the three methods.

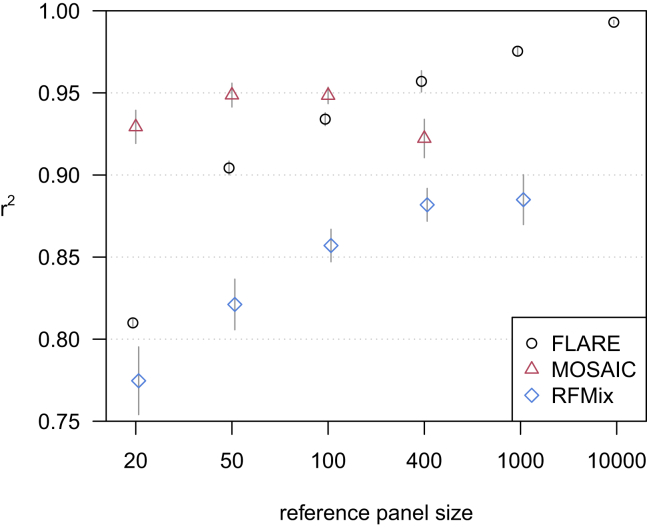
Figure 2 shows accuracy results for the three-ancestry simulation with sequence data. With large reference panel sizes, FLARE is the most accurate method (r² = 0.993 with 10,000 individuals per reference panel). For small reference panel sizes (up to 100 individuals per ancestry), MOSAIC is the most accurate method. For FLARE and RFMix, we see an increase in accuracy with increasing reference panel size.

Figure 2.

Accuracy when increasing reference panel size for simulated sequence data with three-way admixture

The y axis shows squared correlation between true and inferred local ancestry dose averaged over ancestries and across four replicate simulations (details in subjects and methods). Error bars (±2 standard errors) are shown as gray lines. Each of the three ancestries is represented by a reference panel of size shown on the x axis, and each analysis includes 100 admixed individuals. MOSAIC could not analyze the data with 1,000 or more individuals per reference panel within the available 384 GB of computer memory. RFMix could not analyze the data with 10,000 individuals per reference panel within the allotted two days.

With simulated array data instead of sequence data, r² accuracy generally decreases slightly (Figure S1). With the array data as for the sequence data, FLARE has higher r² accuracy than the other two methods for larger reference panel sizes, while MOSAIC has the highest accuracy among the three methods for the smallest reference panel sizes.

Simulation studies typically employ reference panels of equal size for each ancestry, whereas in real analyses some ancestries typically have fewer reference individuals. We thus investigated the accuracy when reference panels have unequal sizes. We found that all three methods performed well, with MOSAIC and FLARE having the highest accuracy performance (Figure S2).

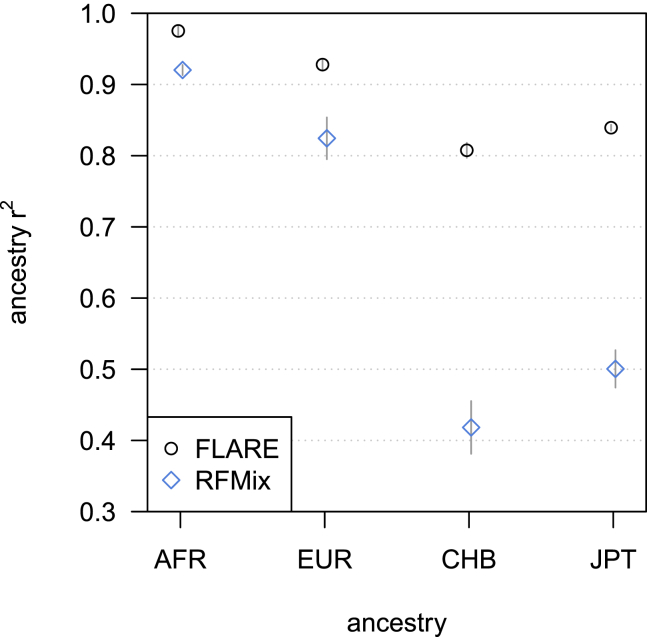
We used the four-ancestry model to assess the ability of the methods to infer local ancestry in situations with less genetic divergence. For the sequence data, we find that FLARE has good resolution to distinguish all four ancestries (r² = 0.888), whereas RFMix’s accuracy is severely reduced (r² = 0.666), with most of this reduction being driven by lower r² for the two Asian ancestries (Figure 3). MOSAIC was excluded from this comparison because it could not analyze the simulated four-ancestry sequence data within the available 384 GB of computer memory. For the array data, FLARE still performs the best (r² = 0.866), with MOSAIC (r² = 0.820) and RFMix (r² = 0.779) being slightly less accurate (Figure S3).

Figure 3.

Accuracy by ancestry for simulated sequence data with four-way admixture

The y axis is the squared correlation between the true and inferred ancestry dose for a single ancestry, averaged across four replicate simulations. Error bars (±2 standard errors) are shown as gray lines. The ancestry is shown on the x axis (AFR is simulated West African, EUR is simulated European, CHB is simulated Han Chinese, JPT is simulated Japanese). The simulated sequence data have 100 admixed individuals and 400 individuals in each of the four reference panels. Results are averaged over four replicate simulations. MOSAIC could not analyze these data within the available 384 GB of computer memory

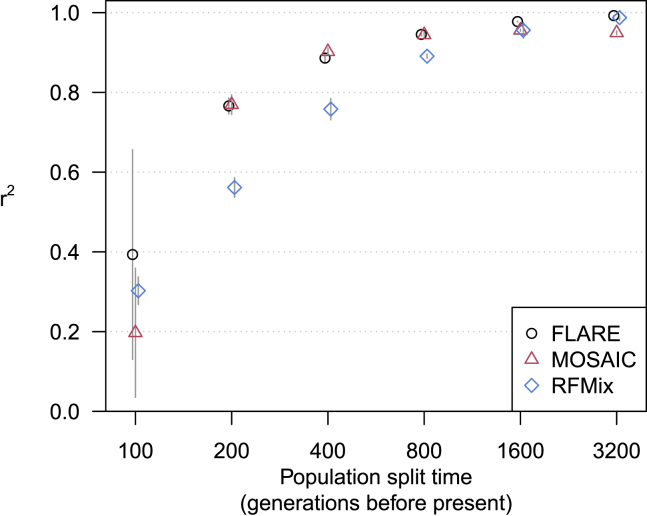
The two-population models include a range of divergence between ancestral populations, with split times ranging from 100 generations ago to 3,200 generations ago. For comparison with human populations, the split time between African and out-of-Africa populations was approximately 4,000 generations ago, while the split time between the Japanese from Tokyo and Han Chinese from Beijing populations was approximately 300 generations ago.⁴¹ All methods have high accuracy for the most diverged ancestral populations (Figure 4). At lower levels of divergence (split times of 200–800 generations ago), FLARE and MOSAIC are most accurate. All methods have difficulty distinguishing the most closely related populations (split time of 100 generations ago).

Figure 4.

Accuracy for simulated sequence data with two-way admixture

The y axis shows squared correlation between true and inferred local ancestry dose averaged over ancestries and across four replicate simulations (details in subjects and methods). Error bars (±2 standard errors) are shown as gray lines. The x axis shows the split time for the two ancestral populations. Each of the three ancestries is represented by a reference panel of size 200, and each analysis includes 100 admixed individuals.

We found that MOSAIC is well calibrated in terms of its reported posterior ancestry probabilities (Figure S4). In contrast, RFMix’s output probabilities are not well calibrated. FLARE’s calibration performance is intermediate and improves with increasing reference panel sizes.

1000 Genomes local ancestry analysis

We inferred local ancestry for each of the 26 populations of the 1000 Genomes Project using six regional reference panels from the HGDP. Estimated ancestry proportions from this analysis are shown in Table 1. Results generally match expectation. For example, the unadmixed African populations are inferred to have 98%–100% African ancestry. Native American ancestry originally derives from Siberia,⁴⁷ which may partially explain the inferred East Asian ancestry in the admixed American populations, although post-colonial migration from Asia may also play a role.⁴⁸ Finns (FIN) are inferred to have 2% East Asian ancestry, which is concordant with previous studies that have found evidence of an Asian contribution to the gene pool in Finns.^49,50 Spaniards (IBS) are inferred to have 2% African ancestry, which matches previous reports of gene flow into southern Europe from North Africa.⁵¹

Table 1.

Inferred ancestry proportions in 1000 Genomes Project chromosome 1 data for six ancestries using HGDP reference panels

Region	Population	African	East Asian	European	Central/South Asian	American	Middle Eastern
Africa	ACBa	0.89∗	0.00	0.10	0.01	0.00	0.00
	ASWa	0.76∗	0.01	0.20∗	0.00	0.03	0.00
	ESN	1.00∗	0.00	0.00	0.00	0.00	0.00
	GWD	0.99∗	0.00	0.01	0.00	0.00	0.00
	LWK	0.98∗	0.00	0.00	0.00	0.00	0.02
	MSL	1.00∗	0.00	0.00	0.00	0.00	0.00
	YRI	1.00∗	0.00	0.00	0.00	0.00	0.00
America	CLMa	0.09	0.01	0.63∗	0.00	0.26∗	0.01
	MXLa	0.06	0.03	0.47∗	0.01	0.44∗	0.00
	PELa	0.04	0.04	0.21∗	0.01	0.69∗	0.00
	PURa	0.16∗	0.01	0.69∗	0.00	0.14∗	0.01
East Asia	CDX	0.00	1.00∗	0.00	0.00	0.00	0.00
	CHB	0.00	1.00∗	0.00	0.00	0.00	0.00
	CHS	0.00	1.00∗	0.00	0.00	0.00	0.00
	JPT	0.00	1.00∗	0.00	0.00	0.00	0.00
	KHV	0.00	1.00∗	0.00	0.00	0.00	0.00
Europe	CEU	0.00	0.00	1.00∗	0.00	0.00	0.00
	FIN	0.00	0.02	0.98∗	0.00	0.00	0.00
	GBR	0.00	0.00	1.00∗	0.00	0.00	0.00
	IBS	0.02	0.00	0.98∗	0.00	0.00	0.00
	TSI	0.00	0.00	1.00∗	0.00	0.00	0.00
South Asia	BEB	0.00	0.00	0.00	1.00∗	0.00	0.00
	GIH	0.00	0.00	0.00	1.00∗	0.00	0.00
	ITU	0.00	0.00	0.00	1.00∗	0.00	0.00
	PJL	0.00	0.00	0.00	1.00∗	0.00	0.00
	STU	0.00	0.00	0.00	1.00∗	0.00	0.00

Ancestry proportions >10% are indicated with an asterisk (^∗). Descriptions of the populations can be found in Supplementary Information Table 1 of the 1000 Genomes Project’s phase 3 paper.⁵²

^aRecently admixed populations from the Americas.

Our initial analyses of chromosome 1 with parameter estimation took 16.6 h (38 min per population on average). Analyses of other chromosomes that use the parameters estimated from the chromosome 1 data would use much less time. For example, when we repeated the chromosome 1 analysis using the parameters estimated in the first analysis, the second analysis took only 2.4 h (6 min per population on average). The first and second analysis produced identical estimated ancestry probabilities, which is expected because the only randomization that occurs within FLARE is in the parameter estimation. Parameter estimation is needed only for one autosomal chromosome, with analyses of the other autosomal chromosomes using the same parameters.

Discussion

We have presented FLARE, a method for local ancestry inference. We showed that FLARE has superior accuracy, computing efficiency, and scalability compared to RFMix and MOSAIC. FLARE was able to analyze a 40 cM simulated chromosome with 10,000 admixed individuals and three 50,000-member reference panels in 35 min on a computer with 24 CPU cores. FLARE’s analysis of simulated chromosome 20 data with 100 admixed individuals and three 10,000-member reference panels took 13 min, while RFMix was unable to complete analysis of these data within two days on the same computer. MOSAIC was even more limited in the data that it could analyze due to memory constraints and was significantly slower than RFMix. Overall, FLARE and MOSAIC had similar accuracy, while RFMix’s accuracy was lower. RFMix utilizes called ancestry from the admixed individuals to augment the reference panels, so it is likely that RFMix’s accuracy would increase with larger numbers of admixed individuals.

A notable feature of the results of the simulation studies is that FLARE can better distinguish ancestries with lower levels of genetic divergence, such as distinguishing between Japanese and Chinese ancestry. In contrast, RFMix had difficulty distinguishing these ancestries. This suggests the potential to accurately infer local ancestry in admixtures that are subtler than the continental-level admixtures that have previously been the focus of attention.

Our model and algorithm borrow heavily from HAPMIX.²⁷ However, there are several significant differences between FLARE and HAPMIX. The two most obvious differences are that FLARE handles multiple ancestries, while HAPMIX is restricted to two, and that FLARE implements a range of computation techniques that are not included in HAPMIX and that allow FLARE to scale to large-scale whole-genome sequence data. In addition, FLARE has a procedure for estimating the matrix of copying probabilities (the p_ij) and the switch rates (the ${\rho }_i$) directly from the reference panel data, while HAPMIX provides an option to estimate all parameters iteratively with an EM approach. Also, HAPMIX allows only for bi-allelic SNPs while FLARE can analyze multi-allelic markers.

FLARE is a user-friendly java program with a command-line interface similar to Beagle.³² When there is a one-to-one matching of ancestries and reference panels, the only input data required by FLARE are phased reference and target VCF files,⁵³ a genetic map file, and a file specifying the reference panel assignment for each reference individual. FLARE outputs a VCF file containing the input genotypes and phased local ancestry calls. As an option, the posterior local ancestry probabilities can also be included in the output VCF file. FLARE also outputs a model file giving the estimated parameters. The model can be used in future analyses of the same study to reduce computing time and ensure consistency between analyses.

FLARE’s user-friendly and robust software implementation, its computational speed and ability to scale to extremely large datasets, and its high accuracy make it a useful tool for local ancestry inference in the increasingly large and diverse genetic data that are being generated.

Published: January 6, 2023

Web resources

1000 Genomes Project high-coverage sequence data, http://ftp.1000genomes.ebi.ac.uk/vol1/ftp/data_collections/1000G_2504_high_coverage/working/20190425_NYGC_GATK/

Beagle, http://faculty.washington.edu/browning/beagle/beagle.html.

HapMap GRCh38 map, http://bochet.gcc.biostat.washington.edu/beagle/genetic_maps/plink.GRCh38.map.zip

Human Genome Diversity Project high-coverage sequence data, ftp://ngs.sanger.ac.uk/production/hgdp/hgdp_wgs.20190516/

msprime, https://github.com/tskit-dev/msprime.

MOSAIC, https://maths.ucd.ie/∼mst/MOSAIC/

Stdpopsim, https://github.com/popsim-consortium/stdpopsim

RFMIX, https://github.com/slowkoni/rfmix.

Supplemental information

Document S2. Article plus supplemental information

Data and code availability

The FLARE software is available from https://github.com/browning-lab/flare. The simulation and analysis pipeline used in this study is available from https://github.com/rwaples/lai-sim.