Construct Identification in the Neuropsychological Battery: What Are We Measuring?

Abstract

Objective:

Major obstacles to data harmonization in neuropsychology include lack of consensus about what constructs and tests are most important and invariant across healthy and clinical populations. This study addressed these challenges using data from the National Neuropsychology Network (NNN).

Method:

Data were obtained from 5,000 NNN participants and Pearson standardization samples. Analyses included variables from four instruments: Wechsler Adult Intelligence Scale, 4^th Edition; Wechsler Memory Scale, 4^th Edition (WMS-IV); California Verbal Learning Test, 3^rd Edition; and Delis-Kaplan Executive Function System (D-KEFS). We used confirmatory factor analysis to evaluate models suggested by prior work and examined fit statistics and measurement invariance across samples. We examined relations of factor scores to demographic and clinical characteristics.

Results:

For each instrument, we identified four first-order and one second-order factor. Optimal models in patients generally paralleled the best-fitting models in the standardization samples, including task-specific factors. Analysis of the NNN data prompted specification of a Recognition-Familiarity factor on the WMS-IV and an Inhibition-Switching factor on the D-KEFS. Analyses showed strong to strict factorial invariance across samples with expected differences in factor means and variances. The Recognition-Familiarity factor correlated with age more strongly in NNN than in the standardization sample.

Conclusions:

Factor models derived from healthy groups generally fit well in patients. NNN data helped identify novel Recognition-Familiarity and Inhibition-Switching factors that were also invariant across samples and may be clinically useful. The findings support efforts to identify evidence-based and optimally efficient measurements of neuropsychological constructs that are valid across groups.

A major challenge for clinical neuropsychology is posed by the diversity of assessment tasks and strategies, hampering our capacity to harmonize and aggregate data at a scale that would enable application of modern psychometric methods to support stronger generalization of results and development of better tests. Flexible assessment approaches are considered important by most clinicians, but the lack of consensus about exactly which neuropsychological constructs are most important and what measurement methods best index those constructs has slowed knowledge and methods development. Neuropsychology has so far lacked infrastructure to aggregate data on a scale that would help overcome these challenges.

The National Neuropsychology Network (NNN), a multi-center, multiple-PI project supported by the NIMH (R01MH118514), was established specifically to promote the use of common data elements and data aggregation to advance the empirical basis of neuropsychological (NP) assessment (see www.nnn.ucla.edu) (Loring et al., 2021). Key aims of the NNN are to leverage advanced psychometric methods to determine the most salient cognitive components of test batteries for use across the heterogeneous diagnostic conditions commonly referred for NP assessment. Four sites (Emory University, Medical College of Wisconsin, University of Florida, and UCLA) are aggregating data from clinical NP batteries and depositing these data at the item level into the NIMH Data Archive, where the results will be available freely to the research community. We have so far enrolled more than 6,400 participants and have item level data available on more than 2,400 participants on some measures.

Because the NNN was designed to aggregate real-world NP data from clinics and does not prescribe a fixed battery of tests, the data reflect the heterogeneity of assessment methods seen in clinical practice. For the analyses reported here, we included tests that are published by Pearson, enabling comparison of our results to prior analyses conducted on the original standardization samples. These included the Wechsler Adult Intelligence Scale, Fourth Edition (WAIS-IV)(Wechsler, 2008a; Wechsler et al., 2008), Wechsler Memory Scale, 4th Edition (WMS-IV; Logical Memory, Visual Reproductions, Verbal Paired Associate Learning)(Wechsler, 2008b), California Verbal Learning Test, 3rd Edition (CVLT3)(Delis et al., 2017); and Delis-Kaplan Executive Function System (D-KEFS; Color-Word Interference, Trail Making, and Verbal Fluency tests)(Delis et al., 2001). Even though our sites employ flexible rather than fixed batteries, we note that the same tests are among the most widely administered not only in our clinics but nationwide, with almost identical measures having been the most popular for more than 15 years (Rabin et al., 2007; Rabin et al., 2016).

The analyses tested the goodness of fit of competing models describing the factor structure of each test or group of tests, based on work originally published in the test manuals (for WAIS-IV and WMS-IV) or published in subsequent work using data from the standardization samples (CVLT3 and D-KEFS). We compared our findings in the NNN clinical samples to findings from the prior analyses of the healthy participants in the Pearson standardization samples. The factor solutions from the Pearson samples have had a strong influence on conceptualizations used widely in clinical neuropsychology. For example, the WAIS-IV Index scores, based on factor analytic studies, are now widely used in clinical interpretation, while Verbal and Performance IQ scores have been abandoned due to lack of psychometric support, despite decades of prior use (Weiss et al., 2010).

While widely used, the existing factor analytic evidence in healthy groups is not definitive. Some factor analytic studies have revealed structures that do not fit well with a priori conceptualizations, and some have shown both low loadings of predicted scores on factors, and high correlations among factors, leading to questions about dimensionality and calling into question how best to understand the precise construct(s) measured by each test.

The factor analytic studies conducted in healthy groups also leave open questions about whether the same factor structures generalize to patient populations or may differ in people with specific brain disorders. Neuropathology is expected to alter covariance among tests relative to that observed in healthy groups. For example, in a cognitively healthy sample, the correlations may be so high between immediate and delayed recall measures that delayed recall may not add much information beyond that provided by immediate recall (Millis et al., 1999; Price et al., 2002). But in samples of patients with mesial temporal lobe dysfunction associated with accelerated long-term forgetting, immediate and delayed recall might emerge as separable factors (Delis et al., 2003). Further factor analytic studies in patient groups have generated interesting results but it has been difficult for most studies to ascertain sufficiently large samples to enable robust analysis (Collinson et al., 2017; Staffaroni et al., 2018). Unfortunately, few studies so far have conducted formal assessments of measurement invariance to determine if the factor structure in clinical groups is the same as that observed in the standardization samples that typically comprise healthy people screened to exclude neuropsychological disorders.

The work presented here reflects an initial step to characterize similarities and differences in the factor structures of NP tests between cognitively healthy participants and patients referred for neuropsychological assessment. This work also provides insight into the number of dimensions that are likely represented in batteries with different numbers of measures and how each test performs psychometrically in the assessment of those dimensions. By using formal assessments of measurement invariance, we aimed to determine how closely the factor structures in our clinical samples follow those observed in the standardization samples. The results of these analyses aimed to inform future development of adaptive versions of widely used test batteries, by first identifying what constructs are being measured in current clinical practice and then assuring that our assumptions about these constructs are justified beyond the standardization samples, in real-world clinical applications.

Method

Participants

Inclusion/Exclusion

Given that this project involved care-as-usual there were no a priori restrictions on inclusion, except that the study included only adults (ages 18 or older) and only those whose primary language was English. Initially we obtained informed consent (for the first 2,138 cases), and during that period we excluded participants if there were concerns about capacity to provide informed consent. Subsequently we received a waiver of informed consent so all clinic patients could be included. For participants older than 89, we coded age as “90+”, consistent with our IRB’s definition of personal identifying information (given the small number of individuals in this age group, those older than 89 might be more readily identified).

Demographic and Clinical Variables

We recorded age, educational attainment, sex, race and ethnicity following protocols developed by the National Human Genome Research Institute’s “PhenX” (phenotypes and genotypes) project (McCarty et al., 2014), and/or that were endorsed by the NIMH as Common Data Elements for demographic variables (Barch et al., 2016). Our coding of educational attainment deviated slightly from that of the PhenX protocol to enable closer matching of our education variable with normative standards that require specification of “years of education.” The code we used for this, and complete data dictionaries for the NNN database, are available online at www.nnn.ucla.edu).

When a new patient is enrolled in the NNN project, their site inputs up to 10 diagnostic entries for “Pre-Exam Diagnoses.” Derived from the referral or the medical record, these are the presumptive diagnoses prior to the NP exam; some of these are non-specific and used primarily for administrative purposes (e.g., ICD-10-CM R41.3, Memory Disorder Not Otherwise Specified). The pre-examination diagnoses were recoded into a series of 10 diagnosis “types” by pooling relevant ICD-10-CM codes. The types identified included: (1) neoplasms; (2) cerebrovascular disorders; (3) seizure disorders; (4) traumatic brain injuries/closed head injuries; (5) anxiety or mood disorders; (6) attention deficit/hyperactivity disorders (ADHD); (7) movement disorders; (8) mild cognitive impairment (MCI); (9) other amnestic syndromes; and (10) other unspecified symptoms and signs. The code specifying which specific diagnostic codes were included in each category are provided in Supplemental Table 2. This study was not preregistered.

Human Subjects

All procedures were conducted with approval from the Institutional Review Boards at each site, using reliance agreements implemented by SmartIRB. The UCLA IRB served as the IRB of record and submitted the master reliance agreement that the other institutions relied upon. Participants are identified by Global Unique Identifiers (GUIDs) or pseudo-GUIDs, as defined by the NIMH. While these identifiers can enable linkage of data for the same person across different studies, personal identifying information cannot be reconstructed from GUIDs or pseudo-GUIDs. Some participants had multiple neuropsychological evaluations during their clinical care; in these cases, results of the first examination only were included for each examinee. An “examination” was operationally defined as a set of tests administered within a period of 30 days, intended to represent a single episode of care.

Measures Included and Analysis Plan

Our analysis plan focused first on confirmatory factor analysis of each instrument¹ to determine if our clinical data fit existing conceptualizations of these measures, mostly based on analyses of findings from the original standardization samples used in the construction of these instruments. We expected that our results might differ from existing data for several reasons, including: (a) our sample was a clinical sample, while the standardization samples specifically excluded individuals with known neuropsychiatric disease; and (b) our samples were assessed using flexible clinic procedures that did not demand administration of every subtest within each battery of tests, reflecting practice standards to administer only selected subtests. In contrast, the standardization datasets included all variables that can be derived from a complete administration of the tests. To be included in our analyses, tests had to have at least 100 observations.

The following subsections describe the target factors and groups of test variables we considered for each instrument. For WAIS-IV, WMS-IV and D-KEFS, each instrument contains multiple subtests, and each subtest yields one or more score. The CVLT3 is one test but generates multiple scores.

WAIS-IV

We tested a series of models based on results presented in the WAIS-IV Technical and Interpretive Manual (Wechsler et al., 2008)(pp 64–73). In the NNN, an adequate number of participants were administered all 10 core subtests, so our analyses attempted to replicate the factor models for the 10 core subtests as described in the WAIS-IV manual. It should be noted, because we did not have all 15 possible subtests from the WAIS-IV, we were unable to evaluate and compare certain models, such as the five-factor model of Benson and colleagues (Benson et al., 2010).

WMS-IV

The WMS-IV was designed to improve upon the factor structure of the WMS-III, given that the index score structure was called into question (see Pearson, 2009, p. 6). The revised structure focused on the Auditory and Visual Memory Index Scores, and on Immediate and Delayed Memory Index Scores, all separately from the Visual Working Memory Index. Our clinics, however, collected sufficient data using only Logical Memory, Verbal Paired Associates, and Visual Reproductions subtests. Therefore, we were able to evaluate only the factor structure of the Auditory Memory Index, had only two of the four indicators for the Visual Memory Index (I.e., VR I and VR II, but not Designs I and Designs II), and for the Immediate and Delayed Memory index scores we had only 3 of the 4 relevant variables for each index (I.e., LM I, VPA I, VR I for Immediate Memory; and LM II, VPA II, and VR II for Delayed Memory). We did collect the recognition memory scores for LM, VPA, and VR. The manual notes that these scores tend to be highly skewed, and no index scores were computed from these. We were interested, however, in examining their psychometric properties relative to the other variables.

CVLT3

Since our clinics administered the CVLT3 in standardized fashion, we had all the variables used in other studies. We examined our data to see how well they would replicate the findings of Donders (Donders, 2008). Donders used 13 CVLT-II variables, similar to those used in prior work on the children’s version (Donders, 1999) and in a clinical sample (Mottram & Donders, 2005). We used the same variables but from the CVLT3: List A Trial 1; List B; Middle region recall; List A, Trial 5; Semantic Clustering; Recall consistency; Short-delay free recall; Short-delay cued recall; Long-delay free recall; Long-delay cued recall; Recognition hits; Total intrusions; and Recognition false positives. Donders used maximum likelihood confirmatory factor analysis to test the goodness of fit for each of four models and found best fit for a solution with four factors, labeled “Attention Span”, “Learning Efficiency”, “Delayed Recall”, and “Inaccurate Recall.”

D-KEFS

Our clinics vary considerably in their use of the D-KEFS subtests and administer other versions of specific tests (e.g., other versions of Trail Making Test, verbal fluency tests, and “Stroop” color-word interference tests). We had more than 100 cases each on the D-KEFS Trail Making, Verbal Fluency, and Color-Word Interference tests. There have been several factor analytic studies of the D-KEFS (Camilleri et al., 2021; Floyd et al., 2006; Karr et al., 2019; Latzman & Markon, 2010). Latzman and Markon (2010) used exploratory factor models to identify D-KEFS structure. Their best-fitting solution included a “Conceptual” factor dependent largely on their inclusion of the Sorting Test, which we did not include. Their solution also included a “Monitoring” factor that had loadings on the switching variables from the Verbal Fluency test, and an “Inhibition” factor with primary loadings on Color Word Inhibition variables and lower loadings on Trail Making Test scores. The D-KEFS Technical Manual also provides information about the correlations among variables within each subtest of the D-KEFS (see pp 55–81). Our ability to replicate these studies was limited by the fact that our clinics collected data on only a subset of all measures rather than the entire D-KEFS instrument. Our analyses were therefore limited to analysis of Verbal Fluency, Trail Making Test, and Color Word Interference test scores. The results from Camilleri et al (2021), who used EFA and machine learning approaches to examine D-KEFS structure, would suggest that we might expect a two-factor solution based on these tests, with one factor reflecting “Inhibition” and loading on both CWI and TMT and another “Fluency” factor. Savla and colleagues (Savla et al., 2012) also found EFA to yield a two-factor solution with “Flexibility” and “Abstraction” components, but we do not include any of the tests that loaded heavily on their Abstraction factor. Most amenable to our data is probably the study of Karr et al (2019) that found best fit for a three-factor model with “Inhibition” (CWI), “Shifting” (TMT) and “Fluency” (fluency scores).

Confirmatory Factor Analysis Methods

For each battery, we specified a series of confirmatory factor analytic models based on prior research, theory, or a combination of the two, following the rationale outlined above for each instrument. We used full information maximum likelihood (FIML) estimation in all models, due to the presence of missing data. FIML estimation uses all available data from all individuals. FIML is an efficient method of estimation and leads to less biased, more accurate estimates of parameters than do other common approaches to handling missing data, such as listwise deletion (Enders & Bandalos, 2001).

To evaluate the fit of factor models to data, we report the standard Chi-Square (χ²) test of model fit. The χ² test is a test of model misfit to the data, so a significant test statistic value provides a statistical basis for rejecting a model. One problem with the χ² statistic is that it is a direct function of sample size. Thus, if sample size is large, model misfit of trivial magnitude may lead to a significant χ² value. Because sample sizes in our NNN data tended to be fairly large, we supplemented the statistical test with a number of practical fit indices, including the comparative fit index (CFI)(Hu & Bentler, 1998), the Tucker-Lewis index (TLI)(Tucker & Lewis, 1973), the root mean square error of approximation (RMSEA) (Browne & Cudeck, 1992), the standardized root mean square residual correlation (SRMR), and the Bayesian information criterion (BIC). To index close fit of a model to data, simulation studies (e.g., Hu & Bentler, 1999) lead to the following recommendations: CFI and TLI values should be .95 or higher, and SRMR values should be less than .08. For the RMSEA, values of .05 or lower indicate close fit, .05 to .08 good fit, .08 to .10 poor fit, and values over .10 indicate unacceptable fit. BIC values do not fall on any standard distribution but have a notable correction for model complexity, and lower values are better, making this useful for comparing models. For additional information on fit indices, see (Hu and Bentler, 1999) and (Widaman & Thompson, 2003).

When reporting fit statistics in later sections, we provide only select indices to avoid unnecessary detail. Tables of model fit with all fit statistics are available in Supplemental Table 5. In addition, we developed confirmatory factor models for each battery based on the NNN data, and then used data supplied by Pearson to replicate our results using the standardization data from each battery, and to perform measurement invariance analyses.

The measurement invariance analyses used multigroup confirmatory factor analysis, with assessment at four levels that are nested hierarchically within each other, as recommended by Widaman and Olivera-Aguilar.

1. The first level, configural invariance, is achieved if the same number of factors are present for each group and the same pattern of fixed and free loading are specified for each group.

2. The second level, referred to as weak factorial invariance, restricts factor loadings to be the same across groups. This has also been referred to as metric invariance or pattern invariance.

3. The third level, referred to as strong factorial invariance, places additional invariance constraints on measurement intercepts. This has also been called scalar invariance. To appreciate this form of invariance in terms of regression of manifest variables on their respective latent variables, weak factorial invariance assures the slopes of these regressions are parallel, while strong invariance implies that the intercepts are also invariant. This level of invariance is important because it helps assure that tests of differences between group means are more easily interpretable because factors are on the same scale.

4. At the fourth and final level, referred to as strict invariance, invariance constraints are also imposed on unique variances, so only the factor means and factor covariance matrices are permitted to vary across groups. If this level of invariance is achieved, differences in group means or variances on manifest variables can be attributed to group differences on the common factors rather than other unknown influences.

For models that satisfied strong or strict invariance criteria, we evaluated differences in means and variances of the factors between the NNN and Pearson samples. These calculations were generally performed after setting factor means to zero and standard deviation to one in the Pearson sample, so that the resulting factor means would represent differences approximately interpretable as Cohen’s d, that is a group difference in standard deviations. If standard deviations differed markedly across groups, we used the SD for the group with greater variance to estimate the group difference.

Finally, although the primary models being evaluated included specification of first-order and second-order factors, following the legacy analyses in the standardization samples, we also evaluated alternative oblique first-order models (i.e., models specifying only first-order factors, and permitting correlations among these factors).

Associations of Factor Scores with Participant Characteristics

We generated factor scores in Mplus using the maximum a posteriori method (using the posterior distribution of latent factor scores given the observed data) to examine relations with selected demographic and clinical variables. It should be noted that these scores are only estimates, and that the correlations of these scores with other variables will not necessarily yield the same result as correlation of the factor with other variables. The standardized factor scores generated by MPlus for the best-fitting models were correlated with age and educational achievement, and group differences in each of the factors were examined by comparing group differences using independent samples t-tests, ANOVAs, or χ² tests, depending on the variables of interest. Given that correlations and tests of group differences were examined across all 20 factors, we used a Bonferroni correction to consider significant only those tests with nominal p < .05/20 = .0025. Demographic and clinical variables examined were: age, education, sex, race, and primary pre-examination diagnosis.

Results

Participant Flow and Test Data Availability

Among the 5,000 individuals who were enrolled in the NNN project, the analyses reported here included results from variable numbers of participants from whom we had data on the variables of interest (as specified above, with n > 100 per variable). Patient characteristics are shown in Table 1. By using the FIML method we were able to include cases with missing data if the cases had at least one non-missing test variable within a given CFA, resulting in estimated sample sizes for WAIS-IV (n = 1,911), WMS-IV (n = 1,635), CVLT3 (657), and D-KEFS (n = 535). We used age-corrected scaled scores except where these were not available, which was true only for the recognition variables of the WMS-IV subtests. Descriptive statistics for all the scores used in our CFAs are shown in Supplemental Table 3. Correlation matrices for these measures, separately for the NNN and Pearson samples, are provided in Supplemental Table 4.

Table 1.

Patient Characteristics

Characteristic	N	Mean (SD)
Age1	5000	57.04 (18.57)
Education2	685	14.82 (2.65)
Characteristic	N	Percent
Sex
Male	2376	47.5%
Female	2615	52.3%
Intersex	3	0.1%
None of these describe me	6	0.1%
Race
White	4014	80.3%
Black	597	11.9%
Asian	103	2.1%
Native Hawaiian/Other Pacific Islander	3	0.1%
Native American/Alaskan Native	16	0.3%
Other	95	1.9%
Unknown	145	2.9%
Prefer Not to Answer/Declined to Specify	27	0.5%
Ethnicity
Hispanic or Latino	176	3.5%
Not Hispanic or Latino	4648	93.0%
Unknown/Missing	176	3.5%

Notes.

¹Age was recoded as 90 for those with age > 89.

²Education was coded using an adaptation of the PhenX Toolkit; a score of 14 indicates an Associate’s Degree and 15 indicates completion of 3 years but not graduating from college (full code available at www.nnn.ucla.edu).

Given that this study does not involve a fixed protocol or battery of tests administered to all participants, we examined cross-tabulations of the tests administered, to characterize clinicians’ preferences in selecting which patients received which tests. Patients receiving the WAIS-IV were highly likely to have WMS-IV tests (Cohen’s weighted kappa = .87), and those receiving CVLT3 were also highly likely to have D-KEFS subtests (kappa = .61). The overlap in administration of WAIS-IV and WMS-IV with CVLT3 and D-KEFS was lower but still common (kappas ranging from .26 to .39).

Recruitment Dates and Data Availability

The patients included in these analyses were enrolled between 08/01/2019 and 10/01/2021. The NNN deposits all available data to the NIMH Data Archive (NDA) and interested researchers may request access at https://nda.nih.gov/get/access-data.html. Data definitions are available on the NDA, and a current data codebook is available at https://www.nnn.ucla.edu/downloads/codebook.pdf.

Missing Data

It is important to note that the data reported here do not represent complete data on all patients who have enrolled in the NNN. As indicated above, the care-as-usual assessment strategy meant that most patients did not have data on all measures. The availability of data depended on: (1) whether tests were administered to the patient; (2) whether results of the tests administered were available in our database. The latter was facilitated for Pearson tests because some of our sites used Q-Interactive extensively, and the NNN project team developed an Application Programming Interface (API) that enabled direct transfer of deidentified Q-Interactive data to the UCLA and NDA servers. The available data underestimates the actual use of these instruments, because some of our participating clinics continued to use paper-pencil administration, and some data from those exams require further data entry. Data may be missing for many reasons, including test selection practices that differ by clinician, clinic, center, and patient factors including their age, education, and level of ability. To our knowledge, missingness was not driven by any systematic factor that would be expected to skew or invalidate the results.

We examined the demographic and clinical characteristics of patients who were included versus those not included in each set of analyses for WAIS-IV, WMS-IV, CVLT3, and D-KEFS, including patients who had one or more score on these instruments. These comparisons are shown in Supplemental Table 5. These analyses revealed that the patients who had these Pearson tests tended to be younger than the rest of enrolled patients. Education level was similar but tended to be slightly lower in the group who had these tests. Males and females were equally represented. There were some differences in race distributions between those who received these tests compared to those who did not, but this varied from test to test. Patients who identified as Hispanic or Latino did not receive these tests as often as others. We examined the distribution of those who had scores on these tests compared to those who did not across sites; the University of Florida had lower rates of administration of these tests relative to their overall enrollment, as clinicians at this site were more likely to favor paper-and-pencil administration.

Factor Analysis Results

The detailed results of our confirmatory factor analyses in the NNN sample are summarized in Supplemental Table 6, for the WAIS-IV, WMS-IV, CVLT3 and D-KEFS variables, respectively. These tables provide the model fit statistics for each of the examined models for each set of test variables. In addition to the models that specify optimal combinations of first-order and second-order factors, which follow from prior literature examples, we also show the fit statistics for models that specify a series of correlated first-order factors. The best fitting models for the NNN sample are presented in Figures 1a-4a, while the best fitting models for the standardization samples are shown in Figures 1b-4b. The fit statistics for the correlated first-order factor results are included in these tables, and in each case the fit statistics for each of the correlated first-order factor models was virtually identical to those for the preferred models with first- and second-order factors.

Figure 1.

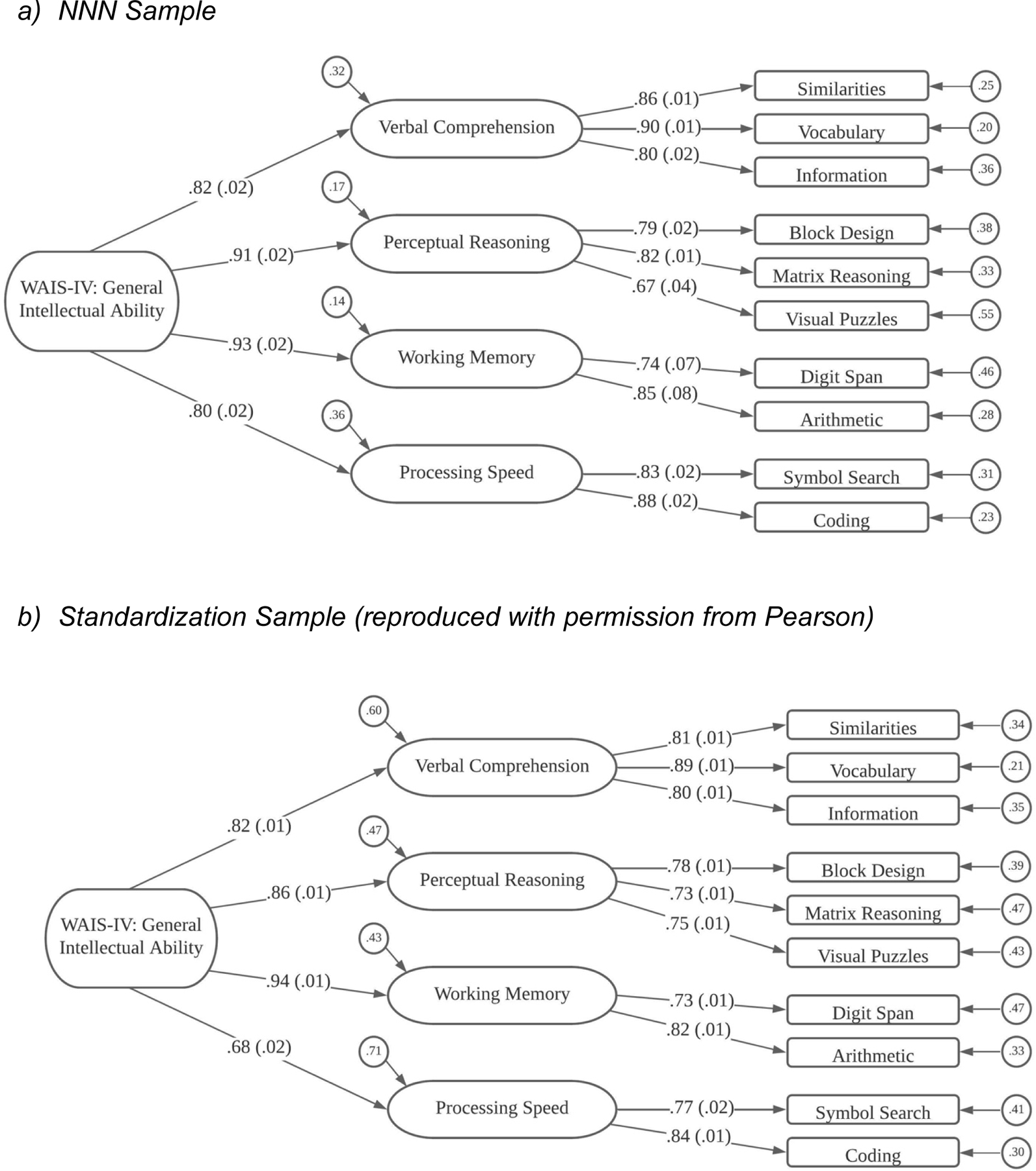
WAIS-IV Structural Model

Figure 4.

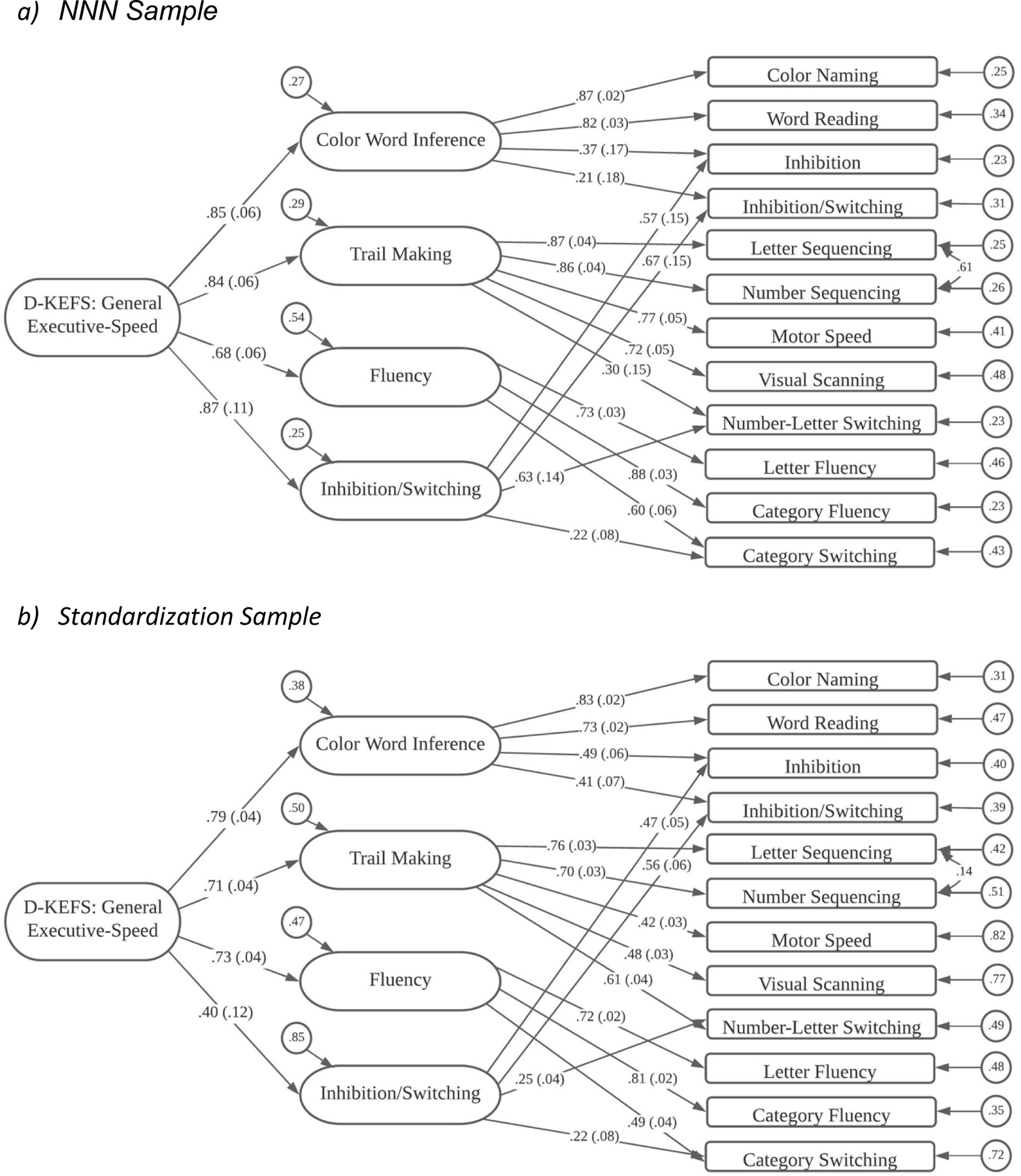
D-KEFS Structural Model

Below we summarize results from the best fitting model for each set of variables. It is worth noting that we used terms that had previously been used to label the factors in this section but have considered alternate labels that we believe may fit the structure better in our figures and discussion.

For each set of results, we also present the primary results of the measurement invariance analyses. Complete results of these analyses are provided in Supplemental Tables 7a (Measurement Invariance Analysis Narrative) and 7b (Factorial Invariance Analysis Tables).

WAIS-IV

NNN Results.

A total of 1,911 Individuals were assessed with subtests from the WAIS-IV so were included in these analyses. Following the models reported in the WAIS-IV technical manual, the first model we fit was a model with a single factor. This model, termed Model 1, had rejectable fit, χ²(35) = 691.59, p < .0001, and poor practical fit to the data, with TLI = .840 and RMSEA = .099.

Model 2 posited the presence of two first-order factors and a second-order factor to account for the correlation between the first-order factors. One first-order factor was a Verbal factor, with subtests from Verbal Comprehension and Working Memory as indicators; and the other first-order factor was a Performance factor, with Perceptual Reasoning and Processing Speed subtests as indicators. Model 2 had better fit than Model 1, χ²(34) = 503.52, p < .0001, but practical fit to the data was still poor, with TLI = .883 and RMSEA = .085.

Model 3 hypothesized the presence of three first-order factors and the second-order factor. One first-order factor was a Verbal Comprehension factor, the second was a Perceptual Reasoning factor, and the third factor had Working Memory and Processing Speed subtests as indicators. Model 3 had improved fit to the data, χ²(32) = 227.56, p < .0001, and practical fit index values of borderline acceptability, with TLI = .948 and RMSEA = .057.

The fourth model, Model 4, was a model that matched the subtest structure of the WAIS-IV, with four first-order factors, one each for Verbal Comprehension, Perceptual Reasoning, Working Memory, and Processing Speed, and then a second-order factor to account for correlations among first-order factors. Model 4 had much improved statistical fit to the data, χ²(31) = 86.24, p < .0001. Although the statistical fit suggested the model was rejectable, the model had very close fit to the data, with TLI = .985 and RMSEA = .031.

Standardized estimates from Model 4 are shown in Figure 1a. As shown in the figure, Similarities (SI), Vocabulary (VC), and Information (IN) subtests loaded on the Verbal Comprehension factor; Block Design (BD), Matrix Reasoning (MR), and Visual Puzzles (VP) loaded on the Perceptual Reasoning factor; Digit Span (DS) and Arithmetic (AR) were indicators on the Working Memory factor; and Symbol Search (SS) and Coding (CD) loaded on the Processing Speed factor. Loadings on the first-order factors were all rather large, ranging from .67 to .90. The second-order factor is an analog of General Intelligence, and all four loadings on the second-order factor were large. The two highest loadings were for Perceptual Reasoning (.914) and Working Memory (.926), but the loadings of Verbal Comprehension (.823) and Processing Speed (.802) were also substantial.

Pearson Results.

As mentioned above, these results are similar to those reported in the WAIS-IV Technical and Interpretive Manual (Wechsler, 2008) from an analysis performed on 2,200 individuals between the ages of 16–90 in the standardization sample. The standardized estimates from the WAIS-IV standardization data are shown in Figure 1b. The factor loadings in the WAIS-IV standardization sample are very close to those obtained in the clinical NNN sample with the exception that in the normative data, the best model allowed Arithmetic to load on both Verbal Comprehension and Working Memory factors.

Measurement Invariance Results.

Starting with the preferred model (see Figure 1), we found the configural and weak factorial invariance models had close fits to the data. When evaluating the strong invariance model, we found poorer fit and modification indices indicated that two intercepts differed across samples (for Information and Block Design subtests). When the invariance constraints were freed on those two intercepts, the resulting partial strong factorial invariance model had much improved fit. In evaluating the fourth, strict factorial invariance model, we continued to allow the intercepts for Information and Block Design to vary across groups, so this model should be called a partial strict invariance model. This model had non-significant loss in fit relative to the partial strong invariance model, and the other indicators (TLI, RMSEA and BIC) were better than any other models considered for the WAIS-IV.

Group differences in factor mean levels are of notable importance in these WAIS-IV analyses, as these were the only model parameter estimates that differed across groups. Relative to the Pearson sample, the NNN sample had a mean on the General factor that was about one-third of a SD lower (M = −0.326, SE = 0.036). Interestingly, the NNN sample exhibited little mean difference from the Pearson sample on the Verbal Comprehension (M = 0.027, SE = .041), and Perceptual Reasoning factors (M = −0.118, SE = 0.044). However, relative to the Pearson sample, the NNN sample had mean levels on the Working Memory and Processing Speed factors that were substantially lower, more than a half standard deviation in magnitude lower (M = −0.598, SE = 0.043 and M = −0.615, SE = 0.046, respectively).

WMS-IV

NNN Results.

For the WMS-IV, 1,635 participants had scores on at least one of the nine scores from this battery that were collected under the NNN protocol. The first model, Model 1, specified a single, general factor, and had poor fit to the data statistically, χ²(27) = 1178.45, p < .0001, and practically, with TLI = .718 and RMSEA = .162.

Based on models presented in the WMS-IV technical manual, we evaluated a second model, which had two first-order factors, Visual and Auditory, and a second-order factor that accounted for their correlation. This Model 2 had much improved statistical fit, χ² (26) = 528.19, p < .0001, but levels of practical fit were still unacceptable, with TLI = .872 and RMSEA = .109.

Our third model posited three first-order factors and the single second-order factor. In this Model 3, the Immediate Recall (I), Delayed Recall (II), and Recognition scores from the Visual Reproduction subtest loaded on a Visual Reproduction factor, and similar specifications were made to define a Logical Memory factor and a Verbal Paired Associates factor. Thus, the three first-order factors were subtest factors. Model 3 had improved fit to the data, χ² (24) = 243.71, p < .0001, and levels of practical fit that neared acceptability, with TLI = .940 and RMSEA = .075.

The fourth and final model fit to the WMS-IV data was largely the same as Model 3 but added a fourth first-order factor that was correlated with the second-order factor. This additional first-order factor had loadings from the recognition tasks from each of the subtests (e.g., Visual Reproduction recognition, Logical Memory recognition, and Verbal Paired Associates recognition). Model 4 also allowed correlated residuals between the Visual Reproduction and Logical Memory immediate recall tasks and between the Visual Reproduction and Logical Memory delayed recall tasks. Model 4 had much improved statistical fit to the data. Although the χ² index was significant, χ² (18) = 51.64, p < .0001 all practical fit indices indicated close fit to the data, with TLI = .988 and RMSEA = .034.

Standardized estimates from Model 4 for the WMS-IV data are shown in Figure 2a. As shown, the Immediate Recall (I), Delayed Recall (II), and Recognition (II) Visual Reproduction indicators loaded on the Visual Reproduction factor; Immediate Recall (I), Delayed Recall (II), and Recognition (II) scores for Logical Memory loaded on the Logical Memory factor; and Immediate Recall (I), Delayed Recall (II), and Recognition (II) variables loaded on the Verbal Paired Associates factor. For the three subtest-related first-order factors – Visual Reproduction, Logical Memory, and Verbal Paired Associates, the immediate recall (I) and delayed recall (II) tasks loaded strongly (ranging between .79 and .97), and the recognition indicators had lower, but not trivial loadings on these factors (ranging between .42 to .54). Then, for the Recognition-Familiarity factor, the loadings were moderate (ranging from .36 to .69). Because of the model specification, the three task-related first-order factors represent the ability to recall the specific items on each of the tests, and the second-order factor is a General Recall factor. The Recognition-Familiarity factor had loadings selectively from the three recognition tasks.

Figure 2.

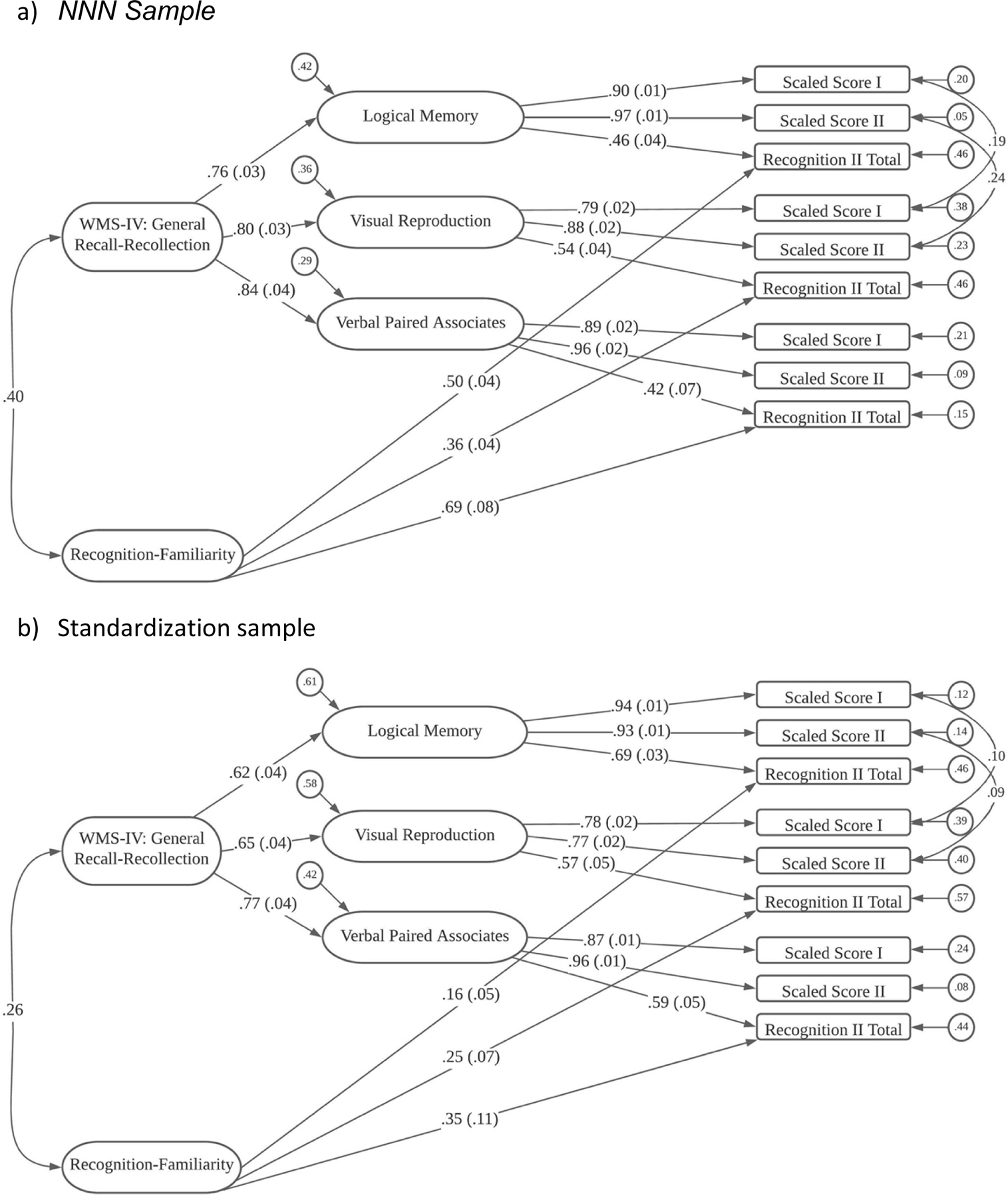
WMS-IV Structural Model

Pearson Results.

The models above were run using the same subtests from 898 individuals in the WMS-IV standardization sample (Wechsler, 2009). These individuals completed the WMS-IV Adult Battery and were between the ages of 16–69. Like the NNN analyses, Model 4 represented the best fit to the normative data, with χ² (18) = 57.44, p < .0001, TLI = .983 and RMSEA = .049. The standardized estimates are shown in Figure 2b. Overall, the loadings are largely similar to those obtained in the NNN clinical sample. One notable exception is that the loadings of the three recognition tasks onto the Recognition-Familiarity factor ranged from .16 to .34, which is substantially lower than the loadings in the NNN clinical sample, which ranged from .50 to 77.

Measurement Invariance Results.

Due to highly skewed distributions of the recognition manifest variables, we used Weighted Least Square Mean and Variance (WLSMV) adjusted estimators rather than ML estimation for these models in Mplus (Suh, 2015). We found that the first two models (configural and weak factorial invariance models) had good fit to the data. The strong factorial invariance model, also fit fairly well and the three measures of practical fit (TLI, RMSEA and SRMR) were essentially unchanged. The strict invariance model fit only slightly worse than the strong invariance model and all the practical fit indices indicated close model fit to the data.

Group differences in factor means and factor variances across groups were present in these WMS-IV analyses. Compared to the Pearson sample, the NNN sample had a large mean difference on the General factor that was about one full SD in magnitude (M = −0.986, SE = 0.075). The NNN sample exhibited similar large differences on the first-order Visual (M = −1.077, SE = .096), Logical Memory (M = −0.897, SE = .085), and Verbal Paired Associates factors (M = −0.983, SE = .126). Because the NNN sample exhibited substantially larger variance on the Recognition-Familiarity factor, we identified the scale of this factor with a mean of 0 and SD of 1.0 in the NNN sample. With this specification, the Pearson (standardization) sample had M = 1.026 (SE = 0.061) and SD = .25. Thus, the Pearson sample scored, on average, about one SD above the NNN sample on this factor and exhibited much less variability.

CVLT3

NNN Results.

As noted previously, we used 13 scores from the CVLT3 to determine whether we could replicate in our NNN data (N = 657) the sequence of models evaluated by Donders (2008). Model 1 for the CVLT3 specified a single, general factor, and this had poor statistical fit, χ² (65) = 654.52, p < .0001, and poor practical fit as well, with TLI = .898 and RMSEA = .117. Model 2 allowed two correlated factors, one identified as Accurate Memory with 11 indicators, and a second labeled Inaccurate Memory with 2 indicators. Although Model 2 had improved fit, its levels of statistical fit, χ² (64) = 577.27, p < .0001, and practical fit – TLI = .909 and RMSEA = .110 -- were still poor.

Model 3 identified three correlated factors, which were labeled Immediate Memory (6 indicators), Delayed Memory (using Donders terminology; 5 indicators), and Inaccurate Memory (2 indicators). Model 3 had improved statistical fit, but fit was still unacceptable, both statistically, χ² (6-) = 431.54, p < .0001, and practically, with TLI = .930 and RMSEA = .097.

Our fourth model (to be described below) was essentially identical to the final, most acceptable model presented by Donders (2008), containing four correlated first-order factors. Model 4 had fit that was similar to fit reported by Donders (2008) in his analyses. In our NNN analyses, Model 4 had a significant test statistic, χ² (56) = 299.84, p < .0001, and practical fit indices that were not as high as for our final WAIS-IV and WMS-IV models, but were acceptable, with TLI = .951 and RMSEA = .081.

Donders (2008) retained as most acceptable his four-factor model but did not pursue the question of a possible second-order factor. Because final models for the WAIS-IV and the WMS-IV based on NNN analyses incorporated a second-order factor, we fit one final model, Model 5, which included a general factor to account for or explain the correlations among the first-order factors. This model had slightly worse statistical fit, χ² (58) = 303.08, p < .0001, but the change in statistical fit was non-significant, Δχ² (2) = 3.24, p =.20, and slightly improved practical fit, with TLI = .951 and the lowest BIC value of any of the models considered (see Supplemental Table 6 for BIC values).

The final form of Model 5 for the CVLT3 is shown in Figure 3a. In this model, List A Trial 1, List B, and middle region recall (Recall Middle) were indicators for an Attention Span factor; List A Trial 5, Semantic Clustering, and Recall Consistency loaded on a Learning Efficiency factor; Short-Delay Free Recall, Long-Delay Free Recall, Short-Delay Cued Recall, Long-Delay Cued Recall, and Recognition Discrimination Hits loaded on the “Delayed Memory” (using Donders’ term) factor; and Recognition False Positives and Total Intrusions were indicators for the Inaccurate Memory factor. Three correlated residuals were estimated: between the Short-Term and Long-Term Free Recall measures, between the Short-Term and Long-Term Cued Recall scores; and between the Recognition Hits and Recognition False Alarms (this last correlated residual was not included in the Donders, 2008, model).

Figure 3.

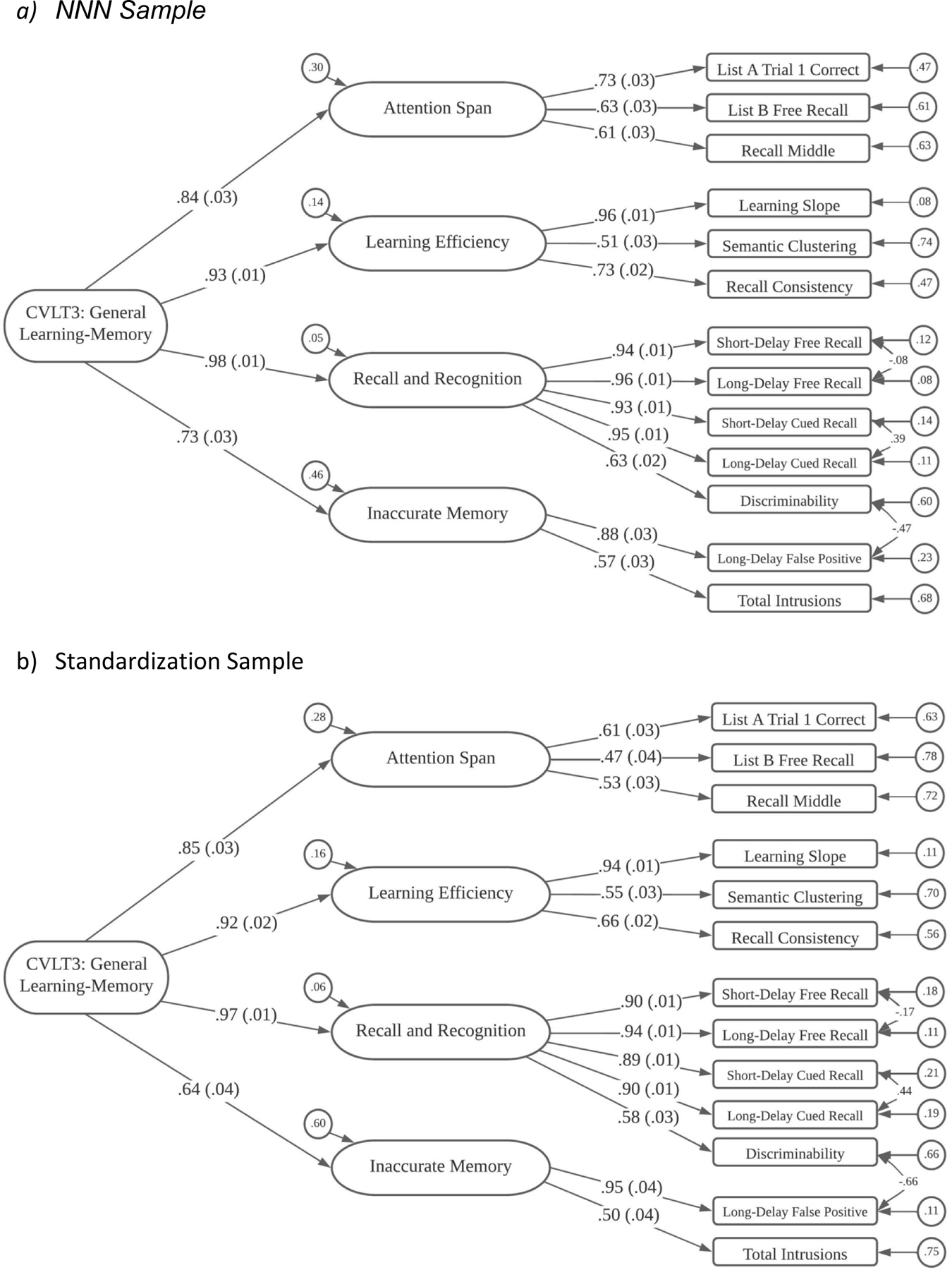
CVLT3 Structural Model

Factor loadings on the first-order factors were moderate to large, ranging from .51 to .94 (median = .73). Loadings on the second-order General factor were even stronger. The loadings for the “Delayed Memory” (.975) and Learning Efficiency (.925) were the strongest, Attention Span had a middling loading (.836), and Inaccurate Memory has the lowest loading (.733).

Pearson Results.

Similar models were run on the CVLT3 standardization sample, which included data from 698 individuals between the ages of 16–90 who were administered the Standard Form. Similar to the NNN sample, Donders (2008) four-factor model yielded a better fit to the data than his other three models. In the Pearson standardization sample, Model 4 yielded a χ² (56) = 234.03, p < .0001, with TLI = .957 and RMSEA = .067. Model 5, which included the general factor accounting for correlations between the first-order factors, was also applied to the CVLT3 standardization data. Like the NNN data, this model did not yield a significantly different fit compared to Model 4, with χ² (58) = 244.22, p < .0001, TLI = .957, and RMSEA = .068. Model 4 is shown in Figure 3b.

Measurement Invariance Results.

The configural and weak factorial invariance models showed good fit to the data, and the strong factorial invariance model showed only a oderate increase in model misfit and slight worsening of practical fit criteria, so modifications were not pursued. The fourth, strict factorial invariance model showed a worsening of statistical model fit but the practical fit indices were improved.

Group differences in factor mean levels were the only model parameter estimates that differed substantially across groups. Relative to the Pearson sample, the NNN sample had a mean on the General factor that was about one-third of a standard deviation lower (M = −0.337, SE = 0.059). The NNN sample had a medium sized differences on the Attention Span factor (M = −0.583; SE = 0.078) and the Inaccurate Memory factor, (M = −0.384, SE = 0.075), and small differences on the Learning Efficiency (M = −0.181, SE = .061) and Delayed Memory factors (M = −0.200, SE = 0.057).

D-KEFS

NNN Results.

For D-KEFS analyses, we had a sample of 535 individuals who had been administered at least one of the subtests. As described above, we had adequate data from just three of the subtests: Color-Word Interference (4 scores), Trail Making Test (5 scores), and Verbal Fluency (3 scores). The D-KEFS technical manual does not provide any factor analytic evidence for the subtests, so we approached our analyses in similar fashion to those for the other batteries. For example, our first model, Model 1, had only a single, general factor. Model 1 had very poor fit to the data, both statistically, χ² (54) = 340.91, p < .0001, and practically, with TLI = .791 and RMSEA = .100.

As a second model, we fit three first-order factors that were specified in a test-based pattern, so all four indicators from the Color-Word Interference test loaded on a Color-Word Interference factor, all five scores from the Trail Making Test loaded on a like-named factor, and the three scores from the Verbal Fluency test loaded on a Verbal Fluency factor. In addition, we retained a second-order factor to explain the correlations among the first-order factors. This model, Model 2, had much improved statistical fit, χ² (49) = 80.45, p = .003, and practical indicating close fit, with TLI = .975.

Because assessment of the ability to deal with tasks involving inhibition or switching is a key aspect of the D-KEFS battery, we engaged in a final model specification to identify an Inhibition-Switching factor. In this model (Model 3; shown in Figure 4a), the major alteration was the addition of an Inhibition-Switching factor that had loadings from the Inhibition and Inhibition-Switching scores from Color-Word Interference, the Number-Letter Switching score from the Trail Making Test, and the Standard version Category Switching from the Verbal Fluency test. This model had very good fit to the data, both statistically, χ² (45) = 54.37, p = .10, and practically, with TLI = .992 and RMSEA = .020.

Standardized estimates from D-KEFS Model 3 are shown in Figure 4a. Factor loadings on first-order factors were quite strong, averaging about .80, except for the rather small loading (.22) for Category Switching on the Inhibition-Switching factor. Loadings on the second-order factor were relatively strong. Interestingly, the loading of the Inhibition-Switching factor (.87) on the General factor was the highest loading among the four first-order factors, but only slightly higher than for two of the other first-order factors.

Pearson Results.

These same models were run on 890 individuals between the ages of 18–89 from the D-KEFS standardization sample. Like the NNN data, Model 1 represented a poor fit statistically, χ² (54) = 938.31, p < .0001, and practically, TLI = .741 and RMSEA = .136. Model 2 was a significantly better fit to the data, with χ² (49) = 195.76, p < .0001, and TLI = .942 and RMSEA = .058. Model 3, which specified an Inhibition-Switching factor, exhibited improved fit to the data, with χ² (45) = 125.10, p < .0001, and TLI = .966 and RMSEA = .045. This model is shown in Figure 4b.

Measurement Invariance Results.

The configural and weak invariance models both showed good fit, but the strong invariance model showed both a decline in statistical fit and much poorer practical fit indices. Modification indices indicated that the intercept for the Motor Speed variable from the Trail Making Test was responsible for the weaker model fit. When the constraints on this intercept were freed, the resulting partial strong invariance model showed improved statistical and practical fit indices. The fourth model, which preserved the freed intercept for Motor Speed from the strong invariance model, and is therefore termed a partial strict invariance model, had improved statistical and practical fit.

Group differences in factor means and factor variances were evident in these D-KEFS models. Relative to the Pearson sample, the NNN sample had a mean on the General factor that was over one-half of a standard deviation lower (M = −0.569, SE = 0.098). The NNN had its lowest mean level on a first-order factor on the Color-Word Interference factor, with M = −0.906 (SE = 0.108). The NNN sample exhibited smaller, but still medium sized mean differences from the Pearson sample on the Trail Making (M = −0.594, SE = .147), Fluency (M = −0.316, SE = .109), and Perceptual Reasoning factors (M = −0.459, SE = 0.135).

Correlated First-Order Factor Models

In addition to the best fitting models in NNN that paralleled models previously specified in the literature, we examined the fit of correlated first-order factor models (see Supplemental Table 6). The fit of these correlated first-order factor models was almost identical to the fit of the best-fitting models that included both first- and second-order factors.

Relations of Factor Scores to Demographic and Clinical Characteristics

Age and Education

The correlations of the twenty best-fitting factor scores with age and educational achievement are shown in Supplemental Table 8.

After Bonferroni correction we found age was correlated significantly with multiple variables from: (1) CVLT3 (including the General, Attention, Learning, Delay, and Inaccuracy factors); (2) WMS-IV (General Recall-Recollection and Recognition-Familiarity factors); and (3) D-KEFS (Verbal Fluency factor). There were no significant correlations with any of the WAIS-IV factors. All significant correlations were negative, indicating poorer performance in older patients, but effects were small (with |r| < .18, except for the Recognition-Familiarity factor from the WMS-IV, which had a correlation with age of r = −.527 (95% confidence interval: .49 - .56). Given this large correlation was observed on a factor derived from subtest scores that were not age corrected, we examined the relations of age with the contributing variables in the standardization sample data, to determine if we could create age-corrected scaled score for these variables even though these are not routinely reported by the Pearson scoring programs. We found the correlations of age with Logical Memory recognition (r = −.02), and with Verbal Paired Associates and Visual Reproductions (r = −.20) were substantially below the 95% confidence interval for the observed correlation of age with Recognition-Familiarity in the NNN sample. As noted in the manual, these recognition test scores are also negatively skewed in the standardization sample. Therefore, we did not attempt to construct age-corrected scores on these measures. We did examine the scatterplot of Recognition factor scores as a function of age and noted an apparent acceleration of age-related decline in patients over the age of 60 (see Figure 5). This impression was corroborated by fitting a quadratic equation to the curve, which increased the shared variance with age from R² = .278 to R² = .372.

Figure 5.

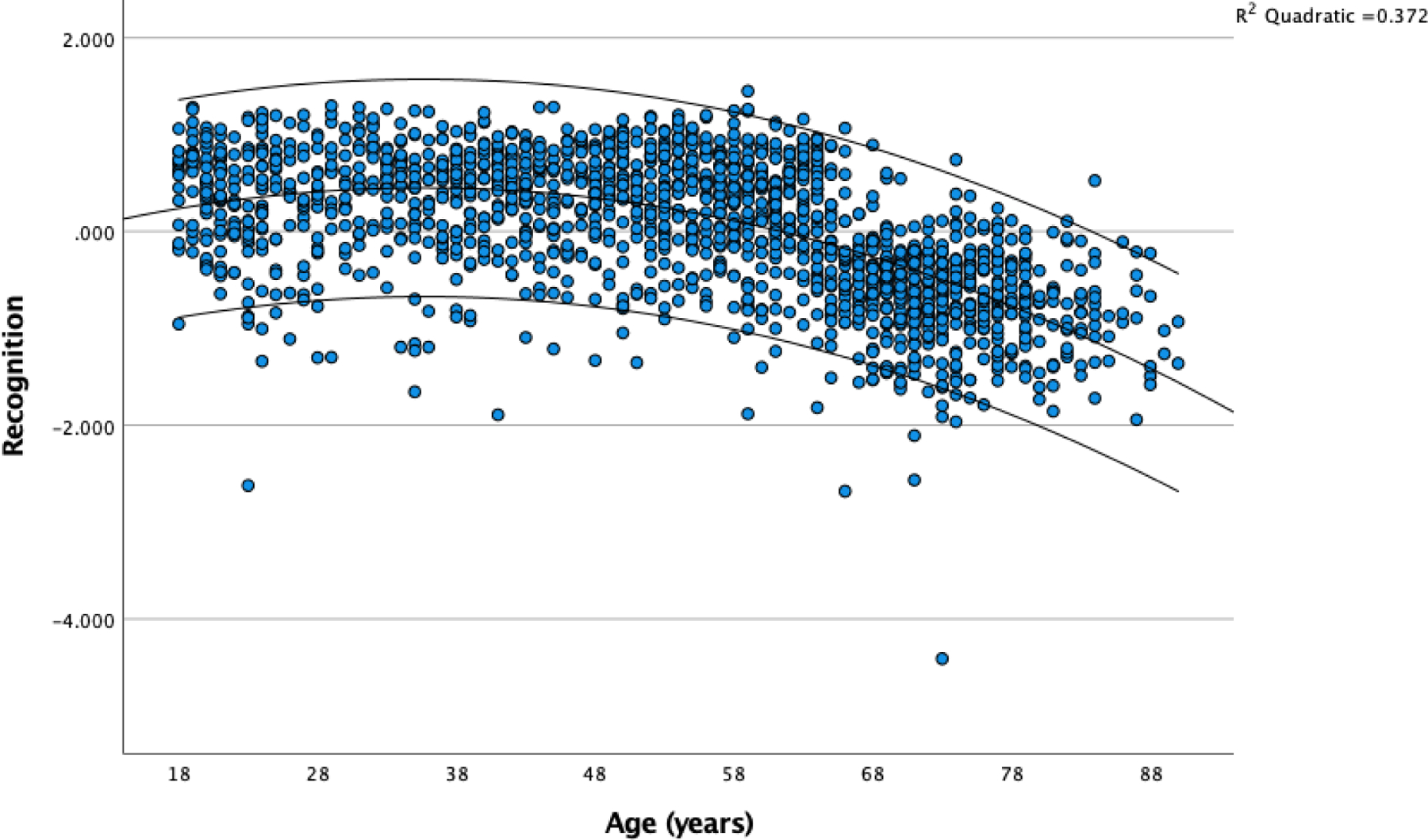
Recognition Factor Scores as a Function of Age in the NNN Sample

After Bonferroni correction we found educational achievement was correlated significantly with every factor, with minimum r = .172, and maximum r = .481. These positive correlations all indicate better performance is associated with higher education. These correlations tended to be higher for the WAIS-IV factors (range of r = .398 to .481), followed by WMS-IV (range of r = .172 to .351), and lower for CVLT3 and D-KEFS factor scores (range of r = .226 to .255).

Sex

Due to the small numbers of individuals who identified as Intersex or other responses we tested for differences on the factors between those who indicated identification as males or females (see Supplemental Table 9). There were significant (Bonferroni corrected) differences on: (1) all WAIS-IV factors except Processing Speed; these differences were small (Cohen’s d < .20) with males having higher scores; (2) WMS-IV Logical Memory and Recognition factors; these differences were small (absolute value of Cohen’s d < .22) with females having higher scores; and (3) all CVLT3 factors; these differences were of medium size (absolute value of Cohen’s d ranging from .29 to .34) with females having higher scores. There were no sex differences on D-KEFS factors.

Race and Ethnicity

As an NIH-sponsored research project, we collect self-report data about race and ethnicity following NIH guidelines but remain concerned that these labels and categories fail to capture important information about individual and cultural differences. We are collecting further data systematically on social determinants of health that we hope may be more informative, but meanwhile, we report our findings to help highlight the importance for research on neuropsychological function to move beyond the NIH categories. For the analyses reported here, due to small sample sizes in all races other than White and Black, we collapsed all individual who did not identify as members of either of these groups as “Other”, and examined group differences across the three categories: White (total n = 4,014), Black (total n = 597), and Other (total n = 389)(note these totals are for the entire sample of 5,000, and the number of people taking specific tests was lower; see Supplemental Table 10)3. Because several factors showed heterogeneity of variance across groups, we used the IBM SPSS Statistics Version 27 robust tests of equality of means and interpreted the Welch tests, using a Bonferroni corrected alpha level of p < .0025 to claim a difference as significant. Most factors showed significant effects across groups, including all WAIS-IV factors, all WMS-IV factors, and all CVLT3 factors except Inaccuracy. None of the D-KEFS factors passed our significance test, but there were trends in the same direction. In all these analyses scores in the Black group were lower than those in the White and Other groups. Effect sizes for these overall group differences were small to medium Eta Squared < .10), but the pairwise differences between groups (e.g., White compared to Black; Black compared to other) were sometimes large (e.g., for the WAIS-IV Verbal Comprehension factor, White/Black Cohen’s d = .945; and Other/Black Cohen’s d = 1.038).

We had small samples of people who identified as Hispanic or Latino, or who indicated their ethnicity as “unknown.” Because many of the cell sizes had fewer than 50 observations, we did not analyze these data further.

Pre-Exam Diagnoses

We examined the effects of Pre-Exam Diagnosis Type (9 categories, including: neoplasms, Cerebrovascular disorders, seizure disorders, traumatic brain injury or closed head injury, mood or anxiety disorder, ADHD, movement disorders, MCI, and other unspecified symptoms and signs of neurological disease (see Supplemental Table 11) on each of the 20 factors, using ANOVA. Tests of between-groups effect on each of the 20 factors revealed main effects with p < .0025 for most WAIS-IV, WMS-IV and CVLT3 factors but not on D-KEFS, with effect sizes ranging up to eta-squared > .12. We did an additional MANOVA on the WAIS-IV first-order factor scores, which showed significant main effects of diagnosis (F[8,1310] = 20.57, p < .001) and a diagnosis by factor interaction (F[18.3, 3930] = 2.45, p < .001, with Greenhouse-Geisser df adjusted due to a violation of sphericity (Mauchly’s W = .579, df=5, p < .001), but the main effect of diagnosis reflected relatively large effect sizes (up to 1 SD difference in factor means between groups, while the within diagnostic group means differed by less than 0.2 standard deviations (see Supplemental Figure 1). The lowest scores were observed in the seizure disorder group (with average scores about .5 SD below the grand mean) and highest scores in the anxiety and mood disorders and ADHD groups (approximately .5 SD above the grand mean). Cerebrovascular and MCI groups had intermediate values that were about 0.2 SD below the grand mean.

Discussion

Overview

The results demonstrate generally strong measurement invariance of the factor models identified in prior work using data from healthy participants across the Pearson standardization samples and the National Neuropsychology Network (NNN) patient sample. These results are striking, given the fact that the NNN clinical samples involved a broad range of patients with heterogeneous disorders, and that the constituent tests were administered in various combinations at the NNN sites. These findings are reassuring that many widely held assumptions about the NP constructs assessed by these instruments are valid in “real world” clinical settings.

Our analyses of the NNN sample further identified several interesting and potentially novel factors, which also showed strong invariance across NNN and standardization samples. The fact that these new models were initially identified in our clinical samples suggests that some factors may emerge more clearly in samples where neuropathology has disrupted the healthy patterns of association among test variables. While many clinical neuropsychologists would have suspected this would be the case based on their clinical experience, there have so far been few empirical studies demonstrating the validity of this intuition. The sample sizes already available through the NNN appear to help make this kind of analysis feasible. Follow-up studies carry the potential to further specify the conditions under which normative patterns of association may break down, opening the possibility that NP batteries of the future might incorporate branching logic based on discrepancies between scores that signal the likelihood of specific forms of pathology.

Factor Analytic Findings

We found that for each instrument or set of tests (i.e., group of tests often administered together, such as WAIS-IV, WMS-IV, and D-KEFS subtests), the best-fitting solution involved four first-order factors and one second-order factor. The first-order factors generally replicated prior findings on these tests. The second-order factors, reflecting shared variance across the first-order factors, may be considered “general” in the context of the instrument(s) from which they emerged. We also highlight that some factors, as in previous factor analyses of these test scores and similar test variables, are test-specific, reflecting the strong correlations among variables that are due to shared test procedures rather than the variance that might be specific to their measurement of a shared construct. These test-specific effects have sometimes been referred to as “method effects” or “method factors” (Campbell & O’Connell, 1967; Pohl & Steyer, 2010), but we believe in neuropsychological testing it may be helpful to specify more precisely the ways in which these methods are the same or different.²

It is important to recognize that the preference for the models that include both first- and second-order factors is based on the relevance of these models to prior work and legacy conceptualizations of function. For example, there is widespread clinical use of both WAIS-IV Index scores and continued use of Full Scale IQ as a broad measure of intellectual ability. Our results show that the correlated first-order factors have almost identical fit statistics, and it is primarily the legacy interpretations of these measures that leads the models with second-order factors to be “preferred.” It is not clear, however, how clinicians could easily use knowledge of the correlations among first-order factors to interpret patterns of performance. In contrast, the specification of “general” factors and cognitive “domains” has enjoyed long clinical use. The specification of “domains” of cognitive ability, similar to the second-order factors specified in the current analyses, is also codified in the current diagnostic taxonomy as expressed in the Diagnostic and Statistical Manual of Mental Disorders, Fifth Edition (DSM-5)(American Psychiatric Association, 2013) for the diagnosis of neurocognitive disorders. For example, the DSM-5 criterion A for diagnosis of Major Neurocognitive Disorder requires: “Evidence of significant cognitive decline from a previous level of performance in one or more cognitive domains (complex attention, executive function, learning and memory, language, perceptual-motor, or social cognition)… preferably documented by standardized neuropsychological testing…” (APA, 2013; page 602).

WAIS-IV

Analysis of the ten WAIS-IV core subtests generally validated the “four-domain” structure that is specified in the WAIS-IV Technical Manual, and that has been codified in the WAIS-IV Index scores: Verbal Comprehension, Perceptual Reasoning, Working Memory, and Processing Speed. The results of measurement invariance analysis show that this model showed strong invariance, and with minor modifications, strict factorial invariance across NNN and Pearson standardization samples. Analysis of factor means show that the NNN sample had General Intellectual Ability factor scores (comparable to FSIQ) about one third of a standard deviation lower than the standardization sample, while the Verbal Comprehension factor score did not differ between groups, and other factors had modestly lower scores (e.g., Perceptual Reasoning factor, M = −0.118) and others showed larger relative deficits (both Working Memory and Processing Speed factors had means of about −0.6). These WAIS-IV factor scores conform to the “classic” pattern identified by Wechsler (Wechsler, 1958); see also (Bilder, 1985; Bilder et al., 1992; Bilder et al., 1985) where “hold” tests (e.g., Information, Vocabulary) are considered insensitive to pathological processes, while others are more sensitive (e.g., Digit Symbol or Coding). This pattern of factor scores can be appreciated clinically by observing the details of the original manifest variables. Thus, in the NNN sample we see that Vocabulary, Visual Puzzles and Similarities all have Age Corrected Subtest Scores (ACSS) of 10 or higher (at or above the standardization sample mean), while Letter Number Sequencing, Block Design, and Coding all have ACSS less than 9, revealing up to about ½ standard deviation deficit relative to normative standards (see Supplemental Table 3). We would caution, however, against drawing the conclusion that the observed pattern of factor scores reflects a “patient” profile, because there are many potential uncontrolled differences, and potential confounds, between the standardization samples and our clinical groups, in which sampling was not experimentally controlled.

The WAIS-IV factor analysis also suggests that 8 subtests might work as well and be more efficient than the currently recommended 10 core subtests to specify both index scores and FSIQ. Specifically, for the factors that currently require 3 subtests, it may be possible to reduce assessment to two indicators per factor without a major sacrifice of measurement precision. For the Verbal Comprehension factor, the Information subtest had the lowest loading and highest measurement error, while for the Perceptual Reasoning factor, Visual Puzzles had the lowest loading and highest measurement error. Elimination of these two subtests would save approximately 11 to 16 minutes, based on estimates of administration time from Q-Interactive and from the comparable subtests on the WISC-V in 16-year-olds (Wechsler, 2014). Reliability of the Verbal Comprehension factor in the NNN sample would drop from standardized alpha = .88 to standardized alpha = .87 if Information were not included. Similarly, the reliability of the Perceptual Reasoning factor would drop from standardized alpha = .81 to standardized alpha = .79 if Visual Puzzles were dropped. The reliability of the second-order WAIS-IV factor (i.e., the factor most closely related to FSIQ) would drop only from a standardized alpha of .941 to .935 after excluding both subtests. These results parallel those reported by Umfleet and colleagues who showed that two-subtest prorated scores correlated highly (r=.96 to .97) with three-subtest index scores (Umfleet et al., 2012)). The WISC-V provides another example in which only two subtests were used to identify index scores with good precision of measurement and clinical utility (Wechsler, 2014; Weiss et al., 2015).

Our results are compatible with the idea that shorter tests might enable similar specification of meaningful neuropsychological constructs, and we believe recasting these assessments in light of developments in modern psychometric theory, particularly item response theory, offers many potential advantages, including the promise of enabling adaptive testing (Reise & Waller, 2009). The practical advantages of fixed short forms for instruments like the WAIS-IV are questionable now that we possess computerized supports enabling administration of adaptive tests that flexibly administer individual items based on their contributions of useful information about an individual’s ability level on a specific latent trait.

It is also important to highlight that the factor loadings on the general factor are so high that if the assessment goal is to measure general ability, more parsimonious measurement methods probably can be specified. The NNN sample may be useful to determine what adaptive testing strategies may be effective in clinical populations. In our sample Verbal Comprehension and Processing Speed factors had slightly lower loadings and higher error relative to Working Memory (WM) and Perceptual Reasoning (PR) factors. The same pattern appeared also, however, in the Holdnack et al (2011) analysis combining variables from WAIS-IV and WMS-IV, with highest loadings on ‘g’ from WM and PR factors. It may be that this feature holds across both healthy and clinical samples, but further work with subpopulations may lead to discovery of syndrome-specific indicators. Meanwhile, our findings in the clinically heterogeneous NNN sample, which appear to replicate the findings of Holdnack and colleagues, suggest that measures of WM and PR alone might characterize ‘g’ with relatively high precision and efficiency.

WMS-IV

Confirmatory factor analysis of the WMS-IV identified four first-order factors, and 3 of these 4 were subtest-specific, reflecting shared variance within the Logical Memory (LM), Visual Reproductions (VR) and Verbal Paired Associates (VPA) variables. It is likely that these three factors are best understood as test-specific effects. The lack of fit for models specifying “auditory” and “visual” learning and memory factors is probably linked to our inclusion of only three of the WMS-IV subtests, and particularly only a single visual memory subtest. It should be recognized that studies including additional visual memory variables, or studies including participants with specific deficits in verbal and visual memory functions, may well identify meaningful factors reflecting auditory-verbal and visual-nonverbal learning and memory.

Our data were not consistent with a separate “delayed recall” factor, replicating prior work on the WMS-III (Millis et al., 1999; Price et al., 2002) that was subsequently corroborated in CFA of the WMS-IV and WAIS-IV (Holdnack et al., 2011). These findings illustrate how the high correlations between immediate and delayed recall variables make it difficult to justify the inclusion of delayed recall measures on purely psychometric grounds in either the standardization sample or our clinically heterogeneous NNN sample. This psychometric evidence conflicts with a legacy of expert clinical opinion that decrements in recall over delays are essential to the diagnosis of amnestic syndromes (Butters et al., 1995; Milner et al., 1968), along with evidence that hippocampal volume reductions are linked to delayed recall deficits even after accounting for immediate recall (Kramer et al., 2004). Millis and colleagues (1999) highlighted the need for larger samples of clinical cases that might reveal separable delayed recall factors and noted that there were so far limited data available to address this problem. Delis and colleagues (2003) used separate principal components analyses in healthy people and people with Alzheimer’s disease. They found that immediate recall, delayed recall, and recognition variables all loaded on a single factor in the healthy group, but the same variables emerged on different factors in the Alzheimer’s group. Specifically, the Alzheimer’s group had separate factors for immediate recall variables, delayed recall variables, and recognition memory variables. Larrabee (2003) discussed this work with special attention to the role played by “method variance” and elaborated on Delis and colleagues’ proposal to employ multiple different measures of immediate and delayed recall and conduct parallel confirmatory factor analyses with some methods applied in the first analysis, and the other methods applied in the second (replication) analysis. Bowden (2004) provided further clarification of the psychometric issues, and usefully pointed out that correlations among latent variables may change, even when the factor structure is the same across two groups, a phenomenon articulated formally by Widaman and Reise (1997). While these initial analyses of the NNN sample do not support the separate identification of a delayed recall factor, as the NNN study progresses we aim to have sufficient samples of patients with memory deficits including amnestic syndromes, and with a wide range of unique methods that we hope will serve to better examine these hypotheses and the best psychometric strategies to distinguish “method” effects from the effects of the underlying processes we aim to measure.

One factor identified in our analyses that was not found clearly in prior work but was identified in our re-analysis of the WMS-IV standardization sample, is the Recognition-Familiarity factor. This is particularly interesting given a long history highlighting “recollection” and “familiarity” as potentially dissociable processes (James, 1890) and more recent work in cognitive neuroscience emphasizing the value of dual-process recollection/familiarity models that explain many aspects of recognition memory (Yonelinas, 2002; Yonelinas et al., 2010). In brief, these models indicate that recall involves active search and retrieval checking, whereas recognition memory can rely on perceived familiarity of presented items in addition to active search and retrieval checking. Of high importance to clinical neuropsychology is the assertion that the hippocampus is critical for recollection processes that facilitate active recall, while familiarity sufficient to enable recognition performance may be mediated by non-hippocampal cortical systems, and some investigators have focused on perirhinal regions as particularly important (Quamme et al., 2004; Yonelinas et al., 2010; Yonelinas et al., 2007). “Remember/know” task paradigms have further promoted understanding of these distinctions (Dudukovic & Knowlton, 2006; Tulving, 1985). Recent formulations further emphasize the possibly unique roles of “binding”, “pattern completion/separation”, and “contextual precision” as contributors to episodic memory with potentially specific functional anatomic correlates (Ekstrom & Yonelinas, 2020).

These distinctions are of high theoretical interest, but controversy remains about their validity and some investigators suggest that an integrated declarative memory system better explains the evidence (Squire, Stark and Clark, 2004; Squire, Wixted & Clark, 2007). There are also psychometric concerns, specifically it has been suggested that differences between recall and recognition tests are confounded by difficulty level, because recall-recollection tasks are usually more difficult than recognition-familiarity tasks, and thus have greater discriminating power (Calev & Monk, 1982). Classic studies also have shown task manipulations can make recognition more difficult than recall (Tulving, 1968). This evidence suggests that preserved recognition relative to recall in many assessments may be explained by the severity of generalized deficit rather than a differential deficit in a specific anatomic system. Similar arguments have been made to suggest that delayed recall deficits may simply be artifacts of more severe generalized deficits at the encoding stage that are not effectively controlled when assessing immediate versus delayed recall, and that psychometric matching is critical to reveal differential deficits (Javitt et al., 2007; Lencz et al., 2002).

Despite these reservations, there is evidence supporting possible clinical utility of these results, from demonstrations of double dissociations that support the validity of the recollection/familiarity distinction in studies of patients with temporal lobe epilepsy (Bowles et al., 2010) and patients with Parkinson’s disease (Cohn et al., 2010). We further believe that clinicians usually interpret recognition results relative to other indicators of encoding (learning) and consolidation (forgetting). We hope that these results from the NNN sample and confirmed in the Pearson standardization sample, showing that a Recognition-Familiarity factor is well identified with widely used tests, may help advance these interpretive efforts by enabling more widespread and reliable measurement of recognition relative to learning and recall variables, and lead to further interest in developing new paradigms that enable tests of the recollection/familiarity distinction in everyday clinical NP practice.

In addition to the first-order factors, our CFAs also revealed a second-order factor, that had high loadings on all three of the test-specific recall or “recollection” first-order factors. We suggest that this might best be understood as a general Recall-Recollection factor, given that our CFA results enabled specification of a separate Recognition-Familiarity factor. We note further that the uniqueness of these factors is supported by their external correlations with age, as discussed further below.

The measurement invariance analyses offered insights into the magnitude of differences between the NNN and standardization samples. These results suggested the NNN sample had a General Recall-Recollection deficit of about one standard deviation, and differences of similar magnitude were observed across all three test specific factors (LM, VR, and VPA). The magnitude of the mean difference on the Recognition-Familiarity factor showed that the Pearson sample scored about one standard deviation higher (M = 1.026, SE = .061) relative to the NNN sample.

CVLT3

Our CFAs found good fit for the Donders model with four factor that he specified as “Attention Span”, “Learning Efficiency”, “Delayed Recall”, and “Inaccurate Recall” (Donders, 2008). Attention Span is a label that appears to capture well the capacity for immediate recall of material on CVLT Trial 1 and List B. Like Donders we find the middle recall variable has a slightly lower loading on this factor. It may reflect WM capacity to the extent that those individuals with greater WMC are more likely to have increased recall from regions of the list that are outside primacy and recency regions.

The second factor, with highest loadings on learning slope, semantic clustering, and recall consistency, appears very similar to Donders’ factor, which he appears to have derived from a similar term used in the manual (“Recall Efficiency”). With learning slope having the highest loading on our factor, we believe “learning consistency” may be a more appropriate descriptor.

Not surprisingly, both short and long, cued and free recall measures loaded on a single factor, which Donders referred to as “delayed recall,” but we refer to as “recall and recognition” because it also includes recognition discriminability. This Recall and Recognition factor should be considered in light of the shared methods across the recall conditions. This factor also loaded most strongly on the second-level factor that has high loadings of all four CVLT3 factors. The fit of this model benefited markedly by permitting correlated variances between the short- and long-delay free recall measures, and between the short- and long-delay cued recall measures, further justifying the use of the label “recall and recognition” rather than “delayed recall.” This replicates other work showing that the correlations are so high between short- and long-delay recall measures that it may be challenging to tease out the effects associated with decrement over delay, except in more specific subpopulations (e.g., people with amnestic syndromes)(Millis et al., 1999; Price et al., 2002).

We also replicated Donders’ “inaccurate memory” factor but note that this in part benefited from specifying correlated variances between recognition discriminability and false positive responses. It is interesting that the false alarms fit well on inaccurate memory while recognition hits fit best on the recall-recognition memory factor, suggesting that a positive response bias is more relevant to inaccuracies than misses.

The magnitude of group differences on the CVLT3 factors, as estimated from our measurement invariance analyses, suggested general impairments of about one-third of a standard deviation in the NNN relative to the standardization sample. The difference was larger for the Attention Span factor (−0.58 SD), while Learning Efficiency and Delayed Memory factors were both smaller (near −0.2 SD), and Inaccurate Memory was in between (−.38 SD). These estimates are all reasonable with respect to the composition of the NNN clinical sample.

D-KEFS

The best solution for D-KEFS measures we included (Color-Word Interference (CWI); Trail Making Test (TMT); and Verbal Fluency (VF)) is similar to that of Karr and colleagues (Karr et al., 2019). We found: (1) A first-order factor with loadings from all four scores from the CWI, probably best understood as speed of processing for automatized language skills; (2) A first-order factor including all TMT components, (3) another first-order factor loading the VF components. We consider all of the preceding factors to be task-specific factors. Finally, we clearly identified: (4) a first-order factor including inhibition and switching measures from VF, TMT and CWI tests. In contrast, other investigators identified two-factor solutions that essentially separated timed tasks from abstraction tests. Our analysis would be unlikely to identify an “abstraction” factor given we did not include Word Context, Twenty Questions, Proverb, Sorting, or Tower Tests (Camilleri et al., 2021; Savla et al., 2012). Our solution is also simpler than a model that emphasized CHC theory and had representations of other tasks that likely highlighted non-executive cognitive abilities (Floyd et al., 2010).

We note also that Category Switching from the Verbal Fluency subtest had cross-loadings, with strong loadings on the Fluency factor and weak loadings on the Inhibition-Switching factor (i.e., only .22; while the loadings of other three variables on the Inhibition-Switching factor in the NNN sample ranged from .57 to .67). This raises a question about the utility of this condition, given that it may be more closely related to fluency than to switching. It seems likely that verbal fluency is already adequately measured by Category and Letter fluency tests, and that the addition of the switching condition adds little to the measurement of the Inhibition-Switching construct.

The magnitude of group differences on the D-KEFS was also in line with expectations based on the composition of the NNN sample, with General factor scores moderately lower (M = −0.569) than the Pearson sample, substantially lower on the CWI factor (M = −0.906), and more modest, but still notable differences on the TMT (M = −0.504), Fluency (M = −0.316, and Inhibition-Switching (M = −0.459 SD) factors.

Relations of Factor Scores with Demographic and Clinical Characteristics

Age

Given that we used age-corrected scores for most of the variables used in our analyses, normal age-associated trends should be removed and our findings may be interpreted best as the additional associations of age with the factors, that may be attributed to age-associated neuropathology, particularly given clinical referral and sampling issues (i.e., older patients are more likely to have Alzheimer’s disease, Mild Cognitive Impairment, and Movement Disorders, while younger patients are more likely to have ADHD, Anxiety/Mood Disorders, Seizure Disorders, and Traumatic Brain Injury). Thus, it was not surprising that we saw modest correlations (|r| < .18) with multiple factor scores.

In contrast, there was the large correlation of age with the Recognition factor, showing worse recognition performance with age and possible steeper decline at ages over 60 (Pearson r = −.527; linear R² = .278; quadratic R² = .372). We examined the possibility that this might reflect the fact that the WMS-IV recognition subtest variables were not age-corrected, but examination of the standardization sample data showed this could not account for a correlation of this magnitude. It seems likely that this reflects a clinically significant difference between the NNN and standardization samples, either due to age or the neuropsychological syndromes that are most associated with age in our patients. Regardless of the cause of this association, it indicates that recognition memory performance might be highlighted for its sensitivity in clinical samples. Further, as discussed above with respect to the recollection/familiarity distinction, we believe our findings support further development of quantitative indicators of recognition memory performance that can help further investigate possibly dissociable causes of memory impairment.

Sex

We found small sex differences on multiple variables, including all WAIS-IV factors except processing speed, all CVLT3 factors, and all WMS-IV factors except the Visual factor, but there were no sex effects on the D-KEFS factors. On the WAIS-IV factors there were small effects (Cohen’s d < 0.2) with scores of males higher. The CVLT3 factor effects were slightly larger (d ~ 0.3) and favored females, while WMS-IV differences were also small (d < 0.22) with females doing better. It is tempting to speculate that males may tend to manifest slightly greater preservation of some crystallized intellectual abilities, while females may possess great resilience against age-associated declines in memory function, but further examination of these differences would be necessary to determine if these sex differences are primarily attributable to clinical conditions, site differences or other possible confounds.

Race & Ethnicity

Given that our overall sample was 80.3% White, 11.9% Black, and the balance of patients indicated other racial group identities, indicated race was unknown or preferred not to specify, our analyses were limited in examining effects of race, and we could only examine effects of race by comparing NIH categories of White, Black and “Other” combining all other groups of respondents. Effect sizes, specified using the omega-squared random-effects point estimate, ranged up to 5% variance explained in factor scores by race. In these comparisons the group identified as Black tended to have lower scores than the White and Other groups, and direct comparisons suggested that patients who identified as Black had scores almost one standard deviation lower than the White or Other groups. These disparities are of great concern, and it is not possible given the structure of our study to determine what biases in referral processes (i.e., patients from racial minority groups may not be referred until their cognitive disorders are more severe), diagnostic confounds (i.e., Black patients were more likely to be seen for cerebrovascular disorders and epilepsy than for ADHD or Anxiety and Mood Disorders), or other factors, including test measurement biases. Our results are compatible with the recent analyses of race and ethnicity effects on the Wechsler IQ tests, which highlight the complex combination of factors and emphasize the role of inequitable access (including parental education, income, academic expectations, and opportunity) that explains substantial variance in these testing outcomes (Weiss & Saklofske, 2020). It is also important to recognize that our discipline needs to engage in much more work to assess measurement invariance across groups differing in race, ethnicity, culture, language and vulnerability to stereotype threat (Wicherts, 2016). We hope that by accumulating more data, the NNN can contribute constructively to this work, and help us to examine the psychometric properties of our tests to help overcome biases that are probably built into our current assessments. Given that our inclusion-exclusion criteria limited our sample only to those who had English as their primary language, our analyses of ethnicity were further limited by small sample sizes of groups identified as Hispanic or Latino (n’s < 50), so we do not interpret these. We believe it will be important in the future to expand the NNN sampling strategy to include patients who speak other languages and create special outreach to Hispanic/LatinX communities to learn more about neuropsychological profiles and psychometric issues that may impact interpretation of neuropsychological findings in these patients.

Pre-Exam Diagnoses

This study was limited to inspection of some effects associated with diagnoses provided prior to the NP exam. These “referral diagnoses” are not definitive, and often considered tentative pending results of the NP exam and other diagnostic procedures. With those reservations, it is interesting that we observed substantial differences between patients who prior to our exams had diagnoses of Epilepsy (and had lower factor scores) relative to groups who had diagnoses of Anxiety or Mood disorders (who had higher scores), and patients with Cerebrovascular disorders or Mild Cognitive Impairment had intermediate scores. The discrepancy between the highest and lowest performing groups was about 1 standard deviation – a large difference. While we look forward to conducting more definitive studies of diagnostic outcomes in the future, it is interesting that these differences exist already at the stage of referral for NP assessment. These observations are consistent with the suggestion that NP examinations should be tailored flexibly to the diagnostic questions at hand, given that different test procedures are more likely to enhance sensitivity and specificity of findings in groups that vary so widely in ability. We believe this practice is already common in many NP clinics nationwide but believe results like these from the NNN may help provide an empirical basis for the creation of flexible and efficient batteries that are informed by referral issues.

Next Steps

We believe the current results from the NNN sample are promising and indicate that this emerging data resource can be useful for the field. We see multiple avenues for future investigation based on the findings reported here, including:

1. Examining factor structures in samples that represent specific, more homogeneous diagnostic groups; for example, comparisons of left vs. right hemisphere temporal lobe epilepsy, comparisons of patients with amnestic vs non-amnestic MCI, and examination of groups defined by specific psychiatric syndromes or comorbidities.

2. Direct comparisons of individual case data between the NNN and standardization samples to estimate the most efficient methods for identification of patients with specific neuropsychiatric syndromes.

3. Extending the analyses shown here that were performed within specific instruments (WAIS-IV, WMS-IV, CVLT3, and D-KEFS) to examine factors that can be defined across instruments (e.g., what memory factors might be defined by indicators from WMS-IV, CVLT3 and other tests of learning and memory).

4. Analyses to specify cross-walks from one instrument to another, to identify the same construct (e.g., to enable harmonization of different versions of the Trail Making Test, color word interference tests, and word list learning tests).

5. Examining the multiple possible causes of test-score disparities leading to observed differences between groups defined by race, ethnicity, language or other social determinants of health.

6. Examining reasons for missing data and assessing the possibilities that non-random missing data may impact the findings. There are myriad potential sources of bias and confound given the clinical ascertainment strategy and care as usual assessment methods. With sufficiently large samples, however, we hope to determine how much these factors limit generalization from our findings.

7. The current results focus only on test-level findings, and from only a subset of all tests. We are eager to examine complete batteries, and to extend this work to the item level, that may help determine substantially more efficient methods, both within test and across tests, for the future.

8. The current findings have included only the pre-assessment diagnosis and have not included outcome measures. We are eager to continue our project and have available sufficient data on important outcomes to assess the predictive validity and ecological validity of NP tests. Similarly, we are eager to combine these data with other datasets including biomarkers, neuroimaging data, and other variables that may help validate NP test methods with respect to biological indicators of neuropathology.

Limitations and Constraints on Generality

There are several limitations to this work that should be recognized. First, the NNN is unusual in its primary aim to reflect clinical practice in real-world settings and therefore necessarily does not incorporate the kinds of constraints on sampling inclusion/exclusion criteria and methods that are customarily involved in research studies. The ascertainment of cases so far reveals racial and ethnic disparities that we believe should be followed up with specific outreach strategies. Second, while our clinics were selected to provide a diversity of cases and regional perspectives, the four initial sites for the NNN are all major academic centers that serve as tertiary referral hubs, and this may bias cases seen. Third, the NNN is still in the process of aggregating data, so this paper includes only part of all information that will be available in the future, and that will more fully represent the scope of both the examinations and diagnostic outcomes for our patients. Fourth, this work faces psychometric challenges inherent in factor analyses involving missing data, and future work can usefully consider how to develop models of missing data generation mechanisms that may have caused part of the data to be missing due to site, clinician, or patient characteristics. We hope that continued ascertainment within the NNN and extension of the NNN to include additional sites will help overcome these limitations and help maximize the yield of this project.

Key Points.

• Question: This paper asks what neuropsychological constructs are identified by a clinical test battery (comprising 17 tests from the WAIS-IV, WMS-IV, CVLT3 and D-KEFS), if patterns seen in patients and healthy people are the same, and what specific variables are most important to define each construct.

• Findings: Models in a heterogeneous clinical sample and the standardization sample are very similar, but models including Recognition-Familiarity and Inhibition-Switching factors were prompted by analyses in the NNN patient sample, and these factors may be clinically relevant.

• Importance: The findings are important because they provide a basis for development of better and more efficient assessment strategies, particularly when seeking to measure specific cognitive constructs in neuropsychological evaluations.

• Next Steps: Next steps include examining factors across instruments, specifying the most efficient adaptive methods to measure these constructs, and determining what specific individual and cultural differences, and what clinical conditions, may deviate from these construct definitions, and/or demand development of additional novel strategies.