Significance
Data from human subjects as well as animals show that working memories are associated with a sense of uncertainty. Indeed, a sense of uncertainty is what allows an observer to properly weigh new evidence against their current memory. However, we do not understand how the brain tracks uncertainty. Here, we describe a simple and biologically plausible network model that can track the uncertainty associated with working memory. The representation of uncertainty in this model improves the accuracy of its working memory, as compared to conventional models, because it assigns proper weight to new conflicting evidence. Our model provides an interpretation of observed fluctuations in brain activity, and it makes testable predictions.
Keywords: working memory, ring attractor networks, head direction neurons, Bayesian inference, Kalman filter
Abstract
Working memories are thought to be held in attractor networks in the brain. These attractors should keep track of the uncertainty associated with each memory, so as to weigh it properly against conflicting new evidence. However, conventional attractors do not represent uncertainty. Here, we show how uncertainty could be incorporated into an attractor, specifically a ring attractor that encodes head direction. First, we introduce a rigorous normative framework (the circular Kalman filter) for benchmarking the performance of a ring attractor under conditions of uncertainty. Next, we show that the recurrent connections within a conventional ring attractor can be retuned to match this benchmark. This allows the amplitude of network activity to grow in response to confirmatory evidence, while shrinking in response to poor-quality or strongly conflicting evidence. This “Bayesian ring attractor” performs near-optimal angular path integration and evidence accumulation. Indeed, we show that a Bayesian ring attractor is consistently more accurate than a conventional ring attractor. Moreover, near-optimal performance can be achieved without exact tuning of the network connections. Finally, we use large-scale connectome data to show that the network can achieve near-optimal performance even after we incorporate biological constraints. Our work demonstrates how attractors can implement a dynamic Bayesian inference algorithm in a biologically plausible manner, and it makes testable predictions with direct relevance to the head direction system as well as any neural system that tracks direction, orientation, or periodic rhythms.
Attractor networks are thought to form the basis of working memory (1, 2) as they can exhibit persistent, stable activity patterns (attractor states) even after network inputs have ceased (3). An attractor network can gravitate toward a stable state even if its input is based on partial (unreliable) information; this is why attractors have been suggested as a mechanism for pattern completion (4). However, the characteristic stability of any attractor network also creates a problem: Once the network has settled into its attractor state, it will no longer be possible to see that its inputs might have been unreliable. In this situation, the attractor state will simply represent a point estimate (or “best guess”) of the remembered input, without any associated sense of uncertainty. However, real memories often include a sense of uncertainty, (e.g., refs. 5–7), and uncertainty has clear behavioral effects (8–10). This motivates us to ask how an attractor network might conjunctively encode a memory and its associated uncertainty.
A ring attractor is a special case of an attractor that can encode a circular variable (11). For example, there is good evidence that the neural networks that encode head direction (HD) are ring attractors (12–19). In a conventional ring attractor, inputs push a “bump” of activity around the ring, with only short-lived changes in bump amplitude or shape (20, 21); the rapid decay to a stereotyped bump shape is by design, and, as a result, a conventional ring attractor network is unable to track uncertainty. However, it would be useful to modify these conventional ring attractors so that they can encode the uncertainty associated with HD estimates. HD estimates are constructed from two types of observations—angular velocity observations and HD observations (11, 22). Angular velocity observations arise from multiple sources, including efference copies, vestibular or proprioceptive signals, as well as optic flow; these observations indicate the head’s rotational movement and, thus, a change in HD (13, 18, 23, 24). These angular velocity observations are integrated over time (“remembered”) to update the system’s internal estimate of HD, in a process termed angular path integration. Ideally, a ring attractor would track the uncertainty associated with angular path integration errors. Meanwhile, HD observations arise from visual landmarks or other sensory cues that provide information about the head’s current orientation (12, 16). These sensory observations can change the system’s internal HD estimate, and once that change has occurred, it is generally persistent (remembered). But like any sensory signal, these sensory observations are noisy; they are not unambiguous evidence of HD. Therefore, the way that a ring attractor responds to each new visual landmark observation should ideally depend on the uncertainty associated with its current HD estimate. This type of uncertainty-weighted cue integration is a hallmark of Bayesian inference (25) and would require a network that is capable of keeping track of its own uncertainty.
In this study, we address three related questions. First, how should an ideal observer integrate uncertain evidence over time to estimate a circular variable? For a linear variable, this is typically done with a Kalman filter; here, we introduce an extension of Kalman filtering for circular statistics; we call this the circular Kalman filter. This algorithm provides a high-level description of how the brain should integrate evidence over time to estimate HD, or indeed any other circular or periodic variable. Second, how could a neural network actually implement the circular Kalman filter? We show how this algorithm could be implemented by a neural network whose basic connectivity pattern resembles that of a conventional ring attractor. With properly tuned network connections, we show that the bump amplitude grows in response to confirmatory evidence, whereas it shrinks in response to strongly conflicting evidence or the absence of evidence. We call this network a Bayesian ring attractor. Third, how does the performance of a Bayesian ring attractor compare to the performance of a conventional ring attractor? In a conventional ring attractor, bump amplitude is pulled rapidly back to a stable baseline value, whereas in a Bayesian ring attractor, bump amplitude is allowed to float up or down as the system’s certainty fluctuates. As a result, we show that a Bayesian ring attractor has consistently more accurate internal estimates (or “working memory”) of the variable it is designed to encode than a conventional ring attractor.
Together, these results provide a principled theoretical foundation for how ring attractor networks can be tuned to conjointly encode a memory and its associated uncertainty. Although we focus on the brain’s HD system as a concrete example, our results are relevant to any other brain system that encodes a circular or periodic variable.
Results
Circular Kalman Filtering: A Bayesian Algorithm for Tracking a Circular Variable.
We begin by asking how an ideal observer should dynamically integrate uncertain evidence to estimate a circular variable, specifically head direction ϕt. Additional information being absent, the ideal observer assumes that HD follows a random walk or diffusion on a circle: across small consecutive time steps of size δt, the current HD ϕt is assumed to be drawn from a normal distribution, ϕt|ϕt − δt ∼ 𝓝(ϕt − δt, δt/κϕ) (constrained to a circle) centered on ϕt − δt and with variance δt/κϕ. This diffusion prior assumes smaller HD changes for a larger precision (i.e., inverse variance), κϕ, and for smaller time steps, δt. Just like the brain’s HD system, the ideal observer receives additional HD information through HD observations zt and angular velocity observations, vt (Fig. 1A). HD observations provide noisy, and thus unreliable, measurements of the current HD drawn from a von Mises distribution, zt|ϕt ∼ 𝓥𝓜(ϕt, κzδt) (i.e., the equivalent to a normal distribution on a circle), centered on ϕt, and with precision κzδt. A higher precision κz means that individual HD observations provide more reliable information about the current HD. Angular velocity observations provide noisy measurement of the current HD change ϕt − ϕt − δt drawn from a normal distribution, centered on the current angular velocity and with precision κvδt. While higher-precision measurements yield more reliable information, they only do so about the current HD change rather than the HD itself.
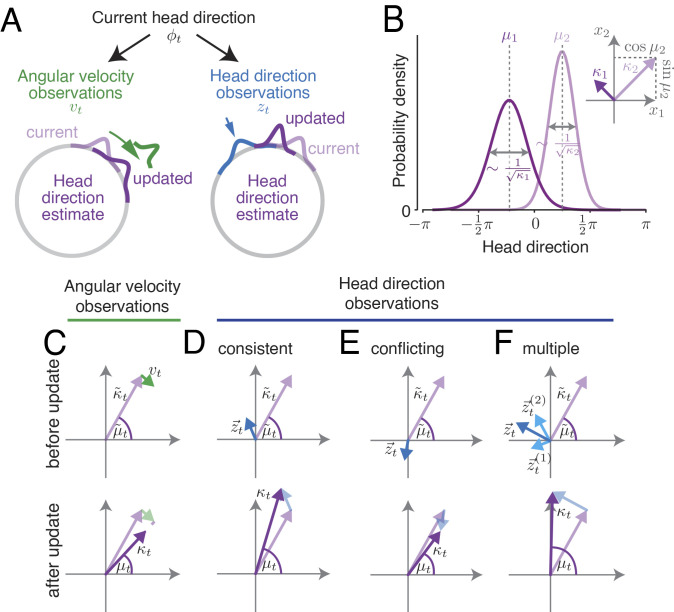
Fig. 1.
Tracking HD with the circular Kalman filter. (A) Angular velocity observations provide noisy information about the true angular velocity , while HD observations provide noisy information about the true HD ϕt. (B) At every point in time, the posterior belief p(ϕt) is approximated by a von Mises distribution, which is fully characterized by its mean μt (location of distribution’s peak) and its precision/certainty parameter κt. Interpreted as the polar coordinates in the 2D plane, these parameters provide a convenient vector representation of the posterior belief (inset). (C) An angular velocity observation vt is a vector tangent to the current HD belief vector. Angular velocity observations continually rotate the current HD estimate; meanwhile, noise accumulation progressively decreases certainty. (D) Each HD observation zt is a vector whose length quantifies the observation’s reliability. Adding this vector to the current HD belief vector produces an updated HD belief vector. HD observations compatible with the current HD estimate result in an increased certainty (i.e., a longer belief vector). (E) HD observations in conflict with the current belief (e.g., opposite direction of the current estimate) decrease the belief’s certainty. (F) Multiple HD cues can be integrated simultaneously via vector addition.
The aim of the ideal observer is to use Bayesian inference to maintain a posterior belief over HD, p(ϕt|z0:t, v0:t) given all past observations, z0:t and v0:t (25, 26). Assuming a belief p(ϕt − δt|z0:t − δt, v0:t − δt) at time t − δt, the observer updates this belief upon observing vt and zt in two steps. First, it combines its a priori assumption about how HD diffuses across time with the current angular velocity observation vt to predict ϕt at the next time step t, leading to p(ϕt|z0:t − δt, v0:t). As both the diffusion prior and angular velocity observations are noisy, this prediction will be less certain than the previous belief it is based on. (SI Appendix for formal expression.) Second, the ideal observer uses Bayes’ rule to combine this prediction with the current HD observation zt to form the updated posterior belief p(ϕt|z0:t, v0:t). These two steps are iterated across consecutive time steps to continuously update the HD belief in the light of new observations.
The two steps are also the ones underlying a standard Kalman filter (27, 28). However, while a standard Kalman filter assumes the encoded variable to be linear, we here use a circular variable which requires a different approach. Because filtering on a circle is analytically intractable (29), we choose to approximate the posterior belief by a von Mises distribution, with mean μt and precision κt, so that p(ϕt|z0:t, v0:t) ≈ 𝓥𝓜(ϕt|μt, κt) (Fig. 1B). Then, the mean μt, which we will call the HD estimate, determines the peak of the distribution. The precision κt quantifies the width of the distribution and, therefore, our certainty in this estimate (larger κt = indicating higher certainty). This approximation allows us to update the posterior over a circular variable ϕt using a technique called projection filtering (30, 31), resulting in,
| [1] |
| [2] |
Here, f(κt) is a monotonically increasing nonlinear function that controls the speed of decay in certainty κt (Methods). Eqs. 1 and 2 describe an algorithm that we call the circular Kalman filter (31) (Methods/SI Appendix for a continuous-time formulation). This algorithm provides a general solution for estimating the evolution of a circular variable over time from noisy observations.
To understand the circular Kalman filter intuitively, it is helpful to think of the observer’s belief as a vector in the 2D plane (Fig. 1B), whose direction represents the current estimate μt, and whose length represents the associated certainty κt. The circular Kalman filter tells us how this vector should change at each time point, based on new observations of angular velocity and HD. Here, we outline the intuition behind the circular Kalman filter, focusing on the HD system as a specific example.
Angular Velocity Observations.
We can think of each angular velocity observation as a vector that points at a tangent to the current HD belief vector (Fig. 1C) and rotates this belief vector (first term in parenthesis on RHS of Eq. 1). Angular velocity observations are noisy and, together with the diffusion prior, decrease the belief’s certainty (κt), meaning that the observer’s belief vector becomes shorter (Fig. 1C). Thus, when angular velocity observations are the only inputs to the HD network—i.e., when HD observations are absent—the HD belief’s certainty κt will progressively decay, with a speed of decay that depends on both κv and κϕ (first term in parenthesis on RHS of Eq. 2).
HD Observations.
We can treat each HD observation as a vector whose length κz quantifies the observation’s reliability (e.g., the reliability of a visual landmark observation). This HD observation vector is added to the current HD belief vector to obtain the updated HD belief vector. The updated direction of the belief vector depends on the relative lengths of both vectors. A relatively longer HD observation vector, i.e., a more reliable observation relative to the current belief’s certainty, results in a stronger impact on the updated HD belief (Fig. 1D, second term in parenthesis on RHS of Eqs. 1 and 2). In line with principles of reliability-weighted Bayesian cue combination (25), HD observations increase the observer’s certainty if they are confirmatory (i.e., they indicate that the current estimate is correct or nearly so, Fig. 1D). Interestingly, however, if HD observations strongly conflict with the current estimate (e.g., if they point in the opposite direction), they actually decrease certainty (Fig. 1E). This notable result is a consequence of the circular nature of the inference task (32). It stands in contrast to the standard (noncircular) Kalman filter, where an analogous observation would always increase the observer’s certainty (33) and is thus a key distinction between the standard Kalman filter and the circular Kalman filter.
To summarize, the circular Kalman filter describes how a nearly ideal observer should integrate a stream of unreliable information over time to update a posterior belief of a circular variable. This algorithm serves as a normative standard to judge the performance of any network in the brain that tracks a circular or periodic variable. Specifically, in the HD system, the circular Kalman filter tells us that angular velocity observations should rotate the HD estimate while reducing the certainty in that estimate. Meanwhile, HD observations should update the HD estimate weighted by their reliability, and they should either increase certainty (if compatible with the current estimate) or reduce it (if strongly conflicting with the current estimate). Note that the circular Kalman filter can integrate HD observations from multiple sources by simply adding all their vectors to the current HD belief vector (Fig. 1F).
Neural Encoding of a Probability Distribution.
Thus far, we have developed a normative algorithmic description of how an observer should integrate evidence over time to track the posterior belief over a circular variable. This algorithm requires the observer to represent their current belief as a probability distribution on a circle. How could a neural network encode this probability distribution? Consider a ring attractor network where adjacent neurons have adjacent tuning preferences so that the population activity pattern is a spatially localized “bump.” The bump’s center of mass is generally interpreted as a point estimate (or best guess) of the encoded circular variable (12, 34). In the HD system, this would be the best guess of head direction. Meanwhile, we let the bump amplitude encode certainty so that higher amplitude corresponds to higher certainty. Of course, there are other ways to encode certainty—e.g., using bump width rather than bump amplitude. However, there are two good reasons for focusing on bump amplitude. First, as we will see below, this implementation allows the parameters of the encoded probability distribution to be “read out” in a way that supports the vector operations underlying the circKF (Fig. 1C–F). Second, recent data from the mouse HD system show that the appearance of a visual cue (which increases certainty) causes bump amplitude to increase; moreover, when the bump amplitude is high, the network is relatively insensitive to the appearance of a visual cue that conflicts with the current HD estimate, again suggesting that bump amplitude is a proxy for certainty (19, 35).
Formally, then, the activity of a neuron i with preferred HD ϕi can be written as follows (Fig. 2A):
| [3] |
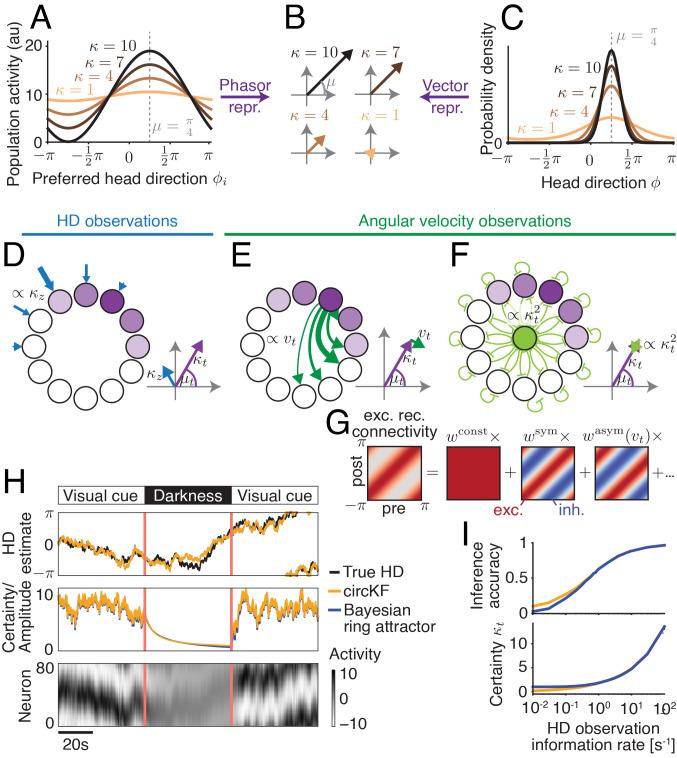
Fig. 2.
A recurrent neural network implementation of the circular Kalman filter. The HD belief vector (B; Fig. 1B) is the “vector representation” of the HD belief (C), and the “phasor representation” (obtained from linear decoding) of sinusoidal population activity (A; neurons sorted by preferred HD ϕi), here shown for HD estimate μ = π/4 (shift of activity/density) and different certainties κ (height of activity bump in A/sharpness of distribution in C). Using this duality between population activity and encoded HD belief, the circular Kalman filter can be implemented by three network motifs (D–F). (D) A cosine-shaped input to the network (strength = observation reliability κz) provides HD observation input. (E) Rotations of the HD belief vector are mediated by symmetric recurrent connectivities, whose strength is modulated by angular velocity observations. (F) Decay in amplitude, which implements decreasing HD certainty, arises from leak and global inhibition. (G) Rotation-symmetric recurrent connectivities (here, neurons are sorted according to their preferred HD) can be decomposed into constant, symmetric, asymmetric, and higher-order frequency components (here dots). (H) The dynamics of the Bayesian ring attractor implement the dynamics of the ideal observer’s belief, as shown in a simulation of a network with 80 neurons. The network received angular velocity observations (always) and HD observations (only in “visual cue” periods). (I) The Bayesian ring attractor network tracks the true HD with the same accuracy (Top; higher = lower average circular distance to true HD; 1 = perfect, 0 = random; Methods) as the circular Kalman filter (circKF, Eqs. 1 and 2) if HD observations are reliable and, therefore, more informative but with slightly lower accuracy once they become less reliable, and therefore less informative. This drop co-occurs with an overestimate in the belief’s certainty κt (Bottom). HD observation reliability is measured here by the amount of Fisher information per unit time. The accuracies and certainties shown are averages over 5,000 simulation runs (Methods for details).
where μt is the encoded HD estimate, κt is the associated certainty, and the “other components” might include a constant (representing baseline activity) or minor contributions of higher-order Fourier components. Note that Eq. 3 does not imply that the tuning curve must be cosine-shaped. Rather, it implies that the cosine component of the tuning curve is scaled by certainty. This is satisfied, for example, by any unimodal bump profile whose overall gain is governed by certainty. A particularly interesting case that matches Eq. 3 is a linear probabilistic population code (36, 37) with von Mises-shaped tuning curves and independent Poisson neural noise (SI Appendix, Fig. S1).
Importantly, this neural representation would allow downstream neurons to read out the parameters of the probability distribution p(ϕt|z0:t, v0:t) in a straightforward manner. Specifically, downstream neurons could take a weighted sum of the population firing rates (i.e., a linear operation; Methods) to recover two parameters, x1 = κtcos(μt) and x2 = κtsin(μt). This is notable because x1 and x2 represent the von Mises distribution p(ϕt|z0:t, v0:t) in terms of Cartesian vector coordinates in the 2D plane, whereas μt and κt are its polar coordinates (Fig. 1B). Having them accessible as vector coordinates makes it straightforward to implement the vector operations underlying the circKF (Fig. 1C –F) in neural population dynamics. For example, as we will see in the next section, the vector sum required to account for HD observations in the circKF (Fig. 1 D and E) can be implemented by summing neural population activity (36). Overall, the vector representation of the HD posterior belief is related to the phasor representation of neural activity (38), which also translates bump position and amplitude to polar coordinates in the 2D plane (Fig. 2B). If the amplitude of the activity bump scales with certainty, the phasor representation of neural activity equals the vector representation of the von Mises distribution (Fig. 2 B and C).
Neural Network Implementation of the Circular Kalman Filter.
Now that we have specified how our model network represents the probability distribution p(ϕt|z0:t, v0:t) over possible head directions, we can proceed to considering the dynamics of this network—specifically, how it responds to incoming information or the lack of information. The circular Kalman filter algorithm describes the vector operations required to dynamically update the probability distribution p(ϕt|z0:t, v0:t) with each new observation of angular velocity or head direction. In the absence of HD observations, the circKF’s certainty decays to zero. By Eq. 3, this implies that neural activity would also decay to zero, such that a network implementing the circKF would not be an attractor network. While we consider such a network in Methods, we here focus on the “Bayesian ring attractor” which approximates the circKF in an attractor network, thus establishing a stronger link to previous working memory literature (1, 2). We describe the features of this network with regard to the HD system, but the underlying concepts are general ones which could be applied to any network that encodes a circular or periodic variable. The dynamics of the Bayesian ring attractor network are given by
| [4] |
where denotes a population activity vector, with neurons ordered by their preferred HD ϕi, τ is the cell-intrinsic leak time constant, is the matrix of excitatory recurrent connectivity that is modulated by angular velocity observations vt, is a vector of HD observations, and g(⋅) is a nonlinear function that determines global inhibition and that we discuss in more detail further below. Let us now consider each of these terms in detail.
First, HD observations enter the network via the input vector in the form of a cosine-shaped spatial pattern whose amplitude scales with reliability κz (Fig. 2D). This implements the vector addition required for the proper integration of these observations. Specifically, the weight assigned to each HD observation is determined by the amplitude of , relative to the amplitude of the activity bump in the HD population. Thus, observations are weighted by their reliability, relative to the certainty of the current HD posterior belief, as in the circular Kalman filter (Fig. 1 D and E). An HD observation that tends to confirm the current HD estimate will increase the amplitude of the bump in HD cells and, thus, the posterior certainty.
Second, the matrix of recurrent connectivity has spatially symmetric and asymmetric components (Fig. 2G). The symmetric component consists of local excitatory connections that each neuron makes onto adjacent neurons with similar HD preferences. This holds the bump of activity at its current location in the absence of any other input. The overall strength of the symmetric component (wsym) is a free parameter which we can tune. Meanwhile, the asymmetric component consists of excitatory connections that each neuron makes onto adjacent neurons with shifted HD preferences. This component tends to push the bump of activity around the ring (Fig. 2E). Angular velocity observations vt modulate the overall strength of the asymmetric component (wasym(vt)), so that positive and negative angular velocity observations push the bump in opposite directions.
Third, the global inhibition term, (Fig. 2F), causes a temporal decay in HD posterior certainty. Here, the function g’s output increases linearly with bump amplitude in the HD population, resulting in an overall quadratic inhibition (Methods). Together with the leak, this quadratic inhibition approximates the nonlinear certainty decay f(κt)/(2(κϕ+κv)) in the circular Kalman filter, Eq. 2, that accounts for both the diffusion prior “noise” 1/κϕ and the noise 1/κv induced by angular velocity observations, both of which are assumed known and constant. The approximation becomes precise in the limit of large posterior certainties κt.
With the appropriate parameter values, the amplitude of the bump decays slowly as long as new HD observations are unavailable, because global inhibition and leak work together to pull the bump amplitude slowly downward (Fig. 2H). This is by design: The circular Kalman filter tells us that certainty decays over time without a continuous stream of new HD observations. This situation differs from conventional ring attractors, whose bump amplitudes are commonly designed to rapidly decay to their stable (attractor) states. In a hypothetical network that perfectly implemented the circular Kalman filter, the bump amplitude would decay to zero. However, in our Bayesian ring attractor, which merely approximates the circular Kalman filter, the bump amplitude decays to a low but nonzero baseline amplitude (κ*).
As an illustrative example, we simulated a network of 80 HD neurons (Methods). We let HD follow a random walk (diffusion on a circle), and we used noisy observations of the time derivative of HD (angular velocity) to modulate the asymmetric component of the connectivity matrix . As HD changes, we rotate the cosine-shaped bump in the external input vector , simulating the effect of a visual cue whose position on the retina depends on HD. This network exhibits a spatially localized bump whose position tracks HD, with an accuracy similar to that of the circular Kalman filter itself (Fig. 2H). Meanwhile, the amplitude of the bump accurately tracks the fluctuating HD posterior certainty in the circular Kalman filter, reflecting how noisy angular velocity and HD observations interact to modulate this certainty, Eq. 2. When the visual cue is removed, the bump amplitude decays toward baseline (Fig. 2H). In the limit of infinitely many neurons, this type of network can be tuned to implement the circular Kalman filter exactly for sufficiently high HD certainties. What this simulation shows is that network performance can come close to benchmark performance even with a relatively small number of neurons (SI Appendix, Fig. S2).
Interestingly, when we vary the reliability of HD observations, we can observe two operating regimes in the network. When HD observations have high reliability, bump amplitude is high and accurately tracks HD certainty (κt). Thus, in this regime, the network performs proper Bayesian inference (Fig. 2I). Conversely, when HD observations have low reliability, bump amplitude is low but constant, because it is essentially pegged to its baseline value (the network’s attractor state). In this regime, bump amplitude exaggerates the HD posterior certainty, and the network looks more like a conventional ring attractor. We will analyze these two regimes further in the next section.
Bayesian vs. Conventional Ring Attractors.
Conventional ring attractors (1, 12, 39) are commonly designed to operate close to their attractor states, so that bump amplitude is nearly constant. This is not true of the Bayesian ring attractor described above, where bump amplitude varies by design. The motivation for this design choice was the idea that, if bump amplitude varies with certainty, the network’s HD estimate would better match the true HD, because evidence integration would be closer to Bayes-optimal. Here, we show that this idea is correct.
Specifically, we measure the average accuracy of the network’s HD encoding for different HD observation reliabilities for both the Bayesian ring attractor and a conventional ring attractor. We vary the HD observation information rate from highly unreliable, leading to almost random HD estimates (circKF inference accuracy close to zero in Fig. 3B), to highly reliable, leading to almost perfect HD estimates (circKF inference accuracy close to one), respectively. To model a conventional ring attractor, we use the same equations as we used for the Bayesian ring attractor, but we adjust the network connection strengths so that the bump amplitude decays to its stable baseline value very quickly (Fig. 3A). Specifically, we strengthen both local recurrent excitatory connections (wsym) and global inhibition () while maintaining their balance, because their overall strengths are what controls the speed (β) of the bump’s return to its baseline amplitude (κ*) in the regime near κ*, assuming no change in the cell-intrinsic leak time constant τ (Methods). With stronger overall connections, the bump amplitude decays to its stable baseline value more quickly. We then adjust the strength of global inhibition without changing the local excitation strength to maximize the accuracy of the network’s HD encoding; note that this changes κ* but not β. This yields a conventional ring attractor where the bump amplitude is almost always fixed at a stable value (κ*), with κ* optimized for maximal encoding accuracy. Even after this optimization of the conventional ring attractor, it does not rival the accuracy of the Bayesian ring attractor. The Bayesian attractor performs consistently better, regardless of the amount of information available to the network, i.e., the level of certainty in the new HD observations (Fig. 3B).
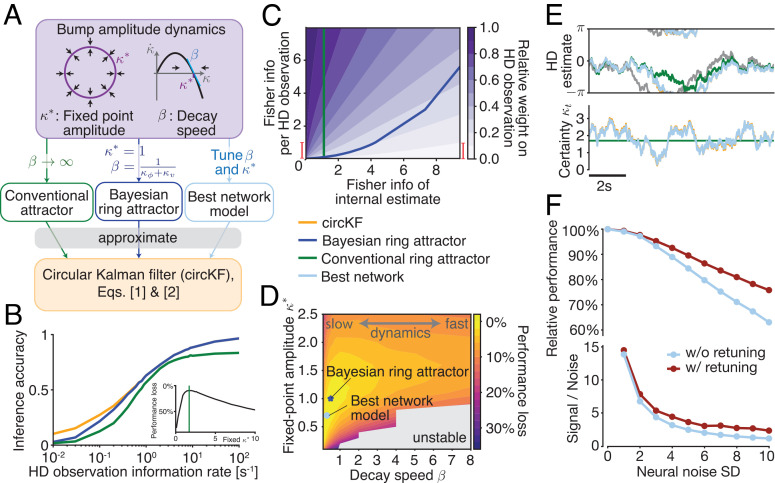
Fig. 3.
Ring attractors with slow dynamics approximate Bayesian inference. (A) The ring attractor network in Eq. 4 can be characterized by fixed point amplitude κ* and decay speed β, which depend on the network connectivities. Thus, the network can operate in different regimes: a regime, where the bump amplitude is nearly constant (“conventional attractor”), a regime where amplitude dynamics are tuned to implement a Bayesian ring attractor, or a regime with optimal performance (“best network,” determined numerically). (B) HD estimation performance as measured by inference accuracy as a function of the HD observation information rate (as in Fig. 2I). κ* for the “conventional” attractor was chosen to numerically maximize average accuracy, weighted by a prior across HD information rates (Inset/Methods). (C) The weight with which a single observation contributes to the HD posterior belief varies with informativeness of both the HD observations (Fisher information for 10-ms observation) and the current HD posterior (weight 1 = HD observation replaces HD estimate; 0 = HD observation leaves HD estimate unchanged). The update weight of the Bayesian attractor is close to optimal, visually indistinguishable from the circKF; not shown here, but SI Appendix, Fig. S3. Fisher information per 10-ms observation is directly related to the Fisher information rate, and the vertical red bar shows the equivalent range of information rate shown in panel B. (D) Overall inference performance loss (compared to a particle filter; performance measured by average inference accuracy, as in B, 0%: same average inference accuracy as a particle filter, 100%: random estimates), averaged across all levels of observation reliability (Methods) as a function of the bump amplitude parameters κ* and β (only for κ* > 0 and β > 0 as infinite network weights arise otherwise). (E) Simulated example trajectories of HD estimate/bump positions of HD estimate/bump positions (Top) and certainties/bump amplitudes (Bottom). The Bayesian ring attractor (not shown) is visually indistinguishable from the circKF and best network. (F) Relative performance (Top; 100% = inference accuracy without neural noise; performance measured as in panel D) and signal-to-noise ratio (Bottom; average κt divided by κt SD due to neural noise) drop with increasing neural noise (noise SD for additive noise in the network of 64 neurons). Retuning β and κ* to maximize performance (purple vs. light blue = optimal parameters for noise-free network, panel D) reduces the drop in inference accuracy and S/N.
This performance difference arises because the conventional ring attractor does not keep track of the HD posterior’s certainty. Ideally, the weight assigned to each HD observation depends on the current posterior certainty, as well as the reliability of the observation itself (Fig. 3C). A conventional ring attractor will assign more reliable observations a higher weight but does not take into account the posterior certainty. By contrast, the Bayesian ring attractor takes all these factors into account (Fig. 3C). The Bayesian ring attractor’s performance drops to that of the conventional ring attractor only once HD observations become highly unreliable. In that regime, the Bayesian ring attractor operates close to its attractor state and thus stops accurately tracking HD certainty, making the attractor–network approximation to the circKF most apparent. Effectively, it becomes a conventional attractor network.
To obtain more insight into the effect of bump decay speed (β) on network performance, we can also simulate many versions of our network with different values of β, which we generate by varying the overall strength of balanced local recurrent excitatory (wsym) and global inhibitory connections (). We in turn vary the overall strength of global inhibition in order to find the best baseline bump amplitude (κ*) for each value of β. The network with the best performance overall had a slow bump decay speed (low β), as expected (Fig. 3 D and E). While it featured similar performance to the Bayesian ring attractor, it had slightly different β and κ* parameters. This is because the Bayesian ring attractor was analytically derived to well approximate the circKF for sufficiently high certainties, whereas the “best network” was numerically optimized to perform well on average. As the bump decay speed β increased further, performance dropped. However, this could be partially mitigated by increasing baseline bump amplitude (κ*) to prevent overweighting of new observations.
We have seen that a slow bump decay (low β), i.e., the ability to deviate from the attractor state, is essential for uncertainty-related evidence weighting. That said, lower values of β are not always better. In the limit of very slow decay (β → 0), bump amplitude would grow so large that new HD observations have little influence rendering the network nearly “blind” to visual landmarks. Conversely, in the limit of fast dynamics (β → ∞), the network is highly responsive to new observations; however, it also has almost no ability to weight those new observations relative to other observations in the recent past. In essence, β controls the speed of temporal discounting in evidence integration. Ideally, the bump decay speed β should be matched to the expected speed at which stored evidence becomes outdated and thus loses its value, as controlled by κϕ and κv.
To summarize, we can frame the distinction between a conventional ring attractor and a Bayesian ring attractor as a difference in the speed of the bump’s decay to its stable state. In a conventional ring attractor, the bump decays quickly to its stable state, whereas in a Bayesian ring attractor, it decays slowly. Slow decay maximizes the accuracy of HD encoding because it allows the network to track its own internal certainty. Nonetheless, reasonable performance can be achieved even if the bump’s decay is fast because a conventional ring attractor can still assign more informative observations a higher weight; it simply fails to assign the current HD estimate its proper weight.
The Impact of Neural Noise on Inference Accuracy.
So far, we have assumed that the only sources of noise in our network are noisy angular velocity and HD observations. However, biological networks consist of neurons that are themselves noisy, resulting in another source of noise (40). What is the impact of that noise on inference accuracy?
If the network contains a sufficient number of similarly tuned neurons, their noise can be easily averaged out (37, 41), so that neural noise does not have a noticeable impact on the accuracy of inference. That said, for smaller networks, like those of insects (42), neural noise might significantly decrease inference accuracy. Indeed, simulating a network of 64 noisy neurons shows that, once the noise becomes sufficiently large, inference accuracy drops to below 70% of its noise-free value (Fig. 3F).
To better understand how neural noise perturbs inference, we derived its impact on the dynamics of the HD estimate μt and its certainty κt (SI Appendix). The derivations revealed that, irrespective of the form of the neural noise (additive, multiplicative, etc.), this noise has two effects. First, it causes an unbiased random diffusion of μt and, thus, an increasingly imprecise memory of the HD estimate. Second, it causes a positive drift and random diffusion of κt, which, if the drift is not accounted for, results in an overestimation of one’s certainty and thus overconfidence in the HD estimate. These results mirror previous work that has shown a diffusion of μt in ring attractors close to the attractor state (41). We here show that such a diffusion persists even if the network operates far away from the attractor state, as is the case in our Bayesian ring attractor. While it is impossible to completely suppress the impact of neural noise, the derivations revealed that we can lessen its impact by retuning the network’s connectivity strengths. Indeed, doing so reduced the drop in inference accuracy by about 35% when compared to the network tuned to optimize noise-free performance (Fig. 3 D and F) and also boosted the network’s signal-to-noise ratio (Fig. 3F). Lastly, our derivations show that the impact of noise vanishes once the network’s population size becomes sufficiently large, in line with previous results (41). For example, increasing the network size four-fold would halve the effective noise’s SD (assuming additive noise, SI Appendix). Overall, we have shown that neural noise causes a drop in performance that can in part be mitigated by retuning the network’s connectivity strengths or by increasing its population size.
Tuning a Biological Ring Attractor for Bayesian Performance.
Thus far, we have focused on model ring attractors with connection weights built from spatial cosine functions (Fig. 2G) because this makes the mathematical treatment of these networks more tractable. However, this raises the question of whether a biological neural network can actually implement an approximation of the circular Kalman filter, even without these idealized connection weights. The most well-studied biological ring attractor network is the HD system of the fruit fly Drosophila melanogaster (Fig. 4A) (17), and the detailed connections in this network have recently been mapped using large-scale electron microscopy connectomics (42). We therefore asked whether the motifs from this connectomic dataset—and, by extension, motifs that could be found in any biological ring attractor network—could potentially implement dynamic Bayesian inference.
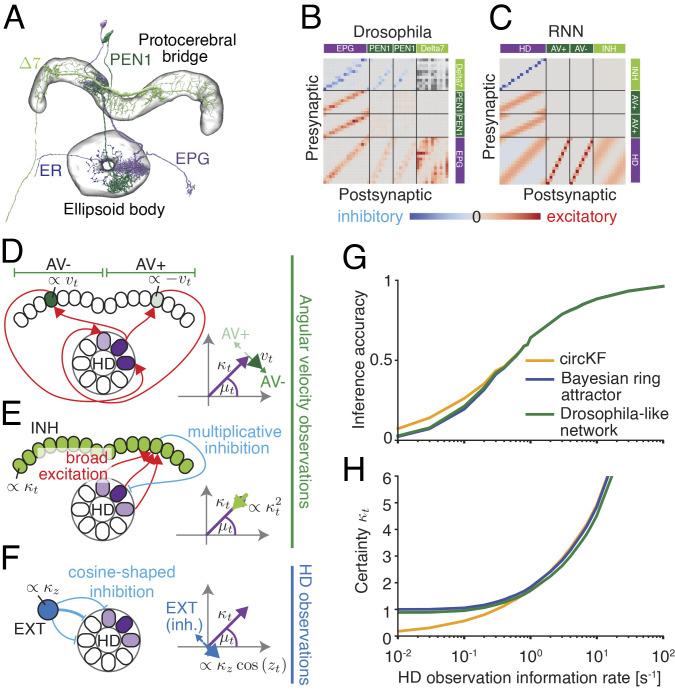
Fig. 4.
A Drosophila-like network implementing the circular Kalman filter. (A) Cell types in the Drosophila brain that could contribute to implementing the circular Kalman filter. (B) Connectivity between EPG, Δ7, and PEN1 neurons, as recovered from the hemibrain:v1.2.1 database (43). Neurons were sorted by their spatial position as a proxy for their preferred HD. The total number of synaptic connections between each cell pair was taken to indicate the functional connection strength between these cells. The polarity of Δ7 → Δ7 connections is unknown, and therefore, these connections are omitted. (C) The connectivity profile of a recurrent neural network (RNN) (Fig. 2D–F) that implements an approximate circKF is strikingly similar to the connectivity of neurons in the Drosophila HD system. To avoid confusion with actual neurons, we refer to the neuronal populations in this idealized RNN as head direction (HD), angular velocity (AV+ and AV-, in reference to the two hemispheres), inhibitory (INH), and external input (EXT) populations. (D) Differential activation of AV populations (left/right: high/low) across hemispheres as well as shifted feedback connectivity from AV to HD populations effectively implements the asymmetric (or shifted) connectivity needed to turn the bump position (here, clockwise shift for anticlockwise turn). (E) Broad excitation of the INH population by the HD population, together with a one-to-one multiplicative interaction between INH and HD population, implements the quadratic decay of the bump amplitude needed for the reduction in certainty arising from probabilistic path integration. (F) External input is mediated by inhibiting HD neurons with the preferred direction opposite to the location of the HD observation, effectively implementing a vector sum of belief with HD observation. (G and H) The inference accuracy of the Drosophila-like network is indistinguishable from that of the Bayesian ring attractor. Inference accuracy, certainty, and HD observation information rate are measured as for Fig. 2I.
To address this issue, we modeled the key cell types in this network (42–44) (HD cells, angular velocity cells, and global inhibition cells), using connectome data to establish the patterns of connectivity between each cell type (Fig. 4B –F and SI Appendix, Text). We then analytically tuned the relative connection strengths between different cell types such that the dynamics of the bump parameters in the HD population implement an approximation of the circular Kalman filter. We also added a nonlinear element in the global inhibition layer as this is required to approximate the circular Kalman filter. We found that this network achieves a HD encoding accuracy which is indistinguishable from that of our idealized Bayesian ring attractor network (Fig. 4 G and H). Thus, even when we use connectome data to incorporate biological constraints on the network, the network is still able to implement dynamic Bayesian inference.
Discussion
Uncertainty can affect navigation strategy (45, 46), spatial cue integration (47, 48), and spatial memory (49). This provides a motivation for understanding how uncertainty is represented in the neural networks that encode and store spatial variables for navigation. There is good reason to think that these networks are built around attractors. Thus, it is crucial to understand how attractors in general—and ring attractors in particular—might track uncertainty in spatial variables like head direction.
In this study, we have shown that a ring attractor can track uncertainty by operating in a dynamic regime away from its stable baseline states (its attractor states). In this regime, bump amplitude can vary because local excitatory and global inhibitory connections in the ring attractor are relatively weak. By contrast, stronger overall connections produce a more conventional ring attractor that operates closer to its attractor states. Because the “Bayesian” ring attractor has a variable bump amplitude, bump amplitude grows when recent HD observations have been more reliable; in this situation, the network automatically ascribes more weight to its current estimate, relative to new evidence. Importantly, we have shown that nearly optimal evidence weighting does not require exact tuning of the network connections. Indeed, even when we used connectome data to implement a network with realistic biological connectivity constraints, the network could still support near-optimal evidence weighting.
A key element of our approach is that bump amplitude is used to represent the internal certainty of the system’s Bayesian HD posterior belief. In our framework, internal certainty determines the weight ascribed to new evidence, relative to past evidence. As such, the representation of internal certainty plays a crucial role in maximizing the accuracy of our Bayesian ring attractor. This stands in contrast to recent network models of the HD system that do not encode internal certainty, even though they weigh HD observations in proportion to their reliabilities (50, 51). Notably, our network also automatically adjusts its cue integration weights to perform close-to-optimal Bayesian inference for HD observations of varying reliability. Recent work (52) described how observations of a circular variable (such as HD) could be integrated across brief time periods, provided that these observations all have the same reliability; however, this work considered neither the problem of integrating observations of differing reliability nor the role of angular velocity observations. Moreover, the network described in that study operated below the fixed point of the bump amplitude, and therefore, it can only correctly weight incoming observations over a short period before reaching the fixed point.
Another important element of our approach was that we benchmarked our network model against a rigorous normative standard, the circular Kalman filter, which was derived analytically in ref. 31 and described here in terms of intuitive vector operations. Being able to rely on the circular Kalman filter was important because it allowed us to analytically derive the proper parameter values of our network model, so that the network’s estimate matched the estimate of an ideal observer. A remarkable property of the circular Kalman filter is that new HD observations will actually decrease certainty if they conflict strongly with the current estimate. This is not a property of a standard (noncircular) Kalman filter or a neural network designed to emulate it (33). The power of conflicting evidence to decrease certainty is particular to the circular domain. Our Bayesian ring attractor network automatically reproduces this important aspect of the circular Kalman filter. Of course, the circular Kalman filter has applications beyond neural network benchmarking, as the accurate estimation of orientation or any other periodic variable has broad applications in the field of engineering.
When adequately tuned, our network can implement a persistent working memory of a circular variable, as, for example, the orientation of a visual stimulus in a visual working memory task. Recent models for such tasks attribute memory recall errors to the stochastic emission of a limited number of spikes (7, 53). As in our network, neural noise can be averaged out once the network has a sufficiently large number of neurons; for this reason, memory errors can be attributed only to the noise of individual neurons in small networks with few neurons. Significant memory errors in larger Bayesian ring attractors thus have to result from other sources of noise, such as imperfect connectivity weights, or correlated input noise from, e.g., shared inputs, that fundamentally limits the amount of information that these inputs provide to the network (54).
In the brain’s HD system, the internal estimate of HD is based on not only HD observations (visual landmarks, etc.) but also angular velocity observations. The process of integrating these angular velocity observations over time is called angular path integration. Angular path integration is inherently noisy, and therefore, uncertainty will grow progressively when HD observations are lacking. Our Bayesian ring attractor network is notable in explicitly treating angular path integration as a problem of probabilistic inference. Each angular velocity observation has limited reliability, and this causes the bump amplitude to decay in our network as long as HD observations are absent, in a manner that well approximates the certainty decay of an ideal observer. In this respect, our network differs from previous investigations of ring attractors having variable bump amplitude (55).
Our work makes several testable predictions. First, we predict that the HD system should contain the connectivity motifs required for a Bayesian ring attractor. Our analysis of Drosophila brain connectome data supports this idea; we expect similar network motifs to be present in the HD networks of other animals, such as that of mice (15, 19), monkeys (56), humans (57), or bats (58). In the future, it will be interesting to determine whether synaptic inhibition in these networks is nonlinear, as predicted by our models.
Second, we predict that bump amplitude in the HD system should vary dynamically, with higher amplitudes in the presence of reliable external HD cues, such as salient visual landmarks. In particular, when bump amplitude is high, the bump’s position should be less sensitive to the appearance of new external HD cues. Notably, an experimental study from the mouse HD system provides some initial support for these predictions (19). This study found that the amplitude of population activity in HD neurons (what we call bump amplitude) increases in the presence of a reliable visual HD cue. Bump amplitude also varied spontaneously when all visual cues were absent (in darkness); intriguingly, when the bump amplitude was higher in darkness, the bump position was slower to change in response to the appearance of a visual cue, suggesting a lower sensitivity to the cue. In the future, more experiments will be needed to clarify the relationship between bump amplitude, certainty, and cue integration. In particular, it is puzzling that multiple studies (16, 18, 19, 24, 59, 60) have found that bump amplitude increases with angular velocity, as higher angular velocities should not increase certainty.
In the future, more investigation will be needed to understand evidence accumulation on longer timescales. The circular Kalman filter is a recursive estimator: At each time step, it considers only the observer’s internal estimate from the previous time step as well as the current observation of new evidence. However, when the environment changes, it would be useful to use a longer history of past observations (and past internal estimates) to readjust the weight assigned to the changing sources of evidence. Available data suggest that Hebbian plasticity can progressively strengthen the influence of the external sensory cues that are most reliably correlated with HD (17, 49, 61, 62). The interaction of Hebbian plasticity with attractor dynamics could provide a mechanism for extending statistical inference to longer timescales (13, 63–69).
In summary, our work shows how ring attractors could implement dynamic Bayesian inference in the HD system. Our results have significance beyond the encoding of head direction—e.g., they are potentially relevant for the grid cell ensemble, which appears to be organized around ring attractors even though it encodes linear rather than circular variables. Moreover, our models could apply equally to any brain system that needs to compute an internal estimate of a circular or periodic variable, such as visual object orientation (6, 70) or circadian time. More generally, our results demonstrate how canonical network motifs, like those common in ring attractor networks, can work together to perform close-to-optimal Bayesian inference, a problem with fundamental significance for neural computation.
Materials and Methods
Ideal Observer Model: The Circular Kalman Filter.
Our ideal observer model—the circular Kalman filter (circKF) (31)—performs dynamic Bayesian inference for circular variables. It computes the posterior belief of an unobserved (true) HD ϕt ∈ [ − π, π] at each point in time t, conditioned on a continuous stream of noisy angular velocity observations v0:t = {v0, vdt, …vt} with vτ ∈ ℝ, and HD observations z0:t = {z0, zdt, …zt} with zτ ∈ [ − π, π]. In contrast to the discrete-time description in Results, we here provide a continuous-time formulation of the filter. Specifically, we assume that these observations are generated from the true angular velocity and HD ϕt, corrupted by zero-mean noise at each point in time, via
| [5] |
| [6] |
Here, 𝓝(μ, σ2) denotes a Gaussian with mean μ and variance σ2, 𝓥𝓜(μ, κ) denotes a von Mises distribution of a circular random variable with mean μ and precision κ, and κv and κz quantify reliabilities of angular velocity and HD observations, respectively. Note that as dt → 0, the precision values of both angular velocity and HD observations approach 0, in line with the intuition that reducing a time-step size dt results in more observations per unit time, which should be accounted for by less precision per observation to avoid “oversampling” (SI Appendix for a subtlety for how κz scales with time).
To support integrating information over time, the model assumes that current HD ϕt depends on past HD ϕt − dt. Specifically, in the absence of further evidence, the model assumes that HD diffuses on a circle,
| [7] |
with a diffusion coefficient that decreases with κϕ.
The circKF in Eqs. 1 and 2 assumes that the HD posterior belief can be approximated by a von Mises distribution with time-dependent mean μt and certainty κt, i.e. p(ϕt|v0:t, z0:t)≈𝓥𝓜(ϕt; μt, κt). Such an approximation is justified if the posterior is sufficiently unimodal and can, for instance, be compared to a similar approximation employed by extended Kalman filters for noncircular variables.
An alternative parametrization of the von Mises distribution to its mean μt and precision κt is its natural parameters, xt = (κtcosμt, κtsinμt)T. Geometrically, the natural parameters can be interpreted as the Cartesian coordinates of a “HD belief vector” and (μt, κt) as its polar coordinates (Fig. 1B). As we show in SI, the natural parameter parametrization makes including HD observations in the circKF straightforward. In fact, it becomes a vector addition. In contrast, including angular velocity observations is mathematically intractable, such that the circKF relies on an approximation method called projection filtering (30) to find closed-form dynamic expressions for posterior mean and certainty (see ref. 31 for technical details and SI Appendix for a more accessible description of the circKF).
Taken together, the circKF for the model specified by Eqs. 5–7 reads
| [8] |
| [9] |
which is the continuous-time equivalent to Eqs. 1 and 2 in Results and where f(κ) is a monotonically increasing nonlinear function,
| [10] |
and I0(⋅) and I1(⋅) denote the modified Bessel functions of the first kind of order 0 and 1, respectively.
For a sufficiently large κ (i.e., high certainty), the nonlinearity f(κ) approaches the linear function, f(κ)→2κ − 2. In our quadratic approximation, we thus replace the nonlinearity with a quadratic decay:
| [11] |
which well approximates the circKF in the high certainty regime.
Network Model.
We derived a rate-based network model that implements (approximations of) the circKF, by encoding the von Mises posterior parameters in activity rt ∈ ℝN of a neural population with N neurons. Thereby, we focused on the simplest kind of network model that supports such an approximation, which is given by Eq. 4. In that equation, τ is the cell-intrinsic leak time constant, g : ℝN → ℝ+ is a scalar nonlinearity, and the elements of rt are assumed to be ordered by the respective neuron’s preferred HD, ϕ1, …, ϕN (Eq. 3). We decomposed the recurrent connectivity matrix into , where 11T is a matrix filled with 1’s, and Wcos and Wsin refer to cosine- and sine-shaped connectivity profiles (Fig. 2G). The network’s circular symmetry makes the entries of these matrices depend only on the relative distance in preferred HD, and the entries are given by , and . The scaling factor was chosen to facilitate matching our analytical results from the continuum network to the network structure outlined here. We further considered a cosine-shaped external input of the form Itext(ϕi)=It(dt)cos(Φt − ϕi) that is peaked around an input location Φt. Here, It(dt) denotes the input pattern in the infinitesimal time bin dt.
As described in Results, we assume the population activity rt to encode the HD belief parameters μt and κt in the phase and amplitude of the activity’s first Fourier component. As we show in SI Appendix, the described network dynamics thus lead to the following dynamics of the cosine-profile parameters μt and κt:
| [12] |
| [13] |
To derive these dynamics, we make the following three assumptions. First, we assume the network to be rate based. Second, our analysis assumes a continuum of neurons, i.e., N → ∞. For numerical simulations, and the network description below, we used a finite-sized network of size N that corresponds to a discretization of the continuous network. SI Appendix, Fig. S2 demonstrates only a very weak dependence of our results on the exact number of neurons in the network. Third, our analysis and simulations focused on the first Fourier mode of the bump profile and is thus independent of the exact shape of the profile (as long as Eq. 3 holds).
Network parameters for Bayesian inference.
Having identified how the dynamics of μt and κt encoded by the network, Eqs. 12 and 13 depend on the network parameters, we now tuned these parameters to match these dynamics to those of the mean and certainty of the circKF, Eqs. 8 and 9. Here, we first do so to achieve an exact match to the circKF, without the quadratic approximation. After that, we describe the quadratic approximation that is used in the main text and leads to the Bayesian ring attractor network. Specifically, an exact match to the circKF requires the following network parameters:
Asymmetric recurrent connectivities are modulated by angular velocity observations, , which shifts the activity profile without changing its amplitude (12, 13).
HD observations zt are represented as the peak position Φt of a cosine-shaped external input whose amplitude is modulated by the reliability of the observation, i.e., It = κz dt. The inputs might contain additional Fourier modes (e.g., a constant baseline), but those do not affect the dynamics in Eqs. 12 and 13.
The symmetric component of the recurrent excitatory input needs to exactly balance the internal activity decay, i.e., .
The decay nonlinearity is modulated by the reliability of the angular velocity observations and is given by , where f(⋅) equals the nonlinearity that governs the certainty decay in the circKF, Eq. 10. This can be achieved, for example, through interaction with an inhibitory neuron (or a pool of inhibitory neurons) with activation function f(⋅) that computes the activity bump’s amplitude κ(rt).
A network with these parameters is not an attractor network, as its activity decays to zero in the absence of external inputs.
To arrive at the Bayesian ring attractor, we approximate the decay nonlinearity by a quadratic approximation that takes the form , where [ ⋅ ]+ denotes the rectification nonlinearity. The resulting recurrent inhibition can be shown to be quadratic in the amplitude κt and has the further benefit of introducing an attractor state at a positive bump amplitude (below). In the large population limit, N → ∞, this leads to the amplitude dynamics (SI Appendix for derivation)
| [14] |
The dynamics of the phase μt does not depend on the form of g(⋅) and thus remains to be given by Eq. 12. If we set the network parameters to and , while sensory input, i.e., angular velocity vt and HD observations zt, enters in the same way as before, the network implements the quadratic approximation to the circKF, Eqs. 8 and 11.
General ring-attractor networks with fixed point κ* and decay speed β.
In the absence of HD observations (It = 0), the amplitude dynamics in Eq. 14 has a stable fixed point at and no preferred phase, making it a ring-attractor network. Linearizing the κt dynamics around this fixed point reveals that it is approached with decay speed . Therefore, we can tune the parameters to achieve a particular fixed point κ* and decay speed β by setting wsym = β + 1/τ and . A large value of β requires increasing both wsym and wquad, yields faster dynamics, and thus indicates more rigid attractor dynamics. In the limit of β → ∞, the attractor becomes completely rigid in the sense that, upon any perturbation, it immediately moves back to its attractor state. In the main text, we assume conventional ring attractors to operate close to this rigid regime. For the Bayesian ring attractor, we find κ* = 1 and . Further, in our simulations in Fig. 3, we explored network dynamics with a range of κ* and β values by adjusting network parameters accordingly.
Assessing the Impact of Neural Noise on Inference Accuracy.
In SI Appendix, we show that neural noise results in an unbiased diffusion of μt and a diffusion and positive drift of κt. We assessed the impact of this noise on inference accuracy by simulating a network with N = 64 neurons and κ* and β tuned to maximize noise-free inference accuracy (“Best network model” in Fig. 3D) and by adding Gaussian zero-mean white noise with variance σnn2δt in each time step δt to each neuron, for different levels of σnn (Fig. 3F, light blue lines). We computed the signal-to-noise ratio for each simulation as the average κt divided by the diffusion noise SD that additive neural noise causes in κt (SI Appendix for derivation). The impact of this noise can be reduced by retuning the network’s connectivity strengths. We did so for each neural noise magnitude separately by a grid search over κ* and β (SI Appendix, Fig. S4), similar to the previous section (Fig. 3F, purple lines).
Drosophila-like multipopulation network.
We extended the single population network dynamics, Eq. 4, to encompass five populations: a HD population, which we designed to track HD estimate and certainty with its bump parameter dynamics; two angular velocity populations (AV+ and AV-), which are tuned to HD and are differentially modulated by angular velocity input; an inhibitory population (INH); and a population that mediates external input (EXT), corresponding to HD observations. The network parameters were tuned such that the activity profile in the HD population tracks the dynamics of the circKF quadratic approximation, in the same way as for the single-population network, Eq. 4. To limit the degrees of freedom, we further constrained the connectivity structure between HD and AV+/- and INH populations by the known connectome of the Drosophila HD system (hemibrain dataset in ref. 42) and tuned only across-population connectivity weights. For further details on the network dynamics and with- and across-population connectivity weights, please consult SI Appendix.
Simulation Details.
Numerical integration.
Our simulations in Figs. 2–4 used artificial data that matched the assumptions underlying our models. In particular, the “true” HD ϕt followed a diffusion on the circle, Eq. 7, and observations were drawn at each point in time from Eqs. 5 and 6. To simulate trajectories and observations, we used the Euler–Maruyama scheme (71), which supports the numerical integration of stochastic differential equations. Specifically, for a chosen discretization time step Δt, this scheme is equivalent to drawing trajectories and observations from Eqs. 7, 5, and 6 directly while substituting dt → Δt. The same time-discretization scheme was used to numerically integrate the SDEs of the circKF, Eqs. 8 and 9 and its quadratic approximation, Eq. 11.
Performance measures.
To measure performance, in Figs. 2I, 3 B and D and 4 G and H, we computed the circular average distance (72) of the estimate μT from the true HD ϕT at the end of a simulation of length T = 20 from P = 5′000 simulated trajectories by . The absolute value of the imaginary-valued circular average, 0 ≤ |m1|≤1, is unitless and denotes an empirical accuracy (or “inference accuracy”) and thus measures how well the estimate μT matches the true HD ϕT. Here, a value of 1 denotes an exact match. The reported inference accuracy is related to the circular variance via Varcirc = 1 − |m1|. In SI Appendix, Fig. S5, we provide histograms with samples μT − ϕT with different numerical values of |m1| to provide some intuition for the spread of estimates for a given value of the performance measure.
We estimated performance through such averages for a range of HD observation information rates in Figs. 2I, 3B and 4G. This information rate is a simulation time-step size-independent quantity, which measures the Fisher information that HD observations provide about true HD per unit time. For individual HD observations of duration dt, Eq. 6, this Fisher information approaches Izt(ϕt)→(κzdt)2/2 with dt → 0 (31, Theorem 2]. Per unit time, we observe 1/dt independent observations, leading to a total Fisher information (or information rate) of γz = κz2dt/2. As in simulations, γz needs to remain constant with changing Δt to avoid increasing the amount of provided information, the HD observation reliability κz needs to change with the size of simulation time-step size Δt. To keep our plots independent of this time-step size, we thus plot performance as a function of the HD observation information rate rather than κz. For the inset of Fig. 3B, and for Figs. 3 D and F, we additionally performed a grid search over the fixed-point κ* (Fig. 3B, inset) or both the fixed-point κ* and of the decay speed β (Figs. 3 D and F). For each setting of κ* and β, we assessed the performance by computing an average over this performance for a range of HD observation information rates, weighted by how likely each observation reliability is assumed to be a priori. The latter was specified by a log-normal prior, p(γz)=Lognormal(γz|μγz, σγz2), favoring intermediate reliability levels. We chose μγz = 0.5 and σγz2 = 1 for the prior parameters, but our results did not strongly depend on this parameter choice. The performance loss shown in Fig. 3D also relied on such a weighted average across information rates γz for a particle filter benchmark (PF, SI for details). The loss itself was then defined as .
Update weights for HD observations.
In Fig. 3C, we computed the weight with which a single HD observation with |zt − μt|=90° changes the HD estimate. We defined this weight as the change in HD estimate, normalized by the value of the maximum possible change, . To make units intuitively comparable between the two axes, we chose to scale the y-axis in units of Fisher information of a single HD observation of duration Δt = 10ms, given by Izt(ϕt)=γz Δt where γz = κz2Δt/2. Thus, the weight is plotted as a function of the Fisher information of a single HD observation (how reliable is the observation?) and the Fisher information of the current HD posterior belief (how certain is the current estimate?), which is given by (31).
Simulation parameters.
In our network simulations, we set the leak time constant τ to an arbitrary, but nonzero, value. Effectively, this resulted in a cosine-shaped activity profile. Note that by setting higher-order recurrent connectivities accordingly, other profile shapes could be realized, without affecting the validity of our analysis from the neural activity vector rt, we retrieved the natural parameters xt with a decoder matrix A = (cos(ϕ),sin(ϕ))T, such that xt = A ⋅ rt, and subsequently computed the position of the bump by ϕt = arctan2(x2, x1) and the encoded certainty (length of the population vector) by .
In all our simulations, times are measured in units of inverse diffusion time constant κϕ, where we set κϕ = 1s for convenience. We used the following simulation parameters. For Fig. 2H, we used κv = 2 and information rate of HD observations of γz = 10/s (equaling κz ≈ 45; during “Visual cue” period) and κz = 0 (during “Darkness” period). For Figs. 2I and 3 B and D we used κv = 1, T = 20, and averaged results over P = 5, 000 simulation runs. For Fig. 3E, we used κv = 1, information rate of γz = 1/s (equaling κz ≈ 14), T = 10. In the network simulations in Fig. 2 H and I and Fig. 3 B and D, we translated these parameters into network connectivity parameters according to our analytical results in SI Appendix, section 3B. Without loss of generality, we set all connectivity parameters that are not explicitly mentioned, to zero (including wconst). Please consult SI Appendix for details on the Drosophila network simulation parameters. We used Δt = 0.01 for all simulations.
Trajectory simulations and general analyses were performed on a MacBook Pro (Mid 2019) running 2.3 GHz 8-core Intel Core i9. Parameter scans were run on the Harvard Medical School O2 HPC cluster. For all our simulations, we used Python 3.9.1 with NumPy 1.19.2.
Supplementary Material
Appendix 01 (PDF)
Acknowledgments
We would like to thank Habiba Noamany for assisting us in navigating the neuPrint database and for informed comments on the manuscript. We would further like to thank Johannes Bill and Albert Chen for discussions and feedback on the manuscript, Philipp Reinhard for going on a typo hunt in SI Appendix, and the entire Drugowitsch lab for valuable and insightful discussions. The work was funded by the NIH (R34NS123819; J.D. & R.I.W), the James S. McDonnell Foundation (Scholar Award #220020462; J.D.), the Swiss NSF (grant numbers P2ZHP2 184213 and P400PB 199242; A.K.), and a Grant in the Basic and Social Sciences by the Harvard Medical School Dean’s Initiative award program (J.D. & R.I.W.).
Author contributions
A.K., M.A.B., R.I.W., and J.D. designed research; A.K., M.A.B., R.I.W., and J.D. performed research; A.K. and J.D. contributed new reagents/analytic tools; A.K. and J.D. analyzed data; and A.K., M.A.B., R.I.W., and J.D. wrote the paper.
Competing interests
The authors declare no competing interest.
Footnotes
This article is a PNAS Direct Submission.
Contributor Information
Anna Kutschireiter, Email: anna.kutschireiter@gmail.com.
Jan Drugowitsch, Email: jan_drugowitsch@hms.harvard.edu.
Data, Materials, and Software Availability
Computer simulations and data analysis were performed with custom Python code, which has been deposited in Zenodo, DOI: 10.5281/zenodo.7615975.
Supporting Information
References
- 1.Wang X. J., Synaptic reverberation underlying mnemonic persistent activity. Trends Neurosci. 24, 455–463 (2001). [DOI] [PubMed] [Google Scholar]
- 2.Compte A., Computational and in vitro studies of persistent activity: Edging towards cellular and synaptic mechanisms of working memory. Neuroscience 139, 135–151 (2006). [DOI] [PubMed] [Google Scholar]
- 3.D. Hansel, H. Sompolinsky, “Modeling feature selectivity in local cortical circuits” in Methods in Neuronal Modeling: From Ions to Networks, Computational Neuroscience Series, C. Koch, I. Segev, Eds. (1998), p. 69.
- 4.Hopfield J. J., Neural networks and physical systems with emergent collective computational abilities. Proc. Natl. Acad. Sci U.S.A. 79, 2554–2558 (1982). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Rademaker R. L., Tredway C. H., Tong F., Introspective judgments predict the precision and likelihood of successful maintenance of visual working memory. J. Vision 12, 21 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Li H. H., Sprague T. C., Yoo A. H., Ma W. J., Curtis C. E., Joint representation of working memory and uncertainty in human cortex. Neuron 109, 3699–3712.e6 (2021). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.P. Bays, S. Schneegans, W. J. Ma, T. Brady, Representation and computation in working memory. PsyArXiv (2022). [DOI] [PubMed]
- 8.Ernst M. O., Banks M. S., Humans integrate visual and haptic information in a statistically optimal fashion. Nature 415, 429–433 (2002). [DOI] [PubMed] [Google Scholar]
- 9.Piet A. T., Hady A. E., Brody C. D., El Hady A., Brody C. D., Rats adopt the optimal timescale for evidence integration in a dynamic environment. Nat. Commun. 9, 1–12 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Fetsch C. R., Turner A. H., DeAngelis G. C., Angelaki D. E., Dynamic reweighting of visual and vestibular cues during self-motion perception. J. Neurosci. 29, 15601–15612 (2009). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Knierim J. J., Zhang K., Attractor dynamics of spatially correlated neural activity in the limbic system. Ann. Rev. Neurosci. 35, 267–285 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Zhang K., Representation of spatial orientation by the intrinsic dynamics of the head-direction cell ensemble: A theory. J. Neurosci. 16, 2112–2126 (1996). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.W. Skaggs, J. Knierim, H. Kudrimoti, B. McNaughton, “A model of the neural basis of the rats sense of direction” in Advances in Neural Information Processing Systems, G. Tesauro, D. Touretzky, T. Leen, Eds. (MIT Press, 1994), vol. 7. [PubMed]
- 14.A. D. Redish, A. N. Elga, D. S. Touretzky, A coupled attractor model of the rodent head direction system. Network: Comput. Neural Syst. 7, 671–685 (1996), 10.1088/0954-898X/7/4/004. [DOI]
- 15.Peyrache A., Lacroix M. M., Petersen P. C., Buzsáki G., Internally organized mechanisms of the head direction sense. Nat. Neurosci. 18, 569–575 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Seelig J. D., Jayaraman V., Neural dynamics for landmark orientation and angular path integration. Nature 521, 186–191 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Kim T. D., Kabir M., Gold J. I., Coupled decision processes update and maintain saccadic priors in a dynamic environment. J. Neurosci. 37, 3632–3645 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Turner-Evans D., et al. , Angular velocity integration in a fly heading circuit. eLife 6, e23496 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Z. Ajabi, A. T. Keinath, X. X. Wei, M. P. Brandon, Population dynamics of the thalamic head direction system during drift and reorientation (bioRxiv, Tech. rep. 2021).
- 20.Amari Si., Dynamics of pattern formation in lateral-inhibition type neural fields. Biol. Cybern. 27, 77–87 (1977). [DOI] [PubMed] [Google Scholar]
- 21.Ermentrout B., Neural networks as spatio-temporal pattern-forming systems. Rep. Progr. Phys. 61, 353–430 (1998). [Google Scholar]
- 22.Heinze S., Narendra A., Cheung A., Principles of insect path integration. Curr. Biol.?: CB 28, R1043–R1058 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Xie X., Hahnloser R. H., Seung H. S., Double-ring network model of the head-direction system. Phys. Rev. E - Stat. Phys. Plasmas Fluids Relat. Interdiscip. Topics 66, 9–9 (2002). [DOI] [PubMed] [Google Scholar]
- 24.J. Green et al., A neural circuit architecture for angular integration in Drosophila. Nature 546, 101–106 (2017). [DOI] [PMC free article] [PubMed]
- 25.Knill D. C., Pouget A., The Bayesian brain: The role of uncertainty in neural coding and computation. Trends Neurosci. 27, 712–719 (2004). [DOI] [PubMed] [Google Scholar]
- 26.Dehaene G. P., Coen-Cagli R., Pouget A., Investigating the representation of uncertainty in neuronal circuits. PLOS Comput. Biol. 17, e1008138 (2021). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Kalman R. E., A new approach to linear filtering and prediction problems. Trans. ASME J. Basic Eng. 82, 35–45 (1960). [Google Scholar]
- 28.Kalman R. E., Bucy R. S., New results in linear filtering and prediction theory. J. Basic Eng. 83, 95–108 (1961). [Google Scholar]
- 29.G. Kurz, F. Pfaff, U. D. Hanebeck, “Kullback-Leibler Divergence and moment matching for hyperspherical probability distributions” in 2016 19th International Conference on Information Fusion (FUSION). No. July (2016), pp. 2087–2094.
- 30.Brigo D., Hanzon B., Le Gland F., Approximate nonlinear filtering by projection on exponential manifolds of densities. Bernoulli 5, 495–534 (1999). [Google Scholar]
- 31.Kutschireiter A., Rast L., Drugowitsch J., Projection filtering with observed state increments with applications in continuous-time circular filtering. IEEE Trans. Signal Proc. 70, 686–700 (2022). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Murray R. F., Morgenstern Y., Cue combination on the circle and the sphere. J. Vision 10, 15–15 (2010). [DOI] [PubMed] [Google Scholar]
- 33.Wilson R., Finkel L., A neural implementation of the Kalman filter. Adv. Neural Inf. Proc. Syst. 22, 9 (2009). [Google Scholar]
- 34.Ben-Yishai R., Bar-Or R. L., Sompolinsky H., Theory of orientation tuning in visual cortex. Proc. Natl. Acad. Sci. U.S.A. 92, 3844–3848 (1995). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Johnson A., Seeland K., Redish A. D., Reconstruction of the postsubiculum head direction signal from neural ensembles. Hippocampus 15, 86–96 (2005). [DOI] [PubMed] [Google Scholar]
- 36.Ma W. J., Beck J. M., Latham P. E., Pouget A., Bayesian inference with probabilistic population codes. Nat. Neurosci. 9, 1432–8 (2006). [DOI] [PubMed] [Google Scholar]
- 37.Beck J. M., Latham P. E., Pouget A., Marginalization in neural circuits with divisive normalization. J. Neurosci. 31, 15310–15319 (2011). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Lyu C., Abbott L. F., Maimon G., Building an allocentric travelling direction signal via vector computation. Nature 601, 92–97 (2022). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Compte A., Synaptic mechanisms and network dynamics underlying spatial working memory in a cortical network model. Cereb. Cortex 10, 910–923 (2000). [DOI] [PubMed] [Google Scholar]
- 40.Faisal A. A., Selen L. P. J., Wolpert D. M., Noise in the nervous system. Nat. Rev. Neurosci. 9, 292–303 (2008). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Burak Y., Fiete I. R., Fundamental limits on persistent activity in networks of noisy neurons. Proc. Natl. Acad. Sci. U.S.A. 109, 17645–17650 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.B. K. Hulse et al., A connectome of the Drosophila central complex reveals network motifs suitable for flexible navigation and context-dependent action selection. eLife 10, e66039 (2021). [DOI] [PMC free article] [PubMed]
- 43.L. K. Scheffer et al., A connectome and analysis of the adult Drosophila central brain. eLife 9, e57443 (2020). [DOI] [PMC free article] [PubMed]
- 44.Turner-Evans D. B., et al. , The neuroanatomical ultrastructure and function of a biological ring attractor. Neuron 108, 145–163.e10 (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Merkle T., Wehner R., Desert ants use foraging distance to adapt the nest search to the uncertainty of the path integrator. Behav. Ecol. 21, 349–355 (2010). [Google Scholar]
- 46.Merkle T., Uncertainty about nest position influences systematic search strategies in desert ants. J. Exp. Biol. 209, 3545–3549 (2006). [DOI] [PubMed] [Google Scholar]
- 47.Campbell M. G., Attinger A., Ocko S. A., Ganguli S., Giocomo L. M., Distance-tuned neurons drive specialized path integration calculations in medial entorhinal cortex. Cell Rep. 36, 109669 (2021). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.K. Cheng, S. J. Shettleworth, J. Huttenlocher, J. J. Rieser, Bayesian integration of spatial information. Psychol. Bull. 133, 625–637 (2007). [DOI] [PubMed]
- 49.Knight R., et al. , Weighted cue integration in the rodent head direction system. Philosop. Trans. R. Soc. B: Biol. Sci. 369, 20120512 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.X. Sun, M. Mangan, S. Yue, An analysis of a ring attractor model for cue integration. Lecture Notes Comput. Sci. (including subseries Lecture Notes in Artificial Intelligence and Lecture Notes in Bioinformatics). LNAI (2018), vol. 10928, pp. 459–470.
- 51.X. Sun, S. Yue, M. Mangan, A decentralised neural model explaining optimal integration of navigational strategies in insects. eLife 9, e54026 (2020). [DOI] [PMC free article] [PubMed]
- 52.J. M. Esnaola-Acebes, A. Roxin, K. Wimmer, Flexible integration of continuous sensory evidence in perceptual estimation tasks. Proc. Natl. Acad. Sci. U.S.A. 119, e2214441119 (2022). [DOI] [PMC free article] [PubMed]
- 53.W. J. Ma, M. Husain, P. M. Bays, Changing concepts of working memory. Nat. Neurosci. 17, 347–356 (2014). [DOI] [PMC free article] [PubMed]
- 54.Moreno-Bote R., et al. , Information-limiting correlations. Nat. Neurosci. 17, 1410–1417 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 55.Carroll S., Josić K., Kilpatrick Z. P., Encoding certainty in bump attractors. J. Comput. Neurosci. 37, 29–48 (2014). [DOI] [PubMed] [Google Scholar]
- 56.R. G. Robertson, E. T. Rolls, P. Georges-François, S Panzeri, Head direction cells in the primate pre-subiculum. Hippocampus 9, 206–219 (1999). [DOI] [PubMed]
- 57.Baumann O., Mattingley J. B., Medial parietal cortex encodes perceived heading direction in humans. J. Neurosci. 30, 12897–12901 (2010). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 58.Finkelstein A., et al. , Three-dimensional head-direction coding in the bat brain. Nature 517, 159–164 (2015). [DOI] [PubMed] [Google Scholar]
- 59.Zugaro M. B., Tabuchi E., Fouquier C., Berthoz A., Wiener S. I., Active locomotion increases peak firing rates of anterodorsal thalamic head direction cells. J. Neurophysiol. 86, 692–702 (2001). [DOI] [PubMed] [Google Scholar]
- 60.Shinder M. E., Taube J. S., Self-motion improves head direction cell tuning. J. Neurophysiol. 111, 2479–2492 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 61.Knierim J. J., Kudrimoti H. S., McNaughton B. L., Interactions between idiothetic cues and external landmarks in the control of place cells and head direction cells. J. Neurophysiol. 80, 425–446 (1998). [DOI] [PubMed] [Google Scholar]
- 62.Fisher Y. E., Lu J., D’Alessandro I., Wilson R. I., Sensorimotor experience remaps visual input to a heading-direction network. Nature 576, 121–125 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 63.Keinath A. T., Epstein R. A., Balasubramanian V., Environmental deformations dynamically shift the grid cell spatial metric. eLife 7, e38169 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 64.M. Milford, G. Wyeth, D. Prasser, “RatSLAM: A hippocampal model for simultaneous localization and mapping” in IEEE International Conference on Robotics and Automation, 2004. Proceedings. ICRA 2004 (IEEE, New Orleans, LA, USA, 2004), vol. 1, pp. 403–408.
- 65.Mulas M., Waniek N., Conradt J., Hebbian plasticity realigns grid cell activity with external sensory cues in continuous attractor models. Front. Comput. Neurosci. 10 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 66.Ocko S. A., Hardcastle K., Giocomo L. M., Ganguli S., Emergent elasticity in the neural code for space. Proc. Natl. Acad. Sci. U.S.A. 115 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 67.Page H. J. I., et al. , A theoretical account of cue averaging in the rodent head direction system. Philosop. Trans. R. Soc. B: Biol. Sci. 369, 20130283 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 68.Page H. J. I., Jeffery K. J., Landmark-based updating of the head direction system by retrosplenial cortex: A computational model. Front. Cell. Neurosci. 12, 191 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 69.Cope A. J., Sabo C., Vasilaki E., Barron A. B., Marshall J. A. R., A computational model of the integration of landmarks and motion in the insect central complex. PLoS One 12, e0172325 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 70.R. J. van Beers, A. C. Sittig, J. J. D. vd. Gon, Integration of proprioceptive and visual position-information: An experimentally supported model. J. Neurophysiol. 81, 1355–1364 (1999). [DOI] [PubMed]
- 71.P. E. Kloeden, E. Platen, Numerical Solution of Stochastic Differential Equations, Applications of Mathematics (Springer, Berlin, ed. 3, 2010), No. 23.
- 72.K. V. Mardia, P. E. Jupp, Directional Statistics (John Wiley& Sons, 2000), p. 3.
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Appendix 01 (PDF)
Data Availability Statement
Computer simulations and data analysis were performed with custom Python code, which has been deposited in Zenodo, DOI: 10.5281/zenodo.7615975.