Principled, practical, flexible, fast: a new approach to phylogenetic factor analysis

Abstract

1. Biological phenotypes are products of complex evolutionary processes in which selective forces influence multiple biological trait measurements in unknown ways. Phylogenetic comparative methods seek to disentangle these relationships across the evolutionary history of a group of organisms. Unfortunately, most existing methods fail to accommodate high-dimensional data with dozens or even thousands of observations per taxon. Phylogenetic factor analysis offers a solution to the challenge of dimensionality. However, scientists seeking to employ this modeling framework confront numerous modeling and implementation decisions, the details of which pose computational and replicability challenges.

2. We develop new inference techniques that increase both the computational efficiency and modeling flexibility of phylogenetic factor analysis. To facilitate adoption of these new methods, we present a practical analysis plan that guides researchers through the web of complex modeling decisions. We codify this analysis plan in an automated pipeline that distills the potentially overwhelming array of decisions into a small handful of (typically binary) choices.

3. We demonstrate the utility of these methods and analysis plan in four real-world problems of varying scales. Specifically, we study floral phenotype and pollination in columbines, domestication in industrial yeast, life history in mammals, and brain morphology in New World monkeys.

4. General and impactful community employment of these methods requires a data scientific analysis plan that balances flexibility, speed and ease of use, while minimizing model and algorithm tuning. Even in the presence of non-trivial phylogenetic model constraints, we show that one may analytically address latent factor uncertainty in a way that (a) aids model flexibility, (b) accelerates computation (by as much as 500-fold) and (c) decreases required tuning. These efforts coalesce to create an accessible Bayesian approach to high-dimensional phylogenetic comparative methods on large trees.

1. Introduction

Biological phenotypes are the result of numerous evolutionary forces acting in complex and often conflicting ways throughout an organism’s evolutionary history. Phylogenetic comparative methods seek to untangle this web of selective pressures and elucidate the forces that have shaped organisms over time. As implied by their name, these methods compare phenotypes across numerous biological taxa connected by a phylogenetic tree that captures their shared evolutionary history. Accounting for shared evolutionary history via the phylogeny is necessary to avoid biased inference, as this shared history implies phenotypes are non-independent across taxa. Statistical models that inappropriately ignore this dependence can identify spurious associations between phenotypes (Felsenstein, 1985). However, accounting for these relationships between taxa poses challenges to statistical inference.

Starting with Felsenstein (1985), there has been much work developing computationally efficient phylogenetic comparative methods (see Rohlf, 2001; Revell and Harmon, 2008; Pybus et al., 2012; Ho and Ané, 2014). While methods development has typically focused on scaling inference to large trees, these methods struggle to accommodate data with a large number of traits or high-dimensional phenotypes. The computational complexity (i.e. run time) of most approaches scales quadratically or cubically with the number of traits, making inference intractable as the number of traits increases. Additionally, methods that estimate the evolutionary correlation structure between traits are difficult to interpret for data sets with high-dimensional phenotypes, as the number of pairwise correlations requiring interpretation scales quadratically with the number of traits.

1.1. Why phylogenetic factor analysis?

Phylogenetic factor analysis (PFA, Tolkoff et al., 2017) provides an all-in-one approach to high-dimensional comparative analyses that simultaneously simplifies complex data via dimension reduction, similar to phylogenetic principal component analysis (pPCA, Revell, 2009), and statistically evaluates evolutionary correlations between groups of phenotypes, as with phylogenetic independent contrasts (Felsenstein, 1985). In Section 6.1, for example, we use PFA to understand the relationship between 11 floral phenotypes and pollinator species in columbines. We identify two axes along which floral phenotypes evolve: a first differentiating hummingbird pollination from hawk moth pollination and a second capturing phenotypes differentiating bumblebee pollination from the latter two pollination strategies. Similarly, in Section 6.2, we explore evolutionary relationships between 82 phenotypes of industrial yeast: growth rates under 62 different stress conditions, production of 16 metabolites and 4 metrics related to reproduction. In this example, we identify a group of phenotypes characterizing the early domestication of beer yeast. Additionally, PFA allows for flexible model specifications. For example, in Section 6.3 we study the evolution of life history strategies in mammals. We structure the PFA model to isolate the influence of a particular trait (body size) so that we can infer size-independent patterns of life history evolution. Finally, as with pPCA, researchers can employ PFA as a descriptive technique useful for identifying and visualizing low-dimensional structure in high-dimensional data (see Section 6.4 for an example of this with New World monkey brain shape). Unlike pPCA, however, Bayesian PFA incorporates uncertainty into the loadings (the analogs of the pPCA weights) and factors (the analogs of the pPCA scores).

1.2. Statistical developments in high-dimensional trait analyses

As the primary motivation of PFA is analyzing high-dimensional trait data, we briefly discuss existing methods that deal with the computational and interpretive burden of high-dimensional phenotypes. As mentioned above, pPCA (Revell, 2009) is one such solution that constructs a low-dimensional, phylogenetically-informed summary of the relationships between traits. More recently, several distance-based methods have been developed by Adams (2014a,b,c) to study phylogenetic signal, high-dimensional phylogenetic regression and evolutionary rates, respectively. While these methods are statistically efficient for high-dimensional phenotypes, they rely on operations that scale cubically with the number of taxa and may struggle computationally with very large trees or in cases where they must be applied over many large trees. Additionally, existing implementations of pPCA and the Adams (2014a,b,c) distance-based methods do not readily accommodate missing data, a common scourge in many relevant data sets. PFA (Tolkoff et al., 2017) adapts the Bayesian latent factor model of Aguilar and West (2000) to the phylogenetic context. Like pPCA, PFA is a linear dimension reduction approach that assumes the P-dimensional data arise from K latent factors that evolve independently along a phylogenetic tree. Unlike pPCA, PFA readily accommodates missing data without data imputation or augmentation. Additionally, PFA fits seamlessly into Bayesian phylogenetic inference and estimates the uncertainty of the influence of a particular factor on a particular trait. However, the inference regime proposed by Tolkoff et al. (2017) scales quadratically with the number of taxa and is intractable for large trees.

Finally, Clavel et al. (2019) propose a penalized likelihood framework for studying high-dimensional phenotypes. While this procedure involves an operation that scales quadratically in number of taxa, the rate-limiting calculations scale linearly in the number of taxa but cubically in the number of traits. Nevertheless, Clavel et al. (2019) demonstrate success handling data sets with more than a thousand traits. While PFA reduces the size of the parameter space by assuming the between-trait covariance is low-rank, the penalized likelihood approach of Clavel et al. (2019) achieves a similar goal by assuming a priori that relatively few of the between-trait covariances are non-zero. The specific implementations also differ in that Clavel et al. (2019) rely on maximum likelihood inference while our work here and Tolkoff et al. (2017) approach PFA from a Bayesian perspective.

1.3. A new approach to PFA

We propose two new PFA inference regimes that each scale linearly with both the number of traits P and the number of taxa N. While Tolkoff et al. (2017) rely on data augmentation, our new methods rely on a novel likelihood-calculation algorithm that analytically integrates out the latent factors. We also address two other shortcomings of PFA and latent factor models generally. First, Tolkoff et al. (2017) constrain the factor loadings matrix to be upper triangular, which induces an implicit ordering to the phenotypes. Specifically, the first trait is influenced only by the first factor, the second trait is influenced only by the first two factors, etc. until the K^th trait and beyond which are influenced by all K factors (see Table 1 for an example). As justifying a specific ordering of the phenotypes a priori can be difficult, we extend an alternative constraint proposed by Holbrook et al. (2016) that eliminates such ordering. Second, a common challenge in exploratory factor analysis generally is determining an appropriate number of factors. As such, we implement a cross-validation model selection procedure that identifies the number of factors that confers the best predictive performance.

Table 1:

Example of how the ordering of three hypothetical traits (A, B and C) influences results in a simple two-factor model under the assumptions made by Tolkoff et al. (2017).

	trait order 1: A, B, C	trait order 2: B, A, C
first factor	captures relationships of trait A with traits B and C	captures relationships of trait B with traits A and C
second factor	captures relationships between traits B and C independent of A	captures relationships between traits A and C independent of B

To facilitate use among researchers seeking to employ these methods, we develop an analysis plan with practical guidance on the most significant modeling and inference decisions. We codify this plan in the Julia package PhylogeneticFactorAnalysis.jl, which uses relatively simple instructions to automatically perform model selection and run more complex analyses in the Bayesian phylogenetic inference software BEAST (Suchard et al., 2018).

For clarity, we emphasize which methods below are completely new statistical innovations and which are novel applications of previously developed statistical practices. The calculations in Sections 3.1.2 and 3.2.1 that allow inference of the loadings without conditioning on the latent factors are novel, and we are unaware of any similar work in the statistics literature. The fast likelihood calculations in Section 2.1.1 are based on earlier work by Hassler et al. (2020) but require non-trivial adjustment for application to this context (see Supplemental Information (SI) Section 1). Finally, the modeling decisions described in Section 2.2 and inference techniques described in Sections 3.1.1, 3.1.3 and 3.2 are previously developed statistical procedures that find novel application to phylogenetic comparative methods here.

1.4. Brief overview

PFA allows researchers to identify high-dimensional patterns of trait variation using a model that reduces the computational and interpretive burden of high-dimensional analyses. We begin by specifying the technical details of the PFA model in Section 2. Intuitively, PFA assumes that the evolution of high-dimensional trait data can be approximated by the evolution of some small number of latent (unobserved) factors, with each of these latent factors influencing the observed traits in some estimable way. In Section 3 we present the technical details of several approaches to statistical inference under this model, and in Section 4 we compare the computational efficiency of these various approaches. As we recognize that researchers seeking to use these methods face an array of technical modeling and inference decisions, we devote Section 5 to practical guidance on how to make these decisions. Finally, in Section 6 we demonstrate the utility of PFA on 4 real-world examples.

2. Phylogenetic Latent Factor Model

We approach inference from a Bayesian perspective and propose two statistical models which share a likelihood but have distinct priors. As we discuss below, each model has advantages under different circumstances, and allowing researchers to choose a model (with our guidance) offers maximum flexibility while keeping modeling decisions to a minimum.

2.1. Likelihood

Both statistical models share the same latent factor likelihood introduced by Tolkoff et al. (2017). This likelihood assumes the N × P trait data Y = (y₁, …, y_N)^t arise from N × K latent factors F = (f₁, …, f_N)^t via the linear transformation Y = FL + ϵ, where L is a K × P loadings matrix that must be inferred and ϵ ~ MN (0, I_N,Λ⁻¹) is matrix-normally distributed with mean 0, between row variance I_N and diagonal between column precision Λ = diag[λ₁, …, λ_P ]. The latent factors F arise from K independent Brownian diffusion processes on the phylogenetic tree $ℱ$. The tree $ℱ$ is rooted and bifurcating with degree-two root node ν_2N−1, degree-three internal nodes {ν_N+1, …, ν_2N−2} and degree-one leaf nodes {ν₁, …, ν_N}. Under the Brownian diffusion model, all internal and tip factors are normally distributed as ${\mathbf{f}}_j~𝒩\left({\mathbf{f}}_{\text{pa}(j)},t_j{\mathbf{I}}_K\right)$ where f_pa(j) are the factors of the parent of node ν_j and t_j is the distance (time) between nodes ν_pa(j) and ν_j. Following from Pybus et al. (2012), we assume the ancestral root traits ${\mathbf{f}}_{2N-1}~𝒩\left({\mathbf{\mu }}_0,\frac{1}{{\kappa }_0}{\mathbf{I}}_K\right)$, where κ₀ is some (typically small) predetermined prior sample size. This construction implies the tip factors are jointly matrix-normally distributed as $\mathbf{F}~\mathrm{MN}\left({\mathbf{1}}_N{\mathit{\mu }}_0^t,\mathbf{\Psi }+\frac{1}{{\kappa }_0}{\mathbf{J}}_N,{\mathbf{I}}_K\right)$, where 1_N is an N-vector of ones, ${\mathbf{J}}_N={\mathbf{1}}_N{\mathbf{1}}_N^t$ and Ψ is the standard variance-covariance (VCV) representation of the phylogeny $ℱ$. Specifically, the diagonal elements Ψ_ii are the sum of the edge lengths connecting ν_i to the root ν_2N−1. The off-diagonal elements Ψ_ij are the total amount of shared evolutionary history or time from the most recent common ancestor of ν_i and ν_j to the root node ν_2N−1.

Given this model, the vectorized data vec(Y) are multivariate normally distributed as

$$\mathrm{vec}(\mathbf{Y})\mid \mathbf{L},\mathbf{\Lambda },ℱ~𝒩\left(\mathrm{vec}\left({\mathbf{1}}_N{\mathit{\mu }}_0^t\right),{\mathbf{L}}^t\mathbf{L}\otimes \left[\mathbf{\Psi }+\frac{1}{{\kappa }_0}{\mathbf{J}}_N\right]+{\mathbf{\Lambda }}^{-1}\otimes {\mathbf{I}}_N\right),$$ (1)

where ⊗ is the Kronecker product operator. Computing the likelihood in this form, however, requires inverting the NP × NP dimensional variance matrix, which has computational complexity $𝒪\left(N^3{P}^3\right)$. Tolkoff et al. (2017) avoid this by treating the latent factors F as model parameters that they integrate out via Markov chain Monte Carlo (MCMC) simulation. This augmented likelihood $p(\mathbf{Y},\mathbf{F}\mid \mathbf{L},\mathbf{\Lambda },ℱ)=p(\mathbf{Y}\mid \mathbf{L},\mathbf{\Lambda },\mathbf{F})p(\mathbf{F}\mid ℱ)$ is far easier to compute, but sampling from the full conditional distribution of F (i.e. the posterior distribution of F conditional on the data and all other model parameters) as proposed by Tolkoff et al. (2017) scales quadratically with the size of the phylogenetic tree and is intractable for big-N.

2.1.1. Fast Likelihood Calculation

To avoid costly data augmentation, we adapt the likelihood-computation algorithm independently developed by Bastide et al. (2018), Mitov et al. (2020) and Hassler et al. (2020). This algorithm analytically integrates out latent traits (in our case factors) and missing data to compute the likelihood $p\left({\mathbf{Y}}^{\text{obs}}\mid \mathbf{L},\mathbf{\Lambda },ℱ\right)$ of the observed data Y^obs in $𝒪\left(NP{K}^2+N{K}^3\right)$ via a post-order traversal of the tree (i.e. computations start at the tips and are carried up the tree to the root). This procedure naturally accommodates missing data assuming an ignorable missing data mechanism (Rubin, 1976). We also utilize a more numerically stable modification of this post-order algorithm proposed by Bastide et al. (2021). We detail these calculations in SI Section 1.

2.1.2. Loadings Identifiability

A major challenge in latent factor models generally is the non-identifiability of the loadings matrix L (see Shapiro, 1985). In statistical models, non-identifiability occurs when there are multiple parameter values that result in the same probability density over the data. In these cases, inference procedures cannot distinguish between the equally valid parameter values. This lack of identifiability in PFA stems from the fact that the likelihood as defined in Equation 1 depends only on L^tL rather than L itself. As such, for any K×K orthonormal matrix Q (i.e. Q^tQ = I_K), p(Y |L,…) = p(Y |QL,…) because (QL)^t (QL) = L^tL. This identifiability problem inspires our choice of priors below.

2.2. Priors

We assume the diagonal precisions λ_j ~ Gamma(a_Λ,b_Λ) for j = 1, …, P (shape/rate parameterization). For the loadings L = {l_kj}, we propose two different priors. Each prior on L admits a different inference regime for sampling from L which in turn have their own strengths and weaknesses that we discuss in Section 3.

2.2.1. Independent Gaussian Priors on the Loadings L

The standard assumption in Bayesian latent factor models is that each element of the loadings ${\ell }_{kj}\stackrel{\text{i}.\text{i.d.}}{~}𝒩\left(0,{\sigma }^2\right)$, where typically σ² = 1. As this prior is also invariant with respect to orthogonal rotations, additional constraints are required for posterior identifiability. One solution is to assume certain elements of the loadings matrix L (typically those below the diagonal) are fixed at zero (Geweke and Zhou, 1996; Aguilar and West, 2000). This approach solves the identifiability problem, but it induces an implicit ordering to the data (see Table 1). While this ordering may be well-informed in some cases, there is typically no principled way to choose such an ordering a priori.

An alternative to the sparsity constraint is to assume that the loadings matrix has rows that 1) are orthogonal and 2) have decreasing norms (Holbrook et al., 2016). This constraint does not require any a priori ordering of the traits. However, it does require sampling from the space of orthogonal matrices, which is a notoriously challenging problem (see Hoff, 2009; Byrne and Girolami, 2013; Jauch et al., 2021; Pourzanjani et al., 2021). We address this challenge via post-processing in Section 3.1.3.

2.2.2. Orthogonal Shrinkage Prior

While post-processing to orthogonality is often sufficient, we find in practice that the loadings may be only loosely identifiable with this procedure in small-N problems. As such, we seek an alternative prior that enforces the orthogonality constraint directly. Following from Holbrook et al. (2017), we decompose the loadings L = ΣV where Σ = diag[σ] is a K × K diagonal matrix whose diagonals σ have descending absolute values and V is a K × P orthonormal matrix (i.e. VV^t = I_K). We assume V^t is uniformly distributed over the Stiefel manifold ${𝒱}_K\left({ℝ}^P\right)$ (i.e. the space of P × K orthonormal matrices). For the scale component Σ = diag[σ₁, …, σ_K] we assume a multiplicative gamma prior inspired by Bhattacharya and Dunson (2011):

$$\begin{array}{l}{\sigma }_k~𝒩\left(0,{\tau }_k^{-1}\right)\text{for}k=1,\dots ,K,\text{where}\\ {\tau }_k=\prod _1^k{\nu }_{\ell }\text{and}\\ {\nu }_{\ell }~\mathrm{Gamma}\left(a_{\ell },b_{\ell }\right)\text{for}\ell =1,\dots ,K.\end{array}$$ (2)

For l > 1, we constrain the prior shape a_l and rate b_l such that a_ℓ > b_ℓ (i.e. $\mathbb{E}\left[{\nu }_{\ell }\right]>1$). This constraint implies that the τ_k are (stochastically) increasing with k, which results in scale parameters σ_k with (stochastically) decreasing magnitudes.

This prior induces posterior identifiability, as it is not invariant under rotations of the loadings. However, in some cases we find that this prior does not induce sufficient identifiability in practice, particularly when K is relatively large (i.e. > 5). For these cases, we multiply the joint prior on Σ by an indicator function 1{|σ_k| < α|σ_k−1| for k = 2, …, K}. Setting α < 1 forces spacing between the diagonals of Σ, which results in more identifiable posteriors.

3. Inference

Our Bayesian inference regime seeks to approximate the posterior distribution of the parameters of scientific interest via MCMC simulation. We typically use molecular sequence data S to simultaneously infer the factor model parameters and phylogenetic tree by approximating

$$p\left(\mathbf{L},\mathbf{\Lambda },ℱ\mid {\mathbf{Y}}^{\text{obs}},\mathbf{S}\right)\propto p\left({\mathbf{Y}}^{\text{obs}}\mid \mathbf{L},\mathbf{\Lambda },ℱ\right)p(ℱ,\mathbf{S})p(\mathbf{L})p(\mathbf{\Lambda }),$$ (3)

where the model of sequence evolution $p(ℱ,\mathbf{S})$ is developed elsewhere (see Suchard et al., 2018). For cases where we lack sequence data or $ℱ$ is too large to infer efficiently, we simply fix the tree $ℱ$.

3.1. Loadings Under the i.i.d. Gaussian Prior

We propose two different samplers to draw from the full conditional distribution of the loadings L under the i.i.d. Gaussian prior from Section 2.2.1. The first relies on the Gibbs sampler used by Tolkoff et al. (2017), where we sample from LY^obs, F, Λ. The second avoids data augmentation and can sample directly from the full conditional distribution LY^obs, F, Λ, $ℱ$ without conditioning on the latent factors F.

3.1.1. Gibbs Sampler with Data Augmentation

Tolkoff et al. (2017) use the conjugate Gibbs sampler of Lopes and West (2004) to sample from LY^obs, F, Λ. As this sampler conditions on the latent factors F, Tolkoff et al. (2017) simultaneously infer the factors by sequentially drawing from f_i | F_/i,Y^obs, L, Λ, $ℱ$ for i = 1, …, N, where F_/i represents all factors except f_i. As sampling f_i for all N taxa requires $𝒪\left(N^2{K}^2\right)$ work, this procedure quickly becomes intractable with increasing taxa.

Rather than relying on this per-taxon sampling scheme, we employ the pre-order data augmentation algorithm of Hassler et al. (2020) that uses statistics from the post-order likelihood computation to draw jointly from F | Y^obs, L, Λ, $ℱ$ in $𝒪\left(N{K}^3\right)$ via a single pre-order traversal of the tree (see SI Section 2.1 for details). After sampling from F | Y^obs, L, Λ, $ℱ$, we can draw directly from L | Y^obs, F, Λ using the procedure developed by Lopes and West (2004) with computational complexity $𝒪\left(NP{K}^2\right)$ (see SI Section 2.2 for details).

3.1.2. Hamiltonian Monte Carlo Sampler

We also propose an alternative Hamiltonian Monte Carlo (HMC; Neal, 2010) sampler for the loadings that does not require data augmentation. Intuitively, HMC (a form of MCMC) treats parameter values as the position of a particle in a landscape informed by the posterior distribution. Parameter proposals are the end-point of a trajectory initiated by “kicking” the particle and allowing it to traverse this landscape according to Hamiltonian dynamics for a pre-determined amount of time. As the parameter trajectories are informed by the geometry of the posterior, HMC tends to propose parameter updates that are both relatively far away from the current position and have high acceptance probabilities.

While we cannot compute these continuous trajectories analytically, we can approximate them numerically. Each trajectory approximation, however, requires numerous gradient calculations, and we must efficiently compute the gradient ${\nabla }_{\mathbf{L}}\log p\left(\mathbf{L}\mid {\mathbf{Y}}^{\text{obs}},\mathbf{\Lambda },ℱ\right)={\nabla }_{\mathbf{L}}\log p\left({\mathbf{Y}}^{\text{obs}}\mid \mathbf{L},\mathbf{\Lambda },ℱ\right)+{\nabla }_{\mathbf{L}}\log p(\mathbf{L})$ to effectively employ HMC to update the loadings L. As we assume each element of the loadings are a priori i.i.d. $𝒩(0,1)$, the gradient of the log-prior ∇_L logp(L) can be computed simply as $\frac{\partial }{\partial {\ell }_{kj}}\log p(\mathbf{L})=-{\ell }_{kj}$ for j = 1, …, P, k = 1, …, K.

As computing ${\nabla }_{\mathbf{L}}\log p\left({\mathbf{Y}}^{\text{obs}}\mid \mathbf{L},\mathbf{\Lambda },ℱ\right)$ directly via Equation 1 scales $𝒪\left(N^3{P}^3\right)$ and is intractable for most problems, we use the highly structured nature of the phylogeny to compute this gradient in $𝒪\left(NP{K}^2+N{K}^3\right)$. We calculate the gradient of the likelihood with respect to each column of the loadings l_j individually to accommodate variation in the missing data structure across traits.

$${\nabla }_{{\ell }_j}\log p\left({\mathbf{Y}}^{\text{obs}}\mid \mathbf{L},\mathbf{\Lambda },ℱ\right)={\lambda }_j\mathbb{E}\left[{\mathbf{F}}^t\mid {\mathbf{Y}}^{\text{obs}},\mathbf{L},\mathbf{\Lambda },ℱ\right]{\mathit{\delta }}_j^{\prime }{\mathbf{y}}_j^{{\text{obs}}^{\prime }}-{\lambda }_j\mathbb{E}\left[{\mathbf{F}}^t{\mathit{\delta }}_j^{\prime }\mathbf{F}\mid {\mathbf{Y}}^{\text{obs}},\mathbf{L},\mathbf{\Lambda },ℱ\right]{\ell }_j,$$ (4)

where ${\mathbf{y}}_j^{{\text{obs}}^{\prime }}$ is the j^th column of Y^obs and ${\mathit{\delta }}_j^{\prime }=\mathrm{diag}\left[{\delta }_{1j},\dots ,{\delta }_{Nj}\right]$ is a diagonal matrix of observed-data indicators (i.e. δ_ij = 1 if y_ij is observed and 0 otherwise). Note that these calculations rely only on the conditional mean and variance of the factors, not the factors themselves. We compute the expectations using statistics from the post-order likelihood calculation (see SI Section 1) in a pre-order tree traversal (Bastide et al., 2018; Fisher et al., 2020) that takes $𝒪\left(N{K}^3\right)$ additional time. See SI Section 3 for detailed calculations.

3.1.3. Orthogonality Constraint and Post-Processing

While both the Gibbs and HMC samplers above can enforce the structured sparsity constraint, neither can enforce the orthogonality constraint directly. However, as both the likelihood and i.i.d. prior are invariant with respect to orthonormal rotations of L, applying such a rotation to all posterior samples via post-processing results in a valid posterior. We can easily rotate the loadings to have orthogonal rows with descending norms via singular value decomposition (see SI Section 4 for details).

3.2. Loadings Under the Orthogonal Shrinkage Prior

Both samplers above are incompatible with the orthogonal shrinkage prior from Section 2.2.2 as 1) they cannot enforce the orthogonality constraint directly and 2) post-processing is invalid because the prior is not rotationally invariant. Therefore, we sample directly from the full conditional distributions of both Σ and V rather than their product L.

3.2.1. Geodesic HMC Sampler on the Orthonormal Component V

Requiring V^t to be orthonormal allows us to employ existing techniques for sampling from the Stiefel manifold (i.e. the space of orthonormal matrices). Geodesic HMC (Byrne and Girolami, 2013) uses the same fundamental principles of standard HMC, but progresses parameters along geodesics on manifolds (e.g. an arc on a sphere) rather than through Euclidean space. This procedure also relies on the gradient of the log-posterior with respect to the parameter of interest. As such, to efficiently employ geodesic HMC to update the orthonormal matrix V, we must efficiently compute the gradient

$${\nabla }_{\mathbf{V}}\log p\left(\mathbf{V}\mid {\mathbf{Y}}^{\text{obs}},\mathbf{\Sigma },\mathbf{\Lambda },ℱ\right)={\nabla }_{\mathbf{V}}\log p\left({\mathbf{Y}}^{\text{obs}}\mid \mathbf{V},\mathbf{\Sigma },\mathbf{\Lambda },ℱ\right)+{\nabla }_{\mathbf{V}}\log p(\mathbf{V}).$$ (5)

As noted in Section 2.2.2, we place a uniform prior on V and can therefore ignore ∇_V logp(V). Using our calculations for ${\nabla }_{\mathbf{L}}\log p\left({\mathbf{Y}}^{\text{obs}}\mid \mathbf{L},\mathbf{\Lambda },ℱ\right)$ from Section 3.1.2, the chain rule provides a simple formula for the gradient of the likelihood with respect to V as L = ΣV:

$${\nabla }_{\mathbf{V}}\log p\left({\mathbf{Y}}^{\text{obs}}\mid \mathbf{V},\mathbf{\Sigma },\mathbf{\Lambda },ℱ\right)=\mathbf{\Sigma }{\nabla }_{\mathbf{L}}\log p\left({\mathbf{Y}}^{\text{obs}}\mid \mathbf{L},\mathbf{\Lambda },ℱ\right)$$ (6)

We then use this gradient in the geodesic HMC algorithm of Holbrook et al. (2016) to sample from the full conditional distribution of V.

3.2.2. Gibbs Sampler on the Diagonal Scale Component Σ

While we can employ HMC to sample from Σ | Y^obs, V, Λ, $ℱ$, our implementation did not mix well in practice. We develop a Gibbs sampler to draw from Σ | Y^obs, V, Λ, F as an efficient alternative that relies on the data augmentation of F in SI Section 2.1. See SI Section 5 for details.

3.2.3. Gibbs Sampler on the Precision Multipliers

We must also sample from the shrinkage multipliers ν₁, …, ν_K when using the shrinkage prior on the loadings. Bhattacharya and Dunson (2011, Section 3.1, Step 5) develop a conjugate Gibbs sampler for these multipliers that we apply directly to this model.

3.3. Sign Constraint on the Loadings

Regardless of which prior (i.i.d. vs. orthogonal shrinkage) or constraint (sparsity vs. orthogonality) we choose, we must enforce a sign constraint on a single element in each row of L for full identifiability (see SI Section 6 for details).

3.4. Gibbs Sampler on the Error Precisions Λ

We sample from Λ | F, Y^obs, L using the same procedure as Tolkoff et al. (2017) in conjunction with the data augmentation algorithm in SI Section 2.1 (see SI Section 7 for details).

4. Computational Efficiency

We compare the computational efficiency of the inference regimes discussed in Sections 3.1.1, 3.1.2 and 3.2 with that of Tolkoff et al. (2017). To understand performance across a wide range of situations, we simulate three unique data sets for all 36 combinations of N ∈ {50, 100, 500, 1000}, P ∈ {10, 100, 1000} and K ∈ {1, 2, 4} (see SI Section 8.1 for simulation details). To understand the relative performance of each inference regime, we compare the effective sample size (ESS) per second of the loadings across all four samplers (see SI Section 8.2 for details) and report our results in Figure 1.

Figure 1:

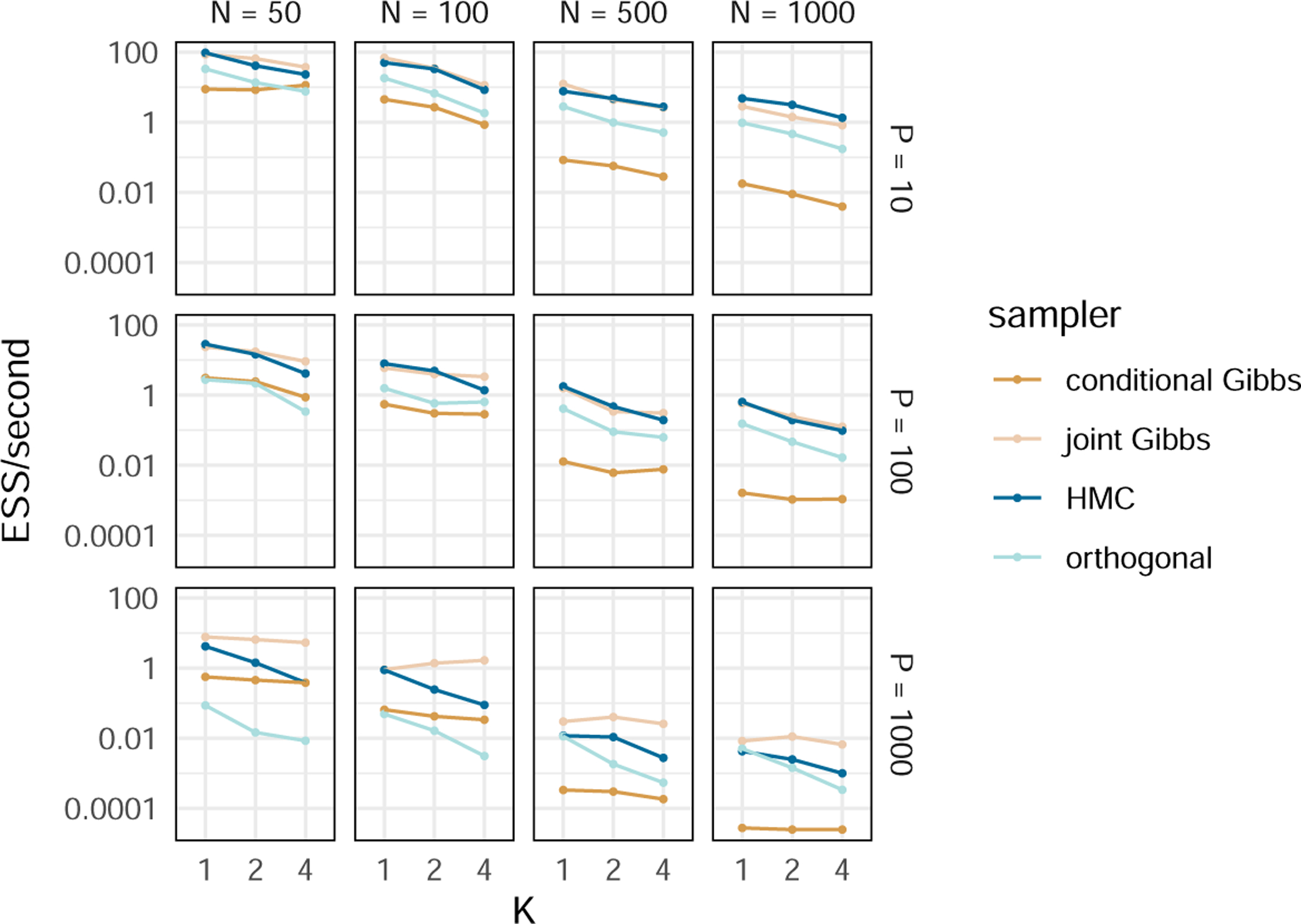
Timing comparison between inference regimes. We run three MCMC chain simulations for each combination of N (the number of taxa), P (the number of traits), K (the number of factors) and sampler and present the average minimum ESS per second for each. The “conditional Gibbs” sampler refers to the methods used by Tolkoff et al. (2017). The “joint Gibbs”, “HMC” and “orthogonal” samplers refer to the methods presented in Sections 3.1.1, 3.1.2 and 3.2 respectively. Our joint Gibbs and HMC samplers are an order of magnitude faster than the conditional Gibbs sampler with relatively few taxa (N = 50) but more than two orders of magnitude faster with many taxa (N = 1000). The orthogonal sampler is slower than the joint Gibbs and HMC samplers (and even the conditional Gibbs in the case of small-N, big-P) but scales well to large trees. Values are available in SI Table 1.

Compared against the conditional Gibbs sampler of Tolkoff et al. (2017), both our joint Gibbs and HMC samplers under the i.i.d. prior consistently yield efficiency gains of an order of magnitude in small-N data sets and two orders of magnitude in big-N data sets. While the sampling regime under the orthogonal shrinkage prior is slower than either the joint Gibbs or HMC sampler (and even the conditional Gibbs sampler for small-N, big-P), it has clear advantages over the others that we discuss in Section 5.2.

5. Principled Analysis Plan

The modeling decisions required for Bayesian factor analysis can be daunting. In addition to the priors, identifiability constraints and sampling procedures discussed above, researchers must also choose an appropriate number of factors K. Making such choices in a principled manner is challenging, and experimenting with different combinations to determine which “work best” is time consuming and opens the door to modeling decisions based on publication concerns. We propose a generalizable analysis plan to guide researchers through this process. To aid researchers seeking to employ phylogenetic factor analysis specifically, we also develop software tools that codify this plan and automate core procedures.

5.1. Choosing the Loadings Constraint

The decision to apply the sparsity constraint versus the orthogonality constraint depends on the biological question of interest. While the sparsity constraint induces ordering onto the traits, this ordering can be desirable under certain circumstances. For example, if one is trying to isolate the effects of a particular set of traits, placing those traits first in conjunction with the upper triangular constraint ensures that they will load only onto the first few factors and all subsequent factors will be independent of their influence. If one does not want to apply such an ordering, the orthogonality constraint may be a better alternative. We emphasize, however, that the orthogonality constraint is no less restrictive than the sparsity constraint; rather, it replaces a series of potentially arbitrary modeling decisions (i.e. the ordering of the first K traits) with a single, perhaps equally arbitrary, constraint.

Researchers can also apply a hybrid approach where one or more traits load only onto a certain factor(s) while the remaining traits are free to load onto all factors. If the specific sparsity structure is not sufficient to induce identifiability, then any unconstrained sub-matrices of the loadings would require rotation to orthogonality. We present a simple example of this in Section 6.3, where the the first trait (body mass) loads only onto the first factor and the remaining traits load onto all K factors. In this case, the first row of the loadings is identifiable and captures mass-dependent relationships, while the sub-matrix composed of rows 2, …, K and columns 2, …, j is rotated to orthogonality via post-processing.

5.2. Choosing the Loadings Prior

Those choosing the sparsity (or hybrid) constraint must use the i.i.d. prior on the loadings, as orthogonality is implicit in our definition of the shrinkage prior. For those opting for the orthogonality constraint, we recommend choosing a prior based on the characteristics of the specific application. For big-N data sets (N > 1000) the geodesic HMC sampler on V under the shrinkage prior may be prohibitively slow (particularly when combined with big-P), and we suggest using the i.i.d. prior with post-processing.

One serious limitation of the post-processing regime, however, is the potential for label switching (Celeux, 1998). This phenomenon occurs when the posterior distributions of certain scale parameters σ overlap enough that a given factor switches its ordering. When this occurs, the resulting estimated factor (e.g. factor 1) may actually be a mixture of factors that shuffle in order during MCMC and post-processing. Figure 2 provides an example of this phenomenon and shows how the orthogonal shrinkage prior can address it. Examining the MCMC trace plots (i.e. plots of parameter values over each sample from the MCMC chain) in software such as the CODA R package (Plummer et al., 2006) or Tracer (Rambaut et al., 2018) is the best way to check for label switching. If the trace plot of the scale parameters σ appear to be touching (as in the top, left panel of Figure 2), then label switching is likely occurring. See SI Section 9 for a more thorough discussion of identifying label switching in the context of PFA.

Figure 2:

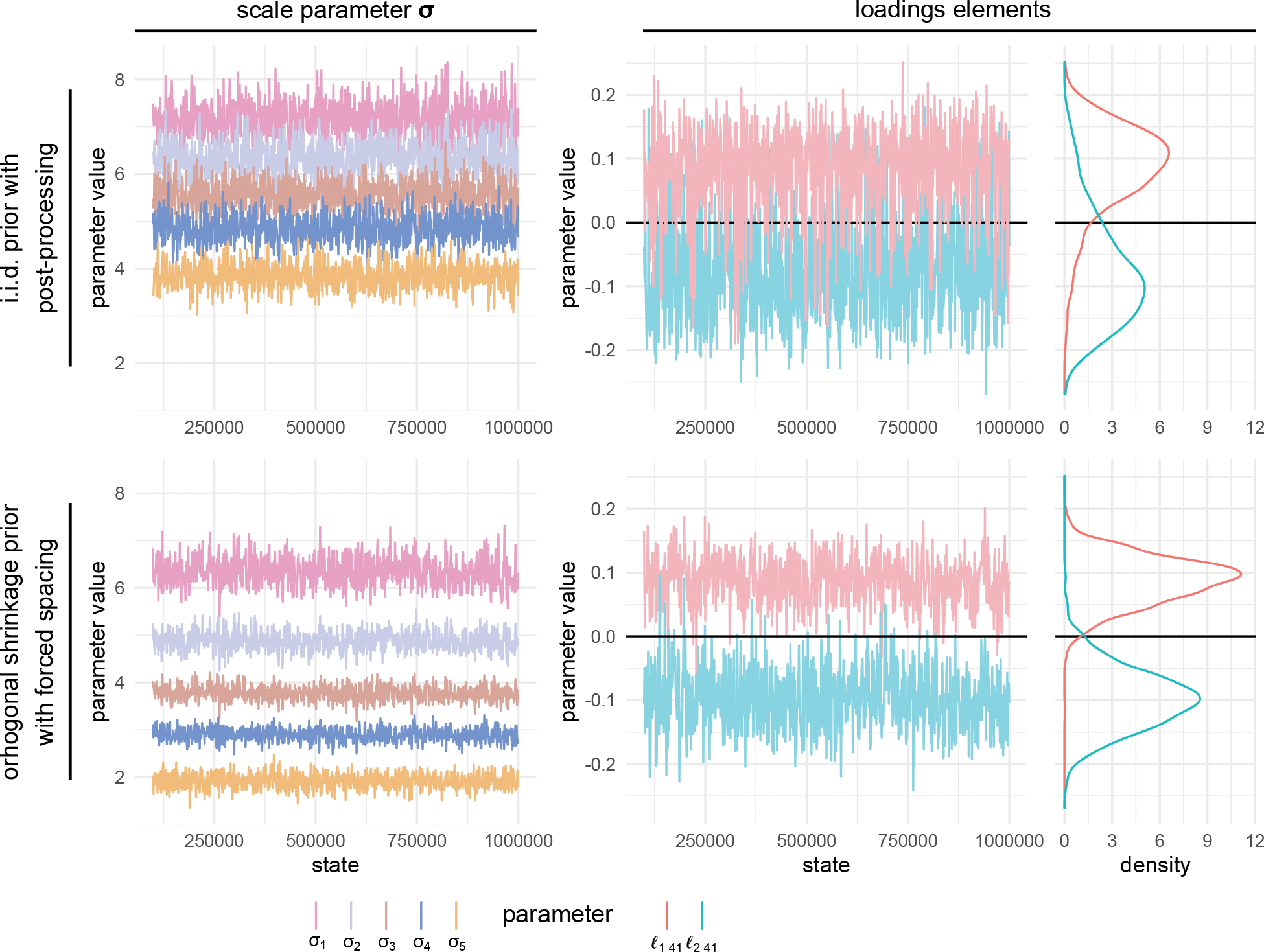
Trace plots of relevant parameters from analysis in Section 6.2. Estimates under the i.i.d. Gaussian prior are characteristic of poorly-identifiable conditions (the scales σ are overlapping resulting in label switching / row-wise convolution of the loadings). The shrinkage prior with forced spacing (α = 0.8) largely eliminates this problem.

Conveniently, label switching does not typically occur in big-N analyses, so we recommend the more computationally efficient i.i.d. prior with post-processing in these situations. For small- or moderate-N analyses, we still suggest attempting the i.i.d. sampler with post-processing, but we caution users to look for evidence of label switching. If such evidence exists, we recommend using the shrinkage prior with forced ordering and separation.

5.3. Constraining the Number of Factors

We propose cross-validation for identifying the number of factors with optimal predictive performance. In the case of the i.i.d. prior, this procedure compares models with different number of factors directly, while in the case of the orthogonal shrinkage prior it tunes the strength of the shrinkage on the loadings scales. See SI Section 10 for details.

We fully recognize that complex evolutionary processes do not, in reality, conform exactly to the phylogenetic latent factor model (or any tractable statistical model) and caution against seeking to identify the “true” number of underlying evolutionary processes driving the phenotypes of interest, as such ground truth likely does not exist. Rather, we encourage researchers to use this model selection procedure to identify the limitations of the information available in a particular data set and the model’s ability to extract it. For example, if model selection determines that a four factor model provides optimal predictive performance, one should be wary of interpreting results from a model with greater than four factors as it is likely some of the perceived signal is an artifact of noise in the data.

Prior to model selection, one must choose some maximum number of factors K_max that balances model interpretability, flexibility, identifiability and tractability. Models with more factors are inherently more flexible and can potentially capture more information about underlying biological phenomena. However, interpretation becomes challenging as the number of factors increases. While the model with optimal predictive performance may have K < K_max, one should be open to interpreting a model where K = K_max. Limiting K_max provides additional benefits, as 1) the identifiability challenges discussed in Section 5.2 intensify with increasing K and 2) inference scales cubically with K and some big-K models may be intractable. In practice, we settle on K_max = 5 for most examples below, as we find that the computation time and identifiability issues are typically manageable at K = 5 and feel most researchers would rarely need to interpret more than five factors.

5.4. Software Implementation

We implement all inference procedures in Section 3 in the Bayesian phylogenetic inference software BEAST (Suchard et al., 2018). While BEAST is an extraordinarily flexible tool, this flexibility can result in a user experience that is overwhelming for the uninitiated.

We develop the Julia package PhylogeneticFactorAnalysis.jl to both simplify the BEAST user experience (in the context of PFA) and automate model selection, post-processing, diagnostics and plotting. Users must input the trait data, a phylogenetic tree, the identifiability constraint on the loadings and the prior on the loadings. Users may also optionally specify other modeling decisions such as whether to standardize the trait data (which we recommend) and the model selection meta-parameters as well as a BEAST input file with instructions for inferring the phylogenetic tree from sequence data.

After receiving appropriate input, PhylogeneticFactorAnalysis.jl automatically performs model selection and outputs a series of files including the sub-sampled MCMC realizations and plots of both the loadings (see Figures 3B, 4A and 5A) and factors on the tree (see Figures 4B, 5B and 6B) using the ggplot2 (Wickham, 2016) and ggtree (Yu et al., 2017) plotting libraries. PhylogeneticFactorAnalysis.jl is registered under the Julia General registry. Source code and documentation can be accessed at:

Figure 3:

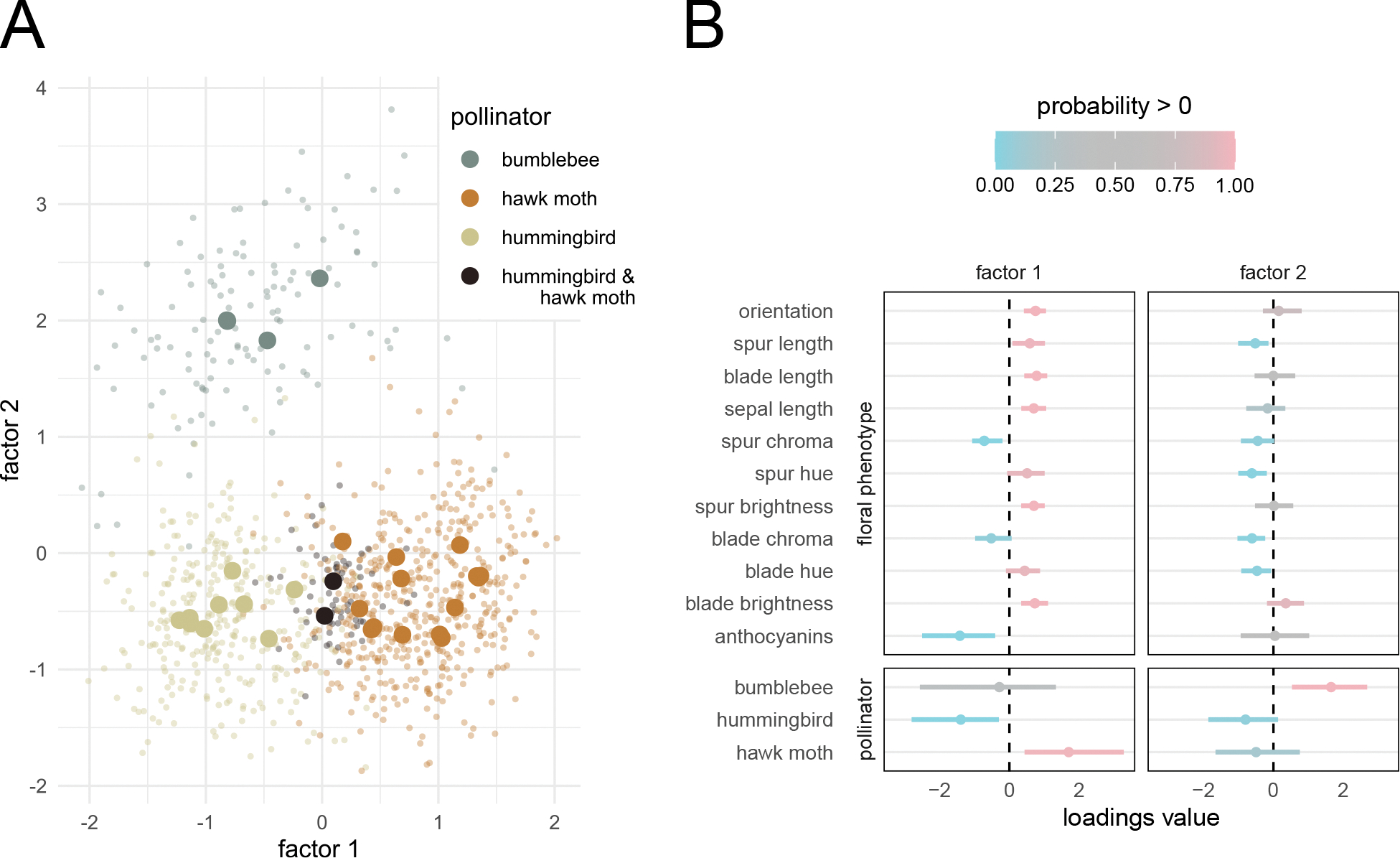
Aquilegia results. A) Factor values colored by pollinator(s) for each species of Aquilegia. Large, solid points represent posterior means for each species. Small, transparent points represent a random sample from the posterior distribution of the factors. B) Posterior summary of the loadings matrix. Dots represent posterior means while bars cover the 95% highest posterior density (HPD) interval. Colors represent the posterior probability that the parameter is greater than 0. While the second factor clearly separates the bumblebee-pollinated plants from the others, the first factor captures a more gradual transition from hummingbird pollination to hawk moth pollination.

Figure 4:

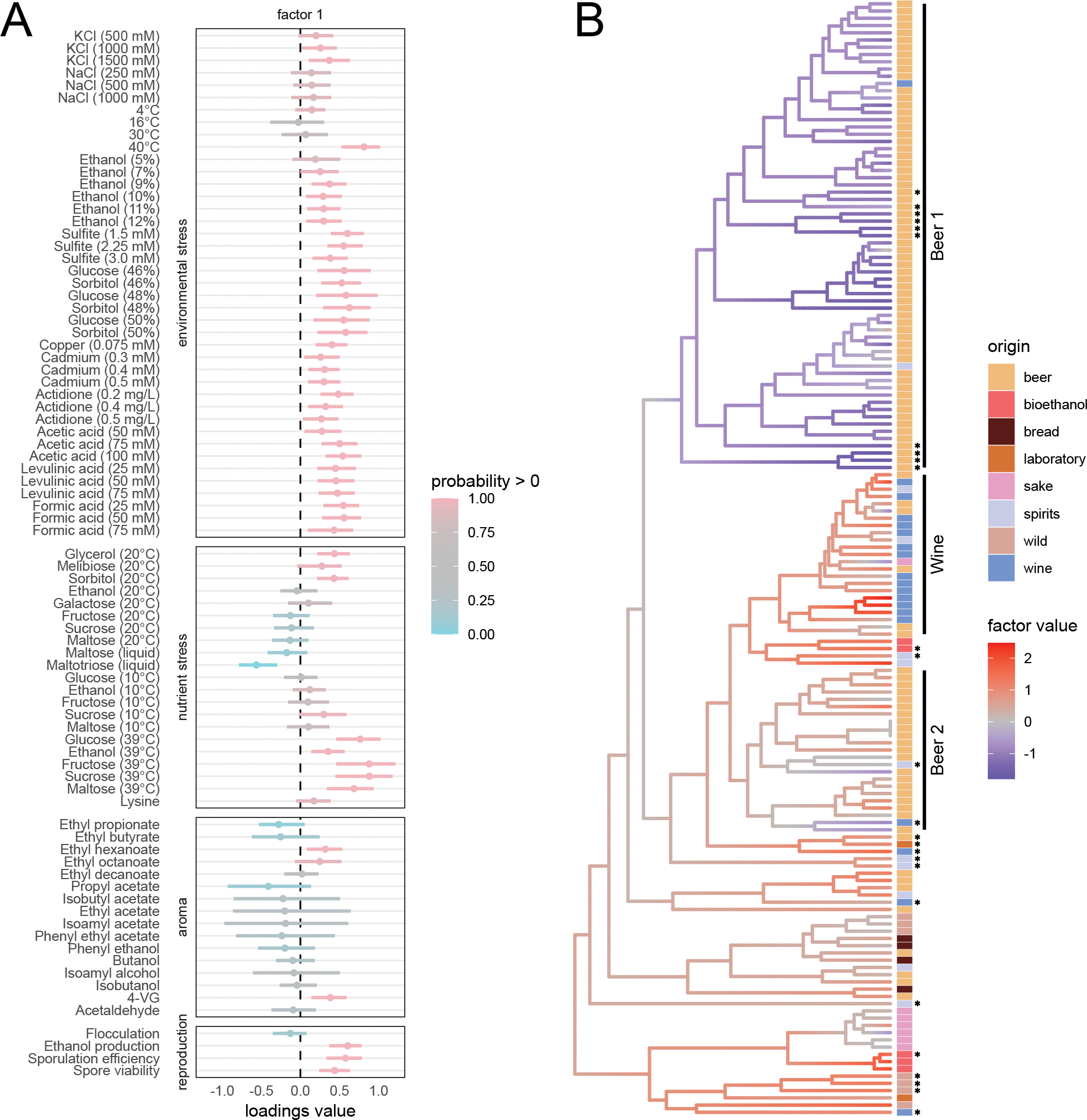
Results associated with first factor in yeast analysis. A) Posterior summary of first row of the loadings of 5-factor PFA on yeast data set. This first factor primarily captures differences associated with tolerance to environment and nutrient stress as well as reproductive ability. See Figure 3B for description of plot elements. B) The first factor plotted on yeast phylogeny with strain origin. Stars at the tips indicate mosaic strains as identified by Gallone et al. (2016). Low factor values in the Beer 1 clade indicate poor tolerance of environmental and nutrient stress generally and a lower capacity to reproduce sexually, all of which are signs of domestication. The Beer 1 clade includes strains from Belgium, Germany, Britain and the United States, and Gallone et al. (2016) estimate its origin ca. 1590 AD that coincides with the transition from home-brewing to large-scale beer production across Europe.

Figure 5:

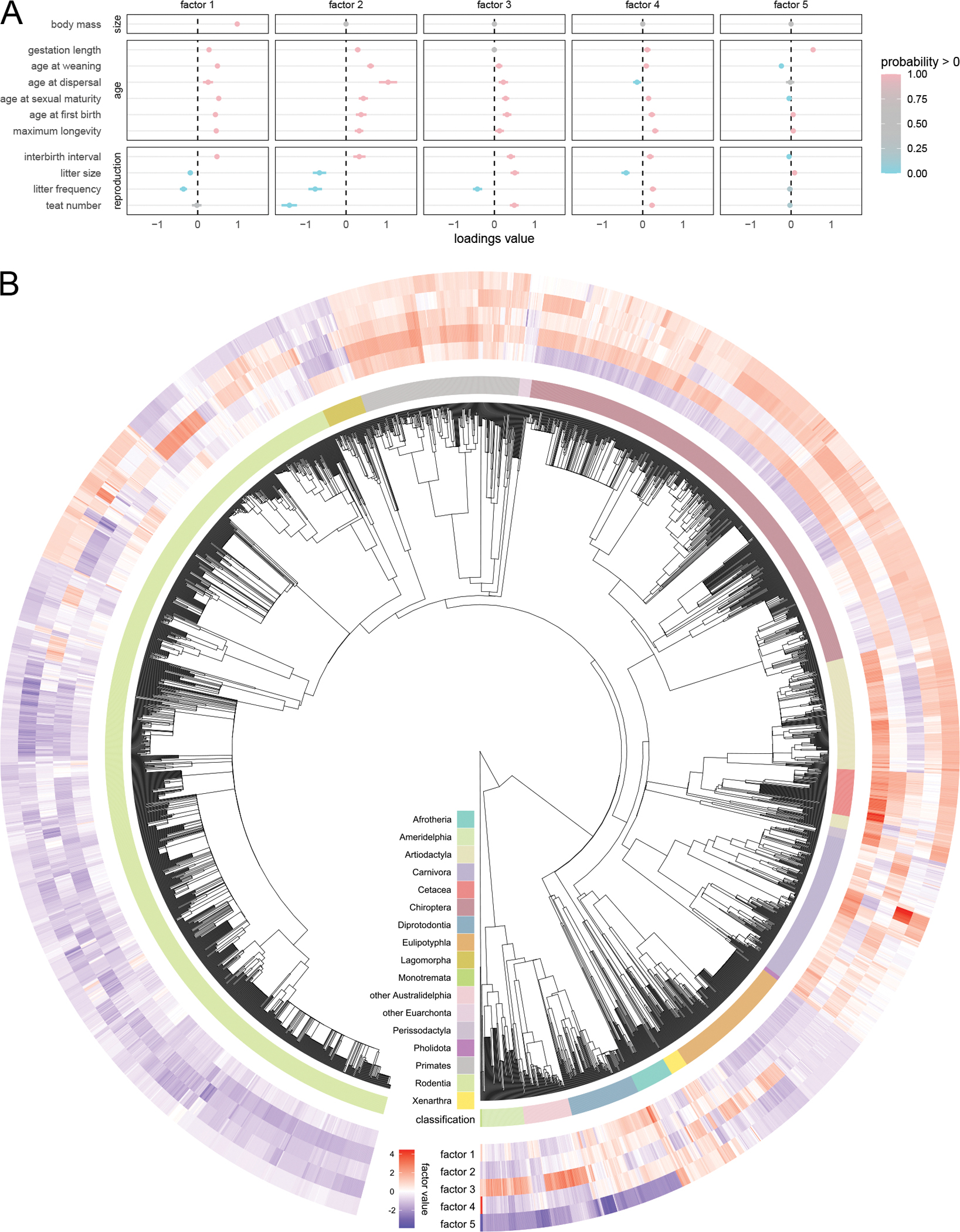
Mammalian life history results. A) Posterior summary of the loadings. Loadings of body size onto factors 2–5 is set to 0 a priori. See Figure 3B for detailed description of figure elements. The first factor captures allometric relationships (by design) and explains only 16% of the heritable variance, while the remaining factors capture size-independent relationships. The second factor, accounting for the plurality (46%) of the heritable variance, captures a fast-slow life history axis. Remaining factors capture more specific strategies (e.g. factors three and four appear to support the energy trade-off between litter size and litter frequency). This suggests that body size is not the main driver of life history evolution and that natural selection primarily acts on life history directly. B) Evolution of factors along the mammalian phylogeny. Most factors are strongly phylogenetically conserved throughout the tree, with large clades sharing similar factor values. There is relatively little correlation between the the first and second factors, with clades of small, slow species (e.g. bats) and large, fast species (e.g. lagomorphs).

Figure 6:

A) Influence of each factor on New World monkey brain shape. B) Brain shape factors plotted along New World monkey phylogeny. The coefficients of the first three principal components (PCs) from Aristide et al. (2016) are highly correlated with the corresponding rows of the loadings matrix. While we do not explore such an analysis here, Aristide et al. (2016) provide evidence of association of PC1 (strongly correlated with our first factor) with relative brain size and PC2 (strongly correlated with our second factor) with diet.

https://github.com/gabehassler/PhylogeneticFactorAnalysis.jl

6. Example Analyses

We demonstrate the utility of these methods in the four examples below. Unless otherwise noted, all data are standardized on a per-trait basis (i.e. subtracting the trait mean and dividing the by the trait standard deviation) prior to analysis.

6.1. Pollinator-Flower Co-evolution in Aquilegia

The intimate relationship between plants and their pollinators has played a defining role in the evolution of angiosperms (see Kay and Sargent, 2009; Van der Niet and Johnson, 2012). Here we re-evaluate the relationship between floral phenotypes and pollinators in the genus Aquilegia (columbines). Whittall and Hodges (2007) identify three primary Aquilegia “pollination syndromes” associated with bumblebees, hummingbirds and hawk moths respectively. Tolkoff et al. (2017) apply phylogenetic factor analysis to study the relationship between 11 floral phenotypes and these pollination syndromes in Aquilegia and identify two factors, only one of which is associated with pollinator type.

We re-evaluate this previous work for two reasons. First, Tolkoff et al. (2017) assume the upper-triangular constraint on the loadings which requires that the vertical angle of the flower loads only onto the first factor. Our orthogonality constraint eliminates arbitrarily singling out this phenotype. Additionally, we compare our cross-validation model selection procedure with the marginal likelihood-based approach of Tolkoff et al. (2017), which identifies a two-factor model as having greatest posterior support.

As four of the traits (anthocyanin production and the three pollination syndromes) are binary, we follow Tolkoff et al. (2017) in adapting the latent-liability model of Cybis et al. (2015) to the latent factor model (see SI Section 11). We use the i.i.d. prior with orthogonality constraint, and our model selection procedure, indeed, identifies two factors. We present our results in Figure 3. The first factor captures patterns differentiating hummingbird-pollinated plants from hawk moth-pollinated plants, while the second factor appears to separate the bumblebee pollinated flowers from the other two pollination syndromes. Note that in Figure 3A, the first factor falls along a relatively uniform continuum, while the second factor has a clear out-group consisting of the bumblebee-pollinated plants. While only two taxa are coded as being pollinated by both hummingbirds and hawk moths, this suggests that non-bumblebee Aquilegia pollination strategies may lie on a continuum rather than strict a hawk moth/hummingbird dichotomy, and it is possible that many of the plants listed as having a single pollinator in reality attract both hummingbirds and hawk moths.

6.2. Yeast Domestication

The brewer’s yeast Saccharomyces cerevisiae is essential to a variety of industrial applications due to its ability to convert sugars into ethanol, carbon dioxide and aroma compounds. In addition to its well-known role in the production of fermented food and beverages, it also plays a key role in the production of of bio-fuels and serves as model organism for basic biological research. Industrial strains within this species adapted to thrive within specialized environments and can withstand stress conditions often suited to the specific industrial niche they evolved in, such as ethanol, osmotic, acidic and temperature stresses.

Recent work by Gallone et al. (2016) and Gallone et al. (2019) uses phylogenetic methods to study the domestication of S. cerevisiae within industrial environments. To elucidate the effects of domestication on yeast phenotypes, Gallone et al. (2016) sequence and phenotype 154 strains of industrial and wild S. cerevisiae. The 82 phenotypes include numerous measurements of growth rates under varying environmental and nutrient stresses, the levels of production of various metabolites and the ability to reproduce sexually.

Domestication in plants and animals is typically characterized by limited reproduction outside of domestic contexts, increased yield and decreased tolerance to rare or novel environmental stressors (Doebley et al., 2006; Larson and Fuller, 2014). Gallone et al. (2016) observe these same patterns in the yeast strains they study, with additional niche-specific patterns of covariation. While their analysis examines the specific hypotheses above, they do not employ a data-generative model of phenotypic evolution capable of studying broad changes across all measured phenotypes.

The phylogenetic latent factor model, however, is ideally suited for such a task. We first infer a phylogenetic tree for the 154 phenotyped strains using the 2.8 megabase DNA sequence alignment of Gallone et al. (2016) (see SI Section 12.1). We fix this tree during model selection due to the computational costs of inferring the phylogeny. Based on the principles discussed in Section 5, we opt for the orthogonality constraint, the orthogonal shrinkage prior with forced spacing (α = 0.8) and K_max = 5. Our model selection procedure yields a final model with five significant factors. For the final analysis we infer the tree jointly with factor model parameters using the same tree model in SI Section 12.1. As the number of significant factors K is equal to the maximum K_max, we are confident any signal is biologically relevant but recognize we have not completely captured the full phenotypic covariance structure. That being said, the final factor captures only 7% (5%−9% HPD interval) of the heritable variance and 3% (2%−4%) of the total variance, suggesting that adding additional factors will yield diminishing returns at the expense of exacerbating identifiability challenges.

We plot the loadings associated with the first factor and the first factor on the tree in Figure 4 (see SI Figures 2 and 3 for the full results). For the first factor that accounts for 44% (33%−52%) of the heritable variance, we observe a clear separation between strains in the Beer 1 clade and strains isolated from other fermentation processes and from the wild. Notably, the domestication of beer strains in this clade led to an impaired sexual cycle as observed in the reduced sporulation efficiency and spore viability. This loss of a functional sexual cycle is paired with the additional loss of tolerance to environment and nutrient stresses generally. These stresses are not encountered during continuous growth in the nutrient-rich wort medium. The higher tolerance to high temperature outside of Beer 1 might reflect other more cryptic specializations of non-Beer clade 1 strains selected for different industrial processes (e.g. bioethanol or cocoa fermentation). Beyond these general patterns, we also note specific traits selected for in the Beer 1 clade. For example: strains within this clade do not produce 4-vinyl guaiacol (4-VG), a renown off-flavor in beer that is less relevant to other industrial niches. Additionally, the first factor in this clade is associated with efficient utilization of maltotriose, an important carbon source in beer wort but rarely found in high concentrations in natural environments. These results overall recapitulate one of the main findings of Gallone et al. (2016): the transition from complex and variable natural niches to the stable, nutrient-rich, beer medium favored certain adaptations (e.g. efficient utilization of maltotriose) and accentuation of certain traits (lost of beer off-flavours) at the cost of becoming sub-optimal for survival in the wild.

We emphasize that in this dataset there are different domestication trajectories targeted to very diverse industrial processes, and the life histories of the different clades took separate paths that the additional factors likely capture.

6.3. Mammalian Life History

Life history strategies vary greatly across the tree of life. Generally speaking, organisms exist along a spectrum between fast-reproducing species that produce many offspring with little investment into any single child and slow-reproducing species that invest relatively great time and energy into each of their (comparatively fewer) offspring (Pianka, 1970). While allometric (size-dependent) constraints clearly influence these life history strategies (Boukal et al., 2014), pace-of-life theory predicts size-independent life-history variation as a major driver of phenotypic covariation (Reynolds, 2003; Réale et al., 2010). Much work has been done evaluating these hypotheses across numerous taxonomic groups (see Blackburn, 1991; Bielby et al., 2007; Salguro-Gómez, 2017), but most studies are limited by methodologies that require complete data and scale poorly to very large trees and many traits.

We explore the evolution of mammalian life history using the PanTHERIA ecological database (Jones et al., 2009). We select a sub-set of this data including body mass and 10 life history traits for the 3,691 species with at least one non-missing observation. While Hassler et al. (2020) explore a similar subset of the PanTHERIA data using a multivariate Brownian diffusion (MBD) model, the MBD model cannot partition the covariance structure into size-dependent and size-independent components.

PFA, however, is ideally suited to this task as we can structure the loadings matrix a priori to reveal these relationships. Specifically, we apply the hybrid constraint introduced in Section 5.1 where elements l₂₁, …, l_K1 are fixed to zero, forcing body mass to load only onto the first factor. To avoid ordering the other life-history traits, we assume that the sub-matrix consisting of rows 2, …, K and columns 2, …, P is orthogonal (which we enforce via post-processing). We use the fixed tree of Fritz et al. (2009), which we prune to include only the 3,691 taxa for which we have trait data. We perform model selection assuming K_max = 5, with the optimal model having K = 5. However, the first three factors explain 85% of the heritable variance (with the last factor explaining only 4%), suggesting that K = 5 is sufficient to capture the major patterns of variation in mammalian life-history evolution. We plot our results in Figure 5.

Consistent with the Hassler et al. (2020) analysis, body size is clearly associated with the “slow” life history strategy (i.e. smaller and less frequent litters, longer lives). Notably, this allometric factor is not the dominant factor and explains only 16% (14%−18%) of the heritable variance. The second factor, however, explains 46% (42%−51%) of this variance and clearly captures a size-independent fast-slow life history axis, suggesting that size-independent life-history strategies play a major role in mammalian evolution. As evident in Figure 5, this primary life-history axis (factor 2) varies independently of the allometric one (factor 1) with examples of large/slow (cetaceans), large/fast (lagomorphs), small/slow (bats) and small/fast (rodents) taxonomic groups. This primary life-history factor is well-conserved across the phylogenetic tree, with large taxonomic groups sharing life-history strategies.

Factors 3, 4 and 5 explain comparatively less of the heritable variance (23%, 11% and 4% respectively). Factors 3 and 4 appear to capture trade-offs between litter size and litter frequency, while the 5^th factor primarily captures a negative relationship between weaning age and gestation length and is strongly expressed in monotremes and marsupials that employ different reproductive strategies than placental mammals.

6.4. New World Monkey Cranial Morphology

While much effort has been devoted to studying the evolution of primate brain size, relatively few studies have focused on understanding diversity in brain morphology or shape. Notable exceptions to this trend include Aristide et al. (2016) and Sansalone et al. (2020). Here we re-analyze the data presented in Aristide et al. (2016), that consist of 399 endocranial landmarks in 3-dimensional Euclidean space (standardized by generalized Procrustes analysis) for 48 species of New World monkey (NWM). While Aristide et al. (2016) perform principal component analysis on the Procrustes coordinates and use the principal component scores as traits in a larger evolutionary analysis, this procedure lacks a complete data-generative statistical model that explicitly accounts for uncertainty or noise in the shape data.

We simultaneously infer the phylogeny with the PFA parameters using DNA sequence alignments from Aristide et al. (2015) (see SI Section 12.2 for details). Preliminary results suggest 1) optimal predictive performance requires a very large number of factors (> 20), which is unsurprising given the complexity of this data set, and 2) identifiability poses an unusually great challenge due to the “small-N big-P” nature of the data. As such, we settle on a 3-factor model with orthogonal shrinkage prior and strong shrinkage to maximize identifiability. To maintain differences in scale between traits, we do not re-scale on a per-trait basis but rather divide all traits by the maximum per-trait standard deviation.

We plot the influence of each factor on brain shape and the evolution of these factors on the tree in Figure 6. These three factors capture similar patterns of variation as the first three principal components in Aristide et al. (2016), who identify several ecological processes associated with the evolution of these principal components. As the latent factor model can capture uncertainty that PCA cannot, we are eager to re-evaluate these relationships via a more structured latent factor model that directly models the relationship between the brain shape factors and ecological phenotypes such as social structure or diet. While preliminary results suggest that the first factor is correlated with relative brain volume (i.e. brain volume divided by body mass) and social group size and that the second factor is correlated with body mass and absolute brain volume, we leave this more structured analysis as future work.

7. Discussion

We develop a practical and scalable analysis plan requiring minimal user decisions enabled by computationally innovative inference procedures. Previously, researchers performing phylogenetic factor analysis were limited by computational constraints and had to determine a priori the ordering of the traits and optimal number of factors. These computational and modeling advances are not independent but rather complement each other. Our default model selection procedure requires 26 individual MCMC chain simulations (5-fold cross validation with 5 sets of meta-parameters plus the final run). Such an analysis would be intractable for all but the smallest data sets using existing inference techniques. However, our new inference procedures take only a few hours to run all 26 simulations for even the largest data sets we analyze. Additionally, we have made these tools both flexible and accessible with the Julia package PhylogeneticFactorAnalysis.jl, which assembles and runs all BEAST input files, automatically performs model selection, plots the results and performs basic quality control. Our implementation allows researchers to focus on big-picture modeling decisions and leave low-level implementation details to the software.

Limitations of this work that we plan to address in the future include the following. First, while we can accommodate discrete phenotypes through the latent probit model of Cybis et al. (2015) (see SI Section 11), we notice both in our analysis and Tolkoff et al. (2017) that the discrete parameters tend to have a far higher influence than their continuous counterparts (i.e. the loadings entries associated with the discrete traits have greater magnitude than those associated with continuous traits). This is likely due to the fact that we control the variance of the latent liabilities indirectly by fixing the discrete trait precisions Λ to a constant as do Tolkoff et al. (2017). It is possible that the (potentially) inflated significance of these discrete traits can influence the loadings structure in unexpected ways, and we seek an alternative solution that places the continuous and discrete traits on more equal footing.

Second, there may be cases where label switching persists despite our efforts to induce identifiability. Additional post-processing procedures developed for Bayesian mixture models (Rodíguez and Walker, 2014) or multidimensional scaling (Okada and Mayekawa, 2018) may serve as solutions to these unusually convolved posteriors. While preliminary work suggests that these methods can efficiently identify and deconvolve individual modes of multi-modal posteriors, we are concerned about their potential to identify non-existent signal in the data and believe a careful analysis of their properties is warranted.

Additionally, as proposed in Section 6.4, this work can be readily extended to incorporate parallel evolutionary models for different suites of traits. In this framework, we could simultaneously perform factor analysis on a high-dimensional trait (e.g. brain shape) and infer the evolutionary correlation between the latent factors and other phenotypes of interest (e.g. brain size, diet, group size) using an MBD model. Note that we could study relationships between multiple, distinct high-dimensional phenotypes as well from structural equation modeling paradigm (Lee and Song, 2012). While likelihood calculations under such models are straightforward given this and previous work, inferring the joint evolutionary covariance matrix requires additional inference machinery that we leave as future work.

Finally, while we focus on the multivariate Brownian diffusion model of phenotypic evolution for simplicity, all inference machinery can be readily adapted to other Gaussian processes, such as the multivariate Ornstein–Uhlenbeck (OU) process (Hansen, 1997). Indeed, the OU model and inference procedure of Bastide et al. (2018) have already been implemented in BEAST and are easily integrated with the methods presented in this paper.

Data Availability

The data and code necessary for reproducing our analyses are available in the GitHub repository https://github.com/suchard-group/PhylogeneticFactorAnalysis and archived at Hassler et al. (2022b, https://doi.org/10.5281/zenodo.6617733). The Julia package PhylogeneticFactorAnalysis.jl is registered under the Julia General registry. Source code for PhylogeneticFactorAnalysis.jl is available on GitHub at https://github.com/gabehassler/PhylogeneticFactorAnalysis.jl and archived at Hassler et al. (2022a, https://doi.org/10.5281/zenodo.6617738).