The Impact of Arterial Input Function Determination Variations on Prostate Dynamic Contrast-Enhanced Magnetic Resonance Imaging Pharmacokinetic Modeling: A Multicenter Data Analysis Challenge

Abstract

Dynamic contrast-enhanced MRI (DCE-MRI) has been widely used in tumor detection and therapy response evaluation. Pharmacokinetic analysis of DCE-MRI time-course data allows estimation of quantitative imaging biomarkers such as K^trans(rate constant for plasma/interstitium contrast reagent (CR) transfer) and v_e (extravascular and extracellular volume fraction). However, the use of quantitative DCE-MRI in clinical prostate imaging islimited, with uncertainty in arterial input function (AIF, i.e., the time rate of change of the concentration of CR in the blood plasma) determination being one of the primary reasons. In this multicenter data analysis challenge to assess the effects of variations in AIF quantification on estimation of DCE-MRI parameters, prostate DCE-MRI data acquired at one center from 11 prostate cancer patients were shared among nine centers. Each center used its site-specific method to determine the individual AIF from each data set and submitted the results to the managing center. Along with a literature population averaged AIF, these AIFs and their reference-tissue-adjusted variants were used by the managing center to perform pharmacokinetic analysis of the DCE-MRI data sets using the Tofts model (TM). All other variables including tumor region of interest (ROI) definition and pre-contrast T₁ were kept the same to evaluate parameter variations caused by AIF variations only. Considerable pharmacokinetic parameter variations were observed with the within-subject coefficient of variation (wCV) of K^trans obtained with unadjusted AIFs as high as 0.74. AIF-caused variations were larger in K^trans than v_e and both were reduced when reference-tissue-adjusted AIFs were used. The parameter variations were largely systematic, resulting in nearly unchanged parametric map patterns. The CR intravasation rate constant, k_ep (= K^trans/v_e), was less sensitive to AIF variation than K^trans (wCV for unadjusted AIFs: 0.45 for k_ep vs. 0.74 for K^trans), suggesting that it might be a more robust imaging biomarker of prostate microvasculature than K^trans.

Introduction

Dynamic contrast-enhanced magnetic resonance imaging (DCE-MRI) is widely used in studies of cancer and other pathologies. Often included as one component of aprostate multiparametric MRI protocol (1), DCE-MRI is routinely used in clinical MRI examination of the prostate. Nevertheless, its use as a quantitative diagnostic imaging modality remains limited. In clinical practice, only qualitative estimations of contrast reagent (CR) wash-in and wash-out are generally used in interpreting prostate DCE-MRI data. Though pharmacokinetic modeling approaches have been under extensive investigation for more than a decade (2-10), pharmacokinetic analysis of prostate DCE time-course data is not currently recommended for routine use under the Prostate Imaging-Reporting and DataSystem (PI-RADS) version 2 guidelines (11,12). Improved reproducibility and standardization in pharmacokinetic analysis of prostate DCE-MRI data is needed for the translation of this quantitative data analysis method into clinical settings.

Quantitative DCE-MRI data analysis using pharmacokinetic models allows extraction and mapping of quantitative parameters of tissue biology in vivo. The most commonly estimated parameters are usually variants of K^trans, a rate constant for passive CR molecule plasma/interstitium transfer, and v_e, the volume fraction of interstitial space (extravascular extracellular space, the putative CR distribution volume). The CR intravasation rate constant, k_ep, can be calculated as K^trans/v_e. Unlike qualitative or semi-quantitative analysis, the parameters derived from pharmacokinetic modeling of DCE-MRI time-course data are in principle independent of MRI scanner platform (vendor and field strength), data acquisition details (pulse sequence and parameters), CR dose and/or injection protocol, personnel skills, etc. This makes them promising imaging biomarkers in multicenter clinical trials as imaging endpoints for results standardization and comparison. However, the accuracy and precision of these parameters can be affected by a plethora of factors contributing to the process of pharmacokinetic modeling, including errors in quantification of pre-contrast T₁ (13) and determination of arterial input function (AIF) (14-20), inadequate temporal resolution (21), selection of pharmacokinetic models to fit the data (22,23), and differences in DCE-MRI acquisition time duration (24,25).

As a requirement in quantitative estimation of DCE-MRI pharmacokinetic parameters, the time-dependences of the plasma and tissue CR concentrations, C_p(t) and C_t(t), respectively, need to be determined from the DCE-MRI images. The former is the AIF and its direct quantification from an imaged blood vessel is not straight forward due to, for example, partial volume effect (signal from a selected image voxel, ideally from 100% blood, is contaminated with signal from non-blood tissues) and in-flow effect (the measured blood signal is affected by signal from the “fresh” blood outside the imaging volume that flows into the imaging volume during data acquisition). Nonetheless, as the driving force that causes in vivo DCE-MRI signal changes in the tissue, accurate AIF determination is fundamental for accurate estimation of pharmacokinetic parameters, especially for in vivo systems like the prostate where CR extravasation is substantial (9). Significant research effort has been devoted to the development of AIF quantification methods. The most commonly used method is to measure AIF directly from a feeding artery if it is clearly detected within the image field of view (FOV). Other methods include blinded AIF estimation (14,15), reference tissue and double reference tissue approaches (16,26), direct blood sampling (23,27), empirically derived population averaged AIF (28), and automated vessel region identification (27). However, given these various methods for AIF quantification, there is a lack of studies investigating the impact of variations in AIF determination on pharmacokinetic analysis of DCE-MRI data, which may potentially lead to best-practice guidelines for analysis of DCE-MRI data acquired from different organs.

The National Cancer Institute (NCI) has recently founded the Quantitative Imaging Network (QIN) for the development and validation of quantitative imaging methods for evaluation of cancer therapy response. The main mission of the QIN Image Analysis and Performance Metrics Working Group is to provide guidance and reach consensus on quantitative image analysis methods through comparison and validation of analysis algorithms. For quantitative DCE-MRI data analysis, it is important to understand the variations of DCE-MRI pharmacokinetic parameters caused by specific error-prone steps encountered during data analysis. Arecent QIN multicenter study demonstrated the effects of variations in pharmacokinetic models and software tools on assessment of breast cancer response to neoadjuvant chemotherapy (23). Here we report the results and experience from a DCE-MRI AIF challenge project, in which nine QIN centers performed AIF quantifications independently from the same prostate DCE-MRI data sets and submitted the AIFs to one managing center for central pharmacokinetic analysis of the shared data. The goal of this study is to assess variations in estimated prostate K^trans, v_e, and k_ep parameters resulted from various AIF extraction approaches.

Materials and Methods

AIF Challenge Participating QIN Centers

The QIN centers that participated in this DCE-MRI AIF challenge project were Oregon Health and Science University (OHSU)- managing center, Brigham and Women's Hospital (BWH) in collaboration with General Electric Research and Development, Medical College of Wisconsin (MCW), Icahn School of Medicine at Mount Sinai (MS), University of Michigan center #1 (UM1), University of Michigan center #3 (UM3), University of Pittsburgh (UPitt), Vanderbilt University (VU), and University of Washington (UW). Hereafter, except for where is explicitly indicated, these nine institutions are denoted as, not necessarily in the order listed above, QIN1 to QIN9.

Although some centers may have used more than one method for AIF determination from the shared data, only one AIF method from each participating center was included in this study. In addition, we also included a population averaged AIF published by Geoff Parker (GP) et al. (28) for comparison. This AIF was selected because it is extensively cited. The analytical expression of GP AIF was implemented at the managing center and temporally resampled to match the temporal features of the shared prostate DCE-MRI data.

Human Prostate DCE-MRI Data Acquisition and Sharing

As part of the IRB-approved BWH quantitative imaging studies, multiparametric MR images were collected for the purposes of detection and/or staging of prostate cancer. The images were obtained with a GE SignaHDx 3.0 T system (GE Healthcare, Waukesha, WI) using a combination of 8-channel abdominal array and endorectal coil (Medrad, Pittsburgh, PA). The MRI sequences included T₁- and T₂-weighted imaging, diffusion weighted imaging, and DCE-MRI as described in (29). The axial DCE-MRI acquisition with full prostate gland coverage utilized a 3DSPoiled Gradient Recalled (SPGR) sequence with TR/TE/α = 3.6 ms/1.3 ms/15°, FOV = (26 cm)², 6 mm slice thickness, and reconstructed image voxel size of 1×1×6 mm. DCE-MRI frames were acquired at approximately 5 s intervals (the number of slices per frame varied between 12 and 16, resulting in time resolution between 4.4 and 5.3 seconds) to achieve a clinically appropriate compromise between spatial and temporal resolutions. Gadopentetatedimeglumine (Magnevist, Berlex Laboratories, Wayne, New Jersey) was injected intravenously (0.15 mmol/kg) using a syringe pump at a rate of 3 mL/s followed by 20 mL saline flush at the same rate. The DCE protocol included approximately 5 baseline frames prior to contrast injection.

A subset of the imaging data from the BWH prostate DCE-MRI database were uploaded to the TCIA (The Cancer Imaging Archive) server for data sharing (10). From these, 11 data sets (from 11 patients) with known prostate cancer diagnosis, tumor region of interest (ROI), and relatively consistent acquisition time length (4.5 – 6 min) were downloaded by participating QIN centers for this AIF challenge project.

AIF Determination by QIN Centers

Although the AIF challenge participants were informed of the single image slice in each data set where the tumor ROI had been drawn and the ROI time-course data would be subjected to pharmacokinetic analysis by the managing center, there was no restriction on which image slice(s) to be used for the AIF quantification. Participating centers were required to extract an AIF time-course using their own methodology for each DCE data set. For example, when measuring AIF directly from a femoral artery within the image FOV, the actual number of voxels used to derive the final AIF time-course varied substantially among all centers. Generally, the following results were saved and submitted to the managing center: 1) extracted AIF signal intensity time-course saved as a single column text (‘.txt’ file), 2) converted blood plasma CR concentration time-course (see Eq. 1 below), and 3) screen-captured images showing the ROI/voxel locations for AIF measurement. Item 2) was optional and both items 2) (if submitted) and 3) served as quality control references for the managing center when performing final pharmacokinetic data analyses with the AIFs from different centers. Details of the AIF determination methods (including references) used by the participating centers are summarized in Table 1.

Table 1.

Arterial Input function (AIF) quantification methods by participating QIN centers

Center	Method
OHSU	A single fixed-size ROI was manually placed inside the femoral artery within the field of view (FOV). Averaged blood intensity time-course was extracted from the ROI, which is further converted to Cp(t) using the parameter values provided in the Materials and Methods section.
BWH	GE's OncoQuant prototype tool was used, which includes: 1) AIF Search Region Slice Localization; 2) AIF Search Mask Localization; 3) AIF Detection Using Shape Based Statistics; and 4) AIF Signal to Concentration Conversion. See (27) for more details.
MCW	Motion corrected DCE series were processed using probabilistic independent component analysis implemented in the FSL(FMRIB's Software Library, www.fmrib.ox.ac.uk/fsl). These were further whitened and projected into a 20-dimensional subspace using Principal Component Analysis. The AIFs were manually chosen from the results (4, 36-38).
MS	ROIs were manually placed inside the iliac arteries within the FOV using Osirix (v5.8; Pixmeo, Switzerland). For each AIF determination, one ROI was drawn on one DCE frame, and its position was adjusted when necessary to account for inter-frame subjection motion. Blood intensity time-course was extracted from the ROIs.
UM1	ROIs of 5 × 5 voxels were manually placed in two to four slices showing the highest artery conspicuity on maximum intensity projection (MIP) displays of the baseline-subtracted DCE images. Voxel time-courses within the ROI were individually displayed on a 5 × 5 panel. Voxels with time-courses demonstrating an AIF curve shape were then individually selected and their locations and time-courses automatically saved.
UM3	ROIs were manually drawn on both left and right femoral arteries on the central four slices. To minimize the in-flow effect, the inferior and superior slices were excluded. Twenty voxels within the ROIs with the highest signal increases were determined by thresholding the histogram of intensity changes. The average signal intensity time curve of the 20 voxels yielded the final AIF signal intensity time-course.
UPitt	Images were loaded into PMOD 3.505 (PMOD Technologies Ltd), a commercial software package. Images were examined to search for an artery near the lesion. A region including the identified artery was surveyed using the voxel browser of PMOD to identify an area with high signal intensity change, followed by AIF ROI delineation.
UW	An adapted version of a PET AIF extraction scheme (39)which does not require user-specified AIF ROI was used. The approach was implemented in R (open-source). The extracted input function was then scaled so that the Apparent Extraction of Gd CR based on the analysis of the entire tissue volume signal is 2.5%.
VU	A seed point was placed manually inside an artery and then a region growing method was applied to select the AIF voxels automatically. The intensity range for the region growing method was set as 80% to 120% of that of the seed point, and the voxel distance from the seed was <10 voxels. Mean signal intensity time course of the selected voxels was obtained.

Prior to performing pharmacokinetic analysis of the shared DCE-MRI data, the managing center first converted the AIF signal intensity time-course to blood R₁ (≡ 1/T₁) time-course, R_1,b(t), using the SPGR steady-state signal intensity equation (30) and a fixed pre-contrast blood R₁ of 0.61 s⁻¹ (31), and then to plasma CR concentration time-course, C_p(t), using the following equation:

$${\mathrm{R}}_{1,\mathrm{b}}\left(\mathrm{t}\right)={{\mathrm{r}}_1}^{\ast }{\mathrm{h}}^{\ast }{\mathrm{C}}_{\mathrm{p}}\left(\mathrm{t}\right)+0.61$$ [1]

where r₁ is the CR relaxivity at 3T, set at 3.8 mM⁻¹s⁻¹ ; and h is the hematocrit, set at 0.45.

Pharmacokinetic Analysis of Human Prostate DCE-MRI Data

Using a single in-house Matlab-based software package the managing center performed pharmacokinetic analysis of the shared 11 sets of prostate DCE-MRI data using the AIFs determined by the 9 QIN centers as well as the literature based GP AIF. All AIF arrival times were manually aligned with the uptake phase of the tissue response curves. The most commonly used pharmacokinetic model, the Tofts model (TM) (32), was applied to data analysis and its basic formulation is shown in Equation [2]:

$${\mathrm{C}}_{\mathrm{t}}\left(\mathrm{t}\right)={\mathrm{K}}^{\mathrm{trans}}{\int }_0^t{\mathrm{C}}_{\mathrm{p}}\left(\mathrm{t}’\right)\exp (-{\mathrm{K}}^{\mathrm{trans}}{{\mathrm{v}}_{\mathrm{e}}}^{-1}(\mathrm{t}-\mathrm{t}’))\mathrm{dt}’$$ [2]

where C_t(t) represents tissue CR concentration at time t; C_p(t’) is the AIF obtained from Eq. [1]. The fast-exchange-limit (FXL) condition intrinsic to the TM (23) implies a linear relationship between R₁(t) and C_t(t):

$${\mathrm{R}}_1\left(\mathrm{t}\right)={\mathrm{r}}_1{\mathrm{C}}_{\mathrm{t}}\left(\mathrm{t}\right)+{\mathrm{R}}_{10}$$ [3]

where R₁(t) is tissue R₁ measured at time t, and R₁₀ is the pre-contrast tissue R₁ (assumed to be 0.63 s⁻¹ (10)).

For each DCE-MRI data set, the voxel intensity time-courses within the pre-defined prostate tumor ROI on a single image slice, drawn by the center (BWH) that acquired the data, were subjected to the TM pharmacokinetic analysis. The mean values of the tumor ROI pharmacokinetic parameters (K^trans, v_e, and k_ep) were obtained by averaging the corresponding voxel parameter values.

Because of different approaches (Table 1) used by participating centers in direct measurement of the AIF, large variations in AIF amplitude were observed due to differences in measurement locations, number of voxels used, inflow effects, etc. As an alternative approach for pharmacokinetic analysis, an ROI (Figure 1 inset) in the adjacent obturator muscle area on the same image slice as the tumor ROI was used as a reference tissue for AIF amplitude adjustment (9,33). The AIF (including the literature GP AIF) amplitude was adjusted until the TM fitting of the muscle ROI DCE-MRI data returned a v_e value of 0.1, which is within the range of literature-reported values (34). Therefore, in total twenty AIFs representing unadjusted and reference-tissue-adjusted AIFs from the 9 centers and the GP population AIF were applied for pharmacokinetic modeling of each prostate DCE-MRI data set using the TM, resulting in 20 sets of K^trans, v_e, and k_ep parameters that were then separated into two groups of results obtained with adjusted and unadjusted AIFs.

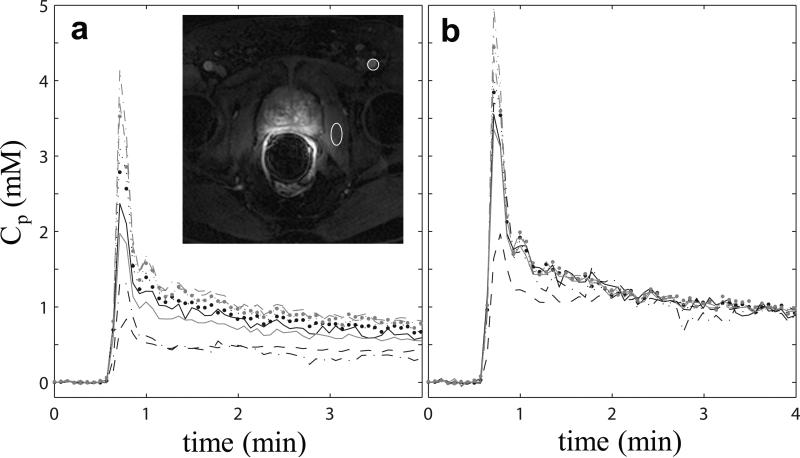
Figure 1.

a.Individual AIFs extracted from one subject's DCE-MRI data by nine participating QIN (Quantitative Imaging Network) centers. The smaller circular ROI in the zoomed image inset (with the prostate in the center of the view) indicates the general location where blood signals are most frequently measured for the final AIF time-courses, and the larger elliptical ROI indicates the general location for the obturator muscle reference tissue ROI. Noticeable variations are evident for both the shape and magnitude of the AIF curves. 1b The reference-tissue-adjusted AIFs of the same subject. The agreement among the individually measured AIFs is clearly improved following the adjustment.

All voxel fitting results were included in calculating the mean tumor ROI pharmacokinetic parameter values since it was difficult to set optimal criteria for excluding voxel fittings obtained with AIFs determined by a diverse array of methods. Using the prior knowledge that a physically meaningful v_eis between 0.0 and 1.0, the lower and upper boundaries for v_e fitting were set accordingly for each voxel. When the reference-tissue-adjusted-AIFs (from all participating centers) were used, all fitted voxel v_e values for all DCE-MRI data sets were within the limits (none returned boundary values). When the unadjusted AIFs were used, on average there were < 3% voxels (ranging from 0 - 6.6% by site for all the AIF and data set combinations) where the returned v_e values reached the upper boundary of 1.0. In these limited number of voxels, the v_e value of 1.0 and the returned K^trans values were taken as the fitted parameter values.

Statistical Analysis

The original parameter values returned from all fittings were used for statistical analysis. Descriptive statistical analysis was conducted to summarize the pharmacokinetic parameter values returned by different AIFs, with the distribution graphically assessed by boxplots. Intraclass correlation coefficients (ICC), within-subject coefficient of variation (wCV), and concordance correlation coefficients (CCC) were calculated, and reported with the corresponding 95% confidence intervals (CIs). While all three were computed to assess the reproducibility of the pharmacokinetic parameter values from different AIFs, each has different focus. The ICCs measure the proportion of total variation contributed by between-subject differences, with high ICCs indicating good agreement. The wCV is the ratio of within-subject standard deviation to the mean of the corresponding parameter. A smaller wCV suggests good reproducibility. The CCCs are closely related to ICCs. They were estimated to represent the level of pairwise linear agreement to a 45 degree line of which the intercept is forced to be zero. A larger CCC (close to 1) suggests good reproducibility. Bland-Altman plots were used to graphically demonstrate pairwise agreements of different AIF measures. SAS 9.4 (Cary, NY) was used for all statistical analysis. SAS macro %ICC9 and %mccc were used for the estimations of ICC, wCV and CCC.

Results

Pharmacokinetic Parameter Variations due to AIF Differences

Figure 1a plots the AIFs extracted from the DCE-MRI data of one subject by the nine participating QIN centers. The inset shows a post-CR DCE image slice zoomed to the prostate area. The smaller circular ROI indicates a common location – the femoral artery - where blood signals were measured for AIF determination, while the larger elliptical ROI indicates the general location of the reference tissue ROI in the obturator muscle. Noticeable variations are evident in both the shape and the amplitude among the C_p time-courses, converted from the measured signal intensity time-course using Eq. [1]. Figure 1b shows the reference-tissue-adjusted AIFs of those shown in Fig. 1a. The agreement among the individually measured AIFs is clearly improved following the adjustment. The standard deviation of the nine measured AIFs over the DCE time course is significantly smaller for the reference-tissue-adjusted AIFs compared to the unadjusted ones (Wilcoxon signed rank test, p < 0.0001). Similar findings are observed for AIFs from the other 10 subjects.

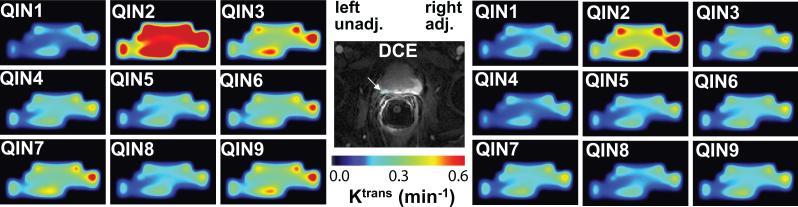
In the center of Figure 2, a zoomed post-CR image slice of the prostate of another subject is shown. The cyan-colored ROI demarks the lesion area used for subsequent TM modeling and parameter comparisons. K^trans color maps generated by TM analysis of the DCE-MRI data using unadjusted AIFs from the nine centers are shown on the left panels and those with reference-tissue-adjusted AIFs are shown on the right. Under the same color scale, substantial variations, mostly in the magnitude of K^trans value, can be seen among the K^trans maps obtained with different unadjusted AIFs (Figure 2, left). These differences are lessened when the K^trans parameter was derived with reference-tissue-adjusted AIFs (Figure 2, right). It is interesting to observe that despite considerable variations in K^trans value caused by AIF differences, the pattern of voxel K^trans distribution largely remains the same.

Figure 2.

Grey-scale image at the center shows a zoomed DCE-MRI slice of another subject. The cyan-colored ROI demarks the lesion area used for subsequent TM modeling and parameter comparisons. K^trans color maps generated by TM analysis of the DCE-MRI data using unadjusted (unadj.) AIFs from the 9 centers are shown on the left panels and those with reference-tissue-adjusted (adj.) AIFs are shown on the right. All 18 panels used the same color scale.

Illustrating the variations seen in Fig. 2 for one parameter from a single DCE-MRI data set, Figure 3 displays the boxplots for K^trans, v_e and k_ep parameters obtained from the eleven subject data sets with adjusted and unadjusted AIFs (including those from the GP AIF). For most measurements, the mean is greater than the median, which is commonly seen when distributions are skewed towards the right (the larger parameter values). The dispersions of the estimated metrics vary substantially across institutions (or AIFs). Examining the results from the same institution (or from one set of unadjusted and adjusted AIFs), it can be observed that the agreement in parameter dispersion between the unadjusted and adjusted AIFs is better for k_ep than K^trans. In fact, k_ep dispersion is hardly affected by the difference in AIF scaling.

Figure 3.

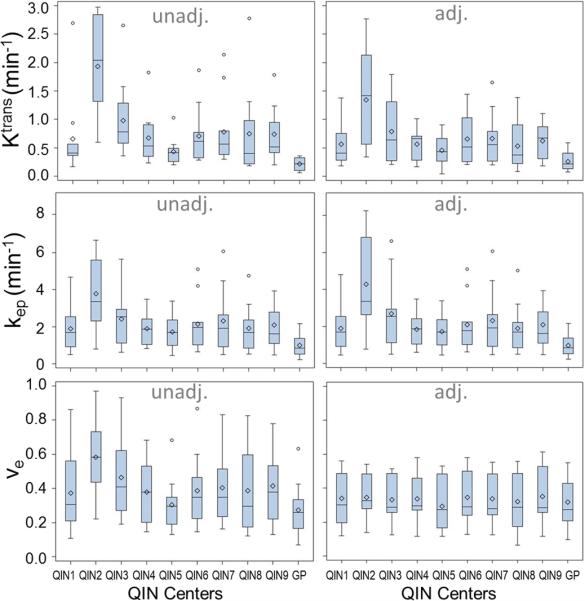
Boxplots of the tumor mean K^trans, v_e, and k_ep parameters for the 11 subjects obtained with unadjusted (unadj.) and adjusted (adj.) AIFs from the 9 centers and the population averaged GP AIF from the literature (28). The diamond and bar symbols represent the mean and median values, respectively. The body of the box is bounded by the upper 25% and lower 25% quartiles, representing the interquartile range of the middle 50% of the measurements. The upper and lower whiskers define the range of non-outliers. The outliers are plotted as dots beyond the whiskers.

Figure 4 shows the column graphs of wCV for K^trans, v_e and k_ep obtained with the unadjusted (shaded light gray) and adjusted (dark gray) AIFs. The error bars are the 95% CIs. A smaller wCV value indicates less variation in measurements on the same subject by different approaches. In this study, the wCV values range from 0.15 for v_e with adjusted AIFs to 0.74 for K^trans with unadjusted AIFs. The wCV of v_e is the smallest, while that of K^trans is the largest among the three pharmacokinetic parameters with either unadjusted or adjusted AIFs. From unadjusted to adjusted AIFs, the parameter variations decrease for K^trans and v_e (wCV values decrease from 0.74 to 0.60 and from 0.33 to 0.15, respectively) while increase slightly for k_ep (wCV value increases from 0.45 to 0.54).

Figure 4.

Column graphs of wCV for the K^trans, v_e and k_ep parameters obtained with the unadjusted (unadj., shaded light grey) and adjusted (adj., dark grey) AIFs. The respective 95% confidence intervals (CI) are shown as error bars.

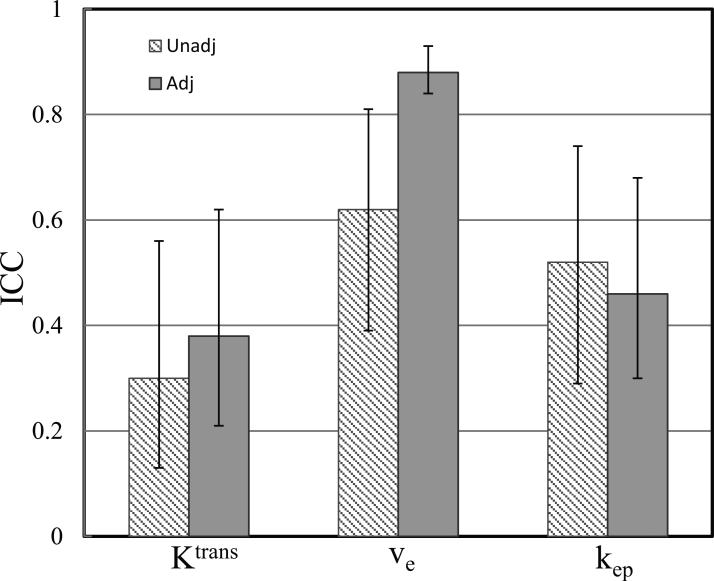
Figure 5 shows the column graphs of ICC values for K^trans, v_e and k_ep obtained with unadjusted (light gray) and adjusted (dark gray) AIFs. The respective 95% CIs are shown as error bars. Consistent with the results shown in Fig. 4, K^trans has the smallest ICC value compared to k_ep and v_e with either unadjusted or adjusted AIF, indicating its high dependence on AIF quantification for prostate DCE-MRI. From unadjusted to adjusted AIFs, the ICC value increases from 0.30 to 0.38 and from 0.62 to 0.88 for K^trans and v_e, respectively, while decreases from 0.52 to 0.46 for k_ep.

Figure 5.

Column graphs of ICC for the K^trans, v_e and k_ep parameters obtained with the unadjusted (unadj., shaded light grey) and adjusted (adj., dark grey) AIFs. The respective 95% CIs are shown as error bars.

Concordance Analysis

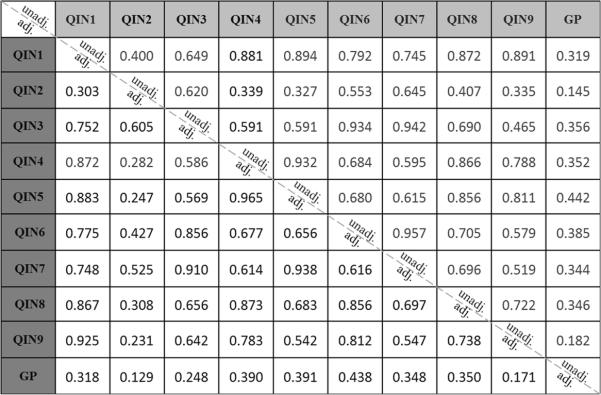
Concordance correlation analysis was conducted to assess parameter agreement between any two AIFs within the same group (adjusted or unadjusted). The K^trans CCC values are tabulated in Table 2a. CCC values for the unadjusted AIFs are listed above the dashed diagonal line, and those for the adjusted AIFs are listed below the diagonal line. Tables 2b and 2c show the 2a equivalents for the v_e and k_ep parameters, respectively. The CCC ranges are 0.031 – 0.944, 0.334 – 0.986, and 0.145 – 0.957 for K^trans, v_e, and k_ep, respectively, obtained with unadjusted AIFs; and 0.082 – 0.965, 0.554 – 0.993, and 0.129 – 0.965 for K^trans, v_e, and k_ep, respectively, obtained with adjusted AIFs. In general, the CCC values increase from unadjusted to adjusted AIFs for the K^trans and v_e parameters, though little changes are observed for the k_ep parameter. In addition, the CCC value resulted from pairing of the GP AIF with any other AIF (unadjusted or adjusted) is usually among the smallest in the above described CCC ranges.

Table 2a.

CCC Values of the K^trans Parameter Obtained with Unadjusted and Adjusted AIFs

CCC: concordance correlation coefficient; unadj: unadjusted AIF; adj: reference-tissue-adjusted AIF

Table 2b.

CCC Values of the v_e Parameter Obtained with Unadjusted and Adjusted AIFs

CCC: concordance correlation coefficient; unadj: unadjusted AIF; adj: reference-tissue-adjusted AIF

Table 2c.

CCC Values of the k_ep Parameter Obtained with Unadjusted and Adjusted AIFs

CCC: concordance correlation coefficient; unadj: unadjusted AIF; adj: reference-tissue-adjusted AIF

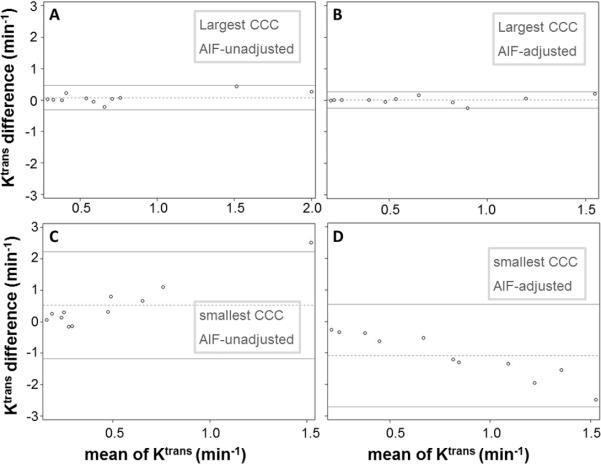
Bland-Altman plots are shown in Figure 6 to demonstrate examples of the agreement in K^trans for AIF pairs with the largest (Figs. 6A and 6B) and smallest (Figs. 6C and 6D) CCC values within the unadjusted (Figs. 6A and 6C) and adjusted (Figs. 6B and 6D) AIF groups. While the differences between measurements are mostly within the 95% confidence limits for all plots, it is rather visually clear (with all four plots having the same vertical axis scale) that the width of confidence bands differs substantially between AIF pairs with greater CCC values (Figs. 6A and 6B) and those with smaller CCC values (Figs. 6C and 6D): narrower for the former; wider for the latter. For the AIF pairs with the largest CCCs (Figs. 6A and 6B), or the best agreements in the estimated K^trans values, the means of K^trans differences between the two AIFs represented by the dotted lines are close to zero at 0.076 and 0.009 min⁻¹, respectively, for unadjusted and adjusted AIFs. For the AIF pairs with the smallest CCCs (Figs. 6C and 6D), or the worst agreements in the estimated K^trans values, the means of K^trans differences are 0.529 and −1.085 min⁻¹, respectively, for unadjusted and adjusted AIFs, considerably different from zero. In addition, in cases of poor K^trans agreement (Figs. 6C and 6D), there seems to be a pattern of correlation between the difference in K^trans and the mean of K^trans with larger differences corresponding to larger mean values.

Figure 6.

Bland-Altman plots are shown to demonstrate agreement in K^trans for AIF pairs with the largest (A and B) and smallest (C and D) CCC values within the unadjusted (A and C) and adjusted (B and D) AIF groups. The two solid horizontal lines represent the upper and lower limits of the 95% confidence interval, while the dotted horizontal line represents the mean value of K^trans differences between the two measurements.

Discussion

The main goal of this multicenter AIF data analysis challenge was to evaluate variations of estimated pharmacokinetic parameters in prostate cancer due to differences in AIF determination. Individually measured AIFs were obtained for each DCE-MRI data set with different QIN center-specific methods which include manual AIF-voxel selection, semi-automatic AIF-voxel identification, automated AIF region identification, and AIF determination using commercial software packages. Quality control measures such as fixed tumor ROI definition, fixed tumor T₁₀, and central data analysis with a commonly used pharmacokinetic model were adopted to ensure that DCE-MRI parameter variations are mainly due to AIF differences only. Although the software package used by the managing center for central pharmacokinetic data analysis was an in-house developed version of the TM (32), its mathematical formulation was validated using DRO (digital reference object) phantom data in a previous DCE-MRI data analysis challenge (23).

The results from this multicenter study clearly show that variations in AIF quantification result in variations in the estimated pharmacokinetic parameter values for prostate DCE-MRI data. Among the K^trans, k_ep, and v_e parameters, K ^trans has the largest while v_e has the smallest AIF uncertainty-caused variations. The wCV values ranged from as low as 0.33 for v_e to as high as 0.74 for K^trans with unadjusted AIFs while the ICC ranged from 0.30 for K^trans to 0.62 for v_e. Similar results of v_e being the most “robust” parameter to AIF variation have been reported in a simulation study (35) previously and its “robustness” may be the direct consequence that v_e is the most influential parameter within the K^trans range (33) seen in prostate cancer. That is, when comparing the effects of the same percentage change in a single parameter on the DCE-MRI time-course, v_e change causes the most noticeable DCE-MRI time-course deviation than the other parameters (33), suggesting that the v_e parameter is shaped more by the tissue DCE time-course during modeling fitting. Another probable reason that K^trans is more susceptible to AIF variation than v_e is that quantification of K^trans strongly depends on the initial AIF spike while v_e quantification relies more on the entire AIF time-course. This work complements a recent study comparing AIF determinations with fully-automated and semi-automated approaches for prostate DCE-MRI data analysis (10). Both efforts show that K^trans variation due to AIF uncertainty is the most prominent compared to variations of other parameters in pharmacokinetic analysis of prostate cancer DCE-MRI data.

It is important to point out that AIF influence on K^trans estimation is CR extravasation (K^trans magnitude) dependent (33), underscoring the importance of accurate AIF measurement in K^trans modeling when CR extravasation is extensive. This CR-extravasation-dependent characteristic is more clearly illustrated in the extreme cases such as normal brain tissue where Gadolinium based CR acts as intravascular agent during the short period after CR injection. Under this condition of no CR extravasation, the AIF has no effect on K^trans (which is undetectable). For organs with extensive CR extravasation, like the prostate (10), the initial AIF curve shape strongly influences the estimation of K^trans. This is possibly the reason that the K^trans values obtained with a fixed, population based GP AIF shows the least agreement (lowest CCC values) with those obtained with individually measured AIFs. After all, the individually measured AIFs (mostly from the femoral artery voxels) more or less captured similar initial AIF curve shapes from the actual DCE-MRI data despite the use of different quantification methods and potential errors from partial volume and inflow effects. The data-acquisition specific details may not be well characterized by the GP AIF, which is modeled based on data from the aorta or iliac arteries, acquired with different pulse sequence parameters and generated at different field strength. Thus, in cases of substantial CR extravasation pharmacokinetic parameters should be estimated with individually determined AIFs whenever possible instead of a generic population averaged AIF unrelated to a specific acquisition protocol.

As shown by this study, there are, however, steps one can take to lessen the effects of AIF variations on estimation of pharmacokinetic parameters. The agreement in the K^trans and v_e parameters obtained with muscle-reference-tissue-adjusted AIFs is improved compared to that with unadjusted AIFs. This is a direct result of better agreement in AIF amplitude among the individually measured AIFs following the muscle reference tissue adjustment. However, the reference tissue approach is far from a perfect solution to AIF-uncertainty caused parameter variations. High wCV, low ICC, and low CCC values are still prevalent after the reference tissue method was used, especially for K^trans, of which the estimated value is strongly influenced by both the magnitude and the initial curve shape of the AIF.

The results from this multicenter challenge project are supported by findings from a recent simulation study (unpublished results), which aims to identify pharmacokinetic parameters that are relatively insensitive to AIF variations. In fact, the simulations demonstrate complete k_ep insensitivity to AIF magnitude errors (unpublished results). The current study shows that for TM analysis, k_ep is less sensitive to AIF uncertainty compared to K^trans. k_ep is the CR intravasation rate constant and is predominantly characterized by the washout phase of the DCE time-course. Since k_ep is often calculated as K^trans/v_e and not as an independent variable in model fitting of the DCE time-course data, it is sometimes under used in clinical DCE-MRI studies. Results from this work, however, suggest that, taking into consideration of uncertainties in AIF determination, k_ep may be a more reproducible DCE-MRI parameter than the K^trans parameter and thus a more robust imaging biomarker of perfusion and permeability. For prostate DCE-MRI, k_ep can offer a different perspective of prostate microvasculature, especially when the K^trans ranges of benign and cancerous tissue overlap (5).

It is important to note that DCE-MRI parameter variations caused by AIF variations are mostly systematic. As an example shown in Fig. 2, the differences among the prostate tumor K^trans maps obtained with different AIFs are mostly in voxel K^trans values. The pattern of voxel K^trans distribution largely remains similar for all the maps. This suggests that assessment of tumor heterogeneity through texture analysis of DCE-MRI parametric maps may not be affected greatly by variations in AIF determination. Additionally, for longitudinal DCE-MRI studies to assess cancer therapy response, the systematic errors caused by AIF quantification variations may be largely cancelled in the calculation of percent changes of DCE-MRI parameters before and after therapy. In a multicenter breast DCE-MRI data analysis challenge study (23), we demonstrated that DCE-MRI parameter percent changes before and after first cycle of neoadjuvant chemotherapy were substantially less sensitive to variations in pharmacokinetic model and software package used for data analysis, compared to absolute parameter values.

Due to its unique temporal signatures and often superior image contrast, DCE-MRI is widely used in prostate imaging as part of a multi parametric prostate MRI protocol. DCE-MRI data analysis with qualitative and/or semi-quantitative assessment is favored in current clinical practice largely due to their relative simplicity. However, the rich information embedded in the DCE-MRI data is likely underutilized. Pharmacokinetic data analysis for estimation of tissue biology specific parameters has the potential to provide more consistent results for broad cross-vendor and cross-scanner platform applications. Robust and reliable AIF determination remains a real challenge for adoption of pharmacokinetic modeling of prostate DCE-MRI data in clinical settings. The results from this study provide useful information on how to minimize errors in estimation of prostate DCE-MRI parameters caused by uncertainties in AIF determination and which parameters are less sensitive to AIF variations.

There are limitations in this multicenter effort. The study cohort size was small (11 patients) and the AIF determination methods were mostly constrained to the approach of direct measurement from an artery. Additionally, no longitudinal data were available and, as a result, the effects of AIF variation on DCE-MRI assessment of prostate cancer progression and/or response to treatment were not investigated. The current study only summarizes the results of AIF variations for a single pharmacokinetic model (TM) and thus parameter reproducibility from different models and relevant model comparisons with AIF variations are beyond the scope of this work. Finally, voxel DCE-MRI parameter distribution patterns were assessed visually without the use of a quantitative texture analysis method.

Conclusion

In conclusion, this multicenter data analysis study highlights one (not all) significant challenge in quantitative pharmacokinetic analysis of DCE-MRI data: considerable variations in DCE-MRI parameter values were observed as a result of variations in AIF determination. The AIF-caused parameter variations are higher in K^trans than v_e. One solution that can be used to reduce parameter variation is to adjust AIF amplitude following its measurement using a reference tissue method. k_ep is less sensitive to AIF uncertainty than K^trans, suggesting that k_ep might be a more robust pharmacokinetic parameter for characterization of prostate microvasculature. The variations in parameter estimates caused by differences in the AIF are systematic and thus the patterns of voxel-based DCE-MRI parametric maps were largely unaffected. In multicenter clinical trials involving quantitative DCE-MRI, central data analysis with a fixed AIF determination method should be adopted for a single time-point study to minimize the undesirable effects due to uncertainty in AIF determination. This approach may introduce systematic errors in estimated pharmacokinetic parameters, but avoids random errors resulted from data analysis by individual centers with different AIF determination methods, which could be detrimental in addressing biological questions. In a longitudinal multicenter study, percent changes of pharmacokinetic parameters instead of their absolute values should be used as imaging endpoints to more accurately evaluate biological changes.

Abbreviations

AIF

arterial input function

CCC

concordance correlation coefficient

CR

contrast reagent

DCE-MRI

dynamic contrast-enhanced magnetic resonance imaging

ICC

intra-class correlation coefficient

K^trans

rate constant for plasma/interstitium contrast reagent transfer

k_ep

rate constant for contrast reagent intravasation

R₁₀

= 1/T₁₀, pre-contrast tissue longitudinal relaxation rate constant

ROI

region of interest

TM

Tofts model

v_e

extravascular, extracellular volume fraction

wCV

within-subject coefficient of variation