Analysis of the “thermodynamic information content” of a Homo sapiens structural database reveals hierarchical thermodynamic organization

Abstract

Classification of the amounts and types of lower order structural elements in proteins is a prerequisite to effective comparisons between protein folds. In an effort to provide an additional vehicle for fold comparison, we present an alternative classification scheme whereby protein folds are represented in statistical thermodynamic terms in such a way as to illuminate the energetic building blocks within protein structures. The thermodynamic relationship is examined between amino acid sequences and the conformational ensembles for a database of 159 Homo sapiens protein structures ranging from 50 to 250 amino acids. Using hierarchical clustering, it is shown through fold-recognition experiments that (1) eight thermodynamic environmental descriptors sufficiently accounts for the energetic variation within the native state ensembles of the H. sapiens structural database, (2) an amino acid library of only six residue types is sufficient to encode >90% of the thermodynamic information required for fold specificity in the entire database, and (3) structural resolution of the statistically derived environments reveals sequential cooperative segments throughout the protein, which are independent of secondary structure. As the first level of thermodynamic organization in proteins, these segments represent the thermodynamic counterpart to secondary structure.

The ability to define a protein fold in terms of elementary units or building blocks is the cornerstone to effective structure comparison. By cataloging the frequency and length of these building blocks within each fold, similarities and differences can be noted and quantitatively evaluated. Indeed such classification schemes as structural classification of proteins (SCOP; Murzin et al. 1995) and families of structurally similar proteins (FSSP; Holm and Sander 1996) have proven invaluable as a means of comparing and contrasting folds. A hallmark feature of traditional descriptions of fold space is that the building blocks are described in terms of structural attributes. For example, each position in a protein is part of a primary structural unit (e.g., α-helix, β-sheet, etc.), each structural unit is, in turn, part of a higher order structural motif (e.g., α/β), and the motifs are arranged to form unique folds. Although structural descriptions of fold space have proven to be effective in fold recognition as well as homology studies (Bowie et al. 1991; Godzik and Skolnick 1992; Jones et al. 1992; Bryant and Lawrence 1993; Defay and Cohen 1996; Huang et al. 1996; Rost et al. 1997; Kelley et al. 2000; Mallick et al. 2002), such approaches do not account (at least not explicitly) for the well-known experimental observation that proteins display regional differences in conformational heterogeneity, even under native conditions (Wuthrich 1989; Bai and Englander 1996). This result suggests that the canonical structure alone may not provide the required determinants for fold specificity, and that a classification scheme that accounts explicitly for this heterogeneity could be of significant value.

In the early 1970s Anfinsen (1973) reported that under the proper solvent conditions, amino acid sequences fold spontaneously into functional three-dimensional protein structures, thus introducing the “thermodynamic hypothesis.” An important implication of the thermodynamic hypothesis is that all of the information required for specifying a protein fold is contained in the primary sequence, and that the information is thermodynamic in nature. An extension, or perhaps even a consequence, of the thermodynamic hypothesis is that in addition to considering a protein as a sequence of structural building blocks (i.e., secondary structure), “a parallel view can be adopted, wherein a protein can be represented as a sequence of thermodynamic building blocks.” Indeed, as shown previously (Wrabl et al. 2002), a database of proteins can be represented in purely thermodynamic terms, and the thermodynamic environments can be implemented successfully into a fold recognition approach, thus providing a proof of principle for the notion of an entirely thermodynamic description of protein folds.

The success of these initial studies (Wrabl et al. 2001,Wrabl et al. 2002) and the unique nature of the environmental descriptors leaves open the possibility that a hierarchical thermodynamic classification scheme similar to SCOP (Murzin et al. 1995) or FSSP (Holm and Sander 1996), but independent of structure, can be developed that will serve as the basis for evaluating thermodynamic similarities between folds. Toward this end, the following questions must be addressed: How many distinct energetic environments are present across a database of proteins? Do hierarchical thermodynamic elements exist that are analogous to secondary structure? What is the relationship between the structural and the thermodynamic building blocks? How many amino acid types are needed to encode the thermodynamic environments across the entire structural database? In the present study, cluster analysis and fold recognition are used as tools to address these questions, which constitute the cornerstone of a thermodynamic classification scheme that can be used as the basis for comparison between folds (Holm and Sander 1996).

Results and Discussion

Position-specific energetics as calculated by the COREX algorithm

The strategy for characterizing proteins in energetic terms is based on determining the regional differences in stability for a database of Homo sapiens proteins (Table A1) using the COREX algorithm (Hilser and Freire 1996). Briefly, the COREX algorithm models the native state of a protein as a statistical thermodynamic ensemble of partially unfolded conformational microstates. For each microstate i in the ensemble, the Gibbs free energy is calculated from a previously calibrated and validated parameterization based on surface area and conformational entropy terms (Baldwin 1986; Lee et al. 1994; Xie and Freire 1994; Gomez et al. 1995; D’Aquino et al. 1996; Habermann and Murphy 1996). From the free energies, the probability of each state can be represented by

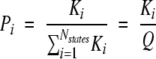(1)

Where K_i= [exp^(−ΔGi/RT)] is the statistical weight of each microstate and the summation in the denominator is the partition function, Q, for the system (Wrabl et al. 2002).

An important feature of the COREX algorithm is that it provides a means of describing a protein structure by position-specific values that can be ascertained directly from the probabilities described in equation 1. One such quantity, known as the stability constant, κ_f,j, is the ratio of the summed probability of states in the ensemble in which a particular position, j, is folded (∑P_f,j) to the summed probability of states in which that position is not folded (∑P_nf,j):

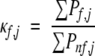(2A)

The importance of the stability constant is twofold. First, it can be compared directly to hydrogen exchange protection factors, thus representing an experimentally verifiable energetic description of the protein (Hilser and Freire 1996; Hilser et al. 1998). The good agreement between calculated and experimental protection factors demonstrates that the native state ensemble, as calculated by the COREX algorithm, provides a reasonable representation of the actual native state ensemble (Wrabl et al. 2001).

The most important aspect of the stability constant, however, is that it provides a means of characterizing the regional differences in stability within the protein, at the level of each residue position. In energetic terms, the stability constant reports on the difference in energy between the subensemble of states in which position j is in a folded region and the subensemble of states in which position j is in a nonfolded region (Fig. 1 ▶):

Figure 1.

Position-specific thermodynamic environments in proteins. The COREX algorithm converts the high-resolution structure into an ensemble of states (top; see Materials and Methods). To calculate the position-specific thermodynamic descriptors, the ensemble of states is first divided into folded and nonfolded subensembles (middle left and middle right) with respect to a particular position j in the protein. Position j is colored blue in the folded subensemble and yellow in the nonfolded subensemble. The position specific observables ([ΔG]_j) have been defined as the difference in energy between the subensembles in which position j is folded (〈ΔG_f,j〉) and the subensemble of states in which position j is not folded (〈ΔG_nf,j〉). Highlighting the statistical nature of the position-specific quantities, we note that each of the states in the different subensembles may have different position-specific energetics, indicating that the average value within a subensemble does not necessarily correspond to the energetics of a particular conformational state.

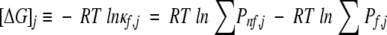(2B)

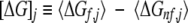(2C)

Likewise, position-specific reporters of the component thermodynamic functions can also be defined; the polar enthalpy ([ΔH]_pol,j), apolar enthalpy ([ΔH]_ap,j), and conformational entropy ([TΔS]_conf,j), like the stability constant, report on the difference in energetics between the folded and nonfolded subensembles for each position (Materials and Methods; Wrabl et al. 2002). The unique and quintessential feature of these quantities, which is shown in Figure 1 ▶, is that they are ensemble averaged thermodynamic reporters of the energetics at each position, which implicitly account for the effects of all regions of the protein on the energetics at a particular position (Wrabl et al. 2002). In contrast, they do not represent the energetic contribution of an amino acid to the stability of the molecule. This is highlighted in Figure 2 ▶ and Table 1, which show the relationship between the position-specific descriptors of the proteins in the H. sapiens database and the contribution of the amino acid at that position to the accessible surface area (ASA) of the native structure. Because the energetic contribution of each amino acid is calculated from the ΔASA, as described in Materials and Methods, the absence of a correlation between the position-specific descriptors and the energetic contributions indicates that position-specific quantities provide a means of characterizing the fold of a protein in a way that effectively separates the amino acid at a position in the protein from the position itself. As such, the position-specific energetics are a property of the ensemble as a whole, and the sequence of properties constitutes the thermodynamic signature of that fold.

Figure 2.

Residue-specific accessible surface area vs. position-specific thermodynamic descriptors. Each point of the scatter plot is a residue position in the human lysozyme protein (PDB: 1JSF). The ordinate is the accessible surface area (ASA) of the apolar atoms for each residue of the protein taken from the X-ray crystal structure. The static ASA values represent the residue-specific energetic contribution to the thermodynamics of the protein. The abscissa is the thermodynamic descriptor, ([ΔH]_ap,j), for each residue position of the protein calculated by the COREX algorithm. These values are ensemble averaged reporters of the apolar enthalpy at each position in the protein. The correlation coefficient (R²) for the static residue-specific ASA vs. the ensemble-averaged position-specific thermodynamic descriptors is 0.0932, indicating no correlation. Correlation statistics for the entire database of proteins is summarized in Table 1.

Table 1.

Correlation (R²) table of accessible surface area contributors versus ensemble-averaged thermodynamic reporters

Correlations R2	〈ln Kr〉	〉Δap〉	〈ΔHpol〉	〈Δ Sconf〉	〈ΔHtot〉	〈TΔStot〉
ASAap	0.0757	0.0763	0.0269	0.0067	0.0180	0.0852
ASApol	0.0388	0.0452	0.0081	0.0002	0.0218	0.0612
ASAsc	0.0388	0.0498	0.0087	0.0014	0.0244	0.0640

Statistically derived thermodynamic environments of the native state ensemble

Each of the 23,944 residue positions in the 159-protein H. sapiens database was assigned a vector of thermodynamic parameters calculated as described in Materials and Methods. The database was subjected to a series of clustering analyses, and all of the residues in the database were successively binned (in separate experiments) into 2, 4, 6, 8, 10, 12, 14, 16, and 18 clusters based on dissimilarities of the thermodynamic descriptors at each position. Cluster analysis reveals the natural distributions of thermodynamic environments (TEs) within the data and therefore eliminates biases associated with defining environment groups in empirical (or even arbitrary) ways as was done in our previous analyses (Wrabl et al. 2001,Wrabl et al. 2002). The significance of this result is discussed below.

Previous studies from this laboratory have revealed that the propensities of amino acids for empirically defined thermodynamic environments can provide significant structure encoding information (Wrabl et al. 2002). This was demonstrated by successfully matching sequences to folds using a thermodynamics-based threading approach. In this study, separate experiments were performed, using the different clustering results, wherein the propensities of the 20 amino acids for each environment cluster were determined. The resultant log-odds probabilities were used in fold recognition experiments to determine the minimum number of thermodynamic environments necessary to sufficiently describe the structure encoding energetics of the proteins analyzed in the database.

Figure 3 ▶ shows fold recognition results obtained by threading a library of sequences onto protein folds that have been defined by different numbers of thermodynamic environment clusters. Fold recognition success is represented by the percent of proteins in which the correct sequence scored in the top 1 percentile (i.e., was among the top four scoring sequences out of 431 decoys) when matched with its corresponding fold. Two features are apparent in Figure 3 ▶. First, fold recognition success saturates at ~84% (dotted line) as the number of environments increases. Second, eight thermodynamic environments provide more than 95% (80%/84%) of the structure encoding information with 80% (128/159) of the sequences correctly matched with structure. Of note is that the choice of criteria for success does not dramatically impact the results. Defining success as scoring in the top 5th and 10th percentiles increases the fraction of proteins that are correctly matched to 87% (139/159) and 91% (145/159), respectively. These results are reproducible using randomly and nonrandomly jackknifed data sets (not shown), indicating that the results are not sensitive to the choice of proteins used. As no size- or structure-related bias in the analysis has been identified (Wrabl et al. 2002), these results suggest that within the database of H. sapiens proteins, eight distinct thermodynamic environments are sufficient to account for virtually all of the thermodynamic diversity captured by this analysis.

Figure 3.

Fold recognition success as a function of thermodynamic environment number. Fold recognition experiments (solid squares) using scoring matrices composed of the log-odds probability of the 20 amino acids for a series of thermodynamic environments. A successful fold recognition experiment is one in which the native amino acid sequence of the target protein scores higher than 99% of the sequences in the sequence library (i.e., one of the top four out of 431 scoring sequences). The dotted line indicates where fold recognition success saturates. The X-axis indicates the number of thermodynamic environments used to generate the scoring matrix for the associated fold recognition experiment. The large open square denotes the minimum number of thermodynamic environments necessary to capture 95% of the structure encoding information for the proteins used in this study (see text for details).

Characterization of the statistically derived thermodynamic environments in proteins

The Partitioning Around Medoids (PAM; Kaufman and Rousseeuw 1990) clustering algorithm was applied to the raw position-specific thermodynamic data when assigning each position to a thermodynamic environment cluster. For illustration purposes, the mean thermodynamic properties of the eight thermodynamic environments are listed in Table 2 and plotted in Figure 4 ▶ so as to highlight key differences. The thermodynamic environments are plotted in order of increasing stability constants. As noted, a low stability constant is obtained for positions that are unfolded in the majority of highly probable states. Consequently, Figure 4 ▶ is ordered from high flexibility (i.e., low stability) to low flexibility (i.e., high stability). When plotted in this fashion, the enthalpy ratio ([ΔH]_ap/[ΔH]_pol), which provides a metric of the relative polarity of a position-specific environment, appears to oscillate as a function of thermodynamic environment. This means that the cluster analysis is discriminating between apolar and polar environments at each level of stability, and suggests that proteins have evolved multiple energetic mechanisms to achieve a particular stability.

Table 2.

Mean energetic properties of the eight thermodynamic environments

Figure 4.

Normalized mean energetic properties of the eight requisite thermodynamic environments. Each thermodynamic environment has been statistically derived based on its component thermodynamic descriptors (see Materials and Methods). Plotted are the eight thermodynamic environments (clusters) listed in order of increasing stability. The two thermodynamic descriptors are the stability constant (closed circles) and enthalpy ratio (open circles). The Y-axis is the normalized mean value of the corresponding thermodynamic descriptors. Due to the relationship between enthalpy and surface area, lower enthalpy ratios denote higher apolar content environments.

The structural distribution of the thermodynamic environments is of special interest. Shown in Figure 5 ▶ is a schematic representation of the COREX thermodynamic characterization for one of the proteins in the database (PDB: 1KAO). For illustration purposes, the eight thermodynamic environments have been threaded over both the sequence (Fig. 5A ▶) and the structure (Fig. 5B ▶) of the molecule. Of note is the existence of stretches of residue positions with identical thermodynamic environments. It should be pointed out that this behavior is in no way predetermined by the calculation. To the contrary, the ensemble is parsed into folded and nonfolded subensembles for the calculation of each residue quantity (Fig. 1 ▶), thereby providing position-specific resolution. The origin of the behavior, instead, stems from the fact that groups of residues, which are folded or nonfolded in the same states, will have the same thermodynamic environment profile. In other words, the stretches of residues with identical environments represent sequential cooperative segments within the protein, wherein cooperative refers to the fact that the residues within each segment behave in an overall coupled fashion in the context of the native state ensemble.

Figure 5.

Thermodynamic environment characterization for the GTP binding protein (PDB: 1KAO). (A) The primary sequence has been colored according to cooperative segments, where each color represents a different thermodynamic environment. The mean energetic properties of the thermodynamic environments comprising the segments are listed in Table 2. Above the sequence is a cartoon representation of the secondary structural units of the protein (gray). It is important to note that the sequential cooperative segments can bridge multiple structural elements, and structural elements can span multiple sequential cooperative segments. In essence, the segments identified here are the thermodynamic counterpart to secondary structure, as they represent the first level of thermodynamic organization in proteins. (B) The ensemble-based energetics have been mapped onto the high-resolution structure, providing a quantitative “single-molecule view” of a fluctuating ensemble.

The fact that the COREX analysis has been shown to capture cooperativity in proteins (Hilser et al. 1998) as well as the determinants of site–site communication (Pan et al. 2000) suggests that the definition of these sequential cooperative segments is not an artifact of the calculation. Indeed, recent studies (Babu et al. 2004) have shown that the ensemble-based descriptions used in this analysis can identify the subglobal units of cooperative structure in a way that can be directly validated using NMR. Thus, the success of this algorithm at capturing such a diverse array of biophysical and functionally relevant phenomena within a unified framework suggests that the sequential segments are physically meaningful.

Interestingly, comparison of the boundaries for the sequential cooperative segments and the boundaries for secondary structure elements reveals that although some segments correspond directly to structural elements, most segments are independent of traditional structural classifications. In several cases the sequential cooperative segments correspond to the ends of β-strands or α-helices and the adjacent loops. In short, sequential cooperative segments can bridge multiple structural elements, and structural elements can span multiple sequential cooperative segments. The lack of correspondence between the two is important because it demonstrates that each secondary structural element does not obligatorily behave as a cooperative unit. Instead, the cooperative building blocks in proteins are more accurately represented by the segments depicted in Figure 5 ▶. In essence, the sequential cooperative segments identified here are the thermodynamic counterpart to secondary structure, as they represent the first level of thermodynamic organization in proteins.

Comparison of the sequential cooperative segments to secondary structure is useful because it highlights several important aspects of the segments. First, like secondary structure, which reports on the local structure in the context of the overall fold, the sequential cooperative segments report on the local energetics in the context of the entire conformational manifold of the protein. As such, they are a representation of the overall structure but are merely defined in energetic terms at the level of groups of amino acids. This leads to a second similarity, which is that the sequential cooperative segments are not reporting only on the intrinsic properties of the local sequence. Rather, the boundaries and thermodynamic properties of the segments are influenced by a combination of local and global factors. Finally, all residues in a sequence are not found to be part of sequential cooperative segments. Much like secondary structure, which can be flanked by residues with more or less nonregular structure, the energetically defined segments are often abutted by amino acids with no discernible energetic similarity to neighboring positions. The qualitative similarities between the segments described here and secondary structure are therefore compelling, as they appear to illuminate a novel way of dissecting proteins into their elementary building blocks.

Hierarchical clustering of amino acids in thermodynamic environments

As the position-specific thermodynamic descriptors in the H. sapiens protein database are independent of the contributions of the amino acids at each site (Fig. 2 ▶; Table 1), the propensities of each amino acid for the different environments cannot be predicted de facto from the properties (i.e., size, charge, hydrophobicity, etc.) of the amino acids. It is therefore of significant interest to know the distributions of amino acids in each environment, as well as which amino acids share similar propensities across all environments. To address these issues, the probabilities of the 20 amino acids for the eight thermodynamic environments were subjected to double hierarchical clustering as described in Materials and Methods. The resultant hierarchical groupings (i.e., dendrograms) and heat map illustrate amino acid propensities for the eight thermodynamic environments (Fig. 6 ▶). Inspection of the row dendrogram shows that the first separation of amino acid clusters is based on hydrophobicity. The aromatic amino acids (Trp, Phe, and Tyr) and the branched aliphatic amino acids (Leu, Ile, and Val) make up the hydrophobic group, and the remaining amino acids comprise the hydrophilic group. Although noted above, it should be emphasized that the separation by hydrophobic and hydrophilic is not predetermined by the method of analysis. As the contribution of each amino acid is not correlated to the thermodynamics of the environment to which it belongs (Fig. 2 ▶; Table 1), the hierarchical cluster analysis is reporting on a selection mechanism that is not specifically determined by the chemistry of the amino acid at that position.

Figure 6.

Double hierarchical cluster analysis of amino acid log-odds probabilities for eight thermodynamic environments. The 20 amino acids make up the rows and the eight thermodynamic environments comprise the columns of the heat map. The heat map is a qualitative representation of the amino acid log-odds probabilities for the thermodynamic environments. Negative log-odds probabilities are green, log-odds probabilities near zero are black, and positive log-odds probabilities are red. The color intensity reflects the magnitude of the log-odds probabilities. The row dendrogram shows groupings of amino acids with similar log-odds probabilities for the thermodynamic environments. The gray scale above the amino acid dendrogram is the cluster scale; the values below the scale indicate the calculated dissimilarity measures, and the values above the scale correspond to the number of amino acid clusters at different positions in the dendrogram. The red dotted line is positioned at the level of six amino acid clusters. Each of the six amino acid cluster nodes is indicated by a red dot. The column dendrogram reveals similarities in the thermodynamic environments.

When further divided into six clusters, as indicated by the red dotted line in Figure 6 ▶, the propensities of aromatic amino acids split from the branched aliphatic amino acids forming two independent hydrophobic classes. The primary discriminating factor between the two hydrophobic clusters is the relative infrequency of the aromatic groups in environments of medium stability with moderate [ΔH]_ap/[ΔH]_pol ratios (i.e., TE1, TE2, and TE4). Once again, this discrimination cannot be predicted on the basis of side chain properties, suggesting that the results are not a simple consequence of the energy function used to determine the ensemble. Further inspection of the row dendrogram reveals that the propensity of Pro is unique, as it is found often in low stability environments (i.e., TE2) at the expense of high stability (i.e., TE7 and TE8). Gly, Thr, and Ala form a fourth cluster, trending with the stability dimension and being found more often in medium- to low-stability environments. The fifth cluster consists of Met, His, Glu, and Arg residues, which are found in medium- to high-stability and high-enthalpy-ratio environments (i.e., TE5 and TE7). The sixth and final cluster is composed of amino acids with charged and uncharged polar side chains (Ser, Asp, Asn, Lys, Glu, and Cys). The frequency of occurrence of these residues does not track with the stability of a cluster, but they are found frequently in environments with high [ΔH]_ap/[ΔH]_pol ratios (i.e., TE3, TE5, and TE7).

Interestingly, comparison of the propensities of chemically and structurally similar amino acids such as Lys and Arg reveal distinct differences in environmental preferences (Fig. 6 ▶). TE3 illustrates one of the differentiating factors between Lys and Arg; Arg is seldom found in the low-stability environment that has a high enthalpy ratio, although Lys shows no preference. Indeed, throughout the entire database, numerous differences in thermodynamic usage are found for amino acids with apparently similar chemistry.

One of the most compelling features of the pattern of propensities (Fig. 6 ▶; Table 2) is that the propensities of some amino acids are strongly influenced by the stability of the particular region of the protein, whereas others are more strongly influenced by the polarity of the environment and are independent of stability. The latter result is especially noteworthy as it further indicates that the propensity of an amino acid for an environment is not simply recapitulating the stability contribution of that amino acid to the environment (as implemented in the energy function). Although we have no definitive explanation for these results, it is, nonetheless, further indication of a degree of independence between the position in a fold and the amino acid that is encoded at that position. If this is indeed the case, then it would leave open the possibility that the thermodynamic signature of a fold is coded in the primary sequence, but not at the level of the individual residue. In other words, it would appear to suggest that the thermodynamic signature of a fold is encoded at the level of “groups” of residues.

Statistically derived amino acid clusters

The double hierarchical clustering of amino acids in the eight thermodynamic environments (Fig. 6 ▶) reveals both traditional and nontraditional groupings of amino acid types. Underlying questions are whether these groupings provide sufficient resolution to encode structure, and if so, how many amino acid clusters are required to describe the eight thermodynamic environments of the proteins in the H. sapiens structural database. To determine the thermodynamic information content of the hierarchical clustering analysis, simple fold recognition experiments were performed based on the observed amino acid distributions within the eight thermodynamic environments in a manner similar to the analysis of the environment clusters described above. Figure 7 ▶ shows fold recognition results obtained by threading sequences, which are defined as having 2–20 amino acid clusters (in separate experiments), into folds that are defined in terms of the eight thermodynamic environment clusters. The amino acid clusters came directly from the nodal divisions of the hierarchical clustering analysis (row dendrogram in Fig. 6 ▶). As stated previously, the first division of the 20 amino acids was correlated with hydrophobicity (Fig. 6 ▶), in which one group was comprised of the aromatic and branched aliphatic amino acids, and the second group was made up of the remaining 14 amino acids. Fold recognition based on this binary hydrophobicity scale was poor (~50% success), indicating that simple hydrophobic versus hydrophilic was not sufficient to match sequence to fold, even with the eight thermodynamic environments (Fig. 7 ▶). Indeed, fold recognition based on the threading of the two amino acid clusters into just two environmental clusters (which, as seen in the column dendrograms in Fig. 6 ▶, reduces to polar versus apolar) results in no fold recognition success (open symbols in Fig. 7 ▶). This result shows that the environmental resolution provided by the current thermodynamic descriptors represents a dramatic improvement over classification schemes that simply identify hydrophobic versus hydrophilic or inside versus outside, and it does so without detailed structural specifications at each position.

Figure 7.

Fold recognition success as a function of amino acid cluster number. The solid squares represent fold recognition experiments using scoring matrices composed of the log-odds probability of a series of amino acid clusters for the eight thermodynamic environments. The open squares represent fold recognition experiments using scoring matrices composed of the log-odds probability of a series of amino acid clusters for two thermodynamic environments. A successful fold recognition experiment is one in which the actual amino acid sequence of the target protein scores higher than 99% of the sequences in the decoy library (i.e., one of the top four out of 431 scoring sequences). The dotted line indicates where fold recognition success saturates. The X-axis indicates the number of amino acid clusters used to generate the scoring matrix used in the associated fold recognition experiment. The large open square denotes the minimum number of amino acid groups necessary to encode the eight thermodynamic environments of the proteins in the H. sapiens database.

The threading curve (Fig. 7 ▶) reveals that the overall success of the fold recognition experiments saturates at ~80% (dotted line) as the number of amino acid groups increases. This result is especially intriguing as it indicates that for the H. sapiens database, >90% (76%/84%) of the thermodynamic variability is captured with a combination of eight thermodynamic environments (large open square in Fig. 3 ▶) and only six amino acid clusters (large open square in Fig. 7 ▶). The implication of this finding is that the genetic code, which consists of 64 codons (20 amino acids), is overdetermined with respect to fold specificity, and that the remaining resolution of the genetic code into the 20-aminoacid library is most likely necessary for functional chemistry and/or to provide a library of chemically similar but structurally variable groups, which can facilitate good packing in the different environments throughout the protein.

Position-specific thermodynamics of chaperone Hsp90

The use of the ensemble-based, position-specific energetics is an important facet of the current analysis, and represents a critical element in the interpretation of the data. As noted previously, the position-specific environmental descriptors are more appropriately viewed as reporters rather than contributors to the energetics at that position. However, of particular significance is that the information is not captured through a structural definition of the environments. Figure 8 ▶ highlights the Phe residues in the chaperone Hsp90 protein (PDB: 1BYQ). As noted, F34, F108, and F160 are nearly identical in terms of their accessible surface area contribution to the energetic calculations as provided by the static representation. The ensemble-based characterization reveals, however, that these three “structurally” similar positions have significantly different thermodynamics in the native state ensemble. The differences in natural log of the stability constants illustrate this point. F160 has a ln κ_f of ~13 whereas F34 has a ln κ_f of ~24 (i.e., F34 is in a more stable environment). Contrary to the canonical representation of these two residues afforded by the high-resolution structure, F160 is far more dynamic than F34 and has a much higher probability of being unfolded in the native state ensemble. Similarly, residues F160 and F203 are found in different regions of the Hsp90 chaperon protein. F160 is buried in the core of the protein and has nearly zero surface area exposure. F203 is located on the surface of the protein with approximately 70% surface area exposure. The ensemble-based characterization of these structurally different residues reveals the energetics of these positions to be similar in the native state ensemble.

Figure 8.

Position-specific thermodynamics of heat shock protein 90 (PDB: 1BYQ). Six phenylalanine residues are represented in space-fill and colored according to their thermodynamic environment. The accompanying table summarizes the ensemble-averaged thermodynamics at each position as well as the static properties of these six residues. The thermodynamic environments do not report on static structural properties of the system (see text for details).

Based on the independence of the thermodynamic and structural classifications (Fig. 5 ▶), it is not surprising that the thermodynamic environments of each Phe residue also have no relationship to secondary structural elements. F160 and F203 are energetically similar in the native state ensemble, but F160 is completely buried in an extended β-strand, whereas F203 is 70% exposed and is located in a turn just C-terminal to an α-helix. F10 and F108 have analogous thermodynamic environments, but F10 is surface exposed in an extended β-strand and F108 is completely buried in an α-helix. Furthermore, F10 and F160 are both found in extended β-strands but belong to different thermodynamic environments. Finally, F34 and F108 are both located in α-helices, but exhibit vastly different energetics in the native state ensemble.

Although anecdotal, Figure 8 ▶ illustrates the fundamental difference between the thermodynamic descriptors and structural classifications of each position. By definition, classic structural descriptions of the positions within proteins are describing some facet of the structure itself. The descriptors used here provide a metric of the thermodynamic susceptibility of each position. This is an essential aspect of the ensemble-based description because it provides a means of quantitatively accounting for the fact that although all regions of the molecule are seen in a unique conformation within the context of the canonical structure, some regions are more dynamic and have a higher proclivity to adopt other conformations. Just as important, proteins utilize different thermodynamic mechanisms (eight, to be precise; Fig. 3 ▶) to achieve the regional differences in stability and dynamics, and the approach described here captures these differences. Finally, the fact that the environments are described in units of energy means that this approach provides a direct quantitative connection with the biophysical and functional properties, opening a venue for experimental validation (Hilser and Freire 1996; Pan et al. 2000; Babu et al. 2004).

Conclusions

The results presented here reveal that a database of H. sapiens protein structures can be represented as sequences of eight thermodynamic environment descriptors, which, when applied to the high-resolution structure, reveal sequential cooperative segments within the proteins. As these segments represent the first level of thermodynamic organization in proteins, they can be considered the thermodynamic equivalent to secondary structure. Interestingly, the boundaries for the sequential cooperative segments and traditional secondary structural elements are not identical, suggesting that secondary structures, although representing elementary structural units, are not the thermodynamic building blocks. Identification of the number and types of thermodynamic building blocks in proteins, as well as the pattern of these building blocks within the protein structure, is a prerequisite to a classification scheme that can be used to compare thermodynamic similarity between folds.

Finally, the results indicate that almost all of the structure encoding information in the thermodynamic analysis can be conferred with six amino acid clusters. This result is intriguing as it implies that the full spectrum of thermodynamic diversity could have been achieved with a much simpler genetic code. In effect, the results indicate that although proteins (and the genetic code) may have increased in complexity during the evolution process, the thermodynamic architecture of the resultant proteins can nonetheless be explained in the context of a primordial library.

Materials and methods

Selection of a Homo sapiens structural database

As described below, an ensemble of conformational states was generated for a database of proteins using the COREX algorithm (Hilser and Freire 1996; Wrabl et al. 2002). Because organism-specific differences in nucleotide content and codon usage (Grantham et al. 1980; Sharp et al. 1988) may affect the distributions of amino acids within different energetic environments in proteins, the current studies were conducted on a database of H. sapiens proteins (Table A1). Selected for these studies were single-chain proteins with sizes ranging from 50 to 250 amino acids, with a maximum sequence identity of 50% (the size limit of 250 residues was chosen based on CPU time required for calculations; Wrabl et al. 2002). To control for structure quality, only X-ray structures with a resolution of 2.5 Å or better were used. This study constitutes the first large-scale COREX analysis of proteins greater than 100 residues. Neither the results reported previously (Wrabl et al. 2002) nor those presented here display a dependence on protein size (data not shown), suggesting that the 250-amino-acid cutoff, although dramatically curtailing the computational resources required, does not impact the conclusions.

The COREX algorithm and accessible surface area calculations

Each of the 159 proteins in the database was analyzed using the COREX algorithm (Hilser and Freire 1996), which models the native state ensemble of a protein molecule in solution. In the present analysis a Monte Carlo sampling method was used to select states, in order to accommodate large ensembles that would be computationally intractable with a full COREX enumeration. The total number of states saved was 50,000 per partition, except for proteins less than 80 residues. For proteins less than 80 residues the Monte Carlo sampling method is still used, but the total number of saved states is lowered accordingly. The Monte Carlo sampling method preferentially selects lower energy states at the expense of high-energy states. The selection subroutine uses the free energy of the completely unfolded state as a reference. The probability of selecting states with an energy equal to the reference state is 75%. The probability of selecting a higher energy state drops exponentially to 1%. Similarly, the probability of selecting a state lower in energy than the reference state increases exponentially to 100%.

The free energy for any state in the ensemble relative to the fully folded state is calculated using equation 3:

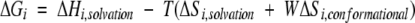(3)

COREX uses accessible surface-area-based parameterizations to calculate the relative apolar and polar free energies of each enumerated state (Gomez et al. 1995; Hilser and Freire 1996):

(4)

(5)

The conformational entropy (ΔS_conf) for each state has three contributing factors: (1) ΔS_bu→ex, the entropy change associated with the transfer of a side chain that is buried in the interior of the protein to its surface; (2) ΔS_ex→u, the entropy change gained by a surface-exposed side chain when the peptide backbone unfolds; and (3) ΔS_bb, the entropy change gained by the backbone itself upon unfolding (D’Aquino et al. 1996; Hilser and Freire 1996). The simulated temperature of all the analyses was 25°C, the window size was 5, and the entropy weighting factor (W) was 0.500. The entropy weighting factor is a scaling variable used in the fold recognition experiments to minimize contributions of the completely unfolded states from the position-specific calculations (equation 3). Inquiries or requests for the COREX algorithm can be made to the corresponding author.

Ensemble-averaged thermodynamic descriptors

To arrive at the position-specific descriptors, an average excess quantity is first defined, which represents the probability distribution of all states in the ensemble (Wrabl et al. 2002):

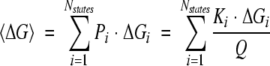(6)

(7)

(8)

Taking the difference in average excess quantities of the folded (Q_f) and unfolded (Q_nf) subensembles yields the position-specific values as described previously (Wrabl et al. 2002):

(9)

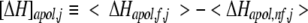(10)

(11)

Equations 9–11 reflect the average thermodynamic environments of a particular position in the protein, accounting implicitly for the contribution of all the amino acids over all the states in the ensemble.

Statistical derivation of the thermodynamic environments

The thermodynamic environments were statistically defined using S-Plus 6.0 professional software. The clustering analysis algorithm used was Partitioning Around Medoids (PAM; Kaufman and Rousseeuw 1990). The position-specific [ΔG]_j, [ΔH]_ap,j, [ΔH]_pol,j, and [TΔS]_conf,j were the variables used to cluster all 23,944 residue positions in the database. The dissimilarity metric was Manhattan, which calculates the sum of the absolute differences between clusters. The number of medoids was set to 2, 4, 6, 8, 10, 12, 14, 16, and 18 in separate cluster analyses.

Statistics for the 20 amino acids as a function of thermodynamic environment cluster number were tabulated for all the residue positions in the database (data not shown). The differential distribution of the 20 amino acids within the thermodynamic environments was used to calculate the log-odds probability of finding an amino acid type within a particular thermodynamic environment cluster. The log-odds probability (LOP) is double normalized to account for differences in amino acid and thermodynamic environment counts as calculated below:

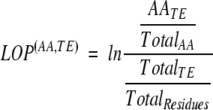(12)

Double hierarchical cluster analysis

SpotFire DecisionSite Statistics 7.2 software was used to visualize and cluster the calculated log-odds probabilities of the 20 amino acids for the eight thermodynamic environments. The heatmap (Fig. 6 ▶) illustrates the relative intensities of the calculated log-odds probabilities. The color range is set to continuous coloring and spans from green to black to red. The range is set so that log-odds probabilities equal to zero are colored black, log-odds probabilities less than zero are green, and log-odds probabilities greater than zero are colored red. The relative intensity of the colors reflects their distance from zero.

SpotFire uses agglomerative hierarchical clustering to generate dendrograms showing the similarity between rows of the heatmap (amino acids) and columns of the heatmap (thermodynamic environments). The agglomerative approach iteratively merges the closest pair of records according to the selected clustering method and dissimilarity measure. The clustering method is complete linkage that computes the distance between any two clusters, x and y, as the maximum distance between a member of cluster x and a member of cluster y. The similarity measure is city block distance (Manhattan), which is the distance between two points measured along axes at right angles.

Fold recognition experiments based on amino acid propensities for thermodynamic environments

Fold recognition experiments are performed using PROFILESEARCH of Eisenberg and coworkers (Bowie et al. 1991), which implements the Smith–Waterman local alignment algorithm (Smith and Waterman 1981) as described previously (Wrabl et al. 2002). The three-dimensional profiling method is used as a proof-of-principle assessment of the amino acid propensities for the thermodynamic environments as seen in Figure 6 ▶. The three-dimensional profiling method characterizes the high-resolution structure of a protein as a one-dimensional string of “environmental classes” as a function of residue position (Bowie et al. 1991). There are 431 decoy sequences in each fold recognition experiment that were obtained from the Protein Data Bank (Berman et al. 2000). The sequence library was inclusive for all H. sapiens fold types coding for experimentally solved structures ranging from 50 to 250 residues in length and having a maximum sequence identity of 50% (Berman et al. 2000). The PROFILESEARCH algorithm dynamically aligns each decoy amino acid sequence plus the native sequence to the one-dimensional string of thermodynamic environments. Each combination of amino acid and thermodynamic environment in the alignment receives a score from a scoring matrix derived from the log-odds probabilities calculated by equation 12. The cumulative score over all positions in the alignment is the score for a particular sequence to a target protein. A successful fold recognition experiment is one in which the native sequence had a greater cumulative score than 99% of the sequences in the sequence library.

Abbreviations

• PDB, Protein Data Bank

• PAM, Partitioning Around Medoids

• ASA, accessible surface area

• SCOP, structural classification of proteins

• FSSP, families of structurally similar proteins

Appendix

Table A1

Table A1.

Homo sapiens proteins used in the COREX thermodynamic database

PDB	Length	Resolution (Å)	SCOP class	SCOP family
1A17	159	2.45	All α	Tetratricopeptide repeat (TPR)
1A3K	137	2.10	All β	Galectin (animal Slectin)
1A7S	221	1.12	All β	Eukaryotic proteases
1AD6	185	2.30	All α	Retinoblastoma tumor suppressor domains
1ALU	157	1.90	All α	Long-chain cytokines
1ALY	146	2.00	All β	TNF-like
1AX8	130	2.40	All α	Long-chain cytokines
1B56	133	2.05	All β	Fatty acid binding protein-like
1B8K	90	2.15	Small	Neurotrophin
1B90	123	1.15	αand β (a + b)	C-type lysozyme
1BD8	156	1.80	αand β (a + b)	Ankyrin repeat
1BIK	110	2.50	Small	Small Kunitz-type inhibitors & BPTI-like
1BKF	107	1.60	α and β (a + b)	FKBP immunophilin/proline isomerase
1BKR	108	1.10	All α	Calponin-homology domain, CH-domain
1BR9	182	2.10	All β	Tissue inhibitor of metalloproteinases, TIMP
1BUO	121	1.90	α and β (a + b)	BTB/POZ domain
1BY2	111	2.00	α and β (a + b)	Scavenger receptor cysteinerich (SRCR)
1BYQ	213	1.50	α and β (a + b)	Heat shock protein 90, N-terminal domain
1CBS	137	1.80	All β	Fatty acid binding protein-like
1CDY	178	2.00	All β	C2 set domains
1CLL	144	1.70	All α	Calmodulin-like
1CTQ	166	1.26	α and β(a/b)	G proteins
1CY5	92	1.30	All α	DEATH domain
1CZT	160	1.87	All β	Coagulation factor C2 domain
1D2S	170	1.55	All β	Laminin G-like module
1D7P	159	1.50	All β	Coagulation factor C2 domain
1DG6	149	1.30	All β	TNF-like
1DV8	128	2.30	α and β (a + b)	C-type lectin domain
1E21	119	1.90	αand β (a + b)	Ribonuclease A-like
1E87	117	1.50	α and β (a + b)	C-type lectin domain
1EAX	241	1.30	All β	Eukaryotic proteases
1EAZ	103	1.40	All β	Pleckstrin-homology domain (PH domain)
1ESR	75	2.00	αand β (a + b)	Interleukin 8-like chemokines
1EVS	163	2.20	All α	Long-chain cytokines
1F2Q	167	2.40	All β	I set domains
1FAO	100	1.80	All β	Pleckstrin-homology domain (PH domain)
1FIL	139	2.00	α and β(a + b)	Profilin (actin-binding protein)
1FL0	163	1.50	All β	Myf domain
1FNA	89	1.80	All β	Fibronectin type III
1FNL	172	1.80	All β	I set domains
1FP5	208	2.30	All β	C1 set domains
1FW1	208	1.90	All α	Glutathione S-transferases, C-terminal
1G0X	192	2.10	All β	I set domains
1G1T	157	1.50	α and β (a + b)	C-type lectin domain
1G96	111	2.50	α and β (a + b)	Cystatins
1GEN	200	2.15	All β	Hemopexin-like domain
1GGZ	144	1.50	All α	Calmodulin-like
1GH2	107	2.22	α and β (a/b)	Thioltransferase
1GLO	217	2.20	α and βprotein	Cathespin
1GNU	117	1.75	α and β (a + b)	GABARAP-like
1GP0	133	1.40	All β	Mannose 6-phosphate receptor domain
1GQV	135	0.98	α and β (a + b)	Ribonuclease A-like
1GR3	132	2.00	All β	TNF-like
1GS4	244	1.95	α and βprotein	Androgen receptor
1GSM	202	1.90	All β	I set domains
1H4W	224	1.70	All β	Eukaryotic proteases
1H6H	143	1.70	α and β (a + b)	PX domain
1HDO	205	1.15	α and β (a/b)	Tyrosine-dependent oxidoreductases
1HDR	236	2.50	α and β (a/b)	Tyrosine-dependent oxidoreductases
1HMT	131	1.40	All β	Fatty acid binding protein-like
1HNA	217	1.85	All α	Glutathione S-transferases, C-terminal
1HUP	141	2.50	α and β (a + b)	C-type lectin domain
1HZ1	129	1.05	All α	Short-chain cytokines
1I1N	223	1.50	α and β (a/b)	Protein-L-isoaspartyl O-methyltransferase
1I27	69	1.02	All α	C-terminal domain of the rap74 subunit
1I2T	61	1.04	All α	PABC (PABP) domain
1I4M	108	2.00	α and β (a + b)	Prion-like
1I71	83	1.45	Small	Kringle modules
1I76	163	1.20	α and β (a + b)	Matrix metalloproteases, catalytic domain
1IAM	185	2.10	All β	I set domains
1IAP	190	1.90	All α	Regulator of G-protein signaling, RGS
1IFR	110	1.40	All β	Lamin A/C globular tail domain
1IHK	157	2.20	All β	Fibroblast growth factors (FGF)
1IJR	103	2.20	α and β (a + b)	SH2 domain
1IJT	128	1.80	All β	Fibroblast growth factors (FGF)
1IKT	115	1.75	α and β (a + b)	Sterol carrier protein, SCP
1IMJ	208	2.20	α and β (a/b)	Ccg1/TafII250-interacting factor B (Cib)
1IMX	56	1.82	Small	Insulin-like
1IPC	186	2.00	α and β (a + b)	Translation initiation factor eIF4e
1J55	88	2.00	α and β	S-100P
1J74	139	1.90	α and β (a + b)	Ubiquitin conjugating enzyme, UBC
1JHJ	160	1.60	All β	Anaphase-promoting complex
1JK3	158	1.09	α and β (a + b)	Matrix metalloproteases, catalytic domain
1JNX	207	2.50	α and β (a/b)	Breast cancer associated protein, BRCA1
1JSF	130	1.15	α and β (a + b)	C-type lysozyme
1JSG	111	2.50	All β	Oncogene products
1JWF	139	2.10	All α	VHS domain
1JWO	97	2.50	α and β (a + b)	SH2 domain
1K04	142	1.95	All α	FAT domain of focal adhesion kinase
1K1B	228	1.90	α and β (a + b)	Ankyrin repeat
1K59	122	1.80	α and β (a + b)	Ribonuclease A-like
1K95	161	1.90	All α	EF-hand modules in multidomain proteins
1KAO	167	1.70	α and β (a/b)	G proteins
1KCQ	103	1.65	α and β (a + b)	Gelsolin-like
1KEX	155	1.90	All β	B1 domain of Neuropilin-1
1KGD	173	1.31	α and β (a/b)	Nucleotide and nucleoside kinases
1KHX	200	1.80	All β	SMAD domain
1KMV	186	1.05	α and β (a/b)	Dihydrofolate reductases
1KPF	111	1.50	α and β (a + b)	HIT protein kinase-interacting proteins
1KTH	58	0.95	Small	Small Kunitz-type inhibitors & BPTI-like
1L2H	144	1.54	All β	Interleukin 1 β
1L3K	163	1.10	α and β (a + b)	Canonical RBD
1L8J	170	2.00	α and β (a + b)	MHC antigen-recognition domain
1L9L	74	0.92	All α	NKL-like
1LB4	153	2.40	All β	TRAF domain
1LCL	141	1.80	All β	Galectin (animal Slectin)
1LDS	96	1.80	All β	C1 set domains
1LF7	164	1.20	All β	Retinol binding protein-like
1LN1	203	2.40	α and β (a + b)	STAR domain
1LO6	221	1.56	All β	Eukaryotic proteases
1LPJ	133	2.00	α and β	Human Crbp IV
1LSL	113	1.90	All β	Thrombospondin-1
1M47	122	1.99	All α	Short-chain cytokines
1M5I	105	2.00	Coiled coil	Tumor suppressor gene product Apc
1M7B	179	2.00	α and β (a/b)	G proteins
1M9Z	104	1.05	Small	Extracellular domain, cell surface receptor
1MAZ	143	2.20	Membrane and cell surface	Bcl-2 inhibitors of programmed cell death
1MEM	215	1.80	α and β (a + b)	Papain-like
1MEO	200	1.72	α and β	Glycinamide ribonucleotide transformylase
1MFM	153	1.02	All β	Cu,Zn superoxide dismutase-like
1MH1	180	1.38	α and β (a/b)	G proteins
1MH9	194	1.80	α and β	Deoxyribonucleotidase
1MJ4	79	1.20	α and β	Cytocrome B5 sulfite oxidase
1MWP	96	1.80	α and β (a + b)	A heparin-binding domain
1MZA	240	2.23	α and β	Pro-Granzyme K
1N6H	167	1.51	α and β	Rab5A
1NKR	195	1.70	All β	I set domains
1OR3	136	1.73	All α	Apolipoprotein
1PBK	116	2.50	α and β (a + b)	FKBP immunophilin/proline isomerase
1PBV	195	2.00	All α	Sec7 domain
1PHT	83	2.00	All β	SH3-domain
1PKR	80	2.48	Small	Kringle modules
1POD	124	2.10	All α	Vertebrate phospholipase A2
1QB0	177	1.91	α and β (a/b)	Cell cycle control phosphatase
1QDD	144	1.30	α and β (a + b)	C-type lectin domain
1QGV	130	1.40	α and β (a/b)	Spliceosomal protein U5-15Kd
1QKT	248	2.20	All α	Nuclear receptor ligand-binding domain
1QUU	245	2.50	All α	Spectrin repeat
1RBP	174	2.00	All β	Retinol binding protein-like
1RGP	189	2.00	All α	BCR-homology GTPase activation domain
1RLW	124	1.40	All β	PLC-like (P variant)
1SRA	151	2.00	All α	Osteonectin
1TEN	89	1.80	All β	Fibronectin type III
1TN3	137	2.00	α and β (a + b)	C-type lectin domain
1UCH	206	1.80	α and β (a + b)	Deubiquitinating enzyme
1YGS	190	2.10	All β	SMAD domain
1ZON	181	2.00	α and β (a/b)	Integrin A (or I) domain
1ZXQ	192	2.20	All β	C2 set domains
2ABL	162	2.50	α and β (a + b)	SH2 domain
2CPL	164	1.63	All β	Cyclophilin (peptidylprolyl isomerase)
2FCB	173	1.74	All β	I set domains
2FHA	172	1.90	All α	Ferritin
2ILA	145	2.30	All β	Interleukin-1 (IL-1)
2ILK	155	1.60	All α	Interferons/interleukin-10 (IL-10)
2PSR	96	2.05	All α	S100 proteins
2TGI	112	1.80	Small	Transforming growth factor (TGF)- β
3FIB	249	2.10	α and β (a + b)	Fibrinogen C-terminal domain-like
3IL8	68	2.00	α and β (a + b)	Interleukin 8-like chemokines
5PNT	157	2.20	α and β (a/b)	Phosphotyrosine protein phosphatases