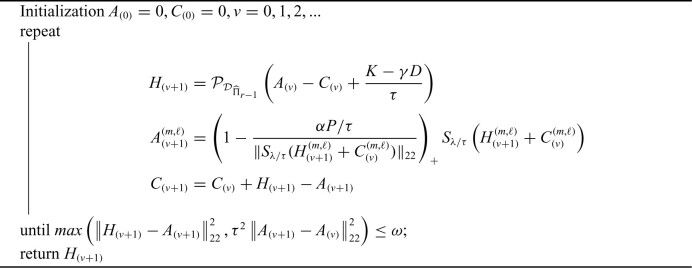Summary
Many studies collect functional data from multiple subjects that have both multilevel and multivariate structures. An example of such data comes from popular neuroscience experiments where participants’ brain activity is recorded using modalities such as electroencephalography and summarized as power within multiple time-varying frequency bands within multiple electrodes, or brain regions. Summarizing the joint variation across multiple frequency bands for both whole-brain variability between subjects, as well as location–variation within subjects, can help to explain neural reactions to stimuli. This article introduces a novel approach to conducting interpretable principal components analysis on multilevel multivariate functional data that decomposes total variation into subject-level and replicate-within-subject-level (i.e., electrode-level) variation and provides interpretable components that can be both sparse among variates (e.g., frequency bands) and have localized support over time within each frequency band. Smoothness is achieved through a roughness penalty, while sparsity and localization of components are achieved by solving an innovative rank-one based convex optimization problem with block Frobenius and matrix  -norm-based penalties. The method is used to analyze data from a study to better understand reactions to emotional information in individuals with histories of trauma and the symptom of dissociation, revealing new neurophysiological insights into how subject- and electrode-level brain activity are associated with these phenomena. Supplementary materials for this article are available online.
-norm-based penalties. The method is used to analyze data from a study to better understand reactions to emotional information in individuals with histories of trauma and the symptom of dissociation, revealing new neurophysiological insights into how subject- and electrode-level brain activity are associated with these phenomena. Supplementary materials for this article are available online.
Keywords: Convex optimization, Functional principal component analysis, Multilevel models, Psychological trauma, Regularization
1. Introduction
Functional principal components analysis (FPCA) is arguably one of the most popular tools for analyzing functional data, providing low-dimensional, parsimonious measures that account for the majority of variation. There has been growing interest in FPCA for multiple dependent functional processes, such as when multiple curves are observed for each subject. Depending on the characteristics of the data and the scientific questions of interest, multiple functional processes are typically analyzed either through multivariate FPCA, aiming to describe joint variation of different processes (Rice and Silverman, 1991; Ramsay and Silverman, 2005; Chiou and others, 2014; Happ and Greven, 2018) or through multilevel FPCA, aiming to characterize variation from repeatedly observed curves with a multilevel hierarchical structure (e.g., between- and within-subject level principal components) (Crainiceanu and others, 2009; Di and others, 2009; Greven and others, 2010; Staicu and others, 2010; Zipunnikov and others, 2011; Shou and others, 2015; Goldsmith and others, 2015; Scheffler and others, 2019).
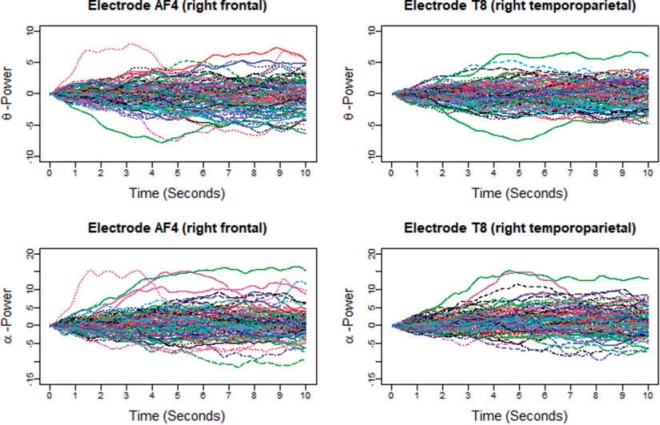
An increasing number of studies collect and wish to analyze functional data that can be viewed simultaneously as multilevel and multivariate. A popular example is from electroencephalography (EEG), which measures electrical activities that take the form of multiple curves over time, defined over multiple prespecified frequency bands, and recorded from multiple locations across the scalp Our motivating example, which is described in further detail in Section 2, involves the analysis of such data from a study to better understand biological mechanisms of feelings of numbness and being removed from reality. To illustrate these data, Figure 1 displays data from two of four time-varying frequency-band measurements of brain activity, at 2 of 14 measured locations across the scalp. Such data can be considered multivariate across frequency-band measures, where we desire a summary of the joint information across the multiple frequency bands, as well as multilevel across locations, where we consider both whole-brain variability between participants as well as location-variation within participants.
Fig. 1.
Illustration of the Blunted and Discordant Affect (BADA) study data: time-varying power in two (theta and alpha power) of four considered bands at two (AF4, right frontal and T8, right temporoparietal) locations.
Although methods for multivariate FPCA and for multilevel FPCA have been individually extensively studied, and methods for FPCA of other data structures such as longitudinally observed functional data (Chen and Müller, 2012; Hasenstab and others, 2017; Scheffler and others, 2019) have also been studied, there is a dearth of methods that are able to jointly deal with both multivariate and repeatedly measured functional processes. A contribution of this article is the introduction of a method for FPCA of multilevel multivariate functional data. Specifically, we extend the multilevel decompositions in Di and others (2009) and Shou and others (2015) to multivariate processes through latent random multivariate subject-specific processes and replicate-within-subject processes and assume a separable replicate-temporal covariance structure that can account for correlation among data from the same subject, such as spatial correlation among data from different locations across the scalp.
The major contribution of this article is the development of an interpretable approach to the PCA of multiple functional processes that is not only smooth but also localized within time and among the variates. Existing approaches to conducting FPCA on multivariate functional data are limited in that they are not localized, or that each component is a nontrivial function of each variate at all time points. This lack of localization, which is a common issue across most classical procedures for analyzing functional data, can be problematic in that it obstructs interpretation. The benefit of localized procedures, both for providing scientifically interpretable measures and for improving statistical performance, have been previously discussed in the context of functional linear regression (James and others, 2009; Zhao and others, 2012; Zhou and others, 2013) and in the context of univariate FPCA (Chen and Lei, 2015; Lin and others, 2016). However, to the best of our knowledge, localization for the PCA of multivariate functional data has yet to be addressed. The problem of conducting an interpretable FPCA for multivariate processes is considerably more challenging than for univariate, as it needs to allow for localization not only within time, but also for localization among the variates.
Towards the goal of conducting an interpretable multivariate FPCA, we introduce a novel localized sparse-variate FPCA (LVPCA). The LVPCA incorporates a roughness penalty to assure smoothness, and matrix  and block-wise Frobenius norm-based penalties to achieve localization within time and variate, respectively. The use of this combination of penalties can be viewed as a multivariate FPCA analogue of the vector
and block-wise Frobenius norm-based penalties to achieve localization within time and variate, respectively. The use of this combination of penalties can be viewed as a multivariate FPCA analogue of the vector  and block-wise vector
and block-wise vector 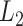 norms that are used to achieve within- and between-group sparsity in high-dimensional regression by the sparse-group Lasso (Simon and others, 2013). There are two main challenges when incorporating localization or sparsity into a PCA: direct approaches via rank-one projection matrices provide solutions that, if they exist, are NP-hard and they provide components that are not orthogonal. The LVPCA overcomes the first issue through the use of the Fantope, which is the convex hull of rank-one projection matrices and has been adapted to overcome analogous problems in localized univariate FPCA (Chen and Lei, 2015) and sparse high-dimensional PCA (Vu and others, 2013). The separation of the smoothness penalty and the localization and sparsity penalties enables the problem to be embedded into the Fantope and allows the LVPCA to be formulated as a convex optimization problem. The second issue is overcome through Fantope-deflation, which assures orthogonality of successive components. The formulation as a convex optimization problem allows for the development of an alternating direction method of multipliers (ADMM) algorithm (Boyd and others, 2011) for easy implementation. For multilevel multivariate FPCA, LVPCA is applied to the MoM estimators of the subject-specific and replicate-within-subject covariance operators to provide interpretable FPCA at each level.
norms that are used to achieve within- and between-group sparsity in high-dimensional regression by the sparse-group Lasso (Simon and others, 2013). There are two main challenges when incorporating localization or sparsity into a PCA: direct approaches via rank-one projection matrices provide solutions that, if they exist, are NP-hard and they provide components that are not orthogonal. The LVPCA overcomes the first issue through the use of the Fantope, which is the convex hull of rank-one projection matrices and has been adapted to overcome analogous problems in localized univariate FPCA (Chen and Lei, 2015) and sparse high-dimensional PCA (Vu and others, 2013). The separation of the smoothness penalty and the localization and sparsity penalties enables the problem to be embedded into the Fantope and allows the LVPCA to be formulated as a convex optimization problem. The second issue is overcome through Fantope-deflation, which assures orthogonality of successive components. The formulation as a convex optimization problem allows for the development of an alternating direction method of multipliers (ADMM) algorithm (Boyd and others, 2011) for easy implementation. For multilevel multivariate FPCA, LVPCA is applied to the MoM estimators of the subject-specific and replicate-within-subject covariance operators to provide interpretable FPCA at each level.
The rest of the article is organized as follows. The motivating BADA Study is introduced in Section 2. A principal components model for multilevel multivariate functional data is presented in Section 3 and an accompanying estimating procedure is developed in Section 4. The proposed method is used to analyze simulated data in Section 5 and data from the motivating BADA Study in Section 6. Finally, we discuss and conclude in Section 7.
2. Motivating study
Data were examined from the Blunted and Discordant Affect (BADA) study, which was conducted to better understand individual differences in emotional information processing. Multiple psychopathologies such as depression and post-traumatic stress disorder (PTSD) are characterized by intense repetitive negative self-thoughts (rumination), which is increasingly well understood. These same conditions are also characterized by blunted emotional reactions and feelings of distance from the self and reality (dissociation) in response to negative information, particularly in the presence of chronic trauma or abuse backgrounds. The neural basis of such blunted reactions are less well understood. As treatments for depression and PTSD are commonly devoted to reducing negative emotion, if some individuals are already neurally disengaged or blunted in their responses, this traditional approach may not be beneficial. Thus, the BADA study examined individuals selected for a variety of psychopathologies, including those with and without chronic trauma, on tasks that could yield with blunted reactions in vulnerable individuals.
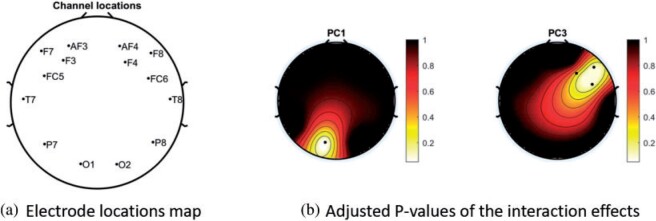
We consider data from 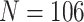 study participants whose brain activity was recorded via EEG while ruminating on a negative thought for 10 s. The EEG montage included 14 electrodes placed in selected locations on the scalp (Figure 4(A)). Data were recorded at 128 Hz. Frequency-band measures, or the amount of variability within an EEG time series due to osculations within an interval of frequencies, provide interpretable measures that are used by researchers and clinicians to elucidate neurophysiological mechanisms. Frequency-band measures are not independent and rather, often have high correlation. We consider four measures: theta power (4–7 Hz) linked to memory and emotional regulation (Knyazev, 2007), alpha power (8–12 Hz) that reflects relaxation, disengagement, or a lack of cognitive activity (Davidson and others, 1990), beta power (18–25 Hz) linked to a variety of attentional processes (Neuper and others, 2009), and gamma power (39–45 Hz) associated with feature integration and fundamental cognitive processes (Tallon-Baudry and Bertrand, 1999). Additional technical details with regards to data processing are provided in Supplementary material available at Biostatistics online.
study participants whose brain activity was recorded via EEG while ruminating on a negative thought for 10 s. The EEG montage included 14 electrodes placed in selected locations on the scalp (Figure 4(A)). Data were recorded at 128 Hz. Frequency-band measures, or the amount of variability within an EEG time series due to osculations within an interval of frequencies, provide interpretable measures that are used by researchers and clinicians to elucidate neurophysiological mechanisms. Frequency-band measures are not independent and rather, often have high correlation. We consider four measures: theta power (4–7 Hz) linked to memory and emotional regulation (Knyazev, 2007), alpha power (8–12 Hz) that reflects relaxation, disengagement, or a lack of cognitive activity (Davidson and others, 1990), beta power (18–25 Hz) linked to a variety of attentional processes (Neuper and others, 2009), and gamma power (39–45 Hz) associated with feature integration and fundamental cognitive processes (Tallon-Baudry and Bertrand, 1999). Additional technical details with regards to data processing are provided in Supplementary material available at Biostatistics online.
Fig. 4.
(A) Locations of the 14 electrodes on the brain. (B) Adjusted p-values for the interaction effect of electrode-level PC 1 and PC 3 scores across 14 electrodes displayed on their corresponding locations. White color indicates locations with p-value 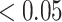 .
.
We desire an analysis of these data to address three questions. First, we desire low-dimensional measures that can be used to describe variability in neurophysiological reactivity in participants while ruminating on negative thoughts. We are specifically interested in neurally meaningful phenomena that could vary anywhere throughout the brain ( i.e., have different topographies across participants) and across participants, but have unique time and frequency-band characteristics. Second, we desire an understanding of the association between these measures with clinical measures of dissociation, measured through the square-root transformed score on the Dissociative Experiences Scale (DES) (Bernstein and Putnam, 1986), in order to better understand neurophysiological mechanisms behind blunted reactions and lack of normal integration of thoughts, feelings and experiences into the stream of consciousness and memory. Lastly, blunted affect has been observed in individuals with a history of trauma and the mechanism driving blunted affect could be different among those with and without a history of trauma (Miniati and others, 2010). We are interested in understanding the potential role that trauma plays in moderating the relationship between dissociation and neurophysiology.
3. Model
The primary methodological question considered in this article is how to conduct interpretable principal component analyses that summarize the variability of multilevel multivariate functional data, 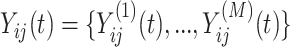 , observed from
, observed from 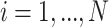 subjects, with
subjects, with 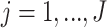 repeated measures taken for each subject at
repeated measures taken for each subject at  variates. In the motivating study, there are
variates. In the motivating study, there are 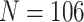 participants,
participants, 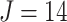 electrodes and
electrodes and 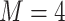 frequency band measures. We consider the scenario where curves for each variate from each subject are observed over a common dense grid of
frequency band measures. We consider the scenario where curves for each variate from each subject are observed over a common dense grid of 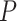 time points as is typical for EEG data,
time points as is typical for EEG data, 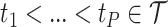 , and where the design is balanced with an equal number of repeated measures
, and where the design is balanced with an equal number of repeated measures 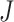 for each subject. Discussions with regards to the unbalanced design and to the setting where curves are observed either sparsely or over different time points are given in Section 7.
for each subject. Discussions with regards to the unbalanced design and to the setting where curves are observed either sparsely or over different time points are given in Section 7.
Consider a two-way functional ANOVA model
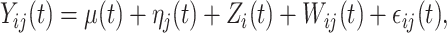 |
(3.1) |
where 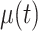 and
and 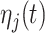 are fixed effects. In our motivating example, they represent the overall mean function and electrode-specific shifts from the overall mean function. The random process
are fixed effects. In our motivating example, they represent the overall mean function and electrode-specific shifts from the overall mean function. The random process 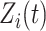 is the zero-mean subject-level deviation from the electrode-specific mean function, with a between-subject covariance function
is the zero-mean subject-level deviation from the electrode-specific mean function, with a between-subject covariance function 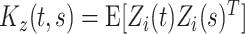 . The random process
. The random process 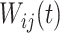 is the zero-mean correlated electrode-level deviation from the subject-level mean, with a within-subject covariance function
is the zero-mean correlated electrode-level deviation from the subject-level mean, with a within-subject covariance function 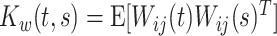 . The processes
. The processes 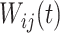 and
and 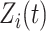 are assumed to be uncorrelated, and
are assumed to be uncorrelated, and 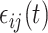 is white noise with mean 0 and variance
is white noise with mean 0 and variance 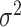 .
.
Within each subject, we assume that the covariance between 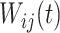 and
and 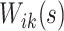 at electrode
at electrode 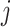 and
and 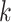 is separable, and takes the form
is separable, and takes the form
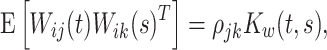 |
where 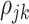 is the correlation coefficient between electrode-level deviations. Another interpretation for
is the correlation coefficient between electrode-level deviations. Another interpretation for 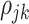 is the correlation between observations at electrode
is the correlation between observations at electrode 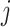 and
and 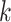 beyond the dependency accounted by the subject-level random process. We assume that
beyond the dependency accounted by the subject-level random process. We assume that 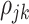 is sparse such that
is sparse such that 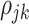 is nonzero for only a subset of pairs of electrodes. Two things should be noted. First, sparsity in
is nonzero for only a subset of pairs of electrodes. Two things should be noted. First, sparsity in 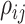 assures identifiability. If no structure was assumed on the correlation between
assures identifiability. If no structure was assumed on the correlation between 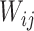 and
and 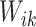 , then it would be unidentifiable with
, then it would be unidentifiable with 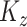 . Second, this assumption is different than the assumption made in other multilevel principal component models where within-subject correlation is modeled as a vanishing stationary function of known structural distance (Staicu and others, 2010). In the analysis of EEG, data from different electrodes from the same subject are expected to be correlated not only due to the structural spatial location of the electrodes but also due to functional relationships and networks. Although the spatial distance between different electrodes are known, functional relationships are not. Thus, we make the nonparametric assumption that
. Second, this assumption is different than the assumption made in other multilevel principal component models where within-subject correlation is modeled as a vanishing stationary function of known structural distance (Staicu and others, 2010). In the analysis of EEG, data from different electrodes from the same subject are expected to be correlated not only due to the structural spatial location of the electrodes but also due to functional relationships and networks. Although the spatial distance between different electrodes are known, functional relationships are not. Thus, we make the nonparametric assumption that 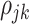 is sparse.
is sparse.
When the processes 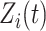 and
and 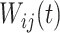 are square-integrable, the Karhunen–Loeve expansion allows the model in 3.1 to be expressed as
are square-integrable, the Karhunen–Loeve expansion allows the model in 3.1 to be expressed as
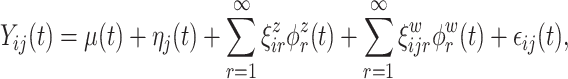 |
(3.2) |
where 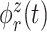 and
and 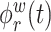 are the
are the 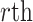 eigenfunctions of
eigenfunctions of 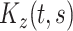 and
and 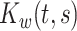 , respectfully. The principal component scores
, respectfully. The principal component scores 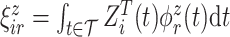 and
and 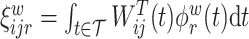 are mean-zero random variables with
are mean-zero random variables with 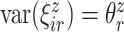 ,
, 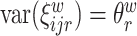 ,
, 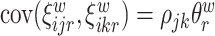 and are uncorrelated otherwise.
and are uncorrelated otherwise.
The goal of our analysis is to conduct a FPCA by obtaining interpretable estimates of the level-specific weight functions 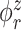 and
and 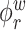 , which provide a low-dimensional representation of the major modes of variation, and of the level-specific principal component scores
, which provide a low-dimensional representation of the major modes of variation, and of the level-specific principal component scores 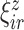 and
and 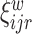 . This FPCA is multivariate in that the weight functions are
. This FPCA is multivariate in that the weight functions are 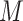 -dimensional and it is multilevel in that it provides subject-level components to describe subject-average variability and electrode-within-subject-level scores to describe within-subject variation.
-dimensional and it is multilevel in that it provides subject-level components to describe subject-average variability and electrode-within-subject-level scores to describe within-subject variation.
4. Estimation
In this section, we develop a two-stage estimation procedure for conducting interpretable multilevel multivariate FPCA. The first stage discussed in Section 4.1 obtains MoM estimators of the between- and within-subject covariances, 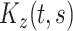 and
and 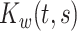 . The second stage discussed in Section 4.2 utilizes a novel penalized decomposition of the level-specific MoM estimator, which we refer to as localized sparse-variate functional principal component analysis (LVPCA), that produces interpretable components and weight functions that are smooth as functions of time, sparse among variates, and localized in time within variates. An optimization algorithm for computing LVPCA is offered in Section 4.3.
. The second stage discussed in Section 4.2 utilizes a novel penalized decomposition of the level-specific MoM estimator, which we refer to as localized sparse-variate functional principal component analysis (LVPCA), that produces interpretable components and weight functions that are smooth as functions of time, sparse among variates, and localized in time within variates. An optimization algorithm for computing LVPCA is offered in Section 4.3.
4.1. Covariance matrix estimation
To aid computation, we introduce additional notation and vectorize values of the 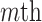 variate from electrode
variate from electrode  from subject
from subject 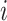 as
as 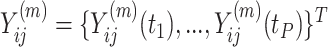 , then concatenate these
, then concatenate these 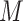 vectors to formulate a
vectors to formulate a 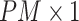 vector
vector 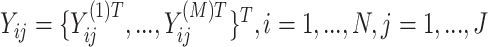 . The
. The 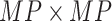 matrices
matrices 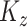 and
and 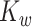 are defined using the same concatenation such that the
are defined using the same concatenation such that the 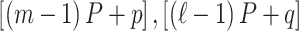 elements of
elements of 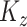 and
and 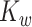 are the
are the 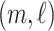 elements of
elements of 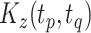 and
and 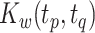 , respectively. Similarly, we vectorize values of the
, respectively. Similarly, we vectorize values of the  eigenfunction within the
eigenfunction within the 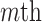 variate
variate 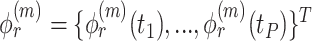 , then concatenate these M vectors to obtain the
, then concatenate these M vectors to obtain the 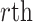 eigenvector
eigenvector 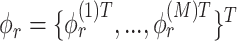 . Lastly, we let the
. Lastly, we let the 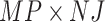 matrix
matrix 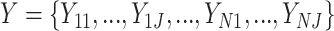 .
.
Without loss of generality, we assume that 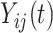 has been demeaned by subtracting the electrode-specific mean, so that
has been demeaned by subtracting the electrode-specific mean, so that 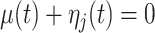 , in order to focus on the estimation of
, in order to focus on the estimation of 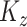 and
and 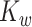 . We begin by noting that
. We begin by noting that
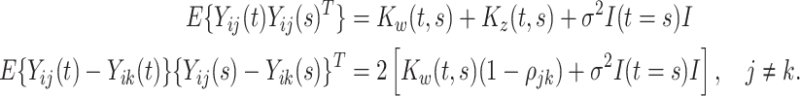 |
The estimation procedure depends on an initial unbiased estimator of the within-subject correlation 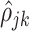 . Details with regards to the estimation of
. Details with regards to the estimation of 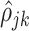 are provided in Supplementary material available at Biostatistics online. Define the matrices
are provided in Supplementary material available at Biostatistics online. Define the matrices 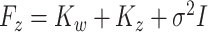 and
and 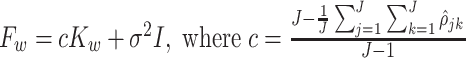 . The explicit MoM estimators of
. The explicit MoM estimators of 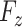 and
and 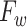 are given by
are given by
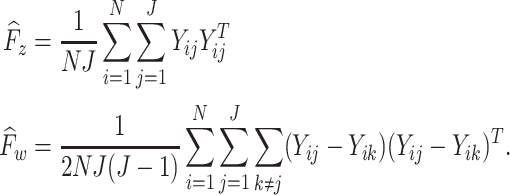 |
The covariance estimators can then be obtained as 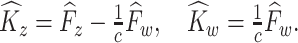
If there is no measurement error, 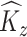 and
and 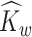 are consistent estimators of
are consistent estimators of 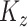 and
and 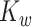 . In the presence of noise, as in our case, the off-diagonal terms are consistent estimators, but there exists a nugget effect on the diagonal. This nugget effect will be explicitly accounted for through a smoothing penalty when estimating eigenvectors.
. In the presence of noise, as in our case, the off-diagonal terms are consistent estimators, but there exists a nugget effect on the diagonal. This nugget effect will be explicitly accounted for through a smoothing penalty when estimating eigenvectors.
4.2. LVPCA: localized sparse-variate functional principal component analysis
In the second stage, we obtain interpretable principal component and weight function estimates at each level via LVPCA individually for the matrices 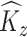 and
and 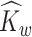 obtained in the first stage. To ease notation, in this and following sections, we will use
obtained in the first stage. To ease notation, in this and following sections, we will use 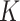 and
and 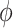 to represent an estimated covariance function and its eigenvector, which can represent either the between-subject quantities
to represent an estimated covariance function and its eigenvector, which can represent either the between-subject quantities 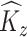 and
and 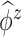 or the within-subject
or the within-subject 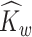 and
and 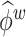 .
.
4.2.1. Methodological motivation
As previously discussed, many approaches for conducting a multivariate FPCA have been developed. To motivate the proposed LVPCA, here we discuss one such approach introduced by Rice and Silverman (1991) where the roughness across each variate of the eigenvectors is penalized. Formally, given a tuning parameter 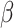 , the first eigenvector is estimated by maximizing
, the first eigenvector is estimated by maximizing 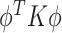 such that
such that 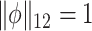 and
and 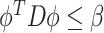 , where
, where 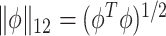 is the
is the 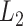 vector norm and D is a roughness matrix penalizing the sum of squared second differences across time. Specially,
vector norm and D is a roughness matrix penalizing the sum of squared second differences across time. Specially, 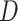 is the PM
is the PM 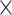 PM block diagonal matrix with
PM block diagonal matrix with 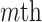 block
block 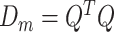 , and
, and 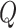 is the
is the 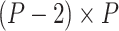 matrix where
matrix where 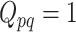 when
when 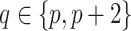 ,
, 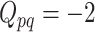 when
when 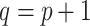 , and is zero otherwise.
, and is zero otherwise.
It will be advantageous to consider two additional formulations of this estimator. The first, which was used by Rice and Silverman (1991) and allows for the estimator to be computed from a simple singular value decomposition, can be obtained through Lagrange multipliers by maximizing the equivalent problem 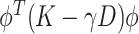 such that
such that 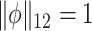 for some smoothing parameter
for some smoothing parameter 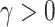 . Alternatively, this problem can also be expressed as maximizing
. Alternatively, this problem can also be expressed as maximizing 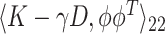 such that
such that 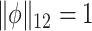 , where
, where 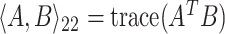 . This last formulation will facilitate the convex relaxation of the problem when localization is introduced, assuring the existence of a solution and enabling efficient computation.
. This last formulation will facilitate the convex relaxation of the problem when localization is introduced, assuring the existence of a solution and enabling efficient computation.
The estimated eigenfunctions previously described are smooth, but not localized, either in time or among variates, in the sense that the estimated eigenfunction at every time point within each variate is nonzero with probability 1. An intuitive approach for obtaining localized estimates of the first eigenfunction is to, in a manner similar to the sparse-group Lasso (Simon and others, 2013), use a combination of 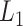 Lasso and
Lasso and 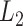 group-Lasso penalties to maximize
group-Lasso penalties to maximize
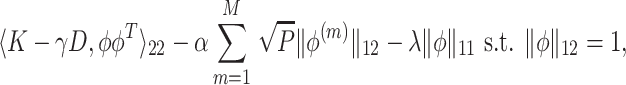 |
where 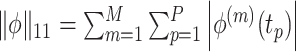 is the
is the 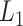 vector norm. The tuning parameters
vector norm. The tuning parameters 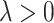 and
and 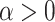 control the degree of within- and between-variate localization, respectively.
control the degree of within- and between-variate localization, respectively. 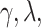 and
and 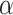 can be selected either through cross-validation to obtain an accurate estimate or by requiring more sparsity with some sacrifice of the fraction of variance explained (FVE). Details for tuning parameter selection are provided in Section 1.2 of the Supplementary material available at Biostatistics online.
can be selected either through cross-validation to obtain an accurate estimate or by requiring more sparsity with some sacrifice of the fraction of variance explained (FVE). Details for tuning parameter selection are provided in Section 1.2 of the Supplementary material available at Biostatistics online.
4.2.2. Penalized deflated Fantope estimation
Unfortunately, the previously considered problem is non-convex, it is not clear if or when a solution exists, and if a solution existed, it would be computationally intractable. A computationally tractable and consistent approach can be formulated through a convex relaxation. Approaches for conducting penalized PCA that consider problems embedded within the convex hull of projection matrices have been explored for sparse PCA of high-dimensional multivariate data (Lei and others, 2015) and for localized PCA of univariate functional data (Chen and Lei, 2015). Here, we extend this approach to our setting of localized sparse-variate PCA of multivariate functional data.
Rather than attempting to maximize the objective function over the space of rank-one projection matrices of the form 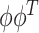 , we can maximize an analogous objective function over the convex hull of rank-one projection matrices, or over the Fantope
, we can maximize an analogous objective function over the convex hull of rank-one projection matrices, or over the Fantope 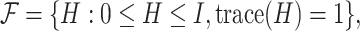 where
where 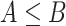 means
means 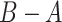 is positive semidefinite for symmetric matrices A and B. Formally, we define our estimate as the first eigenvector of the matrix
is positive semidefinite for symmetric matrices A and B. Formally, we define our estimate as the first eigenvector of the matrix 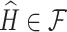 that maximizes
that maximizes
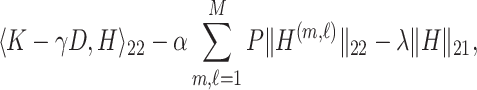 |
where 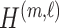 is the
is the 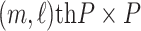 submatrix of
submatrix of  and
and 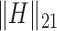 is the
is the 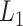 matrix norm that is the sum of the absolute values of all elements.
matrix norm that is the sum of the absolute values of all elements.
This approach produces estimates of the first eigenfunction, but we also desire estimates of higher-order eigenfunctions and require the collection of estimated eigenfunctions to be orthogonal. This can be easily achieved within the Fantope framework via successive Fantope-deflation. The deflated Fantope around a projection matrix 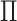 is defined as
is defined as 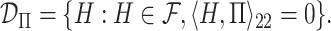 Formally, define
Formally, define 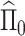 as a matrix of zeros and successively estimate
as a matrix of zeros and successively estimate 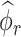 for each
for each 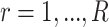 as
as
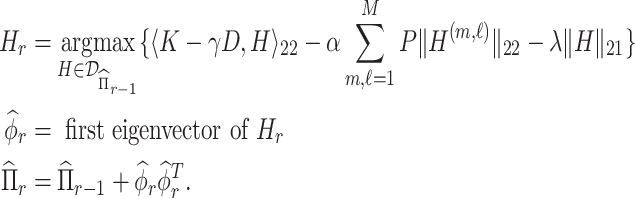 |
(4.3) |
Once the eigenvectors are obtained, scores 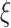 can be obtained through the best linear unbiased predictor (BLUP) and eigenvalues
can be obtained through the best linear unbiased predictor (BLUP) and eigenvalues 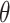 through empirical moments of the scores. Details for the estimation of
through empirical moments of the scores. Details for the estimation of 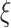 and
and 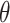 are provided in Section 1.3 of the Supplementary material available at Biostatistics online.
are provided in Section 1.3 of the Supplementary material available at Biostatistics online.
4.3. Optimization using ADMM
The first step in our procedure (4.3) is a convex optimization problem. However, the deflated Fantope constraint makes it difficult to directly employ block-wise subgradient strategy on the penalty terms. To solve this problem, we use the ADMM algorithm to separate the penalty terms and the deflated Fantope constraint. Define 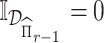 if
if 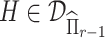 and
and 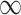 otherwise, the augmented Lagrangian with auxiliary parameter
otherwise, the augmented Lagrangian with auxiliary parameter 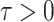 is of the form
is of the form 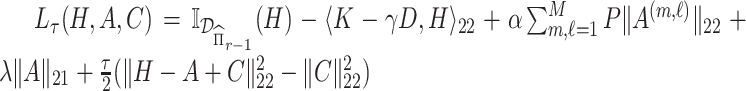 . Letting
. Letting  be the element-wise soft-thresholding operator such that, for each element
be the element-wise soft-thresholding operator such that, for each element 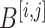 of a matrix
of a matrix 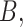
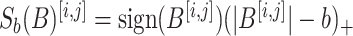 , and letting
, and letting 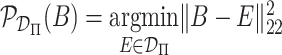 be the Frobenius projection operator, a closed form of which is given in Supplemental Material, this can be solved through Algorithm 1.
be the Frobenius projection operator, a closed form of which is given in Supplemental Material, this can be solved through Algorithm 1.
Algorithm 1:
Penalized deflated Fantope estimation using ADMM
5. Simulation
To better understand the empirical performance of the multilevel LVPCA, we conducted simulations based on the following model:
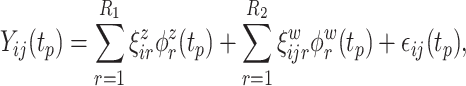 |
(5.4) |
where 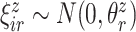 ,
, 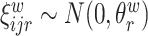 ,
, 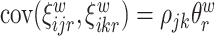 ,
, 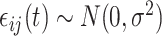 , and
, and 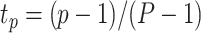 ,
, 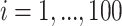 ,
, 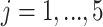 ,
, 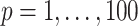 .
. 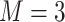 variates. The true eigenvalues are taken as
variates. The true eigenvalues are taken as 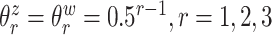 , the true correlation coefficient as
, the true correlation coefficient as 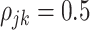 when
when 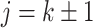 ,
, 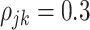 when
when 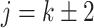 , and is zero otherwise, and the noise as
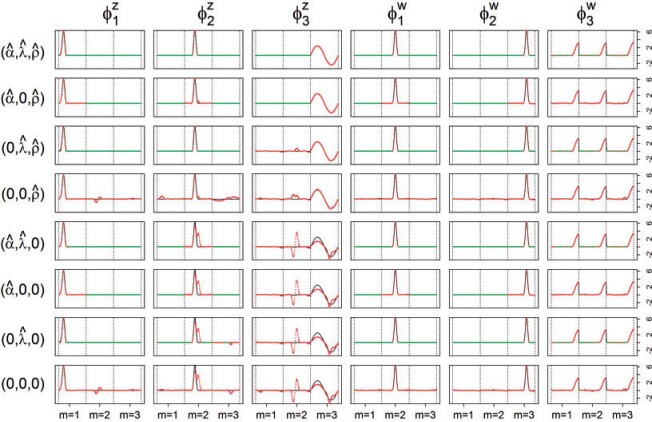
, and is zero otherwise, and the noise as 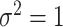 . The true eigenfunctions are displayed as black lines in Figure 2. To evaluate the relative contributions of the localization and sparsity penalties, and of the estimation of within-subject correlation, we consider eight estimation procedures denoted as:
. The true eigenfunctions are displayed as black lines in Figure 2. To evaluate the relative contributions of the localization and sparsity penalties, and of the estimation of within-subject correlation, we consider eight estimation procedures denoted as: 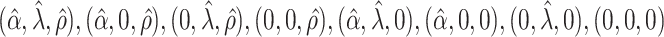 . The first procedure
. The first procedure 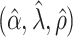 corresponds to the proposed LVPCA with
corresponds to the proposed LVPCA with 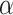 ,
, 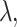 and
and 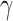 selected by 5-fold cross-validation, and
selected by 5-fold cross-validation, and 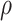 estimated as described in Appendix A.3 of the Supplementary material available at Biostatistics online. Other procedures restrict one or more of
estimated as described in Appendix A.3 of the Supplementary material available at Biostatistics online. Other procedures restrict one or more of 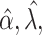 or
or 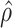 to
to 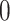 .
.
Fig. 2.
True (black solid) and estimated (green and red dot) eigenfunctions from one simulated data set by the described eight estimation procedures. Solid black lines are the true eigenfunctions, green lines indicate estimated zero elements, and red lines indicate estimated nonzero elements.
Figure 2 displays estimated eigenfunctions 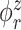 and
and 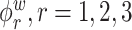 , from one simulated data set. The eight rows correspond to the eight methods. The solid black lines are the true eigenfunctions, green lines indicate estimated zero elements and red lines indicate estimated nonzero elements. Visually, in the top row of Figure 2, it can be seen that the proposed LVPCA, which includes within-variate localization, between-variate sparseness penalties and accounting for within-subject correlation between electrode-specific deviations, leads to favorable recovery of eigenfunctions. Removing either penalty appears to potentially increase bias and select more nonzero elements of
, from one simulated data set. The eight rows correspond to the eight methods. The solid black lines are the true eigenfunctions, green lines indicate estimated zero elements and red lines indicate estimated nonzero elements. Visually, in the top row of Figure 2, it can be seen that the proposed LVPCA, which includes within-variate localization, between-variate sparseness penalties and accounting for within-subject correlation between electrode-specific deviations, leads to favorable recovery of eigenfunctions. Removing either penalty appears to potentially increase bias and select more nonzero elements of 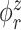 than the truth. Failing to adjust for within-subject correlation between electrode-specific deviations can negatively affect the accuracy of the shape of
than the truth. Failing to adjust for within-subject correlation between electrode-specific deviations can negatively affect the accuracy of the shape of 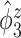 , since the between-subject variation is contaminated by the within-subject variation, specifically
, since the between-subject variation is contaminated by the within-subject variation, specifically 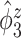 is contaminated by
is contaminated by 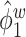 . This trend is further quantified in Table 2, where we report the median of the errors
. This trend is further quantified in Table 2, where we report the median of the errors 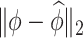 , as well as in Table 3, where we report the median specificity and sensitivity (proportion nonzero/zero elements correctly estimated as nonzero/zero). The proposed LVPCA outperforms the other methods in eigenvector estimation particularly for the higher-level of the hierarchy, and also has the highest specificity among all the methods, and a reasonable level of sensitivity. This result demonstrates the advantage of the proposed LVPCA, which combines localization and between-variate sparsity penalties, in terms of both estimation and variable selection.
, as well as in Table 3, where we report the median specificity and sensitivity (proportion nonzero/zero elements correctly estimated as nonzero/zero). The proposed LVPCA outperforms the other methods in eigenvector estimation particularly for the higher-level of the hierarchy, and also has the highest specificity among all the methods, and a reasonable level of sensitivity. This result demonstrates the advantage of the proposed LVPCA, which combines localization and between-variate sparsity penalties, in terms of both estimation and variable selection.
Table 2.
Median errors 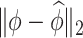 for
for 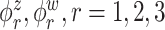 (with median absolute deviations in parenthesis) over 200 simulation runs.
(with median absolute deviations in parenthesis) over 200 simulation runs.
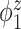
|
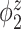
|
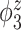
|
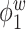
|
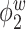
|
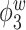
|
|
|---|---|---|---|---|---|---|
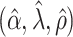
|
0.49 (0.15) | 0.91 (0.41) | 2.18 (1.15) | 0.34 (0.04) | 0.41 (0.04) | 0.66 (0.10) |
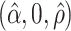
|
0.60 (0.15) | 1.89 (0.68) | 2.54 (1.50) | 0.66 (0.08) | 1.11 (0.11) | 0.91 (0.10) |
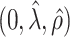
|
1.25 (0.31) | 0.96 (0.44) | 3.49 (1.13) | 0.41 (0.09) | 0.41 (0.05) | 0.60 (0.09) |
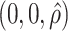
|
2.67 (0.78) | 3.89 (1.00) | 4.46 (1.23) | 1.43 (0.43) | 2.14 (0.58) | 1.57 (0.44) |
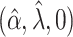
|
0.48 (0.14) | 1.09 (0.62) | 23.14 (1.56) | 0.33 (0.03) | 0.42 (0.05) | 0.66 (0.10) |
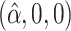
|
0.61 (0.15) | 3.46 (1.73) | 11.71 (5.99) | 0.66 (0.08) | 1.11 (0.11) | 0.90 (0.09) |
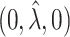
|
1.30 (0.37) | 1.19 (0.72) | 15.15 (8.45) | 0.42 (0.09) | 0.41 (0.05) | 0.60 (0.09) |
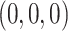
|
3.02 (0.88) | 5.52 (1.71) | 12.73 (4.39) | 1.43 (0.43) | 2.14 (0.58) | 1.57 (0.44) |
Table 3.
Median of specificity (proportion of zero elements correctly estimated as zero) and sensitivity (proportion of nonzero elements estimated as nonzero) for 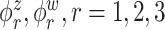 , over 200 simulation runs.
, over 200 simulation runs.
| Specificity | Sensitivity | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
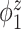
|
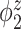
|
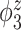
|
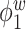
|
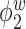
|
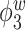
|
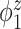
|
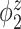
|
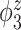
|
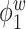
|
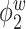
|
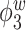
|
|
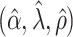
|
0.99 | 0.99 | 1.00 | 0.99 | 1.00 | 0.75 | 0.87 | 0.83 | 1.00 | 0.92 | 0.92 | 0.85 |
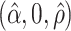
|
0.75 | 0.73 | 1.00 | 0.73 | 0.73 | 0.01 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 |
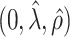
|
0.97 | 1.00 | 0.03 | 1.00 | 1.00 | 0.75 | 0.71 | 0.83 | 1.00 | 0.76 | 0.80 | 0.85 |
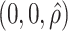
|
0.02 | 0.01 | 0.02 | 0.02 | 0.02 | 0.01 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 |
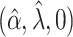
|
0.99 | 0.98 | 0.86 | 1.00 | 1.00 | 0.74 | 0.87 | 0.88 | 0.56 | 0.88 | 0.92 | 0.85 |
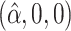
|
0.75 | 0.73 | 0.50 | 0.73 | 0.73 | 0.01 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 |
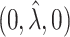
|
0.97 | 0.99 | 0.82 | 1.00 | 1.00 | 0.75 | 0.71 | 0.79 | 0.91 | 0.76 | 0.80 | 0.85 |
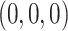
|
0.02 | 0.01 | 0.02 | 0.02 | 0.02 | 0.01 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 |
Table 1.
True eigenfunctions in the simulation setting presented in Section 5. The function 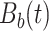 is the
is the 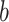 th cubic B-spline basis on
th cubic B-spline basis on 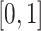 , with 16 equally spaced interior knots, and
, with 16 equally spaced interior knots, and 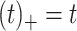 when
when 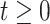 and is zero otherwise.
and is zero otherwise.
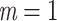
|
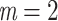
|
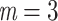
|
|
|---|---|---|---|
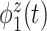
|
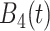
|
0 | 0 |
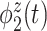
|
0 |
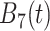
|
0 |
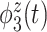
|
0 | 0 |
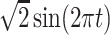
|
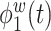
|
0 |
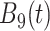
|
0 |
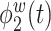
|
0 | 0 |
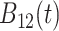
|
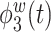
|
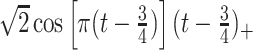
|
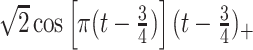
|
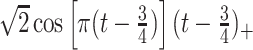
|
In terms of estimation of subject- and electrode-level eigenvalues, the four methods that adjust for within-subject correlation between electrode-specific deviations can recover eigenvalues with relatively little bias; median bias for these methods ranged from  0.006 to 0.022. On the contrary, the four methods without adjusting for within-subject correlation over-estimate
0.006 to 0.022. On the contrary, the four methods without adjusting for within-subject correlation over-estimate 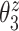 , with median bias ranging from 0.082 to 0.088, and highly underestimate
, with median bias ranging from 0.082 to 0.088, and highly underestimate 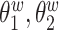 , and
, and 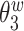 , with median bias ranging from
, with median bias ranging from  0.290 to
0.290 to  0.072. This can be attributed to part of the within-subject variation is mistakenly counted as between-subject variation. Additional details including empirical performance in estimating principal component scores, noise level and within-subject correlation, boxplots of estimated eigenvalues, as well as simulation results for additional settings are provided in Section 3 of the Supplementary material available at Biostatistics online. The primary factor affecting run time is
0.072. This can be attributed to part of the within-subject variation is mistakenly counted as between-subject variation. Additional details including empirical performance in estimating principal component scores, noise level and within-subject correlation, boxplots of estimated eigenvalues, as well as simulation results for additional settings are provided in Section 3 of the Supplementary material available at Biostatistics online. The primary factor affecting run time is 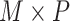 , with
, with 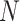 and
and 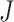 having little relative effect. In our simulations, the mean run time for the proposed procedure including automated tuning parameter selection with
having little relative effect. In our simulations, the mean run time for the proposed procedure including automated tuning parameter selection with 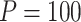 and
and 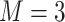 using R Version 3.4 and Windows 10 on a desktop computer with a 3.6 GHz Intel Core i7 processor and 8 GB RAM is 3 min, while the data analysis of the motivating study in Section 6 where
using R Version 3.4 and Windows 10 on a desktop computer with a 3.6 GHz Intel Core i7 processor and 8 GB RAM is 3 min, while the data analysis of the motivating study in Section 6 where 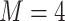 and
and 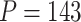 took approximately 25 min.
took approximately 25 min.
6. Application to the BADA study
We applied the proposed methodology to analyze brain reactivity while ruminating on a negative thought from the participants in the BADA study described in Section 2. These data are available from the corresponding author upon request. EEG data considered for each of the 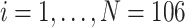 study participants are of the form
study participants are of the form 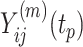 for
for 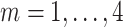 frequency bands (theta, alpha, beta, and gamma), at
frequency bands (theta, alpha, beta, and gamma), at 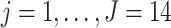 electrodes (locations displayed in Figure 4(A)). Data were pre-centered around each electrode at each time point to remove fixed effects. In Section 6.1, LVPCA was conducted on both the between-subject and within-subject levels to elucidate variability in neurophysiological activity in patients while ruminating on negative thoughts. Then, in Section 6.2, regression analyses were conducted using the scores obtained from the LVPCA to quantify associations between brain activity and clinical dissociation, and for assessing moderation of this relationship by a history of trauma.
electrodes (locations displayed in Figure 4(A)). Data were pre-centered around each electrode at each time point to remove fixed effects. In Section 6.1, LVPCA was conducted on both the between-subject and within-subject levels to elucidate variability in neurophysiological activity in patients while ruminating on negative thoughts. Then, in Section 6.2, regression analyses were conducted using the scores obtained from the LVPCA to quantify associations between brain activity and clinical dissociation, and for assessing moderation of this relationship by a history of trauma.
6.1. LVPCA
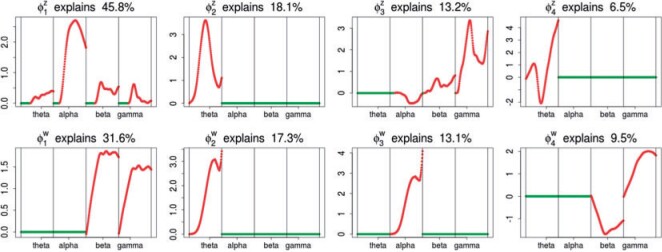
Four principal components at both within- and between-subject levels were selected to account for 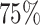 of total variation (Figure 3). The top four subject-level principal components explain
of total variation (Figure 3). The top four subject-level principal components explain 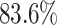 of the total between-subject variation. The first estimated subject-level eigenfunction
of the total between-subject variation. The first estimated subject-level eigenfunction 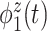 explains
explains 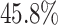 of the variation. It is localized within each variate, being zero for each frequency band in the first 3 s of the trial, with an emphasis on alpha power. The second estimated subject-level eigenfunction
of the variation. It is localized within each variate, being zero for each frequency band in the first 3 s of the trial, with an emphasis on alpha power. The second estimated subject-level eigenfunction 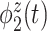 , accounting for
, accounting for 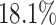 of the variation, is sparse among bands and is a measure of total theta power, with greatest emphasis given to power in the middle of the trial. The third component
of the variation, is sparse among bands and is a measure of total theta power, with greatest emphasis given to power in the middle of the trial. The third component 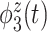 is a contrast between beta and gamma power compared to alpha power. The fourth eigenfunction
is a contrast between beta and gamma power compared to alpha power. The fourth eigenfunction 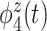 is a contrast in theta power at the beginning and end of the trial.
is a contrast in theta power at the beginning and end of the trial.
Fig. 3.
Estimated subject-level (top row) and electrode-level (bottom row) eigenfunctions for the BADA Study. Green lines indicate estimated zero elements and red lines indicate estimated nonzero elements.
Subject-level eigenfunctions represent the major directions of subject-specific deviation from the overall mean power function. It is not entirely unexpected that they are largely driven by theta and alpha power. Participants were observed while ruminating on a negative memory. Theta power has been linked to memory (Knyazev, 2007), and alpha power has been associated with a lack of emotional regulatory control (Klimesch, 2012), two processes underlying rumination.
The electrode-level components represent ways individual participants vary from population mean and subject-specific whole-brain responses to rumination at specific electrodes. Estimated mean topologies of responses to the rumination instruction across all frequency bands 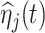 are displayed in Section 2.4.2 of the Supplementary material available at Biostatistics online. The top four estimated electrode-level principal components explained
are displayed in Section 2.4.2 of the Supplementary material available at Biostatistics online. The top four estimated electrode-level principal components explained 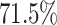 of the total within-subject variation. All four estimated components are sparse among frequency bands. The first estimated electrode-level eigenfunction
of the total within-subject variation. All four estimated components are sparse among frequency bands. The first estimated electrode-level eigenfunction 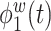 is a positive function of beta and gamma power, or of high-frequency power. Rapidly increasing sustained high-frequency activity could represent effortful cognition associated with trying to ruminate or to regulate emotional reactions. The estimated second and third electrode-level eigenfunctions
is a positive function of beta and gamma power, or of high-frequency power. Rapidly increasing sustained high-frequency activity could represent effortful cognition associated with trying to ruminate or to regulate emotional reactions. The estimated second and third electrode-level eigenfunctions 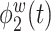 and
and 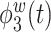 are positive functions of theta and alpha power, respectively. The fourth estimated electrode-level eigenfunction
are positive functions of theta and alpha power, respectively. The fourth estimated electrode-level eigenfunction 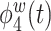 is a positive function of gamma and a negative function of beta power, which could reflect emotional engagement or feature binding.
is a positive function of gamma and a negative function of beta power, which could reflect emotional engagement or feature binding.
6.2. Association between principal component scores and dissociation
Since the principal component scores are correlated, we fit individual regression models for each principal component so that results can be interpreted marginally. In total, there are 60 principal component scores per subject: the four subject-specific scores 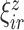 together with the
together with the 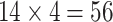 subject-electrode-specific scores
subject-electrode-specific scores 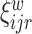 ,
, 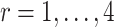 ,
, 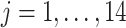 . All reported p-values are adjusted to control the false discovery rate (FDR) at 0.05 with the adaptive group Benjamin and Hochberg procedure (details in Section 2.2 of the Supplementary material available at Biostatistics online).
. All reported p-values are adjusted to control the false discovery rate (FDR) at 0.05 with the adaptive group Benjamin and Hochberg procedure (details in Section 2.2 of the Supplementary material available at Biostatistics online).
Let 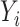 be the square root transformed DES score,
be the square root transformed DES score, 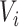 be an indicator variable for a history of trauma, and
be an indicator variable for a history of trauma, and 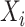 be a principal component score for subject
be a principal component score for subject 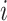 . We fit the linear regression model
. We fit the linear regression model 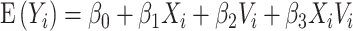 through least squares individually for each of 60 principal component scores. The coefficient
through least squares individually for each of 60 principal component scores. The coefficient 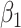 , which quantifies the association between principal component score and square root transformed DES score among participants without a history of trauma, was not statistically significant for any of the principal component scores. The coefficient
, which quantifies the association between principal component score and square root transformed DES score among participants without a history of trauma, was not statistically significant for any of the principal component scores. The coefficient 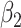 , which is the main effect of trauma, was statistically significant and positive for all principal component scores adjusting for multiple comparisons. This is not unexpected, since dissociation is more common among those with a history of trauma. There were two principal component scores with significant interactions after adjusting for multiple comparisons, indicating that the relationship between brain activity and dissociation is moderated by trauma: one subject-level and one electrode-level. Table 4 displays estimates from the two models with significant interactions and two models with borderline significant trend of interaction effects. Estimates from all 60 models are provided in Section 2.3 of the Supplementary material available at Biostatistics online, as well as scatter plots of principal component scores vs. transformed DES for the models presented in Table 4.
, which is the main effect of trauma, was statistically significant and positive for all principal component scores adjusting for multiple comparisons. This is not unexpected, since dissociation is more common among those with a history of trauma. There were two principal component scores with significant interactions after adjusting for multiple comparisons, indicating that the relationship between brain activity and dissociation is moderated by trauma: one subject-level and one electrode-level. Table 4 displays estimates from the two models with significant interactions and two models with borderline significant trend of interaction effects. Estimates from all 60 models are provided in Section 2.3 of the Supplementary material available at Biostatistics online, as well as scatter plots of principal component scores vs. transformed DES for the models presented in Table 4.
Table 4.
Coefficients, standard errors, and adjusted p-values from univariate models with significant interaction effects and borderline significant trend of interaction effects.
| Score | Trauma | Score 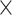 Trauma Trauma |
||||
|---|---|---|---|---|---|---|
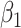 (SE)
(SE) |
p-value |
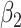 (SE)
(SE) |
p-value |
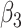 (SE)
(SE) |
p-value | |
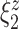
|
0.65 (0.56) | 0.999 | 1.66 (0.25) |
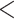 0.001
0.001 |
 2.67 (0.89)
2.67 (0.89) |
0.027 |
|
1.01 (0.40) | 0.098 | 1.62 (0.25) |
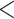 0.001
0.001 |
 1.73 (0.59)
1.73 (0.59) |
0.036 |
|
 0.43 (0.39)
0.43 (0.39) |
0.27 | 1.68 (0.26) |
 0.001
0.001 |
2.10 (0.80) | 0.082 |
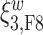
|
 0.31 (0.40)
0.31 (0.40) |
0.45 | 1.74 (0.26) |
 0.001
0.001 |
2.21 (0.84) | 0.082 |
Among the four subject-level principal component scores, the sole model with a significant interaction was 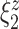 . For this component, the adjusted p-value of
. For this component, the adjusted p-value of 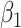 of 0.999 suggests no association between the score and dissociation in people without a history of trauma, while
of 0.999 suggests no association between the score and dissociation in people without a history of trauma, while 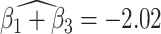 with adjusted p-value 0.028 indicates a negative association in people with a history of trauma. More specifically, recalling that the estimated second subject-level component is a measures of whole-brain theta power, if a person has a history of trauma, the higher his/her theta power, the lower their expected dissociation level. Theta power is associated with memory and emotional control and has been shown to be elevated in participants with a history of PTSD (Bangel and others, 2017). This result may suggest that during instructed rumination, if a person has a history of trauma, not engaging memory related circuitry, perhaps failing to reinvoke trauma recollections, even when a person wants to, may involve dissociation. In the absence of a trauma history, dissociation during rumination may be due to processes other than intensive memory recall, and thus theta power is not so strongly related to dissociation. However, it should be noted that whole-brain theta variability may also represent noise sources (Kappel and others, 2017; Zeng and others, 2013; Jansen and others, 2012) from outside the brain (e.g., movement). Further study is needed to confirm if the moderating effect of trauma on the relationship between dissociation and this score is due to neural processes, or the result of a confounding artifact.
with adjusted p-value 0.028 indicates a negative association in people with a history of trauma. More specifically, recalling that the estimated second subject-level component is a measures of whole-brain theta power, if a person has a history of trauma, the higher his/her theta power, the lower their expected dissociation level. Theta power is associated with memory and emotional control and has been shown to be elevated in participants with a history of PTSD (Bangel and others, 2017). This result may suggest that during instructed rumination, if a person has a history of trauma, not engaging memory related circuitry, perhaps failing to reinvoke trauma recollections, even when a person wants to, may involve dissociation. In the absence of a trauma history, dissociation during rumination may be due to processes other than intensive memory recall, and thus theta power is not so strongly related to dissociation. However, it should be noted that whole-brain theta variability may also represent noise sources (Kappel and others, 2017; Zeng and others, 2013; Jansen and others, 2012) from outside the brain (e.g., movement). Further study is needed to confirm if the moderating effect of trauma on the relationship between dissociation and this score is due to neural processes, or the result of a confounding artifact.
Figure 4 displays the adjusted p-values of the interaction effects for the 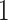 st and
st and 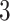 rd electrode-level components at the 14 locations of the brain. The
rd electrode-level components at the 14 locations of the brain. The 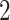 nd and
nd and 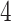 th components have no effect near significant, therefore they are not shown. The model with the
th components have no effect near significant, therefore they are not shown. The model with the 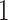 st principal component score
st principal component score 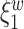 at electrode O1 has a significant interaction effect with a history of trauma on dissociation. Specifically, among patients without a history of trauma,
at electrode O1 has a significant interaction effect with a history of trauma on dissociation. Specifically, among patients without a history of trauma, 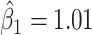 suggests elevated beta and gamma power within the occipital cortex relative to the rest of the brain has a trend of being associated with increased dissociation, though the adjusted p-value is not significant (adjusted p-value
suggests elevated beta and gamma power within the occipital cortex relative to the rest of the brain has a trend of being associated with increased dissociation, though the adjusted p-value is not significant (adjusted p-value  0.098). However this association is significantly different (adjusted p-value = 0.036) among patients with a history of trauma, where elevated beta and gamma power within the occipital cortex relative to the rest of the brain has a negative effect on dissociation with
0.098). However this association is significantly different (adjusted p-value = 0.036) among patients with a history of trauma, where elevated beta and gamma power within the occipital cortex relative to the rest of the brain has a negative effect on dissociation with 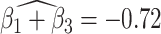 . The reason for an occipital distribution of beta and gamma power is not clear but may suggest that failure of cognitive concentration and regulation of emotional reactions may involve dissociation among individuals with a history of trauma, while this association may have an opposite effect in the absence of trauma history. Other scores that have different directions of associations include
. The reason for an occipital distribution of beta and gamma power is not clear but may suggest that failure of cognitive concentration and regulation of emotional reactions may involve dissociation among individuals with a history of trauma, while this association may have an opposite effect in the absence of trauma history. Other scores that have different directions of associations include 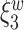 at electrode FC6 and F8. Although such differences are not significant after adjusting for multiple testing (adjusted p-value = 0.082), it is worth noticing that elevated alpha power within the right frontal cortex relative to the rest of the brain has a trend of positive effect on the increased dissociation in patients with a history of trauma (
at electrode FC6 and F8. Although such differences are not significant after adjusting for multiple testing (adjusted p-value = 0.082), it is worth noticing that elevated alpha power within the right frontal cortex relative to the rest of the brain has a trend of positive effect on the increased dissociation in patients with a history of trauma (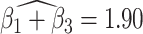 ), which did not appear among patients without a history of trauma (
), which did not appear among patients without a history of trauma (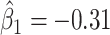 , adjusted p-value = 0.45).
, adjusted p-value = 0.45).
7. Discussion
This article introduces a novel approach to conducting interpretable principal component analysis on multilevel multivariate functional data. The proposed localized sparse-variate FPCA (LVPCA) is combined with a multilevel covariance decomposition to provide subject-level and replicate-within-subject-level components that can be both sparse among variates as well as localized in time. The method was motivated by a study to uncover subject- and electrode-level brain activity that elucidates neurophysiological mechanisms connected to the phenomena of trauma patients shutting down when presented with emotional information.
The proposed method can be easily reduced to useful special cases and generalized to handle more complicated data structures. By restricting 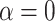 and/or
and/or 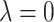 , the method reduces to localized FPCA, sparse-variate FPCA or FPCA without any localization. When
, the method reduces to localized FPCA, sparse-variate FPCA or FPCA without any localization. When 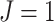 or
or 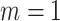 , the method reduces to FPCA on single level or univariate functional data. The proposed method together with all the special cases are implemented into an R package “LVPCA” to facilitate future research. The method can be extended by incorporating other penalty terms to take into account special structures induced by biological information (Beer and others, 2019). Further, the method can be generalized from two-way to multiway, nested or crossed study designs, as introduced in Shou and others (2015). If the design is unbalanced with different number of repeated measures per subject, we can modify the covariance estimators by including only available
, the method reduces to FPCA on single level or univariate functional data. The proposed method together with all the special cases are implemented into an R package “LVPCA” to facilitate future research. The method can be extended by incorporating other penalty terms to take into account special structures induced by biological information (Beer and others, 2019). Further, the method can be generalized from two-way to multiway, nested or crossed study designs, as introduced in Shou and others (2015). If the design is unbalanced with different number of repeated measures per subject, we can modify the covariance estimators by including only available 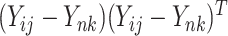 as each of the cross-products independently contributes a same estimator when estimating the between- and within-subject covariance.
as each of the cross-products independently contributes a same estimator when estimating the between- and within-subject covariance.
Finally, in our motivating example, curves were observed over a common dense grid of 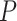 time points. When curves are observed over different time grids, presmoothing can be used to obtain data over a common grid of time points (Ramsay and Silverman, 2005). If each subject is only observed over a sparse collection of random time points, a direct smoothed covariance estimator for sparse functional data (Yao and others, 2005) could be used in lieu of the sample covariance and smoothing penalization component of the proposed procedure.
time points. When curves are observed over different time grids, presmoothing can be used to obtain data over a common grid of time points (Ramsay and Silverman, 2005). If each subject is only observed over a sparse collection of random time points, a direct smoothed covariance estimator for sparse functional data (Yao and others, 2005) could be used in lieu of the sample covariance and smoothing penalization component of the proposed procedure.
8. Software
Software in the form of R code, together with a sample input data set, is available at https://github.com/juz30/MLVPCA.
Supplementary Material
Acknowledgments
Conflict of Interest: None declared.
Contributor Information
Jun Zhang, Department of Biostatistics, University of Pittsburgh, 130 De Soto Street, Pittsburgh, PA, 15261, USA.
Greg J Siegle, Department of Psychiatry, University of Pittsburgh, 3811 O’Hara Street, Pittsburgh, PA, 15213, USA.
Tao Sun, Center for Applied Statistics, School of Statistics, Renmin University of China, 59 Zhongguancun Street, Beijing, 100872, China.
Wendy D’andrea, Department of Psychology, New School for Social Research, 80 Fifth Avenue, New York, NY, 10011, USA.
Robert T Krafty, Department of Biostatistics and Bioinformatics, Emory University, 1518 Clifton Road NE, Atlanta, GA, 30322, USA.
Supplementary material
Supplementary material is available online at http://biostatistics.oxfordjournals.org.
Funding
National Institutes of Health (R01GM113243 and R01MH096334).
References
- Bangel, K. A., van Buschbach, S., Smit, D. J. A., Mazaheri, A. and Olff, M. (2017). Aberrant brain response after auditory deviance in PTSD compared to trauma controls: an eeg study. Scientific Reports 7, 16596. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Beer, J. C., Aizenstein, H. J., Anderson, S. J. and Krafty, R. T. (2019). Incorporating prior information with fused sparse group lasso: application to prediction of clinical measures from neuroimages. Biometrics 75, 1299–1309. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bernstein, E. M. and Putnam, F. W. (1986). Development, reliability, and validity of a dissociation scale. Journal of Nervous and Mental Disease 174, 727–735. [DOI] [PubMed] [Google Scholar]
- Boyd, S., Parikh, N., Chu, E., Peleato, B. and Eckstein, J. (2011). Distributed optimization and statistical learning via the alternating direction method of multipliers. Foundations and Trends® in Machine learning 3, 1–122. [Google Scholar]
- Chen, K. and Lei, J. (2015). Localized functional principal component analysis. Journal of the American Statistical Association 110, 1266–1275. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chen, K. and Müller, H.-G. (2012). Modeling repeated longitudinal observations. Journal of the American Statistical Association 107, 1599–1609. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chiou, J.-M., Chen, Y.-T. and Yang, Y.-F. (2014). Multivariate functional principal component analysis: a normalization approach. Statistica Sinica 24, 1571–1596. [Google Scholar]
- Crainiceanu, C. M., Staicu, A.-M. and Di, C.-Z. (2009). Generalized multilevel functional regression. Journal of the American Statistical Association 104, 1550–1561. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Davidson, R. J., Ekman, P., Saron, C. D., Senulis, J. A. and Friesen, W. V. (1990). Approach-withdrawal and cerebral asymmetry: emotional expression and brain physiology: I. Journal of Personality and Social Psychology 58, 330. [PubMed] [Google Scholar]
- Di, C.-Z., Crainiceanu, C. M., Caffo, B. S. and Punjabi, N. M. (2009). Multilevel functional principal component analysis. The Annals of Applied Statistics 3, 458. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Goldsmith, J., Zipunnikov, V. and Schrack, J. (2015). Generalized multilevel function-on-scalar regression and principal component analysis. Biometrics 71, 344–353. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Greven, S., Crainiceanu, C., Caffo, B. and Reich, D. (2010). Longitudinal functional principal component analysis. Electronic Journal of Statistics 4, 1022–1054. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Happ, C. and Greven, S. (2018). Multivariate functional principal component analysis for data observed on different (dimensional) domains. Journal of the American Statistical Association 113, 649–659. [Google Scholar]
- Hasenstab, K., Scheffler, A., Telesca, D., Sugar, C. A., Jeste, S., DiStefano, C. and Şentürk, D. (2017). A multi-dimensional functional principal components analysis of eeg data. Biometrics 73, 999–1009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- James, G. M., Wang, J. AND Zhu, J. (2009). Functional linear regression that’s interpretable. The Annals of Statistics 37, 2083–2108. [Google Scholar]
- Jansen, M., White, T. P., Mullinger, K. J., Liddle, E. B., Gowland, P. A., Francis, S. T., Bowtell, R. and Liddle, P. F. (2012). Motion-related artefacts in EEG predict neuronally plausible patterns of activation in fMRI data. Neuroimage 59, 261–270. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kappel, S. L., Looney, D., Mandic, D. P. and Kidmose, P. (2017). Physiological artifacts in scalp EEG and ear-EEG. Biomedical Engineering Online 16, 103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Klimesch, W. (2012). Alpha-band oscillations, attention, and controlled access to stored information. Trends in Cognitive Sciences 16, 606–617. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Knyazev, G. G. (2007). Motivation, emotion, and their inhibitory control mirrored in brain oscillations. Neuroscience & Biobehavioral Reviews 31, 377–395. [DOI] [PubMed] [Google Scholar]
- Lei, J. AND Vu, V. Q. (2015). Sparsistency and agnostic inference in sparse PCA. The Annals of Statistics 43, 299–322. [Google Scholar]
- Lin, Z., Wang, L.g and Cao, J. (2016). Interpretable functional principal component analysis. Biometrics 72, 846–854. [DOI] [PubMed] [Google Scholar]
- Miniati, M., Rucci, P., Benvenuti, A., Frank, E., Buttenfield, J., Giorgi, G. and Cassano, G. B. (2010). Clinical characteristics and treatment outcome of depression in patients with and without a history of emotional and physical abuse. Journal of Psychiatric Research 44, 302–309. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Neuper, C., Scherer, R., Wriessnegger, S. and Pfurtscheller, G. (2009). Motor imagery and action observation: modulation of sensorimotor brain rhythms during mental control of a brain–computer interface. Clinical Neurophysiology 120, 239–247. [DOI] [PubMed] [Google Scholar]
- Ramsay, J. O. and Silverman, B. W. (2005). Functional Data Analysis, 2nd edition. Springer Series in Statistics. New York: Springer. [Google Scholar]
- Rice, J. A. and Silverman, B. W. (1991). Estimating the mean and covariance structure nonparametrically when the data are curves. Journal of the Royal Statistical Society: Series B (Methodological) 53, 233–243. [Google Scholar]
- Scheffler, A., Telesca, D., Li, Q., Sugar, C. A., Distefano, C., Jeste, S. and Şentürk, D. (2019). Hybrid principal components analysis for region-referenced longitudinal functional EEG data. Biostatistics. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shou, H., Zipunnikov, V., Crainiceanu, C. M. and Greven, S. (2015). Structured functional principal component analysis. Biometrics 71, 247–257. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Simon, N., Friedman, J., Hastie, T. and Tibshirani, R. (2013). A sparse-group lasso. Journal of Computational and Graphical Statistics 22, 231–245. [Google Scholar]
- Staicu, A.-M., Crainiceanu, C. M. and Carroll, R. J. (2010). Fast methods for spatially correlated multilevel functional data. Biostatistics 11, 177–194. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tallon-Baudry, C.e and Bertrand, O. (1999). Oscillatory gamma activity in humans and its role in object representation. Trends in Cognitive Sciences 3, 151–162. [DOI] [PubMed] [Google Scholar]
- Vu, V. Q., Cho, J., Lei, J. and Rohe, K. (2013). Fantope projection and selection: a near-optimal convex relaxation of sparse PCA. In: Burges C. J. C. and Bottou L. and Welling M. and Ghahramani Z. and Weinberger K. Q. (eds) Advances in Neural Information Processing Systems. Curran Associates, Inc. pp. 2670–2678. [Google Scholar]
- Yao, F., Müller, H.-G. and Wang, J.-L. (2005). Functional data analysis for sparse longitudinal data. Journal of the American Statistical Association 100, 577–590. [Google Scholar]
- Zeng, H., Song, A., Yan, R. and Qin, H. (2013). EOG artifact correction from eeg recording using stationary subspace analysis and empirical mode decomposition. Sensors 13, 14839–14859. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhao, Y., Ogden, R. T. and Reiss, P. T. (2012). Wavelet-based lasso in functional linear regression. Journal of Computational and Graphical Statistics 21, 600–617. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhou, J., Wang, N.-Y. and Wang, N. (2013). Functional linear model with zero-value coefficient function at sub-regions. Statistica Sinica 23, 25. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zipunnikov, V., Caffo, B., Yousem, D. M., Davatzikos, C., Schwartz, B. S. and Crainiceanu, C. (2011). Multilevel functional principal component analysis for high-dimensional data. Journal of Computational and Graphical Statistics 20, 852–873. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.