Covariate adjustment in continuous biomarker assessment

Abstract

Continuous biomarkers are common for disease screening and diagnosis. To reach a dichotomous clinical decision, a threshold would be imposed to distinguish subjects with disease from nondiseased individuals. Among various performance metrics, specificity at a controlled sensitivity level (or vice versa) is often desirable because it directly targets the clinical utility of the intended clinical test. Meanwhile, covariates, such as age, race, as well as sample collection conditions, could impact the biomarker distribution and may also confound the association between biomarker and disease status. Therefore, covariate adjustment is important in such biomarker evaluation. Most existing covariate adjustment methods do not specifically target the desired sensitivity/specificity level, but rather do so for the entire biomarker distribution. As such, they might be more prone to model misspecification. In this paper, we suggest a parsimonious quantile regression model for the diseased population, only locally at the controlled sensitivity level, and assess specificity with covariate-specific control of the sensitivity. Variance estimates are obtained from a sample-based approach and bootstrap. Furthermore, our proposed local model extends readily to a global one for covariate adjustment for the receiver operating characteristic (ROC) curve over the sensitivity continuum. We demonstrate computational efficiency of this proposed method and restore the inherent monotonicity in the estimated covariate-adjusted ROC curve. The asymptotic properties of the proposed estimators are established. Simulation studies show favorable performance of the proposal. Finally, we illustrate our method in biomarker evaluation for aggressive prostate cancer.

1 |. INTRODUCTION

Continuous biomarker is often utilized for disease screening and diagnosis, where a threshold is imposed to reach a dichotomous clinical decision. For its performance assessment, the receiver operating characteristic (ROC) curve provides a comprehensive evaluation across all possible thresholds. Area under the ROC curve (AUC) is a popular performance metric, but it may not be clinically sensible (Hanley and McNeil, 1982). Obviously, a continuous biomarker would not operate at all thresholds, because a diagnostic test typically needs to reach a certain sensitivity (or specificity) level to be clinically useful. Therefore, specificity at a controlled sensitivity level (or vice versa) would be a more desirable performance metric in practice. For example, for the noninvasive diagnosis of aggressive prostate cancer, the cost of a false negative is usually much higher than that of a false positive as a positive test result would be confirmed with biopsy. Thus, the clinical utility of a continuous biomarker would be best measured with specificity at a controlled high sensitivity level, for example, 95% (Sanda et al., 2017). In this work, we mainly focus on specificity at a controlled sensitivity level. The same methods proposed can be directly applied to sensitivity at a controlled specificity level by switching the roles of cases and controls.

Platt et al. (2000) and Zhou and Qin (2005), among others, studied the estimation of such a metric, in the absence of covariates. However, factors, such as age and ethnicity as well as specimen collection condition, may influence a biomarker. For example, prostate-specific antigen (PSA), as a prostate cancer biomarker, tends to be higher in older men (Partin et al., 1996). In addition, African American men have higher PSA than men of other racial backgrounds (Henderson et al., 1997; Sanda et al., 2017). While intrinsically they do not discriminate diseased from nondiseased, these covariates may impact the performance of a biomarker in a number of ways (Pepe, 2003). In fact, covariates may confound the association between the biomarker and disease status when the covariate distributions differ between diseased and nondiseased individuals. Even when the two covariate distributions are the same, ignoring the covariates may lead to biased accuracy assessment. At a minimum, when a test is intended to operate at a controlled sensitivity level, covariate adjustment for the threshold would be necessary to ensure a uniform sensitivity level across subpopulations.

There are many existing methods for covariate adjustment in the assessment of continuous biomarkers. Most of them model covariate effects on biomarker beyond the specific sensitivity/specificity level of interest. As such, they might be prone to model misspecification. For example, Tosteson and Begg (1988) and Pepe (1998) modeled the covariate effects on the diseased and nondiseased populations, and then derived covariate-specific ROC curve. Some other methods directly estimate covariate-adjusted ROC curve through generalized linear regression, for example, Pepe (1997, 2000); Cai and Pepe (2002). However, the covariate effects could be different at different sensitivity levels, as recognized by some of these authors. For example, Cai and Pepe (2002) discussed the possibility of including interactions between false-positive rates and covariates. An exception is Janes and Pepe (2009), who developed a nonparametric estimator in the case of discrete covariates. Nevertheless, when continuous covariates are involved, they used a semiparametric estimator to adjust for covariate effects over the entire biomarker distribution, not specifically targeting the sensitivity/specificity of interest. A few previous works have also adopted Bayesian modeling framework by incorporating the covariate effects in the parameters of the ROC curve associated data distributions (de Carvalho et al., 2013; de Carvalho and Rodriguez-Alvarez, 2018).

In this paper, we develop a covariate adjustment method for specificity at a controlled sensitivity level, by adopting the quantile regression model (Koenker and Bassett, 1978) at the given sensitivity for the diseased population. As such, minimal assumptions are imposed. The proposal also extends readily to the continuous spectrum of sensitivity levels so as to address covariate adjustment for the ROC curve. In the special case that the covariates have a finite number of values, the quantile regression model becomes saturated and thus does not actually impose any assumptions. Accordingly, our method then reduces to the nonparametric method as considered by Janes and Pepe (2009). However, with continuous covariates, the semiparametric model of Janes and Pepe (2009) is different as indicated before. This seemingly natural model has not been favorably considered previously due to a few technique difficulties particularly in the circumstance of covariate adjustment for the ROC curve (Pepe, 2003, p. 139). First, the computation burden may be of concern as the covariate effects are allowed to vary over quantiles. Second, the standard quantile regression of Koenker and Bassett (1978) does not respect the inherent monotonicity of the conditional quantile functions. Subsequently, the estimated ROC after covariate adjustment may not even be monotone. Both issues are resolved in our proposal.

This paper is organized as follows. Section 2 presents the proposed covariate adjustment method for specificity at a controlled sensitivity level. Section 3 extends the proposal to global covariate adjustment over all sensitivity levels, resulting in a covariate-adjusted ROC curve. Simulation studies are presented in Section 4, and a real data illustration given in Section 5. Final discussions are provided in Section 6. Technical proofs are relegated to the Web Appendix. The proposed methods are implemented and available as a user-friendly R/CRAN package caROC (https://cran.r-project.org/web/packages/caROC/index.html).

2 |. SPECIFICITY AT A CONTROLLED SENSITIVITY LEVEL

Denote the case biomarker of interest by $M_1$ and its associated covariate by ${\mathit{Z}}_1$. The case sample consists of $n_1$ i.i.d. replicates of $\left(M_1,{\mathit{Z}}_1\right),\left(M_{1i},{\mathit{Z}}_{1i}\right)$, $i=1,\dots ,n_1$. Similarly, denote the control biomarker by $M_0$ and its associated covariate by ${\mathit{Z}}_0$, and the control sample consists of $n_0$ i.i.d. replicates $\left(M_{0j},{\mathit{Z}}_{0j}\right)$, $j=1,\dots ,n_0$. These covariates may be discrete or continuous.

Write the conditional distribution function of the cases as $F_1(t;\mathit{z})\equiv \mathrm{Pr}\left(M_1\le t\mid {\mathit{Z}}_1=\mathit{z}\right)$. The corresponding conditional quantile function is $F_1^{-1}(·;\mathit{z})$. Controlling sensitivity level at ${\rho }_0$, between 0 and 1, yields a test threshold to be the $\left(1-{\rho }_0\right)$ th quantile, $F_1^{-1}\left(1-{\rho }_0;\mathit{z}\right)$. We adopt the following quantile regression model for the relationship between ${\rho }_0$-level sensitivity and the covariates:

$$F_1^{-1}\left(1-{\rho }_0;\mathit{z}\right)=\left(1,{\mathit{z}}^T\right)\mathit{\beta },$$ (1)

where $\mathit{\beta }$ is the regression coefficient; note that 1 is added to the covariate vector to incorporate an intercept. This model imposes a structure only at the controlled sensitivity level ${\rho }_0$. In the case of the $K$-sample problem, that is, with $K-1$ dummy indicator covariates denoting these $K$ samples, this model becomes saturated and no model structure is actually imposed. For controls, we similarly define $F_0(t;\mathit{z})$ as the conditional distribution function, that is, $F_0(t;\mathit{z})\equiv \mathrm{Pr}\left(M_0\le t\mid {\mathit{Z}}_0=\mathit{z}\right)$. Write ${\mathit{\beta }}_0$ as the true value of $\mathit{\beta }$. The covariate-adjusted specificity at controlled sensitivity ${\rho }_0$ is given by

$${\varphi }_0=\mathrm{Pr}\left\{M_0\le \left(1,{\mathit{Z}}_0^T\right){\mathit{\beta }}_0\right\}=E\left[F_0\left\{\left(1,{\mathit{Z}}_0^T\right){\mathit{\beta }}_0;{\mathit{Z}}_0\right\}\right].$$

This measure gives the overall specificity with covariate-specific threshold so as to keep the same controlled sensitivity level for covariate-specific subpopulations.

Standard quantile regression of Koenker and Bassett (1978) gives a point estimator $\stackrel{\mathit{ˆ}}{\mathit{\beta }}$, which is a solution to the following estimating equation:

$$n_1^{-1}\sum _{i=1}^{n_1} \left(\begin{array}{c}1\\ Z_{1i}\end{array}\right)\left[I\left\{M_{1i}>\left(1,{\mathit{Z}}_{1i}^T\right)\mathit{\beta }\right\}-{\rho }_0\right]=O\left(n_1^{-1}\right).$$

Then an estimator of ${\varphi }_0$ can be obtained via the plug-in principle $\hat{\varphi }=n_0^{-1}{\sum }_{j=1}^{n_0} I\{M_{0j}\le \left(1,{\mathit{Z}}_{0j}^T\right)\stackrel{\mathit{ˆ}}{\mathit{\beta }}\}$. In the special case of the $K$-sample problem, our estimator reduces to the nonparametric estimator of Janes and Pepe (2009).

2.1 |. Asymptotic study

Now we consider the asymptotic properties of our proposed estimator. The following regularity conditions are imposed:

• Condition 1. The control and case size ratio $n_0/n_1$ approaches a constant $c>0$ as $n_0+n_1\to \mathrm{\infty }$.

• Condition 2. Covariates ${\mathit{Z}}_1$ and ${\mathit{Z}}_0$ are bounded.

• Condition 3. $E({\tilde{\mathit{Z}}}_1^{\otimes 2})$ is nonsingular, where ${\tilde{\mathit{Z}}}_1={\left(1,{\mathit{Z}}_1^T\right)}^T$ and ${\mathit{v}}^{\otimes 2}=\mathit{v}{\mathit{v}}^T$ for vector $\mathit{v}$.

• Condition 4a. Both $F_1(t;\mathit{z})$ and $F_0(t;\mathit{z})$ are differentiable at the threshold $t=\left(1,{\mathit{z}}^T\right){\mathit{\beta }}_{\mathbf{0}}$ with derivative bounded away from 0 and $\mathrm{\infty }$ uniformly in $\mathit{z}$ over the supports of ${\mathit{Z}}_1$ and ${\mathit{Z}}_0$, respectively.

These conditions are standard and mild. In particular, the differentiability assumption in Condition 4a is only imposed at the threshold of interest, whereas $F_1$ and $F_0$ could be discontinuous elsewhere.

Theorem 1.

Suppose that the quantile regression model for the cases as given in (1) holds locally at the $\left(1-{\rho }_0\right)thquantile,alongwithconditions1,2,3,and4a.Then,\hat{\varphi }$ is consistent for ${\varphi }_0.Inaddition,n_0^{1/2}(\hat{\varphi }-{\varphi }_0)$ converges to a normal distribution with mean zero and variance

$$V=c{\rho }_0\left(1-{\rho }_0\right){\mathit{D}}_2^T{\mathit{D}}_1^{-1}{\mathit{D}}_0{\mathit{D}}_1^{-1}{\mathit{D}}_2+{\varphi }_0\left(1-{\varphi }_0\right),$$ (2)

where

$$\begin{array}{l}{\tilde{\mathit{Z}}}_0={\left(1,{\mathit{Z}}_0^T\right)}^T,{\mathit{D}}_0=E{\tilde{\mathit{Z}}}_1^{\otimes 2},{\mathit{D}}_1=E\{F_1^{\mathrm{\prime }}({\tilde{\mathit{Z}}}_1^T{\mathit{\beta }}_0;{\mathit{Z}}_1){\tilde{\mathit{Z}}}_1^{\otimes 2}\},\\ {\mathit{D}}_2=E\{F_0^{\mathrm{\prime }}({\tilde{\mathit{Z}}}_0^T{\mathit{\beta }}_0;{\mathit{Z}}_0){\tilde{\mathit{Z}}}_0\},\end{array}$$

and $F_1^{\mathrm{\prime }}(\cdot ;\mathit{z}),F_0^{\mathrm{\prime }}(\cdot ;\mathit{z})arethederivativesof{F}_1(\cdot ;\mathit{z}),F_0(\cdot ;\mathit{z})$, respectively.

The second component of $V$ is the variance if ${\mathit{\beta }}_0$ is known and used instead of $\stackrel{\mathit{ˆ}}{\mathit{\beta }}$. Meanwhile, the additional variability as given by the first component arises from the estimation of ${\mathit{\beta }}_0$.

2.2 |. Inference

Theorem 1 provides the asymptotic variance for the proposed estimator. As derivatives of the distribution functions are involved, direct estimation, however, is difficult. To overcome this difficulty, we adopt the method of Huang (2002) for variance estimation with nonsmooth estimating functions. Recast the estimator $(\stackrel{\mathit{ˆ}}{\mathit{\beta }},\hat{\varphi })$ as the solution to the following set of estimating equations:

$${\mathit{G}}_n(\mathit{\nu })=\left(\begin{array}{c}{n}_1^{-1}{\sum }_{i=1}^{n_1} \left(\begin{array}{c}1\\ {\mathit{Z}}_{1i}\end{array}\right)\left[I\left\{M_{1i}>\left(1,{\mathit{Z}}_{1i}^T\right)\mathit{\beta }\right\}-{\rho }_0\right]\\ n_0^{-1}{\sum }_{j=1}^{n_0} \left[I\left\{M_{0j}\le \left(1,{\mathit{Z}}_{0j}^T\right)\mathit{\beta }\right\}-\varphi \right]\end{array}\right),$$ (3)

where $\mathit{\nu }={\left({\mathit{\beta }}^T,\varphi \right)}^T$. Denote the true value by ${\mathit{\nu }}_0={\left({\mathit{\beta }}_0^T,{\varphi }_0\right)}^T$. The asymptotic variance of ${({\stackrel{\mathit{ˆ}}{\mathit{\beta }}}^T,\hat{\varphi })}^T$ is ${\mathbf{\Gamma }}^{-1}\mathbf{\Sigma }{\left({\mathbf{\Gamma }}^{-1}\right)}^T$, where $\mathbf{\Sigma }$ is the asymptotic variance of ${\mathit{G}}_n\left({\mathit{\nu }}_0\right)$ and $\mathbf{\Gamma }$ is the derivative of the limit of ${\mathit{G}}_n\left(\mathit{\nu }\right)$ at ${\mathit{\nu }}_0$. Note that $V$ in (2) corresponds to the last diagonal element of $n_1{\mathbf{\Gamma }}^{-1}\mathbf{\Sigma }{\left({\mathbf{\Gamma }}^{-1}\right)}^T$. Sandwich variance estimation cannot be directly applied, because ${\mathit{G}}_n\left(\mathit{\nu }\right)$ is not differentiable in $\mathit{\beta }$. The method of Huang (2002) resolves this issue. Specifically, start with an estimator for $\mathbf{\Sigma }$ as

$$\widehat{\mathbf{\Sigma }}=\left(\begin{array}{cc}{n}_1^{-2}{\sum }_{i=1}^{n_1} {\left(\begin{array}{c}1\\ {\mathit{Z}}_{1i}\end{array}\right)}^{\otimes 2}{\left[I\{M_{1i}>\left(1,{\mathit{Z}}_{1i}^T\right)\widehat{\mathit{\beta }}\}-{\rho }_0\right]}^2& \mathbf{0}\\ \mathbf{0}& n_0^{-2}{\sum }_{j=1}^{n_0} {\left[I\{M_{0j}\le \left(1,{\mathit{Z}}_{0j}^T\right)\widehat{\mathit{\beta }}\}-\widehat{\varphi }\right]}^2\end{array}\right).$$ (4)

Perform the Cholesky decomposition to give $\widehat{\mathbf{\Sigma }}={\mathit{C}}^{\otimes 2}$. Write $\mathit{C}=\left({\mathit{c}}_1,\dots ,{\mathit{c}}_L\right)$ with column vectors ${\mathit{c}}_1,\dots ,{\mathit{c}}_L$, where $L$ is the length of $\mathit{v}$. Then, a sample-based variance estimator for ${\left({\mathit{\beta }}_0^T,{\varphi }_0\right)}^T$ is given by $({\mathit{G}}_n^{-1}\left({\mathit{c}}_1\right)-\widehat{\mathit{\nu }},\dots ,{\mathit{G}}_n^{-1}\left({\mathit{c}}_L\right)-\stackrel{\mathit{ˆ}}{\mathit{v}}{)}^{\otimes 2}$. This method overcomes the nondifferentiability issue discussed before effectively by a numerical differentiation of the inverse estimating equation ${\mathit{G}}_n^{-1}(\cdot )$ using a data-adaptive bandwidth.

For the variance estimation, a computationally more intensive alternative is bootstrap with resampling for cases and controls drawn separately. This approach has been commonly adopted for related problems (e.g., Janes and Pepe 2009).

3 |. ROC CURVE

The preceding methods target a particular sensitivity level of interest. The same modeling strategy readily extends to each and every sensitivity level in a continuum, resulting in a covariate-adjusted ROC curve. As such, we impose the global model,

$$F_1^{-1}\left(1-\rho ;\mathit{z}\right)=\left(1,{\mathit{z}}^T\right){\mathit{\beta }}_0\left(\rho \right)\forall \rho \in (0,1),$$ (5)

where the regression coefficient function ${\mathit{\beta }}_0\left(\rho \right)$ may vary with $\rho$. The covariate-adjusted specificity also varies with $\rho$,

$${\varphi }_0\left(\rho \right)=\mathrm{Pr}\left\{M_0\le \left(1,{\mathit{Z}}_0^T\right){\mathit{\beta }}_0\left(\rho \right)\right\}.$$ (6)

Clearly, the global model is a submodel of the local one given by (1). Nevertheless, the global model is fairly general itself as being nonparametric. Just the same as the local model, this global model actually imposes no structure whatsoever in the special case of the $K$-sample problem (Huang, 2010).

As the global model implies local models for each $\rho$ value in (0, 1), we apply the estimation procedure described in Section 2 in a pointwise fashion to obtain the estimators. The regression coefficient estimator $\widehat{\mathit{\beta }}(\rho )$ is the solution of

$$n_1^{-1}\sum _{i=1}^{n_{\mathrm{l}}} \left(\begin{array}{c}1\\ {\mathit{Z}}_{1i}\end{array}\right)\left[I\{M_{1i}>\left(1,{\mathit{Z}}_{1i}^T\right)\widehat{\mathit{\beta }}(\rho )\}-\rho \right]=O\left(n_1^{-1}\right).$$

and an estimator of $\varphi (\rho )$ is $\widehat{\varphi }(\rho )=n_0^{-1}{\sum }_{j=1}^{n_0} I\{M_{0j}\le \left(1,{\mathit{Z}}_{0j}^T\right)\stackrel{\mathit{ˆ}}{\mathit{\beta }}(p)\}$. The computation might be perceived as intensive to have a solution at each and every $\rho$. Nevertheless, the estimator $\stackrel{\mathit{ˆ}}{\mathit{\beta }}(\rho )$ is a step function and its computation can be formulated as a parametric programming problem with $~n\mathrm{l}\mathrm{o}\mathrm{g}\left(n\right)$ breakpoints to examine (Koenker 2005, Section 6.3). Starting from $\rho =0$ upward, this algorithm involves alternately solving the equation at the current $\rho$ value and finding the next breakpoint. The computation burden does not impose a real concern for most applications.

3.1 |. Asymptotic study

For the asymptotic study with the global model, we strengthen Condition 4a.

• Condition 4b. Both $F_1(t;\mathit{z})$ and $F_0(t;\mathit{z})$ have density functions $f_1(t;\mathit{z})$ and $f_0(t;\mathit{z})$, respectively, which are continuous in $t$ for given $\mathit{z}$ and bounded uniformly in $t$ and $\mathit{z}$ over the supports of ${\mathit{Z}}_1$ and ${\mathit{Z}}_0$, respectively. Meanwhile, ${\mathit{\beta }}_0(\cdot )$ is continuously differentiable on $\left[{\rho }_1,{\rho }_2\right]$ for any ${\rho }_1$ and ${\rho }_2$ such that $0<{\rho }_1<{\rho }_2<1$.

The existence of density function is a standard condition when ROC curve is of interest (Janes and Pepe, 2009). The differentiability of ${\mathit{\beta }}_0(\cdot )$ is also mild and commonly imposed (Koenker, 2005). Under the condition, there is no zero-density intervals and thus no jump in quantile.

Theorem 2.

Suppose that the quantile regression model for the cases as given in (5) holds globally over $\left(1-{\rho }_2\right)ththrough\left(1-{\rho }_1\right)thquantilefor0<p_1<p_2<1,alongwithConditions1,2,3,and4b.Then,\hat{\varphi }(\rho )$ converges in probability to ${\varphi }_0(\rho )$ uniformly over $\rho \in \left[{\rho }_1,{\rho }_2\right].Furthermore,n_0^{1/2}\{\hat{\varphi }(\rho )-{\varphi }_0(\rho )\}$ converges weakly to a Gaussian process over $\rho \in \left[{\rho }_1,{\rho }_2\right]$.

3.2 |. Monotonization of the estimated ROC curve

As mentioned in the Introduction, lack of monotonicity in the estimated conditional quantile functions could result in that of the estimated covariate-adjusted ROC curve. In fact, a few existing works adopted location-scale models to avoid illogical results in estimating quantiles, for example, He (1997) and Heagerty and Pepe (1999). However, their models become more restrictive. We rather restore monotonicity in the ROC estimation under the original quantile regression model and suggest two approaches below.

The root of the issue is the lack of monotonicity-respecting with the estimated quantile regression coefficient process. Huang (2017) developed a method to restore the monotonicity-respecting property by identifying and interpolating monotonicity-respecting breakpoints of the original estimated coefficient process. We apply this approach to obtain a monotonicity-respecting estimator $\tilde{\mathit{\beta }}(\cdot )$. Plugging this estimator $\tilde{\mathit{\beta }}(\cdot )$ in (6) results in an estimated ROC curve that is monotone. As a note, the resulting monotonized ROC curve is still a step function. The second strategy is to directly apply the method of Huang (2017) to the estimated ROC curve $\{\widehat{\varphi }(\rho ),0\le \rho \le 1\}$. This method results in a piecewise-linear monotonized ROC curve. Web Appendix Section S3 provides more details about the two monotonization methods. We refer these two methods as regression- and ROC-based monotonizations thereafter.

The monotonized estimators are asymptotically equivalent to the original estimators as shown in Huang (2017). For finite sample, the monotonized estimators may have efficiency gain.

3.3 |. Inference

For a point on the estimated ROC curve, one may adopt the same inference procedure with the local model as described in (1). However, note the availability of several point estimates, depending on whether a monotonized ROC is employed. Nevertheless, any choice of these estimates does not make a difference because they are all asymptotically equivalent.

If the whole ROC curve is of interest, it is possible to construct confidence band using bootstrap. To estimate the distribution of $n_0^{1/2}\{\hat{\varphi }(\cdot )-{\varphi }_0(\cdot )\}$, we can use the same bootstrap approach in local model except that the estimand now is functional. Denote the bootstrap estimator by ${\varphi }^{\mathrm{*}}(\cdot )$. The distribution of $n_0^{1/2}\{{\varphi }^{\mathrm{*}}(\cdot )-\hat{\varphi }(\cdot )\}$ conditioning on the data is asymptotically the same as $n_0^{1/2}\{\hat{\varphi }(\cdot )-{\varphi }_0(\cdot )\}$. For $\rho \in \left[{\rho }_1,{\rho }_2\right]$ with ${\rho }_1$ and ${\rho }_2$ satisfying $0<{\rho }_1<{\rho }_2<1$, the 95% equal-precision confidence band of $\hat{\varphi }(\rho )$ is given by

$$\widehat{\varphi }\left(\rho \right)\pm {\eta }_{0.95}\mathrm{SE}\{\widehat{\varphi }\left(\rho \right)\},$$

where $\mathrm{S}\mathrm{E}\{\hat{\varphi }(\rho )\}$ is the standard error of $\hat{\varphi }(\rho )$ and ${\eta }_{0.95}$ is the estimated 95% percentile of ${\mathrm{s}\mathrm{u}\mathrm{p}}_{\rho \in \left[{\rho }_1,{\rho }_2\right]} [\mid {\varphi }^{\mathrm{*}}(\rho )-]\hat{\varphi }(\rho )\mid /\mathrm{S}\mathrm{E}\{\hat{\varphi }(\rho )\}]$. $\mathrm{S}\mathrm{E}\{\hat{\varphi }(\rho )\}$ is also based on bootstrap resamples. One may construct a confidence band based on a monotonized ROC curve as in Section 3.2 in the same fashion, simply with $\widehat{\varphi }(\cdot )$ replaced by the monotonized version.

4 |. SIMULATIONS

We evaluate the finite sample properties of our proposal under practical sample sizes. Assume that the biomarker relies on two independent covariates $Z_1$ and $Z_2$, both following uniform distribution between 0 and 1 among cases and controls. For cases, the biomarkers $M_1$’s are generated from formulation (1) and ${\mathit{\beta }}_0(·)$ consists of an intercept and two slopes ${\mathit{\beta }}_0(\rho )=[\log \left\{-\log \left(\rho \right)\right\},1-\rho ,(1-\rho {)}^2]$. For controls, the biomarkers $M_0$’s are generated from $N(-1-\left.0.5Z_1-0.5Z_2,2^2\right)$. The true specificities at controlled sensitivity levels 0.95, 0.90, 0.85, and 0.80 are 0.24, 0.36, 0.45, and 0.52, respectively.

Table 1 reports the performance of the proposed method in this setting, including bias, sample- and bootstrap-based standard errors, as well as the coverage probability of confidence intervals. We also present the logit transformation-based confidence interval, which is obtained by backtransforming the Wald-type confidence interval of the logit-transformed ${\varphi }_0$. As a comparison, we present the results using the seimiparametric method by Janes and Pepe (2009) (Column “JP-SP”), implemented in R/CRAN package ROCnReg (Rodríguez-Álvarez and Inacio, 2020). All results are summarized over 5000 Monte Carlo datasets. The estimation bias of the proposed method is very small and decreases with the increase of sample size. Both sample- and bootstrap-based standard errors are close to standard deviations. In addition, the coverage rate of confidence intervals is close to the nominal level under all scenarios. These demonstrate the favorable performance of the proposed method. The semiparametric method by Janes and Pepe (2009) shows larger bias and worse coverage probability. Of course, this comparison is not completely fair because the two methods impose different models and the data are simulated under our model. Web Appendix Figure S1 presents the computational time for different sample sizes using sample-based inference versus bootstrap-based inference. We observe that sample-based variance estimation has comparable performance with the bootstrap-based estimation, whereas the sample-based inference has advantages in computational efficiency.

TABLE 1.

Results of the simulation study for estimating specificity ${\varphi }_0$ under controlled sensitivity level ${\rho }_0$

	Proposed method								JP-SP
			Sample-based			BT-based
${\mathit{n}}_1={\mathit{n}}_0$	Bias	SD	SE	Cov	LCov	SE	Cov	LCov	Bias	Cov
${\rho }_0=0.95,{\varphi }_0=0.24$
100	160	784	1111	94.28	95.62	818	94.72	94.22	424	85.98
200	85	570	739	93.14	94.42	597	94.68	95.06	409	80.12
500	43	358	444	94.76	95.24	382	95.52	95.18	396	68.90
1000	19	265	300	93.78	94.18	270	94.36	94.40	388	51.44
${\rho }_0=0.90,{\varphi }_0=0.36$
100	68	777	1037	95.54	96.36	822	95.62	96.58	116	93.48
200	25	557	682	94.64	95.46	582	95.00	95.68	103	91.36
500	13	354	410	95.00	95.22	367	95.08	95.38	103	92.04
1000	4	254	277	94.8	94.98	257	94.82	94.96	95	90.12
${\rho }_0=0.85$, ${\varphi }_0=0.45$
100	17	736	943	95.38	96.28	788	95.64	96.94	−65	94.32
200	1	537	634	95.08	95.74	554	94.94	95.40	−72	92.92
500	5	334	377	95.28	95.66	346	95.28	95.48	−68	93.02
1000	2	238	259	94.82	94.98	243	94.76	94.90	−72	92.82
${\rho }_0=0.80$, ${\varphi }_0=0.52$
100	−10	706	874	95.18	96.24	750	95.36	96.64	−172	94.32
200	−6	510	588	95.20	95.78	525	95.14	95.70	−176	92.34
500	2	315	352	94.98	95.12	326	94.50	94.70	−172	90.64
1000	2	226	242	95.04	95.12	229	94.84	94.92	−173	85.90

BT-based, bootstrap-based; JP-SP, semiparametric method using the normal linear model of Janes and Pepe (2009); Bias, $(\hat{\varphi }-{\varphi }_0)\times {10}^4$; SD, standard deviation (×10⁴); SE, mean standard error (×10⁴); Cov (%) and LCov (%), coverage rates of 95% confidence interval and logit transformation-based confidence interval.

As discussed in Section 3.2, the estimator $\widehat{\varphi }(\cdot )$ may not respect the monotonicity of ${\varphi }_0(\cdot )$, leading to illogical results. We implement the two monotonization methods described in Section 3.2 and evaluate their performance. Table 2 reports the bias and coverage rate related with these two methods where ${\hat{\varphi }}_{reg}$ and ${\widehat{\varphi }}_{ROC}$ correspond to the estimators after adopting regression- and ROC-based monotonization methods, respectively. The confidence intervals of the monotonized estimators are constructed with the sample-based standard error estimates. We find both regression- and ROC-based methods show small bias and good coverage rate under different sample sizes and sensitivity levels. ROC-based approach generally results in better coverage probability than regression-based method. The coverage probability of ROC-based method is comparable or even better than that without applying monotonicity-restoration method (results presented in Table 1). Lastly, applying monotonicity-restoration method may lead to smaller variance than original estimator, as shown for the ROC-based method and largely so for the regression-based method. This observation is consistent with the finding in Huang (2017).

TABLE 2.

Comparison of two monotonization methods in the simulation study

	${\stackrel{\mathbf{ˆ}}{\mathit{\Phi }}}_{\mathit{r}\mathit{e}\mathit{g}}$				${\widehat{\mathit{\Phi }}}_{\mathit{R}\mathit{O}\mathit{C}}$
${\mathit{n}}_1={\mathit{n}}_0$	Bias	SD	Cov	LCov	Bias	SD	Cov	LCov
${\rho }_0=0.95$, ${\varphi }_0=0.24$
100	419	973	88.82	88.64	276	776	94.68	94.58
200	84	616	92.96	93.48	154	562	94.76	94.94
500	27	363	94.52	95.24	56	363	94.58	94.70
1000	26	259	94.94	95.18	34	260	95.02	95.10
${\rho }_0=0.90$, ${\varphi }_0=0.36$
100	52	810	94.44	95.44	131	768	95.00	95.96
200	24	556	94.90	95.60	69	551	95.30	95.82
500	20	349	95.22	95.34	27	350	95.02	95.18
1000	16	246	95.14	95.28	18	248	95.08	95.12
${\rho }_0=0.85$, ${\varphi }_0=0.45$
100	6	732	95.66	96.46	66	724	95.86	96.72
200	24	525	95.22	95.78	43	526	95.46	96.00
500	14	328	95.32	95.56	16	329	95.24	95.54
1000	10	231	95.44	95.52	10	232	95.20	95.34
${\rho }_0=0.80$, ${\varphi }_0=0.52$
100	−14	685	95.92	96.68	22	685	96.08	96.96
200	13	495	95.96	96.40	21	499	95.74	96.16
500	5	311	95.82	95.98	5	312	95.80	95.94
1000	7	218	95.64	95.74	7	218	95.82	95.90

${\hat{\varphi }}_{reg}$, the estimator with regression-based monotonization; ${\hat{\varphi }}_{ROC}$, the estimator with ROC-based monotonization; Bias, $(\hat{\varphi }.-{\varphi }_0)\times {10}^4$; SD, standard deviation ×10⁴; Cov (%) and LCov (%), coverage rates of 95% confidence interval and logit transformation-based confidence interval.

We also consider the case with discrete covariates only. In this case, our proposed estimator coincides the nonparametric estimator in Janes and Pepe (2009) as indicated in the Introduction. The focus is on comparing the performance of our inference methods to Janes and Pepe (2009), under their simulation setup. The details of this simulation study are presented in Web Appendix Section S1 and the results in Web Tables S1 and S2. Our sample-based variance estimation shows comparable coverage rate as our bootstrap-based inference, whereas their kernel density-based inference has worse performance than the bootstrap-based approach. Thus, our sample-based method outperforms the kernel density-based variance estimation in Janes and Pepe (2009). Such advantage is especially obvious when the controlled specificity is large (${\varphi }_0=0.95$ and 0.90).

5 |. ILLUSTRATION WITH A CLINICAL STUDY

Data from a clinical study for aggressive prostate cancer (Sanda et al., 2017) are used for illustration. This was a prospective, multicenter cohort of male participants for first-time prostate biopsy without preexisting prostate cancer. After excluding 14 subjects with missing values, the data consist of 150 subjects with aggressive (Gleason score ≥ 7) prostate cancer, per biopsy, and 352 controls. The biomarker under consideration herein is PSA. Figure 1a shows the density of PSA from cases and controls.

FIGURE 1.

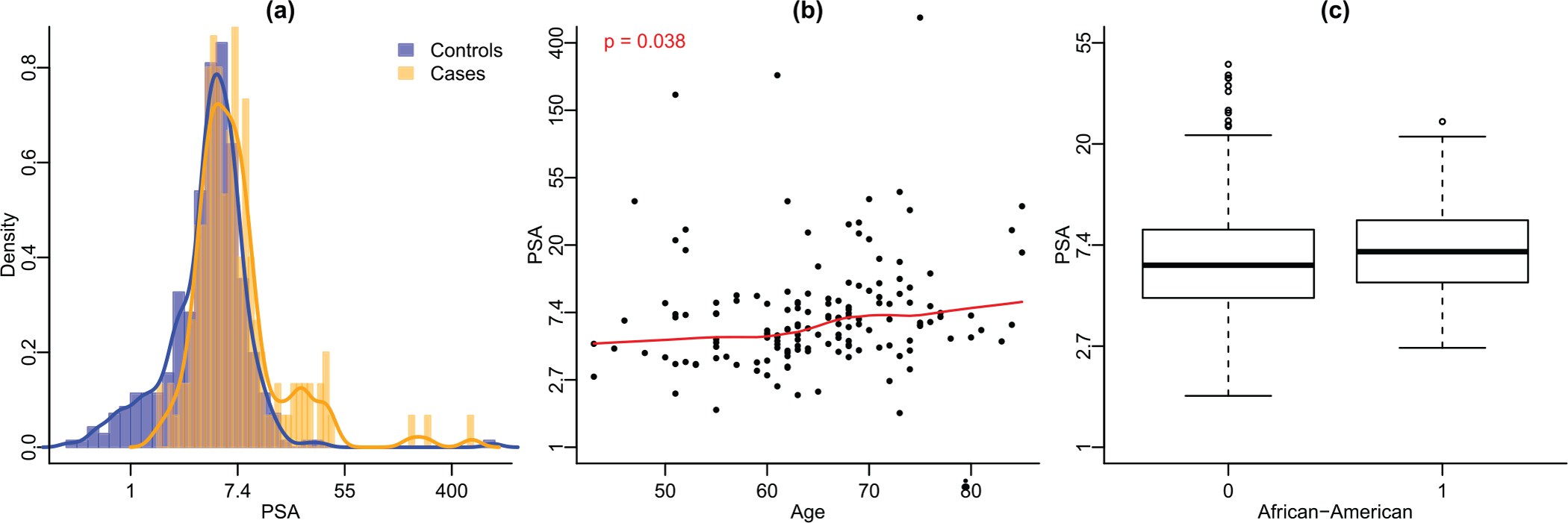
Exploratory plots for the clinical study. Panel (a): Histograms of PSA for cases and controls with density curves overlaid. Panel (b): Scatterplot of PSA versus age, cases only. The red solid line is fitted by loess and the p-value is obtained from testing zero Pearson’s correlation coefficient. Panel (c): Boxplot of PSA of African American population and non-African American group, cases only. This figure appears in color in the electronic version of this article, and any mention of color refers to that version

As mentioned in the Introduction, elder men tend to have higher PSA values than younger men (Oesterling et al., 1993; Lilja et al., 2008). Among the cases of our study, we observe significant $(p=0.038)$ elevation in PSA with the increase of age (Figure 1b). In addition to age, African-American men were also reported to have higher PSA than white men (Henderson et al., 1997). Figure 1c shows a small increase in PSA among African American cases compared to non-African American cases, although the increase is not statistically significant. In the following analysis, age and being African-American (AA) are included as covariates. For model checking, we have considered additional terms of squared age and the interaction of age and AA. They are not significant at the sensitivity levels of interest, ${\rho }_0=0.80,0.85,0.90$, and 0.95, and thus not included in the model.

The ROC curves with and without adjusting for covariates are shown in Figure 2a (black and blue curves; this figure appears in color in the electronic version of this article, and any mention of color refers to that version). The adjusted ROC curves after regression- and ROC-based monotonization are also presented (red and purple curves). Adjusting for covariates leads to different ROC curve compared to the one without covariate adjustment. Covariate-adjusted specificity is higher than no-adjustment when sensitivity is between 0.7 and 0.9, and lower when that is between 0.2 and 0.7. Imposing the monotonicity does not make much difference. The exact specificity estimations for all the methods at controlled sensitivity levels 95%, 90%, 85%, and 80% are reported in Table 3. Consistent with the observations in Figure 2a, the covariate-adjusted specificity is lower than no-adjusted specificity for ${\rho }_0=95\mathrm{\%}$ but higher for ${\rho }_0=90\mathrm{\%},85\mathrm{\%}$, and 80%.

FIGURE 2.

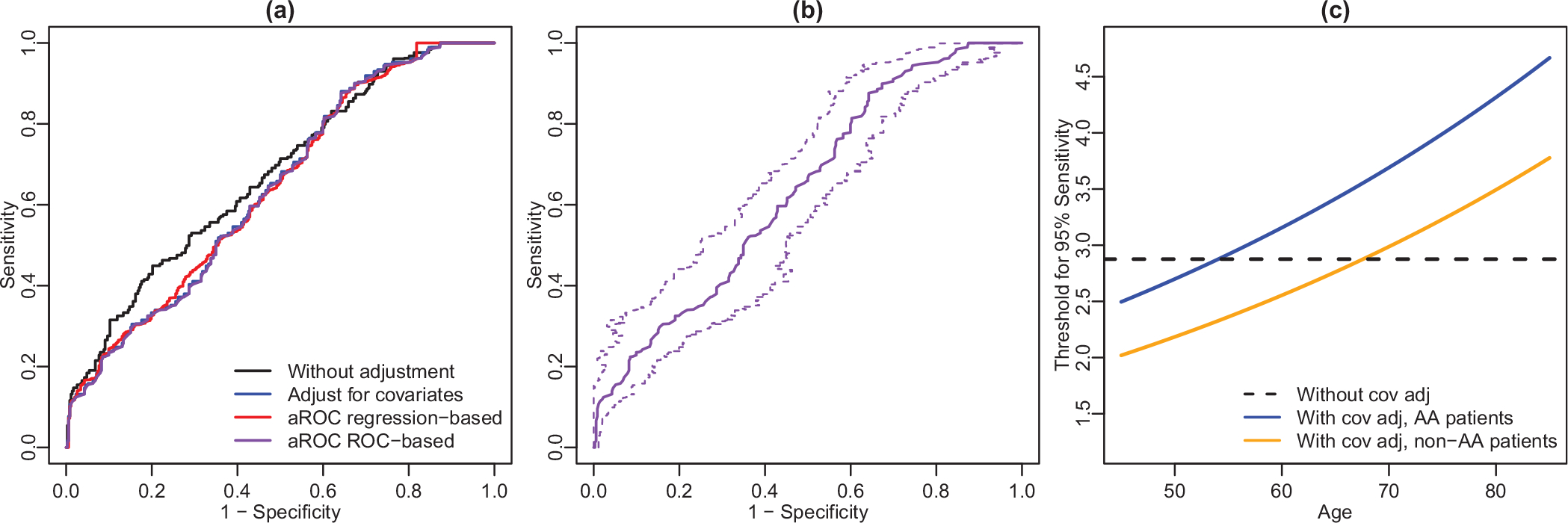
ROC curve and threshold results for the prostate study. Panel (a): ROC curve without and with adjustment for covariates (black and blue curve, respectively). Red and purple curves are adjusted ROC curves after applying regression- and ROC-based monotonization. Panel (b): Covariate-adjusted ROC curve with ROC-based monotonization is in solid purple. Dashed purple lines are the 95% confidence band. Panel (c): Estimated PSA threshold at controlled 95% sensitivity level by age based on the local model. This figure appears in color in the electronic version of this article, and any mention of color refers to that version

TABLE 3.

Estimated specificity along with 95% confidence interval at controlled sensitivity level ${(\rho }_0)$ in the aggressive prostate cancer application

${\mathit{\rho }}_0$	${\widehat{\mathit{\varphi }}}_{\mathit{n}}$	$\stackrel{\mathit{ˆ}}{\mathit{\varphi }}$	${\stackrel{\mathit{ˆ}}{\mathit{\varphi }}}_{\mathit{r}\mathit{e}\mathit{g}}$	${\widehat{\mathit{\varphi }}}_{\mathit{R}\mathit{O}\mathit{C}}$
0.95	0.239	0.196 (0.108, 0.330)	0.208 (0.118, 0.340)	0.218 (0.127, 0.348)
0.90	0.284	0.318 (0.225, 0.429)	0.316 (0.223, 0.427)	0.321 (0.228, 0.431)
0.85	0.332	0.361 (0.297, 0.430)	0.358 (0.294, 0.428)	0.361 (0.297, 0.430)
0.80	0.392	0.398 (0.320, 0.481)	0.398 (0.320, 0.480)	0.400 (0.323, 0.483)

${\hat{\varphi }}_n$, estimated specificity without covariate adjustment; $\hat{\varphi }$, estimated specificity adjusting for age and AA without applying monotonicity restoration; ${\hat{\varphi }}_{reg}$ and ${\hat{\varphi }}_{\text{ROC}}$, covariate-adjusted specificity after applying regression- and ROC-based monotonization methods, respectively. The confidence interval is logit transformation-based with sample-based standard error

In contrast to pointwise confidence intervals, we also construct 95% confidence bands for the covariate-adjusted ROC curves. As the confidence bands are similar for the ROC curves with or without monotonicity restorations, we only present the confidence band for the ROC curve after applying ROC-based monotonization in Figure 2b. The confidence band works well in providing inference for the whole ROC curve.

Lastly, we present the estimated covariate-adjusted thresholds for PSA at controlled sensitivity level 95%in Figure 2c. Such thresholds could be useful for physicians to identify subjects with aggressive prostate cancer. For example, given a non-African American patient of age 50, an estimated PSA threshold of 2.2 may be used for controlled sensitivity level of 0.95. The design of our method ensures that the sensitivity is equally controlled among covariate-specific subpopulations. The covariate-adjusted threshold increases with age and is higher in African Americans, which aligns with existing understanding of these covariates.

Our implementation has excellent computational performance. With this prostate cancer data, which contain 150 diseased and 352 nondiseased samples, computing a covariate-adjusted ROC curve takes less than 1 s on a laptop computer with 4GB RAM and Intel Core i5 CPU. Computing the confidence band takes less than 3 s.

6 |. DISCUSSION

Our contributions are fourfold. First, we provide a covariate adjustment approach for a clinical utility-sensible performance metric, specificity at controlled sensitivity or vice versa, with minimal modeling assumptions. Compared with existing methods that assume uniform covariate effects across the ROC curve, our method only models the covariate effect specific to the corresponding threshold and thus is less prone to model misspecification. Second, this method extends to covariate adjustment for the whole ROC curve, where the issues of computation and monotonicity have been addressed. Third, we develop a sample-based variance estimation using a numerical differentiation with data-adaptive bandwidth. The proposed samples-based inference demonstrates comparable performance as bootstrap-based inference but is more computationally efficient. Lastly, we adopt the monotonization restoration methods of Huang (2017) and develop two strategies for restoring monotonicity in the covariate-adjusted ROC curves. These strategies are generally applicable in ROC estimation.

It is worthwhile to point out that our methods focus on the overall specificity with covariate-adjusted threshold at a controlled sensitivity level. This is different from covariate-specific performance evaluation as for subpopulations, as considered by Toledano and Gatsonis (1995), Pepe (1997), Pepe (1998), Pepe (2000), Cai and Pepe (2002), and Cai and Moskowitz (2004). Our notion of covariate adjustment is similar to that in Janes and Pepe (2009). As pointed by one of the reviewers, by analogy to Janes and Pepe (2009), the pooled specificity at the controlled sensitivity can be formulated as ${\varphi }_0(\rho )=\int {\mathrm{R}\mathrm{O}\mathrm{C}}_{Sp}(\rho \mid \mathit{z})\mathrm{d}{H}_0\left(\mathit{z}\right)$. ${\mathrm{R}\mathrm{O}\mathrm{C}}_{Sp}$ denotes the covariate-specific specificity at sensitivity $\rho$ and is defined as ${\mathrm{R}\mathrm{O}\mathrm{C}}_{Sp}(\rho \mid \mathit{z})=F_0\left\{F_1^{-1}(1-\right.\rho ;\mathit{z});\mathit{z}\}$, where $H_0\left(\mathit{z}\right)=\mathrm{Pr}\left({\mathit{Z}}_0\le \mathit{z}\right)$ is the distribution function of ${\mathit{Z}}_0$.

Our model may be extended to accommodate nonlinear covariate effects. Koenker (2005, 14, Chapter 6.6 and 7) discussed nonparametric quantile regression methods, including kernel-based approximation, additive models, penalized splines, and penalized triogram. In addition, a few recent works have also developed strategies to solve quantile regression with splines (Yoshida, 2013; Andriyana et al., 2014; Lian et al., 2015). They may be incorporated in our proposed method.

Supplementary Material

Supplementary material

• S1 Simulation study with discrete covariates

• Table S1 Results under the simulation setting with discrete covariate values. Sensitivity ${\varphi }_0$ under controlled specificity ${\rho }_0$ is estimated and presented.

• Table S1 Results under the simulation setting with discrete covariate values. Specificity ${\rho }_0$ under controlled sensitivity ${\varphi }_0$ is estimated and presented.

• S2 Proof of Theorems

• S3 Details about two monotonization methods

• Figure S1 Summarization of computational time using two inference methods at different sample size selections.

DATA AVAILABILITY STATEMENT

Data subject to third-party restrictions. Restrictions apply to the availability of these data, which were used under permission for this paper. The data that support the findings of this paper are available from Dr. Martin G. Sanda (martinsanda@emory.edu) with the permission of the Emory Prostate Cancer study. The proposed methods are implemented and available as a user-friendly R/CRAN package caROC (https://cran.r-project.org/web/packages/caROC/index.html).