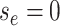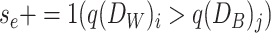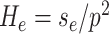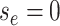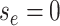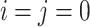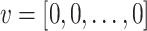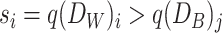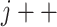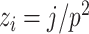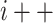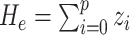Summary
A standard unsupervised analysis is to cluster observations into discrete groups using a dissimilarity measure, such as Euclidean distance. If there does not exist a ground-truth label for each observation necessary for external validity metrics, then internal validity metrics, such as the tightness or separation of the clusters, are often used. However, the interpretation of these internal metrics can be problematic when using different dissimilarity measures as they have different magnitudes and ranges of values that they span. To address this problem, previous work introduced the “scale-agnostic”  discordance metric; however, this internal metric is slow to calculate for large data. Furthermore, in the setting of unsupervised clustering with
discordance metric; however, this internal metric is slow to calculate for large data. Furthermore, in the setting of unsupervised clustering with  groups, we show that
groups, we show that  varies as a function of the proportion of observations assigned to each of the groups (or clusters), referred to as the group balance, which is an undesirable property. To address this problem, we propose a modification of
varies as a function of the proportion of observations assigned to each of the groups (or clusters), referred to as the group balance, which is an undesirable property. To address this problem, we propose a modification of 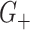 , referred to as
, referred to as 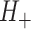 , and demonstrate that
, and demonstrate that 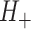 does not vary as a function of group balance using a simulation study and with public single-cell RNA-sequencing data. Finally, we provide scalable approaches to estimate
does not vary as a function of group balance using a simulation study and with public single-cell RNA-sequencing data. Finally, we provide scalable approaches to estimate 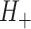 , which are available in the
, which are available in the  R package.
R package.
Keywords: Clustering, Discordance, Dissimilarity, Single cell
1. Introduction
Quantifications of discordance such as Gamma (Goodman and Kruskal, 1979) and Tau (Kendall, 1938) have historically been derived to assess fitness from contingency tables. (The terms “discordance” and “disconcordance” have been used interchangeably to describe related metrics for contingency tables (Rohlf, 1974; Goodman and Kruskal, 1979), but here we use “discordance.”)
In this article, we explore the problem of unsupervised clustering (also known as observation partitioning). A typical clustering algorithm seeks to optimally group 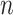 observations into
observations into 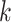 groups (or clusters) using a dissimilarity matrix
groups (or clusters) using a dissimilarity matrix 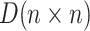 (e.g., Euclidean distance) or
(e.g., Euclidean distance) or 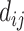 for each
for each 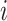 ,
, 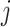 observations with
observations with 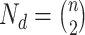 unique pairs of distances. If there does not exist a ground-truth label for each observation, internal validity metrics are often used to evaluate the performance of a set of predicted cluster labels
unique pairs of distances. If there does not exist a ground-truth label for each observation, internal validity metrics are often used to evaluate the performance of a set of predicted cluster labels 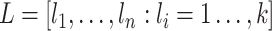 for a fixed
for a fixed  . Many internal fitness metrics quantify the tightness or separation of partitions with functions such as within-cluster sums of squares or mean Silhouette scores (Rousseeuw, 1987). However, when comparing multiple dissimilarity measures, the interpretation of these performance metrics can be problematic as different dissimilarity measures have different magnitudes and ranges, leading to different ranges in the tightness of the clusters.
. Many internal fitness metrics quantify the tightness or separation of partitions with functions such as within-cluster sums of squares or mean Silhouette scores (Rousseeuw, 1987). However, when comparing multiple dissimilarity measures, the interpretation of these performance metrics can be problematic as different dissimilarity measures have different magnitudes and ranges, leading to different ranges in the tightness of the clusters.
One solution is to use discordance as an internal validity metric that depends on the ranks of the dissimilarities, rather than on the dissimilarities themselves, thereby making it a “scale-agnostic.” For example, the discordance metric  (Williams and Clifford, 1971; Rohlf, 1974) uses the following to assess how well a given predicted cluster label
(Williams and Clifford, 1971; Rohlf, 1974) uses the following to assess how well a given predicted cluster label  fits a dissimilarity
fits a dissimilarity 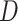 induced from the same observations (Rohlf, 1974; Desgraupes, 2018) (Note 1 of the Supplementary material available at Biostatistics online):
induced from the same observations (Rohlf, 1974; Desgraupes, 2018) (Note 1 of the Supplementary material available at Biostatistics online):
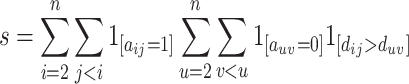 |
(1.1) |
given fixed 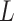 , an adjacency matrix
, an adjacency matrix 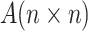 is defined using the predicted cluster label
is defined using the predicted cluster label 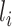 ,
, 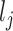 for the
for the 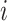 ,
, 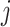 observations, where
observations, where 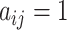 if
if 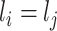 or
or 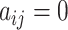 otherwise. We can define the set of within-cluster distances as
otherwise. We can define the set of within-cluster distances as 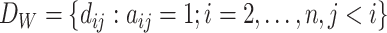 and between-cluster distances as
and between-cluster distances as 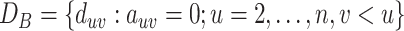 with the total number of distances in each set as
with the total number of distances in each set as 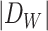 and
and 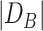 , respectively. As we know that each upper triangular entry of
, respectively. As we know that each upper triangular entry of 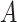 is binary (every distance is either between- or within-cluster), then
is binary (every distance is either between- or within-cluster), then 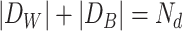 . Here, we define
. Here, we define 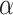 as the proportion of total distances
as the proportion of total distances 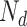 that are within-cluster distances, or
that are within-cluster distances, or 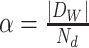 .
.
In the following sections, we first consider properties of 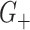 and show how
and show how 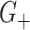 is a function of
is a function of 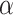 (Section 2), which has an explicit relationship with what we refer to as
(Section 2), which has an explicit relationship with what we refer to as 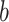 (the group balance, Section 2.4.1), where
(the group balance, Section 2.4.1), where 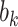 is the proportion of observations assigned to each of
is the proportion of observations assigned to each of 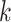 groups (or clusters) and
groups (or clusters) and 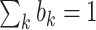 . We illustrate how this is an undesirable property for
. We illustrate how this is an undesirable property for 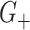 to vary as a function of
to vary as a function of 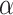 , thereby also the vector
, thereby also the vector 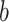 and
and 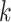 . For example, when simulating “null” data (random Gaussian data with no mean difference between
. For example, when simulating “null” data (random Gaussian data with no mean difference between 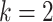 groups), the expected mean (and the interpretation itself) of the
groups), the expected mean (and the interpretation itself) of the 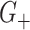 discordance metric varies depending on
discordance metric varies depending on 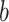 (e.g., if the groups are balanced or
(e.g., if the groups are balanced or 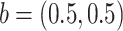 , then
, then 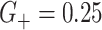 , but if the groups are imbalanced, such as
, but if the groups are imbalanced, such as 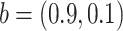 , then
, then 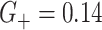 using simulated data) (Figure 1). In addition, we demonstrate that
using simulated data) (Figure 1). In addition, we demonstrate that 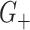 is slow to calculate for large data (due to the pairwise comparisons of dissimilarities in (1.1)). To ameliorate these challenges, we propose a modification to
is slow to calculate for large data (due to the pairwise comparisons of dissimilarities in (1.1)). To ameliorate these challenges, we propose a modification to 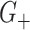 , referred to as
, referred to as 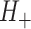 (Section 3) and demonstrate that
(Section 3) and demonstrate that 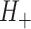 does not vary as a function of group balance using a simulation study and with public single-cell RNA-sequencing (scRNA-seq) data (Section 4). Finally, we provide scalable approaches to estimate
does not vary as a function of group balance using a simulation study and with public single-cell RNA-sequencing (scRNA-seq) data (Section 4). Finally, we provide scalable approaches to estimate 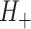 , which are available in the
, which are available in the  R package.
R package.
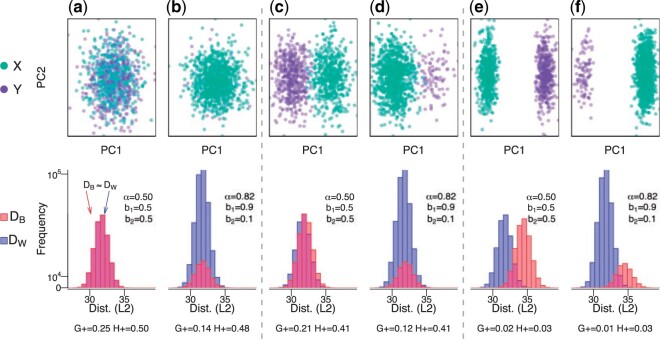
Fig. 1.
The 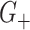 discordance metric varies as function of
discordance metric varies as function of 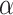 (proportion of within-cluster distances), which is a function of the group balance. We randomly sampled
(proportion of within-cluster distances), which is a function of the group balance. We randomly sampled 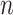 = 1000 observations with 500 features from a mixture distribution
= 1000 observations with 500 features from a mixture distribution 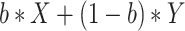 with
with 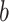 being the probability of an observation coming from
being the probability of an observation coming from 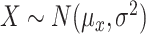 and
and 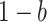 coming from
coming from 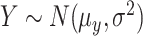 with (a,b) no mean difference (
with (a,b) no mean difference (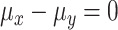 ) (or a “null” setting), (c,d) a small mean difference (
) (or a “null” setting), (c,d) a small mean difference (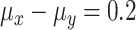 ), and (e,f) a large mean difference (
), and (e,f) a large mean difference (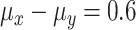 ). We simulate data with (a,c,e) balanced groups (
). We simulate data with (a,c,e) balanced groups (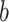 = 0.5) and (b,d,f) imbalanced groups (
= 0.5) and (b,d,f) imbalanced groups (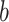 = 0.9). For each simulation, the top row contains observations belonging to a group (
= 0.9). For each simulation, the top row contains observations belonging to a group (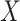 and
and 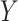 ) along the first two principal components (PCs) and the bottom row contains histograms of the within- (
) along the first two principal components (PCs) and the bottom row contains histograms of the within- (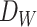 ) and between- (
) and between- (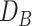 ) cluster distances (Euclidean) for the balanced and imbalanced groups. Refer to Figure S1 of the Supplementary material available at Biostatistics online for an illustration of (and Section 2.4.1 for the explicit relationship between) the proportion of within-cluster distances (
) cluster distances (Euclidean) for the balanced and imbalanced groups. Refer to Figure S1 of the Supplementary material available at Biostatistics online for an illustration of (and Section 2.4.1 for the explicit relationship between) the proportion of within-cluster distances (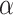 ) and the group balance (
) and the group balance (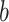 ). For each simulation, the bottom row includes
). For each simulation, the bottom row includes 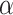 and the two discordance metrics
and the two discordance metrics 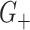 and
and 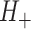 . Generally, values close to zero represent more concordance, while a larger values represent more discordance.
. Generally, values close to zero represent more concordance, while a larger values represent more discordance.
2. The 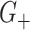 discordance metric
discordance metric
The discordance metric 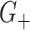 (Williams and Clifford, 1971; Rohlf, 1974) scales
(Williams and Clifford, 1971; Rohlf, 1974) scales 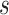 (1.1) by
(1.1) by 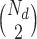 , the number of ways to compare each unique distance to every other.
, the number of ways to compare each unique distance to every other.
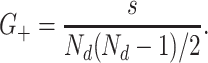 |
(2.2) |
Generally, 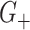 close to zero represents high concordance, while a larger
close to zero represents high concordance, while a larger 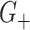 is more discordant. In this way,
is more discordant. In this way, 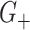 can be used to quantify the cluster fitness for a given
can be used to quantify the cluster fitness for a given 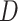 and
and 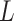 (that is, a designation of each pairwise dissimilarity as within- or between-cluster), where a small
(that is, a designation of each pairwise dissimilarity as within- or between-cluster), where a small 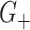 value would be interpreted as good performance with tight, separate clusters.
value would be interpreted as good performance with tight, separate clusters.
2.1. Applications of 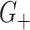
As noted above, if 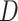 is fixed, smaller values of
is fixed, smaller values of 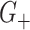 among many sets of labels
among many sets of labels 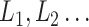 indicate increased cluster fitness (or the generated labels with smaller
indicate increased cluster fitness (or the generated labels with smaller 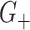 have more accurately described the dissimilarity structure of the data) (Rand, 1971; Williams and Clifford, 1971). If we instead fix
have more accurately described the dissimilarity structure of the data) (Rand, 1971; Williams and Clifford, 1971). If we instead fix 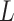 , we can also use
, we can also use 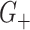 to assess the fitness of multiple dissimilarity matrices
to assess the fitness of multiple dissimilarity matrices 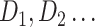 (Rohlf, 1974).
(Rohlf, 1974).
Because 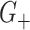 depends on the relative rankings of pairwise distances, this transformation enables a “scale-agnostic” approach to compare dissimilarity measures through the structure they impose on the data, rather than by the exact values of the distances themselves. This allows distances to be compared on varying scales without imposing bias from the expected magnitude of distances.
depends on the relative rankings of pairwise distances, this transformation enables a “scale-agnostic” approach to compare dissimilarity measures through the structure they impose on the data, rather than by the exact values of the distances themselves. This allows distances to be compared on varying scales without imposing bias from the expected magnitude of distances.
2.2. Properties of 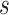
Consider 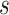 (1.1) with an adjacency matrix
(1.1) with an adjacency matrix 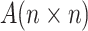 and dissimilarity matrix
and dissimilarity matrix 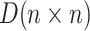 , with induced within-cluster distances
, with induced within-cluster distances 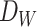 and between-cluster distances
and between-cluster distances 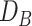 where
where 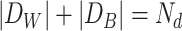 . We can define
. We can define 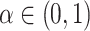 as the proportion of total distances
as the proportion of total distances 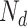 that are within-cluster distances. In this way,
that are within-cluster distances. In this way, 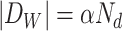 , and similarly,
, and similarly, 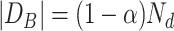 . Then, conditional on
. Then, conditional on 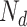 and
and 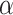 , the
, the 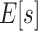 is (Note 1 of the Supplementary material available at Biostatistics online):
is (Note 1 of the Supplementary material available at Biostatistics online):
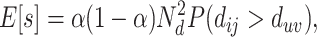 |
(2.3) |
where 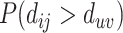 is the probability that a within-cluster distance
is the probability that a within-cluster distance 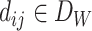 is greater than a between-cluster distance
is greater than a between-cluster distance 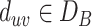 . This is the quantity we are interested in estimating, but there is a scaling factor
. This is the quantity we are interested in estimating, but there is a scaling factor 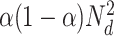 that depends on both
that depends on both 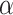 and
and 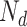 . Next, we consider properties of first
. Next, we consider properties of first 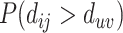 and then
and then 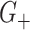 .
.
2.3. Properties of 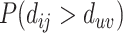
If we know the expected mean and variance for 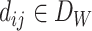 and
and 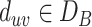 , we can estimate
, we can estimate 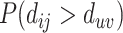 . In the simple case where
. In the simple case where 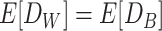 , we can consider
, we can consider 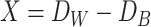 , then
, then 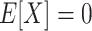 and a standardization of
and a standardization of 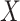 demonstrates (assuming [co]variances exist) that
demonstrates (assuming [co]variances exist) that 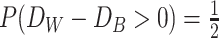 . As we might expect, there is a
. As we might expect, there is a 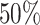 chance that
chance that 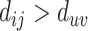 when
when 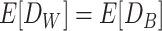 .
.
2.4. Properties of 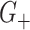
Using (2.2) and (2.3), the expected value of 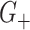 is (Note 1 of the Supplementary material available at Biostatistics online):
is (Note 1 of the Supplementary material available at Biostatistics online):
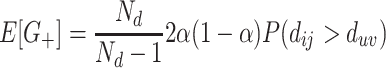 |
As 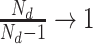 for large enough
for large enough 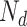 , then we see that
, then we see that 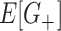 is a function of
is a function of 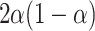 . Next, we derive the relationship between
. Next, we derive the relationship between 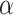 and
and 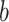 (group balance) (Section 2.4.1). Then, we provide an illustration of how
(group balance) (Section 2.4.1). Then, we provide an illustration of how 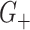 varying as function of
varying as function of 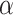 and
and 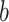 is an undesirable property (Section 2.4.2).
is an undesirable property (Section 2.4.2).
2.4.1. Relationship between 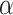 and
and 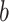
Herein, we derive the relationship between 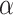 (the proportion of total distances
(the proportion of total distances 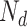 that are within-cluster distances) and the group balance
that are within-cluster distances) and the group balance 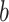 (the proportion of observations assigned to each of the
(the proportion of observations assigned to each of the 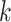 groups). For an arbitrary label
groups). For an arbitrary label 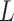 (a vector of length
(a vector of length 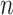 ,
, 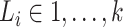 ) where
) where  indicates that the
indicates that the 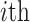 observation is assigned membership to the
observation is assigned membership to the 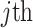 cluster group, we can define the portion of observations in group
cluster group, we can define the portion of observations in group 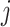 using
using 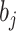 defined as
defined as
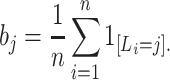 |
By definition, we know 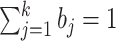 . Each of the
. Each of the 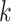 clusters will contribute to the quantity
clusters will contribute to the quantity 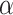 , which is a fraction of the
, which is a fraction of the 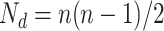 unique pairs of distances. Now, for the
unique pairs of distances. Now, for the 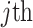 cluster, this contribution (
cluster, this contribution (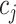 ) is the upper triangular elements of a matrix block with size
) is the upper triangular elements of a matrix block with size 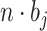
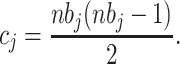 |
Finally, we can express 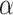 as a sum over each of
as a sum over each of 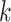 contributions
contributions 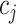 for
for 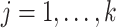 for the explicit relationship between
for the explicit relationship between 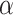 and the
and the 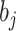 s (and consequently
s (and consequently 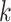 )
)
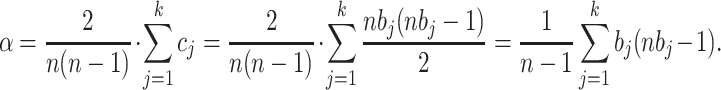 |
(2.4) |
2.4.2. 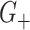 as a function of
as a function of 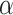 and
and 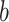 is an undesirable property
is an undesirable property
Because 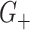 is a function of
is a function of 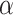 and thereby the group balance
and thereby the group balance 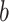 (and consequently
(and consequently 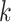 ), the interpretation of what we expect
), the interpretation of what we expect 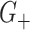 to mean, for example, in a null setting without any true difference between groups, changes across data sets with different group balances
to mean, for example, in a null setting without any true difference between groups, changes across data sets with different group balances 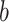 .
.
For example, assume we randomly sampled 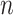 = 1000 observations with 500 features from a mixture distribution
= 1000 observations with 500 features from a mixture distribution 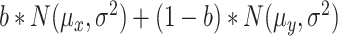 with no mean difference (
with no mean difference (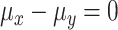 ) and balanced classes (
) and balanced classes (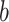 = 0.5 and
= 0.5 and 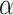 = 0.5) then, we know
= 0.5) then, we know 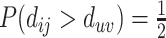 and
and 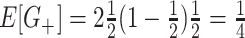 . This can be thought of as a “null” simulation where we expect no difference in class character or balance, yet
. This can be thought of as a “null” simulation where we expect no difference in class character or balance, yet 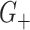 will (perhaps unintuitively) equal
will (perhaps unintuitively) equal 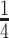 . However, if there is an imbalance in class sizes (
. However, if there is an imbalance in class sizes (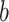 = 0.9 and
= 0.9 and 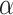 = 0.82) then
= 0.82) then 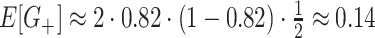 (Figure 1). An illustration of the relationship between
(Figure 1). An illustration of the relationship between  and
and 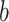 for this example can be seen in Figure S1A,B of the Supplementary material available at Biostatistics online, which shifts the majority of the distances to within-cluster distances simply due to the imbalance of the classes.
for this example can be seen in Figure S1A,B of the Supplementary material available at Biostatistics online, which shifts the majority of the distances to within-cluster distances simply due to the imbalance of the classes.
However, if we consider the same scenario as above, but if we change 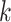 from
from 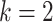 to
to 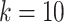 , we see that because there are a larger number of groups, this changes
, we see that because there are a larger number of groups, this changes 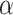 (the portion of within-cluster distances) for both the balanced (Figure S1C of the Supplementary material available at Biostatistics online) and imbalanced simulations (Figure S1D of the Supplementary material available at Biostatistics online).
(the portion of within-cluster distances) for both the balanced (Figure S1C of the Supplementary material available at Biostatistics online) and imbalanced simulations (Figure S1D of the Supplementary material available at Biostatistics online).
3. The proposed method
3.1. An unbiased discordance metric with 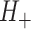
To ameliorate this effect, we propose 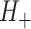 , which replaces the scaling factor
, which replaces the scaling factor 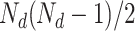 in the denominator in
in the denominator in 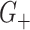 with
with 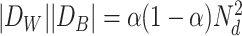 :
:
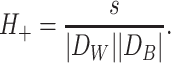 |
(3.5) |
In other words, instead of scaling 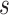 by the total number of ways to compare every distance to every other distance, we divide by the number of ways to compare within-cluster distances to between-cluster distances. Hence,
by the total number of ways to compare every distance to every other distance, we divide by the number of ways to compare within-cluster distances to between-cluster distances. Hence, 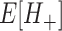 is not a function of
is not a function of 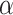 :
:
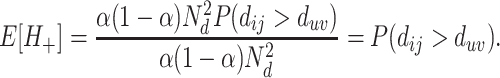 |
In fact, we can empirically verify that while 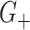 varies as a function of
varies as a function of 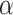 (and
(and 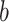 ) (Figure 2a),
) (Figure 2a), 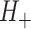 does not (Figure 2b), regardless of difference in expectation between the groups.
does not (Figure 2b), regardless of difference in expectation between the groups.
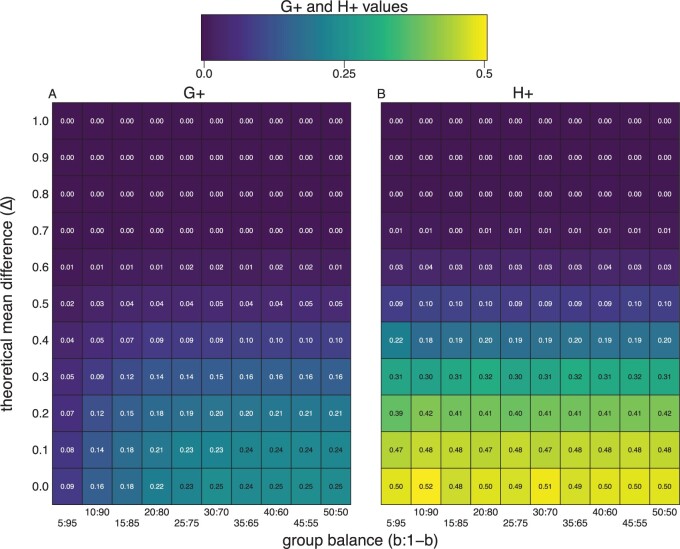
Fig. 2.
The 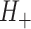 discordance metric does not change as a function of class balance. We randomly sampled
discordance metric does not change as a function of class balance. We randomly sampled 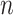 = 1000 observations with 500 features from a mixture distribution
= 1000 observations with 500 features from a mixture distribution 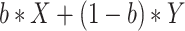 with
with 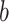 being the probability of an observation coming from
being the probability of an observation coming from 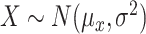 and
and 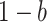 coming from
coming from 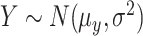 with a true mean difference (
with a true mean difference (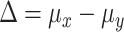 ) (
) (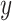 -axis). Along the
-axis). Along the 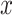 -axis we change group (or class) balance from balanced (e.g.,
-axis we change group (or class) balance from balanced (e.g., 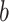 = 0.50) and to imbalanced (e.g.,
= 0.50) and to imbalanced (e.g., 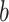 = 0.05) groups. The plots are heatmaps of true
= 0.05) groups. The plots are heatmaps of true 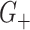 (left) and
(left) and 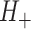 (right) discordance metrics, which shows
(right) discordance metrics, which shows 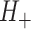 does not change as a function of class balance (
does not change as a function of class balance (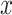 -axis), only as a function of the true effect size (
-axis), only as a function of the true effect size (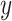 -axis).
-axis).
3.2. Generalizing properties of 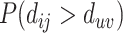
More generally, consider the function 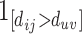 . For some constant
. For some constant 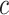 , we can decompose this event as a joint event
, we can decompose this event as a joint event 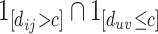 or
or 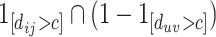 (Jardine and Sibson, 1968; Rohlf, 1974). Therefore, as
(Jardine and Sibson, 1968; Rohlf, 1974). Therefore, as 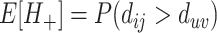 , we can decompose
, we can decompose 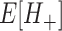 into two quantities:
into two quantities: 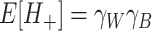 where
where 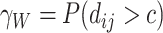 and
and 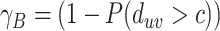 . In other words,
. In other words,  empirically states a
empirically states a  of
of 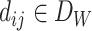 is strictly greater than
is strictly greater than 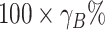 of
of 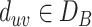 . This implies
. This implies 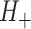 is not uniquely determined. For example, if
is not uniquely determined. For example, if  , we could have
, we could have 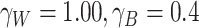 or
or 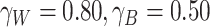 . It should be noted that one can construct examples where two distinct pairs of
. It should be noted that one can construct examples where two distinct pairs of 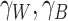 will have the same product, but do not imply each other.
will have the same product, but do not imply each other.
3.3. Two algorithms to estimate 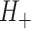 and
and 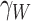 ,
, 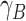
One problem with the 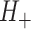 (and
(and 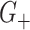 ) discordance metric (3.5) is that it requires the calculation of both (i) the dissimilarity matrix
) discordance metric (3.5) is that it requires the calculation of both (i) the dissimilarity matrix 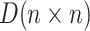 which scales
which scales 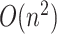 and (ii)
and (ii) 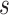 (1.1) which scales with the number of ways to compare within-cluster distances to between-cluster distances (or
(1.1) which scales with the number of ways to compare within-cluster distances to between-cluster distances (or 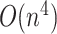 comparisons). For example, with data sets of sizes
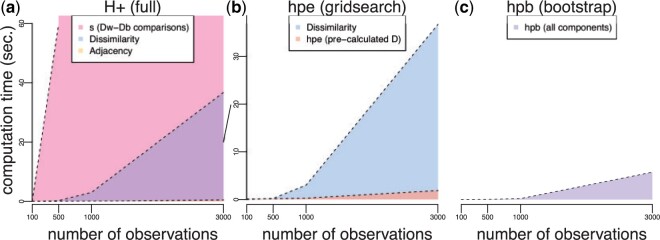
comparisons). For example, with data sets of sizes 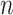 = 100 and 500, it takes 0.01 and 0.22 s, respectively, to calculate
= 100 and 500, it takes 0.01 and 0.22 s, respectively, to calculate 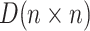 and it takes 0.08 and 59.68 s, respectively, to calculate
and it takes 0.08 and 59.68 s, respectively, to calculate 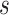 (Figure 3a, Table S1 of the Supplementary material available at Biostatistics online). For data sets with more than
(Figure 3a, Table S1 of the Supplementary material available at Biostatistics online). For data sets with more than 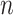 = 500 observations, this quickly becomes computationally infeasible.
= 500 observations, this quickly becomes computationally infeasible.
Fig. 3.
Computation times (seconds) for exact and approximate 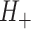 calculations as a function of increasing number of observations
calculations as a function of increasing number of observations 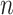 . Computational time (
. Computational time (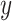 -axis) as a function of observations (
-axis) as a function of observations (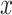 -axis) to calculate the individual components of (a) exact
-axis) to calculate the individual components of (a) exact 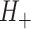 including (i) the dissimilarity matrix
including (i) the dissimilarity matrix 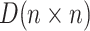 (purple) scaling
(purple) scaling 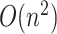 , (ii) the adjacency matrix (orange), and (iii) the most expensive operation
, (ii) the adjacency matrix (orange), and (iii) the most expensive operation 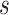 (pink) scaling
(pink) scaling 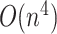 . Note,
. Note, 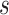 is only shown for
is only shown for 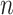 = 100 and 500 observations, but the trend is shaded in for the other observations; (b,c) have different y-axes than (a). The diagonal line between (a) and (b) connects the 20-s ticks of these two axes. (b) Approximate
= 100 and 500 observations, but the trend is shaded in for the other observations; (b,c) have different y-axes than (a). The diagonal line between (a) and (b) connects the 20-s ticks of these two axes. (b) Approximate  estimation (HPE) using the grid search procedure including (i) the dissimilarity matrix
estimation (HPE) using the grid search procedure including (i) the dissimilarity matrix 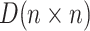 (blue) scaling
(blue) scaling 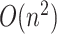 and (ii) the HPE algorithm to estimate
and (ii) the HPE algorithm to estimate 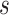 (orange) scaling
(orange) scaling 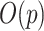 ; (c) approximate
; (c) approximate 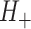 estimation using the bootstrap procedure (HPB) (purple), which scales similarly to HPE without the computational expense required for calculating
estimation using the bootstrap procedure (HPB) (purple), which scales similarly to HPE without the computational expense required for calculating 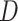 . Note (b) and (c) have a different
. Note (b) and (c) have a different 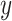 -axis scale than (a) for an zoomed in visualization of time.
-axis scale than (a) for an zoomed in visualization of time.
To address this, we propose two algorithms to estimate 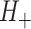 , both referred to as an “h-plus estimator” or (HPE): (i) a brute force approach inspired by the Top-Scoring Pair (Leek, 2009; Magis and Price, 2012) algorithms, which use relative ranks to classify observations with
, both referred to as an “h-plus estimator” or (HPE): (i) a brute force approach inspired by the Top-Scoring Pair (Leek, 2009; Magis and Price, 2012) algorithms, which use relative ranks to classify observations with 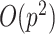 comparisons and (ii) a grid search approach with
comparisons and (ii) a grid search approach with 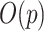 comparisons, where
comparisons, where 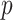 refers to percentiles of the data (rather than the
refers to percentiles of the data (rather than the 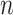 observations themselves). Typically,
observations themselves). Typically, 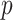 is chosen such that
is chosen such that 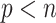 , leading to significant improvements in the computational speed to calculate
, leading to significant improvements in the computational speed to calculate 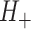 . Specifically, both algorithms estimate
. Specifically, both algorithms estimate 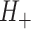 (referred to as
(referred to as 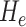 or HPE) assuming
or HPE) assuming 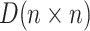 has been precalculated and provide faster ways to approximate
has been precalculated and provide faster ways to approximate 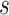 (Figure 3b). Both algorithms are implemented in the hpe() function in the fasthplus R package.
(Figure 3b). Both algorithms are implemented in the hpe() function in the fasthplus R package.
Finally, in a later section (Section 3.5), we introduce a third algorithm based on bootstrap sampling to avoid calculating the full dissimilarity matrix 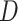 , thereby leading to further improvements in computational speed to estimate
, thereby leading to further improvements in computational speed to estimate 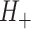 (referred to as
(referred to as 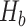 or HPB) (Figure 3c). The bootstrap algorithm is implemented in the hpb() function in the fasthplus R package.
or HPB) (Figure 3c). The bootstrap algorithm is implemented in the hpb() function in the fasthplus R package.
3.3.1. Intuition behind HPE algorithms
The estimator 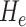 (or HPE) assumes
(or HPE) assumes 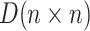 has been precalculated and then provides faster ways to approximate
has been precalculated and then provides faster ways to approximate 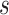 (the pairwise comparisons of
(the pairwise comparisons of 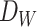 and
and 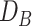 ). Specifically, we let the two sets
). Specifically, we let the two sets 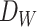 and
and 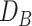 represent the ordered (ascending) dissimilarities
represent the ordered (ascending) dissimilarities 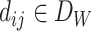 and
and 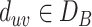 , respectively. Then, we bin the sets
, respectively. Then, we bin the sets 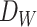 and
and 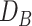 into
into 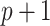 percentiles where
percentiles where 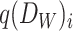 and
and 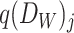 are the percentiles for
are the percentiles for 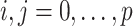 . Note,
. Note, 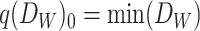 and
and 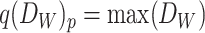 . In both algorithms below, we check if
. In both algorithms below, we check if 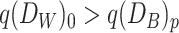 , then
, then 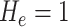 , and similarly, if
, and similarly, if 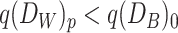 then
then 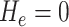 .
.
Next, we provide a graphical intuition for the two HPE algorithms by performing a simulation study. First, we simulate observations from two Gaussian distributions, namely 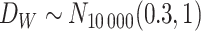 and
and 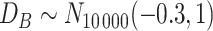 and calculate the quantiles
and calculate the quantiles 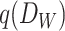 and
and 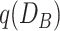 for each of the sets with
for each of the sets with 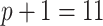 (Figure 4a),
(Figure 4a), 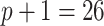 (Figure 4b), and
(Figure 4b), and 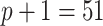 (Figure 4c). The calculation of these quantiles seeks to approximate the true ordered inequality information for each
(Figure 4c). The calculation of these quantiles seeks to approximate the true ordered inequality information for each 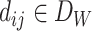 and
and 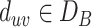 . That is, if
. That is, if 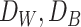 were both given in ascending order, the white line in Figure 4 shows the percent of
were both given in ascending order, the white line in Figure 4 shows the percent of 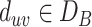 that is strictly less than each
that is strictly less than each 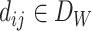 . The true
. The true 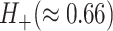 is then given by the area under the white curve (the true rank orderings for each pair). Our goal is to use the following two algorithms to estimate the true
is then given by the area under the white curve (the true rank orderings for each pair). Our goal is to use the following two algorithms to estimate the true 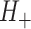 (fraction of blue area in the grid).
(fraction of blue area in the grid).
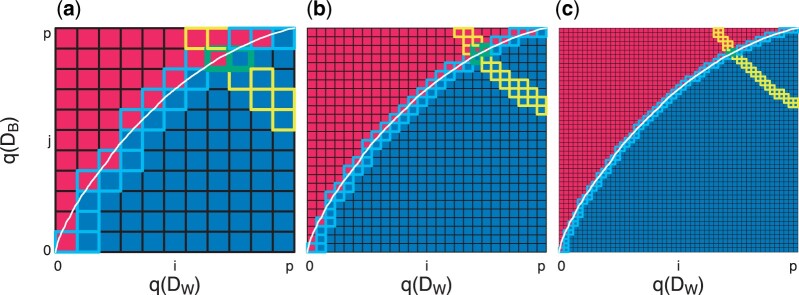
Fig. 4.
Graphical representation of two HPE algorithms to estimate 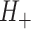 . We simulate observations from two Gaussian distributions, namely
. We simulate observations from two Gaussian distributions, namely 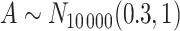 and
and 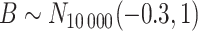 and calculate the quantiles
and calculate the quantiles 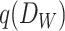 and
and 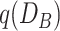 for each of the sets with (a)
for each of the sets with (a) 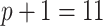 , (b)
, (b) 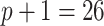 , and (c)
, and (c) 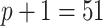 . The white curve represents the percent of elements in
. The white curve represents the percent of elements in 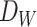 that are strictly less than each element in
that are strictly less than each element in 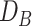 . The goal is to estimate the true
. The goal is to estimate the true 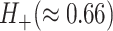 (area under the white curve) using one of two HPE algorithms. The brute force approach (HPE algorithm 1) uses Riemann integration to approximate the white curve by summing the area of the blue squares below the curve. The grid search approach (HPE algorithm 2) starts at the minimum of
(area under the white curve) using one of two HPE algorithms. The brute force approach (HPE algorithm 1) uses Riemann integration to approximate the white curve by summing the area of the blue squares below the curve. The grid search approach (HPE algorithm 2) starts at the minimum of 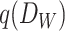 and
and 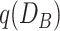 and moves along the red–blue border to approximate the white curve (path followed represents the squares with the light blue borders). The HPE contour
and moves along the red–blue border to approximate the white curve (path followed represents the squares with the light blue borders). The HPE contour 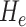 (or estimate of
(or estimate of 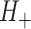 )
) 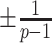 is given by yellow-bordered squares. In other words, every pair
is given by yellow-bordered squares. In other words, every pair 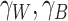 such that
such that 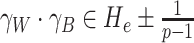 , the interval guaranteed to contain
, the interval guaranteed to contain  . The intersection of this yellow contour (
. The intersection of this yellow contour (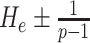 ) and blue contour (grids visited by HPE algorithm 2) are the green-bordered squares, which represents the numerical estimate for
) and blue contour (grids visited by HPE algorithm 2) are the green-bordered squares, which represents the numerical estimate for 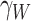 and
and 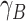 .
.
3.3.2. HPE algorithm 1: 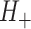 (brute force)
(brute force)
Algorithm 1 numerically approximates 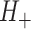 with Riemann integration. Specifically, using a double
with Riemann integration. Specifically, using a double 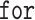 loop with
loop with 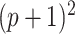 comparisons, this brute force approach sums the area of the squares that are blue in Figure 4, resulting in an algorithm on the order of
comparisons, this brute force approach sums the area of the squares that are blue in Figure 4, resulting in an algorithm on the order of 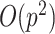 . The path taken by our implementation of this algorithm is given by the squares with light blue borders, and the contour corresponding to the true
. The path taken by our implementation of this algorithm is given by the squares with light blue borders, and the contour corresponding to the true 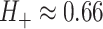 is (approximately) represented by the squares with yellow outlines (Figure 4).
is (approximately) represented by the squares with yellow outlines (Figure 4).
Algorithm 1
(brute force)
1.
2. for
do
3. for
do
4.
5. end for
6. end for
7.
3.3.3 HPE algorithm 2: 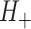 (grid search)
(grid search)
An alternative and faster approach (on the order of 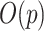 comparisons) is to sketch the surface (blue–red border) that defines
comparisons) is to sketch the surface (blue–red border) that defines 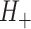 . By starting at the minimum of
. By starting at the minimum of 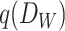 and
and 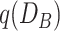 , Algorithm 2 moves along the blue–red border that defines
, Algorithm 2 moves along the blue–red border that defines 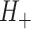 using grid search to determine whether to increase
using grid search to determine whether to increase 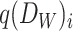 or
or 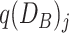 with each iteration.
with each iteration.
Algorithm 2
(grid search)
1.
2.
3.
4.
5. while
and
do
6.
7. if
then
8.
9. else
10.
11.
12. end if
13. end while
14.
3.4. Convergence of HPE algorithms 1 and 2
Next, we provide a numerical bound for the accuracy of 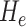 for both the brute force and grid search approaches. For each
for both the brute force and grid search approaches. For each 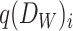 ,
, 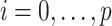 , HPE algorithm 2 (and intrinsically algorithm 1) ascertains one of the following:
, HPE algorithm 2 (and intrinsically algorithm 1) ascertains one of the following:
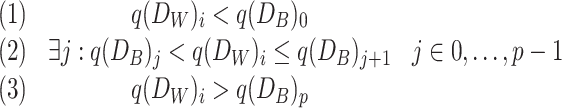 |
(3.6) |
In (1), we have confirmed that 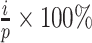 of
of 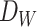 are less than
are less than 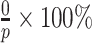 of
of 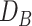 and the
and the 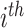 addition to the numerical integral will be zero, that is,
addition to the numerical integral will be zero, that is, 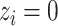 in HPE algorithm 2. In (3), we see that
in HPE algorithm 2. In (3), we see that 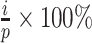 of
of 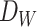 are greater than
are greater than 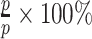 of
of 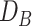 and
and 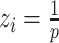 in HPE algorithm 2. In (2), we know that
in HPE algorithm 2. In (2), we know that 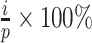 of
of  are bigger than
are bigger than 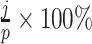 of
of  , but not greater than
, but not greater than 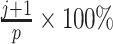 of
of  , and
, and 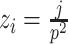 in HPE algorithm 2. Recall that
in HPE algorithm 2. Recall that  is estimated as the sum over each
is estimated as the sum over each 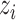 where
where 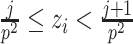 . We denote
. We denote 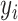 as the true value of this sum for column
as the true value of this sum for column 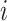 , that is, for some
, that is, for some 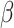 ,
, 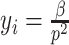 where
where 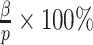 of
of 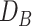 are less than or equal to
are less than or equal to 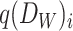 and
and 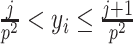 . Thus, for (2), we have the condition
. Thus, for (2), we have the condition 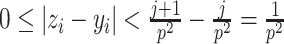 , in other words, the addition to
, in other words, the addition to  from the
from the 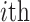 column will differs from the true value (
column will differs from the true value (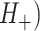 by at most
by at most 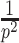 . Thus, for all
. Thus, for all 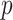 :
:
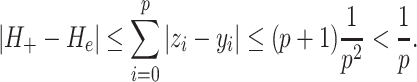 |
(3.7) |
That is, by taking 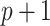 percentiles of
percentiles of 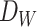 and
and 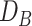 , our estimate for HPE algorithm 2 will be within
, our estimate for HPE algorithm 2 will be within  of
of 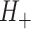 . This follows when one considers HPE algorithms 1 and 2 are approximations of the paired true rank comparisons (white curve in Figure 4) using Riemann integration with increasing accuracy as a function of
. This follows when one considers HPE algorithms 1 and 2 are approximations of the paired true rank comparisons (white curve in Figure 4) using Riemann integration with increasing accuracy as a function of 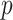 . An additional argument for the convergence of these algorithms is presented in Note 2 of the Supplementary material available at Biostatistics online.
. An additional argument for the convergence of these algorithms is presented in Note 2 of the Supplementary material available at Biostatistics online.
3.4.1. Estimating 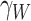 and
and 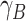
To estimate 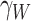 and
and 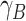 , we use the intersection of the yellow contour (
, we use the intersection of the yellow contour (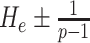 ) and blue contour (path visited by HPE algorithm 2), which are the green-bordered squares in Figure 4. As our approach guarantees that
) and blue contour (path visited by HPE algorithm 2), which are the green-bordered squares in Figure 4. As our approach guarantees that 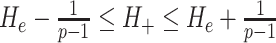 , we can identify every pair
, we can identify every pair 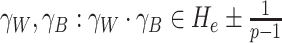 as potential values of
as potential values of 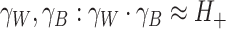 . Our algorithm also identifies the values of
. Our algorithm also identifies the values of 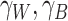 that are true for the observed data (all areas below the white line in Figure 4) or those which have been verified as false (all area above the white line in Figure 4). Our estimate for
that are true for the observed data (all areas below the white line in Figure 4) or those which have been verified as false (all area above the white line in Figure 4). Our estimate for 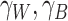 is then the intersection of
is then the intersection of  that are empirically verified in HPE algorithm 2 such that
that are empirically verified in HPE algorithm 2 such that 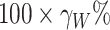 of
of 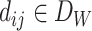 is strictly greater than
is strictly greater than 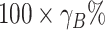 of
of 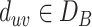 (blue squares in Figure 4) and
(blue squares in Figure 4) and 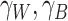 which satisfy
which satisfy 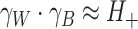 (yellow squares in Figure 4).
(yellow squares in Figure 4).
3.5. Bootstrap algorithm to estimate 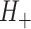
As noted in Section 3.3, while the computational speed of the HPE algorithms for identifying ways to approximate 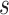 is significantly faster than calculating the full
is significantly faster than calculating the full 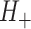 (Figures 3(a) and (b)), both of these algorithms assume the dissimilarity matrix
(Figures 3(a) and (b)), both of these algorithms assume the dissimilarity matrix 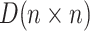 has been precomputed and that an adjacency matrix
has been precomputed and that an adjacency matrix 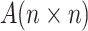 must be calculated. Unfortunately, the
must be calculated. Unfortunately, the 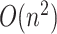 computational requirements for full pairwise dissimilarity calculation to quickly becomes infeasible (Figure 3, Table S1 of the Supplementary material available at Biostatistics online).
computational requirements for full pairwise dissimilarity calculation to quickly becomes infeasible (Figure 3, Table S1 of the Supplementary material available at Biostatistics online).
To address the limitation of computing and storing all pairwise dissimilarities, we implemented a bootstrap approximation of 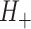 (HPB or
(HPB or 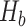 ) that samples with replacement from the original
) that samples with replacement from the original 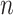 observations
observations 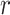 times (bootstraps) with a per-bootstrap sample size
times (bootstraps) with a per-bootstrap sample size 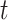 . We sample proportionally according to the vector
. We sample proportionally according to the vector 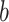 as described in Section 2.4.1, that is, each of the
as described in Section 2.4.1, that is, each of the 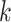 clusters is randomly sampled
clusters is randomly sampled 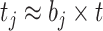 times (where
times (where 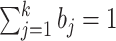 ) such that
) such that 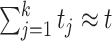 . For each of
. For each of 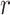 iterations, the
iterations, the 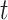 sampled observations are used to generate dissimilarity and adjacency matrices which are then used to calculate a point estimate of
sampled observations are used to generate dissimilarity and adjacency matrices which are then used to calculate a point estimate of 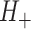 . The mean over these
. The mean over these 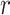 bootstraps is
bootstraps is 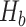 , the bootstrap
, the bootstrap 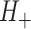 estimate. The bootstrap approach scales substantially better than full dissimilarity calculation (Figure 3c). In our simulations, bootstrap parameters
estimate. The bootstrap approach scales substantially better than full dissimilarity calculation (Figure 3c). In our simulations, bootstrap parameters 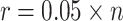 ,
, 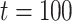 yield
yield 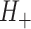 estimates within
estimates within 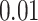 of that given by HPB with
of that given by HPB with 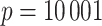 (
(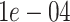 accuracy) with economical performance improvements. For example, we saw a reduction in computation time from
accuracy) with economical performance improvements. For example, we saw a reduction in computation time from 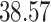 s with HPE to
s with HPE to 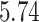 s with HPB at 3000 observations) (Figure S2 and Table S1 of the Supplementary material available at Biostatistics online).
s with HPB at 3000 observations) (Figure S2 and Table S1 of the Supplementary material available at Biostatistics online).
4. Application of 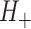 to the analysis of single-cell RNA-sequencing data
to the analysis of single-cell RNA-sequencing data
In this section, we demonstrate the use of 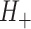 as an internal validity metric in the application of scRNA-seq data with predicted cluster labels. Also, we compare
as an internal validity metric in the application of scRNA-seq data with predicted cluster labels. Also, we compare 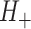 to other widely used validity measures, including both (i) external (i.e., comparing predicted labels to ground-truth clustering known a priori) and (ii) internal (derived from the data itself) measures (Halkidi and others, 2001; Theodoridis and Koutroumbas, 2008).
to other widely used validity measures, including both (i) external (i.e., comparing predicted labels to ground-truth clustering known a priori) and (ii) internal (derived from the data itself) measures (Halkidi and others, 2001; Theodoridis and Koutroumbas, 2008).
4.1. Motivation
Consider a scRNA-seq data set with 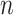 observations (or cells) each with
observations (or cells) each with 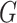 features (or genes). We introduced and formulated
features (or genes). We introduced and formulated 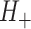 an internal validity metric to assess the fitness of a single dissimilarity measure
an internal validity metric to assess the fitness of a single dissimilarity measure 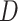 and label
and label 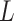 . Here, we introduce two scenarios where the goal is to compare the performance of either (i) two label sets
. Here, we introduce two scenarios where the goal is to compare the performance of either (i) two label sets 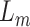 ,
, 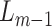 and a fixed dissimilarity
and a fixed dissimilarity 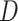 or (ii) two dissimilarity measures
or (ii) two dissimilarity measures 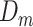 ,
, 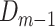 with a fixed label
with a fixed label 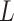 . In the first scenario,
. In the first scenario, 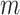 and
and 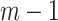 could represent two iterations in a single clustering algorithm or they could be labels from two separate clustering algorithms. As
could represent two iterations in a single clustering algorithm or they could be labels from two separate clustering algorithms. As 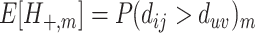 (and similarly with
(and similarly with 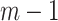 ), the condition
), the condition 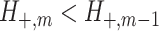 can be rewritten as follows
can be rewritten as follows
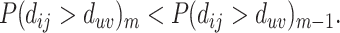 |
(4.8) |
As 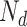 is fixed in the following subsections, we offer interpretations of the condition in (4.8) for fixed
is fixed in the following subsections, we offer interpretations of the condition in (4.8) for fixed 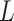 with varying
with varying 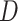 and fixed
and fixed 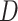 with varying
with varying 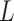 .
.
4.2. Data
We used the 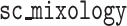 (Tian and others, 2019) scRNA-seq data set, which provides an experimentally derived “gold standard” true cell type identity (label) for each cell (https://github.com/LuyiTian/sc_mixology/).
(Tian and others, 2019) scRNA-seq data set, which provides an experimentally derived “gold standard” true cell type identity (label) for each cell (https://github.com/LuyiTian/sc_mixology/).
The UMI counts and cellular identities were obtained for 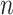 = 902 cells comprised of three cell lines (H1975, H2228, and HCC827). The cell lines are used as the true cell type labels. Raw counts were
= 902 cells comprised of three cell lines (H1975, H2228, and HCC827). The cell lines are used as the true cell type labels. Raw counts were 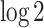 -normalized with a pseudocount of 1, and per-gene variance was calculated using
-normalized with a pseudocount of 1, and per-gene variance was calculated using 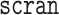 (Lun and others, 2016). For comparison of distances, five dissimilarities (Euclidean, Maximum Manhattan, Canberra, and Binary) were calculated using
(Lun and others, 2016). For comparison of distances, five dissimilarities (Euclidean, Maximum Manhattan, Canberra, and Binary) were calculated using 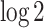 -normalized counts and the top 1000 most variant genes. For comparison of induced labels, dendrograms were induced directly from Euclidean distances using four hierarchical clustering methods (Ward’s method, single linkage method, complete linkage method, and unweighted pair group method with arithmetic mean). Cluster labels were induced by cutting each dendrogram at the true value of
-normalized counts and the top 1000 most variant genes. For comparison of induced labels, dendrograms were induced directly from Euclidean distances using four hierarchical clustering methods (Ward’s method, single linkage method, complete linkage method, and unweighted pair group method with arithmetic mean). Cluster labels were induced by cutting each dendrogram at the true value of 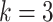 .
.
4.3. Fixed 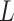 varying
varying 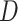
If a user were generating an analysis pipeline, prior to deployment, it may be insightful to compare the performance of several dissimilarity measures on a previously validated label–data set pair (Baker and others, 2021). In this case, fixing 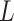 will imply that
will imply that 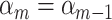 , then from (4.8), we know that
, then from (4.8), we know that 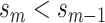 for two dissimilarity matrices
for two dissimilarity matrices 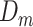 and
and 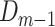 . That is, the number of within-cluster distances greater than between-cluster distances will have strictly decreased. To illustrate this capacity, we used
. That is, the number of within-cluster distances greater than between-cluster distances will have strictly decreased. To illustrate this capacity, we used 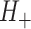 to compare the fitness of five dissimilarity methods induced from the same data and using the same “gold standard” true cell identities. These values may be found in Table S2 of the Supplementary material available at Biostatistics online. Further valuation of dissimilarities in this setting is outside the scope of this work, and we refer the reader to (Baker and others, 2021) for an exploration of this topic.
to compare the fitness of five dissimilarity methods induced from the same data and using the same “gold standard” true cell identities. These values may be found in Table S2 of the Supplementary material available at Biostatistics online. Further valuation of dissimilarities in this setting is outside the scope of this work, and we refer the reader to (Baker and others, 2021) for an exploration of this topic.
4.4. Fixed 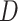 varying
varying 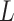
Similarly, 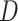 can be fixed (e.g., Euclidean distance) with the goal to compare the fitness of one generated label set
can be fixed (e.g., Euclidean distance) with the goal to compare the fitness of one generated label set 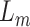 (i.e., iteration
(i.e., iteration 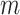 of a clustering algorithm) to a previous label
of a clustering algorithm) to a previous label 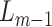 . In this scenario, Equation (4.8) does not imply an explicit relation for
. In this scenario, Equation (4.8) does not imply an explicit relation for 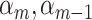 ; however, the discordance has still decreased. To demonstrate the use of
; however, the discordance has still decreased. To demonstrate the use of 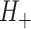 as a cluster fitness metric, we induce labels using four hierarchical clustering methods (Ward’s method, single linkage method, complete linkage method, unweighted pair group method with arithmetic mean) (Figures 5(a–d)), and compare against well-known both external and internal validity metrics (Figure 5(e) and (f)).
as a cluster fitness metric, we induce labels using four hierarchical clustering methods (Ward’s method, single linkage method, complete linkage method, unweighted pair group method with arithmetic mean) (Figures 5(a–d)), and compare against well-known both external and internal validity metrics (Figure 5(e) and (f)).
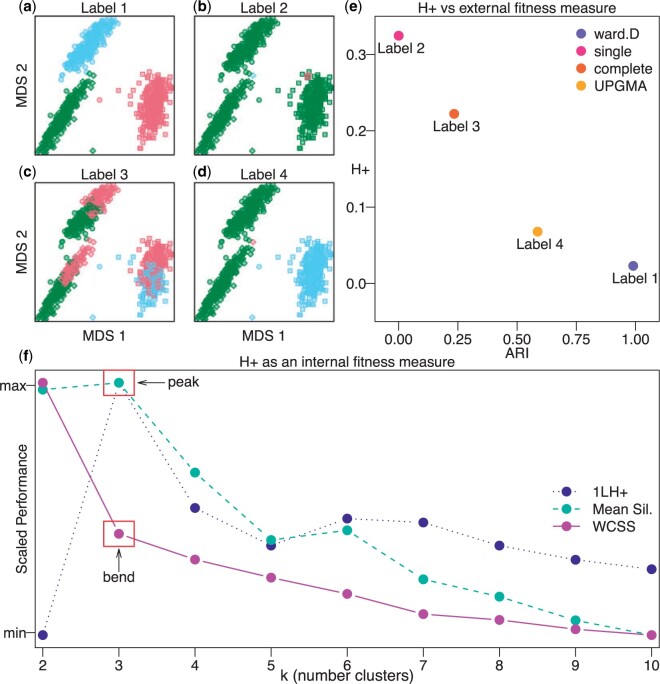
Fig. 5.
The 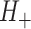 metric is an internal validity measure for assessing the performance of induced cluster labels. Multidimensional scaling (MDS) plots with shapes representing true cell type labels from the
metric is an internal validity measure for assessing the performance of induced cluster labels. Multidimensional scaling (MDS) plots with shapes representing true cell type labels from the  scRNA-seq data set and colors representing induced (or predicted) cluster labels from four hierarchical clustering methods implemented in the hclust() function in the base R stats package including (a) Ward’s method, (b) single linkage method, (c) complete linkage method, and (d) unweighted pair group method with arithmetic mean (UPGMA). (e) Scatter plot of
scRNA-seq data set and colors representing induced (or predicted) cluster labels from four hierarchical clustering methods implemented in the hclust() function in the base R stats package including (a) Ward’s method, (b) single linkage method, (c) complete linkage method, and (d) unweighted pair group method with arithmetic mean (UPGMA). (e) Scatter plot of 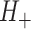 (an internal validity metric) compared to Adjusted Rand Index (ARI) (an external validity metric) demonstrating shared information between the two metrics, which
(an internal validity metric) compared to Adjusted Rand Index (ARI) (an external validity metric) demonstrating shared information between the two metrics, which 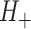 (calculated with the HPE algorithm 1 using
(calculated with the HPE algorithm 1 using 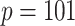 ) recovers without the need of an externally labeled set of observations. (f) A performance plot with three internal validity metrics (
) recovers without the need of an externally labeled set of observations. (f) A performance plot with three internal validity metrics (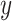 -axis scaled between 0 and 1): (i)
-axis scaled between 0 and 1): (i) 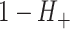 (for ease of comparison) calculated from labels induced using with
(for ease of comparison) calculated from labels induced using with 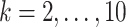 (
(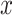 -axis), (ii) mean silhouette score, and (iii) within-clusters sums of square (WCSS). The “peak” of the
-axis), (ii) mean silhouette score, and (iii) within-clusters sums of square (WCSS). The “peak” of the 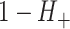 metric at the correct
metric at the correct 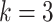 indicates that
indicates that 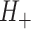 accurately identifies the most accurate label in a comparable fashion to established internal fitness measure, namely a “peak” at the mean silhouette score and a “bend” in the WCSS curve.
accurately identifies the most accurate label in a comparable fashion to established internal fitness measure, namely a “peak” at the mean silhouette score and a “bend” in the WCSS curve.
First, we compare 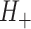 as an internal validity metric to an external validity metric, namely the Adjusted Rand Index (ARI), which assesses the performance of the induced cluster labels using a gold-standard set of cell type labels in the
as an internal validity metric to an external validity metric, namely the Adjusted Rand Index (ARI), which assesses the performance of the induced cluster labels using a gold-standard set of cell type labels in the  (Tian and others, 2019) scRNA-seq data set. Here, the induced labels with better (higher) ARI also yield better (less)
(Tian and others, 2019) scRNA-seq data set. Here, the induced labels with better (higher) ARI also yield better (less) 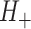 discordance (Figure 5(e)). In this sense,
discordance (Figure 5(e)). In this sense, 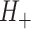 (an internal validity measure without the dependency of a gold-standard set of labels) captures similar information as ARI (an external validity measure that depends on the use of a gold-standard set of labels).
(an internal validity measure without the dependency of a gold-standard set of labels) captures similar information as ARI (an external validity measure that depends on the use of a gold-standard set of labels).
Next, we compare 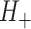 as an internal validity measure to other internal validity measures. Specifically, we induce labels using partition around medoids (
as an internal validity measure to other internal validity measures. Specifically, we induce labels using partition around medoids (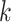 -medoids clustering) for values of
-medoids clustering) for values of 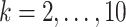 . For each label and
. For each label and 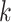 , the mean Silhouette score (Rousseeuw, 1987) and
, the mean Silhouette score (Rousseeuw, 1987) and 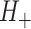 were calculated. We found that
were calculated. We found that 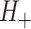 accurately identifies the correct
accurately identifies the correct 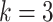 for induced labels when compared to an internal validity metric (i.e., how well the data are explained by a single set of labels) using either the within-cluster sum of square “bend" (or “elbow") criterion or the mean Silhouette score (Figure 5(f)).
for induced labels when compared to an internal validity metric (i.e., how well the data are explained by a single set of labels) using either the within-cluster sum of square “bend" (or “elbow") criterion or the mean Silhouette score (Figure 5(f)).
5. Discussion
Quantifying how well a generated clustering fits the observed data is an essential problem in the statistical and computational sciences. Most methods for measuring cluster fitness are explicitly valued on the dissimilarity induced from the data. While appealing in their simplicity and interpretation, these approaches are potentially more susceptible to numerical bias between observations or types of dissimilarity measures. Discordance metrics, such as  and
and 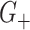 circumvent this issue by assessing label-dissimilarity fitness implicitly on the dissimilarity values. In this work, we show
circumvent this issue by assessing label-dissimilarity fitness implicitly on the dissimilarity values. In this work, we show 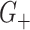 is an estimator for the probability that a within-cluster dissimilarity is strictly greater than a between-cluster dissimilarity,
is an estimator for the probability that a within-cluster dissimilarity is strictly greater than a between-cluster dissimilarity, 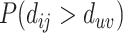 . However, we also show that
. However, we also show that 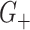 varies as a function of the proportion of total distances that are within-cluster distances (
varies as a function of the proportion of total distances that are within-cluster distances (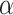 ) and thereby also the group balance (
) and thereby also the group balance (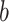 ) and number of groups
) and number of groups 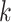 , which an undesirable property of the discordance metric.
, which an undesirable property of the discordance metric.
Here, we present 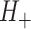 , a modification of
, a modification of 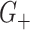 that retains the scale-agnostic discordance quantification while addressing problems with
that retains the scale-agnostic discordance quantification while addressing problems with 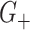 . Explicitly,
. Explicitly, 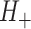 is an unbiased estimator for
is an unbiased estimator for 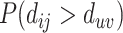 . This benefit is most easily seen in the manner that
. This benefit is most easily seen in the manner that 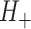 will be unaffected by the value of
will be unaffected by the value of 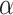 (the portion of distance pairs that are within the same cluster), a formulation that permits the user to assess fitness for an arbitrary value of
(the portion of distance pairs that are within the same cluster), a formulation that permits the user to assess fitness for an arbitrary value of 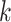 . We discuss the theoretical properties of this estimator, provide two simple algorithms for implementation, and ascertain a strict numerical bound for their accuracy as a function of a simple user-defined parameter. We also introduce an estimator of
. We discuss the theoretical properties of this estimator, provide two simple algorithms for implementation, and ascertain a strict numerical bound for their accuracy as a function of a simple user-defined parameter. We also introduce an estimator of 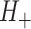 based on bootstrap resampling from the original observations that does not require the full dissimilarity and adjacency matrices to be calculated.
based on bootstrap resampling from the original observations that does not require the full dissimilarity and adjacency matrices to be calculated.
As 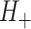 can be used to assess the fitness of multiple dissimilarities for a fixed label, or to compare multiple labels given a fixed dissimilarity, we envision that
can be used to assess the fitness of multiple dissimilarities for a fixed label, or to compare multiple labels given a fixed dissimilarity, we envision that 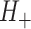 can be employed in both development and analysis settings. If the true observation identities (labels) are known for a data set,
can be employed in both development and analysis settings. If the true observation identities (labels) are known for a data set, 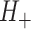 could be utilized in the development stages of analytical software and pipelines to ascertain the most advantageous dissimilarity measure for that specific problem. In the alternate setting, we envision that
could be utilized in the development stages of analytical software and pipelines to ascertain the most advantageous dissimilarity measure for that specific problem. In the alternate setting, we envision that 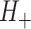 can be used to quantify performance in clustering/classification scenarios. If the true labels are unknown,
can be used to quantify performance in clustering/classification scenarios. If the true labels are unknown, 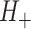 could be used to identify the clustering algorithm which produces the tightest clusters for a fixed dissimilarity measure. As a possible future direction, one could imagine directly minimizing discordance as the objective criteria within a clustering algorithm for optimizing iterative labels.
could be used to identify the clustering algorithm which produces the tightest clusters for a fixed dissimilarity measure. As a possible future direction, one could imagine directly minimizing discordance as the objective criteria within a clustering algorithm for optimizing iterative labels.
Due to its generalizability to the number of clusters 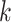 or the portion of within to within-cluster dissimilarity pairs
or the portion of within to within-cluster dissimilarity pairs  ,
, 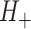 may be susceptible to degenerate cluster labels. For example, in the hierarchical clustering portion of Figure 5, Label 4 is less discordant than Label 3 in terms of both
may be susceptible to degenerate cluster labels. For example, in the hierarchical clustering portion of Figure 5, Label 4 is less discordant than Label 3 in terms of both 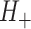 and ARI. Label 4 has simply merged two true clusters, and placed a single point in a third identity. While Label 4 is more accurate than Label 3, it achieves this by exploiting an opportunity to increase the proportion of same-cluster pairs, that is, maximizing
and ARI. Label 4 has simply merged two true clusters, and placed a single point in a third identity. While Label 4 is more accurate than Label 3, it achieves this by exploiting an opportunity to increase the proportion of same-cluster pairs, that is, maximizing 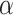 . One could also imagine a scenario where an algorithm simply makes
. One could also imagine a scenario where an algorithm simply makes 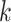 very large to minimize
very large to minimize 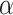 . In both scenarios, the labels generated are unlikely to be particularly informative for the user. We posit that some form of penalization for
. In both scenarios, the labels generated are unlikely to be particularly informative for the user. We posit that some form of penalization for 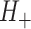 may help to alleviate these degenerate cases. For example, dividing
may help to alleviate these degenerate cases. For example, dividing 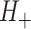 by
by 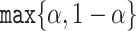 is a penalty for degeneracy in the case of putting many observations in the same label. Conversely, a division by
is a penalty for degeneracy in the case of putting many observations in the same label. Conversely, a division by 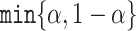 is a potential penalty for the other degeneracy of making many very small clusters.
is a potential penalty for the other degeneracy of making many very small clusters.
We also imagine that discordance measures can be synthesized with probabilistic dissimilarity frameworks such as locality-sensitive hashing (LSH) and coresets (Datar and others, 2004; Har-Peled and Mazumdar, 2004). For example, it could be useful if theoretical (probabilistic) guarantees of observation proximity from LSH algorithms could be extended to similar guarantees for the discordance of observations embedded in the hash space. It may also prove fruitful to explore discordance outside the scope of the clustering/classification problem, such as pseudotime (1-dimensional ordering) or “soft” (weighting membership estimation) clustering problems.
In practice, 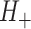 could provide an additional means to consider the termination of a clustering algorithm in a distance-agnostic manner. For example, the
could provide an additional means to consider the termination of a clustering algorithm in a distance-agnostic manner. For example, the 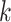 -means algorithm (Hartigan and Wong, 1979) and its variants seek to minimize a form of the total within-cluster dispersion (dissimilarity). These algorithms with similar objective functions are subject to changes in behavior as the distance function changes. The extent to which minimizing discordance such as
-means algorithm (Hartigan and Wong, 1979) and its variants seek to minimize a form of the total within-cluster dispersion (dissimilarity). These algorithms with similar objective functions are subject to changes in behavior as the distance function changes. The extent to which minimizing discordance such as 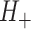 provides benefits regarding sensitivity to noise and magnitude of the distances is intriguing and outside the scope of this work.
provides benefits regarding sensitivity to noise and magnitude of the distances is intriguing and outside the scope of this work.
Supplementary Material
Acknowledgments
The authors would like to thank Kasper Hansen for the pre-print template and the Joint High Performance Computing Exchange (JHPCE) for providing computing resources.
Conflict of Interest: None declared.
Contributor Information
Nathan Dyjack, Department of Biostatistics, Johns Hopkins Bloomberg School of Public Health, 615 N Wolfe St, Baltimore, MD 21205, USA.
Daniel N Baker, Department of Computer Science, Johns Hopkins University, 3400 N Charles St, Baltimore, MD 21218, USA.
Vladimir Braverman, Department of Computer Science, Johns Hopkins University, 3400 N Charles St, Baltimore, MD 21218, USA.
Ben Langmead, Department of Computer Science, Johns Hopkins University, 3400 N Charles St, Baltimore, MD 21218, USA.
Stephanie C Hicks, Department of Biostatistics, Johns Hopkins Bloomberg School of Public Health, 615 N Wolfe St, Baltimore, MD 21205, USA.
Code and software availability
All analyses and simulations were conducted in the  programming language. Code for reproduction of all plots in this article is available at https://github.com/stephaniehicks/fasthpluspaper. Both HPE and HPB have been implemented in the
programming language. Code for reproduction of all plots in this article is available at https://github.com/stephaniehicks/fasthpluspaper. Both HPE and HPB have been implemented in the  package in
package in  available on CRAN at https://CRAN.R-project.org/package=fasthplus and for developmental versions on GitHub at https://github.com/ntdyjack/fasthplus.
available on CRAN at https://CRAN.R-project.org/package=fasthplus and for developmental versions on GitHub at https://github.com/ntdyjack/fasthplus.
Supplementary material
Supplementary material is available online at http://biostatistics.oxfordjournals.org.
Funding
The National Institutes of Health (R00HG009007 to N.D. and S.C.H.); the Chan Zuckerberg Initiative DAF, an advised fund of Silicon Valley Community Foundation (CZF2019-002443 to N.D. and S.C.H.); the National Institutes of Health (R35GM139602 to DNB and BL); NSF CAREER (1652257), ONR Award (N00014-18-1-2364), and the Lifelong Learning Machines program from DARPA/MTO to V.B., in part.
References
- Baker, D. N., Dyjack, N., Braverman, V., Hicks, S. C. and Langmead, B. (2021). Fast and memory-efficient scRNA-seq k-means clustering with various distances. In: Proceedings of the 12th ACM Conference on Bioinformatics, Computational Biology, and Health Informatics (BCB ’21). New York, NY, USA:Association for Computing Machinery,Article 24, pp. 1–8. 10.1145/3459930.3469523 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Datar, M., Immorlica, N., Indyk, P. and Mirrokni, V. S. (2004). Locality-Sensitive Hashing Scheme Based on p-Stable Distributions, SCG ’04. New York, NY, USA: Association for Computing Machinery. [Google Scholar]
- Desgraupes, B. (2018). clusterCrit: Clustering Indices. R package version 1.2.8. https://CRAN.R-project.org/package=clusterCrit [Google Scholar]
- Goodman, L. A. and Kruskal, W. H. (1979). Measures of Association for Cross Classifications. New York, NY: Springer New York. [Google Scholar]
- Halkidi, M., Batistakis, Y. and Vazirgiannis, M. (2001). On clustering validation techniques. Journal of Intelligent Information Systems 17, 107–145. [Google Scholar]
- Har-Peled, S. and Mazumdar, S. (2004). On coresets for k-means and k-median clustering. In: Proceedings of the Thirty-Sixth Annual ACM Symposium on Theory of Computing (STOC ’04). New York, NY, USA: Association for Computing Machinery, pp. 291–300. 10.1145/1007352.1007400 [DOI] [Google Scholar]
- Hartigan, J. A. and Wong, M. A. (1979). Algorithm as 136: a k-means clustering algorithm. Journal of the Royal Statistical Society. Series C (Applied Statistics) 28, 100–108. [Google Scholar]
- Jardine, N. and Sibson, R. (1968). The construction of hierarchic and non-hierarchic classifications. The Computer Journal 11, 177–184. [Google Scholar]
- Kendall, M. G. (1938). A new measure of rank correlation. Biometrika 30, 81–93. [Google Scholar]
- Leek, J. T. (2009). The tspair package for finding top scoring pair classifiers in R. Bioinformatics 25, 1203–1204. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lun, A. T. L., McCarthy, D. J. and Marioni, J. C. (2016). A step-by-step workflow for low-level analysis of single-cell RNA-seq data with bioconductor. F1000Research 5, 2122. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Magis, A. T. and Price, N. D. (2012). The top-scoring ‘N’ algorithm: a generalized relative expression classification method from small numbers of biomolecules. BMC Bioinformatics 13, 1–11. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rand, W. M. (1971). Objective criteria for the evaluation of clustering methods. Journal of the American Statistical Association 66, 846–850. [Google Scholar]
- Rohlf, F. J. (1974). Methods of comparing classifications. Annual Review of Ecology and Systematics 5, 101–113. [Google Scholar]
- Rousseeuw, P. J. (1987). Silhouettes: a graphical aid to the interpretation and validation of cluster analysis. Journal of Computational and Applied Mathematics 20, 53–65. [Google Scholar]
- Theodoridis, S. and Koutroumbas, K. (2008). Pattern Recognition, 4th edition. USA: Academic Press. [Google Scholar]
- Tian, L., Dong, X., Freytag, S., Lê Cao, K.-A., Su, S., Jalalabadi, A., Amann-Zalcenstein, D., Weber, T. S., Seidi, A., Jabbari, J. S.. and others. (2019). Benchmarking single cell RNA-sequencing analysis pipelines using mixture control experiments. Nature Methods 16, 479–487. [DOI] [PubMed] [Google Scholar]
- Williams, W. T. and Clifford, H. T. (1971). On the comparison of two classifications of the same set of elements. Taxon 20, 519–522. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.