A Phylogenetic Framework to Simulate Synthetic Interspecies RNA-Seq Data

Abstract

Interspecies RNA-Seq datasets are increasingly common, and have the potential to answer new questions about the evolution of gene expression. Single-species differential expression analysis is now a well-studied problem that benefits from sound statistical methods. Extensive reviews on biological or synthetic datasets have provided the community with a clear picture on the relative performances of the available methods in various settings. However, synthetic dataset simulation tools are still missing in the interspecies gene expression context. In this work, we develop and implement a new simulation framework. This tool builds on both the RNA-Seq and the phylogenetic comparative methods literatures to generate realistic count datasets, while taking into account the phylogenetic relationships between the samples. We illustrate the usefulness of this new framework through a targeted simulation study, that reproduces the features of a recently published dataset, containing gene expression data in adult eye tissue across blind and sighted freshwater crayfish species. Using our simulated datasets, we perform a fair comparison of several approaches used for differential expression analysis. This benchmark reveals some of the strengths and weaknesses of both the classical and phylogenetic approaches for interspecies differential expression analysis, and allows for a reanalysis of the crayfish dataset. The tool has been integrated in the R package compcodeR, freely available on Bioconductor.

Introduction

The study and analysis of gene expression differences across species is a long-standing problem (King and Wilson 1975). The development of microarray technologies led to the gathering of the first large scale across species gene expression datasets, that allowed for the formulation and study of various hypotheses regarding the link between gene expression and evolution (Enard 2002; Khaitovich et al. 2004; Gilad et al. 2006; Whitehead and Crawford 2006). RNA-Sequencing technologies have changed the way to measure gene expression (Wang et al. 2009), making comparisons across several species easier, even for species with no reference genome available (Perry et al. 2012; Romero et al. 2012). Interspecies gene expression data are increasingly common, with well-curated resources, such as the Bgee database (Bastian et al. 2021), that make it available to the community.

Since changes in expression may underlie complex phenotypes, across species gene expression datasets can be used to test a wide range of evolutionary scenarios (Romero et al. 2012; Dunn et al. 2013). Tested hypotheses include, for instance, expression divergence (Gu 2004); the strength of expression conservation (Gu et al. 2019); the coevolution of gene expression (Cope et al. 2020); test of the orthology conjecture (Rogozin et al. 2014; Dunn et al. 2018); the detection of “phylogenetic signal” (Musser and Wagner 2015); equality of within-species variance (Catalán et al. 2019); constant stabilizing selection, loss through drift, parallel, or divergent selection (Stern and Crandall 2018a, 2018b); or the detection of duplication-specific effects in expression evolution (Fukushima and Pollock 2020).

In this work, we focus only on the detection of change in gene expression levels across species, in a specific lineage or between different groups of species. This problem can be formalized as an interspecies differential expression analysis, and has been studied in various groups of organisms (Cáceres et al. 2003; Zheng-Bradley et al. 2010; Blake et al. 2018; Stern and Crandall 2018b; Chen et al. 2019; Alam et al. 2020; Blake et al. 2020). For instance, difference in gene expression levels was found between mammalian lineages and birds (Brawand et al. 2011), across nonmodel primates species (Perry et al. 2012), between Drosophila species (Torres-Oliva et al. 2016) or Heliconius butterflies (Catalán et al. 2019). Note that the biological interpretation of changes in the level of expression of a gene across species is not easy (Romero et al. 2012). Shifts in gene expression across species could be molecular signatures of ecological adaptation, associated with a directional selection scenario, or a relaxation of evolutionary constraints.

From a bioinformatic point of view, the comparison of RNA-Seq samples between multiple species requires, first, the detection of orthologous relationships between genes (Tatusov 1997; Tekaia 2016), second, the consideration of differences in genome mappability (Zhu et al. 2014) and, third, the adaptation of alignment and quantification pipelines (LoVerso and Cui 2015; Chung et al. 2021). Multi-species alignments techniques have also been developed (Bradley et al. 2009; Brawand et al. 2011). In this work, we name orthologous genes (OG), or simply genes, the set of genes having orthologous relationship across species. Once the orthologous gene expression matrix has been created, the level of expression can be transformed into a discrete variable to detect the presence vs. absence of gene expression (Bastian et al. 2021). Other approaches perform separate differential expression for each species (Dunn et al. 2013; Kristiansson et al. 2013) or focus on pairwise comparisons only (Zhou et al. 2019; Chung et al. 2021). However, direct comparisons of expression between species can be complicated by batch effects (Gilad and Mizrahi-Man 2015), or potential confounding factors (Roux et al. 2015; Cope et al. 2020), and comparative gene expression studies should be carefully designed (Romero et al. 2012; Dunn et al. 2013; Chung et al. 2021).

In the present study, we assume that the alignment has already been performed, and we focus our attention on genes having a one-to-one relationship across several species (more than two species). We consider the level of expression of genes as a quantitative trait evolving across several species, and we detect genes with a shift in the level of expression across species as performed in for example, Brawand et al. (2011), Perry et al. (2012), Torres-Oliva et al. (2016), and Stern and Crandall (2018a). The specificities of interspecies RNA-Seq data are multifold. RNA-Seq data are counts, usually measured on a low number of samples. In addition, several technical biases affect the measured level of expression of a given gene in a given sample, either gene-specific (such as heterogeneity of gene length and GC content across genes and samples), or sample-specific (such as heterogeneity in library size across samples). Finally, since the level of expression of a gene is measured across several species, the phylogenetic relationships between species induce some correlations in the data. While, ideally, all these specificities should be taken into account in the statistical analysis, to our knowledge, there exist no model that includes all these constraints in its hypotheses. The user has the choice between methods specifically designed for analyzing gene expression data such as limma, DESeq2, or edgeR (Smyth 2004; Smyth et al. 2005; Anders and Huber 2010; Robinson and Oshlack 2010; Love et al. 2014); or phylogenetic comparative methods (PCMs) such as phylolm (Ho and Ané 2014a), that implement a phylogenetic regression or ANOVA (Martins and Hansen 1997; Rohlfs and Nielsen 2015), designed for analyzing quantitative traits across species. Although PCMs have already been described for gene expression analysis (Gu 2004; Gu and Su 2007; Bedford and Hartl 2009; Rohlfs et al. 2014; Gu et al. 2019), and applied in particular for differential expression detection (Brawand et al. 2011; Stern and Crandall 2018a; Catalán et al. 2019; Chen et al. 2019), these methods do not explicitly account for count data, which can lead to biased results.

To benchmark these methods, a common strategy is to simulate RNA-Seq count data. There are several well-established tools to simulate RNA-Seq count data in the classical, intraspecies case (Dillies et al. 2013; Soneson and Delorenzi 2013; Soneson 2014; Frazee et al. 2015), which allowed for the benchmark of many differential expression analysis models (Anders and Huber 2010; Robinson and Oshlack 2010; Law et al. 2014). Although some methodological questions remain open (Van den Berge et al. 2019), these extensive simulation studies helped setting good practices in terms of model choice or normalization methods in various intraspecies RNA-Seq settings. To our knowledge, there exists no extension of these frameworks to the interspecies setting. Simulation of gene expression across species has been performed using linear models and Gaussian variables (Rohlfs et al. 2014; Rohlfs and Nielsen 2015; Gu et al. 2019), but without taking into account the specificity of RNA-Seq count data and without focusing on the detection of shifts across species. In this work, we propose a framework to simulate RNA-Seq data across species. We use this framework to compare different strategies to detect genes with a expression level shift across multiple species, and draw recommendations for interspecies gene expression comparison.

New Approach

Simulation Framework

We designed and implemented a new simulation framework, that we used to benchmark and calibrate differential analysis methods on synthetic datasets that exhibit features specific to interspecies RNA-Seq dataset. Our approach is based on a phylogenetic Poisson log-normal (pPLN) model, that relies on two layers. First, latent variables are simulated using a Brownian motion (BM) or an Ornstein-Uhlenbeck (OU) stochastic process on the phylogenetic tree, using well-studied tools from the PCM literature. This layer can account for correlations induced by the phylogenetic relationships, including intraspecies-independent variations. Second, the $\log$ values of these latent variables are used to define the parameter of a Poisson distribution, from which the final simulated count values are drawn. Built on top of tools tailored for RNA-Seq, the framework can simulate realistic count data that reproduce some of the important characteristics of a given empirical dataset, with genes of possibly varying lengths between samples. The simulation can include genes that are differentially expressed in different a priori specified groups of species. (See Section “A framework to simulate interspecies RNA-seq datasets” in the Materials and Methods for more details on the simulation framework.)

Impact of Tree Group Design

Contrary to classical differential analysis, where all the samples are independent, we showed that the specific group design on the tree had a strong influence on the signal present in the data. The phylogeny indeed acts as a confounding factor, as species within a clade tend to look alike while differing from species in other clades, just because of the tree structure. The differential effect of a group that spans over a single clade was hence more difficult to distinguish from a simple evolutionary random drift than the differential effect of a group with species present in various clades (see, e.g., the “block” vs. “alt” designs in fig. 1). To help practitioners having to design new interspecies RNA-Seq studies, we propose a new “differential analysis phylogenetic asymptotic effective sample size” ($\text{dapaESS}$) score. This score takes into account the tree and the group design at the tips of the tree only, so that it can be computed prior to any data collection. Using simulations, we showed that this score was a good predictor of the performance of differential analysis methods in a specific dataset. (See Section “Differential Analysis Phylogenetic Asymptotic Effective Sample Size” in the Materials and Methods for a complete derivation of this effective sample size.)

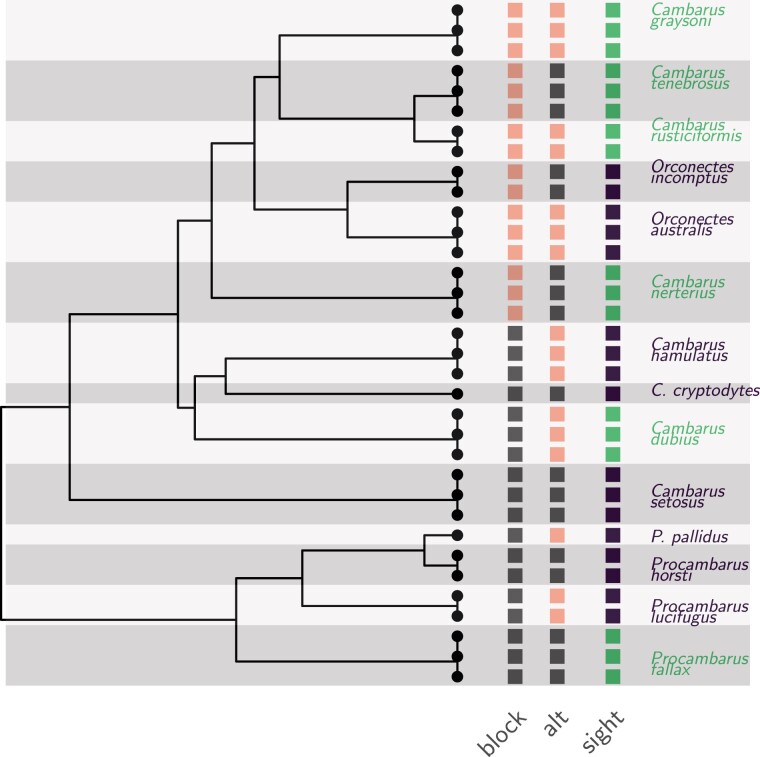
Fig. 1.

Time-calibrated phylogenetic tree of eight blind (dark purple) and six sighted (light green) crayfish species (Stern et al. 2017). The root was dated to $65$ million years before the present (Stern et al. 2017), but the tree was rescaled to unit height for the analyses. The “sight” design (dark purple and light green squares) matches with the biological vision status of the species studied (Stern and Crandall 2018a). The “block” and “alt” designs (light pink and gray squares) are artificial extreme scenarios representing, respectively, a situation where the design is almost un-distinguishable from the phylogeny-induced grouping (block), and a situation where groups are distributed evenly on the tree to maximize the contrast between sister species (alt).

Reanalysis of the Crayfish Dataset

We applied our simulation framework with parameters empirically drawn from a recent study on the evolution of gene expression underlying vision loss in cave animals (Stern and Crandall 2018a). The synthetic datasets had characteristics similar to the original data, while allowing us to control the actual simulation parameters, and hence assess the performance of various differential expression analysis tools. We tested some of the most popular methods, along with several normalization and transformation strategies, both issued from the RNA-Seq or the PCM literature. (See supplementary section A, Supplementary Material online for a survey of all the methods used.) Enlightened by this focused benchmark, we proposed a reanalysis of the original dataset, resulting in a list of possibly differentially expressed genes that is much shorter than previously published one, and that we believe is more robust.

Results

Simulation Studies

Stern and Crandall (2018a) collected an interspecies RNA-Seq dataset to study the molecular mechanisms involved in vision loss in the North American family Cambaridae of crayfish species. We exploited our new simulation framework to generate realistic synthetic datasets following a base scenario, that was set to mimic the features of the crayfish dataset, using the estimated crayfish tree with the observed vision status design (“sight” design, see fig. 1), and matching the empirical counts and gene lengths moments. From this base scenario, we varied several parameters in order to study the impact of evolutionary dependence on the simulated data. In all simulated datasets, we could control exactly which genes were generated as differentially expressed, and which genes had a constant expression across clades (see section “A framework to simulate interspecies RNA-seq datasets” in the Materials and Methods). This allowed us to compare the list of truly differentially expressed genes with the list of candidate genes found by the various statistical methods tested. We tested the performance of the following differential expression analysis methods: DESeq2 (Love et al. 2014); limma (Ritchie et al. 2015), or limma cor (Smyth et al. 2005); and phylolm (Ho and Ané 2014a) with BM or OU processes. See Materials and Methods Section “Simulations and Empirical Studies” and supplementary section A, Supplementary Material online for a detailed presentation of the parameters and methods used. We did not aim at a comprehensive comparison of all the methods available, and chose these tools as representing the three main approaches used in an interspecies context, and available in R. Using the framework implemented in compcodeR, other methods could however easily be added to the comparison.

PLN and NB Simulation Frameworks Produce Similar Datasets

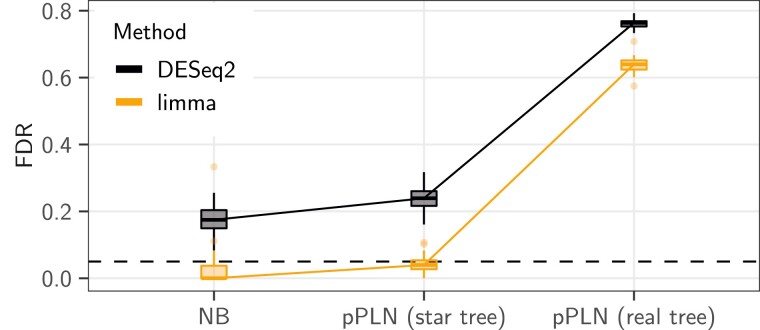
To check that our new pPLN framework produced datasets with properties similar to the well known NB framework as implemented in compcodeR (Soneson 2014), we replaced the crayfish tree with a star-tree, that mimics the NB situation where all species and replicates are independent. When parametrized to produce the same moments, the pPLN framework on a star tree produced datasets that were similar in difficulty to the classical NB framework (fig. 2, first two columns). While limma controlled the FDR to the nominal rate, DESeq2 failed to control the FDR. However, both methods had a better TPR under the pPLN model (see supplementary fig. S1, Supplementary Material online), and DESeq2 had the best MCC score under the pPLN on a star tree. As showed by the countsimQC (Soneson and Robinson 2018) analysis, the datasets simulated with the pPLN and the NB frameworks had similar features, and were comparable to the original empirical dataset (see supplementary section D, Supplementary Material online).

Fig. 2.

The base scenario [pPLN (real tree), right] had empirical moments drawn from (Stern and Crandall 2018a), with an effect size of $3$, a BM model of evolution with added intraspecies variation accounting for $20\text{\%}$ of the total variance, on the maximum likelihood tree, with the observed “sight” groups (see fig. 1). It is compared with a pPLN model with the same parameters, but in a case where all samples were independent [pPLN (star tree), middle], and to a NB model with the same moments and effect size (NB, left). The DESeq2 (black) and limma (light orange) inference methods were applied to each scenario. The black dashed line represents the nominal rate of $5\text{\%}$ used to call positives. For limma, the counts were normalized using ${\log }_2(\text{TPM})$ values. Boxplots are based on $50$ replicates.

Phylogenetic Data Requires Correlation Modeling

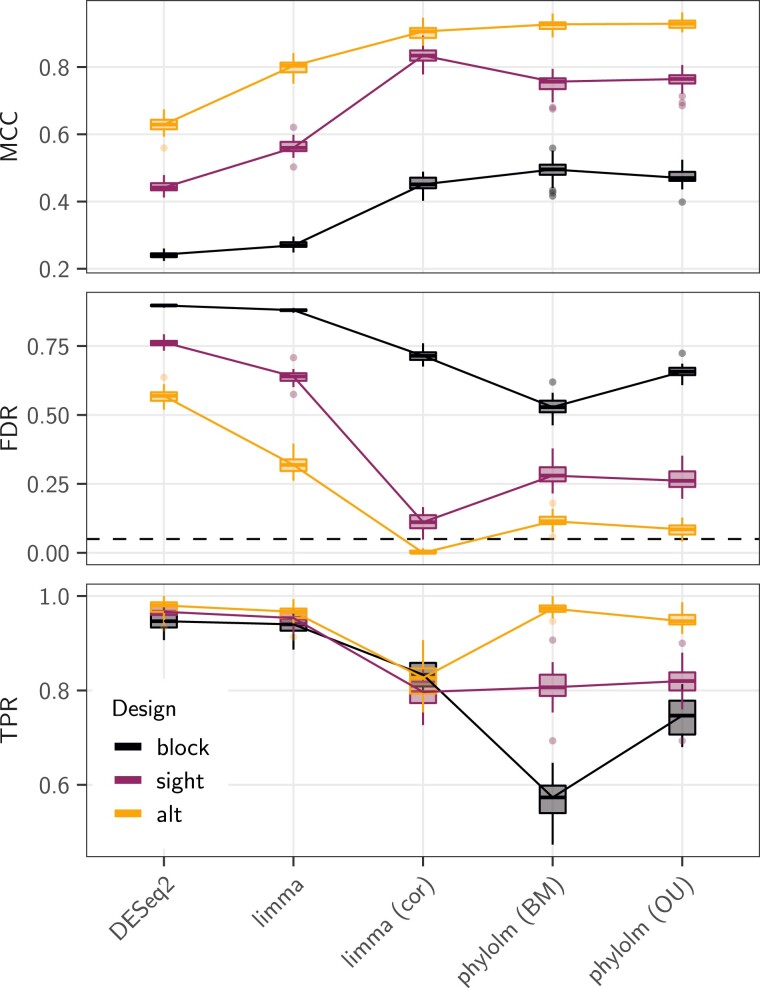
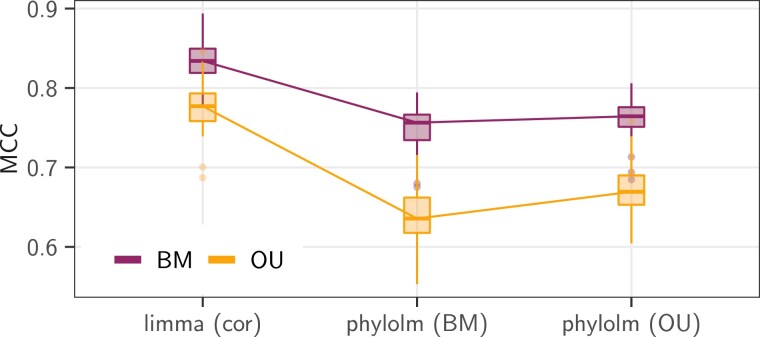
For data simulated according to the base scenario, that is, when the real tree was used to generate the data instead of the star-tree, both DESeq2 and limma methods, that do not take any correlation into account, exhibited very high rates of false discoveries (more than three quarters, fig. 2, last column). In this setting, methods that explicitly model correlations between samples (limma cor and phylolm) performed best (fig. 3, dark purple line). limma cor exhibited the best behavior with the highest MCC, and a TPR reaching about $80\text{\%}$. Its FDR was still above the nominal rate (median around $10\text{\%}$).

Fig. 3.

Results in terms of MCC (top), FDR (middle), and TPR (bottom) scores of the five selected statistical methods (x axis) on the pPLN base scenario, that has an effect size of $3$, a BM model of evolution with added intraspecies variation accounting for $20\text{\%}$ of the total variance, on the maximum likelihood tree (Stern and Crandall 2018a), with the observed “sight” groups (dark purple line, see fig. 1). The “alt” (light orange line) and “block” (black line) groups were also tested, with the same parameters. For the FDR, the black dashed line represents the nominal rate of $5\text{\%}$ used to call positives. When required, the counts were normalized using ${\log }_2(\text{TPM})$ values. Boxplots are based on $50$ replicates.

Tree Group Design Matters

The group design on the tree is known to strongly impact the properties of the data, in particular through its “phylogenetic effective sample size” (Ané 2008; Bartoszek 2016). To study its effect in a gene expression context, we replaced the “sight” design with a “block” and “alt” design (see fig. 1), that were chosen to model two extreme situations. In the “block” design, all the species with a given group are nested within a single clade, so that the differential expression signal is redundant with the phylogenetic signal. At the other end of the spectrum, the “alt” design was chosen so that sister species are in different groups, in order to maximize the contrast between organisms that share a long common history. We expect the “alt” design to produce datasets with a stronger signal.

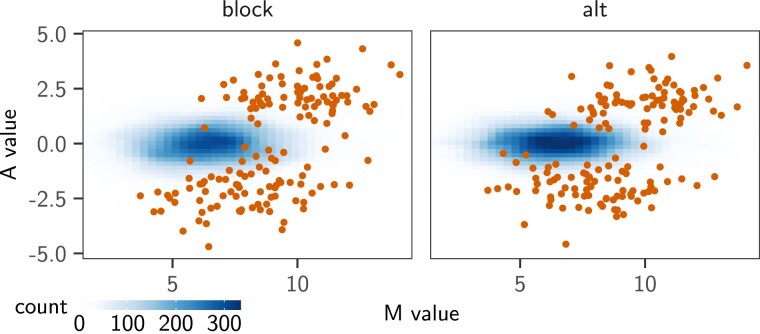
The “alt” designs produced datasets with the clearest signal (fig. 3, light orange line). In this case, limma cor was able to correctly control for the FDR. Although phylolm methods had slightly higher FDR, they achieved a better TPR, reaching almost $100\text{\%}$, leading to a better overall MCC score. At the opposite of the spectrum, the “block” design produced datasets with a very weak signal, with differentially expressed genes counts M-A values strongly overlapping the nondifferentially expressed genes distribution, which was very diffuse (fig. 4). All methods applied to the “block” design had FDR higher or equal to about $50\text{\%}$ (fig. 3, black line). The BM phylolm tool had the least bad MCC score (about $0.5$), although with the worst TPR (around $50\text{\%}$). The relative difficulties of each design was correctly captured by the normalized $\text{dapaESS}$ ($\text{dapaESSn}=\text{dapaESS}/\text{dapaESS}(\text{Ind})$, so that $\text{dapaESSn}=1$ in the independent case). While the “block” design had a lower $\text{dapaESS}$ than the independent case ($\text{dapaESSn}=0.69$), the “alt” design had a higher one ($\text{dapaESSn}=5.1$), and the “sight” design lay in the middle ($\text{dapaESSn}=1.4$).

Fig. 4.

M-A plots (log2 fold change as a function of the mean of normalized counts for each gene) of the datasets produced with base pPLN parameters (effect size of $3$, BM model with added intraspecies variation accounting for $20\text{\%}$ of the total variance), on the maximum likelihood tree (Stern and Crandall 2018a), with the “block” (left) and “alt” (right) designs. The M-A values distribution for the 3,410 nondifferentially expressed genes is shown as a tile plot, with deeper blues representing high probability values. The M-A values of the $150$ differentially expressed genes are shown as red dots.

OU Makes the Signal Weaker and is Hard to Correct For

The simulation process impacts the tree-induced correlation between species (Blomberg et al. 2003; Harmon 2019). To study the impacts of this modeling choice, we replaced the BM process with an OU, with a phylogenetic half-life (Hansen 1997) $t_{1/2}=\log (2)/\alpha$ fixed equal to $50\text{\%}$ of the tree height.

When simulating the counts using an OU model of trait evolution for the latent trait instead of a BM, the signal became weaker, and all methods achieved lower MCC scores (fig. 5). The limma cor methods performed the best in this case, even when compared with a phylolm method that explicitly takes the OU model into account. Further results of data simulated under the OU for different group designs are presented in supplementary figure S3, Supplementary Material online.

Fig. 5.

Results in terms of MCC scores of the three correlation-aware statistical methods (x axis) on the pPLN base scenario (effect size of $3$, intraspecies variation accounting for $20\text{\%}$ of the total variance), with a BM (dark purple line) or an OU (light orange line) model of evolution on the maximum likelihood tree (Stern and Crandall 2018a), with the observed “sight” groups (see fig. 1). The counts were normalized using ${\log }_2(\text{TPM})$ values. Boxplots are based on $50$ replicates.

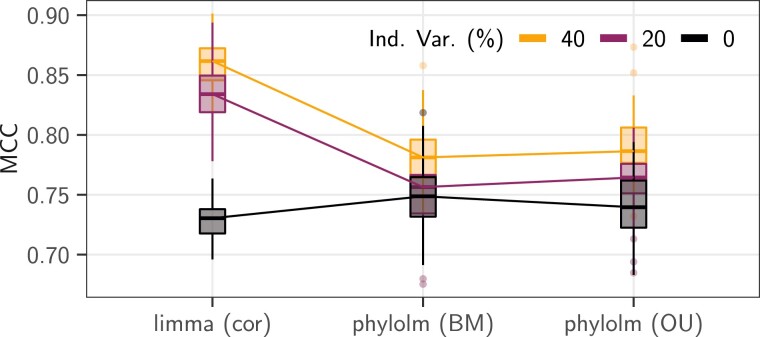
Phylogenetic Methods are Robust to Intraspecies Variations

We mitigated the effect of the BM model on the tree by varying the level of the independent individual variation representing $s_g^2$, from $40\text{\%}$ to $0\text{\%}$. When reducing the intra-species variance to $0$ (inducing a correlation of $1$ between sample values of the same species), the limma cor method lost its advantage compared with the phylolm methods, whose performances were less affected by the level of intraspecies noise (fig. 6).

Fig. 6.

Results in terms of MCC scores of the three correlation-aware statistical methods (x axis) on the pPLN base scenario with an effect size of $3$, a BM model of evolution on the maximum likelihood tree (Stern and Crandall 2018a), with the observed “sight” groups, and intraspecies variation accounting for $40\text{\%}$ (light orange line), $20\text{\%}$ (dark purple line), or $0\text{\%}$ (black line) of the total variance). The counts were normalized using ${\log }_2(\text{TPM})$ values. Boxplots are based on $50$ replicates.

${\log }_2(\text{TPM})$ Normalization is Slightly Better on Phylogenetic Data

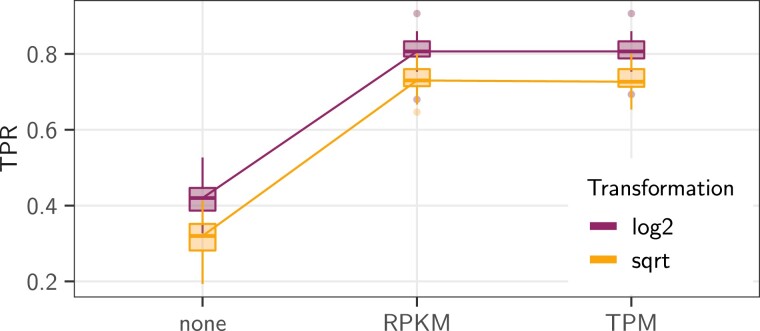
Normalization and transformation of RNA-Seq count data is known to strongly impact the analysis (Musser and Wagner 2015). We studied the effect of these choices by testing combinations of length normalization methods [$\text{TPM}$ (Wagner et al. 2012), $\text{RPKM}$ (Mortazavi et al. 2008), or a simple $\text{CPM}$, i.e., no length normalization], and transformation function [${\log }_2$ (Law et al. 2014) or square root (Musser and Wagner 2015)]. (See Materials and Methods Section “Simulations and Empirical Studies” and supplementary section A, Supplementary Material online for a detailed presentation of these normalization techniques.)

Taking gene lengths into account, using either TPM or RPKM, significantly improved the power of the methods, in particular in terms of TPR (fig. 7). Although TPM normalization led to a slightly better MCC median, its performances were largely similar to the RPKM normalization. On this base scenario, the ${\log }_2$ transformation led to a consistent gain of about $10\text{\%}$ in TPR compared with the square root (increasing from around $70\text{\%}$ to $80\text{\%}$, fig. 7).

Fig. 7.

Results in terms of TPR score of the phylolm (BM) method on the pPLN base scenario (effect size of $3$, BM model of evolution on the maximum likelihood tree (Stern and Crandall 2018a), with the observed “sight” groups, and added intraspecies variation accounting for $20\text{\%}$ of the total variance). The counts were length-normalized (x axis) using $\text{CPM}$ (length not taken into account, none), $\text{RPKM}$ or $\text{TPM}$, and transformed using the square root (light orange) or the ${\log }_2$ (dark purple) functions. Boxplots are based on $50$ replicates.

No Small Counts in De Novo Assembled Data

Including a mean-variance trend correction in the limma cor method did not change its performance on the base scenario, producing very similar MCC values (the median MCC on all $50$ runs differ by less than $0.002$). This is consistent with the fact that the original dataset uses de novo assembled data, that naturally exclude any small counts, and hence the need for a mean-variance trend correction (see Discussion).

Reanalysis of the Crayfish Dataset

While Stern and Crandall (2018a) found a list of $93$ differentially expressed genes (see supplementary table S2, Supplementary Material online in Stern and Crandall 2018a), the limma cor method found evidence for only $6$, with only one gene that was not in the previous list. Among those, one gene was clearly associated with vision (coding for the Rhodopsin protein). The phylolm OU method found evidence for $17$ differentially expressed genes, including the same $5$ genes common to OUwie and limma cor. Raising the threshold from $0.05$ to $0.1$ (respectively, $0.2$), the limma cor method selected another $4$ (resp., $25$) genes, including $1$ (resp., $6$), matching with the list from Stern and Crandall (2018a). Using the ${\log }_2$ RPKM instead of TPM gave a list of $4$ proteins, including two genes that were not in the previous lists.

Discussion

Simulation Study

Our targeted simulation study illustrates some of the specificities of interspecies RNA-Seq differential expression analysis. First, it is essential to take the correlation between replicates within a given species into account. Failure to do so leads to very high rates of false discoveries (fig. 3), that make the analysis unreliable and hard to exploit. Indeed, the limma method with added correlation seems to outperform other tools, including PCMs, in many settings. These results tend to indicate that, even if the full tree is not included in the analysis, incorporating these simple correlations between replicates might be sufficient to efficiently analyze interspecies datasets, at least for some simulation designs.

The group design on the tree was indeed found to be extremely important (fig. 3). A balanced design, where the groups are evenly spread over all clades, has a stronger signal (fig. 4), and allows the analysis to be abstracted from the phylogeny to some extent, as classical tools for differential expression analysis work best in this configuration. On the other hand, when the groups are clustered in the phylogeny, the signal is weaker as it becomes more difficult to distinguish the real group effect from the simple drift that tends to isolate clades from one another. This is in particular the case of designs where one clade or species is tested against out-groups, that is sometimes encountered in the literature (Brawand et al. 2011; Rohlfs and Nielsen 2015). In this configuration, PCMs, although imperfect, are essential.

Finally, this study confirms the importance of length normalization for interspecies differential gene expression analysis to achieve acceptable power detection levels (fig. 7). Although we did not find any significant difference in performance between RPKM and TPM normalizations, the ${\log }_2$ transformation seemed to have a slight advantage over the square root in this simulation setting. This advantage could however be simply an effect of the simulation framework, which is based on a pPLN distribution.

Simulation Design

In this work, we proposed a method to simulate RNA-Seq gene expression across multiple species. Similar to intraspecies simulation tools (Dillies et al. 2013; Soneson and Delorenzi 2013; Soneson 2014), our simulation method can use empirical datasets to set the value of parameters such that the simulated datasets are as close as possible to the real ones, with matching empirical marginal expectation and variance. When applied to independent species, our pPLN model produces datasets with features comparable to the classical NB model (fig. 2 and supplementary section D, Supplementary Material online). In our specific simulation studies, we use the dataset from Stern and Crandall (2018a). This dataset was obtained using de novo assembled data. In addition, we focused on genes with one-to-one orthologuous relationships across species. As a consequence, this dataset had a low number of zeros and small counts, and a large variance across samples (empirical dispersion ranged from $0.1$ to $5$, see fig. 4). The simulated datasets had similar characteristics, which could explain the low performance of DESeq2 in terms of FDR, even when the data were simulated without correlation (fig. 2), and the fact that the trend procedure did not add any power to the limma method. In addition, as DESeq2 explicitly assumes a NB distribution of the counts, it suffers from the deviation from this model, as opposed to limma, which controlled the FDR to the nominal rate in both the NB and pPLN models (fig. 2). Interspecies RNA-Seq gene expression datasets are very diverse, with specificities depending on the underlying biological question being studied. This work provides a first step toward realistic simulation of such datasets.

Simulation Tool

Compared with classical intraspecies simulation tools (Dillies et al. 2013; Soneson and Delorenzi 2013; Soneson 2014), our simulation framework incorporates the species tree and the gene length, which may vary across species. It makes it possible to model the evolution of gene expression on the tree using two different processes (BM or OU), and it allows for additional independent variation, that can model, for example, interspecies variation or measurement error. This complex model leads to new effects, that can be difficult to predict. In particular, we showed that the distribution of the groups on the tree had strong effects on the ability of all methods to detect a group expression shift. We proposed a normalized criterion ($\text{dapaESS}$) to assess the difficulty of the group design for the differential gene expression analysis problem. Although it does not take into account the number of replicates or the specific evolution model, we showed that it could well represent the difficulty of an experimental design. The strength of this criterion is that it only depends on the timed species tree and the tips group allocation, and can be computed before any statistical inference or even data collection. It can hence be used as a practical guide on the expected power of the experimental design. In particular, if the normalized $\text{dapaESSn}$ is lower than one, results from methods that do not take the phylogeny into account should be interpreted with particular caution.

In this work, we focused our attention on the detection of shifts of expression between groups spanning across species. However, interspecies datasets are also used to address many other questions, such as equality of within-species variance, expression divergence, or detection of neutral vs. directed evolution regimes. Several tools from the PCM literature have been used to this end, that rely on various models of trait evolution with appropriate parameter constraints. Since our simulation tool is modular, those various processes could be implemented, in order to produce realistic RNA-Seq datasets with the desired structure. More generally, our tool could be extended to take into account any correlation structure between samples, not necessarily deriving from a phylogenetic model. Such an extended framework could help researchers to test the statistical properties of these complex inference models.

Inference Tools

In this study, we focused on a few inference tools, that come either from the RNA-Seq or the PCM literature, limiting ourselves to methods implemented in R and that can do differential analysis. Although a more comprehensive simulation design would be needed to draw stronger conclusions, our results show that simulations under the OU model could lead to more difficult datasets for some group designs, and that even methods that include the OU model in their framework fail to completely correct for this effect. This could be linked with the fact that the estimation of the selection strength in an OU model is a notoriously difficult question, especially on an ultrametric tree (Ho and Ané 2014b; Cooper et al. 2016). Having to estimate this parameter for thousands of genes is bound to generate some instability, and to deteriorate the performance of those tools. Gu et al. (2019) recently proposed an empirical Bayes approach to deal with this parameter in an RNA-Seq setting. One possible direction could be to adapt this method to a differential analysis problem. More generally, our simulation study seems to show that none of the methods presented here had really satisfactory results, but that taking gene lengths and sample correlation into account was essential. This study illustrates the need for new statistical tools for interspecies differential analysis, that would combine the strengths of both the classical RNA-Seq literature, that can deal with the specificities of this noisy data, and the PCM literature, that takes into account the phylogeny, an information that can be crucial to correctly interpret interspecies data.

Reanalysis of the Crayfish Dataset

In the setting that was most similar to the empirical Crayfish dataset, we found that the limma cor method worked best, with a similar TPR but smaller FDR compared with phylogenetic methods. When we applied this method to the Crayfish dataset, we found a list of only $6$ differentially expressed genes between sighted vs. blind species across all clades. This list was robust to the choice of the detection threshold, as raising it from $0.05$ to $0.1$ only added $4$ candidates. Allowing more false discoveries with a threshold of $0.2$ output a total of $31$ genes including only approximately a third matching the original list of $93$ genes found by Stern and Crandall (2018a), comforting our suspicion that the data only support a limited number of differentially expressed genes. However, such a small list, containing only one gene directly associated to vision, might not be enough to explain the complex mechanisms of vision loss in cave animals. There are at least two factors that could explain this result. First, our model was designed to find genes that are differentially expressed in all clades, that is, it assumed that the mechanisms underlying vision loss were the same for all groups of organisms, which is a very strong assumption. A different design could be to assume that each clade that went through vision loss have their own differentially expressed genes. In the linear model of limma, this simply amounts to adding one group factor per clade of interest, and to test for the coefficient associated with each group. Such an analysis gave us a different list for blind species of each genus Procambarus, Cambarus, and Orconectes, with only one gene that was common to all three lists (see supplementary section B, Supplementary Material online). The fact that only a few genes overlap between each group could indicate that different sets of genes are associated with vision loss in each clade, that is, that evolution has taken different genomic routes to vision loss in cave crayfish. This finding could be consistent with Stern and Crandall (2018a), which concluded that convergent vision loss among blind species was driven by increased gene expression variance (i.e., loss of selective constraint) rather than directional selection on a common set of genes. A second limitation to this study is that we only tested for differentially expressed genes, that is, difference in mean gene expression between groups. This is only one of the many possible ways evolution can impact gene expression (see, e.g., table 1 in Stern and Crandall 2018a). Other tools, designed to test for other patterns of evolution as mentioned above, might be able to detect other genes. Finally, when using RPKM instead of TPM normalization, we found a list of genes that only partially matched with the previous ones. Although TPM and RPKM seemed to performed similarly well on the simulated data (see fig. 7), this result shows that normalization can have a strong impact when analyzing biological datasets, and the robustness of these methods should be carefully assessed, when possible. Unfortunately, still little is known regarding the evolutionary genetics of vision loss in crayfishes, which makes the biological validation of the results difficult.

Table 1.

Differentially expressed genes across blind and sighted crayfish species found by the limma cor method on ${\log }_2$ transformed TPM values (adjusted $P$ values below $0.05$). OG0001281 (OPSD PROCL) is associated with the rhodopsin protein, involved in vision mechanisms.

Orthogroup	Adj. $P$ value	Uniprot Top Hit	Protein Name
OG0002505	$2.3\times {10}^{-9}$	XYLA ARATH	Xylose isomerase
OG0001105	$4.4\times {10}^{-3}$	PIPA DROME	1-phosphatidylinositol 4,5-bisphosphate phosphodiesterase
OG0000233	$6.2\times {10}^{-3}$	RTBS DROME	Probable RNA-directed DNA polymerase from transposon BS
OG0002370	$1.8\times {10}^{-2}$	ARRH LOCMI	Arrestin homolog
OG0006977	$2.3\times {10}^{-2}$	CSK2B RAT	Casein kinase II subunit beta
OG0001281	$2.9\times {10}^{-2}$	OPSD PROCL	Rhodopsin

Materials and Methods

A Framework to Simulate Interspecies RNA-Seq Datasets

Building on existing RNA-Seq methods (Robles et al. 2012; Soneson and Delorenzi 2013; Soneson 2014), we developed a new interspecies simulation framework that can generate realistic count datasets, and takes into account, first, the gene expression correlations induced by the phylogeny and, second, the different lengths a given gene can have in different species.

Realistic Simulations using the Negative Binomial Distribution

We briefly recall here the simulation framework detailed in (Soneson and Delorenzi 2013), and implemented in compcodeR (Soneson 2014).

Negative Binomial Distribution

Let $Y_{gi}$ be the random variable representing the count for gene $g$ ($1\le g\le p$) in sample $i$ ($1\le i\le n$), with true expression level ${\lambda }_{gi}$ and sampling depth $M_i$. Following Robinson and Oshlack (2010), we model each count independently by a negative binomial (NB) distribution with expectation ${\mu }_{gi}$ and dispersion ${\alpha }_g$, such that $Y_{gi}\sim \mathsf{N}\mathsf{B}({\mu }_{gi},{\alpha }_g)$ with

$${\mu }_{gi}=\frac{{\lambda }_{gi}}{{\displaystyle \sum _{h=1}^p}{\lambda }_{hi}}{M}_i.$$ (1)

Differential Expression

To model differential expression, we assume that the samples are partitioned into two groups $S_1$ and $S_2$. For each gene $g$, the dispersion parameter ${\alpha }_g$ is the same for all samples, while the expression level ${\lambda }_{gi}$ can only take two values: ${\lambda }_{g{S}_1}$ if $i$ is in $S_1$ and ${\lambda }_{g{S}_2}$ if $i$ is in $S_2$. Given ${\lambda }_{g{S}_1}$, we take ${\lambda }_{g{S}_2}$ as

$$\begin{array}{r}{\lambda }_{g{S}_2}=\{\begin{array}{cc}{\lambda }_{g{S}_1}& \text{if }g\text{ is not differentially expressed;}\\ {\lambda }_{g{S}_1}\times (e+X_g^e)& \text{if }g\text{ is up-regulated in }{S}_2;\\ {\lambda }_{g{S}_1}\times (e+X_g^e{)}^{-1}& \text{if }g\text{ is down-regulated in }{S}_2;\end{array}\end{array}$$

with $e$ the minimal differential effect size, and $X_g^e$ random variables independent identically distributed according to an exponential distribution with parameter $1$. The values of the parameters are set to match the empirical counts expectation and dispersion of a real datasets.

Realistic Simulations using the Poisson Log-Normal Distribution

The Poisson log-normal (PLN) distribution has been advocated as an alternative to the NB distribution for the analysis of RNA-Seq data. Being more flexible, it is particularly well suited in the presence of correlations (Gallopin et al. 2013; Zhang et al. 2015), which proves essential for interspecies datasets, as demonstrated in the next section. We show here how the parameters of a PLN model can be chosen to match first- and second-order moments of the NB model described above, making it possible to simulate realistic datasets under this more flexible framework.

The PLN Distribution

Under the PLN model, for each gene $g$ and sample $i$, we assume that the observed count random variable $Y_{gi}$ follows a Poisson distribution, with log parameter a Gaussian latent variable $Z_{gi}$, such that

$$\begin{array}{c}{Z}_{gi}\sim \mathcal{N}(m_{gi},{\sigma }_g^2)\\ Y_{gi}|Z_{gi}\sim \mathcal{P}(\exp (Z_{gi})).\end{array}$$ (2)

This model is similar in spirit to the NB distribution, that can be seen as Gamma-Poisson mixture (see, e.g., Holmes and Huber 2019, Chap. 4). Note that in both models, the coefficient of variation of the mixing distribution is constant across samples for a given gene (Chen et al. 2014).

Matching Moments

Using standard moments expressions for the NB (Holmes and Huber 2019) and PLN (Aitchison and Ho 1989) distributions, it is straightforward to show that a PLN distribution with parameters $m_{gi}$ and ${\sigma }_g^2$ yields the same first- and second-order moments as a NB distribution with expectation ${\mu }_{gi}$ and dispersion ${\alpha }_g$ if and only if

$$\{\begin{array}{c}{\sigma }_g^2=\log (1+{\alpha }_g)\\ m_{gi}=\log ({\mu }_{gi})-\frac{1}{2}\log (1+{\alpha }_g).\end{array}$$ (3)

These equations allow us to readily use the framework developed in the previous section also in the case of a PLN simulation.

Phylogenetic Comparative Methods

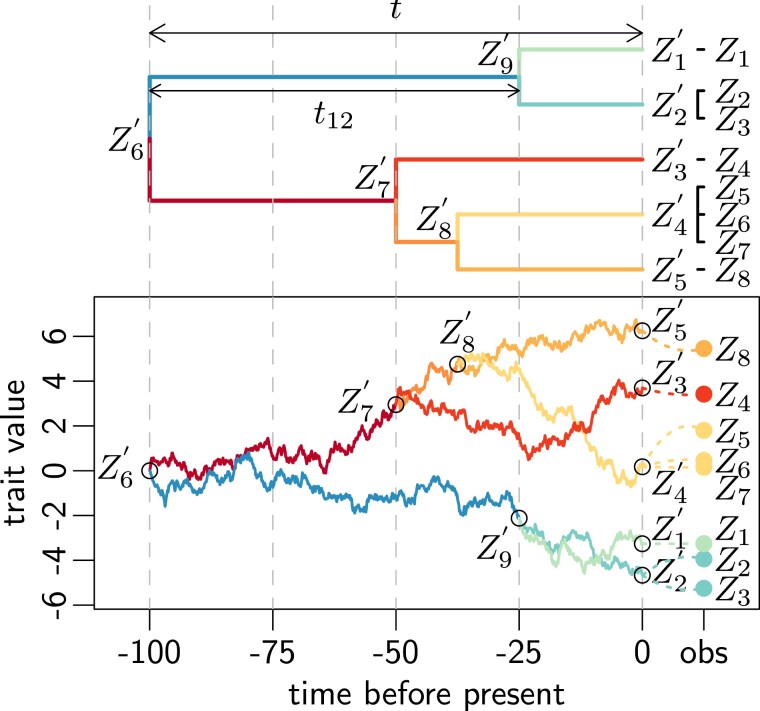
Phylogenetic relationships are known to induce correlations between observed quantitative traits on several species (Felsenstein 1985). The field of PCMs specializes in the comparative study of such phylogenetically related traits, and has been flowering over the last decades [see, e.g., Harmon (2019) for a recent review]. Conditionally on a phylogenetic tree that links a set of species, PCMs model the evolution of a quantitative trait as a stochastic process along the branches of the tree (see fig. 8). This generative model induces a multivariate Gaussian structure of the observed vector of traits across species, with a correlation structure that depends on the tree and on the chosen process. The values of the trait are only observed at the tips of the tree. The values at the root or at the internal nodes are unobserved and are modeled using latent variables.

Fig. 8.

Realization of a Brownian motion (BM) process (bottom), on a time-calibrated ultrametric tree with total height $t=100$ (top), with replicates and within-species variation. The BM process on the tree controls the distribution of the internal nodes, including ancestral nodes $Z_6^{\prime },\dots ,Z_9^{\prime }$, and latent tip traits $Z_1^{\prime },\dots ,Z_5^{\prime }$. The ancestral root value of the BM is $\mu =0$, and its variance is ${\sigma }_{\mathrm{BM}}^2=0.1$, so that the latent (unobserved) tip trait variance is $\mathbb{V}\text{ar}[Z_1^{\prime }]=\dots =\mathbb{V}\text{ar}[Z_5^{\prime }]={\sigma }_{\mathrm{BM}}^{2}t=10$. The covariance of the latent tips trait is proportional to their time of shared evolution, for instance $\mathbb{C}\text{ov}[Z_1^{\prime };Z_2^{\prime }]={\sigma }_{\mathrm{BM}}^2{t}_{12}=7.5$. Replicated measurements are added on the tree as tips with zero branch lengths (top), with an extra variance of $s^2=0.5$. For instance, $Z_2$ and $Z_3$ are replicates of the latent tip $Z_2^{\prime }$, and their conditional distribution is Gaussian with expectation $Z_2^{\prime }$ and variance $s^2$. The total sample traits variance is hence given by $\mathbb{V}\text{ar}[Z_1]=\dots =\mathbb{V}\text{ar}[Z_8]={\sigma }_{\mathrm{BM}}^{2}t+s^2=10.5$, and the sample traits covariance is given by the tree structure, for instance $\mathbb{C}\text{ov}[Z_1;Z_2]=\mathbb{C}\text{ov}[Z_1^{\prime };Z_2^{\prime }]={\sigma }_{\mathrm{BM}}^2{t}_{12}=7.5$, and $\mathbb{C}\text{ov}[Z_2;Z_3]=\mathbb{C}\text{ov}[Z_2^{\prime };Z_2^{\prime }]={\sigma }_{\mathrm{BM}}^{2}t=10$. Note that on this figure, latent internal nodes (internal and external) are numbered from $1$ to $9$, and observations are numbered from $1$ to $8$, but these set of indices are distinct. For instance, $Z_1$ is indeed an observation of $Z_1^{\prime }$, but $Z_4$ is an observation of $Z_3^{\prime }$ and is unrelated to $Z_4^{\prime }$.

Brownian Motion on a Tree

The most commonly used process is the BM (Felsenstein 1985). Under this model, for a given continuous trait Z′ measured at the tips of the tree, the covariance between traits $Z_i^{\prime }$ and $Z_j^{\prime }$ is simply proportional to the time of shared evolution between species $i$ and $j$, that is, the time $t_{ij}$ between the root of the tree and the most recent common ancestor of $i$ and $j$: $\mathbb{C}\text{ov}[Z_i^{\prime };Z_j^{\prime }]={\sigma }_{\mathrm{BM}}^2{t}_{ij}$, where ${\sigma }_{\mathrm{BM}}^2$ is the variance of the BM process. The expectation of each trait is equal to $\mu$, the ancestral value of the process at the root.

Ornstein-Uhlenbeck on a Tree

To model stabilizing selection, the OU process is often used (Hansen and Martins 1996; Hansen 1997). Compared with the BM, it has an equilibrium value $\beta$, that represents the “optimal value” of the trait in a given environment. The trait is attracted to this optimum with a speed that is controlled by the selection strength $\alpha$, or better the phylogenetic half-life $t_{1/2}=\log (2)/\alpha$ (Hansen 1997). This process induces a different correlation structure than the BM, with stronger selection strength inducing weaker interspecies correlations (Hansen 1997; Ho and Ané 2013). Specifically, conditionally on a fixed root, $\mathbb{C}\text{ov}[Z_i^{\prime };Z_j^{\prime }]={\gamma }^2(1-e^{-2\alpha t_{ij}})e^{-\alpha (t_i+t_j-2t_{ij})}$, with ${\gamma }^2={\sigma }_{\mathrm{OU}}^2/(2\alpha )$ the stationary variance of the process, and $t_i=t_{ii}$ the time between the root and node $i$ (Ho and Ané 2013).

Within-Species Variation

The traditional PCM framework assumes that only one measurement is available for each species, and that there is no measurement error, that is, that all the observed variation can be explained by the evolution process on the tree. However, ignoring measurement error can lead to severe biases (Silvestro et al. 2015; Cooper et al. 2016). In addition, in an interspecies RNA-Seq differential analysis, it is usual to have access to replicated measurements, that is, to measurements for several individuals of the same species. There is a vast literature on the subject of within-species variation (Grafen 1989, 1992; Lynch 1991; Housworth et al. 2004; Ives et al. 2007; Hadfield and Nakagawa 2010; Goolsby et al. 2017). One simple way to look at the problem in a univariate setting is to assume that all the individuals from a same species are placed on the tree as tips linked to a same species node with a branch of length zero (Felsenstein 2008) and to add a uniform Gaussian individual variance $s^2$ to all the tip samples traits (see figs. 8 and 1). In such a framework, the total variance of a sample trait $Z_i$ attached to a latent tip with trait $Z_{\mathrm{sp}(\mathrm{i})}^{\prime }$ is given by $\mathbb{V}\text{ar}[Z_i]=\mathbb{V}\text{ar}[Z_{\mathrm{sp}(\mathrm{i})}^{\prime }]+s^2$, where $\mathbb{V}\text{ar}[Z_{\mathrm{sp}(\mathrm{i})}^{\prime }]$ is determined by the chosen stochastic process to model the latent trait (BM or OU). Similarly, the covariance between two-sample traits $Z_i$ and $Z_j$ attached, respectively, to latent tip traits $Z_{\mathrm{sp}(\mathrm{i})}^{\prime }$ and $Z_{\mathrm{sp}(\mathrm{j})}^{\prime }$ is given by $\mathbb{C}\text{ov}[Z_i;Z_j]=\mathbb{C}\text{ov}[Z_{\mathrm{sp}(\mathrm{i})}^{\prime };Z_{\mathrm{sp}(\mathrm{j})}^{\prime }]$.

The Phylogenetic Poisson Log-Normal Distribution

In an interspecies framework, various samples come from various species, which implies a specific correlation between measures, that can be taken into account in a multivariate PLN model.

Continuous Trait Evolution Model

The models of trait evolution used in PCMs are generative, and can be used to simulate continuous traits at the tips of a tree (with possible replicates) such that their correlation structure is consistent with their phylogeny (see fig. 8). Using a simple uniform Gaussian individual variance $s_g^2$ to model within-species variation, the trait variance ${\mathbf{\Sigma }}_g$ for the vector ${\mathbf{Z}}_g$ of continuous traits at the tips of the tree generated by such a process can be expressed as

$$\{\begin{array}{cc}[{\mathbf{\Sigma }}_g{]}_{ij}=\mathbb{C}\text{ov}[Z_i;Z_j]={\sigma }_g^2(\mathrm{sp}(\mathrm{i});\text{sp}(\mathrm{j}))& \text{if }\text{sp}(i)\ne \text{sp}(j),\\ [{\mathbf{\Sigma }}_g{]}_{ii}=\mathbb{V}\text{ar}\left[Z_i\right]={\sigma }_g^2(\text{sp}(i);\text{sp}(i))+s_g^2& \text{otherwise,}\end{array}$$

where ${\sigma }_g^2(\text{sp}(i);\text{sp}(j))$ is the phylogenetic variance between species $\text{sp}(i)$ and $\text{sp}(j)$ of samples $i$ and $j$ (see fig. 8), with a structure given by the evolution process (BM or OU, see expressions above), and $s_g^2$ the added intraspecies variation. Note that the variance parameters do depend on the gene $g$ (for instance, ${\sigma }_g^2(\text{sp}(i);\text{sp}(j))={\sigma }_g^2{t}_{ij}$ in the BM case), which allows us to tune the marginal moments to realistic values for count data, as detailed below.

The Phylogenetic Poisson Log-Normal Distribution

The models described above are well suited for quantitative traits, but need to be adapted for count measures, such as the one produced by a RNA-Seq analysis. To handle such counts, we propose to add a Poisson layer to the trait evolution models described above, defining a “phylogenetic” Poisson log-normal (pPLN) distribution. More specifically, for a given gene $g$, we simulate a vector of $n$ latent traits ${\mathbf{Z}}_g$ as the result of such a process running on the tree, and then, conditionally on this vector, draw the observed counts $Y_{gi}$ from a Poisson distribution with parameter $\exp (Z_{gi})$

$$\begin{array}{c}{\mathbf{Z}}_g\sim \mathcal{N}({\mathbf{m}}_g,{\mathbf{\Sigma }}_g)\\ Y_{gi}|Z_{gi}\sim \mathcal{P}(\exp (Z_{gi})).\end{array}$$ (4)

In other words, the vector of counts ${\mathbf{Y}}_g$ for each gene is drawn from a multivariate PLN distribution, with parameters ${\mathbf{m}}_g$ and ${\mathbf{\Sigma }}_g$ obtained from the evolutionary models described above, ${\mathbf{\Sigma }}_g$ being the structured variance matrix of both phylogenetic and independent effects, and ${\mathbf{m}}_g$ a vector or expectations values at the tips, that can be set independently from the process.

Matching Moments for Realistic Simulations

Assuming that the diagonal coefficients of ${\mathbf{\Sigma }}_g$ are all equal to a single value ${\sigma }_g^2$, equation (3) can be used to ensure that the pPLN model above yields the same marginal expectation and variance as a NB model with expectation ${\mu }_{gi}$ and dispersion ${\alpha }_g$. At a macro-evolutionary scale, most of the dated phylogenetic trees encountered are ultrametric, that is, are such that all the tips are at the same distance $t$ from the root. In that case, all the phylogenetic models described above verify this variance homogeneity assumption. For instance, for the simple BM model with an extra layer of independent variation, we have ${\sigma }_g^2={\sigma }_{\mathrm{BM}}^{2}t+s^2$. Note that although the NB and pPLN models are set to have the same expectations and variance, they differ significantly in their covariances: while in the standard NB model, all the samples are independent from one another, in the proposed pPLN framework, the measurements are correlated, with a structure reflecting both the tree and the selected evolutionary process.

Taking Differential Gene Lengths into Account

Length Normalization of Counts

Let ${\ell }_{gi}$ denote the length of the gene $g$ for sample $i$. Following Robinson and Oshlack (2010), we take this length into account by changing equation (1) to

$${\mu }_{gi}=\frac{{\lambda }_{gi}{\ell }_{gi}}{{\displaystyle \sum _{h=1}^p}{\lambda }_{hi}{\ell }_{hi}}{M}_i.$$ (5)

Note that the same overall sequencing depth $M_i$ is attributed to each sample, but that, because of the weighted average, it is preferentially allocated to longer genes.

Lengths Simulation

The lengths are simulated according to the pPLN model described above, with expectations and dispersions empirically estimated from the dataset at hand.

Differential Analysis Phylogenetic Asymptotic Effective Sample Size

To quantify the intrinsic difficulty of a design compared with another, we propose a new “differential analysis phylogenetic asymptotic effective sample size” ($\text{dapaESS}$). Given a phylogenetic tree $\mathcal{T}$, we first remove all replicates, so that there are no zero-length branches. Then, given a design vector $\mathbf{x}$, we postulate a simple BM model for an hypothetical continuous trait $\mathbf{y}$ at the tips: $\mathbf{y}={\theta }_0\mathbf{1}+{\theta }_1\mathbf{x}+\sigma {\mathbf{e}}^{BM},$ with $\mathbb{V}\text{ar}\left[{\mathbf{e}}^{BM}\right]={\mathbf{V}}^{\mathrm{tree}}=[t_{ij}{]}_{i,j}$. From standard linear model theory, the variance of the maximum likelihood estimator of the coefficient ${\theta }_1$ is given by Ané (2008): $\mathbb{V}\text{ar}\left[{\hat{\theta }}_1\right]={\sigma }^2({\mathbf{X}}^T{{\mathbf{V}}^{\mathrm{tree}}}^{-1}\mathbf{X}{)}_{2,2}^{-1},$ with $\mathbf{X}=(\mathbf{1}\mathbf{x})$ the matrix of predictors. We hence define: $\text{dapaESS}(\mathcal{T},\mathbf{x})=1/({\mathbf{X}}^T{{\mathbf{V}}^{\mathrm{tree}}}^{-1}\mathbf{X}{)}_{2,2}^{-1}$. In the case where all the species are independent (star-tree ${\mathcal{T}}^{*}$), we fall back on a standard differential expression analysis, and we get, assuming that there are $n$ species and that the groups are balanced: $\text{dapaESS}({\mathcal{T}}^{*},\mathbf{x})=n/4,$ which is the standard effective sample size for a balanced two-sample t-test with uniform variance. This gives us a base-line for a “standard” difficulty, and we use in the following the normalized $\text{dapaESS}$: $\text{dapaESSn}(\mathcal{T},\mathbf{x})=\text{dapaESS}(\mathcal{T},\mathbf{x})/\text{dapaESS}({\mathcal{T}}^{*},\mathbf{x})$. A value lower than $1$ indicates a design that is deemed more difficult than a standard independent design (larger asymptotic variance of the estimator), while a value greater that $1$ indicates a problem where the phylogeny actually helps in finding the significant differences. Note that this score can be computed a priori, and, as shown below, can be used to assess the quality of the experimental design.

Simulations and Empirical Studies

Gene Expression Underlying Vision Loss in Cave Animals

The real dataset used to set simulation parameters and for the real data analysis case study was extracted from (Stern and Crandall 2018a). In this study, the authors selected eight blind and six sighted crayfish species, for which a time-calibrated maximum likelihood phylogeny is known (Stern et al. 2017). 3,560 orthologous gene expressions were estimated using the method RNA-Seq by Expectation Maximization (RSEM) (Li and Dewey 2011), with one to three replicates per species (see fig. 1).

Base Simulation Parameters

We used the real dataset to set the parameters of our simulations. We took the estimated crayfish tree rescaled to unit height ($t=1$), with the observed vision status design (“sight” design, see fig. 1), and matching the empirical counts and gene lengths expectation and dispersion. The expression level ${\lambda }_{g{S}_1}$ and the dispersion ${\alpha }_g$ were estimated from the dataset for each gene $g$, while for each sample $i$ the simulation sequencing depth $M_i$ was independently drawn from a uniform distribution with bounds $M_{\min }$ and $M_{\max }$ the observed empirical minimal and maximal values of the library size across all samples. We used a BM model of trait evolution, with an independent layer of individual variation $s_g^2$ representing $20\text{\%}$ of the total tip variance ${\sigma }_g^2$ for each gene $g$: $s_g^2=0.2\times {\sigma }_g^2$, with ${\sigma }_g^2=({\sigma }_{\mathrm{BM}}^2{)}_{g}t+s_g^2$. We chose a base effect size of $3$, with $150$ differentially expressed genes out of the 3,560 simulated ones. From this base scenario, we varied several parameters in order to study their impacts on the simulated data. Each scenario was replicated $50$ times.

Inference Methods Parameters

We used the following statistical inference methods: DESeq2 (Love et al. 2014) assumes a NB distribution on independent counts; limma (Ritchie et al. 2015) applies an Empirical Bayes moderation (without a mean-variance trend correction, unless otherwise specified) on independent normalized counts, possibly assuming that all the samples in a same species are correlated [limma cor (Smyth et al. 2005)]; and phylolm (Ho and Ané 2014a) uses a phylogenetic regression framework based on a BM or OU process, with measurement error. We refer to supplementary section A, Supplementary Material online for a detailed presentation of these methods. For phylolm, the differential analysis relied on a t statistic computed for each gene independently, conditionally on the estimated maximum likelihood parameters ($s_g^2$ and ${\alpha }_g$ for the OU). The raw P values computed by all methods were adjusted using the BH method (Benjamini and Hochberg 1995), using the R function p.adjust. Inferred gene expression differences across groups were marked as significant if their associated adjusted P value was below the threshold of $0.05$.

Length Normalization and Transformation

In DESeq2 (Love et al. 2014), we used the default RLE method (Anders and Huber 2010) to compute the sample-specific normalization factor $m_i$. We followed the recommendations of the section “Sample-/gene-dependent normalization factors” from the DESeq2 vignette to compute the coefficients $c_{gi}$ from the coefficients $m_i$ and gene lengths ${\ell }_{gi}$ detailed in supplementary section A, Supplementary Material online. For methods requiring a preprocessing normalization of the count data (limma and phylolm), we used the TMM method (Robinson and Oshlack 2010) implemented in the calcNormFactor function in edgeR, and a $\text{TPM}$ length normalization with a ${\log }_2$ transformation.

Scores Used to Assess the Performance of the Inference Methods

To assess the performance of the inference methods, based on the list of true (simulated) differentially expressed genes, we computed the number of true positives (TP), true negatives (TN), false positives (FP), and false negatives (FN). We used the Matthews correlation coefficient ($\text{MCC}=[\text{TP}\cdot \text{TN}-\text{FP}\cdot \text{FN}]\cdot [(\text{TP}+\text{FP})(\text{TP}+\text{FN})(\text{TN}+\mathrm{FP})(\text{TN}+\text{FN}){]}^{-1/2}$) as advised in Chicco and Jurman (2020). We also computed the true positive rate ($\text{TPR}=\text{TP}/(\text{TP}+\text{FN})$) and the false discovery rate ($\text{FDR}=\text{FP}/(\text{FP}+\text{TP})$). In addition, we compared the features of the simulated datasets with the empirical one using the countsimQC R package (Soneson and Robinson 2018).

Reanalysis of the Crayfish Dataset

Stern and Crandall (2018a) used the OUwie package (Beaulieu et al. 2012) on each gene to compare an OU model with a single optimal value to a model with two optimal values, one for the sighted species and one for the blind. This method is similar to the phylogenetic ANOVA, but differs on two important aspects. First, it takes as entry the within-species empirical means and variance instead of the individual values. Second, it uses a likelihood ratio test assuming a chi-square distribution with one degree of freedom, instead of the conditional $t$-test used in phylolm. In a mixed model setting, such likelihood ratio test have been shown to be anticonservative (see, e.g., Section 2.4 in Pinheiro and Bates 2006), and can hence lead to many false discoveries. We applied the limma cor method on the ${\log }_2$ TPM values, that performed best on the realistic simulations above, to the same dataset, and compared the list of differentially expressed genes to the one found in Stern and Crandall (2018a). We also applied the phylolm OU method, that is the most similar to the OUwie method, for comparison.

Supplementary Material

Supplementary data are available at Molecular Biology and Evolution online.

Data Availability

The simulation tool is integrated into the compcodeR package, that is freely available on the Bioconductor platform, and documented through a specific vignette (https://doi.org/10.18129/B9.bioc.compcodeR). The data and code used for the simulation study are available on the following GitHub repository: https://github.com/i2bc/InterspeciesDE, and was deposited on Zenodo: www.doi.org/10.5281/zenodo.7311523.