Abstract
As individuals age, death is a competing risk for Alzheimer’s disease (AD) but the reverse is not the case. As such, studies of AD can be placed within the semi-competing risks framework. Central to semi-competing risks, and in contrast to standard competing risks, is that one can learn about the dependence structure between the two events. To-date, however, most methods for semi-competing risks treat dependence as a nuisance and not a potential source of new clinical knowledge. We propose a novel regression-based framework that views the two time-to-event outcomes through the lens of a longitudinal bivariate process on a partition of the time scales of the two events. A key innovation of the framework is that dependence is represented in two distinct forms, local and global dependence, both of which have intuitive clinical interpretations. Estimation and inference are performed via penalized maximum likelihood, and can accommodate right censoring, left truncation, and time-varying covariates. An important consequence of the partitioning of the time scale is that an ambiguity regarding the specific form of the likelihood contribution may arise; a strategy for sensitivity analyses regarding this issue is described. The framework is then used to investigate the role of gender and having ≥1 apolipoprotein E (APOE) allele on the joint risk of AD and death using data from the Adult Changes in Thought study.
Keywords: alzheimer’s disease, b-splines, discrete-time survival, longitudinal modeling, penalized maximum likelihood
1 |. INTRODUCTION
Alzheimer’s disease (AD) is a brain disorder characterized by progressive dementia that slowly destroys memory and cognitive function. In 2018, an estimated 5.7 Americans were living with AD (Alzheimer’s Association, 2018). First described in 1906, factors that have been shown to be associated with AD include: age, family history, the apolipoprotein E (APOE) allele, midlife obesity, midlife hypertension, diabetes, education, and physical activity (Baumgart et al., 2015). Many of these factors are also strongly associated with mortality, suggesting that AD and mortality may be dependent within individuals and, furthermore, that this dependence may be influenced by a range of factors.
Practically, studies of risk factors for AD often focus on the timing of a diagnosis and thus use survival analysis methods. Such analyses typically treat death as a censoring mechanism. An alternative is the semi-competing risks paradigm, within which AD and mortality are considered simultaneously. In general terms, semi-competing risks refer to settings where interest lies in some nonterminal event, the occurrence of which is subject to a terminal event (Fine et al., 2001; Varadhan et al., 2014; Haneuse and Lee, 2016). Let and denote the time to the nonterminal and terminal events, respectively. Key to semi-competing risks is that one can potentially observe both and on individual study units. As such, in contrast to the standard competing risks setting (Tsiatis, 1975), there is partial information on the joint distribution of the two events (Jazić et al., 2016). This, in turn, provides an opportunity to learn about the dependence structure between and .
Beyond the usual challenges of time-to-event analyses (i.e., structuring covariate effects, handling functions of time, and accommodating various forms of censoring and truncation), key challenges that arise in the analysis of semi-competing risks data are: (i) respecting the terminal event as a competing risk and (ii) structuring dependence between and . In the statistical literature, numerous frameworks for the analysis of semi-competing risks data have been proposed, including: methods grounded in causal inference (Egleston et al., 2006; Tchetgen Tchetgen, 2014; Nevo and Gorfine, 2020); methods based on structuring dependence via a copula (Fine et al., 2001; Peng and Fine, 2007; Li and Peng, 2015); the use of illness-death models (Xu et al., 2010; Lee et al., 2017, 2015); and the recently proposed cross-quantile residual ratio (Yang and Peng, 2016). While additional review details are provided in Section A.1 of the Supporting Information, we note that these methods either: (i) view dependence as a statistical nuisance, and not a potential source of new clinical knowledge; or (ii) focus on the role of the nonterminal event as a risk factor for the terminal event, thereby reframing the nonterminal event away from being an outcome of interest. As such, collectively, these methods fail to take advantage of the opportunity to learn about dependence between the two outcomes that semi-competing risks data provide.
In this paper, we propose a novel regression-based framework for semi-competing risks data based on a partitioning of the time scales for the two events that simultaneously structures covariate effects on , and the dependence between the two. A key innovation of the proposed framework is that dependence is represented in two distinct forms, termed the local and global dependence, both of which have intuitive clinical interpretations. Practically, since modeling within the framework is based upon probabilities conditional on survival, left truncation, right censoring, and time-varying covariates may be accommodated in a straightforward manner. An important consequence of the partitioning of the time scale is that an ambiguity regarding the specific form of the likelihood contribution may arise; a strategy for sensitivity analyses regarding this issue is described. Finally, in addition to a series of simulation studies, we illustrate the approach with a case study investigating the complex interplay between gender, APOE, AD diagnosis, and death using data from the Adult Changes in Thought (ACT) study (Kukull et al., 2002).
2 |. A LONGITUDINAL BIVARIATE MODELING FRAMEWORK
This paper proposes a novel longitudinal bivariate modeling framework for semi-competing risks within which dependence between and is characterized in a meaningful and interpretable way, and is permitted to be a function of covariates. Prior to describing the framework, we note how semi-competing risks data are typically represented: letting and denote study entry and right censoring times, respectively, the observed outcome data for the th study participant is , where and . Furthermore, and indicate whether the nonterminal and terminal events, respectively, are observed.
2.1 |. A novel representation of semi-competing risks data
The capacity of the proposed framework to investigate dependence between and hinges on a novel representation of semi-competing risks data that follows from a discretization or partitioning of the analysis time scale. Toward this, let be a set of user-specified points, with for , that define a partition. For example, in analyzing data from ACT one could choose age beyond 65 years as the time scale and . As will become clear, the specification of has important implications, and we return to this task in Section 3.
Given , one can query whether the nonterminal and/or the terminal event was observed to occur within or by the end of any given interval. Toward this, let and be indicators of whether the th study participant experiences the nonterminal and terminal events by time , respectively. In practice, depending on when a study participant contributes person-time on the analysis time scale, they may or may not provide direct information about risk during each of the intervals defined by . For example, an ACT participant enrolled at age 74 years cannot provide direct information about the (65, 70] interval. Thus, the observed outcome data for the th study participant on partition will consist of a longitudinal bivariate process on a subset of the intervals, specifically , where and . The determination of and represents a nontrivial task, and we return to it in Section 3.
Finally, let denote a vector of possibly time-varying covariates measured at time , and the history of all such information at time .
2.2 |. The joint distribution of the observed data
Under the novel representation, we assume that the joint distribution of the observed outcome data, , can be decomposed as the product:
| (1) |
and , and where we define . Underpinning this decomposition is a Markovtype assumption, specifically that, conditional on the totality of the covariate information to that point, the joint probability of the two events in a given interval depends on the history of the two events solely through the status at the start of the interval. As shown in Section A.2 of the Supporting Information, the components of expression (1) can be written in terms of:
| (2) |
| (3) |
| (4) |
for and where
We emphasize that the interpretations of these three quantities are specific to the partition is the cumulative probability of experiencing the nonterminal event by time , given that neither event had occurred by time is the cumulative probability of experiencing the terminal event by time , given that the individual is alive at time ; finally, is the cross-sectional odds ratio for the 2×2 table corresponding to the four possible observed outcome vectors at time , given that neither event had occurred by time . Note that both and are quantities that are modeled in discrete time survival analyses (Prentice and Gloeckler, 1978).
2.3 |. Regression structure
We proceed by placing regression structure on and , specifically:
| (5) |
| (6) |
| (7) |
where , , and are user-specified link functions (e.g., the logistic or log link); , and are each subsets of ; and, , , and are user-specified functions that characterize how the respective quantities depend on the covariates. For example, one may adopt a linear specification with no interactions between the components of and in model (6) by setting .
While their precise interpretations will depend on the partition of the analysis time scale and the chosen link functions, characterize the impact of covariates; Section 2.4 considers the role and interpretation of components of that correspond to . Finally, , and represent baseline time trends in , and , respectively, with their precise interpretation again depending on the choice of , the link functions and covariates included in the models.
From a practical perspective, that consists of parameters may result in computational and/or convergence issues unless the observed data are rich (i.e., a large sample size or high event rates) or the initial partition is coarse. To mitigate such issues, we propose that a B-spline structure be adopted across the components of each of , and (Eilers and Marx, 1996). Focusing on , let denote a collection of user-specified knots on the interior of the range () and the user-specified degree of the local polynomial basis functions. Given these choices, we specify the th component of as , where is the value of the th B-spline at time and is total number of spline terms. Thus, this specification requires estimation of coefficient terms, specifically . Applying the same strategy to and will result in unknown coefficients, collectively denoted as . Finally, to distinguish between specifications, we refer to the model based on with unknowns as the unstructured model while that based on as the -spline model.
2.4 |. Dependence
The central innovation of the framework in expressions (5)–(7) is that dependence between the nonterminal and terminal events is quantified in two distinct and yet complementary ways. The first is captured through which can be viewed as a measure of local dependence in that it quantifies the risk of co-occurrence of the two events, via the odds ratio (Lipsitz et al., 1991; Carey et al., 1993; Ten Have and Morabia, 1999), during the ( interval; a large positive value of indicates that if the nonterminal event (e.g., AD) occurs during then the terminal event (e.g., death) is likely to subsequently occur during the same interval. Because of the novel parameterization, we emphasize that the local dependence can vary over the time scale or as a function of covariates. As such, one could investigate whether local dependence between AD and death is weaker at younger ages relative to older ages. Furthermore, one could investigate whether the probability that the two events co-occur changes in response to key life events such as the death of a partner. The second quantification of dependence is through the components of in expression (6) that correspond to how the status of the nonterminal event, , influences . Labeling these components as , analogous to how one interprets covariates effects in regression models, these parameters capture the extent to which whether the non-terminal event has occurred is associated with a change in risk of the terminal event; for this reason, we refer to as capturing global dependence. Note that global dependence is conceptually similar to the explanatory hazard ratio and cross-quantile residual ratio (see section A.1 of the Supporting Information) in that it concerns the role that the nonterminal event plays in modifying risk of the terminal event.
3 |. KEY PRACTICAL TASKS
The development in Section 2 indicated two practical tasks that analysts must engage in, specifically the choice of and the determination of and .
3.1 |. Choice of partition,
The partition, , plays a critical role in the proposed framework in that it provides the foundation for being able to distinguish between local and global dependence, as we conceptualize them in Section 2.4, and for being able to investigate the role that covariates play. In Section A.2 of the Supporting Information, we show that the underlying distribution for induces the quantities (2)–(4) for any . Thus, regardless of the choice of , the components of the proposed model are well-defined mathematical objects and are, therefore, valid targets for estimation and inference. An important consequence of this is that one cannot say that any given partition corresponds to the “truth.” As indicated in Section 2.2, however, the choice of dictates the numerical values and interpretation of the quantities given by (2)–(4), and correspondingly (in part, at least) the numerical values and interpretation of the parameters in the regression structure given by expressions (5)–(7). As such the choice of requires careful consideration.
In principle, one could approach choosing through consideration of the clinical condition under investigation such as the pace at which the disease progresses. In the ACT study, for example, the choice to schedule follow-up biennially was made in part for logistical considerations but also because AD is a slowly-developing condition. Alternatively, one may pursue a data-driven strategy where, for example, some goodness-of-fit criterion is specified and then optimized as a function of . Our perspective is that the decision should be based primarily, if not exclusively, on clinical considerations. Central to this position is that, in addition to their interpretation, the numerical values of (2)–(4) change with . To see this, we again note that the probabilities in each of (2)–(4) speak to the cumulative incidence of events during the interval . If the length of the interval is decreased then the incidence will necessarily decrease. The corresponding new interpretation and numerical value will not be “wrong,” however, but just different. Put another way, the change in the interpretation and the numerical values of the model parameters that result from, say, adopting a finer partition of the time scale should, arguably, be viewed as a change in the question that is being answered. Thus, in our view, purely data-driven approaches, while they may have some initial intuitive appeal, should be avoided. Nevertheless, we do acknowledge that it may not be easy to elicit a single partition, from the literature or collaborators, on which to base the analyses and conclusions. If it is the case that there is no clear choice, analysts may opt to perform a range of analyses over different partitions, both in terms of how fine the partition is and in terms of where the cut-points are for a given (common) interval length. We pursue this strategy in conducting the analyses of the data from ACT in Section 6.
3.2 |. Determination of and
While the act of partitioning the analysis time scale provides the basis for learning about dependence, there is a trade-off in that there is a loss of information that impacts how one approaches setting and . To illustrate this, and the framework more generally, Figure 1 provides a graphical representation of observed outcome data for two hypothetical study participants; an expanded figure, with five hypothetical participants, is provided in Section A.2 of the Supporting Information. From the top half of the figure, we see that the first participant was observed to enter the study in the interval, experience the nonterminal event in the interval and subsequently experience the terminal event in . From the bottom half of the figure, the second participant was observed to enter the study in the interval and subsequently experience the nonterminal event in (. In contrast to participant , however, they are censored prior to being observed to experience the terminal event, specifically in (.
FIGURE 1.

Graphical representation of the interplay between standard notation for semi-competing risks outcome data and the proposed bivariate longitudinal framework; see Sections 2 and 3.2 for details.
In considering the value of , it seems clear that setting for the first participant is appropriate, so that their outcome data in the interval are . For the second participant, one could follow suit and set so that, acknowledging that they had previously been observed to experience the nonterminal event but not the terminal event, their outcome data in the interval would be . Doing so, however, assumes that the terminal event did not occur in the subinterval . Alternatively, one can interpret the choice as assuming complete person-time in the interval when this was not, in fact, the case. With this latter interpretation, there is an argument to be made that one should not attempt to learn about expressions (2)–(4) for and that, instead, one should adopt a more conservative stance by setting and forgoing the partial information regarding this particular interval.
Figure 1 also helps illustrate similar considerations regarding . Specifically, in considering which of the intervals the first participant can be said to first contribute to, since setting seems a natural choice and, coupled with , would result in observed outcome data in four intervals, specifically . Problematic with setting , however, is that complete person-time for the interval was not observed since . As such, there is, arguably, incomplete data regarding the quantities given by expressions (2)–(4) for this particular interval and a more conservative approach would be set so that, again coupled with , the observed outcome data would be restricted to three intervals, specifically , and that the partial information in is ignored.
To summarize, in setting both and analysts have an option that can be viewed as being conservative, in which partial information is ignored. In contrast, analysts have the option to be anticonservative by including the intervals with partial person-time as if they had complete person-time. One common feature of both of these strategies is that they are agnostic to the amount of partial information; that is how close and are to the right-hand limit of the interval in which they were observed. We therefore propose a third strategy, labeled the nearest neighbor strategy in which the partial information is acknowledged. Focusing initially on , suppose . While the anti-conservative and conservative strategies would always set and , respectively, the nearest neighbor strategy takes if and otherwise. Similarly, suppose . While the anticonservative and conservative strategies would always set and , respectively, the nearest neighbor strategy takes if and otherwise.
To highlight the impact adopting each of the three proposed strategies have, Figure 1 provides the corresponding outcome information for the two hypothetical study participants. In practice, analysts will need to base the decision of which strategy to use by balancing the information gain/loss with their own conservatism regarding taking person-time to be complete in an interval when it is not. Since the nearest neighbor strategy represents, in a sense, a compromise, it is the primary strategy that we would recommend. Of course, analysts may consider other strategies or, as we do in Section 6, consider a range of strategies and examine their impact. Finally, we note that the extent to which this is a concern depends, in part at least, on how coarse the partition is; with finer and finer partitions, the information loss associated with the conservative strategy will decrease.
4 |. ESTIMATION AND INFERENCE
4.1 |. The observed data likelihood
Building on the notation developed in Section 2, the first two columns of Table 1 provide the six possible outcome data scenarios in the th interval of the partition given by as a function of the outcome vector in the previous interval (i.e., as a function of ). The third column provides the corresponding likelihood contributions, that is the interval-specific components in the decomposition given by expression (1), with
where (Ten Have and Morabia, 1999).
TABLE 1.
Six possible data scenarios for the kth interval in the partition given by (see Section 2)
| Likelihood contribution | ||
|---|---|---|
|
| ||
| (0, 0) | (0, 0) | |
| (0, 0) | (1, 0) | |
| (0, 0) | (0, 1) | |
| (0, 0) | (1, 1) | |
| (1, 0) | (1, 0) | |
| (1, 0) | (1, 1) | |
Let denote the collection of unknown parameters in the specification of model (5)–(7). Note that if the unstructured form of the model is fit then while if the B-spline model is fit. For either specification, the observed data likelihood for a random sample of study participants from the population of interest, is the product of terms, each of the form:
See Section A.2 of the Supporting Information for further details.
4.2 |. Estimation
If the unstructured form of model (5)–(7) is adopted, estimation can proceed in a straightforward manner by finding the maximizer of , denoted by . Under the proposed B-spline model, however, care is needed to avoid overfitting. To resolve this, we maximize the observed data likelihood subject to a penalty that imposes smoothness in resulting estimated functions. One such penalty is the integrated squared second derivative which, following Eilers and Marx (1996), can be approximated by penalizing coefficient differences. Let be the difference operator so that, for example, . Then, letting , consider the penalized likelihood:
where corresponds to the difference operator having been applied times; for example, . Note that letting denote the matrix representation of , such that, for example, can be written as (Section A.2 of the Supporting Information), the penalized likelihood can be written as:
| (8) |
Let be the -penalized likelihood. Furthermore, let be the gradient of with respect to and the corresponding matrix of second partial derivatives (i.e., the Hessian matrix). For a given value of , the penalized maximum likelihood estimator, which we denote by , is the solution to . Note, since the penalty is quadratic in , and , gradient-based maximization is relatively straightforward to carry out. This penalization induces smoothing in the estimated function as it approximates penalization of the th derivatives of the functions (Eilers and Marx, 1996).
Finally, toward choosing the value of on which the final results are to be based, say , one can proceed using any standard model-selection criteria such as the Akaike Information Criterion (AIC) or cross-validation (Gray, 1992; Eilers and Marx, 1996). In our implementation of the methods, we follow Gray (1994) by taking the trace of as the effective degrees of freedom when calculating the AIC.
4.3 |. Asymptotic properties
For the unstructured model, under standard regularity conditions, the asymptotic distribution of follows from standard likelihood theory. That is, is consistent and, letting denote the value of induced from the partition, is asymptotically normal with variance equal to the inverse of Fisher information matrix.
For the B-spline model, careful consideration of the asymptotic properties of requires specification of how the number of knots, , and the penalty, , change with the sample size . This has been the focus of a large body of work, much of which is concerned with error estimation for the nonparametric function(s) (e.g., Li and Ruppert, 2008). Here, however, primary interest lies with inference for . Given this, we consider the behavior of in settings where both and are fixed. With this, henceforth, we denote the estimator as .
In Section A.3 of the Supporting Information, assuming standard regularity conditions, we show that ) is asymptotically normal with variance that can be consistently estimated by
| (9) |
where is the solution of and where is the gradient of the log-penalized likelihood of a single observation . For individual parameters, the appropriate entry in the diagonal of (9) is used for estimating the variance. For the baseline time trends, let be the submatrix corresponding to the estimated variance matrix of . Note that can be written as with being a matrix with elements . Therefore, to construct a 95% confidence interval (CI) for the AD time-varying reference probability, , one can use where here to be understood as operating entrywise on the vector, and returns the diagonal of a matrix.
5 |. SIMULATION STUDIES
We conducted a series of simulations to investigate: (i) finite-sample properties of the methods proposed in Section 4; and (ii) the potential bias-variance trade-off that analysts will have to contend with when choosing the degree of regularization in . We note that we make no attempt to perform a comparison with existing methods since the proposed framework was developed to investigate dependence in a way that is distinct from how existing methods approach it. Due to space constraints, we present brief details and a summary of the main conclusions; see Section A.4 in the Supporting Information for full details.
Building on features of the observed data from the ACT study, we generated the data according to models (5)–(7) as a function of both time-fixed and time-dependent covariates under three scenarios for dependence: a null scenario, a simple dependence scenario, and a complex dependence scenario. A range of right-censoring rates (0–30%) and sample sizes (500–5000) were considered. For each scenario, 1000 data sets were generated. All simulations were carried out using code available in the LongitSemiComp package for R. Simulation code, seeds, and results are all available online via the Github repository of the first author.
Figures A.2 and A.3 in the Supporting Information summarize performance regarding estimation of time-varying functions. The time-varying terminal event probability function was generally well-estimated. The time-varying nonterminal probability function was also well-estimated except when the number of knots was small and a substantial amount of regularization were used (i.e., and ); in this case the B-spline estimator was oversmoothed, resulting in bias for later time points where less information is available. The time-varying odds ratio function was well-estimated by the 10 knots B-spline estimator for large enough sample size, as well as by the five knots B-spline estimator when sample size was large enough and there were no oversmoothing. Similar to the nonterminal probability, the five knots over-smoothed estimator suffered from bias. A model with completely unrestricted , and performed well for but not for , for which considerable bias was found for low and moderate sample sizes. Instability of the undersmoothed estimators for time-varying odds ratio, and biased, yet stable, estimators when using excessive smoothing were found when the sample size was small. Using AIC to choose , more smoothing was desired for compared with (Table A.2).
Turning to the coefficients (Tables A.3–A.10), small finite-sample bias for and was mitigated under larger sample sizes. The global dependence parameter was well-estimated, with negligible bias for all sample sizes and censoring rates. A small finite-sample bias was observed for in some of the scenarios, although it decreased as the sample size increased. Furthermore, the bias was more substantial when the sample size was low and the unrestricted model was used for the time-varying functions. Unpenalized estimation under B-spline representation also resulted in bias for . However, penalization largely mitigated this and also reduced the standard error. For larger sample sizes, this bias disappeared. These results were consistent with the performance of the time-varying component estimator of the odds ratio. Finally, in most cases the proposed variance estimators performed well, with empirical coverage of confidence intervals close to the nominal level.
We conducted additional simulations to compare the different strategies in setting and (Section 3.2). Details are presented in Section A.4.4 of the Supporting Information.
6 |. ANALYSIS OF DATA FROM THE ACT STUDY
The ACT study is an ongoing community-based prospective study of incident all-cause dementia and AD among the elderly in western Washington state (Kukull et al., 2002). Initiated in 1994, the goals of the study are to learn about how the brain ages and to identify risk factors for AD. In this paper, we consider data on ACT participants enrolled between 1994 and 2015, and who were aged 65 years or older and cognitively intact at the time of enrollment. Table A.12 in the Supporting Information summarizes key characteristics measured at study entry, including: age, gender, race, marital status, education, comorbid depression, and APOE- carrier status. Follow-up in ACT consists of biennial visits during which participants undergo a comprehensive neurological evaluation. For the purposes of this paper, follow-up time was administratively censored at the first of December, 2016 or age 99 years. Based on these criteria, 205 (5%) were diagnosed with AD during follow-up but were censored prior to death, 818 (19%) were diagnosed with AD and died during follow-up, 1613 (37%) died during follow-up without a diagnosis of AD, and 1731 (39%) were censored prior to either a diagnosis of AD or experiencing death. Figure A.5 in the Supporting Information provides a summary of the observed person-time.
Having ≥1 APOE allele is well-established as a genetic risk factor for AD (Baumgart et al., 2015). The extent to which having ≥1 APOE allele is associated with mortality, however, is unclear (Helzner et al., 2008). Since, to the best of our knowledge, no previous studies have examined the role of the APOE allele through the lens of semicompeting risks, the opportunities that semi-competing risks analyses provide, particularly in terms of explicit acknowledgment of death as a competing risk and in terms of being able to learn about dependence, have not been taken advantage of.
With this backdrop, we present a case study with the goal to investigate the role of having ≥1 APOE allele on the joint risk of AD and death, and whether this varies by gender. Throughout, we use data from ACT with the time scale taken to be “time since age 65” or “time since a diagnosis of AD,” as appropriate. In reporting results, we focus on those that pertain to dependence; additional details, results, and sensitivity analyses are provided in Section A.6 of the Supporting Information. In addition, we performed a series of analyses based on a range of existing methods, including a standard illness-death model, the explanatory hazard ratio, and the cross-quantile residual ratio; Section A.6 of the Supporting Information provides details on the different analyses, results, and discussion.
6.1 |. Analyses based on the proposed framework
As emphasized in Section 3.1, the choice of the partition is important. Toward illustrating the role of this choice, and recalling that participants in ACT underwent biennial visits, we considered two partitions of the time scale [65, 100): , for which ; and, , for which . See Tables A.13 and A.14 in the Supporting Information for the 2×2 outcome tables.
Toward specification of models (5)–(7), we used logit links for and , and a log link for the cross-sectional odds ratio, . In these models, , and were specified with the overarching goal of assessing the joint impact of having ≥1 APOE allele and gender on the joint risk of AD and death. As such, the models for and included main effects for having ≥1 APOE allele and gender, and their interaction, while the model for included main effects, two-way interactions and the three-way interaction between AD diagnosis, having ≥1 APOE allele and gender. For , we additionally included all other variables available in data set.
To complete the models specifications, we considered unstructured and B-spline baseline parameters, , and . For the latter, we used 10 knots for and five knots for , with a cubic spline and a second-order difference penalty (i.e., in ), and considered varying degrees of penalty, specifically setting , with . Finally, following the discussion of Section 3.2, we considered all three strategies for determining and . Table A.19 in the Supporting Information reports AIC from the various fitted models from which we see that the optimal values of were and for and , respectively, across all three strategies for determining and . While there were no convergence issues in the data analysis, in our experience with the simulation studies adding a small penalty may mitigate potential convergence issues (see Section A.4.2 in the Supporting Information).
6.1.1 |. Baseline time trends
Figures 2 and 3 report estimated baseline time trends, with the latter focusing on the estimates obtained based on the nearest neighbor strategy. Note that the interpretation of these quantities is specific to a population of individuals who are cognitively intact at age 65 and have the following characteristics: male, nonwhite, non-college-educated, married without depression, and no APOE alleles.
FIGURE 2.
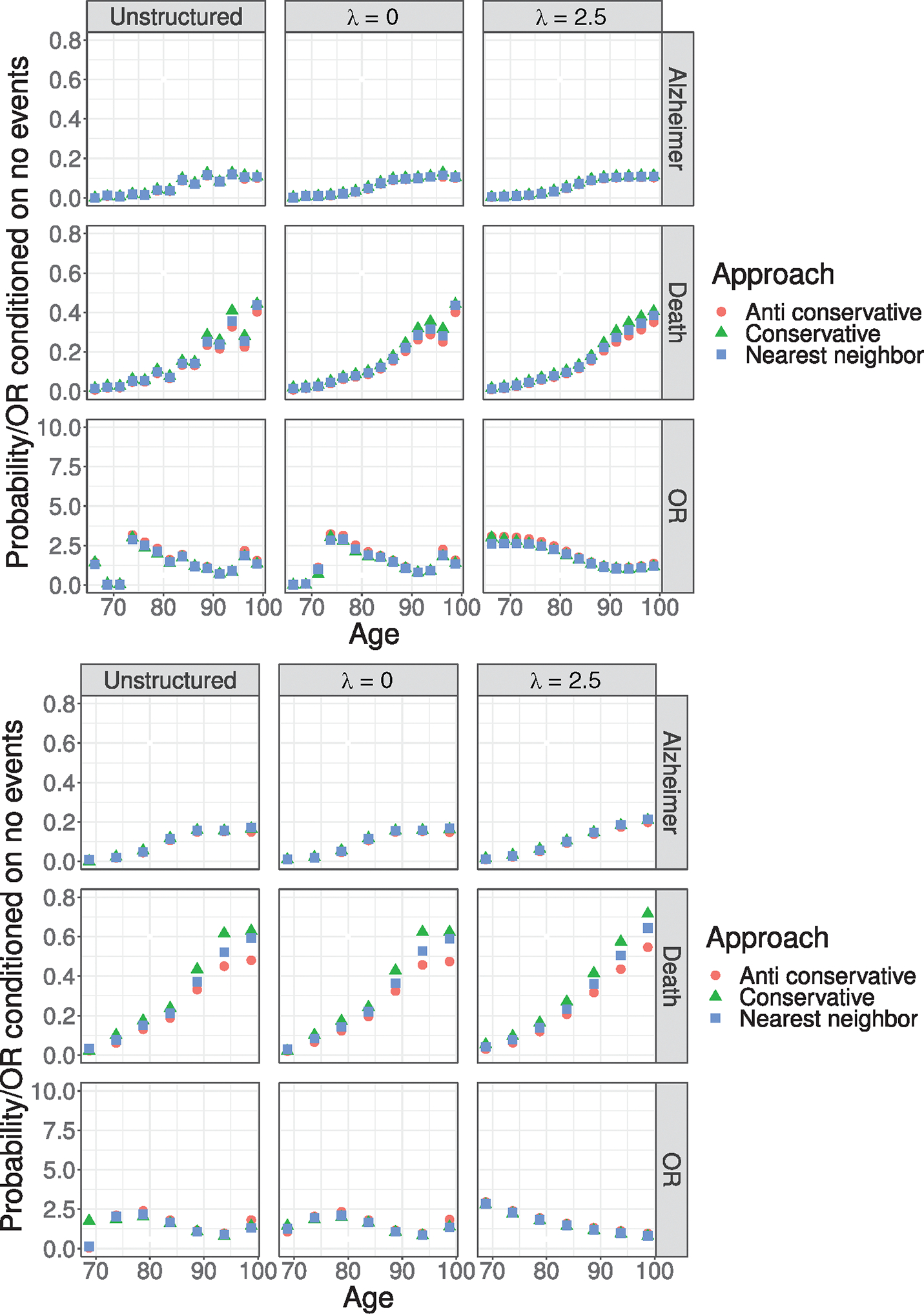
Comparison in the ACT data between the three approaches to overcome within-interval censoring and study entry times. The figures present the estimated baseline time trends, , and , under the unstructured specification and the B-spline specification with and under the two partitions (top panel) and (bottom panel). Note that the -axis has been truncated at 0.8 for and at 10 for .
FIGURE 3.
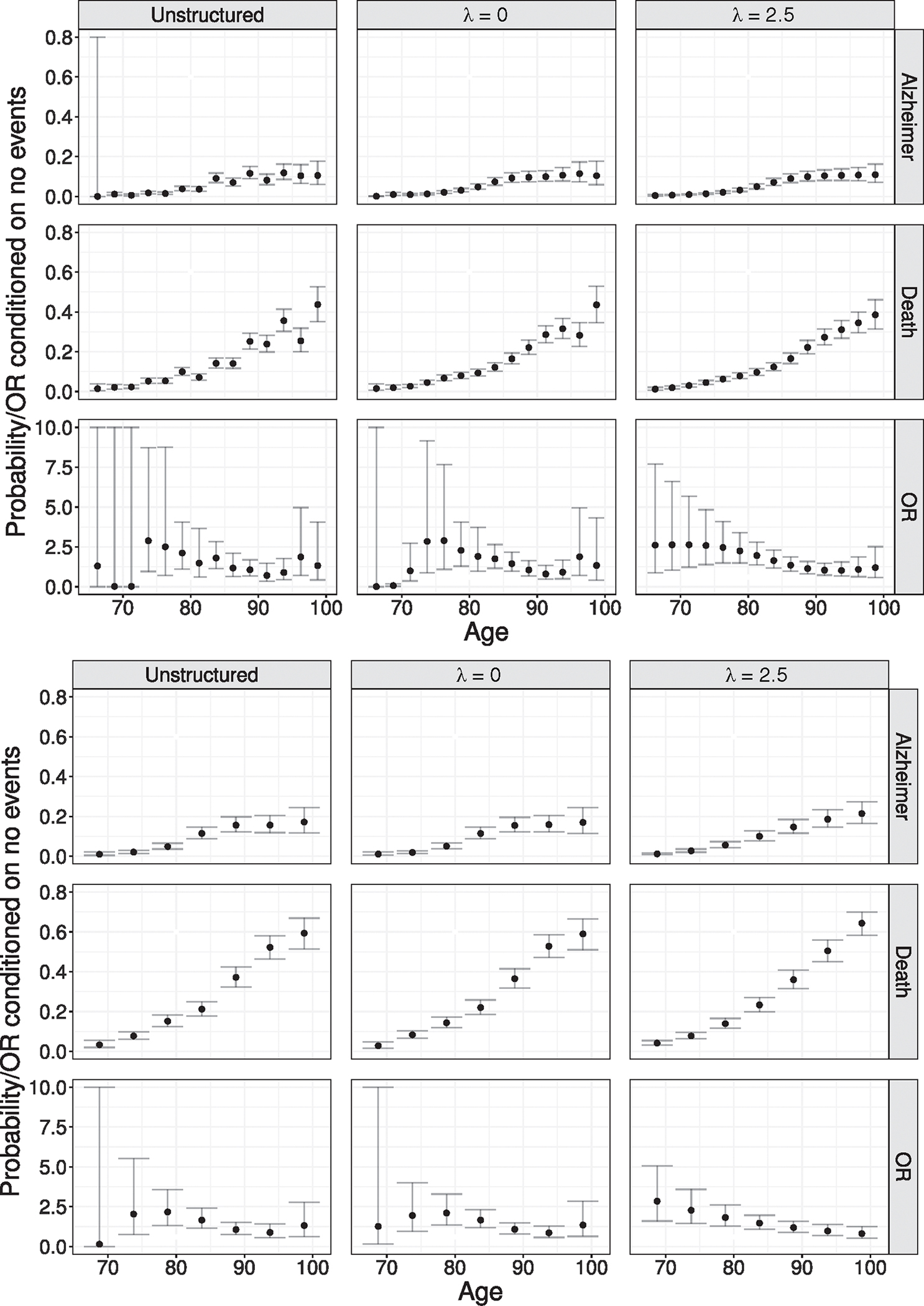
Estimated baseline time trends, , and from a series of analyses to the ACT data, under the unstructured specification and the B-spline specification with and under the two partitions (top panel) and (bottom panel). See Section 6.1 for details. Also shown are 95% confidence intervals. Note that the -axis has been truncated at 0.8 for and at 10 for . For results under more values, see Supplementary Figures A.10 and A.11. Results presented under the nearest neighbor strategy
From Figure 2, we find little overall sensitivity in the estimates across the three strategies for determining and , with the sole exception being in the tails of the conditional probability of death. That this is the case may not be surprising, however, given that overall probability is larger and that the sample size is smaller as the population ages into their 90s. As expected, however, the nearest neighbor strategy provides a reasonable compromise between the conservative and anticonservative strategies.
From Figure 3, the unstructured models, not surprisingly, exhibit greater uncertainty, especially in information-poor parts of the age scale (i.e., early on when there are relatively few AD events). From the top panel of Figure 3, under the B-spline analysis with , the estimated baseline probability of an AD diagnosis during a given 2.5 year age interval, conditional on being AD-free and alive at the start of the interval, increases from 0.005 in (65.0, 67.5] to 0.11 in (97.5, 100.0]. From the bottom panel of Figure 3, the same increasing pattern emerges under partition with , specifically from 0.01 in (65.0, 70.0] to 0.17 in (95.0, 100.0]. Note that this is as expected since the intervals are longer and, correspondingly, the cumulative number of events higher. Also from Figure 3, we see that the estimated baseline probability of death conditional on being event free during a given 2.5-year age interval increases from 0.01 in (65.0, 67.5] to 0.38 in (97.5, 100.0]. Again, the same general pattern is observed under , with the probability increasing from 0.03 in (65.0, 70.0] to 0.59 in (95.0, 100.0].
6.1.2 |. Covariate effects for AD
Table 2 reports estimated covariate associations from the B-spline fits for the main effects and interactions corresponding to gender, having ≥1 APOE allele and AD diagnosis (as appropriate). Results based on all three strategies regarding and are presented; complete results, including those from the unstructured models, are given in Tables A.20–A.24 of the Supporting Information.
TABLE 2.
Select results, specific to the role of gender and having ≥1 APOE allele on the joint risk of AD and death, based on the proposed framework applied to the data from the Adult Changes in Thought study
| Alzheimer’s Disease, |
Death, |
Cross-sectional odds ratio, |
||||
|---|---|---|---|---|---|---|
|
|
|
|
||||
|
| ||||||
| Conservative a | ||||||
| Female | 0.98 (0.82, 1.16) | 1.13 (0.94, 1.36) | 0.58 (0.51, 0.65) | 0.55 (0.48, 0.64) | 0.76 (0.50, 1.17) | 0.82 (0.55, 1.22) |
| APOEb | 1.85 (1.44, 2.36) | 1.96 (1.48, 2.58) | 0.97 (0.80, 1.18) | 0.97 (0.78, 1.22) | 0.57 (0.28, 1.13) | 0.72 (0.39, 1.34) |
| Female × APOEb | 0.98 (0.72, 1.34) | 0.91 (0.64, 1.29) | 1.13 (0.87, 1.46) | 1.19 (0.89, 1.59) | 1.24 (0.50, 3.04) | 1.16 (0.53, 2.53) |
| ADc | 2.54 (1.99, 3.24) | 2.69 (1.88, 3.87) | ||||
| ADc × Female | 1.52 (1.12, 2.06) | 1.95 (1.22, 3.11) | ||||
| ADc × APOEb | 1.55 (0.99, 2.44) | 2.01 (0.99, 4.06) | ||||
| ADc × Female ×APOEb | 0.66 (0.38, 1.14) | 0.55 (0.23, 1.29) | ||||
| Anti-conservative a | ||||||
| Female | 0.97 (0.82, 1.14) | 0.99 (0.83, 1.17) | 0.57 (0.51, 0.64) | 0.55 (0.48, 0.62) | 0.78 (0.51, 1.19) | 0.96 (0.67, 1.38) |
| APOEb | 1.84 (1.45, 2.32) | 1.83 (1.44, 2.34) | 0.97 (0.81, 1.17) | 0.98 (0.81, 1.20) | 0.58 (0.29, 1.14) | 0.78 (0.44, 1.38) |
| Female × APOEb | 1.03 (0.77, 1.38) | 1.03 (0.76, 1.41) | 1.10 (0.85, 1.41) | 1.13 (0.87, 1.46) | 1.20 (0.49, 2.91) | 1.01 (0.49, 2.09) |
| ADc | 2.61 (2.06, 3.31) | 2.77 (2.01, 3.82) | ||||
| ADc × Female | 1.56 (1.16, 2.09) | 1.82 (1.21, 2.73) | ||||
| ADc × APOEb | 1.69 (1.09, 2.62) | 2.33 (1.24, 4.41) | ||||
| ADc × Female ×APOEb | 0.62 (0.36, 1.06) | 0.49 (0.23, 1.05) | ||||
| Nearest Neighbor a | ||||||
| Female | 0.95 (0.81, 1.12) | 1.03 (0.87, 1.22) | 0.57 (0.50, 0.64) | 0.56 (0.49, 0.64) | 0.79 (0.52, 1.21) | 0.91 (0.62, 1.31) |
| APOEb | 1.87 (1.48, 2.37) | 1.91 (1.48, 2.45) | 0.96 (0.79, 1.16) | 0.98 (0.80, 1.19) | 0.56 (0.28, 1.10) | 0.70 (0.39, 1.26) |
| Female × APOEb | 1.00 (0.74, 1.35) | 0.95 (0.69, 1.30) | 1.12 (0.87, 1.44) | 1.12 (0.86, 1.47) | 1.24 (0.51, 3.04) | 1.18 (0.56, 2.47) |
| ADc | 2.63 (2.07, 3.34) | 2.80 (2.00, 3.92) | ||||
| ADc × Female | 1.51 (1.12, 2.04) | 1.94 (1.26, 2.99) | ||||
| ADc × APOEb | 1.56 (1.00, 2.43) | 2.34 (1.19, 4.58) | ||||
| ADc × Female ×APOEb | 0.66 (0.38, 1.15) | 0.42 (0.19, 0.96) | ||||
An indicator of having at least one APOE allele.
An indicator of whether the patient has previously had a diagnosis of Alzheimer’s disease
Based on the optimal λ of λ*=2.5 for and λ*=0.0 for .
Note Results are shown for the B-spline approach. Complete results are given in Tables A.20–A.24 of the Supporting Information
From the first two columns of Table 2, the results regarding risk of AD are largely consistent between the two partitions as well as across the three strategies for determining and . Specifically, we find that, while having ≥1 APOE allele is a strong risk factor, there is no evidence that gender is a risk factor nor that it is an effect modifier of the APOE effect. Note that the results under the unstructured model are similar (see the Supporting Information).
6.1.3 |. Covariate effects for death and global dependence
The middle set of results in Table 2 report on how gender, having ≥1 APOE allele and having a diagnosis of AD jointly influence risk of mortality. Note the four components involving a diagnosis of AD correspond to in model (6) and, thus, jointly represent global dependence between AD and mortality. As with the results regarding the risk of AD, the results for death are largely consistent across the three strategies for determining and . Interestingly, there are some differences between those based on the partition and those based on the partition, although the overarching conclusion that there is an important interplay between the three factors in determining risk of mortality is consistent between the two.
To further facilitate discussion of the results, Table 3 reports odds ratio estimates and 95% confidence intervals for mortality, based on the B-spline model with the nearest neighbor strategy for determining and , across combinations of whether the patient has had an AD diagnosis, their gender, and whether they have ≥1 APOE allele. From the first four rows, in the absence of a diagnosis of AD, female gender is associated with approximately 40% lower odds of mortality while there is no evidence to indicate that the number of APOE alleles play a role.
TABLE 3.
Odds ratio estimates and 95% confidence intervals for mortality across combinations of whether the patient has had an AD diagnosis, their gender, and whether they have ≥1 APOE allele
| Odds ratio (95% CI) |
||||
|---|---|---|---|---|
| AD status | Gender | # APOE alleles | ||
|
| ||||
| No AD | Male | 0 | 1.00 | 1.00 |
| No AD | Male | ≥ 1 | 0.96 (0.79, 1.16) | 0.98 (0.80, 1.19) |
| No AD | Female | 0 | 0.57 (0.50, 0.64) | 0.56 (0.49, 0.64) |
| No AD | Female | ≥ 1 | 0.61 (0.52, 0.73) | 0.61 (0.51, 0.74) |
| AD | Male | 0 | 2.63 (2.07, 3.34) | 2.80 (2.00, 3.92) |
| AD | Male | ≥ 1 | 3.94 (2.79, 5.56) | 6.42 (3.66, 11.28) |
| AD | Female | 0 | 2.26 (1.87, 2.75) | 3.04 (2.29, 4.04) |
| AD | Female | ≥ 1 | 2.51 (1.97, 3.18) | 3.28 (2.32, 4.65) |
Note. Results are based on the B-spline models under the nearest neighbor strategy as reported in Table 2.
From the lower half of Table 3, the odds of mortality among those patients with a diagnosis of AD diagnosis, and, thus, extent of global dependence, is substantially higher with the magnitude depending on the interplay between gender and the number of APOE alleles. Moreover, while having at least APOE alleles seems to be associated with higher odds, the increase is substantially larger for males.
6.1.4 |. Local dependence
Turning to the assessment of local dependence, the third row in the two subfigures of Figure 3 suggest that there are meaningful time trends in the co-occurrence of AD and death, specifically that the risk of co-occurrence within a given interval are highest at the early ages. From the B-spline specification with applied to partition , for example, the odds ratio among males with no APOE alleles decreases from 2.61 (95% CI: 0.89, 7.69) during the (65.0, 67.5] interval to 1.20 (95% CI: 0.57, 2.51) during the (97.5, 100.0]. From Table 2, although the confidence intervals all include 1.00, the point estimates for all three covariates in the model applied to the partition are indicative of clinically meaningful associations. For example, the local dependence odds ratio is estimated to be 44% smaller among males with ≥1 APOE allele compared to those without. The corresponding odds ratio for females is estimated to be approximately 31% smaller (0.56 × 1.24 ≈ 0.69) for those with ≥1 APOE allele compared to those without.
Finally, Tables 2 and 3 highlight that the choice of partition can have a meaningful impact on the conclusions regarding local. In particular, under the evidence regarding an interaction between gender and having ≥1 APOE allele on local dependence is weaker when the partition intervals are 5 years in length.
7 |. DISCUSSION
Although less familiar than competing risks, semi-competing risks arise in a wide range of clinical settings, including: AD, as illustrated in this paper; hospital readmission (Lee et al., 2015, 2016); shock among patients with implanted cardiac devices (Reeder et al., 2019); and graft-versus-host disease (Jazić et al., 2020; Lee etal., 2020). One distinguishing feature of semi-competing risks is that there is partial information about the joint distribution between and . To leverage that information, we have proposed novel framework that seeks to gain interpretable insight into dependence between the two events. Because the interpretation of the model components, including the proposed notions of global and local dependence, are distinct from those obtained from existing methods, we view the framework as being scientifically complementary to existing methods. Moreover, we view the proposed framework as being in-line with recent work that seeks to better understand whether and how specific factors confer risk jointly on multiple outcomes, such as the dual hazard rate (Prentice and Zhao, 2020).
The foundation for the proposed framework is the discretization of the time scale. As discussed in Sections 2.2 and 3.1, one cannot say that a given choice of is the “truth” and yet the specific choice dictates the numerical values and interpretation of the results. This results in a tension that is illustrated in Table 2: one cannot claim that either or is the “right” choice and yet there are instances where the numerical results differ in meaningful ways. Our view of this dilemma is that consideration of multiple partitions should be viewed as an opportunity to obtain additional insight. Consider, for example, the main effect of female gender in the model for based on the B-spline specification: under the estimated impact of female gender is to reduce the local dependence odds ratio by 20% while the reduction is only 10% under . Thus, ignoring (for the purpose of discussion) the lack of statistical significance, there is an indication that among individuals with no APOE alleles, gender plays a role in the co-occurrence of AD and death over relatively short time frames (i.e., 2.5 years) and over longer time frames (i.e., 5 years), although the magnitude of the effect attenuates over the longer time frame. Conceptually, this is analogous to the results that one might see in a Cox model for a univariate outcome if the effect of a covariate varies over time (i.e., nonproportional hazards) and yet proportional hazards is adopted; in such settings, the value of the common hazard ratio that is being estimated will depend on the interval over which data are available.
While the proposed framework provides researchers with a flexible approach to investigating dependence in semi-competing risks data, one trade-off is that, as discussed in detail in Section 3.2, a degree of ambiguity arises regarding the specific form of the contribution to the likelihood for select individuals. Our approach to addressing this challenge, one that is similarly faced in other time-to-event analyses based on a discretization of the time scale (Prentice and Gloeckler, 1978; D’Agostino et al., 1990; Hernán et al., 2000), is via sensitivity analyses. While the simulations we present and data application point to little sensitivity for the contexts they are based on, in other settings (e.g., when there is substantial censoring and/or when the intervals of the partition are wide) the results may indeed be sensitive. For these settings, researchers may opt to report all results and attempt to glean insight from the specifics of the context or to view the sensitivity as an indicator that there is insufficient information on which to base definitive conclusions regarding dependence.
A number of extensions to the proposed framework are possible. The Markov assumption (1) could be relaxed, for example, by having in (3) depend on the entire disease status history . More broadly, a topic for future research is developing methods for testing of assumptions and assessment goodness of fit. From a theoretical perspective, an interesting alternative to having fixed is to consider ; that is the amount of regularization decreases as more data become available. This framing of the asymptotics, however, leads to a variance expression that does not involve and thus has been perceived as of less useful in practice (Gray, 1992; Yu and Ruppert, 2002). Another issue concerns interval-censoring of the data. As mentioned in Section 6 follow-up in ACT consists of biennial visits. As such, while the date of death can be precisely ascertained through death records, AD is subject to interval censoring. Therefore, generalizing our approach to interval-censored data will be of interest. A related problem may arise in defining covariate values when time-dependent covariates are observed only intermittently (Nevo et al., 2020).
Supplementary Material
ACKNOWLEDGMENTS
The authors thank the Associate Editor and Reviewer for helpful comments and gratefully acknowledge funding from National Institutes of Health Grant R-01 CA181360.
Footnotes
SUPPORTING INFORMATION
Web Appendices, Tables, and Figures referenced in Sections 1–6 are available with this paper at the Biometrics website on Wiley Online Library. All simulations were carried out using code available in the LongitSemiComp package for R. Simulation code, seeds and results are all available online via the Github repository of the first author (https://github.com/daniel258/CausalSemiCompReproduce).
DATA AVAILABILITY STATEMENT
The data that were used in this paper are available from Kaiser Permanente Washington Health Research Institute. Restrictions may apply to the availability of these data. Further information can be found at https://www.kpwashingtonresearch.org.
REFERENCES
- Alzheimer’s Association., (2018) 2018 Alzheimer’s disease facts and figures. Alzheimer’s & Dementia, 14, 367–429. [Google Scholar]
- Baumgart M, Snyder H, Carrillo M, Fazio S, Kim H and Johns H (2015) Summary of the evidence on modifiable risk factors for cognitive decline and dementia: a population-based perspective. Alzheimer’s & Dementia, 11, 718–726. [DOI] [PubMed] [Google Scholar]
- Carey V, Zeger S and Diggle P (1993) Modelling multivariate binary data with alternating logistic regressions. Biometrika, 80, 517–526. [Google Scholar]
- D’Agostino R, Lee M-L, Belanger A, Cupples L, Anderson K and Kannel W (1990) Relation of pooled logistic regression to time dependent Cox regression analysis: the Framingham heart study. Statistics in Medicine, 9, 1501–1515. [DOI] [PubMed] [Google Scholar]
- Egleston B, Scharfstein D, Freeman E and West S (2006) Causal inference for non-mortality outcomes in the presence of death. Biostatistics, 8, 526–545. [DOI] [PubMed] [Google Scholar]
- Eilers P and Marx B (1996) Flexible smoothing with B-splines and penalties. Statistical Science, 11, 89–102. [Google Scholar]
- Fine J, Jiang H and Chappell R (2001) On semi-competing risks data. Biometrika, 88, 907–919. [Google Scholar]
- Gray R (1992) Flexible methods for analyzing survival data using splines, with applications to breast cancer prognosis. Journal of the American Statistical Association, 87, 942–951. [Google Scholar]
- Gray R (1994) Spline-based tests in survival analysis. Biometrics, 50, 640–652. [PubMed] [Google Scholar]
- Haneuse S and Lee K (2016) Semi-competing risks data analysis: accounting for death as a competing risk when the outcome of interest is nonterminal. Circulation: Cardiovascular Quality and Outcomes, 9, 322–331. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Helzner E, Scarmeas N, Cosentino S, Tang M, Schupf N and Stern Y (2008) Survival in Alzheimer disease: a multi-ethnic, population-based study of incident cases. Neurology, 71, 1489–1495. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hernán MÁ, Brumback B and Robins JM (2000) Marginal structural models to estimate the causal effect of zidovudine on the survival of HIV-positive men. Epidemiology, 11, 561–570. [DOI] [PubMed] [Google Scholar]
- Jazić I, Lee S, and Haneuse S (2020) Estimation and inference for semi-competing risks based on data from a nested case-control study. Statistical Methods in Medical Research, 29, 3326–3339. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jazić I, Schrag D, Sargent D and Haneuse S (2016) Beyond composite endpoints analysis: semi-competing risks as an underutilized framework for cancer research. Journal of the National Cancer Institute, 108, djw154. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kukull W, Higdon R, Bowen J, McCormick W, Teri L, Schellenberg G, et al. (2002) Dementia and Alzheimer disease incidence: a prospective cohort study. Arch of Neurology, 59, 1737–1746. [DOI] [PubMed] [Google Scholar]
- Lee C, Lee SJ and Haneuse S (2020) Time-to-event analysis when the event is defined on a finite time interval. Statistical Methods in Medical Research, 29, 1573–1591. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lee K, Dominici F, Schrag D and Haneuse S (2016) Hierarchical models for semi-competing risks data with application to quality of end-of-life care for pancreatic cancer. Journal of the American Statistical Association, 111, 1075–1095. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lee K, Haneuse S, Schrag D and Dominici F (2015) Bayesian semiparametric analysis of semi-competing risks data: investigating hospital readmission after a pancreatic cancer diagnosis. Journal of the Royal Statistical Society Series C, 64, 253–273. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lee K, Rondeau V and Haneuse S (2017) Accelerated failure time models for semi-competing risks data in the presence of complex censoring. Biometrics, 73, 1401–1412. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Li R and Peng L (2015) Quantile regression adjusting for dependent censoring from semi-competing risks. Journal of the Royal Statistical Society Series B, 77, 107–130. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Li Y and Ruppert D (2008) On the asymptotics of penalized splines. Biometrika, 95, 415–436. [Google Scholar]
- Lipsitz S, Laird N and Harrington D (1991) Generalized estimating equations for correlated binary data: using the odds ratio as a measure of association. Biometrika, 78, 153–160. [Google Scholar]
- Nevo D and Gorfine M (2020) Causal inference for semi-competing risks data. arXiv preprint arXiv:2010.04485. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nevo D, Hamada T, Ogino S and Wang M (2020) A novel calibration framework for survival analysis when a binary covariate is measured at sparse time points. Biostatistics, 21, e148–e163. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Peng L and Fine J (2007) Regression modeling of semi-competing risks data. Biometrics, 63, 96–108. [DOI] [PubMed] [Google Scholar]
- Prentice R and Gloeckler L (1978) Regression analysis of grouped survival data with application to breast cancer data. Biometrics, 34, 57–67. [PubMed] [Google Scholar]
- Prentice R and Zhao S (2020) Regression models and multivariate life tables. Journal of the American Statistical Association, 1–16. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Reeder H, Shen C, Buxton A, Haneuse S and Kramer D (2019) Joint shock/death risk prediction model for patients considering implantable cardioverter-defibrillators: a secondary analysis of the SCD-HeFT trial. Circulation: Cardiovascular Quality and Outcomes, 12, e005675. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tchetgen Tchetgen EJ (2014) Identification and estimation of survivor average causal effects. Statistics in Medicine, 33, 3601–3628. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ten Have T and Morabia A (1999) Mixed effects models with bivariate and univariate association parameters for longitudinal bivariate binary response data. Biometrics, 55, 85–93. [DOI] [PubMed] [Google Scholar]
- Tsiatis A (1975) A nonidentifiability aspect of the problem of competing risks. Proceedings of the National Academy of Sciences, 72, 20–22. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Varadhan R, Xue Q-L and Bandeen-Roche K (2014) Semi-competing risks in aging research: methods, issues and needs. Lifetime Data Analysis, 20, 538–562. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Xu J, Kalbfleisch J and Tai B (2010) Statistical analysis of illness–death processes and semi-competing risks data. Biometrics, 66, 716–725. [DOI] [PubMed] [Google Scholar]
- Yang J and Peng L (2016) A new flexible dependence measure for semi-competing risks. Biometrics, 72, 770–779. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yu Y and Ruppert D (2002) Penalized spline estimation for partially linear single-index models. Journal of the American Statistical Association, 97, 1042–1054. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data Availability Statement
The data that were used in this paper are available from Kaiser Permanente Washington Health Research Institute. Restrictions may apply to the availability of these data. Further information can be found at https://www.kpwashingtonresearch.org.


