Abstract
Background
The accurate deciphering of spatial domains, along with the identification of differentially expressed genes and the inference of cellular trajectory based on spatial transcriptomic (ST) data, holds significant potential for enhancing our understanding of tissue organization and biological functions. However, most of spatial clustering methods can neither decipher complex structures in ST data nor entirely employ features embedded in different layers.
Results
This article introduces STMSGAL, a novel framework for analyzing ST data by incorporating graph attention autoencoder and multiscale deep subspace clustering. First, STMSGAL constructs ctaSNN, a cell type–aware shared nearest neighbor graph, using Louvian clustering exclusively based on gene expression profiles. Subsequently, it integrates expression profiles and ctaSNN to generate spot latent representations using a graph attention autoencoder and multiscale deep subspace clustering. Lastly, STMSGAL implements spatial clustering, differential expression analysis, and trajectory inference, providing comprehensive capabilities for thorough data exploration and interpretation. STMSGAL was evaluated against 7 methods, including SCANPY, SEDR, CCST, DeepST, GraphST, STAGATE, and SiGra, using four 10x Genomics Visium datasets, 1 mouse visual cortex STARmap dataset, and 2 Stereo-seq mouse embryo datasets. The comparison showcased STMSGAL’s remarkable performance across Davies–Bouldin, Calinski–Harabasz, S_Dbw, and ARI values. STMSGAL significantly enhanced the identification of layer structures across ST data with different spatial resolutions and accurately delineated spatial domains in 2 breast cancer tissues, adult mouse brain (FFPE), and mouse embryos.
Conclusions
STMSGAL can serve as an essential tool for bridging the analysis of cellular spatial organization and disease pathology, offering valuable insights for researchers in the field.
Keywords: spatial transcriptomics, graph attention autoencoder, deep subspace clustering, multiscale self-expression, self-supervised learning, latent embedding feature learning, cell type–aware spatial neighbor network, differential expression analysis, trajectory inference
Key Points.
A graph attention autoencoder is fully utilized to effectively integrate spatial locations and gene expression information by collectively incorporating information between neighboring spots.
A multiscale self-expression module is explored to learn the associations between node representations in all encoder layers and further obtain a more distinct self-expression coefficient matrix for mapping these features into a more precise subspace.
A self-supervised learning method is designed to help spot latent feature learning by utilizing the clustering label as a supervisor.
Background
The tissues in the human body comprise various cell types, where each cell type implements a particular function [1]. The activation of a cell is mainly affected by its surrounding environment [2–5]. Exploring relative positions of these cells contributes to analyzing cell–cell communication [6–9] and their spatial organization and disease pathology [10–13]. The rapid advance of single-cell RNA sequencing (scRNA-seq) technologies enables us to investigate the gene expression patterns of various cells within a tissue/organ [14–22]. However, scRNA-seq technologies fail to provide spatial location information [23]. In contrast, spatial transcriptomics (ST) technologies provide a large number of gene expression data and cellular location information for a tissue and have witnessed tremendous development in the past several years [24–26]. Based on data generation methods, ST technologies mainly contain image-based methods and next-generation sequencing (NGS)–based methods [27].
Image-based methods use in situ sequencing or in situ hybridization to retain spatial locations of cells and further obtain RNA transcripts based on images from the stained tissues. MERFISH [28] can detect gene expression information of about 40,000 human cells in a single 18-hour measurement. STARmap [29] can capture more than 1,000 genes in the mouse cortex through an error-robust sequencing-by-ligation approach. seqFISH+ [30] combined sequential hybridization and standard confocal microscope–based imaging technique to obtain super-resolution imaging and multiplexing data for 10,000 genes.
NGS-based methods depend on the number of spatial barcodes before library preparation [31]. Slide-seq [32, 33] obtained randomly barcoded positions through in situ indexing and captured mRNAs through depositing onto a slide. High-definition ST (HDST) [34] replaced the glass slides using beads deposited in wells. The DBiT-seq [35] technique utilized polyT barcodes in the tissue section based on microfluidics. Stereo-seq [36] obtained nanoscale resolution through randomly barcoded DNA nanoballs. 10x Genomics Visium [37] demonstrated increased resolution with a diameter of 55 µm and a 100-µm center–center, as well as improved sensitivity in more than 10,000 transcripts per spot. It detected more unique molecules for each spot compared with Slide-seq and HDST.
One main challenge in ST data analysis is to capture spatial domains with similar expression patterns. For example, the laminar organization in human cerebral cortex has a close relationship with its biological functions. In this tissue, cells within different cortical layers have different expressions, morphology, and physiology [38]. One efficient way to identify spatial domains is to cluster ST data. These clustering methods mainly fall into 2 categories. The first category adopts conventional clustering methods, for example, K-means clustering [39] and Louvain algorithms [40]. These algorithms are susceptible to the small size of spots and sparsity data, and the detected clusters may be discontinuous in sections. The other category uses cell-type labels obtained from scRNA-seq data to deconvolute spots [41, 42], but these types of methods cannot analyze ST data from the perspective of cellular or subcellular resolution.
It is crucial to learn a discriminative representation for each spot by combining gene expression and spatial contexts when clustering ST data. Recently, several clustering algorithms have been developed to identify spatial domains. For example, BayesSpace [43] assumed that spots belonging to the same cell type may be closer to each other and built a Markov random field model with Bayesian approach. stLearn [44] first proposed a spatial morphological gene expression normalization algorithm to normalize ST data and then employed a standard Louvain clustering approach to partition broad clusters into several subclusters. SEDR [45] exploited a deep autoencoder network to learn gene representations and adopted a variational graph autoencoder to embed spatial information. CCST [46] explored a graph convolutional network to transfer gene expression information as cellular embedding vectors and trained a neural network to encode cell embedding features for clustering. STAGATE [47] developed a adaptive graph attention autoencoder (GATE) [48] to accurately identify spatial domains by integrating gene expression information and spatial neighbor network. DeepST [49] incorporated gene expression, spatial context, and histology to model spatially embedded representation and further capture spatial domains. GraphST [50] integrated graph self-supervised contrastive learning and a graph neural network [51, 52] for spatial clustering, multisample integration, and cell-type deconvolution. ConGI [53] adopted gene expression with histopathological images to accurately capture spatial domains based on contrastive learning. STGIC is a graph- and image-based spatial clustering method. It can generate pseudo-labels for spatial clustering but does not depend on any trainable parameters. SPACEL [54] deconvoluted cell-type composition based on a multiple-layer perceptron, identified spatial domains via a graph convolutional network and adversarial learning, and constructed a 3-dimensional architecture for each tissue. PRECAST [55] integrated a few ST datasets that have complex batch effects and biological effects. SRTsim [56] is spatially resolved transcriptomics-specific simulator for spatial clustering and expression pattern analysis. Tang et al. [57] developed an image-augmented graph transformer for spatial elucidation. The methods mentioned above have significantly promoted the studies of tissue physiology from cell centroid to structure centroid and are state-of-the-art spatial clustering methods. In prticular, Yuan et al. [58] considered that current computation-based ST clustering is a lack of a comprehensive benchmark and systematically benchmarked a collection of 13 spatial clustering methods on 7 ST datasets (34 ST data). Their work has provided guidance for future progress in the ST data analysis field.
Although the aforementioned clustering methods obtained impressive performance, their learned latent node representation failed to achieve the most useful information because they did not use current clustering labels. In addition, some methods, including SEDR and CCST, only used the representation in the final hidden layer of an encoder for clustering ST data, which failed to consider helpful features in the other layers. Although graph attention autoencoder-based methods [59, 60] have elucidated better performance in integrating node attributes and graph structure information, they could not decipher the complex structures in ST data or did not entirely employ features embedded in different layers. Moreover, some models did not utilize a clustering-oriented loss function, while others did not fully use the clustering labels for node representation learning. The problems produced the suboptimal clustering results. Here, we introduce STMSGAL, an ST analysis framework by combining a graph attention autoencoder and multiscale deep subspace clustering network.
Materials and Methods
Overview of STMSGAL
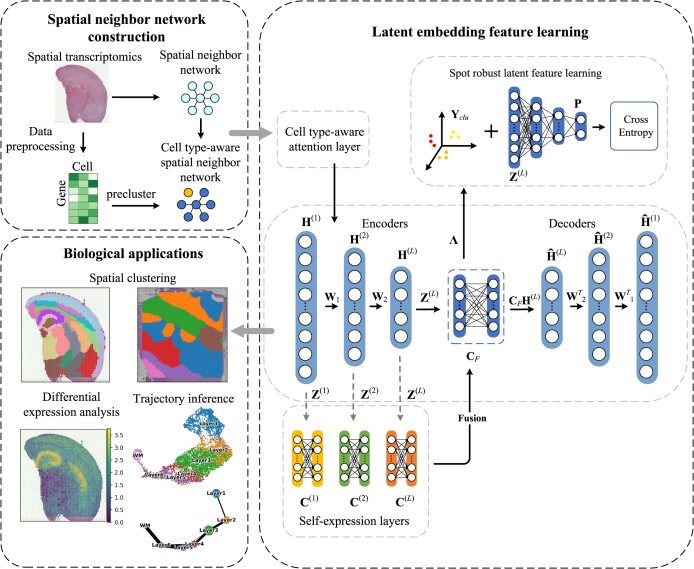
As shown in Fig. 1, STMSGAL is composed of 3 main steps: (i) Spatial neighbor network construction. STMSGAL constructs a spatial neighbor network (SNN) based on spatial contexts and obtains a cell type–aware SNN called ctaSNN through Louvain clustering exclusively based on gene expression data. (ii) Latent embedding feature learning. This mainly comprises spot embedding feature matrix construction, subspace clustering combining multiscale self-expression coefficient learning and affinity matrix construction, and spot robust latent feature learning based on self-supervised learning. (iii) Biological applications. ST data are clustered, and differential expression analysis and trajectory inference are implemented. Similar to STAGATE [47], STMSGAL still constructs a ctaSNN and embedding feature matrix using GATE. However, different from STAGATE, STMSGAL adopts the multiscale deep subspace clustering algorithm to obtain cluster labels based on multiscale information from each encoder layer for spots and then adopts a self-supervised module to learn robust latent features of spots with clustering information.
Figure 1:
Pipeline for clustering ST data based on GATE and deep subspace clustering network. (i) Spatial neighbor network construction. (ii) Latent embedding feature learning. (iii) Biological applications.
Datasets
Four available 10x Genomics Visium datasets, 1 mouse visual cortex STARmap dataset, and 2 Stereo-seq datasets are used to evaluate the STMSGAL performance. The former four 10x Genomics datasets are from Adult Mouse Brain (FFPE) [61], Human Breast Cancer (Block, A Section 1) [62], Human Breast Cancer (Ductal Carcinoma In Situ [DCIS]) [63], and Human Dorsolateral Prefrontal Cortex (DLPFC) tissues [64]. The former 2 datasets have no clustering labels, and the latter 2 datasets are known to be labeled. The Adult Mouse Brain (FFPE) dataset contains 2,264 spots and 19,465 genes. The Human Breast Cancer (DCIS) dataset includes 3,798 spots and 36,601 genes. The Human Breast Cancer (Block A, Section 1) dataset detects 2,518 spots and 19,743 genes. The DLPFC dataset contains 12 tissue slices. It captures 33,538 genes with different spot numbers ranging from 3,460 to 4,789 in each slice. Each slice contains 5 to 7 regions by manual annotation [38]. The mouse visual cortex STARmap dataset provides the expression information of 1,020 genes from 1,207 cells [29]. The Stereo-seq dataset [65] from mouse embryos at E9.5 is obtained based on high-resolution full-transcriptome coverage technologies (i.e., Stereo-seq technology). The number of spots and one of genes are 5,913 and 25,568 (E9.5_E1S1), as well as 4,356 and 24,107 (E9.5_E2S2), respectively.
Spatial neighbor network construction
Data preprocessing
To preprocess ST data, first, spots outside main tissue regions are removed. Next, raw gene expressions are log-transformed and normalized based on library size through the SCANPY package [66]. Finally, multiple highly variable genes are selected as inputs.
Cell type–aware SNN construction
To integrate the similarity between a neighboring spot and a given spot, similar to STAGATE [47], STMSGAL constructs an undirected neighbor network based on a predefined radius r and spatial contexts. Let  denote an adjacency matrix of the constructed SNN, and
denote an adjacency matrix of the constructed SNN, and 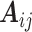 = 1 when the Euclidean distance between 2 spots i and j is less than r. For 10x Genomics Visium data, an SNN where each spot contains 6 nearest neighbors is built. Next, self-loops are added to each spot. Finally, the SNN is pruned based on preclustering and a ctaSNN is constructed. In particular, the preclustering of spots is conducted by Louvain clustering [40] exclusively based on gene expression profiles. The edges where 2 spots linking them belong to different clusters are pruned.
= 1 when the Euclidean distance between 2 spots i and j is less than r. For 10x Genomics Visium data, an SNN where each spot contains 6 nearest neighbors is built. Next, self-loops are added to each spot. Finally, the SNN is pruned based on preclustering and a ctaSNN is constructed. In particular, the preclustering of spots is conducted by Louvain clustering [40] exclusively based on gene expression profiles. The edges where 2 spots linking them belong to different clusters are pruned.
Latent embedding feature learning
Wang et al. [67] presented a multiscale graph attention subspace clustering model and obtained superior performance on 3 graph datasets and 2 real-world datasets. The clustering model fully explored the associations between node representations in all encoder layers and obtained a more accurate self-expression coefficient matrix. To more accurately cluster spots, in this section, we utilize the multiscale graph attention subspace clustering model [67] to learn latent embedding features of spots. First, a spot embedding feature matrix in each encoder layer is constructed via GATE. Second, spot cluster labels are obtained through subspace clustering. Finally, spot robust latent features are learned by self-supervised learning.
Embedding feature matrix construction
Similar to STAGATE [47], we use GATE to construct an embedding feature matrix. For spot i, an encoder with L layers takes its normalized gene expressions 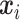 as inputs to generate its embedding features by collectively incorporating information from its neighbors. Taking gene expressions as initial spot embeddings, that is,
as inputs to generate its embedding features by collectively incorporating information from its neighbors. Taking gene expressions as initial spot embeddings, that is, 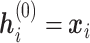 ,
, 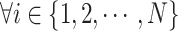 , the embedding of i in the kth (
, the embedding of i in the kth (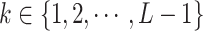 ) encoder layer is denoted by Eq. (1):
) encoder layer is denoted by Eq. (1):
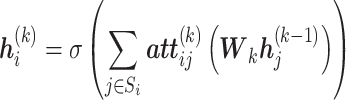 |
(1) |
where 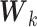 ,
, 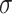 ,
, 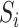 , and
, and 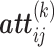 denote the trainable weight matrix, nonlinear activation function, a spot set that includes neighbors of i in SNN and
denote the trainable weight matrix, nonlinear activation function, a spot set that includes neighbors of i in SNN and 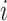 itself, and weight of the edge between spot
itself, and weight of the edge between spot 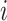 and spot
and spot 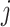 in the
in the 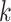 th graph attention layer, respectively. The output
th graph attention layer, respectively. The output 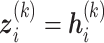 of the encoder is taken as the final spot embedding in the encoder part. The
of the encoder is taken as the final spot embedding in the encoder part. The 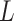 th layer in the encoder does not use the attention layer by Eq. (2):
th layer in the encoder does not use the attention layer by Eq. (2):
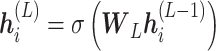 |
(2) |
In the decoder part, a decoder transforms the learned latent embedding back into a normalized expression profile to reconstruct the spot features. Suppose that 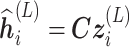 , where
, where 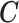 denotes a self-expression matrix, and
denotes a self-expression matrix, and 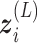 denotes the embedding of
denotes the embedding of 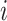 in the
in the 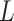 th encoder layer. Next,
th encoder layer. Next, 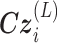 is fed into the decoder to reconstruct the spot embeddings. In the
is fed into the decoder to reconstruct the spot embeddings. In the 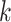 th decoder layer, the embedding features of spot
th decoder layer, the embedding features of spot 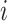 are constructed by Eq. (3):
are constructed by Eq. (3):
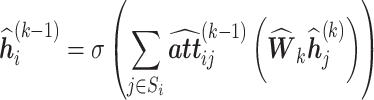 |
(3) |
The L layer in the decoder is denoted by Eq. (4):
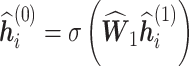 |
(4) |
Its output is the reconstructed normalized expressions. In addition, we set 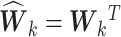 and
and 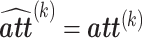 to avoid overfitting.
to avoid overfitting.
The attention mechanism is a 1-layer feed-forward neural network that is parametrized by a weight vector. A self-attention mechanism [68] is used to compute the similarity between neighboring spots in an adaptive way. In the kth decoder layer, the edge weight between spot 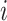 and its neighbor spot
and its neighbor spot 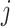 is computed by Eq. (5):
is computed by Eq. (5):
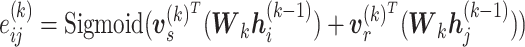 |
(5) |
where 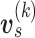 and
and 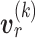 are 2 trainable weight vectors. Next, the similarity weights between spots are normalized by a softmax function by Eq. (6):
are 2 trainable weight vectors. Next, the similarity weights between spots are normalized by a softmax function by Eq. (6):
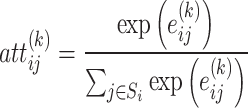 |
(6) |
The obtained weights are applied to further update the latent embedding of spots in the encoder and decoder.
In addition, STMSGAL adopts a self-attention mechanism and constructs a ctaSNN. Let 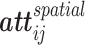 and
and 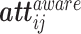 denote the learned spot similarity using SNN and ctaSNN, respectively, and the final spatial similarity is computed by combining the above 2 similarities by Eq. (7):
denote the learned spot similarity using SNN and ctaSNN, respectively, and the final spatial similarity is computed by combining the above 2 similarities by Eq. (7):
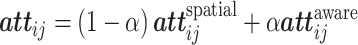 |
(7) |
where 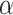 is a hyperparameter used to weigh the importance of SNN and ctaSNN.
is a hyperparameter used to weigh the importance of SNN and ctaSNN.
The reconstructed loss is minimized based on the residual sum of squares by Eq. (8):
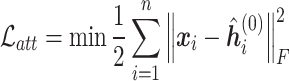 |
(8) |
In particular, weight decay equally imposes a penalty to the 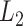 norm; thus, the regularized loss is minimized. The total loss is represented as Eq. (9):
norm; thus, the regularized loss is minimized. The total loss is represented as Eq. (9):
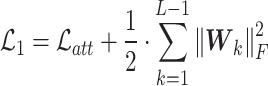 |
(9) |
Multiscale deep subspace clustering
Different from STAGATE [47], in this section, we adopt the multiscale deep subspace clustering algorithm to obtain cluster labels based on multiscale information from each encoder layer for spots. The self-expression property of data greatly influences the performance of subspace clustering. In a union subspace, each datum can be represented as a linear combination of the other data. Thus, we use a multiscale self-expressive module to obtain the final self-expression coefficient matrix based on the spot embedding feature matrix: 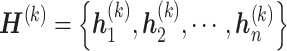 .
.
In deep subspace clustering network [69], a self-expression layer is a full connection layer without bias and activation. Its objection function is represented by Eq. (10):
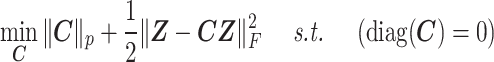 |
(10) |
where 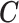 indicates a self-expression coefficient matrix used to build an affinity matrix
indicates a self-expression coefficient matrix used to build an affinity matrix 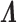 for the following spectral clustering,
for the following spectral clustering, 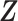 indicates the output feature matrix in the encoder, and
indicates the output feature matrix in the encoder, and 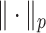 indicates an arbitrary regularization norm.
indicates an arbitrary regularization norm.
Although deep subspace clustering obtains better clustering performance, it fails to consider the multiscale features existing in the other encoder layers. Here, we integrate the multiscale features into the original self-expression module. Given the input normalized gene expressions in the ith encoder layer 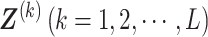 , the self-expression coefficient matrix
, the self-expression coefficient matrix 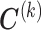 in the kth encoder layer can be computed by Eq. (11):
in the kth encoder layer can be computed by Eq. (11):
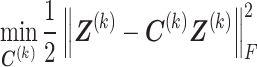 |
(11) |
Next, the multiscale self-expression matrix 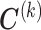 in different layers is fused based on an adaptive approach by Eq. (12):
in different layers is fused based on an adaptive approach by Eq. (12):
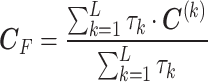 |
(12) |
where 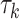 denotes a trainable variable used to balance the importance of each self-expression matrix.
denotes a trainable variable used to balance the importance of each self-expression matrix.
Based on the obtained final self-expression matrix 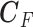 , a deep subspace clustering model builds an affinity matrix
, a deep subspace clustering model builds an affinity matrix 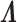 for spectral clustering [70] by Eq. (13):
for spectral clustering [70] by Eq. (13):
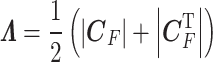 |
(13) |
Consequently, the clustering result 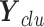 can be obtained by spectral clustering based on
can be obtained by spectral clustering based on  .
.
In particular, the multiscale self-expression loss is represented as Eq. (14):
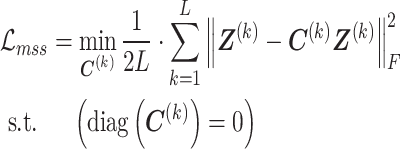 |
(14) |
Besides, a regularization loss is introduced to avoid  being too sparse:
being too sparse:
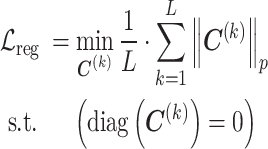 |
(15) |
Thus, the total loss in the multiscale self-expression module is denoted as Eq. (16):
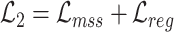 |
(16) |
Spot robust latent feature learning
Furthermore, distinct from [47], we employ a self-supervised module to learn spot robust latent features. First, spots are classified based on 3 full connection layers. Let the dimensions of all full connection layers be denoted as 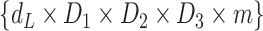 , where
, where 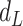 denotes the dimension of
denotes the dimension of 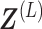 , and
, and 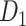 ,
, 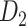 , and
, and 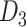 denote the dimensions of 3 full connection layers, respectively. We obtain the classification results
denote the dimensions of 3 full connection layers, respectively. We obtain the classification results 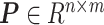 of n spots based on the 3 full connection layers.
of n spots based on the 3 full connection layers.
Next, we use the cross-entropy loss between the classification results 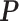 and the clustering results
and the clustering results 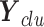 to constrain a self-supervised learning module by Eq. (17):
to constrain a self-supervised learning module by Eq. (17):
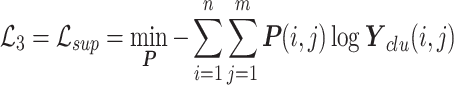 |
(17) |
where 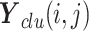 denotes the jth clustering label of spot i obtained from spectral clustering, and
denotes the jth clustering label of spot i obtained from spectral clustering, and 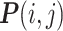 denotes the jth classification label of spot i based on 3 full connection layers.
denotes the jth classification label of spot i based on 3 full connection layers.
Finally, by integrating Eqs. (9), (14), (15), and (17), the total loss function of multiscale GATE is denoted as Eq. (18):
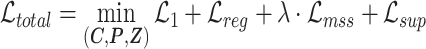 |
(18) |
where 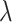 is a trade-off parameter used to measure the importance of
is a trade-off parameter used to measure the importance of 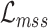 .
.
Biological application
STMSGAL first identifies spatial domains using Leiden clustering [71], Louvain clustering [40] or mclust clustering [72] based on the obtained spot embedding feature matrix. Second, it implements differential expression analysis using the t-test in the Scanpy package. Finally, it conducts trajectory inference.
Spatial clustering
Based on the learned spot embedding feature matrix, we use different strategies to identify spatial domains. For the DLPFC dataset, mclust clustering [72] is applied to spatial clustering. For other datesets, Louvain or Leiden clustering [40, 71] is used to implement ST clustering.
In addition, although the spot embedding feature matrix is obtained by integrating both gene expressions and spatial contexts, several spots may be incorrectly assigned to spatially diametrical domains, which may cause noise and influence downstream analysis. To solve this problem, an optional optimization step is used to further optimize spatial clustering results obtained from Louvain clustering on the DLPFC dataset: for a given spot i, its surrounding spots within an r radius circle are taken as its neighbors. Next, we reassign i to a spatial domain with the most frequent label of its neighbors. In addition, the clustering results are visualized using UMAP [73].
Differential expression analysis
Differential expression analysis is one primary downstream analysis method on transcriptomic data [74–76]. It helps identify biomarkers for novel cell types or detect gene signatures for cellular heterogeneity, and it further provides data for other secondary analyses (such as gene set or pathway analysis and network analysis). We use the t-test implemented in the SCANPY package [66] to identify differentially expressed genes for spatial domains.
Trajectory inference
ST technologies help depict tissues and organisms in great detail. Tracking the transcriptomic profiles of cells over time and studying their dynamic cellular process contribute to the computational reconstruction of cellular developmental processes. Trajectory inference enables us to better study the potential dynamics of a query biological process, for example, cellular development, differentiation, and immune responses [77]. It can detect a graph-like structure existing in the dynamic process from the sampled cells. Properties of cells are compared over pseudotime [78] by mapping them to the captured structure. Trajectory inference allows us analyze how cells evolve from one cell state to another, as well as when and how cells should make cell fate decisions. In this section, the PAGA algorithm [79] in the SCANPY package [66] is employed to depict the spatial trajectory. The obtained trajectory figures are visualized using the scanpy.pl.paga_compare() function.
Results
Experimental setting
In STMSGAL, both the encoder and the decoder with the activation function of the exponential linear unit (ELU) [80] included neural networks with 2 graph attention layers, where the number of neurons was 512 and 30, respectively. The Adam optimizer [81] was employed to minimize their reconstruction loss. In the self-supervised module, the activation function was set to rectified linear units (ReLu) [82]. For Louvain clustering, the radius r was set to 50 when STMSGAL obtained the best clustering performance on the DLPFC dataset.
STMSGAL adopted the same data preprocessing as those of SCANPY. Both used log-normalization and constructed the nearest neighbor network. SCANPY obtained spatial clustering with the scanpy.tl.louvain() function. Table 1 shows parameter settings of STMSGAL on 5 ST datasets. For each dataset with labels, the resolution parameter was tuned manually to ensure the cluster number was equal to the ground truth. Thus, the cluster number in each method was set to the same as one of ground truth layers. For other clustering methods, we adopted their default settings.
Table 1:
Parameter settings
| Datesets | Parameter settings |
|---|---|
| DLPFC | rad_cutoff = 150 |
| cost_ssc = 0.1 | |
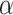 = 0
= 0 |
|
| method = ‘Louvain’ | |
| Human Breast Cancer | rad_cutoff = 300 |
| (Block A, Section 1) | cost_ssc = 1 |
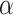 = 0.7
= 0.7 |
|
| method = ‘leiden’ | |
| Adult Mouse Brain | rad_cutoff = 300 |
| (FFPE) | cost_ssc = 0.1 |
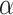 = 0.5
= 0.5 |
|
| method = ‘Louvain’ | |
| Human Breast Cancer | rad_cutoff = 300 |
| (DCIS) | cost_ssc = 1 |
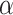 = 0.5
= 0.5 |
|
| method = ‘Louvain’ | |
| Mouse visual cortex | rad_cutoff = 400 |
| cost_ssc = 0.1 | |
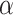 = 0
= 0 |
|
| method = ‘mclust’ | |
| Stereo-seq mouse embryo | rad_cutoff = 3 |
| cost_ssc = 0.1 | |
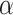 = 0
= 0 |
|
| method = ‘Louvain’ |
Evaluation metrics
For 3 datasets with labels (Human Breast Cancer [Block A, Section 1], DLPFC, and mouse visual cortex STARmap), we employed adjusted Rand index (ARI) [83] to evaluate the performance of different spatial clustering algorithms. ARI computes the similarity between the predicted clustering labels and reference cluster labels by Eq. (19):
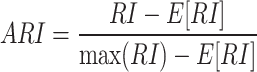 |
(19) |
where the unadjusted Rand index is 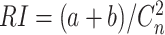 , where
, where 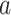 and
and 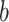 indicate the number of pairs correctly labeled in the same dataset and not in the same dataset, respectively.
indicate the number of pairs correctly labeled in the same dataset and not in the same dataset, respectively. 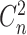 indicates the total number of possible pairs.
indicates the total number of possible pairs. 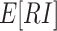 indicates the expected
indicates the expected 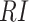 based on random labeling. A higher
based on random labeling. A higher 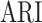 score denotes better performance.
score denotes better performance.
For 2 datasets whose spatial domain annotations are unavailable (Adult Mouse Brain [FFPE] and Human Breast Cancer [DCIS]), we evaluated the performance of spatial clustering algorithms based on 3 clustering metrics: Davies–Bouldin (DB) score [84], Calinski–Harabasz (CH) score [85], and S_Dbw score [86, 87]. DB was computed by averaging all cluster similarities, where the similarity between each cluster and its most similar cluster was taken as its cluster similarity. The similarity was computed by the ratio of within-cluster distances to between-cluster distances. CH is used to measure the cluster validity by averaging the squares of within- and between-cluster distance sum of all spots. S_Dbw evaluates intraclass compactness and interclass density of each spot. Small DB and S_Dbw and large CH indicate the optimal cluster clustering.
Performance comparison of STMSGAL with 6 other methods on 2 datasets without labels
To investigate the clustering performance of STMSGAL, we compared it with 6 other clustering algorithms—that is, SCANPY [66], SEDR [45], CCST [46], STAGATE [47], DeepST [49], and GraphST [50]—on two 10x Genomics Visium datasets without labels (i.e., Adult Mouse Brain [FFPE] and Human Breast Cancer [DCIS]). The former one method obtained broad applications in single-cell clustering, and the remaining 5 methods were widely applied to spatial clustering. Table 2 shows the DB, CH, and S_Dbw scores computed by STMSGAL and other methods on the above 2 datasets. The best performance in each column was denoted using the bold font. The results demonstrated that STMSGAL computed the smallest DB and S_Dbw and the highest CH on Adult Mouse Brain (FFPE) and the highest CH and the smallest S_Dbw on Human Breast Cancer (DCIS), suggesting its optimal clustering performance.
Table 2:
Performance comparison of STMSGAL with 6 other clustering methods on Adult Mouse Brain (FFPE) and Human Breast Cancer (Ductal Carcinoma In Situ [DCIS])
| Metrics | ||||
|---|---|---|---|---|
| Datasets | Methods | DB | CH | S_Dbw |
| Adult Mouse Brain | SCANPY | 1.442 | 358.67 | 0.481 |
| (FFPE) | SEDR | 1.951 | 84.569 | 0.652 |
| CCST | 1.173 | 507.421 | 0.453 | |
| DeepST | 1.166 | 842.033 | 0.328 | |
| STAGATE | 1.467 | 495.547 | 0.427 | |
| GraphST | 1.470 | 310.860 | 0.501 | |
| STMSGAL | 1.155 | 1,010.724 | 0.311 | |
| Human Breast Cancer | SCANPY | 2.069 | 379.084 | 0.593 |
| (DCIS) | SEDR | 2.627 | 54.778 | 0.742 |
| CCST | 1.469 | 507.421 | 0.453 | |
| DeepST | 1.263 | 611.567 | 0.48 | |
| STAGATE | 1.916 | 430.630 | 0.587 | |
| GraphST | 1.951 | 369.594 | 0.610 | |
| STMSGAL | 1.451 | 1,190.850 | 0.332 | |
* The bold font indicates the best performance in each column. Lower Davies–Bouldin (DB) and S_Dbw and higher Calinski–Harabasz (CH) denote better performance.
STMSGAL demonstrates robust clustering performance across ST datasets with different spatial resolutions
To evaluate the STMSGAL performance on spatial domain identification, we compared it with existing 7 state-of-the-art methods on 4 DLPFC sections. Particularly, in complex networks, nodes are clustered into relatively dense communities through the clustering algorithm. Louvain clustering is a nonspatial clustering algorithm. It assigns each spot to a significantly differential community and achieves the desired clusters by iteratively merging and splitting communities. It exhibits powerful clustering performance compared with spectral clustering when clustering ST data, such as DLPFC. Thus, we used the Louvian clustering for performing clustering again on DLPFC.
Moreover, the DLPFC dataset provides high-resolution images and satisfies the need of spatial clustering methods, including SiGra, that must combine high-resolution images for clustering ST data. The results elucidated that spatial domains captured by STMSGAL were consistent with manual annotation on human DLPFC sections and the definition of cortical stratification in neuroscience (Fig. 2).
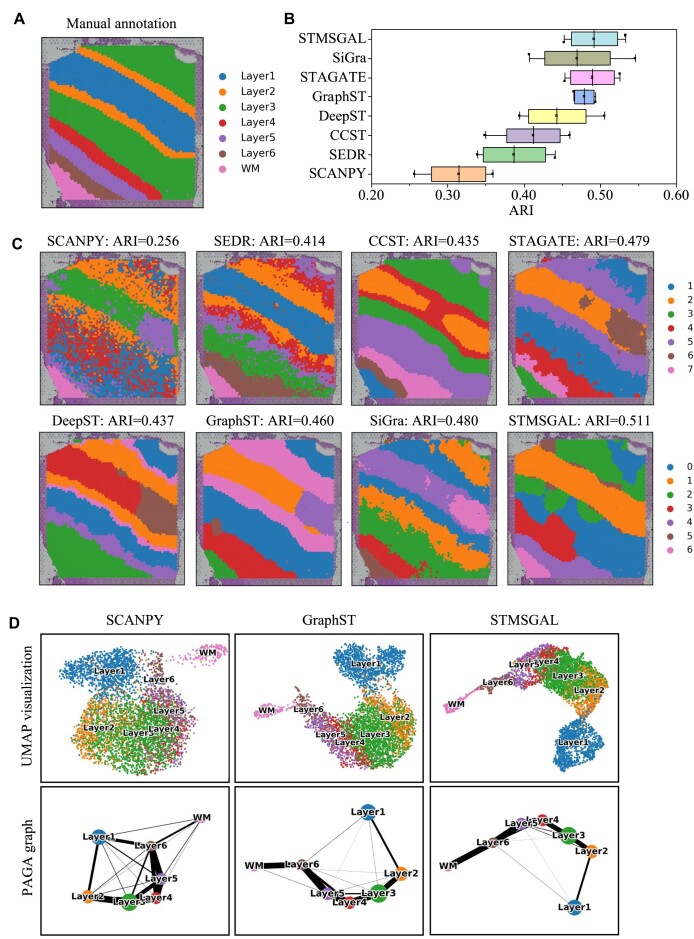
Figure 2:
STMSGAL improves the identification of layer structures in the DLPFC tissue. (A) Ground-truth segmentation of 6 cortical layers and 1 white matter layer in the DLPFC section 151509. (B) Boxplots of ARI computed by STMSGAL and other 7 methods in the DLPFC sections, from 151507 to 151510. (C) Cluster assignments generated by SCANPY, SEDR, CCST, STAGATE, DeepST, GraphST, SiGra, and STMSGAL in the DLPFC section 151509. (D) UMAP visualizations and PAGA graphs generated by SCANPY, GraphST, and STMSGAL embeddings in the DLPFC section 151509.
In addition, STMSGAL effectively captured the expected cortical layer structures and significantly improved spatial clustering performance in comparison with SCANPY, SEDR, CCST, STAGATE, SiGra, DeepST, and GraphST (Fig. 2 and Supplementary Fig. S1). For average ARIs, STMSGAL achieved the best performance (Fig. 2B). In the DLPFC section 151509, STMSGAL clearly depicted the layer borders and obtained the best average ARI of 0.511. In the section, although the clustering results of SCANPY roughly adhered to the expected layer structures, its cluster boundary was discontinuous with many noises, which greatly influenced its clustering accuracy. Moreover, SCANPY is a nonspatial clustering algorithm, and SEDR, CCST, DeepST, STAGATE, SiGra, and GraphST are spatial clustering algorithms. Interestingly, the performance of the above 6 spatial clustering algorithms, especially STMSGAL, is better than the clustering method, elucidating STMSGAL’s powerful spatial domain identification ability (Fig. 2C).
STMSGAL manifested the distance between spatial domains and characterized the spatial trajectory in a UMAP plot [73] by integrating spatial contexts. For example, in the DLPFC section 151509, the UMAP plots delineated by STMSGAL embeddings elucidated well-organized cortical layers and consistent spatial trajectories, which was in accord with functional similarity between adjacent cortical layers and the chronological order [88]. Furthermore, in the UMAP plots delineated by SCANPY embeddings, spots that belong to different layers were not clearly divided while GraphST and STMSGAL could well divide most spots into different layers (Fig. 2D). Finally, we used a trajectory inference approach named PAGA [79] to verify the inferred trajectory. The PAGA graphs depicted by both STMSGAL and GraphST embeddings had a approximately linear development trajectory from layer 1 to layer 6. In addition, the identified adjacent layers by STMSGAL and GraphST showed similarity while ones from SCANPY embeddings were mixed (Fig. 2D).
We further evaluated the performance STMSGAL on the mouse visual cortex STARmap dataset, which is an image-based ST dataset at single-cell resolution and is generated by the STARmap technique [29]. mclust is a widely used R package applied to model-based clustering through finite Gaussian mixture modeling. It is more suitable to single-cell resolution data with fewer samples, such as mouse visual cortex STARmap dataset. Thus, we used mclust for performing clustering again on STARmap. Using the gold standard annotated by experts, as shown in Fig. 3, STMSGAL obtained the best ST clustering performance with an ARI of 0.568 compared to SCANPY, SEDR, CCST, STAGATE, and GraphST, while STAGATE achieved the second-best ranking with ARI of 0.563 (Fig. 3).
Figure 3:
Spatial domains identified by SCANPY, SEDR, CCST, GraphST, STAGATE, and STMSGAL in the mouse visual cortex STARmap dataset.
We also validated the performance of STMSGAL for identifying tissue structures on the Stereo-seq dataset from mouse embryos at E9.5. Tissue domain annotations of mouse embryos were obtained from [65].
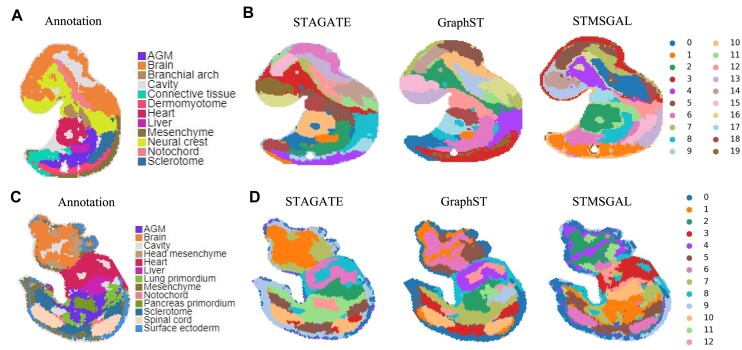
We investigated the clustering results of STAGATE, GraphST, and STMSGAL on the E9.5_E1S1 embryo. As shown in Fig. 4A, although the original annotation had 12 reference clusters, we set the number of clusters in our testing to 20 to acquire a higher resolution of tissue segmentation. The clusters identified by both STAGATE and STMSGAL matched the annotation well (Fig. 4B). As shown in Table 3, however, compared to STAGATE, STMSGAL computed the smallest DB and S_Dbw and the highest CH.
Figure 4:
STMSGAL improves accurately identification of different organs in the Stereo-seq mouse embryo. (A) Tissue domain annotations of the E9.5_E1S1 mouse embryo data. (B) Cluster assignments generated by STAGATE, GraphST, and STMSGAL on E9.5_E1S1 mouse embryo data. (C) Tissue domain annotations of the E9.5_E2S2 mouse embryo data. (D) Cluster assignments generated by STAGATE, GraphST, and STMSGAL on the E9.5_E2S2 mouse embryo data.
Table 3:
Performance comparison of STMSGAL with STAGATE and GraphST on the Stereo-seq mouse embryos
| Metrics | ||||
|---|---|---|---|---|
| Datasets | Methods | DB | CH | S_Dbw |
| E9.5_E1S1 | STAGATE | 1.579 | 582.733 | 0.585 |
| GraphST | 1.396 | 686.177 | 0.549 | |
| STMSGAL | 1.957 | 1,915.695 | 0.355 | |
| E9.5_E2S2 | STAGATE | 1.708 | 603.290 | 0.608 |
| GraphST | 1.686 | 563.371 | 0.632 | |
| STMSGAL | 1.861 | 1,171.402 | 0.488 | |
* The bold font indicates the best performance in each column. Lower Davies–Bouldin (DB) and S_Dbw and higher Calinski–Harabasz (CH) denote better performance.
Moreover, we compared the clustering results of STAGATE, GraphST, and STMSGAL on the E9.5_E2S2 mouse embryo. Here, we set the number of clusters to 13, matching the original annotation (Fig. 4C). The results demonstrated that STMSGAL computed the smallest DB and S_Dbw and the highest CH (Table 3). STAGATE produced more smoother clusters but failed to reveal any fine-grained tissue complexity (Fig. 4D). For example, STAGATE failed to identify cavity in the brain (domain 2). In contrast, STMSGAL’s clusters better matched the annotated regions.
STMSGAL can accurately dissect spatial domains on 2 breast cancer tissues
Differed from the cerebral cortex with clear and known morphological boundaries, breast cancer tissues are remarkably heterogeneous and consist of a complex tumor microenvironment. Consequently, manually labeling cancer data only via tumor morphology cannot fully depict the complexity. Thus, we utilized STMSGAL to find spatial domains on two 10x Genomics Visium datasets with respect to Human Breast Cancer (Block A, Section 1) and Human Breast Cancer (DCIS).
Particularly, Louvain clustering may produce arbitrarily badly connected communities. In the worst case, the obtained communities may even be discontinuous, especially when performing clustering iteratively. Moreover, due to the limitation of resolution, smaller communities may be clustered into larger communities. That is, smaller communities may be hidden, resulting in obtained communities containing significant substructures.
Leiden clustering is a modified version of Louvain clustering and can yield well-connected communities based on the smart local move strategy. Cancer tissues with tumor heterogeneity contain many small substructures. Thus, we used the Leiden clustering for cancer tissues with tumor heterogeneity, such as human breast cancer.
Human Breast Cancer (Block A, Section 1) data have obvious intratumoral and intertumoral differences. It was manually annotated by SEDR [45] (Fig. 5A) and divided into 20 regions. It contains 4 main morphotypes: ductal carcinoma in situ/lobular carcinoma in situ (DCIS/LCIS), invasive ductal carcinoma (IDC), tumor surrounding regions with low features of malignancy (tumor edge), and healthy tissue (healthy).
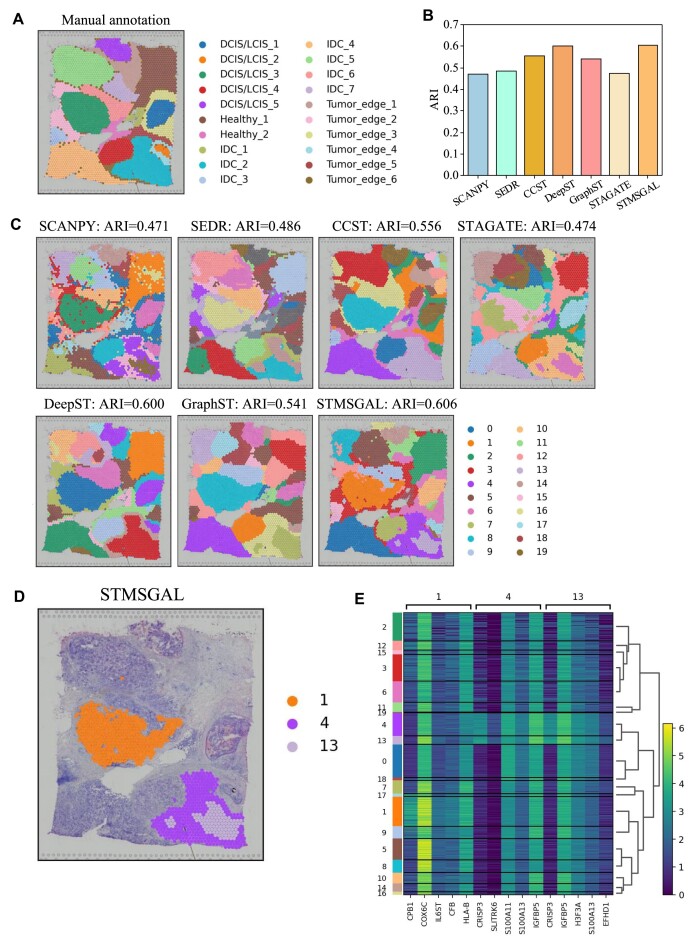
Figure 5:
STMSGAL can accurately dissect spatial domains on Human Breast Cancer (Block A, Section 1). (A) Manual pathology labeling via hematoxylin and eosin staining. (B) The average ARI values computed by SCANPY, SEDR, CCST, STAGATE, DeepST, GraphST, and STMSGAL on Human Breast Cancer (Block A, Section 1). (C) Cluster assignments generated by SCANPY, SEDR, CCST, STAGATE, DeepST, GraphST, and STMSGAL on Human Breast Cancer (Block A, Section 1). (D) Spatial domains identified by STMSGAL. (E) Heatmap of the top 5 differentially expressed genes of domains 1, 4, and 13 on Human Breast Cancer (Block A, Section 1).
We compared the clustering accuracy of STMSGAL with SCANPY [66], SEDR [45], CCST [46], STAGATE [47], DeepST [49], and GraphST [50] in terms of average ARI. The results show that STMSGAL computed the best ARI, significantly outperforming 5 other clustering methods (Fig. 5B).
Figure 5C shows spatial domains identified by SCANPY, SEDR, CCST, STAGATE, DeepST, GraphST, and STMSGAL. The results demonstrate that the identified domains by STMSGAL were highly consistent with manual annotations in Fig. 5A and had more regional continuity. In addition, compared with other methods, STMSGAL obtained the best clustering accuracy with an ARI of 0.606. Furthermore, STMSGAL identified several subclusters within the tumor regions, such as spatial domains 4 and 13 (Fig. 5D). Furthermore, STMSGAL identified some spatial domains with low heterogeneity (i.e., healthy regions) that were remarkably consistent with the manual annotations in Fig. 5A.
We also analyzed intratumoral transcriptional differences among domains 1 (DCIS/LCIS), 4, and 13 (IDC) based on differential expression analysis (Fig. 44E). In domain 1, we identified 3 differentially expressed genes, that is, CPB1, COX6X, and IL6ST. CPB1 can obviously differentiate DCIS from the other subtypes of breast cancer [89]. COX6X may help the differentiation between estrogen receptor–positive and estrogen receptor–negative subtypes [90]. The expression of IL6ST is closely associated with a lower risk of invasion, metastasis, and recurrence [91]. In domains 4 and 13, 2 differentially expressed genes, IGFBP5 and CRISP3, have dense linkages with the treatment of mammary carcinoma [92, 93]. The knockdown of CRISP3 can greatly inhibit the migration and invasion of mammary carcinoma cells and the ERK1/2 MAPK signaling pathway. CRISP3 was also considered a marker for clinical outcomes in patients with mammary carcinoma [92]. IGFBP5 helps manage tamoxifen resistance in breast cancer [93]. The above results suggested that STMSGAL can accurately identify spatial regions with different biological functions.
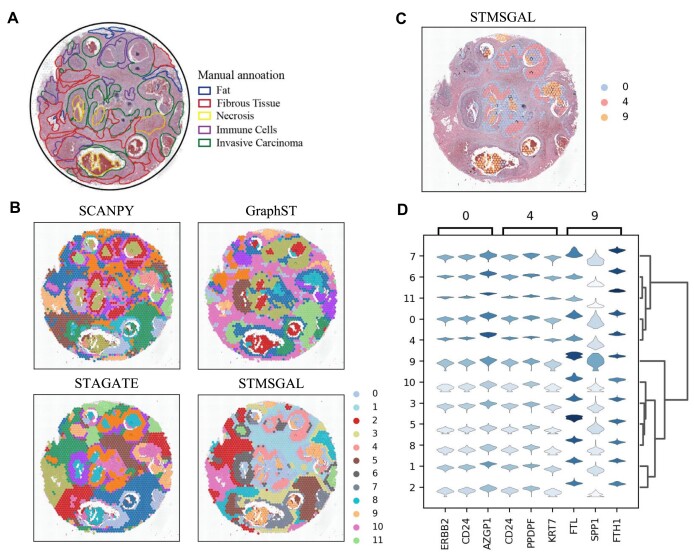
We further investigated ST data on Human Breast Cancer (DCIS). Figure 6A gives its manually annotated areas. STMSGAL identified more fluent and continuous regions than other algorithms and better matched the annotated areas (Fig. 6B, Supplementary Fig. S2, and Table 2). Figure 6D lists the top 3 differentially expressed genes (i.e., AZGP1, CD24, and ERBB2) in domain 0 (Fig. 6C). The expression of AZGP1 determines the histologic grade of tumors in breast cancer [94]. CD24 is a key indicator of triple-negative breast cancer [95–97]. In particular, the overexpression of ERBB2 categorizes ERBB2/HER2-positive, a subclass of breast cancer. The subclass accounts for about 20–30% among all types of breast malignancies and is usually linked to poor prognosis [98]. Targeting ERBB2 contributes to the treatment of ERBB2-positive breast cancers [99].
Figure 6:
STMSGAL can accurately dissect spatial domains on Human Breast Cancer (DCIS). (A) Hematoxylin and eosin staining figures annotated by Agoko’s telepathology platform on Human Breast Cancer (DCIS). (B) Spatial domains identified by SCANPY, GraphST, STAGATE, and STMSGAL on Human Breast Cancer (DCIS). (C) Spatial domains 0, 4, and 9 identified by STMSGAL. (D) Stacked violin plots illustrate the top 3 differentially expressed genes on spatial domains 0, 4, and 9 and their expressions on all spatial domains.
STMSGAL helps to better delineate the similarity between neighboring spots on Adult Mouse Brain (FFPE)
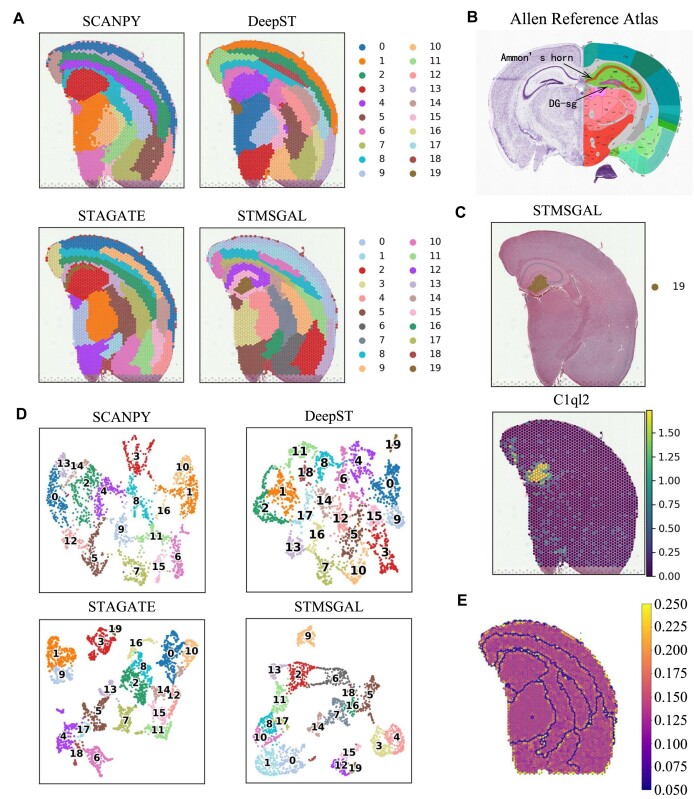
STMSGAL was still applied to provide insights into more complex tissues on a 10x Genomics Visium dataset from Adult Mouse Brain (FFPE) (Fig. 7 and Supplementary Fig. S3). Figure 7A shows spatial domains identified by SCANPY, DeepST, STAGATE, and STMSGAL. In the hippocampal region, the clustering results generated by SCANPY roughly separated the brain tissue structures composed of different cell types but failed to capture small spatial domains. SCANPY did not observe the “cord-like” structure (i.e., Ammon’s horn) and the “arrow-like” structure (i.e., dentate gyrus) within the hippocampus. DeepST only smoothed the spatial domain boundaries but failed to delineate small spatial domains. STMSGAL without ctaSNN captured Ammon’s horn but did not characterize smaller spatial domains. However, STMSGAL with ctaSNN clearly identified both Ammon’s horn and dentate gyrus structures in the hippocampus, in accord with annotations about the hippocampus structures from the Allen Reference Atlas [100] (Fig. 7B). The above results suggested that STMSGAL significantly improved spatial domain identification. Furthermore, even for ST data composed of heterogeneous cell types with low spatial resolution, STMSGAL with ctaSNN can still accurately decipher the spatial similarity.
Figure 7:
STMSGAL reveals spatial domains on Adult Mouse Brain (FFPE). (A) Spatial domains identified by SCANPY, DeepST, STAGATE, and STMSGAL. (B) The annotation of hippocampus structures from the Allen Reference Atlas on mouse brain. (C) Visualization of domains identified by STMSGAL and the corresponding marker genes. (D) UMAP visualization generated by SCANPY, DeepST, STAGATE, and STMSGAL embeddings, respectively. (E) Visualization of all attention layers of STMSGAL with the ctaSNN module. In each attention layer, nodes were arranged based on spatial contexts of spots, and edges were colored by corresponding weights.
Additionally, the expressions of multiple known gene markers validated the cluster partitions of STMSGAL (Fig. 7C and Supplementary Fig. S4). For example, C1ql2 was highly expressed on the identified DG-sg region [101]. Hpca, which mediates calcium-dependent translocation of brain-type creatine kinase in hippocampal neurons, was highly expressed in Ammon’s horn region [102]. Notably, STMSGAL also captured several well-separated spatial domains and deciphered their spatial expression patterns based on differential expression analysis. Domain 15 within the hippocampus, except for the “cord-like” and “arrow-like” structures, delineated high expressions of 2 astrocyte gene markers 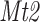 and
and 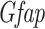 [103]. The spatial domain 14 surrounding the hippocampus expressed multiple oligodendrocyte-related gene markers, including
[103]. The spatial domain 14 surrounding the hippocampus expressed multiple oligodendrocyte-related gene markers, including 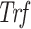 and
and 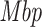 [104] (Supplementary Fig. S4). The above results elucidated that STMSGAL can efficiently detect spatial heterogeneity and further decompose spatial expression patterns. Notably, the cell type–aware module obviously boosted the partition of tissue structures on Adult Mouse Brain (FFPE) based on its UMAP plot [73], while those of DeepST were more like a smooth version of the nonspatial method SCANPY (Fig. 7D).
[104] (Supplementary Fig. S4). The above results elucidated that STMSGAL can efficiently detect spatial heterogeneity and further decompose spatial expression patterns. Notably, the cell type–aware module obviously boosted the partition of tissue structures on Adult Mouse Brain (FFPE) based on its UMAP plot [73], while those of DeepST were more like a smooth version of the nonspatial method SCANPY (Fig. 7D).
Finally, all attention layers of STMSGAL with ctaSNN were visualized. In each layer, nodes were arranged based on spot spatial locations, and edges were colored by corresponding weights. The results demonstrated that the combination of attention mechanism and ctaSNN boosted the characterization of the boundaries of main tissue structures on Adult Mouse Brain (FFPE) (such as the cortex, hippocampus, and midbrain) (Fig. 7E). Collectively, attention mechanism and ctaSNN contributed to delineating the similarity between neighboring spots (Fig. 7E).
Ablation Study
In our STMSGAL method, the combination of a graph attention autoencoder (GATE) and multiscale deep subspace clustering aims to obtain multiscale feature information of spots. The self-supervised module aims to learn robust latent features with clustering information for each spot.
To justify the contribution and necessity of these components, we conducted the ablation study to further investigate the effects of GATE, multiscale deep subspace clustering, and the self-supervised module on spatial clustering performance on the DLPFC sections from 151507 to 151510. As shown in Table 4, 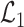 denotes the reconstruction loss of normalized expressions based on GATE.
denotes the reconstruction loss of normalized expressions based on GATE. 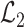 denotes the loss of the multiscale deep subspace clustering module, which contains regularization loss
denotes the loss of the multiscale deep subspace clustering module, which contains regularization loss 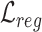 and multiscale self-expression loss
and multiscale self-expression loss 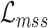 , and
, and 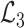 is the loss of the self-supervised module.
is the loss of the self-supervised module.
Table 4:
Ablation study on different loss terms
| Loss function | ||||
|---|---|---|---|---|
| Datasets |
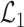
|
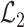
|
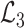
|
ARI |
| 151507 |
|
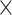
|
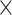
|
0.508 |
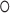
|
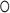
|
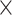
|
0.518 | |
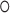
|
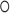
|
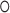
|
0.533 | |
| 151508 |
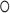
|
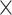
|
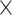
|
0.405 |
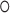
|
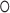
|
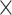
|
0.444 | |
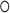
|
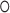
|
|
0.473 | |
| 151509 |
|
|
|
0.392 |
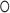
|
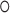
|
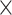
|
0.447 | |
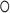
|
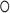
|
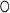
|
0.511 | |
| 151510 |
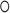
|
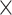
|
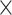
|
0.437 |
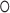
|
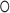
|
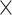
|
0.442 | |
|
|
|
0.452 | |
* The bold type indicates the best performance in each column.
From Table 4, we found that both the multiscale deep subspace clustering module and the self-supervised module cooperated well with GATE and greatly improved the clustering performance. The results demonstrated that the self-supervised module, which utilized the clustering labels to self-supervise the learning of spot embeddings, obtained more accurate clustering ability. The multiscale deep subspace clustering module fully utilized the embedded multiscale information and manifested an obvious effect on spatial clustering, suggesting that a proper clustering-oriented loss function can efficiently enhance the clustering performance.
Moreover, to analyze the effect of the multiscale strategy on spatial clustering performance, we compared the difference between individual self-expression layers and multiscale self-expression layers. Table 5 gives the ARI values of STMSGAL with or without the multiscale strategy for the DLPFC sections from 151507 to 151510. We applied a controlled variable approach to make the rest of the modules the same. The results indicated that the performance of STMSGAL with the multiscale strategy was better than one from a single self-expression layer on the 4 DLPFC sections, verifying that the multiscale strategy fully utilized the embedding features in different layers. In addition, the adaptive fusion method still significantly improved the spatial clustering performance.
Table 5:
Ablation study on the multiscale strategy
| Datasets | Strategy | ARI |
|---|---|---|
| 151507 | Without the multiscale strategy | 0.485 |
| With the multiscale strategy | 0.533 | |
| 151508 | Without the multiscale strategy | 0.394 |
| With the multiscale strategy | 0.473 | |
| 151509 | Without the multiscale strategy | 0.437 |
| With the multiscale strategy | 0.511 | |
| 151510 | Without the multiscale strategy | 0.407 |
| With the multiscale strategy | 0.452 |
* The bold type indicates the best performance in each column.
Since some spots could be erroneously assigned to spatially diametrical domains and cause noise during spot embedding feature learning, we used an additional optimization step to further optimize spatial clustering results obtained from Louvain clustering on the DLPFC dataset.
To further investigate the effect of the additional optimization step on the spatial clustering performance, we compared the performance of STMSGAL with or without the additional optimization step for sections 151507 to 151510 of DLPFC. Table 6 gives the ARI values of STMSGAL with or without the additional optimization step for DLPFC. The results demonstrated that STMSGAL with the additional optimization step significantly outperformed STMSGAL without the step. Thus, the additional optimization step could help spatial clustering.
Table 6:
Ablation study on the additional optimization step
| Datasets | Strategy | ARI |
|---|---|---|
| 151507 | Without the additional optimization step | 0.509 |
| With the additional optimization step | 0.533 | |
| 151508 | Without the additional optimization step | 0.450 |
| With the additional optimization step | 0.473 | |
| 151509 | Without the additional optimization step | 0.484 |
| With the additional optimization step | 0.511 | |
| 151510 | Without the additional optimization step | 0.430 |
| With the additional optimization step | 0.452 |
* The bold type indicates the best performance in each column.
When performing clustering again, we used Louvian clustering on DLPFC, Leiden clustering on Human Breast Cancer, and mclust on STARmap. To analyze why different clustering algorithms were used on different datasets, we conducted ablation experiments on the above 3 datasets. Tables 7 and 8 demonstrated ablation analysis results based on different clustering methods when performing clustering again on DLPFC 10x Genomics Visium datasets, STARmap, and Human Breast Cancer (Block A, Section 1), respectively. The results demonstrated that STMSGAL significantly improved ST clustering accuracy when using Louvian clustering on DLPFC, Leiden clustering on Human Breast Cancer, and mclust on STARmap.
Table 7:
Ablation analysis under different clustering methods on DLPFC 10x Genomics Visium datasets
| Datasets | |||||
|---|---|---|---|---|---|
| Methods | 151507 | 151508 | 151509 | 151510 | Average ARI |
| Louvain clustering | 0.533 | 0.473 | 0.511 | 0.452 | 0.492 |
| mclust | 0.520 | 0.475 | 0.354 | 0.403 | 0.438 |
| Leiden clustering | 0.511 | 0.489 | 0.471 | 0.393 | 0.469 |
| Subspace clustering | 0.216 | 0.325 | 0.395 | 0.284 | 0.294 |
* The bold type indicates the best performance in each column.
Table 8:
Ablation analysis under different clustering methods on STARmap and Human Breast Cancer (Block A, Section 1)
| Datasets | Methods | ARI |
|---|---|---|
| STARmap | Louvain clustering | 0.282 |
| mclust | 0.568 | |
| Leiden clustering | 0.273 | |
| Subspace clustering | 0.067 | |
| Human Breast Cancer | Louvain clustering | 0.534 |
| (Block A, Section 1) | mclust | 0.512 |
| Leiden clustering | 0.606 | |
| Subspace clustering | 0.588 |
* The bold type indicates the best performance in each column.
Discussion
Accurately detecting spatial domains and identifying differentially expressed genes can greatly boost our understanding about tissue organization and biological functions. In this article, we developed a spatial domain identification framework called STMSGAL based on GATE and multiscale deep subspace clustering. STMSGAL can been accurately incorporated to the standard analysis pipeline by using the “anndata” object in the SCANPY package [66] as inputs.
Different from classical autoencoders, STMSGAL utilized an attention mechanism in multiple hidden layers of the encoder and decoder. First, it constructed ctaSNN through Louvain clustering exclusively based on gene expression profiles. The weights of edges in the ctaSNN depicted the similarity between neighboring spots and were adaptively learned. Next, it integrated expression profiles and the constructed ctaSNN to form spot latent embedding representation based on GATE. It mainly includes spot embedding feature matrix construction, subspace clustering combining self-expression coefficient learning and affinity matrix construction, and spot robust latent feature learning based on self-supervised learning. Finally, it implemented biological applications, including spot clustering, differential expression analysis, and trajectory inference.
In the STMSGAL method, the multiscale self-expression module was used to fully explore the associations between spot representations in all encoder layers. The deep subspace clustering module was utilized to obtain the clustering labels for each spot through a clustering-oriented loss function. The self-supervised module was introduced to effectively learn spot latent representation. The combination of the above 3 modules helps to learn more discriminative features with clustering information for each spot. The more discriminative features obtained with clustering information were used as the input of spectral clustering and conducted the final clustering.
Traditional subspace clustering mainly contains 2 procedures: constructing an affinity matrix through representation learning and spectral clustering. However, spectral clustering is sensitive to the construction of a similarity matrix and the selection of various parameters, but the Leiden/Louvain/mclust clustering methods are more appropriate to biological data and exhibit a powerful spatial clustering performance. Consequently, Leiden/Louvain/mclust clustering has been widely used in the field of spatial clustering. Thus, our proposed STMSGAL framework used Leiden/Louvain/mclust for performing clustering again to identify spatial domains after obtaining more discriminative features with clustering information based on multiscale deep subspace clustering.
We compared the performance of STMSGAL with 7 other clustering methods on four 10x Genomics Visium datasets from Adult Mouse Brain (FFPE), Human Breast Cancer (DCIS), Human Breast Cancer (Block A, Section 1), and the DLPFC tissues, as well as 1 mouse visual cortex STARmap dataset. The 7 comparison methods include SCANPY, GraphST, SEDR, CCST, STAGATE, DeepST, and SiGra. The SCANPY has been widely applied to single-cell clustering. The remaining are state-of-the-art spatial clustering methods. The results demonstrated that our proposed STMSGAL method obtained impressive performance over other competing methods in terms of 4 evaluation metrics (i.e., DB, CH, S_Dbw, and ARI). STMSGAL significantly improved the identification of layer structures in 4 DLPFC sections, mouse visual cortex STARmap data, and mouse embryo data; accurately dissected spatial domains on 2 breast cancer tissues; and efficiently depicted the similarity between neighboring spots on Adult Mouse Brain (FFPE).
STMSGAL greatly boosted ST data analysis. It may be mainly attributed to the following features: first, although existing methods (such as stLearn) took histological images as inputs, they achieved limited performance. For example, stLearn adopted a pretrained neural network to obtain spot features from images and further computed their morphological distances via cosine distance. However, the predefined strategy in stLearn was not flexible and resulted in its poor spatial clustering performance. In contrast, STMSGAL adopted an attention mechanism to adaptively integrate spatial locations and gene expression profiles.
Second, a multiscale self-expression module was designed to train a self-expression coefficient matrix in different encoder layers. SEDR and CCST merely adopted the representations in the encoder final hidden layer for spatial clustering tasks, wasting much useful information embedded in its other layers. Comparatively, the multiscale self-expression module fully explored the associations between node representations in all encoder layers. Thus, it fully adopted the embedded multiscale information and obtained a more distinct self-expression coefficient matrix. Furthermore, it mapped these features into a more precise subspace for spatial clustering.
Finally, a deep subspace clustering module was proposed to obtain the clustering labels with a clustering-oriented loss function, and a self-supervised module was introduced to effectively guide spot latent representation learning. Thus, the learned spot latent embedding representation greatly improved the clustering performance.
In summary, STMSGAL is a powerful spatial clustering framework that constructs an integrated representation for spots by aggregating both transcriptomic data and spatial context. STMSGAL derived low-dimensional embedding, enabling to conduct spatial clustering and trajectory inference more accurately. Moreover, STMSGAL facilitates deciphering new principles in a spatially organized context.
Although STMSGAL achieved accurate spatial clustering performance, the deep subspace clustering algorithm can be further developed. In the near future, motivated by the linkages between spatial domain identification and single-cell segmentation used to image-based ST data, we anticipate that STMSGAL can be further extended to a single-cell segmentation task applied to the subcellular resolution technologies. We also hope to enhance its applicability on other datasets generated by new sequencing technologies.
Moreover, self-supervised learning can effectively learn spot representations, but optimizing the spot representations by combining the pseudo labels can affect the convergence of the model. The contrastive learning algorithm is a promising paradigm of the self-supervised learning model. In the future, we will introduce contrastive learning to facilitate spot representation learning and spatial clustering.
Finally, the accumulation of ST data generates spatial omics big data, which pose many technical challenges to data integration and analysis. To enable STMSGAL to deal with larger datasets, we will further alleviate the computational burden of STMSGAL using a graph convolutional network mini-batch or parallel techniques to construct large-scale graphs for spatial omics data.
Availability of Source Code and Requirements
Project name: STMSGAL
Project homepage: https://github.com/plhhnu/STMSGAL
Operating system(s): Platform independent
Programming language: Python
License: MIT license for the code, Creative Commons CC0 1.0 Public Domain Dedication for the filtered spatial transcriptomic data
RRID: SCR_025422
biotools: stmsgal
Supplementary Material
Qianqian Song -- 4/3/2024
Qianqian Song -- 7/24/2024
Zixuan Cang -- 4/8/2024
Zixuan Cang -- 8/7/2024
Acknowledgments
We thank the reviewers for their valuable comments and all authors of the cited references.
Contributor Information
Liqian Zhou, School of Computer Science, Hunan University of Technology, Zhuzhou 412007, Hunan, China.
Xinhuai Peng, School of Computer Science, Hunan University of Technology, Zhuzhou 412007, Hunan, China.
Min Chen, School of Computer Science, Hunan Institute of Technology, Hengyang 421002, Hunan, China.
Xianzhi He, School of Computer Science, Hunan University of Technology, Zhuzhou 412007, Hunan, China.
Geng Tian, Geneis (Beijing) Co. Ltd., Beijing 100102, China.
Jialiang Yang, Geneis (Beijing) Co. Ltd., Beijing 100102, China.
Lihong Peng, School of Computer Science, Hunan University of Technology, Zhuzhou 412007, Hunan, China; College of Life Science and Chemistry, Hunan University of Technology, Zhuzhou 412007, Hunan, China.
Additional Files
Supplementary Fig. S1. Comparison of spatial domains identified by SCANPY, SEDR, CCST, DeepST, STAGATE, SiGra, GraphST, and STMSGAL and manual annotations in 3 sections of human DLPFC tissues.
Supplementary Fig. S2. Cluster assignments generated by SCANPY, SEDR, CCST, STAGATE, DeepST, GraphST, and STMSGAL on Human Breast Cancer (Ductal Carcinoma In Situ [DCIS]).
Supplementary Fig. S3. Cluster assignments generated by SCANPY, SEDR, CCST, STAGATE, DeepST, GraphST, and STMSGAL on Adult Mouse Brain (FFPE).
Supplementary Fig. S4. Visualizations of spatial domains and expressions of the corresponding marker genes identified by STMSGAL with Louvain clustering on adult mouse hippocampus tissue.
Abbreviations
ARI: adjusted Rand index; CH: Calinski–Harabasz; DB: Davies–Bouldin; DCIS: ductal carcinoma in situ; DCIS/LCIS: ductal carcinoma in situ/lobular carcinoma in situ; ELU: exponential linear unit; GATE: graph attention autoencoder; HDST: high-definition spatial transcriptomics; IDC: invasive ductal carcinoma; NGS: next-generation sequencing; ReLu: rectified linear units; scRNA-seq: single-cell RNA sequencing; SNN: spatial neighbor network; ST: spatial transcriptomics.
Author Contributions
Conceptualization: L.Q.Z., X.H.P., L.H.P., M.C., and J.L.Y. Methodology: L.Q.Z., X.H.P., X.Z.H., and G.T. Supervision: L.H.P., J.L.Y. Writing—original draft: L.Q.Z., L.H.P., and X.H.P. Writing—review and editing: L.Q.Z., X.H.P., L.H.P., M.C., and J.L.Y.
Funding
Liqian Zhou was funded by National Natural Science Foundation of China under Grant 62072172 and Natural Science Foundation of Hunan province under Grant 2021JJ30219. Min Chen was supported by National Natural Science Foundation of China under Grant 62172158. Lihong Peng was supported by National Natural Science Foundation of China under Grant 61803151 and Natural Science Foundation of Hunan province under Grant 2023JJ50201.
Data Availability
Source codes and datasets of STMSGAL are available in the GitHub repository [105]. Specifically, the DLPFC dataset is accessible within the spatialLIBD package [64]. The Adult Mouse Brain (FFPE), Human Breast Cancer (DCIS), and Human Breast Cancer (Block A Section 1) datasets are collected from the 10x Genomics website [61–63]. An archival copy of the code and supporting data are also available via the GigaScience repository, GigaDB [106]. DOME-ML (Data, Optimization, Model and Evaluation in Machine Learning) annotations are available via a link in GigaDB [106] and via accession cji1mirt7b in the DOME registry [107].
Competing Interests
G. Tian and J-L. Yang are employees and shareholders of Geneis (Beijing) Co. Ltd. The remaining authors declare no competing interests.
References
- 1. Hu J, Schroeder A, Coleman K et al. Statistical and machine learning methods for spatially resolved transcriptomics with histology. Comput Struct Biotechnol J. 2021;19:3829–41. 10.1016/j.csbj.2021.06.052. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2. Ren X, Wen W, Fan X, et al. COVID-19 immune features revealed by a large-scale single-cell transcriptome atlas. Cell. 2021;184(7):1895–913. 10.1016/j.cell.2021.01.053. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3. Yang W, Wang P, Luo M,et al. DeepCCI: a deep learning framework for identifying cell–cell interactions from single-cell RNA sequencing data. Bioinformatics. 2023;39(10):btad596. 10.1093/bioinformatics/btad596. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4. Qi R, Wu J, Guo F et al. A spectral clustering with self-weighted multiple kernel learning method for single-cell RNA-seq data. Brief Bioinf. 2021;22(4):bbaa216. 10.1093/bib/bbaa216. [DOI] [PubMed] [Google Scholar]
- 5. Xu J, Xu J, Meng Y, et al. Graph embedding and Gaussian mixture variational autoencoder network for end-to-end analysis of single-cell RNA sequencing data. Cell Rep Methods. 2023;3(1):100382. 10.1016/j.crmeth.2022.100382. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6. Peng L, Yuan R, Han C et al. Cellenboost: a boosting-based ligand-receptor interaction identification model for cell-to-cell communication inference. IEEE T NanoBiosci. 2023;22(4):705–15. 10.1109/TNB.2023.3278685. [DOI] [PubMed] [Google Scholar]
- 7. Peng L, Tan J, Xiong W, et al. Deciphering ligand–receptor-mediated intercellular communication based on ensemble deep learning and the joint scoring strategy from single-cell transcriptomic data. Comput Biol Med. 2023;163:107137. 10.1016/j.compbiomed.2023.107137. [DOI] [PubMed] [Google Scholar]
- 8. Peng L, Xiong W, Han C, et al. CellDialog: a computational framework for ligand-receptor-mediated cell-cell communication analysis. IEEE J Biomed Health Inform. 2024;28(2):1–12. 10.1109/JBHI.2023.3333828. [DOI] [PubMed] [Google Scholar]
- 9. Peng L, Gao P, Xiong W et al. Identifying potential ligand–receptor interactions based on gradient boosted neural network and interpretable boosting machine for intercellular communication analysis. Comput Biol Med. 2024;171:108110. 10.1016/j.compbiomed.2024.108110. [DOI] [PubMed] [Google Scholar]
- 10. Jing J, Feng J, Yuan Y, et al. Spatiotemporal single-cell regulatory atlas reveals neural crest lineage diversification and cellular function during tooth morphogenesis. Nat Commun. 2022;13(1):4803. 10.1038/s41467-022-32490-y. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11. Shang L, Zhou X. Spatially aware dimension reduction for spatial transcriptomics. Nat Commun. 2022;13(1):7203. 10.1038/s41467-022-34879-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12. Peng L, Huang L, Su Q, et al. LDA-VGHB: identifying potential lncRNA-disease associations with singular value decomposition, variational graph auto-encoder and heterogeneous Newton boosting machine. Brief Bioinform. 2024;5(1):bbad466. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13. Peng L, Ren M, Huang L, et al. GEnDDn: an lncRNA–Disease association identification framework based on dual-net neural architecture and deep neural network. Interdiscip Sci. 2024;16:418–438. 10.1007/s12539-024-00619-w. [DOI] [PubMed] [Google Scholar]
- 14. Svensson V, Vento-Tormo R, Teichmann SA. Exponential scaling of single-cell RNA-seq in the past decade. Nat Protoc. 2018;13(4):599–604. 10.1038/nprot.2017.149. [DOI] [PubMed] [Google Scholar]
- 15. Ding Q, Yang W, Luo M, et al. CBLRR: a cauchy-based bounded constraint low-rank representation method to cluster single-cell RNA-seq data. Brief Bioinf. 2022;23(5):bbac300. 10.1093/bib/bbac300. [DOI] [PubMed] [Google Scholar]
- 16. Wang P, Yao L, Luo M,et al. Single-cell transcriptome and TCR profiling reveal activated and expanded T cell populations in Parkinson’s disease. Cell Discovery. 2021;7(1):52. 10.1038/s41421-021-00280-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17. Wang J, Zou Q, Lin C. A comparison of deep learning-based pre-processing and clustering approaches for single-cell RNA sequencing data. Brief Bioinf. 2022;23(1):bbab345. 10.1093/bib/bbab345. [DOI] [PubMed] [Google Scholar]
- 18. Yan S, Si Y, Zhou W et al. Single-cell transcriptomics reveals the interaction between peripheral CD4+ CTLs and mesencephalic endothelial cells mediated by IFNG in Parkinson’s disease. Comput Biol Med. 2023;158:106801. 10.1016/j.compbiomed.2023.106801. [DOI] [PubMed] [Google Scholar]
- 19. Hu H, Feng Z, Lin H, et al. Gene function and cell surface protein association analysis based on single-cell multiomics data. Comput Biol Med. 2023;157:106733. 10.1016/j.compbiomed.2023.106733. [DOI] [PubMed] [Google Scholar]
- 20. Tang X, Zhou C, Lu C, et al. Enhancing drug repositioning through local interactive learning with bilinear attention networks. IEEE J Biomed Health Inform. 2023;1–12. 10.1109/JBHI.2023.3335275. [DOI] [PubMed] [Google Scholar]
- 21. Xu J, Xu J, Meng Y, et al. Graph embedding and Gaussian mixture variational autoencoder network for end-to-end analysis of single-cell RNA sequencing data. Cell Rep Methods. 2023;3(1):100382. 10.1016/j.crmeth.2022.100382. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22. Yang Q, Xu Z, Zhou W et al. An interpretable single-cell RNA sequencing data clustering method based on latent Dirichlet allocation. Brief Bioinf. 2023;24(4):bbad199. 10.1093/bib/bbad199. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23. Zhang C, Gao J, Chen HY et al. STGIC: A graph and image convolution-based method for spatial transcriptomic clustering. PLoS Comput Biol. 2024;20(2):e1011935. 10.1371/journal.pcbi.1011935. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24. Qiu Y, Yan C, Zhao P, et al. SSNMDI: a novel joint learning model of semi-supervised non-negative matrix factorization and data imputation for clustering of single-cell RNA-seq data. Brief Bioinf. 2023;24(3):bbad149. 10.1093/bib/bbad149. [DOI] [PubMed] [Google Scholar]
- 25. Wang P, Luo M, Zhou W et al. Global characterization of peripheral B cells in Parkinson’s disease by single-cell RNA and BCR sequencing. Front Immunol. 2022;13:814239. 10.3389/fimmu.2022.814239. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26. Jiang J, Xu J, Liu Y, et al. Dimensionality reduction and visualization of single-cell RNA-seq data with an improved deep variational autoencoder. Brief Bioinf. 2023;24(3):bbad152. 10.1093/bib/bbad152. [DOI] [PubMed] [Google Scholar]
- 27. Rao A, Barkley D, França GS et al. Exploring tissue architecture using spatial transcriptomics. Nature. 2021;596(7871):211–20. 10.1038/s41586-021-03634-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28. Moffitt JR, Hao J, Wang G et al. High-throughput single-cell gene-expression profiling with multiplexed error-robust fluorescence in situ hybridization. Proc Natl Acad Sci. 2016;113(39):11046–51. 10.1073/pnas.1612826113. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29. Wang X, Allen WE, Wright MA, et al. Three-dimensional intact-tissue sequencing of single-cell transcriptional states. Science. 2018;361(6400):eaat5691. 10.1126/science.aat5691. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30. Eng CHL, Lawson M, Zhu Q et al. Transcriptome-scale super-resolved imaging in tissues by RNA seqFISH+. Nature. 2019;568(7751):235–39. 10.1038/s41586-019-1049-y. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31. Larsson L, Frisén J, Lundeberg J. Spatially resolved transcriptomics adds a new dimension to genomics. Nat Methods. 2021;18(1):15–18. 10.1038/s41592-020-01038-7. [DOI] [PubMed] [Google Scholar]
- 32. Rodriques SG, Stickels RR, Goeva A et al. Slide-seq: a scalable technology for measuring genome-wide expression at high spatial resolution. Science. 2019;363(6434):1463–67. 10.1126/science.aaw1219. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33. Stickels RR, Murray E, Kumar P, et al. Highly sensitive spatial transcriptomics at near-cellular resolution with Slide-seqV2. Nat Biotechnol. 2021;39(3):313–19. 10.1038/s41587-020-0739-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34. Vickovic S, Eraslan G, Salmén F et al. High-definition spatial transcriptomics for in situ tissue profiling. Nat Methods. 2019;16(10):987–90. 10.1038/s41592-019-0548-y. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35. Liu Y, Yang M, Deng Y, et al. High-spatial-resolution multi-omics sequencing via deterministic barcoding in tissue. Cell. 2020;183(6):1665–81. 10.1016/j.cell.2020.10.026. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36. Xia K, Sun HX, Li J et al. The single-cell stereo-seq reveals region-specific cell subtypes and transcriptome profiling in Arabidopsis leaves. Developmental Cell. 2023;57(10):1299–1310. 10.1101/2021.10.20.465066. [DOI] [PubMed] [Google Scholar]
- 37. 10x Genomics . https://www.10xgenomics.com/resources/datasets. Accessed 18 November 2024.
- 38. Maynard KR, Collado-Torres L, Weber LM, et al. Transcriptome-scale spatial gene expression in the human dorsolateral prefrontal cortex. Nat Neurosci. 2021;24(3):425–36. 10.1038/s41593-020-00787-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39. Hartigan JA, Wong MA. Algorithm AS 136: a k-means clustering algorithm. J R Stat Soc Ser C Appl Stat. 1979;28(1):100–8. 10.2307/2346830. [DOI] [Google Scholar]
- 40. Blondel VD, Guillaume JL, Lambiotte R, et al. Fast unfolding of communities in large networks. J Stat Mech Theory Exp. 2008;2008(10):P10008. 10.1088/1742-5468/2008/10/P10008. [DOI] [Google Scholar]
- 41. Elosua-Bayes M, Nieto P, Mereu E, et al. SPOTlight: seeded NMF regression to deconvolute spatial transcriptomics spots with single-cell transcriptomes. Nucleic Acids Res. 2021;49(9):e50. 10.1093/nar/gkab043. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42. Cable DM, Murray E, Zou LS et al. Robust decomposition of cell type mixtures in spatial transcriptomics. Nat Biotechnol. 2022;40(4):517–26. 10.1038/s41587-021-00830-w. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43. Zhao E, Stone MR, Ren X, et al. Spatial transcriptomics at subspot resolution with BayesSpace. Nat Biotechnol. 2021;39(11):1375–84. 10.1038/s41587-021-00935-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44. Pham D, Tan X, Balderson B, et al. Robust mapping of spatiotemporal trajectories and cell–cell interactions in healthy and diseased tissues. Nat Commun. 2023;14(1):7739. 10.1038/s41467-023-43120-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45. Fu H, Xu H, Chong K et al. Unsupervised spatially embedded deep representation of spatial transcriptomics. bioRxiv. 2021. 10.1101/2021.06.15.448542. Accessed 1 November 2023. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46. Li J, Chen S, Pan X et al. Cell clustering for spatial transcriptomics data with graph neural networks. Nat Comput Sci. 2022;2(6):399–408. 10.1038/s43588-022-00266-5. [DOI] [PubMed] [Google Scholar]
- 47. Dong K, Zhang S. Deciphering spatial domains from spatially resolved transcriptomics with an adaptive graph attention auto-encoder. Nat Commun. 2022;13(1):1–12. 10.1038/s41467-021-27699-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48. Wang T, Sun J, Zhao Q. Investigating cardiotoxicity related with hERG channel blockers using molecular fingerprints and graph attention mechanism. Comput Biol Med. 2023;153:106464. 10.1016/j.compbiomed.2022.106464. [DOI] [PubMed] [Google Scholar]
- 49. Xu C, Jin X, Wei S, et al. DeepST: identifying spatial domains in spatial transcriptomics by deep learning. Nucleic Acids Res. 2022;50(22):e131. 10.1093/nar/gkac901. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50. Long Y, Ang KS, Li M et al. Spatially informed clustering, integration, and deconvolution of spatial transcriptomics with GraphST. Nat Commun. 2023;14(1):1155. 10.1038/s41467-023-36796-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51. Meng Y, Wang Y, Xu J, et al. Drug repositioning based on weighted local information augmented graph neural network. Brief Bioinf. 2024;25(1):bbad431. 10.1093/bib/bbad431. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 52. Zeng P, Zhang B, Liu A et al. Drug repositioning based on tripartite cross-network embedding and graph convolutional network. Expert Syst Appl. 2024;252:124152. 10.1016/j.eswa.2024.124152. [DOI] [Google Scholar]
- 53. Zeng Y, Yin R, Luo M et al. Identifying spatial domain by adapting transcriptomics with histology through contrastive learning. Brief Bioinf. 2023;24(2):bbad048. 10.1093/bib/bbad048. [DOI] [PubMed] [Google Scholar]
- 54. Xu H, S Wang, M Fang, et al. SPACEL: deep learning-based characterization of spatial transcriptome architectures. Nature Communications. 2023;14(1):7603. 10.1038/s41467-023-43220-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 55. Liu W, Liao X, Luo Z, et al. Probabilistic embedding, clustering, and alignment for integrating spatial transcriptomics data with PRECAST. Nat Commun. 2023;14(1):296. 10.1038/s41467-023-35947-w. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 56. Zhu J, Shang L, Zhou X. SRTsim: spatial pattern preserving simulations for spatially resolved transcriptomics. Genome Biol. 2023;24(1):39. 10.1186/s13059-023-02879-z. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 57. Tang Z, Li Z, Hou T et al. SiGra: single-cell spatial elucidation through an image-augmented graph transformer. Nat Commun. 2023;14(1):5618. 10.1038/s41467-023-41437-w. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 58. Yuan Z, Zhao F, Lin S, et al. Benchmarking spatial clustering methods with spatially resolved transcriptomics data. Nat Methods. 2024;21(4):712–22. 10.1038/s41592-024-02215-8. [DOI] [PubMed] [Google Scholar]
- 59. Salehi A, Davulcu H. Graph attention auto-encoders. arXiv preprint arXiv:190510715. 2019. 10.48550/arXiv.1905.10715. Accessed 18 November 2024. [DOI]
- 60. Kou S, Xia W, Zhang X et al. Self-supervised graph convolutional clustering by preserving latent distribution. Neurocomputing. 2021;437:218–26. 10.1016/j.neucom.2021.01.082. [DOI] [Google Scholar]
- 61. Adult Mouse Brain (FFPE) . 2021. https://www.10xgenomics.com/datasets/adult-mouse-brain-ffpe-1-standard-1-3-0. Accessed 18 November 2024.
- 62. Human Breast Cancer (Block A Section 1) . 2020. https://www.10xgenomics.com/datasets/human-breast-cancer-block-a-section-1-1-standard-1-1-0. Accessed 18 November 2024.
- 63. Human Breast Cancer (DCIS) . 2021. https://www.10xgenomics.com/datasets/human-breast-cancer-ductal-carcinoma-in-situ-invasive-carcinoma-ffpe-1-standard-1-3-0. Accessed 18 November 2024.
- 64. Human Dorsolateral Prefrontal Cortex Dataset . 2024. http://spatial.libd.org/spatialLIBD/. Accessed 18 November 2024.
- 65. Chen A, Liao S, Cheng M et al. Spatiotemporal transcriptomic atlas of mouse organogenesis using DNA nanoball-patterned arrays. Cell. 2022;185(10):1777–92. 10.1016/j.cell.2022.04.003. [DOI] [PubMed] [Google Scholar]
- 66. Wolf FA, Angerer P, Theis FJ. SCANPY: large-scale single-cell gene expression data analysis. Genome Biol. 2018;19(1):1–5. 10.1186/s13059-017-1382-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 67. Wang T, Wu J, Zhang Z, et al. Multi-scale graph attention subspace clustering network. Neurocomputing. 2021;459:302–14. 10.1016/j.neucom.2021.06.058. [DOI] [Google Scholar]
- 68. Veličković P, Cucurull G, Casanova A, et al. Graph attention networks. arXiv preprint arXiv:171010903. 2017. 10.48550/arXiv.1710.10903. Accessed 18 November 2024. [DOI]
- 69. Ji P, Zhang T, Li H, et al. Deep subspace clustering networks. Adv Neur Inf Proc Syst. 2017;30:23–32. [Google Scholar]
- 70. Ng A, Jordan M, Weiss Y. On spectral clustering: analysis and an algorithm. Adv Neur Inf Proc Syst. 2001;14:849–856. [Google Scholar]
- 71. Traag VA, Waltman L, Van Eck NJ. From Louvain to Leiden: guaranteeing well-connected communities. Sci Rep. 2019;9(1):1–12. 10.1038/s41598-019-41695-z. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 72. Fraley C, Raftery AE, Murphy TB et al. mclust version 4 for R: normal mixture modeling for model-based clustering, classification, and density estimation. Technical report. 2012. 10.32614/CRAN.package.mclust. Accessed 18 November 2024. [DOI]
- 73. McInnes L, Healy J, Melville J. Umap: Uniform manifold approximation and projection for dimension reduction. arXiv:1802.03426. 2018. 10.48550/arXiv.1802.03426. Accessed 18 November 2024. [DOI]
- 74. Mou T, Deng W, Gu F, et al. Reproducibility of methods to detect differentially expressed genes from single-cell RNA sequencing. Front Genet. 2020;10:1331. 10.3389/fgene.2019.01331. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 75. Vu TN, Wills QF, Kalari KR et al. Beta-Poisson model for single-cell RNA-seq data analyses. Bioinformatics. 2016;32(14):2128–35. 10.1093/bioinformatics/btw202. [DOI] [PubMed] [Google Scholar]
- 76. Das S, Rai SN. SwarnSeq: an improved statistical approach for differential expression analysis of single-cell RNA-seq data. Genomics. 2021;113(3):1308–24. 10.1016/j.ygeno.2021.02.014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 77. Cannoodt R, Saelens W, Saeys Y. Computational methods for trajectory inference from single-cell transcriptomics. Eur J Immunol. 2016;46(11):2496–506. 10.1002/eji.201646347. [DOI] [PubMed] [Google Scholar]
- 78. Trapnell C, Cacchiarelli D, Grimsby J et al. The dynamics and regulators of cell fate decisions are revealed by pseudotemporal ordering of single cells. Nat Biotechnol. 2014;32(4):381–86. 10.1038/nbt.2859. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 79. Wolf FA, Hamey FK, Plass M, et al. PAGA: graph abstraction reconciles clustering with trajectory inference through a topology preserving map of single cells. Genome Biol. 2019;20:1–9. 10.1186/s13059-019-1663-x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 80. Clevert DA, Unterthiner T, Hochreiter S. Fast and accurate deep network learning by exponential linear units (elus). arXiv preprint arXiv:151107289. 2015. 10.48550/arXiv.1511.07289. Accessed 18 November 2024. [DOI]
- 81. Kingma DP, Ba J. Adam: a method for stochastic optimization. arXiv preprint arXiv:14126980. 2014. 10.48550/arXiv.1412.6980. Accessed 18 November 2024. [DOI]
- 82. Nair V, Hinton GE. Rectified linear units improve restricted boltzmann machines. In: Proceedings of the 27th international conference on machine learning (ICML-10), 807–814. Springer Nature: Haifa, Israel, 2010. https://www.cs.toronto.edu/~hinton/absps/reluICML.pdf. [Google Scholar]
- 83. Hubert L, Arabie P. Comparing partitions. J Classif. 1985;2(1):193–218. 10.1007/BF01908075. [DOI] [Google Scholar]
- 84. Davies DL, Bouldin DW. A cluster separation measure. IEEE T Pattern Anal Mach Intell. 1979;1(2):224–227. 10.1109/TPAMI.1979.4766909. [DOI] [PubMed] [Google Scholar]
- 85. Caliński T, Harabasz J. A dendrite method for cluster analysis. Commun Stat Theory Methods. 1974;3(1):1–27. 10.1080/03610927408827101. [DOI] [Google Scholar]
- 86. Halkidi M, Vazirgiannis M. Clustering validity assessment: finding the optimal partitioning of a data set. In: Proceedings 2001 IEEE International Conference on Data Mining, p. 187–194. San Jose, CA, USA: IEEE, 2001. [Google Scholar]
- 87. Peng L, He X, Peng X et al. STGNNks: Identifying cell types in spatial transcriptomics data based on graph neural network, denoising auto-encoder, and k-sums clustering. Comput Biol Med. 2023;166:107440. 10.1016/j.compbiomed.2023.107440. [DOI] [PubMed] [Google Scholar]
- 88. Gilmore EC, Herrup K. Cortical development: layers of complexity. Curr Biol. 1997;7(4):R231–34. 10.1016/S0960-9822(06)00108-4. [DOI] [PubMed] [Google Scholar]
- 89. Kothari C, Clemenceau A, Ouellette G et al. Is carboxypeptidase B1 a prognostic marker for ductal carcinoma in situ?. Cancers. 2021;13(7):1726. 10.3390/cancers13071726. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 90. Gruvberger S, Ringnér M, Chen Y et al. Estrogen receptor status in breast cancer is associated with remarkably distinct gene expression patterns. Cancer Res. 2001;61(16):5979–84. [PubMed] [Google Scholar]
- 91. Martínez-Pérez C, Leung J, Kay C et al. The signal transducer IL6ST (gp130) as a predictive and prognostic biomarker in breast cancer. J Pers Med. 2021;11(7):618. 10.3390/jpm11070618. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 92. Wang Y, Sheng N, Xie Y et al. Low expression of CRISP3 predicts a favorable prognosis in patients with mammary carcinoma. J Cell Physiol. 2019;234(8):13629–638. 10.1002/jcp.28043. [DOI] [PubMed] [Google Scholar]
- 93. Ahn BY, Elwi AN, Lee B, et al. Genetic screen identifies insulin-like growth factor binding protein 5 as a modulator of tamoxifen resistance in breast cancer IGFBP5 reverses tamoxifen resistance. Cancer Res. 2010;70(8):3013–19. 10.1158/0008-5472.CAN-09-3108. [DOI] [PubMed] [Google Scholar]
- 94. Díez-Itza I, Sánchez LM, Allende MT et al. Zn-α2-glycoprotein levels in breast cancer cytosols and correlation with clinical, histological and biochemical parameters. Eur J Cancer. 1993;29(9):1256–60. 10.1016/0959-8049(93)90068-Q. [DOI] [PubMed] [Google Scholar]
- 95. Zhang P, Zheng P, Liu Y. Amplification of the CD24 gene is an independent predictor for poor prognosis of breast cancer. Front Genet. 2019;10:560. 10.3389/fgene.2019.00560. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 96. Kwon MJ, Han J, Seo JH, et al. CD24 overexpression is associated with poor prognosis in luminal A and triple-negative breast cancer. PLoS One. 2015;10(10):e0139112. 10.1371/journal.pone.0139112. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 97. Sheridan C, Kishimoto H, Fuchs RK et al. CD44+/CD24-breast cancer cells exhibit enhanced invasive properties: an early step necessary for metastasis. Breast Cancer Res. 2006;8:1–13. 10.1186/bcr1610. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 98. Segovia-Mendoza M, González-González ME, Barrera D et al. Efficacy and mechanism of action of the tyrosine kinase inhibitors gefitinib, lapatinib and neratinib in the treatment of HER2-positive breast cancer: preclinical and clinical evidence. Am J Cancer Res. 2015;5(9):2531–61. [PMC free article] [PubMed] [Google Scholar]
- 99. Rimawi MF, Schiff R, Osborne CK. Targeting HER2 for the treatment of breast cancer. Annu Rev Med. 2015;66. 111–28. 10.1146/annurev-med-042513-015127. [DOI] [PubMed] [Google Scholar]
- 100. Sunkin SM, Ng L, Lau C, et al. Allen Brain Atlas: an integrated spatio-temporal portal for exploring the central nervous system. Nucleic Acids Res. 2012;41(D1):D996–98. 10.1093/nar/gks1042. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 101. Iijima T, Miura E, Watanabe M, et al. Distinct expression of C1q-like family mRNAs in mouse brain and biochemical characterization of their encoded proteins. Eur J Neurosci. 2010;31(9):1606–15. 10.1111/j.1460-9568.2010.07202.x. [DOI] [PubMed] [Google Scholar]
- 102. Kobayashi M, Hamanoue M, Masaki T et al. Hippocalcin mediates calcium-dependent translocation of brain-type creatine kinase (BB-CK) in hippocampal neurons. Biochem Biophys Res Commun. 2012;429(3–4):142–47. 10.1016/j.bbrc.2012.10.125. [DOI] [PubMed] [Google Scholar]
- 103. Li D, Liu X, Liu T, et al. Neurochemical regulation of the expression and function of glial fibrillary acidic protein in astrocytes. Glia. 2020;68(5):878–97. 10.1002/glia.23734. [DOI] [PubMed] [Google Scholar]
- 104. White R, Gonsior C, Kram̎er-Albers EM et al. Activation of oligodendroglial Fyn kinase enhances translation of mRNAs transported in hnRNP A2–dependent RNA granules. J Cell Biol. 2008;181(4):579–86. 10.1083/jcb.200706164. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 105. STMSGAL . GitHub repository. https://github.com/plhhnu/STMSGAL. Accessed 18 November 2024.
- 106. Zhou L, Peng X, Chen M et al. Supporting data for “Unveiling Patterns in Spatial Transcriptomics Data: A Novel Approach Utilizing Graph Attention Autoencoder and Multi-Scale Deep Subspace Clustering Network.” GigaScience Database. 2024. 10.5524/102582. [DOI] [PMC free article] [PubMed]
- 107. DOME registry . https://registry.dome-ml.org/search. Accessed 28 November 2024.
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Data Citations
- Human Dorsolateral Prefrontal Cortex Dataset . 2024. http://spatial.libd.org/spatialLIBD/. Accessed 18 November 2024.
- Zhou L, Peng X, Chen M et al. Supporting data for “Unveiling Patterns in Spatial Transcriptomics Data: A Novel Approach Utilizing Graph Attention Autoencoder and Multi-Scale Deep Subspace Clustering Network.” GigaScience Database. 2024. 10.5524/102582. [DOI] [PMC free article] [PubMed]
Supplementary Materials
Qianqian Song -- 4/3/2024
Qianqian Song -- 7/24/2024
Zixuan Cang -- 4/8/2024
Zixuan Cang -- 8/7/2024
Data Availability Statement
Source codes and datasets of STMSGAL are available in the GitHub repository [105]. Specifically, the DLPFC dataset is accessible within the spatialLIBD package [64]. The Adult Mouse Brain (FFPE), Human Breast Cancer (DCIS), and Human Breast Cancer (Block A Section 1) datasets are collected from the 10x Genomics website [61–63]. An archival copy of the code and supporting data are also available via the GigaScience repository, GigaDB [106]. DOME-ML (Data, Optimization, Model and Evaluation in Machine Learning) annotations are available via a link in GigaDB [106] and via accession cji1mirt7b in the DOME registry [107].