Dynamic pattern evolution on scale-free networks

Abstract

A general class of dynamic models on scale-free networks is studied by analytical methods and computer simulations. Each network consists of N vertices and is characterized by its degree distribution, P(k), which represents the probability that a randomly chosen vertex is connected to k nearest neighbors. Each vertex can attain two internal states described by binary variables or Ising-like spins that evolve in time according to local majority rules. Scale-free networks, for which the degree distribution has a power law tail P(k) ∼ k^-γ, are shown to exhibit qualitatively different dynamic behavior for γ < 5/2 and γ > 5/2, shedding light on the empirical observation that many real-world networks are scale-free with 2 < γ < 5/2. For 2 < γ < 5/2, strongly disordered patterns decay within a finite decay time even in the limit of infinite networks. For γ > 5/2, on the other hand, this decay time diverges as ln(N) with the network size N. An analogous distinction is found for a variety of more complex models including Hopfield models for associative memory networks. In the latter case, the storage capacity is found, within mean field theory, to be independent of N in the limit of large N for γ > 5/2 but to grow as N^α with α = (5 - 2γ)/(γ - 1) for 2 < γ < 5/2.

The biosphere contains many complex networks built up from rather different elements such as molecules, cells, organisms, or machines. Despite their diversity, these networks exhibit some universal features and generic properties, a topic of much recent interest (1-6). One important result of this recent activity is a classification scheme for the structure of networks in terms of their topology and connectivity (5, 6). The basic elements of each network can be represented by nodes or vertices and their interrelations by edges between these vertices. By definition, the degree, k, of a given vertex is equal to the number of edges connected to it. In this way, each network is characterized by its graph, a well defined mathematical object (7). Four large subsets of network graphs have been characterized in terms of their connectivity properties: regular ordered and random networks, which have been studied for a long time, as well as small-world (1) and scale-free (4) networks. The latter types of networks are characterized by a degree distribution, P(k), that decays as P(k) ∼ 1/k^γ with decay exponent γ.

Many biological, social, and technological networks are found to be scale-free (5, 6). To explain this abundance, several mechanisms have been proposed, some of which are related to the growth of networks with preferential attachment rules (5, 8). The impact of network architecture on network integrity or resilience has also been investigated (6, 9-11). Upon random removal of a finite fraction of vertices, a scale-free network with decay exponent 2 < γ < 3 will always keep a giant component. In contrast, if a tiny fraction of the most highly connected vertices is selectively removed, such a network will also break up into many small components. Applying this insight to the case of disease spreading on networks, one realizes that infective diseases have a high probability to affect the whole network (12) unless one immunizes the most highly connected vertices (13).

Random removal of vertices is equivalent to the process of site percolation on the initial network (9, 10). Likewise, disease spreading is intimately related, in the long time limit, to bond percolation (6, 10). In general, the elements of real networks are dynamic and exhibit various properties that change with time. A more detailed description of the network dynamics is then obtained in terms of dynamical variables associated with each vertex of the network. We will consider processes on networks that evolve fast compared with any changes in the network topology, which is therefore taken to be time-independent. Two examples for such dynamical processes are provided by the regulation of genetic networks that exhibit a changing pattern of active and inactive genes (see, e.g., ref. 14) or by neural networks that can be characterized by firing and nonfiring neurons (see, e.g., ref. 15).

To identity universal features and generic properties, it is often convenient to use discrete dynamical variables and to allow each vertex to attain several distinct states. The network is then characterized, at each moment in time, by a certain pattern of these internal vertex states, and the time evolution of these patterns represents the global dynamics of the whole network.

The study of discrete dynamical processes on ordered and random networks has a long history. Ordered networks have been studied in the context of neural computation (16, 17), cellular automata or Boolean dynamics (18, 19), and dynamic Ising models (20). Random networks with random Boolean dynamics were introduced in the context of gene expression and studied as prototypes of random cellular automata (21-23). Discrete dynamic processes on small-world networks were discussed in ref. 2, whereas analogous processes on scale-free networks have only been addressed rather recently (24-26).

Random networks as originally studied in mathematics (5-7) are characterized by a Poissonian degree distribution as given by P(k) =〈k〉^ke^-〈k〉/k!, where 〈k〉≡∑kP(k) denotes the mean value of the vertex degree k. In contrast, scale-free networks are characterized by P(k) ∼ k^-γ with decay exponent γ for an intermediate range of k-values that can be defined as follows. To avoid disconnected subgraphs, it is useful to introduce a certain minimal degree k₀ > 0. Furthermore, a large but finite network containing N vertices is also characterized by a certain maximal degree k_N. These two “cutoffs” can be incorporated in a particularly simple way via the explicit form (9)

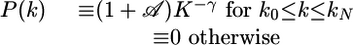[1]

with the normalization factor and k_N = k₀N^{1/(γ - 1)} (see Degree Distribution and Maximal Vertex Degree in Supporting Text, which is published as supporting information on the PNAS web site).

Many scale-free networks are characterized by decay exponents γ that fall into the narrow range 2 < γ ≤ 5/2 as observed in ref. 24. Indeed, table 2 of ref. 5 contains a list of ten scale-free networks with 2 < γ < 5/2, one with γ = 2.5, and only three with 2.5 < γ < 3. The lower boundary value γ = 2 is easy to understand since it ensures that the mean vertex degree 〈k〉 = ∑kP(k) remains finite in the limit of large N. The upper boundary value γ = 5/2 is less obvious. To gain some insight into this latter value, Aldana and Cluzel (24) studied the Kauffman model, i.e., random Boolean dynamics for binary variables or Ising-like spins (21, 22) on scale-free networks. They suggested the criterion that scale-free networks with decay exponent 2 < γ < 5/2 are located on the boundary between order and chaos (24). However, for random Boolean dynamics, the phase boundary between order and chaos turns out to be independent of the network architecture but depends only on the mean vertex degree 〈k〉. Indeed, this phase boundary is determined by the simple relation 2〈k〉ρ(1 - ρ) = 1 between 〈k〉 and the model parameter ρ, which represents the probability that the output of a Boolean function with random input will be equal to 1 (22). As long as 〈k〉 > 2, this equation has two solutions in the physical range 0 < ρ < 1 that determine the boundaries between the ordered and the chaotic phases. Since scale-free networks with γ > 5/2 as well as random Poissonian networks can have 〈k〉 > 2, all of these networks can exhibit transitions between ordered and chaotic phases if the binary patterns evolve according to random Boolean dynamics (21, 22).

In this article, we consider dynamic network models for binary variables or Ising-like spins which evolve in time according to local majority rules on scale-free networks. The latter rules are equivalent to the so-called Glauber dynamics (20) for Ising-models at zero temperature. In addition, we extend our study to finite temperature in the context of Hopfield models (17, 27) for associative memory networks and to networks with directed edges. The main results of our study are as follows.

First, using mean field theory and computer simulations, we show that scale-free networks with γ = 5/2 represent a sharp boundary for the local majority dynamics. This boundary is defined with respect to the decay of strongly disordered patterns and the associated growth of order within these patterns. For γ < 5/2, the disordered patterns decay within a finite time even in the limit of infinite networks. For γ > 5/2, on the other hand, this decay time diverges as ln(N) with the vertex number N. The latter behavior is consistent with recent results for opinion spreading on social networks (28). The different dynamic behavior of scale-free networks with γ < 5/2 and γ > 5/2 provides a new light on the empirical observation that most real-world networks are scale-free with 2 < γ < 5/2.

Second, our simulations give strong evidence that, for scale-free networks, disordered patterns typically evolve toward the two completely ordered patterns (or ground states) provided the networks are connected, the minimal vertex degree k₀ > 1, and the mean vertex degree 〈k〉 is sufficiently large. This is rather different from the behavior found previously for tree-like networks (29) and for d-dimensional hypercubic networks with d ≥ 3 (30), where the evolving patterns are typically trapped in metastable states with many domain boundaries and “blinkers,” but is consistent with the behavior observed in random Poissonian networks (31).

Third, we determine the minimal fraction of spins which one has to flip to transform the all-spin-down pattern into another pattern that evolves toward the all-spin-up pattern under the local majority dynamics. We derive an analytical expression for this minimal fraction and show that it vanishes very rapidly as ∼ exp(-|const|/(γ - 2)) as the decay exponent γ approaches the value γ = 2. This sensitivity of ordered spin patterns to selective spin flips has been independently observed in ref. 25. In contrast to the behavior of the decay time for strongly disordered patterns, the minimal fraction varies smoothly with the decay exponent γ in the vicinity of γ = 5/2.

Fourth, when extended to Hopfield models on scale-free networks, our mean field theory predicts that γ = 5/2 represents a sharp boundary for these models as well. For γ > 5/2, the maximal storage capacity of the network does not grow with the network size N in the limit of large N. In contrast, for 2 < γ < 5/2, the maximal storage capacity grows as N^α with α = (5 - 2γ)/(γ - 1) for large N. Very recently, it has been argued that functional networks in the human brain resemble scale-free networks with γ ≃ 2.1 (32). For the latter networks, our mean field theory predicts the storage capacity to grow as N^α with α ≃ 0.73. This growth of the storage capacity with network size N is almost as fast as in the original Hopfield model (17) on complete graphs with vertex degree k = N - 1 for which α = 1.

Models and Methods

To proceed, consider random scale-free networks with N vertices and M edges with degree distribution P(k) as obtained from the so-called configuration model (6) (see Numerical Generation of Scale-Free Networks in Supporting Text and Fig. 5, which is published as supporting information on the PNAS web site). Each vertex i of such a network has two internal states described by the Ising spin σ_i = ±1. The network architecture is embodied in the network's adjacency matrix I with matrix elements I_ij = 1 if the two vertices i and j are nearest neighbors, i.e., if they are connected by an edge, and I_ij = 0 otherwise. At each vertex i, we define the field h_i ≡∑_j I_ijσ_j. The sign of the field h_i is positive and negative if the majority of the nearest neighbor spins is positive or negative, respectively. The time evolution of the spin pattern is now defined by the local majority rule as given by

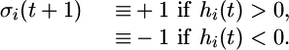In the special case h_i(t) = 0, we choose σ_i(t + 1) = +1 or -1 with equal probability. These local majority rules are equivalent to Glauber dynamics (20) at zero temperature as studied, e.g., on d-dimensional hypercubic networks (30) and on random Poissonian networks (31). Recently, similar dynamic models were also used in the context of opinion spreading (28), network robustness and sensitivity (25), and the yeast cell-cycle regulation system (26).

In general, the graph of a random scale-free network may be disconnected and consist of several components. In such a situation, the pattern evolution in one network component is completely independent of the evolution in all of the other components. To avoid this division of the evolving patterns into several subpatterns, we will focus on degree distributions characterized by minimal vertex degree k₀ ≥ 2 and mean vertex degree 〈k〉 ≥ 10 for which graphs with several components are rather unlikely. In general, random graphs with 〈k〉> 1 have one giant component and several small ones; for Poissonian graphs, the giant component contains φ(〈k〉)N vertices, where φ(〈k〉) approaches φ(∞) = 1 exponentially fast with increasing 〈k〉 (5). For such disconnected networks, our analysis applies to the pattern evolution on the giant components as long as k₀ > 1. Random scale-free networks with k₀ = 1 are special since they tend to be tree-like with many surface sites.

To study the time evolution of the spin patterns in more detail, we consider the probabilities q_k(t) that a vertex with degree k is in the spin-up state, and the probability Q(t) that, for any vertex in the network, a randomly chosen nearest neighbor vertex is in the spin-up state. As will become clear below, the probability Q is directly related to the order parameter of the system and will, thus, be called the ordering probability. Since a vertex associated with a randomly chosen edge has degree k with probability kP(k)/〈k〉 in a random network with no vertex degree correlations, the probabilities q_k and the ordering probability Q satisfy the simple relation

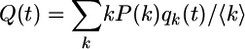[3]

with 0 ≤ Q(t) ≤ 1. Note that the ordering probability Q differs, in general, from the overall probability to find any vertex in the spin-up state. The latter probability is given by 〈q〉 ≡ ∑_k P(k)q_k. Special patterns for which 〈q〉 = Q are provided by k-independent probabilities q_k = q. In particular, for the all-spin-down pattern with q_k = 0 for all k and for the all-spin-up pattern with q_k = 1 for all k, one has Q = 〈q〉 = 0 and Q = 〈q〉 = 1, respectively.

If we know the ordering probability Q at a certain time t, we can calculate the probabilities q_k at the next time step. Indeed, it follows from the majority rule dynamics as defined by Eq. 2 that

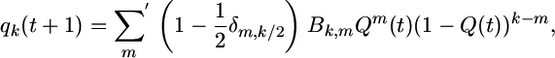[4]

where the prime at the summation symbol indicates that this sum runs over all integer m with k/2 ≤ m ≤ k, δ is the Kronecker symbol, and B_k,m ≡ k!/[m!(k - m)!] are the binomial coefficients. Finally, summation of the left-hand side of Eq. 4 leads to the evolution equation

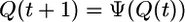[5]

for the ordering probability Q with the evolution function

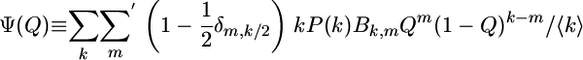[6]

for random graphs with no vertex degree correlations as considered here.

The evolution equation (5) has two stable fixed points at Q = 0 and Q = 1, and an unstable one at Q = 1/2. The fixed points with Q = 0 and Q = 1 correspond to the all-spin-down and all-spin-up patterns, respectively. The unstable fixed point with Q = 1/2 represents the phase boundary between these two ordered patterns; the corresponding boundary patterns are characterized by probabilities q̂_k, which satisfy

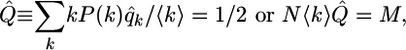[7]

where M is the total number of edges. A subset of these boundary patterns is provided by those patterns for which the probabilities q̂_k = 1/2 for all vertex degrees k. Therefore, the order parameter of these systems is taken to be

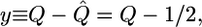[8]

which vanishes for all boundary patterns.

In the next section, we will compare the mean field trajectories obtained from the evolution equation (5) with the pattern evolution obtained from computer simulations. In the latter case, one starts from a certain initial pattern and applies the majority rule dynamics as given by Eq. 2 to each vertex of the network. Since we want to be able to use the same initial pattern for both mean field theory and computer simulations, we will define the enlarged set of strongly disordered patterns that consists (i) of the boundary patterns characterized by Eq. 7 and (ii) of additional patterns characterized by probabilities q̃_k that lead to Q = Q̃ = 1/2 ± 1/2M and, thus, to the order parameter

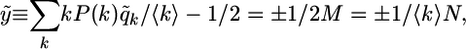[9]

which vanishes in the limit of large network size N. A pattern with probabilities q̃_k can be obtained from a boundary pattern by simultaneously flipping two spins with opposite orientations on a k and (k + 1) vertex.

The evolution equation for the order parameter y = Q - 1/2 can be directly obtained from the corresponding equation (7) for Q and is given by y(t + 1) =Ψ(1/2 + y(t)) - 1/2. In the vicinity of the unstable fixed point with Q = 1/2 and Ψ(1/2) = 1/2, the latter equation can be linearized and becomes

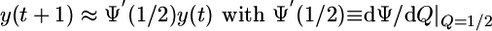[10]

for small y(t). Iterating this equation n times from an initial time t₀ up to a final time t₁, one obtains the time difference

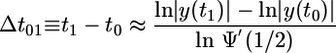[11]

in the limit of small y(t₀).

It follows from the explicit expression (Eq. 6) for the evolution function Ψ(Q) that the derivative Ψ′(1/2) at the unstable fixed point with Q = 1/2 diverges for a scale-free network with decay exponent γ ≤ 5/2 in the limit of large network size N. More precisely, one obtains the asymptotic behavior

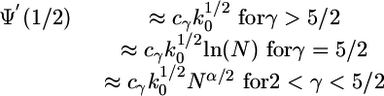[12]

in the limit of large N with α = (5 - 2γ)/(γ - 1), where c_γ is a dimensionless γ-dependent coefficient (see Derivation of Eq. 12 in Supporting Text).

Results and Discussion

Decay of Strongly Disordered Patterns. Now, consider an initial state of the network at time t = t₀ that corresponds to a strongly disordered pattern with order parameter y(t₀) = ỹ = ±1/2M ∼ 1/N as in Eq. 9. For t > t₀, such an initial pattern evolves according to the majority rule dynamics that leads to an increase in the absolute value of the order parameter y and, thus, to the growth of order. We will characterize this decay of the strongly disordered patterns by the decay time t_d, which is the time it takes to reach a pattern with an order parameter y_* that satisfies |y_*| ≥ 1/4. In addition, we have also estimated the probability to reach the completely ordered patterns when one initially starts from strongly disordered ones.

Within mean field theory, the decay time t_d follows from Eq. 11 and is given by t_d ≈ ln(〈k〉N)/ln(Ψ′(1/2)) for large 〈k〉 or large N. This expression behaves as

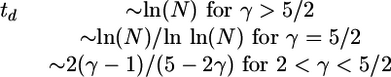[13]

in the limit of large network size N. Thus, for scale-free networks with decay exponent 2 < γ < 5/2, strongly disordered patterns always decay after a finite number of iteration steps even in the limit of large N. In contrast, for networks with γ > 5/2, the decay time diverges as ln(N). The latter behavior for γ > 5/2 also applies to Poissonian networks and is, thus, consistent with recent results for opinion spreading on social networks (28).

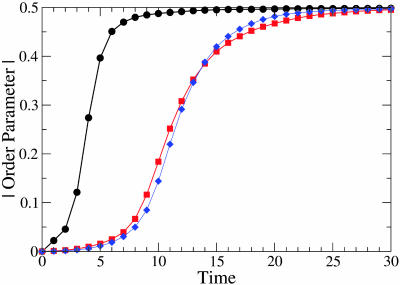
We have confirmed these mean field predictions by computer simulations. To avoid both disconnected and tree-like network graphs, the simulations were performed for networks with a relatively large mean vertex degree 〈k〉 and minimal vertex degree k₀ > 1. In Fig. 1, we display the time evolution of the absolute value of the order parameter, |y| = |Q - 1/2|, as obtained for three different networks that have the same size n = 2¹⁸ and the same mean vertex degree 〈k〉 = 20 but are distinguished by their degree distributions: These networks are scale-free with γ = 2.25 and k₀ = 5, scale-free with γ = 3 and k₀ = 10, and Poissonian, respectively. For each network, 2,000 initial spin patterns are generated, which are all strongly disordered and characterized by the initial order parameter |y(t₀)| = |ỹ| = 1/〈k〉N as in Eq. 9. For each of these initial patterns, the local majority dynamics leads to an increase of |y| with time t. Finally, the time evolution as shown in Fig. 1 is obtained, for each network, via an average over all 2,000 trajectories.

Fig. 1.

Absolute value of order parameter as a function of time measured in units of iteration steps for (i) scale-free network with γ = 2.25 and k₀ = 5 (circles), (ii) scale-free network with γ = 3 and k₀ = 10 (squares), and (iii) Poissonian network (diamonds). All three networks have the same vertex number N = 2¹⁸ and the same mean vertex degree 〈k〉 = 20. Each data set represents an average over 2,000 individual trajectories that all start initially from strongly disordered spin patterns as defined in Eq. 9.

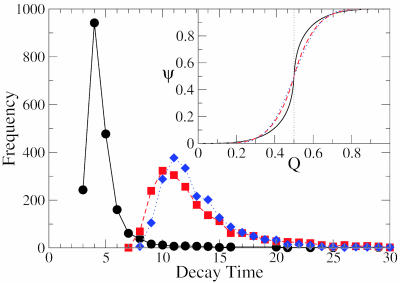
The distributions of the decay times t_d corresponding to the individual trajectories of the three networks are displayed in Fig. 2. Inspection of this figure shows that the decay time distribution for the scale-free network with γ = 2.25 has a narrow peak around t_d ≃ 4, whereas the decay time distributions for the scale-free network with γ = 3 and for the Poissonian network are much broader and shifted toward larger values. The three histograms shown in Fig. 2 correspond to all trajectories with a decay time t_d up to 30 iteration steps. For the scale-free network with γ = 2.25, 9 of 2,000 trajectories have a decay time between 30 and 100 iteration steps, and 2 of 2,000 trajectories have a decay time that exceeds 100 steps. Likewise, for the scale-free network with γ = 3 and for the Poissonian network, only one and no trajectory, respectively, had a decay time above 100 steps.

Fig. 2.

Distribution of decay times for the individual pattern trajectories. The decay time is measured in units of iteration steps. The three data sets correspond to the same networks as in Fig. 1: (i) scale-free with γ = 2.25 (circles), (ii) scale-free with γ = 3 (squares), and (iii) Poissonian (diamonds). (Inset) The evolution function Ψ as a function of Q as in Eq. 6 for the three cases i-iii.

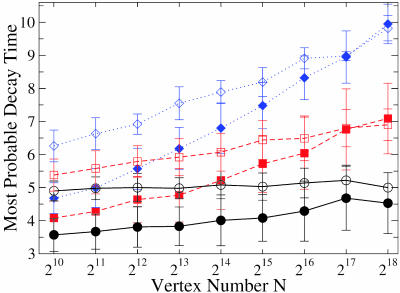
The maximum of the decay time distribution defines the most probable decay time. This time scale was determined for three ensembles of scale-free networks with (i) γ = 2.25 and k₀ = 5, (ii) γ = 2.5 and k₀ = 7, and (iii) γ = 3 and k₀ = 10. All three ensembles are characterized by the same mean vertex degree 〈k〉 = 20. Each ensemble consists of 100 different random networks. For each of these networks, 1,000 different pattern trajectories were determined starting from 1,000 strongly disordered spin patterns as in Eq. 9. The most probable decay times obtained in this way are displayed in Fig. 3 as a function of the network size N. In this figure, we compare the results obtained by numerical iterations of the majority rule dynamics as in Eq. 2 with the mean field results corresponding to the evolution equation (5). Inspection of Fig. 3 shows that the most probable decay time is indeed very insensitive to the vertex number N for γ = 2.25 but grows with N as ∼ ln(N) for γ = 3.0. For the borderline case with γ = 5/2, the decay time grows more slowly than ln(N).

Fig. 3.

Semilogarithmic plot of the most probable decay time (in units of iteration steps) versus vertex number N. The filled symbols were obtained by numerical iterations of the majority rule dynamics (Eq. 2), and the open symbols represent the mean field results as obtained from the evolution equation (Eq. 5). The three sets of filled and open symbols correspond to three ensembles of scale-free networks with γ = 2.25 and k₀ = 5 (filled circles); γ = 2.5 and k₀ = 7 (filled squares); and γ = 3.0 and k₀ = 10. In all three cases, the mean vertex degree has the same value 〈k〉= 20. For the numerical iterations, 100 different random networks were generated for each vertex number N. Furthermore, for each of these networks, 1,000 different pattern trajectories were determined starting from different strongly disordered patterns.

We have also studied the approach of the evolving patterns toward the completely ordered patterns (or ground states) with Q = 0 or Q = 1. For the three networks just discussed, which are characterized by vertex number n = 2¹⁸ and mean vertex degree 〈k〉 = 20, the probability to reach these ordered patterns is very close to 1: In all three cases, we find that the probability of not reaching the completely ordered patterns within 100 steps is smaller than 10^-2 (see Fig. 6, which is published as supporting information on the PNAS web site). For the scale-free networks with γ = 2.25 and 〈k〉 = 20, we have also determined this latter probability as a function of the network size N and found that it is smaller than 0.6 × 10^-2 for 2¹⁰ ≤ n ≤ 2¹⁸ (see Fig. 7, which is published as supporting information on the PNAS web site).

To see how the time evolution of the order parameter depends on the mean vertex degree 〈k〉, the same set of simulations was also performed for three networks with 〈k〉= 10 and k₀ ≥ 2. The corresponding decay time distributions are found to be rather similar to those displayed in Fig. 2 (see Fig. 8, which is published as supporting information on the PNAS web site). The main difference is that the approach to the completely ordered patterns is slowed down (see Figs. 9 and 10, which are published as supporting information on the PNAS web site). Additional simulations for mean vertex degree 〈k〉= 7 and 〈k〉= 5 show that the time to reach the completely ordered patterns further increases with decreasing 〈k〉. These simulation results are consistent with those obtained for random Poissonian networks (31) but are rather different from the behavior found for tree-like networks (29) and for d-dimensional hypercubic lattices with d ≥ 3 (30).

As emphasized in refs. 30 and 31, spin patterns, which evolve according to local majority dynamics, can be trapped in meta-stable states corresponding to several spin-up and spin-down domains. In addition, the domain boundaries may not be completely frozen but may contain “blinkers,” i.e., single spins that continue to flip after each time step. It is not difficult to see that domain boundaries and blinkers are likely to occur for spin patterns on tree-like graphs (33), leading to the glassy dynamics found for Cayley trees (29). Somewhat surprisingly, multidomain patterns with blinkers are also typical for d-dimensional hypercubic lattices with d ≥ 3 as shown in ref. 30. In contrast, our simulations give strong evidence that, for scale-free networks with k₀ > 1, disordered patterns typically evolve toward the two completely ordered patterns provided the networks are connected and the mean vertex degree 〈k〉 is sufficiently large. The case k₀ = 1 is special since the graphs tend to be tree-like, and their dynamics is presumably characterized by blinkers as well.

Selective Spin Flips. Now, let us look at a different aspect of the response behavior. We start from the all-spin-down pattern and ask how many spins we have to flip to reach another pattern that evolves toward the all-spin-up pattern under the local majority dynamics.

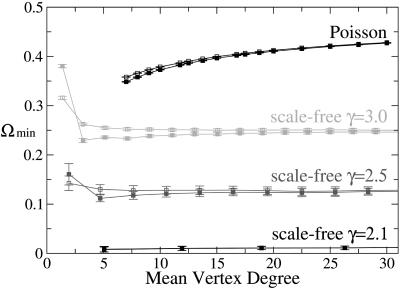
If we flipped the spins on a randomly chosen set of vertices, we would have to flip, in general, of the order of N/2 spins. However, we can induce such a global transition in a much more efficient way if we flip primarily those spins that are located on the highly connected vertices. This is illustrated in Fig. 4, which displays the minimal fraction of spins, Ω_min, which one has to flip to transform the all-spin-down pattern into the all-spin-up pattern. An analytical estimate for this minimal fraction can be obtained from the explicit relation for the boundary patterns as given by Eq. 7 if one considers such patterns with q̂_k = 0 for k₀ < k < k_* and q̂_k = 1 for k_* < k < k_N, where the intermediate k-value k_* is determined by the requirement that the spin pattern represents a boundary pattern with ordering probability Q = Q̂ = 1/2 (see Derivation of Eq. 14 in Supporting Text). For large vertex number N, this leads to the asymptotic estimate

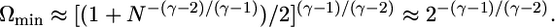[14]

Fig. 4.

Minimal fraction Ω_min of spins that one has to flip to induce a transition from the all-spin-down to the all-spin-up pattern. All networks have N = 10⁵ vertices but differ in their degree distribution, which was Poissonian or scale-free with γ = 3.0, γ = 2.5, and γ = 2.1. The open squares were obtained from the analytical expression (Eq. 14); the filled squares were obtained through exact enumerations where each data point represents an average over 100 network realizations.

This minimal fraction does not depend on the mean vertex degree 〈k〉 and vanishes very rapidly as ∼ exp(-|const|/(γ - 2)), i.e., as an essential singularity in γ - 2. Both properties are fully confirmed by the numerical results (see Fig. 4). For γ = 3, for example, the asymptotic estimate (Eq. 14) leads to Ω_min ≈ 1/4 in perfect agreement with the numerical results shown in Fig. 4. This sensitivity of ordered spin patterns to selective spin flips has been independently observed in ref. 25.

Thus, a scale-free network with a decay exponent γ that is close to γ = 2 has the additional property that one needs to selectively flip only a very small fraction of the spins to induce a transition from one ordered pattern to the other. This property provides a very efficient way for the system to adapt its state in response to varying external conditions. Note, however, that in contrast to the behavior of the response time, the dependence of the minimal fraction Ω_min on the decay exponent γ does not exhibit a sharp borderline at γ = 5/2.

Dynamic Behavior of More Complex Models. The main features of the pattern evolution described above are quite generic and remain valid for various extensions and generalizations of the majority rule dynamics. One particularly interesting generalization is obtained if we extend our mean field theory to Hopfield models (17, 27) that address the maximal storage capacity S_max of associative memory networks. This capacity, which represents the largest possible number of patterns that can be stored in the network, is found to behave as

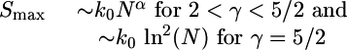[15]

with α = (5 - 2γ)/(γ - 1) in the limit of large network size N (see Hopfield Models on Scale-Free Networks in Supporting Text). In contrast, for γ > 5/2, the maximal storage capacity S_max does not grow with the network size N for large N. It has been recently argued that some functional networks in the human brain are indeed scale-free with γ ≃ 2.1 (32, 34). Thus, for these latter networks, our mean field theory predicts that the storage capacity grows as N^α with α ≃ 0.73, which is almost as fast as in the original Hopfield model on complete graphs that have the constant vertex degree k = N - 1 and are characterized by α = 1.

We have also extended our analysis of the majority rule dynamics to a variety of other models including Potts models on nondirected networks as well as to Ising models on directed networks (see Extension to Directed Scale-Free Networks in Supporting Text). For all of these generalizations, we find that γ = 5/2 represents a borderline case for the dynamic pattern evolution.

Summary. In summary, we have studied the response behavior of a large class of dynamic network models. We found that scale-free networks are characterized by very rapid response provided γ < 5/2. As far as the decay time of strongly disordered patterns is concerned, γ = 5/2 represents a sharp borderline. For γ < 5/2, all of these patterns decay within a finite decay time even in the limit of infinite vertex number. For γ > 5/2, on the other hand, this time diverges as ln(N) for large vertex number N. We also determined the minimal fraction of spin flips to induce a transition from one ordered pattern to another ordered pattern. This fraction becomes very small as one reduces the value of γ and vanishes as an essential singularity in γ - 2. These results are generic and can be generalized to more complex models that involve more than two vertex states and/or directed edges.

One particularly interesting extension is to Hopfield models for associative memory on scale-free networks. In this latter case, we find that the storage capacity is independent of network size N for γ > 5/2 but grows as N^α with α = (5 - 2γ)/(γ - 1) for 2 < γ < 5/2. For the functional networks of the human brain with γ ≃ 2.1 (32), this implies that the storage capacity grows as N^α with α ≃ 0.73. These mean field predictions should be accessible to simulation studies that have been restricted, so far, to the special case γ = 3 > 5/2 (35).

Our results shed light on the empirical observation that many real-world networks are scale-free with decay exponent 2 < γ < 5/2. Further extensions of our study should address possible effects of vertex-vertex correlations, which are present in real-world networks and lead to clustering (1) and modularity (3, 36). We expect that correlations between vertices of high degree will make the response of scale-free networks with γ < 5/2 even more rapid, but this remains to be studied in more detail. Likewise, it will be interesting to investigate how the response behavior is influenced by weighted edges (see, e.g., ref. 37) corresponding to variable nearest neighbor couplings.

Note Added in Proof. For the special case of scale-free networks with minimal vertex degree k₀ = 1, additional simulations have confirmed that the decay of strongly disordered patterns is characterized by persistent oscillations of the order parameter y around y = 0.