Features of Evolution and Expansion of Modern Humans, Inferred from Genomewide Microsatellite Markers

Abstract

We study data on variation in 52 worldwide populations at 377 autosomal short tandem repeat loci, to infer a demographic history of human populations. Variation at di-, tri-, and tetranucleotide repeat loci is distributed differently, although each class of markers exhibits a decrease of within-population genetic variation in the following order: sub-Saharan Africa, Eurasia, East Asia, Oceania, and America. There is a similar decrease in the frequency of private alleles. With multidimensional scaling, populations belonging to the same major geographic region cluster together, and some regions permit a finer resolution of populations. When a stepwise mutation model is used, a population tree based on T_D estimates of divergence time suggests that the branches leading to the present sub-Saharan African populations of hunter-gatherers were the first to diverge from a common ancestral population (∼71–142 thousand years ago). The branches corresponding to sub-Saharan African farming populations and those that left Africa diverge next, with subsequent splits of branches for Eurasia, Oceania, East Asia, and America. African hunter-gatherer populations and populations of Oceania and America exhibit no statistically significant signature of growth. The features of population subdivision and growth are discussed in the context of the ancient expansion of modern humans.

Introduction

The distribution of genetic variation within and among human populations has long been an important tool for inferring the evolutionary history of modern humans. Dramatic improvements in genotyping technologies over the past 15 years have facilitated the development of many types of DNA markers. Considerable attention has been devoted to both uniparental and autosomal genetic markers. Because of their lack of recombination, uniparental markers—mtDNA and the nonrecombining region of the Y chromosome (e.g., see R. L. Cann et al. ¹⁹⁸⁷; Ingman et al. ²⁰⁰⁰; Underhill et al. ²⁰⁰⁰)—and their genealogical histories are perhaps easier to study than are recombining markers. Although recombination introduces additional uncertainty regarding the history of any individual autosomal locus, consideration of a large collection of polymorphic loci spread across the genome enables more general inference about demographic history and population relationships than does study of the Y chromosome and mtDNA, loci whose histories may be anomalous when compared with that of an “average” locus in the genome. Studies of autosomal variation that are based on protein polymorphisms, blood groups, restriction-site polymorphisms, and Alu insertions have revealed much about within- and among-population genetic diversity of humans (Cavalli-Sforza et al. ¹⁹⁹⁴; Relethford ²⁰⁰¹).

Among autosomal markers, ever since the pioneering study of Bowcock et al. (1994), special attention has been paid to polymorphisms of short tandemly repeated DNA (i.e., STRs, or microsatellites). These loci are numerous, highly polymorphic, and densely distributed across the genome, and they mutate at a high rate, facilitating inferences about short-term evolution. Furthermore, their distribution in populations can be described by existing population-genetic theory. This has led to the development of statistical tools, based on population genetics, that treat the number of repeats as a quantitative variable. Among these tools are the R_ST statistic for population differentiation (Slatkin 1995), the genetic distance (δμ)² (Goldstein et al. 1995), the T_D estimator of divergence time (Zhivotovsky 2001), and higher statistical moments of the allele-size distribution (Zhivotovsky and Feldman 1995). Microsatellite statistics have been exploited to study population expansion (e.g., see Kimmel et al. ¹⁹⁹⁸; Reich and Goldstein ¹⁹⁹⁸; Gonser et al. ²⁰⁰⁰; Jin et al. ²⁰⁰⁰; King et al. ²⁰⁰⁰; Zhivotovsky et al. ²⁰⁰⁰) and migration (Slatkin 1995; Michalakis and Excoffier ¹⁹⁹⁶; Rousset ¹⁹⁹⁶; Feldman et al. ¹⁹⁹⁹). An important finding from these studies is that dozens or hundreds of microsatellite loci are required in order to make reliable inferences about relationships of closely related populations (Zhivotovsky and Feldman 1995; Goldstein et al. ¹⁹⁹⁶; Jorde et al. ¹⁹⁹⁷). Specifically, for the dating of population separations and expansions in size, hundreds of loci may be required in order to reduce large statistical errors (Zhivotovsky et al. 2000; Zhivotovsky ²⁰⁰¹). Here, we examine variation at 377 autosomal STR loci in 52 worldwide populations and discuss what this variation reveals about the population history of modern humans.

Material and Methods

We studied 1,056 individuals from 52 populations of the Human Genome Diversity Project–CEPH human genome diversity cell line panel (H. M. Cann et al. ²⁰⁰²)—excluding, from the 1,064 individuals of the panel, 8 individuals who were from populations with small sample sizes and 1 individual (1331) who was not genotyped but including 1 additional individual (1026) who was omitted from the panel because of technical difficulties with maintenance of the cell line. The samples were genotyped by the Mammalian Genotyping Service (Marshfield panel 10; see the Human STRP Screening Sets Web site) at 404 loci, not including the locus D11S1985 of the panel of markers. In the present study, we have employed 377 autosomal STRs: using the classifications provided by the Mammalian Genotyping Service, this collection includes 45 di-, 58 tri-, and 274 tetranucleotide repeat loci. The genotypes used in the present study are available at the Human Diversity Panel Genotypes Web site.

The data set includes populations (with population reference numbers) from sub-Saharan Africa (hunter-gatherer Biaka Pygmy [47] [from the Central African Republic], Mbuti Pygmy [48] [from the Congo], and San [50] [from Namibia]; and farming Bantu [49] [from Kenya], Yoruba [51] [from Nigeria], and Mandenka [52] [from Senegal]), North Africa (Mozabite [44] [from Algeria]), the Middle East (Druze [41] [from the Carmel region of Israel], Palestinian [42] [from Central Israel], and Bedouin [43] [from the Negev region of Israel]), Central/South Asia (Uygur [20] [from northwestern China] and the Pakistani populations Balochi [24], Brahui [25], Burusho [26], Hazara [27], Kalash [28], Makrani [29], Pathan [30], and Sindhi [31]), Europe (Basque [33] and French [34] [both from France]; Bergamo [35], Sardinian [36], and Tuscan [37] [all from Italy]; Orcadian [38] [from the Orkney Islands]; Russian [39] [northwestern Russia]; and Adygei [40] [from the Caucasus region of Russia]), East Asia (Cambodian [6] [from Cambodia]; Dai [7], Daur [8], and Han [9] [sampled from northern China]; Han [10] [sampled from the United States]; Hezhen [11], Lahu [12], Miao [13], Mongola [14], Naxi [15], Oroqen [16], She [17], Tu [18], Tujia [19], Xibo [21], and Yi [22] [all from China]; Japanese [23] [from Japan]; and Yakut [32] [from Siberia]), Oceania (Melanesian [45] [from Bougainville] and Papuan [46] [from New Guinea]), and America (South American Karitiana [1] [from Brazil], Surui [2] [from Brazil], and Colombian [3] [from Colombia]; and Central American Maya [4] and Pima [5] [both from Mexico]). Sample sizes and a description of genetic variation in these populations have been provided elsewhere (Rosenberg et al. 2002).

The software package GDA (see the Lewis Lab Software Web site) was used to produce a 52 × 52 matrix of pairwise F_ST values (actually, θ values; see Weir ¹⁹⁹⁶, chap. 5), from which six principal coordinates (PCs) were obtained by multidimensional scaling performed using the SPSS 8.0.0 package. From the 15 possible pairs of PCs, 3 (PC1-PC2, PC1-PC4, and PC2-PC5) were chosen as two-dimensional projections that gave the clearest separation of groups of populations. The corresponding 52 × 52 matrix of R_ST values (Slatkin 1995) was also calculated. To estimate times of divergence and population expansion, we used the T_D estimator (Zhivotovsky 2001), the imbalance index −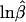 (Kimmel et al. 1998; King et al. ²⁰⁰⁰), and the expansion index S_k (Zhivotovsky et al. 2000). The last of these allows estimation of the preexpansion population size and the time of expansion, assuming mutation-drift equilibrium prior to sudden (infinite) expansion (eqq. [7] and [8] in Zhivotovsky et al. ²⁰⁰⁰). Estimates using S_k should be regarded as lower bounds of expansion times; these times would be greater if the population-size increase were not sudden and/or if there were variation in (effective) mutation rate across loci. Mutation-rate variation increases the average unnormalized within-locus kurtosis in repeat scores (Zhivotovsky et al. 2001) and thus decreases S_k. To model the dynamics of these statistics, we used the program Mathematica (Wolfram 1996). Private (population-specific) alleles can provide useful statistics for the analysis of population structure (e.g., see Barton and Slatkin ¹⁹⁸⁶), although conclusions drawn from them may depend on sample sizes. We examined five private-allele statistics: S1 is the number of different private alleles summed across loci in the sample; S2 is the average frequency of private alleles, or the summed frequencies of private alleles in the sample divided by S1; S3 is S1 divided by sample size; S4 is the frequency of private alleles per locus (in percent), or 100 times S1 times S2 divided by the number of loci; and S5 is the frequency of the most abundant private allele in the sample (the frequency of allele A refers to the number of alleles A observed in the sample divided by the total number of chromosomes examined). The correlation coefficients between the statistics and sample sizes (for the 377 loci, over 52 populations) were 0.45, −0.58, −0.10, −0.04, and −0.18, respectively. Thus, the statistics S3 and S4 appeared to be nearly independent of sample size and were used in the present analysis.

Results

STR Variation

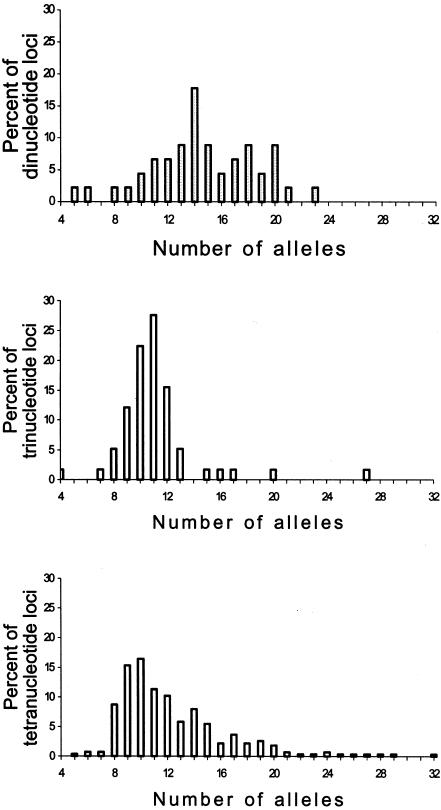
The 377 STR loci show large variation in the number of alleles found among 1,056 individuals—from 4 to 32 alleles. The three kinds of loci (i.e., those with di-, tri-, and tetranucleotide repeats) have different distributions for the number of alleles, with dinucleotide repeats having the most alleles (fig. 1). One hundred thousand permutations with Fisher’s exact test showed no significant difference between the distributions of the tri- and tetranucleotide repeats (P∼.33), although a t test indicated that the latter had a significantly larger mean value (12.4±0.21 vs. 11.1±0.41). The distribution of dinucleotide repeats differed significantly from the two other distributions: the permutation test gave P<10^-5 and P∼.011 for comparisons with distributions of tri- and tetranucleotides, respectively, and the mean ± SE number of alleles for dinucleotides was 14.6±0.59. Because allele-size variance is proportional to mutation rate under stepwise mutation models (Moran 1975; Slatkin ¹⁹⁹⁵; Zhivotovsky and Feldman ¹⁹⁹⁵), the higher variances of dinucleotide loci (table 1 and fig. 2) suggest that these loci are more mutable. The distributions of within-population variance in repeat score show behavior similar to those of the number of alleles (fig. 2): the broadest distribution was observed for dinucleotide repeats, and the narrowest distribution was observed for tetranucleotides, although the latter contained a few outliers. The worldwide distributions of heterozygosity at the three kinds of STRs are more similar to each other than are those of the numbers of alleles. Within-population variation at the STR loci shows a distinct trend across regions, the greatest being in sub-Saharan Africa and the smallest being in America (table 1). For these markers, 7.4% of the nonsingleton alleles were region specific, and the median frequency of region-specific alleles was only 1% (Rosenberg et al. 2002).

Figure  1.

Among-locus distribution of the total number of alleles observed in 1,056 individuals at di-, tri-, and tetranucleotide STRs.

Table 1.

Regional Trends of Within-Population STR Variation^[Note]

	Sub-Saharan Africa
	Hunter-Gatherers	Farmers	Eurasia	East Asia	Oceania	America
WPV at tetranucleotide locia	3.65	3.53	3.19	2.88	2.50	2.24
WPV at trinucleotide loci	3.90	3.87	3.19	2.86	2.73	2.12
WPV at dinucleotide loci	7.57	7.42	6.78	6.34	5.16	5.36
Heterozygosityb	.77	.78	.75	.72	.68	.60

Note.— WPV = within-population variance. The heterozygosities and WPVs are averages of estimates across the populations in the regions.

^aAll 274 tetranucleotide loci.

^bAll 377 loci.

Figure  2.

Among-locus distribution of the within-population variance in the repeat scores at di-, tri-, and tetranucleotide STRs. For each STR, the values of the within-population variance were averaged over all 52 populations.

Population Clusters

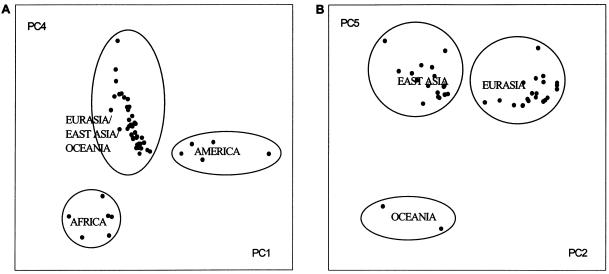
Groups of genetically related populations are revealed by multidimensional scaling of pairwise F_ST values (figs. 3 and 4) computed using all 377 markers. The most important feature of the present analysis is that populations from the same geographic region are clustered together. PC1 and PC2 clearly separate three large groups: Africa/Eurasia, East Asia/Oceania, and America (fig. 3). Africa is well distinguished by PC4, and Oceania is well distinguished by PC5 (fig. 4), although their separation is also satisfactorily indicated by the first two PCs (fig. 3). These results agree with the analysis of the same data by Rosenberg et al. (2002), who used another procedure, the clustering algorithm of Pritchard et al. (2000), to identify geographic clustering.

Figure  3.

Distribution and clusters of 52 populations from the first two PCs in the multidimensional-scaling plot of F_ST values at 377 STRs. Most populations are indicated with numbers (see the “Material and Methods” section). The X- and Y-axes represent PC1 and PC2, respectively. ⧫ = Mozabite; ◊ = three Middle East samples; □ = Basque, Sardinian, and Orcadian samples; ○ = five other samples from Europe; ▵ = East Asian Altaic-speaking populations; ▴ = two Han populations; * = Kalash; ● = remaining samples.

Figure  4.

Multidimensional scaling on the F_ST values at 377 STRs. A, Separation of sub-Saharan African and American populations in a plot of PC4 versus PC1. B, Separation of Oceania in a plot of PC5 versus PC2 (samples from Africa and America are suppressed).

The positions of populations within some clusters correspond well to their predefined assignments to specific regional groups. The sub-Saharan African farming populations (these may include pastoralists; we use the term “farmers” to encompass both) are closer to each other than to the hunter-gatherer San and Mbuti populations—50 and 48, respectively, in the plot (fig. 3). The San and the Mbuti are at the boundary of the sub-Saharan Africa cluster, somewhat apart from another hunter-gatherer population, Biaka (47), which lies within a subcluster of the farmers.

Eurasia, which includes the Middle East, Europe, Central/South Asia, and North Africa, clearly separates from other major groups, and its internal structure is reflected by distinctive subdivision into regional groups. Despite the genetic proximity of North Africa, the Middle East, and Europe that is highlighted in figure 3, North Africa (represented by a single population, the Mozabite) separates from the rest and lies at the edge of the cluster. The populations from the Middle East are placed close together. European populations form a contiguous subcluster, but Basques (33), Sardinians (36), and Orcadians (38) deviate from other European populations and are closer to populations from the Middle East. The Kalash, a Pakistani group that may have considerable ancestry from the Middle East or Europe, deviates from the Central/South Asia samples and lies in the European group (fig. 3). The other populations of Central/South Asia are represented by a subcluster in figure 3, with Balochi, Brahui, Makrani, Pathan, and Sindhi differentiated from Uygur, Hazara, and Burusho (20, 27, and 26, respectively). The plot indicates that the latter group deviates from the remaining Central/South Asian populations whereas the former group is located between the latter and the Middle East/North Africa/Europe cluster. Note that Uygur, Hazara, and Burusho, which are populations that have been found to be genetically intermediate between Eurasia and East Asia (Rosenberg et al. 2002), also have intermediate locations in the multidimensional-scaling analysis; the position of the Uygur and Hazara populations, at the edge of the Central/South Asia group and closer to the East Asia cluster, perhaps reflects a shared contribution of Mongol ancestry.

The East Asian populations form a distinctive group (fig. 3). Like Eurasia, this group also exhibits some internal structure. The Lahu, She, Naxi, and Miao, from southern China, appear in the lower part of the East Asia cluster, whereas most of the northern, Altaic-speaking populations (Daur, Hezhen, Mongola, Oroqen, Tu, and Xibo) form a group in its upper part. (In the analysis of Rosenberg et al. [2002], populations of northern China were largely grouped together, separate from those of southern China, although there were some exceptions, e.g., the Lahu and the Tu.) Oceania also shows clear separation from other continents in figure 4, although its populations are placed close to those of East Asia in figure 3. The populations of America separated from those of other regions (fig. 3) and show much greater within-region genetic differentiation than populations on other continents (fig. 3; see also Rosenberg et al. ²⁰⁰²). The Amazonian Surui population (2) greatly deviates from the other American populations, perhaps because of genetic drift caused by its extremely small population size. Another Amazonian population, Karitiana (1), also deviates considerably from the rest of the worldwide samples. The Mayan population (4) shows some affinity to the Eurasia/Africa cluster, which may reflect the impact of post-Columbian migration to the Americas.

Effective Mutation Rates

To incorporate time into a phylogenetic analysis of populations evolving under stepwise mutation, we need an estimate of the effective mutation rate, w, at the STRs—that is, the product of the mutation rate and the variance in the size distribution of mutational changes in repeat scores (Zhivotovsky and Feldman 1995). Previously, using pedigree data on >5,000 dinucleotide repeat loci by Dib et al. (1996), we estimated the average effective mutation rate as 1.52×10^-3 per dinucleotide locus per generation. Comparison of variation at tri- and tetranucleotide repeat loci with that at dinucleotide loci for the same set of populations and individuals then led to estimates of the average effective mutation rates of 0.85×10^-3 for trinucleotides and 0.93×10^-3 for tetranucleotides (Zhivotovsky et al. 2000). That the mutation rate at dinucleotide loci is higher than at tetranucleotides and at trinucleotides that are not associated with diseases is also supported by the analysis of Chakraborty et al. (1997).

However, effective mutation rates may vary substantially among loci, and, therefore, the average effective mutation rate for one set of loci may differ from that for another set. This probably happens because, in different studies, different criteria are used to choose genetic markers. Indeed, the tetranucleotide loci employed in the present study were selected for use in linkage mapping (Weber and Broman 2001). In contrast, the dinucleotide loci were included in Marshfield panel 10 to make the genetic map more dense when a chromosomal segment could not be finely mapped using tetranucleotides (Weber and Broman 2001), and thus were not specifically selected. This procedure might have introduced systematic differences in variation across the three types of markers. Leaving potential biases aside and applying the same figure for the effective mutation rate at dinucleotide loci as had been estimated from the data of Dib et al. (1996), 1.52×10^-3, to the 45 Marshfield dinucleotide loci and comparing variation at the three kinds of loci (as described in Zhivotovsky et al. ²⁰⁰⁰), we estimated the average effective mutation rates at the 58 tri- and 274 tetranucleotide loci as 0.71×10^-3 and 0.70×10^-3, respectively. Among the tetranucleotide loci, we found three loci (D21S2055, D11S1986, and D12S297) that had extraordinarily large values of the within-population variance across the majority of populations (see fig. 2). Excluding these from the analysis produced an average effective mutation rate of 0.64×10^-3 among the remaining 271 loci and reduced the coefficient of variation in effective mutation rates from 62.1% to 37.9%, estimated by the method of Zhivotovsky et al. (2001), using values of (δμ)² between African and non-African populations. This method assumes mutation-drift equilibrium, so the coefficients of variation must be regarded cautiously. Because the expansion index S_k is based on higher statistical moments of repeat scores, which are sensitive to such outliers, these 271 tetranucleotide repeats with the effective mutation rate w=0.00064 were used in the analysis of population divergence and expansion. For this set of loci, the ratio of the fourth to the second statistical moments due to mutational changes in the repeat scores of parental alleles, k_m/σ²_m, which is required for estimation of the expansion index S_k, was estimated, using the method of Zhivotovsky et al. (2000), to be 1.4.

Analysis of Population Divergence and Expansion in Size

We have used the T_D estimator to estimate time since divergence of a pair of populations and ΔT_D to estimate the time difference between the adjacent nodes on a population tree (Zhivotovsky 2001). The most important features of T_D are that it depends little on changes in population size, that it does not require the assumption of mutation-drift equilibrium, and that it is robust to weak migration, up to 0.1% per generation, between diverging populations; the last property is especially important because of possible intercontinental gene flows. (It should be noted that, if two diverging populations were influenced by migration from the same third source, then the estimates would still be robust to gene flow; however, if the populations were influenced by different migration sources, then the estimates would be biased.)

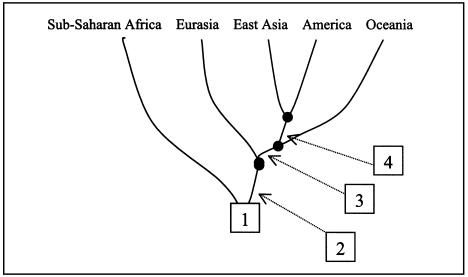
T_D can provide a “phylogenetic,” rooted population tree if one chooses a tree with a nonnegative value of the average (across-locus) ΔT_D for each of its branches. The population tree for major regions, together with the estimated divergence times, is presented in figure 5A. A formal application of the procedure to the within-region subdivision is given by figure 5B, but this assessment must be regarded with caution since it is not known to what extent major migration within regions from different sources may influence estimates of divergence time.

Figure  5.

Population tree based on T_D estimates of divergence time. A. Divergence among major groups. The time estimates are based on 374 STRs (three outlying STRs with tetranucleotide repeats were omitted). Arrows indicate the time (lower bounds, in ky) between adjacent nodes, assuming a generation length of 25 years. B, Schemes of divergence within the major groups, based on the 374 STRs. Time estimates within each continental group were omitted, because they may be biased owing to possible differential gene flows from other groups.

The most ancient branch suggested by the T_D analysis represents African hunter-gatherer populations, from which the branch leading to contemporary African farming populations and non-African populations separates. After the separation of African farmers from non-Africans, the non-African branch divides into Eurasia, Oceania, East Asia, and America, in that order (fig. 5A).

The major problem in the use of T_D is estimating the time of the first, ancient division (at the root), because T_D is defined in terms of the total, among- and within-population variance in repeat scores that has accumulated in both populations since their divergence from a common ancestor (Zhivotovsky 2001). Therefore, T_D requires knowledge of V₀, the variance in the (African) ancestral population that gave rise to all humans. This is unknown, resulting in uncertainty in the dating of the root. The uncertainty can be quantified by using reasonable lower and upper bounds for V₀ (fig. 5A). First, equating V₀ to 0 gives an upper bound for T_D of 141.7 ± 5.7 thousand years (ky) for the time of the first division. Second, if the value of V₀ exceeds that of an ancient African ancestral population from which the hunter-gatherer and farming populations diverged, then the corresponding value of T_D can serve as a lower bound for the divergence time between the African hunter-gatherers and populations of the rest of the world. The problem is the selection of an appropriate upper bound for V₀. The isolated populations of South America (Karitiana and Surui) may provide a model of such an ancestral population, because they perhaps maintain similar lifestyle and population size. (An additional argument for using the South American populations to give an upper bound for V₀ is given below, in the “Discussion” section [see “An Evolutionary Scenario for Ancient Expansion of Modern Humans”].) Therefore, using their variance to estimate an upper bound of V₀, we obtained the lower bound for the age of the root of 71.2±4.4 ky. Both bounds are well within the widely accepted range for the age of the most recent population that is ancestral to all modern humans, between 50 and 200 thousand years ago (kya) (Harpending et al. 1998).

Estimating the time between two adjacent nodes on the tree, ΔT_D (Zhivotovsky 2001) does not require knowledge of actual values of the variance in repeat scores at the nodes but instead assumes that the values are equal to each other. If the populations grew in size (actually, if the within-population variance in repeat scores increased) during the period between two adjacent nodes, then ΔT_D would underestimate the time between them, and, if they declined, then ΔT_D would be an overestimate (Zhivotovsky 2001). If two adjacent nodes are close to one another, then this assumption of equal variances does not appear to produce much bias. However, summation over many nodes along a phylogenetic lineage may lead to an accumulation of substantial bias. The summation should therefore be regarded with caution. In the “Discussion” section, we provide some arguments that the within-population variance in repeat scores was increasing along the branches of the population tree. Therefore, all the estimates of time between adjacent nodes in figure 5A can be regarded as lower bounds for the actual times between the subsequent branch separations.

We computed the imbalance index − (Kimmel et al. 1998) and the expansion index S_k (Zhivotovsky et al. 2000), to test whether the populations grew in size: for growing populations, both indices are positive. The two statistics are positively correlated (the correlation coefficient across the regional groups was 0.86; see table 2). However, two differences can be seen: the imbalance index indicates growth for hunter-gatherer populations of sub-Saharan Africa and decrease in size for populations of America, whereas the expansion index does not differ significantly from 0 for these populations (table 2). Significantly positive values of the expansion index S_k in sub-Saharan African farmers, Eurasia, and East Asia (table 2) indicate that these populations have been expanding in size. The populations of Oceania and America show no such signature of expansion. The hunter-gatherer populations of sub-Saharan Africa show a minor, very recent expansion in size, although it is not statistically significant. Table 2 indicates that the sub-Saharan African farming populations expanded earlier than did the populations of Eurasia and East Asia and that the effective size of the former populations prior to expansion was rather small, <2,000, or a census size of perhaps 6,000 by the “triple rule” of Cavalli-Sforza et al. (1994).

Table 2.

Statistics of Population Growth^[Note]

	Sub-Saharan Africa
Statistic	Hunter-Gatherers	Farmers	Eurasia	East Asia	Oceania	America
Imbalance index, −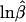	.215	.385	.319	.241	.084	−.288
Expansion index, Sk	.024	.177	.148	.117	−.016	−.046
Variance in repeat scores, V	3.45	3.31	2.90	2.61	2.27	2.11
Estimated expansion time (in kya)	4.3	35.3	25.3	17.6	…	…
Effective population size prior to growth	2,609	1,883	1,760	1,688	…	…

Note.— Estimation of expansion time and effective population size assumes mutation-drift equilibrium prior to sudden large (infinite) expansion. These analyses were done on individual populations, using data on 271 tetranucleotide repeat loci, and then the estimates were averaged over populations within each region.

Discussion

Comparison of Different STRs

The set of 377 autosomal STR loci was able to effectively separate populations into regional clusters (present study and Rosenberg et al. ²⁰⁰²). Importantly, different STRs may have different abilities to distinguish populations. Indeed, STRs with di-, tri-, and tetranucleotide repeats differ from each other, and, within each class of markers, the number of alleles and the within-population variance vary greatly from locus to locus (figs. 1 and 2). (Note that the number of alleles observed in the total sample of 1,056 individuals and the within-population variance in repeat scores show positive correlation across loci; e.g., for 271 tetranucleotide loci, the correlation coefficient was 0.55.) Also, systematic differences among sets of loci used in different studies may influence the relative ease of differentiating among populations. For example, in the present study, the total mean ± SE of within-population variances (across all populations and all tetranucleotide loci) is 3.01±0.032, whereas the average variances for the 60 tetranucleotide loci of Jorde et al. (1997) and the 21 tetranucleotides of Bowcock and Bennett (Zhivotovsky et al. 2000) are 4.43±0.20 and 3.52±0.17, respectively. Nevertheless, any STRs, regardless of motif size, as long as they are polymorphic, can contribute to inferences about differentiation of populations. Table 3 also shows that different kinds and sets of loci give fairly similar estimates of divergence times for the first major splits. They may differ in the later splits, however, which tells us that, although the total variation has a decreasing trend (table 1), different loci differ in the fractions of among- and within-population variation. Furthermore, a subset of loci with a small number of alleles shows lower values of divergence time than a subset that includes markers that are more polymorphic (but with the same assumed effective mutation rate). For example, for 71 loci selected from 271 tetranucleotide loci to have the smallest numbers of alleles (from 5 to 9), the upper and lower bounds for divergence of sub-Saharan African and non–sub-Saharan African populations (event 1 in table 3 and fig. 6) and the time for event 2 were 72.9±4.6, 29.0±4.3, and 7.5±2.1 ky, respectively (using w=0.00064). In contrast, for the 58 (of these 271) loci selected for the largest numbers of alleles (from 15 to 32), the corresponding estimates were 240.1±20.1, 119.9±14.9, and 39.4±9.1 (using the same value for w). These should be compared to estimates based on all 271 loci (table 3). The ascertainment scheme of microsatellite loci does not appear to have much effect on heterozygosity or F_ST estimates (Rogers and Jorde 1996; Urbanek et al. ¹⁹⁹⁶). In our case, the number of alleles correlates positively with the variance in allele size, as well as with heterozygosity: for the 271 loci, the corresponding correlation coefficients are 0.55 and 0.58, respectively. Choosing loci with lower (greater) variation may also select for lower (higher) mutation rates, which, in turn, causes the shift in estimated divergence times, whereas choosing loci for low (high) mutability may select for smaller (greater) variation.

Table 3.

Estimates of the Time of Split of Major Branches^[Note]

	Time ± SE of Separation Event(kya)
STRs	1a	2b	3b	4b
271 tetranucleotide loci	135.9 ± 6.8	19.8 ± 3.4	5.3 ± 2.3	3.1 ± 2.7
	65.6 ± 5.3
58 trinucleotide loci	140.2 ± 9.8	21.7 ± 5.4	8.5 ± 6.5	9.2 ± 5.1
	70.7 ± 8.2
45 dinucleotide loci	142.9 ± 17.4	20.9 ± 7.0	1.0 ± 6.6	5.8 ± 7.5
	69.8 ± 11.0
131 loci of Zhivotovsky (2001)	134.6 ± 9.4	19.8 ± 6.5	…	…
	57.0 ± 8.6

Note.— To compare the data of the present study with those of Zhivotovsky (2001), we have, in figure 6, reduced the tree of figure 5 by considering populations of sub-Saharan Africa as a single group.

^aIn each pair of rows, the first row gives the upper bound, and the second row gives the lower bound.

^bThese times refer to internodal times (see fig. 6).

Figure  6.

Reduced population tree, showing four separation events (see table 3)

Genetic Distances and Methods of Clustering

Reconstruction of population history should rely on genetic information from the entire genome (Barbujani and Bertorelle 2001) and may require a large number of loci (Zhivotovsky and Feldman 1995; Goldstein et al. ¹⁹⁹⁶; Jorde et al. ¹⁹⁹⁷). If, in a DNA-based evolutionary study, only a small amount of genetic variation is available, then the resolution of population differentiation may be poor and, under the assumption that a branching model is appropriate for the populations in question, a particular population may be assigned an incorrect position in a tree. The present study apparently includes enough genetic information on populations to give some assurance of accuracy (figs. 2 and S2 in Rosenberg et al. ²⁰⁰²). Table 3 shows that using a larger number of STRs in the analysis considerably lowers the SEs of statistics associated with divergence of populations. Moreover, this data set confirms that the clustering patterns of individuals converge as the number of loci is increased (Rosenberg et al. 2002). The present analysis (figs. 3 and 4) and that of Rosenberg et al. (2002) demonstrate that the 377 STR loci, the majority of which are tetranucleotide repeats, effectively separate continental groups from each other.

Populations within regions generally cluster together in trees based on similarity indices or genetic distances (e.g., see Cavalli-Sforza et al. ¹⁹⁸⁸; Nei and Roychoudhury ¹⁹⁹³; Bowcock et al. ¹⁹⁹⁴; Deka et al. ¹⁹⁹⁵; Takezaki and Nei ¹⁹⁹⁶; Jorde et al. ¹⁹⁹⁷; Pérez-Lezaun et al. ¹⁹⁹⁷; Jin et al. ²⁰⁰⁰; Watkins et al. ²⁰⁰¹), with the topology depending somewhat on the method of clustering. We compared four trees constructed with the UPGMA (unweighted pair group method using arithmetic averages) and neighbor-joining methods, using 52×52 matrices composed of pairwise F_ST and R_ST values, and found that populations within a region usually clustered together in each of the four trees. However, gene flow, population dynamics, deviation from mutation-drift equilibrium, and other violations of the requirements for interpretation of genetic distances may bias estimates of divergence time that are based on genetic distances and thus may result in incorrect tree topologies. Importantly, estimates based on T_D are largely independent of population dynamics in the absence of migration and do not assume mutation-drift equilibrium (Zhivotovsky 2001). Also, such estimates are robust to weak gene flow between diverging growing populations; this has been checked for migration rates of <0.1% per generation (Zhivotovsky 2001).

An Evolutionary Scenario for Ancient Expansion of Modern Humans

The following are important features of tables 1 and 2 and figure 5: First, the hunter-gatherer populations of sub-Saharan Africa have the highest variance in repeat scores, although their expansion index does not show statistically significant growth and their current population sizes (of perhaps 30–50 thousand each; see Cavalli-Sforza et al. ¹⁹⁹⁴) are much smaller than those of the farming populations of sub-Saharan Africa (many millions). Second, the much larger populations of Asia have less genetic variation than do the African hunter-gatherers (and the African farmers, as well). Third, neither Oceania nor America shows a signature of expansion; although the latter has a greater capacity to maintain large human populations than the former, genetic variation is lower in American populations. Fourth, the decrease in genetic variation along the chain Africa-Asia-Oceania-America follows their divergence in the population tree. Fifth, an effective population size of, at most, 2,700 is required in order to account for the maximal value of the variance in repeat scores (3.45 at 271 tetranucleotide loci) observed in the contemporary hunter-gatherer populations.

How small was the ancestral African population? Under the assumptions that the time of the split is the mean of the lower and upper bounds in figure 5A and that the ancestral population was in mutation-drift equilibrium, the effective size of the ancestor population might have been as low as 700. This estimate—which is in agreement with those of Pritchard et al. (1999), Zhivotovsky et al. (2000), and H. Tang, R. Thomson, L. L. Cavalli-Sforza, P. Shen, P. Oefner, and M. W. Feldman (unpublished data)—is lower than estimates that have been suggested in some other studies (e.g., 10,000 in Harpending et al. ¹⁹⁹⁸). The estimate does not preclude the presence of other populations of Homo sapiens sapiens in Africa, although it suggests that they were probably isolated from one another genetically and that contemporary worldwide populations descend from one or very few of those populations. Contemporary hunter-gatherer populations are larger than the suggested ancestral effective size of 700, enabling growth of genetic variation. Also, these populations appear to have accumulated more genetic variation (Cavalli-Sforza and Feldman ²⁰⁰³). However, they were expanding slowly and perhaps fluctuated dramatically in size. Because the expansion index is more sensitive to such fluctuation than the variance is (Zhivotovsky et al. 2000), the sub-Saharan African hunter-gatherer populations do not show a significant signature of growth. Analogously, growth in size of all other regional groups could allow them to increase genetic variation as compared with that in the putative ancestral population. The decrease in contemporary genetic variation along the chain Africa-Asia-Oceania-America can be explained by the successive splits of populations whose small size caused retardation in the increase of variance. Note that a size of 700 for the ancient ancestral population would produce an expected value of variance in the number of repeats of approximately 2×700×0.00064=0.90, which is smaller than the average variance at the 271 tetranucleotide loci in Karitiana and Surui, 1.8. This suggests that the variance in repeat scores in an ancestral population, V₀, was smaller than that in these American populations and provides an additional argument for using variances in these populations as an upper bound for V₀ in dating the first population split in the deep history of modern humans. This low population size in the suggested ancestral population may also explain why the contemporary human population is not as genetically variable as other closely related species. For example, mtDNA variation in the entire human population is much lower than has been observed within a small social group of chimpanzees (Gagneux et al. 1999). Therefore, the lineage leading to an ancestral sub-Saharan African population of modern humans must have maintained a low size (see Gagneux et al. ¹⁹⁹⁹; Yang ²⁰⁰²), and the time since the expansion of the common ancestral population has not been sufficient to develop a large amount of genetic variation.

Notably, a more conservative bound for the ancestral population size and for the age of the root of the population tree in figure 5A may be obtained by assuming that STR variation in the most variable sub-Saharan African hunter-gatherer populations is equal to the variation in the African ancestral population prior to its differentiation. This, in turn, assumes that the hunter-gatherer populations have remained of constant size and have been in mutation-drift equilibrium during their evolutionary history. Under this assumption, when data on 271 tetranucleotide loci are used, the estimate for ancestral effective population size is ∼2,700 (N = 3.45/2 × 0.00064, where 3.45 is the average variance in repeat size for hunter-gatherers and 0.00064 is the effective mutation rate; a similar figure is obtained using sub-Saharan African farming populations, whose average STR variance is 3.31). However, under this assumption, the age of the root of the population tree of figure 5A would be 7.9±2.6 ky. This figure is incompatible with estimates of the other divergence times in figure 5A, which are obtained relative to the estimate for the root and which do not depend on the value selected for the variance in the ancestral population. Indeed, the second split is estimated to have occurred ∼8.7 ky more recently than the first (the root), and the estimate for the time of the third split is 15.8 ky after the second split: by definition, each of these times, as well as their sum, must exceed the root age (7.9 ky), which would not be the case if the ancestral variance was similar to the variance in modern African populations. Therefore, under the assumption that the model on which T_D estimates are based is appropriate, STR variation in the African ancestral population cannot have been as large as STR variation is in Africa today. If the ancestral variance was larger than the current variances in American hunter-gatherer populations (but smaller than modern African variances), then our lower-bound estimate of divergence time would decrease. Our results (table 2) on recent expansion of major population groups (African farmers, Eurasians, and East Asians) agree with some studies (Jorde et al. 1997; Di Rienzo et al. ¹⁹⁹⁸; Excoffier and Schneider ¹⁹⁹⁹; Gonser et al. ²⁰⁰⁰; Jin et al. ²⁰⁰⁰; Shen et al. ²⁰⁰⁰), although others did not detect signals of expansion outside Africa (Reich and Goldstein 1998; Jin et al. ²⁰⁰⁰). Some studies suggest signatures of bottlenecks prior to expansion (Kimmel et al. 1998; Watkins et al. ²⁰⁰¹; Gabriel et al. ²⁰⁰²), although bottlenecks and population subdivision may have similar effects on expansion tests (Frisse et al. 2001; Reich et al. ²⁰⁰¹; Pluzhnikov et al. ²⁰⁰²). Because the tests that we used only estimate the timing of expansions and do not distinguish among different types of demography prior to expansion, our results do not preclude the possibility of a bottleneck prior to expansion.

Antiquity of Sub-Saharan African Hunter-Gatherers

The principal features of the reported population tree, based on autosomal variation, of contemporary human populations are statistically robust, owing to the large number of STRs. The population tree in figure 5 is consistent with the “out-of-Africa” theory, according to which a sub-Saharan African ancestral population gave rise to all populations of anatomically modern humans through a chain of migrations to the Middle East, Europe, Asia, Oceania, and America. Genetic studies of mtDNA sequences, SNPs of the nonrecombining region of the Y chromosome, and autosomal dinucleotide repeat loci (e.g., see Bowcock et al. ¹⁹⁹⁴; Ingman et al. ²⁰⁰⁰; Underhill et al. ²⁰⁰⁰) have generally been consistent with this view, although the data do not exclude the possibility that archaic humans may have contributed to the modern gene pool. The present analysis places the hunter-gatherers as descendants of the root of the tree, indicating that they descend from the most ancient of the sub-Saharan African populations (fig. 5A). This observation is also supported by the distribution of private alleles, which are most frequent among hunter-gatherers and next most frequent among the sub-Saharan African farming populations (table 4). That private alleles at multiallelic microsatellite loci are most numerous in sub-Saharan Africa is consistent with the data of Stephens et al. (2001), who found the frequency of population-specific haplotypes formed by intragenic SNPs to be highest in the African-American sample as compared with populations of Asian, European, and Hispanic-Latino descent.

Table 4.

Distribution of Private Alleles at 377 Loci in Different Populations

	Sub-Saharan Africa
Statistic	San	Mbuti	Biaka	Farmers	Eurasia	East Asia	Oceania	America
S3:
Single populationsa	5.71	2.93	1.75	1.29	.40	.45	.70	.26
Pooled groupsb				1.64	.66	.64	.74	.30
S4:
Single populationsa	1.25	.69	.61	.21	.07	.07	.21	.08
Pooled groupsb				.36	.25	.16	.25	.20

^aAveraged over populations of the group.

^bEstimated for the whole group by pooling the populations.

The San and the Mbuti may represent the oldest branch of modern humans studied here (fig. 5B). The San appear to have separated prior to the Mbuti, although the difference between the two separation times does not differ significantly from 0 (data not shown). The Biaka lineage appears to diverge from them significantly later, although this observation could be the result of strong gene flow between the farming populations and the Biaka (Cavalli-Sforza ¹⁹⁸⁶). The Biaka and the farming populations of sub-Saharan Africa are genetically close to one another and are separate from the San and the Mbuti, according to the multidimensional-scaling analysis (fig. 4). Further evidence of the antiquity of the San comes from the private-allele statistics (table 4), which are highest among the sub-Saharan African populations. Also, the San include the most-basal extant Y-chromosome lineages in high frequency (Underhill et al. 2000; Cruciani et al. ²⁰⁰²; Semino et al. ²⁰⁰²). Nevertheless, it is not clear which populations descend from the most ancient separation from the lineage that has led to most extant populations, although studies generally identify one or more African hunter-gatherer populations as “ancient.” Indeed, analysis of RFLP data and SNPs from the mtDNA control region suggested that the Biaka branch is the oldest, followed by the San, and that the Mbuti separated later (Chen et al. 2000); however, analysis of complete mtDNA sequences clustered the San and the Mbuti together and placed the Biaka in a different clade (fig. 2 in Ingman et al. ²⁰⁰⁰). An additional argument for the antiquity of hunter-gatherers is suggested by their largest value of the within-population variance in allele scores averaged over populations and loci, 3.45±0.119 (see table 2). Although it is not significantly greater than that for the African farming populations, 3.31±0.108, it is significantly larger than allele-size variances for other regions—2.90 ± 0.035, 2.61 ± 0.036, 2.27 ± 0.100, and 2.11 ± 0.070, for Eurasia, East Asia, Oceania, and America, respectively.

The sub-Saharan hunter-gatherers show almost no signature of population growth: the expansion index S_k is very low (table 2), which is in agreement with the conclusions of Excoffier and Schneider (1999). Unlike the hunter-gatherers, the sub-Saharan African farming populations exhibit the signature of growth. Numerical analysis of the dynamics of V and S_k shows that the observed values in these populations could be attained if their ancestral population started to grow ⩾35 kya from an effective size of ∼2,000 (table 2), corresponding to a census size of ∼6,000. This estimate can be regarded as a lower bound for expansion time, because of possible variation among loci in mutation rate and because the method of estimation assumes a sudden large expansion. This increase in population sizes might have been preceded by technological innovations that led to an increase in survival and then an increase in the overall birth rate. Hunting and gathering could not support a significant increase in population size, and the ancestral population was probably steady at close to its saturation density (see Cavalli-Sforza et al. ¹⁹⁹⁴, p. 106). An increase in the carrying capacity of the land could have resulted from better stone-tool technology that might have been developed ∼50 kya (Cavalli-Sforza et al. ¹⁹⁹⁴, p. 64), which corresponds well to our suggested lower bound of 35 kya for the onset of exponential growth of an ancestor of the farming populations. This bound would increase if there were variation in effective mutation rates and can be compared to the figure of 70 kya for the expansion of sub-Saharan African populations, derived from mtDNA analysis (Excoffier and Schneider 1999), and to the lower bound of ∼60 kya for expansion of major population groups, derived from earlier analysis of di-, tri-, and tetranucleotide repeat polymorphisms (Zhivotovsky et al. 2000).

Settlement of Other Continents

Each of the large population groups (the sub-Saharan African farmers, Eurasia, and East Asia) can be considered as a metapopulation consisting of populations with some genetic exchange between them and with a common ancestry. This is suggested by the value of the statistic S4, which is substantially greater for the pooled regional groups than for single populations within those regions (table 4). In contrast, the corresponding values of S4 for the hunter-gatherers are very close to each other (0.89 for the pooled San, Biaka, and Mbuti vs. 0.85 for the average of their individual values), which may reflect their relative genetic isolation from each other.

The populations of Oceania are estimated to have branched at the time of formation of the Central/South Asian populations (fig. 5); archaeological evidence suggests that humans reached New Guinea ∼40–60 kya. The Oceanic populations have greater frequencies of private alleles than other non–sub-Saharan African populations (table 4). One possibility is that, rather than a single exit from Africa with subsequent migrations to other regions, a few different waves of ancient migration out of Africa might have occurred in the peopling of the world, one of which was to Oceania; this is in agreement with the suggestion of Jin et al. (1999). Alternatively, with a single wave of migration, this distribution of private alleles could be explained by long-term isolation of these Oceanic populations.

The timing and the number of waves of migration into America is a controversial issue: one to three main waves 12–40 kya have been postulated. Because the archaeological evidence suggests a rapid increase in abundance of inhabited sites starting ∼12 kya and because the expansion index for the American populations was not significantly different from 0 (table 2), one can conjecture that the increase in the total number of humans in the Americas was due to an increase in the number of different small populations with low gene flow between them. Some American populations probably went through genetic bottlenecks; at the least, this applies to the Surui population, whose expansion index (S_k = −0.221 ± 0.138) is the lowest in the present study. Although this value is not statistically significant, there is other support for this claim; namely, the Surui population is an outlier on the multidimensional-scaling plot (fig. 4), and its allele-size variance is the smallest among the studied populations, 1.68±0.139. In addition, at the tetranucleotide locus D9S1120, there is a private allele, 275, that is present in each of the five American populations studied but not in the non-American populations. The frequency of this allele is ∼0.2–0.3 in the American populations, except for Surui, in which it is almost fixed (0.30 in Maya, 0.22 in Pima, 0.19 in Colombians, 0.25 in Karitiana, and 0.97 in Surui). The widespread distribution of this allele within the Americas at similar frequencies in different populations suggests that the allele may have originated with the founders of American populations.

Allele 275 can be considered as a genetic marker for American populations. It has the lowest number of repeats of alleles at this locus: all other alleles found at this locus have sizes of ⩾279. Another American private allele at this locus is one repeat longer—namely, allele 279. The next alleles, 283 and 287, have very low frequencies in all populations. Therefore, allele 275 probably occurred as a mutation in a population ancestral to American populations and then increased in frequency. The frequencies of ∼1/5 to ∼1/3 in most American populations suggest that, if genetic drift has not substantially altered the allele frequency since the initial entry into the Americas, then American copies of this locus might trace back to a few lineages (see also Ribeiro-dos-Santos et al. ²⁰⁰⁰). Other populations and population groups do not have such clear population-specific markers, although some private alleles exist at substantial frequency. For example, sub-Saharan African populations have two private alleles with frequencies >10%, whereas sub-Saharan hunter-gatherers have their own private alleles, one of which reaches a frequency of ∼16%. The San have many private alleles, two of which are at >30% (note that private alleles in the San sample must have frequencies of ⩾1/14, owing to the small sample size of seven individuals). Oceania has two private alleles with frequencies >10%, and the New Guinean and Melanesian populations each have their own private alleles at substantial frequencies. Eurasia and East Asia have no private alleles at frequencies >3%. In sub-Saharan African farmers, no frequency of a private allele is >5%, except for one at ∼8%. In these data, none of the populations or regional groups has a private marker that would separate it from the others; the groups can be distinguished, however, by using the combinations of hundreds of nonprivate alleles (Rosenberg et al. 2002) (figs. 3 and 4).

Our findings suggest very complex population structures and complex population histories for the three population groups of largest present size: sub-Saharan African farming populations, Eurasia, and East Asia. This picture is highlighted by the distribution of private alleles: Many pairs or groups of populations have additional private alleles when the populations are pooled together. For example, among the sub-Saharan hunter-gatherers and farmers, there are 160 and 100 different private alleles, respectively; however, when pooled together, they showed 321 different private alleles (i.e., there are 61 additional alleles found only in sub-Saharan Africa that are common to both groups). The same is true for Central/South Asia and East Asia, and Central/South Asia and Europe (32 and 24 additional alleles, respectively), probably as a consequence of gene flow. This is consistent with the suggestion, of Karafet et al. (2001) and Wells et al. (2001), that the Central Asian populations seem to be a significant source of migrants to East Asia and to Europe. Further analysis of the distribution of private alleles among pairs of populations also shows that the Middle East/North Africa has analogous relationships with Europe and Asia. Private alleles also revealed strong relationships between the sub-Saharan African populations and the populations of the Middle East/North Africa, Central/South Asia, and East Asia consistent with some backward migration to Africa, even to sub-Saharan Africa, as suggested by the recent analysis of Y-chromosome haplogroup lineages (Cruciani et al. 2002), although differential loss of alleles through random drift in different regions could also explain our data.

Although the distribution of private alleles may indicate a complicated pattern of gene flow and/or shared ancient ancestry, the frequencies of common alleles in the worldwide populations provide useful information about principal features of population history with the help of population-genetic methods. The present study indicates clear genetic differentiation between major regional groups—sub-Saharan Africa, Eurasia, East Asia, Oceania, and America (figs. 3 and 4)—and suggests possible evolutionary relationships (fig. 5).