The ensemble folding kinetics of protein G from an all-atom Monte Carlo simulation

Abstract

Protein G is folded with an all-atom Monte Carlo simulation by using a Gō potential. When folding is monitored by using burial of the lone tryptophan in protein G as the reaction coordinate, the ensemble kinetics is single exponential. Other experimental observations, such as the burst phase and mutational data, are also reproduced. However, more detailed analysis reveals that folding occurs over three distinct, three-state pathways. We show that, because of this tryptophan's asymmetric location in the tertiary fold, its burial (i) does not detect certain intermediates and (ii) may not correspond to the folding event. This finding demonstrates that ensemble averaging can disguise the presence of multiple pathways and intermediates when a non-ideal reaction coordinate is used. Finally, all observed folding pathways eventually converge to a common rate-limiting step, which is the formation of a specific nucleus involving hydrophobic core residues. These residues are conserved in the ubiquitin superfamily and in a phage display experiment, suggesting that fold topology is a strong determinant of the transition state.

Balancing realism and computational tractability has been the central issue when simulating protein folding on the computer. Recently, an impressive parallelization effort led to a 1-μs full-scale molecular dynamics (MD) trajectory of the 36-residue villin headpiece (1). Unfortunately, the use of such simulations to rigorously study folding is still several years away because single domain proteins fold on timescales that are at least two orders of magnitude longer (2). Moreover, because folding is a stochastic process, averaging over multiple runs is required. These computational problems can be partly alleviated by investigating folding kinetics indirectly by using the construction of free energy landscapes (3) or unfolding at high temperatures (4).

Recently, two complementary approaches have directly accessed the timescales relevant to folding. The first makes use of ensemble dynamics (5), whereby the long waiting times associated with rare events—which plague any simulation being run serially in time—are eliminated by running parallel simulations and allowing them to exchange states whenever a barrier crossing occurs. The second approach extends existing off-lattice coarse-grained Monte Carlo (MC) simulations (6) by introducing all-atom structural realism. Computational costs are minimized by (i) moving only backbone and sidechain torsional degrees of freedom (which are the “softest” modes in a polymer) and (ii) by using coarse-grained potentials. This simulation has been used with the Gō (7) and sequence-based potentials (8) to fold helices, hairpins, crambin, and protein A.

In this paper, we present ensemble kinetic data of the well-characterized 57-residue protein G (9) (Fig. 1A) by using this all-atom MC technique with a Gō potential. Under this potential, only interactions present in the native conformation are attractive. Although the native state is the global energy minimum by construction, no physical principles guide the classification between attractive/repulsive interaction types. As a result, unphysical interactions are possible. Furthermore, the folding landscape may be strongly biased toward the native state. However, there are two a priori reasons for using the Gō model to study protein G. First, when used in conjunction with a structurally realistic model, the Gō model should adequately capture topological frustration (10) on various levels, such as the incorporation of secondary structure elements into a tertiary fold and the satisfaction of packing constraints in the protein interior (7). Second, although significant efforts directed toward predictive folding models have led to sequence-based potentials that can fold isolated helices (11, 12) and hairpins (13, 14), as well as helix bundles (8, 15, 16), sequence-based potentials for folding α-β and all β structures are yet to be reported. For this reason, a Gō potential is currently the best choice for folding small non-helical proteins (17). Many studies have thus used the Gō model in the past few years to propose folding mechanisms (18), predict folding rates (19–21), and interpret φ-value data (19–22).

Fig 1.

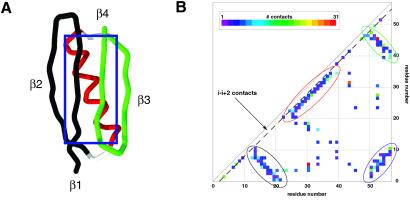
(A) The 57-residue protein G and (B) its contact matrix. The protein (PDB code ) features two anti-parallel β hairpins [N-terminal (colored in black; residues 0–20) and C-terminal (green; 42–55)] packed against a central helix (red; 23–36). The β1 and β4 strands also form a parallel β-sheet. In the contact matrix, a colored square at position (i, j) indicates the number of contact made between residue i and j. The contacts contributing to each of the major secondary structure elements are circled according to the color scheme in A. The i − (i + 2) contacts lie along the dotted line.

The true test of a Gō model simulation, and of any other simulation, is extensive agreement with experimental data. With this in mind, our study was conducted as follows. First, calibrate the Gō potential, if necessary, so that relative thermodynamics of protein G and its constituent secondary structure units match published thermodynamic data, and then record the refolding kinetics. Because only the thermodynamics according to the Gō potential were calibrated, comparison of the simulation kinetic data with experimental observations is a valid test of this simulation. Unfortunately, the folding mechanism of protein G is still under debate. After initial reports that protein G folds in a two-state manner (23), significant burst phase signals (24) for stopped-flow fluorescence experiments were observed. These signals were shown to constitute a distinct kinetic phase by a recent capillary flow experiment (25) (dead time of ≈170 μs), suggesting protein G folds via an on-pathway, intermediate. Soon afterward, strictly based on stopped-flow data collected under less stabilizing conditions, protein G chevron plots featured minimal curvature at low denaturant, as is consistent with two-state kinetics (26).

As shown below, the detailed events recorded by our simulation reveal a complex mechanism: protein G folds through multiple pathways, each of which passes through an on-pathway intermediate. To our surprise, when these trajectories were reexamined through the same reaction coordinate as in fluorescence experiments, the computed ensemble averages were consistent with both the stopped- and capillary-flow data (24–26), as well as φ-value (26) and protein design (27) experiments. This extensive agreement with apparently conflicting experimental data points to the inherent difficulty of inferring microscopic folding events from ensemble averaged data.

Simulation Method

All-Atom MC Gō Folding Simulation.

The characteristic features are that: (i) all heavy atoms are represented as impenetrable hard spheres whose sizes are atom type specific; (ii) the move set consists of small, localized backbone and sidechain torsional rotations; (iii) each MC step consists of 1 backbone and 10 sidechain moves; and (iv) correct bond connectivities and geometries (e.g., planar peptide bonds) are always maintained. The Gō energy of a conformation was obtained by subtracting the number of native from non-native atom–atom contacts. Two atoms separated by a distance R are in contact if σ < R < 1.8σ, where σ is the hard core distance. For example, σ = 2.8 Å for methyl carbons. More details are given in ref. 7. The distance rms (drms) is calculated by , where D and D₀ are pairwise C-α distances in the given and native conformations, respectively. The basic unit of all reported energies is the Gō interaction strength.

Thermodynamic Calibration of the Wild-Type Structure.

Under the Gō potential, protein G unfolds cooperatively at T ≈ 2.1. Calibrating temperature scales against the experimental T_f ≈ 360 K (9), we determined that 278 K corresponds to T ≈ 1.6. At this temperature, hairpin 2 is ≈40% native, whereas the helix and hairpin 1 are negligibly stable. This finding agrees with experiments (28, 29) that have shown that hairpins 1 and 2 are ≈0% and <42% stable (at pH 6.3, 278 K), and with an independent empirical calculation (30) that predicts <10% stability for the helix (at pH 7.0, 278 K).

Thermodynamic Calibration of the Hairpin 2 Mutant.

To test the main conclusions of φ-value analysis (26), we examined the folding of a mutant where hairpin 2 was weakened. This mutant was generated by excluding all contacts involving residues separated by fewer than two positions (Fig. 1B). This mutation had the effect of weakening only the β turns, particularly the second: 2 (0.2% of the total energy) and 41 contacts (8%) involving the residues in hairpins 1 and 2, respectively, were lost, whereas the number of contacts made in the helix and between β-strands 1-2, 3-4, and 1-4 did not change. The resulting mutant featured a helix that was too unstable, and we therefore introduced a generic backbone hydrogen bonding interaction. Every amide N-carbonyl O pair within the contact distance was assigned a particular energy (h) whereas all other backbone atom–atom pairs remained noninteracting. The total energy of a mutant conformation was therefore given by E = E_G + N_hh, where N_h corresponds to the number of hydrogen bonds. Only the stability of the helix was significantly affected as the interaction strength h was increased. Because h > −0.4 resulted in a stability that was too low for the helix and h < −0.8 overstabilized the helix relative to hairpin 2, we were required to choose h = −0.6. At the equivalent of 278 K, the helix and hairpins 1 and 2 are ≈7, 0, and 20% native, respectively. With h = −0.6, the mutated native state (E = −900.4) was slightly less stable (T_f ≈ 1.95) than wild type (E = −890; T_f ≈ 2.1).

Kinetic Folding Runs.

Random coil conformations were first obtained by simulating the native state for 10⁶ steps with an extremely high temperature. Folding runs were then initiated by quenching the temperature to T = 1.6 and allowed to continue for 2 × 10⁹ MC steps. We deemed that folding was complete when the following conditions were all satisfied: (i) drms < 3 Å, (ii) E < −500, and (iii) the fraction of native contact for the helix, hairpin 1, hairpin 2, and the β1-β4 sheet were all >0.4. Conditions i and iii ensure that the backbone topology is essentially native, whereas condition ii guarantees native-like sidechain packing. Fifty runs were completed for both the wild type and mutant.

Determination of the Transition State Ensemble.

For each trajectory, structures near the folding transition as defined by the particular reaction coordinate being used were collected. Twenty folding runs of 10 × 10⁶ MC steps (0.005% of a complete run) were then initiated from these structures, and p_fold was given by the fraction of these runs that folded.

Results

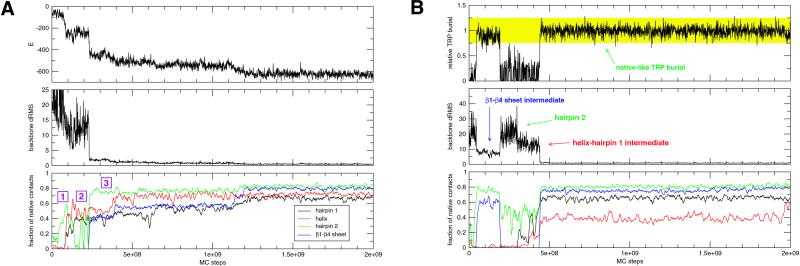
The fastest folding occurred when no kinetic traps, which consisted generally of helix and hairpin misfolds and/or sidechain packing traps (7), were encountered (Fig. 2A). Forty-eight, 72, and 88% of the runs folded to less than 1, 2, and 3 Å drms of the native state, respectively. Three folding pathways were observed: the majority (≈59% of folded runs) passed through a helix-hairpin 1 complex (“major” intermediate; Fig. 2A), whereas the intermediates (“minor”) encountered in the remaining runs were either a helix-hairpin 2 complex or a β1-β4 sheet complex (Fig. 2B). In general, because of its stability and relatively fast folding time, hairpin 2 was observed repeatedly folding to a frayed-end state (31). The major intermediate likely forms before intermediates involving the more stable hairpin 2 because of the larger number of contacts hairpin 1 shares with the helix (132 vs. 103).

Fig 2.

(A) A typical “fast-folding” trajectory, which passes through the helix-hairpin 1 (major) intermediate. Folding occurs to less than 1 Å drms. In this particular trajectory, hairpin 2 folds and unfolds independently (labeled by a purple “1” in the Bottom panel), until the helix-hairpin 1 complex folds (“2”) and stabilizes hairpin 2 (“3”). Note that kinetic traps are not encountered. (B) A trajectory monitored by tryptophan burial. The Top panel tracks the burial of tryptophan 43 (W43) relative to the native state for a typical trajectory. Relative burial is computed as follows: (total number of contacts made by W43)/(total number of native contacts made by W43). Significant events encountered in this trajectory are labeled.

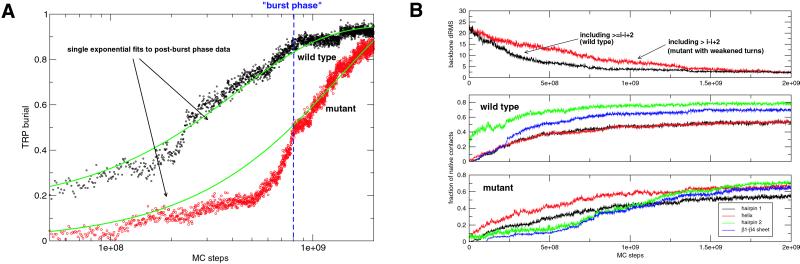
To mimic fluorescence experiments (23–26), we reexamined our trajectories by using tryptophan 43 (W43) burial as the reaction coordinate. Relative burial was computed as the total number of W43 contacts divided by the total number of W43 native contacts. Surprisingly, native W43 burial levels did not strictly correspond to the completion of folding: as shown in Fig. 2B, the β1−β4 sheet intermediate formation results in a native-like signal. The other minor intermediate also completely buries W43 (data not shown). In contrast, despite being on-pathway, the hairpin 1-helix intermediate is not seen by W43 burial. Consequently, the ensemble W43 signal is given by the weighted average of buried (native and two minor intermediates) and non-buried (coil and major intermediate) signals. Runs along two minor pathways therefore contribute to the W43 signal relatively quickly, whereas the majority of runs lag behind as they pass through the helix-hairpin 1 intermediate. This finding results in an early increase in the buried species population, which we believe is the likely explanation for the burst phase (Fig. 3A). As in experiments, two-state models can be satisfactorily fit to the post-burst-phase W43 data. In addition, the burst phase, which is due to intermediates, evolves at a rate (≈10⁹ MC steps) on the same order as folding (≥2 × 10⁹ MC steps). This result is consistent with capillary-flow data (25), where an on-pathway intermediate featuring near-native fluorescence develops in 600–700 μs, whereas the second folding phase finishes in 2–30 ms.

Fig 3.

Ensemble wild-type and hairpin 2 mutant kinetics as seen from different reaction coordinates. (A) W43 burial. The end of the burst phase (labeled as “burst phase”) was determined by matching the wild-type W43 burial with the burst phase value reported in ref. 25. The wild-type and mutant post-burst-phase data were fitted with single exponential rates of 2.56 × 10⁻⁹ and 9.51 × 10⁻¹⁰, respectively. (B) Backbone drms, and secondary structure details. The wild-type ensemble settles to low drms faster than the mutant ensemble (Top). Under ensemble averaging, the wild-type hairpin 2 appears to form earlier than the other three secondary structure features (Middle), whereas this sequence is reversed in the mutant (Bottom).

In a separate set of simulations, we folded a protein G mutant (see Simulation Method) that was slightly destabilized and featured a significantly weakened hairpin 2, in analogy to the mutations analyzed by Baker and coworkers in their φ-value analysis (26). Forty-six of 50 mutant runs folded, with roughly 83% of the runs passing through the helix-hairpin 1 intermediate, whereas the remaining 17% all passed through the helix-hairpin 2 intermediate. The third pathway via the β1-β4 sheet intermediate was not observed. On average, the mutant folds slower and the sequence of folding events appears reversed compared with wild type (Fig. 3B). On mutation, the buried species are populated slower by a factor of ≈2.6 according to the post-burst-phase fit, and the burst phase dropped significantly from 0.85 to 0.4 (Fig. 3A). This finding agrees with the experimental observation that the D46A mutation lowered the burst phase to baseline levels (≈0.4; ref. 26).

Although there is extensive agreement between ensemble-averaged simulation and experiment data, the conclusions drawn from such data do not accurately reflect how protein G actually folds. One reason for this discrepancy is that W43 burial is not a good reaction coordinate. As shown in Fig. 4A, the effective free energy landscape as a function of W43 burial and drms shows only two pronounced minima bridged by a transition region occurring over a broad drms range. Consistent with this fact was that the rise of buried species in the wild type (including both pre- and post-burst-phase data) was single exponential (rate = 2.21 × 10⁻⁹). On the other hand, three minima (unfolded, major + minor intermediate, and native) are present on the L-shaped drms-energy landscape (Fig. 4B). Energy is therefore a better reaction coordinate, because it properly identifies an intermediate. We note that even the combined use of drms and energy as the reaction coordinates is somewhat deficient, because it fails to resolve the major and minor intermediates.

Fig 4.

Qualitative free energy landscapes. All wild-type runs were histogrammed to compute the normalized probability p(X, Y) as a function of the reaction coordinates X and Y. These probabilities were then converted to an effective free energy via the relation F_eff ∼ −ln P. The free energies are given relative to the unfolded state. Although not an exact calculation, it gives a rough idea of where the minima and the saddle regions are located. When drms and energy are the reaction coordinates (Left), there are three distinct minima: unfolded, intermediate, and the native states. In contrast, when drms and W43 burial are used (Right), only two distinct minima (buried and exposed) are seen.

Another important reason lies in the limited information one obtains from ensemble averages. As we have shown, it is difficult to resolve parallel folding pathways by looking at ensemble data, especially if the reaction coordinate being used is imperfect. When the underlying kinetics are quite complex, many of the analyses performed on experimental data, such as φ-value analysis, can break down. From the ensemble point-of-view, both simulation and mutational data show strong agreement: (i) weakening hairpin 2 slows down the folding rate and eliminates the burst phase (26); (ii) both wild type and mutant show apparent single-exponential post-burst-phase kinetics (24, 26); and (iii) protein G can be made to “switch” pathways by weakening hairpin 2 (27). Based on these data alone, hairpin 2 appears to be the kinetically important step, as reported in ref. 26. However, the picture of protein G folding that this ensemble perspective provides is misleading. First, the rise in the true population of the folded species is well fit by a non-two state, multipathway kinetic model (Fig. 5). The rates of formation and depletion of the three intermediates all fall within the same magnitude (≈10⁻⁹), and it is clear that all three pathways are relevant kinetically. Second, the decrease in the folding rate on mutation is actually due to a non-trivial combination of shifts in formation and depletion rates of several different intermediates, and not simply an effect localized to hairpin 2. The main kinetic effect of the mutation was to slow down the formation of the intermediates, particularly the minor ones. This result is not surprising, given that the mutation slows down the formation of hairpin 2 (Fig. 3B). In contrast, the depletion rates of major and helix-hairpin 2 intermediates remained virtually unchanged. Local contacts, including those in hairpin 2, thus do not appear to be important for the final folding step. And third, the switching of pathways is only apparent, because the majority of mutant and wild-type trajectories pass through the hairpin 1-helix intermediate. The faster rise in the wild-type hairpin 2 nativity is simply explained by the higher traffic through the minor pathways and greater stability of hairpin 2.

Fig 5.

Complex time evolution of intermediate populations. The wild-type and mutant fractional populations were fit with a kinetic model featuring multiple three-state pathways [unfolded → I₁ (helix-hairpin 1) or I₂ (helix-hairpin 2) or I₃ (β1-β4 sheet) → N]. The model fitting was done in the following manner: (i) a single exponential was first fitted to the unfolded population data; (ii) the observed pathway branching ratios were then used to determine the three U → I₁ or I₂ or I₃ rates; and (iii) the I₁, I₂, and I₃ population curves were then each separately fitted to determine the I₁, I₂, and I₃ → N rates. For the wild type, the fit is very good for the first billion MC steps, but systematic deviation is observed afterward. This result is best explained by the presence of low-energy sidechain packing traps (7), which results in slower, non-exponential relaxation of the unfolded state. The fit of the model for the mutant was worse overall. We did not find a straightforward explanation for this finding, and we thus attribute it to statistical error. For wild type, k_U→I1 = 1.56 × 10⁻⁹, k_U→I2 = 7.91 × 10⁻¹⁰, k_U→I3 = 2.90 × 10⁻¹⁰, k_I1→F =7.56 × 10⁻⁹, k_I2→U =1.09 × 10⁻⁸, k_I3→F =1.55 × 10⁻⁹; for the mutant: k_U→I1 = 8.63 × 10⁻¹⁰, k_U→I2 = 1.82 × 10⁻¹⁰, k_I1→F =6.71 × 10⁻⁹, and k_I2→F =1.33 × 10⁻⁸.

We also compared our data with quenched flow ¹H–²H exchange experiments (32), because they are not complicated by some of the problems associated with W43 burial. In general, our data were consistent with the observed amide protection factors: (i) hairpin 2 is better protected than hairpin 1 and the β1-β4 sheet (see Fig. 3B); (ii) the protection factors decline as one approaches the hairpin ends presumably because of frayed-end states; (iii) the presence of a structured helix in the large majority of intermediates results in the high average protection value for the helix; and (iv) the β1-β4 sheet amides are weakly protected because they are the last to form in the large majority of trajectories.

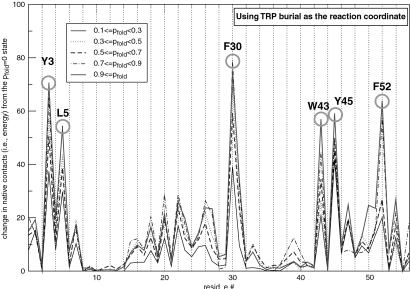
Finally, to directly test the major conclusion from φ-value analysis, we rigorously determined the transition state ensemble for both the wild type and mutant by identifying those conformations with probability to fold (p_fold) = 0.5 (33). In both cases, the rate-limiting step involves the formation of a specific nucleus (34–37) involving a small number of residues that are nonlocalized along the sequence (Fig. 6). The nucleus we identified brings together residues in hairpin 1 (Y3 and L5), the helix (F30), and hairpin 2 (W43, Y45, and F52). Its central location in the native structure makes the nucleation event common to all pathways we have seen (Fig. 7). The specific nucleus positions we have identified are also conserved among structures with homologous folds. Of the residues we have identified, Y3, L5, F30, W43, and F52 show low sequence entropy over aligned sequences in the ubiquitin superfamily (38). A phage display experiment on the structurally homologous protein L also found that positions I6 (Y3 in protein G), A8 (L5), A33 (F30), and L58 (F52) are highly conserved (39).

Fig 6.

Characterization of the transition state ensemble. For each trajectory, the five structures closest to the transition state (i.e., that have a probability to fold (p_fold) = 0.5) were collected and then partitioned into groups having a certain p_fold range. Here, the total number of native contacts made by a particular residue from an average member in each group (relative to the p_fold = 0 state) is plotted. In other words, a rising peak as p_fold increases from 0 to 1, such as F30, suggests a residue that participates in the transition state. Because the number of native contacts is proportional to energy, the height of the peak corresponds to the energetic importance of a residue to the transition state. In this particular plot, W43 burial was used as the reaction coordinate to monitor folding, to mimic the protocol used in ref. 26. The results did not change when energy and drms were used as the reaction coordinates. Similar nucleus residues were obtained when this analysis was repeated for the mutant trajectories.

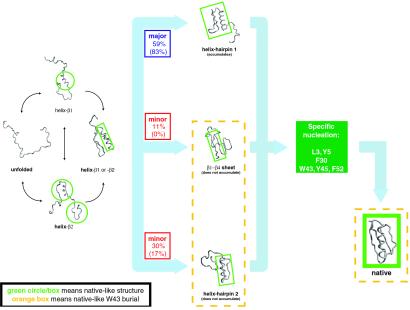
Fig 7.

Summary of the folding kinetics. The observed folding pathways, with their branching ratios, are illustrated. The ratios for the mutant are indicated in parentheses. For each structure, the native-like features are circled or boxed in green. Just before entering two of the three pathways (i.e., the helix-hairpin 1 and helix-hairpin 2 pathways), the helix forms as a result of stabilization by contacts with the β1 or β2 strand (labeled “helix-β1 or -β2”). As expected from its marginal stability (see Simulation Method), helix formation is initiated only when it makes contacts with the strands. After formation of the intermediate, all three pathways converge to a common rate-limiting step, which is the formation of the specific nucleus. Structures exhibiting native-like W43 burial are enclosed in a dotted orange box.

In light of our previous analysis, it is not surprising that this nucleus differs from the nucleus residues proposed by φ-value analysis. This result illustrates the difficulty of inferring microscopic structural features from ensemble mutational data, particularly when the folding reaction is complex. If multiple pathways and intermediates are properly taken into account, φ-value analysis will likely yield the correct transition state.

Discussion

Our all-atom Gō simulations indicate that protein G folds in a manner considerably more complicated that experiments have suggested. Whereas the possibility for on-pathway intermediates has been actively debated in the literature, multiple folding pathways have never been proposed for protein G. However, given protein G's non-trivial chain topology, it is reasonable to expect that there should be a statistical distribution of topologically allowed pathways for assembling the tertiary fold. Remarkably, the presence of multiple pathways does not appear to unnecessarily complicate how protein G folds. We observed that, after the initial divergence into multiple pathways, all pathways appeared to converge to a common rate-limiting step: the assembly of a specific nucleus.

Because sequences with similar folds are likely to share the same set of topologically allowed pathways, we expect them to fold via topologically similar specific nucleation events. Contrary to this assertion, protein L was shown to have a sequence-specific nucleus by using φ-value analysis (40). In light of the difficulties associated with interpreting mutational data when multiple pathways are present, it would be interesting to reexamine protein L by using a similar computational approach.

Despite the coarse-grained energetics and MC dynamics, we believe this simulation yielded folding kinetics that were consistent with experimental data for two main reasons. First, a realistic separation of time scales was maintained (7): helices fold in ≈1 × 10⁶ [≈100 ns, experimentally (41)], hairpins in ≈10 × 10⁶ [≈1 μs (41)], protein G intermediate in ≈1 × 10⁹ [600−700 μs (25)], and protein G in ≈2 × 10⁹ [2−30 ms (25)]. Second, we verified that the thermodynamics as dictated by the Gō potential matched published measurements (9, 28–30) fairly well. Most importantly, at temperatures where protein G is stable, only hairpin 2 is stable (29). It is likely that detailed observations, such as the relative populations and rates associated with each pathway, are Gō model dependent, whereas topological issues were adequately captured by this model.

In general, structural probes that are asymmetrically located in the tertiary fold (such as W43 in protein G) may not capture important details of the folding reaction. Furthermore, a poor choice of the reaction coordinate may not register fast kinetic events, such as the folding of secondary structure elements and particular intermediates. These issues may have important consequences for experiments, whereby folding kinetics have traditionally been measured by using stopped-flow techniques, with which early events cannot be resolved because of experimental dead times (≈1 ms; ref. 42). At the very least, this study has demonstrated the important role high-resolution simulations can play in revealing what lies hidden behind ensemble averages, particularly given that simple reaction coordinates cannot capture the complexity of the folding process (33).

Abbreviations

• MC, Monte Carlo

• drms, distance rms