Skip to main content
PMC home page
Biophysical Journal logoLink to Biophysical Journal
. 2004 Oct;87(4):2552–2563. doi: 10.1529/biophysj.104.043059

Twisting and Untwisting a Single DNA Molecule Covered by RecA Protein

Renaud Fulconis *, Aurélien Bancaud *, Jean-Francois Allemand †, Vincent Croquette †, Marie Dutreix ‡, Jean-Louis Viovy *
PMCID: PMC1304674  PMID: 15454450

Abstract

We study dsDNA-RecA interactions by exerting forces in the pN range on single DNA molecules while the interstrand topological state is controlled owing to a magnetic tweezers setup. We show that unwinding a duplex DNA molecule induces RecA polymerization even at moderate force. Once initial polymerization has nucleated, the extent of RecA coverage still depends on the degree of supercoiling: exerting a positive or negative torsional constraint on the fiber forces partial depolymerization, with a strikingly greater stability when ATPγS is used as a cofactor instead of ATP. This nucleofilament's sensitivity to topology might be a way for the bacterial cell to limit consumption of precious RecA monomers when DNA damage is addressed through homologous recombination repair.

INTRODUCTION

RecA protein is the central enzyme involved in homologous recombination in Escherichia coli. It has been extensively reviewed, for instance by Kuzminov (1999), Lusetti and Cox (2002), and Dutreix et al. (2003). In vitro, RecA interacts with DNA in several ways: i), it readily binds to single-stranded DNA (ssDNA) to form a nucleofilament; ii), the nucleofilament can search for homologous sequences among neighboring DNA molecules, and then align and pair either with a complementary ssDNA or with a homologous double-stranded DNA (dsDNA); iii), in the case of a three-strand reaction, strand exchange can occur spontaneously after proper alignment; only for strand exchange over >∼2000 basepairs does the process need the energy derived from ATP hydrolysis (Menetski et al., 1990); and iv), after strand exchange is completed RecA remains bound to the newly formed heteroduplex and is finally removed via ATP hydrolysis.

RecA-dsDNA complexes are thus a product of homologous recombination. Such complexes can also be formed directly by RecA polymerization on the DNA molecule, although such a process is kinetically very unfavorable. Indeed the nucleation of the first RecA monomers on dsDNA is so slow that polymerization seldom occurs spontaneously. Nevertheless the nucleation barrier can be overcome if the dsDNA has a single-stranded tail, in which case polymerization can then proceed cooperatively along the entire molecule (Shaner and Radding, 1987). The barrier can also be overcome by local defects that tend to destabilize the DNA, such as mismatches, A/T-rich sequences, polypurine tracts, pyrimidine dimers, etc. (Pugh and Cox, 1988), or by the presence of a D-loop on the DNA. A D-loop is produced by homologous recombination with a single-stranded probe, and it can then serve as an initiation site for further RecA polymerization on the double-stranded DNA (Shibata et al., 1982; Register and Griffith, 1988). Once they are formed, nucleofilaments with a dsDNA core are presumed to be energetically more stable than those with an ssDNA core (Klapstein and Bruinsma, 2000).

Two different forms of nucleofilaments have been described: the active (or extended) filaments, that are formed with ATP or its poorly hydrolyzable analog ATPγS as a cofactor, and the inactive (or collapsed) filaments, that are formed with ADP or no cofactor at all (Heuser and Griffith, 1989). For dsDNA filaments, only the active form is stable, unless the molecule is stretched at >20 pN (Hegner et al., 1999). In these active filaments the stoichiometry is 1 RecA monomer per 3 basepairs (3 bases in the case of ssDNA filaments). The DNA molecule follows the helical structure imposed by RecA (with ∼6 monomers per turn on average), so that the DNA helix inside the filament is: i), overstretched by a 1.5 factor relative to the canonical B-DNA (Stasiak et al., 1981); and ii), untwisted by an amount of 15° per basepair (Stasiak and DiCapua, 1982).

Single-molecule studies of RecA-DNA complexes have enabled one to gain insight into the kinetics of RecA binding on DNA as well as the mechanical properties of the nucleofilaments. It was shown in particular that the time lag before the start of polymerization on dsDNA as well as the rate of RecA growth are dependent on the external force applied (Léger et al., 1998; Hegner et al., 1999; Bennink et al., 1999): the greater the external force, the faster the polymerization. There seems to be a force threshold at ∼65 pN. In the absence of a single-stranded tail, a very slow polymerization or even no polymerization at all (Hegner et al., 1999) was observed under the 65 pN threshold, whereas polymerization occurred instantaneously after applying even transiently a force greater than the threshold. Above 65 pN, duplex DNA undergoes a cooperative transition from the normal B-state toward an overstretched state (Smith et al., 1996) that is either modeled as an overextended helix termed S-state (Cluzel et al., 1996) or as a melted duplex (Rouzina and Bloomfield, 2001). The existence of the force threshold for RecA polymerization suggests that the transition to the overstretched state helps the enzyme cross the activation barrier for nucleation. Other observations also include the shape of the growth phase, which is different depending on whether the cofactor is ATP or the poorly hydrolyzable analog ATPγS. Polymerization in the presence of ATP is thought to occur from a single nucleus whereas there are several nuclei in the ATPγS case (Shivashankar et al., 1999). Mechanical properties of RecA fibers were also reported (Hegner et al., 1999; Bennink et al., 1999; Shivashankar et al., 1999). Estimates of the persistence length of nucleofilaments range from ∼200 to 1000 nm, the discrepancy being assumably attributable to complete versus incomplete RecA coverage. As for the stretch modulus, it is thought to be of the order of 2 nN, with remarkable variations whether ssDNA or dsDNA lies at the core, and whether ATP or ATPγS is used as a cofactor.

The single-molecule experiments that we present here shed new light on the behavior of RecA-DNA fibers. In a magnetic tweezers setup, a DNA molecule is tethered between a magnetic particle and the glass surface inside a microfluidic chamber. The whole chamber is then placed in a magnetic field with a strong upward gradient, which is created by a pair of magnets set above the channel. Both the external force applied on the DNA molecule and the topology of the molecule (the word “topology” exclusively referring here to the “interstrand” topological state of the duplex DNA) can thus be imposed via the bead, by moving the magnets along the z axis or by rotating them around the same axis (Strick et al., 1996). Our device permits a more convenient control of both parameters than optical tweezers or micropipettes. Because dsDNA molecules are usually topologically constrained in vivo, whether they are plasmids or just long molecules embedded in other parts of the cell machinery, torsional studies of DNA by itself and of DNA-protein interactions have a strong biological relevance. Since their first description (Smith et al., 1992), magnetic tweezers have permitted one to understand the behavior of a single supercoiled dsDNA (Strick et al., 1998a; Allemand et al., 1998) and to probe its interactions with a complementary ssDNA (Strick et al., 1998b) or with various enzymes such as topoisomerases (Dekker et al., 2003; Charvin et al., 2003), Gal repressor (Lia et al., 2003), or histones (Leuba et al., 2003).

A few experimental facts hint that being able to monitor the effect of both the external force and the topological constraint on a single DNA molecule should be essential when addressing its interaction with RecA protein. First, dsDNA is not only stretched but also underwound upon binding of RecA, which suggests that artificially altering the torsional state of the molecule should affect its interaction with RecA (the same way applying an external force also affects it). Then, there is already evidence that RecA polymerization on DNA depends on topology: negatively supercoiled circular DNA has been proven to be the most favorable substrate, regarding both the extent of RecA binding (Stasiak and DiCapua, 1982) and the binding kinetics (Pugh and Cox, 1988). Last but not least, topology seems to play a major role in other aspects of RecA-DNA interactions, such as homology recognition (Cai et al., 2001) or heterologous DNA probing during the search for homology (Rould et al., 1992).

Our results bring a new contribution to the understanding of torsional effects on DNA-RecA interactions. We show in particular that untwisting a DNA molecule enables a fast start of RecA polymerization, even if the applied external force is far below the 65 pN overstretching threshold. We then investigate the response of a DNA molecule covered by RecA to supercoiling and show that RecA monomers tend to be removed or added to relieve the torsional constraint. Topology therefore seems to be a way of controlling the RecA coverage of dsDNA. We discuss the biological implications of this observation. Interestingly, the torsional behavior of nucleofilaments formed with ATPγS as a cofactor differs dramatically from that of filaments formed with ATP. Estimates of the torques and binding energies involved in both cases are proposed. Finally we qualitatively describe the behavior of more complex structures, such as molecules only partially covered by RecA, that can be writhed at low force.

A few facts about supercoiled DNA

The topology of torsionally constrained DNA molecules such as the ones used in our experimental device is described by two quantities (Boles et al., 1990): 1), the twist, Tw, that is the number of times the two strands of the double helix twist around each other; and 2), the writhe, Wr, which describes the coiling of the axis of the DNA about itself (so-called plectonemes). The linking number Lk = Tw + Wr is a topological constant. For unconstrained DNA, Lk = Lk0 = Tw0 (equals the number of helical turns), and Wr0 = 0. It is convenient to define the degree of supercoiling as σ = (Lk − Lk0)/Lk0. When σ ≠ 0, a torque is applied, which results in a change in Tw and Wr. At low forces the torque is limited by the DNA buckling instability leading to the formation of plectonemes (Wr ≠ 0). In this regime the DNA extension decreases linearly with |σ|. At higher forces the plectoneme torque threshold increases significantly and can even become greater than the critical torque leading to denaturation (when σ < 0) or to the formation of locally overwound DNA (when σ > 0), a structure coined P-DNA by Allemand et al. (1998). In this regime (in which Wr = 0) the DNA extension shows little variation with σ; the process can be respectively envisioned as a phase transition between canonical B-DNA and denatured DNA (with locally σd = −1) and a phase transition between B-DNA and P-DNA (with locally σP = +3). Now, taking RecA into account, RecA-covered DNA is yet in another state with a relative degree of supercoiling σR = −0.43 (deduced from the 15° unwinding per basepair relative to B-DNA).

MATERIALS AND METHODS

Magnetic tweezers setup

In our experiments, we first design a PDMS flow cell with a channel 2-mm wide and 80-μm high. The PDMS cell is then attached on a (3-mercaptopropyl)-trimethoxysilane (Sigma, Lyon, France) treated coverslip for 12 h at 65°C. The final step in surface treatment takes place in the channel and consists in nonspecific binding of anti-digoxigenin (Roche, Basel, Switzerland) for 2 h at 37°C, followed by BSA blocking. Single digoxigenin- and biotin-modified DNA molecules, coupled at one end to streptavidin magnetic particles of diameter 2.8 μm (Dynal Biotech, Oslo, Norway), are incubated in the channel for 30 min at room temperature (buffer: 10 mM Tris-HCl at pH 7.5, 50 mM NaCl, 0.05% Tween 20). The DNA/bead ratio is ∼1:60 to ensure single molecule micromanipulation. Unreacted material is rinsed with a syringe pump (KD Scientific, Boston, MA) at 500 μL/h. The PDMS flow cell is placed beneath two NdFeB permanent magnets separated by 0.8 mm. Images are grabbed by a charge-coupled device camera (JAI, Copenhagen, Denmark) and the (x-, y-, z-) position of the bead is measured in real time. From the transverse fluctuations magnitude 〈δx2〉 and the molecule length l, we deduce the exact force acting on the bead: 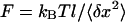Inline graphic (Strick et al., 2000). To eliminate microscope drifts, differential tracking is performed via a second bead stuck to the surface. The vertical force is controlled by the relative position of the magnets to the sample, and rotating the magnets around the optical axis allows control of the degree of supercoiling, σ. By moving the magnets down by ∼5 mm, we can explore a range of forces from 0.1 pN to 15 pN.

DNA construction

The DNA sample is produced by ligating three fragments. The central fragment is ∼14,000 basepairs long and is obtained by polymerase chain reaction (PCR) from phage-λ DNA. Amplification is achieved between positions 21,844 and 35,984 (λ-DNA and the enzyme mix, namely Expand Long Template PCR System, are purchased from Roche). The external fragments are ∼600 basepairs long; they are also obtained by PCR (Roche Expand High Fidelity System) from a linearized plasmid template (pXΔII). One of these fragments is amplified with digoxygenin-modified dUTP, whereas the other is amplified with biotin-modified dUTP (Roche). All fragments are digested at nonpalindromic sites by BsmBI (New England Biolabs, Beverly, MA) and purified on Centricon YM-100 spin columns (Millipore, Billerica, MA) before being ligated together (T4 DNA ligase purchased from New England Biolabs). The final ligation is conducted with excess multidigoxygenin and multibiotin fragments to ensure optimal reaction of most of the central fragments. The excess external fragments are not inconvenient during our experiments because they are not able to bind both the glass surface and the magnetic particles.

The final product is an unnicked DNA molecule ∼5-μm long, with multiple biotin labels on one end and multiple digoxigenin labels on the other end.

Typical experimental conditions

After grafting DNA-bead complexes to the surface and extensively rinsing the channel with the RecA buffer (25 mM Tris-HCl at pH 7.5, 50 mM NaCl, 6 mM MgCl2, 1 mM DTT) to get rid of excess magnetic particles, the magnets are moved near the channel to exert a force in the pN range on the particles: those that are attached to the surface via DNA molecules are positioned ∼5 μm above the surface. We then rotate the magnets by ∼−100 turns: if a magnetic particle goes down to the surface at a force <0.5 pN and goes back to 5 μm above the surface at a force >1 pN, it generally means that we are dealing with a single DNA molecule sensitive to supercoiling. We then plot extension versus supercoiling at various forces and extension versus force at various linking numbers for the “naked” molecule and obtain results similar to those exposed by Allemand et al. (1998). The exact magnet angular position corresponding to a torsionally relaxed molecule (σ = 0) can be determined owing to the extension versus supercoiling curve at low force, and the exact number of basepairs of the molecule can be deduced by fitting a worm-like chain model to the extension versus force measurement in the torsionally relaxed state.

RecA protein (purchased from Sigma) is then injected at a final concentration of 6 μM (in the RecA buffer described above) along with either 1 mM ATPγS or 2 mM ATP. No ATP regeneration system seems to be required within experimental time, because RecA ATPase activity is DNA dependent and very few DNA molecules are present in the channel. The final pH is slightly acidic (pH ∼6). All buffers are filtered before use.

RESULTS

Untwisting dsDNA allows for initiation of polymerization at moderate force

One of our first major observations is that polymerization of RecA on dsDNA can be initiated at a force of ∼8 pN (far below the 65-pN threshold) by merely underwinding the DNA molecule. Indeed, at this force, the extension of naked DNA is nearly equal to that at σ = 0 because denaturation prevents plectoneme formation. RecA polymerization is then primarily monitored as a progressive increase in the length of the molecule, due to the 1.5 factor stretching of DNA upon RecA binding. Polymerization in the presence of ATP cofactor often starts within seconds after untwisting the DNA and maintaining it at 8 pN. When ATPγS is used, the polymerization onset is observed to be much less regular.

The extent of the polymerization in the presence of ATP is roughly proportional to the number of negative turns imposed to the duplex DNA: when N turns are imposed, the increase in the length is very roughly equal to 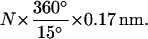Inline graphic Because the coverage of 1 basepair (bp) by RecA amounts to an increase of ∼0.17 nm in length (at a 10-pN force) and a 15° decrease in helicity, this means that the number of RecA monomers added to the DNA is approximately that needed to relieve the torsional constraint imposed on the molecule. This result confirms earlier observations by more traditional methods: only on nicked plasmids can RecA fully polymerize on duplex DNA, whereas covalently closed molecules can only be partially covered (Stasiak et al., 1981). Furthermore, a linear relation between the number of DNA negative supercoils and RecA coverage similar to the one established here was derived by Stasiak and DiCapua (1982). These early experiments were conducted with a successive addition of ATP and ATPγS: we show here that the same quasilinear correspondence applies to molecules exclusively formed with ATP. Oddly, in our own experiments the polymerization extent with ATPγS is much less predictable, and molecules are often incompletely covered even when greatly underwound, probably because the equilibrium takes time to be reached. Therefore, the DNA topological state is probably not the only strong energy barrier to the polymerization on duplex DNA when ATPγS is the cofactor.

The polymerization efficiency is also seen to be dependent on the temperature: experiments conducted at a temperature of 27°C typically result in fast polymerization, whereas at a temperature of 20°C some DNA molecules are never covered by RecA within experimental time (even in the presence of ATP).

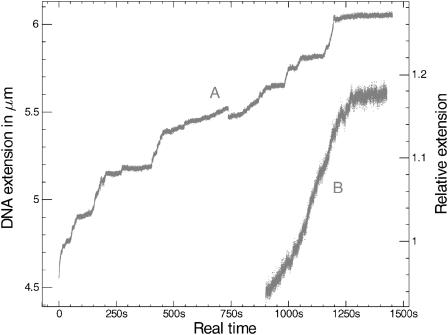
The shape of the growth phase after the initial DNA underwinding is dramatically different according to whether ATP or ATPγS is the cofactor (Fig. 1). Our results are consistent with previous observations by Shivashankar et al. (1999), who stated that RecA-ATP polymerization occurs from a single nucleus and is quasilinear, whereas RecA-ATPγS polymerization occurs from multiple nuclei and is sigmoidal. In addition, our data reveal details that were not apparent in previous work: local variations in the polymerization velocity are conspicuous in the ATPγS case, whereas in the ATP case the rate is much more regular and consistent with the measurement by Shivashankar et al. (1999) (typical velocity ∼12 monomers/s). With ATPγS the total polymerization time is subject to much variation because of long pauses in the process. The rate is often less than the 12 monomers/s rate observed with ATP, but for short bursts of a few seconds it can be bigger (∼25 monomers/s). The level of fluctuations observed with ATP is two to three times larger than with ATPγS, which strongly suggests that RecA binding is highly dynamic, and involves local polymerization and depolymerization at the same time. This rearrangement of RecA monomers is impeded with ATPγS, which might explain why the net polymerization is slower.

FIGURE 1.

FIGURE 1

Open in a new tab

(A) Initial polymerization of RecA on a DNA molecule unwound by 580 turns (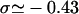Inline graphic), in the presence of ATPγS. (B) Initial polymerization of RecA on a DNA molecule unwound by 400 turns (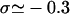Inline graphic), in the presence of ATP (arbitrary time origin). The external force applied is ∼6 pN for both molecules. Fluctuations are observed to be considerably larger in the ATP case, which hints at a very rich dynamics via ATP hydrolysis.

At present the exact process by which nucleation occurs after unwinding DNA is still unclear. It can be assumed that RecA binds to one strand of a denaturation bubble and then closes it by renaturing complementary strands, or alternatively it could directly bind to double-stranded regions with a lower activation barrier owing to the negative torsional stress.

Torsional response of a single DNA-RecA-ATP fiber at equilibrium

After the initial polymerization has been completed in the presence of ATP, we are able to plot the molecule length versus the force at a given number of turns, or conversely the length versus the number of turns at a given external force. The molecule length is now maximal at ∼−580 turns (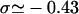Inline graphic) instead of 0 for naked DNA, and the maximal length is slightly smaller than 1.5 times that of the naked DNA molecule at 0 turn. Both observations are consistent with a polymerization over most of the 14,000 basepairs of the molecule, the new helix being elongated by a 1.5 factor and untwisted by 15°/bp relative to the naked DNA helix.

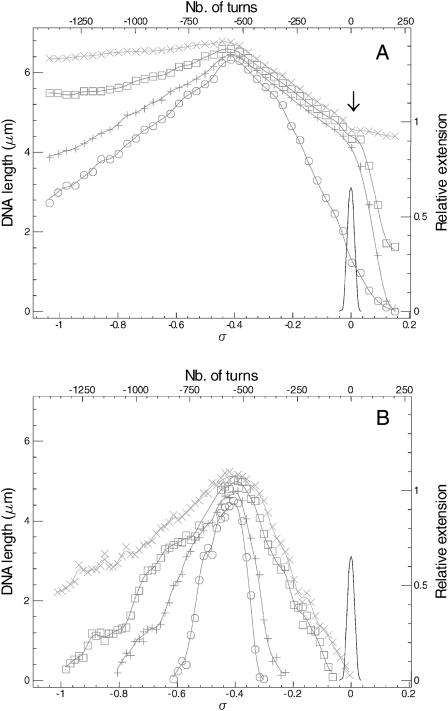
When turns are imposed at a constant force from the new relaxed state (−580 turns), the length of the molecule decreases in an asymmetric way whether supercoiling is positive or negative (Fig. 2). In the case of negative turns (untwisting the DNA further than the natural RecA underwinding), the slope decreases with increasing force, from 21 nm per turn at 0.1 pN to 0.6 nm per turn at 8 pN. In the case of positive turns (retwisting the molecule toward the natural naked DNA helicity and further), the slope also decreases with increasing force from 55 nm per turn at 0.1 pN to ∼3.9 nm per turn at 2 pN and then it remains at this level for higher forces up to at least 10 pN. An intermediate regime has been observed for forces in the 1–2-pN range, with a slope break after a certain number of turns have been made. We interpret the decrease in the DNA length upon twisting in the medium force regime (F ≥ 2 pN) as mere RecA depolymerization. At a number of turns N > −580 the release of part of the RecA monomers relieves some of the torsional constraint. This can be envisioned as an exchange between an R phase (RecA-covered DNA, with σR = −0.43) and a B phase (naked DNA, with σB = 0). Upon arriving at σ = 0, all the R phase has essentially been converted into B phase, which explains why the graphs approximately catch up to the naked DNA curves (Strick et al., 1998a) slightly above N = 0 (arrow in Fig. 2 A). The variations in the extension of the molecule are perfectly and instantaneously reversible if the DNA is twisted back to the σ = −0.43 “relaxed” state, except when the amount of winding reaches several hundreds of turns at once; in that case there is a slow length increase very similar to the initial polymerization phase, which strongly supports our interpretation of reversible depolymerization.

FIGURE 2.

FIGURE 2

Open in a new tab

Extension versus supercoiling for a single DNA-RecA-ATP fiber. (A) Medium forces are: 8 pN (×), 4 pN (□), 2 pN (+), 1 pN (○). (B) Low forces are: 0.8 pN (×), 0.4 pN (□), 0.2 pN (+), 0.1 pN (○). The continuous curve represents the reference for naked DNA at 0.3 pN.

For N < −580 we argue that depolymerization also occurs. Transforming R-phase DNA into B-phase DNA is unfavorable because it increases the torsional constraint, but B-phase DNA can then be denatured (d-phase DNA, with σd = −1), which ultimately relieves the constraint. Denatured DNA having a very different elasticity than B-DNA (Strick et al., 1998a; Allemand et al., 1998), differences in the slopes according to the force are easily understandable.

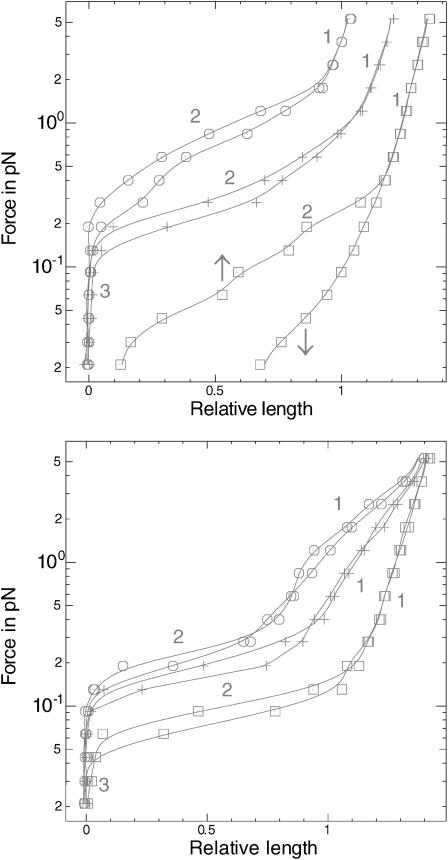
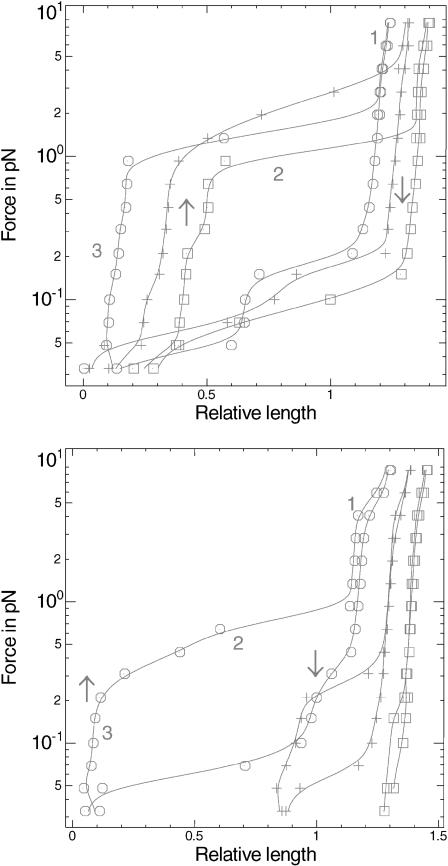
In the low force regime (F < 2 pN) the DNA length tends to decrease to zero upon twisting before reaching N = 0, which means that plectonemes are formed in addition to the depolymerization effect. These plectonemes have to involve both the naked and the RecA-covered part of the DNA. The force versus extension graphs at different σ (Fig. 3) are useful to understand how these plectonemes are formed. Each graph is composed of two parts, one that is obtained by progressively raising the force to a maximum (the extension at any given force being averaged over 10 s or more), and then one that is obtained by progressively decreasing the force from this maximum. An arrow indicates the direction of the force variation when needed. Now three different domains are conspicuous on these graphs (numbered 1–3 on Fig. 3). At the higher forces, writhing is impossible; domain 1 is therefore characteristic of the elasticity of the molecule. It changes very little in the σ > −0.43 regime, where only the length of the molecule diminishes with increasing σ, whereas in the σ < −0.43 regime the slope shows significant variations due to the very different elastic behavior of denatured DNA (created upon RecA depolymerization). Conversely, at very low forces (domain 3) the molecule length is zero, which means that it is extensively writhed. In-between lies domain 2, where the molecule is only partly shortened by plectonemes. The force threshold under which plectonemes start forming is thus designated by the slope change at the frontier between domains 1 and 2. This threshold raises with increasing σ in the σ > −0.43 regime until ∼2 pN, whereas it is much lower in the σ < −0.43 regime (of the order of 0.2 pN).

FIGURE 3.

FIGURE 3

Open in a new tab

Force versus extension for a single DNA-RecA-ATP fiber. (Top) Positive supercoiling relative to the relaxed filament (□, σ = −0.37; +, σ = −0.21; ○, σ = −0.05). (Bottom) Negative supercoiling relative to the relaxed σ ∼ −0.4 filament (□, σ = −0.46; +, σ = −0.62; ○, σ = −0.78). Each curve is obtained by first progressively raising the force to ∼5 pN and then lowering it (downward arrow). Domains 1 and 2, respectively, correspond to the elastic response of the molecule, and to plectoneme formation. In domain 3, the molecule is extensively writhed, and its extension is thus zero.

All these experiments are conducted with RecA and ATP in solution. Rinsing with a buffer that does not contain RecA and/or ATP results in very rapid dissociation of the RecA-DNA complex. We then essentially get back the extension versus force and extension versus supercoiling graphs that could be plotted before injecting RecA (data not shown) and that were already described elsewhere (Strick et al., 1998b; Allemand et al., 1998).

Torsional response of a single DNA-RecA-ATPγS fiber at equilibrium

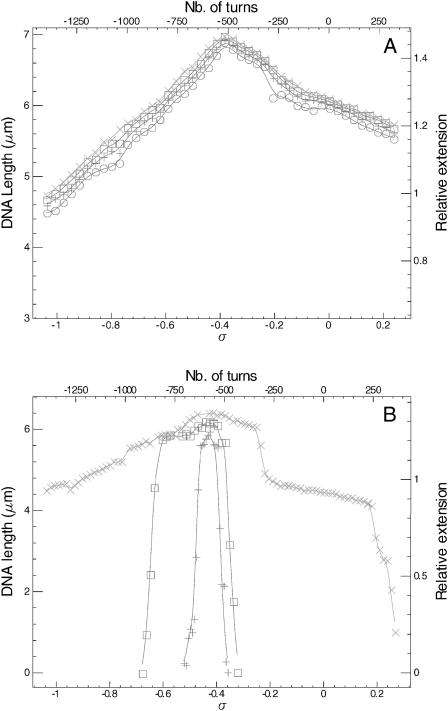
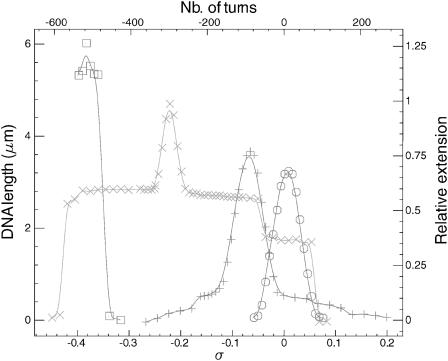
When the same experiment is conducted with ATPγS as a cofactor, the result is qualitatively different (Fig. 4). In the medium force range (1 pN ≤ F ≤ 8 pN), the DNA length depends very little on the force both for negative and positive turns (the molecule is very rigid). The “twisting” slope is evaluated at 1.6 nm per turn. The “untwisting” slope fluctuates more from one experiment to the other and lies between 1.5 and 2.6 nm per turn. Just like in the ATP case, we assume that the length decrease is related to partial depolymerization of RecA, but the filament is more stable, so that RecA depolymerizes to a lesser extent. At low forces (<1 pN) the bead tends to be pulled back to the surface when there is too much over- or underwinding, which implies the formation of plectonemes just like in the ATP case. Yet the transition to zero extension is far less regular than in the ATP case, with abrupt jumps. Actually the behavior of the DNA-RecA-ATPγS fiber shows high hysteresis, especially when it is overwound: the molecule length at a given force is not the same whether it was previously held at a greater or smaller force. Equilibrium length at a given low force can be long to reach (1 min or more), with upwards or downwards jumps in the 500-nm range. Once again, this effect is best seen on the force versus extension graphs at different σ (Fig. 5). When σ > −0.43 plectonemes tend to form rapidly at F = 0.2 pN, but they are efficiently broken only at F ∼ 2–5 pN, hence the huge discrepancy between the upward and downward parts of the graphs. When σ < −0.43 it seems that more supercoiling is needed to form plectonemes. Besides, the curves in this regime differ radically from those obtained with ATP as far as elasticity is concerned. We propose a possible explanation for this fact in the discussion. Note that at the higher forces (for σ close to −0.43) the molecule is strikingly more rigid than when ATP is used, as can be seen by comparing the slopes of domains 1 in Figs. 3 and 5. This is in good agreement with the results of Hegner et al. (1999).

FIGURE 4.

FIGURE 4

Open in a new tab

Extension versus supercoiling for a single DNA-RecA-ATPγS fiber. (A) Medium forces are: 8 pN (×), 4 pN (□), 2 pN (+), 1 pN (○). (B) Low forces are: 0.8 pN (×), 0.4 pN (□), 0.2 pN (+).

FIGURE 5.

FIGURE 5

Open in a new tab

Force versus extension for a single DNA-RecA-ATPγS fiber. (Top) Positive supercoiling relative to the relaxed σ ∼ −0.4 filament (□, σ = −0.30; +, σ = −0.14; ○, σ = +0.02). (Bottom) Negative supercoiling relative to the relaxed filament (□, σ = −0.46; +, σ = −0.62; ○, σ = −0.78). The arrows indicate how the curves are plotted (first raising the force to a maximum, then decreasing it to a minimum). For domain numbering, see Fig. 3.

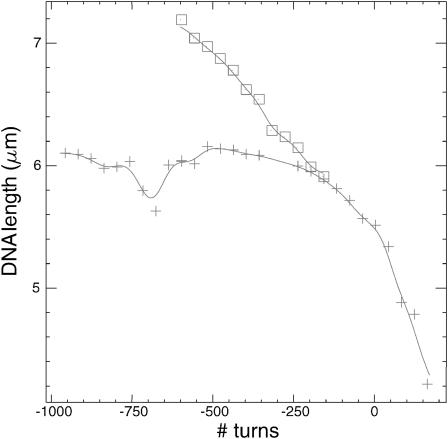
For some reason, some DNA molecules are only partially covered by RecA after the initial polymerization and tend to remain so. Such a partially polymerized molecule shows intermediary features between naked DNA and an ATPγS nucleofilament. The torsionally relaxed state lies at σ0 = −0.43·x (x being the fraction of DNA covered by RecA). For σ close to σ0 the length variation at 0.2 pN is characteristic of B-DNA plectoneme formation (Fig. 6), which means that the naked part of the molecule is the first one to accommodate the torsional constraint. With further supercoiling the molecule length shows the same kind of variations than those observed with a completely covered molecule (milder slopes, abrupt jumps); this is a signature of the torsional response of the RecA-covered part of the molecule. Monitoring extension versus supercoiling curves for different RecA coverage at the same force thus describes how the molecule is progressively deformed during polymerization (Fig. 6): the molecule grows, its helicity is shifted toward negative turns, and the central part of the graph, with the formation of B-DNA plectonemes, shrinks.

FIGURE 6.

FIGURE 6

Open in a new tab

Extension versus supercoiling for molecules with various RecA coverage at 0.2 pN. Estimates of the coverage according to the shift of the maximum of length are: 0% (○), 15% (+), 50% (×), and 90% (□).

Torsional response of a single DNA-RecA-ATPγS fiber without RecA and ATPγS in solution

The filament formed in the presence of ATPγS is rather stable on the timescale of the experiment, which enables us to monitor the torsional response without ATPγS and RecA in solution, thus allowing for depolymerization without allowing for repolymerization. Qualitatively, the length decreases more readily at 8 pN when the molecule is over- or underwound from its relaxed state (Fig. 7) than when the same is achieved with RecA and ATPγS present in solution (Fig. 4). But the main difference is that part of the reversibility is lost: going back from an initial σ ≠ −0.43 state toward the theoretically relaxed σ = −0.43 state only results in a very limited increase in the extension, which then remains more or less constant over a wide range of supercoiling (because RecA cannot repolymerize). However, when the molecule is twisted further away from the initial state, more depolymerization is achieved and the extension decreases again.

FIGURE 7.

FIGURE 7

Open in a new tab

Extension versus supercoiling at 8 pN for a single DNA-RecA-ATPγS fiber in the absence of RecA and ATPγS in solution. The molecule is twisted from ∼−600 turns to −150 turns (□), then untwisted back to −1000 turns (not shown), and retwisted from there up to 150 turns (+).

DISCUSSION

Control of the RecA coverage on dsDNA via positive supercoiling relative to the relaxed DNA-RecA-ATP fiber

Let us consider a preassembled dsDNA-RecA-ATP fiber. At σ = −0.43 the torque is Γ = 0. When we impose positive supercoiling to the structure (σ > −0.43) at a force F > 2 pN, the torque Γ rises, leading to some net depolymerization of RecA (Fig. 2), favored by the plasticity of the RecA coverage (frequent cooperative assembly and disassembly via ATP hydrolysis). As a first approximation we can assume that this process occurs at a constant critical torque Γc, exactly like the B-DNA → d-DNA or B-DNA → P-DNA transitions (Strick et al., 1998a). One indirect way of estimating the value of this critical torque Γc (which is capable of forcing the fiber to depolymerize) relies on the measurement of the slope of the length versus number of turns curve (Fig. 2), as is shown in the following calculation.

First, let us write the three equations that describe the coexistence of a B phase and a RecA phase on the molecule, that is, the conservation of the number of basepairs, the molecule length according to the RecA coverage, and the conservation of the linking number:

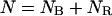graphic file with name M4.gif (4.1)
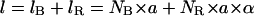graphic file with name M5.gif (4.2)
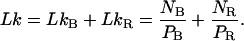graphic file with name M6.gif (4.3)

In these equations a is the standard basepair length (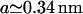Inline graphic in the 2–10-pN range), α stands for the overextension factor of the RecA phase (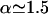Inline graphic), and PB and PR are the number of basepairs per helical turn in the two phases (respectively, 10.4 and 18.4 in the absence of any torsional constraint).

Let us first assume that the fiber has an infinite torsional rigidity (which is equivalent to assuming 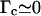Inline graphic). In this case, the change in twist resulting from RecA depolymerization upon positive supercoiling of the fiber must exactly counterbalance the number of turns Δn of the magnets. From Eqs. 4.1 and 4.3 we deduce that the change ΔNR in the number of basepairs covered by RecA is directly proportional to Δn:

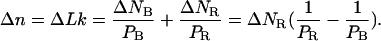graphic file with name M10.gif (4.4)

This produces a change in the molecule length: Δl = a(α − 1)ΔNR (from Eq. 4.2). The slope of the molecule length versus number of turns curve in the 2–10-pN range should therefore be:

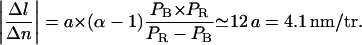graphic file with name M11.gif (4.5)

Let us now acknowledge that the torsional rigidity of B-DNA is finite. The applied torque produces a slight change in the pitch of the molecule. If we conventionally choose to keep PB and PR at the same value as in the absence of torsional constraint, we have to take into account an additional angle Ω corresponding to the elastic torsional response to a torque Γ = Γc, with 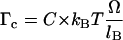Inline graphic (C is the persistence length for torsion). This relation is valid under the assumption that the RecA-covered part of the molecule is torsionally more rigid than the naked part, because the former is firmly held inside the protein helix. Eq. 4.3 is now replaced by:

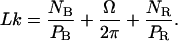graphic file with name M13.gif (4.6)

The total angular variation imposed by the magnets 2πΔn is divided into the depolymerization-related change in twist and the change in the angular deformation of the molecule ΔΩ. Thus:

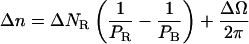graphic file with name M14.gif (4.7)
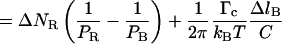graphic file with name M15.gif (4.8)
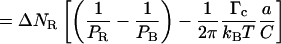graphic file with name M16.gif (4.9)
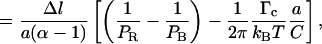graphic file with name M17.gif (4.10)

because ΔlB = −a ΔNR and Δl = a(α − 1)ΔNR. The slope of the molecule length versus number of turns curve in the 2–10-pN range should therefore be

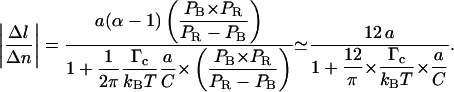graphic file with name M18.gif (4.11)

Equation 4.11 now replaces Eq. 4.5 and includes a corrective term related to the critical depolymerization torque Γc.

Furthermore, owing to measurements and calculations by Strick (1999) as well as to our own data in the absence of RecA, we know that in our 6 mM magnesium-containing buffer, P-DNA appears at a critical force of ∼7 pN and at a critical torque of ∼10 kBT consistently with recent direct torque measurements by Bryant et al. (2003). Hence, we must have 0 < Γc < 10 kBT. Indeed, Γc > 10 kBT would imply that B-DNA turns into P-DNA at F > 7 pN before any RecA monomer is removed. In that case we would come up with a much weaker value of |Δl/Δn| that would be inconsistent with our results (see section entitled “The RecA filament is more resistant to torsion when assembled with ATPγS”). Setting the DNA torsional persistence length C to 85 nm (Strick, 1999), this range in Γc implies that |Δl/Δn| be contained between 3.5 nm/tr (for the strongest critical torque that is possible) and 4.1 nm/tr (for 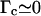Inline graphic). Our own measurements of |Δl/Δn| stand between 3.8 and 3.9 nm/tr, which is consistent with these theoretical limits. The corresponding value of Γc (obtained by inverting Eq. 4.11) stands between 3 and 5 kBT; it is the first estimate of a “RecA depolymerization torque”.

This measurement can in turn give an estimate of the binding energy of one RecA monomer on dsDNA (ERecA). In fact, when one monomer is released, the torsion energy (related to the angular deformation of the molecule Ω by 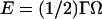Inline graphic) is lowered by ∼Γc × π/8 because the twist is modified by ∼π/4. This gain is compensated at equilibrium by: i), the loss of binding energy 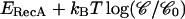Inline graphic where 𝒞 is the RecA bulk concentration and 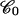Inline graphic the reference concentration (which we can assume to be of the order of 0.1 M, i.e., the close-packing concentration corresponding to perfect availability of the protein); and ii), by the work done by the external force against the shortening of the molecule: F × (3/2)a (this term being small in comparison with the binding term in our experimental conditions). Hence:

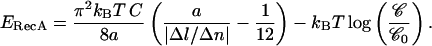graphic file with name M23.gif (4.12)

This yields ERecA ∼ 6 kBT. The only comparison that we can make is with the characteristic energy of RecA-ATPγS binding to ssDNA, which has been estimated by microcalorimetry measurements to be 9.4 kBT per monomer on average (8 kJ/mol of basepairs), with great variations according to the sequence (Wittung et al., 1997)

The RecA filament is more resistant to torsion when assembled with ATPγS

When ATPγS is used instead of ATP, the decrease in the length of the molecule is dramatically reduced: we measure 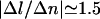Inline graphic nm/tr at F > 2 pN. This leads us to assume that the nucleoprotein filament is more stable and thus less prone to depolymerization. The critical torque for depolymerization Γc is therefore bigger. In particular if it is greater than the 10 kBT torque characteristic of the B-DNA → P-DNA transition in our buffer, then P-DNA (or, more precisely, plectonemed P-DNA as evidenced by Allemand et al., 1998) can be formed at F = 8 pN before RecA is depolymerized. Because P-DNA is able to absorb a great deal of torsional constraint (σP = +3), it is straightforward that more twisting will be needed to depolymerize the same amount of RecA as in the ATP case.

Let us assume that the DNA molecule is again biphasic upon positive supercoiling (σ > −0.43), but that this time the RecA phase coexists with P-DNA. Lets us further assume that both the P-DNA and the RecA regions have their canonical twist (which is a simplification because P-DNA for instance could very well be overwound to accommodate even more torque). If we denote xR, x′R, xP, x′P the fraction of the molecule in the RecA or P phase at two different relative linking numbers separated by Δσ = σ′ − σ, we have:

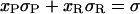graphic file with name M25.gif (4.13)
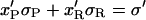graphic file with name M26.gif (4.14)
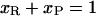graphic file with name M27.gif (4.15)
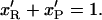graphic file with name M28.gif (4.16)

Hence we get:

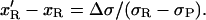graphic file with name M29.gif (4.17)

The extension of the P-DNA region is 0 at F < 25 pN (Allemand et al., 1998). The decrease in the molecule length between σ and σ′ is therefore:

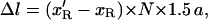graphic file with name M30.gif (4.18)

where N is the total number of basepairs. Now the change in the relative linking number is related to the number of turns made by the magnets by:

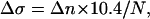graphic file with name M31.gif (4.19)

(because the canonical DNA helix accommodates 10.4 basepairs per turn). Finally:

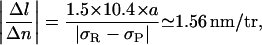graphic file with name M32.gif (4.20)

which is very close from the experimental 1.5 nm/tr result. This supports our initial assumption that the RecA-ATPγS filament is sufficiently resistant to torsion to force the P-DNA transition in naked parts of the molecule before RecA depolymerization. The corresponding lower bound for ERecA according to Eq. 4.12 is 8 kBT, close to the value estimated by Wittung et al. (1997). However, it is not entirely clear at this stage whether the greater stability of RecA-filaments assembled with ATPγS versus those assembled with ATP is due to a stronger binding energy or to a heavy kinetic delay in depolymerization because of a higher activation barrier when hydrolysis of the cofactor is hindered.

Qualitative description of a dsDNA-RecA fiber subject to negative supercoiling

When negative supercoiling is imposed relative to the relaxed nucleofilament (σ < −0.43), the situation is more difficult to describe. Indeed, our results (Figs. 2 and 4) show unambiguously that RecA also depolymerizes, like in the case of positive supercoiling. The molecule probably relaxes torsion via R-DNA → B-DNA → d-DNA, with σd = −1 < σR. However, the interpretation is complicated by the fact that RecA could transiently bind to the denaturation bubbles and renature the complementary strands, or alternatively bind to either or both of the two separated strands.

We have noticed that length fluctuations in the σ < σR regime are considerable, whereas they are greatly reduced if ATPγS is the cofactor. This is consistent with our assumption of unstable depolymerization/repolymerization events occurring with ATP. Another striking feature with ATPγS is the conservation of the slope between 2 and 8 pN, which suggests that the elasticity varies much less upon supercoiling than with ATP, possibly because RecA-ATPγS binds strongly to each strand of denatured DNA, yielding two filaments in parallel, whereas these strands essentially remain naked (or dynamically covered and uncovered) when ATP is used as a cofactor. This could explain the discrepancy between Figs. 3 (bottom) and 5 (bottom). We cannot rule out either that due to the higher resistance of RecA-ATPγS fibers to depolymerization, an even more underwound phase than denatured DNA, actually a left-handed helix coined Z-DNA can appear (Léger et al., 1999).

DNA-RecA plectonemes

At low force, the residual torsional constraint accumulated in the molecule upon supercoiling is converted into Wr. Note that the torsion accumulated is greater with ATPγS than with ATP. It is unclear how these plectonemes are formed, because the DNA molecule is heterogeneous, with a naked part and a much more rigid RecA-covered part. We do not know how the two phases are distributed. What we do know however is that not only the flexible B-DNA part but also the rigid RecA part have to be involved in plectoneme formation, consistently with earlier electron micrographs (Stasiak and DiCapua, 1982; Stasiak et al., 1982). The plectonemes involving nucleofilaments are most likely bigger than those formed with pure B-DNA, the curvature being mostly accommodated by the free basepairs rather than the covered ones, as can be seen on electron micrographs of mixed DNA-filament closed plasmids (Chrysogelos et al., 1983). We would therefore expect the extension versus supercoiling slope at low force to be greater than in the naked DNA case (40–80 nm/tr). Yet in the ATP case it is rather bounded between 10 and 55 nm/tr for positive supercoiling and between 3 and 20 nm/tr for negative supercoiling, which is readily explained by the fact that RecA still partially depolymerizes during supercoiling at low force.

The force threshold under which plectonemes start appearing (ATP) raises from 0.4 pN for σ close to −0.43 to ∼2 pN for σ close to 0 (Fig. 3). This observation is consistent with a progressive decrease in the global persistence length of the molecule upon RecA depolymerization. More complex effects such as an increase of the average ERecA with an increasing level of depolymerization are conceivable. Indeed if RecA has strong sequence preferences on dsDNA just as it has on ssDNA (Bar-Ziv and Libchaber, 2001), the least stable sequences should be depolymerized first, and the most stable ones last. As for the strong hysteresis already noted with ATPγS as a cofactor, it might be attributed to the necessity of creating local defects in the RecA coverage (i.e., “naked” areas) that can accommodate the plectonemes curvature (a need automatically met with ATP because of the plasticity of the structure).

Another striking feature is the asymmetry of the plectoneme regime for positive versus negative supercoiling, which is obvious in Figs. 2–5: the molecule length goes down to zero more readily upon twisting than upon untwisting, and for example in the ATPγS case, negative plectonemes are unstable above ∼0.2 pN whereas positive ones are stable up to 1 pN. This seems to be entirely consistent with previous observations by Stasiak et al. (1982) that ATPγS filaments are able to form regular left-handed helices, either within the same molecule (which is equivalent to positive supercoiling) or between two molecules. Similar effects were demonstrated within bundles of molecules (Egelman and Stasiak, 1988), the superhelical structure being highly sensitive to Mg2+ concentration. On the contrary, right-handed coiling of the filaments does not seem to be energetically favorable. The asymmetry mentioned above could thus be at least partly explained by the filaments' tendency to wind around themselves in a left-handed way and to be stabilized in this form.

CONCLUSION

To the best of our knowledge, this work is the first attempt of investigating topological and torsional effects on DNA-RecA interactions by single-molecule techniques. It was already known that exerting a very large force (>65 pN) on duplex DNA dramatically alters its interaction with RecA. We have proven that the same applies for twisting: underwinding dsDNA favors the onset of polymerization; the extent of the RecA coverage is then closely related to the molecule's degree of supercoiling, especially when filaments are assembled with ATP (which is the biologically relevant case). Not only do these results confirm earlier electron microscopy observations, but they also make possible a more quantitative description of the phenomenon. Applying a torque between 3 and 5 kBT to the molecule is sufficient to force depolymerization. When the poorly hydrolyzable analog ATPγS is used, the nucleofilament is more stable, and the critical torque rises up to >10 kBT according to our estimates. Very little data are available on the average binding energy of one RecA monomer on dsDNA; our experiments allow us to propose a value of 6 kBT when ATP is the cofactor, and a lower bound of 8 kBT when ATPγS is the cofactor.

The possibility of controlling the RecA coverage of dsDNA via torsional constraints could have strong biological implications. Without such a control, a RecA polymerization initiated at a recombination site (induced by a DNA lesion) could propagate indefinitely along dsDNA. But because RecA is sensitive to torsion, and because dsDNA is almost always topologically constrained in vivo, it can probably never be extensively covered by RecA, unless it is actively underwound by another enzymatic process. Because an E. Coli cell has only a limited amount of RecA monomers in store to address potential DNA damage (∼8800 in a noninduced state), the RecA stock has to be used sparingly. Despite the 10- to 20-fold increase in the RecA gene expression after damage detection, the relative concentration of putative RecA binding sites remains in large excess as compared to the number of monomers, with 60 nucleotides per monomer (Gudas and Pardee, 1976). In this respect the strong cooperativity of RecA binding has long been considered an advantage, because it favors the complete coverage of one lesion at a time rather than the incomplete simultaneous coverage of all the lesions. The response of RecA to torsion could be a complementary property that makes sure that RecA is not wasted by polymerizing further on from the lesion site.

Another challenge that the cell has to face after DNA damage repair is to rapidly resume replication and transcription across the repaired region. Moreover, during recombinational repair of stalled replication forks in bacteria, recombination proteins often act to generate substrates for replication restart. It has been recently shown that DNA synthesis is driven by negative superhelicity and is inhibited if disassembly of the RecA filament is prevented (Xu and Marians, 2002). The dynamic structure of the RecA filament is essential to clear the duplex DNA and allow subsequent reactions to take place. Even though further work is required to clearly establish the in vivo interplay between topology and recombination, our results show that torsion could directly act on repair-associated replication by stimulating RecA filament disassembly.

Acknowledgments

The authors thank D. Bensimon (Ecole Normale Supérieure, Paris, France), E. Delagoutte (Institut Curie, Orsay, France), and M. Takahashi (University of Nantes, France) for fruitful discussions, as well as one of our reviewers for enlightening comments on RecA-DNA plectonemes.

R.F. acknowledges a fellowship from DGA-CNRS. This work was partly supported by Institut Curie-PIC “Physics at the cell level” and by CNRS/MENRT Nanosciences program.

Renaud Fulconis and Aurélien Bancaud contributed equally to this work.

References

  1. Allemand, J. F., D. Bensimon, R. Lavery, and V. Croquette. 1998. Stretched and overwound DNA forms a Pauling-like structure with exposed bases. Proc. Natl. Acad. Sci. USA. 95:14152–14157. [DOI] [PMC free article] [PubMed] [Google Scholar]
  2. Bar-Ziv, R., and A. Libchaber. 2001. Effects of DNA sequence and structure on binding of RecA to single-stranded DNA. Proc. Natl. Acad. Sci. USA. 98:9068–9073. [DOI] [PMC free article] [PubMed] [Google Scholar]
  3. Bennink, M. L., O. D. Schärer, R. Kanaar, K. Sakata-Sogawa, J. M. Schins, J. S. Kanger, B. G. de Grooth, and J. Greve. 1999. Single-molecule manipulation of double-stranded DNA using optical tweezers: interaction studies of DNA with RecA and Yoyo-1. Cytometry. 36:200–208. [DOI] [PubMed] [Google Scholar]
  4. Boles, T. C., J. H. White, and N. R. Cozzarelli. 1990. Structure of plectonemically supercoiled DNA. J. Mol. Biol. 213:931–951. [DOI] [PubMed] [Google Scholar]
  5. Bryant, Z., M. D. Stone, J. Gore, S. B. Smith, N. R. Cozzarelli, and C. Bustamante. 2003. Structural transitions and elasticity from torque measurements on DNA. Nature. 424:338–341. [DOI] [PubMed] [Google Scholar]
  6. Cai, L., U. Marquardt, Z. Zang, M. J. Taisey, and J. Chen. 2001. Topological testing of the mechanism of homology search promoted by RecA protein. Nucleic Acids Res. 29:1389–1398. [DOI] [PMC free article] [PubMed] [Google Scholar]
  7. Charvin, G., D. Bensimon, and V. Croquette. 2003. Single-molecule study of DNA unlinking by eukaryotic and prokariotic type-II topoisomerases. Proc. Natl. Acad. Sci. USA. 100:9820–9825. [DOI] [PMC free article] [PubMed] [Google Scholar]
  8. Chrysogelos, S., J. C. Register, III, and J. Griffith.1983. The structure of RecA protein-DNA filaments. 2. RecA protein monomers unwind 17 base pairs of DNA by 11.5°/base pair in the presence of ATPγS. J. Biol. Chem. 258:12624–12631 [PubMed] [Google Scholar]
  9. Cluzel, P., A. Lebrun, C. Heller, R. Lavery, J. L. Viovy, D. Chatenay, and F. Caron. 1996. DNA: an extensible molecule. Science. 271:792–794. [DOI] [PubMed] [Google Scholar]
  10. Dekker, N. H., T. Viard, C. Bouthier de La Tour, M. Duguet, D. Bensimon, and V. Croquette. 2003. Thermophilic topoisomerase I on a single DNA molecule. J. Mol. Biol. 329:271–282. [DOI] [PubMed] [Google Scholar]
  11. Dutreix, M., R. Fulconis, and J. L. Viovy. 2003. The search for homology: a paradigm for molecular interactions? Complexus. 1:89–99. [Google Scholar]
  12. Egelman, E. H., and A. Stasiak. 1988. Structure of helical RecA-DNA complexes. II. Local conformational changes visualized in bundles of RecA-ATPγS filaments. J. Mol. Biol. 200:329–349. [DOI] [PubMed] [Google Scholar]
  13. Gudas, L. J., and A. B. Pardee. 1976. DNA synthesis inhibition and the induction of protein X in Escherichia coli. J. Mol. Biol. 101:459–477. [DOI] [PubMed] [Google Scholar]
  14. Hegner, M., C. B. Smith, and C. Bustamante. 1999. Polymerization and mechanical properties of single RecA-DNA filaments. Proc. Natl. Acad. Sci. USA. 96:10109–10114. [DOI] [PMC free article] [PubMed] [Google Scholar]
  15. Heuser, J., and J. Griffith. 1989. Visualization of RecA protein and its complexes with DNA by quick-freeze/deep-etch electron microscopy. J. Mol. Biol. 210:473–484. [DOI] [PubMed] [Google Scholar]
  16. Klapstein, K., and R. Bruinsma. 2000. RecA force generation by hydrolysis waves. J. Biol. Chem. 275:16073–16083. [DOI] [PubMed] [Google Scholar]
  17. Kuzminov, A. 1999. Recombinational repair of DNA damage in Escherichia coli and bacteriophage λ. Microbiol. Mol. Biol. Rev. 63:751–813. [DOI] [PMC free article] [PubMed] [Google Scholar]
  18. Léger, J. F., J. Robert, L. Bourdieu, D. Chatenay, and J. F. Marko. 1998. RecA binding to a single double-stranded DNA molecule: a possible role of DNA conformational fluctuations. Proc. Natl. Acad. Sci. USA. 95:12295–12299. [DOI] [PMC free article] [PubMed] [Google Scholar]
  19. Léger, J. F., G. Romano, A. Sarkar, J. Robert, L. Bourdieu, D. Chatenay, and J. F. Marko. 1999. Structural transitions of a twisted and stretched DNA molecule. Phys. Rev. Lett. 83:1066–1069. [Google Scholar]
  20. Leuba, S. H., M. A. Karymov, M. Tomschik, R. Ramjit, P. Smith, and J. Zlatanova. 2003. Assembly of single chromatin fibers depends on the tension in the DNA molecule: magnetic tweezers study. Proc. Natl. Acad. Sci. USA. 100:495–500. [DOI] [PMC free article] [PubMed] [Google Scholar]
  21. Lia, G., D. Bensimon, V. Croquette, J. F. Allemand, D. Dunlap, D. E. A. Lewis, S. Adhya, and L. Finzi. 2003. Supercoiling and denaturation in Gal repressor/heat unstable nucleoid protein (HU)-mediated DNA looping. Proc. Natl. Acad. Sci. USA. 100:11373–11377. [DOI] [PMC free article] [PubMed] [Google Scholar]
  22. Lusetti, S. L., and M. M. Cox. 2002. The bacterial RecA protein and the recombinational DNA repair of stalled replication forks. Annu. Rev. Biochem. 71:71–100. [DOI] [PubMed] [Google Scholar]
  23. Menetski, J., D. Bear, and S. Kowalczykowski. 1990. Stable DNA heteroduplex formation catalyzed by the Escherichia coli RecA protein in the absence of ATP hydrolysis. Proc. Natl. Acad. Sci. USA. 87:21–25. [DOI] [PMC free article] [PubMed] [Google Scholar]
  24. Pugh, B. F., and M. M. Cox. 1988. General mechanism for RecA protein binding to duplex DNA. J. Mol. Biol. 203:479–493. [DOI] [PubMed] [Google Scholar]
  25. Register, J. C., III, and J. Griffith.1988. Direct visualization of RecA protein binding to and unwinding duplex DNa following the D-loop cycle. J. Biol. Chem. 263:11029–11032 [PubMed] [Google Scholar]
  26. Rould, E., K. Muniyappa, and C. M. Radding. 1992. Unwinding of heterologous DNA by RecA protein during the search for homologous sequences. J. Mol. Biol. 226:127–139. [DOI] [PubMed] [Google Scholar]
  27. Rouzina, I., and V. A. Bloomfield. 2001. Force-induced melting of the DNA double helix. 1. Thermodynamic analysis. Biophys. J. 80:882–893. [DOI] [PMC free article] [PubMed] [Google Scholar]
  28. Shaner, S. L., and C. M. Radding. 1987. Translocation of Escherichia coli RecA protein from a single-stranded tail to contiguous duplex DNA. J. Biol. Chem. 262:9211–9219. [PubMed] [Google Scholar]
  29. Shibata, T., T. Ohtani, P. K. Chang, and T. Ando. 1982. Role of superhelicity in homologous pairing of DNA molecules promoted by Escherichia coli recA protein. J. Biol. Chem. 257:370–376. [PubMed] [Google Scholar]
  30. Shivashankar, G. V., M. Feingold, O. Krichevsky, and A. Libchaber. 1999. RecA polymerization on double-stranded DNA by using single-molecule manipulation: the role of ATP hydrolysis. Proc. Natl. Acad. Sci. USA. 96:7916–7921. [DOI] [PMC free article] [PubMed] [Google Scholar]
  31. Smith, S. B., Y. Cui, and C. Bustamante. 1996. The elastic response of individual double-stranded and single-stranded DNA molecules. Science. 271:795–799. [DOI] [PubMed] [Google Scholar]
  32. Smith, S. B., L. Finzi, and C. Bustamante. 1992. Direct mechanical measurements of the elasticity of single DNA molecules by using magnetic beads. Science. 258:1122–1126. [DOI] [PubMed] [Google Scholar]
  33. Stasiak, A., and E. DiCapua. 1982. The helicity of DNA in complexes with RecA protein. Nature. 299:185–186. [DOI] [PubMed] [Google Scholar]
  34. Stasiak, A., E. DiCapua, and T. Koller. 1981. Elongation of duplex DNA by RecA protein. J. Mol. Biol. 151:557–564. [DOI] [PubMed] [Google Scholar]
  35. Stasiak, A., E. DiCapua, and T. Koller. 1982. Unwinding of duplex DNA in complexes with RecA protein. Cold Spring Harb. Symp. 47:811–820. [DOI] [PubMed] [Google Scholar]
  36. Strick, T. R. 1999. Mechanical supercoiling of DNA and its relaxation by topoisomerases. PhD thesis. Universite Paris VI, Paris, France.
  37. Strick, T. R., J. F. Allemand, D. Bensimon, A. Bensimon, and V. Croquette. 1996. The elasticity of a single supercoiled DNA molecule. Science. 271:2881–2892. [DOI] [PubMed] [Google Scholar]
  38. Strick, T. R., J. F. Allemand, D. Bensimon, and V. Croquette. 1998a. Behavior of supercoiled DNA. Biophys. J. 74:2016–2028. [DOI] [PMC free article] [PubMed] [Google Scholar]
  39. Strick, T. R., J. F. Allemand, V. Croquette, and D. Bensimon. 2000. Twisting and stretching single DNA molecules. Prog. Biophys. Mol. Biol. 74:115–140. [DOI] [PubMed] [Google Scholar]
  40. Strick, T. R., V. Croquette, and D. Bensimon. 1998b. Homologous pairing in stretched supercoiled DNA. Proc. Natl. Acad. Sci. USA. 95:10579–10583. [DOI] [PMC free article] [PubMed] [Google Scholar]
  41. Wittung, P., C. Ellouze, F. Maraboeuf, M. Takahashi, and B. Norden. 1997. Thermochemical and kinetic evidence for nucleotide-sequence-dependant RecA-DNA interactions. Eur. J. Biochem. 245:715–719. [DOI] [PubMed] [Google Scholar]
  42. Xu, L., and K. J. Marians. 2002. A dynamic RecA filament permits DNA polymerase-catalyzed extension of the invading strand in recombination intermediates. J. Biol. Chem. 277:14321–14328. [DOI] [PubMed] [Google Scholar]

Articles from Biophysical Journal are provided here courtesy of The Biophysical Society

RESOURCES