Interactions of Peptides with a Protein Pore

Abstract

The partitioning of polypeptides into nanoscale transmembrane pores is of fundamental importance in biology. Examples include protein translocation in the endoplasmic reticulum and the passage of proteins through the nuclear pore complex. Here we examine the exchange of cationic α-helical peptides between the bulk aqueous phase and the transmembrane β-barrel of the α-hemolysin (αHL) protein pore at the single-molecule level. The experimental kinetic data suggest a two-barrier, single-well free energy profile for peptide transit through the αHL pore. This free energy profile is strongly voltage- and peptide-length-dependent. We used the Woodhull-Eyring formalism to rationalize the values measured for the association and dissociation rate constants k_on and k_off, and to separate k_off into individual rate constants for exit through each of the openings of the protein pore. The rate constants k_on, and 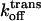decreased with the length of the peptide. At high transmembrane potentials, the alanine-based peptides, which include bulky lysine side chains, bind more strongly (formation constants K_f ∼ tens of M⁻¹) than highly flexible polyethylene glycols (K_f ∼ M⁻¹) to the lumen of the αHL protein pore. In contrast, at zero transmembrane potential, the peptides bind weakly to the lumen of the pore, and the affinity decreases with the peptide length, similar to the case of the polyethylene glycols. The binding is enhanced at increased transmembrane potentials, because the free energy contribution ΔG = −ζδFV/RT predominates with the peptides. We suggest that the αHL protein may serve as a robust and versatile model for examining the interactions between positively charged signal peptides and a β-barrel pore.

INTRODUCTION

The interaction of polypeptides with transmembrane protein pores is of fundamental importance in biology. Examples include protein translocation in the endoplasmic reticulum (1,2), from the cytoplasm into mitochondria (3,4) or across the chloroplast membrane (5).

In particular, the translocation of proteins into mitochondria and chloroplasts occurs through protein channels located in the outer membranes of these organelles (6). Circular dichroism studies demonstrate that these proteins are probably transmembrane β-barrel pores (7,8). These findings set the outer membrane translocases apart from others such as the α-helical translocation pores. A question to be addressed is: how does a signal peptide interact with a β-barrel protein, and cross the channel? There is also considerable interest in examining the transport of polypeptides through β-barrel pores in other circumstances. For example, a β-barrel pore may also serve as a passageway for enzymes to enter the cytosol. Lethal factor (LF) and edema factor (EF) are believed to unfold, at least partially, and translocate through a 14-stranded β-barrel of protective antigen channel PA₇ of anthrax toxin (9–11). The 263-residue N-terminal fragment of LF (LF_N) is translocated across the PA₇ channel even in the absence of cellular proteins, including ATP-driven factors (11). Very recently, the crystal structure of NaIP, a bacterial autotransporter, revealed a 12-stranded β-barrel domain that is filled by an N-terminal α-helix (12). Removal of the N-terminal α-helical domain enhanced the activity of the NaIP autotransporter, indicating that the helix functions in blocking the β-barrel pore.

There is a distinct class of β-barrel proteins that insert spontaneously into membranes without assistance of other proteins. These β-barrels, secreted from bacterial cells, are called pore-forming toxins (β-PFT). In particular, α-Hemolysin (αHL) is a self-assembling, β-PFT secreted by Staphylococcal aureus as a water-soluble monomer of 33.2 kDa (13). The monomer oligomerizes upon binding to the membranes of susceptible cells to form a transmembrane heptamer (14,15). The toxin is an important virulence factor due to its activity against a wide variety of mammalian cells, such as erythrocytes, keratinocytes, granulocytes, monocytes, and endothelial cells (16). The primary mechanisms of cell damage and death are (1) the leakage of water, ions, and other small molecules out of and into the cell, and (2) cell lysis. The αHL forms a relatively large, water-filled pore of known structure (17). The protein contains a roughly spherical vestibule, which measures ∼46 Å in internal diameter, and is located in the extramembranous part (17). In the transmembrane domain, the channel narrows to form a 14-stranded β-barrel with an average diameter of ∼20 Å and a length of ∼52 Å (17).

The knowledge of the crystal structure of the fully assembled αHL heptamer in detergent (17), combined with the wealth of options for membrane protein engineering (13,18,19), has led to approaches for examining single polymer dynamics (20–22), and designing unusual polymer-based nanostructures (20,23–25).

We have recently studied the partitioning of highly flexible neutral polyethylene glycols (PEGs) into the αHL pore. In the dilute regime, the dependence of partitioning on polymer length obeys a simple scaling law (26–28). The polymer moves into the pore by overcoming a free energy barrier of 1.2 k_BT/kDa PEG (28). This barrier presumably arises from a reduction in the number of chain segment configurations (29,30). In the semidilute regime, increased polymer concentration induces an increase in the polymer partition coefficient (31,32). The difference between the results of the equilibrium partitioning experiments in the dilute and the semidilute regime has been attributed to the nonideality of the high concentration polymer solutions (28,33). In contrast to neutral PEGs, the dynamics of the entry and exit of charged polymers with respect to the pore can be substantially altered by applying an external electric field, thus changing the balance between the forces driving polymers into the pore and the forces driving them out (34). How these competing forces act when a charged peptide is transported through a β-barrel protein pore is not yet clarified.

Here, we examine the partitioning of synthetic peptides into the αHL protein pore. Specifically, we probe the exchange of cationic alanine-based peptides between the aqueous phase and the β-barrel, at the single-molecule level. By designing the peptides with a central lysine residue within the repeat unit (Ac-(AAKAA)_mY-NH₂, m = 2–7), the contributions of peptide charge and peptide length to the free energy barrier for the transport of these α-helical peptides across the αHL protein pore are explored.

In this work, we find that the association and dissociation rate constants, and the partitioning data, derived from single-channel electrical recordings of the αHL pore in the presence of micromolar concentrations of peptide, are strongly dependent on transmembrane voltage and peptide-length. We show that the kinetics of partitioning into the αHL protein pore is affected by two contributions: an increase in event frequency due to a more intense transmembrane electric field, and a reduction in event frequency for longer peptides as a result of an entropic penalty for the translocation across the nanometer-scale pore. We propose a semiquantitative model to account for the substantial change in peptide partitioning with transmembrane potential and peptide length.

MATERIALS AND METHODS

Peptide synthesis and purification

The peptides used in this work were Ac-(AAKAA)_mY-NH₂, where m = 2–7. Peptide 1 (m = 1, HPLC purity = 99.1%, M_w = 640 Da), Peptide 2 (m = 2, 99.5%, M_w = 1050 Da), Peptide 3 (m = 3, 98.2%, M_w = 1460 Da), Peptide 4 (m = 4, 99.5%, M_w = 1870 Da), Peptide 5 (m = 5, 95.3%, M_w = 2290 Da), Peptide 6 (m = 6, 95.1%, M_w = 2700 Da), and Peptide 7 (m = 7, 95.0%, M_w = 3110 Da) were synthesized by SynPep Corporation (Dublin, CA). The peptides were purified by HPLC and analyzed by mass spectroscopy (SynPep) and capillary electrophoresis (SynPep). To further confirm the peptide homogeneity, the peptides were analyzed by Tris-Tricine polyacrylamide gel electrophoresis (35) in a 16.5% resolving gel, with a 4% stacking gel (Bio-Rad Laboratories, Hercules, CA). The peptides appeared as discrete narrow bands with only slightly increased broadening with increasing molecular mass.

Circular dichroism of the peptides

CD spectra were recorded on an Aviv 62DS circular dichroism spectropolarimeter (Lakewood, NJ) equipped with a temperature control unit. Quartz cuvettes with a 10-mm-path length were employed. To correlate the CD results with the planar bilayer recordings, the peptides were diluted into 2 M KCl, 10 mM potassium phosphate, pH 7.5, at an amide bond concentration of 0.25 mM. The spectra were corrected by subtracting the spectrum of the buffer alone. The mean molar residue ellipticity, at 222 nm ([θ]₂₂₂), was recorded in the range 0–95 °C, with steps of 2°C. Stock peptide concentrations were determined by measuring tyrosine absorbance in 10 mM potassium phosphate-buffered water (pH 7.5) (36). The observed mean residue ellipticity, [θ]_obs, was converted to fractional helicity f_H for each of the peptides:

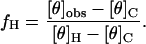(1)

In Eq. 1, the symbols [θ]_H and [θ]_C are the [θ] values, in deg cm² dmol⁻¹, for the complete helix and the complete coil, respectively (37). They are defined by the relations (37)

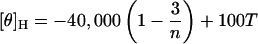(2)

and

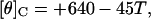(3)

where T is the temperature in °C.

Wild-type α-hemolysin pore

Heptameric wild-type αHL was obtained by treating the monomer, purified from Staphylococcus aureus, with deoxycholate. The heptamer was then isolated from SDS-polyacrylamide gels as previously described (38,39).

Molecular modeling

The β-barrel structure of the αHL pore was generated with SPOCK 6.3 software (40), with coordinates (17) from the Brookhaven Protein Data Bank (PDB ID code 7ahl). The models for the structures of the peptides Ac-(AAKAA)_mY-NH₂, m = 2–7, were generated by INSIGHT II (Molecular Simulations, San Diego, CA), via the BioPolymer Builder module. The SPOCK software was also used to calculate the solvent-accessible volume of peptides and to measure distances between atoms inside the β-barrel domain of the pore.

Single-channel recordings with planar lipid bilayers

Planar lipid bilayers were used for single-channel recordings as described previously (21,41). Both the cis and trans chambers of the apparatus contained 2 M KCl, 10 mM Tris·HCl, pH 7.5, with 100 μM EDTA, unless otherwise stated. A planar lipid bilayer membrane of 1,2-diphytanoyl-sn-glycerophosphocholine (Avanti Polar Lipids, Alabaster, AL) was formed across a 70 μm orifice. The transmembrane potential was applied through Ag/AgCl electrodes connected to the bath with 1.5% agar bridges (Ultra Pure DNA Grade, Bio-Rad Laboratories, Hercules, CA) containing 3 M KCl (Sigma, St. Louis, MO). Measurements were performed at room temperature (24 ± 0.5°C). Protein was added to the cis chamber, which was at ground. Single-channel currents were recorded by using a patch-clamp amplifier (Axopatch 200B, Axon Instruments, Foster City, CA) in the whole-cell mode (β = 1) with a CV-203BU headstage. The signals were lowpass-filtered at 40 kHz with an eight-pole Bessel filter (Model 900, Frequency Devices, Haverhill, MA). A Pentium PC equipped with a DigiData 1322A (Axon Instruments) was used for data acquisition with Clampex 9.2 software (Axon Instruments) at a sampling rate of 200 kHz. The distributions of closed (occupied states) and open (unoccupied states) durations were fitted with sums of exponentials using the maximum likelihood method (42) to estimate the most probable values of the time constants. To determine the number of exponentials for the best fit, we applied the log likelihood ratio (LLR) test, with a confidence level of 0.95, to compare different fitting models (28,42,43). For display and further manipulation of the single-channel currents and histograms, we used pCLAMP 9.2 (Axon Instruments) and Origin 7.0 (Microcal Software, Northampton, MA).

Binding affinities derived from single-channel recordings

We found that the reciprocal of τ_on (the mean inter-event interval) is linearly dependent on the peptide concentration, whereas τ_off (dwell time from the histogram of the occupied states) is independent of the peptide concentration. Thus, a simple bimolecular interaction between peptide and pore can be assumed. The rate constants for association (k_on) were derived from the slopes of plots of 1/τ_on versus [pept], where [pept] is the peptide concentration in the aqueous phase. The rate constants for dissociation (k_off) were determined by averaging the 1/τ_off values recorded over an 80–400-μM concentration range. The equilibrium association constants were then calculated by using K_f = k_on/k_off. The partition coefficients (Π) for the peptides between the aqueous phase and the pore lumen were determined from the equilibrium association constants (K_f) (28). At low occupancies of the pore by the peptide (28)

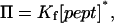(4)

where [pept]^* is the effective molar concentration of a single peptide inside the αHL pore, and has the value

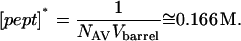(5)

The values N_AV and V_barrel are Avogadro's number and the internal volume of the β-barrel, respectively.

RESULTS AND DISCUSSION

Temperature-dependence of peptide structure in solution

Circular dichroism was used to obtain the helix content of the alanine-rich peptides as a function of temperature. Lysines were included because they are positively charged residues and solubilize the peptides. Alanine has a strong helix propensity (44). The CD spectra of Ac-(AAKAA)_mY-NH₂ exhibit two minima (at 208 and 222 nm) and a single maximum (at 190 nm), which is typical for α-helical peptides. The thermally induced helix-to-coil transition for each peptide was followed by monitoring the CD signal at 222 nm (Fig. 1 A). Identical [θ]₂₂₂ curves were obtained for heating (0–95°C) and cooling (95–0°C). This demonstrates that the thermally induced helix-coil transition is reversible. The weak CD signals for the shortest peptides (P1 and P2) indicate that these molecules are in a random coil conformation. By contrast, the longest peptides (P6 and P7) have a high value of [θ]₂₂₂, confirming extensive helix formation.

FIGURE 1.

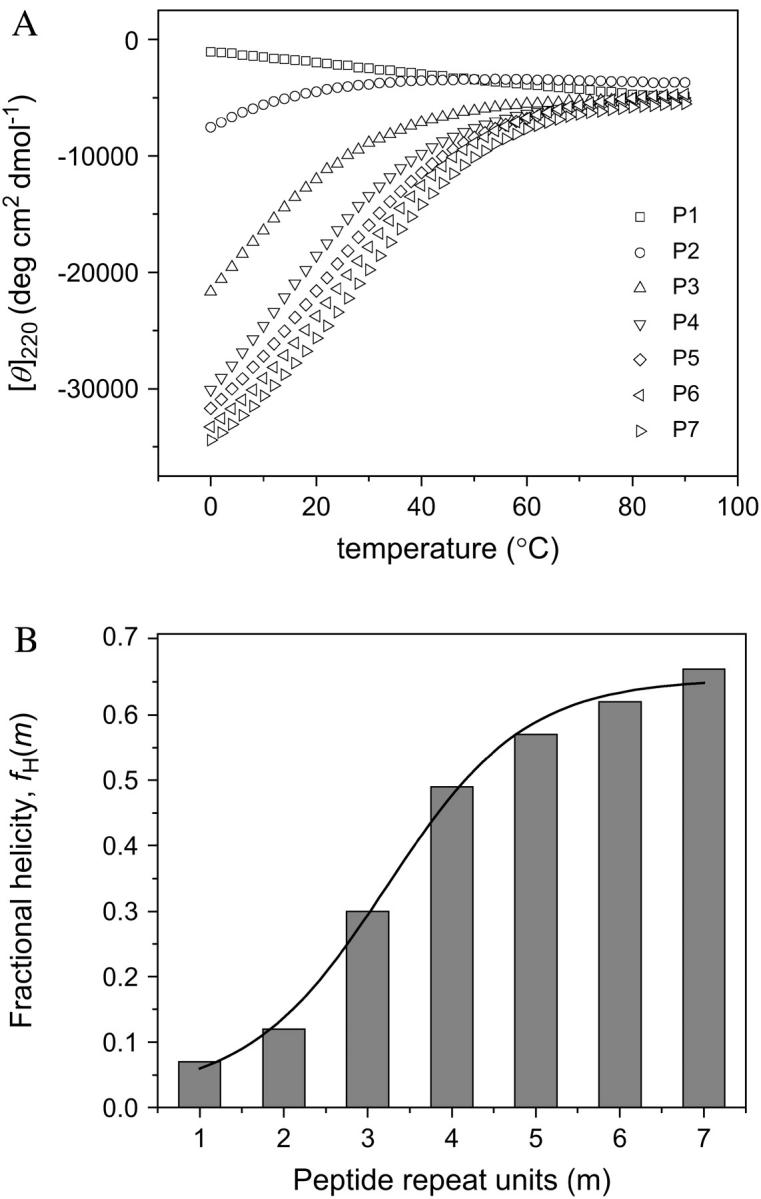
Thermally induced unfolding curves for the α-helical alanine-based peptides Ac-(AAKAA)_mY-NH₂, m = 1–7, determined by circular dichroism. (A) Circular dichroism data collected at 222 nm over a temperature range of 0–95°C; (B) Fractional helicity versus the number of peptide repeat units calculated for 24°C with the data from A. The fractional helicity was calculated by a procedure developed previously (37) for α-helical alanine-rich peptides of varying lengths in water. The buffer was 2 M KCl, 10 mM potassium phosphate, pH 7.5.

The CD spectra were used to calculate the fractional helicity (f_H) according to Eq. 1. The conversion of [θ]₂₂₂ to f_H requires knowledge of the ellipticity of both the complete coil ([θ]_C) and the complete helix ([θ]_H). Both values are slightly temperature-dependent (Eqs. 2 and 3) (37,44). The fractional helicity (f_H) computed at 24°C increases progressively with the peptide length (Fig. 1 B). For the longest peptide that we have used in this work (P7), we found a fractional helicity of 0.67. This result indicates that P7 has a helical core of ∼24 amino acids (44).

Molecular model of a folded peptide in a protein nanopore

The narrowest region of the αHL pore, a β-barrel structure which forms the transmembrane domain, is almost 50 Å long and ∼25 Å wide (based on C_α–C_α dimensions; Fig. 2 A). Because of the amino acid side chains, the actual diameter of the pore is ∼20 Å. The physical properties of the peptides used in this work are listed in Table 1. The widest cross-sectional diameter of the peptides (19 Å), which includes side chains of the lysine residues, is similar to the average diameter of the β-barrel (∼20 Å; Fig. 2, A and B). The average diameter of the peptides including their side chains is ∼13.5 Å, close to the diameter of the most constricted area of the αHL lumen (amino acids Met¹¹³ and Lys¹⁴⁷, Fig. 2 B) near position Glu¹¹¹ (∼15 Å).

FIGURE 2.

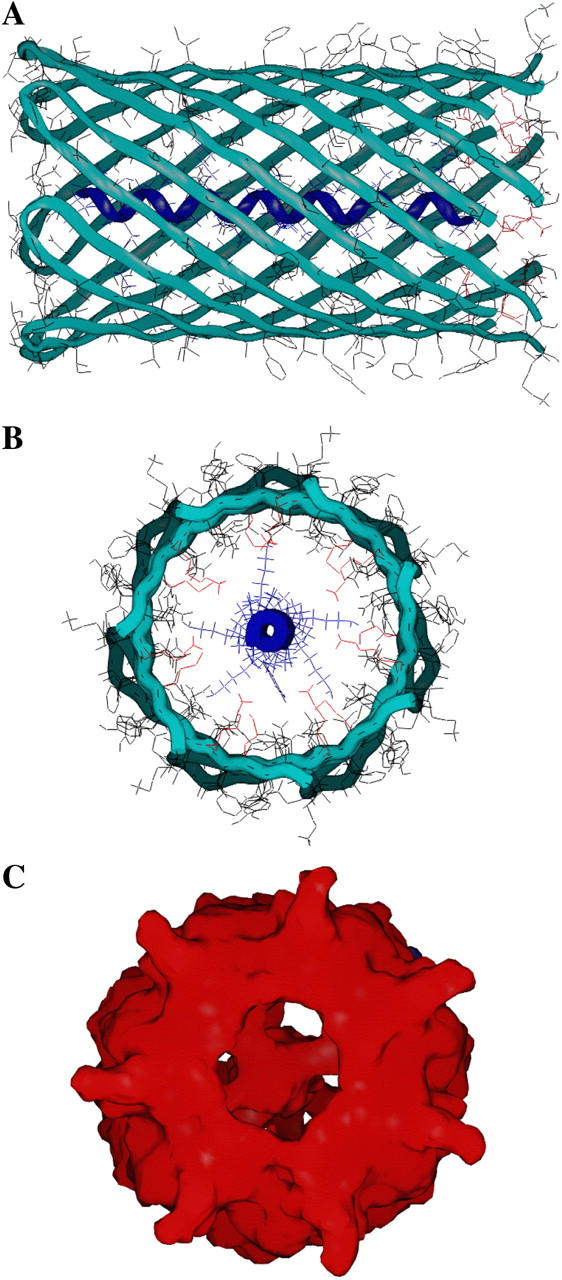
Model of an alanine-based α-helical peptide located in the β-barrel of the αHL pore. (A) A representation of Ac-(AAKAA)₅Y-NH₂ (the backbone is in dark blue) within the β-barrel (green); (B) Cross-sectional view of A in a backbone-bonds graphic representation. The α-helical peptide bonds are colored in blue. (C) Cross-sectional view of accessible surface of B. The large vestibule located within the aqueous phase, in the cis side of the lipid bilayer, is excluded from this figure.

TABLE 1.

Properties of the peptides used in this work

Peptide*	Net charge	Number of residues	Mw†(D)	α-helix length‡ (Å)	van der Waals volume‡ (Å3) × 10−3	Accessible volume‡(Å3) × 10−3
P2	+2	11	1050	16	0.78	2.4
P3	+3	16	1460	23	1.1	3.3
P4	+4	21	1870	31	1.5	4.2
P5	+5	26	2290	38	1.8	5.1
P6	+6	31	2700	46	2.1	6.0
P7	+7	36	3110	54	2.4	7.0

^*Pm is the peptide with the sequence Ac-(AAKAA)_mY-NH₂. The PDB format files of all peptides, forced to be α-helix, were generated in INSIGHT II, Ver. 98.0 (computer simulations, Accelrys, San Diego, CA).

^†The molecular masses of the peptides were determined by mass spectroscopy. The differences between the theoretical molecular masses and the actual molecular masses found by mass spectroscopy were <0.1% of the theoretical values.

^‡The α-helix length, van der Waals volume, and solvent-accessible volume were calculated with SPOCK software (40). The solvent-accessible volume is the volume calculated from the solvent-accessible surface area, which is traced out by the center of a water molecule as it rolls over the surface of the peptide (55). The van der Waals volume is the sum of all van der Waals spheres associated with all atoms in the peptide.

The peptides, as helices, vary in length from 16 Å (P2) to 54 Å (P7) (Table 1); the latter is comparable with the length of the β-barrel. For all peptides, the solvent-accessible volume (Table 1, last column) is smaller than the total solvent-accessible internal volume of the β-barrel. For example, P7 exhibits a solvent-accessible molecular volume of 7 × 10³ ų (Table 1), whereas the total internal volume of the β-barrel is ∼10⁴ ų (28). In general, the solvent-accessible volume overestimates the volume of a protein (in this case, the alanine-based peptide), but it underestimates the volume of a cavity within a protein (in this case, the β-barrel part of the lumen. (45). Therefore, there is a volume, between the peptide and the β-barrel wall, which enables the presence of solvated ions. Thus, the peptides do not produce a full single-channel blockade (see below). It is also true that the peptide may adopt a distorted helical structure when partitioning into the β-barrel region of the lumen. It is more likely that the peptide is loosely packed within the β-barrel.

Transient current blockades of the αHL pore by the alanine-based peptides

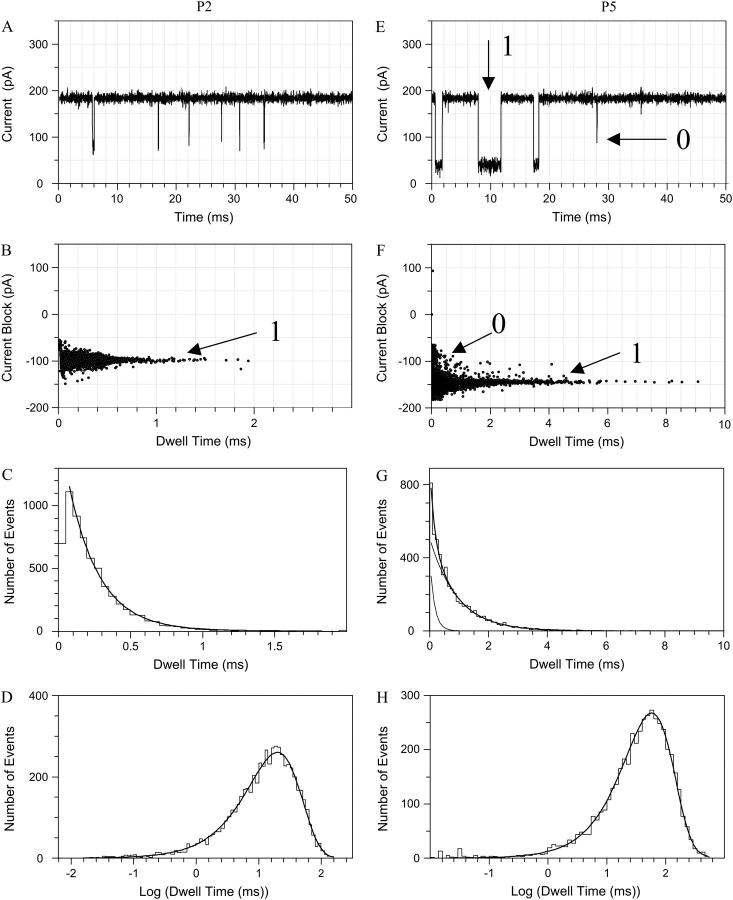
The addition of peptides of various lengths to the trans side of the bilayer, at low micromolar concentrations, produces reversible partial channel blockades of the αHL pore (Fig. 3 A, peptide P2 and Fig. 3 B, peptide P5), at a transmembrane potential of +100 mV.

FIGURE 3.

A typical single-channel recording from the αHL pore in the presence of 80-μM peptide applied to the trans side of the bilayer, at a holding potential of +100 mV. (A) Single channel recording in the presence of P2; (B) scatter plot of current block amplitudes versus dwell time for P2; (C) dwell-time histogram for P2 (τ_off−1 = 216 μs, P < 0.05); (D) semilogarithmic histogram of inter-event intervals for P2 (τ_on = 19.9 ms); (E) single channel recording in the presence of P5; (F) scatter plot of current block amplitudes versus dwell time for P5; and (G) dwell-time histogram for P5 (τ_off−0 = 83 μs and τ_off−1 = 779 μs). The two-exponential fit was statistically significant, as judged by a maximum likelihood ratio test (P < 0.05). (H) Semilogarithmic histogram of inter-event intervals for P5 (τ_on = 64.5 ms).

The partial channel blockades made by the peptides are greater in amplitude and duration for a long peptide than for a short peptide, as illustrated in the scatter plots of Fig. 3, B and F. Interestingly, a second current block peak could be detected for medium-length peptides (peak denoted by 0, Fig. 3 F). Both the amplitude of the current blockade and the dwell time associated with the latter peak are substantially smaller than the corresponding values of the highly populated peak (denoted by 1, Fig. 3 F). The dwell time histogram (τ_off) for P5 could be fitted by a two-exponential function (τ_off−0 = 78 ± 8 μs and τ_off−1 = 790 ± 35 μs, P₀/(P₀ + P₁) = 0.11 ± 0.01, n = 4, Fig. 3 G), which is in contrast with the one-exponential function for short peptides (for P2, τ_off−1 = 220 ± 14 μs, n = 4, Fig. 3 C). The value τ_off−0 corresponds to the low-amplitude blocks, and τ_off−1 to the more substantial blocks. The fits are judged by an LLR test (28,43) to compare the statistical significance of different models. The presence of two population peaks in the electrical recordings is also illustrated by the event amplitude histograms (Fig. 4). The peaks represent the amplitudes of the transient current blockades produced by the peptides when added to the trans side of the bilayer.

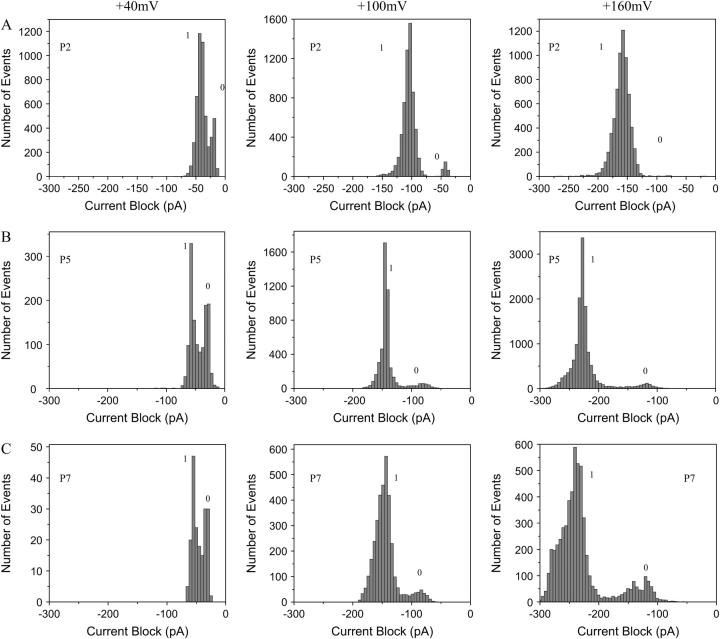
FIGURE 4.

Typical amplitude histograms that document transient single-channel current blocks of the αHL pore produced by cationic alanine-based peptides. (A) Peptide P2. (Left) Two distinct peaks are identified at a transmembrane potential of +40 mV, with current block amplitudes of A₀ = −20.1 pA and A₁ = −41.7 pA; (Middle) +100 mV, with A₀ = −42.5 pA and A₁ = −102.5 pA; and (Right) +160 mV, with A₀ = −75.2 pA and A₁ = −157.5 pA. (B) Peptide P5. (Left) +40 mV, with A₀ = −29.8 pA and A₁ = −55.0 pA; (Middle) +100 mV, with A₀ = −80.5 pA and A₁ = −141.5 pA; and (Right) +160 mV, with A₀ = −117.5 pA and A₁ = −227.5 pA. (C) Peptide P7. (Left) +40 mV, with A₀ = −32.5 pA and A₁ = −57.5 pA; (Middle) +100 mV, with A₀ = −83.5 pA and A₁ = −145.5 pA; and (Right) +160 mV, with A₀ = −130.5 pA and A₁ = −240 pA. In all cases, the bin size was 5 pA and the peptide concentration was 80 μM.

The probability of the events corresponding to peak 0 is strongly voltage- and peptide-length dependent (Fig. 4). For all peptides, excepting P7, we have found that this probability decreases with the transmembrane potential. The probability of the events corresponding to peak 0, P₀/(P₀ + P₁), increases with the peptide length. Taking into consideration the substantially lower current block amplitude (<50% of the current block amplitude of peak 1, Figs. 3 and 4) and the shorter duration of the 0 events, peak 0 can be attributed to peptides that partially enter the αHL pore, but fail to traverse it. The amplitude of the short events is “true” (i.e., not limited by filtering) because their mean duration is well above the risetime T_r, which is ∼33 μs (42).

The semilogarithmic τ_on histograms were fitted by a single-exponential function for all the cases examined in this work, as judged by an LLR test. For example, at +100 mV, for peptide P2, τ_on = 20.1 ± 0.7 ms, n = 4 (Fig. 3 D), whereas for peptide P5, τ_on = 65.3 ± 2.1 ms, n = 4 (Fig. 3 H). Separate τ_on values for the two classes of events (τ_on−0 = τ_on/f₀ and τ_on−1 = τ_on/f₁) were determined by using the relative event frequencies f₀ and f₁ (f₁ = 1–f₀), as determined from the τ_off histograms (28). For short peptides (m = 2,3) and high transmembrane potentials (≥140 mV), we were occasionally able to detect a second peptide within the αHL pore (data not shown here), also noticed with cyclic peptides (46).

Longer peptides are excluded by the αHL pore at low transmembrane potentials

The event frequency from the most populated peak (1, Fig. 3 F) is voltage- and peptide-length dependent (Fig. 5 A), and was normalized to the corresponding value for a transmembrane potential of +40 mV (Fig. 5 B). For long peptides, the event frequency is substantially reduced at low transmembrane potentials, indicating that the association rate constant k_on is low. Strikingly, the normalized event frequency of the longest peptide (P7) undergoes a substantial increase with the transmembrane potential (3015 ± 157% change between +40 and +180 mV, n = 4, Fig. 5 B). In contrast, the normalized frequency of the short peptide (P2) undergoes a smaller change (320 ± 12% change between +40 and +180 mV, n = 4, Fig. 5 B). Below, this is explained in terms of the Eyring-Woodhull formalism applied to the binding of a charged polymer to a protein pore.

FIGURE 5.

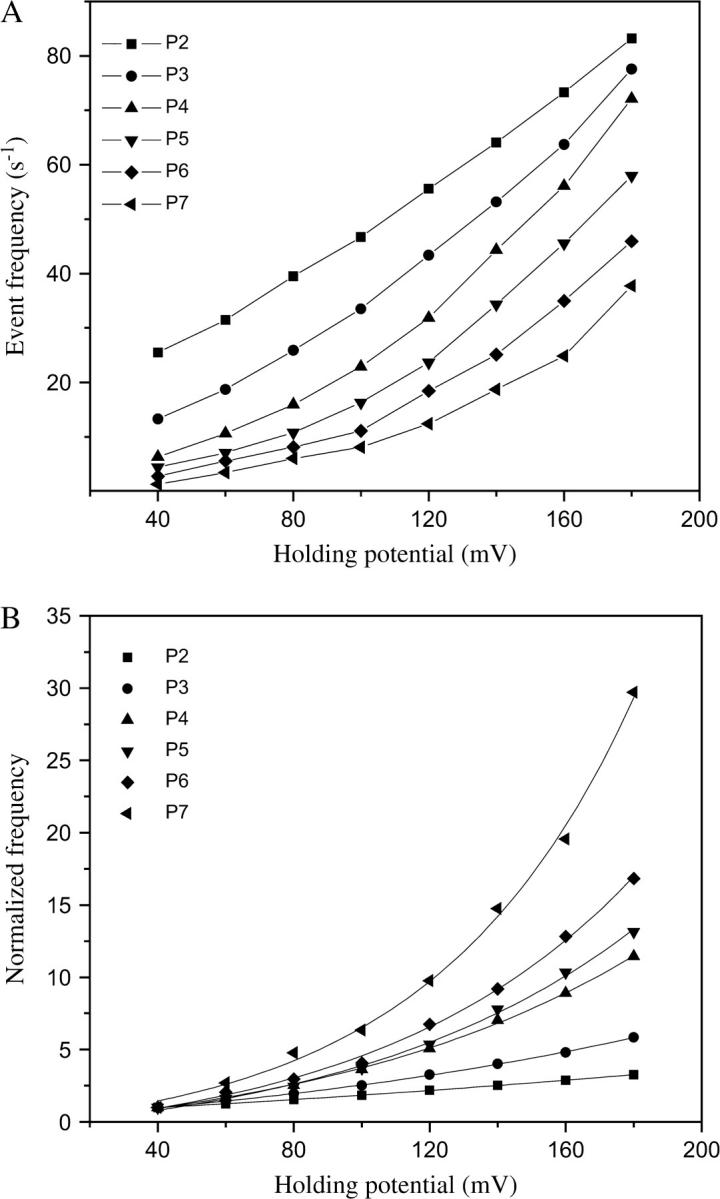
Event frequencies derived from the series of alanine-based peptides interacting with the αHL protein pore. The quantity of 80-μM peptide was added to the trans chamber. (A) Event frequency of the major peak 1; (B) normalized event frequency. The normalization was with respect to the event frequency for each peptide recorded at +40 mV.

Biphasic voltage-dependence of the residence time

For a 1.5-kDa peptide (P3, Table 1), the dwell-time (τ_off) corresponding to the most populated peak (1) is in the range of a few hundreds of microseconds, much longer than the interaction time determined for a neutral and highly flexible polymer such as PEG-1.5 kDa (∼50 μs) (28). In identical experimental conditions, a 1.5-kDa single-stranded oligonucleotide (carrying five negative phosphate charges) traverses the αHL pore in a time interval between several tens of microseconds to one-hundred microseconds (47). We found that the dwell time of the peptides has a biphasic voltage-dependence (Fig. 6). At lower transmembrane potentials, τ_off increases with potential, whereas at higher transmembrane potentials, τ_off decreases with potential. This result suggests a binding interaction between the αHL protein pore and cationic alanine-rich peptides. The value τ_off would be a monotonically decreasing function of the transmembrane potential in the absence of a peptide-pore interaction.

FIGURE 6.

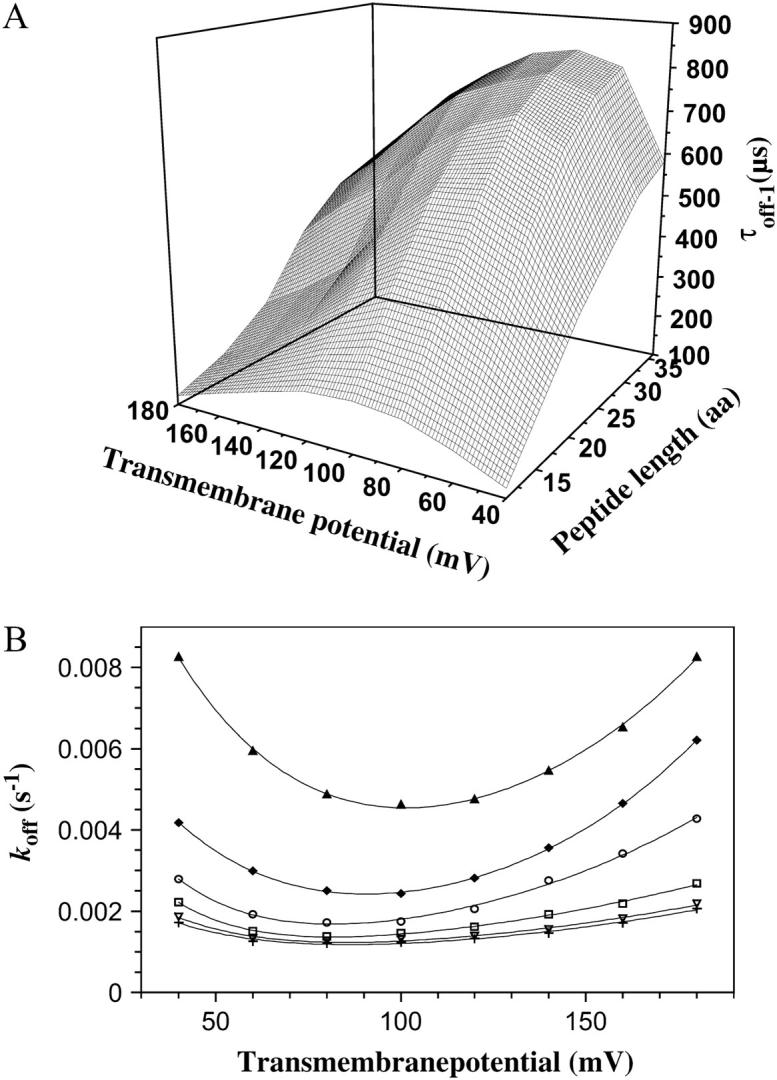
Voltage- and peptide-length-dependence of the dwell time. (A) Three-dimensional plot of the dependence of the peptide residence time τ_off−1 on the transmembrane potential and peptide length. (B) The kinetic constant k_off versus the transmembrane potential. The experimentally determined points for P2 (▴), P3 (♦), P4 (○), P5 (□), P6 (∇), and P7 (+) were fitted by a double-exponential function (see Eq. 10). The standard deviations are not included for the clarity of the plot.

Kinetic rate constants for the interaction between the peptide and the αHL pore

As shown in Table 2 (last two columns), the highly flexible polyethylene glycols (PEGs) bind almost 100-fold more weakly than the cationic alanine-rich peptides, in the dilute concentration regime.

TABLE 2.

Dependence of kinetic constants on peptide molecular mass

Peptide	kon−1 (M−1 s−1) × 10−5	koff−1 (s−1) × 10−3	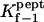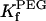* (M−1)	† (M−1)
P2	5.5 ± 0.6	7.5 ± 0.5	75 ± 7	1.8
P3	4.0 ± 0.5	4.4 ± 0.4	94 ± 6	1.2
P4	2.7 ± 0.7	3.3 ± 0.4	81 ± 5	0.78
P5	1.9 ± 0.3	3.2 ± 0.3	62 ± 5	0.52
P6	1.5 ± 0.3	2.9 ± 0.5	48 ± 5	0.34
P7	0.9 ± 0.2	2.8 ± 0.4	31 ± 3	0.23

^*The data were recorded at a holding potential of +100 mV in 1 M KCl, 10 mM Tris·HCl, 100 μM EDTA, pH 7.5, with 80 μM peptide in the trans chamber. Values are the mean ± SD from at least four single-channel experiments.

^†The formation constants between PEGs and the αHL pore were extrapolated from Fig. 7 of Movileanu et al. (28). The data were obtained under similar conditions to the peptide data.

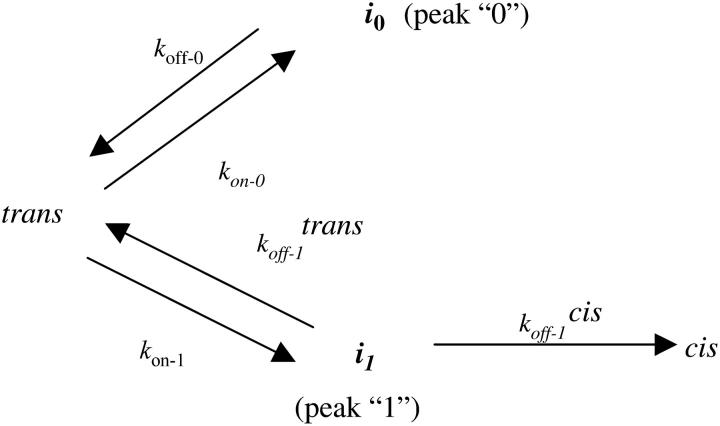
The dependences of the association and dissociation rate constants on peptide molecular mass, derived from single-channel recordings at +100 mV and 1 M KCl, are listed in Table 2. The single-channel data have been fit to a simple model for the interaction of the peptides with the αHL pore (Fig. 7). As mentioned above, the events that correspond to the state i₀ have a low-amplitude current blockade and a very short duration. This duration is much shorter than the translocation time for a polymer with identical molecular mass and charge (see above). These characteristics of state i₀, and its voltage- and peptide length-dependence (Figs. 3 and 4) suggest that the peptide, in this particular state, fails to traverse the αHL protein pore through to the cis side. The state i₁ (that corresponds to peak 1) is characterized by a high-amplitude current blockade, a long duration and a high frequency of occurrence (Fig. 7). In contrast, the extent of the current block amplitude associated with state i₁ suggests a full partitioning of the peptide into the αHL protein pore. Experiments with other polymers, such as DNA and RNA, carried out in similar conditions, show a substantial current blockade when they partition into the αHL protein pore (47,48).

FIGURE 7.

Kinetic model for the interaction of an alanine-based peptide with the lumen of the αHL pore. The two states i₀ and i₁ indicate the two classes of events, 0 and 1 (Fig. 3 F).

Voltage- and peptide-length-dependence of the kinetic rate constants for entry and exit at each of the openings of the pore

It is very instructive to analyze the voltage- and peptide length-dependence of state i_1. By using the Woodhull formalism (48,49), we can calculate the voltage (V)- and peptide length (L)-dependence of the individual rate constants for entry and exit at the cis and trans entrances associated with the most frequent state (i₁). Here, we define δ as the fraction of the transmembrane electrical potential between the trans side of the bilayer and the binding site (49,50). Sometimes this parameter is called the electrical distance to the binding site. However, δ should not be confused with a physical distance, which is harder to calculate because the voltage drop is not linearly dependent on the physical distance. The values of the electrical distance δ are listed in Table 3. The electrical distance is sensitive to the peptide length. Therefore, the binding site is dependent on the peptide length. For example, for the short peptide P2, the electrical distance is 0.39 ± 0.03, whereas for the long peptide P7, the electrical distance is only 0.18 ± 0.03 (Table 3). These values were determined by the assumption that the effective charge of a lysine side chain is reduced to 0.5 due to the screening effect of the high ionic strength of the buffer. This result suggests that the long peptides bind nearer the trans entrance than the short peptides. For the short peptides, we can assume that the central part binds to the β-barrel part of the lumen. However, for the long peptides that bind nearer the trans entrance, it is likely that the binding part is not located centrally.

TABLE 3.

The electrical distance (δ) and the distances from the binding site to the transition states for dissociation to the cis (δ_c) and trans (δ_t) sides, as measured from the trans entrance

Peptide	Net charge*	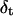†	δ2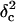
P2	+2	0.08 ± 0.01	0.39 ± 0.03	0.97 ± 0.03
P3	+3	0.07 ± 0.02	0.37 ± 0.03	0.83 ± 0.03
P4	+4	0.09 ± 0.01	0.32 ± 0.02	0.78 ± 0.04
P5	+5	0.09 ± 0.02	0.21 ± 0.02	0.66 ± 0.02
P6	+6	0.09 ± 0.01	0.19 ± 0.02	0.48 ± 0.03
P7	+7	0.10 ± 0.02	0.18 ± 0.02	0.42 ± 0.02

^*This is the net charge of the peptide in aqueous solution, and in the absence of a screening effect (pH 7.5).

^†The values are obtained with the assumption that the effective charge of a single lysine side chain within the pore is reduced to 0.5 due to the screening effect of the high ionic strength of the buffer. Values of the effective charge of a lysine residue higher than 0.6 would give unrealistic δ-values. Values are the mean ±SD from at least four single-channel experiments.

When the peptides bind to the αHL pore from the trans side, the association rate constant k_on−1 is given by (51)

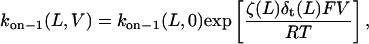(6)

where F, R, and T denote the Faraday's constant, the gas constant, and the absolute temperature, respectively. The values ζ(L) and δ_t(L) are, respectively, the effective charge of the peptide in the pore and the distance from the transition state for dissociation to the trans exit, as measured from the trans side of the bilayer. The values of δ_t(L) are also listed in Table 3. The low values of δ_t(L) indicates that the transition state for dissociation to the trans exit occurs near the trans entrance.

At room temperature,

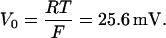(7)

Therefore, Eq. 6 can be written

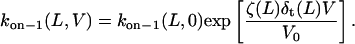(8)

Fitting the curves from Fig. 5 A with single exponentials, we can obtain the values for k_on−1(L,0). These values were also used for the calculation of partition coefficients at 0 mV, Π(L,0) (see below in Fig. 11). The U-shaped dependence of the rate constant k_off−1 on the transmembrane potential (Fig. 6 B) indicates that the peptides in state i₁ bind to the αHL pore and exit through either the trans or cis opening (Fig. 7). If the peptides exit through only the trans side, then k_off−1(V) would be a single-decay exponential (Eq. 10). Alternatively, if the peptides exit through only the cis side, then k_off−1(V) would be a single-growth exponential (Eq. 11). All these considerations are made by the assumption that the transit time is much shorter than the binding (residence) time.

FIGURE 11.

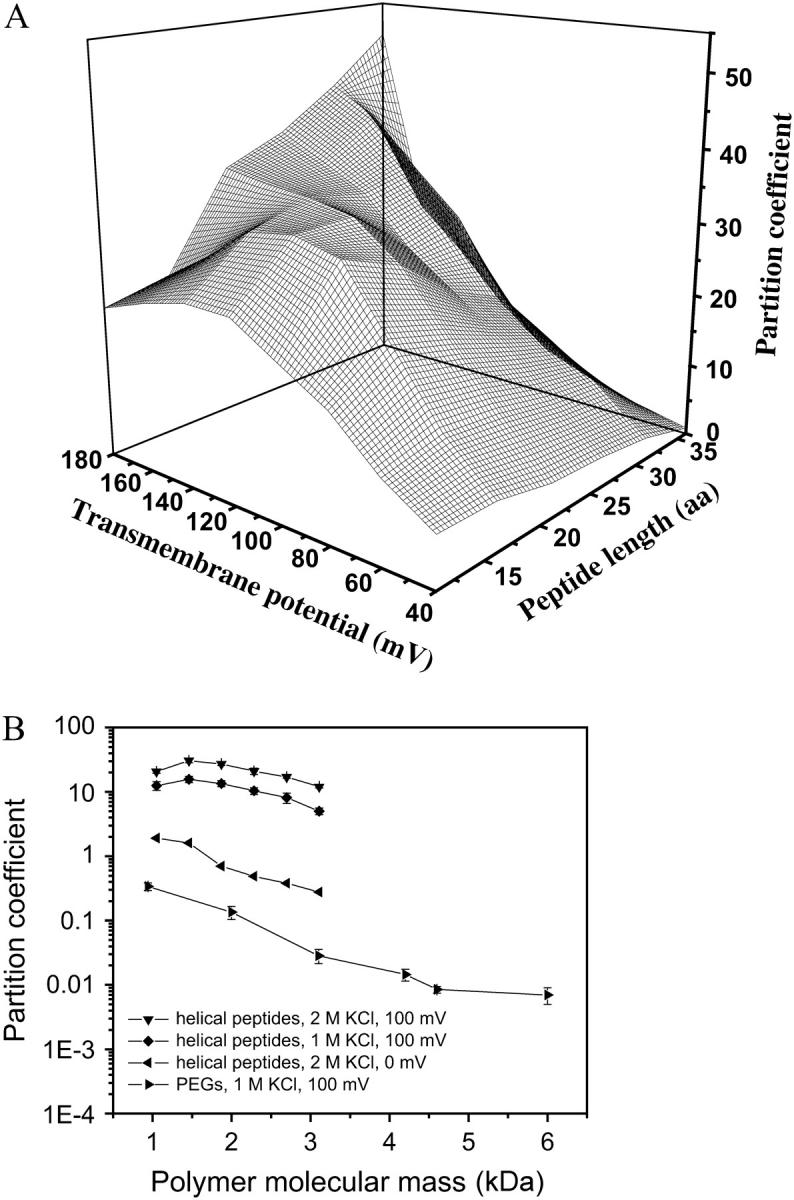
Partition coefficients of the alanine-based peptides between the αHL pore and bulk solution. (A) A three-dimensional plot of the partition coefficients versus transmembrane potential and peptide length calculated from data recorded in 2 M KCl. (B) Comparison of the partition coefficients between peptides in 2 M KCl (▾) and 1 M KCl (♦) and PEGs in 1 M KCl (▸), at +100 mV. The partition coefficients for the peptides in 2 M KCl, at 0 mV (◂) are also shown. The expression aa is the number of amino acids.

The dissociation rate constant associated with peak 1 (see the model in Fig. 7) is given by (51)

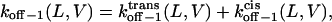(9)

with

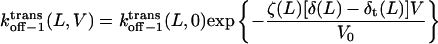(10)

and

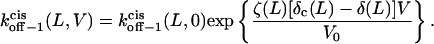(11)

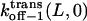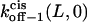Here and are the dissociation rates of the peptides through the trans and cis entrances, respectively, at 0 mV. The values δ(L) and δ_c(L) are the distances from the binding site and the transition state for dissociation to the cis side, respectively, as measured from the trans entrance. For each peptide length L, and a transmembrane potential V, we can determine the dissociation rate constant k_off−1 (L,V) (see Materials and Methods). From the fit of the family of curves k_off−1(L,V) (Eqs. 9–11, and Fig. 6 B) that correspond to individual peptides, we can obtain the dissociation rate constants to the cis and trans sides 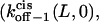and 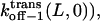respectively, at 0 mV. In addition, we can obtain the exponential coefficients of ζ(L)[δ (L) − δ_t(L)] and ζ(L)[δ_c(L) − δ (L)]. The goodness of all fits was satisfactory (R = 0.97 ± 0.02). These fitting parameters can be used to calculate the dissociation rate constants 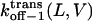and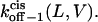

Finally, we can examine the relative exit frequency through the trans and cis sides, respectively, as

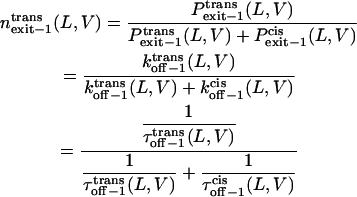(12)

and

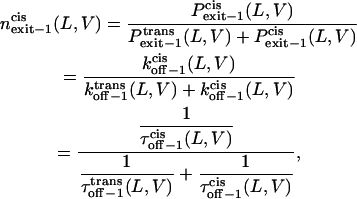(13)

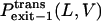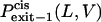where and are the probabilities that the peptides dissociate through the trans and cis sides, respectively. By using the relations in Eqs. 10–13, the relative exit frequencies through the trans and cis sides are plotted as two-dimensional surfaces (Fig. 8, A and B). A two-dimensional plot in Fig. 8 was obtained from a series of one-dimensional plots for each value of L, joined to make a surface.

FIGURE 8.

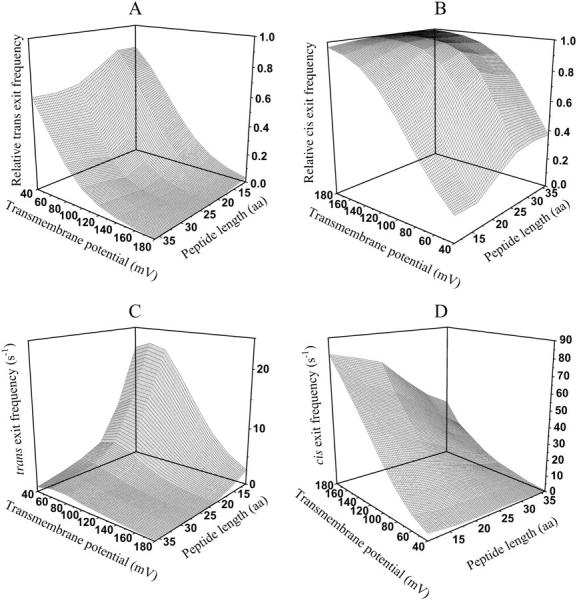
Three-dimensional plots of the relative and absolute frequencies (from peak 1) for the exit of the peptides through either the cis or trans entrance of the αHL pore as functions of transmembrane potential and polymer length. (A) Relative trans exit frequency; (B) relative cis exit frequency; (C) trans exit frequency; and (D) cis exit frequency. The expression aa is the number of amino acids. The other conditions are the same as those in Fig. 5.

Therefore, the exit frequencies through the trans and cis entrances are given by

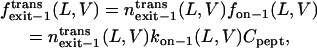(14)

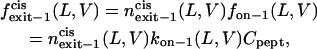(15)

where f_on−1(L,V) is the frequency of on−1 events, and C_pept is the peptide concentration at the trans side of the bilayer. For all peptides, at voltages higher than +80 mV, the cis exit frequency is greater than the trans exit frequency (Fig. 8, C and D). A strong voltage-dependence was observed for the trans exit frequency in the case of the shorter peptides, but not for the longer peptides (Fig. 8 C). A simple interpretation is that the trans exit frequency is very low for long peptides, as a result of a large transition state free energy. In contrast, for short peptides, the trans exit frequency is large, as a result of a small transition state free energy (Fig. 8 C). The cis exit frequency is voltage-dependent for all the peptides examined in this work (Fig. 8 D). The exit frequency through the cis side is substantially enhanced at very high transmembrane potentials (Fig. 8 D). The dissociation rate constants 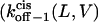and 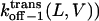are plotted in Fig. 9. For short peptides, both 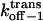and 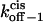are large, as a result of small transition state free energies for the trans and cis exits, respectively. In contrast, for long peptides, the dissociation rate constants are small.

FIGURE 9.

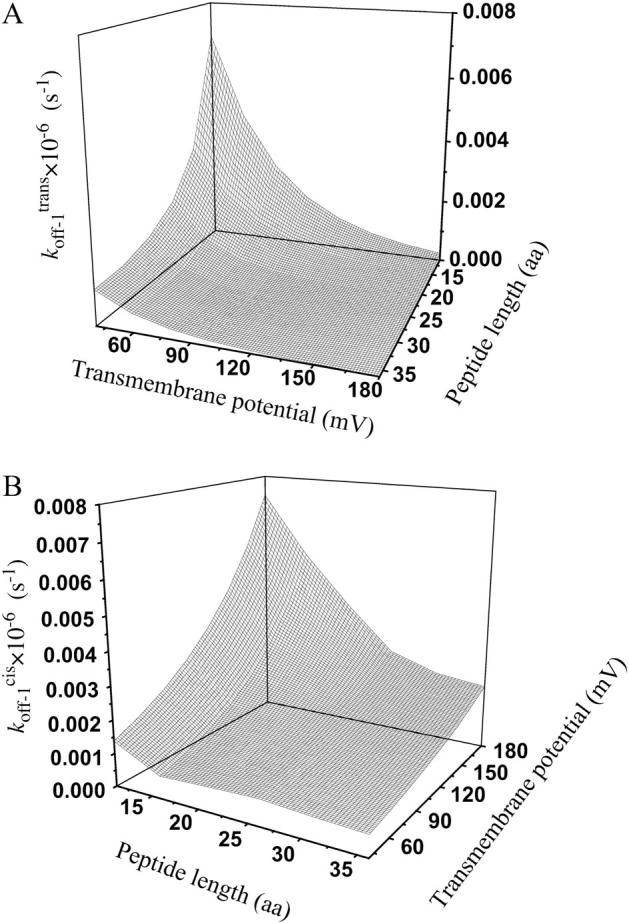
Three-dimensional plots of the off−1 rate constants associated with exit of the peptides through either the cis or trans entrance of the αHL pore as functions of transmembrane potential and polymer length. (A) 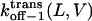; (B) 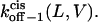The expression aa is the number of amino acids. The other conditions are the same as those in Fig. 5.

The free energy barriers and free energy increments for the transitions of the peptide in the αHL pore

Using Eyring's transition state theory (52, 53), the rate constants that correspond to 0 mV (Eqs. 8–11) can be written (49) as

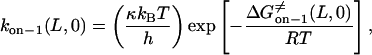(16)

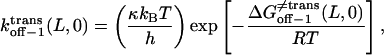(17)

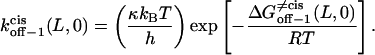(18)

Here, h, k_B, and T are the Planck constant, the Boltzmann constant, and the absolute temperature, respectively. The value κ is the transmission coefficient. We can obtain the increment in activation free energy per peptide repeat for each of the transitions, at 0 mV,

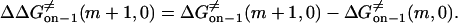(19)

Here, m is the number of peptide repeats, and

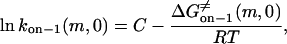(20)

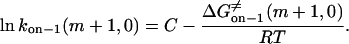(21)

In Eqs. 20 and 21, C is a constant.

Therefore,

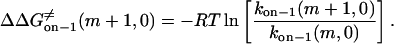(22)

Similarly,

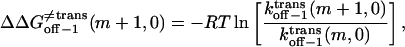(23)

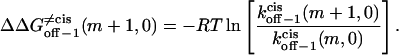(24)

From Eqs. 8–11 and 16–18, the transition state free energies are given by the relations

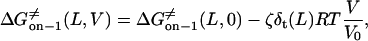(25)

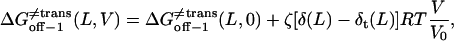(26)

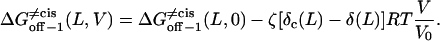(27)

If we consider the Eyring frequency factor,

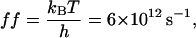(28)

then we can calculate ΔG_on−1 (L,0), and

However, ff from Eq. 29 is only valid for elementary transitions over a distance less than the mean free path of 0.1 Å (52). Therefore, we chose the more suitable value of 10⁹ s⁻¹, which corresponds to diffusional transitions over a distance of 1 nm (52). The activation free energies (Eqs. 26–28), as well as the corresponding rate constants at 0 mV, are plotted in Fig. 10. The kinetic data obtained in this work are consistent with a two-barrier, single-well free energy profile, which has been previously proposed for the voltage-dependent current block of anthrax protective antigen channels by tetraalkylammonium ions (54).

FIGURE 10.

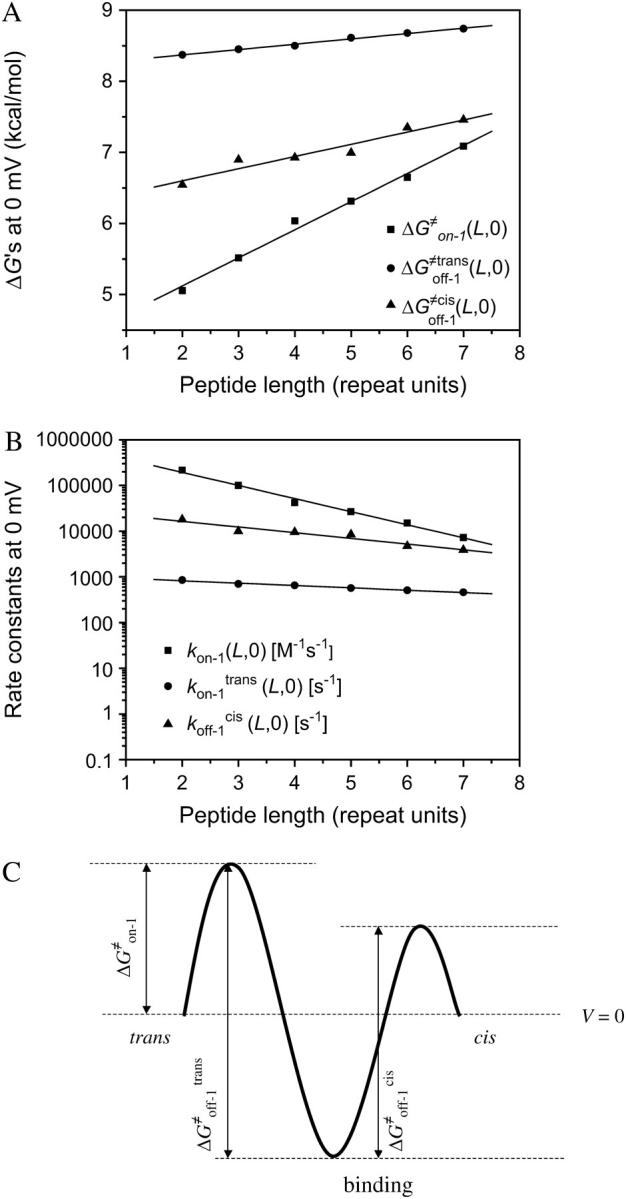
The free energies 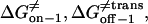and 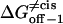at 0 mV, and their corresponding kinetic rate constants k_on−1, 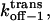and 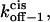as a function of peptide length. (A) The free energies at 0 mV; (B) the kinetic rate constants at 0 mV; and (C) free energy barrier model for the αHL protein pore with a single binding site for alanine-rich peptides at zero transmembrane potential.

Fig. 10 C shows a free energy diagram for three positions of the peptide, in the absence of an applied transmembrane potential (V = 0). The three positions are the trans side, the binding site located in the β-barrel part of the αHL pore, and the cis side. In passing from free aqueous solution on the outside of the membrane (the trans side) to the binding site within the channel, the peptide has to cross a trans energy barrier. Importantly, the location of the energy well that corresponds to the binding site (Fig. 10 C) is dependent on the peptide length (see details in Table 3). The peptide has to overcome a cis energy barrier, when passing from the binding site to the cis aqueous solution, or a trans energy barrier, when returning from the binding site to the trans side of the bilayer. The transition state free energy data shown in Fig. 10 A indicate that the trans barrier is higher than the cis barrier. This is closely similar to the free energy profile corresponding to the voltage-dependent block of anthrax channels by tetraalkylammonium ions (54).

From the relations in Eqs. 16–18, the free energies at 0 mV are given by

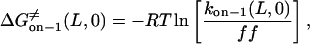(29)

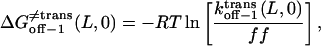(30)

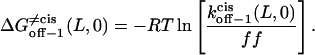(31)

The plots of the kinetic rate constants and the corresponding transition state free energies, at zero transmembrane potential, are shown in Fig. 10. In the absence of a transmembrane potential, a relatively greater change in the k_on value than in both k_off values, versus the length of the peptide, was calculated.

Using the relations in Eqs. 25–27, we can express the final forms for the voltage- and length-dependence of the activation free energies of on, off−1 trans, and off−1 cis events.

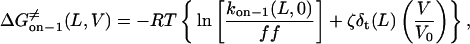(32)

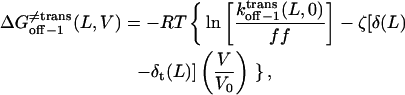(33)

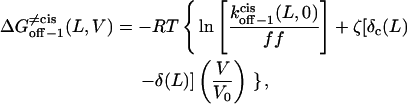(34)

where the parameters k_on−1(L,0), 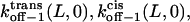ζδ_t(L), ζ[δ(L) − δ_t(L)], and ζ[δ_c(L) − δ(L)] are obtained by direct fitting of k_on−1(L,V) and k_off−1(L,V) (Eqs. 8–11, and Figs. 5 and 6).

Partition coefficients

The equilibrium association constant that corresponds to the state i₁ is given by

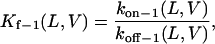(35)

where k_on−1 and k_off−1 are given above (Eqs. 8–11). Therefore, the partition coefficient is a voltage- and peptide-length-dependent function (28):

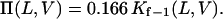(36)

The two-dimensional plot of Π(L,V), obtained from experimentally determined values of k_on and k_off (not from fittings; Eq. 35), is shown in Fig. 11 A. The partition coefficients of the peptides into the αHL pore are larger than unity in all cases (Fig. 11 A). Furthermore, the value of the partition coefficient varies substantially with both transmembrane potential and peptide molecular mass. At low transmembrane potentials (e.g., +40 mV), the partition coefficient decreases with the length of the peptide (Fig. 11 A). This effect is dominated by a reduction in k_on−1 (Figs. 5 A and 10 B). This situation is similar to the case of the neutral and flexible PEGs, which undergo a partitioning decrease as the molecular mass increases (see also the discussion below) (27,28,32).

Conversely, at high transmembrane potentials, the partition coefficient increases substantially with the length of the peptide (Fig. 11 A). In this latter case, both k_on−1 and k_off−1 are peptide-length-dependent: there is a reduction in k_on−1 with the peptide length (Fig. 5 A), but there is also a relatively greater decrease in k_off−1 (Fig. 6 B). Overall, high partition coefficients at increased transmembrane potentials are observed, because ΔG(V) = −ζ(L) δ(L)FV predominates with the peptides. For short peptides, the biphasic behavior of the partition coefficient is due to the strong voltage-dependence of k_off−1 (Fig. 6 B), and also because of a relatively greater change in k_on−1 (Fig. 5 B).

The partition coefficient Π(L,0) was calculated using Eqs. 16–18, 35, and 36 (Fig. 11 B). Interestingly, the alanine-based peptides partition into the lumen of the pore according to a simple linear scaling law at zero transmembrane potential, given by lnΠ(L,0) ∼ −0.98 M_w (Fig. 11 B).

Comparison with other polymers

A comparison of the partitioning data for α-helical cationic peptides and neutral PEGs is presented in Fig. 11 B. The alanine-based peptides exhibit at least a 10-fold higher partition coefficient compared with the neutral and highly flexible PEGs, at +100 mV (Fig. 11 B, the second and fourth curves from the top). For PEGs with a molecular mass <4 kDa, the increment in the Gibbs standard free energy with the polymer length is ΔΔG ≅ 1.2 k_BT/kDa (28). In this work, we calculated an average value for ΔΔG ≅ 0.79 k_BT, which is the Gibbs standard free energy increment that corresponds to an increase in peptide length by one repeat unit. The peptide unit is AAKAA, with a molecular mass of 0.41 kDa. Therefore, the standard free energy for the peptide P7 is 4.0-k_BT greater than that corresponding to the peptide P2. If ΔΔG ≅ 0.79 k_BT, the Gibbs standard free energy increment of ΔΔG ≅ 2.0 k_BT/kDa. This value is greater than the corresponding value for the PEGs, i.e., the partition coefficients for the alanine-based peptides at 0 mV are slightly higher than the partition coefficients for PEGs at 100 mV (Fig. 11 B).

Similar biphasic voltage-dependent behavior of k_off has been observed during the single-channel recordings of the αHL pore in the presence of micromolar concentration of cyclic peptides (46). By contrast, the dwell times of cyclic peptides were quite long, certainly much longer than one would expect for a weakly interacting polymer (e.g., a PEG) with a protein pore (28).

Since the αHL pore maintains an open state for long periods even in extreme conditions (e.g., pH, salt, temperature, etc.) (55), it should be possible to examine the interaction between unfolded peptides and the lumen of the αHL pore. In the present work, we cannot say whether the peptides undergo conformational transitions when they enter the lumen of the αHL pore, but the uniform current blockades do suggest that single conformations are adopted within the pore. Chemical denaturants or temperature ramps could be used to determine the associated enthalpy and entropy changes. A fundamental issue that will be addressed in future experiments is whether the peptides bind to the αHL pore in folded, partially folded, or unfolded conformations. Of course, more computation and theory is required to determine the limits of existing electrical recording instrumentation for probing subtle conformational changes of the translocating peptide. The single-channel current resolution (signal/noise ratio) is important in addressing this issue. First, the rate constant for folding-unfolding transitions might have values in the submicrosecond range (56), which is too fast for the single-channel recording capability. Second, some conformational changes of the confined polypeptide chain might be electrically silent, or simply not detectable, as previously noticed in experiments with single PEGs (21) and elastinlike peptides (Y. Jung, L. Movileanu, and H. Bayley, unpublished) anchored within the large vestibule of the αHL pore. Furthermore, the relationship between confinement and stability of the folded state of the peptide is not simple, because water structure may change under nanometer-scale confinement (57), thus altering the interactions stabilizing the native state.

In this work, we examined the exchange between cationic α-helical alanine-based peptides between the bulk aqueous phase and the transmembrane β-barrel of the αHL protein pore, at the single-molecule level. The peptides, which include bulky lysine side chains, bind more strongly to the pore (formation constant K_f ∼ tens of M⁻¹) than the highly flexible PEGs (K_f ∼ M⁻¹). We think that the binding is enhanced at increased transmembrane potentials, because ΔG(V) = −ζ(L)δ(L)FV dominates with the peptides. We also used the Woodhull-Eyring formalism to rationalize the values measured for the association and dissociation rate constants, k_on and k_off, and to separate the values of k_off into individual rate constants for entry and exit through each of the openings of the protein pore. Therefore, we were able to design a semiquantitative model for the peptide permeation through a β-barrel pore.

Comparison with other peptide translocation systems

Little has been accomplished to clarify the energetic balance that must be overcome for protein translocation through a β-barrel pore in a membrane. The experiments presented in this article have relevance for more complex biological processes such as the translocation of cationic amphiphilic polypeptides across TOM channels located in mitochondrial outer and inner membranes (3,7) and the interaction of transit peptides with the chloroplast protein import channel TOC75 (5). For example, the protein translocases of mitochondrial and chloroplast membranes appear to be β-barrel-type channels (6). In addition, the targeting region of a translocating protein, which is located at the amino-terminus, folds as a cationic amphiphilic α-helix (58,59). In our molecular model, the lysine side chains in the peptide chain (average diameter is 19 Å) and the side chains on the β-barrel wall (average internal diameter is 20 Å) seem to be in intimate contact. Such interactions may occur frequently in nature, as the N-terminus α-helical region of the precursor proteins is rich in positively charged side chains (lysine and arginine residues) (58,59), and the diameter of the translocases is ∼20 Å (3,5,7).

The αHL pore may represent a suitable model to examine polypeptide translocation through a β-barrel pore. The protein translocation channels in mitochondrial and chloroplast membranes are β-barrels that exhibit a moderate cation selectivity (P_K/P_Cl ∼ 5 and ∼7.7 for TOM20 and TOM40, respectively) (3,7), or a stronger cation selectivity (e.g., P_K/P_Cl ∼ 14.3 and 16.0 for TOC75 in outer chloroplast membrane and TIM in inner mitochondrial membrane, respectively) (4,60). By contrast, the αHL protein is a slightly anion selective channel with P_K/P_Cl ∼ 0.65 (61). However, previous mutagenesis work with the αHL protein demonstrated that several additional charges, that change the ionic selectivity of the pore, can be tolerated throughout the β-barrel part without significant alteration in channel activity and stability (62,63). We suggest that the αHL protein may be employed as a robust and versatile β-barrel protein pore for examining peptide translocation in the absence of ATP-driven cellular factors, but with tunable driving forces (e.g., electrochemical, pH gradients), binding interactions between the polypeptide and the lumen (e.g., designed acidic binding sites), unfolding triggers (temperature, urea, guanidinium chloride), and geometric and steric constraints (e.g., a modifiable constricted region).

APPENDIX: SYMBOLS AND ABBREVIATIONS

αHL	α-Hemolysin
β-PFT	β-Barrel pore-forming toxins
CD	Circular dichroism
[pept]	Peptide concentration in bulk solution
dsDNA	Double-stranded DNA
δ	Distance from the binding site, as measured from the trans side of the bilayer
δc	Distance from the transition state for dissociation to the cis exit, as measured from the trans side of the bilayer
δt	Distance from the transition state for dissociation to the trans exit, as measured from the trans side of the bilayer
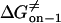	Transition state free energy that corresponds to kon−1
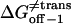	Transition state free energy that corresponds to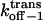
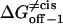	Transition state free energy that corresponds to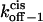
ΔΔG(m+1)	Increment in activation free energy due to increase of the peptide length from m to m+1 repeat units
f0	Event frequency that corresponds to peak 0 (minor peak)
f1	Event frequency that corresponds to peak 1 (major peak)
ff	Eyring frequency factor
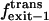	Exit frequency to the trans side of the bilayer
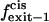	Exit frequency to the cis side of the bilayer
fH	Fractional helicity of the peptide
F	Faraday constant
h	Planck's constant
κ	Transmission coefficient
kB	Boltzmann's constant
kon−1	Association rate constant
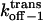	Dissociation rate constant through the trans entrance
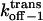	Dissociation rate constant through the cis entrance
Kf	Equilibrium association constant
l	Path length
L	Peptide length
LLR	Log likelihood ratio test
m	Number of repeat units in the polypeptide chain
m°	Measured ellipticity
Mw	Peptide molecular mass
n	Number of amino acids in the polypeptide chain
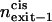	Relative exit frequency through the cis side of the bilayer
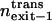	Relative exit frequency through the trans side of the bilayer
NAV	Avogadro's number
OmpF	Outer membrane protein F
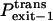	Probability that the peptides dissociate through the trans side of the bilayer
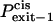	Probability that the peptides dissociate through the cis side of the bilayer
PEG	Polyethylene glycol
[pept]*	Effective molar concentration of a single peptide inside the β-barrel
Π	Partition coefficient
R	Gas constant
ssDNA	Single-stranded DNA
SDS-PAGE	Sodium dodecyl sulphate polyacrylamide gel electrophoresis
[θ]222	Mean molar residue ellipticity at 222 nm
[θ]H	Mean molar residue ellipticity for the complete helix
[θ]C	Mean molar residue ellipticity for the complete coil
T	Absolute temperature
Tr	Risetime of the Bessel filter
TIM	Preprotein translocase of the inner mitochondrial membrane
TOM	Preprotein translocase of the outer mitochondrial membrane
TOC	Preprotein translocase of the outer chloroplast membrane
τ	Dwell time
τon	Inter-event interval (unoccupied state)
τoff	Event duration (of occupied state)
V	Transmembrane potential
Vbarrel	Internal volume of the β-barrel
ζ	Effective charge of the peptide in the pore