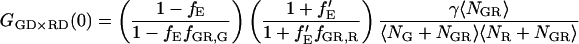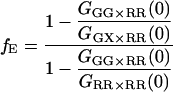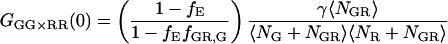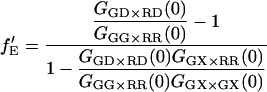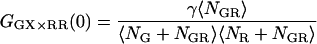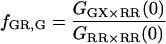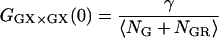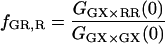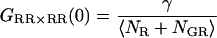Pulsed Interleaved Excitation

Abstract

In this article, we demonstrate the new method of pulsed interleaved excitation (PIE), which can be used to extend the capabilities of multiple-color fluorescence imaging, fluorescence cross-correlation spectroscopy (FCCS), and single-pair fluorescence resonance energy transfer (spFRET) measurements. In PIE, multiple excitation sources are interleaved such that the fluorescence emission generated from one pulse is complete before the next excitation pulse arrives. Hence, the excitation source for each detected photon is known. Typical repetition rates used for PIE are between ∼1 and 50 MHz. PIE has many applications in various fluorescence methods. Using PIE, dual-color measurements can be performed with a single detector. In fluorescence imaging with multicolor detection, spectral cross talk can be removed, improving the contrast of the image. Using PIE with FCCS, we can eliminate spectral cross talk, making the method sensitive to weaker interactions. FCCS measurements with complexes that undergo FRET can be analyzed quantitatively. Under specific conditions, the FRET efficiency can be determined directly from the amplitude of the measured correlation functions without any calibration factors. We also show the application of PIE to spFRET measurements, where complexes that have low FRET efficiency can be distinguished from those that do not have an active acceptor.

INTRODUCTION

Fluorescence has become a powerful tool for investigating the dynamics of biological systems and biomolecules. The availability of high sensitivity photodetectors and small probe volumes obtainable with visible light have contributed to the development of ultrasensitive fluorescence spectroscopy and microscopy methods. Ultrasensitive fluorescence methods allow one to investigate the interactions and dynamics of biomolecules with high accuracy even on the level of single fluorophores. Such ultrasensitive methods include fluorescence correlation spectroscopy (FCS) (1,2) and fluorescence cross-correlation spectroscopy (FCCS)(3,4), burst analysis (5), single-molecule studies (6), single-pair fluorescence resonance energy transfer (spFRET) experiments (7–11), and single virus tracing (12,13).

In ultrasensitive fluorescence measurements, it is important to maximize the information retrievable with each photon. The more information that is recorded during a measurement, the more potential exists in the analysis. In fluorescence spectroscopy, the information available from the photon is its absolute arrival time (intensity information), the position in space where the photon was detected (image information), the energy of the photon (spectral information), its polarization (orientational information), and the delay between excitation and fluorescence emission (lifetime information). Different methods have been developed that utilize various combinations of the available information. Information over the duration of the fluorophore in the excitation state is used in time-gated FCS in connection with the absolute arrival time of the photon to remove background (14,15), to investigate the homogeneity of a sample, and to study the dynamics of heterogeneous distribution (16). Enderlein uses the same information in time-resolved FCS to resolve multiple fluorescence species with FCS (17). In multiparameter fluorescence spectroscopy, all of the above information is recorded and utilized, when necessary, in the analysis (18,19).

Additional information is available when multiple excitation sources are used. Alternating laser excitation (ALEX) was introduced by Kapanidis and colleagues (20). They interleaved two excitation sources on a timescale between 25 and 3000 μs. By switching between both excitation sources on a timescale faster than diffusion of the particle through the probe volume, they can determine the labeling stoichiometry of individual complexes. Recently, they have shown how the accuracy of spFRET measurements can be improved by using ALEX to determine the ratio of detection efficiencies between the donor and acceptor channels (21).

With pulsed interleaved excitation (PIE), we have pushed the alternation timescale into the nanosecond regime. For the experimental conditions given in this article, many excitations pulses from all excitation sources illuminate the sample between the detection of each photon. Hence, on the microsecond timescale, the measurements with the various excitation sources can be considered to be simultaneous. The faster timescale of the interleaved excitation allows FCS experiments to be performed with submicrosecond resolution in addition to all the other possibilities of ALEX. The additional information available from knowing which excitation source is responsible for each detected fluorescence photon provides the capability of detecting multiple fluorophores with a single-channel system. This is useful when measuring colocalization of single molecules, as the same detection optics can be used for imaging all colors and no additional transformation needs to be made to map the image of one channel onto another. PIE can also be used to remove spectral cross talk in a multichannel system, giving better contrast in the longer wavelength channel or channels. PIE-FCCS increases the sensitivity of FCCS by removing any residual cross talk from the cross-correlation function (CCF). FCCS measurements on complexes undergoing FRET can be analyzed quantitatively using PIE, assuming direct excitation of the acceptor at the donor excitation wavelength is negligible, and the detection efficiencies of the donor and acceptor channels are the same. The absolute FRET efficiency can be calculated from the amplitude ratio of correlation functions available from the PIE-FCCS experiments without calibration. As in ALEX, PIE can also be used to determine the labeling stoichiometry in spFRET and perform more accurate FRET measurements by including only samples containing an active donor and acceptor in the analysis.

THEORY

Pulsed interleaved excitation

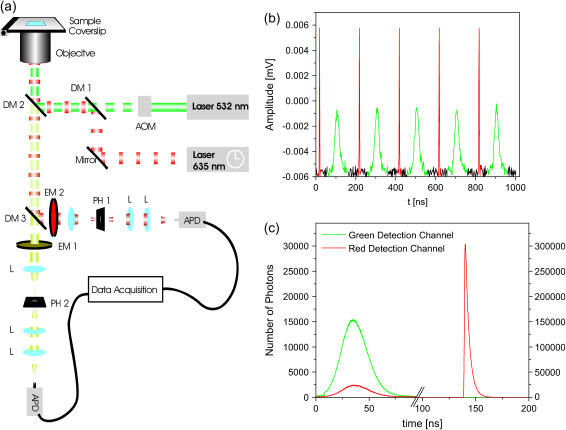
PIE is the use of two or more pulsed excitation sources, alternated with sufficient delay that all the emitted photons from one laser pulse are detected before the next pulse of a different color arrives. A schematic of the apparatus is shown in Fig. 1 a. In our system, we use two excitation sources: a pulsed laser diode at 635 nm (Sepia LDH635, PicoQuant, Berlin, Germany) and a continuous-wave, frequency-doubled Nd:YVO₄ laser (532 nm, Millennia, Spectra Physics, Darmstadt, Germany), which is pulsed by an acousto-optic modulator (N23080-2-LTD, NEOS Technologies, Melbourne, FL). The lasers are synchronized by a master clock and one source is delayed by ∼100 ns with respect to the other. The excitation pulse train recorded with a photodiode is shown in Fig. 1 b. The repetition rate used in the measurements reported here was 5 MHz, although with two, subnanosecond pulsed laser sources, the frequency could be increased. The ultimate limitation in the repetition rate is the interval necessary to collect the photons after excitation, which depends on the lifetime of the fluorophore. Fluorescence decay times are typically 2–10 ns. To collect 99.9% of the photons emitted from a molecule with a fluorescence lifetime of 2.5 ns before exciting with the alternate color, the interval between excitation sources must be at least 18 ns, yielding an overall repetition rate of 27 MHz when using two excitation sources. The photons are detected using time-correlated single-photon counting (TCSPC). The data acquisition card and excitation sources are synchronized with the master clock such that the excitation source responsible for generating the detected photon is encoded into the arrival time of the photon. Fig. 1 c shows the histogram of arrival times with respect to the clock signal for a mixture of Atto532 and Atto647 in buffered solution. Green and red histograms are for the green and red detection channels, respectively. Fluorescence generated from the broad 50-ns green excitation pulse (shown in Fig. 1 b) was collected between 0 and 91.2 ns (Fig. 1 c) whereas fluorescence emission from the Atto647 was collected from 130 to 180 ns (Fig. 1 c). The exponential decay of Atto647 is clearly seen (τ = 2.5 ns) due to the subnanosecond excitation pulse width used, whereas the lifetime information for Atto532 is lost. The use of two, subnanosecond pulsed lasers would allow additional capabilities of PIE by including lifetime information of the fluorophores. From the arrival time, the excitation source for each photon is known and this additional information can be utilized in the data analysis.

FIGURE 1.

Experimental setup (a) Schematic of the dual-color confocal microscope with pulsed interleaved excitation sources. In the diagram, AOM refers to the acousto-optic modulator, DM to the dichroic mirrors, EM to the emission filters, PH to the pinholes, L to the lenses, and APD to the avalanche photodiodes. (b) The excitation pulse train as measured by a photodiode. The repetition rate of the laser pulses was 5 MHz. The green and red excitation pulses are colored accordingly. (c) The histogram of photon arrival times with respect to the master clock is shown in green and red for the green and red detection channels, respectively. Photons arriving in the first ∼100 ns have been generated by the green laser whereas the photons arriving between 130 and 180 ns were generated by the red excitation pulse.

PIE can also be performed on systems without TCSPC. In this case, the data acquisition card is run at a frequency that is an integer multiple of the repetition rate of the lasers. The timing of the excitation pulses are then arranged such that the fluorescence coming from the different excitation pulses are detected in different time bins. The simplest example for two laser sources is to run the data acquisition card at twice the repetition rate of the lasers and detect fluorescence from one excitation source in the odd time bins and those from the other in the even bins. This configuration has the advantage that the dead time of the data acquisition card is typically less, but the lifetime information is no longer available.

FCS and FCCS

FCS measures the fluorescence intensity detected from a small volume as a function of time and analyzes the fluctuations in intensity using correlation analysis. The method was introduced in the 1970s (1,2) and has been used to measure translational diffusion (22), rotational diffusion (23–25), chemical reactions (1,22,26,27), triplet state excitation (28,29), and conformational fluctuations (30,31). The sensitivity of the technique was greatly enhanced when Rigler and co-workers applied the method to the small volume of a confocal microscope (32,33), contributing to its widespread application in the biophysical studies. Several excellent reviews over FCS already exist (34–36) so here we restrict our discussion of the autocorrelation and cross-correlation functions to what is relevant for PIE-FCCS.

In FCS measurements, photons are detected from fluorescent particles diffusing through the small FCS probe volume. The photons arrive in bursts as particles transverse the volume. Hence, there is a correlation in the arrival time of photons that can be calculated from the normalized autocorrelation function (ACF), given by:

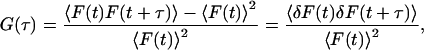(1)

where F(t) is the fluorescence intensity, 〈 〉 refers to the time-averaged value, and 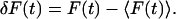The fluorescence intensity is given by:

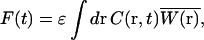(2)

where C(r, t) is the number density of particles at position r, and 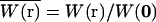is the normalized point-spread function, which is a product of the laser intensity profile, sample extent, and the spatial detection efficiency of the setup. Thus, 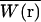describes the shape of the probe volume; ɛ is the molecular brightness of the fluorophore at the center of the point-spread function, which is given by:

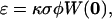(3)

where κ is the detection efficiency of the fluorescence emission, σ is the absorption cross section at the wavelength of excitation, φ is the fluorescence quantum yield of the fluorophore, and 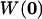is the laser intensity at the center of the point-spread function. Approximating the probe volume by a three-dimensional Gaussian, the normalized ACF for a single, freely diffusing species can be solved analytically and is given by:

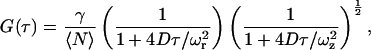(4)

where γ is a factor that depends on the geometry of the probe volume (γ = (1/2)^1.5 for a three-dimensional Gaussian probe volume), 〈N〉 is the average number of particles in the probe volume 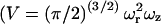where ω_r and ω_z are the distances from the center of the point-spread function to where the intensity decays to 1/e² of its initial value in the lateral and axial directions, respectively), and D is the diffusion coefficient. From the amplitude of the ACF, the average number of particles in the probe volume can be determined and the diffusion coefficient can be calculated when the dimensions of the probe volume are known.

When two detection channels are used, the correlation between the channels, i.e., the CCF, can be investigated. The normalized CCF is given by:

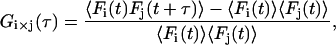(5)

where the subscript i × j refers to the cross-correlation of the i^th channel with the j^th channel; F_k(t) corresponds to the fluorescence intensity of the k^th channel. The CCFs discussed in this article are symmetric, so we make no distinction between G_i×j and G_j×i. Two-color FCCS has been developed to investigate the interaction of biomolecules (3,4,37). In principle, a complex containing both colored fluorophores gives a burst of photons in both channels while it diffuses through the probe volume. The burst from complexes containing only a single fluorophore will only be observed in a single channel. Under ideal conditions, double-labeled complexes will cross-correlate but there is no correlation due to single-labeled molecules. For the discussion, we assume two identical, overlapping, three-dimensional Gaussian probe volumes for the two channels and, unless stated otherwise, that molecular brightnesses of the green and red fluorophores are the same for single-labeled and double-labeled complexes. Under these approximations, the CCF can be determined analytically and is given by:

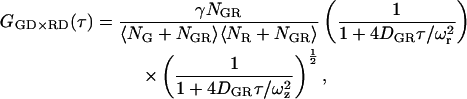(6)

where GD refers to photons detected in the green detection channel (F_GD), RD refers to photons measured in the red detection channel (F_RD), N_GR is the number of double-labeled complexes in the probe volume, and D_GR is the diffusion coefficient of the double-labeled complex. For samples where the total concentrations of green labeled particles and red labeled particles are constant, the amplitude of the CCF is directly proportional to the number of dually labeled complexes.

Fluorophores may undergo a change in molecular brightness when the molecule to which they are attached interacts with other molecules. When the molecular brightness of the green or red labeled complexes is different than the molecular brightness of the green or red fluorophore in the double-labeled complex, the CCF is given by:

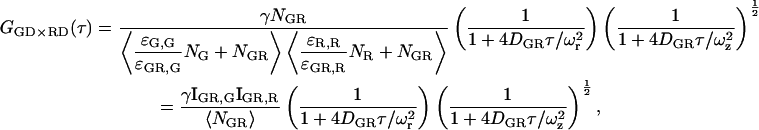(7)

where ɛ_i,j is the molecular brightness of the i^th species in the j^th channel and 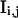represents the fractional intensity of the i^th species in the j^th channel;

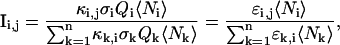(8)

where k is summed over all n species present in the volume. When there is no FRET between fluorophores and the molecule brightnesses of the fluorophores does not depend on labeling or molecular interactions, then ɛ_GR,G = ɛ_G,G, ɛ_GR,R = ɛ_R,R and Eq. 7 reverts to Eq. 6.

Typically in FCCS experiments, there is spectral cross talk of the shorter wavelength fluorophore in the longer wavelength channel. In this case, the fluorescence intensity of the green and red channels are given by:

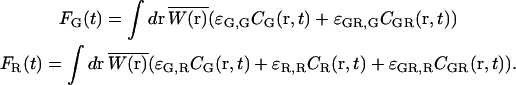(9)

For a mixture of green only, red only, and dually labeled complexes, the CCF, including cross talk, is given by:

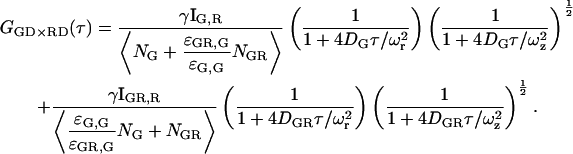(10)

As expected, when the cross-talk term disappears (ɛ_G,R = 0) and thus, 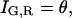the amplitude of the CCF is equal to the amplitude of Eq. 7. When there are no double-labeled particles, N_GR = 0, a residual cross-correlation due to the spectral cross talk is observable. The amplitude of the CCF is given by:

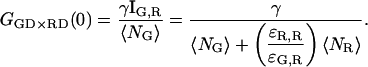(11)

With PIE, we have the additional information of which excitation source generated the detected photon. Hence, PIE yields four distinct time series that can be analyzed individually or added together as desired. The molecular brightness for green and red excitation is in general different. Adding an index to the molecular brightness to describe the excitation source, we define ɛ_i,j,k as the molecular brightness of the i^th species in the j^th channel with k excitation.

In practice, one uses filters where the red fluorescence emission is not detectable in the green channel and a red excitation wavelength that does not excite the green dye. That is, ɛ_R,G,G = ɛ_R,G,R = ɛ_G,G,R = ɛ_G,R,R = 0. With these assumptions, the intensities of the different channels are given by:

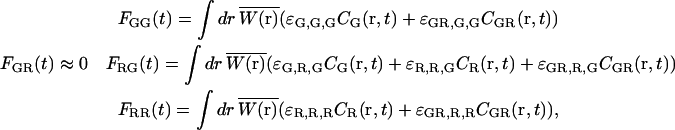(12)

where F_ij refers to photons detected in the i^th channel with j excitation. If we correlate the photons collected in the green channel upon green excitation (F_GG) with those detected in the red channel upon red excitation (F_RR), the cross-talk term disappears and G_GG×RR is identical to Eq. 7. When direct excitation of the red fluorophore with the green laser is not significant, cross talk can be also eliminated by correlating photons detected after green excitation (F_GX = F_GG + F_RG) with those detected after red excitation (F_RX = F_GR + F_RR ≈ F_RR), G_GX×RX. This has recently been demonstrated by Thews et al. using single-channel detection (38).

FRET

When two fluorophores are in close proximity, energy may be transferred between the two fluorophores via dipole-dipole interactions (39). Many excellent reviews over FRET exist in the literature (40–42) and we will only give a short overview. Typically, energy is transferred from the high energy fluorophore, called the donor, to the lower energy fluorophore, referred to as the acceptor. The rate of energy transfer depends on the spectral overlap of the fluorescence emission spectrum of the donor and the absorption spectrum of the acceptor, the orientation of the two dipoles, and their separation. The rate of energy transfer is given by:

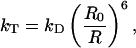(13)

where k_D is the rate of excited state decay from the donor in the absence of acceptor, R₀ is the Förster radius, that is the separation at which 50% of the energy is transferred from the donor to the acceptor, and R is the separation of the donor and acceptor. The FRET efficiency is defined as the fraction of energy transferred from the donor to the acceptor and is given by:

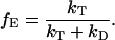(14)

Two popular methods for determining the FRET efficiency are from the amount of donor quenching and from sensitized emission of the acceptor:

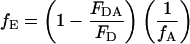(15a)

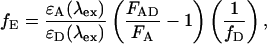(15b)

where F_DA and F_D are the fluorescent intensity of the donor in the presence and absence of the acceptor, respectively, f_A is the fraction of complexes with an active acceptor, ɛ_A(λ_ex) and ɛ_D(λ_ex) are the absorption cross sections of the acceptor and donor at the excitation wavelength, respectively, F_AD and F_A are the fluorescent intensity of the acceptor in the presence and absence of donor, respectively, and f_D is the fraction of complexes with an active donor. For spFRET measurements, the intensities of the donor and acceptor fluorescence are used to determine the FRET efficiency:

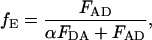(16)

where α is the detection-correction factor between the green and red channels:

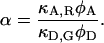(17)

FCCS in the presence of FRET

When performing cross-correlation measurements with complexes that undergo FRET, the molecular brightness of the double-labeled complex in the green channel is reduced while the molecular brightness in the red channel is increased. The intensity of the two channels is given by Eq. 12, but the molecular brightnesses of the double-labeled complexes, ɛ_GR,G,G, ɛ_GR,R,G, and ɛ_GR,R,R, are different than that of the green-only (ɛ_G,G,G) and red-only (ɛ_R,R,G and ɛ_R,R,R) complexes because of energy transfer.

Ignoring cross talk of the green dye into the red channel (ɛ_G,R,G = 0), the cross correlation of the green detection channel (F_GD = F_GG + F_GR ≈ F_GG) with the red detection channel (F_RD = F_RG + F_RR) gives a CCF of (43):

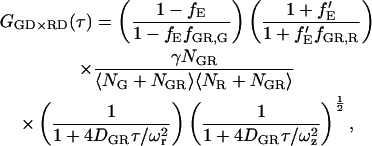(18)

where 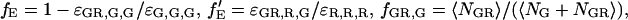and 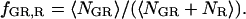f_E is the FRET efficiency, measured from the decrease in the intensity of the donor. It is defined similarly to Eq. 15a, but deals with the molecular brightnesses of the fluorophores and not with the total fluorescence intensities. Hence, no correction for the labeling efficiency is necessary. 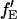is proportional to the FRET efficiency and is the ratio of the molecular brightness of the acceptor in the red channel when excited via FRET to that of direct red excitation. For an appropriate choice of laser powers, 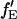= f_E. When there is no FRET, 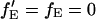and Eq. 18 reduces to Eq. 6. f_GR,G and f_GR,R are the fraction of double-labeled complexes to the total number of complexes containing a green label or red label, respectively. When there are no green-only and red-only labeled complexes, f_GR,G = f_GR,R = 1, and again, Eq. 18 reverts to Eq. 6. However, samples that are purely double-labeled are rare for most FCCS measurements and the fraction of double-labeled species is often the quantity one wishes to determine.

The first term in Eq. 18 arises from the decreased molecular brightness of the double-labeled species in the green channel due to FRET,

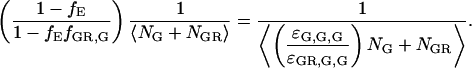(19)

This is the first term in the denominator of Eq. 7. The second term in Eq. 18 comes from the increase in fluorescence intensity of the double-labeled species in the red channel due to FRET,

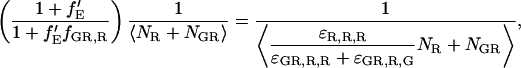(20)

and is equivalent to the second term in the denominator of Eq. 7.

As discussed above, it is possible to remove spectral cross talk using PIE. In this case, correlating the photons detected in the green channel after green excitation (F_GG) with those detected in the red channel with red excitation (F_RR), we remove the increase in the molecular brightness of the acceptor in the red channel due to FRET. The amplitude of the CCF is given by:

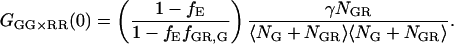(21)

The amplitude still deviates from the CCF in the absence of FRET because of the decrease in molecular brightness of the doubled-labeled complex in the green channel due to FRET. When the detection efficiency in the green and red channels is the same (i.e., the detection-correction factor, α, given in Eq. 17 equals 1), the intensity lost in the green channel due to FRET is detected in the red channel. Cross-correlation of the photons detected after green excitation (F_GX) with the photons detected in the red channel after red excitation (F_RR ≈ F_RX) yields the amplitude of the CCF in the absence of FRET:

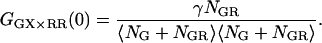(22)

The assumptions given above are not unreasonable for most typical FCCS measurements and quantitative analysis of the FCCS measurements can be performed using PIE when the complex undergoes FRET. As the photons in both the green and red detection channels are summed together after green excitation, cross talk of the green fluorophore in the red channel is automatically corrected. When there is an excess of acceptor in the sample, direct excitation of the acceptor at the wavelength of donor excitation needs to be accounted for.

Determination of FRET efficiency from PIE-FCCS

From Eq. 18, it can be seen that the FRET efficiency affects the amplitude of the CCF and is, in principle, measurable from the CCF. However, only one study has used FCS for determination of FRET efficiencies (44). Extraction of the FRET efficiency from the amplitude of the CCF (Eq. 18) requires knowledge of the labeling efficiency, which is typically a parameter one wishes to determine in the FCCS measurements. Assuming α = 1 (from Eq. 17) and no significant direct excitation of the red fluorophore with green excitation, the FRET efficiency can be directly calculated from the ratio of the amplitude of different correlation functions that are available with PIE. The ratio of Eq. 21 to Eq. 22 gives the following expression for f_E:

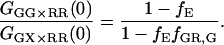(23)

The fraction of double-labeled complexes to the total number of green particles, f_GR,G, is given by the ratio of G_GX×RR(0) to the amplitude of the ACF of photons detected in the red channel after red excitation, G_RR×RR. Solving for f_E, we have:

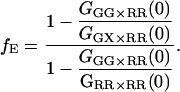(24)

Hence, the FRET efficiency is determined directly from the amplitude of two CCFs and one ACF calculated from the measured data. In contrast to Eq. 15, the labeling efficiency does not need to be known to determine the FRET efficiency. The FRET efficiency is calculated from the molecular brightness of the donor both in the presence and in the absence of an acceptor. Both populations must be present for the measurement to be accurate. When no donor-only species is present in the measurement, f_GR,G = 1, G_GG×RR(0) = G_GX×RR(0), Eq. 24 is no longer valid and the information over the FRET efficiency is no longer available from the FCCS measurement. In the other extreme, where f_GR,G ∼ 0, the amplitude of the CCF goes to zero and determination of the FRET efficiency becomes inaccurate. When f_GR,R ≪ 1, direct excitation of the red fluorophore can become significant and the cross-correlation of green excitation with red detection after red excitation (G_GX×RR) becomes distorted. Hence, determination of the FRET efficiency is the best when donor labeling is not 100%, but between 10 and 90% and the acceptor labeling is high. Although we have ignored spectral cross talk of the donor in the acceptor channel in the above discussion, the determination of the FRET efficiency comes from the different molecular brightnesses in the donor channel and is not influenced by spectral cross talk of the donor into the acceptor channel.

For samples consisting of more than a single FRET species, Eq. 24 returns the weighted average FRET efficiency of the sample. The FRET efficiency determined from Eq. 24 for a sample consisting of two different FRET efficiencies and a donor-only species is:

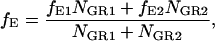(25)

where subscripts 1 and 2 refer to the two species with different FRET efficiencies, f_E1 and f_E2, respectively.

If the proportionality constant between 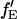and f_E is known, it is possible to determine the FRET efficiency from the sensitized emission of the acceptor, 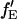from the amplitudes of the measured autocorrelation and CCF:

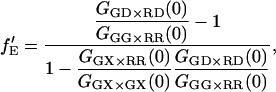(26)

where G_GX×GX is the ACF of the photons detected in the green channel after green excitation. Here again, the labeling efficiency or binding efficiency does not need to be known, but has already been accounted for in the analysis. When f_GR,R ∼ 1, there is no enhancement of the intensity in the red detection channel due to FRET and 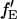cannot be determined. When f_GR,R ∼ 0, the amplitude of the CCF goes to zero and determination of 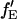becomes inaccurate. For f_GR,G ≪ 1, cross talk of the green dye into the red channel becomes significant and the amplitude of the traditional CCF, G_GD×RD, becomes inaccurate, affecting the calculation of 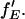The optimal determination of the FRET efficiency occurs when the donor labeling efficiency is high and the acceptor labeling efficiency is ∼50%. A list of relevant auto- and cross-correlation amplitudes for FRET and stoichiometry calculations is given in Table 1.

TABLE 1.

List of relevant auto- and cross-correlation functions for FRET determination

Amplitude of selected auto- and cross-correlation functions	FRET and stoichiometry parameters

Nonidentical probe volumes

For the calculations above, we have assumed identical probe volumes. In practice, the probe volumes will be different. The normal CCF for concentric probe volumes with different sizes has been calculated previously (4). The result is that the probe volume is replaced by an effective probe volume given by:

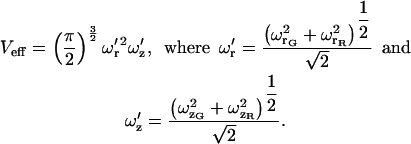(27)

G and R on the subscript refer to the green and red probe volumes, respectively. Concentric probe volumes of different sizes do not affect the use of PIE-FCCS for removing spectral cross talk, but, as above, the probe volume is described by Eq. 27.

When mixing the excitation and detection channels, the influence of different probe volumes needs to be considered in more detail. When the probe volume is defined by the excitation volume rather than the detection volume, we can approximate the probe volume of photons detected in the red channel with green excitation to be the same as the green probe volume. In this case, the expression for G_GX×RR given in Eq. 22 is still correct, but the number of molecules refers to the effective volume given in Eq. 27. The average FRET efficiency is given by:

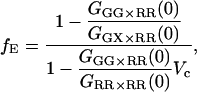(28)

where 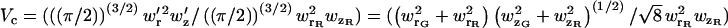is the volume correction factor. When the probe volume is defined by the detection volume (i.e., the detection pinhole) rather than the excitation volume, the correction becomes more complicated.

For the results presented in this article, the red probe volume had a radius of 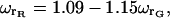leading to volume differences of between 25 and 50%. We did not correct the presented results for the differences in the probe volumes.

MATERIAL AND METHODS

HeLa cells and polyplexes

For the imaging experiments, HeLa cells were stably transfected with DsRed and propagated in DMEM supplemented with 10% FCS and 1% antibiotics (penicillin (10,000 U/ml), streptomycin (10,000 μg/ml), and 400 μg/ml G418). DNA/polyethylenimine polyplexes were labeled with Cy5 as described in Boeckle et al. (45). Cells were seeded in LabTek chamber slides (155411, Nalge Nunc International, Rochester, NY) two days before the experiments. Polyplexes were incubated with the cells for 30 min, the buffer above the cells was exchanged, and images were collected after an additional 30 min.

DNA

For the FCCS studies, a 40-bp double-stranded DNA (dsDNA) was used. The sequence used is shown below:

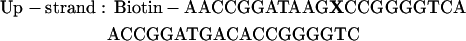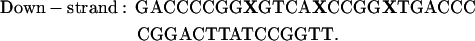Dyes were attached internally to the DNA on the C5 of a thymine modified base with an amino linker. The upper strand was labeled with the acceptor, Atto647 (Atto-Tec GmbH, Siegen, Germany), at the position indicated with an X whereas the lower strand was labeled in one of three locations, also indicated with an X, with the donor molecule, Atto532 (Atto-Tec GmbH). Thus, the distances between the dyes in the double strands were 10 bp (DNA¹⁰), 15 bp (DNA¹⁵), or 20 bp (DNA²⁰). Two other dsDNAs with only one label were also assembled, one with the donor only (DNA^D) and one with acceptor only (DNA^A). All measurements were performed in 10 mM Hepes buffer.

EXPERIMENTAL SETUP

The experimental setup is based on a two-channel confocal microscope, shown schematically in Fig. 1 a. A Nd:YVO₄ laser at 532 nm (Spectra Physics, Millennia, Darmstadt, Germany) and a picosecond-pulsed laser diode at 635 nm (LDM635 and Sepia PDL808, PicoQuant, Berlin, Germany) were used as excitation sources. Pulsing of the Nd:YVO₄ laser was achieved by an acousto-optic modulator (AOM) (N23080-2-LTD, NEOS Technologies, Melbourne, FL). The rise and fall time of our AOM pulse is 20 ns, giving a pulse width of 50 ns, though faster AOMs are currently available. To ensure a good beam profile, both excitation sources were guided through single-mode fibers (QPMJ-A3A,3AF-488-3.5/125-3-5-1 and PMJ-3AF3AF-633-4/125-3-5-1, OZ Optics, Carp, Ontario, Canada) before entering the microscope (Zeiss, Axiovert 200, Göttingen, Germany). After the fiber, the green excitation source was collimated to a smaller diameter (4 mm) than the red excitation beam (6 mm) to generate diffraction limit spots of similar sizes. The light was focused on the sample via a water-immersion objective (C-Apochromat, 63× 1.2, Zeiss). The fluorescence was collected through the same objective and separated from the lasers by a dichroic mirror (DM2, DC532/633xr, AHF Analysetechnik, Tübingen, Germany). In our system, we have separated the green and red detection channels by another dichroic mirror (DM3, 650DCRX, AHF Analysetechnik) and passed the beams through the appropriate emission filters (HQ580/80 (EM 1), HQ700/75 (EM 2), AHF Analysetechnik) before focusing them onto the confocal pinholes (40 μm (PH 1), 50 μm (PH 2), Owis, Staufen, Germany). Here again, the size of the pinholes are adjusted for the different wavelengths to provide similar detection volumes. The fluorescence photons were detected using avalanche photodiodes (SPCM-AQR-14, EG&G Optoelectronics, Vaudreuil, Quebec, Canada) and recorded using a time-correlated single-photon counting card (TimeHarp 200, PicoQuant). The data analysis was performed with our own software routines written in PVWave (Visual Numerics, Houston, TX).

Synchronization of our experiments was performed with an oscillator (SOM808, PicoQuant) providing a master clock frequency of 40 MHz. The output of the master clock was used to trigger a sequencer (SSM808, PicoQuant), which divides the master clock pulse sequentially into eight different outputs, each with a repetition rate of 5 MHz. One output of the sequencer is connected to the driver (SLM808, PicoQuant) of the red diode laser. A second output is connected to a pulse generator (HM 8035, HAMEG GmbH, Mainhausen, Germany) that sends a 50-ns pulse to the AOM, switching on the green laser. A third output is used to synchronize the data collection card.

APPLICATIONS OF PIE

Imaging with PIE

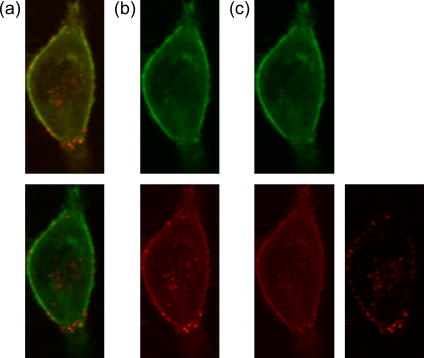
One advantage of PIE is its ability to separate out spectral cross talk. This is advantageous when investigating multiple fluorophores within cells. As the number of available fluorescent proteins is still limited, the amount of spectral cross talk between proteins used in multicolor experiments can be significant. Fig. 2 a, top panel, shows a conventional, two-color image of a DsRed-labeled actin-transfected HeLa cell that has been infected with Cy5-labeled artificial viruses. The image was collected by raster scanning the sample through the confocal volume of the microscope. With two-color detection, we can split the image into the green and red detection channels (Fig. 2 b). When splitting the detection channels, the cross talk of the green channel into the red channel can be readily seen and decreases the contrast of the red detected image. By using PIE, we can further split the data into images collected with green excitation and those with red excitation as shown in Fig. 2 c. The image of red detection with green excitation clearly shows the cross talk of the DsRed-labeled actin filaments into the red channel. In the image recorded in the red channel with red excitation, cross talk from the DsRed-labeled actin is eliminated and the individual artificial virus particles are clearly observed. The improved contrast from PIE can be seen in the lower panel of Fig. 2 a.

FIGURE 2.

Image of a live HeLa cell transfected with DsRed labeled actin and infected with Cy5 labeled polyplexes. (a, top) The two-color image showing all photons detected in the green channel in green and all photons detected in the red channel red. (a, bottom) Same image showing the sharper contrast of PIE where only photons detected in the green channel with green excitation are shown in green and only the photons detected in the red channel after red excitation are shown in red. (b) The same image in the top of panel a split into images of the green detection channel (top) and red detection channel (bottom). (c) Further separation of the image in panel a divided into green detection with green excitation (top left), red detection with green excitation (bottom left), where the cross talk is clearly observable, and red detection with red excitation (bottom right), where the cross talk is not present and the contrast is much improved over the image in the lower part of panel b.

Another imaging application of PIE is two-color detection with a single detector. In this case, green excitation corresponds to detection of the green fluorophore (with a component of direct excitation of the red fluorophore) and red excitation corresponds to detection of the red fluorophore. This application is advantageous when performing nanometer resolution wide-field two-color colocalization measurements on single particles. The identical optical path is used for the detection of both fluorophores and no transformation of the data is necessary to overlap the two channels, which can introduce additional uncertainties in the relative positions of two fluorophores.

FCCS using PIE

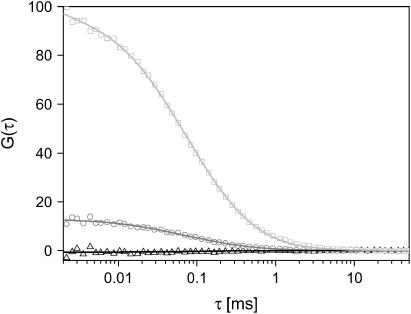
The auto- and cross-correlation of two noninteracting, freely diffusing dyes (Atto532 and Atto647) were measured. The CCF and the ACF of Atto647 are shown in Fig. 3. Due to spectral cross talk, the amplitude of the CCF is 13%. In FCCS, the cross-talk term arises from photons emitted from the green fluorophore being detected in the red channel. Using PIE, we remove the spectral cross talk by correlating photons detected in the green channel after green excitation with red photons detected in the red channel after red excitation. The CCF with PIE is the black curve shown in Fig. 3. The amplitude of the CCF with PIE is −0.7%, or close to zero, as is expected for two, noninteracting species in the absence of spectral cross talk.

FIGURE 3.

Correlation functions of a mixture of freely diffusing, noninteracting dyes: Atto532 (2.5 nM) and Atto647 (2.5 nM). The CCF with (black) and without (gray) the elimination of cross talk are shown, normalized to the ACF of Atto647 (light gray). An amplitude of 13.0% is observed for the CCF without PIE, whereas the cross-correlation amplitude with PIE shows an amplitude of −0.7%.

Dead-time effects of the data acquisition card

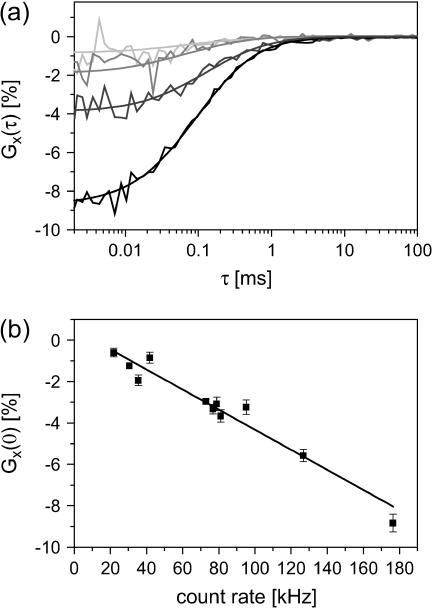
Fig. 4 a shows the CCF measured for different dilutions of samples with free dyes plotted as a percentage of the amplitude of the autocorrelation of Atto647. At count rates above 50 kHz, the amplitude of the CCF becomes noticeably negative and the anticorrelation increases with count rate. This anticorrelation is attributed to a shadowing effect arising from the dead time of the data collection card. To test this hypothesis, we have plotted the amplitude of the CCF with respect to the autocorrelation function of the red channel as a function of count rate (Fig. 4 b). The amplitude of CCF has a linear dependence on the count rate. As the two dyes diffuse independently, arrival of photons in one channel come randomly with respect to the other channel. However, when a green particle is in the probe volume, the number of detected green photons is above average (positive autocorrelation) and the number of detected photons from the red fluorophore decreases due to the dead time of the card and vice versa. From the slope of the graph in Fig. 4 b, the dead time of the card can be approximated at 485 ± 39 ns. This artifact can be avoided by new data collection hardware where the two detection channels are independent.

FIGURE 4.

Influence of the detection card dead time on the amplitude of the CCFs. (a) Normalized CCFs from mixtures of Atto532 and Atto647 at four concentrations. The relative concentration of Atto532 and Atto647 were kept equal for each measurement. (From top to bottom) 2.5 nM (light gray), 5 nM (medium gray), 10 nM (dark gray), and 20 nM Atto532 (black). (b) Normalized amplitudes of the CCF are plotted versus the total count rate (green plus red detection channel). The slope of (485 ± 39 ns) indicates the dead-time of the TCSPC card.

FCCS in the presence of FRET

As discussed in the Theory section, the amplitude of the CCF for complexes undergoing FRET depends on the FRET efficiency, the ratio of the molecular brightnesses of the FRET signal to direct excitation of the acceptor at the wavelength of the acceptor in the red channel, and the fraction of double-labeled species in the sample to the total number of green labeled and red labeled complexes. In the top panel of Fig. 5 a, a series of FCCS measurements with four different mixtures of DNA¹⁰ and DNA^A is shown. The concentrations were adjusted such that the total count rate remained the same, minimizing the influence of the dead time of the data acquisition card. The CCFs have been normalized to the ACF of the red channel. Provided the green and red probe volumes are identical, the amplitude of the normalized CCF in the absence and presence of FRET are given by:

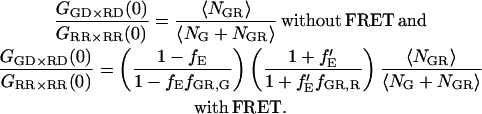(29)

FIGURE 5.

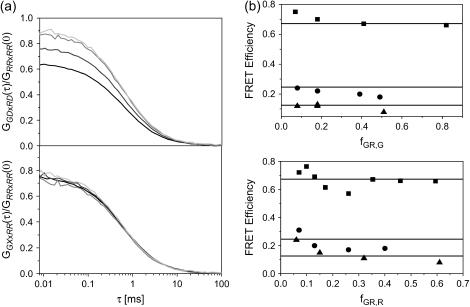
PIE allows a quantitative cross-correlation analysis in the presence of FRET. (a, top) The CCF, G_GDxRD, normalized to the ACF of the red channel upon red excitation (G_RR×RR) is shown for different mixtures of DNA¹⁰ and DNA^A (4 nM DNA¹⁰ (black), 3 nM DNA¹⁰ + 1.67 nM DNA^A (dark gray), 2 nM DNA¹⁰ + 3.33 nM DNA^A (medium gray), 1 nM DNA¹⁰ + 5 nM DNA⁶⁴⁷ (light gray)). (a, bottom) The CCF, G_GX×RR, normalized to G_RR×RR is plotted for the same measurements with the same color scheme. The normalized cross-correlation amplitudes without PIE increase with an increasing concentration of DNA^A whereas the normalized cross-correlation amplitude evaluated with PIE are constant, independent of the concentration of DNA^A. (b) The FRET efficiency of the DNA¹⁰ (▪), DNA¹⁵ (•), and DNA²⁰ (▴) plotted as a function of f_GR,G (top) and f_GR,R (bottom) calculated using Eq. 24. The FRET efficiency determined from spFRET measurements are shown as solid lines.

In the absence of FRET, the amplitude of the normalized CCF is independent of the concentration of acceptor-only species. This is clearly not observed for the CCFs shown in the top panel of Fig. 5 a. Using PIE, we can correlate the photons detected after green excitation (F_GX) with photons detected in the red channel after red excitation (F_RR), which is equivalent to photons detected after red excitation. Hence, all the photons generated from FRET are calculated as if coming from the donor. When the detection correction factor α = 1 (from Eq. 17), the photons lost from the green channel due to FRET are compensated by the photons detected in the red channel after green excitation. The CCFs calculated using PIE are shown in the bottom panel of Fig. 5 a. The amplitudes of the CCF using PIE are independent of the concentration of acceptor-only molecules.

FCCS measurements were also performed with four different concentrations of DNA¹⁰ and DNA^D (data not shown). The amplitudes of G_GG×RR and G_GX×RR were normalized to the amplitudes of the ACF of all photons detected after green excitation (G_GX×GX). As expected, the amplitudes of G_GG×RR varied with f_GR,G whereas the normalized amplitudes of G_GX×RR were independent of the concentration of DNA^D. Hence, quantitatively accurate cross-correlation measurements can be performed in the presence of FRET when no detection correction factor is required between the green and red channels.

A comparison of the amplitudes of G_GG×RR and G_GX×RR show a significant difference even without the addition of DNA^D or DNA^A. This is an indication that the double-labeled species is undergoing FRET and that the sample of double-labeled species was not pure.

Determination of FRET efficiency using FCCS

We have performed FCCS measurements on three different DNA strands with donor-acceptor separations of 10, 15, and 20 bp. The FRET efficiencies were calculated using Eq. 24. A comparison of the calculated FRET efficiencies for different dilutions of donor-only or acceptor-only DNA are shown in Fig. 5 b as a function of f_GR,G (top) and f_GR,R (bottom). The average FRET efficiency determined from spFRET measurements are shown as lines in Fig. 5 b. The results are also listed in Table 2. With only a couple of exceptions, the determined FRET efficiencies are constant and agree with spFRET measurements discussed below. The exceptions come when either f_GR,G or f_GR,R are ≪1. Under these conditions, direct excitation of the acceptor may need to be accounted for. As can be seen from Fig. 5 b and Table2, when f_GR,G ≪ 1, f_E becomes inaccurate.

TABLE 2.

List of results from FRET FCCS measurements using dsDNA complexes

	fɛ	DNA10fG,GR	fR,GR	fɛ	DNA15fG,GR	fR,GR	fɛ	DNA20fG,GR	fR,GR
Initial sample	0.66	0.82	0.46	0.18	0.49	0.40	0.08	0.51	0.61
	0.67	0.41	0.40	0.20	0.39	0.40	0.13	0.18	0.60
Dilution with DNAD	0.7	0.18	0.39	0.22	0.18	0.35	0.12	0.18	0.61
	0.75	0.07	0.35	0.24	0.08	0.36	0.12	0.08	0.59
	0.57	0.74	0.26	0.17	0.49	0.40	0.11	0.49	0.32
Dilution with DNAA	0.69	0.83	0.13	0.20	0.52	0.26	0.15	0.49	0.15
	0.72	0.75	0.07	0.31	0.49	0.13	0.24	0.48	0.06
spFRET	0.672	–	–	0.246	–	–	0.126	–	–

Most studies of FRET using FCS determine the timescale of fluctuations in FRET efficiency from either an autocorrelation analysis of the FRET efficiency and/or a cross-correlation between the donor and acceptor channels (46). Two new methods for determination of the static FRET efficiency from FCS were reported by Widengren and co-workers (44). One method uses the molecular brightness of the acceptor. This method requires a calibration to convert the measured molecular brightness into FRET efficiency, and correction has to be made for the cross talk of the donor into the acceptor channel. This analysis can also be performed with PIE where the molecular brightness of the acceptor is determined from the intensity of the red channel after green excitation and number of molecules undergoing FRET, which is calculated from the amplitude of the ACF of the photons detected in the red channel after green excitation. The second method proposed by Widengren and co-workers (44) uses the influence of the excitation rate from FRET on the trans-cis isomerization transition of the acceptor dye. This method also requires a calibration to convert the measured data into FRET efficiency, but is independent of sample concentration, the labeling efficiency of the acceptor, and donor cross talk into the acceptor channel. The advantage of our method is that the FRET efficiency is determined directly, without any calibration, as long as the assumptions given in the Theory section are reasonably fulfilled.

The signal/noise ratio of the CCF using PIE

One important question is how PIE affects the signal/noise ratio of the CCF. In the absence of FRET, the photons discarded in the analysis do not significantly affect the signal/noise ratio of the measurement. For removal of spectral cross talk, the photons detected in the green channel after green excitation (F_GG) are correlated with photons detected in the red channel after red excitation (F_RR). The photons that are detected in the red channel after green excitation (F_RG) come from either spectral cross talk of a green fluorophore or direct excitation of a red fluorophore. The number of photons detected in the green channel after red excitation is negligible and comes from scattered laser light entering the green channel rather than fluorescence. In the later case, the photons detected are not coming from fluorescence and should not be incorporated in the analysis. In the case of direct excitation of the red fluorophore, we are throwing out photons containing relevant information. However, when a red fluorophore is present, the molecule brightness of the red fluorophore in the red channel upon red excitation (ɛ_R,R,R) is typically much higher then with green excitation (ɛ_R,R,G). Hence, the decrease in the signal/noise ratio is not significant. For FCCS measurements in the presence of FRET, photons detected after green excitation (F_GX) are correlated with photons in the red channel detected after red excitation (F_RR). As the fluorescence photons detected in the green channel after red excitation are not relevant, all of the available photons are used in the analysis and there is no decrease in the signal/noise ratio due to the analysis.

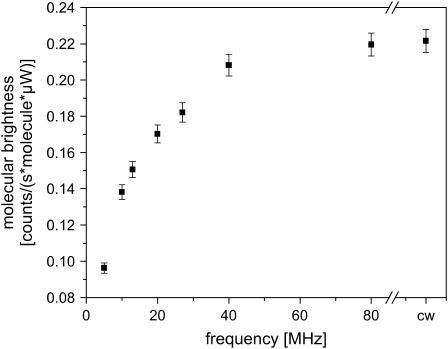
The major factor that affects the signal/noise ratio of the measurements is the decrease in molecular brightness due to the limited excitation cycle. Fig. 6 shows the effect of the excitation rate on the molecular brightness of the fluorophore. The molecular brightness per particle was determined from the average count rate divided by the average number of particles calculated from the ACF. The excitation power entering the microscope was held constant at 50 μW. The molecular brightness with continuous-wave (CW) excitation was performed by aligning a HeNe laser (λ = 633 nm) through the same single-mode fiber we use for pulsed excitation, assuring that the alignment was identical for the two measurements. The molecular brightnesses of Atto647 in solution with CW excitation and with 80 MHz excitation were identical at 11 kHz/mol. As shown in Fig. 6, the molecular brightness decreases with decreasing excitation rate at constant average power. For measurements performed at 27 MHz, the decrease in molecular brightness is <20%. Below 10 MHz, the molecular brightness decreases more severely and at lower repetition rates, varies linearly with the frequency. At 5 MHz, the frequency we used in this work, the molecular brightness is 40% of its value with CW excitation.

FIGURE 6.

Plot of the molecular brightness of Atto647 with red excitation as a function of repetition rate. The excitation power was held constant at 50 μW. There is no significant decrease in the molecular brightness of the fluorophore for excitation rates of 40 MHz and above.

Saturation effects can play an important role on the shape of the ACF as shown by Enderlein (47). For our measurements at constant excitation power, the shape of the ACF did not vary significantly with excitation rate. This suggests that if the molecular brightness measurements are subject to saturation artifacts, the artifact is the same in all measurements. For determination of the FRET efficiency of a sample, the results depend on the amplitude of the CCFs and are not strongly influenced by saturation effects.

Application of PIE to spFRET

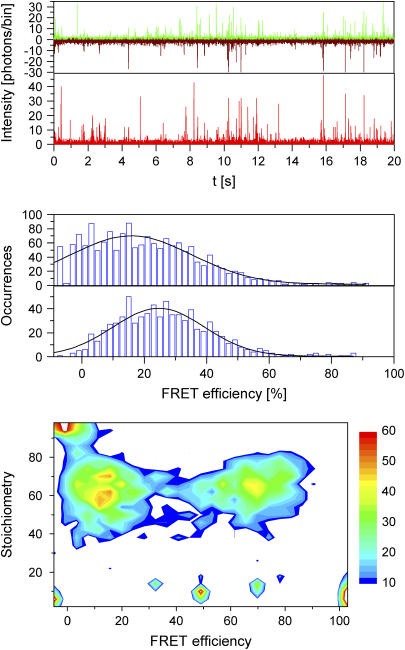
SpFRET measurements were performed on double-stranded DNA with a donor-acceptor separation of 10, 15, and 20 bp. Fig. 7, top panel, shows the time trace of intensity in the green and red channels after green excitation and the intensity of the red channel with red excitation for measurements using DNA¹⁵. Using burst analysis, first introduced by Seidel and co-workers (5), we can analyze individual complexes as they diffuse through our probe volume. A minimum number of photons are required for recognition of a particle in the probe volume and inclusion in the analysis. Fig. 7, middle panel (top), shows the histogram of FRET efficiency, calculated using Eq. 16, for individual DNA¹⁵ strands where a minimum of 25 photons were detected between the green and red channels. One peak is observed with an average FRET efficiency of 15.7 ± 0.9%.

FIGURE 7.

SpFRET analysis with PIE. (top panel) Three time traces of fluorescence intensity with DNA¹⁵ binned with 2-ms resolution: green emission after green excitation (green), red emission after green excitation (dark red), and red emission after red excitation (bright red). The fluorescence bursts are clearly distinguishable from the background. (middle panel, top) Histogram of FRET efficiencies extracted from the time traces in the top panel. All photon bursts were included where a minimum of 25 photons were detected during the burst. (middle panel, bottom) Histogram of FRET efficiencies extracted from the time traces in the top panel with the additional criterion that a minimum of 15 photons were detected in the red channel upon red excitation. (bottom panel) A two-dimensional contour plot indicating the number of molecules detected as a function of stoichiometry and FRET efficiency for a mixture of DNA¹⁰ and DNA²⁰. Stoichiometry values between 35 and 80% indicate double-labeled complexes. The peak with a stoichiometry value close to 1.0 and low FRET efficiency indicates complexes lacking a photoactive acceptor. Molecules with a stoichiometry value below ∼30% are from molecules without an acceptor.

Kapanidis and co-workers have shown how alternating laser excitation can be used to improve the accuracy of FRET measurements (21). With only green excitation, one cannot distinguish between a complex with low FRET efficiency and a molecule that lacks a fluorescently active acceptor. PIE allows us to verify that we have a fluorescently active acceptor as the molecule diffuses through the probe volume. Fig. 7, middle panel (bottom), shows a histogram generated from the same data as in the top panel with the added requirement that a minimum of 15 photons be detected in the red channel after red excitation. With this additional criterion for burst analysis, the contribution from complexes without a photoactive acceptor is removed from the histogram and a clear peak is observed with a FRET efficiency of 24.6 ± 0.7%. Using PIE, spFRET measurements can be performed at donor-acceptor separations where the FRET efficiency is small.

In addition, as shown by Kapanidis and colleagues (20), it is possible to measure the stoichiometry of individual particles using alternating laser excitation. The stoichiometry ratio, S, is defined as (20):

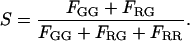(30)

Fig. 7, bottom panel, shows a two-dimensional contour plot of a measurement on a mixture of DNA¹⁰ and DNA²⁰, where the stoichiometry ratio is plotted versus FRET efficiency. From the figure, it can be seen that stoichiometry values between 0.35 and 0.80 indicate double-labeled complexes. The peak at low FRET values with a stoichiometry value above 0.8 is from molecules without a photoactive acceptor. Molecules observed with a stoichiometry value of <∼0.3 have no photoactive donor, and, hence, the FRET efficiency is not defined. The stoichiometry values of 0.61 for DNA¹⁰ and 0.63 DNA²⁰ are very similar, indicating that the detection-correction factor for our system, α, is very close to one. This fulfills one of the assumptions required for quantitative analysis of FCCS measurements as well as determination of the FRET efficiency.

ALEX versus PIE

The difference between ALEX and PIE is that the alternation between green and red excitation occurs faster than the rate of photon detection. In this work, the repetition rate of the excitation was 5 MHz, much higher than the typical count rates of <100 kHz. Hence, the relevant fluorescence information is collected simultaneously. The fast switching rate gives us the ability to perform auto- and cross-correlation analysis on the collected data with submicrosecond time resolution. Even for the spFRET measurements, the measured fluorescence is averaged over the same period in time, and is not affected by significant diffusion of the particle between alternating excitation pulses.

CONCLUSIONS AND OUTLOOK

Accurate determination of the dynamics of single molecules and small ensembles of complexes requires the maximum information to be withdrawn from each photon. PIE provides the information of which excitation source generated each detected fluorescence photon. We have demonstrated the effectiveness of PIE for two excitation sources and one or two detection channels.

In imaging microscopy, two-color experiments can be performed with a single detector, allowing highly accurate distance measurements between two differently labeled molecules without correcting for different optical pathways of the detected light. When using a two-channel imaging system, cross talk from the shorter wavelength fluorophore into the longer wavelength channel can be removed. In addition, FRET analysis can be done using intensity of both the donor and acceptor.

The use of PIE in FCCS allows for cross-correlation experiments to be performed using only a single detector. For a two-channel system, the ability of PIE to remove spectral cross talk allows a cross-talk-free CCF to be determined, improving the sensitivity limit of FCCS experiments. In addition, for FCCS measurements involving complexes that undergo FRET, quantitative analysis of the CCF can be performed. PIE can be used to determine the FRET efficiency from a FCCS measurement without calibration and does not depend on the fraction of double-labeled complexes.

PIE can be applied to spFRET measurements, allowing one to distinguish between individual complexes that have an active donor and acceptor but have a low FRET efficiency and complexes that do not have an active acceptor. This method extends the minimum FRET efficiencies that can be accurately determined, and hence, increases the distances over which FRET measurements can be performed (21).

The applications of PIE are more numerous than we have demonstrated here. Seidel and co-workers demonstrated the use of lifetime information in burst analysis (5) to monitor conformational dynamics. A clear extension of PIE-spFRET is to use subnanosecond laser pulses and utilize the fluorescence lifetime information in determination of the FRET efficiency. This is particularly useful for monitoring changes in the molecular brightness of single fluorophores that occur during spFRET measurements (19). PIE can also be applied to 2-D PCH (48) or 2-D FIDA (49), giving molecular brightnesses in the green and red channels with green and red excitation. PIE can be expanded to three or more excitation sources. This will be particularly useful for three-color FRET measurements (50,51), where the distance between three fluorescent dyes can be determined simultaneously.