Surfing on protein folding energy landscapes

The so-called new view of protein folding describes the process in terms of funnel-shaped energy landscapes (1, 2). In this view, the drive for a protein to fold to its native state originates from a strong slope of the energy landscape toward native conformations. However, this can be counteracted by roughness of the energy landscape that could render the folding reaction less effective, a phenomenon called frustration. A major question occupying the protein folding community in recent years is the relative importance of protein topology and sequence in determining the folding mechanism of proteins. In this issue of PNAS (3), Shea et al. investigate the contribution of protein topology and protein sequence to the frustration of energy landscapes.

Shea et al. investigate the contribution of protein topology and protein sequence to the frustration of energy landscapes.

More than 30 years have passed since the “Levinthal Paradox” (4) was formulated. Levinthal calculated that it is impossible for a polypeptide chain to find its native state by exploring the entire conformational space. Therefore, some kind of search Algorithm has to exist which led to the proposal that proteins fold via specific pathways to the native configuration. Different mechanisms for folding were proposed to solve the paradox. Because a detailed description of all of the models is outside the scope of this commentary, the three main lines of thought are briefly explored. In the nucleation-growth model, (5) one or more critical kinetic nuclei are formed, around which the rest of the structure grows. Another family of models, such as the framework model, (6) envisages the formation of secondary structure elements followed by the docking of those elements to form tertiary interactions in the rate limiting step. Finally, in the hydrophobic collapse model, (7) the hydrophobic effect is considered to be the driving force for folding, squeezing out water in a nonspecific manner, and the subsequent rearrangement of the collapsed state is the rate limiting step. This model predicts an intermediate state that has been called molten globule, which has been characterized both kinetically and at equilibrium as an expanded form of the native state (8, 9).

The framework hypothesis was boosted when it was found that protein fragments corresponding to secondary structure elements could be partly folded in the absence of tertiary interactions (10, 11). The development of new methods in the protein folding field allowed to characterize the folding reaction with high enough resolution to distinguish the proposed models. These were the quenched-flow hydrogen-exchange technology (12) and the protein engineering method (13, 14). The first method provides information about folding intermediates and reports mainly on the consolidation of the protein backbone. The second method deals not only with folding intermediates, but also with the rate-limiting step or transition state ensemble (TSE) and reports mainly on side-chain interactions. After the introduction of these two methods, the first protein to fold by an apparent two-state transition (CI-2) was found (15), followed immediately by others like the spectrin SH3 domain (16) and cold shock protein CspB (17). The simple folding kinetics displayed by these proteins allows the unambiguous application of the protein engineering approach, hence providing information about the kinetically relevant species. So far, the folding of about 30 proteins has been analyzed by using this method. From this work the nucleation-condensation model for protein folding emerged (18, 19). This model suggests that small protein modules fold through an extended nucleus involving the entire module and in which elements of local structure are being formed concomitantly with and stabilized by tertiary interactions. The early steps in the folding reaction are energetically uphill because the entropic cost for restricting the chain to native-like conformations is higher than the energetic compensation donated by nascent native interactions. Only in the transition state the favorable interactions offset the entropic cost of fixing the chain in a given topology and the transition state resembles an expanded version of the native structure. Meanwhile, theoretical groups experimenting in silico with strongly simplified representations of proteins were able to simulate nucleation-condensation-like folding reactions (20). Further, all-atom dynamics simulations of the unfolding reaction of several small proteins by Daggett and coworkers (21–23) yield transition state ensembles that are in excellent agreement with the experimental data. Although nucleation-condensation is the standard mechanism by which small proteins fold, some proteins fold in a more polarized manner with part of the structure forming early on, whereas other parts remain unstructured until the last steps of the reaction. SH3, for example, folds in a two-state transition; but unlike the transition state of CI-2, which is globally diffuse with all residues having some degree of formation, the transition state of SH3 is locally condensed with part of the structure being almost completely formed, whereas another part is almost completely unstructured (24, 25). Still another mechanism is found in Barnase. Barnase first folds to an intermediate, where two folding modules are independently formed according to a nucleation condensation mechanism (13, 26, 27), and subsequently folds to the native state by docking both modules according to a framework mechanism. This modular nucleation–condensation could be a unified scheme applicable to many proteins (28, 29). The knowledge of those different mechanisms allowed the experimental testing of the role of topology for folding mechanisms. The importance of topology in protein folding was triggered by Baker and coworkers (30, 31), who showed that for many proteins the folding speed is related to the ratio between local and nonlocal contacts, the so-called contact order. Faster proteins have relatively more local contacts and consequently can fold through relatively low cost entropic steps, whereas the opposite is true for proteins having a relatively larger number of nonlocal contacts. This was further experimentally tested by designing circular permutants of proteins, which precisely allows to change the ratio of local vs. nonlocal interactions of the residues important for the folding mechanism of a protein, without altering the sequence. Circular permutants of α-spectrin SH3 were all able to fold to the native state, but the folding mechanism changed; each topology folded involving a different part of the protein so as to minimize the entropic cost to attain the native state (32). Recently, circular permutation of the S6 protein switched the mechanism from a globally diffuse to a locally condensed one (33). Monomeric and domain-swapped dimeric suc1 are structurally identical but topologically distinct. Comparison of the folding mechanism of both forms showed that they have the same folding mechanism, but that folding is more locally condensed in the monomer (34, 35).

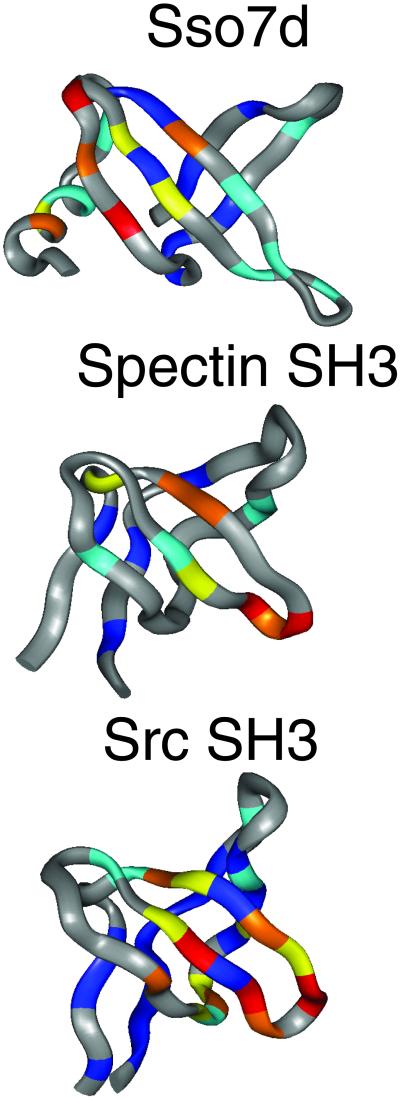
In recent years, theoretical and experimental observations of protein folding have been brought together in a more general theoretical framework that some call the new view of protein folding (36). In this view, energy landscapes are used to describe the kinetics and thermodynamics of the folding reaction. These landscapes are funnel-shaped, with slopes displaying varying degrees of roughness (1, 37). The funnel shape of protein energy landscapes arises from the strong energy drive to the native energy minimum. The roughness on the slope of the energy landscapes reflects the “frustration” of the protein chain. The concept of frustration reflects the inability of a protein to energetically satisfy all its interactions in any given conformation. Frustration in protein folding landscape arises both from topological and sequence specific energetical traps inclining proteins to accumulate intermediates during folding, rendering the process less efficient (38). These theoretical considerations, together with the fact that protein secondary structure elements tend to adopt the same structure in isolation and that it was possible to roughly predict the structure of a protein mainly by using local information and some docking, prompted different groups to develop the so-called Gō models of protein folding. These Gō models assume that for small proteins the degree of energy frustration is minimal, that is that nonnative interactions contribute little. If this is the case, then by computing the energy of all possible protein segments of different length, it should be possible to reconstruct the folding pathway of a protein (39–41). Initially Gō models considered only protein topology-derived force fields, which proved sufficient for predicting the gross features of folding transition states. Comparison of the predicted folding mechanisms for different members of the SH3-fold, however, showed that topological features alone are not enough to account for the observed differences in folding behavior (Fig. 1), and that specific interactions and thus the protein sequence modulate the folding reaction (42, 43). Molecular dynamics simulations on CI2 and SH3 equally demonstrated that the folding reaction is not only geared by topology but that the details of the packing interactions and interactions with water also determine the folding reaction (44, 45). Partly in response to this, Gō models are becoming more sophisticated as more realistic representations of the folding species are being included by allowing movements of the backbone and side chains during the simulation (51). Furthermore, in several recent publications, hybrid approaches between molecular dynamics or Monte Carlo samplings with Gō models have been explored (46, 47). Finally, Monte Carlo sampling with a potential restrained to the experimentally determined transition state structure allows transition state ensembles to be simulated (48). Initial results are confirming that the energy landscape of small proteins do not usually display a large degree of frustration, explaining the success of topological approaches for the prediction of the folding of such proteins. The report of Shea et al. (3) contributes to this discussion by exploring the folding landscape of SH3; starting from unfolding molecular dynamics simulations, several clusters of similar structures are selected of different degrees of “foldedness,” these clusters are then used as starting points for molecular dynamics sampling biased toward the native state. The use of an all-atom representation of the system allows to assess the importance of fold geometry as well as sequence specific interactions. The results confirm the general trend of dominance of topology in the folding of small proteins but some important differences are observed in the finer details of the folding mechanism in comparison with pure Gō models. Interestingly in the work of Shea et al., (3) the authors could not identify a TSE barrier, with folding proceeding downhill. This could be due to small inaccuracies in the force field, or alternatively from an improper consideration of entropy. Experimentally and in simple Gō models, it has been found that one of the main contributors to the TSE barrier is of entropic origin (52). This is a pending question in these more sophisticated Gō-like molecular dynamics approaches and one that needs to be solved.

Fig 1.

Ribbon diagram of three proteins with an SH3-like fold. In color we show the φ values obtained by the “protein engineering” method. The color ranges from blue for low φ values to red for high φ values. The higher the φ value, the more folded is the particular region in the TSE.

One other question that has received increased interest lately is the role of water molecules in the folding process. Experimentally it is documented that molten globules and several intermediates are accessible for binding by fluorescent dye ANS (49, 50), clearly demonstrating the presence of solvent to allow the diffusion of the dye into the protein interior. Further, protein engineering experiments in Barnase have revealed a water molecule bound to a threonine side chain in the intermediate state (27). However, there is no direct data showing how solvated transition states are. This is for the most part due to a technical limitation, because if the water is only expulsed in the very late energetic downhill part of the folding reaction as is suggested by Shea et al., (3) the energetic presence of the water molecules cannot be measured by using the classical protein engineering experiments.

In some cases agreement with experimental φ values is as good for simple Gō models as it is for more sophisticated approaches. The current state of the experimental techniques does not allow the fine resolution already arrived at in folding simulations. Although a lot of progress has been made, the field has arrived at a similar point as before the introduction of φ values and quenched-flow hydrogen exchange: the models can only be rigorously verified when experimental know-how progresses to the next level of sophistication. So it seems we have entered a new era in which experimentalists will need to develop new tools to provide more detail of the folding species in order for theoreticians to benchmark their every day more accurate view of the folding reaction.