On structural transitions, thermodynamic equilibrium, and the phase diagram of DNA and RNA duplexes under torque and tension

Abstract

A precise understanding of the flexibility of double stranded nucleic acids and the nature of their deformed conformations induced by external forces is important for a wide range of biological processes including transcriptional regulation, supercoil and catenane removal, and site-specific recombination. We present, at atomic resolution, a simulation of the dynamics involved in the transitions from B-DNA and A-RNA to Pauling (P) forms and to denatured states driven by application of external torque and tension. We then calculate the free energy profile along a B- to P-transition coordinate and from it, compute a reversible pathway, i.e., an isotherm of tension and torque pairs required to maintain P-DNA in equilibrium. The reversible isotherm maps correctly onto a phase diagram derived from single molecule experiments, and yields values of elongation, twist, and twist-stretch coupling in agreement with measured values. We also show that configurational entropy compensates significantly for the large electrostatic energy increase due to closer-packed P backbones. A similar set of simulations applied to RNA are used to predict a novel structure, P-RNA, with its associated free energy, equilibrium tension, torque and structural parameters, and to assign the location, on the phase-diagram, of a putative force–torque-dependent RNA “triple point.”

In several instances involving DNA, nucleoprotein complexes exert, in vivo, forces or torques that distort it appreciably, for example, by stretching (1), wrapping-around (2), or looping (3). Furthermore, a quantitative assessment of double-stranded DNA deformation can aid in designing novel nanomechanical devices (4), and in perfecting rapid genetic mapping techniques for stretched, surface-immobilized DNA (5, 6). Although less studied in this respect, double-stranded RNA, too, can experience significant structural perturbations; this is likely to play a role in the context of RNA interference (7) and viral RNA capsid compaction (8), as well as in modulating the specific interaction of the RNA duplex with proteins such as the RNA helicases (9), polymerases (10), and nucleases (11).

The development of single-molecule manipulation techniques has spurred a good number of exciting studies on the mechanical response of nucleic acids to tension and torque (12, 13). They have revealed elastic properties otherwise hidden in bulk assays (14), have shown how stretching supercoiled DNA may activate homologous pairing (15), and have assessed the force-dependence of RNA folding (16). They have also demonstrated a unique ability to generate novel macromolecular forms. Outstanding examples are the studies of Cluzel et al. (17) and Smith et al. (18) on stretched DNA (S-DNA), a form 70% longer than B-DNA. The transition was subsequently modeled, with varied abilities to reproduce experimental observables, by computer simulations (19–23). Additionally, an S-RNA form has also been measured and compared with S-DNA (24).

The present study focuses on another form of nucleic acid duplexes, recently revealed in single-molecule experiments that twisted and stretched double-stranded DNA with magnetic or optical beads attached to the ends (14, 25, 26). In the overtwisting case, these experiments produced a structure that was hypothesized to be akin to, (and thereby to somewhat vindicate), an early model of DNA proposed by Pauling (27) (P-DNA). Pauling had modeled three helical backbones inside and the bases flipped outside. Soon after its publication, the P-DNA structure appeared to be untenable in the light of the Watson–Crick model (28) for DNA under physiological conditions. Subsequently, some evidence existed to assume the presence of double-stranded P-DNA, but only under very particular conditions in dry DNA (29) or ethanol solutions (30) (see also ref. 31).

Although the twisting and stretching single-molecule manipulations were instrumental in renewing the interest in P-DNA models, such experiments can only report a limited number of “configurational” observables (e.g., an extension or a bead angle). It is therefore important to complement them by simulations that can reveal atomistic details of any assumed structural transition. The experimental report of double-stranded P-DNA did include a detailed structural model for P-DNA, generated by using molecular mechanics in helical coordinates (25). It involved minimization, in the absence of water and counterions, of a helically symmetric, periodic duplex with twist constraints (the number of degrees of freedom was significantly reduced by fixing bond lengths and many of the bond angles). However, the actual all-atom dynamics and thermodynamics of the transition have not been previously calculated.

Here we report a study of dynamics, structures, energies, entropies, longitudinal stretching forces (from here on interchangeably referred to as “forces,” or “tensions”) and transversal torques calculated from atomistic molecular dynamics simulations. For DNA, the calculated extension, rise, and the underlying forces torques that effect P-DNA transitions match well with experimental data. For RNA, we produce a model for how a P-RNA structure might look, and calculate the forces and torques that could produce it.

Nonequilibrium Structural Transitions

Overtwisting B-DNA Leads to P-DNA.

A large driving torque (600 pN·nm) and a tension of three magnitudes (10, 100, 1,000 pN) was simulated at both strands at the end of a dodecamer duplex (see Methods). In all three cases detailed below, the torque induced overtwisting of DNA and a subsequent transition to a structure with flipped-out bases. However, the magnitude of the pulling force had a significant impact on the details of the transition and the final shape of the DNA backbone.

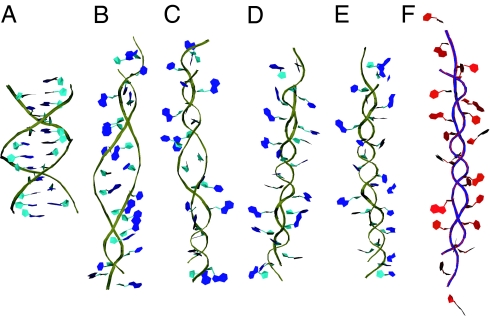
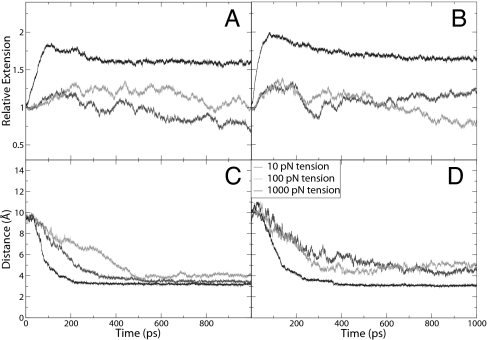
1. With 1,000 pN of force applied over a nanosecond, the initial behavior of the backbone was somewhat similar to that observed in the B- to S-DNA transition (17, 18) in that the backbone is elongated and the bases begin to tilt. A notable exception is that the sugars are forced closer together, whereas the bases flip out of the helix almost concomitantly (Fig. 1B). As the simulation proceeds (see supporting information, which is published on the PNAS web site), the twist propagates through the helix and the bases are exposed to solution, but not flipped all of the way out of the helix (Fig. 1C). By 500 ps, the backbone regularly winds around itself and the bases are all of the way exposed to solution. Between 500 ps and 1 ns, there is no discernible change as the structure settles in a P-form helix. Fig. 2A shows the relative extension of the DNA as a function of time, confirming that the helix is longest at 100 ps with a relative extension of 1.8, before shortening as it winds around itself to an extension of 1.6. The twist of the DNA increases from its initial value to a value fluctuating around 148° between adjacent base pairs, yielding a twist value of 2.25 base pairs per turn. Examination of the backbone spacing in Fig. 2C also shows that most of the transition is completed within the first 400 ps. The final spacing between strands is ≈3.2 Å, which brings the negative charges on the two backbones in much closer proximity than when in the B-DNA form. An atomistic view of the backbone structure (see supporting information) shows that sugar rings become approximately parallel to the helical axis, and that the phosphate anionic oxygens radiate outward to minimize their electrostatic repulsion. Simulation also reveals a longitudinal shift of one of the strands relative to the other by up to one nucleotide unit. Although this staggered configuration might occur in the experiment (base complementarity in P-DNA is lost and staggering could lower phosphate repulsions), it could also be caused by edge effects in our finite-size system. Therefore, calculations of equilibrium properties excluded the terminal bases (see below), and we expect the shift to not alter the structure or energy of the nonterminal bases.

   Given the values of our calculated extension (1.6) and twist (2.25 base pairs per turn), we believe that the simulation has created a P-DNA structure close to that formed in the single molecule experiments. Those reports indicate extension values of 1.6–1.75 and 2.4–2.6 base pairs per turn, depending on the study (14, 25, 26).

2. When only 10 pN of tension is applied to the molecule, DNA transitions to P form proceed at a slower rate than in the 1,000 pN case. This can be seen in the backbone spacing presented in Fig. 2C. The final structure has a buckled backbone (see supporting information) with an extension of only 0.76 of that of B-DNA (Fig. 2A). Due to its writhe, this structure is reminiscent of the supercoiled P-DNA reported in high torque/low pulling force single-molecule DNA experiments in ref. 14.

3. When 100 pN of tension is applied, the backbone still buckles, but not nearly to the extent seen in the 10 pN tension case, generating a middle section of supercoiled P-DNA and a section that consists of single strands extended into solution (see supporting information). When only the middle six bases are included in the analysis, the backbone spacing is 3.2 Å and the extension is 1.03, consistent with slightly supercoiled P-DNA. Although the edge fraying observed is a finite-size artifact of simulation, the structural data obtained from the middle base pairs provide reasonable putative models for the experimentally generated supercoiled structures.

Fig. 1.

Temporal evolution of B-to-P DNA transition. (A–E) Snapshots from temporal evolution of B-to-P transition induced by overtwisting B-DNA with positive driving torque and 1,000 pN tension. For comparison, we present a model of P-RNA in frame (F), produced by a similar driving simulation on A-RNA. Backbone for DNA is in gold with blue bases and RNA has a blue backbone with red bases.

Fig. 2.

Structural properties of B-to-P DNA transitions. (A) Relative extension of DNA under a positive driving torque. (B) Relative extensions of DNA under a negative driving torque. (C) Backbone spacing of DNA under a positive driving torque. (D) Backbone spacing of DNA under a negative driving torque.

Undertwisting B-DNA Leads to Alternative Structures.

We also simulated a negative driving torque (−600 pN·nm) on the dodecamer with the three driving forces.

1. Experiments have indicated (25) that undertwisting DNA leads to its denaturation. In a simulation with the negative driving torque and 10 pN of tension applied on B-DNA, this was observed. As the simulation proceeds (see supporting information), the torque first untwists the helix as the Watson–Crick hydrogen bonds become strained and begin to break. By 200 ps, the strands begin to translate relative to one another; at 500 ps, one strand is extended while the other coils around it with no obvious structure. The average backbone separation (Fig. 2D) is ≈4.6 Å, significantly larger than that for P-DNA, but not close to other types of organized DNA. This simulation indicates that undertwisting with a low tension leads to denatured DNA that could involve an intermediate with one strand twisted around the other in a disorganized fashion.

2. In contrast to the low-tension case, undertwisting while applying a tension of 1,000 pN produces a highly regular structure similar to P-DNA, but with a left-handed helical orientation (shown in supporting information). In the transition to this structure, the relative extension (Fig. 2B) and the backbone spacing (Fig. 2D) follow paths that are similar to those values obtained for by overtwisting with high tension. DNA passes through a state of zero twist before it retwists into a left-handed conformation with a twist of 158° and 2.28 pairs per turn. The undertwisting experiments, performed with low pulling forces, report denatured states and find no evidence for left-handed P states (14, 25). It is formally possible that the left-handed P forms we have generated in the simulations are transient states, and that a longer sampling time would lead to denaturation. However, it is also possible that, in particular, pulling geometries that apply (as done here) tension on both strands, these structures could be generated. We note that the simplified modeling of P-DNA in the original single-molecule report (25) had also proposed the existence of a left-handed P that was close to a mirror-like image of right-handed P-DNA.

3. When the medium pulling force (100 pN) is applied, the structure of DNA becomes a combination of denatured DNA and left-handed P-DNA (possibly supercoiled). The supercoiling reduces the relative extension (Fig. 2B) to 0.8. Although the average backbone separation (Fig. 2D) is at approximately the same level as in the 10 pN tension case, this is a result of the bases in the denatured region; the backbone in the left handed P-DNA region have a separation of ≈3.4 Å.

Model for a RNA Form: P-RNA.

We have performed simulations starting from an A-RNA structure using the same driving forces and torques used for DNA, i.e., 600 pN·nm positive and negative torque, with 10, 100, and 1,000 pN pulling forces (see supporting information). As was the case for DNA, overtwisting RNA with a large driving force produced a P-form structure that we refer to as P-RNA (see Fig. 1F). Although similar in overall shape with P-DNA, it differed in absolute extension, which was greater than P-DNA by ≈10% (see supporting information). Another distinction from the P-DNA simulations was that the backbone spacing, and consequently the atomic structure on the whole, approached the final P-RNA conformation on a slower time scale than in the DNA cases (i.e., around 300 ps for most of the bases and 900 ps for all of them as opposed to 150–300 ps for all DNA bases) for the collapse of the backbone spacing below 4 Å (see supporting information). This observation is in accord with results from umbrella sampling (see below and Fig. 3), which indicate a slightly steeper energy profile along the transition to P-RNA. Simulations with other torques and tensions created structures similar to those in the DNA case (left handed P-form, right handed supercoiled P, and denatured states) but also on a slower time scale when compared with DNA.

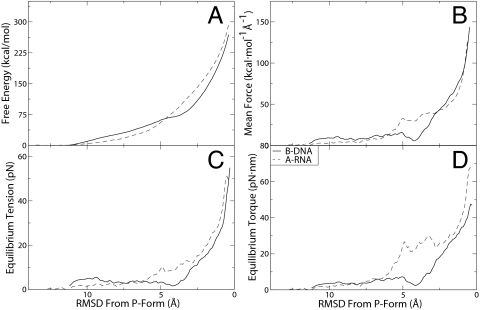
Fig. 3.

Equilibrium calculations of the B-to-P DNA and A-to-P RNA transitions. (A) Free energy profiles of B- to P-DNA and A- to P-RNA transitions. (B) Mean forces calculated from the derivative of the free energies. (C) Calculated equilibrium tensions for formation of P-DNA and P-RNA. (D) Calculated equilibrium torques for formation of P-DNA and P-RNA.

Equilibrium Calculations

Free Energy and Equilibrium Forces and Torques Along a B- to P-DNA Transition Isotherm.

Above, we presented driving simulations, i.e., simulations that induced conformational transitions to P forms on a rapid (irreversible) time scale, and that, therefore, produced trajectories amenable only to qualitative assessment. Here, we use the end-point structures from those simulations to rigorously perform an equilibrium, reversible transition. The underlying free energies are presented in quantitative terms by performing an extensive calculation of the potential of mean force (PMF) along the conformational transitions to the P forms. The transition coordinate, ρ, is chosen as the root-mean squared displacement (RMSD) of backbone atoms relative to a final P structure (see Methods for details). Results obtained by using umbrella sampling in combination with the weighted histogram analysis method are presented in Fig. 3A. Both B-DNA and A-RNA exhibit a large increase in free energy as structures approach the P forms.

For DNA, it is observed that the initial deformation from the B state to a state with ρ = 5 Å away from the P reference requires a relatively weak, linear increase in free energy. Structurally, for DNA conformations with a value of ρ >5 Å, the primary deformation is a lengthening of the axis, whereas the (nonterminal) bases remain at the center of the helix. As ρ decreases toward P values, the bases begin to flip outwards and the backbone twists around itself, causing a large increase in the electrostatic energies of the negatively charged backbones; this sets in over the interval ρ = 4.5 → 0.8 Å, and is characterized by a stronger, quadratic increase in the free energy. Although a gradual, rather than a sharp transition is observed over this interval (as expected due the finite, small size of the simulated dodecamer), visual inspection reveals that a P-DNA state is fully formed at a value of ρ ≈ 1 Å.

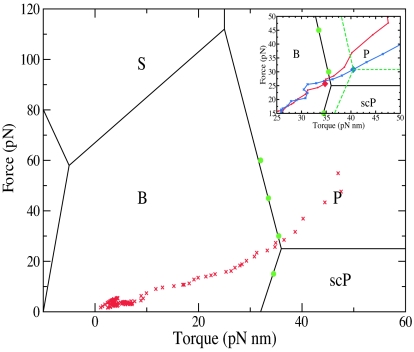
The mean forces obtained from the gradient of the PMF (in Fig. 3B, see Methods for details) are used to calculate the equilibrium tensions and torques (Fig. 3 C and D, respectively). In other words, for each value of ρ, we obtained the thermodynamically averaged force f(ρ) and torque τ(ρ) (where the average was over a constant-temperature ensemble of configurations) that would be needed to maintain the structure in equilibrium at that value of ρ. The reversible transition pathway such produced by umbrella sampling along ρ (in effect, a reversible isotherm in f–τ coordinates with ρ as an order parameter) allowed us to map the calculated force–torque pairs onto an experimentally derived (14) phase diagram of force–torque-dependent DNA states (26, 32) (see Fig. 4). Because the pathway is a result of umbrella sampling calculation that yields the lowest force needed to maintain in equilibrium a P-like structure, the isotherm passes almost through the “triple point” between B, P, and scP. This finding indicates that the lower bound for tensions required to induce P-forms is ≈25 pN, which validates the points on the phase diagram measured experimentally, and the overall features of the borderlines between B, P, and scP derived theoretically (compare figure 4a in ref. 32). Moving along the ρ pathway, structures created around ρ = 1.0 Å reveal the transition of DNA into P form. For them, we calculate an equilibrium tension of 25.7 ± 9.7 pN and an equilibrium torque of 34.8 ± 3.2 pN·nm (with the error estimates being the standard deviation of all structures within 0.25 Å of ρ = 1.0). This compares quite well with the torque-force triple-point experimental values of 25 pN and 34 pN·nm, respectively. In Fig. 4, it is also notable that our predicted f–τ DNA state at ρ = 1.0 Å lies on the border between B- and P-DNA phases exactly where mapped experimentally in ref. 14 (see Fig. 4), whereas structures with a lower ρ are deeper inside the P region. It is worth noting that in the region near the initial B-DNA structure (ρ > 9.5 Å), for which DNA is still in the entropic regime (F ≤ 10 pN), we were also able to calculate (see supporting information for details) a twist/stretch coupling constant of −15 nm. This finding agrees, both in sign and absolute value, with recent single molecule experiments indicating that, near the B form of DNA, an increase in twist leads to an increase in extension (33, 34).

Fig. 4.

The global force-torque phase diagram of DNA overlayed with points in force-torque space from our B to P, reversible, umbrella sampling pathway (or “isotherm”). Points in green have been previously measured experimentally (14). Note that, because the calculated equilibrium pathway yields the lowest force needed to maintain in equilibrium a P-like structure, the isotherm passes almost through the lower right “triple point” between B, P, and scP. This finding indicates that tensions lower than ≈25 pN cannot induce P-forms and validates the experimentally derived phase diagram. (Inset) A zoomed in region of the phase diagram with the value at ρ = 1, an approximate triple point, emphasized with a diamond, and a sketch of what a phase diagram with a triple point at this value may look like with green dashes. For comparison, the DNA isotherm is in red, whereas the RNA isotherm is in blue.

The A- to P-RNA Transition: Free Energy, Forces, Torques, and a Hypothetical Triple Point.

As for DNA, the P-RNA structure generated by the driving simulation was used as reference in defining the RMSD transition coordinate, ρ, and umbrella sampling of ρ was performed to calculate free energies and equilibrium forces and torques. The free energy profile of the transition from A- to P-RNA is initially lower than for the DNA case, but then begins to increase more rapidly at approximately ρ = 6.5 Å, which we attribute to the additional interstrand repulsion between the 2′ oxygen atoms. As RNA extends into P form, this effect becomes less significant but it does cause P-RNA to have a larger free energy than P-DNA. Throughout the second half of the transition, the equilibrium torques and tensions are higher than in the DNA case and we calculate that, at the “borderline” ρ = 1.0 Å, P-RNA has an equilibrium tension and torque of 30.8 ± 12.8 and 40.5 ± 6.4 pN·nm. By analogy with the DNA case, we predict that in an RNA phase diagram (which has not been experimentally mapped), this would correspond to a “triple point” of B, P, and scP RNA with higher forces and torques (see Fig. 4 Inset). Although it is formally possible that this is valid only for the particular sequence we studied, the “up-shift” of the force–torque values for the triple point we predict for RNA is consistent with measurements on a variety of stretched RNA sequences (24), which report an increase in the value of the force required to effect the A- to S-RNA transition by ≈10 pN relative to DNA. Two additional observations are noteworthy. First, the larger extension for RNA that we compute (see Table 2) is also in accord with the larger RNA stretching factor (1.0 relative to 0.7; compare ref. 24) measured in those experiments. Second, when compared with P-DNA, P-RNA has a larger variance in our calculated forces and torques, similarly to the experimental observation (24) of a larger variance in the plateau force for S-RNA.

Table 2.

Equilibrium forces (f), torques (τ), relative extensions (l/l₀), and twist for P-form nucleic acids calculated from umbrella sampling simulations at ρ = 1 (see text for details)

Structure	f pN	τ, pN·nm	l/l0	Twist, bp/turn
B-DNA	—	—	1.0	10.5
P-DNA	25.7 ± 9.7 (30)	34.8 ± 3.2 (34)	1.57 (1.6–1.75)	2.35 (2.4–2.6)
A-RNA	—	—	0.86	10.7
P-RNA	30.8 ± 12.8	40.5 ± 6.4	1.71	3.00

The numbers in parentheses are corresponding experimental data, where available, from refs. 14, 25, and 26.

Qualitative Decomposition of Energy and Entropy Changes.

The DNA internal energy contributions to the enthalpy change (see Methods for calculation details) for various structural transitions are presented in Table 1. Large positive change contributions arise from the van der Waals (Int_VDW) and electrostatic internal (Int_E) energy terms, which are due to the close proximity of the backbones. The other internal energy terms, Int_oth, also contributed significantly to the energy increase, as bonds and angles in DNA were rotated and stretched away from their B-form equilibrium values.

Table 1.

DNA internal energy and entropy changes (in kcal/mol) for structural transition from B-DNA upon simulations with driving torques and forces

fdriving	(−) Torque			(+) Torque
	10 pN	100 pN	1,000 pN	10 pN	100 pN	1,000 pN
ΔIntV DW	112	120	109	105	96	140
ΔIntE	554	515	628	681	551	586
ΔIntoth	396	521	489	490	415	475
−TΔSDNA	−258	−223	−68.4	−176	−170	−76.0

Our conformational entropy calculations (see Methods for details) have revealed an interesting compensation effect. The entropy change from canonical to twisted forms is serving as a significant counterbalance to the large enthalpy change estimated above. All simulations showed an entropy increase in the range of 0.19–0.72 kcal/(K·mol) (corresponding to a free energy decrease ranging from −76.0 kcal/mol to −258 kcal/mol, see supporting information for both DNA and RNA data). This relatively significant increase in entropy is ascribed to the flipped bases being free to move due to their lack of stacking, and is in accord with studies indicating that torsional rigidity of DNA correlates with the stacking energies and not with the melting temperatures (35).

It is important to reemphasize that the numbers in Table 1 are highly approximate. The sampling time of the driving simulations is not sufficient for accurate convergence. As described above, the quantitative description was brought in by the additional umbrella sampling simulations for the calculation of free energy profiles. Although, admittedly, the approximate nature of the decomposition here allows only a qualitative picture, an unequivocally large increase of the enthalpy for the system is expected to exist. In compensation, the increase in entropy helps to offset the enthalpic cost of the new structures created, but the additional, decisive compensation for the (still) high cost of creation of the structures is provided by the external twisting and pulling forces.

Structural Comparison of P-DNA and P-RNA.

Table 2 presents a comparison of forces and structural parameters for DNA and RNA from the configurations gathered during umbrella sampling. This equilibrium sampling has allowed us to create a more accurate calculation of extension and twist for P-DNA and P-RNA. We calculate that P-DNA has an average rise of 5.3 Å and an extension of 1.57 relative to the B-DNA initial structure. For P-RNA there is a slightly higher rise of 5.8 Å with an extension of 1.94 relative to the A-RNA initial structure (and 1.71 relative to the initial B-DNA structure). The additional electrostatic repulsion from the 2′ hydroxyl oxygen with the backbone could be forcing the backbone into a straighter conformation, creating the larger rise for P-RNA. The backbone torsion angles α to ρ were calculated for structures with ρ < 0.4 Å for P forms, ρ = 11.4–11.6 Å for B-DNA, and ρ = 13–13.2 Å for A-RNA (see supporting information). Angles α, β, δ, and ε did not vary significantly between the initial and final conformations. Rotations about the glycosidic bond χ appeared to be unaffected by the P-form backbone and were distributed according to the energy of steric hindrance between base and sugar. We also examined the puckering phase of the sugars in both P-DNA and P-RNA. For both overtwisting and undertwisting, we found that backbone P conformations did not influence the distribution of puckering at various edges in the sugar rings, which were again determined solely by the energy difference between north and south puckers (36, 37). The average counterion–phosphate distance does not change appreciably throughout the transition; however, because the backbone is more condensed, the local sodium concentration does increase from its initial value.

Concluding Discussions

We have presented a series of all-atom simulations concerning the effect of torsion and tension on double-stranded nucleic acids and have shown that that transitions to a P form or denatured states are possible. These forms are energetically disfavored under equilibrium conditions, but become favored when DNA is under the relatively high torque and tension that are applied by single-molecule manipulations or that can, in some instances, arise in nucleoprotein complexes.

We have presented the dynamics of how, in the high tension cases, ordered right-handed or left-handed P structures arise, and we have shown that, in the lower tension cases, the nucleic acid can either go toward a denatured state or a supercoiled P form.

Although the driving torques and forces used in our simulation to induce the overtorqued states were one to two orders of magnitude greater than those used in experiments, we have used them merely to generate the end structures (which agreed, in structural terms, i.e., extension and twist, with the experiments). In other words, we have used the irreversible trajectory generated with large torques/tensions simply as a “transportation” means to overcome the energetic cost to getting to P-DNA (and P-RNA). With the P structure as a target, we have then generated, using umbrella sampling, a reversible, equilibrium transformation pathway, and have calculated its free energy profile. From the free energy profile (a potential of mean force), we have derived the theoretically exact, lower, equilibrium forces and torques, thereby showing that these structures may be created by the forces and torques reported in single-molecule experiments. The good agreement between the calculated and measured parameters (force–torque, extension, rise) for P-DNA, and the passage of our calculated f–τ isotherm through the triple point of the experimentally derived phase diagram suggest strongly that the simulated structures correspond to those generated in the corresponding experiments, and lend credence to a model for the P-RNA structure we generated using similar conditions in the simulation of an A-RNA duplex.

The calculation of the free energy profile in the vicinity of B-DNA has additionally provided an equilibrium twist-elongation dependence (see supporting information) that enabled the calculation, in the low-twist limit, of a negative twist-stretch coupling constant of −15 nm, in accord with recent experiments (33, 34).

The fact that not only the driving torque, but also the driving tension (i.e., the forces applied along the helical axis) needed to be an order of magnitude larger in our nanosecond-time simulation to induce the microsecond-time (or longer) transitions to P forms reported by the experiments indicates that the conformational pathways to P are not perpendicular to the helical axis. Significant energy barriers are expected to exist in directions along the axis. This is not totally unexpected, given twist–stretch coupling in DNA (33, 34, 38, 39), and is in accord with the fact that stretching longitudinally undertwisted DNA induces a flipping out of bases that can activate homologous pairing in physiological conditions (15).

Movies of the structural dynamics to P-DNA, P-RNA, supercoiled P-DNA and denatured DNA, additional figures, and details of the twist-stretch coupling calculation are available on the PNAS web site.

Methods

Molecular dynamics simulations were performed with the program CHARMM (40), using version 27 of the nucleic acid force field parameters (41, 42). A canonical, double-helical B-form DNA of the Drew–Dickerson (43) dodecamer, d(CGCGAATTCGCG)₂ and a canonical, double helical A-form RNA of sequence (CGCGAAUUCGCG)₂ were generated. Their initial structures were aligned so that their primary axis were the x axis. They were overlaid with a previously equilibrated water box, containing TIP3P water molecules (44) and sodium ions, with dimensions 100 Å × 36 Å × 36 Å in the case of B-DNA and 100 Å × 40 Å × 40 Å for A-RNA. Any solvent molecules within 1.6 Å of nucleic acid heavy atoms were deleted and the appropriate number of sodium atoms farthest from the nucleic acid were also deleted to create an electrically neutral solution. Periodic boundary conditions were used, electrostatic interactions were calculated with the particle-mesh Ewald method (45), and Lennard–Jones interactions were truncated at 14 Å with a switch-smoothing function from 12 to 14 Å. For equilibration purposes, the system underwent 500 steps of steepest-descent minimization, followed by 2,000 steps of adopted basis Newton–Raphson minimization. The system was rapidly heated to 300 K over 0.6 ps, followed by an equilibration period of 1 ns with weak harmonic restraints applied to the C3′ carbon atoms at the 5′ and 3′ ends of each DNA strand, to prevent the helical axis from becoming unaligned with the x axis. The leapfrog Verlet algorithm was used with Nosé-Hoover dynamics (46, 47) to keep the temperature constant throughout the simulations. During equilibration, a 2 fs timestep was used with SHAKE (48) to constrain all covalent bonds involving hydrogens, whereas during all other simulations the timestep was reduced to 1 fs and SHAKE was not used.

The center of mass of the C3′ atoms of the terminal bases were restrained within a cylinder of radius 0.5 Å aligned along the x axis using a separate, flat-bottom, geometrical mean field harmonic potentials for each end with force constant of 10 kcal/mol/Ų. To simulate the experimental set-up, a pulling force was applied in the x direction to the C3′ atoms of the two bases at one end of the duplex, whereas the C3′ atoms of the bases at the opposite end were harmonically restrained in the x direction, but were otherwise free to move in the y–z% plane. A torsional force was coded in the CHARMM source. Its implementation followed directly from the definition of torque, τ = r × F and was applied to the C3′ atoms of the terminal bases of each strand such that each end was torqued in an opposite direction. Each individual torque had a magnitude of 300 pN·nm, resulting in a driving torque of 600 pN·nm. We defined the driving torque as positive if it acts in the direction that would increase the twist of the helix, whereas a negative driving torque lies in the direction that would decreases it. For each nucleic acid, we presented the results of six independent simulations, three with overtwisting of the DNA helix with a positive driving torque and pulling forces of 10, 100, and 1,000 pN, and three with a negative driving torque and pulling forces of 10, 100, and 1,000 pN. We analyzed the backbone spacing of the DNA, defined as the distance from a phosphorus atom to the closest backbone atom on the opposite strand, averaged over all bases, and the relative extension as the ratio of the instantaneous length to the initial one. We also examined the puckering phase of the sugar groups, with the definitions of puckering types based on the phase angle (49). Entropy calculations were performed with quasiharmonic analysis (50) using the last 250 ps of the simulation to determine the effective frequencies. The enthalpy change of various energetic contributions were obtained by averaging over the last 250 ps of the trajectories in the P states and subtracting values obtained from averaging over the last 500 ps of the B (or A) trajectories. Helical parameters for twist–stretch coupling were calculated with CURVES (51) and the program VMD (52) was used for the creation of movies and figure images.

The RMSD to the final (reference) structure, ρ = Σ_i=1^N (r_i − r_i^ref)²/N)^1/2, with i indexing the backbone atoms (P, O5′, C5′, C4′, C3′, and O3′, for a total of 142 atoms) was used as a transition coordinate for the conformational change. For both DNA and RNA, the reference structures were created by the simulations for which the driving torque overtwisted the respective duplex and 1,000 pN of tension were applied. The equilibrium forces and torques involved in the transitions were computed from the mean force 〈f(ρ)〉 on the system, where brackets denote canonical-ensemble averaging. The mean force was in turn derived from the potential of mean force (PMF), W(ρ) ≡ −k_BT ln∫ exp(−V(r)/k_BT)δ(ρ(r) − ρ)dr. Umbrella sampling (53) in combination with the weighted-histogram analysis method (54) as implemented by Grossfield (http://dasher.wustl.edu/alan) was used to calculate the potential of mean force W for the transition of B-DNA to P-DNA and A-RNA to P-RNA. Each window began with a snapshot from the overtwisting high/tension driving simulation at a corresponding ρ value in increments of 0.1 Å from their initial value (11.5 in DNA, 13.5 in RNA) to 0 (the reference state). Each window was run at two restraining potentials, one at 50 kcal/(mol·Å). For DNA these were run for 325 ps and for RNA for 305 ps. In the 150 kcal/(mol·Å) simulations, the first 25 ps was used as an initial equilibrium period and, for the 50 kcal/(mol·Å), the first 50 ps was used as an equilibration period. When combined, the windows thereby sampled 66.7 ns in the B-DNA case and 72.8 ns in the A-RNA case. The mean force was calculated by taking the numerical derivative of the free energy with a step size of 0.05 Å. To determine the tension on a single backbone atom i, the mean force along the x direction was computed by taking the derivative of W(ρ) with respect to x_i direction

Tension in the duplex was then computed by adding the two mean forces that acted longitudinally in each strand. The mean force 〈f_xi〉 was calculated for each heavy backbone atom i of nonterminal base pairs at 1-ps increments throughout the sampling periods for the PMF, and all tension values within a 0.125 Å window of the PMF were averaged, followed by averaging over all i atoms, to give the equilibrium tension on the nucleic acid. Similarly, we calculated the equilibrium torque by finding the backbone forces in the y and z directions and adding, for the backbone atoms of each nonterminal base pair (i.e., the kinematic unit involved in nucleobase rotations; ref. 55), the cross products with the radii vectors of the helix