Mapping protein collapse with single-molecule fluorescence and kinetic synchrotron radiation circular dichroism spectroscopy

Abstract

We have used the combination of single-molecule Förster resonance energy transfer and kinetic synchrotron radiation circular dichroism experiments to probe the conformational ensemble of the collapsed unfolded state of the small cold shock protein CspTm under near-native conditions. This regime is physiologically most relevant but difficult to access experimentally, because the equilibrium signal in ensemble experiments is dominated by folded molecules. Here, we avoid this problem in two ways. One is the use of single-molecule Förster resonance energy transfer, which allows the separation of folded and unfolded subpopulations at equilibrium and provides information on long-range intramolecular distance distributions. From experiments with donor and acceptor chromophores placed at different positions within the chain, we find that the distance distributions in unfolded CspTm agree surprisingly well with a Gaussian chain not only at high concentrations of denaturant, where the polypeptide chain is expanded, but also at low denaturant concentrations, where the chain is collapsed. The second, complementary approach is synchrotron radiation circular dichroism spectroscopy of collapsed unfolded molecules transiently populated with a microfluidic device that enables rapid mixing. The results indicate a β-structure content of the collapsed unfolded state of ≈20% compared with the folded protein. This suggests that collapse can induce secondary structure in an unfolded state without interfering with long-range distance distributions characteristic of a random coil, which were previously found only for highly expanded unfolded proteins.

With the discovery of small proteins that fold in the absence of populated intermediates (1), our quantitative understanding of the elementary properties of protein folding reactions has made significant advances, including the structural characterization of transition states for folding (2) and the prediction of folding rates from native structure (3–5). One of the most severe limitations for the further development of these approaches is our ignorance about the energetic or structural properties of unfolded^†† states of proteins. Because of the structural heterogeneity and complexity of the ensembles of conformations populated by unfolded proteins, their experimental characterization has proven extremely difficult. Traditional methods, such as small-angle scattering techniques (6), provide only global physical properties, e.g., the radius of gyration. In some cases, more detailed structural information can be obtained from NMR (7–10), but these studies usually provide information about the denatured state only under nonnative conditions, typically in the presence of large concentrations of denaturant, or through severe destabilization of the native state induced by covalent modification or mutations. The most interesting and physiologically relevant situation, however, is that of an unfolded state of a stable protein under native conditions. Unfortunately, the great majority of molecules will then be present in their native conformation, thus overwhelming the signal from unfolded molecules.

We avoid this problem by using two complementary optical techniques: single-molecule fluorescence and kinetic synchrotron radiation circular dichroism (SRCD) spectroscopy. Single-molecule spectroscopy has the inherent ability to separate the signals from subpopulations in heterogeneous mixtures and equilibria, which makes it ideally suited to analyze protein folding reactions (11, 12). Specifically, by using single-molecule Förster resonance energy transfer (FRET), intramolecular distances of the unfolded state can be measured even in the presence of a majority of folded molecules (13, 14). Recently, the collapse of unfolded molecules of the small cold shock protein CspTm at close to native conditions was discovered with this approach (14). This collapsed unfolded form also can be populated kinetically (15, 16) and has by now been found for a range of small proteins (16–20). It is unclear, however, whether this collapse is a nonspecific random heteropolymer collapse (21) or whether it is accompanied by the formation of specific structure. By placing FRET dye pairs in various positions of the protein, we obtain information on distance distributions in different segments of the unfolded polypeptide chain and their dependence on denaturant concentration.

A versatile method to complement such distance constraints with information about the secondary structure content is circular dichroism (CD) spectroscopy. In this case, however, we have to transiently populate the unfolded state under native conditions by using rapid mixing experiments. For this purpose, we use SRCD spectroscopy with a specifically designed microfluidic continuous-flow mixing system with millisecond dead time. In this way, the collapsed unfolded state, which is populated on a microsecond time scale or faster (14, 16), can be studied spectroscopically without interference from the signal of folded molecules, which form on a slower time scale. Importantly, SRCD gives us access to the far-UV wavelength range, where β-structure can be well distinguished from random coil (22, 23) but which is inaccessible with commercial stopped-flow instruments.

Results

Collapse from FRET Efficiency Histograms.

For the single-molecule FRET experiments, donor (Alexa Fluor 488) and acceptor (Alexa Fluor 594) dyes were placed specifically at different solvent-exposed positions of CspTm via pairs of Cys residues introduced by site-directed mutagenesis (Fig. 1). Upon unfolding of the protein, the average distance between the chromophores increases. As a consequence, the rate of energy transfer between them decreases, resulting in a reduced transfer efficiency E = n_A/(n_A + n_D), where n_A and n_D are, respectively, the number of acceptor and donor photons emitted by the molecule [including corrections (24), see Materials and Methods]. In confocal single-molecule experiments, transfer efficiencies are determined from photon bursts originating from individual molecules freely diffusing through the focal spot of the laser beam (25). A histogram from a large number of such events shows distinct maxima corresponding to the subpopulations present in the sample (Fig. 2). The peak at high E corresponds to folded molecules, and the peak at intermediate E corresponds to unfolded molecules. The additional peak near E = 0 is thought to be caused by molecules lacking an active acceptor chromophore (24, 26) but does not interfere with our analysis.

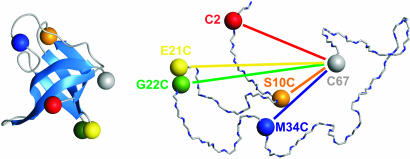
Fig. 1.

Schematic of folded (Left) and unfolded (Right) CspTm with the sites for dye attachment for FRET indicated by colored spheres. For every variant investigated, one dye was reacted with Cys at position 67, and a second dye was reacted with a Cys at one of the other positions shown.

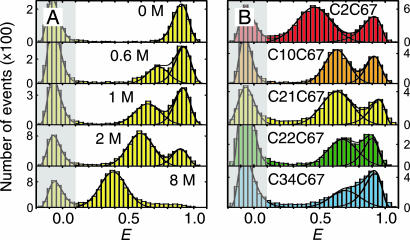
Fig. 2.

Energy transfer efficiency (E) histograms from single-molecule FRET measurements. (A) Examples from a GdmCl titration of variant C21C67, illustrating unfolded state collapse. See SI Movie 1 for a complete data set of C2C67. (B) Histograms of all variants at 1.5 M GdmCl. The peak at E ≈ 0.9 corresponds to folded molecules, and the peak at intermediate E corresponds to unfolded molecules. The peak at E ≈ 0 (shaded) originates from molecules with an inactive acceptor (26). To determine mean transfer efficiencies, the unfolded peak was fit to a normal distribution, and the other two peaks were fit to log normal functions (black lines) (14). The colors used correspond to those used in Fig. 1.

With increasing concentration of the denaturant guanidinium chloride (GdmCl), we observe a change in the relative amplitudes of the signal from native and unfolded molecules, corresponding to the expected redistribution of the two populations (Fig. 2A). However, whereas the mean transfer efficiency 〈E〉 of the folded state is invariant, the peak from unfolded molecules is continuously shifting to higher transfer efficiencies with decreasing GdmCl concentration. By comparison with stiff polyproline peptides, it has previously been shown that this increase in 〈E〉 corresponds to a collapse of the unfolded state in response to the altered solvent conditions (14). To address the question of whether this collapse is a global process that is evenly distributed across the polypeptide chain or whether it is due to compaction of a specific part of the molecule, we measured single-molecule transfer efficiency histograms of the labeled CspTm variants at a wide range of denaturant concentrations. At a given GdmCl concentration, 〈E〉 in the unfolded state shows an overall increase with decreasing sequence separation, as expected (Fig. 2B). Moreover, all variants exhibit the characteristic continuous collapse at low concentrations of denaturant, resulting in an increase in 〈E〉 [Fig. 3A and supporting information (SI) Movie 1].

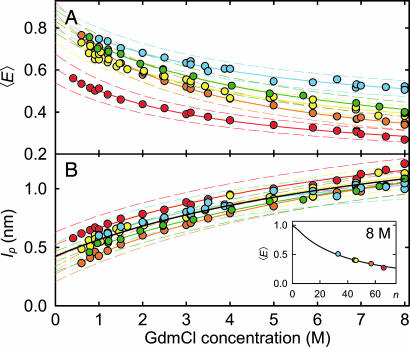
Fig. 3.

Denaturant dependence of the mean transfer efficiencies 〈E〉 and persistence lengths l_p. (A) 〈E〉 of the unfolded state of all variants as a function of GdmCl concentration. (B) l_p calculated from 〈E〉 using Eqs. 1–4. (Inset) Shows the measured values of 〈E〉 for all variants at 8 M GdmCl, and as a black line 〈E〉 for a Gaussian chain calculated from Eqs. 1–4 for l_p = 1.1 nm (the mean value of all variants) as a function of sequence separation n (number of peptide bonds excluding linkers).^‡‡ The solid lines in the GdmCl titrations are fits to the empirical equation y = y₀ [1 + ΔyKx/(1 + Kx)] used for interpolation; the solid black line is a fit to all data. Estimated error ranges for 〈E〉 and l_p are indicated by dashed lines (see SI Materials and Methods). The colors used correspond to those used in Fig. 1.

Distance Distributions from Mean Transfer Efficiencies.

To analyze the mean transfer efficiencies in terms of distance distributions in the unfolded state, we use the Gaussian chain model, the simplest realistic model for describing large-scale properties of macromolecules (21), such as highly unfolded peptides and proteins (6, 27–31). 〈E〉 of the unfolded state at a given GdmCl concentration can be expressed in terms of the end-to-end distance probability distribution function of a Gaussian chain P(r) and the distance dependence of the transfer efficiency E(r) according to^§§

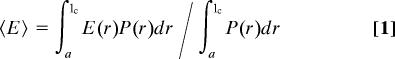with

and

where r is the end-to-end distance, a is the distance of closest approach of the chain ends, l_c is the contour length of the labeled polypeptide segment (with dyes and linkers, see Materials and Methods), and R₀ is the Förster radius of the dye pair at the GdmCl concentration of the solution (R₀ = 5.4 nm at 0 M GdmCl; see SI Materials and Methods for details). The mean squared end-to-end distance 〈r²〉 of a Gaussian chain can be expressed as

where n is the number of peptide bonds between the chromophores, l is the projection of the distance between two consecutive α-carbon atoms on the axis of the fully extended chain (0.38 nm), and l_p (the only free parameter in the model) is a measure for the effective chain stiffness, which in our limit of l_c ≫ l_p is equivalent to the persistence length commonly used in the worm-like chain model (34). Fig. 3B Inset shows the measured 〈E〉 of our CspTm variants at 8 M GdmCl. The continuous line shows 〈E〉 as a function of n calculated according to Eqs. 1–4 with l_p = 1.1 nm. All variants can be described with the same value of l_p, indicative of isotropic distance distributions within unfolded CspTm, and in agreement with previous results on other proteins unfolded at high denaturant concentrations (27–30).

Fig. 3B shows l_p for every variant as a function of GdmCl concentration calculated from 〈E〉 (Fig. 3A) using Eqs. 1–4. The concomitant renormalization for chain length allows a direct comparison of the variants with different sequence separation of donor and acceptor. The values of l_p averaged over all variants range from 1.1 ± 0.1 nm at 8 M GdmCl, to 0.39 ± 0.07 nm extrapolated to 0 M GdmCl (Fig. 3B), close the values found in atomic force microscopy experiments (0.33 to 0.42 nm; summarized in ref. 31) or unstructured peptides [0.64 nm (32)] at 0 M GdmCl. All variants show a similar denaturant dependence of l_p, suggesting isotropic chain collapse. From these data alone we cannot exclude that the more pronounced differences at low denaturant concentrations, especially for variant C10C67, may indicate slight deviations from completely isotropic collapse, but several points suggest otherwise. First, it seems structurally implausible that C2C67 and C21C67, which flank the slightly deviating C10C67, exhibit distance distributions in accord with the remaining variants, whereas a large difference occurs between C2C67 and C10C67. Second, other effects, such as changes in the photophysical properties of the chromophores upon collapse, may play a role; e.g., the two lysine residues directly neighboring Cys-10 may act as fluorescence quenchers (35) whose electrostatic interaction with the negatively charged fluorophores may be shielded at high GdmCl concentrations. In view of the error ranges we estimate for this type of measurement (Fig. 3), we conclude that the data are in agreement with isotropic collapse and do not justify an interpretation beyond this simple model.

Subpopulation-Selective Fluorescence Lifetime Distribution Analysis.

Mean transfer efficiencies obtained from transfer efficiency histograms do not provide direct information about the shape of the distance distribution, because the dynamics of inter-dye distance fluctuations are fast compared with the millisecond observation time per burst (14, 36). Fluorescence intensity decays, on the other hand, do report directly on the shape of the distance distribution (37, 38), because distance fluctuations for long polypeptides are slow relative to the fluorescence lifetimes of the dyes (32, 33). Conventional approaches to the analysis of distance distributions from fluorescence lifetimes suffer from interference with signal from native molecules; however, in combination with the separation of subpopulations by virtue of single-molecule detection, we can selectively analyze distance distributions in the unfolded state while remaining unaffected by native signal (17). For every individual fluorescence burst, the mean donor fluorescence lifetime is estimated (39) in addition to E. From the resulting two-dimensional histograms (Fig. 4A), we select the bursts corresponding to the unfolded state and, by combining the photons from all unfolded molecules, obtain high-resolution fluorescence decays (Fig. 4B). Donor and acceptor decays are then analyzed in a global fit^¶¶ that assumes a distribution of transfer rates resulting from the distribution of donor–acceptor distances (see SI Materials and Methods), analogous to the established procedures for ensemble data (17, 38, 40). Specifically, we use P(r) of a Gaussian chain (Eq. 3) with 〈r²〉 as the only free parameter.

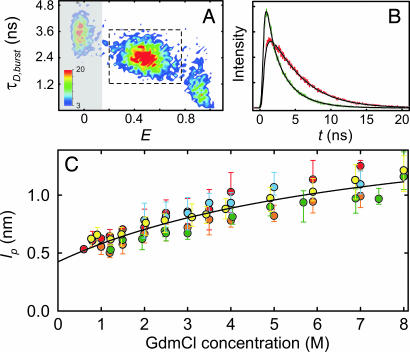
Fig. 4.

Fluorescence lifetime distribution analysis. (A) All events corresponding to unfolded molecules were selected (dashed box) from a two-dimensional histogram (shown is C2C67 at 1.5 M GdmCl) of the number of bursts (color scale) with transfer efficiency E and donor fluorescence lifetime τ_D,burst. (B) The photons were combined to generate time-correlated single-photon counting histograms for donor (green) and acceptor (red) (see SI Movie 2 for a complete data set of C2C67). (C) The rms end-to-end distance was determined and converted to the apparent persistence length l_p (Eq. 4) by using a global fit assuming the distance distribution of a Gaussian chain (black lines). Error bars indicate the uncertainty in the fits. The solid black line in is a fit to all data as described in Fig. 3. The colors used correspond to those used in Fig. 1.

The time-correlated single-photon counting histograms from unfolded molecules are fit well, if we assume the distance distribution of a Gaussian chain (Fig. 4B; see also SI Movie 2), and again we observe a continuous collapse of the chain for all variants, with the expected increase in 〈r²〉 with n (data not shown). To normalize the data for n and to facilitate direct comparison of lifetime and intensity results, we calculate l_p from 〈r²〉 (Eq. 4) (Fig. 4C). The greater demands on the signal-to-noise ratio for this type of analysis reduces the number of suitable data sets, especially at low GdmCl concentrations, where the overlap between native and unfolded subpopulation increases, but nevertheless we again find a similar GdmCl-dependence of l_p for all variants. The good overall agreement of fluorescence intensity (Fig. 3B) and lifetime (Fig. 4C) results and the lack of consistent deviations from the averages in Figs. 3B and 4C provide additional evidence that the remaining differences between variants seen in either analysis are within the errors of the methods. The combined results of single-molecule intensity and lifetime data therefore suggest that the chain dimensions of CspTm are isotropic and Gaussian chain-like on the length scale we are probing, even for strongly collapsed unfolded molecules. But does this random coil behavior exclude the presence of secondary structure in the collapsed unfolded state?

Secondary Structure Content from SRCD.

An ideal method to quantify the secondary structure content of proteins is CD spectroscopy. Collapse of Csp has been shown to occur on a microsecond timescale or faster (12, 14, 16), whereas the folding rate at low GdmCl concentrations is in the tens of milliseconds range (41). In a kinetic mixing experiment with millisecond time resolution, the collapsed unfolded state is therefore formed during the dead time, and only the actual folding process is resolved. The dead time signal amplitude reports on the change in structure during collapse. However, although the formation of α-helical structure is readily observed with stopped-flow CD spectroscopy (typically at 222 nm), formation of β-sheet structure is often not accessible because of the small difference in CD signal between a random coil and β-structure as well as the strong influence of aromatic amino acids at wavelengths of >220 nm (42), the range available in conventional stopped-flow CD. Accordingly, previous attempts to measure secondary structure formation upon collapse of CspTm with CD spectroscopy have failed (B.S., unpublished results). To solve this problem, we have started to establish a methodology for which SRCD is used with microfabricated rapid mixing devices. SRCD has the advantage of high photon flux in the far UV below 220 nm, where the CD signal differences between random coil and β-structure become very pronounced (43), and the Gaussian beam shape allows focusing into microstructures. Microfluidic mixers (44) permit the implementation of sophisticated mixing strategies, making them the fastest method available for rapid-dilution experiments (45). They can be fabricated in fused silica with path lengths in the micrometer range, thus maximizing transmission in the far UV range. Because of the small feature size, sample consumption is drastically reduced compared with conventional continuous-flow mixing experiments (46), some of which have already led to substantial improvements both in time resolution and accessible wavelength range in kinetic CD experiments (47).

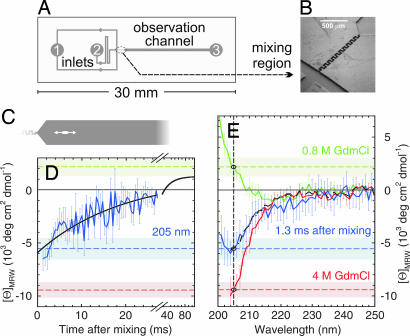
For refolding, CspTm in 4 M GdmCl was diluted to a final concentration of 0.8 M GdmCl (Fig. 5). The actual mixing region (Fig. 5B) consists of a narrow serpentine-shaped channel that performs mixing in the laminar flow regime by virtue of diffusion and chaotic advection (48). CD kinetics were measured by scanning the synchrotron radiation beam along the broader observation channel (Fig. 5C). Different positions in the channel thus correspond to different times after mixing, with a dead time of 1.3 ms. A kinetic trace taken at 205 nm (Fig. 5D), fit to a single exponential decay, resulted in a time constant of 19 ± 4 ms, in good agreement with the folding rates measured with stopped-flow fluorescence under identical conditions (41). However, the CD signal of −6 × 10³ deg·cm²·dmol⁻¹ at 1.3 ms does not coincide with the CD signal of CspTm unfolded in 4 M GdmCl (Fig. 5 D and E, dashed red line), indicating the formation of secondary structure before the actual folding reaction.

Fig. 5.

Secondary structure content of collapsed unfolded CspTm from SRCD. (A) Channel pattern of the microfluidic mixing device. To initiate refolding, unfolded protein injected into inlet 2 is diluted with buffer injected into inlet 1. (B) Rapid mixing occurs in the serpentine-shaped channel shown as a scanning electron micrograph. (C) The synchrotron radiation beam (white ellipse) is positioned in the observation channel. (D) Refolding kinetics of CspTm at 0.8 M GdmCl measured at 205 nm (blue line; error bars give one standard deviation calculated from eight measurements) and a single-exponential fit to the data (solid black line). (E) CD spectrum taken 1.3 ms after mixing (solid blue line), compared with equilibrium spectra under native (solid green line; 0.8 M GdmCl) and unfolding conditions (red line; 4 M GdmCl). The corresponding ellipticities at 205 nm are indicated in the spectra as dashed blue, green, and red lines, respectively. The shaded light blue, green, and red bands indicate one standard deviation from the equilibrium ellipticities of folded and unfolded CspTm, respectively, at 205 nm. The black dashed–dotted curve is a linear combination of the spectra at 0.8 M and 4 M GdmCl used to estimate the secondary structure content of collapsed unfolded CspTm.

For spectral information on collapsed unfolded CspTm, wavelength scans were taken 1.3 ms after mixing (Fig. 5E, solid blue line), when the fraction of native molecules calculated from the folding time is only 7%. Steady-state spectra of CspTm unfolded in 4 M GdmCl (Fig. 5E, solid red line), and native CspTm in 0.8 M GdmCl (Fig. 5E, solid green line) were recorded in the same mixing device and corrected for baselines taken without protein under otherwise identical conditions. These spectra illustrate the advantage gained by extending the wavelength range to <220 nm. Fitting the CD spectrum of collapsed unfolded CspTm to a linear combination of the spectra in 4 M and 0.8 M GdmCl (Fig. 5E, black dash–dotted curve) results in a signal change of ≈27% relative to the native structure (excluding the contribution from the 7% folded molecules). Relating this amplitude quantitatively to β-structure content is complicated by the contribution of aromatic amino acids to the native state signal, but from CD reference spectra for β-sheet (43) and the β-structure content from the NMR structure of CspTm (49), we estimate for the collapsed unfolded protein at 0.8 M GdmCl a β-structure content of ≈20% relative to the native protein (assuming no contribution from aromatic amino acids to the CD of collapsed unfolded CspTm). A very small population of additional α-helical structure cannot be excluded, but from the signal at 222 nm, the α-helix contribution is not more than approximately −1 × 10³ deg·cm²·dmol⁻¹, corresponding to less than ≈3% α-helix (43).

Discussion

Over the past 40 years, many proteins unfolded at high concentrations of denaturant have been shown to obey Gaussian chain statistics on a global scale (6, 27–30, 50, 51). CspTm is no exception in this respect. Its radius of gyration in 6 M GdmCl calculated from all labeled variants [using Eq. 4 and R_g² = 〈r²〉/6 (21)] is 2.9 (±0.1) nm excluding dye linkers, in agreement with the 2.4 (+0.4/−0.2) nm calculated from the scaling law given by Kohn et al. (30, 51). But how does the collapse of the unfolded state at low GdmCl concentrations affect the intramolecular distance distributions? Surprisingly, even under near-native conditions, the agreement with Gaussian chain behavior is good, and l_p is similar for all intramolecular distance pairs (Figs. 3B and 4B). At 1 M GdmCl, for instance, the resulting radii of gyration equal 2.2 (±0.2) nm. The small variance suggests that the distance distributions within the unfolded protein are rather isotropic. We thus have no evidence for native state topology in collapsed unfolded CspTm, in contrast to NMR experiments on staphylococcal nuclease (8) and eglin (52) at high concentrations of urea and in contrast to suggestions from simulations (53). Similarly, there is no obvious relation to the transition state structure (54). Our observation is in contrast to recent measurements on chymotrypsin inhibitor 2 and acyl-CoA-binding protein, where indications were found for a substantial deviation of the collapsed denatured state from Gaussian chain behavior (17) possibly involving folding intermediates (55). In summary, we conclude from the single-molecule fluorescence data that unfolded CspTm is close to a random coil in terms of polymer physics, even under near-physiological conditions.

It may therefore come as a surprise that the collapsed unfolded state contains a significant amount of β-structure, as was observed in our kinetic SRCD experiments. How can we reconcile these two observations? Clearly, global random coil behavior does not exclude the presence of short structured segments (30, 56–58), even more so if these are only populated transiently. This argument has been used to resolve the seemingly conflicting views of residual structure observed in proteins under highly denaturing conditions on the one hand and the successful description of global properties of unfolded polypeptides with the random coil model on the other (59, 60). Our results suggest that there are cases for which we must extend this notion of a random coil with residual structure even to the collapsed unfolded state, populated under conditions that have so far evaded confrontation with the “reconciliation problem” (6). Compaction of the chain would be expected to contribute to the formation of local structure, because the increase in excluded volume effects will introduce more steric interference with non-nearest-neighbor residues (29, 60). As a result, the backbone will be forced even more into the core regions of the Ramachandran map, corresponding to extended structures that avoid such steric conflicts. The largest one of these regions, and thus entropically the most favorable one, is the extended structure of β-strands. The particular preference of CspTm for this conformation is reflected by its extremely low propensity for the formation of α-helices [<1% helical content predicted with AGADIR (61)].

Currently, we have no direct evidence for the detailed conformation and average length of β-strand segments populated in collapsed unfolded CspTm. Because Gaussian-distributed intramolecular distances can only be observed if the segment length is considerably less than the contour length (21), the stretches of β-conformation must be short relative to the sequence separation of our dye pairs. Details about more local distance distributions could be addressed by using FRET pairs with much smaller Förster radii, which are currently inaccessible to single-molecule spectroscopy. In a very recent study, the dead time amplitudes of stopped-flow ensemble FRET experiments were used to probe the first β-hairpin of a closely related cold shock protein for local conformational preferences in the collapsed unfolded state (62). Magg et al. (62) observed a stretching of the second β-strand upon collapse, suggesting that the CD signal observed in our experiments could be due to strands of lengths approaching those in the native state. The question of segment length could possibly also be addressed with new methods for the analysis of CD spectra in terms of the number and size of structured segments in proteins (63, 64), but the current quality of our CD spectra for collapsed unfolded CspTm does not yet warrant such detailed deconvolution. The further development of kinetic SRCD and its combination with single-molecule fluorescence will be an important complementation of NMR methods in clarifying these structural details and the question of whether the behavior of CspTm is an exception or possibly a more general characteristic of such small all-β proteins.

Materials and Methods

Synthesis and Labeling of CspTm Variants.

Cysteine residues were introduced by site-directed mutagenesis to provide functional groups for the specific attachment of the dyes essentially as described previously (14). Expression and purification of Cys variants and wild-type protein were performed as described by Kremer et al. (49) (for details, see SI Materials and Methods).

Confocal Fluorescence Spectroscopy.

Observations of single-molecule fluorescence were made with a MicroTime 200 confocal microscope (PicoQuant, Berlin, Germany) equipped with a 470-nm pulsed diode laser (LDH 470) operated at 40 MHz (average power, 130 μW) and an Olympus (Tokyo, Japan) UplanApo ×60, 1.20-W objective. Sample fluorescence was separated into donor and acceptor components with a dichroic mirror (Chroma 585DCXR) and two final filters (Chroma HQ525/50 and Omega 600ALP). Each component was focused onto an avalanche photodiode (SPCM-AQR-15; PerkinElmer Optoelectronics, Fremont, CA), and the arrival time of every detected photon was recorded relative to the exciting laser pulse with a time resolution of 38 ps. Samples of labeled protein were diluted to a concentration of ≈20 pM in 50 mM sodium phosphate buffer at the appropriate GdmCl (Pierce, Rockford, IL) concentration and individually adjusted to pH 7. Tween 20 (0.001%; Pierce) was added to prevent surface adhesion of the protein (14). Data were taken for 30–60 min.

Single-Molecule Data Reduction and Analysis.

Successive photons detected in either channel separated by <100 μs were combined into one burst. A burst was retained as a significant event if the total number of counts exceeded 50. Identified bursts were corrected for background, differences in quantum yields, the different collection efficiencies of the detection channels, cross-talk, and direct acceptor excitation with the matrix approach (24) (SI Materials and Methods). For determining l_p, the length of dyes and linkers were assumed to be equivalent to an additional 9 aa total, comparable with previous estimates (14, 17, 51, 65). Fluorescence lifetime distribution analysis was performed as described by Laurence et al. (17), except that the time-correlated single-photon counting histograms obtained from the unfolded state subpopulations were analyzed in terms of donor–acceptor distance distributions of a Gaussian chain (38, 40) (for details, see SI Materials and Methods).

Microfluidic Mixing Devices and Synchrotron Radiation Circular Dichroism.

Mixers were fabricated by deep reactive ion etching of fused silica substrates (HPFS Standard Grade, Corning code 7980; Corning, Corning, NY) to a depth of 14.5 μm. Mixers were sealed by direct fusion wafer bonding to another fused silica substrate. A serpentine-shaped channel after the T region joining the inlet channels performs mixing in the laminar flow regime by diffusion and chaotic advection (48). Dean vortices in the transverse plane and corner vortices in the longitudinal plane accomplish mixing by stretching and folding the fluid streamlines. The widening of the channel after mixing slows down the flow, resulting in an accessible time window of ≈27 ms before the solution reaches the exit port (labeled “3” in Fig. 5A).

Microfluidic devices were mounted in the SRCD sample chamber (see SI Materials and Methods) via a custom-designed holder with connections to two syringe pumps (PHD22/2000; Harvard Apparatus, Holliston, MA). Motorized translation stages (M-111.1; PI, Karlsruhe, Germany) allowed reproducible positioning of the mixer relative to the beam. For refolding, a solution of 6.7 mM unfolded CspTm in 4 M GdmCl/50 mM sodium phosphate buffer (pH 7.0) was injected through inlet 2 (Fig. 5) at a flow rate of 30 μl/min and mixed with buffer solution without GdmCl injected through inlet 1 at a flow rate of 120 μl/min. Complete mixing was assessed via absorbance and CD scans orthogonal to the flow direction across the observation channel. Flow rates ≥150 μl/min [corresponding to flow velocities of 6.9 m/s in the mixing channel (25 μm wide) and 0.43 m/s in the observation channel (400 μm wide)] were found to result in uniform concentrations after the mixing region. The dead time calculated from these flow rates and the position of the synchrotron beam is 1.3 ms.

Abbreviations

FRET

Förster resonance energy transfer

CD

circular dichroism

SRCD

synchrotron radiation CD.