Extending the absorbing boundary method to fit dwell-time distributions of molecular motors with complex kinetic pathways

Abstract

Dwell-time distributions, waiting-time distributions, and distributions of pause durations are widely reported for molecular motors based on single-molecule biophysical experiments. These distributions provide important information concerning the functional mechanisms of enzymes and their underlying kinetic and mechanical processes. We have extended the absorbing boundary method to simulate dwell-time distributions of complex kinetic schemes, which include cyclic, branching, and reverse transitions typically observed in molecular motors. This extended absorbing boundary method allows global fitting of dwell-time distributions for enzymes subject to different experimental conditions. We applied the extended absorbing boundary method to experimental dwell-time distributions of single-headed myosin V, and were able to use a single kinetic scheme to fit dwell-time distributions observed under different ligand concentrations and different directions of optical trap forces. The ability to use a single kinetic scheme to fit dwell-time distributions arising from a variety of experimental conditions is important for identifying a mechanochemical model of a molecular motor. This efficient method can be used to study dwell-time distributions for a broad class of molecular motors, including kinesin, RNA polymerase, helicase, F₁ ATPase, and to examine conformational dynamics of other enzymes such as ion channels.

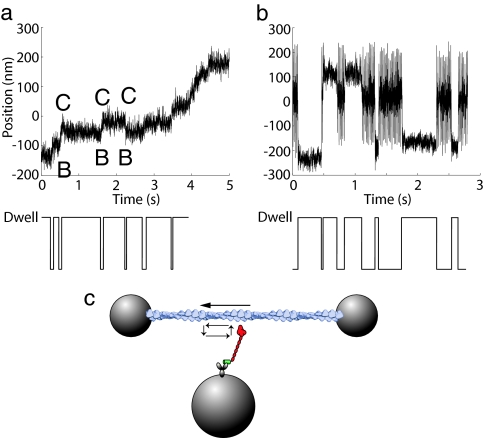
The movements of molecular motors are frequently recorded in biophysical experiments using tools such as optical trap assays and single molecule fluorescence assays. Due to transitions of conformational and chemical states, the motions of molecular motors usually show alternations between an enzyme's moving and pausing behaviors. For example, double-headed myosin VI moving on an actin filament demonstrates a mechanical stepping behavior (Fig. 1a) (1), whereas the events of actin binding and unbinding of a single-headed myosin V construct show alternate phases of oscillating and pausing (Fig. 1b) (2). Collecting a large number of these events and performing statistical analysis provides insight into the kinetics and mechanochemical characteristics of an individual molecule.

Fig. 1.

Dwell events obtained from single-molecule experiments with myosin V and myosin VI. (a) Dwells in mechanical stepping of a double-headed myosin VI. (b) Dwells of actin binding and unbinding for single-headed myosin V. The portions of large oscillations correspond to the actin unbound states, whereas the portions of small fluctuations correspond to the actin bound states. (c) The movement of an actin filament (top arrow) driven by the power stroke of a single-headed myosin V attached to a bead. The arrows on the left of myosin indicate the cyclic behavior of binding, power stroke, unbinding, and recovery.

Dwell events arise from pauses in mechanical stepping (1a) or stochastic delays before a binding–unbinding transition (Fig. 1b). Each dwell represents an experimentally observable event, which can be a single conformational or chemical state, or a collective number of states. The dwell time, or the duration of a dwell, is determined by the probability of exiting a dwell after the time entering it. Histograms of dwell times, also called dwell-time distributions, waiting-time distributions, or distributions of pause durations, are widely used to decipher single molecule kinetics.

The dynamics of an enzyme's activity can be modeled as a number of kinetic states using kinetic equations (3) or mechanical coordinates using diffusion-based (Fokker–Planck) equations (4). For questions addressed in this study, models of kinetic equations were appropriate. All transitions were assumed Markovian (meaning the stochastic processes do not depend on previous transitions), and nonlinear effects, such as changing ligand concentrations during the period of interest, were ignored. As a result, the governing equations were a system of first-order kinetic equations.

Studying the duration of a dwell is a first-passage time problem in stochastic analysis (5, 6). For certain kinetic schemes, dwell-time distributions can be solved analytically, and the solutions are written as multiple exponential formulae (1,2,7–12). Other methods include the backward (adjoint) equation method, the Monte Carlo simulation method, the matrix method (13–15), and the absorbing boundary method.

The backward equation method has been widely used to calculate mean first-passage time and other average values (16–19). However, this method has limited value for obtaining distribution functions such as dwell-time distributions. Monte Carlo simulations, which use stochastic processes to simulate a trajectory (e.g., Fig. 1), perform well for systems with a large number of states when only a small portion of the states are sampled. A dwell-time distribution can then be obtained by binning durations of dwells resulting from the simulation. Achieving a high resolution of dwell-time distributions, however, requires a long trajectory to generate sufficient data for statistical analysis. Even with the efficient Gillespie algorithm (20), the computational cost of simulations for global fitting can be large.

The matrix method has been used to study dwell-time distributions of single ion-channel recordings (13, 14). This method is related to the absorbing boundary method (see below), and uses probability theory to partition the rate matrix into submatrices for open and closed states of a channel. Recently, the matrix method has been applied to dwell-time distribution analysis of molecular motors (21). It is useful for obtaining stochastic properties of systems with a variety of kinetic schemes. However, for molecular motors with complex kinetic schemes (e.g., Scheme 10), partitioning states into groups before and after a dwell is sometimes impossible, as a state can be reached through pathways either exiting a dwell or not.

The absorbing boundary method has been widely applied to study first-passage time problems. This method determines the length of time required to reach a site or a state for the first time, by setting the site or the state as an absorbing boundary. For kinetic models, first-order kinetic equations with absorbing boundary states can be solved to obtain dwell-time distributions. This method is not efficient for obtaining average values such as mean first-passage time, but it is effective for obtaining distribution functions for simple kinetic schemes.

Identifying absorbing boundaries for complex kinetic schemes of molecular motors remains a major challenge. When several kinetic pathways exist from one state to another and not all of them exit a dwell, it is not straightforward to find the absorbing boundary states. Solving this problem is important because cyclic and reverse kinetic pathways are universal for molecular motors. For some motors, branching kinetic pathways are needed to describe the behaviors observed in experiments. Our work extends the absorbing boundary method to solve dwell-time distributions of molecular motors with cyclic, branching, reverse, and even high-dimensional kinetic networks [see examples in the supporting information (SI) Text and SI Figs. 5 and 6]. The extended absorbing boundary (EAB) method enables global fitting of dwell-time distributions from experiments that examine a motor under a variety of different conditions. As a result, it is possible to test different kinetic schemes to find one that best fits a rich set of dwell-time distributions. To demonstrate the utility of this method, we used it to simulate the dwell-time distributions of a single-headed myosin V construct (2) and to globally fit experimental results obtained with different applied loads and ATP concentrations. The method provides very fast computations, and code that implements the method is freely available at www.simtk.org.

Results

Development of the EAB Method.

In the following, we first solve the dwell-time distribution problem for a simple example with the conventional absorbing boundary method. We then solve a problem with a complex kinetic scheme for a molecular motor, where its power stroke (mechanical step) corresponds to the transition exiting a dwell. We use this example to illustrate the extension of the conventional absorbing boundary method, which is especially well suited for such complex kinetic schemes.

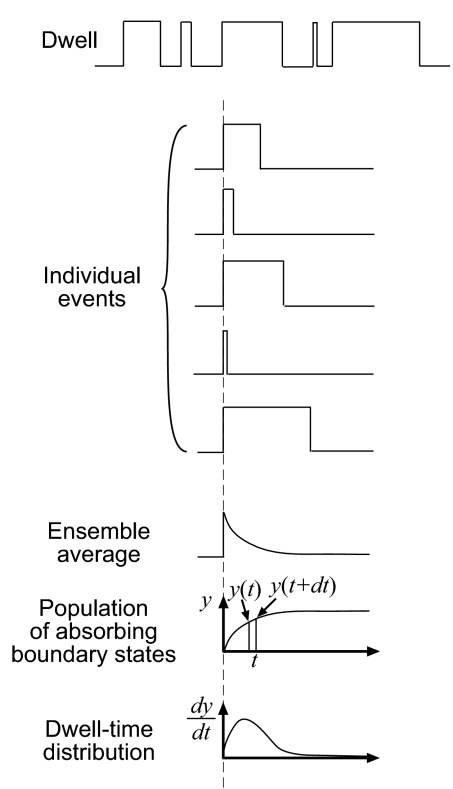
Dwell-time distributions represent the ensemble average behavior of many individual dwell events (Fig. 2). The absorbing boundary method considers the state leaving a dwell as an absorbing boundary state by setting the reverse rate constant to zero. This is equivalent to the constant value after each individual dwell event shown in Fig. 2.

Fig. 2.

Statistics of dwell events. A time trajectory (top trace) is split into individual dwell events. The ensemble average of all these events is proportional to the population of states remaining in the dwell. The population of absorbing boundary states, shown in y, is obtained by subtracting the population remaining in dwells from the total population. Because dwell-time distributions reported in experiments are histograms of events binned within certain time intervals, it is important to also consider calculated results in time intervals. The number of events that exit a dwell during the time interval (t, t + dt) is equal to the number of events that exited dwells before time t + dt excluding those events that exited dwells before time t, or y(t + dt) − y(t). These are the number of dwell events with their dwell time between the time interval t and t + dt. In the limit, the dwell-time distributions at time t are proportional to dy/dt.

A special feature of molecular motors is that their kinetic scheme is cyclic. As an example, consider this simple three-state kinetic cycle:

In this cycle, A, B, and C are three chemical states, and the reactions are all reversible. A possible scenario for this cycle of an ATPase motor is that A → B corresponds to ATP docking, B → C corresponds to the power stroke, the mechanical stroke that drives the load movement, and C → A corresponds to ADP release. This simplified cycle omits several intermediate steps in the ATP hydrolysis cycle, but it is a reasonable approximation for certain cases when intermediate steps are fast. Because B → C is assumed to be the power stroke step, B → C and C → B are steps to exit a dwell corresponding to forward and backward power stroke steps in Fig. 1a. An example for this kinetic scheme is the inchworm movement of a monomeric helicase, such as HCV helicase, translocating on a nucleic acid (22). In this case, B → C represents the mechanical stroke step of the inchworm movement.

An equivalent way to write the kinetic scheme linearly is

According to the absorbing boundary method (5), one incorporates absorbing boundaries into the kinetic scheme to give

In this scheme, states at both ends are absorbing boundary states exiting dwells. Note that the arrows toward boundary states are unidirectional, because once the molecular motor exits a dwell, the reverse step is eliminated to account for the vanishing population within a dwell. To obtain the dwell-time distributions, the population of absorbing boundary states needs to be calculated, as shown in Fig. 2. The governing equations for the kinetic scheme are a system of equations with the form

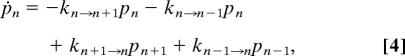where n is any state in Scheme 3, n + 1 is its next state in the forward direction, n − 1 is its previous state in the reverse direction, p_i (i can be n, n + 1 or n − 1) is the population at state i, and k_i→j is the rate constant from state i to state j. The corresponding rate constants of the boundary states are set to 0. The system of equations is detailed in the SI Text. The populations of the left boundary (B in this case) and the right boundary (C in this case) are summed to get the total population of absorbing boundary states. The dwell-time distribution is (6)

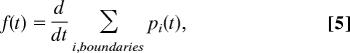where Σ_i,boundaries p_i(t) is the summation of the populations of all absorbing boundary states. This total population accumulates with time. To obtain the dwell-time distribution, or equivalently to calculate how many events happen at a certain time interval, one has to take the time derivative of this total population (Fig. 2).

Initial conditions are required to solve the kinetic equations (Eq. 4). These initial conditions correspond to relative populations of states entering a dwell. Due to the cyclic characteristics of molecular motors, many initial states are possible. There are two possible initial states of a dwell event for this cyclic kinetic scheme (Fig. 1a): either state C, which results from entering a dwell in the forward direction (B → C), or state B, which results from entering in the backward direction (C → B). Three steps are required to obtain the relative initial populations of these two states. The first is to determine the possible initial states (in this case, B and C). The second step is to set the initial conditions of all other states to zero, and the third is to compute the relative populations of those possible initial states.

We implemented a kinetic flux analysis to determine the relative populations. The population of a possible initial state j of a dwell is proportional to a conditional probability p_j = p_ip_i→j, where p_i is the probability in an exiting state i, and p_i→j is the transitional probability from this exiting state i to the initial state j. The probability in an exiting state is proportional to its steady-state concentration of the original kinetic scheme (Scheme 1) because steady-state concentrations represent the average relative populations of all states during the time course of an experiment. The probability of a transition is proportional to its rate constant. Therefore, the populations of the state C after B → C and the state B after C → B are proportional to the kinetic fluxes, i.e., k_B→C × [B]_ss and k_C→B × [C]_ss, where [B]_ss and [C]_ss are steady-state concentrations of Scheme 1. By imposing these initial conditions and a set of rate constants, one can calculate the dwell-time distributions by solving a system of kinetic equation

We will follow these same steps of the conventional absorbing boundary method for a more complex kinetic scheme to illustrate the difficulties encountered, and we will introduce an equivalent but more efficient method that extends the absorbing boundary method for complex kinetic schemes.

An experimental setup (Fig. 1c) shows a single-headed myosin molecule moving an actin filament. The kinetic scheme of the myosin is

In Scheme 6, M is myosin, A is actin, MT is the ATP-bound state, MDP is the ADP·Pi-bound state, and MD is the ADP-bound state. Thus, the chemical cycle includes steps of ATP binding, ATP hydrolysis, Pi release, and ADP release. Each state in this chemical cycle can either bind to actin (the lower row of Scheme 6) or release from it (the upper row of Scheme 6). The power stroke, in which myosin drives actin's motion, can happen only when myosin binds to actin (the states of the lower row). Both mechanical stepping (Fig. 1a) and state transition (Fig. 1b) are possible dwell events depending on the measurement methods. If actin movement by myosin's power stroke is recorded (Fig. 1a), as in the following example, dwell events occur between consecutive mechanical steps. If the amplitude of actin oscillation is recorded to distinguish the states of actin binding and unbinding (Fig. 1b), as shown in Testing the EAB Method, dwell events occur during binding transitions. Different absorbing boundaries must be chosen for these two scenarios.

It is possible to use dwell-time distributions to help identify which step in the chemical cycle is coupled to the mechanical power stroke. One hypothesis is that the power stroke is coupled to the Pi release step (AMDP → AMD) (23). In this case, the trajectory of the actin would be similar to the one shown in Fig. 1a, with jumps corresponding to power strokes. When the actin experiences a forward (AMDP → AMD) or a backward (AMD → AMDP) power stroke from myosin, the trajectory exits a dwell.

According to the conventional absorbing boundary method, absorbing boundaries correspond to states where the trajectory exits a dwell. In this case, the absorbing boundary states are AMD, after an AMDP → AMD transition, and AMDP, after an AMD → AMDP transition. Although these two absorbing boundary states have been identified, how to impose them onto the original kinetic scheme, as was done from Scheme 2 to Scheme 3 in the previous example, is not obvious. Removing the reverse pathways alone results in Scheme 7

Scheme 7 is inaccurate because states AMDP and AMD can proceed to other states. Absorbing boundary states must be states from which no pathway returns, so that the probability of the first-passage time through these dwell-exiting transitions can be monitored.

The correct explicit representation of the kinetic scheme outlined in Scheme 6 is shown below.

where the subscripts represent the position of actin, and arrows on the top represent the cyclic pathways of ATP hydrolysis. The power stroke, AMDP → AMD, moves the actin one step forward (e.g., n → n + 1), whereas ATP hydrolysis can occur without moving actin (i.e., without exiting a dwell) as long as myosin does not go through a power stroke step. With this explicit kinetic scheme, and understanding where the absorbing boundaries are, the kinetic scheme for computing the dwell-time distributions is:

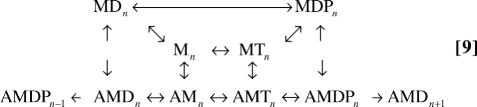where rates of transitions originating from absorbing boundaries are set to zero. Although it is possible to write the cyclic kinetic scheme explicitly for this case, it is impractical to write the explicit kinetic scheme for more complex cases, such as the one shown in SI Text and Figs. 5 and 6.

The EAB method includes three steps to obtain the kinetic scheme for calculating dwell-time distributions. The first is to identify each state exiting a dwell. The second step is to set the rate of that exiting transition to zero. The third step is to add a transition toward an additional state with the original exiting rate; these additional states serve as the absorbing boundary states. Following these steps for Scheme 6 results in

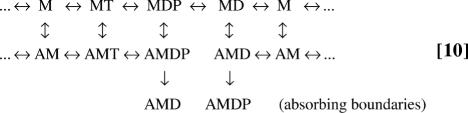The states in the bottom row are the absorbing boundaries. This modification of the kinetic scheme, which identifies the absorbing boundaries and adds exiting pathways to these states, is equivalent to Scheme 9. The same simple procedure can be applied to more complex kinetic schemes by identifying all exiting states and adding the appropriate pathways. In fact, the previous simple three-state case (Scheme 1) can also be treated this way. Identifying the absorbing boundary states (B and C) and diverting transitions across the power stroke to additional states indeed gives Scheme 3.

The extra states introduced in the modified kinetic scheme create extra equations. The governing equations for all states in Scheme 10 are

where j's are adjacent states of state n, Σ_i,out k_ip_n is the summation of all outflux transitions from state n and Σ_i,in k_ip_j is the summation of all influx transitions toward state n. The initial state of a dwell can be AMD or AMDP, and the relative populations of these states can be determined with the kinetic flux analysis shown above. Solving the equations, summing the populations of the absorbing boundary states in the bottom row of Scheme 10, and taking the time derivative gives the dwell-time distribution of the actin movement.

Testing the EAB Method.

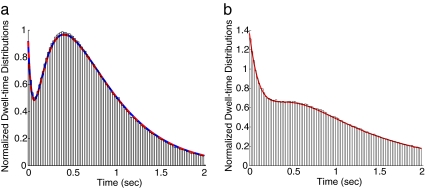
We tested the equivalency of the EAB method with other methods for a simple kinetic scheme. The dwell-time distributions for the cyclic kinetics shown in Scheme 1 were computed using the EAB method, and results agreed well with an analytical solution and a Monte Carlo simulation (Fig. 3a). SI Text provides detailed derivations of the analytical solution, which can be obtained either by transforming into the Laplace domain or by solving the corresponding eigenvalue problem. Both approaches require finding roots of a cubic algebraic equation for this chemical cycle with three species.

Fig. 3.

Agreement of dwell-time distributions results from the EAB method and other methods. (a) The results from the EAB method (red line), the analytical solution (blue dashed line) and the histogram obtained from the Monte Carlo simulation for Scheme 1. The curves from the EAB method and the analytical solution overlap almost perfectly. (b) The results from the EAB method and the histogram from the Monte Carlo simulation for Scheme 10.

The dwell-time distributions for Scheme 10, the power stroke of single-headed myosin, are shown in Fig. 3b. The results from the EAB method agree well with the histogram of a Monte Carlo simulation using Gillespie algorithm, whereas analytical solutions are intractable due to the difficulty of finding roots of high degree polynomials. The time to compute this Monte Carlo simulation was 116 s. The EAB method was >5,000 times faster. This improvement in speed is particularly important when thousands of simulations must be run to find a global optimization of fitting parameters.

We have applied the EAB method to experimental dwell-time distributions. Recently, single molecule experiments were conducted to study the effects of different parameters on the binding and unbinding of actin for a single-headed myosin V construct (2). Fig. 1b shows a sample trajectory from the experimental study. Oscillations represent the states when myosin was not bound to actin and pauses represent actin-bound states. Different directions of forces exerted by an optical trap were imposed on the actin, and different ATP and ADP concentrations were used for different experiments.

The original kinetic scheme is shown in Scheme 6 for a single-headed myosin. In the experiments, dwells are due to actin binding, whereas in the example of Scheme 10, dwells arise from the wait for the next power stroke. To modify the kinetic scheme to account for the absorbing boundaries, we first identified the steps exiting a dwell. In this case, they corresponded to all actin unbinding steps. The kinetic scheme for calculating the dwell-time distributions was thus

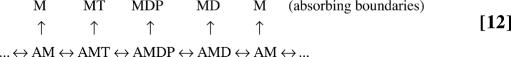Here, all of the actin unbound states (upper row) are absorbing boundaries. The initial conditions were obtained by conducting flux analysis of the original kinetic scheme. Once the corresponding kinetic equations were solved, one can follow the procedure described above to obtain the dwell-time distributions.

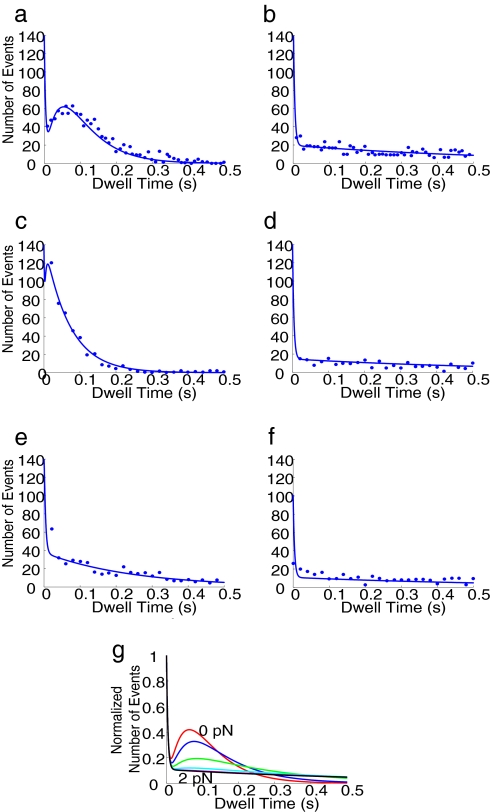
Fig. 4 shows the experimental dwell-time distributions for myosin V (dots) (2) and computational dwell-time distributions (solid lines) in six different experimental conditions. To model the effects of forces exerted by the optical trap, we used Boltzmann factors e^αFΔx/k_BT and e^{(α−1)FΔx/k_BT} for a proposed power stroke step (e.g., see ref. 3). These factors accounted for energy surface adjustments due to forces. More sophisticated models for the force effects could also be incorporated to take the detailed shape of the energy surface into consideration. Many of the rate constants in the kinetic scheme of single-headed myosin have been identified through experimentation (24) and used in our simulations, whereas other unknown ones were obtained by fitting to the dwell-time distributions (SI Text and SI Table 1). We were able to use a single kinetic scheme with a proposed power stroke step to fit all dwell-time distributions (Fig. 4 a–f).

Fig. 4.

Fitting of dwell-time distributions under different conditions using only one kinetic scheme with Boltzmann force factors and the predicted effects of applied forces on dwell-time distributions of single-headed myosin V. Experimental data (dots) are from Purcell et al. (2). (a) Fitting of dwell-time distributions in [ATP] = 10 μM and a forward force 2 pN. (b) Fitting of dwell-time distributions in [ATP] = 10 μM and a reverse force 2 pN. (c) Fitting of dwell-time distributions in [ATP] = 1 mM and a forward forces 2 pN. (d) Fitting of dwell-time distributions in [ATP] = 1 mM and a reverse forces 2 pN. (e) Fitting of dwell-time distributions in [ATP] = 1 mM, [ADP] = 1 mM, and a forward force 2 pN. (f) Fitting of dwell-time distributions in [ATP] = 1 mM, [ADP] = 1 mM, and a reverse force 2 pN. (g) Predictions of dwell-time distributions under different reverse forces when [ATP] is 10 μM.

From the global fitting, we identified the step in the chemical cycle corresponding to the observed rate in each dwell-time distribution. For a low ATP concentration under forward external force (Fig. 4a), two rate-limiting steps observed in the dwell-time distributions were identified as the ATP-binding step and the ADP release step. When the reverse force was applied, the kinetic pathway across the power stroke step was blocked and the kinetic flux turned to an alternative pathway with a slow rate (Fig. 4b). When ATP concentrations were high (Fig. 4c), the rate of ATP binding was fast, and this rate was absent in the dwell-time distributions for the forward force. In Fig. 4d, the reverse force again diverted the flux to the same alternative pathway taken when ATP concentrations were low (Fig. 4b). For [ATP] = 1 mM and [ADP] = 1 mM under a forward force, another characteristic rate was present (Fig. 4e). This rate was identified to be associated with actin unbinding when ADP was in the catalytic site, as high ADP concentrations forced the kinetic flux to go to this pathway.

Discussion

Dwell-time distributions have been reported in many single-molecule biophysical studies. A mathematical or computational representation of the dwell time distribution is needed to gain insight into the function of an enzyme. We extended the absorbing boundary method to produce dwell-time distributions for complex kinetic schemes typical of molecular motors and other enzymes. The key steps in calculating the dwell-time distributions with the EAB method are identifying the absorbing boundaries and modifying the kinetic scheme to include the absorbing boundary states. We have tested the EAB method by comparing it to other methods and have used it to globally fit experimental data describing single-headed myosin V.

There are a variety of methods to characterize dwell time distributions, and each has strengths and weaknesses. When a single dwell-time distribution is examined, an analytical solution, such as a single or double exponential, is usually sufficient to fit it and to obtain one or two critical rate constants. However, when more than one dwell-time distribution is analyzed (e.g., when an enzyme is subjected different experimental conditions) a more sophisticated kinetic scheme is needed to characterize all data at once. Analytical solutions may not be suitable because of the complexity of root finding and inverse Laplace transform. If a kinetic scheme without branching is appropriate, such as Scheme 1, the conventional absorbing boundary method is suitable for representing the dwell-time distributions. If states in a kinetic scheme can be separated to two distinct groups, such as the actin-bound and actin-unbound states in Scheme 12, the matrix method is appropriate to handle the problem. However, for kinetic schemes such as Scheme 10, where branching pathways exist, and the states cannot be divided to two groups before and after a dwell, using the EAB method is appropriate. Many molecular motors require the modeling at this level of complexity for global fitting. The EAB method is especially valuable for high-dimensional kinetic schemes of multimeric molecular motors (see SI Text and SI Fig. 6).

The capability to use a single kinetic scheme to fit all dwell-time distributions observed under different experimental conditions is a powerful tool for identifying the mechanochemical model of a molecular motor. The requirement that a single scheme represents a variety of conditions allows one to eliminate proposed kinetic schemes that are unable to accurately represent all experimental observations. We have applied the EAB method to globally fit the data of myosin V under different ligand concentrations and different directions of external forces. This fitting revealed how force affects the transition rates of its ATP hydrolysis cycle. Also, we have linked the rate observed for [ATP] = 1 mM and [ADP] = 1 mM under a forward force to the rate of an actin unbinding transition (Fig. 4e), demonstrating that the integration of this computational tool and experimental data provides insights into the kinetics and mechanochemical characteristics of myosin V.

The fits shown in Fig. 4 a–f reveal a fast rate in the drop of distributions close to dwell time = 0 sec. This fast rate reflects the Pi release step, which was set as 250 s⁻¹ based on bulk biochemical measurements (24). This fast step has never been reported in dwell-time distributions because it is too fast to capture, and observing it requires an extremely long Monte Carlo simulation trajectory. The examples in Fig. 3 also show three characteristic rate constants. This prediction opens the opportunity to characterize three or more rate constants in one dwell-time distribution.

The EAB method allows us to predict dwell-time distributions under conditions that have not been performed experimentally. For example, Fig. 4g shows the prediction of force dependency, which can be tested by conducting optical trap experiments under different forces. The computer simulation can therefore be used to test whether a proposed power stroke step is indeed valid.

The EAB method can be applied to single molecule dwell-time distributions of other enzymes, such as F₁ ATPase (25), φ29 packaging motor (26), RNA polymerase (27, 28), kinesin (29, 30), and to examine conformational dynamics of other enzymes, such as ion channels. Both mechanical dwells and kinetic dwells have been illustrated, and this method can be easily applied to any of these cases. The software that implements the EAB method is freely available at www.simtk.org.

Abbreviation

EAB

extended absorbing boundary.