Ultrafast dynamics of protein collapse from single-molecule photon statistics

Abstract

We use the statistics of photon emission from single molecules to probe the ultrafast dynamics of an unfolded protein via Förster resonance energy transfer. Global reconfiguration of the chain occurs on a time scale of ≈50 ns and slows down concomitant with chain collapse under folding conditions. These diffusive dynamics provide a missing link between the phenomenological chemical kinetics commonly used in protein folding and a physical description in terms of quantitative free energy surfaces. The experiments demonstrate the potential of single-molecule methods in accessing the biologically important nanosecond time scales even in heterogeneous populations.

The discovery of proteins that fold rapidly in the absence of intermediates (1) has substantially advanced our mechanistic understanding of protein folding. The simplicity of their folding behavior allows thermodynamic and kinetic analyses that have led, e.g., to the characterization of transition states for folding (2) and the prediction of folding rates from native structure (3–5). However, because of their limited experimental accessibility, energetic and dynamic differences between the unfolded states of different proteins have usually been ignored. Similarly, the application of rigorous theories of protein folding in terms of statistical mechanics (6–8) has been hampered by our lack of understanding of structure and dynamics in the unfolded state ensemble. The role of unfolded states in determining protein folding mechanisms is thus largely unknown. Although considerable information about the overall dimensions and residual structure of unfolded proteins has been obtained from methods such as small-angle x-ray scattering and NMR, their dynamics in the submicrosecond range have largely eluded experimental determination. The importance of these time scales has become particularly obvious through the identification of proteins that fold in a few microseconds (9). In this regime, the free energy barrier to folding is assumed to be extremely low or even absent, and diffusive chain dynamics become the dominate factor in folding kinetics. Here, we determine these dynamics for an unfolded protein and investigate how they are affected by the collapse of the unfolded chain under near-physiological conditions.

An ideal way to probe the dynamics of the heterogeneous ensemble of unfolded protein conformations is single-molecule spectroscopy (10). The absence of averaging over many molecules allows spontaneous intramolecular distance fluctuations to be observed at equilibrium, without the need for perturbations to synchronize the ensemble. Förster resonance energy transfer (FRET) between two chromophores attached to the polypeptide chain has been suggested as an approach for investigating its submicrosecond dynamics (11, 12), but has eluded experimental implementation. Here, we use this method to directly probe the unfolded state dynamics of the cold shock protein (Csp) from Thermotoga maritima, a small, 7.5-kDa β-barrel protein that exhibits two-state thermodynamics and kinetics (13–17). The protein was labeled terminally with a green fluorescent donor and a red fluorescent acceptor dye via amino- and carboxyl-terminal cysteine residues, and freely diffusing molecules were observed in confocal single-molecule experiments (Fig. 1). During the transit of the protein through the observation volume, its donor chromophore is excited by the laser beam. Depending on the distance r to the acceptor, energy transfer results with a rate that determines the relative probabilities of photon emission from donor and acceptor. Correspondingly, distance dynamics within the protein can be measured by fluctuations in the transfer efficiency and thus in the fluorescence emission of the chromophores (Fig. 1).

Fig. 1.

Principle of measuring distance fluctuations in unfolded proteins with FRET. Energy level diagram (Left) of the FRET process between two fluorophores (A and D) attached to the termini of a protein (Right) with the relevant transitions between the electronic states. The Förster transfer rate k_F(r) = k_D(R₀/r)⁶ fluctuates on the same time scale as the distance r(t) between the chain ends and thus allows a direct measurement of chain dynamics. k_ex is the excitation rate of the donor D, fk_ex is the rate of direct excitation of the acceptor A, and k_D and k_A are the intrinsic decay rates of donor and acceptor, respectively. The possible role of annihilation processes (66–68) in the state D*A* is to the best of our knowledge currently unknown for these chromophores and has thus not been included in our photophysical model. Note, however, that these processes would be expected to occur on a time scale shorter than or similar to the fluorescence lifetime of the dyes and thus would not affect our analysis of the correlation functions on the time scale of protein dynamics.

Results

Measurement of Unfolded State Dynamics.

In our experiments, we combine the separation of folded and unfolded subpopulations by single-molecule spectroscopy with the high time resolution available from the photon statistics of a FRET-coupled dye pair. First, a transfer efficiency histogram is created from the photon bursts of individual molecules diffusing through the focus (15, 18). Fig. 2A shows an example at a concentration of the denaturant guanidinium chloride (GdmCl) of 1.4 M, where three subpopulations are resolved: folded protein molecules with a transfer efficiency E close to 1, unfolded molecules with E ≈ 0.5, and molecules lacking an active acceptor chromophore with E ≈ 0 (15, 19). A second synchronized counting card continuously records the time intervals τ between consecutive detected photons with picosecond time resolution. Dead times of detectors and counting electronics are avoided by using a Hanbury Brown and Twiss detection scheme (20–22). Under our conditions, normalized histograms of the resulting interphoton times are essentially equivalent to the donor or acceptor intensity autocorrelation functions g_ii(τ)(i = A, D) (23), which report directly on the time scales of fluctuations in fluorescence intensity (see Materials and Methods). We can obtain g_ii(τ) for each of the subpopulations shown in Fig. 2A by using only the interphoton times from molecules assigned to a single subpopulation.

Fig. 2.

Intensity autocorrelation functions of the subpopulations identified in single-molecule experiments. (A) Transfer efficiency histogram at 1.4 M GdmCl fit with three peaks (black lines) corresponding to the folded or native (N; high E) and unfolded (U; E ≈ 0.5) subpopulations, and molecules lacking an active acceptor (E ≈ 0). (B–G) The ranges of E used for extracting the specific normalized donor and acceptor autocorrelation functions g_DD (B–D) and g_AA (E–G) are shaded in blue. Fits to g_DD are shown in green, and fits to g_AA are shown in red (for fit functions, see Materials and Methods). The normalized signal amplitude α for each correlation function is given relative to the unfolded state (α = 1). g_DD and g_AA were calculated from the corresponding interphoton time distributions by correcting for pile-up and triplet-state components (see Materials and Methods).

The resulting intensity autocorrelation functions of donor [g_DD(τ)] and acceptor [g_AA(τ)] emission for every subpopulation are shown in Fig. 2 B–G. In all cases, g_ii(τ) exhibits a drop in amplitude at τ = 0. This photon antibunching is characteristic of individual quantum systems that cannot emit two photons simultaneously; it decays within a few nanoseconds (22, 24). More interestingly, pronounced photon bunching, i.e., an additional component in g_ii(τ) with positive amplitude, is observed in the 50-ns range. The decay of this bunching signal in the unfolded subpopulation (E ≈ 0.5) is described by similar time constants for donor and acceptor autocorrelation functions (Fig. 2 C and F). The behavior of g_ii(τ) agrees with theoretical predictions for a flexible polypeptide chain (11, 12): if, for example, a donor photon is emitted at τ = 0, the chain ends are likely to be far apart at that instant, corresponding to a low rate of energy transfer, k_F. A very short time later, the ends will still be far apart, and the likelihood of emitting another donor photon will still be increased. However, at times much greater than the reconfiguration time τ_r of the chain, the molecule will have lost the “memory” of its initial configuration at τ = 0, and the probability of donor emission will be determined by the average transfer efficiency. In other words, we expect an increased autocorrelation of the emission intensity around τ = 0 that decays approximately on the time scale of chain reconfiguration.^¶

The acceptor autocorrelation function g_AA(τ) of the native subpopulation also exhibits a small, but significant, relative bunching signal (Fig. 2G). This signal may in part be caused by the imperfect separation of subpopulations (Fig. 2A), but the slower relaxation compared with the unfolded state could indicate an additional contribution from interactions of the chromophores with the specific environment presented by the native structure. To exclude an influence of native molecules on the determination of unfolded state dynamics, we restrict our measurements and analysis to the donor signal, where only unfolded molecules contribute to bunching (Fig. 2 B–D). The optimal signal-to-noise ratio is obtained at a protein concentration of 500 pM, where a separation of subpopulations is no longer possible, but the determination of the correlation times is most accurate. An example for such a measurement is shown in Fig. 3B; the pronounced photon bunching yields an intensity autocorrelation time of 44 ± 3 ns. Under identical conditions, this signal is absent in stiff (19) polyproline peptides with the same average transfer efficiency as unfolded Csp (Fig. 2D), confirming that photon bunching is indeed caused by chain dynamics in the unfolded protein. The bunching signal is also absent in Csp labeled only with a donor chromophore (data not shown), excluding dye–protein interactions and rotational dynamics of the entire chain as origins of the bunching signal we observe. An additional slower component with a relaxation time of several microseconds was observed in all data sets, as expected from the triplet-state lifetimes of the chromophores (25). Fluorophore reorientation occurs on the time scale of ≈300 ps (19); resulting fluctuations in the energy transfer rate would thus affect the correlation functions only on time scales much shorter than the range relevant for the dynamics investigated here.

Fig. 3.

Calculated (A and C) and measured (B and D) donor intensity autocorrelation functions for unfolded Csp (A and B) and a stiff polyproline peptide (C and D) at 4 M GdmCl, corroborating that the 44-ns component of g_DD is caused by chain dynamics. The curve in C was calculated based on the photophysics of the FRET process assuming a fixed distance between the fluorophores, whereas in A diffusive end-to-end distance dynamics of a Gaussian chain were included.

Theory and Analysis of Photon Statistics.

To analyze our measurements in terms of protein dynamics, we describe the relative motion of the chain ends as a diffusive process on the potential of mean force that corresponds to the end-to-end distance distribution of the unfolded protein. By combining these diffusive chain dynamics with the distance-dependent stochastic photon emission from the coupled dye pair (Fig. 1), the complete photon statistics of the system can be obtained (12). To avoid time-consuming simulations, we use a recently developed theory (26) that allows us to calculate the intensity correlation functions of donor and acceptor emission numerically. Briefly, if we assume for the unfolded protein the end-to-end distance distribution function of a Gaussian chain [which has recently been shown to be a good approximation for Csp (27)], p_eq(r) = 4πr²(2π〈r²〉/3)^−3/2 exp(−3r²/2〈r²〉) (see Fig. 5), protein dynamics can be combined with the photophysics of FRET in the rate matrix:

where D is the relative diffusion coefficient of the chain ends, K₀(r) describes the distance-dependent kinetics of interconversion between the four electronic states illustrated in Fig. 1, and I is the 4 × 4-identity matrix. The time dependence of all electronic and conformational transitions in the system is then described by the rate equation dp/dt = Kp, where p is the vector of the populations of the four electronic states in Fig. 1. By discretizing the diffusion operator, the problem is reduced to matrix algebra, and the intensity correlation functions can be calculated to high accuracy with numerical methods (for details, see Materials and Methods and SI Text). All parameters needed to define the model in terms of our system are known: the photophysical rate constants of the FRET process (Fig. 1) were measured independently, and p_eq(r) is defined uniquely by the mean square end-to-end distance 〈r²〉, which can be calculated from the average transfer efficiency of the unfolded subpopulation (15, 27) (see SI Text). We can thus determine the only remaining parameter, the effective end-to-end diffusion coefficient D, by adjusting it such that the calculated intensity autocorrelation function fits the experimental result. Finally, the chain reconfiguration time τ_r (the decay time of the end-to-end distance autocorrelation function) for a Gaussian chain is obtained from τ_r ≃ 〈r²〉/6D (see SI Text).

Fig. 5.

Schematic free energy surface of Csp collapse. End-to-end distance distribution functions p_eq (gray filled functions) and the corresponding potentials of mean force G (thick black lines) of unfolded Csp at 8 M GdmCl (Lower) and 0 M GdmCl (Upper) are shown, assuming a Gaussian chain model (27). A 3D plot of the potential of mean force in the range of 8 to 0 M GdmCl illustrates the collapse and increasing roughness calculated from the data in Fig. 4. The Förster radius R₀ (dashed red line) and the rms end-to-end distance (rms r, red line) are indicated. The thin line superimposed on the average free energy surface (thick line) in Upper (0 M GdmCl) shows one representative distribution of energies compatible with the model for the roughness used (37). Note, however, that the discretization of the end-to-end distance is arbitrary and was introduced only for the purpose of illustration. G is given in units of k_BT and scaled to a maximum value of 10 k_BT relative to the minimum of the average potential at 0 M GdmCl, where 10 k_BT is the height of the free energy barrier for folding.

In summary, we can thus determine, from the measured intensity correlation function, the dynamics of an unfolded protein in terms of the diffusion coefficient D and the corresponding reconfiguration time τ_r. Examples for calculated intensity correlation functions both with and without chain dynamics are shown in Fig. 3 A and C, respectively. The excellent agreement between the functional forms of experimental and calculated correlation functions (Fig. 3 A and B) suggests that our single reaction coordinate is a reasonable approximation for the dynamics of unfolded Csp. It is worth stressing that what we observe here are large-scale chain dynamics along this reaction coordinate, whereas the wide range of subnanosecond dynamics known to occur in polypeptides (28, 29), such as dihedral angle rotations, essentially enter into the diffusion coefficient D (or the energetic roughness of the free energy surface; see The Free Energy Surface of Collapse and Implications for Protein Folding).

Effect of Collapse on Unfolded State Dynamics.

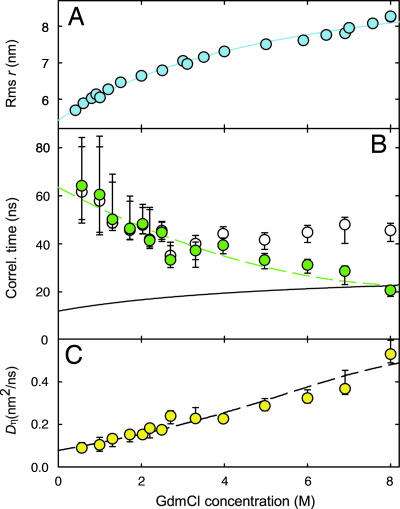
The unfolded state of Csp has been found to collapse in response to decreasing GdmCl concentrations (15, 17, 27, 30). This collapse precedes the folding reaction in kinetic experiments (17, 30), and single-molecule FRET can be used to quantify the resulting change in chain dimensions under equilibrium conditions by virtue of the separation of folded and unfolded subpopulations (15, 27). Fig. 4A shows the corresponding decrease in the rms end-to-end distance 〈r²〉^1/2 determined from the mean transfer efficiencies of the unfolded state (27). For an ideal chain, compaction is expected to lead to faster relaxation of intramolecular distances because of the reduced size of the accessible conformational space (Fig. 4B). This behavior has indeed been observed for some unstructured peptides (31) (however, also see ref. 52), but what happens in the case of a real protein? To answer this question, we measured the change in the decay time of the donor intensity autocorrelation function τ_DD in response to decreasing GdmCl concentrations (Fig. 4B). With the above analysis, we find a decrease in the viscosity-corrected diffusion coefficient D_η from ≈0.5 nm²/ns at 8 M GdmCl to ≈0.1 nm²/ns at low GdmCl concentrations [corrected for change in solvent viscosity η_s with increasing denaturant concentration according to D_η = Dη_s⁻¹ 1 mPa s(31–35)]. The corresponding chain reconfiguration time τ_r increases from ≈20 ns at 8 M GdmCl to ≈65 ns under near-native conditions (Fig. 4B). In conclusion, we find very fast global chain reconfiguration in the unfolded state of Csp, but, concomitant with chain collapse at low denaturant concentrations, we observe a deceleration of these dynamics. This finding is opposite to the behavior expected for an ideal chain with invariant D_η (Fig. 4B), suggesting that interactions within the polypeptide chain, or “internal friction” (36), significantly affect unfolded state dynamics upon chain collapse, similar to what has recently been found for unstructured GlySer-repeat peptides (52).

Fig. 4.

Denaturant dependence of unfolded state collapse and dynamics. (A) rms end-to-end distance r of the unfolded protein as determined from the mean transfer efficiency of the unfolded state in single-molecule fluorescence experiments. The solid line is an empirical fit to the equation rms r = rms r₀ + Ac/(1 + Bc) used to interpolate the values of rms r for further calculations. (B) Donor intensity autocorrelation times τ_DD (open circles) and viscosity-corrected end-to-end distance autocorrelation times τ_r (green circles) of unfolded molecules determined from measurements as shown in Fig. 3. The dashed green line is an empirical second-order polynomial fit to the distance correlation times. The black line shows the calculated reconfiguration time of an ideal Gaussian chain assuming a constant diffusion coefficient and the rms r values in A. (C) Effective viscosity-corrected relative diffusion coefficients of the chain ends D_η, illustrating the slowed chain dynamics upon collapse. The dashed line is calculated from the solid and dashed fits in A and B, respectively, according to D_η = 〈r²〉/6τ_r. Error bars represent our estimate of the combined experimental errors and the systematic uncertainty in data analysis.

The Free Energy Surface of Collapse and Implications for Protein Folding.

With the shape of the end-to-end distance distribution p_eq and the effective end-to-end diffusion coefficient D_η as a function of the denaturant concentration, we have obtained the two key parameters for describing the collapse of Csp in terms of a quantitative free energy surface. The change in D_η upon collapse can be expressed in terms of an effective energetic “roughness”, i.e., a distribution of small energy barriers caused by intramolecular interactions that slow down diffusion along the reaction coordinate. Possible physical origins of the dependence of D_η on denaturant concentration, as captured by the roughness, are changes in the packing and interaction strength of the polypeptide backbone and side chains in the unfolded state. These interactions may also contribute to the increase in the β-structure content recently observed upon collapse of unfolded Csp (27). Assuming a random amplitude with a Gaussian distribution inde-pendent of r, the rms roughness ε is given by ε = k_BT $\epsilon =k_{B}T\sqrt{In(D_0/D_{\eta })}$ (37, 38), where D₀ is the diffusion coefficient in the absence of intramolecular interactions. For D₀, we choose the viscosity-corrected diffusion coefficient of the unfolded state in 8 M GdmCl. At such high denaturant concentrations, the average chain volume is ≈18 times greater than in the folded structure, suggesting complete solvation of the polypeptide chain, and consequently minimal intramolecular interactions. The decrease in D_η we observe upon collapse under native conditions corresponds to an increase in roughness by 1.3 (+0.1/−0.2) k_BT. In Fig. 5, we plot the relative energetic roughness superimposed on the potential of mean force G(r) = −k_BT ln p_eq(r) of unfolded Csp as a function of the denaturant concentration to illustrate the influence of collapse on the energy landscape.

Discussion

The free energy surface in the absence of denaturant (Fig. 5) summarizes the global structure and dynamics of unfolded Csp molecules under folding conditions. The rate of folding is determined both by the effective free energy barrier ΔG ^‡ separating folded and unfolded states, and the “attempt frequency” for crossing the barrier from the unfolded state. In generalized transition state expressions for the folding time τ_f of type τ_f = τ₀ exp(ΔG ^‡/k_BT), the reconfiguration time τ_r of the chain within the unfolded state potential is directly related to the inverse attempt frequency, or the preexponential factor τ₀. In a simplified Kramers description (39–41), where the curvature of the free energy surface and the effective diffusion coefficient are assumed to be similar in the unfolded well and on the top of the barrier, the preexponential factor is given by τ₀ ≈ 2πτ_r. In the absence of a barrier, τ₀ remains as an approximation to the “speed limit” (42), i.e., the minimum time scale of folding. With our value of 65 ns for τ_r of unfolded Csp under native conditions, large-scale chain diffusion thus sets a lower limit of τ₀ ≈ 0.4 μs to the folding time for a protein the size of Csp^‖, remarkably similar to estimates based on the length scaling of folding rates (9, 43). It remains to be clarified whether the decrease in the intramolecular diffusion coefficient we observe upon collapse (Fig. 4) continues toward the transition state region, as suggested from theory (44–47). The rapid folding observed for some proteins [folding times ranging from 0.7 μs for a variant of villin headpiece (48) to several microseconds (9)] suggests that this effect might not be large. This issue could be addressed with a combination of single-molecule experiments of the type described here, and laser temperature-jump experiments, which have been used to determine the molecular time scale of ≈2 μs for the relaxation from the transition state region to the unfolded state in variants of the five-helix bundle protein λ_6–85 (49, 50).

Note, however, that the preexponential factor for Csp folding as approximated above is virtually invariant compared with the nine orders of magnitude decrease in its folding time τ_f from 8 to 0 M GdmCl (13). The large change in τ_f is thus almost entirely caused by a change in ΔG ^‡, supporting the assumption of a linear dependence of ΔG ^‡ on denaturant concentration frequently made in the analysis of protein folding kinetics (2, 13).

Comparison to Peptide Dynamics.

Short unstructured peptides have been investigated intensively as model systems for the chain dynamics of real proteins, using ensemble lifetime fluorometry (51, 52) and quenching methods (32–35, 53, 69, 70). Extrapolating the rates of contact formation observed in quenching experiments of peptides to the length of the Csp chain yields values between ≈0.5 × 10⁶ s⁻¹ and 5 × 10⁶ s⁻¹. For a direct comparison to our results, we estimate the end-to-end contact formation rate for unfolded Csp assuming a Gaussian chain as k_c = 4πDa/(2π〈r²〉/3)^3/2 (54), where a is the contact distance. With our values for D and 〈r²〉 (Fig. 4), and a = 0.4 nm (34, 52), we calculate contact rates of (0.8 ± 0.1) × 10⁶ s⁻¹, within the extrapolated values from peptide dynamics. Similarly, the end-to-end diffusion coefficients between 0.04 and 0.2 nm²/ns, obtained for peptides under a variety of denaturant concentrations (34, 52), are close to the values we find for unfolded Csp**. The similarity of the dynamic time scales observed in unfolded Csp and unstructured peptides, and the single exponential decay of our measured intensity correlation functions (Fig. 3C), indicate the absence of specific interactions and corresponding large energy barriers (55), even in collapsed unfolded Csp under native conditions.

Rate of Collapse.

Finally, we point out that, according to Onsager's regression hypothesis, or, more generally, the fluctuation dissipation theorem, small fluctuations decay on the average in exactly the same way as macroscopic deviations from equilibrium (56). In other words, the time correlation functions of the spontaneous end-to-end distance fluctuations we observe in single molecules (Figs. 2 and 3) decay with the same time constants as the macroscopic signal would in ensemble perturbation experiments, such as rapid changes in solution conditions or laser-induced temperature jumps. The reconfiguration times measured in our experiments are thus equivalent to the collapse time of unfolded Csp. The similarity in time scale to the dynamics of unstructured peptides shows that the collapse of Csp is a purely diffusive, “downhill” process. Conversely, previous observations of denatured state dynamics in the microsecond range (57, 58) thus probably involve the crossing of substantial barriers.

Our measurement of the reconfiguration time of ≈50 ns is in good agreement with the relaxation time expected for an ideal chain (59–61) and theoretical estimates of the collapse times for proteins (43, 62). Additional evidence for the connection between reconfiguration dynamics and the collapse time comes from laser-induced temperature jump experiments on the 40-residue protein BBL; the collapse of its acid-denatured state occurs on a time scale of ≈60 ns (63), remarkably similar to the reconfiguration time of Csp. Future experiments will have to address in more detail issues such as the dependence of collapse times on chain length, temperature, and other parameters (43). For BBL, the enthalpy change involved in collapse evidently is large enough to allow temperature-induced perturbations of chain compactness. For a closely related Csp, laser-induced temperature jump experiments have not resulted in an observable signal (64), raising the possibility that its collapse does not involve a sufficient enthalpy change. Other perturbation methods, such as pressure jump and even the fastest mixing methods, are currently limited to time scales in the tens of microsecond range and above. Spontaneous fluctuations of individual molecules at equilibrium, however, are a universal property of sufficiently thermalized systems. Single-molecule photon statistics thus provide a versatile approach for investigating the dynamics of macromolecules on the biologically important nanosecond time scales.

Materials and Methods

Samples and Instrumentation.

Labeled Csp and polyproline peptides were produced as described (15, 19, 27). All experiments were performed in 50 mM sodium phosphate buffer adjusted to pH 7, containing 0.001% Tween 20 to prevent surface adhesion of the polypeptides. High-purity GdmCl solutions (Pierce, Rockford, IL) were used for denaturation experiments. Single-molecule fluorescence was observed by using a PicoQuant MicroTime 200 confocal microscope equipped with a continuous wave solid-state diode-pumped laser (Sapphire 488-200; Coherent, Santa Clara, CA) operating at 488 nm (average radiant power at the sample: 100 μW), a 1.2 NA, ×60 microscope objective (UplanApo ×60/1.20W; Olympus, Melville, NY), and a 100-μm confocal pinhole. A dichroic mirror (585DCXR; Chroma, Rockingham, VT) separated donor and acceptor fluorescence. Subsequently, each fluorescence component was divided randomly by a 50/50 beam splitter between a pair of two avalanche photodiodes (APDs; Optoelectronics SPCM-AQR-15; PerkinElmer, Wellesley, MA). Additional interference filters [HQ525/50 (Chroma) and 525AF45 (Omega Optical, Brattleboro, VT) for the donor APDs, 600HQLP (Chroma) and HQ640/100 (Chroma) for the acceptor APDs] completed spectral separation of the sample fluorescence and served to suppress the mutual detection of APD breakdown flashes in the infrared (65). Each of the two APD pairs was connected to a photon counter: the donor detectors to a PicoHarp 300 and the acceptor detectors to a TimeHarp 200 (both PicoQuant, Berlin, Germany). In their histogram mode, which we used for the measurements at 500 pM Csp and Pro20, the two input channels of these cards operate as start and stop channels. The measured time intervals Δt between start and stop were histogrammed in 256-ps (PicoHarp) or 304-ps (TimeHarp) bins. To avoid cross-talk between the two channels at short time intervals and simplify data analysis, an electronic time delay Δt₀ was imposed onto the stop channel (SI Fig. 6). Mean transfer efficiency data for calculating rms end-to-end distances (Fig. 4A) were taken from ref. 27. The dependence of the Förster radius R₀ on denaturant concentration was determined by measuring changes in spectral overlap, donor quantum yield, and the refractive index of the solvent and was found to be dominated by the change in refractive index. For more details on data acquisition and analysis and the measurement of subpopulation-specific correlation functions (Fig. 2), see SI Text.

Analysis of Interphoton Time Distributions.

The histograms shown in Fig. 3 B and C (integration time 10 h) represent interphoton time distributions φ̃_ii(Δt) (i = A, D), which are, in the limit of very low mean photon detection rates τ_i⁻¹, proportional to the intensity autocorrelation function g_ii(τ) with the lag time τ = Δt − Δt₀. At higher count rates, shorter interphoton times are detected more frequently than longer ones. To correct for this pile-up effect, we fitted the data to:

where g_ii(τ) was approximated by

assuming separation of time scales. A is an overall amplitude, exp(−Δt/τ_i) accounts for the pile-up effect (compare Eq. 8), g_AB, g_CD, and g_T correspond to the contributions of photon antibunching, chain dynamics, and triplet-state dynamics, respectively, to the overall autocorrelation function g_ii(τ). For each sample, we determined the triplet-state correlation time τ_T from independent conventional fluorescence correlation spectroscopy measurements. Typical values were in the range of 1–4 μs. All remaining parameters of φ̃_ii(Δt) were determined by least-square fitting to the histogram data. The values obtained for τ_i⁻¹ (≈10⁵ s⁻¹) are in good agreement with the mean photon count rates during a photon burst, i.e., during the passage of a molecule through the observation volume. The pile-up-corrected correlation data shown in Fig. 3 were obtained by dividing each histogram value by A exp(−Δt/τ_i).

Calculation of Intensity Correlation Functions and Interphoton Time Distributions.

The intensity autocorrelation functions of fluorescence from donor and acceptor are defined as:

where n_i(τ) is the fluorescence count rate (photon counts per unit time), which fluctuates because of the stochastic processes of photophysics and protein dynamics. The correlation functions are normalized such that g_ii (τ) → 1 as τ → 170). The distribution of the times between donor or between acceptor photons are denoted by φ∞. The distribution of the times between donor or between acceptor photons are denoted by φ_DD(τ) and φ_AA(τ) and are normalized according to ∫₀^∞φ_ii(τ)dτ = 1, i = A, D.

Recently, a general theory of these quantities has been developed (26). In this theory, the rate matrix K describes all electronic and conformational transitions in the system, and the matrix elements of the off-diagonal matrices V_A and V_D specify those transitions that result in the emission of acceptor or donor photons. Let p_ss be the vector of normalized steady-state probabilities obtained by solving Kp_ss = 0 (1^⊤ p_ss = Σ_i p_ss (i) = 1, where 1 is the unit vector). The mean time between detected acceptor (donor) photons, τ_i, and the mean fluorescence count rate 〈n_i〉 (i = A, D) are then given by:

(see equation 2.16 of ref. 26). The intensity correlations are:

(see equation 2.18 of ref. 26). The interphoton time distributions are:

(see equation 2.25 of ref. 26). The interphoton time distributions can be related to the corresponding intensity correlation functions if the mean time between photons τ_i is much longer (in our case on the microsecond time scale) than the relaxation time of the correlation function (in our case on the nanosecond time scale). Then, using the separation of time scales, the interphoton time distribution can be approximated as:

We confirmed numerically that this approximation holds very well under the conditions of our experiments. Thus, the intensity correlation function can be obtained by multiplying the interphoton time distribution by an exponential (pile-up effect correction; compare Eq. 2).^†† Details of the theoretical model used for calculating g_ii(τ) and the procedures for comparing measured and calculated correlation functions are given in SI Text.

Abbreviations

FRET

Förster resonance energy transfer

Csp

cold shock protein

GdmCl

guanidinium chloride

APD

avalanche photodiode.

Note Added in Proof.

Two papers (71, 72) published since submission of this manuscript are closely related to the present work.