Femtosecond direct observation of charge transfer between bases in DNA

Abstract

Charge transfer in supramolecular assemblies of DNA is unique because of the notion that the π-stacked bases within the duplex may mediate the transport, possibly leading to damage and/or repair. The phenomenon of transport through π-stacked arrays over a long distance has an analogy to conduction in molecular electronics, but the mechanism still needs to be determined. To decipher the elementary steps and the mechanism, one has to directly measure the dynamics in real time and in suitably designed, structurally well characterized DNA assemblies. Here, we report our first observation of the femtosecond dynamics of charge transport processes occurring between bases within duplex DNA. By monitoring the population of an initially excited 2-aminopurine, an isomer of adenine, we can follow the charge transfer process and measure its rate. We then study the effect of different bases next to the donor (acceptor), the base sequence, and the distance dependence between the donor and acceptor. We find that the charge injection to a nearest neighbor base is crucial and the time scale is vastly different: 10 ps for guanine and up to 512 ps for inosine. Depending on the base sequence the transfer can be slowed down or inhibited, and the distance dependence is dramatic over the range of 14 Å. These observations provide the time scale, and the range and efficiency of the transfer. The results suggest the invalidity of an efficient wire-type behavior and indicate that long-range transport is a slow process of a different mechanism.

Since the first report on conductive (1) one-dimensional DNA crystals more than 30 years ago (2, 3) different methods have been used for the study of conductivity, the latest of which is the measurement of conductance on the mesoscopic scale, which suggests a large band-gap semiconductor behavior (4). Charge transfer by photoinduced reactions between donors and acceptors has provided a useful methodology for exploring the mechanism in DNA (5, 6); the donor and acceptor were either noncovalently (7–10) or covalently (11–15) bound to DNA. Evidence for long-range oxidative damage was also demonstrated (16–19). However, results for different systems have shown different values for the distance range over which the transfer is efficient, in part because of measurements of the yield in most cases.

Recently, we have studied DNA with covalently tethered ethidium (hole donor) and a base-like acceptor (7-deazaguanine, Z; ref. 20); the rates and yields reflect the different processes involved. Even though these systems have a covalently tethered hole donor, a careful study of the effects of stacking and distance on charge transfer requires DNA assemblies unperturbed by donor/acceptor probes. Here, we report such studies in DNA assemblies with the donor and acceptor being nucleic acid bases (Fig. 1). These systems are unique because (i) there are only minor structural perturbations arising; (ii) no ambiguities occur with respect to distance separating donors and acceptors; (iii) the assemblies are structurally well defined and well characterized (21); and (iv) much is known about the steady-state quenching of fluorescence (15).

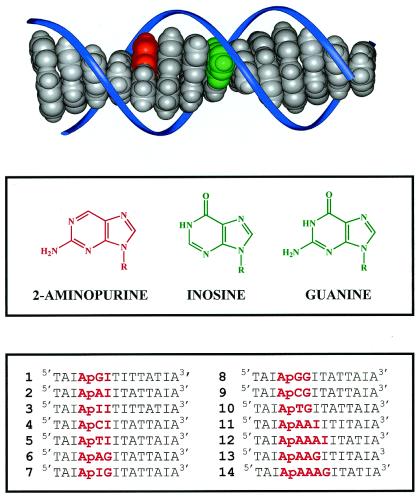
Figure 1.

(Top) Molecular model (INSIGHT II program) schematically illustrating the base pair stack within a DNA-duplex. The bases 2-aminopurine (Ap) and guanine (G) are depicted in red and green, respectively, and the sugar phosphate backbone is depicted schematically in blue. (Middle) Structures of 2-aminopurine, inosine, and guanine. (Bottom) The sequences of 14 DNA duplexes studied in our experiments. The complementary strands are not shown; Ap, as an analogue of adenine, is paired with thymine, and inosine is paired with cytosine.

Experimental Procedures

The femtosecond experimental setup has been published (22). Briefly, in our experiments, a femtosecond laser pulse at 325 nm (0.2 μJ) excites 2-aminopurine (Ap) into its lowest excited state (Ap*) while a second pulse at 600 nm (<0.01 μJ), delayed in time, measures the absorbance of Ap*. This scheme allows us to monitor the decay of the initial population. Other probe wavelengths between 400 and 700 nm showed similar decay characteristics but with smaller amplitudes. The polarization of pump and probe pulses was set at 54.7° (magic angle) to avoid contribution from polarization anisotropy by, e.g., orientational motions (20, 22). All samples contained 0.1 mM duplex DNA in 0.1 M sodium phosphate buffer (pH 7) and were measured in a quartz cell at room temperature. To avoid accumulation of photo products, the samples were stirred during the measurements. The typical transient absorption signal (ΔA) at the initial time was 0.002 under the experimental conditions.

Control Experiments

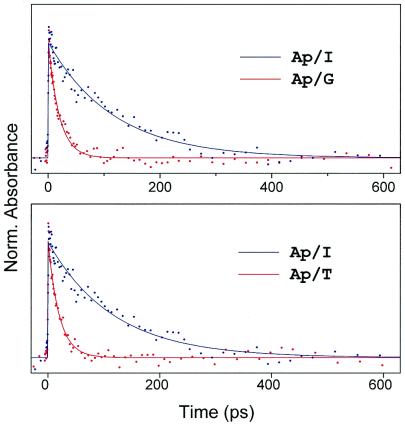
To characterize the nature of the transfer in DNA, we also studied Ap complexes with mononucleotides (without DNA) in water and in buffer solutions. We have measured both the transient absorption and the fluorescence up-conversion in these systems and observed charge transfer dynamics on the time scale of 20 ps to 300 ps depending on the nucleotide (Fig. 2). These time constants describe the forward rate of charge transfer. The important fact that transient absorption reveals the same dynamical behavior as the fluorescence up-conversion (for G, T, A, C) confirms that both methods monitor the excited state dynamics of Ap, because the charge transfer state is nonradiative in nature. Moreover, the rise of all our signals is within the femtosecond pulse correlation, and this is independent of the free energy of the different nucleotides. The quenching of Ap* by the nucleotides was evident in the temporal behavior (Fig. 2). Energy transfer has been excluded because of the lack of spectral overlap between the fluorescence of Ap* and the absorption of the natural DNA bases.

Figure 2.

Normalized transient absorption of Ap/nucleotide complexes in aqueous solutions. (Upper) The ps decay of Ap (≈100 mM) with dGTP (86 mM) and with dITP (75 mM). (Lower) The ps decay of Ap (≈100 mM) with dTTP (86 mM) and with dITP (75 mM). The decay times are 19 ps, 20 ps, and 120 ps for dGTP, dTTP, and dITP, respectively (see text and Fig. 3).

We have also made a thorough study of the Ap in water and other solvents to examine the overall rate of nonradiative decay, by, e.g., internal conversion, and the effect of the solvent on such rates. The measured time constants were found to be longer than nanosecond, consistent with the fact that the nonradiative decay rate of aminopurine is much smaller than that of DNA bases because of the change in ordering of the nπ* and ππ* states (23). To check for the possibility of proton transfer, we have studied the effect of pH, by changing the H⁺ concentration over 5 orders of magnitude, and the isotopic change from H₂O to D₂O. The similarity of the transient again supports our conclusion of electron transfer. To confirm this picture, we have repeated the DNA experiments, but we replaced guanine with 7-deazaguanine, a one-atom change. The change in rates for the latter follows the driving force change of ∼0.3 eV (20).

Dynamics in DNA Assemblies

The decay constants of Ap/G (19 ps) and Ap/T (20 ps) systems are almost the same and are clearly faster than that of Ap/I (120 ps), where I is inosine. This behavior cannot be explained by following the established trend for the oxidation (G > A > I > C, T; refs. 24–26) or the reduction (T > C > A > G; ref. 25) potentials of the nucleotides. Hence, we concluded that these results are an indication that the charge transfer can occur through both oxidative and reductive reactions of the nucleotides with Ap*. It should be noted that in all systems studied, we observed a longer ns component that represents the fraction of molecules which cannot undergo charge transfer, i.e., the unfavorable configurations (20, 22).

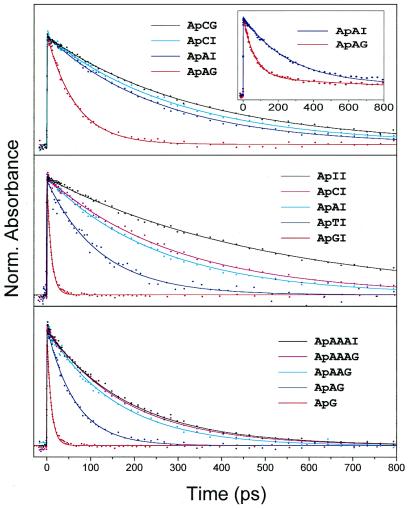
For a synthetic DNA duplex with Ap incorporated in the base stack, Fig. 3 displays the transient absorption decays obtained showing (i) the effect of the driving force, (ii) the effect of the adjacent base, and (iii) the distance dependence of charge transfer rates in the double helix. Specifically, in the top portion we show the decay of ApAI and ApAG. In these systems the driving force for charge transfer is much larger for ApAG, resulting in the clearly observed faster ps decay for ApAG (65 ps) when compared with ApAI (265 ps). The sensitivity of the transfer to the nature of the bridge base becomes apparent by comparing the results of ApCG with ApCI in the figure (3). Replacing A by C changes the decay drastically and results in very similar rates for ApCI (300 ps) and ApCG (335 ps). Analogous behavior was observed for the pair ApTI (124 ps)/ApTG (109 ps). This result indicates the crucial role of intervening bridge states, as discussed below.

Figure 3.

Normalized transient absorption of DNA assemblies. (Top) The ps decay of ApAG, ApAI, ApCI, and ApCG duplex assemblies. (Inset) The measured data for ApAG and ApAI without subtraction of the ns component. (Middle) ApGI, ApTI, ApAI, ApCI, and ApII duplex assemblies. (Bottom) The ps decay of ApG, ApAG, ApAAG, ApAAAG, and ApAAAI duplex assemblies. Note that ApG and ApGI refer to the same molecular assemblies. In DNA the ns component (Inset) is due to stacking and structural disorder. Note that the excited state lifetime of Ap* in water and DNA is >20 ns (23) and >1 ns, receptively. As in Fig. 2, here we also subtracted this ns component to focus on charge transfer.

In Fig. 3 Middle, we show the transients of DNA assemblies where Ap is adjacent to the different bases (G, A, I, C, T). The charge transfer rate is maximum in ApGI (10 ps) and slows down in ApAI (260 ps) and ApII (512 ps), following the established trend for the oxidizability of nucleotides, as given above. Interestingly, upon going from I (512 ps) to C (298 ps) and T (124 ps), the charge transfer is accelerated again, following the trend for the reducibility of nucleotides. This behavior is entirely consistent with our results obtained for the nucleotide complexes without DNA (see Fig. 2); Ap* can undergo oxidative charge transfer with G and A and reductive charge transfer with T and C. The charge transfer to I appears in both directions to be energetically unfavorable, resulting in the slowest dynamics for the ApI sequence (512 ps). Therefore, inosine can function as a calibration base for quantifying the G oxidation rates.

In Fig. 3 Bottom, we show the experimental results for DNA assemblies of varying distance between Ap and G. The DNA assemblies contain different numbers of bridging adenine bases. Clearly, the rates decrease dramatically with increasing distance between Ap and G: 10 ps (ApG); 65 ps (ApAG); 155 ps (ApAAG); 179 ps (ApAAAG); compared with 260 ps (ApAI); 210 ps (ApAAI); and 190 ps for ApAAAI in the reference systems. However, at a Ap-G distance of ≈14 Å (assuming 3.4 Å base-base stacking), no significant difference in the rates between the ApAAAG and ApAAAI could be found.

Three key observations are noteworthy: (i) The results show that all bases can undergo charge transfer when located directly to the 3′ side of Ap in the base stack. (ii) The G oxidation has the largest driving force and is, therefore, the most efficient charge transfer process. It occurs not only locally, but also by mediation via intervening purine bases (A, I), and hardly via the pyrimidine bases (T, C). (iii) The G oxidation exhibits a strong distance dependence and becomes insignificant after three intervening bases (≈14 Å).

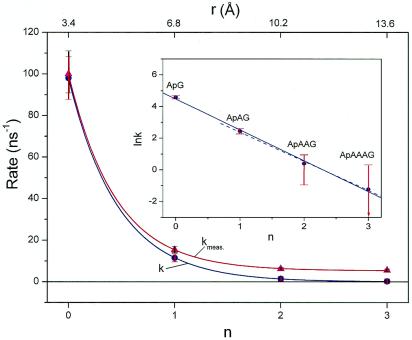
From the experimental point of view, it is evident that the rates highly depend on the nature and the number of the bridging bases; a nearly biphasic behavior with distance over the range of 14 Å was observed (Fig. 4). From a theoretical point view, the DNA assembly can be decomposed into three components, namely the donor (Ap*), the bridge (B), and the acceptor (G). The overall charge transfer dynamics must depend on all possible reaction channels between these components. In this picture:

Figure 4.

Rate of charge transfer from Ap* to G plotted vs. the number (n) of intervening bridge bases adenine. The data of the overall measured rate k_meas for the G-containing assemblies was fitted to a function of an exponential plus a constant (β = 0.63 Å⁻¹). The base-mediated rate k (see text) was fitted to an exponential function (β = 0.59 Å⁻¹). (Inset) The semilogarithmic plot. The linear fit with all four data points (solid line) and with only three data points n = 1 to 3 (dashed line) gives β = 0.57 Å⁻¹ and 0.54 Å⁻¹, respectively. It is interesting to note that in the Inset the first point (ApG) is also located on the slope, although in this system only local charge injection is operative. This suggests that all nearest neighbor base electronic matrix elements in DNA are on average of similar magnitude and that Ap can be treated as an intrinsic DNA base.

(1a) Ap*BG → Ap^⋅−B^⋅+G for B = A (hole injection);

(1b) Ap*BG → Ap^⋅+B^⋅−G for B = T, C (electron injection); and

(2) Ap*BG → Ap^⋅−BG ^⋅+ (superexchange/tunneling).

Channel 1 is the local charge transfer from Ap* to its adjacent B (3′ side). If B = A the charge transfer is a hole injection. If B = T, C the charge transfer is an electron injection process. In these cases, further charge migration from B to G may occur and give Ap^⋅−BG^⋅+. However, it is not observable because only the initial population of Ap* is monitored in our experiment; also, the latter is a faster process because of its exothermicity. Channel 2 is a direct charge transfer from Ap* to G that requires the involvement of B. In the so-called superexchange model (27), the intermediate state of B, which may include the ion pair state {Ap^⋅−B^⋅+G} manifold, will mediate the virtual coupling. Indeed, there is an experimental correlation that suggests the involvement of the ion-pair vibronic states. Such states are energetically favorable if B = A or I; for B = T or C, these states are much higher in energy and provide a much smaller coupling (based on the oxidation potential). Thus, for B = T or C, the resulting rate for base-mediated G oxidation cannot compete with the rate of local electron injection (channel 1b, i.e., the reduction of the adjacent base), and this explains why ApCG and ApCI have very similar rates (see Fig. 3 Top).

Considering the existence of two channels, where one is leading to local charge injection and the other to a charge transfer mediated by the intervening bases, we can extract the rates for the latter process by subtracting the corresponding decay profile of the reference inosine system, the calibration sequence: the rates for ApG, ApAG, ApAAG, and ApAAAG were calibrated against those for ApI, ApAI, ApAAI and ApAAAI. Thus, the system is treated as two population channels with no interference (28–30). However, this may not be significant because our experiments comparing ApGI (10 ps) with ApGG (9 ps) demonstrate that the effect of G on an intervening base is minor. If one plots these calibrated rates versus distance, an exponential dependence was obtained (Fig. 4 Inset). This behavior follows the empirical relationship k(r) ∝ exp(−βr), and from the slope we can obtain a distance range parameter of β = 0.6 ± 0.1 Å⁻¹. It is interesting that this value is very close to that measured in DNA hairpins systems (13).

Nature of Transport

The above results are directly relevant to the description of the nature of the transport (29–31) and striking in a number of ways: (i) the distinct and different order of magnitude in time scale for the behavior of the local injection and the base-mediated transfer, and (ii) the change of the rates with distance and driving force. It may appear counterintuitive that the local hole injection in ApAI from Ap* to A is slower than the mediated G oxidation in Ap*AG. This is particularly the case if one considers the transfer as a superexchange process with an effective coupling V_n (where n is the number of intervening bases) equals (V_DBV_BA/Δ)(V_BB/Δ)ⁿ⁻¹, where V_DB, V_BA, and V_BB are nearest-neighbor electronic matrix elements and Δ is the electronic energy gap. Accordingly, as n increases, the rates should decrease exponentially. However, there are two problems with this simplified description.

First, the effect of exothermicity. Our results show that the exothermicity of the base next to Ap* controls the observed rate (see Fig. 3 Middle). Thus, in the assembly ApAG, the rate for Ap*AG → Ap^⋅−A^⋅+G is not related to the rate for Ap*AG → Ap^⋅−AG^⋅+, because the former process is controlled by the exothermicity and the latter, by both the exothermicity and the electronic coupling V. This point becomes clear if we consider the theory of nonadiabatic electron transfer that expresses the rate in a Fermi Golden Rule as k = 2π/ℏ |V|² F(ΔG, λ), where F is the Franck Condon factor that gives the dependence on the free energy (ΔG) and the reorganization energy (λ). Thus, both V and F are part of a complete rate description. When the distance is varied in the same family of assemblies, e.g., Ap(A)nG, then the exothermicity is about the same and V is the main changing parameter. Our experiments separate these dependencies because of the designed duplexes in the study (see Fig. 1).

Second, the nature of the electronic coupling as the number of intervening bases changes. This is more complex (32) than usually thought because of the range of bridge state energies involved, including those at high energies Δ ≫ V (superexchange limit) and those in near resonance Δ ≈ V (tunneling limit). In the superexchange regime, as discussed above, we expect the exponential dependence on n or distance with β > 1. However, if the mediation through the base involves coherent near resonant states, then β could be less than 1. A coherent mediated transfer utilizes B for transmission but molecular motions will determine the dynamical disorder (dephasing time) or the coherence length of the transport.

It is of interest to compare the results reported here with those published earlier for the system of ethidium (hole donor)/7-deazaguanine (hole acceptor), which gives a rate of (5 ps)⁻¹ for the hole injection (20). In the present system, this injection rate for Ap*G is (10 ps)⁻¹. It should be noted that for the ethidium (cation) system the transport is that of a carrier (+), whereas here it is a charge separation (+ −). Thus, the reorganization energies might be different. Second, stacking of ethidium within the helix is expected to lead to expansion in the duplex. Third, for the ethidium system, the distance studied (10–17 Å) is larger than the range studied here (3–14 Å). This fact, together with the nature of stacking, explains the lack of clear base-mediated (superexchange-type) transfer in the ethidium system. Finally, as far as the efficiency of the transfer in both systems is concerned, we clearly see the fraction of structures which undergo the transfer; for the ethidium systems it is up to ≈60%, but for the Ap systems the efficiency is much higher, reaching ≈90%. The efficiency relates to stacking and dynamical disorder (20).

Conclusions

The experimental results reported here provide direct observation of the femtosecond dynamics of charge transfer in well defined DNA assemblies where donors and acceptors are of the same family as the intrinsic bases. The time scales show the distinct local and base-mediated dynamics over three bridge bases, and the dependence on the nature of the bases involved. The facts that the rates are on the picosecond time scale, the base-mediated (superexchange-type) process significantly slows down with distance (≈14 Å), the overall rate is controlled by the initial charge injection (even if the transfer between bases is faster), and the efficiency decreases for each step because of dynamical disorder, we conclude that DNA does not exhibit an efficient molecular wire behavior. Long-range transport must occur on a longer time scale and with a different mechanism, possibly by hopping migration (17, 18). Currently, we are addressing two related issues: direct measurement of the rates of product formation and the theoretical modeling of the time scale for base-to-base transfer. Very recently Lewis et al. (33) reported rate constants as low as 5 × 10⁶ s⁻¹, and it is important to consider the molecular dynamics (20, 34, 35) and other reaction channels which yield disparity in rates over a wide range, from 10¹¹ to 10⁷ s⁻¹.

Abbreviation

Ap

2-aminopurine