Seasonality, density dependence, and population cycles in Hokkaido voles

Abstract

Voles and lemmings show extensive variation in population dynamics regulated across and within species. In an attempt to develop and test generic hypotheses explaining these differences, we studied 84 populations of the gray-sided vole (Clethrionomys rufocanus) in Hokkaido, Japan. We show that these populations are limited by a combination of density-independent factors (such as climate) and density-dependent processes (such as specialist predators). We show that density-dependent regulation primarily occurs in winter months, so that populations experiencing longer winters tend to have a stronger delayed density-dependence and, as a result, exhibit regular density cycles. Altogether, we demonstrate that seasonality plays a key role in determining whether a vole population is cyclic or not.

Along controversy over the issue of density-dependent versus -independent population regulation has led to the conclusion that both factors are important for understanding population fluctuations (1–8). It is, however, less clear how such density-dependent and -independent factors interact with each other in shaping the dynamic pattern of populations across a larger part of the species range. In an attempt to disentangle these issues, we analyze a set of 30-year seasonal (spring and fall) time series from 84 populations of the gray-sided vole [Clethrionomys rufocanus (Sundevall, 1846)] from Hokkaido, Japan (Fig. 1A) (9, 10). To investigate the role of seasonality in the generation of population cycles, we decompose the annual (fall-to-fall) density dependence, as well as the density-independent stochasticity into their seasonal components. The added detail provided by pinpointing the seasonal arena of population regulation (see supporting information on the PNAS web site, www.pnas.org) provides us with a better basis for suggesting and evaluating hypotheses about the biological mechanisms that cause density dependence, stochasticity, and population fluctuations.

Fig. 1.

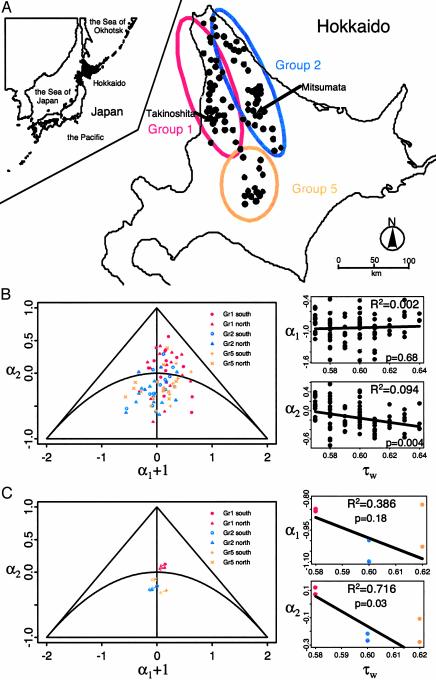
The study area (A) and the dynamics of the gray-sided voles (B and C). (A) Hokkaido is the northernmost island (41° 24′–45° 31′ N, 139°46′–145° 49′ E) of Japan and covers 78,073 km². Average relative length of winter is 0.579 (SD = 0.009) in the western populations of Group 1 (red), 0.595 (SD = 0.010) in the eastern populations of Group 2 (blue), and 0.618 (SD = 0.014) in the southern and mountainous populations of Group 5 (yellow). (B) Population dynamics are investigated by autoregressive coefficients. Below the semicircle the dynamics are cyclic with shorter periods the stronger the density dependence (28). An observed annual scatter-plot of the autoregressive coefficients for 84 Hokkaido time series is shown. To the right of the triangle, the annual density dependencies (α_i) are plotted against the relative length of the winter. Ordinary regressions are shown as lines. (C) Predicted change for an increase of 0.1 in τ_w from the estimated position in the parameter space, using the estimated density dependencies from the pooled analyses (Table 1; see text). For each area (the northern and southern part of Groups 1, 2, and 5), seasonal estimates are divided by average season length to estimate per-time-unit seasonal density dependencies. The direct and delayed annual density dependencies are generally predicted to become stronger the longer the winter. To the right of the triangle, the weighted regressions of annual density dependencies on relative length of winter are given; the weights [based on (WI – ŴI)²; see text] for Group 1, Group 2, and the more mountainous Group 5 are 0.96, 0.85, and 0.19, respectively.

A perennial problem in the study of population dynamics has been the relative lack of extensive and accurate data. In this study we attempt to reach more accurate conclusions than are usually possible by two means. First, we use comparative time-series data from a large number of very similar populations. Second, we address the very substantial problem of biased and imprecise measures of population density through use of a state-space modeling approach (11–13), where time-series observations are related to unobserved “states” of the real population through a probabilistic observation model accounting for sampling variation. Our study confirms and extends an earlier study of ours (14); whereas the earlier study used only fall data (and as a result could cover the entire island of Hokkaido), the present study used both fall and spring data. The greater detail of the data used in this paper makes a much more detailed analysis of the seasonal structure possible; a picture we assume, based on earlier studies (14), applies to the entire island of Hokkaido.

The Study System, Its Seasonal Structure, the Sample Sites, and the Data

Hokkaido is the northernmost island (41° 24′–45° 31′ N, 139° 46′–145° 49′ E) of Japan and covers 78,073 km². It neighbors the Asian continent and is surrounded by the Sea of Okhotsk, the Pacific Ocean, and the Sea of Japan. A southern warm current prevails in the Sea of Japan along the western shore of Hokkaido, whereas northern cold currents prevail in the Pacific Ocean along the northern and eastern shores. Mountain ridges run north–south through the middle of the island; in the southwestern part there is another mountain ridge. Except for the temperate deciduous forests of the southwestern peninsula, most of the natural forests in Hokkaido are regarded as the transition between the temperate and the subarctic zones (15). The dominant tree genera are Abies, Acer, Betula, Picea, and Quercus. Hokkaido represents the easternmost part of the gray-sided voles' distribution, which extends as far as Fennoscandia in the west (16, 17).

The lengths of the seasons vary from one year to the next. Information on this variability is not available. A related measure, an index of vegetation growth called the warmth index (WI) (see supporting information) is, however, available for a large number of meteorological sites, but not for all trapping sites used in our study. This index is used as a basis for developing a measure of relative length of the winter (τ_w), being 1 – (relative length of the summer) (for details, see supporting information).

The gray-sided vole (C. rufocanus) represents a pest on plantations of larch (Larix leptolepis) and todo-fir (Abies sachalinensis). Since 1954, the Forestry Agency of the Japanese Government has carried out censuses of vole populations for management purposes in forests all over Hokkaido. The forests managed by the Forestry Agency cover 28,400 km² [21,500 km² natural forests and 6,900 km² planted forests (1992 figures)]. These forests were in 1992 managed by 76 district offices, which were further divided into several ranger offices, giving a total of 433 ranger offices. The individual ranger office, which also represented our basic unit of analysis, carried out the censuses; personnel at the ranger offices were regularly trained, including in species identification, for performing the censuses (16).

Rodent censuses were carried out twice a year [spring (May or June) and fall (September or October)] on a 0.5-hectare (50 × 100 m) plot [the latter being used for the annual analysis (14, 17, 19)]. At each plot, 50 snap traps were set in 10 × 10-m grids for five or three nights. For each site, one to three separate grids were monitored in fixed preselected natural forests. The census grids were occasionally relocated within the local area. Altogether, 84 time series for both spring and fall covering 30 years (1963–1992) in the central and northernmost part of Hokkaido (the Asahikawa Regional Office, Forestry Agency of the Japanese Government) are used; this region is the one for which cycles occur (10) and for which we have sufficient data. We have grouped these populations according to topographic characteristics in our previous studies (19). Trapping efforts were represented by multiplying the number of traps by the number of nights and the number of census plots (grids). For instance, when three-night censuses were carried out at three grids in a ranger office, the trapping efforts by the ranger office at the census was 450 (= 50 × 3 × 3). The spring-to-fall season (summer) corresponds to the period of population growth (because of reproduction), whereas the fall-to-spring season (winter) corresponds to the period of population decline [winter reproduction is negligible (refs. 17 and 20–25; see supporting information)].

Reliable data are available on food habits of voles (16, 20). C. rufocanus of Hokkaido prefer green plants as food (20). Leaves of bamboo grasses (Sasa senanesis, Sasa kurilensis, and Sasa nipponica) constitute a large part of the winter diet, and their shoots occupy a considerable part of the summer diet (although summer diet is much more varied than winter diet). Thus, bamboo leaves influence survival during the winter and bamboo shoots influence reproduction during the summer (most likely primarily during the spring because other plants do not grow as well at this time of the year). Bamboo grasses may be particularly important during winter when other plants wither, even though their leaves do seem to be nutritionally poor during the winter. Even though there are many predators such as snakes, birds, and mammals in Hokkaido (21), their activity under the snow cover is often restricted. An exception is the least weasel Mustela nivalis, which is a highly efficient predator under the snow cover.

The gray-sided vole is the most common rodent species in Hokkaido (20, 25). Three other microtine and murine rodent species are recorded as an integral part of the census: Clethrionomys rutilus (Pallas, 1779), Apodemus speciosus (Temminck, 1844), and Apodemus argenteus (Temminck, 1844). In addition, Clethrionomys rex Imaizumi, 1971, Apodemus peninsulae (Thomas, 1907), and shrews (Sorex spp.) are occasionally caught. Personnel of the Forestry Agency identified the specimens. Clethrionomys is easily distinguished from other genera. Distinguishing C. rufocanus from its congeners may, however, be difficult, although the abundance of C. rufocanus and C. rutilus was separately reported. The numbers for the other Clethrionomys species is, however, very low in Hokkaido (20, 26), reducing the impact of any misclassification.

The Ecological Model

Let spring and fall abundances in year t (log-transformed and centered around their means) be denoted x_t and y_t, respectively. The seasonal models for the net winter population growth rate, R_wt (= x_t – y_t–1), and the net summer population growth rate, R_st (= y_t – x_t), are given as (27)

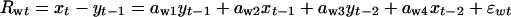[1a]

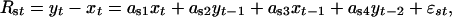[1b]

where ε_wt is the time-independent process noise during the winter 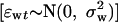and ε_st is the corresponding summer component 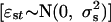. The parameters a_w and a_s define the seasonal density-dependent structure for the winter and summer growth rates, respectively. The annual net growth rate is obtained by rewriting Eqs. 1 and 2 as a model in y only (27):

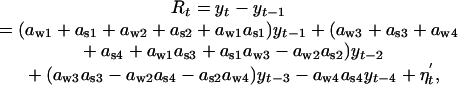[2]

where 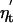is the annual noise term (see supporting information). The two last autoregressive terms in Eq. 2 are typically negligible (as is also the case in this study), rendering a second-order process an appropriate approximation (6, 8, 25):

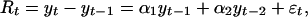[3]

where ε_t is the annual noise term [ε_t ∼ N(0, ρ²)] and the parameters α₁ and α₂ define the direct and delayed annual density dependencies; for this system to correspond to a stationary process, the two autoregressive parameters (1 + α₁) and α₂ must fall within the triangle defined by (–2, –1), (0, 1), and (2, –1) (28).

The link between the annual and the seasonal parameters are given as α₁ = a_w1 + a_s1 + a_w2 + a_s2 + a_w1a_s1 and α₂ = a_w3 + a_s3 + a_w4 + a_a4 + a_w1a_s3 + a_s1a_w3 – a_w2a_s2. Assuming a white-noise term (i.e., no delayed noise in the noise process of Eq. 3), ρ², the annual noise variance may be expressed by 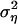given as a function 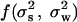(see supporting information).

Linking the Data to the Ecological Model

Sampling variance is known to bias the estimates of, and invalidate tests for, density dependence (5, 29); the degree of direct density dependence is typically overestimated when ignoring sampling variance. Despite this, sampling variance is generally ignored (25) in empirical studies, partly because of availability of data and methodological shortcomings. Sampling variance may be accounted for by adopting a state-space modeling approach where time-series observations are related to unobserved “states” of the real population through a stochastic observation model (11–13). Let the number of voles caught during the spring and fall session at a given site in year t be given by z_s,t and z_f,t, respectively. Similarly, let the trapping effort at a given site in the spring and the fall of year t be given by T_s,t and T_f,t, respectively. Our core data consist of the total number of gray-sided voles caught (z_s,t and z_f,t) and the corresponding trapping effort (T_s,t and T_f,t). The expected number of voles caught during a trapping session will be related to the abundance of voles at the site (y_t and x_t, log-abundances scaled around their respective mean values, μ_y and μ_x) and on the trapping effort. As a first approximation, the ecological process model as described by Eqs. 1a and 1b or Eq. 3 is assumed to be linked to the observed number of voles caught through a Poisson model. For the fall samples this will then be given as: P(z_f,t = z|y_t) = exp(–λ_f,t)λ^z_f,t/z!, where the Poisson mean (assumed to be proportional to the trapping effort and the population abundance) is defined as λ_f,t = qT_f,t exp(μ_y + y_f,t). The trapping effort T_f,t is a known parameter. The parameter μ represents the mean of the logtransformed “true” population abundances. Because of the nature of the data, the average level of the true population (μ) is confounded by the “trappability” (i.e., the average probability for any present individual to be trapped) in the given environment q. However, although μ cannot be directly estimated, we can estimate the product of the average abundance level and the “trappability,” defined as exp(γ) = q exp(μ). This yields the following reparameterization (for the fall; and equivalently for the spring): λ_f,t = T_f,t exp(γ_f + y_f,t).

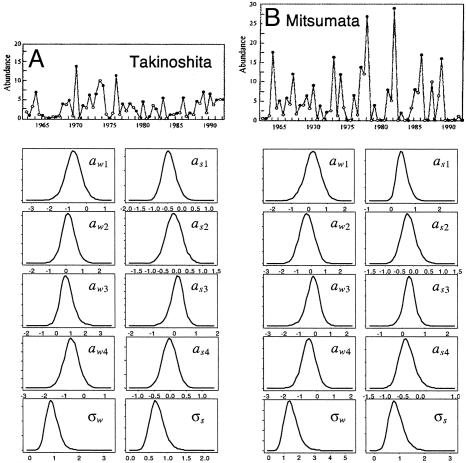
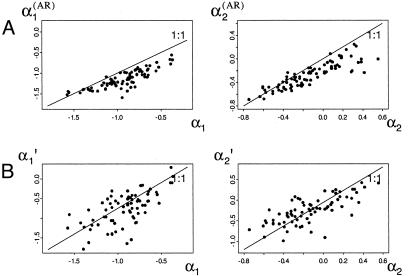
By using the software package bugs (Bayesian inference using Gibbs sampling; ref. 30), a Bayesian framework was adopted to estimate parameters in the state-space model. The resulting posterior distributions of parameters from the seasonal model are shown for two typical populations (Fig. 2). Only vague (i.e., essentially flat) prior distributions were used. For further details, see supporting information. Posterior means are used as parameter estimates and used in further analyses. Seasonal parameter estimates being judged as statistically appropriate were obtained from only 74 sites (see supporting information). All 84 time series are, however, used for obtaining the main results summarized in Table 1, as well as those depicted in Figs. 1 B and C. Notice that the annual density dependencies given by Eq. 3 are both estimated to be stronger when sampling error is not accounted for (Fig. 3A).

Fig. 2.

Kernel density estimates of the posterior distribution of parameters for the seasonal processes (Eqs. 1a and 1b) are shown for two populations. (A) Takinoshita (44° 11′ N, 141° 51′ E). (B) Mitsumata (44° 04′ N, 142° 35′ E). Posterior distributions of parameters from the corresponding observation model (see supporting information) are not shown.

Table 1. Strength of density-dependent processes as estimated by the mean posterior distribution obtained from pooled seasonal (Eqs. 1a and 1b) and annual (Eq. 3) analyses (SD of posterior distribution in parentheses).

Dynamics		Group 1 (south; n = 15)	Group 1 (north; n = 15)	Group 2 (south; n = 14)	Group 2 (north; n = 16)	Group 5 (south; n = 12)	Group 5 (north; n = 12)
Winter	aw1	-0.84 (0.08)	-0.99 (0.09)	-0.98 (0.08)	-0.84 (0.08)	-0.72 (0.10)	-0.82 (0.08)
	aw2	0.16 (0.10)	0.25 (0.09)	0.26 (0.11)	0.09 (0.09)	-0.07 (0.12)	0.03 (0.13)
	aw3	0.09 (0.08)	-0.09 (0.08)	-0.22 (0.07)	-0.23 (0.08)	-0.09 (0.09)	0.08 (0.08)
	aw4	-0.22 (0.09)	-0.05 (0.08)	-0.16 (0.09)	0.07 (0.10)	-0.32 (0.11)	-0.27 (0.11)
Summer	as1	-0.25 (0.06)	-0.47 (0.05)	-0.25 (0.07)	-0.25 (0.06)	-0.24 (0.07)	-0.21 (0.08)
	as2	0.06 (0.08)	0.20 (0.07)	0.07 (0.09)	-0.21 (0.07)	0.16 (0.10)	-0.15 (0.08)
	as3	-0.16 (0.08)	-0.22 (0.06)	-0.27 (0.10)	-0.03 (0.08)	-0.30 (0.10)	-0.07 (0.11)
	as4	0.19 (0.05)	0.15 (0.06)	0.04 (0.06)	-0.14 (0.05)	0.04 (0.06)	-0.08 (0.06)
Annual
Fall-to-fall	α1	-0.85 (0.06)	-0.86 (0.06)	-1.00 (0.06)	-1.10 (0.06)	-0.83 (0.07)	-1.03 (0.07)
	α2	0.12 (0.06)	0.07 (0.06)	-0.22 (0.06)	-0.27 (0.06)	-0.28 (0.06)	-0.11 (0.07)
Spring-to-spring	α1	-0.71 (0.07)	-0.75 (0.07)	-0.74 (0.08)	-0.85 (0.07)	-0.88 (0.07)	-0.84 (0.09)
	α2	-0.17 (0.07)	-0.09 (0.07)	-0.29 (0.07)	-0.14 (0.07)	-0.42 (0.08)	-0.28 (0.09)

A common dynamic structure is assumed within each of six areas (the northern and southern part of Groups 1, 2 and 5; see Fig. 1A). The state-space model is fitted simultaneously to each site within an area, restricting the parameters of density dependence to be common for each of these n sites, allowing the process noise to vary. (Estimates in bold indicate strong evidence for the corresponding density-dependent process. Group 1 tends to exhibit noncyclic dynamics, whereas populations in the other groups are cyclic.)

Fig. 3.

Decomposing the annual density-dependent structure from the seasonal density-dependent structure. Autoregressive coefficients estimated from the annual ecological model (Eq. 3) incorporating an observation model (see text) are given by α₁ (Left) and α₂ (Right). (A) The relation between AR(2) estimates as found by ordinary autoregressive analyses ignoring sampling variance and the corresponding estimates incorporating sampling variance [Left, 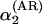vs. α₁; Right, 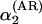vs. α₂]. As expected, the direct density dependence is overestimated when sampling variance is ignored [on average overestimated with –0.23 (SD = 0.14) compared with the state-space model]. As can be seen, this is also the case for the delayed density dependence [on average overestimated with –0.16 (SD = 0.15) compared with the state-space model]. (B) The relation between α^′₁, the first-order coefficients calculated on the basis of seasonal analyses incorporating observation models, and the directly estimated α₁ (R² = 0.417, F_1,77 = 55.2, P < 0.001); Right depicts the equivalent relationship for the second-order coefficients α^′₂ (as given in the text) and α₂ (R² = 0.553, F_1,77 = 95.4, P < 0.001). The direct density dependence calculated on the basis of seasonal analyses is on average underestimated with 0.15 (SD = 0.32) compared with α₁. The delayed density dependence calculated on the basis of seasonal analyses is on average overestimated with –0.13 (SD = 0.23) compared with α₂.

Results

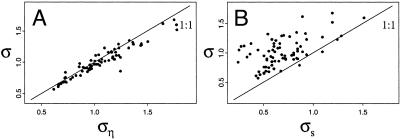
The obtained parameter estimates (Table 1 and Figs. 1B and 2) suggest that a fourth-order process (with the existence of some long lags) underlies the dynamics in at least one of the seasons (see Eqs. 1 and 2). The direct fall-to-spring effect (a_w1) is clearly stronger than the direct spring-to-fall effect (a_s1), suggesting that winter processes are more important than summer processes in determining the annual direct density dependence. These, as well as fall-to-fall effects (a_s2) and spring-to-spring effects (a_w2) all contribute to the annual direct density dependence (see Eq. 2 and supporting information), a result consistent with earlier findings both for Hokkaido (see refs. 25, 31, and 32) and the same species in northern Finland (refs. 27 and 33; also see refs. 34–38). As seen from Fig. 3B, we are able to predict both the direct and delayed annual density dependencies from the seasonal components. Assuming the model given by Eq. 2, the seasonal components explain 70% and 79% of the (deterministic) among-population variability in the direct (α₁) and delayed (α₂) annual density dependencies, respectively. A major part of the among-populations variation in the level of density-independent stochasticity (i.e., among-population variation in ρ) is, however, accounted for by variation in the level of summer stochasticity (i.e., among-population variation in ρ_s; Fig. 4). Variation in degree of summer stochasticity accounts for 32.0% of the total variation in annual stochasticity, whereas the winter stochasticity accounts for 11.7%. If summer stochasticity already is accounted for, the winter stochasticity only accounts for 1.2% of the remaining variation. In the multiple regression of annual stochasticity on the summer and winter stochasticities, the effect of the winter stochasticity is not statistically significantly different from zero.

Fig. 4.

Relating the annual-noise process to its seasonal components. (A) The annual-noise SD (ρ) as estimated from Eq. 3 plotted against the annual noise (ρ_η) calculated on the basis of seasonal analyses (see supporting information). (B) The annual-noise SD (ρ) as a function of its main seasonal noise component, the summer SD (ρ_s).

It should finally be noticed that the fall-to-fall annual density-dependent structure corresponds to the spring-to-spring density-dependent structure (see supporting information). This close correspondence clearly strengthens the validity of the obtained results.

Discussion

The Seasonal Structure of the Population Dynamics. The summer is the main reproductive season for the gray-sided vole; essentially no winter reproduction is observed (see supporting information and refs. 16 and 20). Hence, strong, direct density dependence during the winter must necessarily involve winter survival. Mechanistically, such density dependence may be generated through a functional response of predators or through the limited amount of food (such as bamboo; Sasa spp.) produced during the preceding summer. On the other hand, the strong influence of summer stochasticity (Fig. 4) may stem from a variety of summer events (such as plant production and generalist predation), all of which may be sensitive to erratic temporal and spatial variation in climatic conditions. Notice, however, that when interpreting the statistical parameter a_w1, given a mechanistic process model, this will typically involve direct density dependence of the vole during the winter, in addition to other processes from other seasons. Hence, biological interpretation of these parameters is difficult in the absence of a detailed mechanistic process model. The same applies to the other seasonal statistical parameters.

If we are to explain the observed phenomenological lag-structure, involving four lags (Table 1), in terms of a process model that only allow interactions within a season, we would have to postulate four underlying variables. One of these must be the density of voles. The character of the remaining three variables is unclear. We suggest three possibilities: (i) voles, winter food (bamboo grass), and a specialist predator (the least weasel, M. nivalis) with two age classes (the two age classes of the predator are reasonable on this time scale; weasels require one year to mature); (ii) voles, bamboo grass, specialist predator, and additional members of the small-mammal community that either compete directly with the gray-sided vole or induce apparent competition (39) through some common predator; and, finally, (iii) an interacting web consisting of voles, food plants (e.g., bamboo grass), weasels, and generalist predators. A range of other hypotheses (involving, e.g., intrinsic properties of the vole populations) are certainly possible; however, the three suggested hypotheses are more plausible based on general natural-history insights (see ref. 40 for details). We know, for instance, that the vole specialist (41–43) least weasel is found all across the island (41, 44) and that it may have a particularly strong effect during the winter, because it is able to hunt in the subnivean space where the voles are protected from other predators. Bamboo grass is common all across Hokkaido (45); their new shoots in the spring are known to affect reproduction during the summer, and leaves of bamboo-grass (laid down by the snow) are known to affect survival during the winter. It is difficult to explore these alternatives within a time-series setting, because the number of possible interactions in a four-variable model leads to a large number of parameters. Thus, to further test such process hypotheses, one would need to search for more direct evidence of interacting variables (or perform appropriate experiments; see ref. 40 for further discussion).

The striking difference between population regulation during summer and winter suggests that seasonality may hold a clue to understanding geographic differences in population dynamics. Notice, for instance, that the western populations (Group 1; see Fig. 1 A) tend to fall in the upper right part of the triangle of Fig. 1B (corresponding to stable populations), whereas eastern and the mountainous populations tend to fall further down toward the central part of the triangle (corresponding to periodically fluctuating populations). Because of warm currents along the western coast of Hokkaido, the Group 1 populations are exposed to the longer summers (17). On the other hand, colder currents along the eastern coast expose the Group 2 populations to longer winters (17). The more mountainous Group 5 populations are also exposed to long winters (17). On this basis, it is reasonable to hypothesize that the observed systematic differences in the population dynamics of these groups are influenced by differences in season length, a view that is substantiated by observing the relation between the annual density dependencies and the length of the winter, particularly so when using the pooled estimates (Fig. 1). What we in effect might see is a detailed example of more cyclic dynamics being observed toward the north (18), where the summer season is fairly short.

Incorporating the Length of the Seasons into the Population-Dynamics Model. To further investigate the hypothesis that season length is essential for determining the dynamics, we reparameterized the seasonal model to reveal the relative length of the winter as a parameter τ_w.†† This allows separation of the effects of season length per se from the effect of density dependence per time within the season. A seasonal model will then be given as

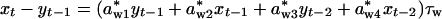[4a]

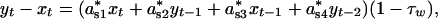[4b]

where seasonal density dependencies a_wi and a_si in Eqs. 1a and 1b now are given as a*_wi·τ_w and a*_si·(1 – τ_w), respectively. The annual direct (α₁) and delayed (α₂) density dependencies expressed in terms of seasonal components are

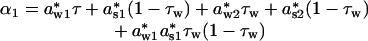and

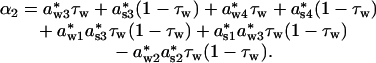The linear effects of winter length on α₁ and α₂ are then

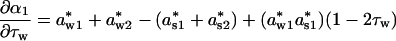and

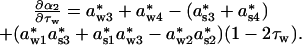Given that density dependencies are stronger (i.e., more negative) during the winter than the summer, and that the winter is the longer season, ∂α₁/∂τ_w and ∂α₂/∂τ_w will quite often be negative.

Using the pooled estimates reported in Table 1, the annual direct and delayed density dependencies typically become smaller (i.e., the strength increases) as winter becomes longer (i.e., dα₁/dτ_w and dα₂/dτ_w both become negative) (Fig. 1C). On this basis, we predict that noncyclic dynamics are more likely in areas with short winters and that periodic cycles are more likely in areas with long winters, just as seen empirically (ref. 9; also see Fig. 1B). Although the density-dependent structure is best explained by whether the population belongs to Group 1, 2, or 5 (Fig. 1B), the length of winter (τ_w) seems to be a good predictor of the density-dependent structure. This dependency of the relative winter length can, however, only be substantiated when using the (better) pooled estimates reported in Table 1, not when using the estimates for the individual populations.

Conclusion

Altogether we have shown that winter length has a clear effect on the population dynamics of Hokkaido voles. Essentially, increasing winter length may be seen as a bifurcation parameter shifting the dynamics from an intrinsically stable regime with irregular fluctuations (generated by density-independent mechanisms) to larger-amplitude, periodic cycles influenced by density-dependent mechanisms. As the required delayed density-dependent structure is widespread in voles (8), such a season-based bifurcation process may apply quite generally. The underlying mechanisms generating this density-dependent structure are the subject of contention, and may differ from one system to another; however, the relative length of the seasons will be a generic bifurcation parameter irrespective of the underlying mechanism. Hence, we suggest that seasonality represent a key for unlocking the mystery of population cycles.