Construction of effective free energy landscape from single-molecule time series

Abstract

A scheme for extracting an effective free energy landscape from single-molecule time series is presented. This procedure uniquely identifies a non-Gaussian distribution of the observable associated with each local equilibrium state (LES). Both the number of LESs and the shape of the non-Gaussian distributions depend on the time scale of observation. By assessing how often the system visits and resides in a chosen LES and escapes from one LES to another (with checking whether the local detailed balance is satisfied), our scheme naturally leads to an effective free energy landscape whose topography depends on in which time scale the system experiences the underlying landscape. For example, two metastable states are unified as one if the time scale of observation is longer than the escape time scale for which the system can visit mutually these two states. As an illustrative example, we present the application of extracting the effective free energy landscapes from time series of the end-to-end distance of a three-color, 46-bead model protein. It indicates that the time scales to attain the local equilibrium tend to be longer in the unfolded state than those in the compact collapsed state.

Energy landscape theory provides a framework for resolving important contemporary issues observed in the dynamics and thermodynamics of complex systems (1–3). The potential energy landscape of biomolecules is a multidimensional hypersurface composed of 3N degrees of freedom (in which N is the number of atoms) associated with a very complex topography. At nonzero temperature the free energy landscape may be more appropriate to reveal the origin of complexity in kinetics of the systems. Recently, Krivov and Karplus (4, 5) revealed in terms of their transition disconnectivity graph (TRDG) of folding–unfolding equilibrium simulations of a β-hairpin that the heterogeneity of the denatured state “ensemble” on the multidimensional free energy landscape is significantly masked by the projection onto a few order parameters (e.g., the fraction of native contacts).

On the contrary, recent experimental developments in single-molecule spectroscopy have provided us with several insights into not only the distribution of the molecular properties but also the dynamical information at the single-molecule level buried in the ensemble-averaged measurements (6–10). For example, some experimental studies have indicated the existence of heterogeneous pathways for protein folding (8) and abnormal diffusion depending on the time scale at which one observes the dynamical events (9).

In fluorescence resonance energy transfer (FRET) experiments, what one can observe is, for example, fluorescence from donor (D) and acceptor (A) molecules embedded in single proteins as a function of time. Such physical quantities are expected to trace the change in the D–A distance at the single-molecule level. The complexity in kinetics observed in single-molecule measurements arises from the morphological features inherent to the underlying multidimensional free energy landscape of the system.

What can one deduce or extract solely from scalar single-molecule time series about the morphological properties of the underlying multidimensional free energy landscape? This is the central question to be addressed in this article. It should be noted that there exist several problems in the single-molecule measurements (11–14) for the elucidation of the underlying free energy landscapes. One of the most cumbersome obstacles is the so-called “degeneracy problem”: even when the system traverses different physical states, the value of the time series (e.g., D–A distance) is not necessarily different and may be degenerate due to the finite resolution of the observation and the nature of the observable onto which the multidimensional nature of the system is projected. It is known that such degeneracy may bring about apparent long-term memory even when the transitions among states are Markovian (14).

In the present article a method is presented for constructing an effective free energy landscape in terms of a given scalar time series as free as possible from the degeneracy problem. The crux is the evaluation of states not solely by the scalar value of the time series at a specific time but by the short-time distributions in the neighborhood of the time. The short-time distributions are expected to differentiate the states that are degenerate in the scalar value (corresponding to first-order moment of the distribution) because the short-time distributions can also reflect the higher-order moments. As shown later, a set of the short-time local distributions can lead the concept of local equilibrium state (LES). Then one can construct an effective free energy landscape by assuming canonical transition state theory (TST). The time window for which the local distributions are constructed may be regarded as the time scale of “observation.” The different time windows can lead to the corresponding different coarse-grained free energy landscapes the system can trace at the different time scales of observation.

In this article, we demonstrate our method with an off-lattice, three-color, 46-bead model protein by Honeycutt and Thirumalai (15), whose energy landscapes have been examined in a number of previous studies (16–22). We scrutinize scalar time series of the end-to-end distance generated by isothermal molecular dynamics (MD) simulation at several temperatures, from which we extract the underlying effective free energy landscape as a function of temperature and the time scale of observation.

Definition of “State” in Terms of Single-Molecule Time Series

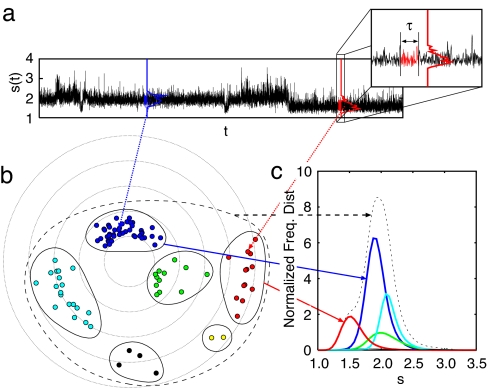
Fig. 1 schematically shows our procedure to construct a set of states from time series of an observable s(t). From the time series s(t) in Fig. 1a, how does one elucidate the number of states? The number of states has often been counted by fitting the whole distribution of the observable s by a combination of Gaussian functions. However, can one define the state as free as possible from any assumption about the form of the distribution function associated with each state?

Fig. 1.

A schematic picture of the state assignment procedure. (a) A single-molecule time series s(t) (taken from an end-to-end time series of the 46-bead model protein at T = 0.3ε). For every mth time step t_m, the short-time probability density function g_m^(τ)(s) [∫ g_m^(τ)(s)ds = 1] is evaluated for a time window (t_m − τ/2, t_m + τ/2] (with τ set to be 10⁴ MD steps). (b) A two-dimensional projection of a set of g_m^(τ)(s) so as to maintain the “metric” relationship among the g_m^(τ)(s) (determined by Eq. 1) as well as possible by using a nonlinear multidimensional scaling method (26). Each node or circle corresponds to each g_m^(τ)(s) at different t_m as indicated by red and blue lines [for visual clarity, not all but every other 10,000 sampled points of g_m^(τ)(s) are plotted from the time series in a]. The set covered by the dashed line indicates the full set of g_m^(τ)(s) corresponding to the full s(t). Different subsets (covered by solid lines) of different colored nodes correspond to the different state “candidate” where the composite g_m^(τ)(s) are classified as the same group on this metric space in the full dimension. (c) The corresponding frequency distributions of the four major state candidates with respect to s. If the average escape times of the system from them in s(t) are sufficiently longer than the time window τ, they are considered to be LES (see text).

Suppose that s(t) is recorded with an equal interval from t₁ to t_n. First, we extract “short segments” in a time window (t_m − τ/2, t_m + τ/2] in the vicinity of t_m and construct the corresponding short-time probability density function g_m^(τ)(s) sequentially. Second, we select a “measure” to quantify the degree of proximity of two probability density functions. In this article, we chose the Kantorovich metric (23) defined by

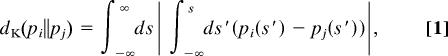where p_i(s) and p_j(s) are two arbitrary probability density functions with respect to s. It was found that the d_K is much more appropriate than the most commonly used measures, e.g., Kullback–Leibler divergence (relative entropy) (24) and Hellinger distance (25), in differentiating the distance between two probability density functions [see the supporting information (SI) Appendix for more detail]. Fig. 1b illustrates the metric relationship (regarding d_K) among the set of g_m^(τ)(s) by the projection onto a two-dimensional plane so as to maintain the metric relationship among them as well as possible (26). Each node corresponds to each g_m^(τ)(s) at a different time t_m. Third, we partition the set of g_m^(τ)(s) into a union of “clusters (subsets)” on the full-dimensional metric space as illustrated by clusters surrounded by solid lines in Fig. 1b (see SI Appendix). Each cluster can be supposed as a candidate of state because all g_m^(τ)(s) in each cluster are classified as almost the same shape as the short-time distribution. In what circumstance may one assign each cluster of g_m^(τ)(s) as state?

Here we incorporate the concept of local equilibrium states (LESs) into our framework: First, we assign which cluster (“candidate of state”) the system traverses at each time t_m along the original s(t) by referring g_m^(τ)(s) centered at t_m, in other words, when the system enters and leaves each cluster along the time series. Second, we check whether the time window τ is shorter than the escape time τ_esc(i) from the ith cluster:

(see SI Appendix). If a cluster in {g_m^(τ)(s)} satisfies Eq. 2 we assign the candidate of state as an LES, otherwise as a non-LES at the given time window τ. This definition of state, based on the short-time distributions in a given time series, is expected to be as free as possible from the degeneracy problem compared with using solely the (scalar) value of the time series.

The state classified as LES should, in principle, provide us with a unique local distribution of the observable whenever the system revisits the same state along the course of time evolution. The uniqueness of the local distribution associated with each LES enables us to evaluate residential probability P_i of the ith LES, that is, how often the system resides or visits in the ith LES. In addition, one can evaluate the transition probabilities P_ij from the ith LES to the jth LES, that is, how often the system escapes or reacts from the ith LES to the jth LES per unit time. When the local detailed balance P_ij ≃ P_ji is satisfied in a given time series, which is the necessary condition to validate canonical transition state theory of the reaction rate, one can translate these probabilities into an effective free energy landscape by the following equations (4):

where F_i and F_ij, respectively, denote the relative free energy of the ith LES and the relative free energy of the barrier linking the ith and jth LES. k_B, h, and T denote the Boltzmann constant, Planck constant, and absolute temperature, respectively. Eq. 5 is derived by assuming canonical TST; the free energy barrier height from the ith LES to the jth LES is obtained by F_ij − F_i. Note that the Kramers theory (27) tells us that the canonical TST provides an upper bound of the rate constant. The free energy barrier derived from Eq. 5 can be affected by the existence of viscosity from the environment (28, 29). An appropriate correction may be required for the better estimation of the free energy barrier (7).

This clustering of the short-time probability density functions satisfying Eq. 2 naturally leads to the probability density function of the ith LES, p_i^(τ)(s), defined as a collection of Dirac delta functions δ(x) of all {s(t_m)} belonging to the same cluster i in {g_m^(τ)(s)}:

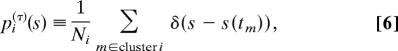where N_i = Σ_{m∈cluster i} ∫_−∞^∞ ds′δ(s′ − s(t_m)) = Σ_{m∈cluster i} 1 (in the absence of any broadening effects of signal in the measurement). Note that the probability density function of LES is not necessarily Gaussian (as indicated in Fig. 1c) and it should depend on the local morphological nature of the underlying free energy landscape. The time window τ in the construction of the local distributions could be regarded as the time scale of “observation.” For example, as the time window increases, it is expected that a set of some LES becomes unified as one larger LES if the associated escape times from there are shorter than the time window τ. The different time windows naturally lead to the corresponding different coarse-grained free energy landscapes the system should find at the different time scales of the observation.

Results and Discussion

As an illustrative example, we apply our method to the scalar time series of the end-to-end distance of an off-lattice, three-color, 46-bead model protein (15) at several temperatures. This system has been examined in a number of previous studies (16–22). This model is composed of hydrophobic (B), hydrophilic (L), and neutral (N) beads and is termed the BLN model hereafter. The global potential energy minimum for the sequence B₉N₃(LB)₄N₃B₉N₃(LB)₅L folds into a β-barrel structure with four strands. The BLN model exhibits a frustrated potential energy landscape (19, 20) and it does not fold easily and uniquely (17, 18). Two peaks are seen in the heat capacity: one corresponds to the collapse temperature, at which the BLN model transitions from the extended to the compact collapsed states, and the other to the folding temperature, where it folds into the global potential energy minimum (17, 18).

The isothermal MD simulation was performed by Berendsen's thermostat (30) for a range of temperatures k_BT = 0.3–2.0ε, which involves the folding and collapse temperature of the BLN model. Here ε is the energy unit of the model (see also the legend of Fig. 2). After 50,000-MD-steps simulation for equilibration, the value of the end-to-end distance was recorded every 100 steps during the course of a 13-million-step trajectory. Here the MD step, Δt, corresponds to ∼1/180 of the time scale of one vibration of the bond. The coupling constant γ with the Berendsen thermostat was chosen as ∼1/(200Δt) such that one can expect that the canonical distribution is quickly attained during the course of MD simulation. The lower the temperature, the longer the system becomes trapped in several metastable states, which make it more difficult to “see” the global morphological nature of the underlying free energy landscape. Hence, to survey the global nature as possible, the end-to-end distance time series was prepared with 20, 10, and 5 trajectories at 0.3–0.4, 0.5–0.8, and 2.0ε, respectively.

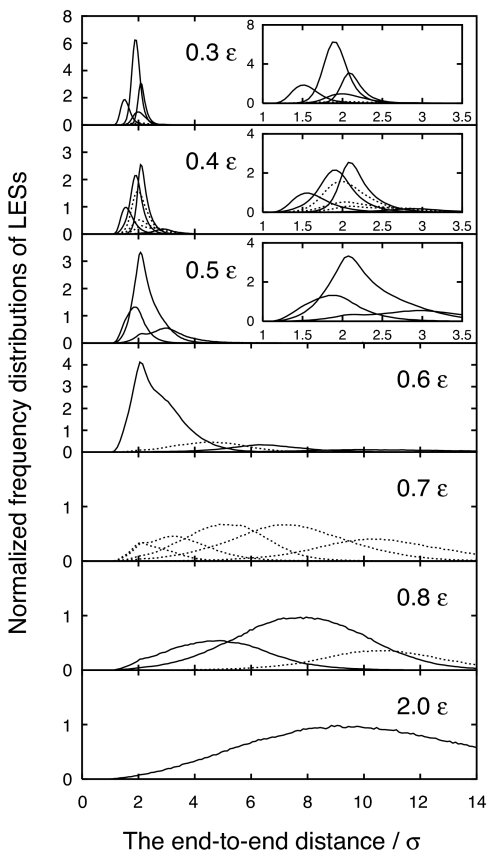
Fig. 2.

The normalized frequency distributions of LES/non-LES constructed from the end-to-end distance time series of the BLN model at different temperatures, that is, 0.3, 0.4, 0.5, 0.6, 0.7, 0.8, and 2.0 ε. The normalized frequency distribution of the ith LES is derived by Σ_{m∈cluster i} δ(s − s(t_m))/Σ_{m∈all clusters} ∫_−∞^∞ ds′ δ(s' − s(t_m)). In the Insets of 0.3–0.5ε, graphs magnified in the horizontal axis are given. The unit of the vertical axis is 10⁻² [−], where the bin size of the horizontal axis is taken to be 0.05σ for 0.3–0.5ε and 0.1σ for 0.6–2.0ε. Note that the distributions indicated by the dotted lines did not satisfy Eq. 2. The potential energy function is described by V = (K_r/2)Σ_i(r_i − r₀ⁱ)² + (K_θ/2)Σ_i(θ_i − θ₀ⁱ)² + Σ_i [A(1 + cos Φ_i) + B(1 + cos 3Φ_i)] + 4εΣ_i<j−3 S₁[(σ/R_ij)¹² −S₂(σ/R_ij)⁶], where S₁ = S₂ = 1 for BB (attractive) interactions, S₁ = 2/3 and S₂ = −1 for LL and LB (repulsive) interactions, and S₁ = 1 and S₂ = 0 for all of the other pairs involving N, expressing only excluded-volume interactions. K_r = 231.2εσ⁻² and K_θ = 20ε/rad², with the equilibrium bond length r₀ⁱ = σ and the equilibrium bond angle θ₀ⁱ = 1.8326 rad.

Extracted LES at Different Temperatures

Fig. 2 presents the normalized frequency distributions of the assigned LES (including non-LES) from the end-to-end distance time series at k_BT = 0.3–2.0ε for the original BLN model. Here the time window τ was set to be 10,000 Δt in evaluating the short-time distributions. This corresponds to ∼55 oscillations of the bond vibration and 50 times longer than the time scale of the coupling between the protein and the thermal bath.

At 0.3ε and 0.4ε, four and three large LESs are identified. The larger the normalized frequency distribution, the more the system resides in the LES. Note that the folding temperature T_f was assigned to be 0.27ε (31) to 0.35ε (32), although reliable sampling could not be expected below 0.4ε because the kinetics are controlled by escape from the long-lived traps at such a low T region (19). As T increases to 0.5ε, one can see the existence of three large LESs, into which some of the LESs observed at 0.4ε are considered to be unified. This temperature falls between T_f and the collapse temperature T_c and, hence, one may expect that the collapsed state is composed of, at least, three large superbasins on the free energy landscape the system can find at the chosen time scale τ.

The three large LESs observed at 0.5ε are interpreted as unified into one large LES at 0.6ε. This unification of the three LESs implies that the system quite often traverses back and forth between the three unified LESs at 0.6ε within the chosen τ. Note also that some “delocalized” distributions start to emerge (with low probabilities) besides this large unified state at 0.6ε.

At 0.7ε, although the “compact” large LES ceases, delocalized distributions become more significant with higher probabilities. Note that from 0.6ε to 0.7ε the “center” of the LES migrates from the short to the long end-to-end distance regions, which corresponds to the transition from the collapsed state to the unfolded state. This migration manifests the existence of T_c between 0.6ε and 0.7ε (32). Note here that none of distributions is classified as LES. This indicates that, in the chosen time scale τ, in neither the compact states nor the more delocalized denatured states can the system be well equilibrated (i.e., the residential times inside them are shorter than τ).

At 0.8ε above T_c, two distributions are classified as LES, whereas the other distributions violate Eq. 2 in the τ. All of the two LES and one non-LES observed at 0.8ε are unified as one distribution delocalized through the configuration space at 2.0ε. Note that if only one cluster is assigned in {g_m^(τ)(s)} the state is always classified as LES because the corresponding escape time formally becomes infinity.

Quite recently, Kinoshita and his coworkers (33) found by using their single-molecule detection technique that iso-1-cytochrome c (known as having a collapsed intermediate state) exhibits relatively slower conformational dynamics in the unfolded state, compared with that in the intermediate state. The consequence observed in a frustrated BLN model may indicate that the time scales to attain the local equilibrium tend to be longer in the (extended) unfolded state than those in the compact collapsed state at the single-molecule level because of the enlargement of the conformation space in which the system should move about in the unfolded state.

A Visualization of the Effective Free Energy Landscape

As temperature increases, one can expect that a certain set of LES/non-LES becomes unified as one LES if the system can wander through the set of LES/non-LES across the barriers linking those LES/non-LES in a much shorter time than the given time window τ. Several visualization techniques have been developed to represent this topographical feature of the multidimensional energy landscape (3, 21, 22, 34). However, there is no appropriate scheme to capture how each state (or superbasin) is related to each of the others through different temperatures. We present a visualization scheme in terms of the d_K distance matrix among probability density functions of LES/non-LES at different temperatures, combined with nonlinear multidimensional scaling (MDS) method (26). This scheme projects the multidimensional abstract space (where each state is represented as a point or node whose position satisfies the mutual d_K relation with all of the other states) onto a two-dimensional space so as to preserve the metric relationship among the nodes on that multidimensional space as much as possible.

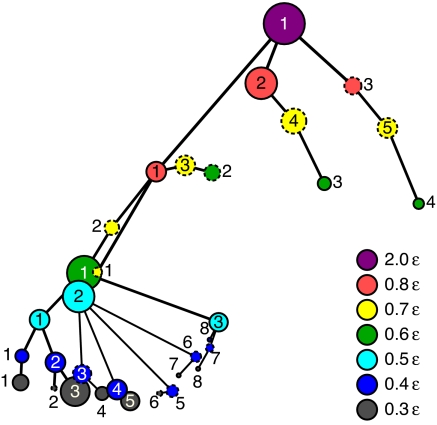
Fig. 3 presents how the LES/non-LES observed at different temperatures are related each other. Here each node or circle represents an LES/non-LES, and its area is proportional to the residential probability at different temperatures. One can see that the single LES at 2.0ε becomes split into three superbasins as the temperature T decreases to 0.8ε. From 0.8ε to 0.6ε through 0.7ε, the largest LES is shifted from the middle to the left superbasins, manifesting the existence of T_c between them. From 0.5ε to 0.3ε via 0.4ε, at which the largest residential probabilities are somewhat delocalized from the second to fourth LES, the shift of the superbasin (where the system resides for the longest period during the simulation) may be identified. This shift of the superbasin, i.e., from the second LES at 0.5ε to the third LES at 0.3ε in Fig. 3, might reflect the existence of T_f, although the sampling should not be sufficient to capture the underlying free energy landscape at such a low T region.

Fig. 3.

A projection of the LES/non-LES network of the BLN model onto a two-dimensional space in terms of nonlinear MDS method using closeness centrality (26). The closeness centrality C_c(i) is obtained by calculating the average (geodesic) distance of the ith node to all other nodes in the network. The vertical and horizontal axes roughly correspond to temperature and the closeness centrality, respectively [a two-dimensional configuration (C_c(i), T(i)), where T(i) is temperature of the ith state (LES/non-LES), was used as an input of the nonlinear MDS calculation]. Here each node or circle represents the corresponding state, and its area is scaled to be proportional to the residential probability of the state at each temperature T. The non-LESs are depicted by dashed circles. The colors of the circles denote the different T: gray, blue, light blue, green, yellow, pink, and purple are 0.3, 0.4, 0.5, 0.6, 0.7, 0.8, and 2.0 ε, respectively. The index associated with each circle is numbered in increasing order with respect to the average value of the end-to-end distance for the corresponding LES/non-LES. Each line connects from each state at a T to the closest state at the adjacent higher T (with respect to d_K).

Note that this visualization scheme is applicable, in general, in revealing the dependency of the LES network structure not only on temperature but also on the other physical variables, e.g., the concentration of denaturant, pH, and the time window τ.

Eq. 5 can also offer the elucidation of free energy barrier height linking two LESs when the local detailed balance is satisfied. Elsewhere, a disconnectivity graph analysis including the information of the barrier height will be presented for each temperature.

The τ Dependency of LES

The LES/non-LES probability density functions depend on the time window τ. Suppose a (symmetric) double-well potential system with an activation potential barrier much higher than k_BT coupled with the thermal bath. The system is expected to possess two LESs corresponding to the two wells when τ is short enough to differentiate the two wells, compared with the escape time τ_esc from one well to another (but the τ should be longer than the local equilibration time in each well). With a τ much longer than τ_esc, the system frequently goes back and forth between the wells through the barrier. If the chosen τ is also long enough to “globally” equilibrate across the two wells, the system should find only a single unified LES. In between the “short” and “long” time windows τ for the system to “see” two and one LES(s), respectively, there exists a time scale in τ neither long enough to attain the global equilibrium across the two wells nor short enough to reside in either of two wells to be locally equilibrated before the escape from one well to the other. Such an intermediate time scale of τ results in a non-LES distribution through the two wells at the chosen time scale.

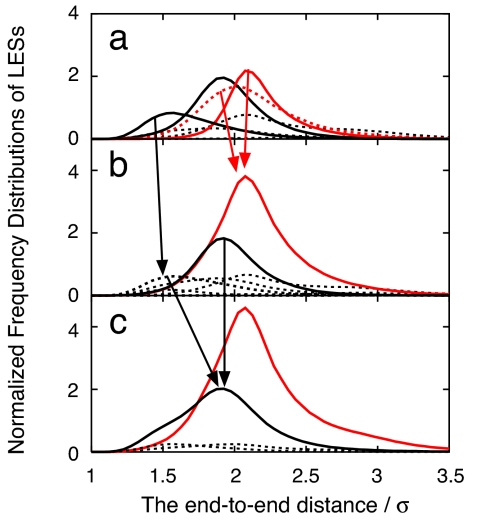
Let us consider a more complicated system with multiple wells. Fig. 4 shows how the LES and non-LES of the BLN model protein depend on τ at 0.4ε. The chosen τ corresponds to 400, 500, and 2,000 sample points (n_S) in evaluating the local distributions of the end-to-end distance time series. From n_S = 100 to 400, the major three LESs were assigned with almost identical distributions (see also the Inset of Fig. 2 at 0.4ε). As τ increases from n_S = 400 to 500, one of the non-LESs and one of the LESs observed at n_S ≤ 400 are unified as one LES. In addition, one LES observed at n_S ≤ 400 turns to a non-LES at n_S = 500 because the escape time becomes shorter than the chosen time window τ. The non-LES at n_S = 500 merges into one of the LESs, resulting in one new LES at n_S = 2,000.

Fig. 4.

The dependency of LES/non-LES on the time window τ at T = 0.4ε. The number of the sample points to evaluate the local distributions (n_S) corresponds to 400 (a), 500 (b), and 2,000 (c). The unit of the vertical axis is the same as in Fig. 2. The solid and dashed lines indicate the LES and non-LES distributions, respectively. The red arrows indicate the merge of a non-LES into an LES as n_S = 400 → 500. The black arrows indicate the change from LES to non-LES as n_S = 400 → 500 and the merge of a non-LES into an LES as n_S = 500 → 2,000.

Such “stepwise” unification of a set of multiple states depending on the time window τ arises from the existence of hierarchical time scales of the escapes on multidimensional free energy landscapes. The most striking consequence is that the topography of the free energy landscape is subject to the time scale of observation and the roughness of the landscape becomes smeared out as the time scale of observation increases. In the glass transition, heterogeneous properties in finite time and space scales have been explored in terms of the so-called random first-order transition theory (35) and space-time thermodynamics (36). The LES network topology depending on time and space scales is expected to relate with such studies in glassy complex systems.

Comparison with a Free Energy Landscape Constructed from the Full Set of Coordinates

The short-time non-Gaussian distributions are expected to lift a certain degeneracy more (which should exist inherently in the projected scalar time series) than by using only the scalar value of the time series. This increase is because the short-time distributions can reflect higher-order moments in the neighborhood of a chosen point along the time series. As shown in the SI Appendix, Kantorovich metric d_K based on the short-time non-Gaussian distributions turned out to be much superior to the other measures such as relative entropy and can differentiate the underlying (multidimensional) morphological features associated with LES more than the scalar value of the time series.

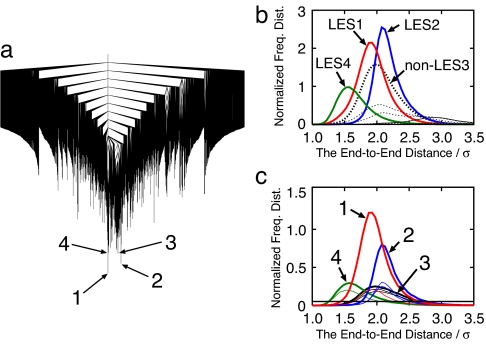
However, how much did the LES/non-LES procedure capture the complexity of the underlying multidimensional free energy landscape? Fig. 5 presents a coarse-grained transition disconnectivity graph (TRDG) (5) for the multidimensional free energy landscape of the BLN model at 0.4ε. We used a coarse-graining procedure (21) in which two free energy basins are unified as one when the TST rate constants evaluated from one basin to another and vice versa are both faster than a chosen threshold. The coarse-grained TRDG exhibits the complexity buried in the free energy landscape. In the low free energy regime, several free energy basins exist, separated by large barriers.

Fig. 5.

A comparison with transition disconnectivity graph (TRDG) constructed from the full set of coordinates. (a) A coarse-grained TRDG for the multidimensional free energy landscape of the BLN model at 0.4ε. This TRDG was constructed in terms of 1.6 × 10⁴ quenched structures and mutual transitions among them obtained along a long isothermal MD trajectory of 2.2 × 10⁸ Δt. We used a coarse-graining procedure (21) with a TST rate constant threshold of τ/5 (all of the LESs merge one after another, resulting in a single LES with the threshold larger than ∼τ/2. As the threshold decreases, the number of the TRDG basin increases more with lesser residential probability. With τ/5, the system mainly (∼50%) resides in the lowest 10 TRDG basins). The index i (1–4) (also shown in c) is numbered as the ith lowest free energy basin. The total numbers of the bare and the coarse-grained TRDG basins are 15,374 and 827, respectively. (b) The normalized frequency distributions of LES and non-LES at 0.4ε, constructed from the end-to-end distance time series. The four major LESs (non-LESs) are represented by bold lines (dotted bold line). The red, blue, black, and green lines indicates LES1, LES2, non-LES3, and LES4, respectively (the index i in LES/non-LES i is numbered as the ith highest residential probability). The total numbers of LESs and non-LESs with τ = 10⁴ Δt are 4 and 4, respectively. (c) The normalized frequency distributions of the end-to-end distance of the quenched structures that belong to each of the lowest 10 free energy basins on the TRDG in a. The first to fourth lowest free energy basins in a are depicted by bold lines with the index i. Each color indicates which LES/non-LES i (i = 1–4) the system traverses most frequently while tracing in the lowest 10 TRDG basins (the color denotes the LES/non-LES i in b) (see also SI Appendix).

The evaluated lowest four LES/non-LES distributions and the end-to-end distance distributions of the lowest 10 TRDG basins are presented in Fig. 5 b and c, respectively. One can see that the relative order in the stability among the lowest four LES/non-LESs coincides with that among the corresponding TRDG basins. Moreover, the lowest four LES/non-LESs constructed in terms of the scalar time series can qualitatively reproduce the shape of the distributions of the end-to-end distance evaluated for the TRDG basins (e.g., both LES4 and the fourth TRDG distributed around 1.5σ have a long tail in the longer distance regime). The relative magnitude of stability, however, cannot be fully captured. This inability is mainly because some short-time probability density functions {g_m^(τ)(s)} (which should belong to distinct free energy basins) still have a certain degeneracy, that is, too close to result in different LESs (see also SI Appendix). This LES technique is expected to lift “degeneracy” as much as possible within the limited source of scalar finite time series. However, a certain degeneracy must remain, in principle, unless one can access the information of the full set of coordinates. Our approach can straightforwardly be generalized to multivariate time series. Highly resolved multivariate detection by single-molecule spectroscopy is required to further lift such inevitable degeneracy if significant.

The interpretation of our LES in terms of the underlying high-dimensional potential energy landscape is important but the exploration of the high-dimensional landscape itself is one of the most intriguing unresolved problems. Shalloway and colleagues (37) demonstrated, by using a six-atoms cluster, that coarse-grained states under Brownian dynamics must have not discrete but “soft” boundaries with smooth overlap between their residential probabilities on the conformational space. The comparison with LES and their “macrostates” by using the same system may be interesting to interpret the LES network in terms of the multidimensional potential energy landscape.

Conclusions

In this article, we have presented a method to extract effective free energy landscapes from single-molecule time series. If the local equilibrium and the local detailed balance are satisfied in a chosen time scale of observation, one can construct the effective free energy landscape for the regions where the system wanders frequently. This method is not based on any a priori assumption of local equilibrium for all substates on that landscape but rather provides us with a time scale at which the system more likely attains the local equilibrium in a set of substates.

The typical time scale of FRET measurements is at the order of 10⁻³ s. In such a time scale, the system can go back and forth frequently among lots of substates that should be averaged out completely. This averaging results in a sharp spike of the FRET efficiency if one can ignore shot noise and other broadening effects not dependent on the interdye distance. There exists no means to single out such unified LES within experimental resolution. However, our method is expected to differentiate the larger substates and establish a coarse-grained effective free energy landscape at the time and space scales where the system can experience their different morphologies. Furthermore, by scrutinizing the variance of each local distributions of measured FRET efficiencies, one may elucidate the time scale of the local equilibration for each state (7). The hierarchical coarse-grained effective free energy landscapes can also be derived as a function of τ. This method can also be applied to a set of short single-molecule time series (typically, with a few tens of transitions), by supposing that each (short) time series is sampled with the same experimental conditions.