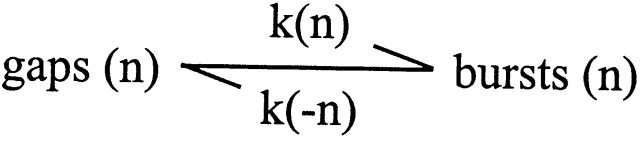Functional Coupling of the β₁ Subunit to the Large Conductance Ca²⁺-Activated K⁺ Channel in the Absence of Ca²⁺

Abstract

Coexpression of the β₁ subunit with the α subunit (mSlo) of BK channels increases the apparent Ca²⁺ sensitivity of the channel. This study investigates whether the mechanism underlying the increased Ca²⁺ sensitivity requires Ca²⁺, by comparing the gating in 0 Ca²⁺ _i of BK channels composed of α subunits to those composed of α+β₁ subunits. The β₁ subunit increased burst duration ∼20-fold and the duration of gaps between bursts ∼3-fold, giving an ∼10-fold increase in open probability (P _o) in 0 Ca²⁺ _i. The effect of the β₁ subunit on increasing burst duration was little changed over a wide range of P _o achieved by varying either Ca²⁺ _i or depolarization. The effect of the β₁ subunit on increasing the durations of the gaps between bursts in 0 Ca²⁺ _i was preserved over a range of voltage, but was switched off as Ca²⁺ _i was increased into the activation range. The Ca²⁺-independent, β₁ subunit-induced increase in burst duration accounted for 80% of the leftward shift in the P _o vs. Ca²⁺ _i curve that reflects the increased Ca²⁺ sensitivity induced by the β₁ subunit. The Ca²⁺-dependent effect of the β₁ subunit on the gaps between bursts accounted for the remaining 20% of the leftward shift. Our observation that the major effects of the β₁ subunit are independent of Ca²⁺ _i suggests that the β₁ subunit mainly alters the energy barriers of Ca²⁺-independent transitions. The changes in gating induced by the β₁ subunit differ from those induced by depolarization, as increasing P _o by depolarization or by the β₁ subunit gave different gating kinetics. The complex gating kinetics for both α and α+β₁ channels in 0 Ca²⁺ _i arise from transitions among two to three open and three to five closed states and are inconsistent with Monod-Wyman-Changeux type models, which predict gating among only one open and one closed state in 0 Ca²⁺ _i.

INTRODUCTION

Large conductance Ca²⁺-activated K⁺ channels (BK channels or maxi-K channels) are found in a wide variety of tissues, where they regulate excitability through a negative feedback mechanism (Meech and Standen 1975; Meech 1978; Adams and Gage 1980; Marty 1981, Marty 1983; Pallotta et al. 1981; Maruyama et al. 1983; Cook 1984; Blatz and Magleby 1987; Petersen and Findlay 1987; Singer and Walsh 1987; Smart 1987; Hudspeth and Lewis 1988; Brayden and Nelson 1992; Wu et al. 1995; Tanaka et al. 1997; Jones et al. 1999; and reviewed by Hille 1991; Conley 1996; Kaczorowski et al. 1996). Both membrane depolarization and increased intracellular Ca²⁺ (Ca²⁺ _i) activate BK channels. Opened BK channels allow the efflux of K⁺, which then hyperpolarizes the membrane potential, reducing excitability and closing Ca²⁺ channels. BK channels can be composed of either α subunits alone (α channels) or of α subunits together with various β subunits (α+β channels). The larger pore-forming α subunits, which are encoded by the gene at the slo locus, were first cloned from Drosophila (slowpoke phenotype), and bear homology to the superfamily of voltage-gated K⁺ channels, including a pore-forming region between the S5 and S6 transmembrane segments, and an S4 voltage-sensing domain (Atkinson et al. 1991; Adelman et al. 1992; Salkoff et al. 1992; Butler et al. 1993; Dworetzky et al. 1994; Pallanck and Ganetzky 1994; Tseng-Crank et al. 1994; Wallner et al. 1995; Jan and Jan 1997; Stefani et al. 1997; Diaz et al. 1998). BK channels differ from strictly voltage-gated K⁺ channels by having a greatly extended COOH terminus that accounts for more than half of the primary sequence. The extended COOH terminus contains at least one Ca²⁺-binding domain involved in activation of the channel (Wei et al. 1994; Schreiber and Salkoff 1997; Schreiber et al. 1999).

Several distinct auxiliary β subunits for the BK channel have been cloned: β₁, β₂, and β₃ (Knaus et al. 1994; Meera et al. 1996; Dworetzky et al. 1996; Tseng-Crank et al. 1996; Oberst et al. 1997; Wallner et al. 1999; Xia et al. 1999). All of these β subunits appear to share a common secondary structure with two transmembrane domains connected by a large, extracellular loop. The different β subunits affect the gating of the α subunits in several ways. The β₁ subunit increases the apparent Ca²⁺ sensitivity by decreasing the Ca²⁺ _i required for half activation of the channel (McManus et al. 1995; Dworetzky et al. 1996; Tseng-Crank et al. 1996; Wallner et al. 1996; Meera et al. 1996; Nimigean and Magleby 1999; Ramanathan et al. 2000). The increased Ca²⁺ sensitivity with the β₁ subunit is reflected in a 5–10-fold leftward shift in plots of open probability (P _o) vs. Ca²⁺ _i (Nimigean and Magleby 1999). In addition to increasing the Ca²⁺ sensitivity like the β₁ subunit, the β₃ subunit produces an inactivating BK channel similar to the BK channels in chromaffin cells (Wallner et al. 1999; Xia et al. 1999). The action of the β₁ subunit requires an S0 transmembrane segment in BK channels that is not present in other voltage-gated K⁺ channels (Wallner et al. 1996; Meera et al. 1997).

In a recent study, we showed that the β₁ subunit increases the apparent Ca²⁺ sensitivity of BK channels by stabilizing the channel in the bursting states (Nimigean and Magleby 1999). The β₁ subunit increased P _o by increasing burst duration ∼20-fold while having little effect on the durations of the gaps between bursts in the presence of Ca²⁺ _i. Increasing P _o by either adding the β₁ subunit or by increasing Ca²⁺ _i gave marked differences in the single-channel kinetics, suggesting that the β₁ subunit does not increase P _o by proportionally increasing all the Ca²⁺-binding rates. These observations of differences in gating kinetics induced by Ca²⁺ _i and the β₁ subunit raise the possibility that the β₁ subunit may not require Ca²⁺ _i to exert its facilitating effects on P _o.

We now investigate this possibility by examining the effects of the β₁ subunit on the gating of unliganded BK channels, by studying the gating of α and α+β₁ channels in the virtual absence of Ca²⁺ _i. Such experiments are possible since BK channels can gate in effective 0 Ca²⁺ _i (Pallotta 1985; Meera et al. 1996; Horrigan et al. 1999; Horrigan and Aldrich 1999; Talukder and Aldrich 2000). We find, in the absence as well as the presence of Ca²⁺ _i, that the β₁ subunit has the same effect of retaining the gating of the channel in the bursting states. Hence, neither Ca²⁺-dependent transitions nor Ca²⁺ binding are required for the β₁ subunit-induced prolongation of bursts, and, consequently, for the functional coupling of the β₁ subunit to the channel. Therefore, the increase in Ca²⁺ sensitivity that arises from the β₁ subunit-induced increase in burst duration arises mainly from a Ca²⁺-independent mechanism. The effects of the β₁ subunit on stabilizing the bursting states were observed over a range of membrane potentials (+30 to +100 mV). Increasing P _o with either the β₁ subunit or by depolarization gave marked differences in the single-channel kinetics, suggesting that the β₁ subunit does not increase P _o by the same alterations in rate constants that voltage induces.

Previous studies (Meera et al. 1996) have indicated that physiological Ca²⁺ _i acts as a switch to functionally couple the β₁ subunits with the α subunits, thus allowing lower levels of Ca²⁺ _i to activate the BK channel by shifting the P _o vs. Ca²⁺ _i curve to the left. We examined the mechanism of this switch and found that the observation that the β₁ subunit increases mean burst duration ∼20-fold, independent of Ca²⁺ _i, is sufficient to account for 80% of the increase in Ca²⁺ sensitivity indicated by the leftward shift in the P _o vs. Ca²⁺ _i curve. The remaining 20% of the leftward shift arises because the β₁ subunit no longer increases (and may decrease slightly) the durations of gaps between bursts in the presence of Ca²⁺ _i. Thus, the functional switch has both Ca²⁺-independent and -dependent components, with the Ca²⁺-independent component accounting for the majority of the increase in Ca²⁺ sensitivity. While the effect of the β₁ subunit on increasing burst duration is always present, independent of Ca²⁺ _i, it is only in the presence of Ca²⁺ _i, when the P _o becomes significant, that this β₁ subunit-induced increase in burst duration has a physiological effect. For example, increasing P _o 20-fold, from 0.0002 to 0.004 in very low Ca²⁺ _i, would have little effect on current, whereas increasing P _o 20-fold, from 0.02 to 0.40 in higher Ca²⁺ _i, could have a dramatic physiological effect.

The complex bursting kinetics in 0 Ca²⁺ _i for both α and α+β₁ channels was found to arise from transitions among a minimum of two to three open states and three to five closed states. Gating among such a large number of unliganded states is inconsistent with gating mechanisms based on Monod-Wyman-Changeux type models for ligand-activated tetrameric allosteric proteins (Monod et al. 1965), which would predict gating among only one open and one closed state in 0 Ca²⁺ _i (Horrigan et al. 1999; Talukder and Aldrich 2000). Gating among multiple open and closed states in 0 Ca²⁺ _i is consistent with a 50-state two-tiered gating mechanism proposed by Rothberg and Magleby 1999 for the gating of BK channels.

METHODS

Heterologous Expression of BK Channels in Human Embryonic Kidney 293 Cells

Human embryonic kidney (HEK) 293 cells were transiently transfected with expression vectors (pcDNA3) encoding the α subunit (mSlo from mouse; Genbank accession number MMU09383) and β₁ subunit (bovine β; Genbank accession number L26101) of the BK channels kindly provided by Merck Research Laboratories, and also with an expression vector encoding the green fluorescent protein (GFP, Plasmid pGreen Lantern-1; GIBCO BRL). Cells were transfected transiently using the Lipofectamine Reagent (Life Technologies) according to the protocol provided by GIBCO BRL. The GFP was used to monitor successfully transfected cells. HEK cells are optimal for transfection and expression after they have been in culture for ∼3–4 wk. The cells are cultured using standard tissue culture media: DMEM with 5% fetal bovine serum (Life Technologies) and 1% penicillin-streptomycin solution (Sigma-Aldrich) and passaged at ∼100% confluency using PBS with 5 mM EDTA to loosen cells from the bottom of the dish. For transfection, cells at 30–40% confluency in 30-mm Falcon dishes used later for recording were first washed with antibiotic and serum-free DMEM, and then incubated with a mixture of the plasmids (total of 1 μg DNA per dish), Lipofectamine Reagent (optimal results at 7 μl) and Opti-MEM I reduced serum medium (Life Technologies). The mixture was left on cells for 1–1.5 h, after which it was replaced with standard tissue culture media. The culture media was again replaced after 24 h to remove debris and dead cells. The cells were patch-clamped 2–3 d after transfection when the culture medium was replaced with standard extracellular saline solution that contained (mM) 2.04 CaCl₂, 2.68 KCl, 1.48 MgCl₂, 0.05 MgSO₄, 125 NaCl, 0.83 NaH₂PO₄, 20 NaHCO₃, and 2 HEPES, pH 7.4.

In the coexpression experiments, a fourfold molar excess of plasmid encoding the β₁ subunit was used to drive coassembly with the α subunits (McManus et al. 1995). Using the same promoter (cytomegalovirus) for the α and β₁ subunits and the GFP increased the probability that if the GFP was expressed, the included subunits would also be expressed.

Solutions

The intracellular solution contained 175 mM KCl, 5 mM TES pH buffer, and 10 mM EGTA and 10 mM HEDTA to buffer the Ca²⁺ (see below). The extracellular solution contained either 150 or 175 mM KCl and 5 mM TES and had no added Ca²⁺ or Ca²⁺ buffers. Both the intracellular and extracellular solutions were adjusted to pH 7.0. The amount of Ca²⁺ added to the intracellular solution to obtain approximate free Ca²⁺ concentrations of 0.001–100 μM was calculated using stability constants for EGTA (Smith and Miller 1985) and for HEDTA (Martell and Smith 1993). The 0 Ca²⁺ solution had no Ca²⁺ added and the same composition as the other solutions. These solutions were then calibrated using a Ca²⁺ electrode (Ionplus; Orion Research, Inc.) standardized against solutions with KCl and TES in which known amounts of Ca²⁺ were added. Before adding Ca²⁺, any contaminating divalent cations were removed from the solution by treatment with Chelex 100 (Bio-Rad Laboratories). The solutions bathing the intracellular side of the patch were changed by means of a valve-controlled, gravity-fed perfusion system using a micro-chamber (Barrett et al. 1982).

Single-Channel Recording and Analysis

Currents flowing through single (or in some cases multiple) BK channels in patches of surface membrane excised from HEK 293 cells transfected with clones for either the α or the α and β₁ subunits were recorded using the patch-clamp technique (Hamill et al. 1981). All recordings were made using the excised inside-out configuration in which the intracellular surface of the patch was exposed to the bathing solution. BK channels were identified by their large conductance and characteristic voltage and Ca²⁺ dependence (Barrett et al. 1982). Endogenous BK channels in nontransfected HEK 293 cells were not seen, but we cannot exclude that they might exist at a low density. Currents were recorded with an Axopatch 200A amplifier and stored on VCR tapes using a VR-10B digital data recorder. The currents were then analyzed using custom programs written in the laboratory. Single-channel patches were identified by observing openings to only a single open-channel conductance level during prolonged recording in which the open probability was >0.4. Experiments were performed at room temperature (20–25°C). For the 0-Ca²⁺ _i experiments, the number of channels in a patch was determined by pulling the patch in a high Ca²⁺ solution and then switching to 0 Ca²⁺ solution.

Single-channel current records were low-pass filtered with a four-pole Bessel filter to give a final effective filtering (−3 dB) of typically 10 kHz (range 4.5–10 kHz), and were sampled by computer at a rate of 125–250 kHz. The methods used to select the level of filtering to exclude false events that could arise from noise, measure interval durations with half-amplitude threshold analysis, and use stability plots to test for stability and identify modes have been described previously, including the precautions taken to prevent artifacts in the analysis (McManus et al. 1987; McManus and Magleby 1988, McManus and Magleby 1989; Magleby 1992). The kinetic analysis in this study was restricted to channel activity in the normal mode, which typically involves 96% of the detected intervals (McManus and Magleby 1988). Activity in modes other than normal, including the low activity mode (Rothberg et al. 1996), was removed before analysis, as were the infrequent transitions to subconductance levels. The numbers of intervals during normal activity analyzed for each experimental condition ranged from 50 to 14,000 in the 0-Ca²⁺ _i experiments, where the open probability and the interval frequency can be very low at less depolarized potentials, to upwards of 200,000 for higher Ca²⁺ _i, where the channel activity was higher.

Data from multichannel patches were only analyzed for very low Ca²⁺ _i, where the activity was so low that simultaneous openings of two or more channels were seldom if ever observed. For the multichannel patches, the open probability was calculated by dividing the total open time by the total record length, and then by the number of channels in the patch. The mean durations of the gaps between bursts for the multichannel patches were estimated by determining these parameters as if the data were from a single channel, and then multiplying the estimates by the numbers of channels in the patch. The mean closed times for the multichannel patches were determined in the following way: the sum of all durations of the gaps between the bursts during the total recording time, multiplied by the number of channels in the patch, was added to the sum of all the durations of the closed intervals within bursts, and then the value was divided by the total number of closed intervals in the record. There was no need to correct estimates of the mean open time and mean number of openings per burst, since at such low P _o, only one channel was open at any given time.

The methods used to log-bin the intervals into dwell-time distributions, fit the distributions with sums of exponential components using maximum likelihood fitting techniques (intervals less than two dead times were excluded from the fitting), and determine the number of significant exponential components with the likelihood ratio test have been described previously (McManus and Magleby 1988, McManus and Magleby 1991; Colquhoun and Sigworth 1995). Dwell-time distributions are plotted with the Sigworth and Sine 1987 transformation, which plots the square root of the number of intervals per bin without correcting for the logarithmic increase in bin width with time. With this transform, the peaks of the individual components fall at the time constants of the components.

The method of defining a critical gap (closed interval) to identify bursts is detailed in Magleby and Pallotta 1983. In brief, the distributions of closed-interval durations were first typically fitted with the sum of five exponential components. The closed intervals from the one or two exponential components with the longest time constants were then defined as gaps between bursts, as there was typically a difference of one to three orders of magnitude in the time constants separating the gaps between bursts from the time constants of the much briefer duration components that generated the closed intervals within bursts. A critical time was then defined so that the number of gap intervals misclassified as closed intervals within bursts was equal to the number of closed intervals within bursts misclassified as gap intervals. With this critical time, errors resulting from misclassification would tend to cancel out. The critical time was found to be relatively insensitive to the numbers of significant exponentials required to fit the dwell-time distribution. Burst analysis was typically restricted to current records from single channels, except for some multichannel patches where P _o was so low (due to low Ca²⁺ _i and/or less positive voltages) that only one channel was open at any time. Burst analysis was restricted to data with P _o < 0.8, as it was difficult to clearly define the gaps between bursts for higher P _o.

RESULTS

The β₁ Subunit Increases both P_o and Burst Duration in the Virtual Absence of Ca²⁺ _i

To investigate whether the β₁ subunit requires Ca²⁺ _i for its action, we used single-channel analysis to examine the gating of α and α+β₁ channels in the effective absence of Ca²⁺ _i (<1 nM), which will be referred to as 0 Ca²⁺ _i. (It will be shown in a later section that effective 0 Ca²⁺ _i was achieved.) Fig. 1 A shows single-channel currents recorded in 0 Ca²⁺ _i at +30 mV from an α channel and also from an α+β₁ channel. The occasional openings and bursts of openings are separated by the long closed intervals of many seconds that form the gaps between bursts. The long gaps between bursts in 0 Ca²⁺ _i give very low open probability. The average P _os for the entire records from which each excerpt was obtained were 0.00056 for the α channel and 0.0039 for the α+β₁ channel, for a sevenfold increase in P _o. The mean P _o for 15 α channels and 21 α+β₁ channels at 0 Ca²⁺ _i is plotted in Fig. 2 A (left-most points), where the presence of the β₁ subunit increased P _o ∼10-fold on average, from ∼0.0002 to 0.002.

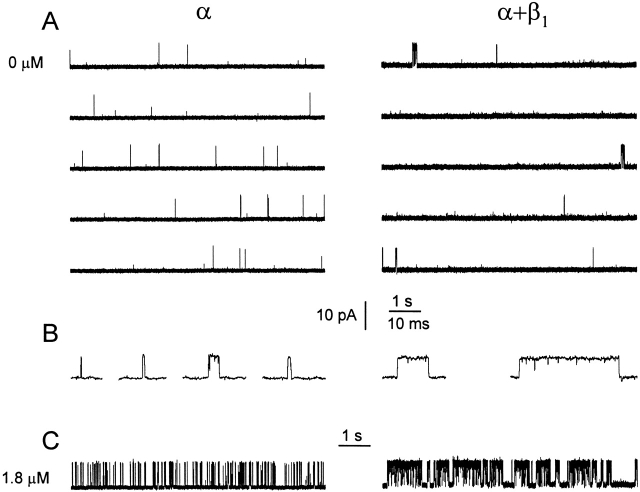
Figure 1.

The β₁ subunit alters the single-channel gating kinetics in both the absence and presence of Ca²⁺ _i. (A) Currents recorded from single α and α+β₁ channels in 0 Ca²⁺ _i. A continuous record in each case was cut into the five presented traces. The β₁ subunit increases both burst duration and the duration of the gaps between bursts. The average P _os for the entire record from which each excerpt was obtained were: 0.00056 for the α channel and 0.0039 for the α+β₁ channel. (B) Bursts from α and α+β₁ channels presented on a faster time base. (C) Currents recorded from α and α+β₁ channels in 1.8 μM Ca²⁺ _i. The traces were filtered at 4 kHz for display in this and subsequent figures, while the filtering for the analysis carried out in this paper was typically 10 kHz. Membrane potential: +30 mV; α channel, C92; α+β₁ channel, C87.

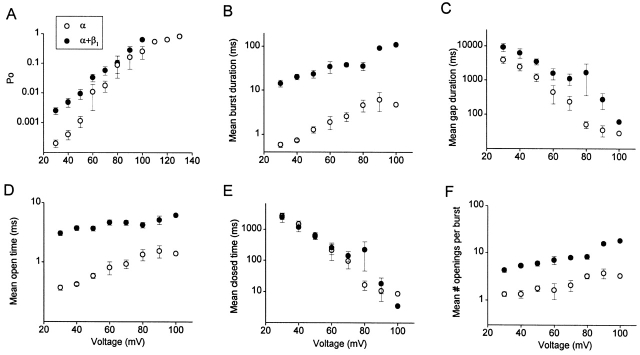
Figure 2.

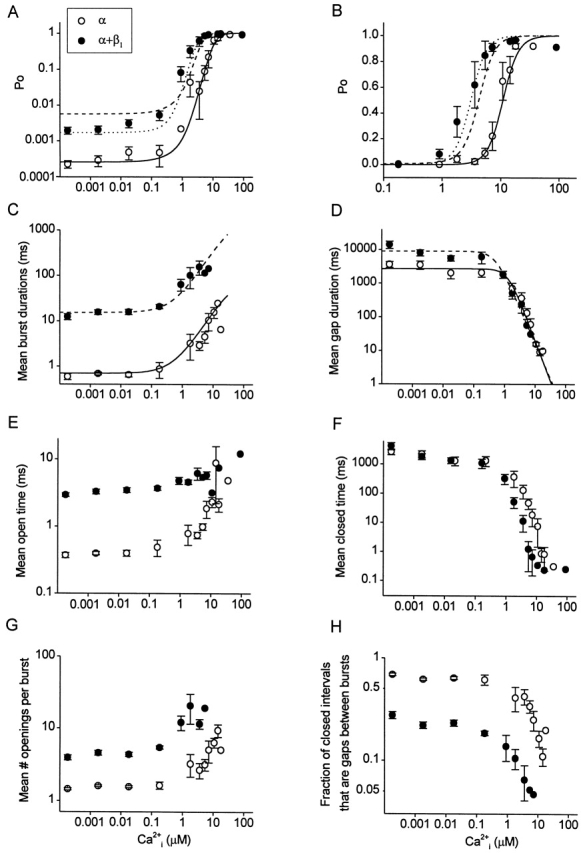
Effects of the β₁ subunit on the gating parameters from 0 to high levels of Ca²⁺ _i. Data is plotted for α channels (○) and α+β₁ channels (•). The lack of effect of Ca²⁺ _i on the parameters from 0.00018 to 0.018 μM Ca²⁺ _i indicates that effective 0 Ca²⁺ _i was achieved in this range. (A and B) Plots of P _o vs. Ca²⁺ _i on double logarithmic and semilogarithmic coordinates. (Continuous lines) Calculated P _o for α channels with using the continuous line in C for burst and the continuous line in D for gaps. (Dashed lines) Calculated P _o for α+β₁ channels with using the dashed line in C for burst and the continuous line in D for gap. The assumption that the β₁ subunit increased burst duration 22-fold in a Ca²⁺-independent manner accounted for 80% of the leftward shift in the P _o vs. Ca²⁺ _i plot. (Dotted lines) Calculated P _o for α+β₁ channels with using the dashed line in C for burst and the dashed line in D for gap. 100% of the shift could be accounted for by also including the smaller Ca²⁺-dependent effect of the β₁ subunit on the duration of the gaps between bursts. (C) Plot of mean burst duration versus Ca²⁺ _i. The burst duration of α channels (continuous line) was described by the empirical expression: Y_α(burst) = 0.7 + 100/[1 + (50/X)^1.1], where X is Ca²⁺ _i in micromolar and burst duration is in milliseconds. Multiplying this line by a constant factor of 22 then described the burst duration of α+β₁ channels (dashed line). (D) Plot of the mean duration of gaps between bursts versus Ca²⁺ _i. The continuous line for α channels is given by the empirical equation: Y_α(gap) = 2,700{1 −1/[1 + (1.3/X)^2.4]}, and the dashed line for α+β₁ channels is given by: Y_α+β(gap) = 9,000{1 −1/[1 + (0.5/X)^2.1]}, where X is Ca²⁺ _i in micromolar and gap duration is in milliseconds. (E–H) Plots of the indicated parameters versus Ca²⁺ _i. For all parts of the figure, the data for α channels are from 15 patches containing 1–12 channels per patch, and the data for α+β₁ channels are from 21 patches containing 1–13 channels per patch. Data from multichannel patches were used only in 0 or very low Ca²⁺ _i, when the P _o was sufficiently low that the bursts did not overlap. Parameters from multichannel patches were corrected for the numbers of channels in each patch, as specified in methods. Data are plotted as the mean ± SEM.

In conjunction with the large increase in P _o, the β₁ subunit stabilized the bursting states, increasing mean burst duration in 0 Ca²⁺ _i. For the channels in Fig. 1, mean burst duration increased from 1.1 to 28.8 ms, for a 26-fold increase. The dramatic increase in mean burst duration can be seen in Fig. 1 B, where selected bursts are presented on a faster time base. The β₁ subunit consistently increased burst duration in 0 Ca²⁺ _i. Mean burst duration for 15 α channels and 21 α+β₁ channels at 0 Ca²⁺ _i is plotted in Fig. 2 C (left-most points). The presence of the β₁ subunit increased mean burst duration 21-fold in 0 Ca²⁺ _i, from 0.59 to 12.4 ms. Thus, the β₁ subunit exerts its characteristic effects of increasing P _o by retaining the gating in the bursting states in 0 Ca²⁺ _i, just as it does in the presence of Ca²⁺ _i. For comparison, the effects of the β₁ subunit on gating in the presence of Ca²⁺ _i (1.8 μM) are shown in Fig. 1 C, where the β₁ subunit also increased burst duration and P _o, as described previously (Nimigean and Magleby 1999).

The β₁ Subunit Alters the Gating Parameters from 0 to Higher Ca²⁺ _i

To examine further the effects of the β₁ subunit on the gating at 0 Ca²⁺ _i and to compare these effects with those at higher Ca²⁺ _i, we measured an array of kinetic parameters (P _o, mean burst duration, mean duration of gaps between bursts, mean open time, mean closed time, and mean number of openings per burst) for α and α+β₁ channels and plotted them against Ca²⁺ _i in Fig. 2. Over the entire range of Ca²⁺ _i, from 0 to higher levels, the β₁ subunit increased mean burst duration ∼20-fold (Fig. 2 C). This increase in the mean burst duration arose from both an increase in mean open time (Fig. 2 E) and in the mean number of openings per burst (Fig. 2 G). The β₁ subunit also increased the mean durations of the gaps between bursts approximately threefold in 0 Ca²⁺ _i, while having little effect on the durations of the gaps at higher Ca²⁺ _i (Fig. 2 D). The mean closed time was little affected by the β₁ subunit in 0 Ca²⁺ _i (Fig. 2 F) because the β₁ subunit-induced increase in the duration of the gaps between bursts (Fig. 2 D) was compensated for by a decrease in the fraction of closed intervals that were gaps between bursts (Fig. 2 H).

Evidence for the Effective Absence of Ca²⁺

In Fig. 2 it can be seen that all the measured kinetic parameters (P _o, mean burst duration, mean duration of gaps between bursts, mean open time, mean closed time, and mean number of openings per burst) remained relatively unchanged as Ca²⁺ _i was increased more than two orders of magnitude (from 0.00018 to 0.018 μM). If Ca²⁺ _i were to bind to the channel and affect activity over this wide range of Ca²⁺ _i, then the kinetic parameters that define gating should change. Since little change was observed, these observations suggest that the channel remained functionally unliganded for Ca²⁺ _i < 0.1 μM. Hence, even though trace Ca²⁺ _i was likely present, functional 0 Ca²⁺ _i was achieved.

The β₁ Subunit Shifts the P_o vs. Ca²⁺ _i Curve to the Left

The characteristic leftward shift in the P _o vs. Ca²⁺ _i curve induced by the β₁ subunit (Nimigean and Magleby 1999; Ramanathan et al. 2000; and equivalent findings in McManus et al. 1995; Dworetzky et al. 1996; Meera et al. 1996; Tseng-Crank et al. 1996; Wallner et al. 1996) is shown in Fig. 2 B. This leftward shift is generally referred to as an increase in Ca²⁺ sensitivity because it indicates that less Ca²⁺ _i is required to half-activate the channel. From the semilogarithmic plot in Fig. 2 B, it appears that the β₁ subunit only alters gating for Ca²⁺ _i > 0.1 μM. Hence, this figure by itself suggests that the mechanism involved in the leftward shift in P _o by the β₁ subunit may be a function of Ca²⁺ _i. However, from the double logarithmic plots in Fig. 2C, Fig. E, Fig. G, and Fig. H, it appears that a major effect of the β₁ subunit is to shift the kinetic parameters associated with burst duration, independent of Ca²⁺ _i. The resulting effect of the β₁ subunit on P _o is shown on double logarithmic coordinates in Fig. 2 A, where P _o is shifted upward both in the absence and presence of Ca²⁺ _i.

β₁ Subunit Exerts Its Effects Over a Range of Voltages

The data in Fig. 2 were obtained at a single voltage of +30 mV. To examine whether the effects of the β₁ subunit in 0 Ca²⁺ _i are dependent on voltage, we collected data in 0 Ca²⁺ _i over a range of voltages. Examples of single-channel currents obtained at +60 and +90 mV for α and α+β₁ channels are shown in Fig. 3. The β₁ subunit increased the durations of the bursts as well as the gaps between bursts at both voltages. The increase in burst duration with the β₁ subunit in 0 Ca²⁺ _i is clearly shown in Fig. 3 C for both voltages, where representative bursts are presented on a faster time base.

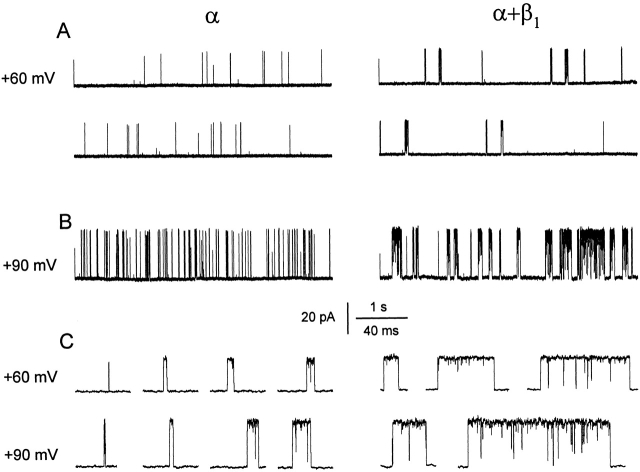
Figure 3.

The β₁ subunit still increases both burst duration and the duration of gaps between bursts in 0 Ca²⁺ _i when P _o is increased by depolarization. (A and B) Currents recorded from single α and α+β₁ channels at two different membrane potentials of +60 mV (A) and +90 mV (B) in 0 Ca²⁺ _i. For the +60-mV data, a continuous record was cut into two traces in each case. The average P _os for the entire records from which the excerpts were obtained were: 0.0042 (+60 mV) and 0.063 (+90 mV) for the α channel, and 0.029 (+60 mV) and 0.37 (+90 mV) for the α+β₁ channel. (C) Representative bursts of openings from A and B on a faster time base. α channel, C96; α+β₁ channel, C100.

The mean effects of the β₁ subunit on the gating kinetics over a range of voltages in 0 Ca²⁺ _i are shown in Fig. 4 for eight patches with α channels and nine patches with α+β₁ channels. For both α and α+β₁ channels, depolarization increased P _o through increases in mean burst duration, mean open time, and the mean number of openings per burst, and decreases in the mean closed time and in the mean duration of the gaps between bursts (Fig. 4). The same characteristic effects of the β₁ subunit that were observed in 0 Ca²⁺ _i in Fig. 2 were then superimposed on these effects of depolarization. Over the examined range of voltage (+30 to +100 mV), the β₁ subunit increased mean burst duration ∼20-fold (Fig. 4 B) and the mean duration of the gaps between bursts two- to threefold (Fig. 4 C). The increase in mean burst duration was due to increases in both mean open time (approximately eightfold, Fig. 4 D), and the mean number of openings per burst (approximately threefold, Fig. 4 F). The β₁ subunit had little effect on mean closed time even though the mean closed time drastically decreased with depolarization (Fig. 4 E).

Figure 4.

The β₁ subunit exerts its characteristic effects on gating in 0 Ca²⁺ _i from +30 to +100 mV. Data are plotted for α channels (○) and α+β₁ channels (•). All data were obtained in 0 Ca²⁺ _i. (A–F) Plots of the indicated kinetic parameters versus membrane potential. The β₁ subunit increased P _o (A), mean burst duration (B), the mean duration of gaps between bursts (C), mean open time (D), and the mean numbers of openings per bursts (F) over the examined range of membrane potentials by shifting the parameters on the double logarithmic plots, while having little effect on the mean closed times (E). The data for α channels are from eight patches containing 1–12 channels and the data for α+β₁ channels are from nine patches containing 1–13 channels. Multichannel patches were used only when the P _o was sufficiently low that bursts did not overlap. Parameters from multichannel patches were corrected for the number of channels in each patch. Data are plotted as the mean ± SEM.

Evident in Fig. 4 is that the estimates of the parameters that describe single-channel kinetics for α and α+β₁ channels (mean open time, mean closed time, mean burst duration, mean duration of gaps between bursts, and mean number of openings per burst) are generally parallel with each other on a logarithmic scale, indicating that the ratios of the kinetic parameters for the α+β₁ to the α channels remain relatively constant over the examined range of +30 to +100 mV. As a first approximation, a constant ratio suggests that the β₁ subunit may act like a gain control, independent of voltage, such that the kinetic parameters measured in the presence of the β₁ subunit are simply the result of multiplication between the kinetic parameters in the absence of the β₁ subunit and a constant factor, which depends on the parameter measured.

Interestingly, the magnitude of the fractional increase in P _o with the β₁ subunit decreased with depolarization (Fig. 4 A). Some decrease with depolarization might be expected since depolarization increases P _o and P _o saturates near 0.96 for both α and α+β₁ channels. However, the decreased effect of the β₁ subunit on P _o with depolarization was apparent at low P _os as well. Projection of imaginary lines through the data in Fig. 4 A suggests that at very depolarized voltages, the β₁ subunit may no longer have an effect of increasing P _o and may even decrease it. A similar trend, however slight, is also apparent in Fig. 4B and Fig. D, for mean burst duration and mean open time, suggesting that the β₁ subunit may have reduced effects on these parameters at greatly depolarized voltages.

The β₁ Subunit Does Not Act Like an Increase in Membrane Potential

Previous results (Nimigean and Magleby 1999) indicated that the β₁ subunit does not act like an increase in Ca²⁺ _i. That is, the β₁ subunit does not increase all the Ca²⁺-binding rates proportionally. This conclusion was reached by showing that α and α+β₁ channels had markedly different gating kinetics at the same P _o, achieved by changing Ca²⁺ _i. We now apply the same type of analysis to investigate whether the β₁ subunit acts like an increase in voltage.

If voltage and the β₁ subunit worked through the same mechanism, α and α+β₁ channels should display identical gating kinetics at the same P _o, achieved by changing voltage. This was not the case. Increasing P _o with the β₁ subunit in 0 Ca²⁺ _i was associated with greatly increased burst duration and a smaller increase in the duration of the gaps between bursts. In contrast, increasing P _o with depolarization was associated with small increases in burst duration and large decreases in the duration of gaps between bursts.

Although these differential effects on kinetics are apparent from the examination of Fig. 1 Fig. 2 Fig. 3 Fig. 4, they are more easily seen in Fig. 5, where the P _o of an α channel was increased with depolarization to match the P _o of an α+β₁ channel. The dramatic differences in single-channel kinetics at similar P _os for α and α+β₁ channels are readily apparent in the current traces inset in Fig. 5. These effects of voltage and the β₁ subunit on kinetics are quantified in Fig. 5 by the open dwell-time distributions (left) and the closed dwell-time distributions (right) for both the α and the α+β₁ channels. At similar P _os, both the mean open times and the mean durations of the gaps between bursts were about an order of magnitude less for the α channel than for the α+β₁ channel (vertical lines), while the relative number of closed intervals that were gaps between bursts was greater for the α channel than for the α+β₁ channel. These marked differences in the kinetics of α and α+β₁ channels at the same P _o (achieved by changing voltage) suggest that depolarization and the β₁ subunit act through different mechanisms.

Figure 5.

Dwell-time distributions obtained from single α and α+β₁ channels, adjusted to have the same P _o by changing the voltage, have different single-channel kinetics. The open- and closed-interval durations were log binned, and the square root of the number of intervals in each bin was plotted against the bin midtimes for one α channel (+80 mV) and one α+β₁ channel (+60 mV) in 0 Ca²⁺ _i. To allow direct comparison of the distributions, the number of intervals in each distribution (from time 0 to infinity) was normalized to 100,000 in each case. The continuous lines are fits with the sums of two significant open and five significant closed exponential components for the α channel and two significant open and four significant closed exponential components for the α+β₁ channel. The vertical dashed lines indicate the mean open times and the mean durations of the gaps between bursts. The time constants and areas of the exponential components are: (A, open) 0.075 ms, 0.10; 1.1 ms, 0.90. (B, open) 0.081 ms, 0.14; 6.3 ms, 0.86. (A, closed) 0.046 ms, 0.55; 0.13 ms, 0.11; 4.5 ms, 0.033; 54 ms, 0.29; 211 ms, 0.016. (B, closed) 0.041 ms, 0.66; 0.24 ms, 0.17; 1.8 ms, 0.027; 607 ms, 0.14. α channel, C96; α+β₁ channel, C98.

The β₁ Subunit Acts as a Gain Control on Bursting Kinetics, Independent of whether the Channel Is Activated by Voltage or Ca²⁺ _i

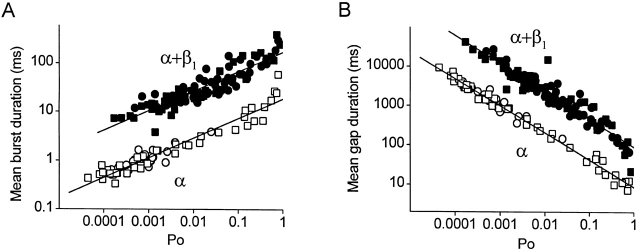
To explore whether the β₁ subunit has the same effect on the bursting kinetics, independent of whether P _o is changed by voltage or Ca²⁺ _i, mean burst duration and the mean duration of gaps between bursts were plotted against P _o for both α and α+β₁ channels in Fig. 6. The circles plot data obtained over a range of Ca²⁺ _i (0 to 18 μM) at +30 mV, and the squares plot data obtained over a range of voltages (+30 to +100 mV) in 0 Ca²⁺ _i. Filled symbols plot data from α+β₁ channels and open symbols plot data from α channels. At any given P _o, both the mean burst duration and the mean duration of gaps between bursts were 10-fold longer in the α+β₁ channels as compared with the α channels, independent of whether the P _o was achieved by changing Ca²⁺ _i or voltage. This 10-fold effect of the β₁ subunit on the bursting parameters was independent of P _o, as indicated by the parallel shifts over four orders of magnitude of change in P _o.

Figure 6.

The β₁ subunit-induced increase in both burst and gap duration is independent of P _o and whether the channel is activated by voltage or Ca. (A) Plot of mean burst duration versus P _o. (B) Plot of the mean durations of gaps between bursts versus P _o. Data in each plot are presented for α channels (open symbols) and for α+β₁α+β₁ channels (filled symbols). P _o was changed by changing Ca²⁺ _i at the same membrane potential of +30 mV (circles), or by changing the membrane potential in the absence of Ca²⁺ _i (squares). Data are from the same patches detailed in the legends of Fig. 2 and Fig. 4.

The results in Fig. 6 suggest that the β₁ subunit acts mainly as a gain control on the bursting parameters, independent of P _o or whether the channel is activated by Ca²⁺ _i or by voltage. This is the case since a parallel shift on a logarithmic coordinate, as in Fig. 2, Fig. 4, and Fig. 6, is consistent with a multiplicative (gain) effect. Hence, as a first approximation, the gain effect of the β₁ subunit appears to be independent of Ca²⁺ _i (Fig. 2), voltage (Fig. 4), and P _o, over the examined range of conditions.

The constant shift in the mean durations of gaps between bursts in Fig. 6 B in the presence of the β₁ subunit may appear paradoxical, since it was observed in Fig. 2 D that the β₁ subunit increased the durations of the gaps between bursts approximately threefold in 0 Ca²⁺ _i, but had little effect on the durations of the gaps once Ca²⁺ _i was increased. The difference between Fig. 6 and Fig. 2 is that the data in Fig. 6 are plotted against P _o rather than Ca²⁺ _i. At a fixed Ca²⁺ _i, the β₁ subunit greatly increased burst duration, leading to an increase in P _o for α+β₁ channels. The same P _o could then be achieved in α channels by increasing their activity through depolarization or increased Ca²⁺ _i. This increased activity is associated with large decreases in the durations of the gaps between bursts and smaller increases in burst duration (Fig. 2 and Fig. 4). Hence, at the same P _o, α channels must have much smaller gaps between bursts than α+β₁ channels, as observed (Fig. 6 B), to compensate for the much longer duration bursts of α+β₁ channels (Fig. 6 A).

Ca²⁺ _i Switches Off the β₁ Subunit-induced Increase in the Duration of Gaps between Bursts

As indicated previously, for 0 Ca²⁺ _i, the β₁ subunit increased the durations of gaps between bursts approximately threefold (Fig. 2 D). For Ca²⁺ _i > ∼0.2 μM, the β₁ subunit no longer lengthened the durations of the gaps between bursts (perhaps even decreased them slightly), consistent with Nimigean and Magleby 1999. Thus, Ca²⁺ _i switches off (inhibits) the β₁ subunit-induced lengthening of the gaps between bursts. It follows that the Ca²⁺-dependent effect of the β₁ subunit on the mean closed time in Fig. 2 F is a consequence of Ca²⁺ _i > 0.2 μM switching off the β₁ subunit-induced lengthening of bursts. Thus, although the major effects of the β₁ subunit on increasing burst duration appear to be independent of Ca²⁺ _i, the observation of a Ca²⁺-dependent effect on the durations of the gaps between bursts raises the question as to what extent the β₁ subunit-induced shift in apparent Ca²⁺ sensitivity is Ca²⁺ dependent.

80% of the β₁ Subunit-induced Increase in Ca²⁺ Sensitivity Is Independent of Ca²⁺ _i

To determine to what extent the β₁ subunit-induced shift in Ca²⁺ sensitivity is Ca²⁺ independent, we examined how much of the β₁ subunit-induced shift in Ca²⁺ sensitivity could be accounted for by assuming that the sole effect of the β₁ subunit was to multiply burst duration a constant amount, independent of Ca²⁺ _i. We first developed an empirical model to generate the P _o vs. Ca²⁺ _i data for α channels, and then calculated the predicted P _o vs. Ca²⁺ _i curve for α+β₁ channels by assuming that the only effect of the β₁ subunit was to multiply burst duration a constant amount, independent of Ca²⁺ _i.

Open probability is defined by :

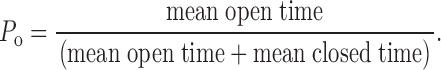1

Since the durations of the closed intervals within bursts are brief compared with both the durations of the open intervals and the durations of the gaps between bursts, P _o can be approximated by:

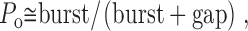2

where burst represents the mean burst duration and gap represents the mean duration of gaps between bursts.

The continuous lines in Fig. 2C and Fig. D, are empirical descriptions of mean burst duration and the mean duration of gaps between bursts, respectively, as functions of Ca²⁺ _i for α channels (see figure legends). These empirical descriptions for burst and gap were then used with to calculate the P _o vs. Ca²⁺ _i curve for the α channels, plotted as continuous lines in Fig. 2A and Fig. B. It can be seen that this method of predicting P _o gave a reasonable description of the P _o vs. Ca²⁺ _i data for the α channels for both semilogarithmic and double logarithmic plots.

To determine to what extent the increased Ca²⁺ sensitivity induced by the β₁ subunit could be predicted by assuming that the sole effect of the β₁ subunit was to increase burst duration a constant (multiplicative) amount, independent of Ca²⁺ _i, the P _o vs. Ca²⁺ _i curve for α+β₁ channels was calculated exactly as it was for the α channels, except that mean burst duration (burst) in was multiplied by a constant factor 22. The results of the calculation (Fig. 2, A–C, dashed lines) show a leftward shift in the P _o vs. Ca²⁺ _i curve that accounts for 80% of the increase in Ca²⁺ sensitivity induced by the β₁ subunit. This simple multiplicative effect also described the effect of the β₁ subunit on burst duration (Fig. 2 C, dashed line). Thus, the assumption that the sole effect of the β₁ subunit was to increase mean burst duration a constant multiplicative amount, independent of Ca²⁺ _i, could describe the β₁ subunit-induced increase in burst duration and 80% of the leftward shift in the P _o vs. Ca²⁺ _i curve induced by the β₁ subunit. It follows, then, that 80% of the β₁ subunit-induced increase in Ca²⁺ sensitivity (the apparent Ca²⁺ switch) can be accounted for by a Ca²⁺-independent mechanism.

The remaining 20% of the β₁ subunit-induced increase in Ca²⁺ sensitivity did appear to be Ca²⁺ dependent. When the Ca²⁺-dependent effect of the β₁ subunit on the gaps between bursts was taken into account by describing gap in with the dashed line in Fig. 2 D (rather than by the continuous line), 100% of the β₁ subunit-induced leftward shift in the Ca²⁺ sensitivity could be accounted for, as shown by the dotted line in Fig. 2A and Fig. B. Furthermore, when the Ca²⁺-dependent component was included, the P _o in 0 Ca²⁺ _i was also correctly predicted (Fig. 2 A, dotted line). (Results essentially indistinguishable from those presented in this section were obtained when the calculations included the effects of the durations of the intervals within bursts.)

We cannot exclude that there may be Ca²⁺-dependent effects of the β₁ subunit on mean open time and on the mean number of openings per burst (Fig. 2E and Fig. G). Unfortunately, estimates of these two parameters, unlike burst duration, are highly dependent on the flickers (brief closed intervals within bursts). Since flickers may arise from closed states beyond the activation pathway (Cox et al. 1997; Rothberg and Magleby 1998, Rothberg and Magleby 1999; Talukder and Aldrich 2000), it is not clear whether there is a Ca²⁺ dependence of the underlying process. Nevertheless, the results of this section indicate that 80% of the β₁ subunit-induced increase in Ca²⁺ sensitivity arises from a Ca²⁺-independent increase in burst duration and 20% arises from a Ca²⁺-dependent inhibition of the lengthening effect of the β₁ subunit on the gaps between bursts at +30 mV.

Unliganded BK Channels Gate in a Minimum of Two to Three Open and Three to Five Closed States

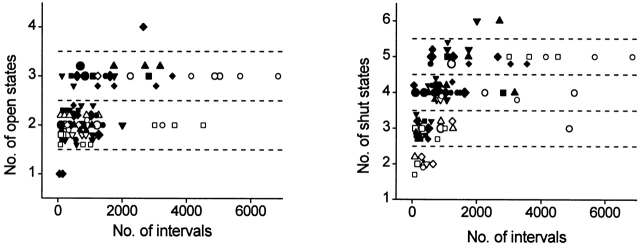
To obtain further insight into the gating mechanism of unliganded α and α+β₁ channels, an estimate of the number of kinetic states entered during gating in 0 Ca²⁺ _i for each channel were obtained by fitting dwell-time distributions of open- and closed-interval durations with sums of exponential components. The number of significant exponential components gives a measure of the minimal number of kinetic states entered during gating (Colquhoun and Hawkes 1981, Colquhoun and Hawkes 1982, Colquhoun and Hawkes 1995; McManus and Magleby 1988). Examples of such dwell-time distributions obtained in 0 Ca²⁺ _i are shown in Fig. 5, where the open distributions were described by two significant open components for both α and α+β₁ channels and the closed distributions were described by five significant closed components for α channels and four significant closed components for α+β₁ channels. Estimates from eight patches containing α channels and 12 patches containing α+β₁ channels are presented in Fig. 7 for data obtained over a range of voltages in 0 Ca²⁺ _i.

Figure 7.

BK channels typically gate in a minimum of two to three open and three to five closed states in 0 Ca²⁺ _i, inconsistent with gating mechanisms based on the Monod-Wyman-Changeux model with Ca²⁺ _i as the allosteric activator, which predicts gating in one open and one closed state in 0 Ca²⁺ _i. The minimal number of significant exponential components required to describe the open and closed dwell-time distributions in 0 Ca²⁺ _i are plotted against the numbers of analyzed intervals. Data for α channels (open symbols) are from 34 sets of data from eight different patches. Data for α+β₁ channels (filled symbols) are from 52 sets of data from 12 patches. A number of data sets, each at a different membrane potential, were typically obtained from each patch. Each symbol type plots estimates obtained from a single patch. Data from patches containing multiple channels were included when the channel activity was so low that channel openings did not occur simultaneously. When the analysis was restricted to the 27 data sets from the seven patches containing a single channel, the same results were obtained, except that only two, rather than three, open states were detected for α channels. There was no obvious effect of voltage on the number of detected states.

Both α and α+β₁ channels typically gated in a minimum of two to three open states and three to five closed states in 0 Ca²⁺ _i. (Similar results were found when analysis was restricted to the 27 data sets from the seven patches containing a single channel.) These estimates can be compared with a minimum of typically three to four open and five to six closed states for α and α+β₁ at higher levels of activity in the presence Ca²⁺ _i (Nimigean and Magleby 1999), and to typically three to four open and five to seven closed states for native BK channels from cultured rat skeletal muscle in the presence of Ca²⁺ _i (McManus and Magleby 1988). The larger numbers of detected states at higher Ca²⁺ _i when compared with 0 Ca²⁺ _i may reflect in part the increased resolution resulting from the increased numbers of intervals (see McManus and Magleby 1988) that could be collected and analyzed in higher Ca²⁺ _i, where the activity was greatly increased.

In 0 Ca²⁺ _i, the estimates of the mean number of detected open states for α channels (2.2 ± 0.4, mean ± SD) was not significantly different (P > 0.25, Mann-Whitney test) from the mean number of detected open states for the α+β₁ channels (2.4 ± 0.6). The estimate of the mean number of detected closed states for α channels (3.4 ± 1.0) was significantly less (P < 0.05) than the number of detected closed states entered for α+β₁ channels (4.1 ± 0.8). An increased number of detected closed states for α+β₁ channels in 0 Ca²⁺ _i could reflect a difference in the actual numbers of states typically entered during gating in 0 Ca²⁺ _i, or an increased ability to detect closed states for α+β₁ channels because the intervals are spread over a greater range of times than for α channels.

Our findings of gating among multiple open and closed states in 0 Ca²⁺ _i are consistent with a study using single-channel recording just published by Talukder and Aldrich 2000, where data were presented for gating in two to three open and three closed states in 0 Ca²⁺ _i for mslo channels composed of only the α subunit. The fewer closed states detected in their study may reflect that fewer closed states were typically entered at the more depolarized voltages used in their study or that the detection of closed states was more difficult because of the compressed dwell time distributions at the higher P _os in their study.

Rejection of the Monod-Wyman-Changeux Model for Gating in 0 Ca

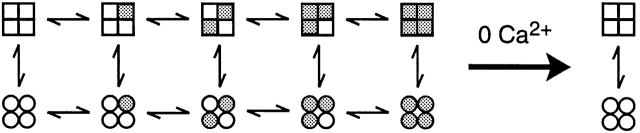
Models considered for the gating of BK channels have often been based on the Monod-Wyman-Changeux (MWC) model for allosteric proteins (McManus and Magleby 1991; DiChiara and Reinhart 1995; Wu et al. 1995; Cox et al. 1997; Cui et al. 1997; Rothberg and Magleby 1998). The MWC model (Monod et al. 1965) is presented in Fig. 1, where the upper row represents closed states, the lower row represents open states, and shaded subunits have bound Ca²⁺ _i.

Scheme S1.

The opening-closing transitions in the MWC model are concerted, with all four subunits undergoing simultaneous conformational changes. From Fig. 1, it can be seen that the gating will be confined to the two unliganded states in the absence of Ca²⁺ _i, giving only one open and one closed state. The observations in Fig. 7, that both α and α+β₁ channels typically gate in a minimum of two to three open and three to five closed states in 0 Ca²⁺ _i are clearly at odds with Fig. 1, and require that the MWC model be rejected as a mechanism for the gating of these channels. Talukder and Aldrich 2000 have also rejected the MWC model for gating of BK channels based on the observation of gating in multiple open and closed states in 0 Ca²⁺ _i. Findings using other types of experimental approaches have previously shown that the gating of BK channels is inconsistent with the MWC model (Fig. 1) or extensions of the MWC model (Horrigan et al. 1999; Horrigan and Aldrich 1999; Rothberg and Magleby 1998, Rothberg and Magleby 1999).

DISCUSSION

The accessory β₁ subunit of BK channels greatly increases their Ca²⁺ sensitivity by reducing the Ca²⁺ _i required for half activation 5–10-fold, giving a characteristic leftward shift in the P _o vs. Ca²⁺ _i plots (McManus et al. 1995; Dworetzky et al. 1996; Meera et al. 1996; Tseng-Crank et al. 1996; Wallner et al. 1996; Nimigean and Magleby 1999; Ramanathan et al. 2000; and Fig. 2 B). Although it is known that the β₁ subunit increases P _o in the presence of Ca²⁺ _i by retaining the gating in the bursting states (Nimigean and Magleby 1999), the method of coupling between the α and β₁ subunits is not yet established. One possibility is that the functional coupling between α and β₁ subunits requires Ca²⁺ _i (Meera et al. 1996). To test this, we examined the effects of the β₁ subunit on the gating in the virtual absence of Ca²⁺ _i for comparison to its effects when Ca²⁺ _i is present. In both the absence and presence of Ca²⁺ _i, the β₁ subunit increased burst duration ∼20-fold, by increasing both mean open time and the mean number of openings per burst (Fig. 2). The β₁ subunit-induced increase in burst duration increased P _o in both the absence and presence of Ca²⁺ _i (Fig. 2A and Fig. B). Since the β₁ subunit still imposed its dominant effects on channel gating in the absence of Ca²⁺ _i when the channel was unliganded, it follows that neither Ca²⁺ binding nor Ca²⁺-dependent steps are required for the dominant action of the β₁ subunit.

If the dominant action of the β₁ subunit does not require Ca²⁺-dependent processes, then the paradoxical possibility arises that the mechanism underlying the β₁ subunit-induced increase in Ca²⁺ sensitivity also does not require Ca²⁺ _i. To explore this possibility, we examined to what extent an assumption of Ca²⁺-independent action could account for the leftward shift that gave rise to the increased Ca²⁺ sensitivity. We found that 80% of the leftward shift could be accounted for by assuming that the only effect of the β₁ subunit was to increase burst duration ∼20-fold, independent of Ca²⁺ _i (Fig. 2A and Fig. C, dashed lines). Thus, a Ca²⁺-independent mechanism was sufficient to account for 80% of the increased Ca²⁺ sensitivity induced by the β₁ subunit.

The remaining 20% of the shift in Ca²⁺ sensitivity reflects a Ca²⁺-dependent mechanism. The β₁ subunit increased the durations of the gaps between bursts approximately threefold in the absence of Ca²⁺ _i, and this increase disappeared (and the gap durations became slightly briefer based on the fitted lines) as Ca²⁺ _i was raised sufficiently to just increase channel activity (Fig. 2 D). When this Ca²⁺-dependent effect of the β₁ subunit on gaps between bursts was taken into account, the remaining 20% of the leftward shift in Ca²⁺ sensitivity could be accounted for (Fig. 2A and Fig. B, dotted lines).

Whatever the mechanism for the Ca²⁺ dependence of the β₁ subunit on the durations of gaps between bursts at the transition between 0 and low Ca²⁺ _i, it seems unlikely to reflect a β₁ subunit-induced increase in Ca²⁺ _i binding rates, as the β₁ subunit then had little effect on the durations of the gaps between bursts for further increases in Ca²⁺ _i that decreased the durations of gaps between bursts two orders of magnitude (Fig. 2 D). This relative lack of effect of the β₁ subunit on the gaps between bursts in the presence of Ca²⁺ _i has been described previously (Nimigean and Magleby 1999) and suggests that the β₁ subunit does not alter the Ca²⁺-dependent transitions that dominate the gaps between bursts in the presence of Ca²⁺ _i. Since gaps between bursts are present both in the absence and presence of Ca²⁺ _i, their durations are determined by both Ca²⁺-independent and -dependent transitions. Consequently, a large increase in the rate constants for the Ca²⁺-dependent transitions as Ca²⁺ _i is increased could mask the effects of the β₁ subunit on the Ca²⁺-independent transitions involved in lengthening the gaps between bursts in 0 Ca²⁺ _i, without directly affecting such transitions.

Our finding that the β₁ subunit was always functionally coupled to the α subunit, independent of Ca²⁺ _i (Fig. 1 Fig. 2 Fig. 3 Fig. 4), differs from that of Meera et al. 1996, who suggest that the functional coupling is exquisitely modulated by Ca²⁺, with Ca²⁺ ions switching the α+ β₁ complex into a functionally coupled state. This difference in conclusions could arise from a number of factors. First, our experiments used single-channel recording, which allowed high resolution analysis at very low P _os, while their experiments used macro currents, where activity at low P _o would be more difficult to study. Using single-channel recording, we observed a 10-fold increase in P _o in 0 Ca²⁺ _i in the presence of the β₁ subunit (from 0.0002 to 0.002 at + 30 mV), while they reported no change in P _o under similar 0 Ca²⁺ _i. Second, we directly measured the effects of the β₁ subunit on the gating in 0 Ca²⁺ _i, while they estimated the effects from the projected voltages required for half activation (V_0.5) in 0 Ca²⁺ _i. Third, our experiments used bovine β₁ and mouse α subunits, while theirs used human β₁ and α subunits. The difference in primary structure of the β₁ subunits (84% homology) and α subunits (96% homology) in the two studies might lead to different mechanisms of modulation by the β₁ subunit.

The contributions of these three factors to the differences in conclusions are not clear, but the most likely explanation is that the β₁ subunit has pronounced effects on P _o in 0 Ca²⁺ _i at moderate depolarized potentials, as we observed, while having little effect on P _o at large depolarizations, as used by Meera et al. 1996 to determine V_0.5 in 0 Ca²⁺ _i. Such an explanation requires that the effect of the β₁ subunit on increasing P _o be weakly voltage dependent, with depolarization decreasing the magnitude of the effect. Support for this possibility comes from the voltage-dependent trend in our data in P _o, mean burst duration, and mean open time (Fig. 4A, Fig. B, and Fig. D). Projections of our data suggest that the effects of the β₁ subunit on P _o may become negligible at large depolarized potentials, and may even reverse. Further support for this possibility comes from observations of Ramanathan et al. 2000 that the β₁ subunit has little effect on estimates of V_0.5 in low Ca²⁺ _i, and observations of Cox, D.H., and R.W. Aldrich (personal communication) that the effect of the β₁ subunit on increasing conductance in macropatches becomes negligible at subnanomolar Ca²⁺ _i as the potential approaches +150 mV, after which the β₁ subunit decreases the conductance at potentials greater than +150 mV.

We did find that the β₁ subunit had a Ca²⁺-dependent component, but this component accounted for only 20% of the increased Ca²⁺ sensitivity, and arose mainly from a Ca²⁺-dependent switching off of the β₁ subunit-induced lengthening of the gaps between bursts (Fig. 2 D). Consistent with our observations of functional coupling in 0 Ca²⁺ _i, Meera et al. 1996 found that the β₁ subunit slowed the activation kinetics threefold in 0 Ca²⁺ _i, just as might be expected from the threefold increase in the duration of gaps between bursts that we observed with the β₁ subunit in 0 Ca²⁺ _i. Other studies have also reported a β₁-induced slowing in activation and deactivation kinetics over a range of Ca²⁺ _i (Dworetzky et al. 1996; Tseng-Crank et al. 1996; Ramanathan et al. 2000).

If the β₁ subunit is always coupled, then it should be possible to predict the effects of the β₁ subunit on the kinetic parameters in the absence of Ca²⁺ _i by projecting data obtained in the presence of Ca²⁺ _i to the abscissa at 0 Ca²⁺ _i. Such projections are difficult on the log–log plots used in this paper to emphasize the kinetics at low Ca²⁺ _i, because a value of 0 Ca²⁺ _i is never reached on a log axis. However, such projections can be made from the semilogarithmic plots presented in our previous study. For example, the predicted value of burst duration for α+β₁ and α channels obtained by projecting a linear regression line to 0 Ca²⁺ _i from the data obtained from 15 to 1.8 μM Ca²⁺ _i was 16 and 0.7 ms, respectively (Nimigean and Magleby 1999; Fig. 4 E). These values are in agreement with the limiting values of mean burst duration of 15 and 0.7 ms observed in the present study as Ca²⁺ _i approached 0 (Fig. 2 C, dashed and continuous lines). Thus, the 23-fold increase in burst duration determined by projection is in agreement with the 21-fold increase in burst duration determined by the limiting values in 0 Ca²⁺ _i. Similar agreement in projected and limiting results for the effect of the β₁ subunit was obtained for mean open time and the mean number of openings per burst.

The direct observations in Fig. 1 and Fig. 2, and the projected observations discussed above, indicate that the β₁ subunit exerts its characteristic effects of increasing P _o and mean burst duration through an increase in the mean open time and the number of openings per burst in Ca²⁺ _i so low that the channel is essentially unliganded. Consequently, since the β₁ subunit imposes its characteristic effects on channel gating in the absence of Ca²⁺ _i, it follows that the β₁ subunit is coupled to the channel in the absence of Ca²⁺ _i, and can generate its signature effects without changing any Ca²⁺-binding rates. Furthermore, the observation on the double logarithmic plots in Fig. 2 A that both the α and α+β₁ channels appear to have similar critical Ca²⁺ _i for initiating the Ca²⁺-dependent activation (between 0.18 and 0.9 μM Ca²⁺ _i) indicates that the β₁ subunit may have relatively little effect on the initial Ca²⁺-binding rates, for if it had a pronounced effect, the Ca²⁺-induced increase in P _o (and underlying changes in the other gating parameters) should occur at appreciably lower Ca²⁺ _i for α+β₁ channels than for α channels. Cox and Aldrich 2000 have also suggested that the β₁ subunit has little effect on the affinity of the channel's Ca²⁺-binding sites.

Consistent with a lack of increase in Ca²⁺-dependent rate constants, observations in our previous study indicate that the β₁ subunit does not act by mimicking the effects of increased Ca²⁺ _i (Nimigean and Magleby 1999). Similar kinetic analysis in this present study showed that the β₁ subunit does not act by mimicking the effects of voltage, as increasing P _o with depolarization gave markedly different single-channel gating kinetics than increasing P _o with the β₁ subunit (Fig. 5). This finding, together with the observation that the voltage dependence of the single channel kinetic parameters is little affected by the β₁ subunit (Fig. 4), suggests that the β₁ subunit does not exert its major effects on gating over the examined range of voltages by changing the apparent voltage sensitivity of the channel. This conclusion is in agreement with previous studies that found little difference in the voltage sensitivity between α and α+β₁ channels (McManus et al. 1995; Dworetzky et al. 1996; Meera et al. 1996; Tseng-Crank et al. 1996).

The observations in this present study indicate that the major effect of the β₁ subunit is to produce approximately parallel shifts (on logarithmic coordinates) in the magnitudes of the examined bursting parameters, when compared with α channels (Fig. 2 and Fig. 4). Such parallel shifts on logarithmic coordinates are consistent with a multiplicative (gain) effect of the β₁ subunit on the examined parameters, and this gain effect was observed over three orders of magnitude of P _o, independent of whether the channel was activated by Ca²⁺ _i or by voltage (Fig. 6). How might such a gain effect on the bursting parameters occur?

The gating of BK channels is described by a model comprised of five parallel subschemes, each with five open and five closed states, in which the subschemes differ from one another by having either 0, 1, 2, 3, or 4 Ca²⁺ _i bound to the states in each subscheme (Rothberg and Magleby 1999). Recent data obtained for the gating of α channels in 0 Ca²⁺ _i by Horrigan et al. 1999, Horrigan and Aldrich 1999, and Talukder and Aldrich 2000 are also consistent with this two-tiered model. For discussion purposes, this complex gating mechanism can be reduced to the simplified Fig. 2, where gaps (n) represent the collection of closed states that generate the gaps between bursts, bursts (n) represent the collection of open and closed states that generate the bursts, k(n) is the forward rate constant for transitions from gaps to bursts, k(-n) is the backward rate constant for leaving bursts, and n, with values of 0, 1, 2, 3 and 4, represents the number of Ca²⁺ _i bound to the states. Note that the rate constants k(n) and k(-n) are composite rate constants that reflect all of the rate constants involved in generating gaps and bursts: k(n) also includes the rate constants among the collection of closed states that generate the gaps, and k(-n) also includes the rate constants among the collection of open and closed states that generate the bursts.

Scheme S2.

In 0 Ca²⁺ _i, none of the states involved in gating would have bound Ca²⁺. Binding Ca²⁺ would then increase P _o by altering the rate constants to decrease the durations of gaps and to increase the durations of bursts, and this would be the case for both α and α+β₁ channels (Fig. 2).

Since the β₁ subunit had little effect on the minimal number of kinetic states entered during gating in 0 Ca²⁺ _i (Fig. 7) or in the presence of Ca²⁺ _i (Nimigean and Magleby 1999), the most parsimonious mode of action of the β₁ subunit would be to modulate gating through changes in one or more of the transition rates among the existing states. Which transitions are altered? The ∼20-fold increase in burst duration, independent of Ca²⁺ _i (Fig. 2 C), suggests that the β₁ subunit slows the rate constant k(-n) of ∼20-fold, and this would be the case independent of the number of bound Ca²⁺ _i, where n = 0–4. Such a slowing would act to retain the gating in the bursting states, increasing P _o. An explanation for the apparent multiplicative (gain) effect of the β₁ subunit now becomes apparent. Whatever the burst duration (which increases with Ca²⁺ _i), the β₁ subunit increases burst duration another ∼20-fold by slowing k(-n) ∼20-fold, independent of bound Ca²⁺ _i.

Whereas the β₁ subunit increases burst duration ∼20-fold, independent of Ca²⁺ _i, its smaller effect of increasing the durations of the gaps between bursts approximately threefold was only observed in 0 Ca²⁺ _i (Fig. 2 D). A threefold increase in the durations of the gaps between bursts in 0 Ca²⁺ _i, but not in higher Ca²⁺ _i, would arise if the β₁ subunit selectively slowed k(n), where n = 0, threefold, while having little effect on k(n) where n = 1–4. If this were the case, Ca²⁺ _i would switch off the lengthening effect of the β₁ subunit on gap duration. Alternatively, the addition of Ca²⁺ _i might remove the lengthening effect of the β₁ subunit by driving the gating away from the altered transition pathways involved in the lengthening, or by selectively changing these pathways. Under conditions of 0 Ca²⁺ _i, the ∼20-fold increase in burst duration overrides the smaller threefold increase in gap duration, giving rise to the observed 10-fold increase in P _o with the β₁ subunit in 0 Ca²⁺ _i. In the presence of Ca²⁺ _i, the β₁ subunit no longer lengthens the duration of the gaps between bursts (and may shorten them slightly), so the increase in burst duration can give rise to an even greater increase in P _o, which becomes limited as P _o saturates near its maximum of 0.96.

As indicated above, the β₁ subunit only slows k(n) in the absence of Ca²⁺ _i when n = 0. The presence of Ca²⁺ _i switches off the inhibitory effect of the β₁ subunit in 0 Ca²⁺ _i of increasing gap duration. This switching occurs over a range of Ca²⁺ _i between 0.2 and 2 μM (Fig. 2 D). This Ca²⁺-dependent removal of the inhibition accounted for ∼20% of the shift in the apparent Ca²⁺ sensitivity, while the Ca²⁺-independent increase in burst duration accounted for the other 80% of the shift in apparent Ca²⁺ sensitivity (Fig. 2A and Fig. B).

Conclusion

Ca²⁺ _i is not required for the coupling of the β₁ subunit to the BK channel. In the absence of Ca²⁺ _i, the β₁ subunit increases mean burst duration ∼20-fold and also increases the duration of the gaps between bursts approximately threefold. The increase in burst duration facilitates channel activity and the increase in gap duration inhibits channel activity, for an increase in P _o of ∼10 fold in 0 Ca²⁺ _i. The β₁ subunit-induced ∼20-fold increase in mean burst duration is Ca²⁺ independent, is retained over wide ranges of Ca²⁺ _i and voltage, and accounts for 80% of the increased Ca²⁺ sensitivity associated with the β₁ subunit. The β₁ subunit-induced approximately threefold increase in the duration of gaps between bursts is switched off (inhibited) by the addition of Ca²⁺ _i. This removal of the β₁ subunit-induced inhibition accounts for the remaining 20% of the increased Ca²⁺ sensitivity associated with the β₁ subunit. Thus, the major effect of the β₁ subunit on increasing Ca²⁺ sensitivity occurs through changes in Ca²⁺-independent rate constants.