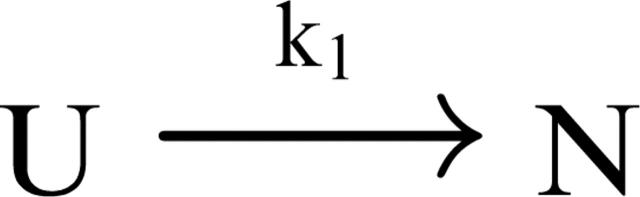Role of unfolded state heterogeneity and en-route ruggedness in protein folding kinetics

Abstract

In order to improve our understanding of the physical bases of protein folding, there is a compelling need for better connections between experimental and computational approaches. This work addresses the role of unfolded state conformational heterogeneity and en-route intermediates, as an aid for planning and interpreting protein folding experiments. The expected kinetics were modeled for different types of energy landscapes, including multiple parallel folding routes, preferential paths dominated by one primary folding route, and distributed paths with a wide spectrum of microscopic folding rate constants. In the presence of one or more preferential routes, conformational exchange among unfolded state populations slows down the observed rates for native protein formation. We find this to be a general phenomenon, taking place even when unfolded conformations interconvert much faster than the “escape” rate constants to folding. Dramatic kinetic deceleration is expected in the presence of an increasing number of folding-incompetent unfolded conformations. This argues for the existence of parallel folding paths involving several folding-competent unfolded conformations, during the early stages of protein folding. Deviations from single-exponential behavior are observed for unfolded conformations exchanging at comparable rates or more slowly than folding events. Analysis of the effect of en-route (on-path) intermediate formation and landscape ruggedness on folding kinetics leads to the following unexpected conclusions: (1) intermediates, which often retard native state formation, may in some cases accelerate folding, and (2) rugged landscapes, usually associated with stretched exponentials, display single-exponential behavior in the presence of late high-friction paths.

Protein folding involves the transition of several unfolded conformations to a native state bearing a much smaller degree of conformational heterogeneity. In-depth knowledge about folding mechanisms has been arising in recent years from investigations directly relating experimental observations to computational predictions (Ansari et al. 1992; Muñoz et al. 1997; Garcia-Mira et al. 2002; Snow et al. 2002; Ma and Gruebele 2005; Naganathan et al. 2005).

Sorting out folding mechanisms

Folding experiments on small water-soluble single-domain proteins often lead to single-exponential kinetics for native state formation. Less frequently, multiple- or stretched-exponential traces are observed (Gillespie and Plaxco 2004; Ma and Gruebele 2005; Naganathan et al. 2005). As often remarked in the literature (Baldwin 1995; Zwanzig 1997; Ozkan et al. 2002; Gillespie and Plaxco 2004), single-exponential kinetics are compatible with both a simple two-state process and more complex mechanistic schemes. Moreover, multiple- or stretched-exponential kinetics may either be due to the presence of folding intermediates or to downhill diffusion-driven folding (Gruebele 2002). The above mechanistic uncertainties pose serious dilemmas to the unequivocal interpretation of experimental folding data. Single-molecule folding experiments (Deniz et al. 2000; Talaga et al. 2000; Schuler et al. 2002; Lipman et al. 2003) show promise to ultimately help differentiate mechanistic hypotheses. However, a systematic analysis of the expected folding kinetics in bulk solution for different key types of energy landscapes is urgently needed. This will provide experimentalists with a better framework to guide data interpretation and aid in the rational design of ad hoc experiments targeting the discrimination of different mechanistic possibilities. Since this type of analysis has been missing to date, we have elected to systematically investigate the predicted protein folding kinetics in response to variations of a broad range of parameters (e.g., rate constants and unfolded state conformations). This analysis has been carried out for several classes of folding models, representative of plausible landscapes proposed in past experimental and computational studies (Gillespie and Plaxco 2004). The definition of kinetic criteria for different classes of folding behaviors and the identification of a number of unexpected trends have emerged.

Role of unfolded state heterogeneity

A key issue for the proper evaluation of folding kinetics is the nominal starting point of the process, i.e., the unfolded state (Dill and Shortle 1991). Recent experiments at equilibrium have provided evidence for a highly dynamic unfolded state (Dyson and Wright 2002, 2004) bearing distinct loosely structured conformational states (Chattopadhyay et al. 2005; Pletneva et al. 2005), under denaturing conditions. Data collected on reduced ribonuclease A, representative of the putative unfolded state populated under native-like conditions (i.e., the most relevant species for folding in a native environment), also indicate the presence of a wide distribution of conformational states (Navon et al. 2001). On the other hand, computational studies by Dill and coworkers (Ozkan et al. 2002) have explicitly shown that even complex folding mechanisms may lead to an observed single-exponential behavior in the presence of multiple unfolded state conformations and a unique native state. Creighton (1988^{, 1994)}) pointed out that the available experimental evidence in protein folding is consistent with the presence of fast conformational changes among several unfolded state conformations, preceding global folding events. Following this lead, Zwanzig (1997) has shown that the fast pre-equilibration of multiple unfolded state conformations relative to folding is a natural consequence of statistical considerations on a simple model encompassing many interconverting unfolded states, some of which escape via gateway pathways to a thermodynamically more stable native conformation. Under these circumstances, a single-exponential apparent two-state behavior is predicted. His demonstration is based on the assumption that there is a statistically higher likelihood of unfolded state interconversion relative to “escape” to the native state. This conclusion applies to the case of identical rates of unfolded state interconversion and escape to folding, for a landscape with a selected number of escape routes. However, the expected folding behavior under more general conditions, not necessarily fulfilling these assumptions, is still open to investigation. The analysis presented here applies to single-domain soluble proteins devoid of kinetic complications such as unusually high barriers between some particular unfolded states. These types of barriers, usually detected when proline isomerization in the unfolded state plays an important role, lead to trapping for long periods of time and obscure the intrinsic kinetics of folding. For simplicity, we will assume a uniform population of initial unfolded conformations and equal exchange rates among all the unfolded species. However, several regimes, comprising different unfolded state exchange rates relative to folding rates, will be analyzed.

Role of intermediates and landscape ruggedness

The role of kinetic intermediates in folding has been controversial (Kim and Baldwin 1982, 1990; Bryngelson et al. 1995; Wolynes et al. 1995). Proteins with > ~110 amino acids are usually more stable than smaller proteins and often fold by populating one or more kinetic intermediates (Jackson 1998). A very fast kinetically unresolvable “burst phase” followed by slower folding has often been experimentally observed in folding experiments. When combined with additional biophysical evidence, the presence of folding intermediates has been confirmed (Jennings and Wright 1993; Evans and Radford 1994; Capaldi et al. 1999). The inability to kinetically resolve early folding stages led to ambiguities regarding the nature of the folding intermediates. Although the “obligatory” nature of folding intermediates can be established (Capaldi et al. 1999; Tsui et al. 1999), under fast pre-equilibrium conditions, off-path routes cannot be discriminated from on-path routes leading to intermediate formation (Roder 2004). However, the recent availability of ultrafast mixing devices has allowed further kinetic resolution, leading to the direct identification of folding intermediates for staphylococcal nuclease (Walkenhorst et al. 1997) and the immunity protein IM7 (Capaldi et al. 2001) as on-path species.

Computational studies best represented by the diffusion–collision model (Karplus and Weaver 1976, 1994) have highlighted the presence of multiple intermediates generated along multiple parallel paths. More recently, the traditional notion of discrete intermediates has been replaced by a downhill folding scenario in the presence of energy landscape ruggedness (Bryngelson et al. 1995; Wolynes et al. 1995). This manifests itself as multiple transiently kinetically trapped intermediates, responsible for folding retardation. Experimental evidence for ruggedness has been hard to gather (Gillespie and Plaxco 2004), although some reports are now available (Sabelko et al. 1999; Nevo et al. 2005).

The significance of intermediates and ruggedness in protein folding is not well understood yet. For instance, it is not clear whether folding intermediates are productive species, which help achieve the native conformation, or whether they are undesired “mistakes.” This report focuses on analyzing how the population of native state and en-route folding intermediates are predicted to vary for different limiting classes of rugged folding landscapes, upon modulating values of relevant kinetic parameters. As already mentioned above, we also address the role of unfolded state heterogeneity for landscape devoid of kinetic intermediates. The simplified kinetic models analyzed here are intended to capture some essential and experimentally testable features of protein folding events under limiting conditions.

Results and Discussion

Unfolded state conformational heterogeneity and folding kinetics

The easiest way to model the complex conformational space of a protein that folds without populating transient intermediates is to start from the simplest two-state kinetic scheme shown below

Scheme 1.

where k₁ is the microscopic rate constant for folding, and U and N are the unfolded and native states, respectively. It is important to note that k₁ and the other rate constants used here are intended to fit the mathematical form of Kramer’s theory, either in the presence or the absence of free energy barriers. Experimental detection of single-exponential kinetics for native state formation follows from Scheme 1, according to the expression

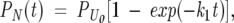(1)

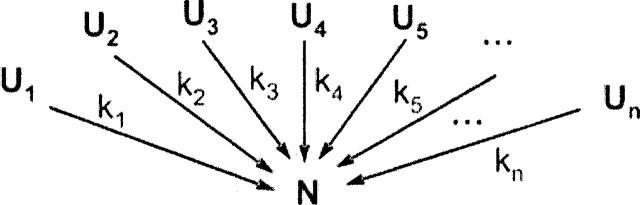
where P_N(t) and P_U0denote the populations of native and initial unfolded state, respectively. In the realistic case of U composed of several microscopic states, e.g., distinct polypeptide conformations, the above simplified view of protein folding is inaccurate, in general. As summarized in the introduction, it is clear that the unfolded state is highly dynamic and comprises a distribution of distances for many of the possible intra-nuclear interaction pairs, pointing to the presence of multiple conformations. Given a heterogeneous unfolded state, one may postulate the existence of multiple parallel folding pathways, supported by both computations (Brooks et al. 1998; Brooks 2002) and experiments (Jackson 1998; Nguyen et al. 2003). Therefore, a more plausible modified version of the two-state folding kinetics is the scheme below, which considers folding as proceeding from a number of unfolded states, from U₁ to U_n.

Each of the unfolded states represents a microscopic state, i.e., a particular region of configuration space. The different conformations may either belong to the same thermodynamic basin or be separated from each other by significant barriers. Since the “escape” rates to folding for each of these conformations is different, according to the above scheme, it makes sense to treat the unfolded conformations separately, from the kinetic standpoint. A peculiar aspect of this model is that the different conformations are not able to mutually interconvert, under the relevant folding conditions. For simplicity, the folding escape reactions are regarded as effectively irreversible under the strongly native-like conditions considered here. Scheme 2 gives rise to multiple exponential kinetics for N formation, according to

Scheme 2.

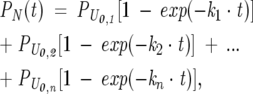(2)

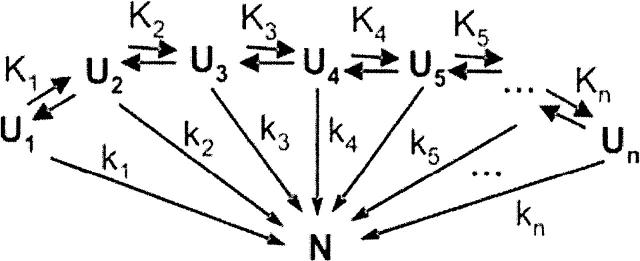
where k₁…k_n represent the microscopic rate constants for folding starting from the P_U0,i…P_U0,n unfolded populations. NMR data on the unfolded state ensemble (Yao 2001) are consistent with the presence of conformational exchange among the different microscopic states. This is an important issue that needs to be taken into account, given that the relative values of these conformational interconversions and folding rates may strongly bias folding to specific paths. Most importantly, this may result in different experimentally observable protein folding rates. A more realistic folding mechanism taking the above into account and assuming folding to be slower than unfolded state conformational interconversion, therefore, assumes the form

where K₁…K_n represent the equilibrium constant for the interconversion among different unfolded state conformations. The unfolded conformations are regarded as mutually exchanging with rate constants k_inter-U. Under the limiting condition of fast pre-equilibrium among the unfolded states, relative to folding (i.e., k_i ≪ k_inter-U), an expression for the formation of N can be derived analytically from the elementary kinetic rate laws for the different steps in Scheme 3, leading to

Scheme 3.

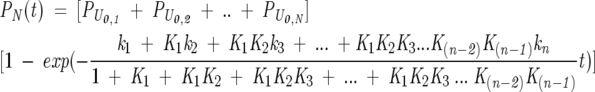(3)

The argument of the exponential in Equation 3 is composed by a time-independent term, serving as an apparent complex rate constant, multiplying the time variable t. Therefore, a folding process involving rapidly interconverting unfolded state conformations is expected to give rise to single-exponential kinetics, just like the much simpler kinetic Scheme 1.

Under the above conditions, though, the observed rate constant for folding is fundamentally different from, and it should not be confused with, the microscopic folding rate constant for folding through specific paths. The observed rate constant for the single-exponential folding event represented by Equation 3, under fast equilibrium conditions, is a complex function of rate and equilibrium parameters. Two important implications of the above are that (1) one should be cautious in interpreting experiments yielding single-exponential kinetics in that the observed rate constant does not necessarily reflect the value corresponding to an individual folding route, and (2) under fast pre-equilibrium conditions, it is impossible to determine the microscopic rate constants for different parallel folding routes by a simple experiment in bulk solution unable to resolve the different relevant kinetic phases.

The above result is consistent with the theoretical treatment by Zwanzig (1997). However, Equation 3 is more general in that it does not require that the number of escape routes to the native state be smaller than the number of unfolded conformations (i.e., the total number of possible folding paths).

A fair question at this point is whether the fast pre-equilibration of unfolded state conformations relative to folding is an acceptable approximation to properly describe the folding of small proteins in solution. This is presently a difficult question to answer, in the absence of a sufficient amount of experimental data on microscopic rate constants for conformational interconversion of unfolded state populations and elementary folding events. NMR experiments on denatured (Dyson and Wright 2002) and natively unfolded proteins (Dyson and Wright 2005) provide an upper limit to the expected average exchange rates. These experiments show that, under refolding conditions and at room temperature, the backbone amide protons in the unfolded state ensemble exchange at an average rate faster than the chemical shift difference between the different conformations, i.e., faster than ~10 msec. This conclusion is supported by backbone dynamics NMR data on the unfolded state (Yao 2001; Schwarzinger et al. 2002), which indicate the presence of conformational exchange on a wide range of timescales, ranging from picosecond to millisecond. On the other hand, the extremely compact nature of the unfolded protein chain observed in aqueous solution under native conditions (Flanagan et al. 1992; Lietzow et al. 2002) suggests that unfolded state interconversion rates might be even slower than generally expected. While more data from single-molecule folding and unfolded state conformational dynamics are being gathered (Deniz et al. 2000; Lipman et al. 2003), it is important to investigate the expected kinetics of folding under a spectrum of exchange rates and more general assumptions than those adopted by the above models.

Modeling kinetic folding pathways for complex energy landscapes

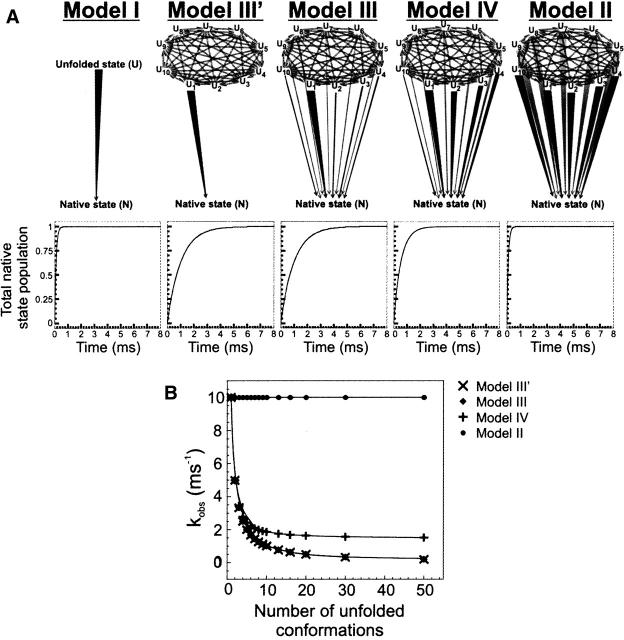
The expected behavior of an unfolded ensemble subject to folding conditions has been examined. The models are general in that they do not necessarily require fast pre-equilibration of unfolded state conformations. Different scenarios for available folding routes have been analyzed. The two-state folding model discussed above (Scheme 1) encompasses a unique path and, in most cases, does not adequately describe folding. A model landscape involving multiple unfolded states, analogous to Scheme 2, is also possible. An alternative model envisions a generalized version of Scheme 3, where all the unfolded conformations mutually interconnect via reversible steps. For simplicity, folding is regarded here as a predominantly irreversible process with no significant back rates, as in folding experiments under native-like conditions. The actual models utilized for the computations are shown in Figure 1. Model I follows the simple two-state kinetics, and Model II includes different mutually interconverting unfolded states. Each unfolded state is in reversible exchange with all the others. For simplicity, we have limited the number of unfolded states to 10 (U₁…U₁₀). All the microscopic folding rate constants are identical, according to this model, as denoted by the identical line thickness. Model III is similar to Model II except that one strongly preferred pathway exists, with a folding rate constant much faster than the others, as indicated by the thickest vertical line in the figure. Finally, Model IV comprises a distribution of rate constants for folding.

Figure 1.

Kinetic models examined in this work for the folding of proteins that do not populate kinetic intermediates. U, U_1…10, and N denote the total unfolded state population, the individual unfolded subpopulations, and the native state, respectively. The thickness of the lines for the folding events correspond to the value of the respective rate constants.

Role of unfolded state interconversion rates

The four models introduced in the previous section have been utilized to test for the role of unfolded state interconversion rates in folding. Figure 2 illustrates the results of folding simulations for the model landscapes I to IV. The representative rate constants used in the different cases are reported in the figure legends and in Table 1. The folding rate constant pertaining to the fastest step has been set to 10⁴ sec⁻¹ for landscapes I to IV. This is a typical value for the experimentally observable folding rate of a small globular protein in aqueous solution (Jackson 1998). The two-state Model I, which serves as a reference for the more complex landscapes, gives rise to fast folding and single-exponential kinetics for the formation of native structure. Model II, which entails multiple unfolded states of equal starting concentration (one-tenth of the total unfolded state concentration) and equivalent parallel pathways for native state formation, shows that the time course of native state population buildup is identical to that for Model I. This is true regardless of the rate of mutual interconversion of the unfolded state conformations. Therefore Models I and II are kinetically indistinguishable in terms of overall flux for native state formation.

Figure 2.

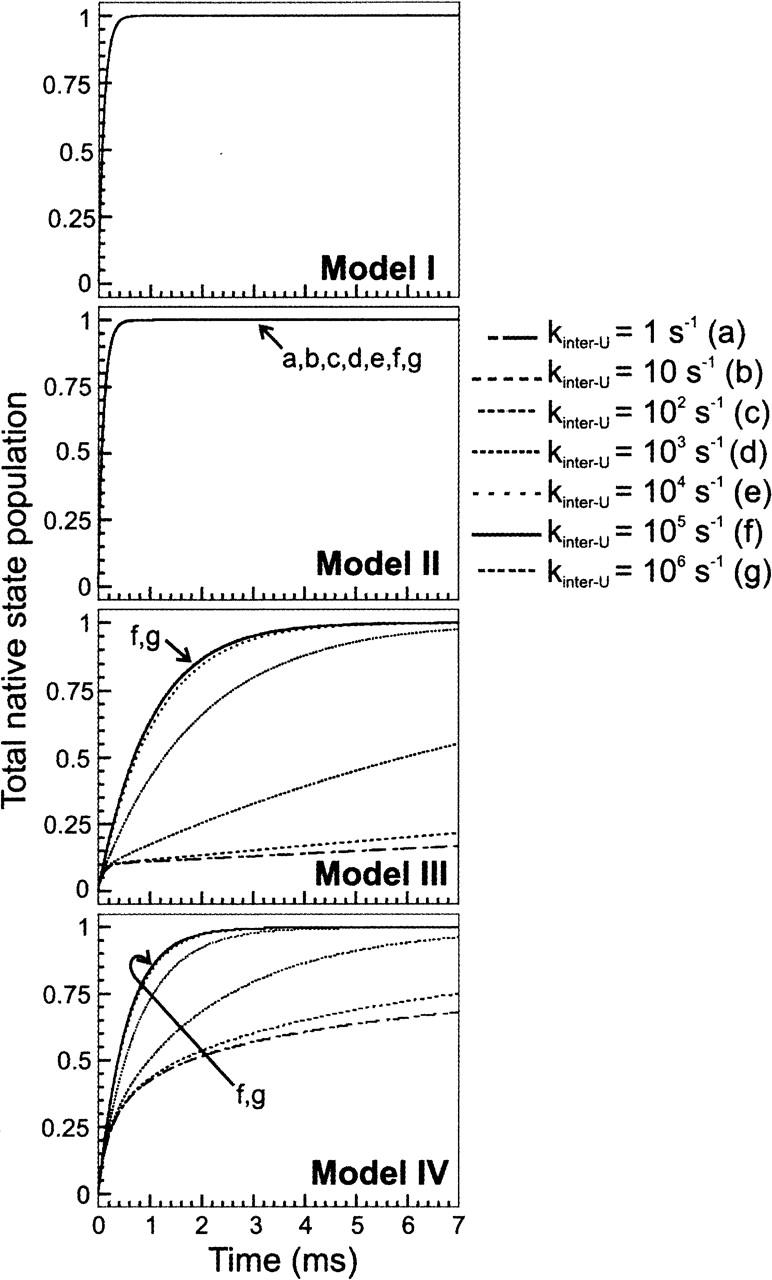
Time course for protein folding according to the kinetic Models I through IV, defined in Figure 1. The rate constants for the folding events in Models I to IV are listed in Table 1. The rate constants for unfolded state interconversion are as labeled on the figure. The initial total unfolded state population was set to one. Initial unfolded state populations for Models II to IV were equally partitioned among the different unfolded states.

Table 1.

Folding rate constants for the simulations in Figure 2

	Kinetic model
Rate constants (sec−1)	I	II	III	IV
kU1N	104	104	104	104
kU2N		104	10	4.6 × 103
kU3N		104	10	2.2 × 103
kU4N		104	10	103
kU5N		104	10	4.6 × 102
kU6N		104	10	2.2 × 102
kU7N		104	10	102
kU8N		104	10	46
kU9N		104	10	22
kU10N		104	10	10

Model III, which comprises one preferential pathway for folding, shows that, regardless of the rates for unfolded state interconversion (i.e., k_inter-U, kept identical for the whole unfolded state ensemble, for exchange in either direction), folding is slower than in the case of Models I and II. This result highlights the importance of conformational heterogeneity in the unfolded state ensemble in the presence of a dominant escape route to the folded state. Under these conditions, the mere existence of this heterogeneity has the property of slowing down the folding process. Folding is fastest in the case when k_inter-U is much greater than the largest folding rate constant (k_i,fastest) defining the preferred folding pathway. As k_inter-U progressively decreases to become equal to the fastest folding rate (k_inter-U = k_i,fastest = 10⁴ sec⁻¹), the overall formation of native state gets slower. In the limiting case of k_inter-U ≪ k_i,fastest = 10⁴ sec⁻¹, formation of native state is considerably slowed down, and it clearly shows a biphasic behavior. The amplitude of the fastest kinetic phase is roughly one-tenth of the total amplitude, indicating that the fastest population to fold is the one corresponding to the U₁ unfolded state basin, followed by the remaining unfolded state population in slow exchange with U₁.

A similar behavior is observed for Model IV, which includes a wide distribution of folding rates. These contribute to a general speeding up of folding relative to Model III, as expected. The limiting trace “g” corresponds to the case of distributed folding pathways under fast pre-equilibration of the starting unfolded state population. Upon comparing the “g” traces for Models III and IV, it is noticeable how the presence of more fast routes of escape to the folded state has the overall effect of speeding up folding.

Figure 3A provides a schematic summary of the kinetic effect of unfolded state heterogeneity on folding time course. The calculations were carried out for fast pre-equilibration relative to folding, with the understanding that slower unfolded state conformational exchange would only further enhance the magnitude of the observed kinetic effects. Briefly, comparison with folding from one unique unfolded state configuration (Fig. 3A, Model I), shows that, surprisingly, the mere presence of a heterogeneous unfolded state conformational ensemble has the effect of slowing down folding, in the presence of a unique (Fig. 3A, Model III′) or a predominant (Fig. 3A, Model III) folding pathway. This effect is not due to kinetic trapping of unfolded populations, since it is present even when the exchange rates k_inter-U for unfolded state conformational interconversion tend to infinity (data not shown). As seen in Figure 2, slower k_inter-U values further slow down folding. In the case of a distribution of folding rate constants, simulated in Model IV, the observed rates are slightly faster. Model II of Figure 3A shows that, for landscapes having all identical parallel folding paths, even in the presence of unfolded state conformational heterogeneity, fast folding is reinstated. This is true regardless of the k_inter-U rate constant values.

Figure 3.

(A) Illustration of the effect of multiple parallel folding pathways on predicted folding kinetics, according to five different kinetic models. Rapid interconversion of unfolded state populations is assumed. Folding rate constants and initial unfolded state populations were set to the same values as in Figure 2. Unfolded state interconversion rates were set to k_inter-U = 10⁶ sec⁻¹. (B) Effect of number of unfolded state conformations on the observed single-exponential kinetic rate constant for folding. Simulations have been run under identical conditions to those used in A except that the number of unfolded state microscopic states has been varied, as shown in the plot. The folding rate constants for Model IV, for different number of unfolded states, were determined according to Equations 5 and 6, as discussed in Materials and Methods.

Effect of number of unfolded conformations on folding kinetics

Figure 3B shows a plot of the expected variations in apparent single-exponential folding rates as a result of varying the number of effective microscopic unfolded states, corresponding to different conformations. Each of the unfolded conformations interconnects to all the others via reversible steps. The rate constants for interconversion among the different microstates have been set to be much greater than the microscopic rate constants for folding.

As shown in the plot of Figure 3B, the folding kinetics according to Model II do not depend on the number of unfolded state conformations, since all of the available microstates are able to escape to folded protein. However, both Models III and III′, which include a preferential path for conversion to native state, experience a dramatic retardation in folding as the number of unfolded conformations increases. Significant retardation is also observed for Model IV–type folding, which is characterized by a distribution of escape rates to folding. The above trend underscores the important fact that highly channeled protein folding, proceeding via a unique or restricted set of conformations, is kinetically very inefficient in the presence of a high number of “inactive” unfolded conformations, no matter how fast they mutually interconvert with the “active” unfolded population. The kinetic penalty is so high that, for the strongly channeled folding represented by Models III and III′, the expected folding rate constant rapidly approaches zero, for >10 unfolded conformations. This argument is in strong support of the presence of parallel pathways in the early stages of protein folding. Kinetic channeling may occur only at later stages, as demanded by the conformational search for the native state of individual proteins.

Flux through different folding routes

Further insights are provided by analysis of the flux for native state formation through individual folding routes for the main kinetic models examined so far. All the unfolded conformations are allowed to mutually interconvert reversibly at equivalent rates (k_inter-U = 10⁶ sec⁻¹) in all directions. Fast (relative to folding) pre-equilibrium conditions are satisfied. Model II is a prototype for folding proceeding through multiple kinetically equivalent parallel paths. The upper panel of Figure 4 shows that, for this model, all escape routes have an equivalent flux, which accounts for the folding of individual unfolded state populations. The total flux, equivalent to the Model II kinetic trace of Figure 2, arises from the sum of all fluxes through the individual paths.

Figure 4.

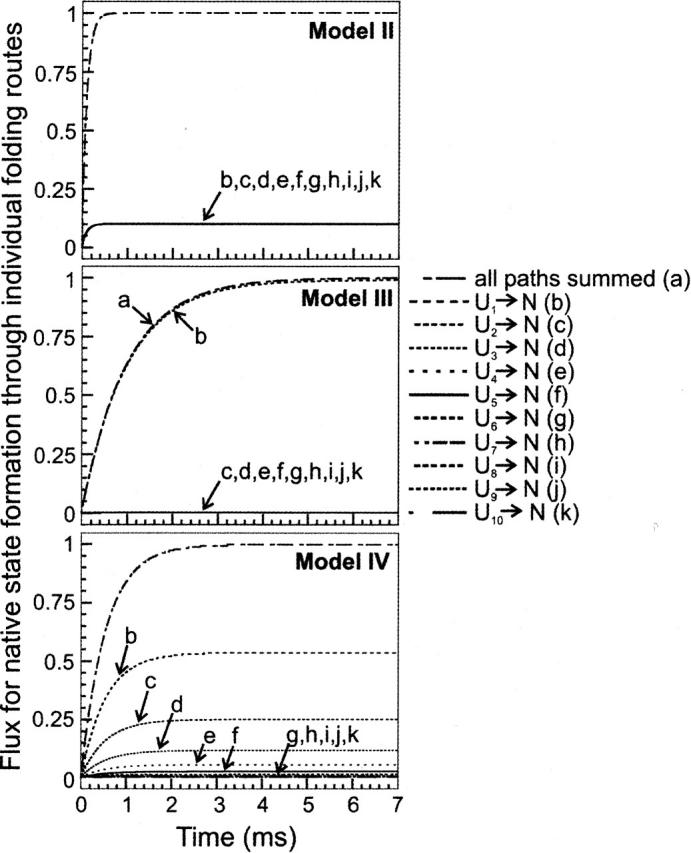
Flux for native state formation through individual folding routes corresponding to Models II (upper panel), III (middle panel), and IV (lower panel) of Figure 1. Folding rate constants and initial unfolded state populations were set to the same values as in Figure 2. Unfolded state interconversion rates were set to k_inter-U = 10⁶ sec⁻¹.

The fluxes for native state formation in Model III distinctly differ for the slow paths (Fig. 4, central panel), which have nearly zero flux, and the fast folding-competent path, which accounts for the large majority of the overall flux. This implies that, under these conditions, folding is effectively routed through the fast path. This model is not significantly different from the two-state scheme according to the “old” view of protein folding, except that the unfolded state heterogeneity, supported by both experimental data and computational predictions, is taken into account here.

Model IV landscapes, which include a diversified ensemble of folding routes, have more diverse profiles for the fluxes leading to native state (Fig. 4, lower panel). Interestingly, the individual routes arising from single unfolded state populations have different final flux amplitudes but similar apparent half-lives. The faster routes level off at higher amplitude than do the slower routes. This reflects the fact that faster folding routes are more efficient at recruiting unfolded state populations from other unfolded state basins, under fast pre-equilibrium conditions. As further detailed in the next section, an immediate consequence of the above is that Model IV landscapes give rise to overall single-exponential kinetics for the formation of native protein.

Single-exponential kinetics and deviations from exponentiality

Given that the unfolded state is experimentally known to be heterogeneous but the exchange rates for the different conformations are not known with certainty, it is important to establish under what conditions folding landscapes involving a heterogeneous unfolded state lead to single-exponential kinetic fits or to deviations from exponentiality. A truly two-state folding mechanism leads to accumulation of native protein according to the single-exponential Equation 1. This model serves as a reference for the calculations shown in Figure 5.

Figure 5.

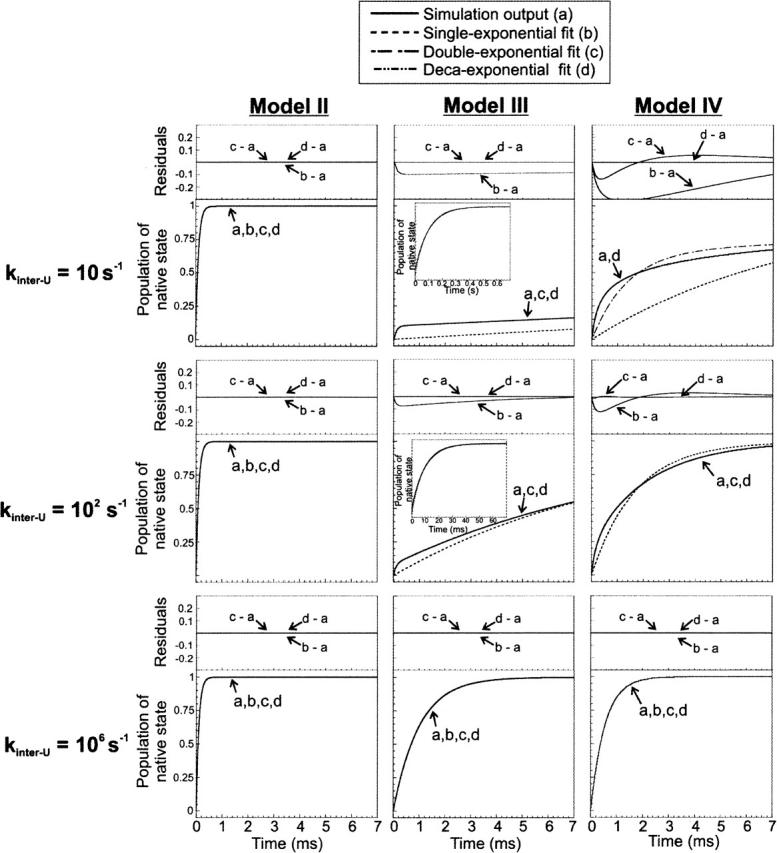
Deviation from exponentiality during the time course of native state formation for the folding of a protein according to kinetic Models II, III, and IV. Rate constants for folding are as in Figure 2, except for the rate constants for the interconversion of unfolded state conformations (k_inter-U), which are as indicated on the figure. The captions to the curves represent (a) kinetic simulation output, (b) single-exponential, (c) double-exponential, and (d) multiple (i.e., deca-) exponential fits to the simulated data. Plot residuals, i.e., differences between computation output and its matching curve fit, are shown above each panel.

As seen in the previous section, Model II landscapes have a uniform identical flux for native state formation. Figure 5 illustrates the fact that the overall flux always gives rise to a perfect single-exponential with negligible residuals at all time points. The overall rates for native state formation are identical to those of Model I, for identical folding rates for the individual pathways.

Model III mechanisms give rise to a perfect single-exponential only in the presence of fast exchange among the unfolded states. For slow exchange rates, folding proceeds according to double-exponential kinetics.

Under the limiting condition of no exchange among unfolded conformations, Model IV displays similar behavior to Model III landscapes, except that deviations from exponentiality are more pronounced and they extend to the whole time course, until equilibrium is reached. This highlights the fact that native state formation may proceed according to multiple exponential kinetics even in the absence of intermediates. Therefore multiple exponential time courses are not, per se, evidence for the presence of folding intermediates. This kinetic scenario fits the case of barrierless downhill folding in the presence of heterogeneous diffusional processes occurring on different timescales (Gruebele 1999). Alternatively, this situation is consistent with activated folding occurring in the presence of a heterogeneous transition state ensemble, due to multiple folding barriers giving rise to a distribution of folding rates (Gruebele 1999). In contrast to the above nonexponential behavior, it is important to notice that the kinetic heterogeneity disappears as the unfolded exchange rate constants become faster than those for folding. Under these conditions, a perfect single-exponential is observed. Interestingly, the presence of single-exponential folding does not depend on the fraction of active escape routes to native state, since it is observed for both kinetic models III and IV.

In summary, this set of results outlines the importance of the exchange rates among different unfolded state populations in protein folding. While single-exponential folding kinetics are quite common for small single-domain proteins < ~110 aminoacids, it is important to keep in mind that this type of kinetics may correspond to a variety of different mechanistic scenarios, as long as the interconversion rates among the different unfolded state populations are fast, relative to folding. Upon modulating the unfolded state exchange rates (k_inter-U) from large to small values, relative to folding, the observed kinetics evolve from single- to multiple-exponential for landscapes supporting either one predominant rate or a distribution of rates for folding. On the other hand, deviations from single-exponential behavior are only observed during the early stages of folding, in the case of landscapes characterized by one predominant folding path.

Folding in the presence of on-path intermediates

Stable proteins comprising > ~110 amino acids are known to convert to their native state via one detectable folding intermediate (Jackson 1998). This scenario is usually accompanied by apparent three-state kinetics. Under these circumstances, in bulk solution one monitors a weighted averaged spectroscopic signal arising from both intermediate and native state. This gives rise to either a double-exponential trace or a single-exponential trace preceded by a burst phase.

Figure 6 illustrates our strategy for simulating the formation of a kinetic folding intermediate in model landscapes that take the unfolded state heterogeneity into account. We focus here on en-route (i.e., on-path) intermediates. Off-path intermediates will be investigated elsewhere. The classical three-state case is illustrated by the scheme in Figure 6A. Given that the unfolded state is known to be heterogeneous, this model is only used here as a reference. A more realistic situation is that illustrated in Figure 6B, which reports the formation of a unique intermediate, followed by conversion to a monodisperse native state. If conformational heterogeneity is present in the folding intermediate, a model such as that of Figure 6C best describes folding for a heterogeneous intermediate whose populations do not mutually interconvert. For mutually interconverting intermediate populations, such as, for instance, those detected for apomyoglobin (Nishimura et al. 2002), folding is best described by the kinetic model in Figure 6D.

Figure 6.

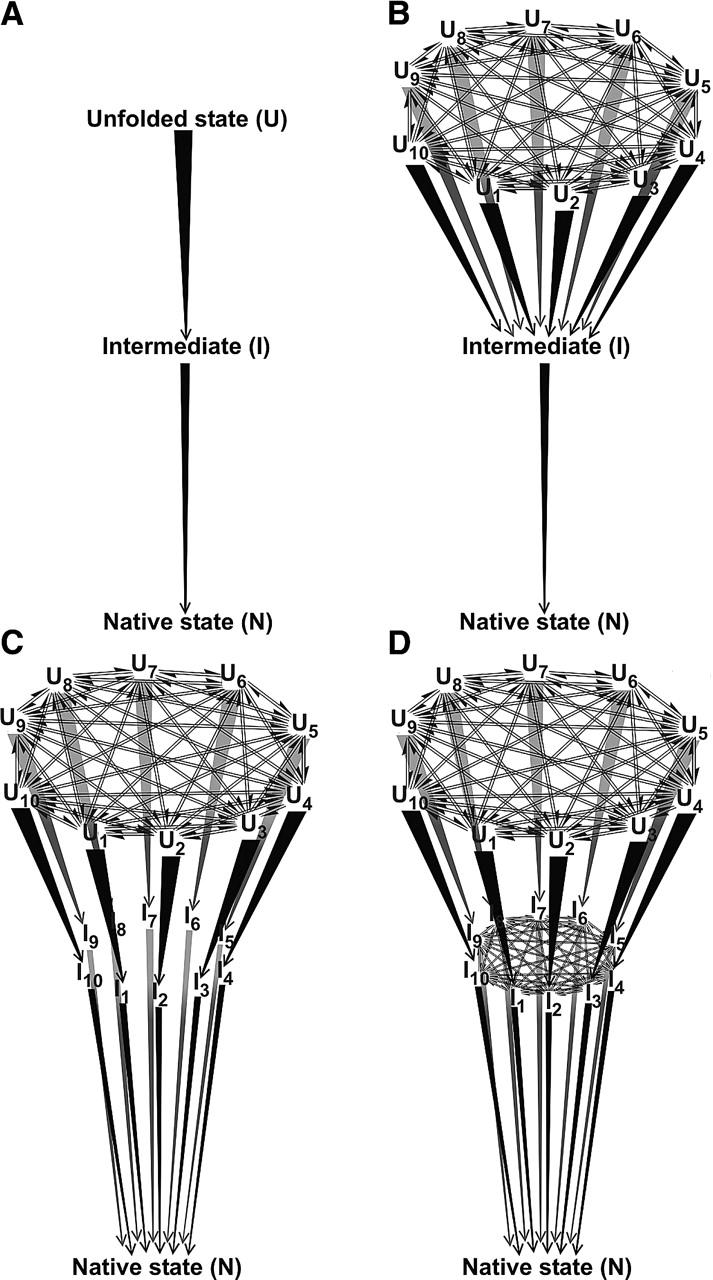
Kinetic models examined in this work for the folding of proteins populating one class of kinetic intermediates. Symbols are defined as in the legend to Figure 1. In addition, I denotes a folding intermediate and I_1…10 denote individual folding intermediates.

Figure 7 illustrates the expected kinetics for a number of mechanistic scenarios pertinent to different types of intermediates and kinetic schemes. All of the simulations in Figures 7–9 have been run with the rate constants reported in Table 2, where it is important to notice that some of the kinetic parameters have been chosen to be larger than typical realistic values. This has been done with the precise intent of keeping either rate constants or transition state energies for the final folding step (linking intermediates to the native state) identical to those in the simulations of Figure 2. The procedure allows direct comparisons, which facilitate estimation of the kinetic effects resulting from introducing intermediates during the early stages of folding. The model landscapes of Figure 7 illustrate rapid intermediate generation followed by slower folding and include parallel pathways of equal magnitude from U to I and from I to N (Table 2). The energetic relations among unfolded states, intermediates, and different regions of a protein’s landscape may be of different nature for different types of intermediates. We have chosen a set of representative cases, illustrated on the left-hand side of Figure 7, as intermediates of types 1 to 6. The different types of intermediates are reported, for simplicity, on a complex section of a protein’s potential energy landscape. This landscape is suitable to illustrate the folding progress through a given kinetic path allowed by the respective folding model. By using this formalism, we abstain from any commitment regarding the presence or the absence of a free energy barrier to folding, to keep the treatment general. In terms of potential energy, the intermediates are either downhill and irreversible (intermediate type 1), downhill and reversible with a reduced excited state energy (intermediate type 2) relative to the reference landscape of Figure 3A (dashed curve in Fig. 7), downhill and reversible with identical excited state energy to the reference landscape (intermediate type 3), reversible and isoenergetic with the unfolded states (intermediate type 4, technically not a true intermediate), uphill and reversible with higher excited state energy to the reference landscape (intermediate type 5), and uphill and reversible with identical excited state energy to the reference landscape (intermediate type 6). Similar definitions apply to the model landscapes of Figures 8 and 9. We adopted systematic criteria to choose the energies for the different types of intermediates represented in Figures 7, 8, and 9. The relevant procedures are discussed in the Supplemental Material.

Figure 7.

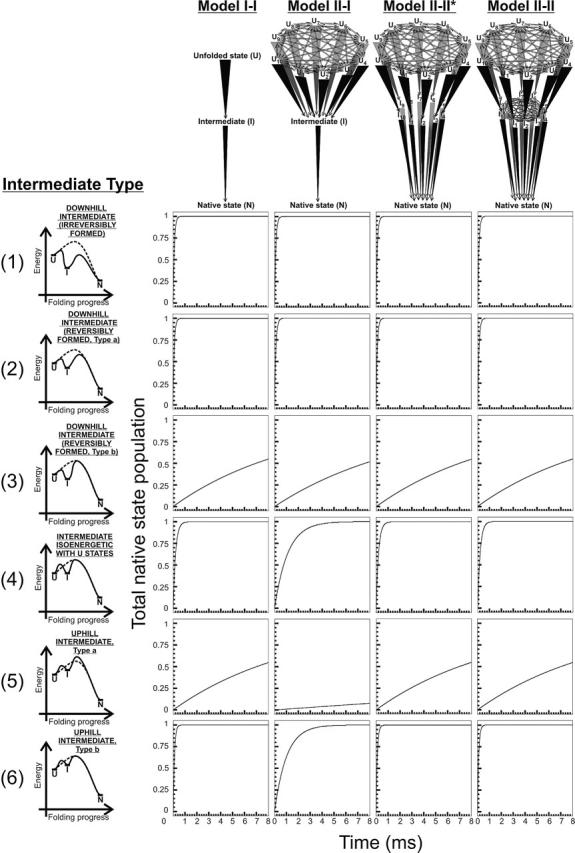
Expected time courses for native state formation according to the kinetic models illustrated in the upper portion of the figure. Each model involves at least one folding intermediate. Specific kinetic parameters are reported in Table 2. The step(s) connecting unfolded and intermediate state(s) are reversible, for intermediates of types 2 to 6. Unfolded state and intermediate interconversion rates were set to k_inter-U = k_inter-I = 10¹⁰ sec⁻¹. The graphs on the left side of the figure illustrate the folding progress through the fastest path for each kinetic model. The different kinetic models are named according to the general models of Figure 1, for the U to I, and I to N steps, respectively. The asterisks refer to modified model types characterized by non–mutually interconverting intermediates.

Figure 8.

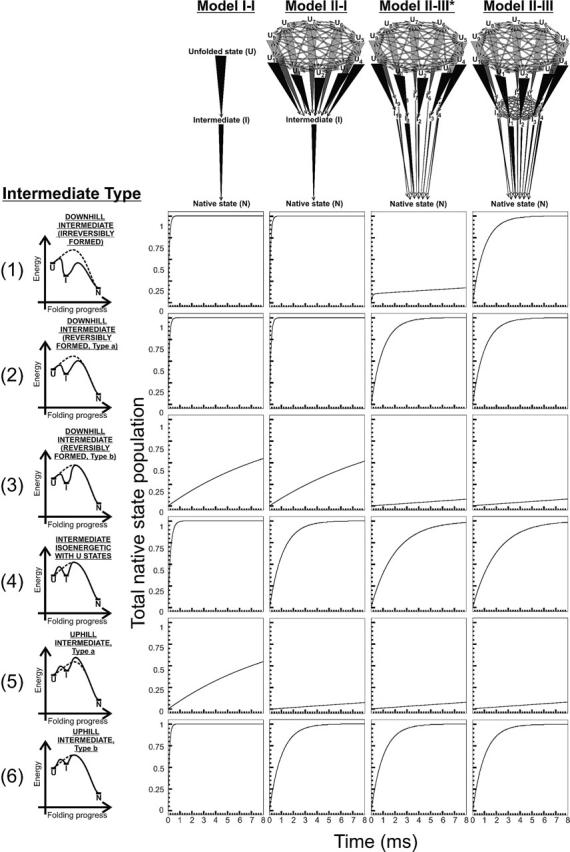
Predicted time courses for native state formation according to kinetic models involving at least one folding intermediate. The specific models are illustrated in the upper portion of the figure. Kinetic parameters are reported in Table 2. Unfolded state and intermediate interconversion rates were set to k_inter-U = k_inter-I = 10¹⁰ sec⁻¹. The graphs on the left side of the figure illustrate the folding progress through the fastest path for each kinetic model. The asterisks have the same meaning as in Figure 7.

Figure 9.

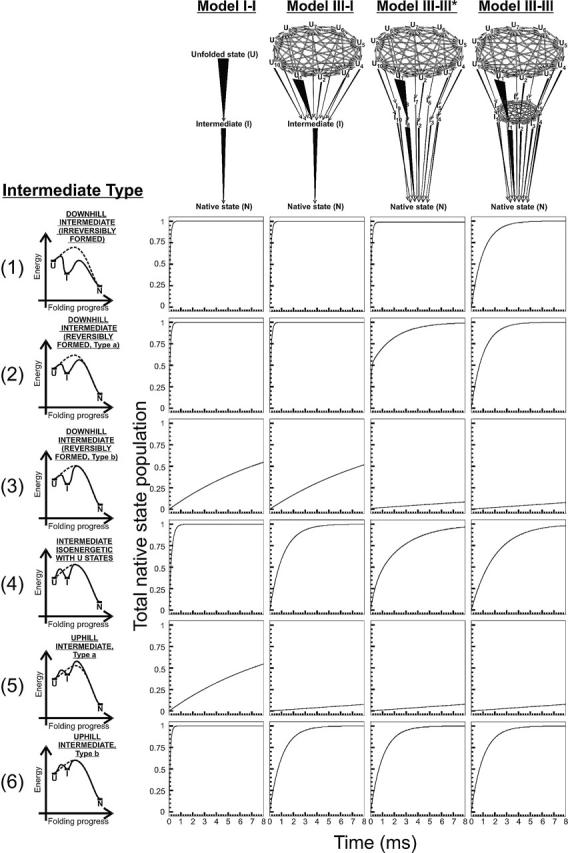
Expected time courses for native state formation according to kinetic models involving one preferential folding pathway and at least one folding intermediate. The specific models are illustrated in the upper portion of the figure. Kinetic parameters are reported in Table 2. Unfolded state and intermediate interconversion rates were set to k_inter-U = k_inter-I = 10¹⁰ sec⁻¹. The graphs on the left side of the figure illustrate the folding progress through the fastest path for each kinetic model. The asterisks have the same meaning as in Figure 7.

Table 2.

Kinetic parameters for the simulations in Figures 7, 8, and 9

		Kinetic Model
		Figure 7	Figure 8		Figure 9
Intermediate type	Rate constants sec−1	I–I, II–I, II–II*, II–II	I–I, II–I	II–III*, II–III	I–I	III–I	III–III*, III–III
	kUI (fast)	108	108	108	108	108	108
(1)	kUI (slow)					105	105
	kIN (fast)	104	104	104	104	104	104
	kIN (slow)			10			10
	kUI (fast)	108	108	108	108	108	108
	kUI (slow)					105	105
(2)	kIU (fast)	106	106	106	106	106	106
	kIU (slow)					103	103
	kIN (fast)	104	104	104	104	104	104
	kIN (slow)			10			10
	kUI (fast)	108	108	108	108	108	108
	kUI (slow)					105	105
(3)	kIU (fast)	106	106	106	106	106	106
	kIU (slow)					103	103
	kIN (fast)	102	102	102	102	102	102
	kIN (slow)			10−1			10−1
	kUI (fast)	106	106	106	106	106	106
	kUI (slow)					103	103
(4)	kIU (fast)	106	106	106	106	106	106
	kIU (slow)					103	103
	kIN (fast)	104	104	104	104	104	104
	kIN (slow)			10			10
	kUI (fast)	106	106	106	106	106	106
	kUI (slow)					103	103
(5)	kIU (fast)	108	108	108	108	108	108
	kIU (slow)					105	105
	kIN (fast)	104	104	104	104	104	104
	kIN (slow)			10			10
	kUI (fast)	106	106	106	106	106	106
	kUI (slow)					103	103
(6)	kIU (fast)	108	108	108	108	108	108
	kIU (slow)					105	105
	kIN (fast)	106	106	106	106	106	106
	kIN (slow)			103			103

The kinetic traces of Figure 7 illustrate the fact that downhill intermediates of types 1 and 2 do not lead to any folding rate variation, relative to the corresponding intermediate-free reference landscapes of Figure 3A, Model I and II. The downhill intermediate of type 3, on the other hand, slows down folding, as expected due to the increased potential energy barrier height. Intermediate of type 4 only slows down folding for Model II-I, while uphill intermediates of type 5 have the general tendency to slow down folding. Interestingly, uphill intermediates of type 6 cause no folding deceleration except for the case of the “focused” intermediate of Model II–I. Therefore in landscape of the type represented in Figure 7, it is convenient to have a distribution of intermediate conformations, to keep folding fast and efficient.

A new set of landscapes, sharing a preferred fast path for the slowest I→N folding step, is shown in Figure 8. In this case, the presence of a preferred rate-determining path, as for Models II–III* and II–III, precludes a number of folding routes from being active and leads to folding deceleration. This is true regardless of the type of intermediate considered. Notably, the slow biexponential folding observed for intermediate of type 1 in landscape II–III* is rendered more efficient by allowing the fast interconversion between the intermediates allowed by Model II–III.

Figure 9 illustrates the case of kinetic models bearing a preferential pathway for both the U-to-I and the I-to-N steps. This situation corresponds to the presence of preferential kinetic paths upon folding. Unexpectedly, for a few of the case scenarios analyzed, folding is actually accelerated by the presence of a folding intermediate. Landscapes III–I and III–III* show fast folding for irreversible downhill intermediates of type 1. This is true despite the fact that the reference landscape of Figure 3A, Model III, bearing no intermediates, shows decreased folding rates in the presence of rapidly interconverting unfolded conformations. So, while fast exchanging heterogeneous unfolded states slows down folding, the matching of this type of unfolded state to an irreversibly formed intermediate allows decoupling the effect of fast unfolded exchange from the rate-determining step of folding. This leads to kinetic acceleration. Kinetic acceleration caused by the presence of a folding intermediate has been experimentally observed (Wagner and Kiefhaber 1999; Spudich et al. 2004). Interestingly, for Model III-III*, this effect disappears when the downhill folding intermediate is formed reversibly (intermediate type 2). In this case folding displays typical biphasic kinetics for native state formation. While a rapid kinetic phase accounts for the fast formation of native state before the equilibrium among U and I conformations is established, a second slow kinetic phase follows, to account for folding in the presence of the coupled inter-U and U–I equilibria. This biphasic kinetics for native state formation is unique to landscape III-III* and intermediate of type 2 and it can be regarded as an experimentally testable kinetic signature for this type of mechanism. The other kinetic traces in Figure 9 show that a kinetically channeled intermediate leads to slower folding, for fast interconverting unfolded states.

We hope that the above kinetic scenarios will serve to stimulate targeted experiments to test specific folding mechanisms. Toward this end, it is important to keep in mind that our simulated traces refer to native state populations only, while most typical experiments in bulk solution collectively monitor all types of populated species (i.e., U’s, I’s, N). This may lead to differences in the observed kinetic profiles. For instance, intermediate type 1 for Model I-I gives rise to a single-exponential for N formation in our case. However, a more complex kinetic trace is to be expected in an experiment reporting on the summation of I and N populations.

Folding kinetics for rugged landscapes

The presence of rugged energy landscapes, rich in intermediates responsible for transient trapping, has been widely supported by computational and theoretical studies (Bryngelson et al. 1995; Wolynes et al. 1995). The predicted multiple intermediates, occurring within otherwise diffusive landscapes, were interpreted as a source of kinetic “frustration,” responsible for slowing down folding and opposing its kinetic optimization. We have examined this issue by studying how the observed kinetics for native protein formation depend on the specific type of rugged landscape. Toward this end, we have constructed five types of representative landscape models, shown in Figure 10, illustrating different kinetic relationships among a number of intermediates. These intermediates have been modeled as being en route to the native state, for simplicity. Recent simulations on the folding of five globular proteins based on Go-like potentials support the prediction of on-path intermediates (Clementi et al. 2000). Two types of intermediates were considered. Type 1 intermediates lie on a downhill (in terms of potential energy) landscape and have identical escape rates, while type 2 intermediates are characterized by a rate-determining slow step right before generation of the native state.

Figure 10.

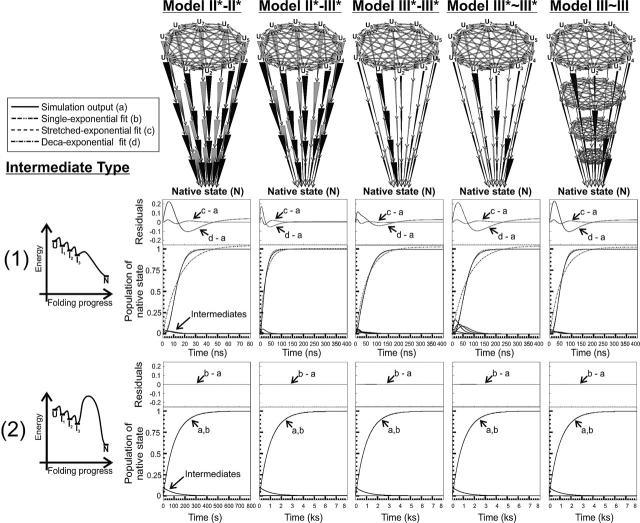
Kinetic impact of folding landscape ruggedness on protein folding. The simulations were carried out for en-route (or on-path) intermediates. The cases of a monotonically downhill (top panels) and a downhill followed by an energy barrier (bottom panels) bumpy landscapes were considered. The predicted populations of native state, kinetic intermediates, and single-, multiple (deca-), and stretched-exponential fits to the computation output are plotted as a function of time. Residuals illustrate differences between simulated outputs and curve fits. The kinetic parameters used in the calculations are provided in Table 3. Unfolded state and intermediate interconversion rates were set to k_inter-U = k_inter-I = 10¹⁰ sec⁻¹. Labels to the intermediates have been omitted in the landscape images, for clarity. The kinetic models were named based on the general nomenclature of Figure 1, according the following additional criteria The first numeral refers to the transitions from U up to I₃. The second numeral refers to the last transition, from I₃ to N. The tilde between numerals indicates that the fast folding routes are not linked to the same intermediate. The asterisk refers to a modified model type with non–mutually interconverting intermediates. The results from stretched exponential curve fitting, for the graphs illustrating type 1 intermediates, are, from left to right: α = 2.2, k = 7.1 × 10⁷ sec⁻¹; α = 1.5, k = 3.6 × 10⁷ sec⁻¹; α = 1.4, k = 1.9 × 10⁷ sec⁻¹; α = 2.1, k = 1.4 × 10⁷ sec⁻¹; and α = 2.2, k = 1.8 × 10⁷ sec⁻¹, respectively.

The simulation results are clear-cut. Intermediates of type 1 are characterized by a lag time preceding formation of the native state, for all five kinetic schemes. The time course for N formation fits best to a stretched exponential, as predicted and observed experimentally for complex folding scenarios (Gruebele 1999; Sabelko et al. 1999). The plots of Figure 10 include the population of transient intermediates. Their transient population correlates with the presence of the lag phase, showing that the intermediates lead to kinetic retardation. In the case of the downhill intermediates of type 1, it is evident that the population of transiently trapped species is greater for Model III*~III*, comprising fast downhill preferential paths not linked to each other. Under these conditions, the kinetic retardation increases. Upon allowing the conformation of the different intermediates to interconvert rapidly, relative to folding, as in Model III~III, faster folding is reinstated.

The landscapes bearing intermediates of type 2 are characterized by a dramatic decrease in the folding rates. From the conceptual viewpoint, the presence of a final slow step, or ensemble of steps, in folding is not unreasonable. This may be the result of a free energy barrier due to loss of conformational entropy and/or enthalpically unfavorable interactions in the transition state ensemble. Alternatively, slow folding in its later stage may arise from the plausible increase in internal friction (due to the protein) during the later stages of folding. The kinetic retardation observed for intermediates of type 2 arises from the presence of a slower rate-determining step, relative to the other cases illustrated in Figure 10 bearing intermediates of type 1. Folding takes place with apparent single-exponential kinetics. Therefore, it is important to notice that (1) experimental single-exponential behavior is compatible with the presence of a rugged energy landscape and, (2) as a consequence of the above, an observed stretched exponential, often invoked as one of the expected experimental signatures of ruggedness (Gillespie and Plaxco 2004), is actually not a necessary requirement for a rugged folding landscape. One important corollary observation confirmed by additional simulations (data not shown) is that, as more downhill intermediates are added, the apparent single-exponential curve turns into a progressively more stretched exponential, even for type 2 scenarios. The key point to keep in mind is that slow bottleneck-type late event(s) may mask the ability to experimentally observe landscape ruggedness. The specific balance between degree of ruggedness (proportional to the number of small bumps) and slow character of the bottleneck step determines the overall detectability of stretched exponentials in rugged landscapes.

It is worth noticing that the stretched exponential constant α (see Equation 4) is invariably >1 in all the predictions discussed here (e.g., Figs. 5, 10). In contrast, α is invariably found to be <1 in experiments detecting deviations from exponentiality upon folding (Gruebele 1999; Sabelko et al. 1999; Ma and Gruebele 2005). This is not surprising, considering that our kinetic predictions assess native state populations, while experimental studies, typically based on relaxation analysis (e.g., after T-jumps), generally detect variations in unfolded state populations. In qualitative agreement with experiments, our computed kinetic time courses display α<1, when the analysis is performed on unfolded state populations.

The kinetic data presented here are undeniably characterized by a high degree of degeneracy. For instance, two or more different models may predict the same qualitative behavior. Therefore, a comparison between predicted kinetics accompanied by experimental observation of native protein populations as a function of time may not be sufficient to discriminate among different landscape types. This highlights the fact that in some cases it is compelling to perform additional experiments, involving the selective detection of distinct population types (by either bulk or single-molecule methods), to unequivocally discriminate among different folding landscapes. One important purpose of this work is to sensitize the reader toward this issue.

Conclusions

This work provides a systematic description of the expected folding time course for a variety of representative landscapes intended to capture some of the key features governing protein folding. A special emphasis has been placed on exploring the effect of unfolded state and intermediate conformational interconversion on folding. In addition to confirming and recapitulating a set of key findings supported by experimental and theoretical work over the last decade, we have also identified a few novel crucial aspects of the folding process, as summarized below.

The presence of distributed conformational heterogeneity in the unfolded state slows down folding for potential energy landscapes with some type of kinetic channeling. These landscapes are characterized by a number of folding “escape” routes much smaller than the number of unfolded state conformations. Most importantly, the above applies even when the rate constants for unfolded state interconversion are much faster than the escape routes to the native state.

For landscapes lacking detectable intermediates, single-exponential kinetics for native state formation are always observed, as long as the unfolded state interconversion rate constants are much faster than any of the escape routes to folding.

Remarkably, the presence of a conformationally heterogeneous unfolded state, now widely supported by both computation and experiments, implies the need for parallel folding paths during the early stages of protein folding. These paths need to involve many of the conformationally diverse unfolded microstates. Otherwise severe folding deceleration is predicted to occur.

Kinetic intermediates of different types may speed up folding, slow it down, or not affect folding rates at all, depending on the specific type of landscape considered. Likewise, the presence of fast conformational equilibration in folding intermediates has variable effects on folding rates. The presence of ruggedness in folding energy landscapes may be undetectable, i.e., by not giving rise to stretched exponential kinetics, if the ruggedness is followed by a slow rate-determining step.

We hope that the findings reported here will serve to stimulate new experiments and folding simulations aimed at testing, tuning, and improving our understanding of the fundamental principles governing protein folding.

Materials and methods

The computational models representing the complex energy landscapes studied in this work include unfolded, intermediate, and native states, interconnected by either reversible or irreversible processes. Folding is viewed as the time-dependent transition of an unfolded state ensemble to the native state through a multitude of parallel pathways, either directly leading to the native state or via a number of kinetic folding intermediates. Each of the steps follows first-order kinetics and is represented by a first-order homogeneous differential equation, defining the rate law for folding. The time dependence for the population of the different species is obtained by solving the system of n differential equations establishing the rate law for each kinetic model, where the parameter n denotes the number of distinct species present in the model.

The system of differential equations defining the pertinent rate laws for each kinetic model was solved by the Gepasi Biokinetics Simulator (version 3.30, running under Microsoft Windows XP [http://www.gepasi.org]) (Mendes 1993, 1997; Mendes and Kell 1998). Gepasi takes advantage of the LSODA (Livermore solver of ordinary differential equations) algorithm, which is part of the ODEPACK package of numerical methods for ordinary differential equations (Hindmarsh 1983; Petzold 1983). By measuring the stiffness of the differential equations and dynamically adjusting its integration method depending on the measured stiffness value, LSODA is capable of solving numerical complex systems of differential equations more efficiently than traditional solvers can. Integration and optimization methods used by the package include simulated annealing, genetic algorithms, Levenberg-Marquardt, Hooke and Jeeves, L-BFGS-B, steepest descent, and random search. In addition to the formal definition of the kinetic models, the input to the Gepasi simulations included values of the pertinent microscopic rate constants, shown in Tables 1–3, and a set of initial conditions defining the initial populations of unfolded state conformations. The total initial unfolded state population was set to one. The initial unfolded populations, P_U0,i, were evenly distributed among unfolded microstates.

Table 3.

Kinetic parameters for the simulations in Figure 10

		Kinetic Model
Intermediate type	Rate constants (sec−1)	II*–II*	II*–III*	III*–III*	III*~III*	III~III
	k↓(fast)a	3.2 × 108	3.2 × 108	3.2 × 108	3.2 × 108	3.2 × 108
	k↑(fast)b	3.2 × 106	3.2 × 106	3.2 × 106	3.2 × 106	3.2 × 106
(1)	k↓(slow)		5.6 × 107	5.6 × 107	5.6 × 107	5.6 × 107
	k↑(slow)			5.6 × 105	5.6 × 105	5.6 × 105
	k↓(fast)	3.2 × 108	3.2 × 108	3.2 × 108	3.2 × 108	3.2 × 108
	k↑(fast)	3.2 × 106	3.2 × 106	3.2 × 106	3.2 × 106	3.2 × 106
(2)	k↓(slow)			5.6 × 107	5.6 × 107	5.6 × 107
	k↑(slow)			5.6 × 105	5.6 × 105	5.6 × 105
	k↓(fast)c	10−2	10−2	10−2	10−2	10−2
	k↓(slow)c		10−5	10−5	10−5	10−5

^a All the k_↓ rates pertain to reactions leading towards the native state.

^b All the k_↑ rates pertain to reactions leading away from the native state.

^c These rates pertain only to the final kinetic folding step.

The Gepasi output was analyzed with the OriginLab package (version 7.5, OriginLab Corp.), which was also utilized for generating curve fits to the simulation outputs. Kinetic data were fit to single, double, deca-, or stretched exponentials,

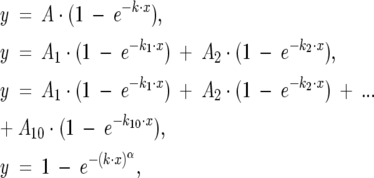(4)

respectively, where As, ks, and α were set as adjustable parameters.

In order to probe curve fit quality, residuals, i.e., differences between Gepasi’s output and Origin’s curve fits, were calculated.

The folding rate constants for type IV model, utilized for the data in Figures 2 through 5, were determined via the relations

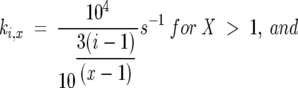(5)

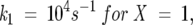(6)

where X is the total number of unfolded state conformations, and i is the specific unfolded state conformation whose folding rate is being considered. In accordance with the nomenclature for the unfolded states shown in Figure 1, 1 ≤ i ≤ X for any X.

Electronic supplemental material

A detailed description of the criteria adopted to choose energies and kinetic rate constants for the folding intermediates in Figures 7, 8, and 9 is available.

Abbreviations

• N, native state

• U, unfolded state

• I, intermediate state

• k_inter-U, rate constant for exchange among different unfolded state conformations

• k_inter-I, rate constant for exchange among different intermediate conformations

• k_i, folding rate starting from the ith unfolded state conformation

• k_UI, rate constant for the transition from a U to an I

• k_IU, rate constant for the transition from an I to a U

• k_IN, rate constant for the transition from an I to an N

• K_i, equilibrium constant for the interconversion among different unfolded state conformations

• P_N(t), time-dependent population of native state P_U0,i

• initial population of ith unfolded conformation

• LSODA, Livermore solver of ordinary differential equations

Article and publication are at http://www.proteinscience.org/cgi/doi/10.1110/ps.051758206.