Quantification of helix–helix binding affinities in micelles and lipid bilayers

Abstract

A theoretical approach for estimating association free energies of α-helices in nonpolar media has been developed. The parameters of energy functions have been derived from ΔΔG values of mutants in water-soluble proteins and partitioning of organic solutes between water and nonpolar solvents. The proposed approach was verified successfully against three sets of published data: (1) dissociation constants of α-helical oligomers formed by 27 hydrophobic peptides; (2) stabilities of 22 bacteriorhodopsin mutants, and (3) protein-ligand binding affinities in aqueous solution. It has been found that coalescence of helices is driven exclusively by van der Waals interactions and H-bonds, whereas the principal destabilizing contributions are represented by side-chain conformational entropy and transfer energy of atoms from a detergent or lipid to the protein interior. Electrostatic interactions of α-helices were relatively weak but important for reproducing the experimental data. Immobilization free energy, which originates from restricting rotational and translational rigid-body movements of molecules during their association, was found to be less than 1 kcal/mole. The energetics of amino acid substitutions in bacteriorhodopsin was complicated by specific binding of lipid and water molecules to cavities created in certain mutants.

Association of α-helices plays an important role during folding, oligomerization, and conformational transitions of membrane proteins (Booth et al. 2001; Arkin 2002; Chin et al. 2002; Engelman et al. 2003; Jiang et al. 2003; Perozo and Rees 2003). Therefore, the physical forces that drive assembly of α-helices in nonpolar media have been a subject of significant interest (Gil et al. 1998; White and Wimley 1999; Popot and Engelman 2000). Nevertheless, there have been relatively few quantitative studies in this area, because of the difficulties with conducting equilibrium unfolding and binding experiments for membrane proteins (Haltia and Freire 1995; Booth et al. 2001). The accumulated data include stabilities of bacteriorhodopsin mutants (Krebs and Isenbarger 2000; Faham et al. 2004; Yohannan et al. 2004) and equilibrium dissociation constants of transmembrane oligomers in bilayers and micelles (Fisher et al. 1999, 2003; Mall et al. 2001; Fleming 2002; Yano et al. 2002; Cristian et al. 2003; DeGrado et al. 2003; Lew et al. 2003). The oligomeric complexes were formed by single-spanning α-helical peptides, such as glycophorin A, designed hydrophobic coiled coils, M2 channel, integrin, synaptobrevin, and others. Unfortunately, except for an NMR structure of the glycophorin A (GpA) dimer, there are no atomic resolution structures of these complexes. Theoretical models of M2 channels, synaptobrevin, and several other oligomers have been calculated by global energy minimization, with a few experimental restraints obtained from mutagenesis and solid-state NMR studies (Fleming and Engelman 2001b; Gottschalk et al. 2002; Nishimura et al. 2002). However, such ab initio models are probably imprecise and differ from each other when developed by independent research teams, as in the case of the M2 tetrameric channel (Wang et al. 2001). More precise homology models can be generated for designed transmembrane coiled coils using crystal structures of their parent water-soluble proteins.

These experimental studies suggest that assembly of transmembrane α-helices is driven mostly by van der Waals (vdW) interactions and H-bonds, whereas hydrophobic forces are insignificant within the nonpolar bilayers or micelles (MacKenzie and Engelman 1998; DeGrado et al. 2003; Lee 2003). The energy of a single H-bond was found to be ~−2 kcal/mole (Lear et al. 2003), whereas the average contribution of vdW interactions to the stability of bacteriorhodopsin mutants was estimated as 26 cal/moleŲ (Faham et al. 2004). These values are nearly the same as in interiors of water-soluble proteins, that is, −1.5 kcal/mole to −2.0 kcal/mole for buried H-bonds (Myers and Pace 1996), and 22 cal/mole, 26 cal/mole, and 29 cal/moleŲ for vdW interactions of aliphatic carbon, aromatic carbon, and sulfur, respectively (Table 5 in Lomize et al. 2002). It was also found that stability of GpA dimer depends on losses of side-chain conformational entropy (MacKenzie and Engelman 1998). These findings can be better understood by considering the aggregation of α-helices as a process similar to crystallization of small organic molecules, an analogy that has often been applied to protein folding (Shakhnovich and Finkelstein 1989; Murphy and Gill 1991; Graziano et al. 1996; Zhou et al. 1999). The crystallization is also driven by the energy of vdW interactions and H-bonds, which is known as enthalpy of fusion, and it is opposed by an entropic contribution originating from immobilization of the molecules in space and restraining of their torsion angles (Dunitz 1994; Sternberg and Chickos 1994). However, the aggregation in bilayers or micelles is complicated by protein–lipid interactions.

Table 5.

Solvation parameters determined for different types of atoms (see Materials and Methods)

	σ (cal/mole Å2)
Combination of media	Nsolutea	C-aliph	C-arom	N	O	S
Water–decadiene	16	13 ± 3b	19 ± 2	−53 ± 3	−57 ± 3
Water–hexadecene	16	13 ± 4b	19 ± 2	−55 ± 4	−63 ± 4
Water–hydrocarbons	34	22 ± 1	18 ± 1	−66 ± 2	−72 ± 2	−13 ± 7
Water–lipidc		25	19	−55	−63	−13
Water–proteind		19	7	−21	−66	−1
Lipid–proteine		−6	−12	34	−3	12

^a Number of solutes applied for fitting.

^b These values must be disregarded, because the solutes, whose transfer energies were applied for fitting, had few aliphatic carbons.

^c Water–lipid parameters were selected as described in the text.

^d Parameters obtained from protein engineering data (Lomize et al. 2002).

^e The differences of values from two upper rows.

In the present work we propose a simplified theoretical approach for estimation of helix–helix binding free energies as consisting of the following components: (1) transfer energy of protein atoms from a solvent (lipid, detergent, or water) to the interior of the protein complex; (2) H-bond, vdW, and electrostatics interactions within the protein interior; and (3) side-chain conformational entropy losses calculated using the discrete rotamer approximation (Pickett and Sternberg 1993). The transfer energy is estimated using an implicit solvation model (Richards 1977), as a sum of buried surface areas of certain atoms multiplied by their empirical solvation parameters (transfer energies per Ų); this contribution depends on protein–lipid interactions. The H-bond, vdW, and electrostatic interactions between the helices are described by pairwise interatomic potentials. Because the interactions occur in condensed medium rather than in vacuum, the parameters of potentials are different from those in molecular mechanics (see Discussion).

The parameters of energy functions, which are required for calculations using this model, were derived previously from mutagenesis data for water-soluble proteins (Lomize et al. 2002). However, it was necessary to address several additional problems that are specific for binding in nonpolar media. First, the lipid–protein solvation parameters were determined by combining the corresponding water–protein values from our previous study (Lomize et al. 2002) and transfer energies of model organic compounds from water to nonpolar solvents (see Materials and Methods). Second, we selected a dielectric constant for calculations of helix–helix electrostatic interactions in bilayers and micelles. Finally, the association of peptide molecules restricts their rotational and translational movements (Murphy et al. 1994; Holtzer 1995; Gilson et al. 1997). The corresponding immobilization free energy has been found to be small (Yu et al. 2001). Therefore it was simply omitted in the calculations. If present, it would appear as a systematic deviation of the experimental and calculated energies. The proposed computational approach (see Materials and Methods) was tested using all appropriate stability data for transmembrane protein complexes whose three-dimensional structures have been experimentally determined or could be modeled by homology with high precision.

Results

Protein–ligand binding in aqueous solution

Because our energy functions were derived from unfolding ΔΔG values, their feasibility for calculation of binding affinities was not clear. Therefore, they were tested for several protein–ligand complexes in aqueous solution. The corresponding association free energies were calculated for nine small ligands that bind to a small nonpolar cavity in L99A lysozyme (Morton and Matthews 1995). Importantly, this cavity does not contain bound water molecules (Eriksson et al. 1993; Morton et al. 1995). Only complexes with available crystal structures have been considered here to take into account perturbation of protein structures during the binding.

The calculated energies of ligand binding agree reasonably well with experiment, but they are systematically overestimated. The obtained discrepancies (last column of Table 1) were less for four smaller ligands in the set, whose volumes match the size of the binding cavity. The average deviation in this case was only ~0.7 kcal/mole and can be attributed to immobilization free energy of the ligands. However, the additional deviation for five larger ligands (an average of ~2.3 kcal/mole) is probably due to the accumulation of conformational strain. Indeed, the binding of all five larger ligands except ethylbenzene leads to formation of a sterically forbidden side-chain conformer of Val 111 in lysozyme, with χ¹ ~+60° in α-helix (Morton et al. 1995). It is also worth noticing that all five complexes with larger ligands have increased B-values of atoms in the area of binding pocket. The interactions of the atoms with higher B-values may be weakened due to dynamic averaging, which might produce the smaller than expected experimental binding energies. Thus, the results obtained suggest that our energy functions are appropriate for calculations of ligand-binding affinities in the absence of significant strain, and that immobilization energies of the ligands are probably less than 1 kcal/mole.

Table 1.

Comparison of experimental and calculated binding free energies (ΔG_expand ΔG_clc) for ligands of L99A lysozyme

Ligand	PDBa	ΔGexpb	ΔGclc	ΔGexp − ΔGclc
Smaller ligands
Benzene	1811	−5.2	−5.5	0.3
Benzofuran	1821	−5.5	−5.0	−0.5
Indene	1831	−5.2	−7.0	1.8
Indole	1851	−4.9	−5.9	1.0
Larger ligands
Ethylbenzene	lnhb	−5.8	−8.5	2.7
Izobutylbenzene	1841	−6.5	−8.8	2.3
n-butylbenzene	1861	−6.7	−9.9	3.2
p-xylene	1871	−4.7	−8.7	4.0
o-xylene	1881	−4.6	−7.3	2.7

^a Ligand-free structure, 1190.

^b From Morton and Matthews (1995).

Association of α-helical peptides in micelles and bilayers

In the next series of tests, we considered formation of α-helical dimers and trimers in bilayers and micelles (Tables 2, 3). This was necessary to verify atomic solvation parameters (see Materials and Methods) and dielectric constant, which varies from 3.5 to 7 in biological membranes (Radu et al. 1996; Polevaya et al. 1999; Ermolina et al. 2001; Hughes et al. 2002). The dielectric constant affects electrostatic interactions of α-helix “macrodipoles” (Hol et al. 1981; Ben-Tal and Honig 1996).

Table 2.

Association energies of α-helical peptides in micelles and bilayers (kcal/mole)

			Components of ΔGclc (kcal/mole)
Model peptides	ΔGexp	ΔGclca	ΔHvdW	ΔHHb	ΔGtrnsf	−TΔSsch	ΔHelectr
Dimers in micelles
GpA	−6.4b	−6.5 (−6.3)	−13.3	0	4.3	0.9	1.6
MS1	−4.0b	−4.1 (−4.4)	−15.5	−2.2	6.2	4.7	2.6
Trimers in micelles
MS1	−5.5b	−6.6 (−6.8)	−24.9	−4.3	12.0	5.1	5.5
V7N MS1	−12.4b	−12.7 (−12.9)	−25.9	−8.3	10.3	5.3	5.5
Dimers in lipid bilayers
L16 + Y16	−1.5– −3c	−1.1 (−1.4)	−14.6	0	6.2	4.7	2.6
L22 + Y22	−1.5– −3c	−2.7 (−4.2)	−18.8	0	7.7	5.4	3.0
Leu-GpA	<−6.4d	−7.4 (−7.2)	−14.5	0	4.7	0.9	1.5
L7NL11	<−6.4d	−6.6 (−7.1)	−19.8	−2.2	6.3	6.2	2.9
L19	<−3.4d	−3.7 (−4.2)	−20.3	0	7.4	6.2	2.9

^a These energies were calculated using ɛ = 4 and ΔG_imm = 0. Values in parentheses are obtained with ɛ = 8 and ΔG_imm = 1 kcal/mole. Only transmembrane segments of α-helices were included in the calculations: 73–95 for GpA and LeuGpA, 3–24 for MS1 and related peptides, 3–25 for L₇NL₁₁ and L₁₉, 4–20 for L₁₆ + Y₁₆, and 6–25 for L₂₂ + Y₂₂).

^b Experimental energies were recalculated using data from the original publications (Fisher et al. 1999; Fleming 2002; Gratkowski et al. 2002; Lear et al. 2003), as described in Materials and Methods and using partial volumes of detergents from Maire et al. (2000). ^c Energies varied between −1.5 and −3 kcal/mole, depending on the length of phosphatidylcholine fatty acyl chains (Mall et al. 2001). ^d An estimation based on results of the TOXCAT assay, as described in the text.

Table 3.

ΔΔG_assocvalues (kcal/mole) of GpA and MS1 mutants in micelles

Glycophorin A dimer			MS1 trimer
Mutant	ΔΔGexpa	ΔΔGclc	Mutant	ΔΔGexpb	ΔΔGclc
L75A	1.3	0.9	N14V/V7N	−0.6	−0.8
I76A	1.8	1.1	N14Q	−1.8	−0.6
I77A	0.1	0.1	N14E	0.0	0.4
F78A	−0.1	0.0	N14L	>1.8	4.2
V80A	0.4	0.7	N14V	>2.1	4.2
M81A	−0.2	0.0	N14T	>2.4	4.5
V84A	1.0	0.5	N14S	>2.4	6.6
I85A	−0.4	0.0	N14A	>3.0	6.8
G86A	−0.1	−0.1
T87A	0.9	1.5

ΔΔG_assoc = ΔΔG_assoc (mutant) − ΔΔG_assoc (wild type); the values are negative for stabilizing replacements.

^a Data of Fleming and Engelman (2001a).

^b Based on data of Gratkowski et al. (2001) and Lear et al. (2003). N14D mutant was not included, because it forms a mixture of monomers, trimers, and hexamers (Gratkowski et al. 2001).

Our test set included the following peptides (Table 2): glycophorin A (GpA), glycophorin A with all interfacial residues simultaneously replaced by Leu (Leu-GpA), a redesigned version of two-stranded coiled coil (MS1 peptide), and several poly-Leu peptides with incorporated polar or aromatic residues (L₁₉, L₇NL₁₁, L₁₆ + Y₁₆, and L₂₂ + Y₂₂). These peptides form dimers with a crossing angle of ~−30° (GpA and Leu-GpA) or coiled coil dimers and trimers with a crossing angle of ~+20°. The structure of GpA dimer was taken from the Protein Data Bank (1afo; MacKenzie et al. 1997), whereas homology models of other dimers and trimers were generated from crystal structures of the corresponding water-soluble coiled coils, that is, PDB files 2zta and 1zim, respectively. In the models of L₁₆ + Y₁₆ and L₂₂ + Y₂₂ heterodimers, two aromatic side chains from different monomers interact with each other but do not interfere with packing of central Leu residues. The models of MS1 mutants (Table 3) were generated from structures of the most closely related water-soluble coiled coils: the 1zim PDB file (Gonzalez et al. 1996b) for N14L, N14D, N14E, and N14Q mutants, 1ij2 (Akey et al. 2001) for N14T and N14V, and 1zij (Gonzalez et al. 1996a) for N14S and N14A. All side-chain conformers were “traced” as in the experimental templates and adjusted to maximize the number of interhelical H-bonds. Small-to-large mutants, such as Gly → Ala in GpA, were not included, because this requires energy optimization of the original experimental structures to relax the arising overlaps, and the resulting models would be insufficiently precise.

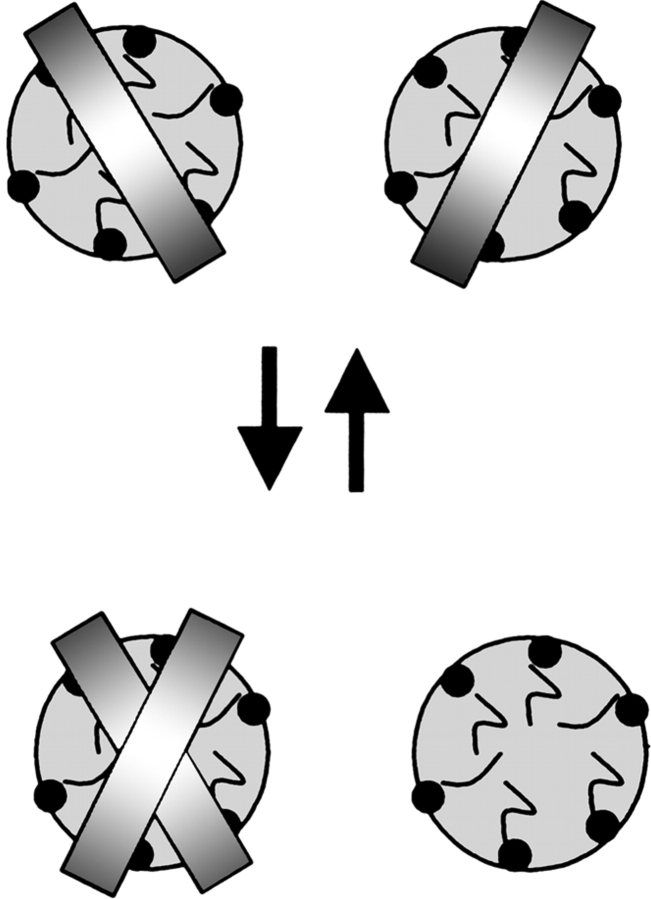
Self-association of GpA and MS1 peptides was studied in the presence of micelles formed by different nonionic or zwitterionic detergents, including C₈E₅, DPC, and C14-betaine (Fig. 1 ▶). Under such conditions, all experimental energies must be defined using mole concentrations of peptides in detergent rather than peptide concentrations in water or mole fractions. Therefore, the energies from original publications were recalculated, as described in Materials and Methods. The obtained values depend on detergent. For MS1 dimer, they were −4.0 and −2.0 kcal/mole in DPC and C₁₂E₈, respectively (Gratkowski et al. 2002). For GpA dimer, they were −6.4, −6.4, −6.8, and −5.2 kcal/mole in C₈E_5, DPC, DDMAB, and C14-betaine, respectively (Fisher et al. 1999; Fleming 2002; Fleming et al. 2004). Dimerization energies of two other peptides, L₁₆ + Y₁₆ and L₂₂ + Y₂₂, were determined in bilayers (Mall et al. 2001). They varied from −1.5 to −3 kcal/mole, depending on the length of phospatidylcholine fatty acyl chains. Table 2 also includes three peptides whose dimerization propensities were estimated qualitatively in biological membranes using a two-hybrid approach. In the TOXCAT assay, L₇NL₁₁ and Leu-GpA dimers were slightly more stable than GpA, whereas L₁₉ was slightly more stable than G83I GpA (Russ and Engelman 1999; Zhou et al. 2001). This can be compared with stabilities of the corresponding GpA and G83I GpA dimers in micelles, that is, −6.4 kcal/mole and −3.4 kcal/mole, respectively, based on data of Fisher et al. (1999) and Bu and Engelman (1999).

Figure 1.

Dimerization of α-helical peptides in micelles. The peptide–detergent ratio is sufficiently low to have less than 1 peptide molecule per micelle.

The calculated stabilities of α-helical dimers and trimers were consistent with the experimental values (Table 2), with an average deviation of 0.4 kcal/mole for oligomers in micelles. The agreement was best with dielectric constant ɛ = 4. However, the value of ɛ could not be defined precisely, because of the uncertain immobilization energy, ΔG_imm. For example, the association energies calculated with ɛ = 8 and ΔG_imm = 1 kcal/mole were very close to ones with ɛ = 4 and ΔG_imm = 0 (Table 2). In the subsequent calculations, we used ɛ = 4. It is worth noting that ΔΔG values in Tables 3 and 4 do not depend on ɛ, because the contribution of backbone electrostatics is identical in wild-type and mutant proteins.

Table 4.

ΔΔG_unfoldvalues (kcal/mole) of bacteriorhodopsin mutants

Mutant	ΔΔGexpa	ΔΔGclc	Mutant	ΔΔGexpa	ΔΔGclc
T24S	−0.3	−0.6	P50A	−0.1	0.6
T24V	0.2	1.4	I52A	1.4	0.6
T24A	−0.6	1.9	F54A	1.0	0.4
F42A	1.6	−0.3 (1.2)b	T55A	0.1	0.0
Y43A	1.3	1.5	M56A	−1.4	0.2
I45A	1.9	0.9 (1.8)b	Y57A	3.7	3.8
T46A	2.2	3.3	L58A	−0.3	0.2
T46S	−0.1	1.2	S59A	−0.1	0.0
T47A	1.0	0.8	M60A	0.8	0.8
L48A	0.1	0.3	L61A	−0.7	0.3
V49A	−0.7	1.3	L62A	−0.5	0.0

Large-to-small replacements with ΔΔG_clc overestimated by >0.5 kcal/mole are indicated by bold.

^a Data from Faham et al. (2004) and Yohannan et al. (2004).

^b Value in parentheses were calculated assuming that the residue is exposed to water in the SDS-unfolded state.

Table 2 shows the different components of free energy. The major stabilizing contribution comes from dispersion attraction of the α-helices (ΔH_vdW). This was expected, because the interactions of uncharged molecules are usually dominated by dispersion forces (Israelachvili 1992). Some of the oligomers are also greatly stabilized by hydrogen bonds (−8.3 kcal/mole in V7N MS1 trimer). The largest destabilizing component was represented by the transfer energy (ΔG_trnsf). This contribution is unfavorable, because surfaces of the α-helices consist mostly of aliphatic and aromatic groups that are more “soluble” in the nonpolar hydrocarbon cores of bilayers or micelles than in the protein interior, judging from the corresponding solvation parameters (bottom row in Table 5). However, the solid-state vdW interactions outweigh this nonspecific solvation effect (|ΔH_vdW | > ΔG_trnsf in Table 2). The contribution of side-chain entropy is also destabilizing, but it strongly depends on flexibility of residues affected by interaction of α-helices. The entropy changes were close to zero for GpA dimer, because its binding interface consists mostly of Val, Gly, and Thr residues, whose side chains are already restrained in isolated α-helices before the association. This contribution is higher for other complexes that contain a number of Leu residues, whose conformations are restrained during formation of the oligomers. However, the entropy changes are still relatively small, because Leu has only two allowed rotamers in an isolated α-helix. Electrostatic interactions of α-helices are also destabilizing, because the helices are roughly parallel in the oligomers.

In the next test, we estimated association energies of GpA and MS1 mutants (Table 3). The calculated ΔΔG_assoc values were consistent with experiment: The average deviation was 0.3 kcal/mole for mutants of GpA. The results obtained for MS1 trimer were more difficult to compare. Some of the ΔΔG values are indicated by inequalities in Table 3, because they were not precisely determined (Lear et al. 2003). The corresponding MS1 mutants form trimers only at relatively high peptide–detergent mole ratios, close to 1:100 (Gratkowski et al. 2001). Such ratios may correspond to more than one peptide molecule per micelle, because the aggregation number of C14-betaine micelles is ~83–130 (Maire et al. 2000). Thus, two or more peptide molecules might be forced to occupy the same micelle, which differs from the situation shown in Figure 1 ▶.

In summary, the results of calculations for 27 peptides (Tables 2, 3) indicate that the implicit solvation model works successfully with parameters derived from transfer energies of model compounds. The experimental binding affinities were satisfied using ɛ of 4 to 8 and immobilization energy <1 kcal/mole.

Stabilities of bacteriorhodopsin mutants

In the last test, we reproduced ΔΔG values of 22 bacteriorhodopsin mutants (Table 4). The protein was dissolved in mixed DMPC/CHAPSO micelles and reversibly unfolded by gradually increasing the concentration of SDS (Faham et al. 2004; Yohannan et al. 2004). Under such conditions, the folded protein exists in a monomeric form that can be crystallized from bicelles (Faham and Bowie 2002). The “unfolded” state of bacteriorhodopsin in SDS micelles probably represents a mixture of four or five nativelike α-helices (A to E), nonnative β-structure, and coil (Hunt et al. 1997; Marti 1998; Booth et al. 2001).

The substituted residues (Table 4) were located in trans-membrane helices A and B of bacteriorhodopsin. These helices are individually stable in SDS, as demonstrated by two-dimensional NMR studies of the corresponding peptides, 1–36, 34–65, and 1–71 (Lomize et al. 1992; Pervushin and Arseniev 1992; Pervushin et al. 1994; Orekhov et al. 1995). Therefore, the unfolding ΔΔG values of residues in these helices were calculated as the differences of free energies describing dissociation of the entire 7α-helical domain into individual α-helices in the wild-type and mutant proteins. The crystal structures of mutants T24S, T24V, T24A, T46S, P50A, and M56A were taken from the PDB (1s51, 1s52, 1s54, 1s53, 1pxr, and 1pxs files, respectively; Faham et al. 2004^; Yohannan et al. 2004). Models of other mutants, without available crystal structures, were generated by substituting the corresponding residues by Ala in wild-type monomer (1py6). Substitutions of residues 37–41 were not included, because this region is disordered in SDS (Lomize et al. 1992).

The results of calculations indicate that stabilities of the mutants were reproduced in most but not all cases (Table 4). For a majority of mutants, the average deviation of ΔΔG values was 0.3 kcal/mole, just as for GpA. However, Phe 42 and Ile 45 residues are probably exposed to water in the denatured state, because their ΔΔG values were reproduced much better using water–protein instead of lipid–protein solvation parameters (the default assumption was that all residues from the hydrophobic segments are buried from water). These two residues are situated at the edge of a hydrophobic segment and separated by a proline kink from the rest of helix B.

Discrepancies were also found for eight large-to-small replacements, whose calculated stabilities were systematically underestimated (indicated by bold in Table 4). These replacements usually improve stability of bacteriorhodopsin, despite the loss of vdW interactions within the protein structure. The observed stabilization can be attributed to tight specific binding of water or lipid molecules to cavities created in these mutants. All the corresponding residues are either buried within the transmembrane α-bundle (46, 49, and 50) or situated at the protein–lipid interface (24, 56, and 61). All crystal structures of mutants from the first group (1s53 and 1pxr) include a bound-water molecule, which spatially substitutes for the removed side chain and forms H-bonds with the protein (the water molecules were not included in the calculations). All residues from the second group (Thr 24, Met 56, and Leu 61) are involved in formation of lipid-binding sites, because they form contacts with crystallized lipids in bacteriorhodopsin trimer (1c3w) or monomer (1kme). The lipid-binding cavities become deeper after substituting these residues by Ala, which would strengthen the lipid–protein association and stabilize the structures of the mutants (however, lipid molecules were not included in PDB entries of the mutants). It is worth noting that no similar deviations of ΔΔG values were observed for mutants of GpA, except possibly I85A (Table 3). The 7α-helical bundle of bacteriorhodopsin is probably more prone to formation of lipid-binding cavities than the small GpA dimer, because it has a more complicated surface geometry.

The obtained results suggest that stabilities of mutants in transmembrane proteins can be theoretically predicted. However, there are certain complications here. The folded protein structure may be stabilized by tight specific binding of water and lipid molecules. In addition, the denatured state may be unfolded in some regions of the polypeptide chain, but form nativelike α-helices in others. These independently stable α-helices are probably dissociated or form a molten globule-like state in SDS micelles.

Discussion

The experimental binding affinities were reproduced successfully in all systems considered, including protein–ligand complexes in aqueous solution, α-helical bundles in micelles, and bacteriorhodopsin mutants (Tables 1–4). Thus, the described theoretical approach can be applied hereafter. For example, the dimerization free energies can now be estimated for any transmembrane oligomers deposited in the PDB (these energies are typically −2 to −8 kcal/ mole according to our preliminary results). In addition, an analysis of helix–helix binding energies within individual transmembrane subunits in the PDB would be important for understanding of protein folding in biological membranes. Finally, an automated membrane protein docking procedure can be developed by combining our method for evaluation of energy with previously developed optimization software (Tuffery et al. 1994; Adams et al. 1995; Pappu et al. 1999; Torres et al. 2001; Kim et al. 2003).

The stability of transmembrane oligomers depends on several factors, most of which were known previously: (1) tight packing of α-helices; (2) formation of hydrogen bonds; (3) formation of aliphatic, aromatic, and polar clusters, in accordance to the “like dissolves like” rule that applies for vdW forces in media (see below); (4) a preferential solvation of aliphatic and aromatic groups by detergents and lipids, as reflected in their protein–lipid transfer energies; (5) content of conformationally constrained Val, Gly, Ala, Thr, or Pro residues; and (6) mutual orientations of helices, which affects electrostatic energy. The corresponding energy contributions are discussed below in more detail.

Protein–protein interactions

All α-helical bundles are stabilized exclusively by helix–helix vdW interactions and H-bonds (ΔH_vdW and ΔH_HB in Table 2). This is a purely enthalpic contribution. Surprisingly, even in aqueous solution, the binding of nonpolar ligands to proteins is usually enthalpy driven (Morton et al. 1995; Klotz 1997; Weber and Salemme 2003), which means it depends more on interactions within the complexes than on hydrophobic effect. Importantly, the corresponding helix–helix interaction energies, for example −13 kcal/mole in GpA dimer, are several times smaller than would be calculated with molecular mechanics potentials, such as CHARMM or OPLS (Torres et al. 2001; Im et al. 2003; Lazaridis 2003). This discrepancy has a simple explanation. The molecular mechanics potentials are derived from enthalpies of sublimation or vaporization describing transfer of organic molecules from molecular crystals or liquids to the gas phase (Jorgensen et al. 1996; Gavezzotti and Filippini 1997; Ewig et al. 1999), or at least they reproduce these enthalpies, when derived from different sources (Momany et al. 1974). Therefore, such potentials are usually regarded as specifying interactions in vacuum (Lazaridis et al. 1995). However, vdW forces are much weaker in condensed media than in vacuum, as evident from theory and experiment, because these forces are of electrostatic origin (Israelachvili 1992; Leckband and Israelachvili 2001). Furthermore, the aggregation and even folding of protein molecules is similar to crystallization or liquid–solid transition (Murphy and Gill 1991; Zhou et al. 1999). Therefore, the corresponding energy gain must be related to enthalpy of fusion (Shakhnovich and Finkelstein 1989; Graziano et al. 1996), which is smaller than the enthalpies of sublimation or vaporization, consistent with the weaker interactions in media. Further, the vdW interactions in media are expected to follow the “like dissolves like” pattern, in which the same types of atoms interact more strongly than different types (Israelachvili 1992). In contrast, all empirical force fields are based on the Slater–Kirkwood equation or “combinatorial rules,” which assume that interaction energy of different types of atoms, A and B, is intermediate between A–A and B–B energies.

As follows from this discussion, the in vacuo molecular mechanics potentials are not appropriate for calculations of interatomic forces and energies in media. For example, all protein–protein and protein–lipid attractive forces are strongly overestimated and conceptually incorrect (they do not follow the “like dissolves like” rule) in molecular dynamics simulations with explicit lipids and water. Better energy functions can be derived from thermodynamic parameters of protein folding, ligand binding, crystal dissolution, or melting (the processes that occur in condensed media), rather than from heats of sublimation or vaporization describing transitions of condensed phases to gases (Murphy and Gill 1991; Eriksson et al. 1992; Robertson and Murphy 1997; Funahashi et al. 2001; Guerois et al. 2002). However, the parameters of distance-dependent (r⁻⁶) potentials have only recently been estimated from such thermodynamic data (Lomize et al. 2002). The depths of the potentials, specifically in the protein interior, were smaller than in molecular mechanics and followed the “like dissolves like” rule, as expected. Apparently, these potentials can also be applied for protein complexes in bilayers and micelles, as follows from results of this work. However, interactions across water would be weaker (Lomize et al. 2002).

We have found that electrostatic interactions of α-helices are relatively weak. Surprisingly, any value of dielectric constant between 4 and 8 could satisfy our limited set of data. These values of ɛ are consistent with experimental measurements of dielectric constant in different biological membranes, which vary from 3.5 to 7 (Radu et al. 1996; Polevaya et al. 1999; Ermolina et al. 2001; Hughes et al. 2002) and represent an average value for the protein and lipid components (Hianik and Passechnik 1995). At first glance, ɛ ~4–6 seems too high, because ɛ is ~2 in pure “black” bilayers (Benz et al. 1975) and often assumed to be between 3 and 4 in proteins (Gilson and Honig 1986). However, the experimental values of ɛ in the protein core can actually vary from 5 to 20, depending on local packing density of the polypeptide chain and penetration of single molecules of water (Ramesh et al. 1997; Dwyer et al. 2000; Mertz and Krishtalik 2000; Cohen et al. 2002). At lower packing densities or higher temperatures, the polypeptide chain becomes more flexible, which facilitates relaxation of the peptide dipoles in the electric field (Sham et al. 1998), thus increasing ɛ of dry synthetic polypeptides up to 20 (Tredgold and Hole 1976). The value of 4 can be considered as a lower limit for proteins that was observed in tightly packed crystals of acetamide and silk-like polypeptides (Tredgold and Hole 1976; Lide 2003).

Protein–lipid interactions

Association of α-helices is also mediated by peptide–lipid interactions. These interactions were treated here using an implicit solvation model, which operates with empirical transfer free energies (per squared Å) for different types of atoms determined from partition coefficients of organic compounds (Table 5). The transfer energies (atomic solvation parameters) include enthalpic and entropic components that may show up in various ways (Seelig 1997; Heerklotz and Epand 2001). For example, the GpA dimer is partially stabilized by a small entropic contribution (Fisher et al. 1999) that may originate from the gain of conformational freedom by detergent molecules that are released during association of the peptides, similar to annular lipids (Marsh and Horvath 1998; Lee 2003). Such entropic effects are difficult to reproduce in simulations with explicit lipids. Therefore, we prefer the implicit solvation model. Importantly, this model yields attractive protein–lipid interactions that destabilize the complexes (ΔG_trnsf > 0 in Table 2).

The implicit solvation model has certain limitations. First of all, the atomic solvation parameters may depend on a specific experimental system. For example, the transition of lipid bilayers to gel phase or addition of cholesterol decreases water-membrane transfer energies of hexane and benzene (DeYoung and Dill 1988, 1990). This can be interpreted as reduced solvation parameters of aliphatic and aromatic carbons, which would promote helix–helix association in the presence of cholesterol, as has actually been observed for several peptides (Mall et al. 2001; Cristian et al. 2003). It has also been found that aggregation of α-helical peptides can be modulated by replacing a detergent or lipid, although the corresponding energetic effects are relatively small, ~1.5 kcal/mole for dimers (Mall et al. 2001; Fleming 2002; Gratkowski et al. 2002), and ~2.7 kcal/mole for M2 tetramer (Cristian et al. 2003), that is, ~0.7 kcal/ mole per α-helix. Such effects may be explained by different factors that were not considered here, such as lateral pressure, hydrophobic mismatch, or specific interactions with detergent head groups.

Furthermore, the implicit solvation model can be applied only in liquid solvents whose interactions with a solute have been reduced and averaged because of the high mobility and lower density of the liquid state. The tight specific binding of a solvent molecule to a protein cavity is an entirely different situation that was observed for certain large-to-small mutants of bacteriorhodopsin (see Results). The stabilities of such mutants are probably improved by solid-state interactions with the water or lipid molecules attached to the rigid protein core, a situation that can be treated only using explicit interatomic potentials.

It is the binding of solvent molecules that probably explains the unusually high proportion of stability-enhancing mutations in membrane proteins (Bowie 2001; Howard et al. 2002). The specific binding of solvent may be more typical for membrane than water-soluble proteins for two reasons. First, the interiors of transmembrane channels, receptors, and transporters have a higher content of polar residues, which facilitate formation of H-bonds with bound water. Second, the lipid molecules can stick to shallow clefts in proteins, because they have a reduced mobility in the liquid crystalline state. The corresponding stability gain associated with tight solvent binding can be as high as 2 kcal/mole, judging from deviations of ΔΔG values in Table 4.

Other energy contributions

The results of our work suggest that immobilization of molecules during their binding costs very little (<1 kcal/mole for a dimer), no matter whether this is protein–ligand binding in water or association of α-helices in micelles (Tables 1, 2). This is in agreement with the earlier cross-linking studies of protein dimers (Yu et al. 2001). The small value of immobilization free energy can be explained by considering it as a sum of the corresponding enthalpic and entropic components ΔH_imm and -TΔS_imm (Yu et al. 2001). The value of -TΔS_imm should not exceed fusion entropy of rigid asymmetric molecules, which can be approximated by a constant of ~3.9 kcal/mole at 300 K, according to Walden’s rule (Chickos et al. 1999). Indeed, the corresponding entropic contributions were found to be ~3.0 kcal/mole and ~2 kcal/mole for dimerization of proteins and crystallization of water, respectively (Dunitz 1994; Tamura and Privalov 1997; Yu et al. 2001). The enthalpy of immobilization, ΔH_imm, originates from loss of kinetic energy that has been transformed to heat during the nonelastic collision of two molecules. The kinetic energy of a molecule is ¹/₂NkT (where N is the number of degrees of freedom; Wannier 1966), that is, ~−1.8 kcal/mole at 300 K (N = 6). Finally, the ΔH_imm - TΔS_imm value must be less than 2 kcal/mole for dimerization of asymmetric molecules in three-dimensional space, and even smaller in two-dimensional membranes.

Importantly, the transmembrane oligomers with larger buried surfaces are not necessarily more stable, just as with complexes of water-soluble proteins (Brooijmans et al. 2002). The energy of vdW interactions and H-bonds increases with the number of interatomic interactions: It is −18 kcal/mole in MS1 dimer and −29 kcal/mole in MS1 trimer (Table 2). However, this energy gain is almost cancelled by the growing destabilizing contributions, such as transfer energy (peptide–lipid interactions) and side-chain conformational entropy. Indeed, all stabilizing and destabilizing energy terms are expected to increase simultaneously with the number of atoms, and their balance depends on fine details of the structure, such as close packing, formation of specific H-bonds, or clustering of aliphatic, aromatic, and polar side chains. The total energy can be zero or positive. Thus, only complementary domains, with negative binding energy, will aggregate in biological membranes.

Materials and methods

Experimental binding free energies

The noncovalent binding of two molecules, A and B, can be considered as a generalized chemical reaction, A + B = AB. The condition for equilibrium is that

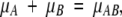(1)

or

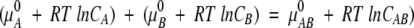(2)

Thus

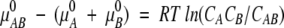(3)

where each C_X is the equilibrium concentration of species X = A, B, or AB, μ_X = μ_X⁰ + RTlnC_X is the chemical potential of X, and μ_X⁰ is the standard chemical potential of X.

The theoretical energy of binding represents the difference of standard chemical potentials, ΔG_clc = μ_AB⁰ − (μ_A⁰ + μ_B⁰), and it should be compared with the corresponding experimental energy determined from the equilibrium concentrations, C_A, C_B, and C_AB:

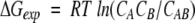(4)

Importantly, all concentrations in equations 2–4 must actually be defined as C_A/C_A⁰, C_B/C_B⁰, and C_AB/C_AB⁰, where C_A⁰ = C_B⁰ = C_AB⁰ = 1 mole (Alberty 1983; Gilson et al. 1997). Therefore, the equilibrium constant, K_AB = C_AB/C_AC_B, is a dimensionless quantity.

Experimental binding energy depends on concentration units applied in equation 4. For example, ΔG_exp describing self-association of a peptide in the presence of detergent can be defined using: (1) mole peptide concentrations in water, (2) mole fractions (moles of peptide per 1 mole of detergent), or (3) moles of peptide in 1 L of detergent. This yields three different values, ΔG^aq, ΔG^MF, and ΔG^deterg, respectively, which are related as follows:

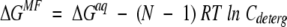(5)

where C_deterg is the concentration of detergent, N is the number of molecules in the complex (N = 2 for dimer, N = 3 for trimer, etc.), and

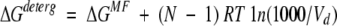(6)

where V_d is the partial volume of the solvent (detergent or lipid), in units of centimeters cubed per mole. For example, the ΔG^aq, ΔG^MF, and ΔG^deterg values for dimerization of glycophorin A in C₈E₅ micelles are −9 kcal/mole (Fleming et al. 1997), −7 kcal/mole, and −6.4 kcal/mole, respectively. The applicability of equation 5 has been justified previously (Fleming 2002; Fleming et al. 2004).

It has been emphasized that only mole concentrations, not mole fractions, can be applied for extracting the standard free energies (Ben-Naim 1980; Holtzer 1994, 1995). Thus, we used molarity units in all cases, including protein–ligand binding in water (Table 1), partitioning of model compounds (Table 5), and oligomerization of α-helical peptides (Table 2). However, because the peptides are highly hydrophobic, they are dissolved in detergent or lipid pseudo-phases, not in water. Therefore we used ΔG^deterg. Nevertheless, the corresponding mole fraction-based energies, ΔG^MF, could also serve as a reasonable approximation (Lear et al. 2001; Mall et al. 2001; Fleming 2002), because they are very close to ΔG^deterg, with a difference of only 0.6 kcal/mole for binding of two molecules in detergents (N = 2, V_d ~350 cm3) and 0.2 kcal/ mole in lipids (V_d ~750cm³), as follows from equation 6.

To summarize, we assumed that hydrophobic peptides are dissolved in the detergent or lipid phases, and that law of mass action can be applied to determine their experimental self-association free energies (Fleming 2002), as long as the following conditions are satisfied: (1) The peptide–detergent molar ratio is sufficiently low to have less than one peptide molecule per micelle (Fig. 1 ▶); (2) C_deterg is significantly higher than the critical micelle concentration (the presence of nonmicellar detergent was neglected); and (3) peptide concentrations are expressed in proper units. All these conditions were satisfied for data in Tables 2 and 3.

Theoretical association free energies

The theoretical binding energies, ΔG_assoc, were calculated using our program Assembl and three-dimensional models of the complexes as input. They represented a difference of the energies calculated for the complex and individual molecules (subunits):

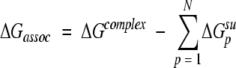(7)

The energies of the complex and subunits were represented as follows:

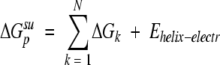(8)

where E_helix-electr is the energy of electrostatic interactions of TM α-helices, ΔG_k is the contribution of residue k, and N is number of residues. The contribution of residue k included transfer and interaction energies of its atoms, averaged over all side-chain conformers of residue k, and conformational entropy of this residue:

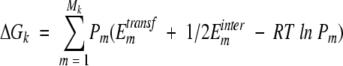(9)

where P_m, E_m^transf, and E_m^inter are occupancy, transfer energy, and interaction energy of conformer m, respectively, and M_k is number of side-chain conformers of residue k. The 1/2 multiplier appears in equation 9 because the interaction energy of residues k and l will be summed twice. The contributions ΔG_k were included only for “active” residues, which form the interaction interface between the subunits in a complex. A residue was considered as active if it had at least one contact (the distance between closest atoms <7 Å) with another subunit. Operating with only active residues served to reduce the errors associated with summation over a large set of pairwise energies dependent on imprecisely determined atomic coordinates. The set of active residues was further limited during calculations of ΔΔG values for bacteriorhodopsin mutants by including only α-helical segments around the substituted residue.

Transfer energy of residue k in conformer m from the external environment (water or lipid) to protein interior was defined as follows:

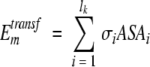(10)

where σ are the corresponding water–protein or lipid–protein atomic solvation parameters from Table 5, and ASA_i is accessible surface area of atom i.

Interaction energy of conformer m of residue k with other active residues was defined as follows:

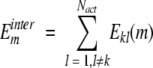(11)

where interaction energy of residues k and l is defined as follows:

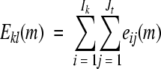(12)

where e_ij is the interaction energy of atoms i and j that belong to residues k and l, respectively, and I_k and J_l are numbers of atoms in residues k and l. During the calculations, side chain of residue k occupies conformer m, whereas residue l occupies its conformer present in the experimental structure or model of the complex. Thus, the averaging of side-chain conformers was done individually for each residue k, rather than for clusters of interacting amino acid residues. We have not included here torsion energy and side-chain–backbone vdW interactions within the same α-helix, which were assumed to be unchanged during binding.

The conformer occupancies, P_m in equation 9 were defined as follows:

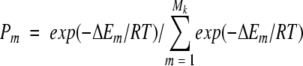(13)

where ΔE_m is the relative energy of conformer m:

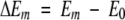(14)

E₀ is the lowest energy, and

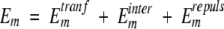(15)

The potentials for vdW interactions and H-bonds were used as 6–12 and 10–12 functions, respectively, with softened repulsions (Kuhlman and Baker 2000; Lomize et al. 2002):

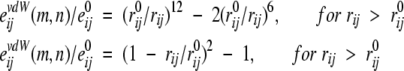(16)

for vdW interactions, and

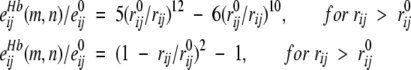(17)

for H-bonds, where r_ij is the distance between atoms i and j, e⁰ _ij is energy at the minimum of the potential, and the equilibrium distances, r⁰_ij, were taken from ECEPP/2 (Momany et al. 1974). The repulsions were softened, because the experimental coordinates of atoms are determined with a precision of ~0.3 Å, which would produce significant errors in the calculated energies.

The electrostatic interactions between large systems of oriented peptide dipoles in α-helices were calculated with partial atomic charges from CHARMM:

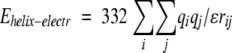(18)

where atoms i and j belong to backbones of different α-helices (including polar hydrogens).

The repulsion energy, E_m^repuls, was added in equation 15 to exclude all sterically forbidden side-chain conformers. It was calculated similar to E_m^inter (equations 11 and 12), except that interaction energy of atoms i and j was defined differently:

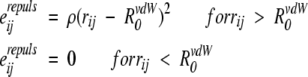(19)

where R₀^vdW are radii of Chothia reduced by 0.1 Å, and the weight factor, ρ, was chosen to be 3 kcal/moleŲ. We have also assumed that repulsion energy does not change during peptide–peptide association. Therefore, E_m^repuls was not included directly in binding energy (equation 9) and could only affect conformer occupancies.

The calculations for ligand–lysozyme complexes were accomplished as described above, using water–protein atomic solvation parameters. The distance cutoff defining the set of active residues was reduced to include only 19 lysozyme residues around the ligands. These residues were mostly inaccessible to water; their side chains were considered as rigid during calculations. The ligand binding energy included interactions between all active lysozyme residues in the bound and ligand-free protein structures, in addition to the protein–ligand interactions, as follows from equations 7 and 8. Conformational entropies of ligands were estimated simply from the number of their conformers, that is, 3 and 9 (0.7 kcal/mole and 1.1 kcal/mole) for izobutylbenzene and n-butylbenzene, respectively. Torsion energy was included for χ angles of active residues, as described previously for protein mutants (Lomize et al. 2002). Total contribution of torsion energy did not exceed 0.5 kcal/mole.

Determination of solvation parameters in membranelike environments

The required σ^{lipid → protein} parameters were defined as differences of the corresponding σ^{water → protein} and σ^{water → lipid} energies, where σ^{water → protein} values were obtained previously from mutagenesis data for water-soluble proteins (Lomize et al. 2002), and σ^{water → lipid} parameters were determined here based on experimental transfer energies of model compounds from water to non-polar solvents. Importantly, all transfer energies had to be obtained based on mole concentrations of the solutes rather than mole fractions (Ben-Naim 1980; Radzicka and Wolfenden 1988; Holtzer 1994).

The required σ^{water → lipid} value was estimated first for aliphatic carbon. Transfer energies of aliphatic compounds from water to nonpolar solvents, micelles, and bilayers are slightly different. For example, transfer energies of hexane from water to hexadecane or DMPC vesicles are −6.1 or −5.4 kcal/mole, respectively, based on data of Abraham et al. (1994) and DeYoung and Dill (1990). The most reliable estimate here can be obtained using the “consensus” increment value of a CH₂ group, which is 0.7 kcal/mole (Heerklotz and Epand 2001). This yields σ = 25 cal/moleŲ for aliphatic carbon with radii of Chothia (ASA of CH₂ group is 28 Ų), consistently with 20–26 cal/moleŲ, which is usually applied for hydrocarbons (Richards 1977). The σ of aromatic carbon was nearly the same in all considered water–solvent systems, ~19 cal/moleŲ (Table 5). This was expected, because transfer energies of benzene (as a representative aromatic solute) from water to hexadecane, SDS micelles, and DMPC vesicles are almost identical, −2.9, −2.8, and −2.8 kcal/mole at 300 K, respectively, judging from the corresponding partition coefficients (DeYoung and Dill 1988; Abraham et al. 1994; Hussam et al. 1995).

Solvation parameters of oxygen and nitrogen are more difficult to determine than for carbon. They cannot be derived directly from the partition coefficients of polar compounds between water and bilayers or micelles, because such compounds occupy a lipid–water interface rather than the hydrophobic interior of the bilayer (Wimley and White 1993). A possible solution here comes from studies of permeability barriers across lipid bilayers. These studies show that the membrane core is much less polar than octanol (Walter and Gutknecht 1986) and can be best approximated by nonpolar solvents with one or two double bonds, such as hexadecene or decadiene (Xiang and Anderson 1994a,b). Therefore, we used partition coefficients of 16 uncharged solutes containing mostly polar and aromatic groups, which have been determined for water/1,9-decadiene and water/hexadecene systems by Xiang and Anderson (1994a^,b). The set included water, acetamide, adenine, 2′3′-dideoxyadenosine, and formic, acetic, benzoic, butyric, p-toluic, α-hydroxy-p-toluic, α-methoxy-p-toluic, α-carboxy-p-toluic, α-carbamido-p-toluic, α-naphtoic, β-naphtoic, and 9-an-throic acids. The atomic solvation parameters were determined by the least square fitting of the corresponding transfer energies, using ASA in the most extended conformers of the solutes generated using QUANTA. ASA were calculated using the subroutine SOLVA from NACCESS (Hubbard and Thornton 1993) with atomic radii of Chothia (1975), probe radius of 1.4 Å, and without hydrogens. The parameters obtained for polar atoms decrease with the number of double bonds in a solvent (zero in decane, one in hexadecene, and two in decadiene; Table 5). The final parameters were taken as for hexadecene.

The solvation parameter of sulfur was estimated using the “water–hydrocarbons” data set, which combined transfer energies from water to decane (16 polar solutes) and from water to hexadecane (18 nonpolar solutes: pentane, hexane, heptane, octane, nonane, benzene, butylbenzene, pentylbenzene, naphthalene, biphenyl, anthracene, phenantrene, pyrene, perylene, phenylmethyl sulfide, buthylthiol, diethyl disulfide, and di-n-propyl sulfide) (data from Abraham et al. 1994^; Xiang and Anderson 1994a).

Abbreviations

• vdW, van der Waals interactions

• ASA, accessible surface area

• PDB, Protein Data Bank

• SDS, sodium dodecylsulfate

• DPC, N-dodecylphosphocholine

• DDMAB, N-dodecyl-N,N-(dimethylammonio) butyrate

• DMPC, 1,2 Dimytristoyl-sn-glycerol-3-phosphocholine

• GpA, glycophorin A

• MS1, QLLIAVLLLIAVNLILLIAVARLRYLVG

• L₇NL₁₁, RARL₇NL₁₁GILIN

• L₁₉, RARL₁₉GILIN

• L₁₆, KKGL₇WL₉KKA

• Y₁₆, KKGL₇YL₉KKA

• L₂₂, KKGL₁₀WL₁₂KKA

• Y₂₂, KKGL₁₀YL₁₂KK.

Article published online ahead of print. Article and publication date are at http://www.proteinscience.org/cgi/doi/10.1110/ps.04850804.