Genetic epidemiology of single-nucleotide polymorphisms

Abstract

On the causal hypothesis, most genetic determinants of disease are single-nucleotide polymorphisms (SNPs) that are likely to be selected as markers for positional cloning. On the proximity hypothesis, most disease determinants will not be included among markers but may be detected through linkage disequilibrium with other SNPs. In that event, allelic association among SNPs is an essential factor in positional cloning. Recent simulation based on monotonic population expansion suggests that useful association does not usually extend beyond 3 kb. This is contradicted by significant disequilibrium at much greater distances, with corresponding reduction in the number of SNPs required for a cost-effective genome scan. A plausible explanation is that cyclical expansions follow population bottlenecks that establish new disequilibria. Data on more than 1,000 locus pairs indicate that most disequilibria trace to the Neolithic, with no apparent difference between haplotypes that are random or selected through a major disease gene. Short duration may be characteristic of alleles contributing to disease susceptibility and haplotypes characteristic of particular ethnic groups. Alleles that are highly polymorphic in all ethnic groups may be older, neutral, or advantageous, in weak disequilibrium with nearby markers, and therefore less useful for positional cloning of disease genes. Significant disequilibrium at large distance makes the number of suitably chosen SNPs required for genome screening as small as 30,000, or 1 per 100 kb, with greater density (including less common SNPs) reserved for candidate regions.

During most of the 20th century geneticists attributed polymorphism to an equilibrium between opposing selective forces (1, 2). This approach was brilliantly successful with sex determination in Hymenoptera (3), inversions in Drosophila pseudobscura (4), and malaria-dependent polymorphisms (5), but it was overtaken by the sheer numbers of polymorphisms revealed through blood groups, isozymes, and, ultimately, by DNA itself. The first human polymorphism was reported in 1901 (6), and it took a generation to identify the second polymorphism (7). There were 17 polymorphic blood groups recognized in the 1960s (8) when isozymes took center stage. About 150 protein polymorphisms were known in the '80s (9), when they were superseded by nucleotide markers. Restriction fragment length polymorphisms (RFLPs) soon were overshadowed by sequence polymorphisms revealed through the PCR. They include variants of repeat number, of which about 30,000 microsatellites have been most useful for positional cloning of disease genes by linkage and allelic association (10, 11).

During the past 3 years interest has shifted to nonrepetitive sequence variants, by far the most common of which are single nucleotide polymorphisms (SNPs). It is generally believed that the complete human sequence will reveal at least a million SNPs in nonrepetitive sequences of coding regions, including introns and promoters (12). Most SNPs must be quasi-neutral, but a proportion contribute to disease susceptibility and resistance. Current technology does not lend itself to SNP identification in repetitive sequences, which account for most of the genome and make an unknown contribution to disease. This uncertainty polarizes human genetics. On the causal hypothesis a large collection of SNPs includes almost all genetic determinants of disease, and, therefore, allelic association among SNPs is of little interest (13). On the proximity hypothesis most genetic determinants of disease will not be included even in a sample of several hundred thousand SNPs, and, therefore, allelic association with nearby SNPs is an essential factor in positional cloning (14). On both hypotheses the magnitude of gene effect, measured as a relative risk, logit, or variance component, is critical. Detection of small effects requires huge samples on the causal hypothesis and much larger samples on the proximity hypothesis. Neither extreme view is plausible, but the roles of local and global polymorphisms, repetitive sequences, and other relevant factors are, at present, too obscure to anticipate how often the causal hypothesis will be correct in any particular collection of SNPs. Therefore, allelic association among SNPs is an object of current interest, which we now address.

Materials and Methods

Although methods are being developed to measure allelic association when haplotypes are unknown, we confine ourselves here to autosomal haplotypes determined through family studies (or perhaps in the future through other methods). Recent studies of SNPs do not ascertain haplotypes, but many haplotypes for nonrepetitive sequences were published in the decade after 1982 and report diallelic RFLPs, most of which are SNPs that alter a restriction endonuclease recognition site. We therefore distinguish two types of markers: diallelic RFLP polymorphisms, which we call SNPs, and multiallelic markers (mostly microsatellites) dichotomized by association with a major disease gene, which we call non-SNPs. There are three samples of data.

(i) Haplotypes bearing a major disease gene and two or more SNPs or non-SNPs. The latter give an estimate of association because they have been dichotomized as in Table 1.

Table 1.

SNP haplotypes (15)

Younger SNP1		Older SNP2
		Allele 1	Allele 2	Total
Allele 1	Number	a	b	a + b
	Frequency	Qρ + QR(1 − ρ)	(1 − ρ)Q(1 − R)	Q
Allele 2	Number	c	d	c + d
	Frequency	(R − Q)ρ + R(1 − Q)(1 − ρ)	(1 − R)[ρ + (1 − Q)(1 − ρ)]	1 − Q
Total	Number	a + c	b + d	N
	Frequency	R	1 − R	1

Covariance: D = ρQ(1 − R). Correlation: Δ = ρ√Q(1 − R)/R(1 − Q). Gene frequency difference: d = ρ(1 − R)/ (1 − Q) or ρQ/R. 

(ii) Case-control studies of major disease genes that have been accurately localized. Cases are heavily enriched, and the major gene is of such large effect that it can be assigned to a haplotype.

(iii) Random haplotypes with two or more SNPs.

For each sample we searched the literature and captured samples without regard to whether they showed a relation between association and physical distance, which was recorded in kb to one decimal place. To measure association we used ρ (Table 1), which (unlike D, Δ, d, etc.) is not confounded with gene frequencies and therefore can take the value 1 for a monophyletic allele (15). This is unambiguous for the first two samples, of which the second makes exact allowance for a known enrichment factor ω. An approximate allowance can be made by δ (16). For sample 3 there is ambiguity about which SNP is of more recent origin and therefore analogous to a major disease gene. Table 1 may be rearranged by interchanging alleles for either or both SNPs, which themselves may be interchanged. The arrangement most consonant with SNP₁ as the younger polymorphism has ad ≥ bc and Q(1 − R) ≤ R(1 − Q), which implies b ≤ c. This is one of the two solutions provided by the statistic D′, the other being negative and irrelevant (17). The objective of D′ is to give a maximum absolute value in the ±1 interval, but the relation to ρ has not been recognized (18). The statistic denoted by λ,δ,δ* and P_excess approaches ρ as Q approaches zero, but is not appropriate for pairs of polymorphisms (15, 16). On the null hypothesis of no association χ₁² = Δ²n = ρ²K, where the information about Δ is n and the information about ρ is K = nQ (1 − R)/R(1 − Q). For a given sample size n there is much variation in K. Neither measure of information allows for accumulated drift or variation among loci and regions. Therefore, a parsimonious model leaves a residual χ² that is often significant, especially when regions are pooled to sample the genome. Then, the ratio r of residual χ² to its degrees of freedom (assumed large) gives an empirical error. If χ_q² is a test of a model with q estimated parameters, χ_q²/r is its adjusted value. If σ is a standard error assuming homogeneity, σ√r is its adjusted value allowing for residual heterogeneity (15).

Single locus tests of association are inappropriate with dense SNPs. The Malecot model provides a multiple-pairwise test based on ρ, making the heavy discount of a Bonferroni correction unnecessary. The Malecot equation, originally proposed for populations isolated by distance (19), is ρ = (1 − L)Me^−ɛd + L, where M = 1 if SNP₁ is monophyletic and less than 1 otherwise, d ≥ 0 is distance on the genetic or physical map, and L is the bias from the constraint ρ ≥ 0. The parameter ɛ ≥ 0 depends on the number of generations during which the haplotypes have been approaching equilibrium and also on the ratio z between the physical and genetic maps if the former is used for d. Each estimate of ρ is weighted by its information to give the composite likelihood (15).

For a single region the estimate of L is usually not significantly greater than 0 on the scale (genetic or physical) chosen to minimize residual χ² (15, 20). However, when regions are pooled, they must have the same scale. We chose the physical map as more useful and usually more accurate. Pooling regions with different values of ɛ generates heterogeneity, and large values of d are preferentially reported from regions with small values of ɛ, inflating L. Estimates of ɛ and M are stable when large values of d are censored. Under the model the estimated duration when d is expressed in kb is 10⁵zɛ generations if z is given as Mb/cM, the scaling factor 10⁵ representing the product of 1,000 kb/Mb and 100 cM/Morgan (15). This analysis was performed by the allass program, which is available with these data from http://cedar.genetics.soton.ac.uk/public_html/.

Results

We found that all samples have residual heterogeneity, which is incorporated in estimates of standard errors and heterogeneity χ² (Table 2). The three samples from haplotypes bearing a major disease locus are in reasonable agreement and closely resemble region-specific analyses except for inflation of L (20). However, heterogeneity among samples is significant (χ₆² = 32.97), presumably because heterogeneity within and among regions is confounded. The estimate of ɛ when the three samples are pooled is .0028, corresponding to a swept radius 1/ɛ of 357 kb. Because tθ = ɛd, the swept radius estimates the distance in kb at which disequilibrium falls to e⁻¹ ≈ .37 of its initial value. This is consistent with many instances of mapping by allelic association over 50- to 500-kb intervals (15, 20–24). Because the duration of major disease loci is short (approximately 10⁵ɛ or 280 generations on the assumption of 1 Mb/cM), it is not surprising that SNPs and non-SNPs give similar results: differences in mutation rate are unlikely to play an important role over such a short time. For SNP × SNP haplotypes the residual χ² is much greater for the correlation Δ weighted by its information n than for ρ weighted by information K.

Table 2.

Estimates of association parameters

Markers		ε	σε	L	σL	M	σM	Residual χ2
First	Second							ρ	Δ	df
Haplotypes with major disease locus
S	S	.0019	.0004	.1505	.0561	.7663	.0319	1316.78	2707.38	352
D	S	.0032	.0040	.1715	.0961	.6378	.2039	482.35	—	48
D	N	.0028	.0008	.2830	.0308	1.0000	.1016	570.41	—	67
All	All	.0028	.0004	.2520	.0207	.7636	.0352	2547.10	—	473
Random haplotypes
S	S	.0038	.0014	.1810	.0621	.6031	.0356	3610.54	5991.64	549
Total		.0032	.0005	.2432	.0204	.6340	.0248	6434.83	—	1025

S, SNP; N, non-SNP; D, major disease locus. 

The only surprising aspect of these data is the close similarly between disease and random haplotypes, with no evidence for a long duration of the latter. The swept radius 1/ɛ is 263 kb, corresponding to a duration of about 380 generations. When distances greater than 1,500 kb are censored, the estimate of L in the whole data drops to .099 and ɛ is reduced to .00187, corresponding to a duration of about 187 generations and a swept radius of 535 kb. These results are in sharp contrast with a recent simulation from which it was inferred that “a useful level (of linkage disequilibrium) is unlikely to extend beyond an average distance of roughly 3 kb in the general population” (14). How can these conflicting results be explained, since they cannot be reconciled?

Discussion

Genetic drift may increase or decrease ρ, but its effect on φ = E(ρ²) is predictable. The general theory for φ was developed by Sved (25), which, with slight modification (26), may be expressed as φ_t = φ_rt + φ_ct, where

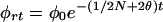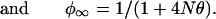The basic parameters are the effective size N, assumed constant, and the recombination rate θ. This may be generalized by replacing t/2N with .5 Σ(1/N_i) = t/2N*, where N* is the harmonic mean of the N_i (27). Although the vector of the N_i determines the opportunity for genetic drift, the order of the elements is irrelevant: a population that contracts from 1,000 to 10 is exactly equivalent to one that expands from 10 to 1,000 so long as the values of the N_i, and, therefore, N*, are the same, although subsequent opportunity for drift is different. Recent interest in nonexpanding populations contravenes this principle (28, 29).

We also may generalize θ to (1 − w)(1 − c) ∼ w + c, where c is the true recombination rate and w is the coefficient of recall resulting from the linear pressure of selection, migration, and mutation (19). Introducing migration and mutation raises the possibility of polyphyletic origin, which multiplies each φ by a function that is estimated in the Malecot equation by M² if φ₀ = 1. Kinship between a pair of SNPs is φ_t in the current population, t generations from founders with kinship φ₀, and E(ρ_t) = √φ_t. Two processes act to make φ_t different from φ₀. First, remote kinship φ_rt diminishes with t, approaching 0 as t approaches ∞. Second, close kinship φ_ct builds up from an initial value of 0 in founders to some equilibrium value φ_∞ that is indeterminate unless effective population size is constant. If Homo sapiens had an effective population size of 710 when migration from Africa took place 5,000 generations (100,000 years) ago, increasing to 10⁹ today, the doubling time would be 245 generations, or nearly 5,000 years, and the effective size would be 10,000, in good agreement with other evidence that does not assume monotonic expansion (30, 31). Even this small value of N* makes 1/2N* negligible by comparison with 2θ at a distance of 10 kb, assuming the rough approximation that 1 cM corresponds to 1 Mb. If θt is small, we therefore may neglect φ_ct for the human species and conclude that kinship between SNPs that are highly polymorphic in all major ethnic groups is almost entirely determined by ρ₀, the association among regional founders (26).

At the opposite extreme are the local polymorphisms that have been a focus for Amerindian studies, with an estimated age of 100–400 generations (32). For small values of N*, the contribution of φ_ct may not be negligible, fueling the hope that isolates may make a special contribution to positional cloning through combination of monophyletic origin (M) ≈1, low age (t), and perhaps subsequent drift (φ_ct). However, this hope is not well supported (26). SNPs that are weakly polymorphic and perhaps limited to a single ethnic group are especially interesting because of the possibility that they are of relatively recent origin and/or reduced fitness. They therefore may contribute disproportionally to disease and to close association with causal SNPs. Many RFLPs that have been used in positional cloning of major genes are weakly polymorphic.

Success in positional cloning of oligogenes is likely to depend less on population structure than on the fraction of SNPs in a candidate region that are causal for a particular disease. A sample of 500,000 SNPs would give a density of about 1 per 6 kb, whereas the density of SNPs in cDNA may be 2–10 times as great, depending on recognition in repetitive sequences (12). Typing a large number of SNPs increases the proportion that are causal, but power to detect noncausal association increases more slowly. Selection of SNPs polymorphic in all major ethnic groups may be counterproductive, because they are likely to be neutral and in weak disequilibrium with causal SNPs.

Although the samples we have examined are remarkably consistent, they are averages over heterogeneous haplotypes. Mutation rates for SNPs vary over more than three orders of magnitude, from 10⁻⁵ per generation for the single nucleotide that causes achondroplasia (34) to 5 × 10⁻⁹ for the typical nucleotide. Effective sizes for defined populations vary from less than 100 to several thousand (33). The ratio of the physical map to the genetic map is nominally 1 Mb/cM (10), but in particular regions of several Mb, it can be as large as 6 (20) or as small as .03 (35). Greater variation is likely in smaller regions. Finally, the duration t is variable, depending on chance and fluctuating population size. However numerous our species, the number of founders for a particular population has been small at critical times. Thompson and Neel (32) conjectured that the number of adults who crossed the Bering Land Bridge 40,000 years ago was less than 1,000, and similar numbers have been suggested for migrants from Africa to Eurasia 100,000 years ago and for occupation of Finland a few thousand years ago (24). Smaller numbers probably were responsible for the first settlement of Australia and the Pacific islands. The spread of agriculture and use of metals may have depended on expansion of a migrant subpopulation at the expense of sparser and less advanced cultures along a narrow frontier. The number of founders for each of these populations is infinitesimal compared with the size of the human population at that time, and the opportunity for establishment of a regional SNP that may not be polymorphic in other ethnic groups (or is associated with a different haplotype) is correspondingly greater. Because the effect of each contraction is dissipated slowly, successive contractions are, to a degree, cumulative but difficult to trace beyond the most recent coalescent. If steady expansion over thousands of years has ever occurred, it would have had different consequences from cycles of expansion and contraction that characterize real populations and haplotypes (36), which experience three types of bottlenecks. Two of these are demographic (in situ and migrational), and the third is selective. The causes of population bottlenecks in situ include epidemics, famines, massacres, ecological changes, and pressure from technologically more advanced or more aggressive neighbors. Migrational bottlenecks include settlement of uninhabited or sparsely inhabited territory and displacement of technologically less advanced or less bellicose groups. Ethnic admixture (in situ or after migration) increases association over the genome but does not require population contraction. Selection of an advantageous gene creates a bottleneck for closely linked loci as the founder haplotype increases. Such “hitchhiking” differs from a demographic bottleneck in being restricted to one small genomic region and not depending on population contraction. We believe that these mechanisms (variable recombination, mutation, and effective population size and population bottlenecks) explain the wide range of linkage disequilibrium in our data, which span many regions and (we have argued) more than one time of origin (Fig. 1). In confirmation, a recent scan of haplotypes in 54 individuals found an excess of significant associations up to several cM (37). These and other observations coincide with predictions for variable t of ρ_t as √φ_t from Sved's theory with ρ₀ = 1 (Fig. 2). The parsimonious Malecot model is a reasonable approximation to the general model with unresolvable parameters (N, θ, t, ρ₀, w).

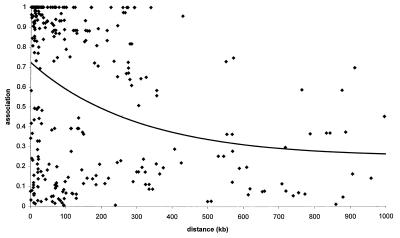
Figure 1.

Allelic association ρ for pairs of loci within 1,000 kb and K > 50, together with the Malecot equation for the whole data (ɛ =.0032, L = .2432, M = .6340).

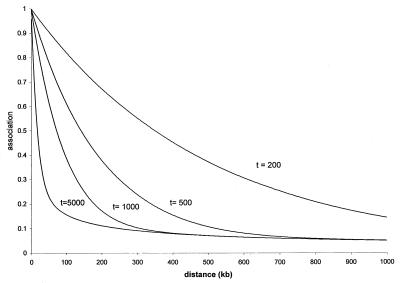
Figure 2.

Predictions of ρ with n = 10,000, ρ₀ = 1, and 200 ≤ t ≤ 5,000 generations (25).

Sved (25) derived φ_t as a probability (his formulae 4–5), but equated it to E(Δ²) in his equation 3a, although he recognized that φ_t “is calculated conditional on the observed genotypic distribution in the present generation.” We see in Table 1 that Δ² = φ only when Q = R, which conflicts with current gene frequencies and therefore with interpretation of SNP₁ as the younger polymorphism. Interchanging SNP₁ and SNP₂ when Q < R gives a smaller estimate of allelic association, say ρ′, where Δ² = ρρ′. Therefore, in a given population Δ is confounded with gene frequencies, even if it were true that on an evolutionary scale, E(R) = E(Q). On the other hand, genetic drift over cycles of expansion and contraction could make Q > R and thereby give an erroneous inference of the younger SNP. In the literature, allelic association φ has been used in two different ways, both stemming from Sved's seminal work (25). One line of descent retains φ as E(ρ²). The other accepts the approximation φ ≃ Δ², which leads to a χ² metric that is especially convenient with multiple alleles when there is insufficient information to dichotomize them (21). An alternative is to make all r!/2 hierarchical dichotomies of r alleles and scale the total information by 2/r!. Although we have been principal offenders in using the χ² metric, we believe that for diallelic loci and dichotomized alleles it should be abandoned in favor of ρ, which has better theoretical qualifications, has been successful in positional cloning of major loci, and in the data reported here gives much smaller values of residual χ².

A far richer body of data will become available as SNP haplotypes are reported from different populations. Effective use of this material requires consensus about how allelic association should be measured. Estimates of parameters that are confounded with allele frequencies should be abandoned. Whatever measure of allelic association is used, the swept radius in which there is useful association is likely to be greater than 100 kb and, therefore, to contain many SNPs. An individual heterozygous for n SNPs has 2ⁿ possible haplotypes, each of unknown history and systematic pressure. The latter is not readily distinguished from low recombination, low mutation, or chance, because in the absence of selection the SD of a conserved segment is large relative to the mean (25). Multiple locus analysis of such material is inconceivable with current methods, but multiple pairwise analysis with the Malecot model is not difficult, even if association is estimated without haplotyping. Such high resolution is feasible after a candidate region has been defined by linkage, sequence, function, or coarse allelic association. Because the swept radius is two orders of magnitude greater than was suggested by simulation of monotonic population expansion, the number of SNPs required for a cost-effective genome scan is correspondingly reduced to 30,000 or less if the gene density and ratio of the physical to the genetic map are used adaptively. Because few of these SNPs would be disease determinants, high-resolution tests within a candidate region are indispensable.

Abbreviations

SNP

single-nucleotide polymorphism

RFLP

restriction fragment length polymorphism