Cooperativity, connectivity, and folding pathways of multidomain proteins

Abstract

Multidomain proteins are ubiquitous in both prokaryotic and eukaryotic proteomes. Study on protein folding, however, has concentrated more on the isolated single domains of proteins, and there have been relatively few systematic studies on the effects of domain–domain interactions on folding. We here discuss this issue by examining human γD-crystallin, spore coat protein S, and a tandem array of the R16 and R17 domains of spectrin as example proteins by using a structure-based model of folding. The calculated results consistently explain the experimental data on folding pathways and effects of mutational perturbations, supporting the view that the connectivity of two domains and the distribution of domain–domain interactions in the native conformation are factors to determine kinetic and equilibrium properties of cooperative folding.

Our understanding of protein folding has been deepened by the combined efforts of experimental, theoretical, and computational studies of the last decade. Energy landscape theory describes folding as the stochastic relaxation process on the free energy surface of conformational change, where the free energy surface is determined by the compromise of conformational entropy of the polymer chain and interaction energies to stabilize the native conformation (1–3). Because proteins can fold when interactions that stabilize the native conformation dominate over the nonnative interactions that may trap the chain into the irrelevant structures, protein folding can be approximately simulated by using the interaction potentials that are derived from the knowledge of the native structure. With such structure-based models, folding of various small proteins has been simulated, and quantitative agreement between simulations and experiments has been reported (3). The agreement has been improved by simulations that further take account of the residue-dependent energetic differences (4), the atomistic packing (5–7), or the hydration structure (8), and such agreement has convinced us that the topology of the native structure is the primary determinant of the equilibrium and kinetic features of folding at least for small proteins (3) although the atomistic details perturb those features or they sometimes change the delicate balance among folding pathways (9, 10).

These intensive studies on folding have been predominantly focused on small, single-domain proteins or isolated single domains of larger proteins. More than 70% of eukaryotic proteins, however, are composed of multiple domains, and hence we should ask whether the principles of folding found in single domains of proteins also apply to connected multidomain proteins as well (11). Anticorrelation between the contact order and the folding rate has been observed in multidomain proteins (12), and the structure-based simulations on multidomain proteins such as the ankyrin family (13–15) and CV-N (16) have provided consistent results with experiments. The importance of interactions between domains in determining the folding behavior of repeat-containing proteins has been shown theoretically (15). These observed and simulated data suggest the decisive importance of topology of the native structure for folding kinetics in multidomain proteins, but more should be investigated to clarify how the topology determines the kinetic features. For example, when isolated individual domains that can fold and unfold independently of other domains are connected to a multidomain protein, domains would still behave independently or behave cooperatively through the domain–domain interactions. Although both cooperative folding and independent folding of domains have been observed (11), whether topology determines the cooperativity has not yet been clarified. To shed light on this problem, we here analyze the folding of the example proteins human γD-crystallin (17–22), protein S (23, 24), and a tandem array of the R16 and R17 domains of spectrin (25–28) by using a simple structure-based model and show that the model indeed captures the essential features of the folding of these multidomain proteins.

Cooperativity of folding should be intrinsically related to the connectivity of the chain. When two regions in a small, single-domain protein approach each other with the native-like steric arrangement to interact as in the native conformation, then the chain connecting these two regions should have more chance to take the native-like configuration. Similarly, when the chain connecting them is native-like, the two regions have more chance to interact to stabilize the native-like configuration. This should lead to a higher probability of realization of two states: the state in which two interacting regions and the chain connecting them are both native-like and the state in which neither two regions nor the chain are native-like. This is the cooperativity arising from the connectivity of the chain. With this cooperativity, the residues that have the native-like configuration should tend to form contiguous domains in the sequence in the course of folding, and such tendency has been highlighted by the structure-based, coarse-grained models of folding (29–39). Success of these models in describing kinetic features of various small proteins showed that connectivity is an important factor to determine the cooperativity. In a similar way, we may expect that the linker region of the chain between two domains and the domain–domain interactions should decide the cooperativity of folding of the connected two domains. In this article, we explore the relation between the cooperativity and connectivity in multidomain proteins by using a structure-based, coarse-grained model.

Results

Description of Free Energy Landscape.

As a coarse-grained variable, using m_i = 1 or 0, which represents the configuration at the ith residue, is convenient: m_i takes unity when two dihedral angles of the backbone at the ith residue are within some narrow range around values in the native state conformation and zero otherwise. The partition function is described by Z = Σ_confΠ_iν^1−m_ie^−βH with Hamiltonian H, which is expressed by a set of coarse-grained variables {m_i}. Σ_conf denotes summation over configurations. β = 1/k_BT is the inverse of temperature T, and ν is the number of nonnative configurations each residue can take. Here, for simplicity, ν is assumed to be independent of the residue position i. Then, the total number of configurations is (1 + ν)^N, with N being the total number of residues. The entropic cost for a residue to take the native configuration is σ = k_B ln ν > 0.

To analyze two-domain proteins, we define a two-dimensional reaction coordinate (x, y) by x ≡ Σ_i=1^n_Im_i and y ≡ Σ_i=n+1^Nm_i, where n_I is the number of residues in the N-terminal domain (domain I) and n_II = N − n_I is the number of residues in the C-terminal domain (domain II). x and y are order parameters to describe the native-likeness (the number of residues that take the native configurations) of domains I and II, respectively. The partition function at a fixed (x, y) is obtained by summing configurations under the constraint of (x, y) as

and the free energy is F(x, y) = −k_BTlnZ(x, y). It is also convenient to decompose the Hamiltonian into the intradomain parts, H_I and H_II, and the interdomain part V as H = H_I + H_II + V, where H_I is a sum of terms belonging to domain I, H_II is a sum of terms belonging to domain II, and V is a sum of terms of interactions between a residue in domain I and a residue in domain II. By defining the free energy surface of separated domains F₀(x, y) = −k_BTlnZ₀(x, y) with

is the difference in free energy between the connected two-domain protein and the separated two noninteracting domains [supporting information (SI) Text], where 〈⋯〉_x,y is the average taken by using Z(x, y).

Entropy at a fixed (x, y) is calculated to be S(x, y) = S_c(x:n_I) + S_c(y:n_II) + S_e(x, y) with

and S_e(x, y) = −k_Bln〈exp[β(H − E(x, y))]〉_x,y ≤ 0, where E(x, y) = 〈H〉_x,y is energy at a fixed (x, y) (the detailed derivation is explained in SI Text). S_c(x; n_I) and S_c(y; n_II) express configuration entropies of domains I and II, respectively, which arise from the total number of configurations that each domain can take under the constraint of (x, y). Notice that S_c(x; n_I) and S_c(y; n_II) do not depend on the form of Hamiltonian, so the effects of the domain–domain interactions on entropy are solely expressed in S_e(x, y): The entropy term of U(x, y) is −T[S_e(x, y) − S_e0(x, y)], where S_e0(x, y) = −k_Bln〈e^{β(H_I+HII−E₀(x, y))}〉_0x,y with E₀(x, y) = 〈H_I + H_II〉_0x,y, and 〈⋯〉_0x,y is the average taken by using Z₀(x, y). S_e(x, y) takes a large negative value when the variance in the energies of the conformations at a given (x, y) is large and S_e(x, y) ≈ 0 in the native or fully unfolded state. S_e(x, y) therefore strongly affects free energy of transition states and therefore controls the folding/unfolding process although it does not affect the free energy of the native or fully unfolded state.

We adopt the Hamiltonian

with m_ij = Π_k=i^jm_k, where Δ_i,j = 1 when ith and jth residues are close in space in the native conformation and Δ_i,j = 0 when those residues are separated in the native conformation (see Methods). When the backbone of the segment from i to j takes the native configuration as m_ij = 1, then the native pair i and j should have a large chance to come close to each other to gain energy of ε > 0 by forming a native contact. With this Hamiltonian, Wako and Saito (29, 30) described folding pathways of proteins, and much later the same Hamiltonian was used by Muñoz and Eaton and other authors to analyze the free energy landscapes and kinetics of the folding of many proteins (10, 31–37) and also was applied to protein mechanical unfolding (38) and conformational changes in protein functioning (39). Although the effects of insertion of an unfolded loop in between the native contacts should be incorporated to further improve the model (37), we here use the model of Eq. 2 that facilitates the thorough survey of free energy landscapes of large proteins. In this model, the relevant parameters are ε/k_BT and σ, where ε/k_BT should take a smaller value when the temperature is increased or denaturant is added, and σ is discussed in Methods. F(x, y), F₀(x, y), U(x, y), and other quantities discussed here can be exactly calculated without introducing any further approximation (31, 34) (SI Text). We compare F(x, y), F₀(x, y), and U(x, y) of example two-domain proteins to discuss the folding mechanisms.

Human γD-Crystallin.

Human γD-crystallin (HγD-Crys) is a 173-aa protein found in the densely packed lens nucleus of human eyes. As shown in Fig. 1, HγD-Crys has two domains, domain I and domain II, each of which consists of two intercalated β-sheet Greek-key motifs, and two domains interact to bury the surface hydrophobic patches (PDB ID: 1HK0). Although an equilibrium folding intermediate has not been observed except for the mutants (18), analyses of kinetics of unfolding and refolding have shown the existence of the intermediate state that has the unstructured domain I and the native-like structured domain II (18–22).

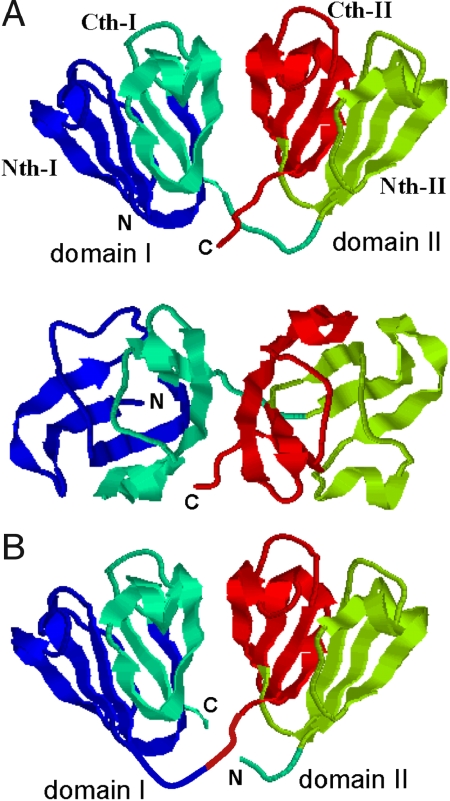
Fig. 1.

Structures of human γD-crystallin and its circular permutant. (A) Structure of human γD-crystallin (PDB ID: 1HK0) is shown by specifying four Greek-key motifs (Nth-I, Cth-I, Nth-II, Cth-II) with different colors. (B) Illustration of the structure of the circular permutant of 1HK0 proposed in this article is shown.

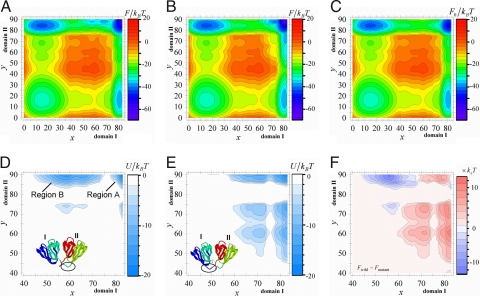
We define order parameters x and y by regarding a midpoint in the linker region as the domain boundary with n_I = 83 and n_II = 90. With this definition of two domains, the free energy landscape, F(x, y), for ε/k_BT = 0.53 is drawn in Fig. 2A. F(x, y) has four distinct minima, which correspond to the native state N_IN_II at (x, y) ≈ (83, 90), the unfolded state U_IU_II around (x, y) ≈ (15, 15), and two partially folded states, U_IN_II at (x, y) ≈ (15, 85), and N_IU_II at (x, y) ≈ (80, 15). Corresponding to two partially folded states, there are two folding pathways: Pathway I (P_I) is the route in which domain I folds first as U_IU_II → N_IU_II → N_IN_II, and Pathway II (P_II) is the route in which domain II folds first as U_IU_II → U_IN_II → N_IN_II. The barrier height of the transition U_IN_II → N_IN_II in P_II is ≈3k_BT lower than that of the transition U_IU_II → N_IU_II in P_I, whereas N_IU_II → N_IN_II in P_I and U_IU_II → U_IN_II in P_II have almost the same barrier height, so P_II is the dominant pathway with the largest folding rate and U_IN_II is the dominant on-pathway kinetic intermediate. This result agrees with the observed data on the features of the kinetic intermediate state (18–21).

Fig. 2.

Free energy profiles of HγD-Crys. (A) Free energy surface, F(x, y) for the wild type. (B) F(x, y) for the circular permutant. (C) The free energy surface of noninteracting two domains, F₀(x, y), where x(y) is the number of residues that take the native configuration in domain I(II). (D) The differences in free energy between the connected two-domain protein and the separated two noninteracting domains, U(x, y), for the wild type. (E) U(x, y), for the circular permutant. (F) The difference in free energy between the wild type and the mutant, F_wild − F_mutant. ε/k_BT = 0.53 and σ = 1.5k_B.

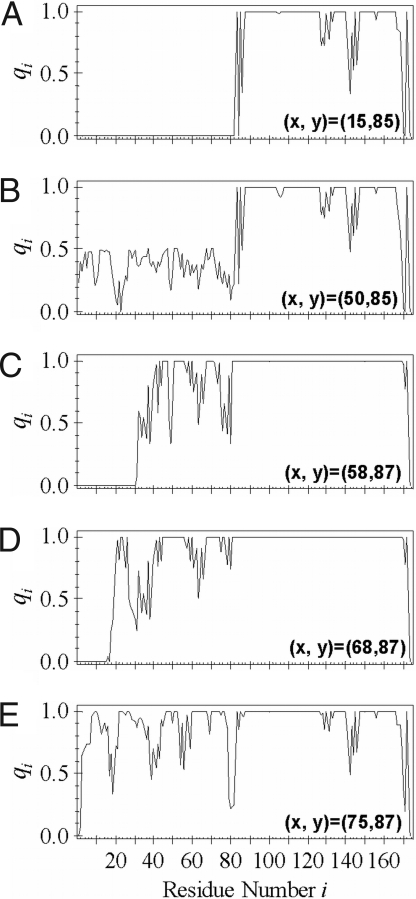
As explained in Methods, the influence q_i(x, y) of the perturbation of interactions on free energy can be used as a structural order parameter of the ith site under the constraint of (x, y). In Fig. 3, q_i(x, y) at minima (x, y) = (15, 85) and at four points around saddles (x, y) = (50, 85), (58, 87), (68, 87), and (75, 87) of the free energy surface are shown to describe how the structure is formed along P_II. As shown in Fig. 3, structure of the C-terminal half of domain I (Cth-I) develops after the completion of the structure formation of the C-terminal half of domain II (Cth-II). In this way, the folded domain II catalyzes folding of Cth-I, which then catalyzes the folding of the N-terminal half of domain I (Nth-I). The linker also should be noted to be unstable when domain I is entirely folded at (x, y) = (75, 87), whereas it is stable when only Cth-I is folded. This result shows that the linker has an important role in the kinetic process of folding of domain I, whose structural fluctuation is closely associated with fluctuation of domain–domain interactions.

Fig. 3.

Structure formation of HγD-Crys along the U_IN_II → N_IN_II process. Structural order parameters q_i(x, y) for each residue at (A) (x, y) = (15,85), (B) (x, y) = (50,85), (C) (x, y) = (58,87), (D) (x, y) = (68,87), and (E) (x, y) = (75,87) for ε/k_BT = 0.53.

Also notable in Fig. 2A is the existence of an additional free energy valley at approximately (x, y) ≈ (65, 85). The last step of folding, the formation of Nth-I catalyzed by the structured Cth-I, is the transition from this free energy valley to N_IN_II. Existence of this additional free energy valley agrees with the experimental data for an intermediate state residing in between U_IN_II and N_IN_II (21). The low free energy valley in F(x, y) at around the native state extends toward the smaller x, indicating that the native state has the larger conformational fluctuation at Nth-I. This result is consistent with the observed large B-factor at Nth-I in the crystal structure.

Asymmetry of P_I and P_II implies that domains I and II are not independent of each other but fold in a cooperative way. This can be clarified by comparing F(x, y) with F₀(x, y) and U(x, y). Because each of the two domains undergoes the two-state folding transition, the free energy surface F₀(x, y) of noninteracting two domains is a composite of two of the two-state transitions and thus has four distinct minima as shown in Fig. 2C. P_I and P_II in this case have an identical folding rate by definition. U(x, y) has negative values at around N_IN_II (Region A in Fig. 2D), showing that the domain–domain interactions stabilize the native conformation. U(x, y) has large negative values at approximately y ≈ 85 and 50 < x < 70 (Region B in Fig. 2D), which is the region around the free energy saddle in F₀(x, y). The free energy of the barrier region of the transition U_IN_II → N_IN_II in P_II is, therefore, lowered by domain–domain interactions. The lowering of the free energy along U_IN_II → N_IN_II by 5 to 10k_BT (≈10 to 20ε) than U_IU_II → N_IU_II gives rise to the dominance of P_II over P_I. In this way, the domain–domain interactions contribute to the stability of the native structure in Region A and catalyze the folding process in Region B. Because U(x, y) is almost zero along U_IU_II → U_IN_II, the model explains the observed data that the mutations that weaken the domain–domain interactions do not affect the folding rate of domain II although they lower the folding rate of domain I (20, 21).

As shown in Fig. 1A, two domains of HγD-Crys associate almost symmetrically around a twofold axis. Asymmetry of U(x, y) arises not from this symmetrical distribution of native contacts but from the asymmetrical chain connectivity. As shown in Fig. 1A, domain–domain interactions are formed mainly between Cth-I and Cth-II, whereas domains are connected from Cth-I to the N-terminal half of domain II (Nth-II). Because the native-like interactions between the two regions are formed with a higher probability when the chain connecting them is native-like, the domain–domain interactions are stabilized when the region from Cth-I through Cth-II becomes native-like. This is the reason why domain II folds first and catalyzes the folding of Cth-I. Thus, the chain connectivity is the origin of asymmetry of U(x, y).

For single-domain proteins, the importance of chain connectivity has been examined by circular permutation (40, 41). Here, we point out that circular permutation also should highlight the effects of connectivity in multidomain proteins: As illustrated in Fig. 1B, we may cut the linker between the 83rd and the 84th residues and connect the N terminus of domain I and the C terminus of domain II without changing the native contacts in the model. We here use the same domain name as in the wild-type protein: The C(N)-terminal domain of the circular permutant is called domain I(II). To stabilize domain–domain interactions in this case, the connected region composed of domain I and Cth-II should be native-like, and hence domain I should fold first. F(x, y), U(x, y), and the difference in free energy between the wild type and the mutant, F_wild − F_mutant, are shown in Fig. 2B, E, and F, respectively. The model predicts that free energy is lowered along N_IU_II → N_IN_II by 5 to 10k_BT than U_IU_II → U_IN_II, and therefore P_I becomes more favored to make N_IU_II the intermediate. In this case, it is expected that the mutations that weaken the domain–domain interactions do not significantly affect the folding rate of domain I although they lower the folding rate of domain II.

Protein S.

Myxococcus xanthus spore coat protein S is a 173-aa protein. As shown in Fig. 4A, protein S has two domains, each of which consists of Greek-key motifs (PDB ID: 1PRS). The overall structure of protein S is, therefore, similar to that of HγD-Crys (23, 24), but protein S has different structural features. Domain–domain interactions are formed mainly between Cth-I and Nth-II. From this structural pattern, we expect that the domain–domain interactions are stabilized when the region from Cth-I through Nth-II becomes native-like. This topological constraint suggests no preference of order of folding of the two domains. There are, however, minor inhomogeneities in distributions of domain–domain interactions arising from interactions between Nth-I and Nth-II in the native conformation.

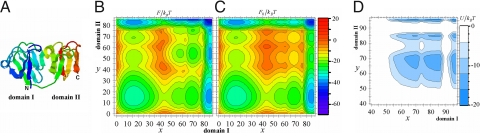
Fig. 4.

Structure and free energy profiles of protein S. (A) Structure of protein S (PDB ID: 1PRS). Shown are F(x, y) (B), F(x, y) (C), and U(x, y) (D) for ε/k_BT = 0.58.

Also shown in Fig. 4 are F(x, y) for ε/k_BT = 0.58 (Fig. 4B), the corresponding U(x, y) (Fig. 4D), and F₀(x, y) (Fig. 4C), where we assume n_I = 87 and n_II = 86. As in HγD-Crys, F(x, y) of protein S has distinct minima at N_IN_II, U_IN_II, N_IU_II, and U_IU_II, and two pathways P_I and P_II connecting them are possible. As is expected from the above topological consideration, the free energy profile along P_I and that along P_II are not significantly different. U(x, y) has the large negative values at the native state and at (50 < x < 87, 50 < y < 86), which lowers the free energy barrier height of both P_I and P_II. Corresponding to the minor distributions of interactions between Nth-I and Nth-II, however, the region in which U(x, y) takes low values is wider for x > y than the region for x < y. Owing to this asymmetrical free energy lowering, the model predicts that P_I that passes N_IU_II should have a larger folding rate than P_II.

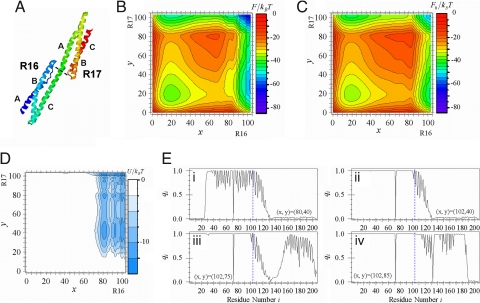
R1617 Spectrin Domain.

As shown in Fig. 5A, each spectrin domain consists of three helices A, B, and C, so helix C of domain I forms a continuous helix with helix A of domain II. Pairs of spectrin domains connected in this way are significantly more stable than the isolated separated domains (26). We here study the connected pair of R16 and R17 (R1617, PDB ID: 1CUN) by truncating 7 residues from the C terminus of 1CUN. Although the folding intermediate does not exist in equilibrium, kinetic analyses showed that domain I (R16) folds first and is followed by domain II (R17) (28). Thus, R1617 shows cooperative folding despite the small number of residues that form the domain–domain interactions.

Fig. 5.

Structure and free energy profiles of the R1617 spectrin domain. (A) structure of R1617 (PDB ID: 1CUN). Each domain consists of three helices A, B, and C. Shown are F(x, y) (B), F₀(x, y) (C), and U(x, y) (D) for ε/k_BT = 0.6. Structural order parameters q_i(x, y) for each residue are (x, y) = (80, 40) (Ei), (x, y) = (102, 40) (Eii), (x, y) = (102, 75) (Eiii), and (x, y) = (102, 85) (Eiv).

By assuming n_I = 103 and n_II = 103, F(x, y), F₀(x, y), and U(x, y) of R1617 for ε/k_BT = 0.6 are shown in Fig. 5B, C, and D, respectively. F(x, y) has four free energy minima, so there are two pathways, P_I and P_II, where P_I passing N_IU_II traverses the surface of free energy lower than that of P_II. Predominance of P_I is consistent with the observed results, showing that the folding intermediate is N_IU_II (27, 28). F₀(x, y) has a symmetrical pattern showing that isolated domains I and II are almost identical in their folding kinetics. Asymmetry of P_I and P_II arises from the large negative values of U(x, y) at large x. The large negative values of U(x, y) are not found in the region of small x, which is consistent with the observed data that the folding rate of R16 in R1617 is similar to that of isolated R16 but the unfolding rate of R16 in R1617 is significantly smaller than that of isolated R16 (28).

Asymmetry of U(x, y) is due to the asymmetric domain–domain interactions. We refer to the contiguous helix connecting domains I and II as the helix C-A. Domain I consists of helix A, helix B, and the N-terminal half of helix C-A, whereas domain II consists of the C-terminal half of helix C-A, helix B, and helix C. The domain–domain interactions are formed between helix C-A and the loop connecting helices A and B of domain I and between helix C-A and the loop between helices B and C of domain II, where the number of native contacts is larger in the former interactions. Such asymmetry inevitably arises from the repeat of almost equivalent domains unless each domain has a special symmetry to allow the same interactions at different sites. With this asymmetry, as shown with q_i(x, y) of Fig. 5E1–E4, helix B of domain I and helix C-A form first, which catalyzes the folding of the remainder of the protein, helix A of domain I and helices B and C in domain II.

Summary and Discussion.

We examined the multidomain proteins HγD-Crys, protein S, and R1617 by using a structure-based, coarse-grained model of folding. The calculated results consistently explained many experimental data showing that the structure-based model captures the essential features of folding of multidomain proteins. Two domains in HγD-Crys interact with each other in an almost symmetrical way, but the asymmetrical chain connectivity between the two domains determines the folding pathway and the intermediate. The model predicted that a change of the connectivity by circular permutation should change the folding pathway. In protein S, two domains are connected in an almost symmetrical way, but the domain–domain interactions are asymmetric, which should determine the relative weight of multiple folding pathways. In R1617, a helix extends from one domain to another. Although the two domains are quite similar to each other, the asymmetric interactions between this helix and the remainder of the protein determines the folding pathway and intermediate. In this way, the connectivity of the two domains and the distribution of domain–domain interactions in the native conformation are factors to determine kinetic and equilibrium properties of folding.

Folding of multidomain proteins resembles the binding of a pair or oligomer of proteins to form complexes. In complex formation, binding proceeds not only as docking of rigidly folded monomers, but there are many cases in which binding and folding occur concomitantly (42, 43). In the latter cases, binding proceeds as a two-state transition from unfolded monomers to a folded complex or via an intermediate depending on the strength of interactions between folding units (i.e., monomers) (44, 45). Also in the present multidomain cases, interactions between folding units (i.e., domains) are important, but, as shown here, the other important factor, which is absent in complex formation, is the chain connectivity between folding units.

Effects of the chain connectivity and the distribution pattern of domain–domain interactions are reflected in the functional form of U(x, y) in the model. In the present model, large cancellation between enthalpy and entropy is already taken into account in calculation of F₀(x, y), so that U(x, y), which is determined by the residual domain–domain interactions and the connectivity, decisively controls the catalytic effect on the folding process and the subtle balance between multiple possible pathways. Although F₀(x, y) depends on the parameters in the model or on the precise definition of native pairs, the overall functional form of U(x, y) is insensitive to changes in these details. We conclude, therefore, that the topology of the native conformation is the primary determinant of the folding and unfolding processes of multidomain proteins. This theoretical conclusion should be verified by further examining different multidomain proteins. Especially interesting would be the examination of artificially designed homodimers connected by linkers.

The present results suggest that the functionally important features of multidomain proteins can be controlled by the topological design: Design of the chain connectivity and the distribution of domain–domain interactions should determine the structural features of folding intermediates and determine which domain is more unstable, which may be relevant to the functional requirements of proteins. This design principle should be useful in protein engineering and in analyzing the evolutionary history of proteins in a family or a superfamily. Combined efforts with the coarse-grained, structure-based models, all-atom simulations, and experiments should help to examine the design principle proposed in this article.

Methods

In the present model, we define Δ_i,j = 1 when a heavy atom other than hydrogen in the ith residue and a heavy atom in the jth residue with j > i + 2 are closer than 5 Å in the native conformation and Δ_i,j = 0 otherwise. Throughout this article we use σ = 1.5k_B (ν ≈ 4.5), but independence of U(x, y) on σ assures the insensitivity of the effects of domain–domain interactions to the choice of the precise value of σ. F(x, y) for σ ≠ 1.5k_B can be obtained by using the free energy function at σ = 1.5k_B as F(x, y) = F(x, y)|_{σ = 1.5kB} + T(N − x − y)(σ − 1.5k_B).

Response to the perturbation of interactions with respect to the ith residue, q_i(x, y), is defined as follows: When the strength of interactions that involve the ith residue is changed from ε to ε + Δε, then energy is modulated as ΔH(i) = ΔεΣ_jΔ_i,jm_ij. q_i(x, y) is defined by q_i(x, y) = ΔF_i(x, y)/ΔεΣ_jΔ_i,j with ΔF_i(x, y) = −k_BT ln〈exp[−βΔH(i)]〉_x,y. From this definition, we can see that q_i(x, y) is normalized to be 0 ≤ q_i(x, y) ≤ 1. At the transition state region of (x, y), q_i(x, y) provides information similar to the Φ value (10). Also, in other regions of (x, y), q_i(x, y) can be used as an order parameter to represent the native-likeness of the ith site under the constraint of (x, y).