Structure, Dynamics, and Branch Migration of a DNA Holliday Junction: A Single-Molecule Fluorescence and Modeling Study

Abstract

The Holliday junction (HJ) is a central intermediate of various genetic processes, including homologous and site-specific DNA recombination and DNA replication. Elucidating the structure and dynamics of HJs provides the basis for understanding the molecular mechanisms of these genetic processes. Our previous single-molecule fluorescence studies led to a model according to which branch migration is a stepwise process consisting of consecutive migration and folding steps. These data led us to the conclusion that one hop can be more than 1 basepair (bp); moreover, we hypothesized that continuous runs over the entire sequence homology (5 bp) can occur. Direct measurements of the dependence of the fluorescence resonance energy transfer (FRET) value on the donor-acceptor (D-A) distance are required to justify this model and are the major goal of this article. To accomplish this goal, we performed single-molecule FRET experiments with a set of six immobile HJ molecules with varying numbers of bps between fluorescent dyes placed on opposite arms. The designs were made in such a way that the distances between the donor and acceptor were equal to the distances between the dyes formed upon 1-bp migration hops of a HJ having 10-bp homology. Using these designs, we confirmed our previous hypothesis that the migration of the junction can be measured with bp accuracy. Moreover, the FRET values determined for each acceptor-donor separation corresponded very well to the values for the steps on the FRET time trajectories, suggesting that each step corresponds to the migration of the branch at a defined depth. We used the dependence of the FRET value on the D-A distance to measure directly the size for each step on the FRET time trajectories. These data showed that one hop is not necessarily 1 bp. The junction is able to migrate over several bps, detected as one hop and confirming our model. The D-A distances extracted from the FRET properties of the immobile junctions formed the basis for modeling the HJ structures. The composite data fit a partially opened, side-by-side model with adjacent double-helical arms slightly kinked at the four-way junction and the junction as a whole adopting a global X-shaped form that mimics the coaxially stacked-X structure implicated in previous solution studies.

INTRODUCTION

The Holliday junction (HJ) is a branched DNA structure with four interwoven nucleotide strands forming a four-way junction. Although Robin Holliday first introduced the structure to explain the mechanisms of homologous and site-specific genetic recombination (2,3), subsequent work has found the four-way arrangement of DNA to be critically involved in DNA replication (4,5) and DNA repair (6). Despite the many advances made in the structural characterization of HJs, our knowledge of the branch-migration mechanism, as a central mechanism of DNA recombination, is quite limited. The majority of known four-way structures (immobile HJs; reviewed in Lilley (7)) cannot undergo branch migration. The lack of information stems from the lack of appropriate experimental approaches that allow for the study of HJs undergoing branch migration (mobile HJs).

Single-molecule biophysics now offers a series of techniques that enable one to follow the dynamics of individual molecules. There are a growing number of examples of the application of atomic force microscopy (AFM) for the observation, in solution, of the dynamics of protein-DNA complexes (8–11), supercoiled DNA (12), cruciforms (13,14), and other alternative DNA structures (14,15). Progress has recently been made in the real-time observation of the dynamics of molecular complexes at the single-molecule level using single-pair fluorescence resonance energy transfer (spFRET) (16–22), including studies (23–25) in which the dynamics of immobile four-way junctions were analyzed with spFRET. The analysis of the structure and dynamics of mobile HJs, made possible by these two single-molecule approaches, has led to a breakthrough in understanding the large-scale mechanism of branch migration. Our group (26) has further shown that time-lapse AFM is capable of detecting a wide range of dynamics in mobile HJs, including branch migration and the separation of homologous DNA molecules, and was the first (to our knowledge) to characterize the structure and dynamics of mobile HJs. Very recently, the power of spFRET for analyzing HJ dynamics in real time was demonstrated by two back-to-back publications (1,27): one focusing on HJs with single-basepair (bp) homology (27), and one (1) analyzing HJs that are capable of migrating over a 5-bp homology region. Of importance, we could observe branch migration directly, separate this pathway from the junction-folding pathways, estimate the branch-migration hopping rate, and propose a mechanism of spontaneous branch migration.

It is widely accepted that branch migration is a random-walk process (28–30) and that this process can be modeled as a one-dimensional discrete hopping event of defined step size. In the case of branch migration, the step size is the number of bases exchanged during one dissociation event. In contrast to mathematical models of branch migration, which propose that the step size is 1 bp (31), our spFRET studies revealed the variability of the FRET steps, prompting us to hypothesize that the branch-migration step size varies and can be larger than 1 bp (1). Indeed, the stepwise pattern of the spFRET data allows us to determine the step size by measuring the FRET-jump values directly. However, to translate the FRET-efficiency data into step sizes in terms of the number of bps, we need to know the dependence of FRET on the donor-acceptor (D-A) distance. Obtaining this dependence and thereby characterizing the sensitivity of spFRET in applications to HJ branch migration is one of the goals of this work.

To accomplish this goal, we designed a set of immobile HJs in which the D-A distances vary by 2-bp increments, corresponding to a branch-migration step size of 1 bp (1). Multiple measurements were performed for each design so that FRET values corresponding to well-defined separations between donor and acceptor could be determined. The analysis of the time-dependent FRET data for mobile HJs using the observed dependence of FRET on the D-A distance leads to two major conclusions: first, branch migration over 1 bp can be reliably measured with the spFRET approach; second, one hop in the branch-migration process does not necessarily involve 1 bp. Rather, the mean hop size for a homologous region of 5 bp is 2.2 bp, and hops corresponding to migration over an entire homology region (5 bp) are observed. Modeling based on the collective FRET data points to two types of three-dimensional structures: 1), the familiar coaxially stacked, crossed HJ configuration with adjacent helical arms associated end-to-end and rotated with respect to the other pair; and 2), a partially opened, side-by-side arrangement with adjacent double-helical arms slightly kinked at the four-way junction. Structures of the latter type not only account for the complete set of dye interactions in the current HJ constructs but also resemble the global X-shaped arrangements implicated in earlier work and modeled by crossed, coaxially stacked structures.

MATERIALS AND METHODS

HJ structures

A set of oligonucleotides (IDT, Coralville, IA) was synthesized for the assembly of mobile and immobile HJs. Internal thymines in two of the four oligonucleotides in each set were amino-labeled for attaching dyes. Immobile junctions were obtained by annealing single-stranded oligonucleotides to give the designs shown in Fig. S1 in Supplementary Material, Data S1. The full set of oligonucleotides used for these studies was the same as published recently (32). Using this set, we were able to obtain immobile HJs with dye-to-dye distances of 10, 12, 14, 16, 18, and 20 bp.

The mobile HJ was obtained by annealing the following four oligonucleotides using the annealing protocol described earlier (1):

• 1: biotin-5′-TCTTTTGATAAGCTTGCAAGCATATATATCTCGTAATTTCCGGTTAGGT

• 2: 5′-ACCTAACCGGAAATTACGAGATATAGATGCATGCAAGCTTCACA

• 3: 5′-TGTGAAGCTTGCA/iAmMC6T/GCATCTATATAATACGTGAGGCCTAGGATC

• 4: 5′-GATCCTAGGCCTCACGTATTATATATATGC/iAmMC6T/TGCAAGCTTATCA

The exchangeable parts of the oligonucleotides that form the mobile HJ are shown in boldface.

Oligonucleotides 3 and 4 were labeled with succinimide esters of Cy3 or Cy5 dyes (GE Healthcare, Buckinghamshire, UK) according to the protocol provided by the company. Labeled oligonucleotides were purified by reverse-phase HPLC, and four-way junctions (Fig. 1 b) were prepared as previously described (1). The yield of the annealing reaction, determined by gel electrophoresis, was ∼80–90%.

FIGURE 1.

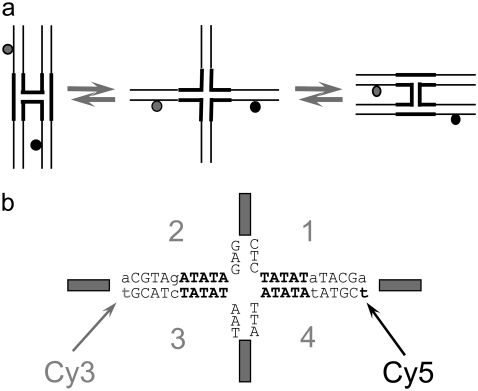
Structure of an HJ. (a) Diagram outlining the principle of immobile-HJ folding used in single-pair FRET studies. (b) Schematic of the HJ central sequence with a 20-bp D-A distance, including Cy3 (donor) and Cy5 (acceptor) dyes marked by arrows. Variable parts of the HJ design are shown in boldface letters (see Materials and Methods for details).

Fluorescence measurements and FRET efficiency calculations

The following procedure was used to acquire the original traces of fluorescence intensity (1,32): Cleaned glass coverslips were treated sequentially with 1 mg/mL biotinylated BSA (Sigma, St. Louis, MO) in pH 7.5 TES buffer (10 mM Tris-HCl, 150 mM NaCl, 1 mM EDTA) for 10 min, rinsed with TES buffer, treated with a 0.5-μM solution of streptavidin in the same buffer for 10 min., and rinsed with TES buffer. A 50-pM solution of biotinylated HJs in TES buffer was added and incubated for ∼10 min. Measurements were performed in TNM buffer (10 mM Tris-HCl, 100 mM NaCl, and 10 mM MgCl₂) containing an oxygen-scavenging system based on glucose oxidase and catalase (33).

Single-molecule FRET measurements were carried out on a confocal single-molecule setup built around an Olympus IX71 (Hitschfel Instruments, Inc., St. Louis, MO) inverted microscope body equipped with a piezo-driving scanning stage (Physik Instrumente GmbH, Karlsruhe, Germany). An oil immersion UPlanApo 100× objective with 1.35 numerical aperture (Olympus, Tokyo, Japan) was used for all measurements. Fluorescence intensities were obtained using incident laser light of ∼100 μW provided by a 532-nm laser (Crystalaser, Reno, NV). This wavelength was optimal for the excitation of the Cy3 dye (donor). Fluorescence was collected through a 30-μm-diameter pinhole placed in the focal plane of the right side port. A dichroic mirror (Chroma 630dcxr, Rockingham, VT) placed after the pinhole separated the emission into either a donor or an acceptor channel, dependent on wavelength. The emission was then focused onto silicon avalanche photodiodes (APD, Perkin Elmer Optoelectronics, SPCM-AQR-15, Freemont, CA) operating in single photon-counting mode. Data acquisition and preliminary analysis were performed using a TimeHarp 200 PCI-board and SymPhoTime software (PicoQuant GmbH, Berlin, Germany).

FRET efficiency was calculated from the fluorescence intensities of the donor (I_D) and acceptor (I_A) using the following equation:

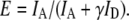(1)

The intensity values were obtained by subtracting the background counts from the raw intensities and correcting for cross talk between the two detection channels according to Ha (34). The γ-factor, 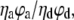accounts for the quantum yields of donor and acceptor emission (ϕ_d and ϕ_a, respectively) as well as the instrument-detection efficiencies in both channels (η_d and η_a). This correction factor was determined as described in Ha et al. (21) from the ΔI_a/ΔI_d ratio, where ΔI_d and ΔI_a are the respective changes in acceptor and donor intensity during acceptor photobleaching. The ΔI_a/ΔI_d ratio was determined for 48 acceptor-photobleaching events, and the γ-factor was found to be 1.8 ± 0.5 for our experimental setup. However, this correction factor value was likely overestimated due to the presence of bleached acceptor in the vicinity of donor, which may effectively decrease the donor intensity even after acceptor photobleaching (T. Ha, Department of Physics, University of Illinois, personal communication, 2007). We therefore used a corrected γ-factor value of 1.6 ± 0.5 for the actual FRET efficiency measurements. This slightly lower value was obtained as a mean value of the correction factors based on the ensemble FRET data (1.4) and spFRET measurements, explained above.

The steps on the FRET time trajectories were identified by the use of the plateau-search algorithm described in Karymov et al. (32). Briefly, a plateau was generated if the FRET values for two adjacent data points were <0.12, a threshold value determined on the basis of the noise level. The mean value for the two-point plateau level was initially calculated. Additional data points that meet the difference criterion were included one by one and the mean value for the plateau level was updated. The process was stopped when two consecutive FRET values deviated by more than 0.12 from the mean. The value for the plateau level was then plotted as a horizontal line, and the procedure was repeated to search for the plateau in the next set of data points. The assignment of the plateau positions to the number of bps between the dyes was performed with the use of the calibration curve (see Figs. 4 and 5; these values are shown as horizontal gray dashed lines in Fig. 5, a and b).

FIGURE 4.

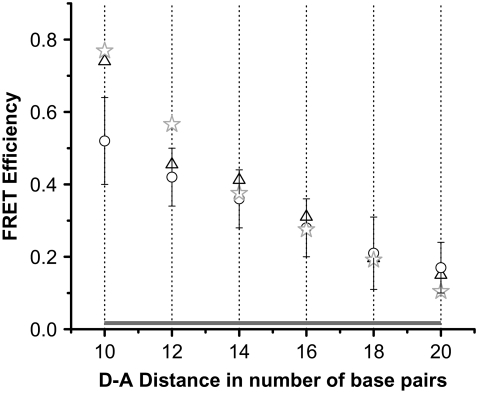
Calibration curve and HJ-modeling schematics. Calibration curve establishing the relationship between FRET efficiency and dye-to-dye distance in terms of the number of bps. Calibration data are based on FRET-efficiency distributions from immobile HJs with known numbers of bps between donor and acceptor. The region covering all six distances is shown as a gray horizontal bar. Here single-molecule data are designated with open circles, SDs with error bars, and SEs within the circles. Ensemble FRET measurements are shown with black triangles, and modeled FRET values corresponding to distances between the tether centers (ϕ = 180°, ψ = 140°) are shown with gray stars.

FIGURE 5.

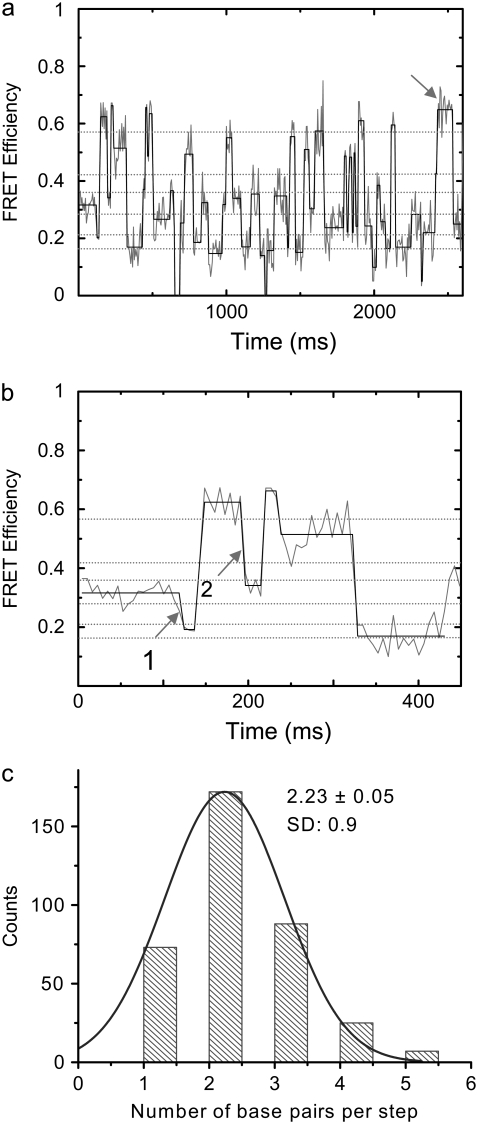
FRET-efficiency plots and hop-size distribution of mobile HJs. (a) Time dependence of spFRET efficiency (gray line) of a mobile HJ with an ATATA exchanging sequence. Original intensity data were binned with a 6-ms binning interval. The black line shows the plateau values calculated using the averaging algorithm described in Karymov et al. (32). The dotted-gray horizontal lines show the measured FRET efficiency values obtained from immobile HJs with even numbers of bps between donor and acceptor. (b) The initial part of the time traces, shown in a, is extended over the timescale to illustrate the data-analysis approach. (c) Histogram of hop sizes in number of bps obtained from a series of time traces; SE = 0.05. A 1-bp hop produces a 2-bp change in the D-A distance (1 bp from each side of the junction). Step positions obtained from the mean FRET efficiency values corresponding to each plateau were rounded to the closest even number of bps taken from the calibration plot (dotted green lines in a and b).

The distance R between donor and acceptor dyes was calculated based on the known Förster radius value of 6.0 nm for Cy3 and Cy5 dyes (35,36) using the equation:

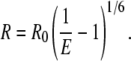(2)

We used the experimentally determined Förster distance for the Cy3-Cy5 pair found for DNA molecules (36) under a wide range of experimental conditions.

Ensemble-FRET measurements

Fluorescence-energy transfer between two Cy-dye molecules (a Cy3 donor and a Cy5 acceptor) attached to different sides of a four-way junction was measured on a Cary Eclipse spectrofluorometer from Varian (Walnut Creek, CA). All fluorescence-emission intensities were background-corrected using the pure buffer fluorescence as a reference. FRET efficiency values were calculated using the following equation (37,38):

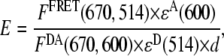(3)

where F^DA(670,600) is the fluorescence emission of a solution of a Cy3-Cy5-labeled HJ at 670 nm when it is excited at 600 nm; 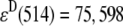M⁻¹cm⁻¹ is the molar extinction coefficient of the donor at 514 nm; 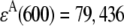M⁻¹cm⁻¹ is the molar extinction coefficient of the acceptor at 600 nm; d is the labeling efficiency; and F^FRET(670, 514) is the acceptor fluorescence due to FRET detected at 670 nm, when the HJ solution is excited at 514 nm. The value of F^FRET(670, 514) was determined by a sum of terms:

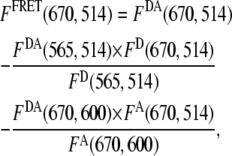(4)

where F^DA(670, 514) is the total fluorescence emission of a solution of a Cy3-Cy5-labeled HJ at 670 nm when it is excited at 514 nm; F^DA(565, 514) is the fluorescence emission of a solution of a Cy3-Cy5 labeled HJ at 565 nm when it is excited at 514 nm; F^D(670, 514) is the fluorescence emission of a solution of a Cy3-only labeled HJ at 670 nm when it is excited at 514 nm; F^D(565, 514) is the fluorescence emission of a solution of a Cy3-only labeled HJ at 565 nm when it is excited at 514 nm; F^DA(670, 600) is the fluorescence emission of a solution of a Cy3-Cy5 labeled HJ at 670 nm when it is excited at 600 nm; and F^A(670, 514) is the fluorescence emission of a solution of a Cy5-only labeled HJ at 670 nm when it is excited at 514 nm; F^A(670, 600) is the fluorescence emission of a Cy5-only labeled HJ solution at 670 nm when it is excited at 600 nm.

The labeling efficiency d is given by:

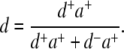(5)

Here d⁺a⁺ is the integral fluorescence intensity of the gel-electrophoresis band corresponding to double-labeled HJ, and d⁻a⁺ is the integral fluorescence intensity of other acceptor-only-labeled species in the lane. HJ samples (12 μL of 0.2 μM solution in 0.5× TBE buffer) were loaded in a 7% polyacrylamide gel and run at 120V for 3.5 h in the same buffer at 4°C. The gel was imaged with a Typhoon 9410 gel scanner (GE Healthcare, Piscataway, NJ) at the Cy5 excitation/emission range. The gel image was background-corrected and quantified using the ImageQuant software from the same company. Labeling efficiency was determined as the ratio of the intensity (multiplied by the band area) of the band containing HJ only to the total fluorescence intensity (multiplied by the total) of the fluorescent species in the corresponding gel lane (Fig. S2 in Data S1).

Modeling procedures

Atomic-level representations of immobile HJ structures were obtained with a generalized procedure that accommodates a four-way junction with arms of variable sequence, conformation, and chain length. A pair of ideal B-DNA duplexes with the sequences specified above is brought into close proximity and computationally nicked at the site of strand exchange by removing the phosphate atoms on antiparallel strands, one from each duplex (39). The relative disposition of the helical arms is controlled by swiveling the two nucleic-acid structures about the recombination site without disruption of base stacking. The angle ϕ (see Figs. 6 and 7) allows the helical arms to interconvert from the two possible antiparallel starting arrangements, where either the (red) acceptor- or the (green) donor-containing strand forms a U-turn at the recombination site, i.e., the upright and (90°-rotated) lazy-H configurations illustrated in Fig. 1 a, toward coaxially stacked-X forms like those detected in high-resolution structures (40–45) and ideal, parallel alignments where ϕ is taken to be zero. Each of the duplexes can also be kinked and repositioned with respect to one another at the recombination site, interrupting the coaxial stacking in the two arms of the antiparallel starting structures and converting the H forms to alternate “〉-〈” crossed arrangements. The latter configurations are obtained by introducing virtual bends in the double-helical axes of the starting duplexes (see Figs. 6 and 7). The angle of bending ψ (about the long axis of the computationally nicked bp step) is defined, following Hohng et al. (25), to be zero when the (green) donor-containing strand is straight and the (red) acceptor-containing strand forms a U-turn (i.e., the upright H), 90° when the HJ adopts the square-planar open form illustrated in the center of Fig. 1 a, and 180° when the (red) acceptor-containing strand is straight (i.e., the lazy H). It should be noted that the U-turns in the dye-labeled strands in the current constructs differ in direction from those used by Hohng et al. (25), i.e., the acceptor-containing turn in the upright-H (ψ = 0°) form is the lower, upside-down U in Fig. 1 a but would be the upper, standard U in the design of Hohng et al. (25). Atomic-level representations of tetrahedral junctions are also considered, with constructs positioned such that ϕ = ±90° and ψ = 70.5°, i.e., cos ψ = 1/3. The values of ϕ and ψ characterizing the arrangements of the helical arms in known high-resolution HJ structures are obtained with the 3DNA software package (46), first extracting the identities and local axes of the four helical arms in each structure and then determining the ϕ,ψ values of a symmetric model that best match the observed angles between helical arms. Corresponding pairs of arms form identical angles in the model, e.g., 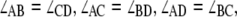where the subscripts A–D refer to the arms of the junction.

FIGURE 6.

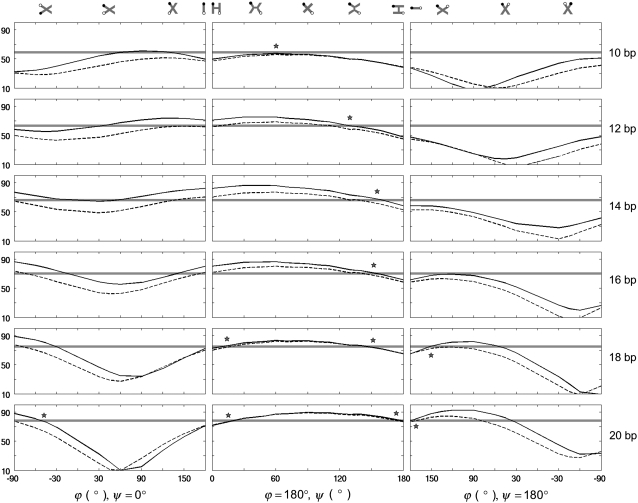
Distances between dyes on opposing arms of immobile, four-way junctions in various three-dimensional arrangements. (Left) Coaxially stacked structures along the pathway that converts the ideal, antiparallel H arrangement (Fig. 1 a, left) to the parallel form. (Center) Kinked structures along the pathway that links the two possible antiparallel arrangements. (Right) coaxially stacked structures along the pathway that transforms the ideal, antiparallel lazy-H configuration (Fig. 1 a, right) to the parallel form. Rotations via ϕ pass through stacked-X forms like those detected in high-resolution HJ structures (40–45). Bending via ψ leads to fully opened, square-planar forms like those found in the presence of different enzymes (51–55) and the partially opened, kinked HJ structure found in the presence of T4 endonuclease VII (56). Angles are defined such that ϕ is 180° in antiparallel states (where unexchanged strands run in opposing directions) and zero in parallel states, and ψ is zero when the acceptor-containing strand is kinked and the HJ assumes the upright-H form, and 180° when the donor-containing strand is kinked and the HJ adopts the lazy-H form (see schematics above the plotted curves, where the solid circle represents the donor and the open circle the acceptor in each arrangement). Asterisks denote models that best match observation. (Solid line) Distance between the centers of rigid, fully extended Cy3 and Cy5 moieties. (Dashed line) Distance between the amide nitrogen atoms on the chemical tethers that link the dyes to DNA. (Gray shading) Distances within ±2.5 Å of the experimental values.

FIGURE 7.

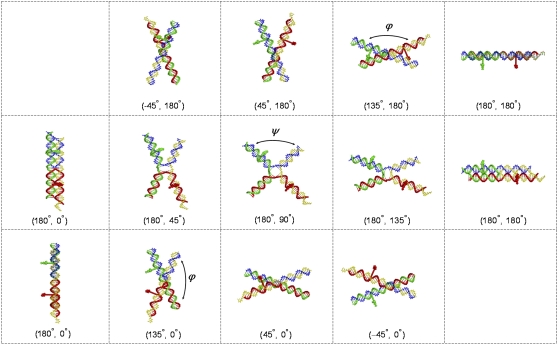
Atomic-level representations of modeled HJ structures with the longest (20 bp) Cy3-Cy5 base separation, i.e., dyes on bases 10 bp from the recombination site. (Top) Coaxially stacked structures, generated by changes in ϕ, linking the antiparallel, lazy-H arrangement to the parallel form. (Middle) Kinked structures, obtained by variation of ψ, joining the two ideal antiparallel arrangements (shown in two views at the ends of the middle and upper/lower rows of images). (Bottom) Coaxially stacked structures, generated by changes in ϕ, linking the antiparallel upright-H configuration to the parallel form. DNA shown as a wireframe model with backbones represented by tubes (Cy3 donor-containing strand 3, green; Cy5 acceptor-containing strand 4, red; biotin-labeled strand 1, yellow; unlabeled strand 2, blue). Dyes depicted as space-filled forms with Cy3 in green and Cy5 in red. (ϕ, ψ) values denoted in parentheses below each image. Note the similar spacing of dyes and overall global fold of the partially kinked lazy-H structure and the nearby stacked-X arrangement where the (ϕ, ψ) values are (180°, 135°) and (135°, 180°), respectively.

The phosphodiester conformations of the exchanged chain backbone and the unexchanged strands at kink sites are found with a chain-closure algorithm developed previously to link pairs of arbitrarily positioned bases (47). Dyes are tethered to the C5 atoms of labeled thymines through fully-extended, all-trans linkers, fixing 1), the centers of Cy3 and Cy5 (located at the midpoints of the respective diene or triene linker between the two indoline rings of each dye) at (23.4, 2.6, 0 Å) and (22.4, 3.6, 0 Å) with respect to a standard coordinate frame (48) on the modified T:A pairs; and 2), the indolenyl-hexanoyal amide nitrogen atoms in the linkers that join the modified thymine (acrylamide) on DNA to the nitrogen on one of the indoline rings at (15.0, −2.6, 0 Å). These points crudely bracket the space sampled by the transition dipoles of flexibly tethered dyes. The pairwise distances between the dye centers and the tether centers in the various HJ models are then compared against the observed D-A distances. Simple geometric models (25) that ignore the positions of backbone and dye atoms, i.e., the “real” spacing of helical arms and dyes, underestimate the experimental data.

RESULTS AND DISCUSSION

HJ design

A schematic of the HJ designed for the spFRET studies is presented in Fig. 1 a and is similar to ones described in our earlier work (32). Briefly, the donor (Cy3) and acceptor (Cy5) labels are placed on opposite arms of the junction, and the sequences are designed in such a way that the distances between the donor and acceptor dyes attached at defined positions are 10, 12, 14, 16, 18, and 20 bp. The complete set of HJs is shown in Fig. S1 in Data S1. As a result, with this set of molecules, we are able to cover the entire range of branch migration of a mobile HJ (1,32) and thus correlate the FRET changes with the migration of the junction. The design of the immobile HJs takes careful consideration of two important factors. First, the sequence around the dye remains identical in all designs. Second, the change in relative orientation of the dyes for two adjacent designs matches the change of orientation during branch migration of the mobile HJ studied previously (1). Our immobile HJ designs differ from each other by a 2-bp increment in D-A placement, changing the relative orientation of the dyes on adjacent designs by ∼68.6°, i.e., 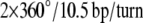of double helix. This value exactly matches the relative rotation values corresponding to a 1-bp branch-migration step in a mobile HJ. Each junction is assembled from four single-stranded oligonucleotides, with the structure assembly examined by gel electrophoresis. The donor and acceptor dyes are covalently attached to the modified thymines indicated by arrows in Fig. 1 b.

FRET-efficiency measurements

Single-molecule fluorescence experiments were performed identically to previously described measurements of mobile HJs, in which the HJs were tethered via a flexible polymeric linker (1) consisting of five deoxynucleotides (TTCT) and a C6 hydrocarbon chain attached to biotin. This flexible linker allows free rotation of the HJ near the BSA-streptavidin coated surface (21,49).

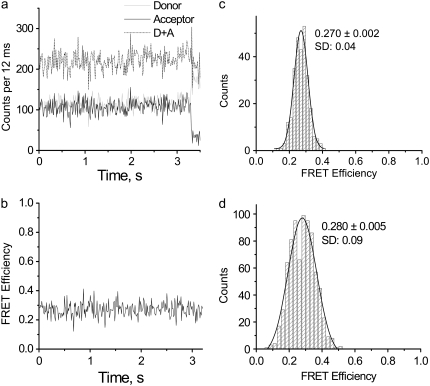
The results of the single-molecule experiments for the junction with 16 bp between the donor and acceptor are shown in Fig. 2. All measurements were performed in TNM buffer. Time traces of the fluorescence intensities of the donor (gray) and acceptor (black) and the sum of the signals (dashed line) are shown in Fig. 2 a. The original intensity data were binned with a 12-ms time interval. The FRET-efficiency time trace calculated for each data point on the time traces for the donor and acceptor is shown in Fig. 2 b. This graph shows that the FRET values constantly fluctuate around a mean value 0.27. The distribution of the FRET values is well approximated by a Gaussian with maximum at 0.270 ± 0.002 and standard deviation (SD) = 0.04 (Fig. 2 c). Such data were obtained for a set of molecules, and the histogram of the combined data for seven molecules is shown in Fig. 2 d. The Gaussian distribution for this data set is characterized by a mean FRET value of 0.280 ± 0.005 and an SD of 0.08.

FIGURE 2.

Time trajectories of the fluorescence intensity with the corresponding FRET-efficiency plot for an immobile HJ with 16 bp between the dyes. (a) Time trajectories of donor (light gray) and acceptor (black) fluorescent intensities, and the sum of the two signals (dashed line). Original intensity data were binned with a 12-ms time interval. (b) FRET-efficiency plot corresponding to intensity time trajectories. (c) Distribution of the FRET-efficiency values for a single four-way junction. The mean value was determined using a Gaussian distribution with a standard error (SE) = 0.002. (d) FRET-efficiency distribution for multiple molecules; here SE = 0.005.

The constant FRET value over time seemingly contradicts earlier findings that HJs flip between two conformations with different relative positions of the arms (50), including a structural transition detected by spFRET analysis (23). However, it is important to note that the labeling methods employed in our work differ from those used previously by other researchers. The structural transition is detected if the dyes are placed on adjacent arms of the junction. To detect branch migration, our designs place the dyes on opposite arms (Fig. 1). Our previous data (1,32) showed that the labeling of opposing arms is insensitive to the HJ transition between the two conformers. The data presented here are consistent with that finding.

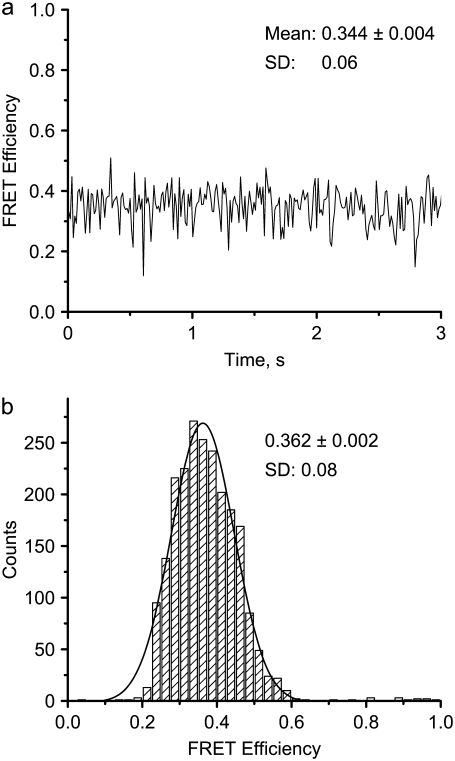
Similar single-molecule experiments were performed with other HJ designs, and the data for HJ-14 with a smaller D-A distance (14 bp) are reported in Fig. 3. The time trace FRET graph, shown in Fig. 3 a, resembles the data reported above, with the FRET value fluctuating around a mean value (here 0.344 ± 0.004). A histogram summarizing the measurements of 12 different HJ-14 molecules is shown in Fig. 3 b. The data are well approximated by a Gaussian with maximum 0.362 ± 0.002 and SD of 0.08. The data shown in Figs. 2 d and 3 b correspond to two samples that differ by 2 bps in the D-A distance and translate to a 1-bp migration of a mobile HJ. Thus, by using the labeling method described above, we are able to measure a 1-bp branch-migration step.

FIGURE 3.

FRET-efficiency data for an immobile HJ with 14 bp between dyes. (a) FRET-efficiency time trajectory. The mean FRET efficiency ± SE for this particular time trajectory and its SD are marked on the figure. (b) Distribution of FRET efficiencies obtained from 12 HJs. The mean value was determined from the maximum of the Gaussian distribution; SE = 0.002.

All other samples were analyzed in the same way. Several dozens of different molecules for each sample were analyzed, FRET values were obtained, and the mean FRET values were calculated for each design. The dependence of the FRET data on the D-A distances is shown in Fig. 4 (open circles). The error bars show the SDs of the measured FRET efficiencies for each design. The highest value of the FRET efficiency corresponds to the smallest D-A distance, 10 bp, with the efficiency decreasing upon an increase in the number of bps between the dyes. Ensemble-FRET efficiency values were obtained for the same set of HJ samples and these data are also shown in Fig. 4 (triangles). The two sets of data correlate fairly well with each other. The modeling results (see below) are also shown on Fig. 4 as gray stars. These points correspond to a partially opened, side-by-side arrangement with adjacent double-helical arms slightly kinked at the four-way junction.

Branch migration pattern

This section describes the results of the single-molecule FRET analysis of the dynamics of a mobile HJ with a homologous (ATATA) sequence that allows for branch migration over a 10-bp homology region (a sequence of one strand is shown). The FRET time trajectories for one experiment are shown in Fig. 5 a. The gray line corresponds to the FRET data calculated from the time traces for the donor and acceptor as described previously (1) and in the Materials and Methods section. In contrast to the FRET values of the immobile junctions, which do not change over time, the FRET values of the mobile junction behave differently, changing over a broad range (between ∼0.2 and ∼0.7). Of importance, the changes exhibit a stepwise pattern qualitatively similar to data obtained previously for a slightly different sequence (1). This pattern is more clearly seen in Fig. 5 b, which is a close-up of the initial section of the time trajectory shown in Fig. 5 a. The FRET efficiency initially fluctuates around a value of 0.32, drops rapidly to a smaller value (0.19), and subsequently jumps to 0.62. After residing at this stage for 48 ms, the FRET value drops again to 0.34, rises after 24 ms to a value of 0.66, and after 24 ms falls to a long-lived state at 0.51, where it resides for 90 ms. The signal then decreases suddenly to a value of 0.17, which remains for ∼108 ms. The stepwise pattern is clearly seen upon application of the plateau-search algorithm described in the Materials and Methods section and in the previous work (32). These data are shown in Fig. 5, a and b, by a black line.

Although we used an immobilization procedure that typically is applied to immobilize a variety of different molecules, the effect of the interaction of the HJs with the surface on the structure and dynamics of the junction cannot be excluded. Note, however, that the FRET values determined for the same samples immobilized on the surface (single-molecule measurements) and in solution (ensemble measurements; see Fig. 4) are very close. This suggests that the effect of immobilization of HJs on their structure and dynamics is not strong.

According to our model (1,26), branch migration is a two-phase process. The migration phase per se requires unfolding of the junction. Folding of the junction, the second phase, terminates this process. The characteristic time of branch migration is much shorter than the lifetime of the folded state (1). The residence time for folded states depends on the concentration of Mg²⁺ cations. In experiments performed in the presence of 10 mM Mg²⁺ cations, the residence time for folded states can be as long as several hundred milliseconds (1). The branch-migration process thus appears on time traces as a vertical line connecting two plateaus corresponding to long-lived folded states. The dependence of the FRET signal on the D-A distance provides additional support for this model. If the plateaus on the time trajectories correspond to the folded states of the junctions, these values should be similar to the FRET values obtained from the calibration curve (Fig. 4). Indeed, the dotted gray lines in Fig. 5, a and b, match the FRET values of donors and acceptors on immobile junctions separated, at increments of 2 bp, between 10 and 20 bp. Note that a 1-bp branch-migration hop leads to a 2-bp change in the D-A distance. The positions of the plateaus in the graphs correlate well with the FRET values corresponding to the anticipated D-A distances for folded immobile HJs.

Branch-migration step size

If the plateaus correspond to the folded conformational states of a stalled, mobile HJ, the size of the vertical step on the time traces is a measure of the size of one migration step, and hence its value can be obtained from the jump size. As shown in Fig. 5, a and b, these values vary over a broad range, suggesting that the migration step may also vary. We used the calibration-curve data, shown by dotted gray lines, to estimate the number of bps per migration step. For example, a FRET difference between 0.32 and 0.19 (arrow 1 in Fig. 5 b) corresponds to a 2-bp change in the D-A spacing, and a FRET difference between 0.62 and 0.34 (arrow 2 in Fig. 5 b) corresponds to a change of 4 bp. These values are equivalent to branch-migration hops of 1 and 2 bp, respectively. Measurements performed over 10 FRET-efficiency time traces are summarized in Fig. 5 c in a histogram of the distribution of the number of bps per branch-migration step (the change in the D-A separation divided by two). The data clearly show that a 1-bp hop is not a dominant event. Instead, the distribution is centered around a value of 2 bp, so that events corresponding to the migration of the junction over the entire sequence-homology region (5 bp) are not excluded. These data suggest that once the junction is unfolded, the migration proceeds over several bps.

Note that there is a visible difference in the maximal FRET-plateau value (∼0.65) obtained for the mobile HJ (indicated in Fig. 5 a with an arrow) and the maximal plateau value obtained for an immobile HJ with a 10-bp D-A distance (0.574 ± 0.002). We hypothesize that such a difference in FRET values is due to a sequence-dependent variability of HJ geometry. Indeed, the bps of the immobile junction with a 10-bp D-A distance differ from those of the corresponding mobile junction (1), namely, (TA)→(AT)→(GC)→(TA) for the 10-bp immobile junction compared to (TA)→(TA)→(GC)→(TA) for the mobile junction with the 10-bp D-A distance (1). To test this hypothesis, we constructed an immobile HJ with a 10-bp D-A distance and a different set of inner bps: (TA)→(CG)→(GC)→(CG). The FRET-efficiency value of 0.5240 ± 0.0007 obtained for the latter sequence differs from the preceding value (0.574 ± 0.002), suggesting that the geometries of mobile and immobile HJs can also differ (within 10% in this case). Such sequence-based variability of FRET may cause a 1-bp uncertainty in the plateau assignment. Note that the observed difference corresponds to the smallest D-A distance, i.e., the highest FRET value, where the measurements are most sensitive to structural changes.

Apparent structure

The FRET data for the full set of immobile junctions were used to find the HJ structure(s) that provide the best fit to the experimental results. Fig. 6 summarizes the extent to which various three-dimensional models account for the observed distances between dyes on opposing arms of the immobile four-way junctions. The models include two series of coaxially-stacked structures along pathways that convert the dye-containing branches between parallel and antiparallel forms (Figs. 6, left and right, and 7, top and bottom), a sequence of kinked structures that link the two possible antiparallel arrangements of labeled junctions (Figs. 6 and 7, center), and an ideal tetrahedral junction (not shown). The virtual rotation ϕ used to effect large-scale configurational changes without disrupting base stacking passes through states reminiscent of the coaxially stacked-X forms detected in high-resolution HJ structures (40–45), in which the four double-helical arms associate in pairs and form two crossed domains. The kink angle ψ used to connect the H and lazy-H (90°-rotated) arrangements of antiparallel junctions (left and right images in Fig. 1 a) describes a different set of crossed arrangements, including fully opened, square-planar forms similar to those induced by the binding of different enzymes (Cre recombinase, FLP recombinase, E. coli RuvA helicase) (51–55) and the partially opened, kinked HJ structure with intact bps found in the presence of T4 endonuclease VII (56).

We report two D-A distances for each model of a given HJ design: 1), the distance between the centers of rigid, fully extended Cy3 and Cy5 moieties at the labeled sites; and 2), the distance between the amide nitrogen atoms on the chemical tethers that link the dyes to DNA (see Materials and Methods). These values roughly bracket the range of distances sampled experimentally in successful models (see Table S1 in Data S1 for the complete set of observed and modeled distances).

The HJ models that best match the expected distance criteria (highlighted by asterisks in Fig. 6) suggest that the four-armed structure preferentially adopts kinked, partially unstacked forms in solution rather than the coaxially stacked-X arrangements seen in many high-resolution HJ structures (40–45) and commonly believed to account for HJ solution properties. Although stacked-X configurations account for the measured distances in designs where the dyes are farthest (8–10 bp) from the recombination site, the open, kinked structures reproduce the observed values between dyes in all designs. The known variability of ϕ and ψ in stacked-X HJ structures, ϕ = 0–10° and ψ = 30–40° in crystalline DNA four-way junctions (40–45), is not broad enough to account for the observed FRET distances. On the other hand, the variation in kinking needed to mimic the D-A distances in different designs suggests that the dyes may perturb the natural HJ configuration if placed too close to the recombination site. The apparent kink angle increases from 20–30° to ∼90° as the dye sites shift toward the HJ center and the bimodal fit found with more widely spaced dyes disappears. Whereas formation of the stacked-X model entails changes in the roll of bps (local bending into the major and minor grooves) at the recombination site, formation of the kinked HJ involves changes in bp tilt (local accordion-like bending that concomitantly compresses and stretches the strands of an intact duplex). Although DNA bends more easily via roll than tilt in ordinary double-helical structures (57), the bending of a four-way junction is less costly, in terms of the electrostatic interactions between phosphate groups, if the recombination site deforms via tilt than roll. The total electrostatic energy between point charges of −1 esu interacting through a sharp, sigmoidal distance-dependent dielectric constant, 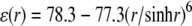(58), is 538 kcal/mol if the four 10-bp arms of a coaxially-stacked, antiparallel HJ undergo a 90° rotation in ϕ, but 465 kcal/mole if the same structure is kinked through an angle ψ of 90°. The distances between dyes in the tetrahedral models are not compatible with the experimental data, being too large when the labels are far from the recombination site and too small when the dyes are closely spaced.

The partially opened HJ structures implicated here are not usually considered in the interpretation of solution studies. Local kinking at the recombination site, nevertheless, yields an X-shaped configuration that is compatible with the observed interactions of dyes on the ends of adjacent arms. Single-molecule experiments, which measure these distances, show that the geometry of an immobile junction is highly labile in solution, undergoing transitions between two distinct states through an extended form that acts as a transient intermediate (23,24). The kinked H and kinked lazy-H models illustrated in Fig. 7 closely resemble the overall configuration of the stacked-X forms used to interpret these data. As shown here, these different configurational forms stem from a common reference state. Specifically, whereas a decrease in ϕ from the ideal, side-by-side, antiparallel lazy-H form, where (ϕ, ψ) = (180°, 180°), leads to a stacked-X structure, a comparable increase in ψ yields a kinked arrangement. Note, in particular, the comparable separation but distinctly different spatial disposition of dyes on opposite arms in the kinked and stacked-X models in Fig. 7 with respective ϕ, ψ values of (180°, 135°) and (135°, 180°) (see also numerical values in Table S1 in Data S1).

Molecular-dynamics studies of the potential conformational pathways linking the observed configurational states of HJ junctions (59) show that magnesium ions stabilize the stacked X-conformation and destabilize open square-planar and tetrahedral intermediates. The calculations, however, omit consideration of modestly kinked HJ configurations among the various starting states, the persistence or disappearance of which during the course of simulation is used as the indicator of stability or instability. The contacts of magnesium and cationic amino acids with the ∼50°-kinked HJ structure found in the crystal complex with T4 endonuclease VII (56) point to the potential role of multivalent cations in stabilizing such structures in solution. It is easy to understand the branch migration of DNA through a series of such kinked structures, with the kink site translating by two or more bp increments along the chain backbone.

CONCLUSIONS

Single-molecule FRET studies of a mobile HJ reveal a stepwise pattern for branch migration in which the fast steps of the process appear on time trajectories as hops between plateaus where the junction resides for relatively long times. The results in this work support this two-phase model and provide values for the hop size. In addition to a hop corresponding to a 1-bp exchange between homologous arms, the time traces reveal hops that span several bps. In fact, the number of 1-bp hops is almost equal to the number of hops with the exchange of 3 bps. Moreover, some hops span the entire homology of the sequence. We pointed to this possibility in an earlier work (1), but could not prove the hypothesis until we collected the present time-resolved data for a set of immobile HJs with different D-A distances. The size of the hop has been an unknown adjustable parameter until now in models of HJ branch migration as a one-dimensional diffusion process (31). The current data provide the requisite hop-size values. Although branch migration appears as a vertical step in the present experiments, the process is very likely quite complex, requiring the formation of transient states that allow for the swap of homologous bps between different arms. Our previous work provided an estimate of the duration of the branch migration step, ∼100 μs, a value suggesting that time-resolved FRET techniques would be an appropriate tool for the analysis of the swap mechanism. In addition, current advances that extend molecular-dynamics simulations to timescales approaching the microsecond range open prospects for atomic-level modeling of this important genetic process. The availability of FRET data for a set of HJs with different D-A distances has also allowed us to refine the models of immobile HJs. The composite data fit a partially opened, side-by-side model with adjacent double-helical arms slightly kinked at the four-way junction and the junction as a whole adopting a global X-shaped form that mimics the coaxially stacked-X structure implicated in previous solution studies. This structural distinction only becomes clear when the donor and acceptor dyes are placed, as here, in opposite arms. Although Hohng et al. (25) recently introduced a kinked model to interpret the interactions of dyes on adjacent arms of a HJ in the transition state, they did not interpret either of the dominant states in terms of a partially kinked (unstacked) structure of the type offered here.

SUPPLEMENTARY MATERIAL

To view all of the supplemental files associated with this article, visit www.biophysj.org.