Chemical, physical, and theoretical kinetics of an ultrafast folding protein

Abstract

An extensive set of equilibrium and kinetic data is presented and analyzed for an ultrafast folding protein—the villin subdomain. The equilibrium data consist of the excess heat capacity, tryptophan fluorescence quantum yield, and natural circular-dichroism spectrum as a function of temperature, and the kinetic data consist of time courses of the quantum yield from nanosecond-laser temperature-jump experiments. The data are well fit with three kinds of models—a three-state chemical-kinetics model, a physical-kinetics model, and an Ising-like theoretical model that considers 10⁵ possible conformations (microstates). In both the physical-kinetics and theoretical models, folding is described as diffusion on a one-dimensional free-energy surface. In the physical-kinetics model the reaction coordinate is unspecified, whereas in the theoretical model, order parameters, either the fraction of native contacts or the number of native residues, are used as reaction coordinates. The validity of these two reaction coordinates is demonstrated from calculation of the splitting probability from the rate matrix of the master equation for all 10⁵ microstates. The analysis of the data on site-directed mutants using the chemical-kinetics model provides information on the structure of the transition-state ensemble; the physical-kinetics model allows an estimate of the height of the free-energy barrier separating the folded and unfolded states; and the theoretical model provides a detailed picture of the free-energy surface and a residue-by-residue description of the evolution of the folded structure, yet contains many fewer adjustable parameters than either the chemical- or physical-kinetics models.

A major challenge to advancing our understanding of how proteins fold is the development of an analytical theoretical model capable of calculating the quantities directly measured in both equilibrium and kinetic experiments. We have approached this problem experimentally by studying a small ultrafast folding protein, the 35-residue subdomain from the villin headpiece (1–7) (Fig. 1). It is the smallest naturally occurring protein that autonomously folds into a globular structure (8–10), so it should have one of the simplest protein-folding mechanisms, which may therefore be amenable to understanding in depth by a theoretical model. Moreover, because folding of this protein occurs in a few microseconds, close to the proposed theoretical speed limit (4, 11), it can be investigated in detail by molecular-dynamics simulations. Our theoretical approach is to calculate the experimentally measured quantities with an Ising-like statistical mechanical model (12, 13), originally developed to explain our results on the β-hairpin from the protein GB1 (14, 15), and similar to models of Baker, Finkelstein, and coworkers (16–18). The key simplifying feature of these models is that they explicitly consider only interactions between residues that are in contact in the native structure [the perfectly funneled energy landscape of Wolynes and Onuchic (19–21)]. These models have been remarkably successful in predicting both the number of observable states and the folding rates for individual proteins and have also had some success in predicting the relative effect on folding rates and equilibrium constants produced by site-directed mutations [i.e., φ-values (22)] (12, 16–18, 23). However, up to now they have not been used to calculate the physical properties that are actually measured experimentally.

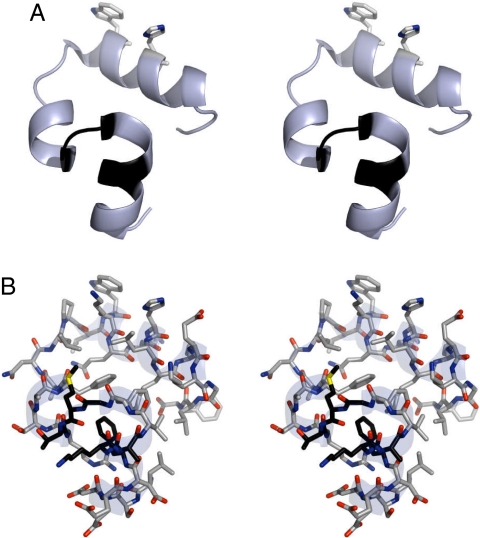
Fig. 1.

Structure of villin subdomain solved by x-ray diffraction (PDB 1WY4) (2). Ribbon diagram of backbone showing the side chains of W23 and H27 (A) and structure with all nonhydrogen atoms (B). Residues F6,K7,A8,G11,M12,T13 are shown in black because their contacts contribute most to the stability of the most populated microstates of the transition state ensemble at 310 K (see Figs. S8 and S9).

In this work, we present and analyze an extensive set of equilibrium and kinetic data on the villin subdomain. The equilbrium data consist of the excess heat capacity (6), tryptophan fluorescence quantum yield (QY), and natural circular-dichroism (CD) spectrum (1, 2, 4) as a function of temperature. The kinetic data consist of time courses of the QY over a wide temperature range from nanosecond-laser-induced temperature-jump experiments. These measured quantities are calculated using a coarse-grained version of the Ising-like model of Muñoz, Henry, and Eaton (12, 13). The kinetics are described by diffusion on a one-dimensional free-energy surface (24), using either the number of ordered residues (25) or the fraction of native contacts (26, 27) as reaction coordinates (28), and a position-dependent diffusion coefficient determined from measurements of the relaxation rate as a function of viscosity (7). We also calculate φ-values for a number of mutants from the change in relaxation rate resulting from the perturbation of the free-energy surface produced by the mutation. To test the validity of our use of order parameters as reaction coordinates, we calculated the splitting probability (also called the p_fold) (29–32) from the rate matrix of the master equation for all 10⁵ microstates of the model.

In addition, we have analyzed the data in terms of a conventional chemical-kinetics model and a model in which the kinetics are described by diffusion on an empirical free-energy surface, similar to what has previously been done for other proteins by Gruebele (33), Muñoz (34), and their coworkers. For lack of a better term, we call this a physical-kinetics model. The chemical- and physical-kinetics models are not only helpful in interpreting experimental results, but they also expose features that support the validity of the theoretical results. We believe that our analysis, using three very different types of models to interpret the data, represents the most comprehensive approach so far to understanding the results of equilibrium and kinetic experiments on protein folding.

Results

Experimental Data to Be Calculated.

The most important equilibrium data to be calculated are the heat capacity as a function of temperature measured by differential scanning calorimetry (6). The reason for its special importance is that the parameters required to fit the data are purely thermodynamic quantities, unlike both equilibrium fluorescence and CD data that require additional parameters to describe the temperature dependence of the QY and CD for each state of the chemical-kinetics model, each position along the reaction coordinate for the physical-kinetics model, or each microstate of the theoretical model. Because the theoretical-kinetics model does not consider the contributions from hydration or internal degrees of freedom arising from bond and angle vibrations, and the chemical-kinetics model considers only differences in heat capacity relative to the native state, the relevant experimental quantity is the heat capacity in excess of that for the fully folded, native state (Fig. 2).

Fig. 2.

Excess heat capacity as a function of temperature. The filled circles are the experimental data. The curves are the fits using the three-state chemical-kinetics (dashed, red), physical-kinetics (continuous, cyan), and theoretical (continuous, blue) models.

Fig. 3 shows the equilibrium thermal unfolding curves measured by fluorescence and CD. To reduce the number of adjustable parameters in fitting with all three models, we also measured the fluorescence of a fragment to simulate the QY for the fully unfolded protein (upper dotted curve in Fig. 3A). The results of the kinetics experiments are shown in Fig. 4. The observed progress curves [QY versus time, supporting information (SI) Fig. S1] are well characterized at each temperature by two exponential processes with relaxation times of ≈100 ns and 1–5 μs. Several lines of evidence, including an independent estimate of the folding rate from an analysis of end-to-end contact measurements (3) and infrared studies by Dyer and coworkers (35, 36), indicate that the slower relaxation corresponds to global unfolding/refolding. Fig. 5 shows φ-values for 10 mutants calculated from simultaneous fitting of fluorescence and CD equilibrium unfolding curves as in reference (1) and relaxation rates assuming a two-state model (equilibrium and rate constants are summarized in Table S1).

Fig. 3.

Tryptophan fluorescence quantum yield and circular dichroism as a function of temperature. The filled circles are the experimental data. The curves are the fits using the three-state chemical-kinetics (dashed, red), physical-kinetics (continuous, cyan), and theoretical (continuous, blue) models. (A) Tryptophan fluorescence: the upper dotted curve corresponds to the measured quantum yield of the fragment (AcWKQQH); the lower dotted curve is the quantum yield of the theoretical-kinetics model for microstates that have a W23-H27 contact. (B) Circular dichroism. The curves are the fits using the three-state chemical-kinetics (dashed, red), physical-kinetics (continuous, cyan), and theoretical (continuous, blue) models.

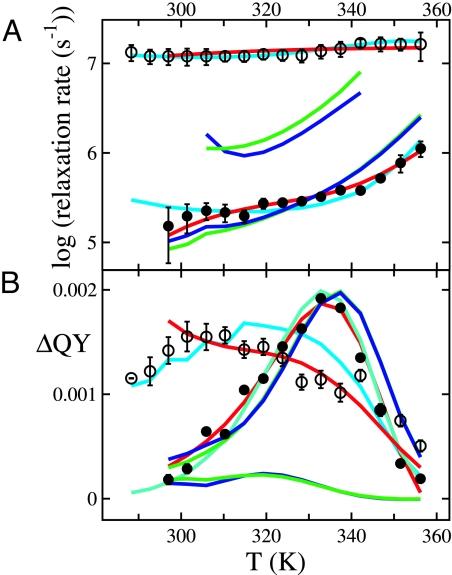
Fig. 4.

Relaxation rates (A) and kinetic amplitudes (B) as a function of temperature. The open and filled circles are the relaxation rates obtained from biexponential fits to the measured kinetic progress curves shown in Fig. S1. The curves are the fits using the three-state chemical-kinetics (red), physical-kinetics (cyan), and theoretical models with P (green) and Q (blue) as reaction coordinates.

Fig. 5.

φ-Values. The red points are the experimental data at 310 K (see Table S1); the continuous blue and green curves are the φ-values calculated for the Q and P reaction coordinates, respectively, assuming a two-state model and a 50 cal/mol perturbation of the stability by altering the contact energy for the mutated residue. The dotted blue and green curves, for Q and P respectively, correspond to the (Boltzmann-weighted) average fraction of native contacts for the microstates at reaction coordinates with free energies within 1 k_BT of the barrier top.

Chemical-Kinetics Model.

The simplest chemical-kinetics model is a two-state model, in which there are only two populations of molecules at equilibrium and at all times in kinetic experiments. However, the observation of two phases in the kinetic progress curves requires consideration of a third state. The conventional three-state folding model is one in which there is an intermediate state (I) on the pathway from the unfolded (U) to folded (F) state, i.e.

This model provides an excellent fit to both equilibrium and kinetic data (Figs. 2–4). The standard equations used and the values of the adjustable parameters of the model are given in SI Appendix and Table S2. The important result of the three-state model, as indicated in the scheme above, is that the intermediate (I) interconverts with the folded state (F) much faster than it does with the unfolded state (U) and therefore lies on the folded side of the major free-energy barrier (the populations of the three states as a function of temperature are shown in Fig. S2).

Physical-Kinetics Model.

Our physical-kinetics model consists of a free energy (G) versus reaction coordinate function, and the values of the observables (QY and CD) at each value of the reaction coordinate (q). We assumed that there are only two deep minima on this free-energy surface, corresponding to the unfolded and folded states, with the position of the minima allowed to move with temperature as a way of generating an additional relaxation. Recognizing that, with the possible exception of the calorimetric data, the information content in the data is insufficient to determine curvatures, we used effectively the same curvature for both wells and barrier top and parameterized the surface with coordinates (q_i,G_i) for the unfolded state, the barrier top, and the folded state. Fig. 6 shows the free-energy surfaces as a function of temperature that optimally fit the experimental data (the coordinate dependencies of the QY and CD are shown in Fig. S3). The calorimetric data (Fig. 2) were fit from the temperature dependence of an equilibrium constant (Fig. S4), defined by the ratio of the populations on either side of the dividing line, taken as the value of q at the free-energy barrier top (see SI Appendix for details).

Fig. 6.

Free-energy surface (continuous) and populations (dashed) of physical-kinetics model.

The physical-kinetics model also provides an excellent fit to all of the equilibrium and kinetic data (Figs. 2–4). The important results of analyzing the data by using this model are that the free-energy barrier to folding is very small (≈2 kcal/mol) and that the ≈100-ns process is explained as relaxation in the folded well to more unfolded conformations as the temperature increases, as indicated by the movement of the folded-well minimum to smaller values of the reaction coordinate.

Theoretical-Kinetics Model.

The model has been described in detail elsewhere (6, 12, 13) (see SI Appendix and Table S3 for details). The principal assumptions of the model are that each residue of the polypeptide chain can exist in one of two possible states—native (n) or nonnative (c), as in an Ising model (37)—and that no more than two continuous stretches of native residues are allowed in each molecule (e.g., …cnnncccnnnccc…). This latter assumption, the so-called double-sequence approximation, greatly reduces the number of possible configurations from 2³⁵ (3 × 10¹¹) to 6 × 10⁴. The free energy and thermodynamic weight of a stretch of native residues of length j beginning at position i are, respectively,

where n_ji is the number of contacts in the stretch, ε is the energy per contact, and Δs_conf is the conformational-entropy cost of fixing a residue in its native conformation. The model allows contacts between residues in a native segment and between residues in two different native segments, so there is an additional destabilizing term in the partition function for connecting the two segments by a disordered loop, but it contains no adjustable parameters. The same energy (ε) was assigned to each interresidue contact and is an adjustable parameter of the model. In the same spirit, the same entropy decrease (Δs_conf) for the nonnative to native transition was assigned to every residue. Allowing Δs_conf and ε to be temperature-dependent to account for hydrophobic interactions gave no improvement to the fits.

A contact between residues exists if the distance between α-carbons of the polypeptide backbone in the folded structure is ≤0.8 nm. This definition results in a rather sparse interresidue contact map (Fig. 7A), with only 13 nonlocal contacts (which we define as contacts between residues separated by five or more residues in the sequence) and 9 contacts between helices. Using atom–atom contacts as a criterion for interresidue contacts, Chiu et al. (2) found the corresponding numbers to be 18 and 13. Importantly, our more coarse-grained contact map does contain contacts by all three of the core phenylalanines (F6, F10, and F17) and two of the three interhelical hydrogen bonds.

Fig. 7.

Results of theoretical-kinetics model. (A) Contact map (PDB 1YRF). (B) Free energy and relative population versus Q reaction coordinate. (C) Free energy and relative population versus P reaction coordinate. (D) Probability that a residue is in its native conformation at each temperature. The thick red bars indicate helical residues. (E) Probability that a residue is in its native conformation at each value of Q relative to all microstates at that value of Q. (F) Probability that a residue is in its native conformation at each value of P relative to all microstates at that value of P. (G–I). Relative probability that contact is formed at Q = 0.09 (barrier top) (G), 0.33 (H), 0.71 (I). See Fig. S5 for corresponding plot for P reaction coordinate.

The excess heat capacity was calculated directly from the partition function of the model (see Eqs. S1–S5 in SI Appendix), whereas calculation of the unfolding curves measured by CD and fluorescence required a model for the CD and the QY for each microstate of the model (see SI Appendix for details). For short helices, there is a large dependence of the CD on the length of the helix. We used the model of Thompson et al. (38), which also considers the contribution to the CD from the lone tryptophan (see Eqs. S7 and S8 in SI Appendix). For the QY of each microstate we assumed that the only source of quenching relative to the fully unfolded state arises from the contact of the tryptophan with the protonated histidine one turn away on the helix (Fig. 1) when all of the intervening residues are in their native conformation. This assumption is based on the well known quenching of tryptophan fluorescence by protonated histidine (38) and our observation of a ≈4-fold decrease in the amplitude for the slower unfolding/refolding relaxation at pH 7, where the histidine is mainly unprotonated (data not shown). For microstates in which this contact is not made, we assumed that the QY is the same as that measured for a short peptide fragment containing the lone tryptophan of the sequence (upper dotted curve in Fig. 3A).

The kinetics were obtained by solving the system of differential equations describing reversible hopping between adjacent discrete values of the reaction coordinate on a one-dimensional free-energy surface, where the reaction coordinate is taken as either the number of ordered residues (P) (25) or the fraction of native contacts (Q) (26) (see Eqs. S9–S12 in SI Appendix) (Figs. 7 B and C). The QY at each position along the reaction coordinate was calculated from the Boltzmann-weighted contribution of the subset of the 92,696 microstates of the partition function having that value of the reaction coordinate. Fig. S1 shows representative fits to the progress curves, with all of the results summarized in Fig. 4, which compares the calculated and experimental values of the relaxation rates and amplitudes at each temperature.

Fig. 5 contains the φ-values predicted by the model using two different types of calculations (see SI Appendix for details). In one, φ-values were calculated in the small-perturbation limit by adjusting the contact energy of the mutated residue to produce a new free-energy surface with a 50-cal/mol decrease in the stability of the folded state, assuming a two-state system with the dividing surface at the barrier top (Q = 0.09 or P = 5). The folding rate was then obtained from the new relaxation rate and equilibrium constant to yield the φ-value, as was done with the experimental data. In the second method, the φ-value was obtained from the (Boltzmann-weighted) fraction of native contacts for each residue for all microstates at and close to the barrier top, assumed to be the transition state. This method corresponds to the conventional interpretation of experimental φ-values and is also similar to what is done to calculate φ-values from simulation results; the correct calculation, namely the determination of the change in folding rate and equilibrium constant produced by the mutation, is much more difficult to calculate from simulations and has not yet been done for any protein.

The important output of the theoretical model (Fig. 7) is mechanistic information, that is, the prediction of how the structure evolves from the unfolded to folded state along the reaction coordinates, P and Q. Fig. 7 E and F show the relative probability at each value of the Q or P reaction coordinate, respectively, that a residue is in its native conformation, whereas Fig. 7 G–I shows the evolution of the interresidue contacts along the Q reaction coordinate (the corresponding contact maps for P are shown in Fig. S5 and are very similar).

Splitting Probabilities.

The splitting probability (or p_fold) is the probability that a given microstate of the model will reach the folded state before reaching the unfolded state (29–32). These probabilities were calculated for the individual microstates from the rate matrix for the master equation of the theoretical model (see SI Appendix) (39). Fig. 8 shows the splitting-probability distribution for those microstates of the model with free energies of 2 k_BT or less above the lowest-free energy microstate for the specified value of the coordinate. Fig. S6 shows the distribution for all microstates at these values of the reaction coordinates.

Fig. 8.

Distribution of spitting probabilities (p_fold) calculated from the rate matrix for microstates <2 k_BT above the most stable one at each value of the reaction coordinate at 310 K. (A) p_fold distribution at Q = 0.03, 0.09 (the barrier top), and 0.27. (B) p_fold distribution at P = 3, 5 (the barrier top), and 10. See Fig. S6 for p_fold distribution for all microstates at the same values of the reaction coordinates.

Discussion

Each of the three models used to simultaneously fit the equilibrium and kinetic data provides information on the mechanism of folding of the villin subdomain. The three-state chemical-kinetics model provides an excellent fit to all of the data (Figs. 2–4), which is not surprising because there are 18 adjustable parameters in the model (Table S2). The important result from this model is that the intermediate interconverts with the fully folded state (≈10⁷ s⁻¹) much faster than with the unfolded state (≈10⁵ to 10⁶ s⁻¹), from which we conclude that it is located on the folded side of the major free-energy barrier. The three-state model also attributes the increase in CD before the main unfolding transition (Fig. 3B) to an increase in the partially unfolded intermediate-state population of lower helix content (Fig. S2). The important feature of a chemical-kinetics model is that there is a straightforward prescription for obtaining information on the ensemble of structures of the transition state from the relative effects of site-directed mutants on the folding rate and equilibrium constant—the φ-value (22), defined as Δlnk_f/ΔlnK_eq. Because of the separation in time scales between the fast phase and the global unfolding/refolding phase, the fast phase could be ignored, permitting the calculation of φ-values from a simple two-state analysis to obtain the folding rate and equilibrium constant for the wild-type and the mutants. None of the mutations are ideal for φ-value analysis, because they do not represent small structural changes, such as simple deletion of a methyl group, as in replacing isoleucine with valine or threonine with serine. Nevertheless, the φ-values are unusually low at 310 K (Fig. 5), suggesting a transition state with little structure formation and therefore one that appears very early along the reaction coordinate. There is, moreover, a significant increase in φ-values for four of the nine residues for which φ-values could be calculated at 340 K (Table S1), suggesting a shift in the transition state toward the folded state at the higher temperature.

The physical-kinetics model, which consists of an empirical one-dimensional free-energy surface with two deep minima (Fig. 6) and the coordinate dependence of the fluorescence QY and CD (Fig. S3) to give a total of 16 adjustable parameters (Table S4), also provides an excellent fit to the equilibrium and kinetic data (Figs. 2–4). According to this model, the position of the folded-well minimum moves toward smaller values of the reaction coordinate with increasing temperature. This motion represents partial unfolding and explains the decrease in helix content before the global thermal unfolding (Fig. 3B). It also explains the ≈100-ns phase in the kinetics (Fig. 4) as reconfiguration in the shifted folded well at the elevated temperature. The lack of temperature dependence for the rate of the ≈100-ns phase is consistent with our a priori assumption that there is no additional barrier on the free-energy surface.

The major result of the physical-kinetics model is the prediction of the height of the free-energy barrier separating folded and unfolded states. According to Kramers' theory, the rate of barrier crossing depends on the curvature of the wells and the barrier top and exponentially on the barrier height (24), so the barrier height dominates. An important result of the physical-kinetics model, then, is that the free-energy barrier to folding (Fig. 6) is small (≈2 kcal/mol). A ≈2-kcal/mol barrier is also simply calculated from Kramers' equation for a two-state system, assuming that the diffusion coefficients and curvatures in the folded and unfolded well and at the barrier top of the free-energy surface are the same, i.e., ΔG_f^‡ = RT_f ln(τ_f/2πτ) = 1.6 kcal/mol, where τ_f (4.6 μs) is the folding time, and τ (70 ns) is the reconfiguration time in the folded well (4). The 1- to 2-kcal/mol barriers at the folding temperature are also obtained by fitting the calorimetric data (Fig. 2) with the variable barrier model of Muñoz and Sanchez-Ruiz (6) or the temperature dependence of the relaxation rates (Fig. 4A) with a mean-field model of Naganathan et al. (34).

The Ising-like theoretical model provides remarkably good fits to all of the experimental equilibrium and kinetic data (Figs. 2–4) and yields the most information about the folding mechanism, yet contains far fewer adjustable parameters than either the chemical-kinetics or physical-kinetics models. Although the fit to the excess heat capacity-vs.-temperature curve (Fig. 2) is not as good as either of the other two models, the theoretical model requires only two adjustable parameters to (nearly) fit the heat-capacity data—a contact energy and a conformational-entropy loss (Eq. 1) that are the same for every residue, compared with eight adjustable parameters of the chemical-kinetics model and nine of the physical-kinetics model. The fitted value of −3.70 cal mol⁻¹ K⁻¹ for the conformational-entropy loss, moreover, is comparable to the average value expected from thermodynamic analysis of many proteins (6).

The kinetics are described by the theoretical model as hopping along the discretized one-dimensional free-energy surface given by the partition function, by using either the fraction of native contacts (Q) or number of native residues (P) as reaction coordinates (25–27). By invoking a linear free-energy relation between the hopping rate and the ratio of equilibrium populations at adjacent values of the reaction coordinate, the additional adjustable parameter required to describe the kinetics is the proportionality constant (γ) and an activation energy for its temperature dependence (Eqs. S10–S12 in SI Appendix). From a recent study of the viscosity dependence of the measured relaxation rates using a viscogen that has no effect on the equilibrium properties, we obtained the reaction-coordinate dependence of γ by fitting the data with the theoretical model (see Fig. S7) (7). The resulting simultaneous fits to all of the equilibrium and kinetic data (Figs. 2–4 and Fig. S1), apart from the CD (see SI Appendix), are not quite as good as the other models, but again there is a large difference in the number of adjustable parameters (7 for the theoretical model, 15 for the physical-kinetics model, and 18 for the chemical-kinetics model). The theoretical model fails to come close to fitting the ≈100-ns phase, attributed by the physical-kinetics model to reconfiguration in the folded well. This relaxation apparently reflects the fine structure of the free-energy surface, which is not captured by this simple theoretical model. The failure of the model may also result from the implicit assumption of the same prefactor independent of the type of motion (40) or from an oversimplification in our treatment of the (W23) quantum yield, which assumes that contact with the protonated histidine (H27) one turn away in the helix (Fig. 1) is the only additional source of fluorescence quenching in the folded state.

A question that immediately arises in describing the kinetics as diffusion on the one-dimensional free-energy surface is: are Q and P good reaction coordinates? A critical test is whether the splitting probability is close to one-half for the microstates at the free-energy barrier tops of these profiles. We therefore calculated the splitting probability (also called the p_fold) from the rate matrix of the master equation of the model (see SI Appendix). Fig. 8 shows the distribution of splitting probabilities for those microstates of the model within 2 k_BT of the lowest free-energy microstate at the barrier top and at positions 1.6 k_BT to the left and right of the barrier top. A substantial fraction of microstates exhibits a p_fold between 0.4 and 0.6 at the barrier top for both Q (28% at Q = 0.09) and P (44% at P = 5) reaction coordinates, with a sharp change in the p_fold distribution at higher and lower values of Q and P. We also asked the question: what fraction of the low lying microstates with a p_fold between 0.4 and 0.6 is within the barrier region, i.e., at reaction coordinates within 1 k_BT of the barrier top? If we identify the low lying microstates as those within 2 k_BT of the lowest free-energy microstate at each value of the reaction coordinate, we find that the barrier region contains 84% of the microstates with a p_fold between 0.4 and 0.6 for Q and 100% for P. If the low lying microstates are identified as those within 3 k_BT of the lowest free-energy microstate at each value of the reaction coordinate, the barrier region contains 48% for Q and 90% for P. All of these results indicate that both Q and P are indeed good reaction coordinates for describing the kinetics.

Another important test of the theoretical model is its ability to predict φ-values, which cannot be calculated from either the chemical- or physical-kinetics model. Fig. 5 shows the φ-values for the 10 mutations studied. Of these, only two (L20V and L28V) might represent a sufficiently small structural perturbation to satisfy the assumption of the φ-value analysis that the mutation does not alter the unfolded state and changes only the interaction of the mutated residues with its contacting neighbors in the transition and folded states without perturbing any other residue–residue interactions. At 310 K the observed φ-values are unusually low compared with all other proteins, which is qualitatively explained by the theoretical model as resulting from the major barrier being very early along the reaction coordinate for both Q and P (Fig. 7 B and C), where there is a very low probability of native contact formation for most residues (Fig. 7G and Figs. S5A, S8, and S9). The model also does a remarkably good job of predicting the low φ-values quantitatively using two different methods (Fig. 5 and Table S1).

Although the system is not far from two-state, as judged by the temperature dependence of the probability that a residue is in its native state (Fig. 7D), we do not have the simple case of a high barrier that remains at the same position along the reaction coordinate at all temperatures. At temperatures above the folding temperature of 340 K, the surface becomes more complex, indicating formation of an intermediate, and a new major barrier appears closer to the folded state (Q ≈ 0.5 and P ≈ 25). (A simple calculation explains almost all of the shift: Increasing the temperature by ΔT results in an increase in free energy at P = 25 relative to P = 5 from the change in the contribution from the conformational entropy of ΔP × Δ T × Δs_conf, which, for a 40°C temperature increase, is 3 kcal/mol). This change in the surface contributes to the denaturant independence (Fig. S10) of the observed relaxation rate because of the relative insensitivity of the folding and unfolding barriers to the contact energy at low and high denaturant concentration, respectively (Fig. 7 B and C) (5). The change in the free-energy surface also results in the decrease in the viscosity dependence of the relaxation rate as the temperature is increased because of an increased contribution of internal friction in the more compact structures at higher values of the reaction coordinate (7) (Fig. S7). The model therefore also predicts that there should be an increase in φ-values with increasing temperature, and in the four mutants where measurements could be made at 340 K, there is indeed a significant increase (Table S1).

Because of the complexity of the surface, both experimental and theoretical φ-values are only approximate. The correct and more rigorous approach is to compare the new thermal unfolding curves and relaxation rates that result from the mutation. That is, vary the contact energy (and possibly also the conformational entropy change) of the mutated residue to optimally fit the new thermal unfolding curve and compare the calculated relaxation rate on the new free-energy surface with the observed relaxation rate. To test this prediction of the model will require more extensive data on the temperature dependence of the kinetics, particularly results from more conservative mutations than are currently available.

The utility of the theoretical model, of course, is that if accurate it provides a detailed description of the mechanism. Unlike φ-value analysis, which, with rare exceptions (21), provides structural information at a single, albeit important point along the reaction coordinate—the transition state—the theoretical model describes the complete evolution of the unfolded to folded structure. This information is shown in Fig. 7 E and F as the probability of a residue being in the native confirmation at each position on the reaction coordinate and the evolution of the contact map (Fig. 7 G–I and Fig. S5 A–C). The model predicts that the N-terminal helix (D3 to F10) forms first, along with an interhelical contact with the first few residues of the second helix (R14 to F17), followed by the middle helix, and finally the C-terminal helix (L21 to E31). The longest-range contacts between the N- and C-terminal helices (V9-K32, F10-L28) do not begin to form until very late along the reaction coordinate. Diagrams of the individual microstates of the transition-state ensemble at 310 K (Figs. S8 and S9) show that for both Q and P reaction coordinates, the interaction between the helical residues F6-K7-A8 with the G11-M12-T13 loop contributes most to the stability (Fig. 1) (reflected in the peaks of the theoretically calculated φ-values in Fig. 5), so that forming the transition state ensemble does not correspond to simple helix nucleation.

There have been a large number of simulations of various types with the aim of describing the dynamical properties and folding mechanism of the villin subdomain (see SI Appendix for a list of simulation references). So an obvious question might be: How does this evolution of the structure compare with the predictions of simulations that provide much more structural detail than can be obtained from our theoretical model? We believe that it is premature to make detailed comparisons for at least two reasons. First, none of the directly measured experimental quantities have been calculated in any of the simulations—most importantly, the temperature dependence of the heat capacity that tests their thermodynamic accuracy. Second, although the agreement between the predictions of our theoretical model and experimental results is impressive, as pointed out above, more extensive mutagenesis will be required to more rigorously test the predicted order of structure formation. Nevertheless, there are two intriguing results that should be mentioned. Shakhnovich and coworkers used Monte Carlo simulations of an atomistic model to calculate φ-values from the fraction of native contacts in the ensemble of microstates with 0.4 < p_fold < 0.6 (41). Although their calculated φ-values are uniformly higher at 300 K than we observe at 310 K (Fig. 5), the pattern of φ-values indicates that the N-terminal and middle helices form before the C-terminal helix. Pande and coworkers have carried out all-atom molecular-dynamics calculations in explicit solvent (42, 43). They find that the native conformation is in fast exchange with ensembles of conformations containing the middle and C-terminal helices and conformations containing only the middle helix, providing a possible explanation of the ≈100-ns relaxation (see also ref. 44).

Concluding Remarks

Our analysis of equilibrium and kinetic data using three different approaches highlights the importance of a theoretical model. Despite having many fewer adjustable parameters than either the chemical-kinetics or physical-kinetics models, the Ising-like model produces an almost equally good fit to a wide range of experimental data. An obvious question is: Why does such a simple model, with a perfectly funneled energy landscape and no distinction between the different amino acid residues, work so well? A possible answer to the first part is that coarse graining works because of enthalpy–entropy compensation. This issue could be explored further by using contact maps generated with different distance or atomistic criteria or with residue-specific potentials (45). The answer to the second part of the question is more biological than physical, and is based on the idea that natural selection minimizes nonnative interactions to prevent traps that will slow folding or lead to aggregation (19).

What can be done to further test and refine the model? One computational test would be to carry out Langevin simulations of a coarse-grained representation of the protein. These calculations could determine how many contiguous sequences would be required in the model to adequately describe the folding process. An experimental test would be to carry out mutational studies that can be interpreted more rigorously, in which the change in the amino acid is a simple methyl-group deletion (e.g., threonine to serine or leucine to norvaline). Finally, a more complete description of the mechanism can, of course, be obtained from the kinetic equations that describe the interconversion of all microstates of the theoretical model (Eq. S13). Solution of these equations will yield the distribution of pathways that the protein takes from the folded to the unfolded state, as can be obtained by molecular simulations, and might be tested by single-molecule FRET experiments (46).

Materials and Methods

The 35-residue villin subdomain (LSDED FKAVF GMTRS AFANL PLWKQ QHLKK EKGLF—helical residues in bold type) was obtained from California Peptide Research. Solutions were buffered with 20 mM sodium acetate at pH 4.9. Details of the differential scanning calorimetry experiments have been described by Godoy-Ruiz et al. (6). The absolute heat capacity for the fully formed native structure was taken from the study of Freire, using C_P^F = (b + c(T − 273.15))M_r cal K⁻¹ mol⁻¹, with b = 0.329 cal K⁻¹ g⁻¹, c = 1.9 × 10⁻³ cal K⁻² g⁻¹, and the molecular weight of the protein M_γ = 4084 g mol⁻¹. Godoy-Ruiz et al. argued that the larger surface-to-volume ratio for this 35-residue protein, with a greater fraction of surface residues having conformational freedom of the side chains compared with the much larger proteins used in the Freire study (47), justified the use of the Freire parameters that produce the highest heat capacity within the experimental uncertainty.

CD was measured with a Jasco J-720 spectropolarimeter at a protein concentration of 0.2 mM. Fluorescence thermal unfolding curves were measured with a SPEX Fluorolog spectrofluorometer at 10 μM concentration. Folding kinetics were measured at 0.5 mM by using a laser-temperature-jump apparatus described in ref. 38. Each kinetic progress curve was obtained from the average of 512 laser shots. The size of the temperature jump (7–10 K) was calibrated by using the temperature dependence of N-acetyltryptophanamide fluorescence.