Distinct mechanisms act in concert to mediate cell cycle arrest

Abstract

In response to DNA damage, cells arrest at specific stages in the cell cycle. This arrest must fulfill at least 3 requirements: it must be activated promptly; it must be sustained as long as damage is present to prevent loss of genomic information; and after the arrest, cells must re-enter into the appropriate cell cycle phase to ensure proper ploidy. Multiple molecular mechanisms capable of arresting the cell cycle have been identified in mammalian cells; however, it is unknown whether each mechanism meets all 3 requirements or whether they act together to confer specific functions to the arrest. To address this question, we integrated mathematical models describing the cell cycle and the DNA damage signaling networks and tested the contributions of each mechanism to cell cycle arrest and re-entry. Predictions from this model were then tested with quantitative experiments to identify the combined action of arrest mechanisms in irradiated cells. We find that different arrest mechanisms serve indispensable roles in the proper cellular response to DNA damage over time: p53-independent cyclin inactivation confers immediate arrest, whereas p53-dependent cyclin downregulation allows this arrest to be sustained. Additionally, p21-mediated inhibition of cyclin-dependent kinase activity is indispensable for preventing improper cell cycle re-entry and endoreduplication. This work shows that in a complex signaling network, seemingly redundant mechanisms, acting in a concerted fashion, can achieve a specific cellular outcome.

One goal of systems biology is to quantitatively understand the dynamics of signaling pathways. As mathematical models of individual pathways emerge, we are challenged to interconnect them into a detailed understanding of how different pathways control the processing of information within the cell. The networks controlling cell cycle progression and the response to DNA damage are natural choices for such an integrative study. Each has been individually modeled successfully, and a great deal is understood about how specific interactions and regulation affect the dynamics of each network. However, in the absence of an extended model bridging these two pathways, the quantitative interaction between them remains undescribed. Here we develop a computational model of the combined networks and use it together with experimental measurements to determine the relative contribution and specific function of different cell cycle arrest mechanisms in response to DNA damage.

During the cell cycle, mammalian cells coordinate cell growth, genome replication, and division. Two irreversible events subdivide the cell cycle into distinct phases: the onset of DNA replication defines S phase; and cell division defines M phase. Cells grow and carry out additional functions during the gap phases G1 and G2. The changing activity states of cyclin-dependent kinases (Cdks) regulate the transition between different stages of the cell cycle (1). Cyclin D/Cdk4 and -6 and cyclin E/Cdk2 complexes drive the sequential progression from G1 to S phase, respectively. Cyclin A/Cdk2 and -Cdk1 complexes become active during S and G2 phase, and cyclin B/Cdk1 complexes control the G2/M transition as well as various processes during mitosis. The cell cycle has long been a fruitful subject for mathematical modeling (2). Models have proven useful for understanding the impact of perturbations to protein levels, network connections, and the cellular environment on cell cycle progression (3, 4).

A separate, well-studied regulatory network senses DNA double-stranded breaks (DSBs) caused by ionizing radiation (IR). DSBs activate the ataxia telangiectasia-mutated (ATM)/checkpoint kinase 2 (Chk2) kinase cascade that phosphorylates p53, contributing to its stabilization and activation (5–7). p53 transcriptionally modulates a variety of genes involved in cell cycle arrest, DNA repair, apoptosis, and in regulating p53 itself (8). The feedback loops between p53, its upstream activating kinases ATM and Chk2, and its downstream regulators Mdm2 and Wip1 generate oscillatory dynamics in single cells (9–11). Mathematical modeling contributed to understanding the dynamic behavior exhibited by this network as well (9, 12).

Upon DNA damage, interactions between the damage-sensing and the cell cycle networks induce cell cycle arrest by modulating cyclin/Cdk activity. These interactions must fulfill three main requirements: first, to prevent alterations to the genome they must relay the damage signal and halt the cell cycle promptly. Second, the arrest must persist as long as damage is present. Last, because cyclin/Cdk activity might be changed during the arrest, cell cycle re-entry should only proceed from a state of cyclin activation that ensures the proper sequence of DNA replication and mitosis.

Multiple mechanisms that connect the DNA damage response to the cell cycle have been identified (13), and there is evidence for cooperation between some of them (14). However, little is known about their relative contribution in the context of the full signaling networks. Furthermore, it is unclear whether individual mechanisms are sufficient to fulfill all of the above criteria, or whether combinations of mechanisms confer specific characteristics to a proper cell cycle arrest.

We address these questions systematically by combining experimental measurements of cell cycle distributions and cyclin levels together with the development of an integrated model of the DNA damage response and cell cycle networks. We find that individual arrest mechanisms act in concert to specifically establish immediate and sustained arrest after damage, as well as to prevent improper cell cycle re-entry.

Results

A Model of the DNA Damage and Cell Cycle Networks.

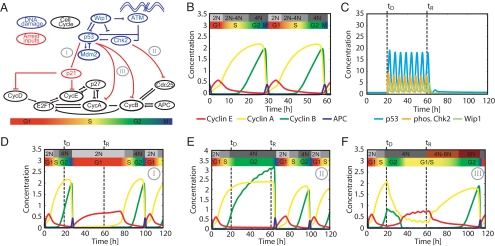
We constructed an integrated model of the DNA damage response network and the cell cycle (Fig. 1A). The model includes interactions previously studied in the context of the p53 network (shown in blue) and the cell cycle (shown in black). The interactions between the two networks represent the effect of DNA damage on the cell cycle (shown in red).

Fig. 1.

Cell cycle and DNA damage models. (A) Diagram of key species in the integrated model of DNA damage signaling (blue) and cell cycle arrest (black). Bridging connections consist of species modulating cell cycle arrest (red). The approximate cell cycle phases are shown below the diagram. Three classes of arrest mechanisms are indicated by numerals: I: G1 arrest by p21 induction; II: G2 arrest by G2 cyclin inactivation; and III: G2 arrest by G2 cyclin transcriptional repression. (B) Cell cycle model simulation showing cyclins E, A, and B and phosphorylated APC. Progression through cell cycle phases and changes in DNA content are indicated above the simulation. (C) Simulation of the DNA damage network after onset of damage at times t_D until the repair time t_R. Nuclear p53, phospho-Chk2, and Wip1 species are shown. (D-F) Simulation of arrest mechanisms (I-III). Dynamics are influenced by the p53 and Chk2 activity from the DNA damage network shown in C.

The topology of the DNA damage model was derived from the model of Batchelor et al. (11), in which oscillations are driven by a combination of 2 negative feedback loops: the core p53-Mdm2 loop and a loop in which the upstream checkpoint kinases are inhibited by a p53-inducible gene product, the phosphatase Wip1. To provide an extensible framework for future modeling of the DNA damage network, we incorporate additional feedback loops (15) in our model [supporting information (SI) Fig. S1A]. With the current parameterization, however, these loops do not significantly affect the network's dynamics.

Our cell cycle model is based on the cell cycle model of Csikasz-Nagy et al. (16). This comprehensive model is composed of generic network modules that have been parameterized to match data from yeast to mammals. To adapt the model as a platform to study cell cycle arrest in human cells, it was necessary to modify it in both parameterization and topology, while ensuring that it remains capable of recapitulating known experimental results.

Three classes of changes are introduced in the present study: (i) species previously treated at quasi-steady state with algebraic expressions were expanded to dynamic differential equations, (ii) protein synthesis and degradation terms were added for each species in the model, and (iii) the intracellular signal resulting from extracellular growth factor present in the medium, M, replaced the dependence between cell size and progression through the cell cycle (17) (SI Appendix, “Model construction”, Table S1, SI MATLAB code).

Simulation of the freely cycling model shows qualitative similarity to trajectories obtained previously (16), with sequential peaks of cyclins E, A, and B defining G1, S, and G2 phase (Fig. 1B). These cell cycle phases are associated with the transition from a 2N DNA content to 4N and the subsequent distribution of chromosomes to daughter cells during mitosis, which is represented by a peak in anaphase-promoting complex (APC) activity (Fig. 1B) (1). The model also matches a variety of experimental results from the literature, including (i) G1 synchronization by serum starvation or cycloheximide treatment (18) (Fig. S1 B and C), (ii) free cycling without cyclin E (19) (Fig. S1D), and (iii) G1 arrest at normal mitogen levels but continued cycling at high mitogen levels for the cyclin D knockout model (Fig. S1E) (20). Taken together, these results demonstrate that our cell cycle model recapitulates a wide range of experimental observations.

The two models were initially joined by incorporating well-described interactions that represent larger classes of G1 and G2 arrest mechanisms (Fig. 1A and SI Appendix, “Modeling cell cycle arrest”). For simplicity, we divided these mechanisms into 3 classes and analyzed one representative mechanism from each class (Fig. 1A): I: G1 arrest represented by p53-dependent inhibition of cyclin E/Cdk and cyclin D/Cdk complexes by p21 (21, 22); II: p53-independent G2 arrest represented by posttranslational inactivation of cyclin A/Cdk and cyclin B/Cdk complexes (23, 24); and III: p53-dependent G2 arrest represented by transcriptional repression of cyclin A, cyclin B, and Cdk1 (25–28).

Computational Analysis of Different Arrest Mechanisms.

To assess the relative contribution of different arrest mechanisms, we implemented each mechanism individually and tested the resulting network behavior (Fig. 1 C-F). Cell cycle arrest was simulated by activating DNA damage between the time of damage (t_D) and recovery (t_R) (SI Appendix, “Model simulation details”). The damage stimulus activated the p53 network, leading to oscillations of p53 and active Chk2 with a period of approximately 5.5 h (Fig. 1C) (11). Each arrest mechanism was capable of halting the cell cycle on its own, but there were distinct differences in the state of the network during the arrest (Fig. 1 D-F).

When damage was applied during G2 phase, mechanism I (implementing p21-dependent inhibition of cyclin E/Cdk2) led to a stable arrest in G1 (2N DNA content) after one cell division (Fig. 1D). During the arrest, p21 and cyclin E reached high levels. After removal of the damage signal, re-entry into S phase was delayed by ≈20 h. Mechanism II (implementing Chk2-mediated G2 cyclin inactivation) induced the arrest of 4N cells with high levels of cyclins A and B; upon re-entry, cells immediately entered mitosis (Fig. 1E). In contrast, p53-dependent G2 cyclin downregulation implemented by mechanism III led to the arrest of 4N cells in which cyclin A and B levels progressively decreased and cyclin E levels were elevated (Fig. 1F). Thus, in cells arrested by mechanism III, the cyclin network uncouples from the status of DNA replication: cyclins switch from a G2 to a G1/S-like state, even though cells do not divide. Upon deactivation of the damage stimulus, these cells increase cyclin A and B levels, thereby progressing twice through the cell cycle without an intervening mitosis. This implies a danger inherent to arrest mechanism III: downregulation of the G2 cyclins might lead to loss of information about the cell cycle phase before damage and endoreduplication.

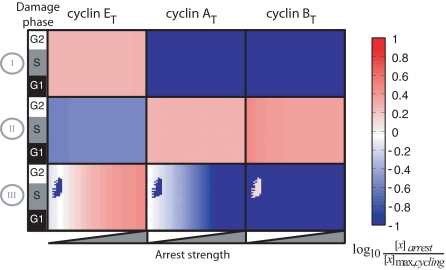
The dynamic behaviors of Fig. 1 were obtained by applying damage at a specific time, with fixed parameters controlling p53's and Chk2's activation of each arrest mechanism (SI Appendix, “Modeling cell cycle arrest”). To expand this analysis, we simulated cell cycle arrest, varying the time of damage induction and the arrest strength. From the resulting trajectories, we determined the steady state levels of cyclins E, A, and B (Fig. 2 and SI Appendix). Mechanism I led to a moderate increase of cyclin E levels with low levels of the G2 cyclins A and B, consistent with arrest in G1. Notably, mechanisms II and III, which are both known to act in G2 cells with 4N DNA content, resulted in distinct cyclin profiles during the arrest: mechanism II led to increased levels of cyclins A and B and low levels of cyclin E, whereas mechanism III showed the reverse pattern in most simulations. At weak arrest strengths this mechanism led to bimodality in cyclin B and E profiles.

Fig. 2.

Steady-state cyclin levels during simulated arrest. Rows indicate the arrest mechanism; columns indicate the cyclin measured. In each square both strength and time of arrest application are varied. Arrest strength was varied by scaling the value of the parameters implementing each arrest mechanism over 2 orders of magnitude from the minimum value required to generate arrest (SI Appendix, “Modeling cell cycle arrest”). Colors indicate the ratio of steady-state cyclin levels to their maximum level during normal cycling.

Experimental Measurements of Cell Cycle Arrest.

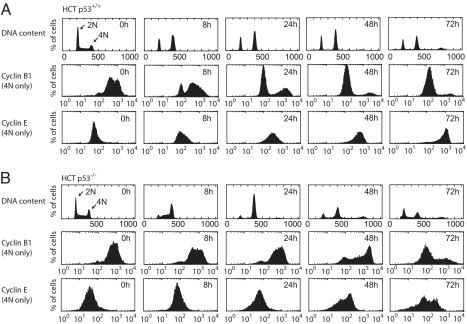
Our modeling results indicate that the dominant arrest mechanism can be uniquely identified by measuring DNA content and cyclin levels in arrested cells. Within 8 h after irradiation, an asynchronous population of wild-type HCT116 cells arrested with ≈30% of the cells in G1 (2N) and 70% in G2 (4N). The cells remained arrested for at least 72 h (Fig. 3A). Notably, we observed only low levels of apoptosis during the period studied (Fig. S2F) (29). Finer temporal sampling showed that the G2 arrest was immediate, whereas the G1 population initially decreased and was stabilized only after 4 h (Fig. S2A). This is consistent with the dependence of the G1 arrest on p53-mediated p21 expression (mechanism I, Fig. S2 B and C). The ratio of cells arrested in G1 vs. G2 thus depends on the initial cell cycle distribution and the kinetics of p21 expression. To determine the contribution of mechanisms II and III for the G2-arrested cells, we measured cyclin levels in the G2 population (4N). In freely cycling cells (Fig. 3A; 0 h time point), most cells with 4N DNA content had high cyclin B1 and low cyclin E levels. Only a small population had low levels of cyclin B1, which likely represents postmetaphase mitotic cells. At 8 h after IR, most of the now-arrested G2 cells maintained high cyclin B1 and low cyclin E levels, suggesting that mechanism II was dominant during this time. At later times, the population of cells with low cyclin B1 increased, with nearly all cells having low cyclin B levels by 48 h. We observed corresponding decreases in cyclin A and Cdk1 levels during these times by Western blot (Fig. S2C). Conversely, the cyclin E distribution increased dramatically, reaching levels that exceeded those observed during G1 in freely cycling cells (Fig. S3A). These results argue that in cells initially arrested in G2, mechanism III gradually becomes dominant over mechanism II during the course of arrest, uncoupling the cyclin state (now G1/S-like) from DNA content (4N). Similar results were obtained in nontransformed RPE-hTERT cells (Fig. S2 D-E).

Fig. 3.

Cell cycle progression and cyclin levels during arrest. Flow cytometry histograms of DNA content and cyclin levels in HCT p53^+/+ (A) and p53^−/− (B) cells after IR. Cells were irradiated and stained for DNA content and cyclin levels. Histograms of cyclin levels are gated from the 4N population only. Quantification of apoptotic cells is shown in Fig. S2F.

These observations led us to ask whether mechanism II remains active at late times after IR, or whether it turns off after mechanism III is initiated. In the first case both pathways play redundant roles, whereas in the second case each mechanism is used at different times during arrest. To distinguish between these cases, we examined DNA content and cyclin levels in HCT116 cells lacking p53, which are restricted to using mechanism II (Fig. 3B and Fig. S2A). These cells arrested in G2 (4N) by 16–24 h, with most cells retaining high cyclin B1 and low cyclin E levels. This is in agreement with a G2 arrest solely mediated by the p53-independent mechanism II. Most noticeably, the G2 arrest was transient: 24 h after irradiation, cells re-enter G1 (2N) and S, which is reflected by changes in cyclin levels. These results show that mechanism II is sufficient to induce an immediate G2 arrest (Fig. 3B and Fig. S2A). However, sustained G2 arrest depends on mechanism III, arguing against redundancy of these mechanisms. Instead, we suggest that mechanisms II and III complement each other, with mechanism II operating on a fast and mechanism III on a slow time scale.

Merging Model and Measurements.

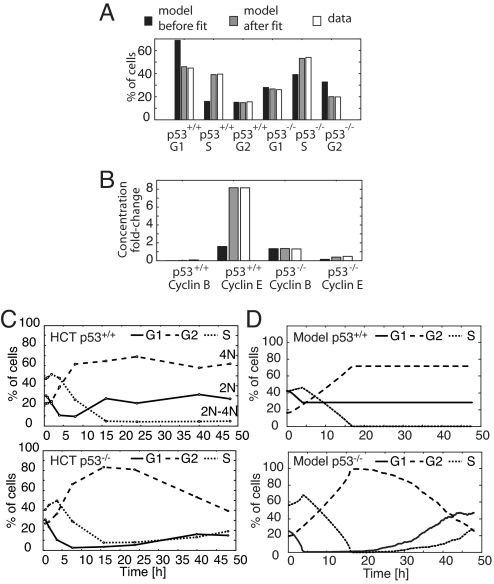
Our original model addressed individual arrest mechanisms in the context of the generic mammalian cell cycle. After acquiring quantitative measurements of the combination of arrest mechanisms and their relative timings, we next set out to parameterize our model to reflect these data. Our fitting procedure accounts for the steady-state concentrations of molecular species during arrest, as well as the relative timing of their induction during cell cycle progression (SI Appendix, “Fitting the Model to Data”, Table S2). The sensitivities of both were calculated efficiently using an adjoint method. The fitted model recapitulated the amount of time spent in G1, S, and G2/M (Fig. 4A) and matched the cyclin levels reached during arrest (Fig. 4B). Cycloheximide treatment, serum starvation, and cyclin knockouts still elicited the appropriate phenotypes (data not shown).

Fig. 4.

Cell cycle model training and prediction. (A) Fractions of G1, S, and G2 cells in freely cycling HCT p53^+/+ and HCT p53^−/− populations are compared with the amount of time spent by the initial and the fitted model in G1, S, and G2. (B) The ratios of cyclins E and B during IR-induced arrest to their maximum level during normal cycling in both HCT p53^+/+ and p53^−/− cells, compared with the ratios calculated from model trajectories. (C) Time courses of DNA content after treatment with 10 Gy IR. HCT p53^+/+ and p53^−/− cells were irradiated, and the fractions of cells with G1, S, and G2 DNA contents were measured by FACS. For apoptotic fraction, see Fig. S2F. (D) Model-generated cell cycle distribution time courses. Individual model trajectories (5 × 10²) were simulated from initial conditions distributed through the cell cycle (SI Appendix, “Simulating populations of cells”).

After fitting, 2 features of the arrest dynamics remained undetermined: the activation and deactivation time of each arrest mechanism. On the basis of the arrest profile of p53^−/− cells (Fig. S2A), we assume that mechanism II is initiated immediately after damage. It is gradually deactivated between 16 and 48 h, as indicated by the slow decrease of the G2-arrested population of p53^−/− cells (Fig. 4C). We modeled mechanism II deactivation times with a mean of 35 h and SD of 10 h, kinetics that are consistent with the stochastic repair of DSBs using repair rates found in the literature (SI Appendix, “Simulating populations of cells”; Fig. S4 A and B) (12). For the p53-dependent mechanisms I and III, we define the activation time to be 4 h after damage, because p53 was induced at that time (Fig. S2B). In wild-type cells, the arrest was sustained through the time course (Fig. 3A), during which p53 levels remained high (Fig. S2C). We therefore assume that mechanisms I and III are activated permanently on the time scale of our simulations.

Our final model implements the combined action of three arrest mechanisms, as well as their temporal organization, allowing direct comparison with experimentally measured distributions of arrested cells over time. Indeed, simulation of an asynchronous population of cells after arrest largely recapitulated the arrest dynamics and cyclin profiles of p53^+/+ and p53^−/− cells (compare Fig. 4 C and D and Fig. S4 D and E). Notably, in contrast to the modeling results, the HCT116 p53^+/+ G1 population increased 8 h after irradiation, although damage was still present, whereas RPE-hTERT cells do not show this behavior (Fig. S2 E and G). This suggests that at early arrest times some cells escaped G2 arrest and entered G1, which may be the result of checkpoint defects in the cancer cell line used, phenomena that are not considered in our model.

Model Validation and Predictions.

To validate the quality of our fitted model, we tested its ability to predict the mean protein levels in irradiated populations of p53^+/+ and p53^−/− cells, and the behavior of freely cycling and arrested cells after silencing individual cell cycle genes (SI Appendix, “Fitted Model Validation”; Fig. S5C; Tables S3 and S4). These results demonstrate that the fitted model accurately reflects features of arrested mammalian cells.

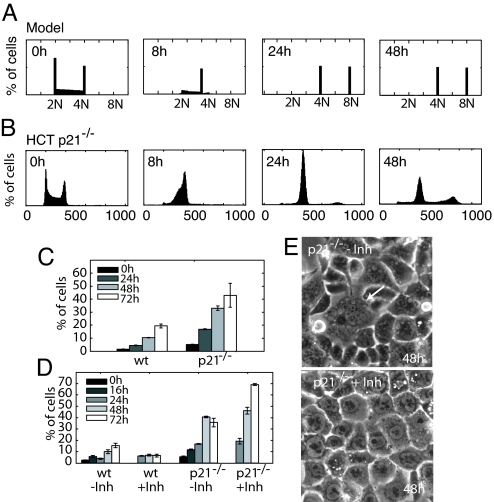
One additional model prediction captured our attention. Simulating mechanism III individually predicted that downregulation of G2 cyclins would prime cells for endoreduplication (Fig. 1F). However, this phenomenon was not observed in the model combining all arrest mechanisms. We next interrogated the model to determine what feature of the combined arrest prevented endoreduplication. Simulations of mechanism III alone and of the final model resulted in high total cyclin E levels and low cyclin A and B1 levels during arrest (Figs. 1F and S5D). However, in the final model, cyclin E was inhibited by p21 through mechanism I, suggesting that p21 prevented initiation of DNA replication of G2-arrested cells (Fig. S5D). Indeed, eliminating p21 from the final model predicted that ≈50% of the cells will initiate a second S phase and endoreduplicate (Figs. 5A and S5E).

Fig. 5.

p21 function in preventing endoreduplication. (A) Model prediction of HCT p21^−/− endoreduplication. Individual model trajectories (5 × 10²) were simulated from initial conditions distributed through the cell cycle. (B) DNA content profiles for HCT p21^−/− cells after irradiation with 10 Gy IR. For apoptotic fraction, see Fig. S2F. (C) Fractions of cells with >G2 DNA content in HCT wild type (wt) and p21^−/− cell lines (mean ± SE) as a function of time after irradiation. (D) Fractions of cells with >G2 DNA content after irradiation followed by addition of Cdk1 inhibitor RO-3306 at 16 h after IR (mean ± SE). The increased endoreduplication of p21^−/− cells after inhibitor treatment can be explained by a decrease in cells entering mitosis prematurely, creating a larger pool of cells able to undergo a second S phase. (E) Phase contrast images of p21^−/− cells 72 h after irradiation. Without added inhibitor, cells are multinucleated (arrow), indicating failures during mitosis. Cells treated with inhibitor are mononucleate but have also undergone endoreduplication.

To test this prediction experimentally, we measured the cell cycle distribution of an HCT116 cell line lacking p21 (21) (Fig. 5B). Consistent with our modeling results and previous reports (29), approximately half of the p21^−/− population had DNA content greater than 4N (Fig. 5C). Surprisingly, approximately 20% of wild-type cells endoreduplicated as well. We suggest that this is caused by cells attempting to re-enter the cell cycle prematurely with remaining damage, leading to failures in mitosis (30).

Simulation of our model suggests that p21 prevents endoreduplication by inhibiting cyclin E/Cdk2 activity in G2-arrested cells. Alternatively, p21 has been implicated in inhibiting Cdk1 activity (30, 31). In this scenario, elimination of p21 may cause cells to prematurely enter mitosis, fail, and ultimately endoreduplicate. Morphologically, a fraction of p21^−/− cells possessed fragmented nuclei, supporting mitotic failure as a cause of endoreduplication (Fig. 5E). To determine whether this is the only source of endoreduplication, we used the Cdk1 inhibitor RO-3306 (32). This drug mimics the effect of p21 on Cdk1 and prevents cells from attempting mitosis. Under these conditions, G2-arrested p21^−/− cells still re-replicated their DNA while remaining mononucleate, suggesting that cyclin E/Cdk2 inhibition by p21 is necessary as well to prevent endoreduplication (Fig. 5 D and E). Taken together, these results suggest that p21 plays an important role in maintaining the sustained G2 arrest by preventing endoreduplication after downregulation of G2 cyclins.

Discussion

An intricate network of protein interactions mediates cellular signaling. To facilitate our understanding, this network is often subdivided into individual units. However, these units do not act in isolation: they influence each other through common interactions and complex feedbacks. Here we present the integration of 2 models of subnetworks by implementing specific, experimentally verified connections supplemented by a thorough investigation of the space of possible arrest mechanisms. We found that a variety of interactions lead to similar arrest profiles and that the specific connections implemented are representative of these larger classes of arrests. One benefit of such an approach lies in the ability to individually study these mechanisms and their effect on the behavior of the integrated network. Furthermore, by fitting to experimental data, the model can be used to analyze the combined action of multiple mechanisms and their relative contribution to the signal processing.

Upon DNA damage, cells must activate arrest immediately, maintain it as long as the insult persists, and be prevented from re-entering into inappropriate cell cycle phases (13). Our analysis shows that a combination of different arrest mechanisms contributes to fulfilling these requirements. However, the requirements seem to pose a paradox for G2-arrested cells: cells undergoing sustained arrest lower their G2 cyclin levels, whereas appropriate cell cycle re-entry depends on these cyclins to convey information about the prearrest state. To resolve this paradox, we propose that in response to high levels of DNA damage, cells that arrest by cyclin downregulation must do so permanently. Downregulation of cyclins by p53 may therefore be the first step in establishing senescence, a terminal cell fate characterized by the irreversible exit from the cell cycle (33). Our model can now be used to generate testable predictions for thresholds in time, damage levels, and cyclin concentration that define the decision between cell cycle re-entry and senescence.

Our integrated model also revealed a function for p21 in sustaining G2 cell cycle arrest. p21's involvement in G2 arrest and endoreduplication has been reported (29, 31, 34), but the exact mechanism remains less well defined. p21 was previously suggested to inhibit Cdk1-activating kinases (35) or alter the subcellular locations of the Cdk1 complex (36). In addition, we now propose that p21 contributes to a sustained G2 arrest by inhibiting G1 cyclins. This function is crucial to prevent DNA replication after downregulation of G2 cyclins and may explain previously observed endoreduplication after mitotic spindle disruption (37) in cells lacking p21.

In the present study we have abstracted certain processes involved in the DNA damage and cell cycle networks. For example, we do not address all of the details of DNA repair but rather rely on a simple stochastic representation of this process. Additionally, we use the activation of APC as a surrogate for the complex process of mitosis. Although this abstracted model was sufficient to characterize the interactions transmitting the DNA damage signal to the cyclin network, a detailed treatment of these processes would allow us to address further questions. For example, we show that p53 activation is sustained for at least 96 h (Fig. S2C) and that cells lacking p53 re-enter the cell cycle after 24 h (Fig. 4C). This indicates either that DNA damage is repaired by 24 h and p53 activity is sustained after DNA repair is complete, or that DNA damage persists and cells lacking p53 adapt to the damage checkpoint. Including the details of mitotic progression and the possibility of mitotic failure would provide the framework necessary to better understand checkpoint adaptation. Accounting for the details of DNA damage and its repair may reveal whether sustained p53 activation is mediated by persistent damage or by the activation of additional network interactions.

Materials and Methods

Cell Culture.

HCT116 p53^+/+, p53^−/−, and p21^−/− cells were grown in McCoy's media including 10% FBS under standard conditions. Cells (5 × 10⁵ in a 6-cm dish or 1.5 × 10⁶ in a 10-cm dish) were plated and irradiated 2 days later with 10 Gy using a Co⁶⁰ source.

Immunoblots.

Western blots were performed as described previously (11). Antibodies used were αp53 DO-1, αCyclinB1 (H433), αCyclinA (C-19), αCdk1 (all Santa Cruz Biotechnology), αp21 (Calbiochem), and αβ-tubulin (E7, Developmental Studies Hybridoma Bank).

Flow Cytometry.

Cells were trypsinized and fixed in 70% ethanol at −20 °C. For DNA content analysis, cells were washed in PBS, incubated with 25 μg/mL propidium iodide (PI), 0.1% Triton, and 0.2 μg/mL RNase, and analyzed on a FACSCalibur flow cytometer (BD Biosciences). For cyclin A, E, and B labeling, fixed cells were washed, permeabilized in 0.25% Triton, and blocked in 0.5% BSA. Cells (1 × 10⁶) were incubated with 1 μg primary antibodies, washed, and incubated with Alexa488-coupled secondary antibody. Cells were stained with PI and analyzed as above [αCyclinE (HE12), Santa Cruz Biotechnology].

Only cell singlets were analyzed, on the basis of the pulse width vs. height ratio. To obtain the percentages of G1, S, G2/M, and endoreduplicated cells, we computationally fit the DNA content distributions using a modification of the Dean-Jett model, augmented to include the 8N and second S phase population (38).

Computational Methods.

For all simulations, numerical integration was performed in MATLAB using ode15s (The Mathworks). Optimization was implemented using fmincon configured to use Quasi-Newton with BFGS in the MATLAB Optimization Toolbox Version 3.0.4.