Abstract
Fibronectin (Fn) is an important mediator of bacterial invasions and of persistent infections like that of Staphylococcus epidermis. Similar to many other types of cell-protein adhesion, the binding between Fn and S. epidermidis takes place under physiological shear rates. We investigated the dynamics of the interaction between individual living S. epidermidis cells and single Fn molecules under mechanical force by using the scanning force microscope. The mechanical strength of this interaction and the binding site in the Fn molecule were determined. The energy landscape of the binding/unbinding process was mapped, and the force spectrum and the association and dissociation rate constants of the binding pair were measured. The interaction between S. epidermidis cells and Fn molecules is compared with those of two other protein/ligand pairs known to mediate different dynamic states of adhesion of cells under a hydrodynamic flow: the firm adhesion mediated by biotin/avidin interactions, and the rolling adhesion, mediated by L-selectin/P-selectin glycoprotein ligand-1 interactions. The inner barrier in the energy landscape of the Fn case characterizes a high-energy binding mode that can sustain larger deformations and for significantly longer times than the correspondent high-strength L-selectin/P-selectin glycoprotein ligand-1 binding mode. The association kinetics of the former interaction is much slower to settle than the latter. On this basis, the observations made at the macroscopic scale by other authors of a strong lability of the bacterial adhesions mediated by Fn under high turbulent flow are rationalized at the molecular level.
Cell-protein adhesion regulates essential processes in multicellular organisms and provides signals that affect the morphology, motility, gene expression, and survival of cells (1). Fibronectin (Fn) is an extracellular matrix protein that is widely distributed in the tissues of all vertebrates and is a potential ligand for most cell types (2). Fn is also an important mediator of bacterial invasions and of persistent infections like that of Staphylococcus epidermidis (3). Until now, S. epidermidis was considered a mere saprophyte, usually harboring on the skin and mucosae. Recently, this organism has been shown to also act as a pathogen, mainly in association with surgical applications of biomaterials (4).
Like many other cell-protein adhesions, the binding between Fn and staphylococci takes place under physiological shear rates (5). It has been reported that the high shear stress characteristic of the turbulent flow at blood vessel entrances and bifurcations can prevent Fn-mediated adhesion of Staphylococcus aureus to the endothelial cells lining the vessel, reducing, in this way, the chances of bacterial invasion (6). Thus, a thorough characterization of the binding/unbinding dynamics of these interactions is necessary to better understand the molecular mechanisms of Fn-mediated pathogenesis. Moreover, specific cell-protein interactions have been selected by nature to mediate different dynamic processes of adhesion of a cell under hydrodynamic flow, as in the case of the rolling adhesion of leukocytes whose velocity in the blood vessels is controlled by transient binding events to the inner walls. It is of interest to understand how different cell/protein adhesions are optimized in their functions through the details of the interactions at the molecular level. In this article, we address this issue by comparing the interaction dynamics of three different adhesion processes: firm adhesion mediated by the biotin/avidin pair, rolling adhesion, which is mediated by the L-selectin/P-selectin glycoprotein ligand 1 (PSGL-1) system, and cell/bacterium adhesion mediated by Fn/adhesin binding.
Traditionally, adhesion interactions have been studied in reversible equilibrium conditions. However, in vivo, these interactions take place under significant shear forces with pulling rates that are much faster than the relaxation rates of the binding pair, and thus, the binding/unbinding process occurs under nonequilibrium, irreversible conditions. The development of single-molecule manipulation methods, such as scanning force microscopy (SFM) and optical tweezers, has made it possible to investigate the dynamics of these processes under nonequilibrium conditions, and to measure their force-dependent dissociation kinetics. Here, we investigate the dynamics of the interactions between individual living S. epidermidis cells and single Fn molecules, map the energy landscape of the binding/unbinding process, and measure the association and dissociation rate constants of the binding pair by using SFM. In particular, we show that two parameters, the bond length extension required to reach the transition state from the minimum energy equilibrium position of the bound state, and the bond survival time extrapolated at zero force, play a crucial role in determining the dynamics of the interaction.
Materials and Methods
Bacterial Strains. Single colonies of each bacterial strain were seeded in 8 ml of triptycase soy broth. After incubation for 24 h at 37°C, the broth culture was fractionated in 1-ml aliquots stored at -80°C. Their genus and species were identified by the Api-Staph test (BioMerieux, Charbonnier les Bains, France) and by PCR methods (7) (see Supporting Materials and Methods, which is published as supporting information on the PNAS web site).
Preparation of Bacterial Confluent Lawns. Slime-producing strains. Polystyrene discs cut from Petri dishes (Bibby Sterilin, Stone, Staffordshire, U.K.) were incubated in 3.5 ml of triptycase soy broth (TSB) with the addition of 350 μl of stored strain aliquot at 37°C. After 24 h, 40% of the culture medium was substituted with fresh TSB and the incubation was continued for another 48 h. With the replacement of part of the culture medium, the period of the exponential growth of the microbial population was prolonged, achieving a complete and uniform colonization of the discs. At the end of the incubation, the discs were washed five times with physiologic solution (saline) to remove nonadherent bacteria.
Non-slime-producing strains. Instead of polystyrene discs, Fn-coated discs were used. The coating was achieved by covering a stainless steel disk (≈1 cm in diameter) with a 5-nm layer of 99.99% titanium (Sigma), followed by a 30-nm layer of 99.99% gold (Sigma), by resistive evaporation in high vacuum (10-6 torr; 1 torr = 133 Pa). These discs were immediately immersed into a 100 μg/ml solution of human Fn (Sigma) in PBS for 20-30 min. The growth of the bacterial lawn was then obtained on these Fn-coated discs as above. To obtain the maximal expression of adhesins on bacterial surface, exponential growth conditions were achieved. After 24 h, 40% of the culture medium was substituted with fresh triptycase soy broth (previously brought to 37°C) and incubation was continued for another 48 h. With the replacement of part of the culture medium, the period of exponential growth of the microbial population is prolonged, achieving a complete and uniform colonization of the disk by staphylococcal cells, which in this growth phase exhibited, besides, their maximal expression of adhesins (8). Although the number of adhesin molecules per cell has not been described for S. epidermidis, in the case of S. aureus, in exponential growth 15,000 adhesins per cell have been estimated by flow cytometry (9). The Fn adhesins are known to be uniformly distributed on the cell surface (10, 11), with different concentrations in the different strains.
Dynamic Force Spectroscopy (DFS) Experiments. Silicon nitride (Si3N4) probes (Microlevers, ThermoMicroscopes; Sunnyvale, CA) were gold-coated, following the same procedure as with the metallic discs (see above). A few Fn molecules were covalently bound to the probe by sulfur-gold bonds. The probes after that functionalization with Fn were made to approach a bacterial confluent lawn, kept in contact for a desired time (see below), and then retracted. This cycle is normally repeated multiple times in sequence. Whenever a molecular bridge is formed because of a bond settled between at least one Fn molecules on the tip and Fn adhesins on the cell surface, the force acting on this bridge is reported vs. the tip displacement, as in Fig. 1. All of the force curves thus obtained were recorded in PBS (150 mM NaCl/150 mM sodium phosphate, pH 7.4), by using a Nanoscope IIIa (Digital Instruments, Santa Barbara, CA). The spring constant (k) of the cantilevers was ≈50 ± 10 pN/nm, determined by the thermal oscillations method (12, 13). The loading rate values were obtained by multiplying the experimental spring constant of the cantilever by the pulling velocity. All of the probe approaches were made at a constant speed of 1 μm/s, and the loading force at the contact point was kept at a value of ≈400 pN. The saturation of the bacterium adhesins with Fn was achieved directly into the Nanoscope III fluid cell by injecting a 10 μg/ml Fn solution in PBS, and, after ≈20 min, the unbound Fn was washed out with PBS before starting recording the force curves.
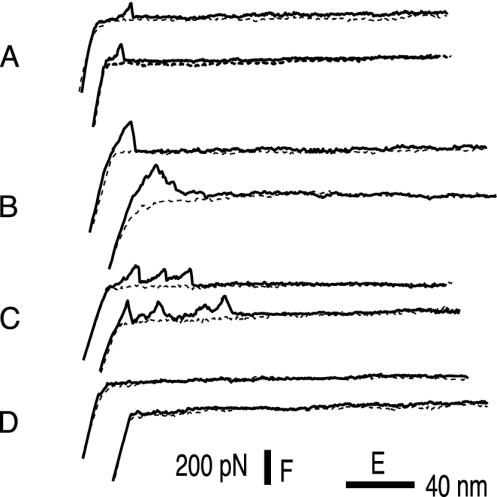
Fig. 1.
Representative profiles of the force (F) vs. extension (E) curves obtained when an SFM tip functionalized with Fn molecules is made to approach (dotted trace) to a living bacterium and then retracted (solid trace). The curves with a single peak (as in A) monitor the rupture of interactions between the tip and the bacterium sustained by single molecular bridges; the peaks in curves with multiple peaks (as in C) may be ascribed either to unfolding and/or to unbinding events. The curves as in B might be due only to nonspecific interactions, and those curves as in D may be due to experiments in which no binding interactions were settled.
Results and Discussion
Force Spectroscopy. Fn exists in the plasma and other body fluids as a soluble dimeric molecule, whereas in the extracellular matrix, it is present in insoluble multimeric forms. The dimeric molecule consists of two 220 to 250-kDa monomers joined by two disulfide bonds at the C terminus of each subunit (2). Fn is rich in sulfur atoms. Besides these two disulfide bridges, each monomer contains 28 additional disulfide bridges and two free cysteine groups (14). We could take advantage of these sulfur atoms to immobilize the Fn molecules on a previously gold-coated tip through covalent sulfur-gold bonds. These bonds do not lead to a loss of the binding ability of Fn molecules to the Fn-adhesins on the surface of S. aureus (11) or of S. epidermidis (15).
DFS measurements on the wall of a single cell were performed on a confluent bacterial lawn to increase the chances that the tip will contact one bacterium in each approach of the SFM tip to the surface, thus circumventing the need for prior imaging and localization of the cells. This strategy also avoided potential tip contamination, which often occurs during imaging, and that can affect the subsequent force measurements, and result in artifacts. The S. epidermidis strains used in the present study were clinically isolated and selected on their ability to bind Fn and to produce slime.
Preliminary DSF experiments were carried out with slime-producing strains, but the force-curves profiles obtained with them were poorly reproducible and acquired the characteristic shapes shown in Fig. 1 only after many approach-retraction cycles. Thus, we decided to carry out the experiments with a non-slime-producing strain. The choice of using bacteria without slime for the experiments obliged us to develop another method of deposition, because non-slime-producing bacteria do not form confluent lawns on polystyrene surfaces. To avoid the use of glutaraldehyde as a cross-linker (16), we took advantage of the dual capability of Fn to bind both to a gold-coated substrate (through the thiol-gold bonds), and to the surfaces of the bacteria. A gold-coated disk was functionalized with Fn and then used as a substrate to immobilize the bacteria by Fn/Fn-adhesin interactions. Confluent bacterial lawns were obtained, as confirmed by SFM imaging.
The surface of the bacteria not adhering to the substrate surface was exposing Fn adhesins. The DFS experiments were carried out on that surface by approaching and retracting the functionalized tip. Force curves were recorded with force loading rates ranging from 5 × 103 to 105 pN/s, which brackets the loading rate range (3 × 104 to 6 × 105 pN/s) acting between a cell moving in a shear flow and a substrate, as described and related to physiological conditions by Chen and Springer (17). The retraction (pulling) traces exhibited either one or multiple peaks. Among the retraction traces with one peak, only those displaying a sign change in curvature after the contact point (Fig. 1 A) were considered for further analysis because they were interpreted as resulting from specific interactions (18, 19). All other traces (see, for example, Fig. 1B) were assumed to result from nonspecific interactions and were discarded. Among the traces with more than one peak (Fig. 1C), only the last peak was included in the analysis (20), because this is the only one that can be unambiguously identified with a single Fn-cell detachment event. In contrast, the other peaks can either result from the breaking of single ligand-receptor interaction, or from the mechanically induced unfolding of the weakest domains in Fn (21, 22).
The possibilities that the Fn-cell detachment events resulted either from the detachment of Fn from the gold coated tip or from the uprooting of the Fn-adhesin from the surface of the bacteria, were excluded because of the following two reasons: First, Fn was covalently attached to the tip and covalent bonds can withstand forces of >2nN (23). Second, the experiments reported in Figs. 2 and 4 were carried out with the same tip: at its end, there were only a few Fn molecules and uprooting events should have resulted in a loss of its functionality. The ability to discriminate between receptor-ligand dissociation and receptor uprooting constitutes one of the advantages of single-molecule mechanical experiments over classical kinetics studies of cellular adhesion, where such distinction is usually very difficult to establish (24).
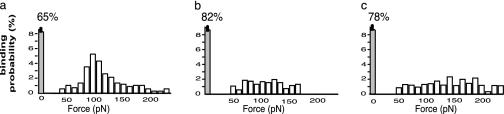
Fig. 2.
(a) Distribution of the binding probability vs. the rupture forces (measured with a 1 μm/s pulling velocity) of the Fn/Fn adhesins interactions. (b and c) The histograms are relative to the two control experiments: one with a passivation of the Fn adhesins by flooding Fn (b), and one with a mutant strain not expressing the Fn adhesins (c). The bars at zero force corresponds to the unsuccessful binding approaches.
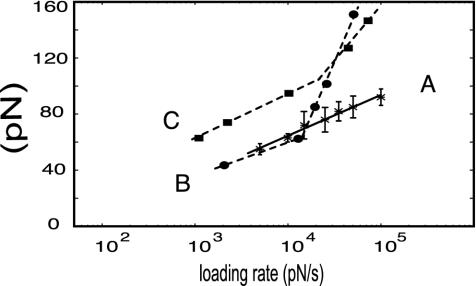
Fig. 4.
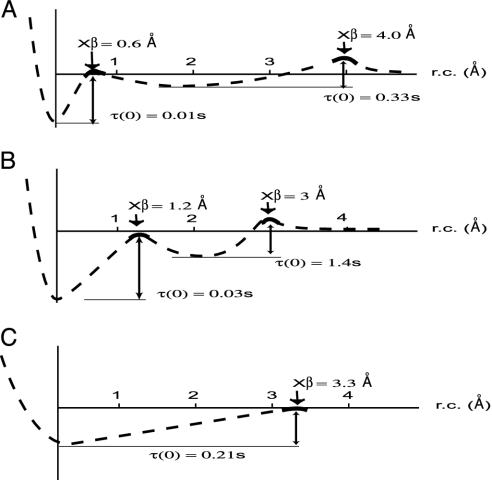
(A) The most probable unbinding forces (pN) (determined by a Gaussian fit of distributions like that in Fig. 2a and reported with their SD) at different loading rates (pN/s) identify for the Fn/Fn-adhesin interaction one linear regime that maps, in an energy landscape, a barrier at xβ = 3.3 Å and a time survival (extrapolated at zero force) τ(0) = 0.21 s. The corresponding plots of L-selectin/PSGL-1 (B), and avidin/biotin (C) are reproduced here from refs. 34 and 35, respectively. The two linear regimes of the avidin/biotin and of L-selectin/PSGL-1 pairs locate two barriers along the unbinding pathways of the two systems. The high-strength regimes locate the inner barriers at 1.2 and 0.6 Å, respectively. The two lower-strength regimes map outer barriers at xβ = 3 and 4 Å, respectively. Extrapolation of each linear regime to zero force yields the koff(0) and therefore the time survival, τ(0), of the bond under those experimental conditions. In biotin/avidin, τ(0) was found to be equal to 0.03 and 1.4 s (35), and in the L-selectin/PLSG-1 case, the values were 0.01 and 0.33s (41), respectively, for the higher- and lower-strength regimes.
The force curves we first recorded with a tip-pulling velocity of 1 μm/s led to the distribution of the rupture forces shown in Fig. 2a (n = 1,000). The zero force bar corresponds to the tip approaches to the surface (65%) that did not result in an adhesion interaction (Fig. 1D), i.e., to the unsuccessful binding events. This distribution of rupture forces shows a single peak centered at ≈85 ± 9 pN (Fig. 2A). This monomodal distribution indicates a well defined and discrete quantum of mechanical force and is consistent with the breaking of interactions between individual molecules of Fn and adhesins on the surface of S. epidermidis.
When the adhesins on the surface of the bacteria were passivated by flooding a concentrated solution of Fn, most (78%) of the curves did not show any adhesion event. The other curves led to a very broad and flat distribution of the rupture forces (Fig. 2b). Moreover, a monomodal distribution, like that in Fig. 2a, reappeared after the passivating molecules of Fn were washed out with a diluted solution of acetic acid (25). When a clinically isolated mutant strain (7) that did not express adhesins was used, a distribution of the rupture forces was obtained (Fig. 2c), which was very similar to that in Fig. 2b. These two independent control experiments confirmed that the 85 pN deadhesion force was associated to a specific interaction between a Fn molecule and S. epidermidis bacterium.
To determine the location of the specific interaction between a Fn molecule and S. epidermidis bacterium, we used specific antibodies against different domains of Fn. We found that the specific peaks in the force curves disappeared when the Fnfunctionalized tip was preincubated for 2-4 h at 37°C with a 100 μg/ml solution of a monoclonal antibody against the 12 type III domain (heparin-binding site) of Fn located near the C terminus (Takara Biomedicals, Tokyo; clone no. FNH3-8). This conclusion was confirmed at a macroscopic level by incubating a Fn-functionalized gold-coated disk with the same antibody; no bacteria adhered to the disk under these conditions. The location of the interaction at the heparin-binding site near the C terminus by these passivating experiments is consistent with surface plasmon resonance (SPR) results that shows the higher affinity of S. epidermidis for the C-terminal fragment of Fn over its N-terminal fragment (26).
Mapping the Deadhesion Energy Landscape Under a Mechanical Force. The value of 85 pN corresponding to the most probable value of the deadhesion force is not a fundamental property of this ligand-receptor pair, but it depends on the loading rate used in these experiments. The loading rate is a measure of the rate at which the force is applied to the sample. An external mechanical force, properly directed, tilts and deforms the energy landscape of the unbinding path (Fig. 3) so that the lifetime of the bond is shortened significantly below its natural lifetime (τ = 1/koff). Under external force, the dissociation rate is modified as described in refs. 27 and 28:
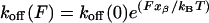 |
[1] |
where koff(F) is the dissociation rate constant of the binding pair under the applied force, (F), xβ is the reaction length over which the force must be applied to reach the transition state from the equilibrium position of the bound state, kB is the Boltzmann constant, and T is the absolute temperature. In this expression, koff(0) is the dissociation rate constant extrapolated to zero force, whose linear correlation with the unbinding force was first demonstrated by Schwesinger et al. (29). For an energy landscape of only one barrier, this force-activated rate, koff(0), becomes equal to the ”natural” koff that can be determined by bulk methods like SPR (30). In the case of rugged energy landscapes with more than one barrier, koff(0) and koff will not necessarily coincide because their values could be related to different barriers.
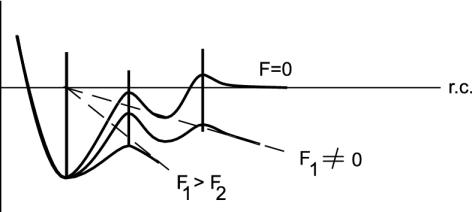
Fig. 3.
A schematic view illustrating how an external mechanical force (F1, F2) deforms the energy landscape of an unbinding path, and how, on increasing the force, one barrier along the reaction coordinate (rc) is reduced and ultimately suppressed. If the highest barrier is located sufficiently out, it is possible for an inner, smaller barrier to emerge as the rate-determining barrier in a mechanical experiment. In principle, by varying the force loading rate on the molecule, one can use direct mechanical manipulation to make different barriers emerge as the rate-determining barriers, and thus map the dissociation landscape.
The bond strength is defined as the most probable value for the rupture force Fmp, (31, 32), i.e., to the maximum of the distribution in Fig. 2 and depends on the loading rate dF/dt on the ligand (28) according to:
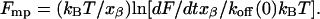 |
[2] |
The most probable rupture forces obtained at loading rates ranging from 5 × 103 to 105 pN/s are plotted against the natural logarithm of the loading rate in Fig. 4. A linear plot is obtained with a slope (kBT/xβ) that corresponds to a barrier located at xβ = 3.3 Å along the reaction coordinate. This same plot yields a value of τ(0) ≡ 1/koff(0) = 0.21 s for the survival time of the bond extrapolated to zero force.
Force Spectra of Cell-Adhesion Proteins. Fig. 4 also shows the force spectra for two representative cases of two other protein/ligand pairs that mediate different dynamic states of adhesion of a cell under a hydrodynamic flow: L-selectin or P-selectin/PSGL-1 that mediate the so-called rolling adhesion (33), and avidin/biotin, which mediates firm cell adhesion, as reported by Evans et al. (34) and by Merkel et al. (35), respectively. Unlike the plot obtained here for the Fn/Fn-adhesin interaction, which shows a single linear regime, these two plots reveal two distinct linear regimes. As shown by Evans and Ritchie (28), each linear regime in a force spectrum corresponds to the overcoming of a single energy barrier along the unbinding pathway of the system. Detachment from a bound state by a ligand confined by more than one sharp barrier should lead to multiple linear regimes in the force spectrum plot, as observed for selectin and avidin interactions. These linear regimes make it possible to locate the barriers along the unbinding pathways, and to yield the koff(0) and therefore the time survival, τ(0), of the bond within each well determined by each barrier. On the basis of these two parameters, potential energy profiles can be temptatively sketched as in Fig. 5.
Fig. 5.
A schematic view illustrating how the position (xβ) and the number of barriers along the reaction coordinate (rc) can determine the dynamic characteristics of adhesion interaction under load. The potential energy curves have been sketched for the L-selectin/PSGL-1, the avidin/biotin, and the Fn/Fn-adhesin interactions on the basis of the plots in Fig. 4. The binding lifetime extrapolated to zero force, τ(0), is reported for each potential well. (A) Rolling adhesion takes place when the cell velocity drops because of transient binding events: barriers characterized by short xβ can sustain high forces but small deformations (brittle character), and large xβ can sustain lower forces but larger deformations (elastic or compliant character). In the case of the L-selectin/PSGL-1 curve, the inner barrier provides the high-strength attachment needed to initiate the leukocyte tethering, but only for very short loading times [τ(0) = 0.01 s]; the additional interaction ensures longer residence at vessels [τ(0) = 0.33 s]. (B) Transition from a transient to a firm adhesion regime can be achieved by carefully tailoring the values of xβ and τ(0) (33). The values of xβ and τ(0) for the inner barrier of the avidin/biotin interaction are about twice as much as those of the inner barrier for L-selectin/PSGL-1. These parameters are consistent with the function of avidin/biotin known to mediate firm adhesion under flow. (C) The Fn/Fn-adhesin values of xβ and τ(0) are much larger than those found for the inner barrier of the biotin/avidin and L-selectin/PSGL-1 and are comparable to those of their outer barriers. This set of values typifies an elastic interaction selected to sustain relatively large deformations at low forces and low loading rates, but for significantly longer times.
Thermally induced dissociation is always controlled by the highest barrier of the landscape. In contrast, mechanically induced dissociation is controlled not only by the height of the barrier but also by the position of the barrier along the reaction coordinate. In particular, the reduction and ultimate suppression of the barrier height by the external force is greater the further the location of the barrier along the reaction coordinate. Thus, if the highest barrier is located sufficiently out, it is possible for an inner, smaller barrier to emerge as the rate-determining one in a mechanical experiment (Fig. 3). In principle, by varying the force-loading rate on the molecule, one can use direct mechanical manipulation to make different barriers emerge as the rate-determining ones, and thus map the dissociation landscape (Fig. 4).
Consequently, the observation of a single linear regime in the force spectrum of the Fn/Fn-adhesin pair (Fig. 4) cannot be interpreted as an unequivocal evidence of a single barrier along the unbinding pathway. If this were the case, both the thermal and the mechanically induced dissociation process would be controlled by this barrier, and the time survival of the bond extrapolated to zero force τ(0) obtained by force spectroscopy experiments would coincide with the bond lifetime, (τ), measured for thermally activated dissociation. In this case, the value of τ(0) = 0.21 s obtained by DSF for Fn is six orders of magnitude smaller than that estimated by SPR (26). The uncertainties in the loading-rate evaluation in the DSF experiments, and rebinding and avidity effects that might have affected the SPR τ(0) value (as suggested by one referee), cannot account for such an enormous difference. This difference proves that the energy landscape of Fn/Fn-adhesin interaction is controlled by more than one potential barrier and that the regime identified by our measurement corresponds to an inner barrier (Fig. 5).
Barriers characterized by short xβ can sustain high forces but small deformations and thus display a ”brittle”character; conversely, barriers possessing large xβ are ”elastic” or compliant, being capable of sustaining low forces but larger deformations (36). The small distance to the first barrier from the equilibrium bound position observed in rolling-adhesion mediated by L-selectin/PSGL-1 (xβ = 0.6 Å) results in a binding mode that can sustain high stress, but only for very short loading times (τ(0) = 0.01 s). Such a binding mode can provide the high strength attachment needed to initiate cell tethering and to interrupt cell translocation in flow, but it requires additional interactions to provide longer residence of leukocytes at vessels after being first arrested by the inner barrier. These additional binding interactions are provided by an outer barrier (xβ = 4 Å), which, although capable of sustaining smaller forces (typically <65 pN), have significantly larger survival times (τ(0) = 0.33 s). Firm adhesions, such as those mediated by the biotin/streptavidin interaction, in contrast, are characterized by an inner barrier whose values for xβ and τ(0) are about twice as much as those of the inner barrier for L-selectin/PSGL-1 (Fig. 5). These parameters are consistent with the function of avidin-biotin known to mediate firm adhesion under flow (33).
In contrast, the Fn/Fn-adhesin values of xβ and τ(0) reported here are much larger than those found for the inner barrier of the biotin-avidin and L-selectin-PSGL-1 and comparable to those of their outer barriers (Fig. 5). The larger value of xβ determined for the Fn/Fn-adhesin thus typifies an elastic interaction selected to sustain relatively large deformations at low forces and low loading rates, but for significantly longer times. This observation rationalizes the strong liability of bacterial adhesion to high, turbulent flow.
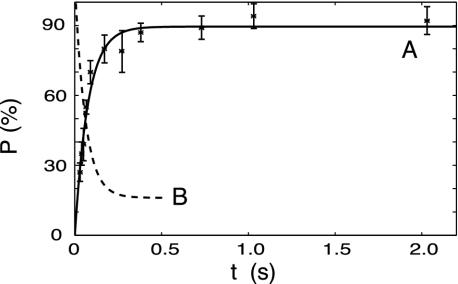
The Adhesion Probability and the Kinetic Rate Constants. Simulations of adhesion dynamics by Chang et al. (33) have shown that for fixed koff(0) and xβ, increasing the association rate, kon, decreases the velocity of cell rolling so that a rolling adhesion can become a firm adhesion. What is the role played by the kinetics of binding in Fn/Fn-adhesin interactions and how do these compare with the binding kinetics of the L-selectin/PSGL-1 pair? Binding kinetics in single-molecule studies can be characterized in terms of adhesion probability (P), that is, the ratio between the number of force curves showing a specific adhesion event (Fig. 1 A and C) to the total number of curves. In these experiments, the Fn-functionalized tip is kept in contact with the surface of the bacteria for different times before it is pulled away with a velocity of 1 μm/s. More than 4,000 force curves were recorded in this way. As shown in Fig. 6, the adhesion probability vanished at zero contact time and increased exponentially with increasing contact time up to 200 ms. Beyond this threshold, the value of the adhesion probability reached a plateau. The adhesive interaction of an SFM tip to a surface due to a specific binding reaction can be described by:
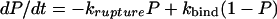 |
[3] |
where krupture and kbind are the rupture and binding rates of the interaction (37). In particular, kbind is assumed to be a pseudo first-order rate constant. Being at zero contact time P(0) = 0, this equation can be integrated to give:
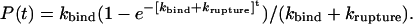 |
[4] |
Eq. 4 accounts for the behavior of the adhesion probability on the contact time observed experimentally for Fn (see Fig. 6). At contact times shorter than 200 ms, the adhesion probability is determined by the on-rate constant, kbind, alone. When the contact times are increased up to values of the same order of magnitude of the lifetime of the interaction in the experimental conditions (τrupture = 1/krupture), the complex starts breaking spontaneously before being stretched significantly, leading to a decrease of observable adhesion events, and in this second regime, as predicted by Eq. 4, a plateau is reached. Using Eq. 4, the rates krupture and kbind can thus be determined by a leastsquare fit of the experimental data of adhesion probability vs. contact time reported in Fig. 6. This analysis yields krupture = 1.38 ± 0.34 s-1 and a kbind = 11.76 ± 0.79 s-1.
Fig. 6.
The dependence of the adhesion probability (P) on the contact time (t) in the case of the binding between Fn and S. epidermidis (curve A), and in that of P-selectin and PSGL-1 (curve B, reproduced from ref. 37). Eq. 4 was fitted (A, solid curve) to the experimental points. Both the approach and the retraction were performed at 1 μm/s velocity. For each contact time three sets of experiments were carried out with at least 400 approach-retraction cycles each. The average values and the SD are reported in the plot.
Whereas the kbind can be converted into an on-rate only if we know the effective concentration of binding partners in the volume of the interaction between the tip and the bacterium surface, krupture directly corresponds to a koff (37). The difference between the value of koff(0) = 4.7 s-1 determined by the binding analysis and estimated from the plot in Fig. 4 with the krupture determined from Fig. 6 is likely due to the fact that the latter is really an apparent rate constant. Indeed, whereas in the first set of experiments the data were selected among those pulling curves in which a rupture event could be unequivocally discerned, in the second set the data included both those curves which displayed and those curves that did not display ruptures. In some cases, when a rupture was not seen, we concluded that there had been no binding. In reality, a binding event might have taken place, but the corresponding rupture event occurred below the force resolution of the SFM (20 pN), leading to an underestimation of krupture.
For comparison, the association kinetics of P-selectin/PSGL-1 reported by Anselmetti and colleagues (37) is reproduced in Fig. 6. It can be seen that these data have a mirror image relationship with that obtained here for Fn/Fn-adhesin. In the former case, the binding probability starts from 100% at zero contact time, then exponentially decreases until a plateau at ≈20% is reached. This behavior indicates that the binding is very fast. As suggested by Anselmetti and colleagues (37), this high-adhesion probability in short contact time, could be a general feature of selectin-ligand interactions, and the underlying molecular property that makes the leukocyte tethering process more effective with increased shear flow. On the contrary, Fn/Fn-adhesins binding probability starts from 0% at zero contact time and increases exponentially until it reaches a plateau. This result explains why and how the bacterial infections mediated by Fn are modulated by the blood velocity as observed at the macroscopic scale by Reddy and Ross (6). These authors found that when the flow rate increases, the Fn/Fn-adhesin binding is greatly decreased. At high shear flow, i.e., when the contact time is very short, the elastic binding mode of Fn/Fn-adhesins resulting from the inner barrier described here is not efficient and fast enough to capture bacterial cells, contrary to the leukocyte rolling adhesion case.
Supplementary Material
Acknowledgments
We thank G. Zuccheri (University of Bologna, Bologna, Italy) for his crucial and helpful advice and F. Grandi (University of Bologna) for technical assistance. This work was supported by Italian Ministry of Health Grant SVE 225/2001; Programmi Biotechnologie legge 95/95 Ministero dell'Universitá e della Ricerca Scientifica e Tecnologica 5%; Ministero dell'Universitá e della Ricerca Scientifica e Tecnologica Progetti di Ricerca di Interesse Nazionale 1999 and 2001; Progetti Pluriennali (2001) Università di Bologna; and Progetto Fondo Integrativo Speciale per la Ricerca (Ministero Tesoro, 2003).
Abbreviations: SFM, scanning force microscopy; Fn, fibronectin; PSGL-1, P-selectin glycoprotein ligand 1.
References
- 1.Gumbiner, B. M. (1996) Cell 84, 345-357. [DOI] [PubMed] [Google Scholar]
- 2.Ruoslahti, E. (1988) Annu. Rev. Biochem. 57, 375-413. [DOI] [PubMed] [Google Scholar]
- 3.Sinha, B., Francois, P. P., Nusse, O., Foti, M., Hartford, O. M., Vaudaux, P., Foster, T. J., Lew, D. P., Herrmann, M. & Krause, K. H. (1999) Cell Microbiol. 1, 101-117. [DOI] [PubMed] [Google Scholar]
- 4.Frere, J., Dubus, A. & Fonze, E. (1999) Nat. Biotechnol. 17, BV17-BV18. [Google Scholar]
- 5.Goldsmith, H. L. & Turitto, V. T. (1986) Thromb. Haemostasis 55, 415-435. [PubMed] [Google Scholar]
- 6.Reddy, K. & Ross, J. M. (2001) Infect. Immun. 69, 3472-3475. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Montanaro, L., Arciola, C. R., Borsetti, E., Collamati, S. & Baldassarri, L. (1999) New Microbiol. 22, 331-336. [PubMed] [Google Scholar]
- 8.Projan, S. J. & Novick, R. P. (1997) in The Staphylococci in Human Diseases, eds. Crossley, K. B. & Archer, G. L. (Churchill Livingstone, New York), pp. 55-82.
- 9.Mohamed, N., Visai, L., Speziale, P. & Ross, J. M. (2000) Microb. Pathog. 29, 357-361. [DOI] [PubMed] [Google Scholar]
- 10.Proctor, R. A. Mosher, D. F. & Olbrantz, P. J. (1982) J. Biol. Chem. 257, 14788-14794. [PubMed] [Google Scholar]
- 11.Vann, J. M., Hamill, R. J., Albrecht, R. M., Mosher, D. F. & Proctor, R. A. (1989) J. Infect. Dis. 160, 538-542. [DOI] [PubMed] [Google Scholar]
- 12.Florin, E. L., Rief, M., Lehmann, H., Ludwig, C., Dornmair, V. T., Moy, V. T. & Gaub, H. E. (1995) Biosens. Bioelectron. 10, 895-901. [Google Scholar]
- 13.Hutter, J. L. & Beckhhoefer, J. (1993) Rev. Sci. Instrum. 64, 1868-1873. [Google Scholar]
- 14.Potts, J. R. & Campbell, I. D. (1996) Matrix Biol. 15, 313-320. [DOI] [PubMed] [Google Scholar]
- 15.Pavey, K. D., Barnes, L. M., Hanlon, G. W., Olliff, C. J., Ali, Z. & Paul, F. (2001) Lett. Appl. Microbiol. 33, 344-348. [DOI] [PubMed] [Google Scholar]
- 16.Razatos, A., Ong, Y. L., Sharma, M. M. & Georgiou, G. (1998) Proc. Natl. Acad. Sci. USA 95, 11059-11064. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Chen, S. & Springer, T. A. (2001) Proc. Natl. Acad. Sci. USA 98, 950-955. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Conti, M., Bustanji, Y., Falini, G., Ferruti, P., Stefoni, S. & Samori, B. (2001) ChemPhysChem 2, 610-613. [DOI] [PubMed] [Google Scholar]
- 19.Hinterdorfer, P., Schilcher, K., Baumgartner, W., Gruber, H. J. & Schindler, H. (1998) Nanobiology 4, 177-188. [Google Scholar]
- 20.Baumgartner, W., Hinterdorfer, P. & Schindler, H. (2000) Ultramicroscopy 82, 85-95. [DOI] [PubMed] [Google Scholar]
- 21.Rief, M., Gautel, M., Schemmel, A. & Gaub, H. E. (1998) Biophys. J. 75, 3008-3014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Oberhauser, A. F., Badilla-Fernandez, C., Carrion-Vazquez, M. & Fernandez, J. M. (2002) J. Mol. Biol. 319, 433-447. [DOI] [PubMed] [Google Scholar]
- 23.Grandbois, M., Beyer, M., Rief, M., Clausen-Schaumann, H. & Gaub, H. E. (1999) Science 283, 1727-1730. [DOI] [PubMed] [Google Scholar]
- 24.Alon, R., Chen, S., Fuhlbrigge, R., Puri, K. D. & Springer, T. A. (1998) Proc. Natl. Acad. Sci. USA 95, 11631-11636. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Flock, J. I., Froman, G., Jonsson, K., Guss, B., Signas, C., Nilsson, B., Raucci, G., Hook, M., Wadstrom, T. & Lindberg, M. (1987) EMBO J. 6, 2351-2357. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Holmes, S., May, K., Johansson, V., Markey, F. & Critchley, I. (1997) J. Microbiol. Methods 28, 77-84. [Google Scholar]
- 27.Bell, G. I. (1978) Science 200, 618-627. [DOI] [PubMed] [Google Scholar]
- 28.Evans, E. & Ritchie, K. (1997) Biophys. J. 72, 1541-1555. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Schwesinger, F., Ros, R., Strunz, T., Anselmetti, D., Guntherodt, H. J., Honegger, A., Jermutus, L., Tiefenauer, L. & Pluckthun, A. (2000) Proc. Natl. Acad. Sci. USA. 97, 9972-9977. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Dettmann, W., Grandbois, M., Andre, S., Benoit, M., Wehle, A. K., Kaltner, H., Gabius, H. J. & Gaub, H. E. (2000) Arch. Biochem. Biophys. 383, 157-170. [DOI] [PubMed] [Google Scholar]
- 31.Izrailev, S., Stepaniants, S., Balsera, M., Oono, Y. & Schulten, K. (1997) Biophys. J. 72, 1568-1581. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Evans, E. & Ritchie, K. (1999) Biophys. J. 76, 2439-2447. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Chang, K. C., Tees, D. F. & Hammer, D. A. (2000) Proc. Natl. Acad. Sci. USA 97, 11262-11267. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Evans, E., Leung, A., Hammer, D. & Simon, S. (2001) Proc. Natl. Acad. Sci. USA 98, 3784-3789. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Merkel, R., Nassoy, P., Leung, A., Ritchie, K. & Evans, E. (1999) Nature 397, 50-53. [DOI] [PubMed] [Google Scholar]
- 36.Liphardt, J., Onoa, B., Smith, S. B., Tinoco, I. J. & Bustamante, C. (2001) Science 292, 733-737. [DOI] [PubMed] [Google Scholar]
- 37.Fritz, J., Katopodis, A. G., Kolbinger, F. & Anselmetti, D. (1998) Proc. Natl. Acad. Sci. USA 95, 12283-12288. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.