Abstract
Diabatic models are widely employed for studying chemical reactivity in condensed phases and enzymes, but there has been little discussion of the pros and cons of various diabatic representations for this purpose. Here we discuss and contrast six different schemes for computing diabatic potentials for a charge rearrangement reaction. They include (i) the variational diabatic configurations (VDC) constructed by variationally optimizing individual valence bond structures and (ii) the consistent diabatic configurations (CDC) obtained by variationally optimizing the ground-state adiabatic energy, both in the nonorthogonal molecular orbital valence bond (MOVB) method, along with the orthogonalized (iii) VDC-MOVB and (iv) CDC-MOVB models. In addition, we consider (v) the fourfold way (based on diabatic molecular orbitals and configuration uniformity), and (vi) empirical valence bond (EVB) theory. To make the considerations concrete, we calculate diabatic electronic states and diabatic potential energies along the reaction path that connects the reactant and the product ion-molecule complexes of the gas-phase bimolecular nucleophilic substitution (SN2) reaction of 1,2-dichloethane (DCE) with acetate ion, which is a model reaction corresponding to the reaction catalyzed by haloalkane dehalogenase. We utilize ab initio block-localized molecular orbital theory to construct the MOVB diabatic states and ab initio multi-configuration quasidegenerate perturbation theory to construct the fourfold-way diabatic states; the latter are calculated at reaction path geometries obtained with the M06-2X density functional. The EVB diabatic states are computed with parameters taken from the literature. The MOVB and fourfold-way adiabatic and diabatic potential energy profiles along the reaction path are in qualitative but not quantitative agreement with each other. In order to validate that these wave-function-based diabatic states are qualitatively correct, we show that the reaction energy and barrier for the adiabatic ground state, obtained with these methods, agree reasonably well with the results of high-level calculations using the composite G3SX and G3SX(MP3) methods and the BMC-CCSD multi-coefficient correlation method. However, a comparison of the EVB gas-phase adiabatic ground-state reaction path with those obtained from MOVB and with the fourfold way reveals that the EVB reaction path geometries show a systematic shift towards the products region, and that the EVB lowest-energy path has a much lower barrier. The free energies of solvation and activation energy in water reported from dynamical calculations based on EVB also imply a low activation barrier in the gas phase. In addition, calculations of the free energy of solvation using the recently proposed SM8 continuum solvation model with CM4M partial atomic charges lead to an activation barrier in reasonable agreement with experiment only when the geometries and the gas-phase barrier are those obtained from electronic structure calculations, i.e., methods i–v. These comparisons show the danger of basing the diabatic states on molecular mechanics without the explicit calculation of electronic wave functions. Furthermore, comparison of schemes i–v with one another shows that significantly different quantitative results can be obtained by using different methods for extracting diabatic states from wave function calculations, and it is important for each user to justify the choice of diabatization method in the context of its intended use.
1. Introduction
A useful starting point for elucidating the factors that determine the activation barrier in many condensed-phase and enzyme-catalyzed reactions is an understanding of the intrinsic reactivity of the uncatalyzed reaction in the gas phase. Subsequently, the effect of solvation and/or catalysis can be considered. For example, a computation of the change of a reaction’s activation barrier from aqueous solution to an enzyme can be very informative, although it is not sufficient to generate a complete picture of enzyme catalysis1 nor adequate to validate the potential energy surface and computational techniques.1,2 Valence bond (VB) theory provides a fundamental framework for this purpose because of its direct connection to concepts such as chemical bonding, reactivity and electronic resonance.3 When ab initio self-consistent field valence bond (VBSCF) is represented in terms of a two-state model,4 describing the interactions between the reactant and the product diabatic states, the intuitive nature of such a simple model is particularly useful both for understanding and for computation. However, when such a multi-configurational VB wave function is reduced to a two-state representation, the construction of these two states is not unique, as we illustrate in this article, and this can lead to different interpretations of chemical reactivity and the origin of solvent effects. Consequently, it is essential to carefully examine the nature of a specific two-state VB model before it is applied to chemical reactions in solution and in enzymes. In this article, we aim to provide a perspective on different ways of constructing diabatic states, and we discuss the limitations on their usefulness for describing the potential energy surface of the adiabatic ground state.
Consider, for a more specific example, the haloalkane dehalogenase catalytic cycle. The haloalkane dehalogenase enzyme catalyzes the hydrolytic cleavage of carbon-halogen bonds in a broad range of halogenated alkanes to yield the corresponding alcohol with concomitant release of the halide anion.5–11 The efficiency of the enzymatic conversion is maximal with 1,2-dichloroethane (DCE) as the substrate.8 The catalytic action of haloalkane dehalogenase has been shown to consist of two chemical reaction steps. The first step involves a nucleophilic substitution (SN2) reaction in which the carboxylate group of Asp124 attacks the halogenated hydrocarbon, displacing the halide anion and forming an enzyme-ester covalent intermediate.5 The second step is the hydrolysis of the intermediate by an activated water molecule, assisted by His289 and Asp260 residues of the enzyme, to yield the alcohol and to return the enzyme to its native form for the next catalytic cycle.6 The factors that affect the catalytic efficiency of the enzyme have been the focus of many theoretical studies.12–32 The reactions of several nucleophiles (hydroxide, formate, and acetate) with substrates such as methyl chloride, chloroethane, and DCE have been used to mimic the attack of the Asp124 residue of haloalkane dehalogenase on a haloalkane.13,14,20,22,23 Many theoretical studies of SN2 reactions in the gas phase and in solution, including those just cited, have made use of ab initio or semiempirical molecular orbital or post-Hartree–Fock electronic structure calculations.33–49 Nucleophilic substitution reactions have also been investigated by density functional theory.41,48,50–53 The use of valence-bond (VB) theory to study these reactions quantitatively is less common because of the higher computational cost and slow convergence (with respect to adding configurations) of VB calculations, but VB theory has the advantage of providing unique insight into the electronic structure.54–59 Examples of nucleophilic substitution reactions studied using VB methodology include the identity X−+ RX′ → XR + X′−reactions (R = alkyl; X, X′ = F, Cl, Br, I);54–57,60–68 nonidentity versions of these reactions (X not the same as X′);54–57 the Cl−+ CH3SH2+ → ClCH3 + SH2 and H3N + CH3SH2+ → H3NCH3+ + SH2 reactions;61 the particular case CH3Cl + NH3 →Cl−+ CH3NH3+ of the general Menshutkin reaction;55,58,69–72 reactions of esters and ketyl radical anions;56,73 reactions at peptide bonds;74 and reaction at phosphorus.75
A challenging question in condensed-phase reaction dynamics is the definition of the reaction coordinate. Arguably, the choices that have been made may be divided into two categories: (1) the use of a set of solute geometrical variables or a combination of approximate functions of relevant bond orders that vary systematically from the reactants to the products, and (2) the use of a generalized solvent coordinate such as, in the Marcus theory of electron transfer reactions, the energy gap between the reactant and product diabatic states. In the first case, two common choices are (i) an analytic function of internal coordinates, such as the breaking and forming bond distances, or the distance between the reactants, and (ii) the distance along a union of the steepest descent paths in mass-scaled coordinates from the saddle point to reactants and products. Choice (i)76–80 is usually called a distinguished reaction coordinate, and choice (ii)80–86 is called a minimum-energy-path (MEP) coordinate or an intrinsic reaction coordinate
Sometimes one considers an ensemble of reaction paths and hence of reaction coordinates, as in ensemble-averaged variational transition state theory87,88 and in the transition path sampling method,89 but we shall not need to consider such theories for the present perspective article.
In category (2), the energy gap is typically defined as the difference in energy between two diabatic states of the reagents (also called “solute” or “primary subsystem”), one representing the reactants and the other representing the products, with both including their interactions with their surroundings (also called “solvent” or “bath” or “secondary subsystem”). For example, for an outer-sphere electron transfer reaction, the product state differs from the reactant state by the rearrangement of one electron, and the energy difference between these states is a function of the coordinates and polarization state of the solvent. Thus a diabatic energy gap can be considered to be a collective solvent coordinate. Such a diabatic gap was originally invoked by Marcus90,91 in electron transfer theory and has subsequently been used more broadly to describe other charge transfer processes in the condensed phase.92–107 Other collective solvent coordinates have also been used.108–116 In addition, diabatic states and diabatic potential energy surfaces (sometimes called quasiadiabatic states and distortion potentials in this context) have sometimes been used for dynamical treatments by using separate coordinate systems for reactants and products.117–121
Although diabatic energy functions for condensed-phase reactions were originally defined in terms of classical models, for example, the nonequilibrium electronic polarization energy of a dielectric medium interacting with a spherical ion,122 progress in the treatment of complex reactions can be achieved by using quantum mechanical electronic structure theory to define the diabatic states and calculate their energies. The present article is primarily concerned with such quantum mechanical calculations. When one uses electronic structure theory to treat the Born-Oppenheimer dynamics of complex systems, the nuclear coordinates are parameters in the electronic Hamiltonian and electronic wave functions. The electronic Hamiltonian (which is defined, as usual, to include the nuclear repulsion) is diagonalized, and the eigenvalues as functions of nuclear coordinates are the (adiabatic) potential energy surfaces for nuclear motion. That is called the adiabatic representation. Here we employ an analogous treatment for a two-state diabatic representation. In this representation, the electronic Hamiltonian (which in general is Hermitean and here is assumed real symmetric, so there is only one unique off-diagonal element) is not diagonal. The diagonal matrix elements are the diabatic potential energy surfaces, and the off-diagonal Hamiltonian matrix element is the diabatic coupling which decreases the energy as compared to the diabatic crossing energy, thereby stabilizing the transition state of the adiabatic ground state.123–126
In previous work, the diabatic potential energy surfaces have often been modeled without explicit calculations of electronic wave functions—for example by molecular mechanics such as in the Warshel–Weiss empirical valence bond formalism92–103 (we shall abbreviate this specific formalism as EVB; other VB treatments—both older and newer— with empirical elements are called semiempirical VB to distinguish them from EVB), by solvent dielectric continuum theory,122 by linear response theory,127 or by phenomenological fitting of reaction rates.62,128,129 The EVB model treats the diabatic coupling as a parametrized function—typically, as for example in the case considered here,21 as a constant. Further, a fundamental assumption of the EVB model is that the overlap integral between the diabatic states is zero. However, this model has been found to be insufficient to reproduce the vibrational frequencies at the transition state.130,131 As a result, the EVB model is not well suited for computing detailed rate quantities such as kinetic isotope effects that require an accurate treatment of the potential energy surface, the zero-point energy (ZPE), and quantum mechanical tunneling.2 In other semiempirical VB models, the overlap-dependence of the diabatic coupling is treated implicitly by parametrizing the off-diagonal element to fit the entire adiabatic potential surface. Methods in the latter category include molecular mechanics with valence bond (MMVB),132 multi-configurational molecular mechanics (MCMM),116,133,134 multi-state empirical valence bond (MS-EVB),135 and the generalized Gaussian algorithm of Chang and Miller130 and Schlegel and Sonnenberg.131
In contrast, the fourfold way and mixed molecular orbital and valence bond (MOVB) methods that we describe in this article use electronic structure theory to derive the diabatic states; the ability of electronic structure theory to predict details of potential energy surfaces (such as vibrational frequencies) is one motivation for using quantum mechanical electronic structure theory in the diabatic formalism.
In comparing theories of diabatic states, it is important to keep in mind that diabatic electronic states are not uniquely defined,4,59,105,136–141 and a number of definitions have proved useful in various contexts. Many of these, whether or not quantum mechanics is explicitly employed, are most easily understood in terms of VB theory.4,59,136,141–149 In VB theory, an electronic configuration state function (CSF) with a definite bonding pattern and set of formal atomic charges is called a VB structure. Note that, depending on the state, a VB structure may be a single Slater determinant or a linear combination of determinants. A resonance structure may be expressed in terms of one or more VB structures. For example, in VB theory, the wave function for the resonance structure of the HCl molecule can be written as a linear combination of a covalent (Heitler-London) VB structure which is described by two Slater determinants for the spin pairing between the two electrons that form the single bond, and two ionic VB structures ([H+ Cl−] and [H− Cl+]), each of which is represented by a single Slater determinant. In discussion, it is important to distinguish between VB structures (single CSFs) and VB resonance wave functions (linear combinations of CSFs); the latter will usually be called configuration interaction wave functions. Although the electronic wave function for a given VB structure changes when the coordinates of the nuclei change, it varies gradually, and it retains a recognizable bonding pattern even globally; Hartree-Fock (HF) wave functions may change suddenly, and they may also change the bonding pattern. Furthermore, HF orbitals, unlike VB orbitals, do not have a definite atomic parentage. In the original VB theory of Heitler, London, Slater, and Pauling, a VB structure changes only because the fixed atomic orbitals in terms of which it is defined move with the nuclei; in modern VB theory, sometimes called generalized valence bond150 (GVB) or valence bond self-consistent field151 (VBSCF), the defining orbitals also breathe and polarize and may even delocalize across a bond.152
One approximation used in the EVB formalism92–103 is that the partial atomic charges of the EVB states are assumed to be independent of the reaction coordinate and are based on reactant and product molecular mechanics parameters. In VB theory, this is equivalent to assuming that the ionic character of a VB structure is invariant to changes in geometry and external field, which is a severe approximation.62,63 Among other consequences, it implies that the partial charges on VB structures are the same in the gas phase, in solution, or in enzymes. Although in principle, it is possible to make the atomic partial charges in EVB-type models dependent on molecular structure, it is rarely done and such a procedure is laborious for chemical reactions.68,75 Overcoming this kind of limitation of molecular mechanics-based treatments is another motivation for calculating diabatic potentials by using quantum mechanical electronic structure theory.
The first wave function approach considered in this article is the mixed molecular orbital and valence bond (MOVB) method.60,141 The MOVB method constructs VB-like diabatic states by a block localization procedure applied to molecular orbital calculations.153–160 Two MOVB schemes are considered:4 in one, called the variational diabatic configuration (VDC) scheme, the energies of the diabatic states are each variationally optimized, and in another, called consistent diabatic configuration (CDC) scheme, the energy of the adiabatic ground state is variationally minimized.
The other approach that we will use to define diabatic states is called the fourfold way;161–163 it is based on the use a threefold density criterion and possibly one or more reference orbitals to construct diabatic molecular orbitals (DMOs), the use of these orbitals to define diabatic CSFs, and the determination of diabatic states in terms of the diabatic CSFs by configurational uniformity. This method has its roots in the theory of photochemical reactions, and it uses the concepts of DMOs161–164 and configurational uniformity161–163,165,166 to determine diabatic states as smoothly varying linear combinations of adiabatic CSFs; since the diabatic states are smooth functions of geometry, they resemble, to some extent, VB states.142 A key feature of this method is that the diabatic states span exactly the same space as the same number N (two in the example considered here) of adiabatic states, which may be chosen as the ground state and the (N − 1) lowest-energy adiabatic states, or—as in the example considered here—as the ground state and an excited adiabatic state with the charge character of the product, so that the diabatic energy gap can serve as a reaction coordinate. A second key feature is that one can base the method on correlated wave functions, which are more accurate than HF ones.
In the present work, we illustrate the diabatization methods by applying them all to the same example. The example chosen is the SN2 reaction of acetate ion with DCE in the gas phase
| (1) |
which is motivated by the haloalkane dehalogenase reaction discussed in the second paragraph. Although the main focus is on the definition of diabatic states for the gas-phase reaction, we also consider the reaction in water to compare the free energies of solvation and activation obtained with the EVB PES with those reported in the literature.21,28 In addition to serving as a model SN2 reaction, reaction (1) is of interest for developing bioremediation strategies. The production of halogenated hydrocarbons for use as herbicides, pesticides, refrigerants, or solvents has given rise to environmental concerns due to their toxicity and possible role as carcinogenic agents.167 A possible route for bioremediation of contaminated soils and waters168–170 involves the action of the haloalkane dehalogenase enzyme5–11,171–173 present in, for instance, the bacterium Xanthobacter autotrophicus GJ10.
The remainder of the article is organized as follows. Section 2.1 reviews the general valence bond framework for the treatment of SN2 reactions. In section 2.2 the electronic structure methods used to determine the adiabatic and diabatic electronic states are introduced. The fourfold way with configuration uniformity algorithm for diabatization is explained in section 2.3, and the details of its application to the acetate + DCE reaction are given in the appendix. The MOVB method is explained in section 2.4. The definition of diabatic coupling for nonorthogonal and orthogonal MOVB wave functions is detailed in section 2.5. The main features of the EVB theory are sketched in section 2.6. The method used to calculate free energies of solvation and activation in water is presented in section 2.7. Sections 2.8 presents the basis sets employed. The main results of the present study are presented in section 3. Section 3.1 contains the definition of reaction coordinate and reaction path for the acetate + DCE reaction. The adiabatic energy profiles obtained along the reaction path are presented and discussed in section 3.2, where the accuracy of the adiabatic reaction energy and barrier height is assessed by comparing them to high-level calculations. Section 3.3 present a detailed comparison of the diabatic energies and couplings obtained with the different methods. Section 3.4 is concerned with the solvation and activation free energies of the reaction in water. Finally, the conclusions are presented in section 4.
2. Theory and Methods
2.1. Valence-Bond Treatment of SN2 Reactions
The general scheme for the treatment of SN2 reactions using VB theory has been developed in a number of previous works.4,55,56,64,174,175 The reaction :X−+ R–Y → X–R + :Y−, where :X− and :Y− are the nucleophile and the leaving group, respectively, and R is an alkyl group, can be used to illustrate the general case. Four electrons participate directly in the nucleophilic displacement, i.e., two from the reactant nucleophile :X− and two from the R–Y bond. If these electrons are distributed among the three frontier orbitals of the three fragments (X, R, and Y), a total of six VB structures can be generated,64 which are depicted below:
| (2) |
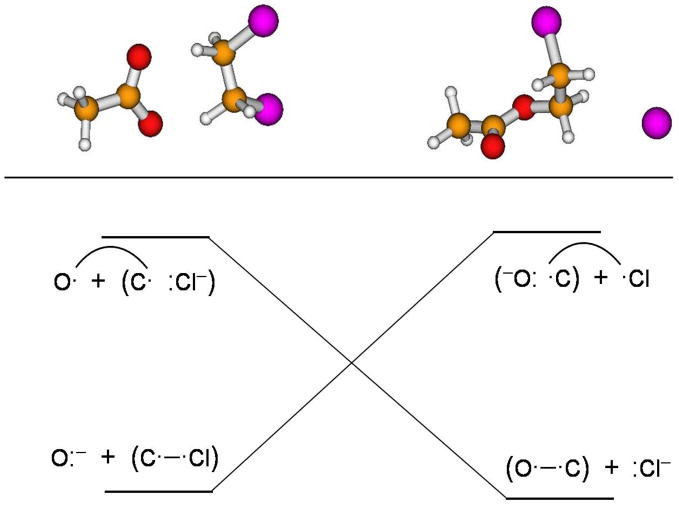
The VB many-electron wave function is expressed as a linear combination of the CSFs that correspond to the six VB structures in eq 2. Structures 1 and 2 represent Heitler-London covalent configurations, each of which consists of two Slater determinants, and have the largest weights, corresponding to the reactant and the product state, respectively. They are the dominant configurations, and a minimal description of the diabatic states must always include them.4,56,174,175 Structure 3 is the triple-ion configuration that is most stable and has the greatest resemblance to the transition state. The VB configuration correlation diagram56 of these resonance structures for the acetate + DCE reaction are shown in Figure 1. The VB picture of an SN2 reaction is that the VB configurations corresponding to structures 1 and 2, “dressed” by the proper ionic configurations,56 experience an avoided crossing along the reaction coordinate and their interaction gives rise to two adiabatic states.56,174,175 The excited adiabatic state assumed in this scheme has in fact been detected in photoexcitation experiments.176,177 The ground state has a reaction barrier, and the excited state has a local minimum at approximately the same geometric location, corresponding to the crossing point of the diabatic states (Figure 1). The VB studies performed on SN2 reactions in the gas phase and in solution have found that the use of structures 1, 2, and 3, is sufficient to obtain quantitative results because in structures 4, 5, and 6, a negative charge is placed on a less electronegative atom, resulting in high energies and relatively small configuration weights in the VB wave function.60,61,64–66 Nevertheless, structures 4 and 6 can play significant roles in the definition and understanding of diabatic states. Note that structure 5 represents a spin paired interaction between two electrons, each localized on one of the non-bonded atoms, in the presence of a doubly occupied orbital.. It corresponds to a charge-transfer excited state that does not contribute to the nominal configuration interaction wave function either for the reactant state or for the product state. Nevertheless, structure 5 can mix with other VB structures to stabilize the adiabatic ground state and it has the largest contribution at the transition state where the molecular geometry is the most compact. We have found that the effect of structure 5 in lowering the reaction barrier is very small, less than 1 kcal/mol for typical SN2 reactions.4 Thus, it is not essential to include structure 5 in defining the diabatic and adiabatic states.
FIG. 1.
Reactant and product VB structures and schematic correlation diagram for the acetate + DCE SN2 reaction.
2.2. Electronic Structure Methods
The fourfold way161–163 and the MOVB60,141 scheme are based on different approaches to the construction of diabatic states.
In the fourfold way with configuration uniformity, adiabatic states are generated first, and they are subsequently transformed to an equivalent set of diabatic states; the transformation also yields the diabatic energies and couplings. In the general cases, to obtain good reaction energies and barrier heights without empirical parameters, dynamic electron correlation effects need to be included in the wave function. In the present implementation, the state-averaged CASSCF, or SA-CASSCF,178,179 method (in the state average, the ground state is weighted 75% and the excited state 25%) has been chosen to define configuration interaction (CI) coefficients and MOs that are then used as the basis for multiconfigurational quasidegenerate perturbation theory at second order (MC-QDPT)180–182 to include dynamic correlation. (Note that MC-QDPT is very similar to another well known method called multi-state complete-active-space second-order perturbation theory183 (MS-CASPT2)). The CASSCF active space has been selected in analogy to the discussion of section 2.1. Thus, the active space is formed by four electrons in three active MOs. The four active electrons correspond to two electrons from one of the attacking oxygen atoms in the acetate ion and the two electrons in the C–Cl bond of DCE. The three active MOs are the oxygen lone pair centered on the attacking oxygen of CH3CO2−, one of the p orbitals of Cl− in the products, and the orbital delocalized over the three atoms that participate directly in the forming and breaking bonds.
It is important to note that the excited electronic state used in the fourfold way analysis is the first excited state of the acetate + DCE system in the CASSCF calculations within the active space chosen, but it is not the first excited state of the system. The spectroscopic first singlet excited electronic state in fact is the one that derives from an n → π* transition of the acetate ion. However, that electronic state is not directly relevant to the nucleophilic substitution reaction and is excluded in the present treatment. Here we formulate the problem in terms of only the two crossing diabatic states that correspond to the different bonding patterns (charge arrangements) of the reactant and product. For this reason, the active space chosen must be considered as a “model space.”
The MC-QDPT calculations use a modified 6-31+G(d)184–187 basis set called 6–31&G(d), which is explained in the Appendix, which contains extra computational details not germane to our focus.
The diabatic states in the MOVB method are generated by following a different strategy. In MOVB, we first construct VB states in terms of block-localized MOs for each fragment in the corresponding VB structure. In the original formulation of the MOVB method, the VB matrix elements are determined analytically using non-orthogonal determinant wave functions.60,141 In the limit of a single fragment in which the MOs are fully delocalized, the MOVB state reduces precisely to the HF limit. (The HF method is accurate enough for the present SN2 example; in cases where electron correlation effects must be included, the method can be applied at the Kohn-Sham level rather than with HF.)
In order to obtain reference values for the relative energies of the acetate + DCE ground-state potential energy surface (PES), we have followed the strategy of choosing an accurate yet computationally affordable method to carry out the stationary point geometry optimizations and then using these geometries to calculate refined relative energies using high-level wave function methods. Thus, the geometry optimizations were performed using the M06-2X188 density functional with the MG3S189 basis set. The M06-2X functional has been shown188 to provide accurate main-group thermochemistry, kinetics, noncovalent interactions, and electronic excitation energies to valence and Rydberg states. The MG3S basis set is a multiply polarized basis of triple-ζ quality that contains diffuse functions centered in all heavy atoms and that was designed to provide accurate relative energies in density functional theory. Three high-level methods were used to perform single-point calculations on the M06-2X/MG3S stationary point geometries, namely, Gaussian-3X with scaled energies (G3SX),190–192 its MP3 version with a reduced order of perturbation theory (G3SX(MP3)),192 and the BMC-CCSD193 multi-coefficient correlation method.194 These high-level calculations will be denoted G3SX//M06-2X, G3SX(MP3)//M06-2X, and BMC-CCSD//M06-2X, respectively.
The M06-2X density functional was also employed to obtain reaction path geometries on the ground-state PES that were then used to compute the MC-QDPT adiabatic and diabatic reaction profiles. The ground-state reaction path was also calculated with the B3LYP195–198 functional for comparison with the other methods. For the MOVB method, diabatic energies were calculated at the optimized ground-state adiabatic reaction path geometries obtained at the HF level.
Note that in this work we are only concerned with the segment of the reaction path that connects the reactant ion-molecule complex and the product ion-molecule complex of the gas-phase SN2 reaction, by analogy with the structures relevant to the SN2 step of the haloalkane dehalogenase catalytic cycle.12–32 Thus, infinitely separated reactants and products are not considered in the present study.
2.3. Fourfold Way Algorithm for Diabatization
The fourfold way161–163 is a direct diabatization method that has been applied successfully in our group to determining the first two singlet diabatic electronic states of the Li + FH → LiF + H162 and the HNCO → HN + CO, H + NCO163 reactions, to the construction of global diabatic PESs for the ground and first singlet excited electronic states of NH3,199,200 and to the calculation of the six lowest singlet diabatic states of the photodissociation reactions of BrCH2C(O)Cl201 and BrCH2Cl202 along the C–Br and C–Cl dissociative reaction coordinates. The key principles of fourfold way with configurational uniformity161–163 are the construction of suitable DMOs and their use to construct diabatic configuration state functions (DCSFs) that are employed to enforce configurational uniformity on the multiconfiguration wave function of the CASSCF or MC-QDPT step; here we use the latter. The DMOs and the DCSFs must have three properties: (1) they must be uniquely defined at each nuclear configuration, (2) they must be smooth along continuous nuclear-coordinate paths, and (3) when the multiconfigurational wave functions are expressed in terms of DMOs, each state must be dominated by at most a few DCSFs in regions where the electronic states are weakly interacting. To construct DMOs, the one-electron density matrices and transition density matrices are used to define the functional
| (3) |
where αN, αR, and αT are parameters usually set to the values 2, 1, and 0.5 (we use the standard values in the present work), D NO is a natural orbital density matrix, D NO is an occupation number density matrix, and DTD is a transition density matrix. The criterion for constructing DMOs based on maximization of the D3 functional is called the threefold density criterion. For some systems (including the present one), one needs additional constraints on MO uniformity. This is done by introducing a set of λ reference MOs and defining a new term, called the reference overlap term, which contains an overlap-like quantity between the MOs at the current geometry and the reference MOs. Use of eq 3 without reference orbitals is called the threefold way; when one or more reference MO is included, the method is called the fourfold way, since it depends on the three functionals in eq 3 and on the set of reference MOs.
The DMOs are used to construct orthonormal DCSFs that are distributed into groups, with each group spanning a characteristic subspace that defines a diabatic state. The basic requirement is that the group list be the same for all nuclear geometries. The adiabatic many-electron wave functions are finally expressed in the basis of the DCSFs, and their CI coefficients are used to define the adiabatic-to-diabatic transformation matrix which is then used to generate the diabatic energy matrix. Diagonalization of the diabatic matrix gives back the adiabatic energy matrix.
The fourfold way yields two VB-like configurations that correspond to the covalent VB structures of eq 2 (i.e., structures 1 and 2, each mixed with structure 3 proportionally); these configurations may be called resonance60,203,204 structures. The bonding patterns of these resonance configurations in the reactant and product regions of the acetate + DCE system are shown in Figure 1.
The role of the reference MOs for the acetate + DCE reaction is somewhat different than for most reactions studied previously199–202 with the fourfold way, but it is analogous to that in the two-arrangement reaction Li + FH → LiF + H.162 In most cases199–202 studied so far, the reference MOs are introduced to fix the orientation of the DMOs that are localized on a given atom but that become degenerate with other orbitals at either reactants or products, and whose coefficients would otherwise mix with the other degenerate orbitals along the reaction coordinate making it impossible to define consistent groups of DCSFs. In the case of acetate + DCE, the reference MOs also play this role, as they help to discriminate between the two degenerate lone pairs on oxygen in the reactant and between the three degenerate orbitals of chloride in the product. However, in this case as well as in the case of the LiFH162 two-arrangement system, there is a complication with the deformation of the DMOs obtained by the threefold way along the reaction path. Applying the threefold way, a DMO that is localized on a given atom in reactants can become delocalized along the path and can transform into a DMO localized on a different atom in products. For the acetate + DCE reaction, reference MOs are essential for obtaining diabatic states that are VB-like states, because they effectively project the delocalized MOs obtained by CASSCF or MC-QDPT onto localized MOs centered on the atoms, and they consequently generate VB-like configurations once the wave function is re-expressed in terms of the fourfold way DMOs. What is required is to obtain two crossing VB-like diabatic states analogous to those in VB theory.
Note that the adiabatic energies obtained by the MC-QDPT fourfold way are different from the energies obtained without applying the fourfold way. The two different sets of energies are denoted MC-QDPT(4) and MC-QDPT, respectively, or when indicating that they are calculated at stationary points or along reaction paths optimized with the M06-2X density functional, they are denoted MC-QDPT(4)//M06-2X or MC-QDPT//M06-2X. That the MC-QDPT and MC-QDPT(4) energies are different can be understood considering the way the MC-QDPT adiabatic energies are calculated. When the fourfold way is not applied, the MC-QDPT wave function is based on the CASSCF canonical MOs,180 whereas when the fourfold way is applied, the MC-QDPT wave function is based on the CASSCF DMOs for the active space and on the canonical MOs for the inactive and virtual subspaces. This causes the adiabatic energies to differ between these two cases, because whereas the CASSCF adiabatic energies are strictly invariant with respect to rotations of active orbitals, this is not true for MC-QDPT.162 In the calculations reported here, only the MC-QDPT(4)//M06-2X adiabatic energies are computed along the reaction path, for consistency with the diabatic energies obtained at the same level.
2.4. Diabatic States from the Molecular Orbital-Valence Bond (MOVB) Method
The MOVB method60,141 is based on a block-localized wave function (BLW) approach.153–160 The BLW method has been applied to a variety of problems including interaction energy decomposition and conjugation delocalization effects.205–208
For each given VB structure, the molecular system is divided into a number of polyatomic fragments, for which MOs are formed by using only basis functions on that fragment; the number of electrons and total charges of each fragment are fully determined by the VB structure. Therefore, for the present SN2 reaction between acetate ion and dichloroethane, the wave functions for the reactant ( ) and product ( ) states are given by
| (4a) |
| (4b) |
where  is an antisymmetrizing operator, and φF specifies a product of molecular orbitals that are expressed as linear combinations of atomic orbitals in fragment F. The Lewis structures for different fragments in the reactant and product diabatic states as well as their associated total charges are defined by square brackets. The MOs within each fragment in eqs 4a and 4b are restricted to be orthogonal as in HF theory, but the MOs of different fragments are not orthogonal – a key feature of conventional valence bond theory, for which the fragments are atoms.
The wave function of each VB structure is defined by a single Slater determinant (eqs 4a and 4b), and the MOs of the MOVB treatment are fragment localized, that is, they are delocalized within each fragment, but by construction they are localized on one or another fragment. Each VB wave function obtained by the BLW method represents a diabatic electronic state. We have shown that the reactant state wave function defined by eq 4a in MOVB corresponds to an ab initio VB wave function containing covalent configuration 1, and ionic configurations 3 and 4 for the C-Cl bond that is cleaved, and the nucleophile CH3CO2− ion acts as a “spectator” ion that interacts and polarizes the C-Cl bond structure.4 In the same vein, the product state wave function defined by eq 4b consists of contributions from covalent structure 2, and ionic structures 3 and 6.4 We note that the outer spin-pairing structure 5 does not contribute to the Lewis bond configuration interaction wave function of either the reactant or the product state; thus, it is not included in the MOVB wave fucntion; however, comparison of the results from ab initio VBSCF calculations, with and without inclusion of structure 5, shows that it only affects the reaction barrier by about one kcal/mol.4 The total MOVB wave function is then written as a linear combination of the diabatic states obtained with BLW:
| (4c) |
where aR and aP are MOVB configuration coefficients for the reactant and product states, respectively. The adiabatic energies are obtained by solving the generalized eigenvalue problem61 in the nonorthogonal MOVB basis of the two diabatic states.
Two different variational schemes are employed to optimize the VB wave functions.4 In the first scheme, the optimal fragment localized MOs at each molecular geometry are obtained so as to minimize the expectation value of the Hamiltonian for each individual VB structure ( and ). In other words, the energy for each VB structure is separately optimized. The resulting VB states are called variational diabatic configurations (VDC). An alternative procedure, called consistent diabatic configuration (CDC) theory, is to simultaneously optimize both VB structures and configurational coefficients, as in the multi-configuration self-consistent field (MCSCF) method, to minimize the ground-state adiabatic energy. The resulting VB states are called consistent diabatic configurations since they are consistently obtained with respect to the variational energy of the adiabatic ground state.
In either scheme we may work in the nonorthogonal or orthogonal representation. In the former case the secular equation is the generalized eigenvalue problem4
| (5) |
where and are the energies of the nonorthogonal VB states, is the nonorthogonal off-diagonal Hamiltonian matrix element, S12 is the overlap integral, and the resonance energy (defined as the stabilization energy at the diabatic state crossing) is the difference between V and the lower of and (Note that S21 = S12, and ). Alternatively, the nonorthogonal diabatic states may be orthogonalized, in which case the off-diagonal Hamiltonian matrix element is the resonance energy itself. Hence there are four combinations, namely orthogonal and nonorthogonal CDC and VDC states.
The MOVB method is more efficient than other self-consistent field valence bond (VBSCF) methods58,66,150,151,209–213 for obtaining the adiabatic ground-state potential energy surface of a reactive system, but the trade-off is lower accuracy since each VB structure is approximated by a single Slater determinant of block-localized MOs. There are at least three ways that the accuracy of the MOVB method can be improved. The first is to use multiconfigurational methods such as generalized valence bond (GVB) theory209 to construct the individual diabatic states; this could provide a better treatment of electron correlation within each fragment. In the limit of this approach in which orbitals are block-localized on individual atoms, MOVB is equivalent to ab initio VBSCF, which is comparable to the familiar CASSCF method with an appropriate choice of active space.214–217 Secondly, computational accuracy can be improved by forming an effective Hamiltonian, in which the off-diagonal Hamiltonian matrix element ( H12 ) is required to reproduce high-level ab initio calculations or experimental data. Thirdly, one can use Kohn-Sham or generalized Kohn-Sham density functional theory instead of HF theory, but this requires additional assumptions to approximate the diabatic coupling. These approaches are not employed in the present examples.
2.5. Diabatic Couplings from MOVB Wave Functions
The calculations described in section 2.4 originally yield H11, H 22, and H12 in a nonorthogonal representation.4,60,127 For dynamics calculations it is often necessary to consider orthogonal states. For example, the usual rate of electron transfer rearrangement in the nonadiabatic limit is derived by Fermi’s Golden rule;218,219 if one used nonorthogonal initial and final states in a Golden Rule calculation, a constant coupling operator would cause a finite rate of charge transfer. If one treats the dynamics to infinite order, i.e., exactly, one can obtain correct results with either orthogonal or nonorthogonal representations, if used consistently. However, much of the literature of charge rearrangements is based on the Golden Rule or other perturbation treatments, and difficulties with formulating such treatments in terms of nonorthogonal representations are well known.220,221
The preferred way to transform to orthogonal states is by the symmetric orthogonalization method of Löwdin222 because, of all possible orthogonalizations, this yields states with the most resemblance to the original nonorthogonal ones. The resulting transformed 2 × 2 Hamiltonian matrix in the symmetrically orthogonalized representation is61,142
| (6) |
where S11 and S22 are unity because the nonorthogonal states are normalized, S12 (= S21) is the overlap between the diabatic states, T denotes a transpose, and Hn is the Hamiltonian in the nonorthogonal representation.
It is useful to compare the eigenvalue problem for the ground-state adiabatic potential energy surface V, in the two representations. In the symmetrically orthogonal representation it is the standard eigenvalue problem
| (7) |
whereas in the nonorthogonal representation it is given by eq 5. Comparing eqs 5 and 7 shows that the off-diagonal element of the Hamiltonian enters the theory in a different way in the orthogonal and nonorthogonal representations. It would be meaningless to specify without also specifying S12.
Interestingly, if one defines (as done above) the resonance energy, B, as the stabilization energy at the diabatic state crossing, it is clear that in the orthogonal diabatic state representation,
| (8) |
On the other hand, in the nonorthogonal diabatic state representation, solving eq 5 analytically shows that the resonance energy is
| (9a) |
where
| (9b) |
Equation 9a, combined with the definition of B, can also be rearranged to
| (10) |
that is, the resonance energy is the absolute value of the difference between the nonorthogonal off-diagonal Hamiltonian matrix element and the adiabatic ground state energy scaled by the overlap integral. If one treats B as a parameter in an effective two-state VB Hamiltonian approach, B is implicitly dependent on the overlap.4,126 (Notice that if one changes the sign of both diabatic wave functions, none of the matrix elements changes sign; whereas if one changes the sign of only one diabatic wave function, then and S12 change sign, but B computed by eq 9a or 10 is invariant to such a sign change.)
2.6. Diabatic Energies from the Empirical Valence Bond (EVB) Method
The EVB method92–103 of Warshel and Weiss has as its main features223 (a) using molecular mechanics to model chemical reactions in the context of VB theory; (b) assuming orthogonality of diabatic states to eliminate unknown overlap integrals; (c) calibrating the energy of the molecular fragments to try to make the method suitable for the study of reactions in solution and large molecules such as enzymes; (d) including solvation effects in the diagonal Hamiltonian matrix elements; and (e) assuming the off-diagonal Hamiltonian matrix elements are independent of environments, for example, the same in the solution as in an enzyme. Note that (b) and (c) are mutually incompatible because if the diabatic states are assumed orthogonal or transformed to be so, they contain orthorgonalization tails from other fragments. If molecular fragments are used to calibrate such orthogonal diabatic states, this treatment of overlap contributes an additional source of error over and above the assumption that the fragments are not internally polarized (distorted by valence interactions and noncovalent effects) when incorporated into the whole system. (Similar errors due to distortion and neglect of overlap have been discussed carefully in the context of diatomics-in-molecules theory,224 which is another semiempirical valence bond method.) If real molecular fragments are used to model the potential energy surfaces of the orthogonalized diabatic states, the neglect of the overlap can be a severe error if electronic structure methods are used as we see below. Furthermore, due to the neglect of internal polarization, if the diabatic coupling is only fitted to reproduce the barrier height of the adiabatic ground state, severe errors may arise in other regions of the potential energy surface.130,131 In step (d), the off-diagonal matrix elements are determined empirically by comparison with experimental kinetics data and are assumed to have generally simple functional forms or are taken as constant. In step (e), they are assumed to be unaffected by the surroundings. These features of the non-diagonal matrix elements are drawbacks of EVB theory.
In this work we characterize the ground-state adiabatic potential energy surface derived from EVB for the acetate + DCE reaction, taking the molecular mechanics parameters for the diabatic states to be the same as those used in Ref. 21 (see the appendix).
2.7. Free energies of solvation and activation in water
The standard-state free energy of activation in water at a temperature T in the separable equilibrium solvation (SES) approximation can be calculated from the geometries of the gas-phase reactants and the TS as follows225
| (11) |
where T is temperature; is the potential energy barrier in the gas phase; is the difference between the internal gas-phase free energies of the TS and reactants, with RVE standing for rotational, vibrational, and electronic degrees of freedom; and is the difference in standard-state free energies of solvation of the TS and reactants. (Note that we include zero point vibrational energies in the term whereas some workers include it in .) We neglect the term in the calculations, as this term is not our focus here and does not affect our discussion. All the calculations presented here are for a temperature of 298.15 K.
We calculate (T) by using the SM8 universal continuum solvation model226 in combination with CM4M,227 which is the parametrization of Charge Model 4228 (CM4) that is specifically designed to be used with the M06 suite (M) of density functionals. The M06-2X functional with the 6-31G(d) basis set has been chosen for the calculations. The SM8/M06-2X/CM4M model has been shown to reproduce free energies of solvation for a set of 120 ions in water with a mean unsigned error of 3.4 kcal/mol.226
2.8. Basis sets
All B3LYP, HF, MC-QDPT, and M06-2X/SM8 calculations in this article use the 6-31+G(d,p), 6-31+G(d,p), 6-31&G(d), and 6-31G(d) basis sets, respectively. The 6-31&G(d ) basis is defined in the appendix For gas-phase M06-2X calculations, MG3S is used for stationary points, and 6-31G(d) has been used for the construction of contour plots.
3. Results
We first define the reaction coordinate used for the plots, and we explain how the reaction path and energies along the reaction path were obtained for each of the methods employed. Then, relative adiabatic ground-state potential energy values at stationary points are presented to evaluate the quality of results at different levels of theory. The free energies of solvation and activation in water are calculated and compared with the dynamical results based on the EVB potential surface reported in the literature. Then, we describe the diabatic states. Finally, we discuss the diabatic state coupling along the reaction path.
3.1. Reaction Coordinate and Reaction Path
The reaction coordinate for reaction 1 is defined as the difference between the bond distances of the breaking bond (C-Cl) and the forming bond (O-C)
| (12) |
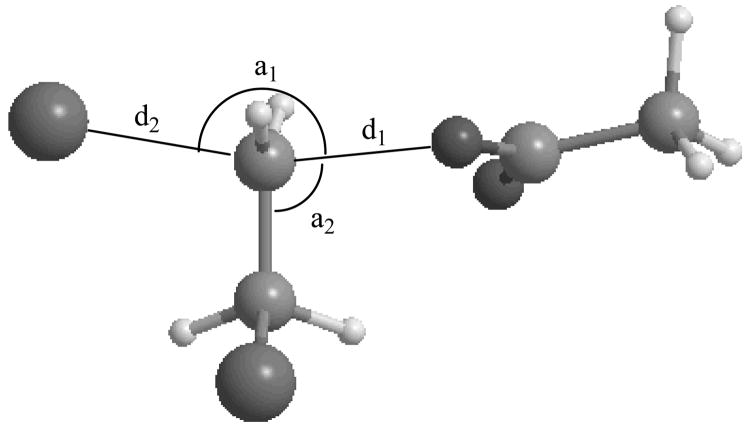
As mentioned in section 1, such a reaction coordinate is sometimes called a distinguished reaction coordinate. The reaction paths were constructed by fixing the value of this distinguished reaction coordinate and optimizing the rest of geometrical variables on the ground-state adiabatic PES. The values of some of the key geometric parameters for the stationary points obtained using the HF, B3LYP, M06-2X, and the EVB computational methods, are presented in Table 1. The definition of these variables is illustrated in Figure 2. Tables containing the Cartesian coordinates of all the points calculated along the reaction paths with these four methods are presented in Tables S2-S5 of Supporting Information. Overall, the optimized M06-2X geometrical parameters are in good agreement with those obtained at the HF and B3LYP levels. The average of the root-mean-square deviations in the O-C and C-Cl bond distances for the HF and B3LYP results at the reactant ion-molecule complex and the transition state, as compared with the more reliable M06-2X results, are 0.12 and 0.08 Å, respectively.
Table 1.
Value of key bond distances (in Å) and angles (in degrees) obtained for the stationary points of the acetate + DCE reaction with the HF, B3LYP, M06-2X, and EVB methods. The geometric parameters are defined in Figure 2. ‘RS’, ‘TS’, and ‘PS’ stand for the reactant ion-molecule complex, the transition state, and the product ion-molecule complex, respectively.
| HF | B3LYP | M06-2X | EVB | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| RS | TS | PS | RS | TS | PS | RS | TS | PS | RS | TS1 | TS2 | PS | |
| C-O(d1) | 3.19 | 2.12 | 1.44 | 3.12 | 2.09 | 1.46 | 3.09 | 2.01 | 1.44 | 2.37 | 1.86 | 1.95 | 1.70 |
| Cl-C(d2) | 1.82 | 2.36 | 3.49 | 1.84 | 2.35 | 3.44 | 1.81 | 2.28 | 3.23 | 2.40 | 2.90 | 3.34 | 4.89 |
| O-C-Cl (a1) | 126 | 164 | 166 | 126 | 164 | 169 | 129 | 166 | 165 | 170 | 124 | 169 | 98 |
| O-C-C (a2) | 86 | 91 | 113 | 91 | 96 | 114 | 72 | 95 | 113 | 95 | 107 | 100 | 118 |
FIG 2.
Geometric variables for the acetate + DCE reaction showing the formation of the O-C bond and the breaking of the C-Cl bond.
The first point along the reaction path is the reactant ion-molecule complex with the DCE molecule in a gauche conformation, because this conformation is preferred for the nucleophilic attack of the acetate ion. The O–C distance at this geometry calculated at the M06-2X level is 3.09 Å, which is slightly shorter than the O–C distance optimized at the other two levels. The O–C distance at the optimized M06-2X transition state is 2.01 Å, which is also shorter than that optimized at the HF and B3LYP levels. The product ion-molecule complex has R(O–C) = 1.44 Å. The C-Cl distances obtained at the M06-2X level are also shorter than those obtained at the HF and B3LYP levels at the three stationary points.
As can be observed in Table 1, the bond distances and angles obtained with EVB are quite different from those obtained with the other methods. As also shown in Table 1, two different transition states (each confirmed by frequency analysis to have only a single imaginary frequency) are found on the ground-state adiabatic potential energy surface instead of the single transition state obtained with HF and with density functional methods. The data presented in Table 1 also show that the EVB stationary point geometries are shifted towards the region of products, as shown most clearly by the O-C and C-Cl bond distances: the EVB reactant complex has distances comparable to those of the TS obtained with the other methods, and the EVB transition states have distances roughly comparable to that of the HF and density functional product complex. The shape of the EVB ground potential surface is therefore quite different to that of the potential surfaces obtained with electronic structure methods. This will be more clearly seen in the next section, where we compare contour plots obtained with density functionals to those obtained with EVB.
3.2. Adiabatic Ground-State Energy
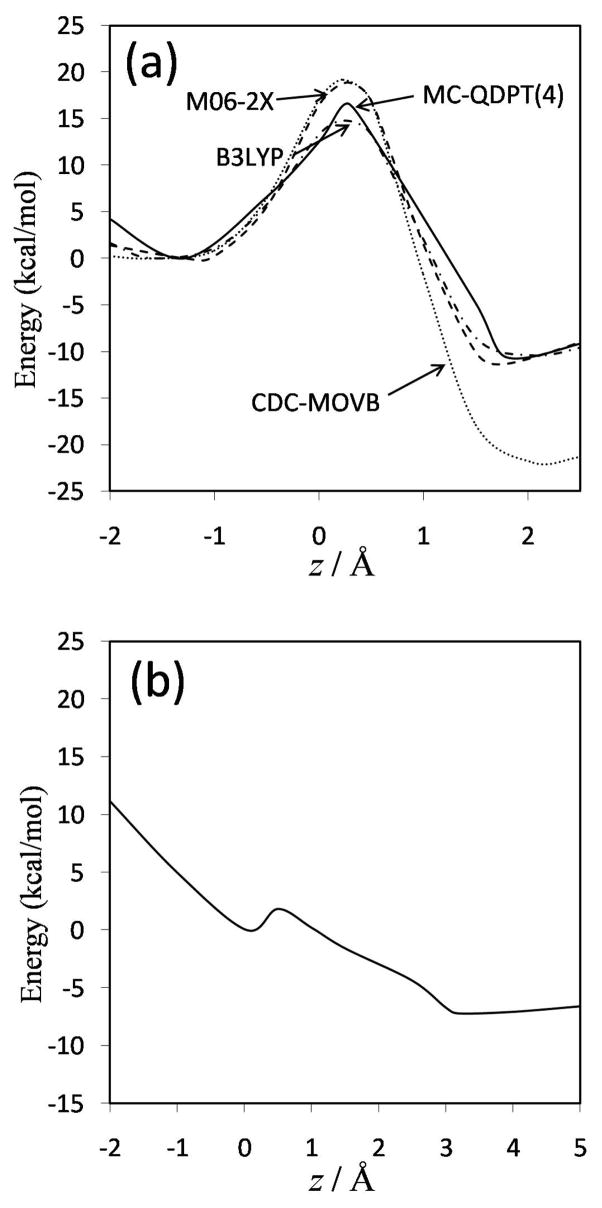
Shown in Figure 3(a) are the ground-state adiabatic potential energies as functions of the reaction coordinate obtained at the B3LYP, M06-2X, and fourfold way (MC-QDPT(4)//M06-2X) levels of theory. In Figure 3(b) we present analogous results obtained with EVB theory; these are given separately because they span a larger range of the reaction coordinate.
FIG. 3.
Ground-state adiabatic potential energy profiles along the reaction coordinate computed with (a) MC-QDPT(4)//M06-2X (full line), M06-2X (dashed line), CDC-MOVB (dotted line), and B3LYP (dashed-dotted line), and (b) EVB. For each method, the zero of energy is taken as the ground-state adiabatic energy of the ion-molecule reactant complex. Note the change in the scale of the abscissa between parts (a) and (b).
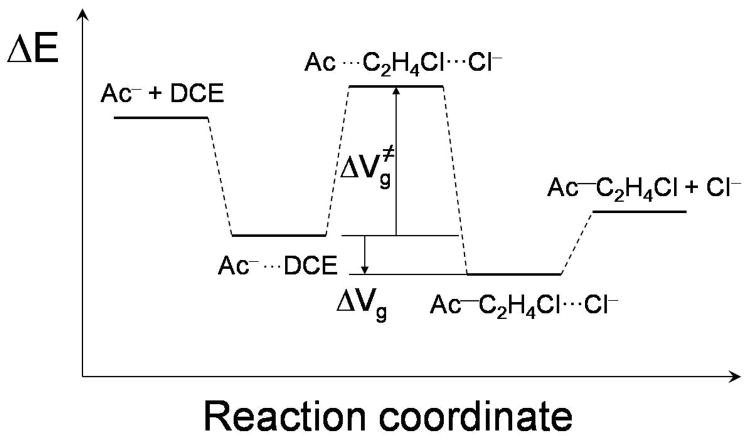
The energies of the stationary points along the gas-phase reaction path are sketched in Figure 4, where ΔVg represents a difference in gas-phase potential energy. The two key electronic energy differences are defined in this scheme, namely, the reaction energy from the reactant complex to the product complex (ΔVg ), and the reaction barrier with respect to the reactant complex ( ). Table 2 summarizes the values obtained in the present work for these quantities. To our knowledge, the product complex has not been reported in the literature, and there are no data to which to compare.
FIG. 4.
Definition of reaction energy and reaction barrier on the ground-state PES used in the present study.
Table 2.
Reaction Energy and Barrier Height (in kcal/mol) of the Acetate + DCE Reaction in the Gas Phase.
| Method | ΔVg | ||
|---|---|---|---|
| M06-2X | −11.3 | 18.9 | |
| BMC-CCSD//M06-2X | −9.9 | 18.0 | |
| G3SX(MP3)//M06-2X | −10.5 | 17.2 | |
| G3SX//M06-2X | −10.7 | ||
| MC-QDPT//M06-2X | −15.1 | ||
| MC-QDPT(4)//M06-2X | −10.6 | ||
| B3LYP | −10.3 | ||
| HF | −18.4 | ||
| MOVB (scheme VDC) | −21.7 | 18.3 | |
| MOVB (scheme CDC) | −22.0 | 23.8 | |
| EVB | −7.0 | 19.2 | |
| 22.9, 2.3a |
The first value corresponds to TS1, and the second value corresponds to TS2 (see Table 1 for the geometries of TS1 and TS2).
The barrier heights and reaction energies obtained with the three high-level wave function methods used as a reference (presented in Table 2) agree reasonably well with each other. The presumably most accurate method, G3SX//M06-2X, gives a barrier height of 16.9 kcal/mol. The MC-QDPT(4)//M06-2X barrier height is in good agreement with this high-level value, whereas density functional theory at the B3LYP level gives too low a barrier and the M06-2X barrier is slightly too large (Table 2 and Figure 3). The energy of reaction predicted by the high-level methods is between about −10.0 and −11.0 kcal/mol, in good agreement with the density functional and MC-QDPT(4)//M06-2X results. The EVB reaction energy of −7.0 kcal/mol is in reasonable agreement with the high-level results. The higher of the two barriers obtained by EVB (22.9 kcal/mol) is about 6 kcal/mol higher than our best estimate and, as mentioned before, the geometry of the saddle point disagrees with all four other calculations. Of particular relevance is the presence of the second EVB saddle point with a barrier of only 2.3 kcal/mol. Following the path of steepest descent from either transition state leads in one direction to the reactant complex and in the other to the product complex. (Thus, the path of steepest descent from the higher saddle point does not lead to the lower one). This implies that there is an alternative, lower-energy path for the reaction to proceed, avoiding the higher barrier. This is most likely an artifact of the fitting of the EVB method to empirical data for its use to study the reaction in water and in the haloalkane dehalogenase enzyme. The relevance of such a low barrier for dynamical studies of the reaction in water and in the haloalkane dehalogenase enzyme will be considered below.
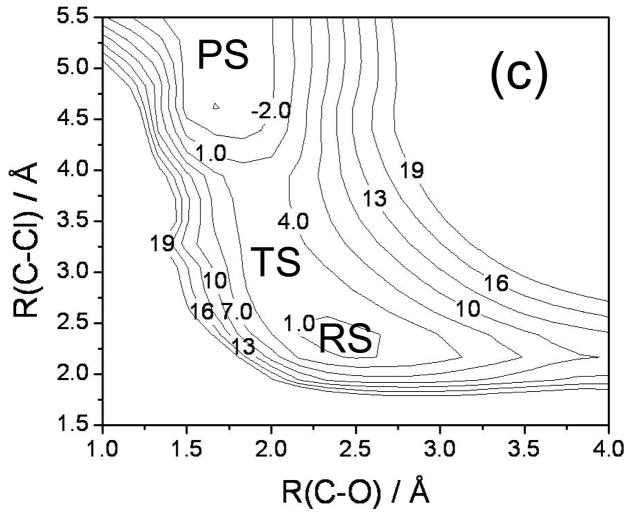
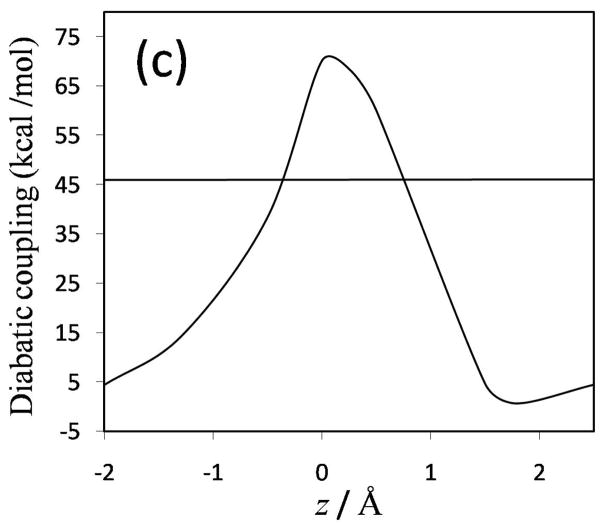
To further examine the shape of the ground-state adiabatic PES, we have constructed 2-D contour plots for the reaction at the B3LYP and M06-2X levels and have compared them to those calculated at the EVB level. To make these plots, a grid of points was defined spanning a range of values of the O-C and C-Cl distances. The ground-state adiabatic energies that are plotted were obtained by fixing the values of these two distances and optimizing the rest of geometric parameters. The contour plots obtained using B3LYP are presented in Figure 5(a), those obtained using M06-2X are shown in Figure 5(b), and the ones obtained from EVB are presented in Figure 5(c). In Figures 5(a) and 5(b), the reactant ion-molecule complex is located in the lower right-hand corner, with an energy which is zero by definition. The system then evolves towards the transition state, which is located at an energy of 14.9 kcal/mol for B3LYP (Table 2) and at an energy of 16.5 kcal/mol for M06-2X, and it reaches the product ion-molecule complex in the upper left-hand corner of the figures. The EVB contour plot presented in Figure 5(c) is substantially different; the most notable features are the shift of the reactant complex toward the region of the B3LYP TS, and the “shelf” located between the contours of 1.0 and 4.0 kcal/mol containing the lower transition state. Note that the TS with the higher barrier is not reflected in the plot, as the optimizations fixing the values of the O-C and C-Cl distances close to those of the TS with the higher barrier always lead to the lower energies observed in the figure. We conclude that the features of the EVB ground-state PES for acetate + DCE reaction in the gas phase do not reflect those obtained with high-level electronic structure theory.
FIG. 5.
Contour plots of the ground-state adiabatic potential surface in the plane of the O-C and C-Cl distances. The levels of calculation used to construct the plots are (a) B3LYP, (b) M06-2X, and (c) EVB. “RS”, “TS”, and “PS” stand for the reactant ion-molecule complex, the transition state, and the product ion-molecule complex, respectively. Note the different ordinate between parts (a) and (b). The energy units used are kcal/mol.
3.3. Diabatic States
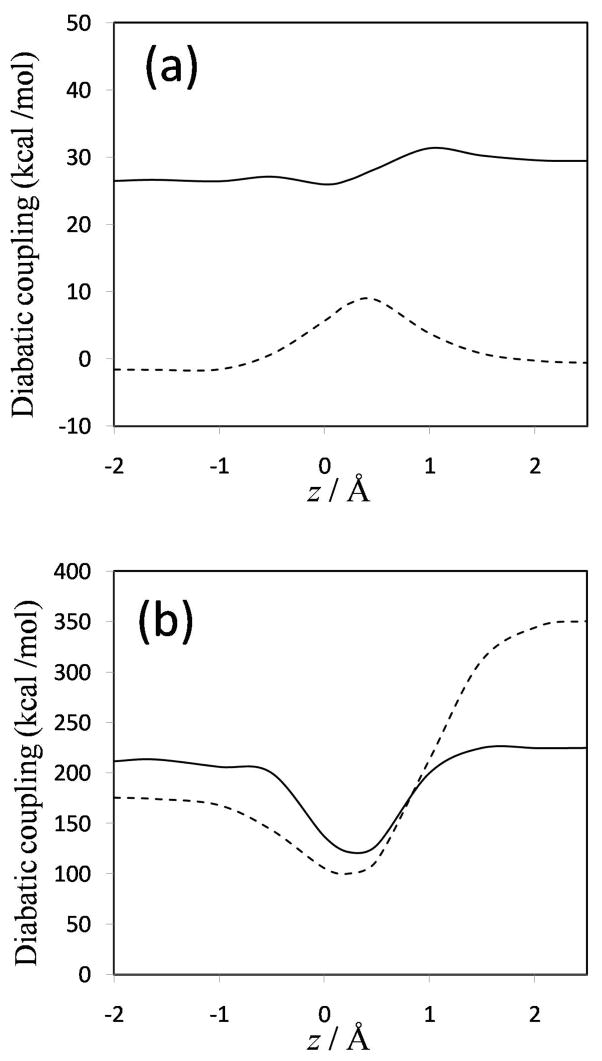
The diabatic potential energy curves (and the ground-state adiabatic potential curves) obtained using the nonorthogonal and orthogonal representations for MOVB with VDC and CDC methods are presented in Figure 6; the diabatic curves and the ground- and first-excited adiabats obtained with the fourfold way are shown in Figure 7; and the analogous curves obtained with the EVB method are presented in Figure 8. In comparing these curves, one should keep in mind that the fourfold way diabatic states span the same space as the ground and selected excited adiabatic states, whereas the MOVB states involve no reference or excited adiabatic states, and the EVB curves involve no electronic structure information at all. The corresponding diabatic couplings for the MOVB method in the nonorthogonal and orthogonal representations and for the fourfold way (MC-QDPT(4)//M06-2X) and EVB calculations are depicted in Figure 9.
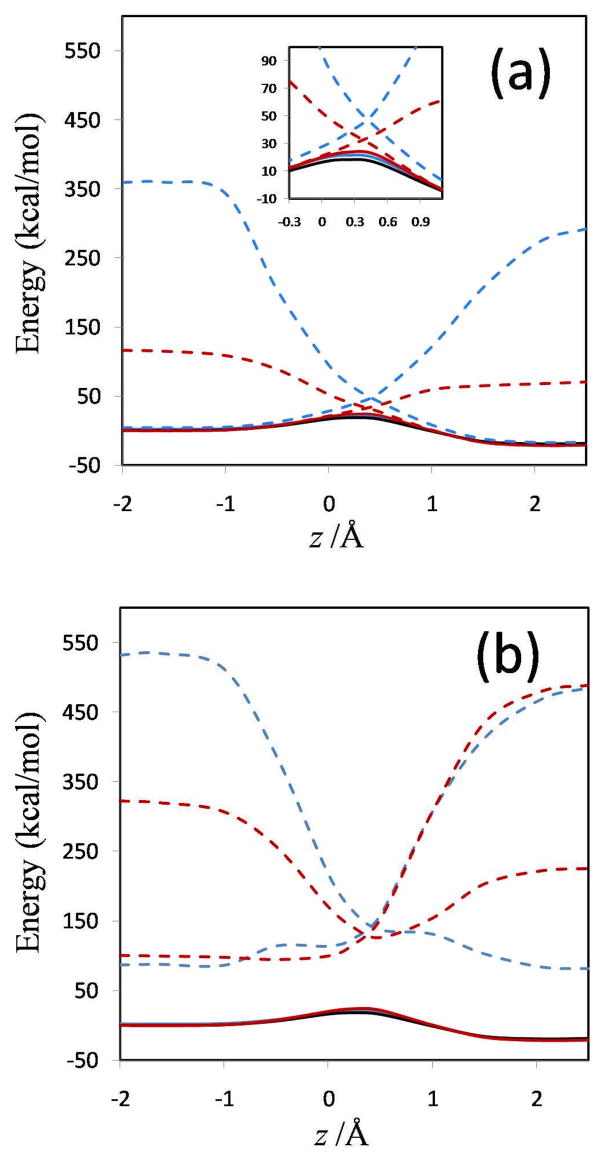
FIG. 6.
Comparison of adiabatic and diabatic potential profiles. (a) Adiabatic HF profile (black line) and adiabatic and diabatic MOVB potential energy profiles obtained by nonorthogonal VDC (red lines) and nonorthogonal CDC (blue lines) schemes. The panel in the center is a blowup of the central region of the larger panel. (b) Same as part (a) except MOVB results are in the orthogonal representation. In both (a) and (b) the zero of energy is chosen as the ground-state HF adiabatic energy of the ion-molecule reactant complex.
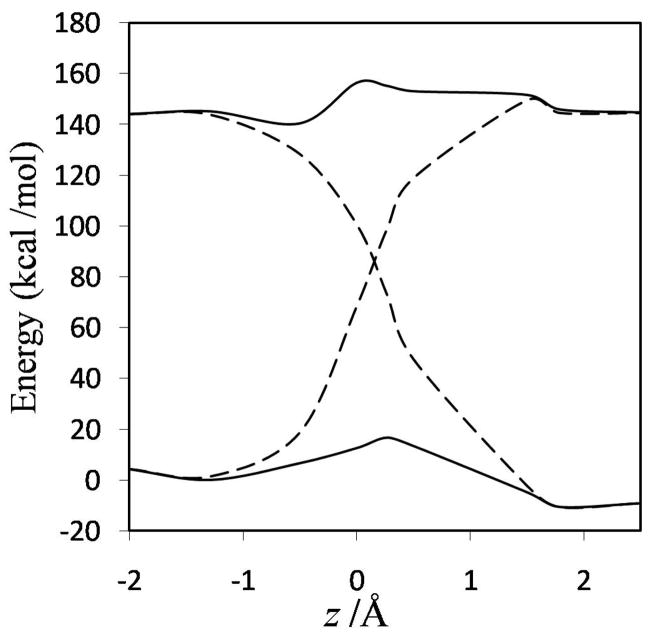
FIG. 7.
Fourfold way (MC-QDTP(4)//M06-2X) adiabatic and diabatic energies along the reaction coordinate. The zero of energy is chosen as the ground-state adiabatic energy of the ion-molecule reactant complex.
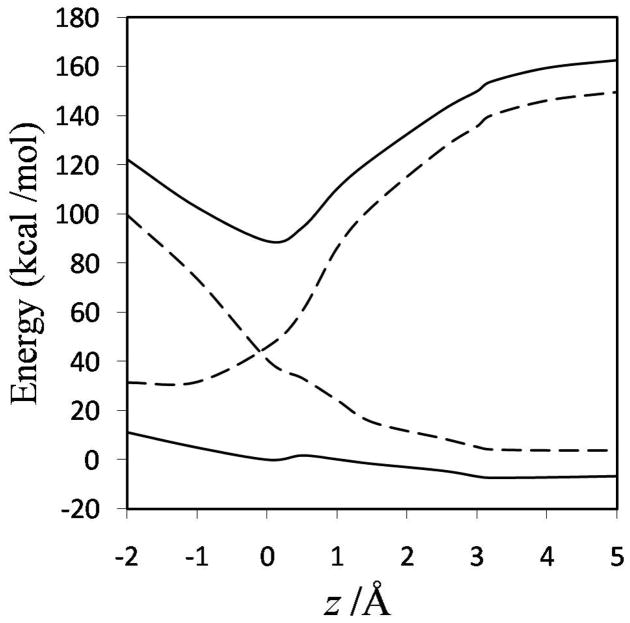
FIG. 8.
EVB adiabatic and diabatic energies along the reaction coordinate. The zero of energy is chosen as the ground-state adiabatic energy of the ion-molecule reactant complex.
FIG. 9.
Diabatic coupling matrix elements as a function of the reaction coordinate. (a) Nonorthogonal MOVB resonance energy of eq 9a or the equivalent eq 10 (full line for the CDC method, and dashed line for the VDC method), (b) orthogonal MOVB (CDC is given as a 12 full line, and VDC is shown by a dashed line), and (c) fourfold way (MC-QDTP(4)//M06-2X) (curve with a peak) and EVB (straight line).
We emphasize that there is no unique way of defining the diabatic states corresponding to the reactant state and the product state, in part because diabatic states are intrinsically nonunique4,59,105,136–141 and in part because it is necessary to apportion the contributions from additional VB structures (such as, in the present example, the key ionic configuration (3) as well as the high-energy covalent configuration 6 in eq 2) into two explicit states along the entire reaction coordinate.
The MOVB reactant and product diabatic energy profiles in VDC and CDC models and in the nonorthogonal and orthogonal representations are presented in Figure 6. Figure 6(a) shows that in the nonorthogonal representation, the diabatic energy increases by about 70 and 290 kcal/mol for VDC and CDC states, respectively, in going from the equilibrium reactant ion-dipole geometry to the equilibrium product state geometry. Similarly, for the reverse reaction, the product state energy increases by 115 and 360 kcal/mol for VDC and CDC schemes, respectively, at the reactant geometry. Thus, optimizing each of the MOVB structures separately affords much smaller energies at geometries far from their respective regions of minimal energy than does optimizing the ground-state energy. The fourfold way values for these quantities are approximately 140 kcal/mol both for the reactant and product diabatic states (Figure 7). The orthogonal representation for MOVB yields results very different to those from the nonorthogonal representation, as can be seen in Figure 6(b). The energies of the orthogonal MOVB states are significantly higher than for the nonorthogonal representation, and the curves do not join the adiabatic ground-state curve in the reactant and product regions. Thus, the energy variations in the fourfold way reactant and product diabatic states are larger than the MOVB results in the VDC method, but smaller than those in the CDC optimization (either nonorthogonal or orthogonal). The maximum energy changes in the reactant and product states of EVB theory are about 140 and 100 kcal/mol, respectively.
Orthogonalization of the MOVB states involves the overlap between the MOVB structures. The overlaps for the reactant complex, the transition state, and the product complex, are presented in Table 3, and overlaps at other locations along the reaction path are presented in Table S6 of Supporting Information. As observed in Table 3, the overlaps are always quite large, especially in VDC states where they go up to 0.94 in the product region. The overlap integrals from the CDC wave functions are significantly smaller than the VDC values (Table 3). Apparently, optimizing the MOVB structures separately causes the fragment orbitals to delocalize more than optimizing the ground-state energy (CDC theory), thereby causing a stronger overlap between the structures. This may also be recognized as increased ionic character in the VDC reactant diabatic state at the product state geometry, which has greater resemblance with the product diabatic state near its minimum.4 Also, the overlaps in VDC states increase continuously along the reaction path, whereas the CDC overlaps are maximal in the transition state region. The values obtained for the overlaps can be compared, for instance, with those obtained in a breathing-orbital VB study of the X−+ CH3X (X = F, Cl, Br, I) identity reactions,64 where for the TS geometry, smaller values oscillating between 0.47 for F and 0.33 for I were obtained for the VB wave function overlap. In yet another study, ab initio VBSCF/6-31+G(d,p) calculations on the ammonia exchange reaction of NH3 and CH3NH3+ show overlap integrals varying from 0.6 to 0.7 from the ion-dipole complex minimum to the transition state.4 Thus, a more conventional VB approach yields smaller, but still significant, overlaps than MOVB, because the VB orbitals are more constrained in the former case and are not allowed to delocalize as extensively as in the MOVB method. Overlap is simply not negligible in VB theory.
Table 3.
Computed overlap integrals using the MOVB wave functions at the reactant complex (RS), transition state (TS), and product complex (PS) geometries optimized at the HF level.
| z | VDC-MOVB | CDC-MOVB |
|---|---|---|
| RS | 0.853 | 0.605 |
| TS | 0.910 | 0.770 |
| PS | 0.938 | 0.659 |
The energy difference between the product and reactant diabatic states at the reactant geometry is called the reorganization energy in condensed phase reactions, and it plays a key role in Marcus theory. In other contexts, this energy difference is called promotion energy, for example by Shaik.56 Figures 6–8 show that the reorganization energy varies from 115 to 440 kcal/mol for the four MOVB schemes and is 140 kcal/mol in both the fourfold way and the EVB model. The close agreement of the reorganization energy from the nonorthogonal VDC-MOVB scheme with that of the fourfold-way is not straightforward to interpret because the orthogonal fourfold way and EVB schemes should strictly be compared only to the orthogonal MOVB results.
Note that the fourfold way states are obtained by following a strategy in which both the ground and the first excited state surfaces are used in the definition of the two diabatic states, whereas in the MOVB schemes no excited adiabatic state plays any role. Nevertheless, both the fourfold way and the MOVB method share the characteristic that the definition of the diabatic states is based on electronic structure considerations. In contrast the EVB diabatic states are based on the value of molecular mechanics analytical energy expressions used in regions far away from equilibrium conformation —where they are not valid and were not designed to be used. The EVB diabatic energy profiles shown in Figure 8 do not agree qualitatively with either the MOVB or the fourfold-way ones in that the region of the transition state does not correspond to the crossing of the diabatic curves although it is typically described in this way. In the present SN2 reaction (chosen to model the haloalkane dehalogenase reaction), the transition state is located at a larger value of the reaction coordinate (about 1.3 Å). As already mentioned, the EVB barrier on the ground-state adiabatic PES is much lower than that obtained with the other methods.
The diabatic couplings obtained by all six schemes are shown in Figure 9. First one notes that some features of the diabatic couplings obtained by the MOVB method, the fourfold way, and the EVB calculations are qualitatively different. Focusing first on the nonorthogonal MOVB method (Figure 9(a)), the diabatic coupling obtained with the CDC scheme, in which it represents the stabilization energy of the transition state at the diabatic energy crossing and is dependent on the overlap integral according to eqs 8a and 10, has a rather different shape from that obtained with the VDC model. The CDC resonance energy remains relatively constant along the reaction path, as in EVB theory, and is nonzero at the reactant and product regions. Interestingly, the quantitative result of about 30 kcal/mol is also close to the EVB constant value of ~45 kcal/mol (Figure 9(c)). On the other hand, the VDC resonance energy curve in Figure 9(a) has very similar shape, but smaller diabatic coupling, in comparison with the fourfold way method. This reflects the more ionic character in the VDC states in which the stabilization energy due to diabatic coupling is partially included in the diabatic energies, and this is mirrored by greater overlap integrals than that between the CDC states. However, when the nonorthogonal CDC and VDC diabatic states are orthogonalized by Lowdin transformation, the couplings, shown in Figure 9(b), have a much larger magnitude than those of B in nonorthogonal representation shown in Figure 9(a), and the former couplings present a minimum around the transition state geometry. The different behavior of as compared with B is probably a consequence of the large overlap between the nonorthogonal MOVB structures, which should cause the nonorthogonal and orthogonal wave functions to differ considerably. Interestingly, while the symmetric transformation enforces orthogonality between diabatic states, the “penalty” of distorting the wave functions is transferred to enhanced diabatic coupling to yield the same ground state energy. In the fourfold way (Figure 9(c)), the diabatic states are orthogonal by construction and—also by construction—are zero at reactants and products, and the diabatic state coupling is most dominant in the strong interaction region where the two VB states become degenerate and have the greatest overlap. This is qualitatively in agreement with the nonorthogonal VDC-MOVB method. The maximum values of the fourfold-way and EVB H12 curves are much smaller than the magnitude of the MOVB couplings in the orthogonal representation but larger than those in the nonorthogonal representation. The fourfold way coupling decays rather rapidly but not at the same rate in the directions towards the reactant state and the product state. This uneven rate of decrease in the diabatic coupling strength is usually not considered in EVB, where either a single exponential function or a constant diabatic coupling are assumed.
3.4. SM8 free energies of solvation and free energies of activation
We have applied the SM8 solvation model to the reactant ion-molecule complex and the TS, and we have calculated free energies of activation by adding the gas-phase reaction barrier to the difference of the free energies of solvation. The results are presented in Table 4. The second row gives the results of molecular dynamics simulations of the free energy of activation in water from Ref. 21, and the corresponding free energies of solvation from Ref. 28. Comparing the values of these quantities shows that the gas-phase free energy of activation (that is, the sum of the first two terms on the right-hand side of eq 11) is only 2 kcal/mol. This value is substantially smaller than expected from the electronic structure calculations presented in this work, which indicate that the value of the electronic gas-phase barrier is about 17 kcal/mol. However, the result would be consistent with the lower electronic barrier of 2.3 kcal/mol found for EVB (see Figure 5(c)), which was pointed out in Refs 1 and 27, and with the general shape of the EVB ground-state PES. Note that the final result, namely, the free energy of activation, is in good agreement with experiment.
Table 4.
Free energies of solvation and activation in water (in kcal/mol), and energies of activation in the gas phase, for the acetate + DCE reaction obtained from EVB and from M06-2X geometries. ‘RS’ and ‘TS’ stand for the reactant ion-molecule complex and the transition state, respectively. The experimental free energy of activation in water is 28.2 kcal/mol.24,27,230
The results presented in the first row of Table 4 have been obtained by optimizing the geometries of the reactant ion-molecule complex and of the TS in the presence of the solvent by SM8. The gas-phase geometries of reactants and of the TS taken as the reference for the calculation of free energies of solvation are those obtained by M06-2X. The value of the electronic gas-phase potential energy barrier has been assumed to be that of the best level of calculation used in the present study, namely, G3SX//M06-2X. Regarding the free energies of solvation, as shown in the table, it is interesting that the values obtained for reactants and for the TS are rather similar, in contrast to other SN2 reactions (for example, the prototype Cl−+ CH3Cl reaction66,229) where reactants are preferentially solvated by a large amount over the TS. This is probably due to the delocalized nature of the charge in the acetate anion. The overall free energy of activation is 21.3 kcal/mol, smaller than the experimental value of 28.2 kcal/mol.24,27,230 at 373 K. Note that solute-solvent charge transfer is not taken into account by the present treatment. For the acetate anion in a microsolvated environment, a charge transfer to water of +0.18 was obtained with the SM8 model also employed here.231 Consideration of this and other factors affecting the solvation free energies could lead to a better agreement with experiment.
The results shown in the third and fourth row of Table 4 employ the EVB PES. In this case, pointwise calculations of free energies of solvation have been performed at the SM8 level at EVB geometries. In the third row, which has been obtained from EVB reactant and TS geometries, one observes that the energy of activation obtained is negative, in strong disagreement with the value obtained from molecular dynamics simulations.21,28 It is noteworthy that the solvation energy for the TS is considerably larger than that for reactants, which is the opposite of that found from the simulations28 and contrary to what is expected for SN2 reactions. This is caused by the already mentioned shift of the EVB reactant and TS geometries with respect to those obtained by electronic structure calculations (see Table 1): the TS has an extended C-Cl distance and the Cl− anion has a large free energy of solvation. The large discrepancy obtained for the free energy of activation is due at least in part to the fact that the geometries chosen are not quite representative of the geometries actually sampled in the liquid-phase molecular dynamics simulations, such as those shown in Figure 1(a) of Ref. 21. To address this point, we have chosen two geometries, one with an O-C distance of 3.2 Å and a Cl-C-O angle of 150.0° as representative of the reactants region, and another one with an O-C distance of 2.2 Å and a Cl-C-O angle of 165.0° as representative of the TS region. These two parameters were fixed while the rest of geometrical parameters were optimized, and pointwise SM8 calculations were again performed on the optimal structures. The results, presented in the fourth row of Table 4, show a free energy of activation close to zero, and a larger solvation energy for the reactant state, as expected for the acetate + DCE SN2 reaction. Note also the negative reaction barrier in the gas phase using these structures (Table 4). Olsson at al. argued in footnote 68 of Ref. 28 that TS structures are similar in the gas phase and in aqueous solution, but the structures of the reactant states are different and the elongated ion-dipole structure in water is 13 kcal/mol higher and the compressed ion-dipole complex in the enzyme is 6 kcal/mol higher in energy than that at the gas-phase minimum.28 According to this analysis28 a negative reaction barrier of about −11 kcal/mol would be obtained in water, in close agreement with the value in the fourth row of Table 4. It is possible that an average over many molecular configurations such as that shown in Figure 1(a) of Ref. 21 could reconcile this result with the gas-phase activation barrier of 2.0 kcal/mol obtained in the first row of the table. However, Olsson et al.28 stated that a gas-phase activation barrier deduced from their “thermodynamic cycle is in excellent agreement with ab initio estimates of this barrier (about 17 kcal/mol)”. The free energy of activation obtained is actually in disagreement with that from molecular dynamics simulations by more than 20 kcal/mol.
Therefore, none of the calculations presented using the EVB PES has been able to reasonably reproduce the results presented in Refs. 21 and 28. We believe that it is mainly the qualitatively wrong shape of the EVB PES in the gas phase which causes the inconsistencies in the computation of free energies of solvation and activation in water. In our opinion, a careful study of the EVB gas-phase reactions should be undertaken prior to reparametrizing the PES for use in studies in condensed phase or in the active center of an enzyme.
3.5. Other methods
It is interesting to compare the present treatments to Voter and Goddard’s generalized resonating valence bond (GRVB) method.232 As compared to MOVB, we note that GRVB uses a multiconfiguration wave function, whereas the MOVB method uses a single Slater determinant. As compared to the fourfold way, we note that GRVB is an approximate way to calculate the ground electronic state, whereas the fourfold way starts with arbitrarily accurate calculations that approximate the ground and excited states and then finds diabatic states that span the same space as the two lowest-energy adiabats.
To construct an accurate and efficient VB-based model for modeling chemical and enzymatic reactions, an effective Hamiltonian MOVB (EH-MOVB) approach has been developed;233 this method can be parameterized similarly as the EVB model, but the molecular structures can be optimized to obtain good agreement with ab initio MO or VBSCF results. The EH-MOVB method can be carried out at either the semiempirical or ab initio level of theory, using either Hartree-Fock or density functional theory. Accuracy is improved by introducing a scaling factor on the diabatic coupling ( ) to yield the correct barrier height, and a diabatic energy shift constant ( ) to reproduce the experimental energy of reaction. The EH-MOVB theory is based on ab initio valence bond theory with a multiconfiguration reduction to generate the diabatic states.4 The level of theory to describe the diabatic states can be systematically improved, and the diabatic coupling is dependent on all 3N degrees of freedom where N is the number of atoms in the system. The method has been illustrated for the SN2 reaction between hydrosulfide and chloromethane at the EH-MOVB/6-31+G(d,p) level, and excellent agreement has been obtained with ab initio VBSCF or other high-level results for optimized structures and the potential energy surface.233
4. Concluding remarks
We hope that the perspective presented here is useful for elucidating the importance of consistently defining diabatic states when using them to discuss condensed-phase properties such as reaction rates of enzymatic reactions. The construction of diabatic states for the gas-phase reaction is often a useful first step for applications where liquid-phase diabatic states are desired for interpretative purposes, but there is no unique method for defining diabatic states in either phase. The main focus of the present study is a comparison between three methods, namely, the molecular orbital valence bond (MOVB) method, the fourfold way, and empirical valence bond (EVB) calculations, of generating diabatic, VB-like states, as illustrated by application to the acetate + DCE system in the gas phase. For the MOVB case, we consider two schemes, called variational diabatic configurations (VDC) and consistent diabatic configurations (CDC). Furthermore, whereas the fourfold way and EVB are defined only in an orthogonal representation, MOVB is directly defined in a nonorthogonal representation, which can be transformed to an orthogonal representation by Löwdin symmetric orthogonalization method.
There are many different motivations for working with diabatic states, and in the case of the EVB calculations presented here the goal of the original workers was to predict the free energy profile in an enzyme reaction for use with a collective reaction coordinate based on an energy gap. It is recognized by all practitioners that all the approaches used here are approximate ones, and when one applies these same methods to other problems, the quality of the results will depend on the quality of the parameterization, the basis set, and various problem-specific details. For parameterized methods, one must keep in mind the nature of the parameterization. If one calibrates an analytic potential energy surface, especially one with an analytic form restricted for computational efficiency, to produce one or two properties one cannot necessarily expect the potential energy surface to be accurate along any coordinate chosen. Thus, one might argue that an EVB surface should be used only for calculating the potential energy surface along the same collective energy-gap coordinate for which it was designed and created. That is one possible way to proceed, but our goal here was to examine the underlying diabatic potential surfaces because they are often interpreted in a physical way as providing information about reorganization energy, promotion energy, and enzyme mechanisms and for understanding the origin of rate acceleration in enzyme catalysis. Thus, in the present paper, we are examining the EVB diabatic curves in a different context using a geometrical reaction coordinate different than that (an energy-gap coordinate) for which they were originally parameterized along. Our justification for this is that we believe that—for many purposes—dynamical methods based on a collective reaction coordinate and dynamical methods based on a valence-coordinate reaction path should both utilize an atomically qualitatively correct description of the potential energy surface as a function of all relevant atomic coordinates, and our goal was to compare—in this context—three classes of methods employing the concept of diabatic states in various ways. By calculating not only the transition state theory rate constant but the transmission coefficient, one can unify treatments based on different choices of the reaction coordinate.1,2,105 It has been shown that the transmission coefficients are close to unity for the present SN2 reaction in water and in haloalkane dehalogenase enzyme when making use of the asymmetric stretch reaction coordinate,27 so this choice of reaction coordinate is a very relevant one.
The diabatic potential energy profiles along the asymmetric stretch reaction coordinate obtained with the fourfold way agree qualitatively but not quantitatively with the nonorthogonal MOVB method with the VDC model; this is very interesting since the underlying electronic structure methods employed in this work for MOVB (ab initio HF) and the fourfold way (ab initio MC-QDPT) are very different and since the fourfold way yields an orthogonal representation. The results obtained with EVB, which is based on a parameterization of MM diabatic states to reproduce free energies in condensed phase, are quite different from those obtained with MOVB and the fourfold way, which are based on electronic structure calculations, but are closer in general magnitude to the fourfold-way results. However, the EVB gas-phase adiabatic reaction path shows a systematic shift towards product geometries with, e. g., the EVB ion-molecule reactant minimum resembling the TS geometry obtained with electronic structure methods. Also EVB has two different reaction paths, one bearing a barrier of 22.9 kcal/mol, in qualitative agreement to the barrier obtained by MOVB and the fourfold way, and a second reaction path of much lower energy, with a barrier of only 2.3 kcal/mol. This second reaction path is an artifact of the EVB parameterization. A calculation of free energies of solvation and activation in water based on the EVB PES has been unable to reproduce the free energy of activation obtained by molecular dynamics simulations (24.9 kcal/mol). These findings cast doubts on the reported EVB results and suggest that a careful parameterization of the gas-phase reaction might have been useful in order to obtain more meaningful results for the condensed-phase reaction by the EVB method.
The energy variations predicted by the two electronic structure methods (MOVB and the fourfold way) for the reactant and product states at the product and reactant equilibrium geometries, respectively, are large. The MOVB values for these quantities depend to a large extent on the representation (nonorthogonal or orthogonal) and on the optimization strategy adopted for the wave functions. An interesting question for future consideration is whether any of the electronic-structure reorganization energies calculated by the methods used here should be used as the solute contribution to the reorganization energies106,107 for the condensed-phase reaction.
The diabatic couplings obtained with the fourfold way decrease steeply from the region of the transition state towards reactants and products, where they are close to zero. In contrast, the couplings obtained with the MOVB method have a much larger magnitude, are either relatively constant along the reaction coordinate or present a minimum in the transition state region, and are nonzero in the reactant and product regions. An exception is the nonorthogonal VDC-MOVB model, which has qualitatively similar features to those found by the fourfold way. These differences reflect the fact that the diabatic coupling absorbs the non-uniqueness in the definition of the diabatic states. No functional form is assumed for the diabatic coupling in MOVB or in the fourfold way since the diabatic coupling (off-diagonal element of the Hamiltonian matrix) is determined by using electronic structure methods; however, the values of the diabatic coupling that are obtained are intimately determined by the specific definition of the diabatic state wave function. This is quite different from the situation in the EVB method, where either an exponential dependence on the distance between the nucleophile and the leaving group involved in an SN2 reaction, or a constant coupling as for the acetate + DCE reaction, is assumed.
The reaction energies obtained by density functional theory and by the fourfold way agree well with the those obtained by the three high-level methods (G3SX, G3SX(MP3), and BMC-CCSD), which predict values ranging from −10 and −11 kcal/mol. The results for the diabatic states are especially significant because in the fourfold way, changes in the exponent of the diffuse basis functions of chlorine and in the weight of the two adiabatic states involved in the underlying SA-CASSCF wave function were carried out to obtain simultaneously a barrier height and reaction energy (on the adiabatic potential energy surface) in good agreement with the high-level ab initio results. The resulting fourfold way barrier (16.7 kcal/mol) agrees very well with the barriers predicted by the high-level methods, especially with the most reliable one, which is the G3SX//M06-2X value, and is somewhat higher than the B3LYP value but lower than the M06-2X value.
Although this perspective has been quantitatively illustrated only with gas-phase diabatic states, most of the considerations are equally valid for condensed-phase reactions, for which a number of valence-bond electronic structure approaches are now available.61,63,65,67,68,72,101,141 In previous work on aqueous SN2 reactions, the MOVB method based on VDC diabatic states led to solute-solvent interaction energies that vary weakly with the reaction coordinate, in contrast to previous studies of other SN2 reactions using the EVB method.94 Further work on the analogy between SN2234 and other types of reactions (such as hydride, proton, or hydrogen atom transfer reactions in enzymes106 or electron-transfer reactions90,91,93,235–241) and on the reorganization energies defined in terms of CDC diabatic states would be useful.
In light of the large quantitative differences between diabatic states obtained by employing different defining equations, algorithms, or representations, we recommend that justification needs to be made for employing specific definitions in specific contexts in cases where the quantitative values are important. For qualitative discussion purposes, one can have more leeway in the definition employed. In applications to enzymatic reactions, it is useful, if possible, to first investigate the corresponding model reaction in the gas-phase to justify the definition of diabatic states and to validate the entire potential energy surface and structures of the adiabatic ground state. Then, a valence-bond-based potential can be used to model the reaction in aqueous solution to validate or even to calibrate the interactions between solute and solvent. Finally, after validation of the potential energy surface in the gas phase and solute-solvent interactions in water, the method can be applied to the enzyme reaction to understand catalysis.
Supplementary Material
EVB parameters, Cartesian coordinates of all the points calculated on the ground-state adiabatic reaction paths, and MOVB overlaps. This material is available free of charge via the Internet at http://pubs.acs.org.
Acknowledgments
The authors are grateful to R. A. Marcus, Yousung Jung, Oksana Tishchenko, and Jonathan Young for stimulating discussions and to Avital Shurki for correspondence about EVB parameters. This work was supported in part by the National Science Foundation under grant No. CHE07-04974 (DGT) and by the National Institutes of Health (JG).
Appendix
Computational Details
In the MC-QDPT calculations, the intruder-state avoidance (ISA)242 method has been used to avoid artifacts due to intruder states in the MC-QDPT wave function. The level shift parameter242 b of the ISA method was set to 0.02 (1 Eh ≡ 1 hartree).
Initially, the MC-QDPT calculations used the 6-31+G(d)184–187 basis set. However, the resulting MC-QDPT reaction profiles had artifacts in either the reactant or the product region, depending on the weights of the electronic states in the CASSCF step. This problem is caused by the diffuse functions, especially those on the carbon and oxygen atoms, because the character of the excited state in the reactant and product regions is that of a resonance embedded in the continuum, as has been explained elsewhere.144 This problem was eliminated by omitting diffuse functions on all atoms except on the two chlorine atoms of DCE. Furthermore, the exponents of the diffuse functions of chlorine were increased from the standard value of 0.483 to 0.09 to obtain a good reaction energy and barrier. The resulting basis set will be denoted as 6-31&G(d).
Several SA-CASSCF(4,3) calculations were performed in which the weight of the two electronic states in the state average was varied in the range 50:50 to 90:10. Other combinations of weights in which the excited state has a higher weight than the ground state yielded an unbalanced description of the adiabatic states and were discarded. The best state weightings were ascertained by comparison to the high-level calculations and were found to be those with 75:25 weights, and these are used in the rest of this article.
The first step in the application of the fourfold way to the acetate + DCE system is to establish a standard orientation so that the Cartesian coordinates of the atoms are uniquely and continuously defined at all nuclear configurations. In the standard orientation, the molecule is situated as follows. The attacking oxygen of CH3CO2−is placed at the origin, the carbon atom of ClCH2CH2Cl that is attacked by that oxygen is on the positive Z axis, and the chlorine atom that is bound to that carbon atom in reactants, acetate + DCE, is on the first quadrant of the XZ axis. The remaining atoms do not have a particular orientation since they do not participate directly in the nucleophilic displacement reaction. Two reference MOs were introduced as follows. The first one is the oxygen lone pair of the attacking oxygen atom of acetate, and it is obtained at the reactant ion-molecule configuration by the threefold way. The second reference MO is obtained by the threefold way at the product ion-molecule configuration as the p orbital of the chloride ion which derives from the cleaved C–Cl bond. In order to keep the character of the DMO centered on the chlorine atom fixed it becomes necessary to define a specific molecular orientation (denoted by primed coordinates), and for a general molecular geometry the reference MO must be transformed to the standard orientation (unprimed). The reference MO centered on the oxygen does not need a specific orientation since the oxygen atom is always located at the coordinate origin. The specific orientation is defined in the same way as the standard orientation, except that the chlorine atom is placed along the positive Z′ axis of the specific orientation. The reference MO centered on the chlorine atom is transformed from the specific to the standard orientation at each point along the reaction coordinate by means of a rotation matrix that depends on the angle between the C–Cl bond and the Z axis.
It is necessary to have a one-to-one correspondence of the fourfold-way DMOs at consecutive geometries. For this, two reference geometries have to be chosen in regions where diabatic states are equal to adiabatic states to a good approximation. The fourfold way is then carried out at each of the reference geometries. The procedure is advanced by taking several consecutive geometries separated by small steps along the minimum energy path that connects reactants and products. This procedure ensures that the DMOs of products are ordered in the same way along the whole reaction path so that they can produce consistent groups of DCSFs.
The matrix elements of the MOVB Hamiltonian are evaluated using methods for nonorthogonal determinants, and the computational details can be found in refs 60 and 141. In the VDC method, the MOs are obtained using a reorthogonalization technique,154 although an iterative sequence of Jacobi rotations approach is also possible.155
The EVB parameters used in this work are presented in Table S1 of Supporting Information. The corrections with respect to the way that the parameters are presented in Ref. 21 are (1) the bond angle force constants have been transformed from (kcal/mol).rad−2 to (kcal/mol).deg−2; (2) the C…O nonbonded van der Waals term is only included in the reactant configurations, and the C…Cl term is only included in the product configuration, and (3) for these terms, the exponents have been changed to α = 3.90 for the reactant configuration, and to α = 4.00 for the product configuration to match the values used in the published21 work. These corrections enable us to generate the EVB potential corresponding to the treatment of Ref. 21.
Software
The fourfold way calculations were carried out with HONDOPLUS, version 5.1;243 the BLW calculations were performed using the Xiamen VB (XMVB) program;244 the Minnesota Gaussian Functional Module (MN-GFM),245,246 version 3.0 was used for the M06-2X calculations; the G3SX, G3SX(MP3), and BCM-CCSD calculations were carried out with MLGAUSS, version 2.0;246,247 and the SM8 solvation free energy calculations were performed with the Minnesota Gaussian Solvation Module (MN-GSM).248
References
- 1.Gao J, Ma S, Major DT, Nam K, Pu J, Truhlar DG. Chem Rev. 2006;106:3188. doi: 10.1021/cr050293k. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Pu J, Gao J, Truhlar DG. Chem Rev. 2006;106:3140. doi: 10.1021/cr050308e. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Hiberty PC, Shaik S. J Comput Chem. 2007;28:137. doi: 10.1002/jcc.20478. [DOI] [PubMed] [Google Scholar]
- 4.Song L, Gao J. J Phys Chem A. 2008 doi: 10.1021/jp803050e. ASAP. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Pries F, Kingma J, Pentenga M, van Pouderoyen G, Jeronimus-Stratingh CM, Bruins AP, Janssen DB. Biochemistry. 1994;33:1242. doi: 10.1021/bi00171a026. [DOI] [PubMed] [Google Scholar]
- 6.Pries F, Kingma J, Krooshof GH, Jeronimus-Stratingh CM, Bruins AP, Janssen DB. J Biol Chem. 1995;270:10405. doi: 10.1074/jbc.270.18.10405. [DOI] [PubMed] [Google Scholar]
- 7.Schanstra JP, Janssen DB. Biochemistry. 1996;35:5624. doi: 10.1021/bi952904g. [DOI] [PubMed] [Google Scholar]
- 8.Schanstra JP, Kingma J, Janssen DB. J Biol Chem. 1996;271:14747. doi: 10.1074/jbc.271.25.14747. [DOI] [PubMed] [Google Scholar]
- 9.Krooshof GH, Ridder IS, Tepper AWJW, Bos GJ, Rozeboom HJ, Kalk KH, Dijkstra BW, Janssen DB. Biochemistry. 1998;37:15013. doi: 10.1021/bi9815187. [DOI] [PubMed] [Google Scholar]
- 10.Schindler JF, Naranjo PA, Honaberger DA, Chang CH, Brainard JR, Vanderberg LA, Unkefer CJ. Biochemistry. 1999;38:5772. doi: 10.1021/bi982853y. [DOI] [PubMed] [Google Scholar]
- 11.Lewandowicz A, Rudzinski J, Tronstad L, Widersten M, Ryberg P, Matsson O, Paneth P. J Am Chem Soc. 2001;123:4550. doi: 10.1021/ja003503d. [DOI] [PubMed] [Google Scholar]
- 12.Damborsky J, Kuty M, Nemec M, Koca J. J Chem Inf Comput Sci. 1997;37:562. [Google Scholar]
- 13.Maulitz AH, Lightstone FC, Zheng YJ, Bruice TC. Proc Natl Acad Sci USA. 1997;94:6591. doi: 10.1073/pnas.94.13.6591. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Lightstone FC, Zheng YJ, Maulitz AH, Bruice TC. Proc Natl Acad Sci USA. 1997;94:8417. doi: 10.1073/pnas.94.16.8417. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Damborsky J, Bohac M, Prokop M, Kuty M, Koca J. Prot Eng. 1998;11:901. doi: 10.1093/protein/11.10.901. [DOI] [PubMed] [Google Scholar]
- 16.Kuty M, Damborsky J, Prokop M, Koca J. J Chem Inf Comput Sci. 1998;38:736. [Google Scholar]
- 17.Lightstone FC, Zheng Y, Bruice TC. Bioorg Chem. 1998;26:169. [Google Scholar]
- 18.Lightstone FC, Zheng Y, Bruice TC. J Am Chem Soc. 1998;120:5611. [Google Scholar]
- 19.Damborsky J, Koca J. Prot Eng. 1999;12:989. doi: 10.1093/protein/12.11.989. [DOI] [PubMed] [Google Scholar]
- 20.Lau EY, Kahn K, Bash PA, Bruice TC. Proc Natl Acad Sci USA. 2000;97:9937. doi: 10.1073/pnas.97.18.9937. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Shurki A, Strajbl M, Villà J, Warshel A. J Am Chem Soc. 2002;124:4097. doi: 10.1021/ja012230z. [DOI] [PubMed] [Google Scholar]
- 22.Kahn K, Bruice TC. J Phys Chem B. 2003;107:6876. [Google Scholar]
- 23.Hur S, Kahn K, Bruice TC. Proc Natl Acad Sci USA. 2003;100:2215. doi: 10.1073/pnas.242721799. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Devi-Kesavan LS, Gao J. J Am Chem Soc. 2003;125:1532. doi: 10.1021/ja026955u. [DOI] [PubMed] [Google Scholar]
- 25.Soriano A, Silla E, Tuñón I. J Phys Chem B. 2003;107:6234. [Google Scholar]
- 26.Kmunicek J, Bohac M, Luengo S, Gago F, Wade RC, Damborsky J. J Comput-Aided Mol Des. 2003;17:299. doi: 10.1023/a:1026159215220. [DOI] [PubMed] [Google Scholar]
- 27.Nam KN, Prat-Resina X, García-Viloca M, Devi-Kesavan LS, Gao J. J Am Chem Soc. 2004;126:1369. doi: 10.1021/ja039093l. [DOI] [PubMed] [Google Scholar]
- 28.Olsson MHM, Warshel A. J Am Chem Soc. 2004;126:15167. doi: 10.1021/ja047151c. [DOI] [PubMed] [Google Scholar]
- 29.Soriano A, Silla E, Tuñón I, Ruiz-López MF. J Am Chem Soc. 2005;127:1946. doi: 10.1021/ja046553h. [DOI] [PubMed] [Google Scholar]
- 30.Rosta E, Klähn M, Warshel A. J Phys Chem B. 2006;110:2934. doi: 10.1021/jp057109j. [DOI] [PubMed] [Google Scholar]
- 31.Silberstein M, Damborsky J, Vajda S. Biochemistry. 2007;46:9239. doi: 10.1021/bi700336y. [DOI] [PubMed] [Google Scholar]
- 32.Otyepka M, Banas P, Magistrato A, Carloni P, Damborsky J. Proteins: Struct Funct Bioinform. 2008;70:707. doi: 10.1002/prot.21523. [DOI] [PubMed] [Google Scholar]
- 33.Jorgensen WL, Buckner JK. J Phys Chem. 1986;90:4651. [Google Scholar]
- 34.Shi Z, Boyd RJ. J Am Chem Soc. 1989;111:1575. [Google Scholar]
- 35.Tucker SC, Truhlar DG. J Phys Chem. 1989;93:8138. [Google Scholar]
- 36.Deng L, Branchadell V, Ziegler T. J Am Chem Soc. 1994;116:10645. [Google Scholar]
- 37.Hu WP, Truhlar DG. J Am Chem Soc. 1995;117:10726. [Google Scholar]
- 38.Glukhovtsev MN, Pross A, Radom L. J Am Chem Soc. 1995;117:2024. [Google Scholar]
- 39.Hu WP, Truhlar DG. J Am Chem Soc. 1996;118:860. [Google Scholar]
- 40.Glukhovtsev MN, Pross A, Schlegel HB, Bach RD, Radom L. J Am Chem Soc. 1996;118:11258. [Google Scholar]
- 41.Strajbl M, Florián J, Warshel A. J Am Chem Soc. 2000;122:5354. [Google Scholar]
- 42.Schmatz S, Botschwina P, Stoll H. Int J Mass Spectrom. 2000;201:277. [Google Scholar]
- 43.Gonzalez JM, Cox RS, III, Brown ST, Allen WD, Schaefer HF., III J Phys Chem A. 2001;105:11327. [Google Scholar]
- 44.Gonzalez JM, Pak C, Sidney Cox R, Allen WD, Schaefer HF, III, Császár AG, Tarczay G. Chem Eur J. 2003;9:2173. doi: 10.1002/chem.200204408. [DOI] [PubMed] [Google Scholar]
- 45.Uggerud E. Chem Eur J. 2006;12:1127. doi: 10.1002/chem.200500639. [DOI] [PubMed] [Google Scholar]
- 46.Laerdahl JK, Civcir PU, Bache-Andreasson L, Uggerud E. Org Biomol Chem. 2006;4:135. doi: 10.1039/b513315g. [DOI] [PubMed] [Google Scholar]
- 47.Ocrhran RA, Uggerud E. Int J Mass Spectrom. 2007;265:169. [Google Scholar]
- 48.Zheng J, Zhao Y, Truhlar DG. J Chem Theory Comput. 2007;3:569. doi: 10.1021/ct600281g. [DOI] [PubMed] [Google Scholar]
- 49.Pliego JR, Jr, Piló-Veloso D. Phys Chem Chem Phys. 2008;10:1118. doi: 10.1039/b716159j. [DOI] [PubMed] [Google Scholar]
- 50.Bickelhaupt FM. J Comp Chem. 1999;20:114. [Google Scholar]
- 51.Zhao Y, Gonzalez-Garcia N, Truhlar DG. J Phys Chem A. 2005;109:2012. doi: 10.1021/jp045141s. [DOI] [PubMed] [Google Scholar]
- 52.Bento AP, Sola M, Bickelhaupt FM. J Comp Chem. 2005;26:1497. doi: 10.1002/jcc.20261. [DOI] [PubMed] [Google Scholar]
- 53.Van Bochove MA, Bickelhaupt FM. Eur J Org Chem. 2008:649. [Google Scholar]
- 54.Shaik S. J Am Chem Soc. 1983;105:4359. [Google Scholar]
- 55.Shaik S, Reddy AC. J Chem Soc Faraday Trans. 1994;90:1631. [Google Scholar]
- 56.Shaik S, Shurki A. Angew Chem Int Ed. 1999;38:586. doi: 10.1002/(SICI)1521-3773(19990301)38:5<586::AID-ANIE586>3.0.CO;2-T. [DOI] [PubMed] [Google Scholar]
- 57.Hiberty PC, Shaik S. Theor Chem Acc. 2002;108:255. [Google Scholar]
- 58.Amovilli C. Valence Bond Theory. In: Cooper DL, editor. Theor Comp Chem Series. Vol. 10. Elsevier; Amsterdam: 2002. pp. 415–445. [Google Scholar]
- 59.Truhlar DG. J Comp Chem. 2007;28:73. doi: 10.1002/jcc.20529. [DOI] [PubMed] [Google Scholar]
- 60.Mo Y, Gao J. J Comp Chem. 2000;21:1458. [Google Scholar]
- 61.Gao J, García-Viloca M, Poulsen TD, Mo Y. Adv Phys Org Chem. 2003;38:161. [Google Scholar]
- 62.Blavins JJ, Cooper DL, Karadakov PB. J Phys Chem A. 2004;108:914. doi: 10.1021/jp047431e. [DOI] [PubMed] [Google Scholar]
- 63.Song L, Wu W, Zhang Q, Shaik S. J Phys Chem. 2004;108:6017. [Google Scholar]
- 64.Song L, Wu W, Hiberty PC, Shaik S. Chem Eur J. 2006;12:7458. doi: 10.1002/chem.200600372. [DOI] [PubMed] [Google Scholar]
- 65.Hong G, Rosta E, Warshel A. J Phys Chem B. 2006;110:19570. doi: 10.1021/jp0625199. [DOI] [PubMed] [Google Scholar]
- 66.Su P, Wu W, Kelly CP, Cramer CJ, Truhlar DG. J Phys Chem A. doi: 10.1021/jp711655k. [DOI] [PubMed] [Google Scholar]
- 67.Sharir-Ivry A, Crown HA, Wu W, Shurki A. J Phys Chem A. 2008;112:2489. doi: 10.1021/jp710395b. [DOI] [PubMed] [Google Scholar]
- 68.Sharir-Ivry A, Shurki A. J Phys Chem A. published online at DOI:10.1021/jp801722e. [Google Scholar]
- 69.Gao J. J Am Chem Soc. 1991;113:7796. [Google Scholar]
- 70.Gao J, Xia X. J Am Chem Soc. 1993;115:9667. [Google Scholar]
- 71.Amovilli C, Mennucci B, Floris FM. J Phys Chem B. 1998;102:3023. [Google Scholar]
- 72.Su P, Ying F, Wu W, Hiberty PC, Shaik S. ChemPhysChem. 2007;8:2603. doi: 10.1002/cphc.200700626. [DOI] [PubMed] [Google Scholar]
- 73.Grochowski P, Lesyng B, Bala P, McCammon JA. Int J Quantum Chem. 1996;60:1143. [Google Scholar]
- 74.Trylska J, Grochowski P, Geller M. Int J Quantum Chem. 2001;82:86. [Google Scholar]
- 75.Kolmodin K, Hansson T, Danielsson J, Åqvist J. Transition State Modeling for Catalysis. In: Truhlar DG, Morokuma K, editors. ACS Symposium Series. Vol. 721. American Chemical Society; Washington: 1999. p. 370. [Google Scholar]
- 76.Rothman MJ, Lohr LL, Jr, Ewig CS, Van Wazer JR. In: Potential Energy Surfaces and Dynamics Calculations. Truhlar DG, editor. Plenum; New York: 1979. p. 653. [Google Scholar]
- 77.Chandrasekhar J, Smith SF, Jorgensen WL. J Am Chem Soc. 1984;106:3049. [Google Scholar]
- 78.Kottalam J, Case DA. J Am Chem Soc. 1988;110:7690. [Google Scholar]
- 79.Steckler R, Truhlar DG. J Chem Phys. 1990;93:6570. [Google Scholar]
- 80.Heidrich D. In: The Reaction Path in Chemistry: Current Approaches and Perspectives. Heidrich D, editor. Kluwer; Dordrecht: 1995. p. 1. [Google Scholar]
- 81.Shavitt I. Theoretical Chemistry Laboratory Technical Report No. WIS-AEC-23. University of Wisconsin; Madison: 1959. [Google Scholar]
- 82.Marcus RA. J Chem Phys. 1966;45:4493. [Google Scholar]
- 83.Truhlar DG, Kuppermann A. J Am Chem Soc. 1971;93:1840. [Google Scholar]
- 84.Fukui K. In: The World of Quantum Chemistry. Daudel R, Pullman B, editors. Reidel; Dordrecht: 1974. p. 113. [Google Scholar]
- 85.Natanson GA, Garrett BC, Truong TN, Joseph T, Truhlar DG. J Chem Phys. 1991;94:7875. [Google Scholar]
- 86.Alhambra C, Gao J, Corchado JC, Villà J, Truhlar DG. J Am Chem Soc. 1999;121:2253. [Google Scholar]
- 87.Truhlar DG, Gao J, Alhambra C, Garcia-Viloca M, Corchado JC, Sánchez ML, Villà J. Acc Chem Res. 2002;35:341. doi: 10.1021/ar0100226. [DOI] [PubMed] [Google Scholar]
- 88.Truhlar DG, Gao J, Garcia-Viloca M, Alhambra C, Corchado JC, Sánchez ML, Poulsen TD. Int J Quantum Chem. 2004;100:1136. [Google Scholar]
- 89.Bolhuis PG, Dellago C, Chandler D. Faraday Discuss. 1998;110:421. [Google Scholar]
- 90.Marcus RA. Discuss Faraday Soc. 1960;29:21. [Google Scholar]
- 91.Marcus RA. Rev Mod Phys. 1993;65:599. [Google Scholar]
- 92.Warshel A, Weiss RM. J Am Chem Soc. 1980;102:6218. [Google Scholar]
- 93.Warshel A. J Phys Chem. 1982;86:2218. [Google Scholar]
- 94.Hwang JK, King G, Creighton S, Warshel A. J Am Chem Soc. 1988;110:5297. [Google Scholar]
- 95.Warshel A, Chu ZT. J Chem Phys. 1990;93:4003. [Google Scholar]
- 96.Yadav A, Jackson RM, Holbrook JJ, Warshel A. J Am Chem Soc. 1991;113:4800. [Google Scholar]
- 97.Warshel A. Computer Modeling of Chemical Reactions in Enzymes and Solutions. Wiley; New York: 1991. [Google Scholar]
- 98.Aqvist J, Warshel A. Chem Rev. 1993;93:2523. [Google Scholar]
- 99.Kong YS, Warshel A. J Am Chem Soc. 1995;117:6234. [Google Scholar]
- 100.Muller RP, Warshel A. J Phys Chem. 1995;99:17516. [Google Scholar]
- 101.Wesolowski T, Muller RP, Warshel A. J Phys Chem. 1996;100:15444. [Google Scholar]
- 102.Kuznetsov A. In: Electron and Ion Transfer in Condensed Media. Kornyshev AA, Tosi MP, Ulstrup J, editors. World Scientific; Singapore: 1997. p. 165. [Google Scholar]
- 103.Warshel A, Bentzien J. Transition State Modeling for Catalysis. In: Truhlar DG, Morokuma K, editors. ACS Symposium Series. Vol. 721. American Chemical Society; Washington: 1999. p. 489. [Google Scholar]
- 104.Billeter SR, Webb SP, Agarwal PK, Iordanov T, Hammes-Schiffer S. J Am Chem Soc. 2001;123:11262. doi: 10.1021/ja011384b. [DOI] [PubMed] [Google Scholar]
- 105.Schenter GK, Garrett BC, Truhlar DG. J Phys Chem B. 2001;105:9672. [Google Scholar]
- 106.Marcus RA. J Chem Phys. 2006;125:194504. doi: 10.1063/1.2372496. [DOI] [PubMed] [Google Scholar]
- 107.Marcus RA. J Phys Chem B. 2007;111:6643. doi: 10.1021/jp071589s. [DOI] [PubMed] [Google Scholar]
- 108.Lee S, Hynes JT. J Chem Phys. 1988;88:6853. [Google Scholar]
- 109.Kim HJ, Hynes JT. J Am Chem Soc. 1992;114:10528. [Google Scholar]
- 110.Schenter GK, McRae RP, Garrett BC. J Chem Phys. 1992;97:9116. [Google Scholar]
- 111.Truhlar DG, Schenter GK, Garrett BC. J Chem Phys. 1993;98:5756. [Google Scholar]
- 112.Basilevsky MV, Chudinov GE, Napolov DV. J Phys Chem. 1993;97:3270. [Google Scholar]
- 113.Garrett BC, Schenter GK. Structure and Reactivity in Aqueous Solution. In: Cramer CJ, Truhlar DG, editors. ACS Symposium Series. Vol. 568. American Chemical Society; Washington: 1994. p. 122. [Google Scholar]
- 114.Mathis JR, Hynes JT. J Phys Chem. 1994;98:5445. [Google Scholar]
- 115.Ruiz-López MF, Rinaldi D, Bertrán J. J Chem Phys. 1995;103:9249. [Google Scholar]
- 116.Chuang YY, Truhlar DG. J Am Chem Soc. 1999;121:10157. [Google Scholar]
- 117.Schatz GC, Ross J. J Chem Phys. 1977;66:2943. [Google Scholar]
- 118.Engler C, Rabe E, Schultz H, Lorenz W. Theor Chim Acta. 1989;75:67. [Google Scholar]
- 119.Halvick P, Zhao M, Truhlar DG, Schwenke DW, Kouri DJ. J Chem Soc Faraday Trans. 1990;86:1705. [Google Scholar]
- 120.Caratzoulas S, Jackson B. J Chem Phys. 1996;105:8639. [Google Scholar]
- 121.Shin C, Shin S. J Chem Phys. 2000;113:6528. [Google Scholar]
- 122.Marcus RA. J Chem Phys. 1956;24:979. [Google Scholar]
- 123.London F. Z Elektrochem. 1929;35:552. [Google Scholar]
- 124.Porter RN, Karplus M. J Chem Phys. 1964;40:1105. [Google Scholar]
- 125.Shaik SS. J Am Chem Soc. 1981;103:3692. [Google Scholar]
- 126.Shaik SS, Hiberty PC. A Chemist’s Guide to Valence Bond Theory. John Wiley & Sons, Inc.; Hoboken, New Jersey: 2007. [Google Scholar]
- 127.Marcus RA. J Chem Phys. 1965;43:679. [Google Scholar]
- 128.Kreevoy MM, Lee ISH. J Am Chem Soc. 1984;106:2550. [Google Scholar]
- 129.Lee ISH, Ji YR, Jeoung EH. J Phys Chem A. 2006;110:3875. doi: 10.1021/jp056745e. [DOI] [PubMed] [Google Scholar]
- 130.Chang YT, Miller WH. J Phys Chem. 1990;94:5884. [Google Scholar]
- 131.Schlegel HB, Sonnenberg JL. J Chem Theory Comput. 2006;2:905. doi: 10.1021/ct600084p. [DOI] [PubMed] [Google Scholar]
- 132.Bernardi F, Olivucci M, Robb MA. J Am Chem Soc. 1992;114:1606. doi: 10.1021/ja00226a011. [DOI] [PubMed] [Google Scholar]
- 133.Tishchenko O, Truhlar DG. J Phys Chem A. 2006;110:13530. doi: 10.1021/jp0640833. [DOI] [PubMed] [Google Scholar]
- 134.Higashi M, Truhlar DG. J Chem Theory Comput. 2008;4:790. doi: 10.1021/ct800004y. [DOI] [PubMed] [Google Scholar]
- 135.Minichino C, Voth GA. J Phys Chem B. 1997;101:4544. [Google Scholar]
- 136.Garrett BC, Truhlar DG. Theory of Scattering: Papers in Honor of Henry Eyring. In: Henderson D, editor. Theor Chem Advances Perspectives Series. 6A. Academic; New York: 1981. p. 215. [Google Scholar]
- 137.Delos JB. Rev Mod Phys. 1981;53:287. [Google Scholar]
- 138.Mead CA, Truhlar DG. J Chem Phys. 1982;77:6090. [Google Scholar]
- 139.Pacher T, Cederbaum LS, Köppel H. J Chem Phys. 1988;89:7367. [Google Scholar]
- 140.Sidis V. Adv Chem Phys. 1992;82:73. [Google Scholar]
- 141.Mo Y, Gao J. J Phys Chem A. 2000;104:3012. [Google Scholar]
- 142.Numrich RW, Truhlar DG. J Phys Chem. 1975;79:2745. [Google Scholar]
- 143.Kubach C, Sidis V. Phys Rev A. 1976;14:152. [Google Scholar]
- 144.Kabbaj OK, Lepetit MB, Malrieu JP, Sini G, Hiberty PC. J Am Chem Soc. 1991;113:5619. [Google Scholar]
- 145.Bianco R, Hynes JT. J Chem Phys. 1995;102:7864. [Google Scholar]
- 146.Dobrovsky I, Levine RD. Chem Phys Lett. 1998;286:155. [Google Scholar]
- 147.Shurki A, Crown HA. J Phys Chem B. 2005;109:23638. doi: 10.1021/jp054913x. [DOI] [PubMed] [Google Scholar]
- 148.Shurki A. Theor Chem Acc. 2006;116:253. [Google Scholar]
- 149.Mo Y, Song L, Lin Y. J Phys Chem A. 2007;111:8291. doi: 10.1021/jp0724065. [DOI] [PubMed] [Google Scholar]
- 150.Goddard WA, III, Dunning TH, III, Hunt WJ, Hay PJ. Acc Chem Res. 1973;6:368. [Google Scholar]
- 151.van Lenthe JH, Balint-Kurti GG. J Chem Phys. 1983;78:5699. [Google Scholar]
- 152.Hiberty PC, Flament JP, Noizet E. Chem Phys Lett. 1992;189:259. [Google Scholar]
- 153.Raimondi M, Gianinetti E. J Phys Chem. 1988;92:899. [Google Scholar]
- 154.Gianinetti E, Raimondi M, Tornagui E. Int J Quantum Chem. 1996;60:157. [Google Scholar]
- 155.Mo Y, Peyerimhoff SD. J Chem Phys. 1998;109:1687. [Google Scholar]
- 156.Gianinetti E, Vandoni I, Famulari A, Raimondi M. Adv Quantum Chem. 1998;31:251. [Google Scholar]
- 157.Mo Y, Zhang Y, Gao J. J Am Chem Soc. 1999;121:5737. [Google Scholar]
- 158.Mo Y, Gao J, Peyerimhoff SD. J Chem Phys. 2000;112:5530. [Google Scholar]
- 159.Khaliullin RZ, Head-Gordon M, Bell AT. J Chem Phys. 2006;124:204105. doi: 10.1063/1.2191500. [DOI] [PubMed] [Google Scholar]
- 160.Khaliullin RZ, Cobar EA, Lochan RC, Bell AT, Head-Gordon M. J Phys Chem A. 2007;111:8753. doi: 10.1021/jp073685z. [DOI] [PubMed] [Google Scholar]
- 161.Nakamura H, Truhlar DG. J Chem Phys. 2001;115:10353. [Google Scholar]
- 162.Nakamura H, Truhlar DG. J Chem Phys. 2002;117:5576. [Google Scholar]
- 163.Nakamura H, Truhlar DG. J Chem Phys. 2003;118:6816. [Google Scholar]
- 164.Garcia VM, Reguero M, Caballol R, Malrieu JP. Chem Phys Lett. 1997;281:161. [Google Scholar]
- 165.Ruedenberg K, Atchity GA. J Chem Phys. 1993;99:3799. [Google Scholar]
- 166.Atchity GA, Ruedenberg K. Theor Chem Acc. 1997;97:47. [Google Scholar]
- 167.National Institute for Occupational Safety and Health 1978, Current Intelligence Bulletin # 25, Publication No. 79–146, pp 91–100.
- 168.Fetzner S, Lingens F. Microbiol Rev. 1994;58:641. doi: 10.1128/mr.58.4.641-685.1994. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 169.Janssen DB, van der Ploeg JR, Pries F. Environ Health Perspect. 1995;103:29. doi: 10.1289/ehp.95103s429. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 170.Leisinger T. Curr Opin Biotechnol. 1996;7:295. doi: 10.1016/s0958-1669(96)80033-4. [DOI] [PubMed] [Google Scholar]
- 171.Keuning S, Janssen DB, Witholt B. J Bacteriol. 1985;163:635. doi: 10.1128/jb.163.2.635-639.1985. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 172.Wischnak C, Muller R. Biotechnology. 2. 11b. 2000. p. 241.p. 271. [Google Scholar]
- 173.Ridder IS, Dijkstra BW. Cattech. 2000;3:126. [Google Scholar]
- 174.Shaik SS, Pross A. J Am Chem Soc. 1982;104:2708. [Google Scholar]
- 175.Shaik S, Schlegel HB, Wolfe S. Theoretical Aspects of Physical Organic Chemistry: The SN2 Mechanism. Wiley; New York: 1992. [Google Scholar]
- 176.Cyr DM, Bailey CG, Serxner D, Scarton MG, Johnson MA. J Chem Phys. 1994;101:10507. [Google Scholar]
- 177.Dessent CEH, Johnson MA. J Am Chem Soc. 1997;119:5067. [Google Scholar]
- 178.Ruedenberg K, Sundberg R. In: Quantum Science. Calais J-L, Goscinski O, Lindenberg J, Öhrn Y, editors. Plenum; New York: 1976. p. 505. [Google Scholar]
- 179.Roos BO. Adv Chem Phys. 1987;68:399. [Google Scholar]
- 180.Nakano H. J Chem Phys. 1993;99:7983. [Google Scholar]
- 181.Nakano H. Chem Phys Lett. 1993;207:372. [Google Scholar]
- 182.Nakano H, Nakajima T, Tsuneda T, Hirao K. J Mol Struct. 2001;573:91. [Google Scholar]
- 183.Finley J, Malmqvist P-Å, Roos BO, Serrano-Andrés L. Chem Phys Lett. 1998;288:299. [Google Scholar]
- 184.Hariharan PC, Pople JA. Theor Chim Acta. 1973;28:213. [Google Scholar]
- 185.Francl MM, Petro JJ, Hehre WJ, Binkley JS, Gordon MS, DeFrees DJ, Pople JA. J Chem Phys. 1982;77:3564. [Google Scholar]
- 186.Clark T, Chandrasekar J, Spitznagel GW, Schleyer PvR. J Comp Chem. 1983;4:294. [Google Scholar]
- 187.Gill PMW, Johnson BG, Pople JA, Frisch MJ. Chem Phys Lett. 1992;197:499. [Google Scholar]
- 188.Zhao Y, Truhlar DG. Theor Chem Acc. 2008;120:215. [Google Scholar]
- 189.Lynch BJ, Zhao Y, Truhlar DG. J Phys Chem A. 2003;107:1384. [Google Scholar]
- 190.Curtiss LA, Raghavachari K, Redfern PC, Rassolov V, Pople JA. J Chem Phys. 1998;109:7764. [Google Scholar]
- 191.Curtiss LA, Raghavachari K, Redfern PC, Pople JA. J Chem Phys. 2000;112:1125. [Google Scholar]
- 192.Curtiss LA, Redfern PC, Raghavachari K, Pople JA. J Chem Phys. 2001;114:108. [Google Scholar]
- 193.Lynch BJ, Zhao Y, Truhlar DG. J Phys Chem A. 2005;109:1643. doi: 10.1021/jp045847m. [DOI] [PubMed] [Google Scholar]
- 194.Fast PL, Corchado JC, Sánchez ML, Truhlar DG. J Phys Chem A. 1999;103:5129. [Google Scholar]
- 195.Becke AD. Phys Rev A. 1988;38:3098. doi: 10.1103/physreva.38.3098. [DOI] [PubMed] [Google Scholar]
- 196.Lee C, Yang W, Parr RG. Phys Rev B. 1988;37:785. doi: 10.1103/physrevb.37.785. [DOI] [PubMed] [Google Scholar]
- 197.Becke AD. J Chem Phys. 1993;98:5648. [Google Scholar]
- 198.Stephens PJ, Devlin FJ, Chabalowski CF, Frisch MJ. J Phys Chem. 1994;98:11623. [Google Scholar]
- 199.Nangia S, Truhlar DG. J Chem Phys. 2006;124:124309. doi: 10.1063/1.2168447. [DOI] [PubMed] [Google Scholar]
- 200.Li ZH, Valero R, Truhlar DG. Theor Chem Acc. 2007;118:9. [Google Scholar]
- 201.Valero R, Truhlar DG. J Chem Phys. 2006;125:194305. doi: 10.1063/1.2363991. [DOI] [PubMed] [Google Scholar]
- 202.Valero R, Truhlar DG. J Phys Chem A. 2007;111:8536. doi: 10.1021/jp072590u. [DOI] [PubMed] [Google Scholar]
- 203.Pauling L. The Nature of the Chemical Bond. Cornell University Press; Ithaca: 1939. [Google Scholar]
- 204.Wheland GW. The Theory of Resonance and Its Applications to Organic Chemistry. Wiley; New York: 1955. [Google Scholar]
- 205.Mo Y, Gao J. J Phys Chem A. 2001;105:6530. [Google Scholar]
- 206.Mo Y, Subramanian G, Gao J, Ferguson DM. J Am Chem Soc. 2002;124:4832. doi: 10.1021/ja0174433. [DOI] [PubMed] [Google Scholar]
- 207.Mo Y, Wu W, Song L, Lin M, Zhang Q, Gao J. Angew Chem, Int Ed. 2004;43:1986. doi: 10.1002/anie.200352931. [DOI] [PubMed] [Google Scholar]
- 208.Mo Y, Gao J. Acc Chem Res. 2007;40:113. doi: 10.1021/ar068073w. [DOI] [PubMed] [Google Scholar]
- 209.Hunt WJ, Hay PJ, Goddard WA., III J Chem Phys. 1972;57:738. [Google Scholar]
- 210.Nakano H, Sorakubo K, Nakayama K, Hirao K. Valence Bond Theory. In: Cooper DL, editor. Theor Comp Chem Series. Vol. 10. Elsevier; Amsterdam: 2002. p. 55. [Google Scholar]
- 211.Garrett J, Cooper DL, Raimondi M. Valence Bond Theory. In: Cooper DL, editor. Theor Comp Chem Series. Vol. 10. Elsevier; Amsterdam: 2002. p. 55. [Google Scholar]
- 212.Li J, McWeeny R. Int J Quantum Chem. 2002;89:208. [Google Scholar]
- 213.Hiberty PC, Shaik SS. Theor Chem Acc. 2002;108:235. [Google Scholar]
- 214.Hunt WJ, Hay PJ, Goddard WA. J Chem Phys. 1972;57:738. [Google Scholar]
- 215.Siegbahn PEM, Almlöf J, Heiberg A, Roos BO. J Chem Phys. 1981;74:2384. [Google Scholar]
- 216.Hiberty PC. Theochem. 1998;451:237. [Google Scholar]
- 217.Tishchenko O, Zheng J, Truhlar DG. J Chem Theory Comput. 2008;4:1208. doi: 10.1021/ct800077r. [DOI] [PubMed] [Google Scholar]
- 218.Marcus RA. J Chem Phys. 1984;81:4494. [Google Scholar]
- 219.May V, Kühn O. Charge and Energy Transfer Dynamics in Molecular Systems. Wiley-VCH; Berlin: 2000. p. 284. [Google Scholar]
- 220.Mittleman MH. Phys Rev. 1961;122:1930. [Google Scholar]
- 221.Truhlar DG, Cartwright DC, Kuppermann A. Phys Rev. 1968;175:113. [Google Scholar]
- 222.Löwdin PO. Adv Quantum Chem. 1970;5:185. [Google Scholar]
- 223.Truhlar DG. J Phys Chem A. 2002;106:5048. [Google Scholar]
- 224.Tully JC. Semiempirical Methods of Electronic Structure Theory, Part A, Techniques. In: Segal GA, editor. Modern Theoretical Chemistry Series. Vol. 7. Plenum; New York: 1977. p. 173. [Google Scholar]
- 225.See for instance Chuang Y-Y, Radhakrishnan ML, Fast PL, Cramer CJ, Truhlar DG. J Phys Chem A. 1999;103:4893.
- 226.Marenich AV, Olson RM, Kelly CP, Cramer CJ, Truhlar DG. J Chem Theor Comput. 2007;3:2011. doi: 10.1021/ct7001418. [DOI] [PubMed] [Google Scholar]
- 227.Olson RM, Marenich AV, Cramer CJ, Truhlar DG. J Chem Theor Comput. 2007;3:2046. doi: 10.1021/ct7001607. [DOI] [PubMed] [Google Scholar]
- 228.Kelly CP, Cramer CJ, Truhlar DG. J Chem Theory Comput. 2005;1:1133. doi: 10.1021/ct050164b. [DOI] [PubMed] [Google Scholar]
- 229.Chandrasekhar J, Smith SE, Jorgensen WL. J Am Chem Soc. 1985;107:154. [Google Scholar]
- 230.Okamoto K, Kita T, Araki K, Shingu H. Bull Chem Soc Jpn. 1967;40:1912. [Google Scholar]
- 231.Marenich AV, Olson RM, Chamberlin AC, Cramer CJ, Truhlar DG. J Chem Theor Comput. 2007;3:2055. doi: 10.1021/ct7001539. [DOI] [PubMed] [Google Scholar]
- 232.Voter AF, Goddard WA., III J Am Chem Soc. 1986;108:2830. doi: 10.1021/ja00269a010. [DOI] [PubMed] [Google Scholar]
- 233.Song L, Mo Y, Gao J. J Chem Theory Comput. submitted. [Google Scholar]
- 234.Marcus RA. J Phys Chem A. 1997;101:4072. [Google Scholar]
- 235.Marcus RA, Sutin N. Biochim Biophys Acta. 1985;811:265. [Google Scholar]
- 236.Kuharski RA, Bader JS, Chandler D, Sprik M, Klein ML, Impey RW. J Chem Phys. 1988;89:3248. [Google Scholar]
- 237.Chandler D, Kuharski RA. Faraday Discuss Chem Soc. 1988;85:329. [Google Scholar]
- 238.King G, Warshel A. J Chem Phys. 1990;93:8682. [Google Scholar]
- 239.Ichiye T. J Chem Phys. 1996;104:7561. [Google Scholar]
- 240.Ungar LW, Newton MD, Voth GA. J Phys Chem B. 1999;103:7367. [Google Scholar]
- 241.Blumberger J, Tavernelli I, Klein ML, Sprik M. J Chem Phys. 2006;124:64507. doi: 10.1063/1.2162881. [DOI] [PubMed] [Google Scholar]
- 242.Witek HA, Choe YK, Finley JP, Hirao K. J Comput Chem. 2002;10:957. doi: 10.1002/jcc.10098. [DOI] [PubMed] [Google Scholar]
- 243.(a) Nakamura H, Xidos JD, Chamberlin AC, Kelly KC, Valero R, Thompson JD, Li J, Hawkins GD, Zhu T, Lynch BJ, Volobuev Y, Rinaldi D, Liotard DA, Cramer CJ, Truhlar DG. HONDOPLUS, version 5.1, based on HONDO, version 99.6. University of Minnesota; Minneapolis, MN: 2007. [Google Scholar]; (b) Dupuis M, Marquez A, Davidson ER. HONDO, version 99.6, based on HONDO, version 95.3, Quantum Chemistry Program Exchange. Indiana University; Bloomington, IN: 1999. [Google Scholar]
- 244.(a) Song L, Wu W, Mo Y, Zhang Q. XMVB: An Ab Initio Nonorthogonal Valence Bond Program. Xiamen University; Xiamen: 1999. [Google Scholar]; (b) Song L, Mo Y, Zhang Q, Wu W. J Comput Chem. 2005;26:514. doi: 10.1002/jcc.20187. [DOI] [PubMed] [Google Scholar]
- 245.Zhao Y, Truhlar DG. MN-GFM 3.0. University of Minnesota; Minneapolis: 2006. [Google Scholar]
- 246.Frisch MJ, Trucks GW, Schlegel HB, Scuseria GE, Robb MA, Cheeseman JR, Montgomery JA, Jr, Vreven T, Kudin KN, Burant JC, Millam JM, Iyengar SS, Tomasi J, Barone V, Mennucci B, Cossi M, Scalmani G, Rega N, Petersson GA, Nakatsuji H, Hada M, Ehara M, Toyota K, Fukuda R, Hasegawa J, Ishida M, Nakajima T, Honda Y, Kitao O, Nakai H, Klene M, Li X, Knox JE, Hratchian HP, Cross JB, Bakken V, Adamo C, Jaramillo J, Gomperts R, Stratmann RE, Yazyev O, Austin AJ, Cammi R, Pomelli C, Ochterski JW, Ayala PY, Morokuma K, Voth GA, Salvador P, Dannenberg JJ, Zakrzewski VG, Dapprich S, Daniels AD, Strain MC, Farkas O, Malick DK, Rabuck AD, Raghavachari K, Foresman JB, Ortiz JV, Cui Q, Baboul AG, Clifford S, Cioslowski J, Stefanov BB, Liu G, Liashenko A, Piskorz P, Komaromi I, Martin RL, Fox DJ, Keith T, Al-Laham MA, Peng CY, Nanayakkara A, Challacombe M, Gill PMW, Johnson B, Chen W, Wong MW, Gonzalez C, Pople JA. Gaussian 03, revision D.01. Gaussian, Inc.; Wallingford, CT: 2004. [Google Scholar]
- 247.Zhao Y, Truhlar DG. MLGAUSS-version 2.0. University of Minnesota; Minneapolis: 2005. [Google Scholar]
- 248.Olson RM, Marenich AV, Chamberlin AC, Kelly CP, Thompson JD, Xidos JD, Li J, Hawkins GD, Winget P, Zhu T, Rinaldi D, Liotard DA, Cramer CJ, Truhlar DG, Frisch MJ. MN-GSM, version 2007-beta. University of Minnesota; Minneapolis: 2007. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
EVB parameters, Cartesian coordinates of all the points calculated on the ground-state adiabatic reaction paths, and MOVB overlaps. This material is available free of charge via the Internet at http://pubs.acs.org.