Abstract
Enveloped viruses enter host cells either through endocytosis, or by direct fusion of the viral envelope and the membrane of the host cell. However, some viruses, such as HIV-1, HSV-1, and Epstein-Barr can enter a cell through either mechanism, with the choice of pathway often a function of the ambient physical chemical conditions, such as temperature and pH. We develop a stochastic model that describes the entry process at the level of binding of viral glycoprotein spikes to cell membrane receptors and coreceptors. In our model, receptors attach the cell membrane to the viral membrane, while subsequent binding of coreceptors enables fusion. The model quantifies the competition between fusion and endocytotic entry pathways. Relative probabilities for each pathway are computed numerically, as well as analytically in the high viral spike density limit. We delineate parameter regimes in which fusion or endocytosis is dominant. These parameters are related to measurable and potentially controllable quantities such as membrane bending rigidity and receptor, coreceptor, and viral spike densities. Experimental implications of our mechanistic hypotheses are proposed and discussed.
Introduction
Entry mechanisms of enveloped viruses (viruses with a surrounding outer lipid bilayer membrane) are usually classified as being either endocytotic or fusogenic (1,2). In fusion, the virus membrane and the host cell membrane become joined by a pore. Once the two membranes are contiguous, the virus can directly enter the host cell. This process is typically mediated by binding of cell surface receptors to glycoprotein spikes on the viral membrane surface, which trigger embedded fusion peptides. In endocytosis, the host cell first internalizes the virus particle, wrapping it in a vesicle before either fusion with the endosomal membrane, or degradation of the virus as the endosome is acidified. Fusion of the endosomal membrane with the viral envelope is often triggered by the acidic environment of the endosome.
While viruses are typically thought to enter host cells via either endocytosis or fusion, there is a growing list of viruses known to enter cells though both pathways. For example, influenza, the avian leukosis virus, and Semliki Forest virus primarily enter cells via endocytosis followed by endosomal fusion triggered by low pH. However, they have also been observed to directly fuse with host cells if the pH of the extracellular environment is lowered (3–5). For some viruses (e.g., Influenza), the glycoprotein-receptor complexes that bind the virus to the cell membrane initiate fusion under acidic conditions encountered later in the process. Many other viruses require the binding of multiple cell surface receptors by multiple viral glycoproteins for entry, and several such viruses have also been observed to enter cells through their nondominant pathway.
At least three of the 12 types of glycoproteins in the envelope of the Herpes Simplex Virus-1 (HSV-1) bind cell surface receptors as integral steps in viral entry. As an initial step, glycoproteins gB and gC bind to heparan sulfate (HS) proteoglycans on the cell surface, attaching the virus to the host cell. Once the viral and host cell membranes are brought close to each other, glycoprotein gD can associate with any of a number of cell receptors, including Herpesvirus entry mediator (a tumor necrosis factor receptor), nectin-1 (a member of the immunoglobulin superfamily), and 3-O-sulfated heparan sulfate (HS), to trigger fusion. HSV-1 is known to exploit at least three entry pathways: direct fusion with the host cell membrane, endocytosis followed by fusion with an acidic endosome, and endocytosis followed by fusion with a neutral endosome (6).
Epstein-Barr virus, another member of the Herpes virus family, requires the binding of multiple glycoproteins to cell surface receptors during entry. When Epstein-Barr virions enter B-cells, the glycoprotein complex gp350/220 binds to complement receptor type II (CR2) to attach the virus to the host B-cell. Fusion of the virus with the cell membrane or endosome requires that glycoprotein gp42 associate with a HLA class II protein on the cell surface (7). It is thought that the virus and cell membranes must be brought close by gp350/220-CR2 binding before gp42 can bind a HLA class II protein. While the Epstein-Barr virus typically enters B cells by endocytosis, eventually fusing with the endosome, it enters epithelial cells by direct fusion with the plasma membrane. There are at least three models for the entry of Epstein-Barr virus into epithelial cells;
-
1.
An interaction between gp350/220 on the virus and CR2 on the cell brings the membranes close. Viral glycoprotein complex gHgL can then interact with gHgL receptor on the cell, triggering fusion.
-
2.
The viral glycoprotein complex may directly interact with its receptor on the cell membrane, triggering fusion.
-
3.
The viral protein encoded by BMRF2 may interact with integrins on the cell surface followed by gHgL-gHgLr binding which triggers fusion (8).
Human immunodeficiency virus (HIV) has also been shown to exploit both entry mechanisms. HIV requires a receptor, CD4, for endocytosis, and both CD4 and a coreceptor, usually CXCR4 or CCR5, to fuse with the host cell membrane (9,10). The HIV coreceptor binds to the viral glycoprotein gp120 with a much higher affinity if the glycoprotein spike is already bound to a CD4 receptor (11–13). HIV infects cells with which it fuses, and is typically inactivated upon endocytosis (10).
A previous study (14) has examined the dynamics of viral entry when a single type of cell receptor attaches the virus to the cell membrane and induces fusion. In this article, we develop a stochastic model that describes viral entry pathways in which binding of a receptor to viral glycoprotein spikes is followed by binding of a coreceptor to viral spikes. In this model, the receptors are only attachment factors and the coreceptors induce fusion. The coreceptors and receptors may both bind to the same viral glycoprotein, as is the case for HIV, or they may bind to different glycoproteins or sets of glycoproteins, as is the case for HSV-1 and the Epstein-Barr virus. The selection of entry pathway is computed as a function of the kinetic rates in the model. We will discuss the sensitivity of pathway selection to the local coreceptor-mediated fusion rate and the rate of coreceptor binding. In Discussion and Conclusions, we will also estimate the role of active cellular processes in viral uptake by introducing separate rates for such active processes.
Table 1 lists relevant physical parameters for HIV-1 and HSV that guide assumptions of our model. Parameter values relevant to our model, but not readily available, are left blank and await future experimental investigation.
Table 1.
Known representative parameter values for virus spikes, receptors, and coreceptors, and their article references
| Quantity | HIV-1 | HSV-1 |
|---|---|---|
| Radius R | 0.05 μm (52) | 0.1 μm (53) |
| Spikes/virus | 8–14 (55,56) | 235–480 gD (54) |
| ∼700 total (44) | ||
| Receptor | KD ≈ 5 nM (57) | |
| Binding | ΔH ≈ −100 kBT (57) | |
| Coreceptor | KD ≈ 4 nM (58) | |
| Binding | ΔH ≈ −300 kBT (59) | |
| Receptor diff. | 0.044 μm2/s (60) | |
| Const. Dr | ||
| Coreceptor diff. | 0.05 μm2/s (60) | |
| Const. Dc | ||
| Host cell radius | T-cell | Epithelial cell |
| 4 μm (61) | 5 μm (62) | |
| Cell receptor | 300–3000 | 6–9 × 106 |
| Density | CD4/μm2 (63) | HS/μm2 (64) |
| Cell coreceptor | 60 CCR5/μm2 (63) | |
| Density |
Kinetic Model for Receptor-Coreceptor Engagement
Here, we derive a stochastic model describing the competition between the endocytic and fusion viral entry pathways. We assume that receptors on a host cell membrane can bind to any one of M spikes uniformly distributed on the surface of a single virus, and that coreceptors can bind to any one of N spikes, which may be different from the spikes to which receptors bind (see Fig. 1). Receptor binding locally attaches the virus envelope to the cell membrane, while coreceptor binding leads to the formation of fusion-enabling complexes. For simplicity, we consider the binding of both receptors and coreceptors to be irreversible. Since binding interactions between receptors and spikes can be very strong and/or have low dissociation constants (see Table 1), this approximation is consistent with physical parameters relevant to many viruses. However, there is also evidence that the CD4-gp120 interaction is weak and can dissociate during coreceptor recruitment (15).
Figure 1.
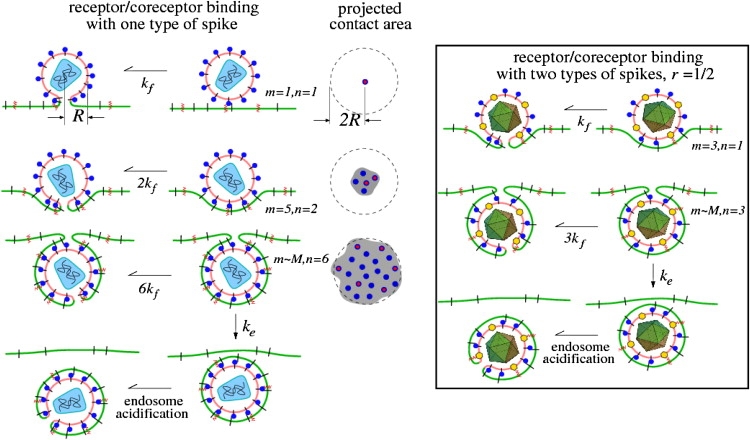
A schematic of the kinetic steps involved in receptor and coreceptor engagement, which ultimately lead to membrane fusion or endocytosis. Receptors and coreceptors in the cell membrane are represented by black line segments and red zigzags, respectively. The projected contact area nucleated by the number of bound receptors is also shown. Only viral spikes that have a coreceptor bound can induce fusion. Endocytosis can occur only when the contact region grows to the surface area of the virus particle. (Left) The receptors and coreceptors both bind to the same viral spikes (blue circles). An example of such a virus is HIV-1, where spikes, likely composed of trimers of gp120/41, bind to both CD4 and CCR5. (Right) An example (such as herpes simplex virus) in which coreceptors and receptors bind to different spikes, with the ratio of receptor-binding spikes (blue circles) to coreceptor-binding spikes (yellow hexagons) defined by r.
We assume that only those coreceptor-binding spikes in a region where spikes are bound to receptors can bind coreceptors. This assumption is appropriate if the receptors act as the attachment factor that brings the viral and cell membranes close enough for the coreceptor to bind. For example, the binding of CR2 receptors to the large gp350/220 glycoprotein complex on the Epstein-Barr virus typically precedes attachment of fusion-inducing HLA class II proteins to the smaller gp42 glycoprotein. This assumption also applies to HIV, since the affinity of coreceptors for viral spikes increases significantly if the spike has already bound a receptor (11–13).
The ratio of coreceptor-binding spikes to receptor-binding spikes is defined by r = N/M. For viruses where attachment receptors and fusion initiating coreceptors attach to the same glycoprotein spike, such as HIV-1, we can simply set r = 1 in our model. Although we assume that each spike can bind at most only one receptor and/or one coreceptor, experimentally inferred stoichiometries range from one to a handful (16–18). Our model can be straightforwardly adapted to describe specific receptor/coreceptor/spike stoichiometries.
For endocytosis to occur, the virus must be fully wrapped by the cell membrane. We assume that when the virus is fully wrapped all receptor-binding spikes have a receptor attached. However, as more of the cell membrane contacts the virus membrane through receptor binding, the rate of binding of fusion-inducing coreceptors increases and fusion is increasingly likely.
Although CD4 is known to coordinate accumulation of leukocyte-specific protein tyrosine kinase enhancing T cell sensitivity to antigens (19), we are not aware of any evidence of such cooperativity at the molecular level in the spike-receptor-coreceptor HIV fusion system. It has been shown that for HIV, viral spike trimers act independently to induce fusion (20), so in this case, we will assume that each spike-receptor-coreceptor complex represents a fusion-enabling trimer. Since we are only interested in the first instant any one of the spike-receptor-coreceptor triggers irreversible fusion, when the fusion entry pathway is chosen, our model assumes the total rate of fusion will be proportional to the number of existing spike-receptor-coreceptor complexes.
Within our stochastic model, the likely pathway of virus entry, endocytosis, or fusion, will also depend on the specific rates of receptor and coreceptor binding. These rates will be first motivated by simple physical considerations. A mathematical framework representing our stochastic model is found by considering, at any given time t, the probability Pm,n(t) that m spikes are bound to a receptor and n spikes are bound to a coreceptor. With the definition of the relevant rates in our problem, as follows,
pm,n, rate of binding an additional receptor;
qm,n, rate of binding an additional coreceptor;
kf, fusion rate for each spike-receptor-coreceptor complex;
ke, rate of endocytosis (membrane pinch-off) when all viral spikes are receptor-bound (m = M);
the probability Pm,n(t) evolves according to the Master equation,
| (1) |
Here, ∂tP0,0 = − p0,0P0,0, ∂tPM,0 = pM−1,0PM−1,0 − (qM,0 + ke)PM,0, and ∂tPM,N = pM−1,NPM−1,N + qM,N−1PM,N−1 − (Nkf + ke)PM,N. The process depicted in Fig. 1 and described by the above expressions in Eq. 1 can be represented by transitions within the m, n-state space shown in Fig. 2.
Figure 2.
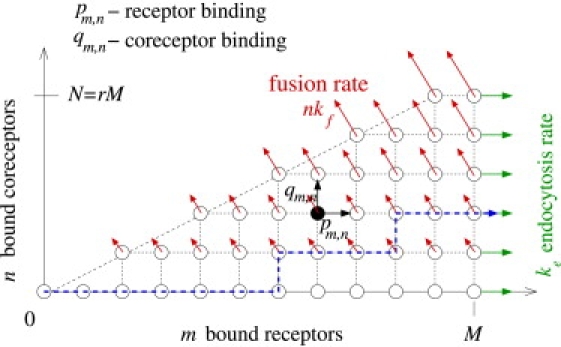
Two-dimensional state space for receptor and coreceptor-mediated viral entry. Each state corresponds to a virus particle bound to m ≤ M receptors and n ≤ N = rM coreceptors. In this example, the fraction of coreceptor-binding spikes to receptor-binding spikes is r = 1/2. The probability fluxes through the fusion and endocytosis pathways are indicated by the red and green arrows, respectively. A representative trajectory of the stochastic process that results in endocytosis is indicated by the blue dashed curve.
We treat all transitions in our model as Markovian, implicitly assuming that they do not depend on past configurations. This assumption is appropriate if the attachment rates are kinetically limited by membrane fluctuations or by receptor/coreceptor binding, rather than by diffusion. Diffusion-limited binding of receptors and coreceptors gives rise to history-dependent kinetics and must be treated within the framework of stochastic moving boundary problems. (Deterministic moving boundary problems relevant for virus wrapping are treated in P.-W. Fok and T. Chou (21) and (22).) For binding kinetics to not be diffusion-limited, receptors and coreceptors must diffuse fast enough to replenish a receptor-depleted region before the next binding event occurs. The time required for concentration variations to diffuse away is ar,c/Dr,c, where ar and ac are the typical areas per receptor and coreceptor on the cell surface, and Dr and Dc are their diffusion coefficients in the cell membrane. Therefore, provided
| (2) |
diffusion will not contribute to history-dependent binding. For the HIV infection systems, CD4 receptor and CCR5 coreceptor concentrations are ∼103/μm2 and 60/μm2, respectively. Upon using the cell surface receptor and coreceptor diffusion coefficients in Table 1, we find that pm,n ≪ 50/s and qm,n ≪ 3/s, and are required for CD4 and CCR5 engagement to be kinetically limited, and not diffusion-limited.
Within our coarse-grained Markov chain, the history-independent binding assumption also requires neglect of active cell processes, such as those involving a signaling cascade, or aggregation of signaling proteins on the cell membrane. However, our coarse stochastic model can still capture the qualitative effects of these active processes provided the rates are interpreted as effective parameters and a new parameter representing the timescale of active processes is introduced. We defer discussion of active processes to Discussion and Conclusions.
Although our main qualitative findings are independent of the precise form for the attachment rates pm,n and qm,n, we nonetheless examine a specific physical model for these rates. First, assume that a receptor binds, with rate pm,n, to only those spikes that are within some small distance ℓ of the contact line L(m) (see Fig. 3) where the membrane detaches from the virus. A functional form for this rate can be derived by considering the number of ways additional receptors can bind, given that there are already m receptor-spike complexes making up the contact region. Fluctuations of the cell membrane will be distributed in size with a typical scale ℓ (Fig. 3). The plasma membrane fluctuations, either thermally excited, or driven by cellular processes such as cytoskeletal reorganization (23), can be caught by the virus if they bring a receptor into the proximity of a spike. As shown in Fig. 3, the membrane-wrapping process is a Brownian ratchet that uses the spikes within a distance ℓ of the contact line of length L(m) to catch the cell membrane fluctuations. The rate of attachment of an additional receptor can be written as pm,n ∼ δrδsωℓL(m)as−1ar−1, where ω is an intrinsic attempt rate for binding and fluctuations of typical size ℓ, δr,s are receptor and spike sizes, as−1 is the viral spike concentration, and ar−1 is the receptor concentration on the cell membrane. The term ℓL(m)as−1 represents the probability that a membrane fluctuation of typical size ℓ will encounter a spike on the viral surface when m receptors have already previously bound. The approximate spherical geometry of this system gives , and since the area per spike is as ≈ 4πR2/M, we find the coreceptor-independent, receptor binding rate to be
| (3) |
where p1M is the intrinsic rate of binding the second receptor when initially one is bound. This intrinsic rate depends on a number of physical parameters such as cell membrane bending rigidity (through ℓ and ω) and cell surface receptor concentration. For stiff membranes under tension, a membrane wrapping a spherical particle encounters an energy barrier near half-wrapping (24). This can be incorporated into the dynamics by assuming p1 has an M dependence with a minimum near m ≈ M/2. Other forms for pm,n can also be motivated (25) by considering the mechanics of wrapping (26).
Figure 3.
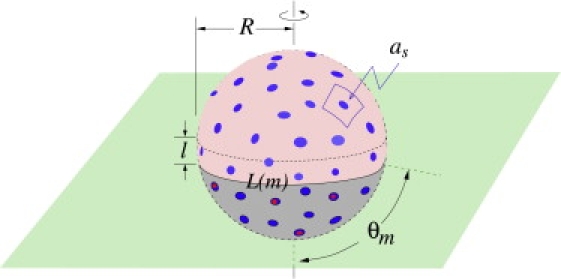
A schematic of a partially wrapped virus particle. The unbound spikes above the contact region are represented by light-blue circles, while the receptor-bound spikes in the contact region are represented by the dark-blue circles. Spikes that are bound to coreceptors are indicated by the red circles. The unbound receptors and coreceptors on the cell membrane (green) are not shown.
The binding rate of coreceptors will be proportional to the integer number of receptor-spike complexes that have not yet bound to coreceptors,
| (4) |
where q1 is the intrinsic rate of a coreceptor binding to a spike-receptor complex.
Finally, we describe the fusion and endocytosis steps. The rates of these processes, kf and ke, are the least well measured. The individual fusion rates kf depend not only on the particular spike-receptor complex, but also may depend on other molecular factors such as the lipid composition. We assume that each spike-receptor-coreceptor complex (or complex trimer) spontaneously and independently triggers fusion with rate kf, after it has formed. In model systems involving the gp41 fusion peptide of the HIV-1 glycoprotein-receptor complex, the fusion rate was found to be ∼kf ∼0.01/s (27). Physical models for kf can also be motivated from phenomenological considerations of fusion intermediates (28–31) and/or estimated from computer simulations (31,32).
The pinching-off of membrane vesicles in endocytosis is potentially a more complex process activated by GTPases such as dynamin (33). The kinetics of this process may be akin to the kiss-and-run fast mode of endocytosis at neuronal synapses. A wide range of rates (0.1/s < ke < 20/s) for synaptic vesicle kinetics has been reported (34).
Numerical Solution of Master Equation
Solutions to Eq. 1 can be found numerically for up to reasonably large values of M and N. From the resulting probabilities, we construct time-independent quantities of interest.
The total time integrated probability Qe that the virus undergoes endocytosis can be constructed from
| (5) |
Similarly, the total time-integrated probability Qf that the virus undergoes fusion is
| (6) |
where the last equality arises from conservation of probability and the assumption of nondetaching receptors.
We solve for Qe and Qf by taking the Laplace transform of Eq. 1 and setting s = 0. If we define , then the endocytosis and fusion probabilities can be expressed as and , respectively. We can also find the mean times 〈Te〉 to viral entry, conditioned upon endocytosis, or 〈Tf〉, conditioned upon fusion,
| (7) |
and
| (8) |
Finally, crucial to experimental considerations of spike-receptor-coreceptor stoichiometry (35), we also compute the mean numbers of receptors and coreceptors bound to the virus at the moment of entry. The mean number of receptors bound at the moment of fusion is found from
| (9) |
The mean numbers of coreceptors bound at the moment of fusion, and the mean number of coreceptors bound at the moment of endocytosis (when all N receptors are bound) can be similarly obtained.
Results and Analysis
In this section, we discuss solutions of the Master equation (Eq. 1). For simplicity, consider that the ratio of the number of spikes that can bind coreceptors to the number of spikes that can bind receptors is r = 1 and that M = N. This implies either that the number of receptor-binding spikes equals the number of coreceptor binding spikes, or that receptors and coreceptors both bind the same spikes, as is the case for HIV. The results for r ≠ 1 are qualitatively similar to the results of r = 1 when the replacement kf → rkf is made (see Appendix).
Pathway probabilities
We first explore how the probability that the virus undergoes endocytosis, Qe, depends on problem parameters. Since Qe + Qf = 1, it is sufficient to consider only Qe. In Fig. 4 a, Qe is plotted as a function of the normalized fusion rate, kf/p1, for different values of the normalized intrinsic coreceptor binding rate, q1/p1. The number of viral spikes, M = N, was chosen to be 100. The probability that the virus undergoes endocytosis decreases with increasing fusion rate, but a small coreceptor binding rate can attenuate fusion even when kf is large. In Fig. 4 b, we plot the probability that the virus undergoes endocytosis as a function of normalized fusion rate, kf/p1, for different values of the normalized endocytosis rate, ke/p1.
Figure 4.
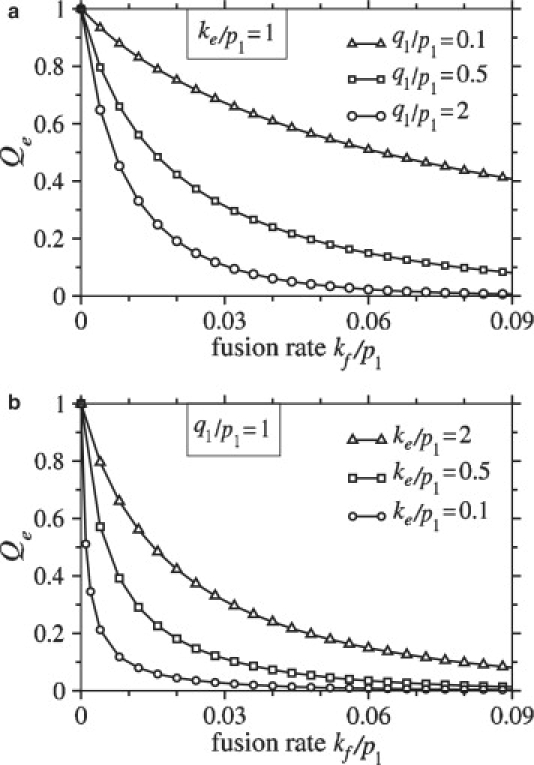
(a) The probability that the virus undergoes endocytosis is plotted as a function of the normalized fusion rate, kf/p1, for different values of the normalized coreceptor binding rate, q1/p1. The probability of endocytosis decreases with increasing fusion rate and, for a given fusion rate, the probability of endocytosis increases with decreasing q1/p1. In this example, the normalized endocytosis rate, ke/p1 = 1. (b) For q1/p1 = 1, the probability of endocytosis is plotted as a function of fusion rate for different values of the normalized endocytosis rate, ke/p1. In both plots, the number of receptor-binding spikes and the number of coreceptor-binding spikes are set to M = N = 100.
The dependence of the endocytosis probability, Qe, on the number of viral spikes, M, is shown in Fig. 5. Although the binding rate, pm increases with M (see Eq. 3), so do the number of spikes that need to be engaged by receptors to achieve the full wrapping required for endocytosis. The time required to fully wrap the virus is therefore constant with respect to M. However, the fusion rate is proportional to the number of spikes with coreceptors bound and is thus proportional to N. As N increases, the probability that the particle undergoes fusion before it becomes fully wrapped increases, as illustrated by Fig. 5. Figs. 4 and 5 clearly show a marked decrease in the endocytosis probability as the fusion rate kf is increased.
Figure 5.
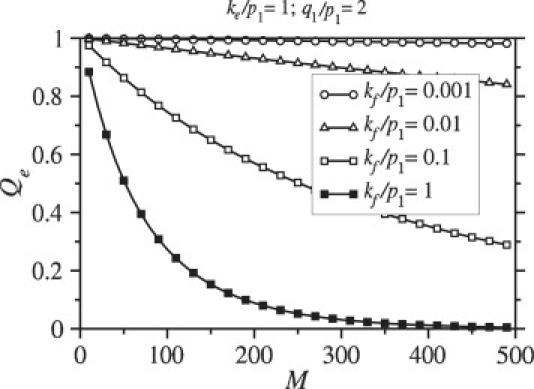
Endocytosis rates are plotted as a function of M = N. During wrapping, the fusion rate is proportional to the number of bound coreceptors, and increases with increasing N (in this case equal to M). The probability that the virus enters the cell through endocytosis decreases with increasing M = N.
Since kf may vary greatly depending on physical chemical conditions, as well as on viral species, it is important to estimate the values of kf for which endocytosis or fusion is the dominant mode of entry. To better understand how Qe depends on kf, we consider the continuum limit of Eq. 1, appropriate for large M, N. The probabilities of full wrapping and endocytosis, as well as times to fusion and endocytosis, can be calculated analytically by the method of characteristics (see Appendix). Fig. 6 compares our continuum limit analytic solution with the exact numeric solution and agreement is good for M, N ≳ 100. The analytic solution (see Eq. 30 in Appendix) provides a guide for estimating the parameters for which endocytosis is likely.
Figure 6.
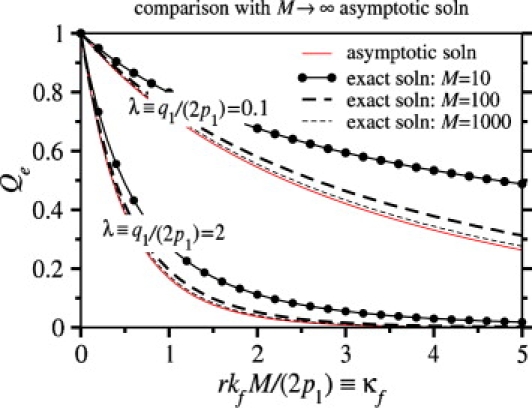
The exact numeric solution of Eqs. 1 and 5 for the probability Qe that the virus undergoes endocytosis is plotted as a function of κf ≡ rkfM/(2p1), the dimensionless fusion rate and compared to the M → ∞ asymptotic solution (thin solid curves). Two sets of curves, corresponding to λ ≡ q1/(2p1) = 0.1, 2 are shown for M = N = 10, 100, and 1000 (r = 1). In these plots, the endocytosis rate was taken to be ke/p1 = 2.
Let us now dissect the entry dynamics and estimate values of ke and kf for which endocytosis will occur. For certain parameters, the virus is likely to fuse before it becomes fully wrapped. In this case, the probability that the virus reaches the fully wrapped state will be small, and fusion will be the dominant mode of entry. Only if the virus is likely to become fully wrapped is endocytosis a possible alternative to fusion. Endocytosis will occur only if the probability that M receptors become bound to the virus, PM, is ∼1 and endocytosis occurs more quickly than fusion once the virus is fully wrapped. For single receptor-spike complexes that attach membranes and induce fusion (14), previous asymptotic analysis showed that
| (10) |
must be satisfied for the virus to become fully wrapped. In that analysis, pm was a typical receptor binding rate.
Analogous conditions for endocytosis can be found when both receptor and coreceptor binding are required for fusion. These conditions can be found numerically by computing Qe from Eqs. 1 and 5. However, upon using the specific forms for the receptor and coreceptor binding rates given by Eqs. 3 and 4, the conditions can also be deduced from the wrapping probability PM in the large M limit. From Eq. 25 in the Appendix,
| (11) |
where λ = q1/(2p1). This asymptotic expression allows us to determine when the wrapping probability is appreciable. If coreceptors are required for fusion, as considered in this study, the expected behavior will be similar to the single receptor model only if coreceptor binding is faster than receptor binding. Indeed, when q1 ≳ p1 (λ ≳ 1), we find that the condition
| (12) |
is required for full wrapping. Since pm ∼ p1M, we recover the condition (Eq. 10 here) given in Chou (14) when r = 1. Fig. 7 a shows the numerically computed probability of full wrapping, PM, as a function of rkf M/p1 (with r = 1). The condition for full wrapping given by Eq. 12 holds even when parameters are individually varied over a wide range of values.
Figure 7.
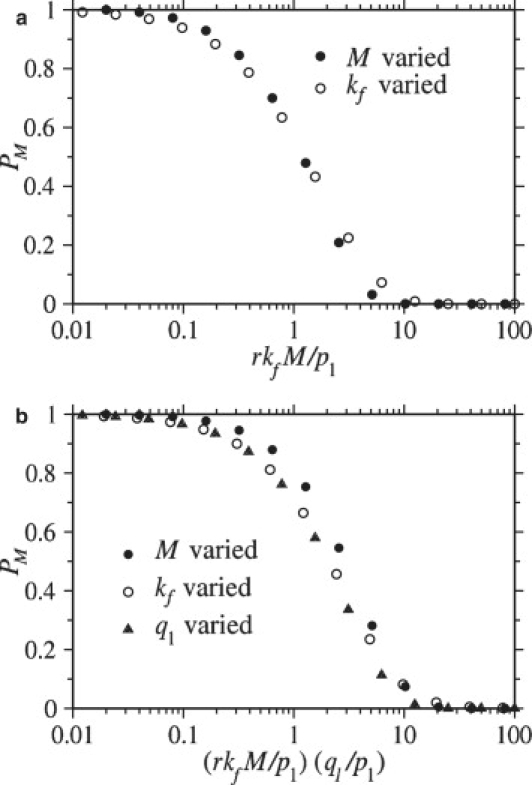
Wrapping probabilities for M = N (r = 1). (a) For q1 ≳ p1, the probability PM that the virus reaches the fully wrapped state is plotted as a function of the dimensionless fusion-rate parameter rkfM/p1. When this parameter is small, PM approaches unity, but when rkfM/p1 ≫ 1, PM is small. (b) When 1/N ≪ q1/p1 ≪ 1, the wrapping probability PM is plotted as a function of the dimensionless expression (rkfM/p1)(q1/p1). In this case, the transition of PM from large to small values occurs at (rkfM/p1)(q1/p1) ∼ O(1). In both plots, only one parameter was varied within a group of symbols of the same color and shape. In a, the number of spikes M was varied within the groups of circles, and the fusion rate, kf was varied within the groups of triangles. In b, the number of spikes M was varied within the groups of solid circles, the fusion rate kf was varied within the groups of open circles, and the coreceptor binding rate q1 was varied within the groups of triangles.
Now consider the condition for full wrapping when coreceptor binding is slow compared to receptor binding. For extremely small q1/p1 = 2λ ≪ 1/N, the M, N → ∞ continuum limit for PM (Eq. 11) is not appropriate. When coreceptor binding is extremely small, no coreceptors bind, and the virus always becomes fully wrapped independent of kf. However, for 1/N ≪ q1/p1 ≪ 1 (or 1/N ≪ λ ≪1). The condition for PM ∼1 derived from Eq. 11 is
| (13) |
If the condition in Eq. 12 is satisfied, the condition in Eq. 13 will be satisfied provided that q1 ≤ p1. Thus, the condition in Eq. 12 is sufficient for the virus to become fully wrapped; however, because slow coreceptor binding can limit the effects of a fast fusion rate, the condition in Eq. 12 is not necessary, particularly when coreceptor binding is slow. In other words, even if rkfM/p1 is large, as long as q1/p1 is small enough, the condition in Eq. 13 can still be satisfied and full wrapping can still occur. In Fig. 7 b, PM is plotted as a function of (rkfM/p1)(q1/p1) with various parameters independently varied. When coreceptor binding is slow, the condition given by Eq. 13 is found to predict whether the virus is likely to reach the fully wrapped state. Although we have used the particular binding rates pm and qm,n from Eqs. 3 and 4, analogous conditions for PM ∼1 can be motivated for general binding rates (see Appendix).
We can now derive sufficient conditions for endocytosis after the virus becomes fully wrapped. In the case where the coreceptor binding rate is large compared to the receptor binding rate, we expect that when the virus reaches the fully wrapped state, nearly all N spikes will be coreceptor-bound. Once the virus is fully wrapped, it fuses with the cell membrane with total (and maximal) rate Nkf, while it is endocytosed by the cell with rate ke. Thus, endocytosis will be the dominant mode of viral entry if
| (14) |
Provided the virus has a high probability of reaching the fully wrapped state, ke ≫ Nkf is always a sufficient, but not always a necessary condition for endocytosis. When coreceptor binding is not fast, we will typically need to consider the full solution given by Eq. 30 to determine when endocytosis is likely. However, we can consider the limiting case where the coreceptor binding rate is small compared to both the receptor binding rate (q1 ≪ p1), and the fusion rate (q1N ≪ kf). In this case, we can assume that fusion is limited by the coreceptor binding rate, and the condition required for efficient endocytosis is
| (15) |
The conditions described above for efficient endocytosis are summarized in Discussion and Conclusions and delineated in a parameter-space phase diagram.
Mean entry times
We now investigate 〈Te〉, the mean viral entry time via the endocytosis pathway, and 〈Tf〉, the mean entry time via the fusion pathway. The normalized mean times are computed from Eqs. 7 and 8 and are plotted in Fig. 8 as a function of the fusion rate per bound coreceptor, kf. Endocytosis is governed by two potentially rate-limiting steps: viral wrapping, and the final endocytosis step (pinching-off of the cell membrane). For small ke, the endocytosis step is rate-limiting, and 〈Te〉 scales as 1/ke when Qe ≈ 1. For the parameters used in Fig. 8 a, the receptor binding rates are much faster than the endocytosis rate; thus, ke is the limiting rate constant. As the fusion rate kf increases, both the probability of endocytosis, Qe, and the mean endocytosis times, 〈Te〉, decrease. One might initially expect 〈Tf〉, but not 〈Te〉, to decrease with increasing kf. However, we expect there to be some distribution of times at which the virus becomes fully wrapped. A larger fusion rate will preferentially annihilate trajectories that take longer to reach the fully wrapped state. Therefore, only trajectories that quickly reach the fully wrapped state survive to m = M and participate in endocytosis, resulting in a decreased 〈Te〉 when kf is increased.
Figure 8.
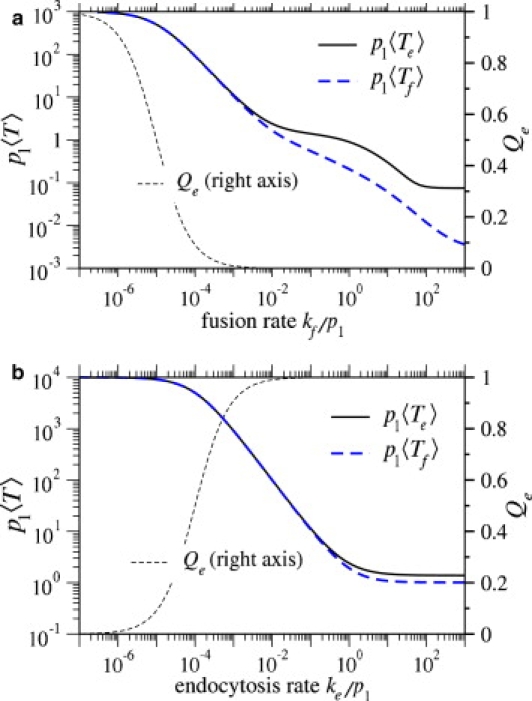
(a) Normalized mean times to fusion and endocytosis plotted as functions of kf/p1, the fusion rate per coreceptor-spike complex. Parameters used were M = N = 100, q1/p1 = 50, ke/p1 = 0.001. (b) Normalized mean times to fusion and endocytosis plotted as functions of ke/p1. Here, M = N = 100, q1/p1 = 5, and kf/p1 = 10−6, were used. For reference, Qe, the corresponding probability that the virus undergoes endocytosis is also plotted.
In Fig. 8 b, we plot the normalized mean entry times as a function of ke/p1, the normalized endocytosis rate. We find that as we increase ke, the mean time 〈Te〉 decreases and then plateaus. The plateau occurs when ke is sufficiently fast that endocytosis is no longer rate-limiting. Rather, membrane wrapping is the rate-limiting step, and 〈Te〉 becomes independent of ke.
Mean receptor/coreceptors bound at entry
Finally, consider the mean numbers of receptors and coreceptors bound to the virus at the time of entry. In Fig. 9 a, we plot 〈mf〉, the mean number of receptors bound when fusion occurs, and 〈m〉, the mean number of receptors bound when the virus enters the cell through either pathway, as functions of q1, the coreceptor binding rate. As q1 increases, Qe decreases, and the virus is more likely to fuse with the host cell. Because the virus fuses more rapidly, there is less time for receptors to bind and 〈m〉 decreases. Fig. 9 b shows the mean number of coreceptors bound to the virus at the time of entry. For very small coreceptor binding rates, the virus typically undergoes endocytosis before a coreceptor can bind, and 〈ne〉 ≪ 1, where 〈ne〉 is the mean number of coreceptors bound when the virus undergoes endocytosis. However, at least one coreceptor must bind for fusion to occur; therefore, when q1 is small, the conditional mean number of bound coreceptors 〈nf〉 ≈ 1. As q1 becomes large, the probability that the virus undergoes endocytosis becomes small, but the mean number of coreceptors bound to the viruses that do undergo endocytosis approaches N = 100. We know that when q1 is large, n ≈ rm. Since full wrapping (m = M) is required for endocytosis to occur, we also expect 〈ne〉 ≈ N.
Figure 9.
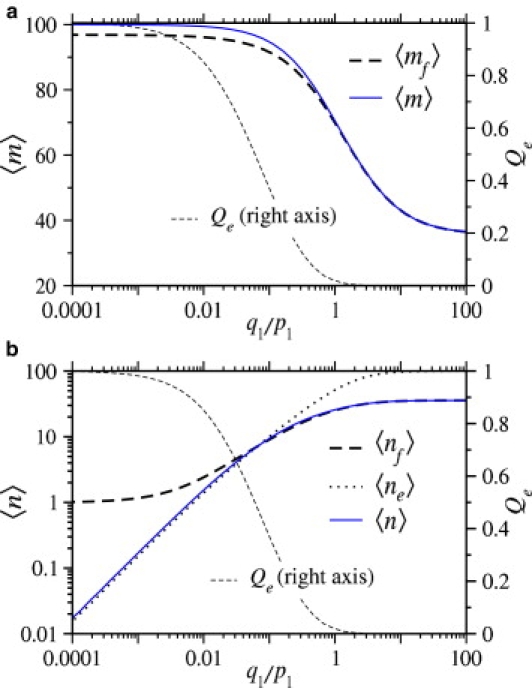
(a) The mean number of receptors bound at the moment of viral fusion, and the mean number of receptors bound at the moment of viral entry (regardless of entry pathway) plotted as functions of the normalized coreceptor binding rate, q1/p1. (b) The mean number of coreceptors bound at the moment of fusion and endocytosis, and the average number of coreceptors bound are plotted as a function of the normalized coreceptor binding rate q1/p1. The probability that the virus undergoes endocytosis, Qe is plotted for reference. For both plots M = N = 100, kf/p1 = 0.1, ke/p1 = 1.
Discussion and Conclusions
We have developed a stochastic model describing the binding of receptors and coreceptors to viral glycoprotein spikes, and the subsequent competition between endocytosis and fusion during entry of enveloped viruses. Receptors function as simple attachment factors in our model, while subsequent binding of coreceptors enables fusion. We found parameter regimes in which endocytosis is favored and derived analytic expressions for the probability of endocytosis in the large spike number limit (M, N → ∞). Since the endocytosis and fusion rates, ke and kf, are difficult to measure, we summarize our results by a (kf − ke) phase diagram defined by the conditions in Eqs. 12–15 and shown schematically in Fig. 10.
Figure 10.
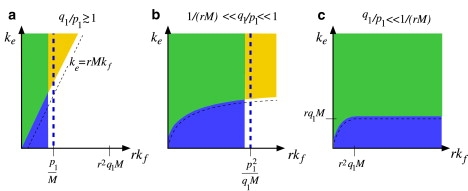
Qualitative phase diagram showing the regimes of parameter space in which endocytosis is dominant. Diagrams a–c correspond to fast, intermediate, and slow coreceptor binding, respectively. In all diagrams, parameters falling within the blue region left of the vertical thick dashed line favor full viral wrapping before fusion occurs (PM ≈ 1). In the yellow sector above the thin-dashed curves, the rate of endocytosis exceeds the effective rate of fusion in the fully wrapped state. In the green intersection of these regions, the virus is likely to reach the fully wrapped state and undergo endocytosis. Note that when coreceptor binding is very slow (c), the virus reaches the fully wrapped state for all values of kf.
Our model provides a mechanistic basis for a number of experimental measurements and observations. For example, the dual entry pathways of certain viruses suggest that under certain conditions (delineated in Fig. 10), inhibition of fusion does not necessarily preclude viral entry through endocytosis. HIV fusion inhibitors such as Enfuvirtide (T-20) bind the intermediary spike-CD4 complex of HIV-1 (36,37), and reduce kf by preventing CCR5 from inducing fusion. Maraviroc binds CCR5 and prevents it from binding the spike-CD4 complex, effectively reducing q1 and also preventing fusion (38). Since the virus may still enter through the endocytosis pathway, our analysis suggests that the effectiveness of fusion inhibitors relies on endocytic entry being less infective than fusion.
The sensitivity of entry of HIV strains to cell CD4 and CCR5 levels have recently been quantitatively studied using cells lines in which expression levels of receptor and coreceptor can be independently varied (S. H. Johnston, M. A. Lobritz, S. Nyugen, Y. J. Bryson, E. J. Arts, T. Chou, and B. Lee, unpublished). This system provides a way of independently varying p1 and q1, and has revealed qualitatively different usage patterns by different HIV strains. Our model provides an additional dimension to the analysis of receptor/coreceptor tropism. If endocytic entry does not significantly diminish the probability of nuclear entry and productive infection, it is possible that strains with similar infectivities actually prefer different entry pathways.
Infection measurements using, for example, luciferase reporting of p24 coat protein levels after productive infection, cannot directly determine entry pathways. However, using single molecule imaging techniques, both the timing and entry pathways can be directly observed (40–42). Such direct imaging techniques may be able to distinguish the mean conditional times to fusion and endocytosis, particularly in systems with large fusion and endocytosis rates as shown in Fig. 8.
Additionally, kinetic studies have been performed to extract the stoichiometry of receptors and coreceptors per spike, per fusion event (16–18,35,43). Even though our analysis was based on an intrinsic molecular stoichiometry of one spike, one receptor, and/or one coreceptor, it implies that the apparent stoichiometry can vary depending on the degree of wrapping, and on average, the number of spikes that are receptor/coreceptor-engaged before fusion or endocytosis. The apparent stoichiometries are defined by 〈mf〉 and 〈nf〉 derived from our model and shown in Fig. 9. Cells with higher surface densities of coreceptors, and hence larger q1, would more likely fuse before significant wrapping and formation of spike-receptor-coreceptor complexes occur. Therefore, a high coreceptor binding rate can present a lower apparent coreceptor stoichiometry. It would thus be interesting to measure kinetics and correlate spike/receptor/coreceptor stoichiometry across viral strains with different apparent usage stoichiometries, and across cell types with varying concentrations of surface receptors and coreceptors.
The assumption that the viral spikes are evenly distributed on the surface of the virus is valid only if the spikes are immobile on the virus surface during the entry process. Freely diffusing glycoprotein spikes will preferentially bind to membrane receptors or coreceptors when the spikes come near the cell membrane. Thus, spikes with receptors and coreceptors bound would tend to cluster near the bottom of the virus, precluding full wrapping. In this case, the probability that the virus enters the cell via fusion would be increased. It is also possible that the viral glycoproteins form functional clusters on the viral envelope (44). It is known that the glycoprotein spikes of recently budded HIV-1 are associated with the underlying matrix proteins, but that proteolysis occurs during the maturation process (45,46). If softening of a maturing virus particle (46) also increases glycoprotein spike mobility, one would expect that mature HIV-1 would be biased toward using the fusion pathway.
The model we have developed considers only the rudimentary receptor engagement processes before fusion or endocytosis. Nonetheless, more-complex mechanisms also can be described by our model, provided the effective rate parameters are properly interpreted, or the model is augmented to include other intermediary processes. For example, consider the possibility that binding of the virus to a cell surface receptor activates an endocytic pathway that increases the rate by which the virus is wrapped by the cell membrane. The increased wrapping rate may be the result of, for example, a decreased effective stiffness of the cytoskeleton that allows the virus to more easily enter the cell (47). An endocytotic pathway may also rely on the clustering cell surface receptors and/or coreceptors, as observed in Qi et al. (48), resulting in a high local receptor/coreceptor concentration near the virus, thereby effectively increasing the rate of receptor, and possibly coreceptor binding.
Activated viral entry processes can be incorporated within our fusion-or-endocytosis model in a qualitative way by assuming that before activation, receptors and coreceptors bind with rates p1i and q1i, and that after activation receptors and coreceptors bind with rates p1a and q1a, respectively. We further assume that activation occurs some time τa after the first receptor binds. And, for simplicity, we will again consider that M = N and r = 1. In the absence of an active endocytosis process, two conditions were required for endocytosis to occur:
Condition 1. The virus had to reach the fully wrapped state; and
Condition 2. Endocytosis had to be faster than fusion in the fully wrapped state.
If, however, the cell must initiate an active process for endocytosis, an additional condition arises:
Condition 3. The cell must reach the activated state without the virus undergoing fusion.
All three conditions must be satisfied if activated endocytosis is to occur. If activation is important, the inactivated receptor binding rate p1i is slow such that on average, few receptors bind before activation occurs and . In this case, the third condition can be described in terms of the effective binding rates as follows.
If the inactivated coreceptor binding rate is fast compared with the timescale on which activation occurs (q1i ≳1/τa), the virus will survive to the activated state provided τakf ≪ 1. If the inactivated coreceptor binding rate is slow (q1i ≪ 1/τa), it is unlikely that a coreceptor will bind before the activated state is reached, and the virus will become activated for any kf. The delay time τa required to activate the cell's endocytosis machinery will be relevant if Condition 3 (that the cell reaches the activated state before viral fusion) is not met, but Conditions 1 and 2 are. In this case, a model without the activation step would predict that the virus should undergo endocytosis when it in fact will undergo fusion. In Table 2, we summarize the criteria under which all three activated endocytosis conditions are met.
Table 2.
Conditions for 1), survival to fully wrapped state after activation; 2), endocytosis being faster than fusion; and 3), reaching the activated state before fusion
| Condition 1 |
Condition 2 |
Condition 3 |
|||||||
|---|---|---|---|---|---|---|---|---|---|
| Fast or slow def. | Survival to fully wrapped state | Fast or slow def. | Endocytosis faster than fusion | Fast or slow def. | Survival to activated state | ||||
| Fast coreceptor binding | ke ≫ Nkf | qi1τa ≳ 1 | τakf ≪ 1 | ||||||
| Slow coreceptor binding | q1aN ≪ kf | ke ≫ Nq1a | q1iτa ≪ 1 | τa2kfqi1 ≪ 1 | |||||
We can also consider the case in which cells undergo clathrin- or caveolin-dependent endocytosis that competes with the fusion process (41,49,50). In these cases, the membrane adhesion, or wrapping rate pm,n is no longer a function receptor concentration, but is rather a function of the rate of assembly of clathrin subunits (51) or calveolin, M of which cover the virus. This rate would be a function of clathrin or caveolin concentration, or of molecules that recruit them. If the formation of clathrin pits or caveolin occurs successively in an approximately axisymmetric manner, we expect the functional form for pm,n would be unchanged from Eq. 3. Three variants of our model could apply to fusion under clathrin or caveolin-mediated endocytosis:
Variant 1. If coreceptors can continue to bind viral spikes and induce fusion in regions of the membrane coated with clathrin or caveolin, the model described in this work is directly applicable. In this case, monomeric clathrin/caveolins are receptors and M is the total number of monomers required to encapsulate the virus.
Variant 2. If receptor binding, but not fusion, is precluded in regions of the membrane coated by clathrin/caveolin, the coreceptor binding rate is no longer given by qm,n = q1(n∗(m) − n). In this case, coreceptors, like monomers of clathrin or caveolin, only bind along the perimeter of the coated membrane region. The coreceptor binding rate then has a form similar to the receptor (monomeric clathrin/caveolin) binding rate and is given by . All other aspects of the model would remain unchanged.
Variant 3. If coreceptors within a region of the membrane coated by clathrin/caveolin cannot induce fusion, the virus can still undergo fusion if coreceptors bind to spikes along the perimeter of the coated region and induce fusion before the coated region grows enough to cover the location of the coreceptor. When coreceptor binding is fast compared to the rate at which the protein scaffold assembles, the instantaneous fusion rate is proportional to the number of spikes near the contact region. Instead of nkf, the effective m-dependent fusion rate arises. The fusion rate depends only on the number m of bound receptors and the total number N of coreceptors. It is independent of the number n of bound coreceptors, rendering the state space effectively one-dimensional.
Acknowledgments
This work was supported by the National Science Foundation (grant No. DMS-0349195) and by the National Institutes of Health (grant No. K25AI058672). S.A.N. also acknowledges support from a National Science Foundation Graduate Research Fellowship. The authors also thank the Institute for Pure and Applied Mathematics at UCLA for sponsoring a program on Cells and Materials during which some of this research was conceived and performed.
Appendix: Method Of Characteristics
Using specific forms for the receptor and coreceptor attachment rates pm,n and qm,n, analytic expressions for the wrapping and endocytosis probabilities can be obtained in the large spike number limit M ≡ 1/ɛ →∞. Assuming binding rates given by Eqs. 3 and 4 and defining x = mɛ, y = rnɛ, and time τ = 2p1t, we find the continuum limit of the Master equation:
| (16) |
In Eq. 16, the convection is defined by
| (17) |
where λ ≡ q1/(2p1) and κf = rkf/(2p1ɛ) are renormalized coreceptor binding and fusion rates. Assuming that the system starts in the state P(x, y, 0) = δ(x − ɛ)δ(y) (only one receptor attached), the total derivative of P(x(τ), y(τ), τ) obeys
| (18) |
provided
| (19) |
First consider times before the virus is fully wrapped by the cell membrane. The components of Eq. 19 give
| (20) |
and
| (21) |
Upon using the initial conditions x(0) = ɛ≈ 0 and y(0) = 0, Eqs. 20 and 21 are solved by
| (22) |
and
| (23) |
Full wrapping of the virus, if it occurs, is defined by x(τ∗) = 1, where τ∗ = π. Therefore, at time τ = τ∗ = π, we can find the fraction of bound coreceptors as
| (24) |
Using the forms for the trajectory r(τ), the probability density for times τ ≤ τ∗ can be found upon solving Eq. 18 to give
| (25) |
The probability density P∗ that the virus reaches the fully wrapped state (the continuum analogue of PM shown in Fig. 7) is found by evaluating P(x(τ∗) = 1, y(τ∗) = y∗, τ∗) ≡ P∗. This evaluation gives Eq. 11 in the large M, N limit.
At times τ > τ∗, additional receptors cannot bind, thus, x(τ > τ∗) = 1, and y(τ) follows
| (26) |
Upon defining z∗ ≡ 1 − y∗, Eq. 26 is solved by
| (27) |
In terms of the renormalized endocytosis rate κe = ke/(2p1), the probability that the virus has not entered the cell through either fusion or endocytosis at time τ follows
| (28) |
which is solved by
| (29) |
The probability Qe that the virus particle undergoes endocytosis is then given by
| (30) |
where γ is the incomplete lower Gamma function. This expression was used to generate the analytic results plotted in Fig. 6.
Besides our results obtained using the specific forms of receptor and coreceptor binding rates, conditions analogous to those in Eqs. 12 and 13 can also be obtained for general coreceptor-independent binding rate pm by using simple scaling arguments. When coreceptor binding is fast, q1 ≳ p1, the probability of fusion is ∼kf〈nf〉t∗, where
| (31) |
is the mean conditional wrapping time, and 〈nf〉 is the mean number of bound coreceptors before fusion. For fast coreceptor binding 〈nf〉 ∼ N, and the necessary (but not sufficient) condition for full virus wrapping (PM ∼ 1) is
| (32) |
When coreceptor binding is slow, 〈nf〉 ≈ q1Nt∗ increases linearly with both time and the number of available coreceptor-biding spikes. In this case, the necessary condition for virus wrapping becomes
| (33) |
Upon inserting the smoothly varying forms for pm from Eq. 3 into the above relationships, they reduce to the conditions in Eqs. 12 and 13, respectively.
References
- 1.Dimitrov D.S. Virus entry: molecular mechanisms and biomedical applications. Natl. Rev. 2004;2:109–122. doi: 10.1038/nrmicro817. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Marsh M., Helenius A. HIV entry inhibitors. Cell. 2006;124:729–740. doi: 10.1016/j.cell.2006.02.007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Duzgunes N., Pedroso de Lima M.C., Stamatatos L., Flasher D., Alford D. Fusion activity and inactivation of influenza virus: kinetics of low pH-induced fusion with cultured cells. J. Gen. Virol. 1992;73:27–37. doi: 10.1099/0022-1317-73-1-27. [DOI] [PubMed] [Google Scholar]
- 4.Diaz-Griffero F., Hoschander S.A., Brojatsch J. Endocytosis is a critical step in entry of subgroup B avian leukosis viruses. J. Virol. 2002;76:12866–12876. doi: 10.1128/JVI.76.24.12866-12876.2002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Marsh M., Bron R. SFV infection in CHO cells: cell-type specific restrictions to productive virus entry at the cell surface. J. Cell Sci. 1997;110:95–103. doi: 10.1242/jcs.110.1.95. [DOI] [PubMed] [Google Scholar]
- 6.Reske A., Pollara G., Krummenacher C., Chain B.M., Katz D.R. Understanding HSV-1 entry glycoproteins. Rev. Med. Virol. 2007;17:205–215. doi: 10.1002/rmv.531. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Haan K.M., Kwok W.W., Longnecker R., Speck P. Epstein-Barr virus entry utilizing HLA-DP or HLA-DQ as a coreceptor. J. Virol. 2000;74:2451–2454. doi: 10.1128/jvi.74.5.2451-2454.2000. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Hutt-Fletcher L.M. Epstein-Barr virus entry. J. Virol. 2007;81:7825–7832. doi: 10.1128/JVI.00445-07. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Daecke J., Fackler O.T., Dittmar M.T., Krusslich H.-G. Involvement of clathrin-mediated endocytosis in human immunodeficiency virus type 1 entry. J. Virol. 2005;79:1581–1594. doi: 10.1128/JVI.79.3.1581-1594.2005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Schaeffer E., Soros V.B., Greene W.C. Compensatory link between fusion and endocytosis of human immunodeficiency virus type 1 in human CD4 T lymphocytes. J. Virol. 2004;78:1375–1383. doi: 10.1128/JVI.78.3.1375-1383.2004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Trkola A., Dragic T., Arthos J., Binley J.M., Olson W.C. CD4-dependent, antibody-sensitive interactions between HIV-1 and its co-receptor CCR-5. Nature. 1996;384:184–187. doi: 10.1038/384184a0. [DOI] [PubMed] [Google Scholar]
- 12.Wu L., Gerard N.P., Wyatt R., Choe H., Parolin C. CD4-induced interaction of primary HIV-1 gp120 glycoproteins with the chemokine receptor CCR-5. Nature. 1996;384:179–183. doi: 10.1038/384179a0. [DOI] [PubMed] [Google Scholar]
- 13.Hill C.M., Deng H., Unutmaz D., Kewalramani V.N., Bastani L. Envelope glycoproteins from human immunodeficiency virus types 1 and 2 and simian immunodeficiency virus can use human CCR5 as a coreceptor for viral entry and make direct CD4-dependent interactions with this chemokine receptor. J. Virol. 1997;71:6296–6304. doi: 10.1128/jvi.71.9.6296-6304.1997. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Chou T. Stochastic entry of enveloped viruses: fusion versus. endocytosis. Biophys. J. 2007;93:1116–1123. doi: 10.1529/biophysj.107.106708. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Chang M.I., Panorchan P., Dobrowsky T.M., Tseng Y., Wirtz D. Single-molecule analysis of human immunodeficiency virus type 1 gp120-receptor interactions in living cells. J. Virol. 2005;79:14748–14755. doi: 10.1128/JVI.79.23.14748-14755.2005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Platt E.J., Durnin J.P., Kabat D. Kinetic factors control efficiencies of cell entry, efficacies of entry inhibitors, and mechanisms of adaptation of human immunodeficiency virus. J. Virol. 2005;79:4347–4356. doi: 10.1128/JVI.79.7.4347-4356.2005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Lineberger J.E., Danielsen R., Hazuda D.J., Simon A.J., Miller M.D. Altering expression levels of human immunodeficiency virus type 1 gp120-gp41 affects efficiency but not kinetics of cell-cell fusion. J. Virol. 2002;76:3522–3533. doi: 10.1128/JVI.76.7.3522-3533.2002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Yang X., Kurteva S., Ren X., Lee S., Sodroski J. Subunit stoichiometry of human immunodeficiency virus type 1 envelope glycoprotein trimers during virus entry into host cells. J. Virol. 2006;80:4388–4395. doi: 10.1128/JVI.80.9.4388-4395.2006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Li Q.-J., Dinner A.R., Qi S., Irvine D.J., Huppa J.B. CD4 enhances T cell sensitivity to antigen by coordinating Lck accumulation at the immunological synapse. Nat. Immunol. 2004;5:791–799. doi: 10.1038/ni1095. [DOI] [PubMed] [Google Scholar]
- 20.Yang X., Kurteva S., Ren X., Lee S., Sodroski J. Stoichiometry of envelope glycoprotein trimers in the entry of human immunodeficiency virus type 1. J. Virol. 2005;79:12132–12147. doi: 10.1128/JVI.79.19.12132-12147.2005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Fok P.-W., Chou T. Interface growth driven by surface kinetics and convection. SIAM J. Appl. Math. 2007 In press. [Google Scholar]
- 22.Gao H., Shi W., Freund L.B. Mechanics of receptor-mediated endocytosis. Proc. Natl. Acad. Sci. USA. 2005;102:9469–9474. doi: 10.1073/pnas.0503879102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Lerner D.M., Deutsch J.M., Oster G.F. How does a virus bud? Biophys. J. 1993;65:73–79. doi: 10.1016/S0006-3495(93)81071-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Deserno M. Elastic deformation of a fluid membrane upon colloid binding. Phys. Rev. E Stat. Nonlin. Soft Matter Phys. 2004;69:031903. doi: 10.1103/PhysRevE.69.031903. [DOI] [PubMed] [Google Scholar]
- 25.D'Orsogna M.R., Chou T. Queuing and cooperativity in ligand-receptor binding. Phys. Rev. Lett. 2005;95:170603. doi: 10.1103/PhysRevLett.95.170603. [DOI] [PubMed] [Google Scholar]
- 26.Sun S.X., Wirtz D. Mechanics of enveloped virus entry into host cells. Biophys. J. 2006;90:L10. doi: 10.1529/biophysj.105.074203. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Haque M.E., Lentz B.R. Influence of gp41 fusion peptide on the kinetics of the poly(ethylene glycol)-mediated model membrane fusion. Biochemistry. 2002;41:10866–10876. doi: 10.1021/bi020269q. [DOI] [PubMed] [Google Scholar]
- 28.Siegel D.P. Energetics of intermediates in membrane fusion: comparison of stalk and inverted micellar intermediate mechanisms. Biophys. J. 1993;65:2124–2223. doi: 10.1016/S0006-3495(93)81256-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Markin V.S., Albanesi J.P. Membrane fusion: stalk model revisited. Biophys. J. 2002;82:693–712. doi: 10.1016/S0006-3495(02)75432-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Monck J.R., Fernandez J.M. The fusion pore and mechanisms of biological membrane fusion. Curr. Opin. Cell Biol. 1996;8:524–533. doi: 10.1016/s0955-0674(96)80031-7. [DOI] [PubMed] [Google Scholar]
- 31.Müller M., Katsov K., Schick M. A new mechanism of model membrane fusion determined from Monte Carlo simulation. Biophys. J. 2003;85:1611–1623. doi: 10.1016/S0006-3495(03)74592-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Jahn R., Grubmüller H. Membrane fusion. Curr. Opin. Cell Biol. 2002;14:488–495. doi: 10.1016/s0955-0674(02)00356-3. [DOI] [PubMed] [Google Scholar]
- 33.Roux A., Uyhazi K., Frost A., Camilli P.D. GTP-dependent twisting of dynamin implicates constriction and tension in membrane fission. Nature. 2006;441:528–531. doi: 10.1038/nature04718. [DOI] [PubMed] [Google Scholar]
- 34.Royle S.J., Lagnado L. Endocytosis at the synaptic terminal. J. Physiol. 2003;553:345–355. doi: 10.1113/jphysiol.2003.049221. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Kuhmann S.E., Platt E.J., Kozak S.L., Kabat D. Cooperation of multiple CCR5 coreceptors is required for infections by human immunodeficiency virus type 1. J. Virol. 2000;74:7005–7015. doi: 10.1128/jvi.74.15.7005-7015.2000. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Moore J.P., Doms R.W. The entry of entry inhibitors: a fusion of science and medicine. Proc. Natl. Acad. Sci. USA. 2003;100:10598–10602. doi: 10.1073/pnas.1932511100. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Reeves J.D., Gallo S.A., Ahmad N., Miamidian J.L., Harvey P.E. Sensitivity of HIV-1 to entry inhibitors correlates with envelope/coreceptor affinity, receptor density, and fusion kinetics. Proc. Natl. Acad. Sci. USA. 2002;99:16249–16254. doi: 10.1073/pnas.252469399. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Este J.A., Telenti A. Virus entry: open sesame. Lancet. 2007;370:81–88. [Google Scholar]
- 39.Reference deleted in proof.
- 40.Brandenburg B., Zhuang X. Virus trafficking-learning from single virus tracking. Nat. Rev. Microbiol. 2007;5:197–208. doi: 10.1038/nrmicro1615. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Sieczarski S.B., Whittaker G.R. Influenza virus can enter and infect cells in the absence of clathrin-mediated endocytosis. J. Virol. 2002;76:10455–10464. doi: 10.1128/JVI.76.20.10455-10464.2002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Seisenberger G., Ried M.U., Endre T., Bning H., Hallek M. Real-time single-molecule imaging of the infection pathway of an adeno-associated virus. Science. 2001;294:1929–1932. doi: 10.1126/science.1064103. [DOI] [PubMed] [Google Scholar]
- 43.Platt E.J., Durnin J.P., Shinde U., Kabat D. An allosteric rheostat in HIV-1 gp120 reduces CCR5 stoichiometry required for membrane fusion and overcomes diverse entry limitations. J. Mol. Biol. 2007;374:64–79. doi: 10.1016/j.jmb.2007.09.016. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Grunewald K., Desai P., Winkler D.C., Heymann J.B., Belnap D.M. Three-dimensional structure of herpes simplex virus from cryo-electron tomography. Science. 2003;302:1396–1398. doi: 10.1126/science.1090284. [DOI] [PubMed] [Google Scholar]
- 45.Bukrinskaya A.G. HIV-1 assembly and maturation. Arch. Virol. 2004;149:1067–1082. doi: 10.1007/s00705-003-0281-8. [DOI] [PubMed] [Google Scholar]
- 46.Kol N., Shi Y., Tsvitov M., Barlam D., Shneck R.Z. A stiffness switch in human immunodeficiency virus. Biophys. J. 2007;92:1777–1783. doi: 10.1529/biophysj.106.093914. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Matarrese P., Malorni W. Human immunodeficiency virus (HIV)-1 proteins and cytoskeleton: partners in viral life and host cell death. Cell Death Differ. 2005;12:932–941. doi: 10.1038/sj.cdd.4401582. [DOI] [PubMed] [Google Scholar]
- 48.Qi S.Y., Groves J.T., Chakraborty A.K. Synaptic pattern formation during cellular recognition. Proc. Natl. Acad. Sci. USA. 2001;98:6548–6553. doi: 10.1073/pnas.111536798. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.Sieczkarski S.B., Whittaker G.R. Dissecting virus entry via endocytosis. J. Gen. Virol. 2002;83:1535–1545. doi: 10.1099/0022-1317-83-7-1535. [DOI] [PubMed] [Google Scholar]
- 50.Rust M.J., Lakadamyali M., Zhang F., Zhuang X. Assembly of endocytic machinery around individual influenza viruses during viral entry. Nat. Struct. Mol. Biol. 2004;11:567–573. doi: 10.1038/nsmb769. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51.Shraimin B.I. On the role of assembly kinetics in determining the structure of clathrin cages. Biophys. J. 1997;72:953–957. doi: 10.1016/s0006-3495(97)78729-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 52.Mahy B.W.J., Compans R.W., editors. Immunobiology and Pathogenesis of Persistent Virus Infections. Taylor & Francis, Abingdon; Oxfordshire, UK: 1996. [Google Scholar]
- 53.Wilson W.R., Sande M.A., editors. Current Diagnosis and Treatment in Infectious Diseases. McGraw-Hill Professional; Chicago, IL: 2001. [Google Scholar]
- 54.Clarke R.W., Monnier N., Li H., Zhou D., Browne H. Two-color fluorescence analysis of individual virions determines the distribution of the copy number of proteins in herpes simplex virus particles. Biophys. J. 2007;93:1329–1337. doi: 10.1529/biophysj.107.106351. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 55.Zhu P., Liu J., Bess J., Chertova E., Lifson J.D. Distribution and three-dimensional structure of AIDS virus envelope spikes. Nature. 2006;441:847–852. doi: 10.1038/nature04817. [DOI] [PubMed] [Google Scholar]
- 56.Zhu P., Chertova E., Bess J., Lifson J.D., Arthur L.O. Electron tomography analysis of envelope glycoprotein trimers on HIV and simian immunodeficiency virus virions. Proc. Natl. Acad. Sci. USA. 2003;100:15812–15817. doi: 10.1073/pnas.2634931100. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 57.Myszka D.G., Sweet R.W., Hensley P., Brigham-Burke M., Kwong P.D. Energetics of the HIV gp 120–CD4 binding reaction. Proc. Natl. Acad. Sci. USA. 2000;97:9026–9031. doi: 10.1073/pnas.97.16.9026. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 58.Choe H., Martin K.A., Farzan M., Sodroski J., Gerard N.P. Structural interactions between chemokine receptors, gp120 Env and CD4. Semin. Immunol. 1998;10:249–257. doi: 10.1006/smim.1998.0127. [DOI] [PubMed] [Google Scholar]
- 59.Liu S., Fan S., Sun Z. Structural and functional characterization of the human CCR5 receptor in complex with HIV gp120 envelope glycoprotein and CD4 receptor by molecular modeling. J. Mol. Model. 2003;9:329–336. doi: 10.1007/s00894-003-0154-9. [DOI] [PubMed] [Google Scholar]
- 60.Finnegan C.M., Rawat S.S., Cho E.H., Guiffre D.L., Lockett S. Sphingomyelinase restricts the lateral diffusion of CD4 and inhibits human immunodeficiency virus fusion. J. Virol. 2007;81:5294–5304. doi: 10.1128/JVI.02553-06. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 61.Shen W.-C., Louie S.G. CRC Press; Boca Raton, FL: 1999. Immunology for Pharmacy Students. [Google Scholar]
- 62.Shaw A.J., editor. Epithelial Cell Culture: A Practical Approach. Oxford University Press; Oxford, UK: 1996. [Google Scholar]
- 63.Platt E.J., Wehrly K., Kuhmann S.E., Chesebro B., Kabat D. Effects of CCR5 and CD4 cell surface concentrations on infections by macrophagetropic isolates of human immunodeficiency virus type 1. J. Virol. 1998;72:2855–2864. doi: 10.1128/jvi.72.4.2855-2864.1998. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 64.Baumann H., Keller R. Which glycosaminoglycans are suitable for antithrombogenic or athrombogenic coatings of biomaterials? Part II: Covalently immobilized endothelial cell surface heparan sulfate (ESHS) and heparin (HE) on synthetic polymers and results of animal experiments. Semin. Thromb. Hemost. 1997;23:215–223. doi: 10.1055/s-2007-996093. [DOI] [PubMed] [Google Scholar]


