X-ray vs. NMR structures as templates for computational protein design

Abstract

Certain protein-design calculations involve using an experimentally determined high-resolution structure as a template to identify new sequences that can adopt the same fold. This approach has led to the successful design of many novel, well-folded, native-like proteins. Although any atomic-resolution structure can serve as a template in such calculations, most successful designs have used high-resolution crystal structures. Because there are many proteins for which crystal structures are not available, it is of interest whether NMR templates are also appropriate. We have analyzed differences between using X-ray and NMR templates in side-chain repacking and design calculations. We assembled a database of 29 proteins for which both a high-resolution X-ray structure and an ensemble of NMR structures are available. Using these pairs, we compared the rotamericity, χ₁-angle recovery and native-sequence recovery of X-ray and NMR templates. We carried out design using RosettaDesign on both types of templates, and compared the energies and packing qualities of the resulting structures. Overall, the X-ray structures were better templates for use with Rosetta. However, for ∼20% of proteins, a member of the reported NMR ensemble gave rise to designs with similar properties. Re-evaluating RosettaDesign structures with other energy functions indicated much smaller differences between the two types of templates. Ultimately, experiments are required to confirm the utility of particular X-ray and NMR templates. But our data suggest that the lack of a high-resolution X-ray structure should not preclude attempts at computational design if an NMR ensemble is available.

Introduction

Protein design was cast in 1983 as an “inverted” folding problem by Pabo, who discussed how finding sequences compatible with a given structure might be easier than predicting how a sequence folds¹. The inverted folding problem requires identifying combinations of amino acids that fit well onto a designated structural template, similar to solving a complex and combinatorial molecular jigsaw puzzle. In the 1990s this approach to protein design was rendered practical for real problems by the advent of powerful algorithms and fast computers^2-4. Since that time, many experimentally validated examples have shown that not only folds, but also functions, can be encoded in protein sequences rationally using such procedures^4-14.

Despite very significant progress, many basic questions related to computational protein-design methodology remain. One important issue is how to choose a structural template for the target^{8, 11, 15}. Building a target structure from scratch (de novo protein design) has been successful in a few cases^{10, 11, 13, 16}, but a much more common approach is to use an existing high-resolution structure. This guarantees that the target backbone is “designable,” i.e. that at least one sequence exists that will adopt the desired structure.

Most protein-design studies have used high-resolution structures solved using X-ray diffraction as templates^{5, 6, 8, 17-19}. In only a few examples have structures solved using nuclear magnetic resonance (NMR) been employed, and even fewer of these examples have been experimentally characterized^{20, 21}. Yet the number of structures solved by NMR in the protein data bank (PDB)²² has significantly increased over the last ten years, and a relatively small fraction of all NMR structures are also solved by X-ray crystallography. This means that for many possible design candidates, only NMR templates are available.

Beyond expanding the range of accessible protein targets, there could be other advantages to using NMR structures for design. Solution structures are free of artifacts from crystal packing interactions, and NMR structural ensembles that result from refinement, in contrast to the single structures from X-ray studies, may also provide a way to account for backbone flexibility in protein design. Backbone flexibility has been shown to be important for increasing the diversity of designed sequences^{8, 23}.

It is not obvious, however, that NMR structures provide suitable templates for current protein-design methods, which have been developed primarily for use with X-ray structures. Many people have suggested that NMR ensembles, which represent sets of structures consistent with measured constraints and stereochemical principles, are less accurate and precise than structures arising from high-resolution X-ray diffraction experiments^24-26. A study comparing the use of NMR and X-ray structures as starting points for molecular dynamics simulations found NMR derived structures to be less stable²⁷. And Lee et al. observed in molecular mechanics-Poisson/Boltzmann calculations that NMR structures of water soluble proteins were energetically less favorable than a significant number of structural decoys, in contrast to results obtained using X-ray structures²⁸. Finally, Kuhlman et al. reported that protein-design results obtained from NMR templates using Rosetta gave higher design energies and lower sequence recoveries than X-ray templates²⁹. A complicating issue is that the validation of NMR structure quality is difficult. There is no equivalent of the R_free value that is used to measure the agreement between the experimental data and the modeled structure in X-ray crystallography^{30, 31}. Although several groups have proposed methods to assess NMR goodness-of-fit^32-35, there is still no metric that is generally accepted and widely applied.

Here we explore whether NMR structures are likely to be suitable as templates for protein design. Although this question can only be answered definitively by carrying out large numbers of experiments, NMR structures can be compared to X-ray structures in terms of their behavior in tests related to protein-design calculations. We used X-ray structures as a standard because of their demonstrated utility in large numbers of published design studies. For our analyses, we compiled 29 proteins with structures solved by both high-resolution X-ray crystallography and NMR. We analyzed the side-chain conformations of these structures and compared the behavior of NMR and high-resolution X-ray structures in side-chain repacking calculations. Then, we designed sequences using RosettaDesign on both types of templates to probe the “designability” of NMR templates. Our results suggest that X-ray structures provide better templates when using Rosetta but that NMR ensemble members may also be suitable for use in real design applications for a subset of structures.

Results

A test set of X-ray/NMR structure pairs for comparison using discrete conformational modeling

We compiled the set of 29 X-ray/NMR structure pairs shown in Table I as described in the Methods. The tested proteins all have X-ray structures with resolution < 2.0 Å, and range in length from 90 to 226 residues. In each case, an ensemble of NMR-derived structures with between 10 and 45 members is available. We used the protein structure validation software suite (PSVS)³⁶ to compute quality scores based on PROCHECK³⁷, PROCHECK NMR³⁸ and MolProbity³⁹. Results were reported as Z-scores relative to values for high-resolution X-ray structures. Z scores of large magnitude indicate high deviations from expected structural properties. All native structures were evaluated and additionally, prior to evaluation, all structures were subjected to a brief minimization procedure to regularize stereochemistry according to the CHARMM param19 force field (referred to as C-RELAX, see Methods). The quality scores before and after minimization are in Table II.

Table I. Test set of X-ray/NMR structure pairs used for comparison calculations.

PDB ID		X-ray Resolution (Å)	Number of NMR structures	Residues	Core residuesa		Cluster sites
X-ray	NMR				Number of core residues	Fraction of total residues	Number of cluster residues	Fraction of total residues
1AGI	1GIO	1.5	10	125	76	0.61	27	0.22
1BED	2IJY	2	22	181	81	0.45	43	0.24
1BP2	1BVM	1.7	20	123	65	0.53	26	0.21
1C44	1QND	1.5	20	123	71	0.58	25	0.20
1CHN	1DJM	1.78	27	126	66	0.52	28	0.22
1EKG	1LY7	1.8	15	119	71	0.60	28	0.24
1FKJ	1FKR	1.7	20	102	58	0.57	21	0.21
1GNU	1KOT	1.75	15	117	57	0.49	28	0.24
1GPR	1AX3	1.9	16	158	83	0.53	38	0.24
1GSV	3PHY	1.75	26	122	65	0.53	26	0.21
1HCV	1G9E	1.85	20	116	56	0.48	34	0.30
1IFB	1AEL	1.96	20	131	67	0.51	30	0.23
1IFR	1IVT	1.4	15	111	64	0.58	30	0.27
1J2A	1CLH	1.8	12	159	80	0.50	37	0.23
1JF4	1VRE	1.4	29	140	79	0.56	34	0.24
1KF5	2AAS	1.15	32	124	70	0.56	30	0.24
1KM8	1BC4	1.9	15	105	55	0.52	17	0.16
1LDS	1JNJ	1.8	20	97	48	0.49	25	0.26
1MG4	1UF0	1.5	20	101	46	0.46	21	0.21
1OPC	2JPB	1.95	20	99	67	0.68	19	0.19
1RRO	2NLN	1.3	20	108	53	0.49	19	0.18
1UOH	1TR4	2	20	223	81	0.36	43	0.19
1WHO	1BMW	1.9	38	89	55	0.62	22	0.25
1YV6	1PU3	1.78	20	103	70	0.68	17	0.17
2CWR	2CZN	1.7	38	97	53	0.55	27	0.28
2E1F	2DGZ	2	20	94	42	0.45	16	0.17
2GRC	2H60	1.5	11	105	50	0.48	14	0.13
2SAK	1SSN	1.8	20	121	68	0.60	29	0.24
2V75	2JPS	1.8	45	89	45	0.51	17	0.19
Min		1.15	10	89	42	0.36	14	0.13
Max		2	45	223	83	0.68	43	0.29
Mean		1.72	21.59	120.97	63.52	0.53	26.59	0.22
Std. dev.		0.22	8.18	29.07	11.86	0.07	7.76	0.04

^aas defined by FindCore (Snyder, Montelione 2005)

Table II. PROCHECK and MolProbity Z-scores for the test set, before and after minimizing the structures.

PDB ID		Quality
		No minimization				Minimized structures
		PROCHECK		Molprobity		PROCHECK		Molprobity		H-bond coincidencea
X-ray	NMR	X-ray	NMRa	X-ray	NMRa	X-ray	NMRa	X-ray	NMRa
1AGI	1GIO	-0.87	-2.28	0.58	1.31	-0.98	-1.22	0.84	0.49	0.61
1BED	2IJY	0.43	0.94	0.02	-22.37	0.83	0.9	0.74	-0.14	0.82
1BP2	1BVM	1.18	-0.43	-1.46	-8.61	0.67	0.28	0.23	0.32	0.79
1C44	1QND	-0.55	-2.32	-9.66	-0.14	-0.63	-1.49	0.43	0.37	0.63
1CHN	1DJM	0.71	-0.31	0.91	0.24	0.75	0.59	1.18	0.32	0.70
1EKG	1LY7	0.28	-3.5	-0.89	-5	-0.24	-1.53	0.88	0.6	0.70
1FKJ	1FKR	-0.55	-4.8	1.09	-3.49	-1.49	-1.22	0.98	0.89	0.77
1GNU	1KOT	0.35	-3.03	-0.56	-17.79	0.04	-0.39	0.92	0.23	0.80
1GPR	1AX3	-1.26	-3.54	-0.71	0.51	-1.61	-2.95	1.02	0.11	0.66
1GSV	3PHY	-0.35	-3.78	-0.31	-20.53	-0.59	-0.47	0.88	-0.09	0.71
1HCV	1G9E	-1.22	-3.82	-1.16	-8.41	-1.53	-2.12	0.62	-0.03	0.73
1IFB	1AEL	-1.18	-7.59	-4.57	-31.53	-1.18	-4.48	0.88	-1.43	0.49
1IFR	1IVT	-1.46	-3.54	-1.17	-1.84	-0.98	-2.36	0.63	-0.23	0.67
1J2A	1CLH	-1.22	-7.12	-1.1	-39.06	-1.61	-1.34	0.82	-0.28	0.61
1JF4	1VRE	2.24	-0.34	0.84	-13.98	2.32	1.57	1.27	0.03	0.78
1KF5	2AAS	-0.2	-1.38	0.51	-1.91	-0.35	-0.87	0.69	0.03	0.75
1KM8	1BC4	-0.83	-4.52	-0.88	-7.85	-1.49	-2.87	0.8	0.08	0.64
1LDS	1JNJ	-1.1	-3.89	0.22	0.38	-1.22	-2.64	1.2	0.09	0.57
1MG4	1UF0	-0.94	-2.32	0.57	-0.97	1.18	-1.61	0.83	0.83	0.65
1OPC	2JPB	-0.43	-2.83	-3.57	-9.29	-1.26	-0.16	1.1	0.39	0.74
1RRO	2NLN	1.65	-1.89	0.58	-22.11	1.06	-1.18	1.21	-0.82	0.59
1UOH	1TR4	0.9	0	0.1	-13.06	0.67	0.55	0.71	0.02	0.78
1WHO	1BMW	-0.71	-6.57	0.78	-7.14	-1.3	-1.97	0.78	0.55	0.59
1YV6	1PU3	-0.63	-2.08	-1.53	-4.19	-1.02	-1.46	0.27	-0.01	0.88
2CWR	2CZN	-1.42	-4.09	-0.02	-32.74	-1.57	-2.36	0.69	0.16	0.76
2E1F	2DGZ	1.46	-1.69	0.14	-5.4	1.18	0.75	0.83	0.6	0.86
2GRC	2H60	2.01	1.38	0.83	-2.31	1.65	1.3	0.95	0.72	0.79
2SAK	1SSN	-0.59	-4.13	0.74	1.45	-0.98	-3.27	0.83	0.49	0.60
2V75	2JPS	2.64	2.12	0.16	-9.45	2.4	1.89	0.9	0.6	0.86
Min		-1.46	-7.59	-9.66	-39.06	-1.61	-4.48	0.23	-1.43	0.49
Max		2.64	2.12	1.09	1.45	2.4	1.89	1.27	0.89	0.88
Mean		-0.06	-2.67	-0.67	-9.84	-0.25	-1.04	0.83	0.17	0.71
Std. dev.		1.19	2.37	2.16	11.04	1.25	1.57	0.25	0.48	0.10

^aValues for NMR structures are averages over members of the ensemble.

PROCHECK and PROCHECK_NMR assess the molecular geometries of main-chain bond lengths, bond angles and dihedral angles. The 29 test-set X-ray-structure PROCHECK Z-scores ranged from -1.46 to 2.46, with an average of -0.06. This confirms the overall good stereochemical quality of the X-ray structures in our test set³⁶.

The relaxed X-ray structures had a similar average Z-score of -0.25. PROCHECK Z-scores for NMR structures ranged from -7.59 to 2.12 with an average of -2.67. This is similar to the mean Z-score for NMR structures reported in a large-scale test by Bhattacharya et al.³⁶. Seven of our 29 NMR structures had PROCHECK Z-scores < -4, indicating unfavorable backbone conformations, but relaxation improved the average over all NMR structures to -1.04, with only one relaxed structure still giving a PROCHECK Z-score < -4 (1AEL).

MolProbity is used to detect unfavorable contacts and atomic overlaps within protein structures³⁹. The MolProbity Z-scores for the X-ray structures in the test set ranged from -9.66 to 1.06, with an average of -0.67, suggesting that there are only minor clashes in the high-resolution structures. Minimization removes most of the clashes, as reflected by the range of 0.23 - 1.27 (mean = 0.83) for the minimized structures. The NMR set has numerous structures with extremely low MolProbity Z-scores (-39.05 - 1.45, mean = -9.84), but the average Z-score for relaxed NMR structures, 0.17, falls in the range expected for high-resolution crystal structures.

We also examined the backbone hydrogen bonds formed in the different structures. Garbuzynskiy et al. have demonstrated backbone hydrogen bonding differences between X-ray and NMR structures⁴⁰. Using the metric proposed by Ramelot et al. for backbone hydrogen-bond coincidence⁴¹, we found an average of 65.2% coincidence between X-ray and NMR structures for our structure set, which was improved to 70.2% following C-RELAX minimization.

Overall, compared with the values reported by Bhattacharya et al.³⁶, the quality of our test set of X-ray and NMR structures agrees well with the average scores of a larger number of structures. Also, a small amount of relaxation via minimization improves the quality of both X-ray and NMR structural templates.

For each structure pair, we selected two different clusters of residues: a buried cluster of 14 - 43 residues and a surface cluster of 7 – 25 residues. For many applications, it is common to redesign a relatively small fraction of the total protein sequence (e.g. in design of a binding site or engineering of protein mutants with higher thermostabilities)⁴². Buried clusters were chosen to reduce the influence of crystal packing on native-χ₁-angle and native-sequence recovery, and to allow the comparison of more accurate side-chain repacking results. Energy functions used in design calculations typically perform better when satisfying packing constraints of the protein core as opposed to modeling solvent interactions and electrostatics on the surface. And core designs tend to give relatively high native-sequence recoveries, which were used in this work to assess candidate templates. For these reasons, most analyses in this work were carried out using only the buried clusters. However, because some applications may require the design of surface sites, surface clusters were included for selected comparisons (where explicitly noted). The design of surface-residue clusters does not reflect expected performance in problems such as protein interface design, or enzyme active site design, because the presence of a protein partner or substrate will introduce significant additional constraints.

Both buried and surface clusters were chosen from core regions of the test-set structures as defined using the program FindCore²⁵. Core regions have only a small amount of coordinate variation between NMR ensemble members and thus identify those parts of the protein that are best defined by an NMR experiment. For example, the average pair-wise backbone RMSD for the buried design cluster residues was < 1.1 Å for all but 2 NMR structures.

NMR ensembles contain highly rotameric structures

We investigated the side-chain configuration of the NMR structures compared to their X-ray counterparts by evaluating the “rotamericity” of each structure. Rotamer libraries compile statistics describing side-chain conformations in high-quality structures in the PDB, and analysis of such libraries shows that most side chains exhibit strong χ₁ and χ₂ preferences. Most rotamer libraries, including the one that we used, are derived using X-ray, not NMR, structures⁴³. A side-chain conformation was defined as “rotameric” in this study if its χ₁ value was within 40 degrees of a member of the rotamer library, using the minimized structures described above and in the Methods (method C-RELAX). The rotamericity of a cluster was defined as the percentage of design-cluster sites that were rotameric. The rotamericity of a structure may be important for protein design because if a residue adopts a non-rotameric conformation, it may not be possible to fit even the native amino acid into its appropriate position in the structure.

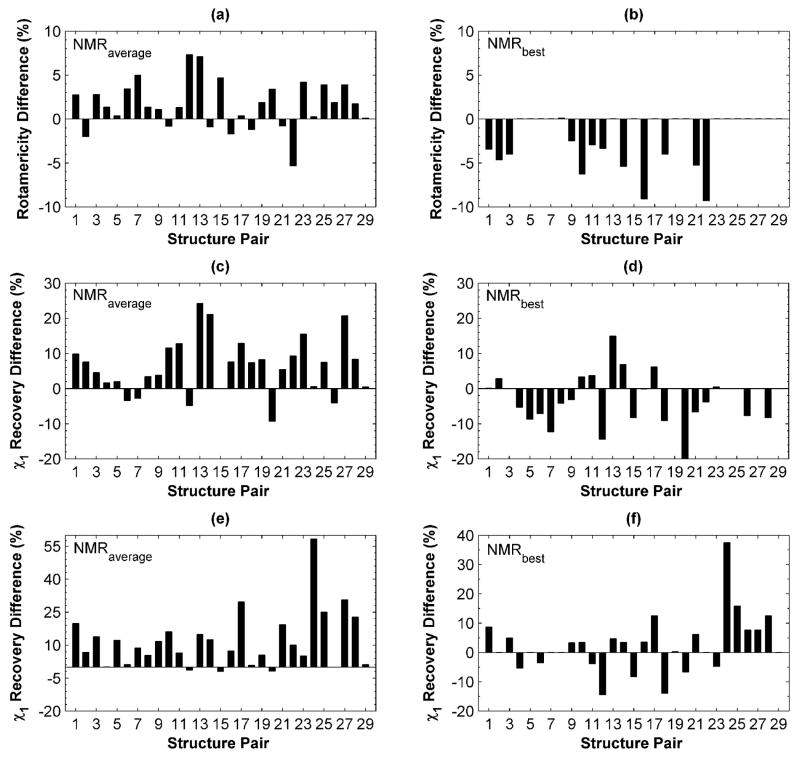
The χ₁ rotamericity for the test-set X-ray structures was high: 100% for 19 of 29 structures and higher than 90% for all but one example, indicating that only one or two design-site χ₁ rotamers were not represented in the rotamer library. Compared to the X-ray set, the average rotamericity of the NMR structures was lower (97.3% for X-ray vs. 91.9% for NMR). The average difference in rotamericity with respect to the X-ray structure, for all members within each NMR ensemble, is shown in Figure 1 (a). Only 7 NMR structures showed higher average rotamericities. However, most (27 of 29) NMR ensembles included at least one structure with 90% rotamericity or higher, and in all cases an ensemble member that was at least as rotameric as the X-ray structure was identified (Figure 1 (b)). Thus, although NMR structures are less rotameric on average, highly rotameric templates can nevertheless be identified.

Figure 1. Side-chain repacking performance on X-ray and NMR templates.

In panels (a), (c) and (e) performance on the X-ray template is compared to the average performance over all NMR templates in the corresponding ensemble. In panels (b), (d) and (f) performance on the X-ray template is compared to performance on the best-performing NMR template. (a) and (b) Differences in rotamericity between X-ray and NMR templates (see text). Values are positive for pairs in which the X-ray structure is better described using the rotamer approximation. (c) - (f) Recovery of the χ₁ angle in the structure upon re-packing the entire cluster. For (c) and (d) repacking was done using the CHARMM-based energy function. For (e) and (f) repacking was done using RosettaDesign.

Many NMR ensembles contain structures that perform well in side-chain repacking tests

Repacking of side chains, i.e. selecting the best rotamer for each residue at each site, given a fixed sequence, is a key step in almost every computational protein design algorithm. Good design protocols applied to good structural templates should recognize that the native sequence fits well on its own backbone, using mostly native-like rotamers for buried residues. We used two different protocols to assess repacking of native sequences on CHARMM-based pre-relaxed X-ray and NMR backbones (C-RELAX, see Methods) in the test set. The first was a CHARMM-based approach that employed dead-end elimination search, similar to that employed by Ali et al.⁵. The second was the widely used program RosettaDesign¹¹. We judged repacking performance using χ₁-angle recovery and compared energies for re-packing NMR templates to re-packing X-ray templates.

Native χ₁-angle recovery was high on X-ray templates: 23 out of the 29 X-ray structures gave better than 90% χ₁ recovery, 4 X-ray structures had recovery rates ≥ 80% and 2 structures performed below 80%. Differences between X-ray and NMR performance are shown in Figure 1, panels (c) – (f). Using either CHARMM-based or RosettaDesign methods, χ₁ recovery averaged over NMR backbones in an ensemble was worse than that for X-ray templates for most structure pairs. As in the rotamericity analysis, however, an NMR template with χ₁ recovery close to the X-ray template was found for many structure pairs. The results varied according to which repacking method was used. In both cases (Figure 1 (d) and (f)) NMR templates could be identified that gave equivalent or higher χ₁ recovery than the X-ray template; there were 22 such test-set examples using the CHARMM method and 15 using Rosetta (13 of which overlapped). Rosetta exhibits a greater preference than the CHARMM procedure for the X-ray structure.

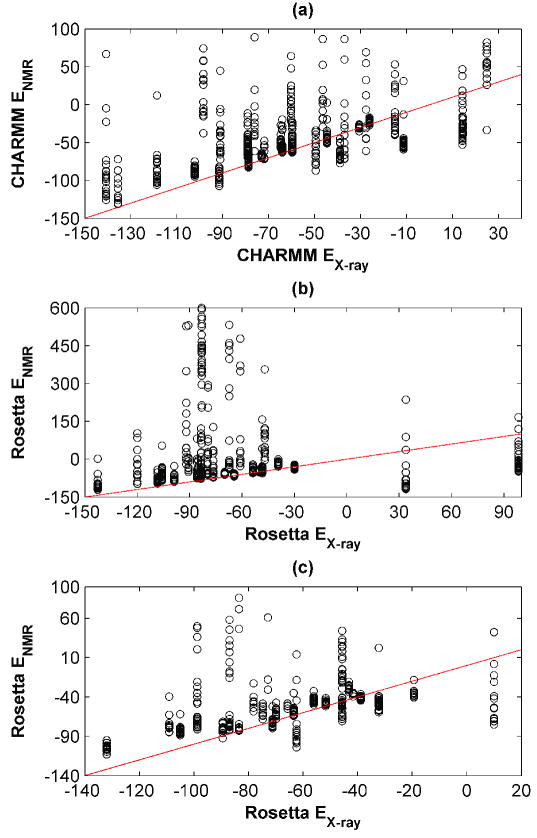
Repacking energies are shown in Figure 2, where the energy obtained using the X-ray structure is plotted against the energy for each NMR ensemble structure. There is a significant difference between repacking methods. Using the CHARMM-based protocol, the repacked energies for most NMR structures were higher than the corresponding X-ray energy. However, for 17 out of 29 structure pairs, the lowest energy NMR solution provided a lower energy than its X-ray counterpart. In contrast, Rosetta showed a greater preference for X-ray templates. The spread of the NMR repacking energies was very large for some ensembles (Figure 2 (b)), suggesting that most of the NMR ensemble members could not accommodate the native sequence well using the approximations of RosettaDesign. Excluding two structure pairs where Rosetta gave extremely large, unrealistic data for the X-ray templates (see Figure 2 (b)), only 7 of the test-set examples included an NMR template that gave an energy less than 2 kcal/mol greater than that for the X-ray template. Here, and below, the arbitrary choice of a 2 kcal/mol cutoff is intended to capture those NMR designs that are “better than or almost as good as” an X-ray design. The trends in the results are not highly sensitive to choice of cutoff in the 0-4 kcal/mol range.

Figure 2. Energies of repacked X-ray vs. NMR structures.

CHARMM (a) or Rosetta (b) were used to re-pack all clusters for all templates. Templates were prepared using the C-RELAX procedure. Repacking results using RosettaDesign with R-RELAX relaxed structures are depicted in panel (c). Repacking energies on NMR templates are plotted as a function of the repacking energy on the X-ray template, for each pair. Unreasonably high-energy outliers (highest 5 % of all energies) are not plotted for the sake of clarity.

In an attempt to better fit the native sequences onto their own native templates using Rosetta, we replaced the C-RELAX CHARMM-based pre-relaxation procedure with one guided by the Rosetta energy function (R-RELAX, see Methods). However, this still left several X-ray template models with very high energies, and also large energy ranges for the NMR ensembles. The R-RELAX procedure reduced the preference of Rosetta for the X-ray templates, however, leaving an average energy difference of just -1.6 ± 24.4 kcal/mol (when two structures with very high X-ray energies were excluded from the analysis). There were 11 out of 27 examples where the lowest-energy NMR model was no more than 2 kcal/mol higher in energy than the X-ray model.

Rosetta gives lower energy designs for X-ray templates than for most NMR templates

Due to the computational demands of treating 655 templates, only the computationally less expensive RosettaDesign method was used for design calculations. Sequences designed using Rosetta were also evaluated using other energy functions. Templates were prepared as for repacking, using the C-RELAX or R-RELAX procedures, and amino acids for all design-cluster sites were selected from an alphabet of 18 residues. Both C-RELAX and R-RELAX calculations gave similar results and showed a strong preference for the X-ray template over most NMR ensemble members, but a quite modest average preference for X-ray structures over the best available NMR template (Table III). For 6 or 9 examples (R-RELAX and C-RELAX, respectively), NMR templates provided a design within 2 kcal/mol of the X-ray design (Figure 3 (a) and (b)).

Table III. Properties of designs on X-ray vs. NMR templates.

	Method	avg. minimum NMR − Xray energy differencea	Native-sequence recovery			SASApack
			X-ray	NMR Bestb	NMR Average	X-ray	NMR Besta	NMR Average
buried	C-RELAX	6.7 ± 7.9	52.9 ± 14.2	49.9 ± 19.7	36.3 ± 13.0	2.7 ± 1.5	2.5 ± 1.8	4.2 ± 1.6
	R-RELAX	6.6 ± 6.8	56.5 ± 13.7	58.2 ± 15.7	45.6 ± 11.4	2.1 ± 1.8	2.0 ± 1.6	4.5 ± 1.8
	R-ITER	5.6 ± 7.1	70.2 ± 14.7	61.8 ± 13.1	53.2 ± 13.1	0.7 ± 2.0	0.8 ± 1.0	3.2 ± 1.6
surface	C-RELAX	2.13 ± 4.1	19.9 ± 8.8	28.5 ± 9.1	16.2 ± 6.5	1.07 ± 0.5	0.80 ± 0.6	1.52 ± 0.7
	R-RELAX	0.17 ± 7.9	22.2 ± 11.1	34.7 ± 9.8	20.8 ± 6.7	0.81 ± 0.6	0.49 ± 0.6	1.42 ± 0.6
	R-ITER	1.12 ± 3.5	30.7 ± 10.1	38.3 ± 9.6	24.1 ± 7.4	0.39 ± 0.6	0.19 ± 0.6	1.00 ± 0.6

^aThe average of the difference {(lowest-energy-NMR-design) − (X-ray design)} over all structure pairs.

^b“NMR Best” refers to the best native-sequence recovery or SASApack score among NMR designs with energies less than 2 kcal/mol above the X-ray design.

Figure 3. Design using RosettaDesign on X-ray vs. NMR templates.

Backbones were prepared in varying ways and sequences were designed on each structure, as described in the text. The design energies from the NMR templates are plotted as a function of the design energy on the X-ray template, for each pair. (a) C-RELAX method, (b) R-RELAX method, (c) R-ITER method. A small number of high-energy outliers are omitted for clarity (C-RELAX: 16, R-RELAX: 3, R-ITER: 0).

The RosettaDesign package has recently been expanded to allow iterative optimization of sequence and structure. This has proven effective in a number of applications^{11, 44, 45} and could make calculations less sensitive to the quality of the input structure. We used iterative sequence-structure optimization (R-ITER, see Methods) with the X-ray and NMR structures as starting geometries for the calculations summarized in Figure 3 (c). Interestingly, this made the range of the design energies significantly smaller and eliminated outliers, but did not alter the overall trends. The lowest energy NMR design was within 2 kcal/mol of the X-ray design for 7 examples. Iterative sequence-structure optimization should significantly expand the accessible sequence and structure space. The fact that our R-ITER derived designs are not much lower in energy may be due to the limited number of runs (ten per template) used. A more extensive search (100 runs) for one selected protein suggests that lower energy designs can be found by more extensive sampling, especially on the NMR template, for which there were larger fluctuations in energy throughout the simulation (data not shown).

The design calculations were repeated for the surface clusters, giving results that showed similar trends but gave better relative performance of the NMR structures compared to the X-ray templates. Tables III and IV summarize the results. While the spread of the design energies within an NMR ensemble remained large (several tens of kcal/mol in most cases), the lowest energy NMR design and the X-ray design were closer in energy, on average, than for buried clusters. A greater fraction of NMR designs have energies not above 2 kcal/mol of the X-ray design (C-RELAX: 13 out of 29; R-RELAX: 14 out of 27; R-ITER: 16 out of 27). It seems reasonable that surface designs would be less sensitive to the detailed structure of the template, as the potential for bad interactions is much lower.

Table IV. Percentage of structure pairs with at least one NMR ensemble member satisfying various criteria.

	Method	ENMR ≤ EX-ray + 2 kcal/mol (1)	(1) AND SASApackNMR ≤ SASApackX-ray + σS (2)	(1) AND NSRNMR ≥ NSRX-ray - σN (3)	All (4) (1) and (2) and (3)
buried	C-RELAX	31.0	27.6	27.6	27.6
	R-RELAX	22.2	18.5	18.5	14.8
	R-ITER	25.9	25.9	18.5	14.8
surface	C-RELAX	44.8	41.8	44.8	41.8
	R-RELAX	51.9	51.9	51.9	51.9
	R-ITER	59.3	48.1	55.6	44.4

For (2), (3) and (4) in columns 3-5, the percentage of structures pairs indicated met the criterion stated in the header for each column as well as criterion (1) in column 2. Symbols σ_S and σ_N indicate the standard deviation for native-sequence recovery and SASApack, respectively, for all X-ray designs. NSR stands for native-sequence recovery.

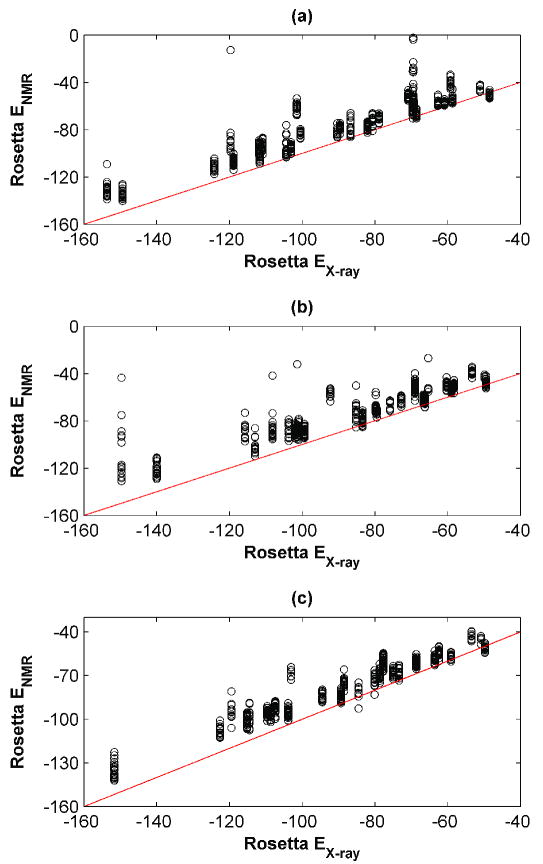
The systematic preference for X-ray designs over most NMR designs could be due to the energy function used in RosettaDesign. To explore this, we re-evaluated the Rosetta-designed buried clusters using a more physical, CHARMM-based energy function (see Methods). The results were very different from the Rosetta results for all three template-relaxation methods. The CHARMM-based function frequently predicted NMR-derived designs to have energies comparable to the corresponding X-ray designs (for 67 out of 83 total examples, considering all three design protocols, the best NMR design was no more than 2 kcal/mol higher than the X-ray, Figure S1; the corresponding number for Rosetta was 22 out of 83). Re-evaluation of the designs with the structure-based energy function FOLDEF⁴⁶ gave results intermediate between Rosetta and CHARMM, with 39 out of 83 of the lowest-energy NMR designs satisfying the 2 kcal/mol cutoff (Figure S2).

Other metrics suggest that the best NMR templates in an ensemble can be appropriate for design

It is not straightforward to interpret the results of Figure 3 in terms of their likely consequences for actual designs. Most protein-design energy functions do not achieve good correlation between predicted and measured energy differences, and design energy functions are very sensitive to the definition of the unfolded reference state⁴⁷. This makes it difficult to judge the significance of energy gaps in absolute terms or to reconcile differences such as those observed between Rosetta, CHARMM and FOLDEF energy evaluations. To partially address this, we compared two other properties of designs resulting from X-ray vs. NMR templates. The frequency with which the native amino acid is recovered at a design site is sometimes used as a metric^{29, 45}. High native-sequence similarity does not guarantee that designs will be of high quality, but the relative sequence recovery of different methods and templates can be used as a basis for comparison. Another measure is the packing of designed residues, which can be compared to packing of similar amino acids in similar environments using the SASApack metric of Hu et al.⁴⁴.

It is striking that although template-preparation methods C-RELAX, R-RELAX and R-ITER gave very similar lowest-energy-NMR vs. X-ray energy differences (Table III), the frequencies of native-sequence recovery were very different. Using Rosetta to modify the starting templates with R-REALX or R-ITER led to higher native-sequence recoveries. This was true for native-sequence recovery on the X-ray templates and for the average recovery on all NMR templates. Interestingly, examining the low-energy NMR designs with the highest native-sequence recovery showed a trend similar to the X-ray-template results (the “NMR best” column in Table III shows the best native-sequence recovery among NMR designs with energies no more than 2 kcal/mol higher than the X-ray design, averaged over structure pairs), These data support the proposition that some low-energy NMR designs behave similarly to X-ray templates and are thus probably suitable for use in protein-design applications.

SASApack data show a similar trend. For this measure, a larger then average difference (> 0) indicates poor packing due to the existence of small voids that cannot be filled with water⁴⁴. Values reported in Table III and below indicate average packing quality values for all designed residues. SASApack averaged over all NMR designs was high compared to that for the X-ray designs, for all methods. In fact, the average SASApack values for both X-ray and NMR designs were greater than for either the native X-ray or NMR structures (which were both very low). The design process increases SASApack values and, because SASApack does not penalize clashes, even the procedure of preparing the templates for design using a small amount of minimization increases these values (mean C-RELAX value of 1.45 for relaxed X-ray templates vs. 0.64 for native X-ray templates). This indicates that SASApack alone is not a good measure of structure quality, but as with native-sequence recovery, it can be used for comparisons.

Compared to the C-RELAX procedure, preparing structures with the Rosetta energy function (R-RELAX) improved the packing scores for X-ray derived designs. Using R-ITER design improved packing further, achieving values very close to the scores for the unchanged original PDB X-ray templates. SASApack scores for NMR structures were poor on average. But the best packed low-energy NMR structures (“NMR best”, Table III) behaved very similarly to the X-ray designs, again suggesting that these may be good templates.

As expected, the surface clusters gave much lower native-sequence recoveries than the core clusters. Compared to surface positions on average, however, both X-ray and the best NMR surface-design residues were of good quality, giving low SASApack values (Table III). Interestingly, although native-sequence recoveries were low at surface sites, NMR surface clusters gave higher recoveries than X-ray surface clusters.

Identifying good NMR templates

Among low-energy NMR designs, templates could be identified that had similar native-sequence recovery and SASApack scores as the X-ray designs. These are likely good candidate design templates, but how common are they? Table IV shows that for only 22 – 31% of test-set proteins was an NMR ensemble member identified that gave an energy comparable to or better than the X-ray design (using the Rosetta energy function, and depending on how the structures were relaxed). The table also quantifies how often at least one of the low-energy NMR designs had X-ray-like native-sequence recovery and/or SASApack scores. Good NMR templates were not very common by these criteria.

For real design applications, a slightly different question may be of interest: How frequently do NMR ensembles yield designs with high native-sequence recovery and low SASApack scores that are also low in energy? This is of interest because native-sequence recovery and SASApack can be evaluated in the absence of an X-ray template for energy comparison. Data are given in Table V. Using Rosetta energies, the frequencies were low (14 – 42%). But because other energy functions do not show as much X-ray bias as Rosetta, it was not uncommon to identify well-packed designs with high native-sequence recovery that had low CHARMM-based or FOLDEF energies. These may be reasonable design candidates.

Table V. Proportion of structure pairs for which at least one NMR design with X-ray-like SASApack and native-sequence recovery^a also had a low design energy.^b.

Method	Rosetta	CHARMM	FoldEF
C-RELAX	0.42 (8/19)	0.74 (14/19)	0.53 (10/19)
R-RELAX	0.27 (4/15)	0.73 (11/15)	0.40 (6/15)
R-ITER	0.14 (3/21)	0.62 (13/21)	0.38 (8/21)

^aNative-sequence recovery and SASApack scores within the range {X-ray value plus/minus one standard deviation} were considered X-ray-like.

^bA low design energy was an energy lower than 2 kcal/mol above the X-ray design energy.

We tested across the 29 structure pairs for correlations with NMR vs. X-ray design energy differences that might be predictive of good template performance. We chose the lowest-energy NMR design to represent each protein. Lowest-energy-NMR vs. X-ray design energy differences for R-RELAX and R-ITER correlated reasonably well with those for C-RELAX (R = 0.92, 0.82 respectively), suggesting that some of the same structure pairs showed good vs. bad performance in these methods. However, the design energy differences did not correlate well with PROCHECK score, rotamericity or χ₁-angle recovery. MolProbity provided some information for C-RELAX templates (R = -0.75) but this was not the case for R-RELAX or R-ITER. The repacking energy of the native sequence correlated quite well with design energy difference for R-RELAX and R-ITER (R = 0.91 and 0.78, respectively) but less so for C-RELAX (R = 0.57).

Significant noise in the calculations may preclude strong overall correlation of structure metrics with design performance, so we also examined whether increasingly stringent cutoffs could enrich templates in good design candidates. In general, good templates could not be confidently identified this way. For example, those NMR structures with the best MolProbity, PROCHECK or χ₁-angle recovery scores often gave designs with high energies, poor native-sequence recovery and/or poor packing (χ₁-angle recovery data are in Figure S3). However, templates with very poor χ₁-angle recovery scores consistently performed poorly in design, suggesting a strategy for identifying and eliminating some templates from consideration. For example, we permissively define as a “good candidate template” any NMR structure with a design energy within 10 kcal/mol of the X-ray design and also X-ray-like native-sequence recovery and SASApack (as defined in Table IV). Applying a χ₁-angle recovery cutoff of 80% can eliminate 29/37/36% of NMR structures from consideration while retaining 88/77/80% of good candidate templates (values are for C-RELAX/R-RELAX/R-ITER procedures). That is, good design templates infrequently have χ₁-angle recoveries less than 80%, and structures with χ₁-angle recovery higher than this are enriched in good templates (Figure S3).

We found that the hydrogen-bond coincidence of an NMR template with its corresponding X-ray structure correlated only very weakly with the difference in design energies between the two. But a high proportion of NMR templates with the very best hydrogen-bond coincidence values were good candidate designs (Figure S4). Also, we found that applying cutoffs based on hydrogen-bond coincidence could eliminate bad templates, much as in the χ₁-angle recovery analysis above. For example, using a hydrogen-bond coincidence cutoff of 70%, 33/47/42% of templates could be eliminated, leaving 82/64/74% of good candidate templates (defined as above, values are given for C-RELAX/R-RELAX/R-ITER). Although hydrogen-bond coincidence cannot be evaluated in the absence of a high-resolution X-ray structure, this nevertheless suggests that structure preparation/refinement methods that improve hydrogen-bond coincidence could potentially enrich NMR ensembles in appropriate design templates (see Discussion). Both C-RELAX and R-ITER gave modest improvements in hydrogen-bond coincidence relative to the initial PDB templates (70.2% and 68.5%, compared to 65.2%, respectively), with R-RELAX giving somewhat less improvement (67.1%).

Discussion

In this work we explored whether NMR structures can serve as good templates for protein design. Because protein-design energy functions and procedures are not highly reliable, it is not possible to answer this definitively without carrying out many experimental tests. In lieu of this, we evaluated a range of computable metrics that allowed us to compare the performance of NMR and X-ray structures. At a minimum, a protein-design procedure should give reasonable results when modeling native structures on native templates, and we explored this using side-chain repacking. An additional requirement, necessary but not sufficient for a good template, is that a design procedure return low-energy sequences with reasonable structural properties. Applying a range of criteria to evaluate design energy, native-sequence recovery and packing quality, our tests indicated that NMR ensemble members are, on average, not as useful as X-ray structures for design. However, in some cases, one or more members of an NMR ensemble could be identified that performed as well as, or better than, a high-quality X-ray structure of the same protein (Table III). These are good candidates for testing as protein-design templates.

Our results support the possible utility of NMR structures, despite an overall strong preference for X-ray templates when using RosettaDesign. Whether this preference reflects inherently higher quality or suitability of X-ray structures for design, or a pro-X-ray bias in RosettaDesign, is difficult to determine. However, a role for bias is suggested by the much better relative performance of NMR structures in the CHARMM-based repacking tests, (Figure 1 and 2) and in the CHARMM- and FOLDEF-based re-evaluations of Rosetta designs (Figures S1 and S2). It is not surprising that Rosetta exhibits a preference for X-ray structures over most NMR ensemble members. The rotamer library and energy function used in RosettaDesign are both parameterized using X-ray structures, and the method relies heavily on statistical terms derived from such structures in the PDB. The critical reference energies are optimized by maximizing the frequency with which native residues are recovered in X-ray-structure-based modeling.

We found significant differences in behavior when preparing the template structures in different ways. Pre-relaxation of the PDB-reported NMR structures consistently lowered the design energy of NMR templates, compared to energies obtained on untreated PDB templates. We recommend that at least this simple procedure be applied prior to any use of NMR structures in design calculations. In contrast, X-ray design energies on native PDB structures were relatively close to their relaxed-template design energies (data not shown). The C-RELAX protocol involved only a small amount of minimization, carried out to relieve steric clashes, and it did not change the structures very much. R-RELAX and R-ITER were introduced to prepare the structures in accord with the Rosetta energy function. In particular, R-ITER is a powerful method in which the template structure can be continuously updated throughout the design process. An interesting observation was that these different methods had little impact on the energy differences between NMR and X-ray designs, but showed a large effect at the sequence level. In particular, native-sequence recovery was higher for the R-RELAX method, and much higher for the R-ITER methods, than for C-RELAX. Also, R-ITER stood out because it achieved a low (native-structure-like) value of SASApack for designs on X-ray templates and for some low-energy NMR designs, in contrast to the other methods. Because the results of Rosetta are non-deterministic, it is appropriate to run a large number of calculations and evaluate the best results. We found that NMR design energies using R-ITER fluctuated more than X-ray design energies across runs (data not shown). Hence, more R-ITER design simulations per structure might be required to achieve a low energy sequence-structure combination on an NMR template. This was not tested here due to the large computational demands.

In the best case, techniques would exist for determining whether an NMR ensemble is likely to provide a good design template before calculations are undertaken, especially in those cases where an X-ray template is not available. We found that correlations between many different structural metrics and measures of design performance were weak. In particular, those NMR ensemble members that gave the lowest energy designs were not the ones with the highest native-sequence recovery or lowest SASApack values, suggesting that multiple criteria must be evaluated to judge the possible utility of an NMR model. MolProbity scores did correlate moderately with C-RELAX NMR vs. X-ray design energies, but didn't work well for R-RELAX or R-ITER. One approach to evaluating a prospective NMR template is to run design calculations and evaluate the results using metrics such as native-sequence recovery and SASApack, which can be compared to what is expected for good X-ray templates. This can be computationally expensive, especially when using iterative design, and good sequence recovery and packing do not indicate that designs will be low in energy. But we have not yet identified a way to determine a priori whether reasonable design energies can be obtained from an input NMR structure.

An alternative is to carry out more extensive pre-minimization or iterative optimization of the starting NMR structures. Recent work by Qian et al. and by Ramelot et al. suggests that NMR structures can be significantly improved by extensive refinement using Rosetta. In an analysis of human protein HSPC034, Ramelot et al. generated 1,000 candidate structures for each ensemble member, varying both backbone and side-chain positions. During this optimization, the average hydrogen-bond coincidence with a high-resolution X-ray structure improved from 65% to 71%. Although such a protocol was too computationally expensive to test extensively in this study, we did observe that templates that gave high hydrogen-bond coincidence were enriched in good candidate designs. This supports re-refinement or more extensive iterative refinement during design as an appealing option for attempting NMR-based design.

In summary, our results support the conclusion that while X-ray templates are to be preferred for protein design, NMR structures can provide promising templates for protein-design calculations in some cases. Of note, we examined design in core and surface regions of NMR structures with relatively low heterogeneity in the ensemble. This may be a best-case scenario. Even then, X-ray template performance was better than the average performance for NMR structures, by many metrics, especially when using RosettaDesign. This work did not address whether and how NMR templates may represent improvements over X-ray templates, because X-ray template performance was used as the standard. It is possible, however, that appropriate use of pre-minimized, pre-refined or iteratively refined NMR backbones may make protein-design calculations more effective by relaxing the fixed-backbone approximation and thus rendering a larger sequence space accessible to the designs. This type of advance may be increasingly important as the demands places on designed proteins, in terms of function, solubility, specificity and other features, increase.

Methods

Test set

The test set consisted of the 29 X-ray/NMR structure pairs listed in Table I. 19 of these were extracted from a data set by Andrec et al.⁴⁸ and 10 were identified directly from the PDB. The following criteria were used to include candidates in the test set: structures contained a single chain in both the X-ray and NMR examples; the X-ray structure had resolution ≤ 2 Ǻ; both proteins were derived from the same organism; structure pairs with significantly different conformations, insertions, deletions or a large number of mutations were excluded. Minor deviations in sequence (e.g. point mutations, if not at one of the cluster sites) were tolerated.

Definition of design/repack cluster sites

Clusters of sites to be repacked or designed were defined with the following procedure. First, FindCore²⁵ was used to identify core atoms within the NMR ensemble. FindCore employs an inter-atomic-variance-matrix (IVM)⁴⁹ to compute an order parameter ε that can be used to define a core atom set via a simple clustering algorithm. These core regions define sets of atoms with minor coordinate deviations within the NMR ensemble. Core residues were defined as those for which their Cα atom was a core atom. Second, the solvent accessible surface area relative to reference residues (SAS) was computed for the first NMR ensemble member and the X-ray structure using the program NACCESS⁵⁰, with a default probe value (1.4 Å). Every core residue with a relative SAS value ≤ 20% in both structures was defined to be a repack/design cluster site. Cluster sizes are given in Table I.

Structure preparation

To prepare the structure pairs for design calculations, we applied the following procedure. The sequences of the X-ray and NMR structures were aligned with ClustalW⁵¹. Non-overlapping sequence at the C- and N-termini, most likely arising from the use of different constructs in the X-ray and NMR experiments, were eliminated to generate structures with the same length. The truncated structures were renumbered to ease site-specific comparisons. Protons were added by using the HBUILD command in CHARMM with the CHARMM 19 parameter set⁵².

Because the deposited structures in the PDB do not necessarily coincide with a global or local minimum in most molecular force fields, structures were pre-relaxed prior to repacking and design calculations. Two different procedures were used.

In the C-RELAX method, energy minimization for each member of the NMR ensemble and for the X-ray structure was carried out using CHARMM. The energy function included van der Waals energy (100% radii), bond-stretching terms, bond-angle terms, dihedral-angle and improper-dihedral potentials. Electrostatics was modeled using the CHARMM Effective Energy Function (EEF1)⁵³ Minimization was carried out using 100 steps of steepest-descent minimization followed by 100 steps of adapted-basis Newton Raphson, with all atoms included (backbone and side-chain atoms). This number of steps was chosen because it accomplished most of the reduction in energy of longer minimizations, without significantly perturbing the structure.

In the R-RELAX method, RosettaDesign was used to re-optimize/fine-tune the structure using the native sequence. For this purpose, the sequence of each protein was used to generate 3- and 9-residue fragment libraries as described^{54, 55} PSIPRED was used for secondary structure prediction⁵⁶, and we excluded near homologs in the fragment search. Given the fragment libraries, RosettaDesign was used to adjust the native-protein structure via iterative side-chain and backbone optimization. During backbone optimization steps, segments of the structure were replaced with members of the fragment library, or small random perturbations in torsion angle space were performed. Ten independent runs for each X-ray or NMR structure were carried out, each consisting of thousands of small backbone adjustments, and the lowest-energy structure from the ten runs was used as input for fixed-backbone design. Sometimes this procedure dramatically altered the experimentally determined structure. This was deemed unrealistic, and an all-backbone atom RMSD limit of 4 Å from the experimental structure was imposed to eliminate some templates. This applied to 134 out of 655 structures.

Side-chain conformation analysis

To characterize the side-chain conformations of the NMR structures compared to the corresponding X-ray structures, we evaluated whether the conformations of design site side-chains were represented in the rotamer library of Dunbrack et al.⁴³. The relative fraction of design site side chains with a conformation represented in the rotamer library is referred to as “rotamericity”. Here a side-chain was defined to be rotameric, if its χ₁-angle was within 40 degrees of a member of the rotamer library using the minimized template structure. Side-chains that have no χ₁ variable, alanine, glycine and proline, were not included in this analysis.

Hydrogen-bond coincidence analysis

We used the method of Ramelot et al. to characterize backbone hydrogen bonding⁴¹. Briefly, those hydrogen bonds with DSSP energies < -0.5 kcal/mol were identified in each structure and a filter was applied to exclude bivalent hydrogen bonds. Hydrogen-bond coincidence between an X-ray and an NMR structure was defined as 100 • (number of hydrogen bonds in both structures)/(total hydrogen bonds, i.e. hydrogen bonds in either the X-ray or NMR structure). Coincidence values were computed for PDB entries (unmodified), C-RELAX and R-RELAX prepared templates, and R-ITER designs. In each case, NMR templates were compared to an X-ray template that was relaxed using the same technique. Because the analysis was applied only to backbone hydrogen bonds, coincidence values were meaningful even when comparing R-ITER designs that had different sequences.

Side-chain repacking calculations

Repack calculations were carried out with two different protocols – one based on a CHARMM energy functions and similar to that used by Ali et al.⁵, and RosettaDesign¹¹. The repack/design cluster residues were allowed to move, while all other residues of the protein were held fixed. The CHARMM-based method used a Dead-End-Elimination/A* algorithm^{2, 57} to find the optimal combination of rotamer conformations, given a rotamer library. The 2002 backbone-dependent rotamer library of Dunbrack et al. ⁴³ was used. The energy function included CHARMM param19 van der Waals (with 90% atomic radii), distance-dependent dielectric electrostatics with ε = 4r and EEF1 solvation. To report the energies of re-packed or designed clusters, we used a cluster energy defined as the full energy contribution of single residues and residue pairs within a cluster, plus 50% of the interaction energy of the cluster residues with the fixed residues.

Because the Monte Carlo search procedure in RosettaDesign is not deterministic, repacking using that program was performed 10 times for each structure and the lowest energy solution was used for analysis. RosettaDesign also used the backbone dependent rotamer library of Dunbrack et al.⁴³, with χ₁ and selected χ₂ angles expanded ± one standard deviation as described by Saunders et. al. ⁴⁵. The energy function used was very similar to that of Kuhlman et al.²⁹ and contained modified attractive and repulsive Lennard-Jones terms (95 % atomic radii), an implicit Lazaridis-Karplus solvation model⁵⁴, an internal rotamer energy derived using statistics⁴³, an intra-residue clash term, a statistics based pair term, a Ramachandran preference term for each amino acid, a side-chain-main chain orientation-dependent hydrogen bond term and a reference energy term. In repacking tests, rotamer-based χ₁ angles were considered to be equivalent to the X-ray or NMR structure values if these differed by < 40°.

RosettaDesign

All redesign calculations were done using RosettaDesign version 2.1. Design-cluster sites were allowed to mutate to any of the 20 common amino acids except proline or cysteine. Fixed-backbone redesign calculations were performed 100 times for each structure and the lowest energy solution was taken for analysis.

We tested the performance of the X-ray/NMR structure pairs in three different protocols that introduced varying amounts of structural variation to the original template. C-RELAX and R-RELAX are described above. The Rosetta flexible-backbone design method R-ITER involved iterative optimization of sequence (of the design-cluster residues) and structure (of all residues). The fragment libraries and torsional sampling described for the R-RELAX method (above) were used to sample backbone structures, and the starting structures were the R-RELAX templates. For R-ITER, changes to the protein sequence were performed and followed by re-optimization of the backbone structure. Starting with random sequences for the design-site residues, ten independent flexible-backbone design calculations, each consisting of ten sequence-design and backbone optimization cycles, were performed for each input template and the lowest energy designed structure was analyzed.

For all methods described above, the final energies reported were those resulting from the RosettaDesign calculations. Rosetta designs were also evaluated with other potential functions. To compute a CHARMM-based energy, designs were subjected to a small amount of relaxation after restoring 100% van der Waals radii. The relaxation was similar to C-RELAX, differing only in the respect that the backbone was held fixed. The re-evaluation was carried out with an energy function that included a CHARMM param 19 van der Waals term (100 % radii), a CHARMM param 19 torsion energy term, a Coulomb energy term with a dielectric constant of 4, CHARMM EEF1 for desolvation only (not interaction) and a polarization energy pair-wise screening term, computed from a generalized Born model⁵⁸ using PEP⁵⁹ to compute Born radii for the transfer of a protein with internal dielectric of 4 from dielectric of 4 to 80. All designs were also re-evaluated with the Fold-X energy function (FOLDEF)⁴⁶.