Comparing Mutational and Standing Genetic Variability for Fitness and Size in Caenorhabditis briggsae and C. elegans

Abstract

The genetic variation present in a species depends on the interplay between mutation, population size, and natural selection. At mutation-(purifying) selection balance (MSB) in a large population, the standing genetic variance for a trait (V_G) is predicted to be proportional to the mutational variance for the trait (V_M); V_M is proportional to the mutation rate for the trait. The ratio V_M/V_G predicts the average strength of selection (S) against a new mutation. Here we compare V_M and V_G for lifetime reproductive success (≈ fitness) and body volume in two species of self-fertilizing rhabditid nematodes, Caenorhabditis briggsae and C. elegans, which the evidence suggests have different mutation rates. Averaged over traits, species, and populations within species, the relationship between V_G and V_M is quite stable, consistent with the hypothesis that differences among groups in standing variance can be explained by differences in mutational input. The average (homozygous) selection coefficient inferred from V_M/V_G is a few percent, smaller than typical direct estimates from mutation accumulation (MA) experiments. With one exception, the variance present in a worldwide sample of these species is similar to the variance present within a sample from a single locale. These results are consistent with specieswide MSB and uniform purifying selection, but genetic draft (hitchhiking) is a plausible alternative possibility.

THE genetic variation present in a species is a composite function of mutation, population size, and natural selection. The relationship between the standing genetic variance (V_G) and the per-generation input of genetic variance by mutation (the mutational variance, V_M) has a straightforward interpretation under two evolutionary scenarios. Under a deterministic mutation-(purifying) selection balance (MSB) model, 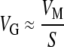, where S is the average selection coefficient against a new mutation (Barton 1990; Crow 1993; Houle et al. 1996). The ratio 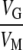(i.e., 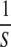) can be interpreted as the “persistence time” (t_P) of a new mutation, i.e., the expected number of generations a mutant allele remains in the (infinite) population before it is eliminated by selection (Crow 1993; Houle et al. 1996). The more deleterious the allele, the faster it is removed from the population. At the opposite extreme, under a strict neutral model of mutation–drift equilibrium (MDE), for self-fertilizing taxa, V_G ≈ 4N_eV_M, where N_e is the effective population size (Lynch and Hill 1986). For a quantitative trait, V_M = UE(a²), where U is the genomic mutation rate and a is the additive phenotypic effect of a new mutation (Lynch and Walsh 1998, p. 329).

The unifying factor in these different scenarios is V_M. Under both the MSB and MDE scenarios, we expect V_G to be proportional to V_M and thus the persistence time to be constant if selection is uniform. Changes in the relationship between V_G and V_M among groups must be due to differences in natural selection. Thus, if t_P differs between groups, the difference must be due to historical differences in the strength or efficiency of natural selection. This principle has been demonstrated by Houle et al. (1996), who found that the average t_P for life history traits was about half that for morphological traits in a variety of taxa, consistent with the expected stronger correlation of life history traits with fitness. Average persistence times differed significantly between species, but the traits differed between species, the species were phylogenetically disparate, and included taxa not likely to be at equilibrium and/or to have experienced recent strong artificial selection. To our knowledge, there has been no comparison of mutational variance and standing genetic variance for the same traits in natural populations of related taxa.

In this study we report the standing genetic variation for two quantitative traits—lifetime reproduction weighted by survivorship (≈ fitness, which we designate W) and body size—in worldwide collections of two species of rhabditid nematodes, Caenorhabditis briggsae and C. elegans. Several lines of evidence suggest that the mutation rate in C. briggsae is greater than that of C. elegans for these traits (Baer et al. 2005, 2006; Ostrow et al. 2007) and for microsatellites (Phillips et al. 2009) and perhaps for single nucleotide substitutions (D. Denver, unpublished data). Thus, we predict that V_G should be proportionally greater in C. briggsae than in C. elegans. If not, it suggests that idiosyncratic natural selection (e.g., genetic draft; Gillespie 2000) is of primary importance in shaping the standing genetic variation.

MATERIALS AND METHODS

Wild isolates:

We initially obtained all publicly available strains of wild-caught nematodes in the species C. briggsae (6 strains) and C. elegans (40 strains) from the Caenorhabditis Genetics Center (CGC) in the spring of 2005; we obtained 50 additional strains of C. briggsae from various sources in the spring of 2007. Recently, it became apparent that six of the “wild” isolates of C. elegans are probably laboratory contaminants recently derived from the N2 strain (Rockman and Kruglyak 2009; see supporting information, Table S1, so we removed those strains from the analysis. Each strain is descended from a single wild-caught individual that was allowed to reproduce to large population size and then cryopreserved. Collection information is presented in Table S1 further details are available from the CGC (http://www.cbs.umn.edu/CGC/). Upon receipt, each strain was allowed to expand to large population size (approximately two generations), at which time three replicate sublines were initiated from a single individual. Each subline was inbred for six generations by randomly picking a single L4 stage (juvenile) worm and allowing it to self-fertilize. This inbreeding protocol is identical to the initial stage of our mutation accumulation (MA) protocol (Baer et al. 2005) and was done both to assure similar starting conditions of wild strains and MA stocks and to account for genetic variation resulting from within-strain heterozygosity.

Mutation accumulation lines and fitness assays:

Details of the MA and fitness assay protocols have been reported elsewhere (Vassilieva and Lynch et al. 1999; Baer et al. 2005, 2006). All 40 C. elegans strains and 6 of the C. briggsae strains were assayed in the summer of 2005; the remaining 50 C. briggsae strains were assayed in the summer of 2007. Worms were assayed under standard conditions (20°, fed on the OP50 strain of Escherichia coli) except that density of agar plates was 30% greater to prevent worms from burying. Worms were counted using the same protocol as in Baer et al. (2005). At the beginning of the assay, each subline was replicated 10 times and taken through an additional three generations of single-worm transfer to account for parental and grandparental effects. If a worm did not reproduce at the first generation the replicate was replaced; if the worm did not reproduce subsequent to the first generation the replicate was not included in the assay. Sample sizes therefore differ between strains and sublines. We define “total fitness” (W) of a worm as the lifetime reproductive output of an individual; W = 0 for worms that failed to reproduce.

Some plates became contaminated with mold prior to counting. Mold contamination was scored as none/some/heavy = 0/1/2 in 2005 and none/present = 0/1 in 2007. On average, plates with mold contamination had fewer worms than uncontaminated plates. There are two potential nonexclusive explanations: we know that worms are more difficult to see on plates with mold present, leading to predictable undercounts. We suspect that worms eat mold spores and newly germinated molds, such that mold grows more quickly on plates with fewer worms. On the basis of extensive observation, we believe that this mold does not have direct deleterious effects on the worms. To account for the effects of mold, we constructed a “mold index” (MI) by weighting the density of mold (0/1/2) by the average fraction of total reproduction contributed by that day's reproduction. For example, for C. elegans in 2005, the first day's reproduction (R1) accounted for 53.0% of total reproduction, R2 accounted for 40.7%, and R3 accounted for 6.3%. Thus, if the three plates representing an individual worm's reproductive output were scored 2/0/1 representing heavy mold, no mold, and some mold on days 1, 2, and 3, respectively, the MI would be (2)(0.53) + (0)(0.407) + (1)(0.063) = 1.123. We included MI as a covariate in subsequent analyses of fitness; the effect was essentially zero for C. briggsae in 2007; it was marginally significant (0.10 < P < 0.11) for C. briggsae in 2005 and highly significant for C. elegans (P < 0.0001) in 2005.

Body size:

Body volume was assayed using a slight modification of the protocol outlined in Ostrow et al. (2007). For each inbred line in each strain, we randomly chose half of the replicates in the fitness assay for inclusion in the body size assay. Approximately 10 age-synchronized young adult worms (72–74 hr postlaying) were randomly placed into a 1.5-ml microcentrifuge tube containing a fixative solution of 4% gluteraldehyde buffered with PBS. Fixed worms were then pipetted onto a slide micrometer and digitally photographed at 20× magnification using a Leica MZ75 dissecting microscope fitted with a Leica DFC280 camera controlled by the Leica IM50 software package (Leica Microsystems Imaging Solutions). Digital images were first manually processed by removing the background surrounding each worm using Adobe Photoshop (v. 6), leaving only the worm/s in the image. Edited images were then batch processed using a custom macro written in the ImageJ64 software package (http://rsb.info.nih.gov/ij/). After processing, the measured outline of each worm was visually inspected and all worms that were damaged were removed from the final analysis. A subset of the images were analyzed by manually adjusting the threshold of the image and then outlining the worm using the “Analyze Particles” option in ImageJ; there was no significant difference between manually analyzed and batch processed images (data not shown). The area (A) and perimeter (P) of each worm were calculated and used to estimate body volume (S) under the assumption that the worm is cylindrical using the equation from Azevedo et al. (2002; note that a typographical error in the original publication omitted the exponent in the numerator):

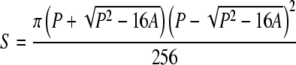Data analysis:

Mutational variance:

For traits under directional selection, the most meaningful measure of genetic variation is the genetic variance divided by the square of the trait mean. This quantity establishes the upper bound on the rate of response to selection and is commonly referred to as the “opportunity for selection,” I_G, where 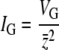and z̄ represents the trait mean (Crow 1958; Houle 1992; Wade 2006). The mutational variance V_M is half the among-line component of variance divided by the number of generations of mutation accumulation (Lynch and Walsh 1998, p. 331). Thus, , where t is the number of generations of MA, V_L,i is the among-line component of variance after i generations of MA, and z̄_i is the trait mean at generation i. Values of I_M presented here are averages of the two strains of each species at t_MA = 200 and are from reanalysis of data reported elsewhere (Baer et al. 2005, 2006; Ostrow et al. 2007). Empirical 95% confidence intervals for I_M were calculated using a bootstrap resampling method outlined in Baer et al. (2005). Briefly, a pseudo-data set was initially constructed by sampling the data with replacement at the level of line (i.e., all replicates within a line were included), maintaining the block structure of the original data. Means and variance components of the pseudo-data set were estimated separately for MA and control lines within each of the four strains by restricted maximum likelihood (REML) as implemented in the MIXED procedure of SAS v. 9.2. For the trait W, we used the model y = Block + Line + Error; for body volume we used the model y = Block + Line + Replicate(Line) + Error. The calculation was repeated 1000 times; the upper and lower 25 pseudoestimates establish the approximate 95% confidence interval. The average of the two strains within each species for each pseudoreplicate is taken as the species average.

Standing genetic variance:

Variance components were estimated for each species using REML as implemented in the MIXED procedure of SAS v. 9.2. Since different strains of C. briggsae were assayed in different years (2005, 2007), for the trait W we initially analyzed the model y = MI + Year + Strain(Year) + Inbred_Line(Strain(Year)) + error, with MI as a covariate, year considered a fixed effect, and the other effects random. Means did not differ significantly among years, so subsequent analyses were done without regard to assay year. For the trait body volume we initially considered the model y = Year + Strain(Year) + Inbred_Line(Strain(Year)) + Replicate(Inbred_Line(Strain(Year))) + error. C. briggsae measured in 2005 were marginally smaller than those measured in 2007, so we retained year in the model for subsequent analyses.

Population genetic structure introduces a potential complication into the analysis. Strictly speaking, the approximation is a statement about within-population variation. However, the model tacitly assumes that deleterious mutations never reach appreciable frequency in the population, so it is reasonable to assume that subpopulations do not diverge substantially due to genetic drift, and positive selection is ignored in any case. Both C. elegans and C. briggsae show a specieswide clade structure, with two deep clades in C. elegans (Denver et al. 2003) and three in C. briggsae (Dolgin et al. 2008). The clades in C. briggsae largely reflect geography, with the three lineages representing temperate, tropical, and equatorial clades (Dolgin et al. 2008), whereas the deep clades in C. elegans are apparently not geographically structured (but see Rockman and Kruglyak 2009). In addition, some collections contain several individuals from the same collecting location, but many locations include only a single individual. Almost half (19/40) of the C. elegans strains were collected in a single location (Roxel; see Table S1). Moreover, because of the nature of Caenorhabditis life history (self-fertile, very short generation time) it is possible that some or all of the strains within a collecting location are descended from the same ancestral worm in the very recent past. To accommodate the variable collecting structure, we further subdivide the data into “locations,” some of which contain multiple strains and some of which do not (Table S1). For the trait W, the full model is: y = MI + Clade + Location(Clade) + Strain(Location(Clade)) + Inbred_Line(Strain(Location(Clade))) + error, with MI as a covariate, clade as a fixed effect, and the others random. Clade identity is unknown for 6/40 C. elegans lines from two locations. The effect of clade was not significant for either trait in either species (C. briggsae, P > 0.13 or greater in all cases) so we omitted clade from further analyses.

In the above analysis, the environmental component of phenotypic variance (V_E) is represented by the error (within inbred line) variance. Under an additive model, the total genetic variance (V_G) is represented by half the sum of the remaining components of variance and can be partitioned into within- and among-group components. Note that we assume that each inbred line is homozygous at all loci, which cannot be strictly true. The among-inbred line component of variance is twice the genetic variance within each strain resulting from polymorphism in the ancestral worm and the among-strain component of variance represents twice the genetic variation among individuals within a sampling location.

Standard errors and 95% confidence limits for I_G were calculated using a delete-one jackknife protocol in which each strain was sequentially deleted from the data and the mean and variance components of the redacted data set recalculated as described above (Knapp et al. 1989). Confidence limits were calculated using the jackknife standard error and the usual Student's t-distribution formulation (Sokal and Rohlf 1981, p. 145).

Standard errors of persistence time (I_G/I_M), average selection coefficient (I_M/I_G), and the ratios of the mutational and standing variances between species (I_M,Cbr/I_M,Cel and I_G,Cbr/I_G,Cel) were determined using the Delta method for the variance of a ratio, where

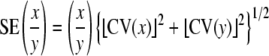and CV(x) is the coefficient of sampling variation (the ratio of the standard error to the estimated value) of x (Lynch and Walsh 1998, equation A1.19b; Vassilieva et al. 2000). Confidence limits were calculated as above. The lower confidence limits calculated in this way are conservative in comparison with likelihood ratio (LR) tests—for example, for the specieswide collection of C. elegans the lower 95% confidence limit on V_G is 0 (Table 1), yet the genetic component of variance is highly significant when the full model is compared by LR test to a model without the genetic terms included (χ² = 28.8, d.f. = 3, P < 0.0001).

TABLE 1.

Total fitness (W)

Species/group	Uā (× 103)	IM (× 104)	VLOC (N)	VLINE (N)	VINLINE	VE
C. briggsae (all lines)	−2.89 (−3.17, −2.60)	8.96 (4.22, 13.91)	252.8 (16)	68.3 (51)	129.4 (0, 287.6)	2034.2
Cbr (Merlet)	—	—	—	392.8 (12)	187.9 (0, 562.7)	1634.3
Cbr (Viosne)	—	—	—	0.13 (12)	23.0 (0, 119.1)	1853.4
C. elegans (all lines)	−1.07 (−1.38, −0.75)	2.24 (1.34, 3.30)	185.1 (13)	280.8 (34)	73.5 (0, 316.6)	4113.1
Cel (Roxel only)	—	—	—	399.5 (19)	306.9 (0, 1171.2)	4433.6
Cel (Roxel omitted)	—	—	131 (12)	192.4 (15)	28.9 (0, 197.8)	3864
Species/group	VG	W̄	IG	H2	tP (=IG/IM)	S
C. briggsae (all lines)	225.3 (20.9, 429.6)	90.8 (80.8, 100.8)	0.027 (0.0008, 0.054)	0.11 (0.007, 0.21)	30.5 (0, 65.0)	0.033 (0, 0.070)
Cbr (Merlet)	290.4 (0, 779.0)	71.0 (55.1, 86.8)	0.058 (0, 0.163)	0.17 (0, 0.49)	65.2 (0, 188.3)	0.015 (0, 0.044)
Cbr (Viosne)	11.6 (0, 59.1)	87.4 (82.4, 92.4)	0.0015 (0, 0.008)	0.006 (0, 0.033)	1.7 (0, 8.8)	0.59 (0, 1)
C. elegans (all lines)	269.7 (0, 548.5)	140.5 (123.8, 157.1)	0.0137 (0, 0.0290)	0.07 (0.0013, 0.130)	61.0 (0, 134.9)	0.016 (0, 0.036)
Cel (Roxel only)	353.2 (0, 779.1)	116.3 (97.1, 135.6)	0.026 (0, 0.063)	0.08 (0, 0.19)	116.8 (0, 291.0)	0.009 (0, 0.021)
Cel (Roxel omitted)	176.4 (0, 418.4)	145.1 (129.5, 160.7)	0.0084 (0, 0.020)	0.05 (0, 0.11)	37.4 (0, 92.0)	0.027 (0, 0.066)

See text for details of calculations. Confidence interval (95%) below point estimate in parentheses. Uā, % per-generation change in the mean with mutation accumulation; I_M, per-generation increase in the genetic (mutational) variance, scaled by the square of the mean; V_LOC, component of genetic variance among locations (N = no. of locations); V_LINE, component of genetic variance among lines within locations (N = no. of lines); V_INLINE, component of genetic variance among inbred lines within lines; V_E, environmental (= error) component of variance; V_G, total genetic variance; W̄, mean lifetime reproductive output; I_G, total genetic variance scaled by the square of the mean; H², broad-sense heritability; t_P, persistence time; S, average selection coefficient against new mutations.

We also report the broad-sense heritability, H², defined as the total genetic variance scaled as a fraction of the environmental variance, i.e., H² = V_G/V_E.

RESULTS and DISCUSSION

Fitness:

Summary statistics are presented in Table 1. First, we can rule out the MDE (V_G ≈ 4N_eV_M) scenario. Given the observed V_G and V_M, worldwide N_e would have to be on the order of a few dozen individuals to explain the results, an implausibly small number (Cutter et al. 2006). This is unsurprising, given that we expect lifetime reproductive output to be closely related to fitness; however, ruling out MDE is a necessary first step in understanding the relationship between V_M and V_G.

The null hypothesis is that V_G is entirely explained by V_M. Thus, we predict the ratio of the standing variances in the two species, I_G,Cbr/I_G,Cel, should equal the ratio of mutational variances, I_M,Cbr/I_M,Cel. The ratio of the mutational variances of C. briggsae to that of C. elegans, I_M,Cbr/I_M,Cel, is 3.99, with the 95% confidence interval between 1.78 and 8.01. The observed ratio of standing variances, I_G,Cbr/I_G,Cel, is 2.00, with 95% confidence interval between 0 and 5.88. Thus, although the ratio of the standing variances in the two species (2.00) is less than predicted from the respective mutational variances (3.99), the null hypothesis of I_G,Cbr/I_G,Cel = 3.99 cannot be rejected.

Looking across species and populations, with one exception (the Viosne population of C. briggsae, see below), estimated (homozygous) selection coefficients (I_M/I_G) are quite consistent and fall within a relatively narrow range of a few percent (Table 1, last column). Broad-sense heritabilities are on the order of 5–15%. These results are similar to analogous results from Drosophila melanogaster and Daphnia pulex, which suggest heterozygous selection coefficients of mutations affecting components of fitness (e.g., viability) on the order of a few percent and comparable heritabilities (Houle et al. 1996; Lynch et al. 1998). Unfortunately, our results cannot be directly compared to results from other taxa, for two reasons. First, because there are no similar estimates of lifetime reproductive success (≈ absolute fitness) for other taxa, and second, because these Caenorhabditis species are (believed to be) predominantly selfing, the relevant selection coefficient against new mutations is presumably the homozygous effect, whereas in obligately outcrossing taxa such as Drosophila it is the heterozygous effect that is estimated by V_M/V_G. We know of no analogous data from any other predominantly selfing organism.

Selection coefficients inferred from the ratio V_M/V_G can be compared to those calculated directly from the MA data (typically referred to as E(a) in the MA literature). Selection coefficients calculated from MA data are widely believed to be overestimates, perhaps gross overestimates, because mutations of very small effect are difficult to detect with the available methods (Davies et al. 1999; Keightley and Eyre-Walker 1999). However, the standing genetic variance has presumably accumulated over a long time, such that the accumulation of many alleles of small effect would contribute to the total genetic variance. If so, we expect V_G to be much larger than V_M and the inferred selection coefficient to be very small. The selection coefficients inferred from this study (≈ 0.02–0.03) are smaller than those estimated directly from the MA data (≈ 0.1–0.2; Keightley and Caballero 1997; Vassilieva et al. 2000; Baer et al. 2006; Begin and Schoen 2006). This implies that estimates of genomic mutation rates (U) calculated from MA data are underestimates of similar magnitude. This conclusion is consistent with indirect estimates of U inferred from direct sequencing of MA lines, in which (diploid) U for C. elegans was estimated to be on the order of 1 per generation (Denver et al. 2004).

The relationship 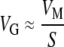(and thus ) is valid only when the population is (1) large, and (2) at mutation–selection balance (Keightley and Hill 1988). Together, these two assumptions imply that the standing genetic variation observed within a single population will be similar to the genetic variation present in the entire species, because deleterious alleles will never achieve appreciable frequency in any population, precluding divergence due to fixation of slightly deleterious alleles. If positive selection and/or genetic drift had caused populations to diverge, there should be substantially more variation present in the species as a whole than in any individual population. Again with one exception, the results appear to lend credence to this assumption. The point estimate for the standing genetic variance for fitness (I_G) in the worldwide collection of C. elegans not including the Roxel population (N = 15 lines) is 0.0084; it is three times that in the Roxel population alone (I_G = 0.026, N = 19 lines). The specieswide standing genetic variance I_G for fitness in C. briggsae (N = 50 lines) is 0.027; within the Merlet population (N = 12 lines) it is 0.058. The nonsignificant effect of clade in either species is consistent with the deterministic MSB scenario.

The inconvenient exception is the Viosne population of C. briggsae (N = 12 lines), which is genetically depauperate (I_G = 0.0015). The point estimate of the selection coefficient (S = I_M/I_G) is 0.59, implying very strong purifying selection acting solely within this population. A more plausible scenario is that the worms in the Viosne sample are not at equilibrium, having descended from a single hermaphroditic founder in the very recent past.

Body volume:

Summary statistics are presented in Table 2. The ratio of the mutational variances for body size in the two species, I_M,Cbr/I_M,Cel, is 1.69, with the 95% bootstrap confidence interval between 0.43 and 3.61. The observed specieswide value of I_G,Cbr/I_G,Cel is 2.76, with the asymptotic 95% confidence interval between 0 and 5.99.

TABLE 2.

Body volume

Species/group	Uā (× 103)	IM (× 104)	VLOC (N)	VLINE (N)	VINLINE	VREP	VE
C. briggsae (all lines)	−1.43 (−1.77, −1.10)	2.48 (0.30, 4.66)	7.85 E-9 (16)	7.03 E-9 (51)	4.53 E-9 (1.49, 7.57 E-9)	4.53 E-9	2.48 E-8
Cbr (Merlet)	—	—	—	1.44 E-8 (11)	5.83 E-9 (0, 1.47 E-8)	3.02 E-8	2.14 E-8
Cbr (Viosne)	—	—	—	3.83 E-9 (12)	4.18 E-9 (0, 1.71 E-8)	4.26 E-8	2.54 E-8
C. elegans (all lines)	−0.68 (−0.96, −0.40)	1.54 (0.89, 2.20)	6.71 E-10 (13)	2.08 E-8 (34)	5.06 E-11 (0, 1.36 E-9)	1.12 E-7	8.86 E-8
Cel (Roxel only)	—	—	—	2.08 E-8 (19)	0	1.42 E-7	1.04 E-7
Cel (Roxel omitted)	—	—	2.12 E-9 (12)	1.86 E-8	8.51 E-11	1.01 E-7	7.55 E-8

Species/group	VG (× 109)	z̄ (× 103)	IG (× 103)	H2	tP(IG/IM)	S
C. briggsae (all lines)	9.71 (4.14, 15.3)	1.23 (1.15, 1.30)	6.45 (2.46, 10.44)	0.15 (0.05, 0.25)	26.0 (0, 55.1)	0.038 (0, 0.081)
Cbr (Merlet)	10.10 (0, 25.2)	1.06 (0.96, 1.15)	9.02 (0, 21.93)	0.20 (0, 0.50)	36.4 (0, 99.2)	0.027 (0, 0.075)
Cbr (Viosne)	4.00 (0, 11.41)	1.20 (1.14, 1.27)	2.76 (0, 7.82)	0.06 (0, 0.17)	11.2 (0, 34.1)	0.090 (0, 0.275)
C. elegans (all lines)	10.74 (4.26, 17.23)	2.15 (2.06, 2.23)	2.33 (0.86, 3.87)	0.053 (0.018, 0.089)	15.2 (3.3, 26.9)	0.066 (0.014, 0.118)
Cel (Roxel only)	10.41 (0, 24.83)	2.15 (20.56, 22.50)	2.25 (0, 5.35)	0.04 (0, 0.10)	14.6 (0, 35.7)	0.069 (0, 0.169)
Cel (Roxel omitted)	10.42 (8.3 E-10, 20.02)	2.12 (2.03, 2.22)	2.32 (0, 7.55)	0.10 (0.01, 0.20)	10.31 (0, 21.3)	0.097 (0, 0.201)

See text for details of calculations. Confidence interval (95%) below point estimate in parentheses. z̄, mean body volume (mm³), all other abbreviations are the same as in Table 1.

Two patterns emerge from the data on body size. First, just as for fitness, the specieswide genetic variance for body size is not substantially larger than the genetic variance present within individual populations, lending credence to the MSB interpretation of the relationship between standing genetic and mutational variance. Second, the inferred selection coefficients for body volume are of the same order as those for fitness, and if anything are slightly larger. This seems counterintuitive; we expect total fitness (W, a function of fecundity and survivorship) to be under strong directional selection and there is no such a priori expectation for body size. Previous MA studies have consistently found a large positive mutational correlation of body volume with W (Azevedo et al. 2002; Estes et al. 2005; Ostrow et al. 2007). However, interpretation of genetic correlations determined from MA experiments is problematic because nonzero correlations are expected to arise for reasons in addition to correlated mutational effects (Keightley et al. 2000; Estes et al. 2005; Estes and Phillips 2006). The relatively strong selection on body volume inferred here from V_M/V_G suggests a functional relationship between body volume and fitness, i.e., “real” pleiotropy.

These species of Caenorhabditis are believed to be primarily self-fertilizing in nature and are expected to be largely homozygous. However, in C. briggsae, for both fitness and body volume, ∼25% of the total genetic variance is among inbred lines within a line; the among-inbred line component is significantly different from 0 for body size but not for fitness. Presumably, the among-inbred line variance results from residual heterozygosity and/or heteroplasmy in the ancestor, although new mutations arising during the six generations of inbreeding could also contribute. For the worldwide collection of C. elegans, the fraction of the genetic variance attributable to variation among inbred lines within a line is ∼14% for fitness and essentially zero for body volume. In the Roxel population of C. elegans, in which all strains were recently isolated from the wild, about half the genetic variance for fitness is among inbred lines, although the REML estimate of the among-inbred line component of variance is 0 for body volume. A prosaic explanation is that some of the C. elegans lines were kept in lab culture before cryopreservation, thus more of the residual genetic variation has been purged in C. elegans than in C. briggsae. The qualitative difference of the Roxel population from the specieswide collection of C. elegans reinforces that interpretation. If some of the genetic variation originally present in C. elegans has been purged subsequent to collection, it implies that the estimates of persistence times are underestimates.

An important caveat is that the mutational properties (i.e., I_M) assigned to each species are derived from estimates from only two genotypes. We can put legitimate confidence limits on the estimates, but they represent a fixed effect. Mutational variance is in reality a random effect and we have little understanding of the scope of the variation in mutational properties within and between species. This consideration is not unique to Caenorhabditis.

Finally, perspective is in order with respect to power. Nesting lines within locations is conservative, providing a sample size of only 13 or 16, respectively. If we accept that genetic variation among locations is not much greater than within locations (the Viosne population notwithstanding), we can legitimately increase power by resampling over lines rather than locations. Interestingly, the results for the basic statistics—V_G, and thus I_G and H²—do not change substantially. For example, the upper 95% confidence limit on V_G in C. briggsae decreases from 2.2 times the point estimate to 1.7 times the point estimate with an increase in sample size from 16 to 50 (the point estimates are within a few percent). This exercise is obviously not the same as actually sampling an additional 34 locations, but it does suggest that doing so might not change the results much.

Summary and conclusions:

There are three main results. First, V_M is notoriously noisy (e.g., Shabalina et al. 1997), and it is reasonable to suppose the difference in the between-species ratio of mutational variances for fitness (I_M,Cbr/I_M,Cel = 3.99) and size (I_M,Cbr/I_M,Cel = 1.69) simply represents sampling variation around a common expected value. The average of the two is 2.84; the average of the two between-species ratios of standing variances (I_G,Cbr/I_G,Cel) is 2.38. This coincidence need not have been the case; for example, we might imagine the specieswide V_G in C. briggsae equaled that found in the depauperate Viosne population, in which case the average I_G,Cbr/I_G,Cel would be 1:10. Second, the strength of selection acting on mutations affecting both fitness and body size is consistently inferred from the relationship V_M/V_G to be on the order of a few percent. This value is broadly compatible with similar results from other taxa and is substantially smaller than estimates of selection coefficients estimated directly from MA data, particularly for fitness. Finally, the total genetic variance in a worldwide collection is not much greater than the genetic variance within sampling locations. Taken together, these results suggest that genetic variation for these traits is maintained by mutation–selection balance. However, there is an alternative possibility. The relative consistency of genetic variance within and between populations and species, and especially between traits, suggests that recurrent hitchhiking events—genetic draft (Gillespie 2000)—may play a predominant role in structuring the genetic variation in these species. Genetic draft is likely to be particularly important in selfing taxa. Moreover, the relative consistency of persistence time (V_G/V_M) across disparate taxa and traits (∼50 for life history traits; Houle et al. 1996; this study) is intriguing. Draft theory predicts relative independence of standing molecular genetic variation from population size (Gillespie 2000). Equivalent theory for quantitative traits does not exist, but the parallels are obvious.

Comparisons of V_G and V_M between taxa and traits provide the best way to disentangle the contributions of neutral and nonneutral processes in shaping quantitative genetic variation. We envision two classes of studies that would be particularly informative. First, the best-characterized metazoan species (D. melanogaster, D. pulex, Caenorhabditis) all have large N_e (>10⁴), such that the deterministic MSB formulation is plausible. It would be useful to perform this kind of study in groups with known large differences in population size. Second, it would be useful to consider multiple traits with different expected levels of selection, in the spirit of Houle et al. (1996). However, discerning among the alternative possibilities (e.g., draft, uniform mutational properties) will require not only estimates of V_G from multiple populations, but estimates of V_M from the same populations.