Chemical Frustration in the Protein Folding Landscape: Grand Canonical Ensemble Simulations of Cytochrome c

Abstract

A grand canonical formalism is developed to combine discrete simulations for chemically distinct species in equilibrium. Each simulation is based on a perturbed funneled landscape. The formalism is illustrated using the alkaline-induced transitions of cytochrome c as observed by FTIR spectroscopy and with various other experimental approaches. The grand canonical simulation method accounts for the acid/base chemistry of deprotonation, the inorganic chemistry of heme ligation and misligation, and the minimally frustrated folding energy landscape, thus elucidating the physics of protein folding involved with an acid/base titration of a protein. The formalism combines simulations for each of the relevant chemical species, varying by protonation and ligation states. In contrast to models based on perfectly funneled energy landscapes that contain only contacts found in the native structure, the current study introduces “chemical frustration” from deprotonation and misligation that gives rise to many intermediates at alkaline pH. While the nature of these intermediates cannot be easily inferred from available experimental data, the current study provides specific structural details of these intermediates thus extending our understanding of how cytochrome c changes with increasing pH. The results demonstrate the importance of chemical frustration for understanding biomolecular energy landscapes.

Specific chemistry often plays a dominant role in folding especially in metalloproteins. Covalent chemistry is clearly discrete while folding is so complex that it often appears to be nearly continuous. A general way to combine detailed coordination chemistry with energy landscape ideas describing the inter-residue forces guiding folding is to employ a grand canonical formalism. The formalism allows the use of discrete simulations using perturbed structure based (native topology based) models to examine how ensemble properties change with pH and metal coordination. Structure based models, utilizing a perfectly funneled energy landscape, have already been used to predict the dominant folding route of cytochrome c which is strongly influenced by its heme cofactor¹ (Figure 1). These models have also been successfully applied to many other naturally occurring proteins without cofactors.^2-8 However, changes in solvent conditions can perturb the energy landscape giving rise to “chemical frustration” that allows chemically distinct intermediates to appear (Figure 2). The observation of non-native protein ligand interactions with the iron of cytochrome c provided one of the first experimentally documented examples of frustration on a biomolecular energy landscape.⁹ Especially beautiful examples of how the folding landscape may be modulated by ligation and misligation events are provided by the alkaline-induced transitions of cytochrome c. Upon increasing pH, the native Met80 ligand is displaced from the heme center resulting in misligation of the heme and eventual unfolding of the protein.^10-13 Experiments that probe cytochrome c mutants with NMR,^13-15 hydrogen exchange,¹⁶ EPR,¹⁵ and resonance Raman¹⁷ have identified Lys73 and Lys79 as ligands for the heme. However, at least under certain conditions, kinetic pH-jump experiments detect an intermediate in which the Met80 ligand is displaced and not replaced by a lysine.¹⁸ A more recent FTIR study¹⁹ based on the incorporation of carbon-deuterium bonds at specific residues has identified a potentially related intermediate under equilibrium conditions.¹⁹ Based on these experiments, the equilibrium alkaline-induced transitions may be written as III ⇌ 3.5 ⇌ (IV_a ⇌ IV_b) ⇌ V ⇌ U. State III is the native state at pH 7, states IV_a and IV_b are misligated by Lys73 and Lys79 respectively, and U is the unfolded state. States 3.5 and V are less well characterized experimentally than the others. The identities of the heme ligands in states 3.5 and V have been suggested^17,19 but this assignment remains tentative. Providing a detailed structural description of these states is the main goal of the present paper.

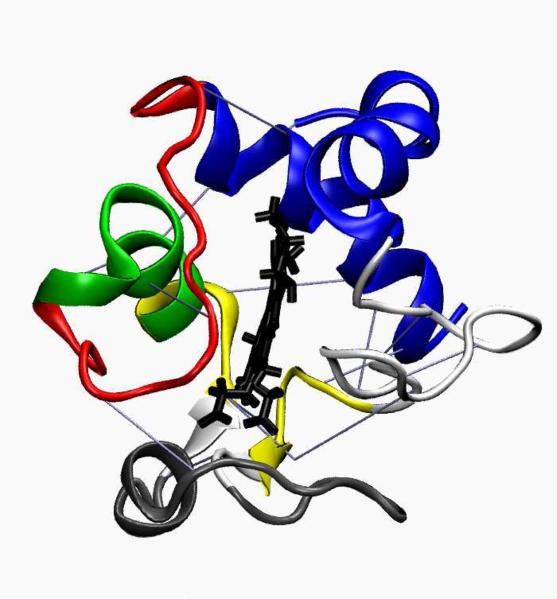
Figure 1.

Crystal structure of cytochrome c colored by the folding units: N- and C-terminal helices (blue), 60's helix (green), two stranded beta sheet (yellow), Met80 loop (red), and the omega loop (grey). H-bonds included into the model are shown with blue lines.

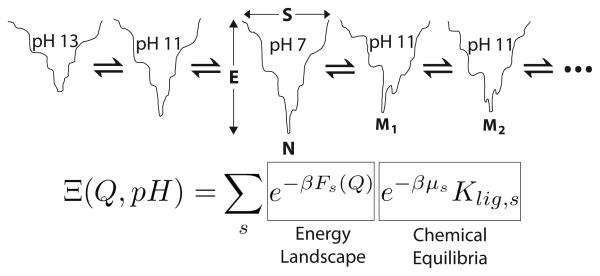
Figure 2.

A scheme for combining energy landscapes for folding individual chemical species with acid/base and coordination chemistry. In the above scheme, each chemical species is represented by its own folding funnel of varying depths. The pH 7 folding funnel has an energy minima at the native state (N), but as the pH or ligation conditions change, the energy landscape is perturbed giving rise to slightly different funnels with distinct minima such as at a misligated state (M₁ or M₂). The grand canonical partition function contains a sum over each chemical species (s). The folding landscape contributions are clearly separated from the terms containing chemical potentials that give rise to the chemical equilibria between species. For more information on the grand canonical partition function see the Methods section.

In order to describe the different partially unfolded states induced by increasing pH, chemical frustration must be introduced into what may be taken otherwise to be a perfectly funneled energy landscape to a good approximation. This frustration can be described by introducing a misligation potential (with an explicit heme) and by accounting for energetic changes due to deprotonation and accompanying electrostatics. Separate simulations are carried out for the relevant chemical species, which are selected by enumerating the probable ligation and protonation states. The simulations are used to generate free energy profiles that determine the stabilities of the different states in various degrees of folding. By knowing the chemical potential balances for the acid/base chemistry and for the heme coordination chemistry, the resulting set of free energy profiles can be combined using the statistical mechanics of the grand canonical ensemble to generate a rather complete description of the alkaline-induced transitions.

The grand canonical formalism allows us to model in a unified way a system which has multiple conformational transitions involving chemically distinct species. All atom simulations have previously been used to determine pH dependent properties and pKa's for relatively static conformations^20-24 but such expensive calculations are not currently feasible to apply to large conformational transitions like those involved in folding. Using a coarse grained model, however, free energy profiles can efficiently be generated. The method allows us to separately analyze each individual species among a complex set of equilibria. The free energy profiles from different chemical species are combined by relating the free energies of completely unfolded ensembles, which in these models consists of structures that are near-random coils, to chemical equilibrium constants involving free amino acids. The free energies of these unfolded ensembles, before accounting for the chemical equilibria, should be the same since entropy dominates these ensembles and is nearly identical for unstructured chains of the same length. The difference in stability between the unfolded ensembles is determined by the relevant chemical potentials, such as for the hydronium ion in the current study (Figure 2). One advantage of employing the grand canonical ensemble method is the flexibility to include or exclude specific chemical species. In this way, we can compare the effects of including different species on the properties of the entire ensemble in order to address experimental results that report on such intermediates, but without structural detail. This method also allows for approximations that can reduce the necessary simulation time by several orders of magnitude. For example, there are 2²⁵ potential protonation states in the alkaline-induced transitions of cytochrome c if one enumerates all 25 basic residues. If we only consider the possible lysine-misligated states then nearly 10⁹ simulations would be needed. An approximation is appropriate given that the majority of those states are not individually observable experimentally. Therefore we include the most probable protonation states (native pH 7, all lysine and tyrosine residues deprotonated, or all lysine and tyrosine and arginine residues deprotonated) and ligation states (native methionine, each lysine, or hydroxide bound). One of the main advantages of the current grand canonical approach is that it utilizes effectively only two free parameters. These correspond to the heme ligation constants which are furthermore restricted by experimental data. Apart from the heme coordination chemistry, the current method provides a simple energy landscape with essentially no adjustable parameters. In effect, the grand canonical ensemble method leads to results that are mostly dependent on features of the funneled part of the energy landscape which in turn is determined by the native state topology.

We therefore employ separate models in order to see which aspects of the energy landscape are most important for reproducing different experimental results. First, the most simple model, or pure-funnel model, consists of, with the exception of a misligation potential, interactions that are based entirely on the native structure of cytochrome c. In a separate model, we try to isolate the effects of long range electrostatic and hydrophobic forces by including Coulomb and hydrophobic collapse potentials in addition to native topology based terms. We explore the role of side chain hydrogen bonding (H-bonding) in yet another model. The use of these three models provides an interesting comparative study of the forces leading to the intermediate structures populated in the alkaline-induced transitions of cytochrome c.

Methods

The grand canonical ensemble is a general statistical mechanical tool that can be used to combine known chemical properties with results from simulation. Especially when dealing with large biomolecules, such a strategy can save tremendous amounts of computing time and in some cases allows calculations that would otherwise be impossible. Grand canonical ensemble simulations have been previously used to simplify the treatment of bulk water in calculations of solvation in proteins and DNA.^25,26 Similar methods have been used to improve the accuracy of calculations involving ligand-protein binding interactions.²⁷

Grand canonical ensemble simulations are used here to describe the alkaline-induced transitions of cytochrome c. The grand canoncial partition function is composed of three terms that describe the folding, the acid/base chemistry, and the heme coordination chemistry: $\Xi (Q,\mathit{pH})={\displaystyle \underset{s}{\Sigma }}{e}^{-\beta F_s\left(Q\right)}{e}^{-\beta {\mu }_s}{K}_{\mathit{lig},s}$. The subscript s runs over each chemical species. These have varying protonation and ligation states that occurs at alkaline pH. β = 1/k_BT. In the current study we include 22 distinct species as shown in Table 1. The free energy profiles (F_s(Q)) that describe folding and stability of each state are generated using the weighted histogram analysis method WHAM.²⁸ Q is a folding reaction coordinate that describes the similarity to the native state topology and is defined as: $Q=\frac{2}{(N-1)(N-2)}{\displaystyle \underset{i<j-1}{\Sigma }}\mathit{exp}\left[\frac{-{(r_{\mathit{ij}}-r_{\mathit{ij}}^{\mathit{nat}})}^2}{2{|i-j|}^{0.3}}\right]$. The summation runs over all C^α residues, $r_{\mathit{ij}}^{\mathit{nat}}$ is the distance between C^α's in the crystal structure, and N refers to the number of residues. Deprotonation is described by the following chemical potential: ${\mu }_s={\displaystyle \underset{j}{\Sigma }}{k}_{B}T(\mathit{pH}-{\mathit{pK}}_{a,j})N_j$. In this equation j indicates three residues that deprotonate (lysine, tyrosine, and arginine) and water, N_j is one if the base is deprotonated within state s and zero if it is not, and the pK_a is set to the value for the free group in solution (Table 1). Ligation is summarized in the disassociation constants, K_lig,s, for each of the potential heme ligands. The values of K_lig,s are not individually known by experiment to high accuracy. Fortunately only the ratios of the disassociation constants are important in the grand canonical method. We chose parameters, consistent with the principles of inorganic chemistry, such that heme is more strongly bound by hydroxide than by deprotonated lysine, which are, in turn, both bound more strongly than methionine or water. The disassociation constants are furthermore restricted by Resonance Raman²⁹ and FTIR experiments¹⁹ which suggest that, for example, two hydroxide bound states dominate in highly alkaline conditions with a midpoint between pH 10.5 and 11. Varying K_OH,s merely shifts the transition midpoint and does not change the structural details or the identity of the intermediates involved. Varying any disassociation constant by less than an order of magnitude does not significantly change the results.

Table 1.

Simulations Performed and Parameters Used

Simulated Chemical Species		Parameters
Ligated Chemical Group	Deprotonated Residues
Met80	None
Lys5	Lys Tyr	Pure-funnel and Electrostatics/ Collapse Models
Lys7	Lys Tyr
Lys8	Lys Tyr
Lysl3	Lys Tyr	pKTYR = 10.0
Lys22	Lys Tyr	pKLYS = 10.5
Lys25	Lys Tyr	pKARG = 12.5
Lys27	Lys Tyr	pKH20 = 15.6
Lys39	Lys Tyr	KLYS = 1 × 10−4
Lys53	Lys Tyr	KOH = 1 × 10−7
Lys55	Lys Tyr	KMET = KH2O = 1
Lys60	Lys Tyr
Lys72	Lys Tyr	Hydrogen
Lys73	Lys Tyr	Bonding Model
Lys79	Lys Tyr	pKTYR = 10.0
Lys86	Lys Tyr	pKLYS = 10.5
Lys87	Lys Tyr	pKARG = 12.5
Lys88	Lys Tyr	pKH20 = 15.6
Lys99	Lys Tyr	KLYS = 1 × 10−4
Lys100	Lys Tyr	KOH = 1 × 10−9
−OH	Lys Tyr	KMET = KH2O = 1
−OH	Lys Tyr Arg

The present simulations are based on the associative memory Hamiltonian (AMH)^30,31 which utilizes structural information in multiple “memory” proteins which is used for ab initio structure prediction. By using only a single memory protein conforming to the native X-ray structure, we ensure a perfect funnel. The structure of horse heart cytochrome c is used for the simulations in this study. The AMH Hamiltonian is written as the sum of backbone and contact terms. The backbone potential, V_back, contains only local terms that maintain backbone geometry (bond angles and distances) and includes excluded volume. The contact potential, V_contact, includes Gaussian well potentials summed over all C^α's and C^β's for protein-protein contacts or C^α's and heme pseudo-atoms for heme-protein contacts. The contact potential includes 40% nonadditivity, which results in barrier heights and cooperativity consistent with those observed in small globular proteins.³² The details of the backbone and contact potentials were laid out in our earlier studies³³ and is also discussed in the supporting information. The heme is introduced explicitly with a potential V_heme that includes terms to maintain the heme geometry as well as ligation terms for the iron to protein residues. The current heme model contains five heme pseudo-atoms. Four atoms are fixed in a square-planar geometry while the fifth atom is placed in the center. Well chosen interactions between the pseudo-atoms of the heme ensure that the heme has a realistic size and shape. Harmonic potentials, k(r − r_o)², account for ligation between the heme center pseudo-atom and the C^α of a residue in which r_o for lysine is set to 7. Simulations are run at a constant temperature near the temperature used in experiment.

We use three models to study the role of electrostatics in the alkaline-induced transitions. A protein's native state at pH 7 is usually optimized electrostatically, but upon deprotonation favorable electrostatic effects are generally lost. Therefore deprotonation of a residue is modeled by energetically destabilizing some of the native state contacts. The pure-funnel model, used in the current study, is structure based and includes a mean field treatment of electrostatics in which the pairwise energy of contacts involving a deprotonated residue is decreased homogeneously. The pure-funnel Hamiltonian can be written as H_{pure−f unnel} = V_back+V_contact+V_heme+V_deprot in which $V_{\mathit{deprot}}=-{\displaystyle \underset{\text{i or j deprot}}{\Sigma }}0.1{\epsilon }_{\mathit{ij}}\left(r_{\mathit{ij}}\right)$. The factor 0.1 was estimated using a calculation of the electrostatic energy change upon deprotonation obtained by placing charges on the C^β's (using a coulomb potential) in the crystal structure. The total destabilization energy distributed among all contacts involving deprotonated residues is about 5 to 15 percent of γ_ij. Neither the nature of the intermediate ensembles nor their relative stabilities change significantly when the γ_ij are varied within this range.

A second model was also employed additionally to account for long range and non-native electrostatic effects by using a simple coulomb potential. In a separate study,³⁴ we compared pair distribution functions calculated from simulation to those derived from experimental FRET data on cytochrome c.^35,36 The results of the previous study suggest that long range electrostatic effects and a general hydrophobic collapse term improve the accuracy of the unfolded and partially unfolded conformations of cytochrome c. The Hamiltonian for the electrostatic/collapse model is given by H_elec/col = V_back +V_contact +V_heme +V_elec +V_Rg +V_deprot where $V_{\mathit{elec}}={\Sigma }_{|i-j|>2}\gamma V_{\mathit{Rg}}\times \frac{q_i{q}_j}{4\pi {\epsilon }_0\epsilon r_{\mathit{ij}}}\times e^{(-r_{\mathit{ij}}∕{\lambda }_D)}$. Solvent and ion screening effects are accounted for using a Debye screening term (e^{(−r_ij/λ_D)}). The charge on residue i is plus or minus one depending on the identity of the residue, r_ij is the distance between C^β's of residues i and j, γ is the strength of a native contact, and λ_D = 2.5. Because the funneled energy terms implicitly contain native electrostatic effects, we chose a dielectric constant so that the long range and non-native electrostatics have a more dominant effect in a similar manner to other studies.^34,37 The dielectric constant (ε = 30) is less than that for water but is still significantly more than the value of 3.5 calculated for ferricytochrome c.³⁸ Furthermore, the electrostatic terms are scaled by the amount of collapse to avoid overcompensating for electrostatics implicitly included in the contact terms. Such a model mimics the expected interplay of electrostatic effects and hydrophobic collapse on the frustration of the energy landscape in the unfolded ensemble and allows for a nearly unfrustrated energy landscape near the native ensemble.

The last model includes the effects of specific side chain H-bonding changes in addition to the local electrostatics in order to capture the large energetic costs of deprotonating a residue and disrupting an H-bond. By increasing pairwise contact energies between residues that participate in side chain H-bonding in the native state, the H-bonding potential captures specific interactions that are affected by deprotonation. The Hamiltonian for the H-bonding model is H_H−bond = V_back + V_contact +V_heme +V_deprot +V_H−bond. The possible H-bonds in the crystal structure were determined using the program WHATIF³⁹ and can be seen in Figure 1. H-bonds are included if either the donor or acceptor is a side chain and the residues are greater than three residues apart. The pairwise contact energies between residues determined to have H-bonds involving a side chain is increased by a factor of 3: $V_{H-\mathit{bond}}={\displaystyle \underset{\mathrm{H}-\text{bonded, not deprot}}{\Sigma }}3{\epsilon }_{\mathit{ij}}\left(r_{\mathit{ij}}\right)$. If the side chain of the residue involved in the H-bond deprotonates, the energetic bonus for the H-bond is removed.

Results

The Alkaline-Induced Intermediates

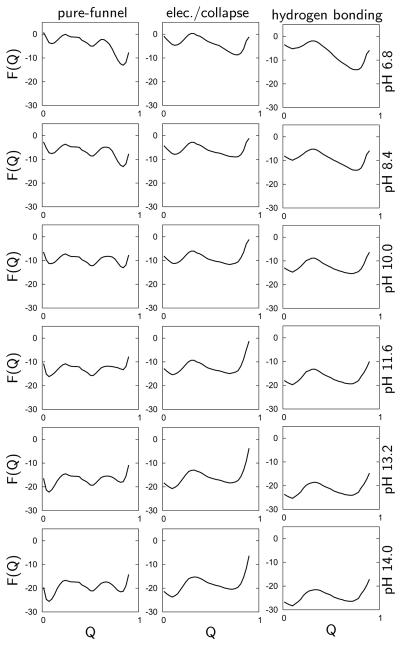
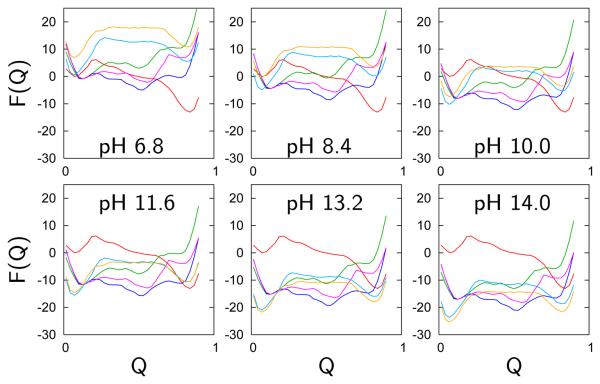
As pH is varied over alkaline conditions, we calculate the most probable structural ensembles as a function of the folding reaction coordinate Q. The appropriate free energy profile is calculated using the grand canonical partition function F(Q, pH) = −k_BTln(Ξ(Q, pH)) (Figure 3). The pure-funnel model clearly reveals a transition at a pH 9 where the depth of the folded state free energy minimum (Q ≈ 0.9) becomes similar to the depth of the partially and globally unfolded state minima (0.5 < Q < 0.6 and Q ≈ 0.1 respectively). The electrostatic/collapse and H-bonding models exhibit a more modest change in Q with pH. A partially unfolded minimum begins to appear around pH 9 (Q ≈ 0.8). This minimum is broader than that associated with the fully folded state at pH 7. A second transition involves the global unfolding of the protein at pH greater than 12. The prediction of several distinct transitions agrees with numerous experimental studies^10-13,17,19 that have identified multiple intermediates at alkaline pH. To analyze the ensemble calculations in more detail we determined the population of each species as a function of pH (Figure 4). The population of species s in a grand canonical ensemble is:

$$P\left(s\right)=\frac{{\displaystyle \underset{Q}{\Sigma }}{e}^{-\beta F_s\left(Q\right)}{e}^{-\beta {\mu }_s}{K}_{\mathit{lig},s}}{{\displaystyle \underset{Q}{\Sigma }}\Xi (Q,\mathit{pH})}$$ (1)

Figure 3.

Free energy curves calculated using the grand canonical partition function as a function of the reaction coordinate Q at specific pH values of 6.8, 8.4, 10.0, 11.6, 13.2, and 14.0. The curves are obtained from simulations using the pure-funnel (left column), the electrostatic/collapse (middle column), and the H-bonding models (right column).

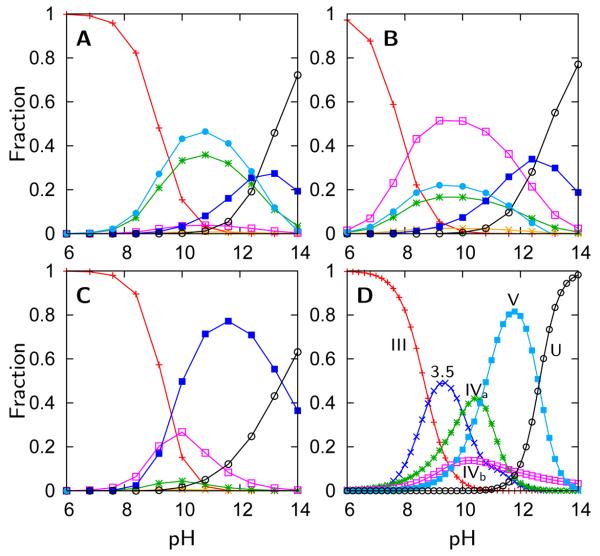
Figure 4.

Fractional concentrations of the most stable chemical species as a function of pH for (A) the pure-funnel model, (B) the electrostatic/collapse model, and (C) the H-bonding model. The native (), Lys73-misligated (), Lys79-misligated (), Lys72-misligated (), unfolded and water/lysine-misligated (), OH-misligated lysine/tyrosine deprotonated (), and OHmisligated lysine/tyrosine/arginine deprotonated (○) states are shown. (D) The probability distribution of states inferred from FTIR studies of semi-synthetic protein with carbon-deuterium labeled residues.¹⁹

Over the entire pH range, four intermediates are found to dominate using either the pure-funnel or the electrostatic/collapse models: the Lys73- and Lys79-misligated states, an unfolded hydroxide-bound state, and an unfolded lysine- or water-bound state. However, only three intermediates are needed to describe the results of the model with explicit H-bonding: the Lys73- and Lys79-misligated states, and a partially folded hydroxide-bound state. The free energy profiles of the most probable species after evaluation by the grand canonical partition function is illustrated in Figure 5. The figure displays the effect of misligation and deprotonation on the shape of the free energy profiles as well as the effect of the grand canonical partition function on the their stability. The predicted presence of several intermediates agrees with many studies^13-17,19 which demonstrate that the transition at pH 9 is an equilibrium between the native state (III), the two lysine-misligated states (IV_a, IV_b), and another state with limited structural information (3.5). The calculations also show that, in agreement with experiment, there is a transition at pH 11-12 that involves a global unfolding event with multiple partially unfolded states.^12,17,19

Figure 5.

Free energy curves of the most stable chemical species as a function of the reaction coordinate Q at specific pH values of 6.8, 8.4, 10.0, 11.6, 13.2, and 14.0. The chemical species depicted are native state (red), Lys73-misligated (blue), Lys79-misligated (magenta), Lys72-misligated (green), hydroxide-misligated lysine/tyrosine deprotonated (cyan), and hydroxide-misligated lysine/tyrosine/arginine deprotonated (yellow). The free energy curves are calculated using the grand canonical partition function based on pure-funnel model simulations.

The Lysine-misligated Intermediates

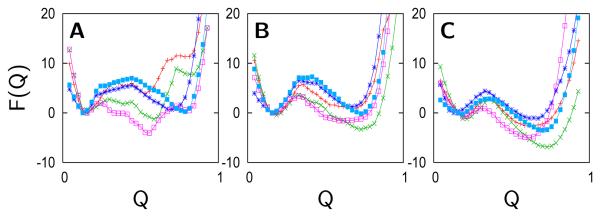
Our simulations provide information about the structures and relative stability of the lysine intermediates. There is much experimental evidence that Lys73 and Lys79 form stable misligates with maximal probability near pH 10.5.^13-17,19,40 Simulations were carried out in which each of the nineteen lysine residues was forced to misligate the heme center and with protonation states corresponding to pH 10.5 (Table 1). Free energy curves were calculated to visualize the relative stability and energy barriers between the unfolded state (Q ≈ 0.1) and the folded state (0.6 < Q < 0.8). The pure-funnel model, as discussed previously,¹⁹ predicts that Lys73- and Lys79-misligated ensembles are more stable than all other lysine misligates (Figure 6). Similar results are obtained with the electrostatic/collapse and H-bonding models but the relative stability of the Lys79 intermediate is increased. Both the electrostatic/collapse and H-bonding models predict that the lysine misligates' free energy minima are at a higher Q than is found with the pure-funnel model which shows a larger number of native contacts. All three models predict that Lys53- and Lys55-misligated species could normally be present in small concentrations and perhaps would dominate if Lys79 and Lys73 were not available (i.e. due to trimethylation⁴¹ or protein binding⁴²).

Figure 6.

Free energy curves as a function of the reaction coordinate Q for the five most stable lysine-misligated intermediates from simulations using (A) the pure-funnel, (B) the electro-static/collapse, and (C) the H-bonding models. The most stable lysine intermediates are Lys53 (), Lys55 (), Lys72 (), Lys73 (), and Lys79 ().

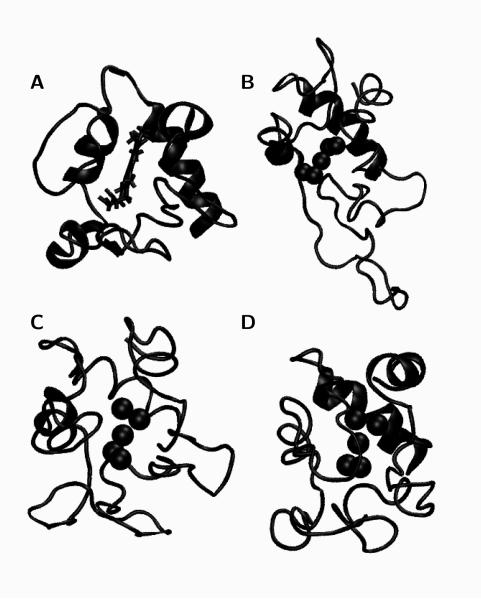
To assess the accuracy of the simulations, we compare the predicted structures from the Lys73-misligated minima to the published NMR structure of this misligated state.⁴³ As shown in table Table 2, the RMSD, the Q score, and the combinatorial extension (CE) score show that the electrostatic/collapse and H-bonding models correspond more closely to the NMR results than does the pure-funnel model. Nevertheless, structures from all three models possess nearly the same average fraction of native contacts, Q_cut, as a measure of the distance pair similarity between the predicted and the NMR structure (with an 8 cutoff). The comparison of the structures from the simulated ensembles and the NMR model deposited in the PDB is shown in Figure 7. The primary difference is that the omega loop (residues 40 to 56) seems to more closely dock to the rest of the protein in the electrostatic/collapse and H-bonding models than it does in the pure-funnel model.

Table 2.

Structural Accuracy of Lys73-Misligated Structures

Model	RMSDa	Qa	Qcuta	CE scorea
Pure-funnel	6.5 +/− 0.6	0.21 +/− 0.01	0.36 +/− 0.01	2.1 +/− 0.6
Electrostatic / Collapse	3.2 +/− 0.4	0.25 +/− 0.01	0.37 +/− 0.02	4.4 +/− 0.3
Hydrogen Bonding	3.5 +/− 0.4	0.25 +/− 0.01	0.36 +/− 0.01	4.2 +/− 0.4

^aThe NMR structure of the Lys79Ala Lys73-misligated structure is compared to 30 structures randomly selected from the free energy minima calculated from each simulation.

Figure 7.

(A) NMR structure of a Lys79Ala Lys73-misligated cytochrome c (PDB code 1LMS). Representative structures of the Lys73-misligated cytochrome c taken from the free energy minima of the (B) pure-funnel, (C) electrostatic/collapse, and (D) H-bonding simulations.

Solvent Exposure Calculations

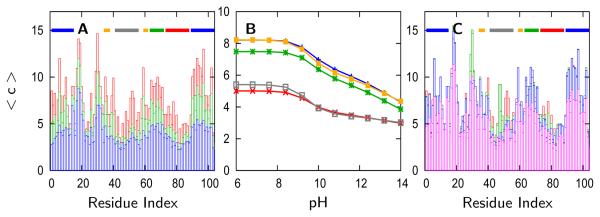
Hydrogen exchange experiments⁴⁴ have been used to infer the dominant folding route of cytochrome c which, in agreement with results of theoretical modeling,¹ involves the sequential folding of five cooperative folding units (Figure 1). However, the hydrogen exchange experiments suggest that the alkaline transition at pH 9 involves the unfolding or restructuring of only the two least stable folding units: the Met80 loop (residues 70 to 88) and the omega loop (residues 40 to 56).^16,45 Calculations involving the number of contacts per residue have been shown to reproduce protection factors determined from hydrogen exchange data^46-52 and will be used in the current work to discuss the degree of solvent exposure. By computing the ensemble average of the number of contacts per residue over all conformations in the ensemble, we confirm that the two least stable units are as exposed to solvent at pH 10.8 as they are at pH 14.0 (Figure 8a). Averaging the number of contacts per residue over each folding unit reveals that the least stable folding units are less protected than the more stable folding units and show unfolding transitions at pH 9 (Figure 8b). The remaining units unfold near pH 12.

Figure 8.

(A) The ensemble average of the number of contacts ($<c>={\displaystyle \underset{c}{\Sigma }}\mathit{cP}\left(c\right)$) per residue at pH 6.0 (red), pH 10.8 (green), and pH 14.0 (blue) calculated using the entire structural ensemble at those pH values. The lines across the top indicate the folding units as defined by hydrogen exchange experiments⁴⁴ and simulation.¹ (B) The value of < c > averaged over each folding unit. (C) The average of the number of contacts per residue calculated for individual species: native (red), Tyr48-misligated (green), Tyr67-misligated (blue), and hydroxide ligated and lysine/tyrosine deprotonated (magenta). Each plot is generated using the H-bonding model simulations. Similar results were calculated for the electrostatic/collapse and pure-funnel models.

We can examine the simulated alkaline-induced ensembles in a manner closely analogous to what is done for the site specific FTIR experiments. FTIR studies of semi-synthetic protein with carbon-deuterium labeled residues provide information about the local environment of the labeled residues because the observed signals are sensitive to solvent exposure, ligation to the heme iron, and protonation changes.^19,53-55 To relate the simulations to FTIR signals that are mainly sensitive to changes in solvent exposure, we determine the probability distributions of the number of contacts at five residues as a function of pH (Figure 9). The probability of c contacts for a residue at a given pH is:

$$P\left(c\right)=\underset{s}{\Sigma }\frac{{\displaystyle \underset{Q}{\Sigma }}{e}^{-\beta F_s\left(Q\right)}{e}^{-\beta {\mu }_s}{K}_{\mathit{lig},s}\theta \left(c_s\left(Q\right)\right)}{{\displaystyle \underset{Q}{\Sigma }}\Xi (Q,\mathit{pH})}$$ (2)

Figure 9.

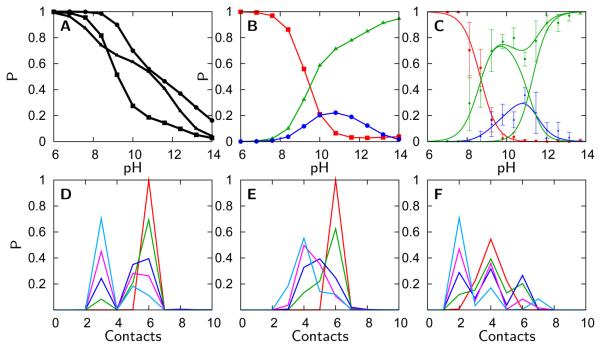
(A) Probability of finding 10 contacts, as found in the native state, with Leu68 calculated using the pure-funnel (squares), electrostatic/collapse (triangles), and H-bonding models (circles). (B) Probability of finding 6 (red), 4 (blue), or 2 (green) contacts with Met80 calculated using the pure-funnel model. (C) Fractional concentrations of the folded (red), high pH solvent exposed (green), and intermediate (blue) signals observed for Met80 by FTIR.¹⁹ (D-F) Probability of the number of contacts (c) with Lys72, Lys73, and Lys79 respectively calculated using the H-bonding model. The curves plotted are for pH 6.0 (red), pH 9.2 (green), pH 10.0 (blue), pH 11.6 (magenta), and pH 14.0 (teal). The complete set of probability distributions of the number of contacts for all models is shown in the supporting information.

The value of θ(c_s(Q)) is usually 0 but is given a value of 1 if c equals c_s(Q), the number of contacts for residue i in which the distance, < r_ij(Q) >, is less than 8 and |i−j| > 1. The results can be qualitatively described via a two state fit at Leu68 and by three state fits at Lys73, Lys79, and Met80 consistent with the observed changes in the FTIR experiment (Figure S1). The electrostatic/collapse and H-bonding models more correctly predict the Leu68 transition midpoint which occurs at 12.7 experimentally, but is predicted to occur at less than pH 10.0 in the pure-funnel model (Figure 9A). In contrast to the Leu68 FTIR signals which are sensitive primarily to changes in solvent exposure and the Met80 signals which are sensitive to both solvent exposure and ligation, the Lys72, Lys73, and Lys79 signals are affected by changes in solvent exposure, ligation, and deprotonation. While comparison of the lysine signals to simulation is difficult, it is interesting to note that the calculated transitions at Lys73 and Lys79 appear to involve more distinct structural ensembles than does the Lys72 transition (Figure 9D-F). This agrees with the interpretations of the experimental IR data that suggest there is a three state transition for Lys73 and Lys79 and a two state transition for Lys72. The simulations also qualitatively capture the character of the transition at Met80 (Figure 9B-C). Experimental evidence suggests that between pH 9 and 11, Met80 experiences two different environments, a buried state that is more heterogeneous than the native state at pH 7 and a solvent exposed state. Another transition near pH 11 results in complete solvent exposure at Met80. The probability distributions of the Met80 contacts shows similar behavior (Figure 9C, Figure S1, and Figure S2).

Discussion

FTIR studies of site-selectively deuterated cytochrome c have resolved the existence of two intermediates, which are maximally populated at pH 9.3 (3.5) and 11.8 (V), in addition to the lysine-misligated intermediates.¹⁹ However the experiments provide only limited structural information about these intermediates. The data suggest that both intermediates are partially folded since the FTIR signal at Leu68 indicates protection from solvent but the Met80 signal indicates significant solvent exposure. Both the pure-funnel and electrostatic/collapse models fail fully to reproduce these structural details because they predict Leu68 is solvent exposed in both 3.5 and V (Table Table 3). In these models, the protein unfolds upon deprotonation of lysine and tyrosine and is only modestly affected by the deprotonation of arginine. However, due to the stabilizing H-bonds between the two most stable folding subunits (the N- and C-terminal helices and the 60's helix),⁴⁴ the model with modified H-bonding captures the global unfolding event upon arginine deprotonation. The modified H-bonding model also predicts that the partially unfolded intermediate structures for 3.5 and V are similar since the distribution of the partially unfolded hydroxide-bound state (Figure 4C), which dominates at intermediate pH, may represent the sum of 3.5 and V as inferred from experiment (Figure 4D). Previous experiments, in fact, suggest that the ligand in state V is hydroxide.¹⁷ An alternative possibility is that the 3.5 intermediate results from a chemical species not included in the current simulations. Another chemical species having a maximum population at pH 9.3 could shift the population of the predicted intermediates so that they form at a higher pH. Due to the lower pK_a of tyrosine as compared to lysine, its deprotonation could favor a tyrosine-misligated intermediate or trigger an unfolding event that is localized to the Met80 loop, both of which could be consistent with experimental observations. Analogous to the calculations of the relative stability between the lysine misligates, we predict that the Tyr48 and Tyr67 misligates would be most stable as indicated by all three models (Figure S3). However, the structures of both misligates do not agree with interpretations of hydrogen exchange and residue specific FTIR data based upon examination of the ensemble average of the number of contacts per residue (Figure 8c). Consistent with experimental interpretations, the predicted structures of the Tyr67 misligate and the hydroxide-bound species (V) demonstrate solvent exposed Met80 and omega loops (residues 70 to 88 and 40 to 56 respectively). In contrast, the Tyr48 misligate has similar solvent exposure to that for the native state. Upon closer analysis, the Tyr67-misligated and the hydroxide-bound species (V) are predicted to have a significantly decreased number of contacts at Met80 but a similar number of contacts at Leu68 when compared to the native state which agrees with interpretations of FTIR experiments. Therefore the current work strongly suggests that the 3.5 intermediate is either a Tyr67 misligate or a hydroxide-bound species. All three models predict that state V is a hydroxide-bound species in agreement with experimental work.¹⁷

Table 3.

Structural Description/Ligation State of the Dominant Species in the Simulation as Compared to the Experiments

		Pure- funnel	Electrostatic/ Collapse	Hydrogen Bonding	Experiment
Experimentally Observed Statesa	III	F/Met80	F/Met80	F/Met80	F/Met80
	3.5	U/H20	U/H20	PF/−OH	PF/?
	IVa	PF/Lys73	PF/Lys73	PF/Lys73	PF/Lys73
	IVb	PF/Lys79	PF/Lys79	PF/Lys79	PF/Lys79
	V	U/−OH	U/−OH	PF/−OH	PF/?
	U	U/−OH	U/−OH	U/−OH	U/−OH

^aStates are either folded (F wtih Q>0.8), partially folded (PF with 0.3<Q<0.8), or unfolded (U with Q<0.3) and are ligated with either an amino acid or solvent molecule

Using these three related but distinct models provides insight into the dominant forces that govern these multiple pH transitions. Protein folding theory indicates that local interactions, interactions close in distance but not necessarily close in sequence, are the most dominant contributors to the funneled nature of the energy landscape. Deprotonation decreases the strength of local interactions that stabilize the native state thereby decreasing the funneled nature of the energy landscape. In the pure-funnel model, long range electrostatic effects are ignored and side chain interactions are treated with homogeneous non-additive terms. Remarkably even this most simplistic model is able to predict intermediate stabilities well because the destabilizing effects of deprotonation are captured in the changes of the local interactions. Thus the homogeneous non-additive pure-funnel model describes well the relative stability of the lysine misligated intermediates in addition to the relative folding sequence of the folding units.¹ However some detailed structural information appears to be poorly captured in this simplest model's prediction. For instance, the agreement of structural features of the Lys73-misligated state with experiment is relatively poor because the omega loop (residues 40 to 56) is predicted to be randomly coiled but appears to be partially folded on the basis of the NMR studies. The electrostatic/collapse model shows better agreement with the Lys73-misligated NMR structure because the collapse potential forces the omega loop to dock more completely with the rest of the structure. While structural accuracy is apparently improved by the addition of the electrostatic and collapse potentials, the more complex model fails to capture the stability change upon arginine deprotonation. This discrepancy is resolved using the model having modified H-bonding because the Arg91 side chain forms a H-bond at the interface of the two most stable folding units of cytochrome c. This H-bond is vital to the stability of the protein since preserving the interface allows a significant part of the folding nucleus to remain intact. In general, the H-bond potential rescales the stabilities of the folding units and the interfaces between folding units so that the dominant folding route correctly predicted with the pure-funnel model is more structurally faithful. Treating H-bonding explicitly results in improved agreement of the Lys73 misligated NMR structure with the simulation as several H-bonds help stabilize the omega loop.

The current study demonstrates the importance of including the full range of chemical species in the analysis of complex multispecies processes such as the alkaline-induced transitions of cytochrome c. While only a few states dominate at any given pH, many different intermediates become populated, albeit at low concentration. Consistent with the funneled landscape picture, mutating the protein to selectively destabilize one intermediate ordinarily gives rise to a competing species of slightly less stability. Also cytochromes c from different species are funneled into slightly different near native state ensembles which may explain experimental discrepancies between measurements of the relative concentrations of the Lys79-, Lys73-, and Lys72-misligated states on different variants of cytochrome c.^14-16,56,57 The current grand canonical ensemble methodology can serve as an explanatory tool for analysis of multistate folding transitions. Since the method requires few free parameters the same methodology can easily be applied to many metalloprotein systems. The introduction of specific non-native contacts, correlated with known inorganic chemistry, into an otherwise perfectly funneled energy landscape demonstrates the importance of energetic frustration in chemically induced unfolding as demonstrated by the alkaline-induced transitions of cytochrome c.

Abbreviations

AMH

associative memory Hamiltonian