LOX: inferring Level Of eXpression from diverse methods of census sequencing

Abstract

Summary: We present LOX (Level Of eXpression) that estimates the Level Of gene eXpression from high-throughput-expressed sequence datasets with multiple treatments or samples. Unlike most analyses, LOX incorporates a gene bias model that facilitates integration of diverse transcriptomic sequencing data that arises when transcriptomic data have been produced using diverse experimental methodologies. LOX integrates overall sequence count tallies normalized by total expressed sequence count to provide expression levels for each gene relative to all treatments as well as Bayesian credible intervals.

Availability: http://www.yale.edu/townsend/software.html

Contact: jeffrey.townsend@yale.edu

1 INTRODUCTION

The quantification of genomic gene expression variation across conditions has become an increasingly common component of diverse research programs. While microarray technology has been widely and successfully applied in the past, high-throughput sequencing technology has garnered significant attention for the identification of differentially expressed transcripts (Creighton et al., 2009). High-throughput sequencing technology facilitates discrete counts of expressed sequences, enabling accurate and precise quantification of differential expression levels, especially for low-abundance transcripts, and is not subject to issues of cross-hybridization. These features represent important advantages over hybridization-based microarray technologies (t Hoen et al., 2008), provided that suitable approaches are applied for data analysis.

Experimentally, sequencing-based expression methodologies differ in RNA isolation and priming strategies (e.g. band-cutting, oligo-dT primers, random primers, gene-specific primers or multi-targeted primers), as well as sequence lengths and coverage (e.g. 454, SOLiD and Solexa). For nearly all expression assays, reverse transcription from messenger RNA (mRNA) to complementary DNA (cDNA) is a key step that contributes considerable experimental variance (Yang and Speed, 2002). Throughput of the reaction is biased for each gene by secondary and tertiary structures of mRNA, affinities specific to the reverse transcriptase, inhibitors present in the sample, priming strategy and variation in priming efficiency (Gonzalez and Robb, 2007; Graf et al., 1997; Stahlberg et al., 2004; Stangegaard et al., 2006; Talaat et al., 2000). To make full use of diverse datasets gathered by different methodologies and to enable accurate and precise expression profiling, therefore, it is necessary to be able to analyze gene expression levels based on data from diverse methodologies. Although several recent tools (Bloom et al., 2009; Robinson et al., 2010; Wang et al., 2010) are appropriate for sequencing-based gene expression data, little attention has been devoted to the development of software that can support of analysis not just of homogeneously gathered datasets, but also of datasets gathered by multiple methodologies (Balwierz et al., 2009). Here, we present open-source, cross-platform software, LOX (Level Of eXpression), enabling powerful, accurate and precise quantification of expression from multiple treatments and/or sequencing methodologies.

2 ALGORITHMS

2.1 Model

LOX is implemented with a Markov chain Monte Carlo (MCMC) algorithm, facilitating integration over multiple treatments when expressed sequence counts have been provided by one or more experimental methodologies. We denote the set of treatments as N, the set of experimental methodologies as M, and the set of genes as G. The expressed tag count c_ijk is the input data for each gene k under treatment i and methodology j, and can range from less than ten to thousands or more. Estimated parameter p_ik is the expression level in treatment i relative to all genes, and q_jk is the correction for the omitted-variable bias imposed on gene k by methodology j, where 0 < p_ik < 1 and 0 < q_jk < 1. The proportion of counts should reflect the proportion of expressed mRNA, modulated by the effect q of the methodology on the gene k. Therefore, the posterior density for p_ik and q_jk for all i and j can be estimated by applying Bayes' rule to the distribution of the data conditioned on the parameters. Assuming an uninformative prior and a binomial distribution of the counts c_ijk with proportion p_ikq_jk (0 < p_ikq_jk < 1) yields

(1)

where input data s_ij is the sum of expression counts across all genes with treatment i and methodology j, formulated as s_ij = ∑_k∈Gc_ijk.

2.2 Implementation

LOX employs a relative expression estimation approach similar to that used for the BAGEL (Bayesian Analysis of Gene Expression Levels) analysis of microarray data (Townsend and Hartl, 2002). Briefly, a Markov chain is constructed by MCMC integration that explores the probability density for the parameters on the basis of Equation (1). Initial values of parameters p_ik and q_jk are set as 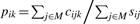and 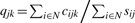, respectively, and their subsequent values in the chain are determined iteratively by choosing successive proposed values. To generate successive proposed values, two of the expression-level parameters are first chosen at random. Second, a triangularly distributed step size with range [−Δ, +Δ] is generated, where the magnitude of Δ is the average of the two chosen parameters' initial values divided by two. These calibrated step sizes facilitate rapid mixing of the Markov chain, because likely values of p and q can vary from gene to gene over orders of magnitude. Third, one of the two chosen parameters is incremented by the generated step size and the other is decremented by the same quantity. Thus, the proposed state differs from the last iteration only for the two chosen parameters.

Next, an acceptance probability is calculated as the ratio of the probabilities of the proposed state to the current state. The acceptance of transition from the current state to the proposed state is indicated by comparing the acceptance probability with a random variable from 0 to 1, viz.,

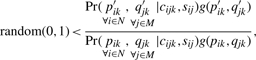(2)

where the prime symbolizes the proposed parameter and g(p′_ik, q′_jk) is an equiprobable (flat) prior distribution of the parameters. If Equation (2) is not satisfied, the current state is retained for the next iteration. After stationarity, this procedure results in a Markov chain of states that stochastically recapitulates the posterior distributions of each parameter, integrated across the probable states of all other parameters (Hastings, 1970; Metropolis et al., 1953). Estimates are derived from the median of the posterior.

3 FEATURES

LOX, written in standard C++, facilitates compilation compliant with GNU standard procedure and execution on Linux/Unix, Macintosh, and Windows platforms. LOX is distributed as open-source software and licensed under the GNU General Public License. The LOX package, including compiled executables, example data, documentation and source codes, is freely available for academic use at http://www.yale.edu/townsend/software.html.

The input data for LOX are expression counts of multiple genes, under one or more treatments and with one or more methodologies. To ease data input, LOX accepts tab-delimited text file with three header rows. Input row one is set aside for user-customized information, row two contains text codes designating the methodology applied and row three includes text codes designating the treatment type. The subsequent rows contain gene ID, gene name and expression counts under corresponding treatments and methodologies. An example data file containing 5525 genes and its results file accompanies the LOX package. To facilitate use of LOX, a basic pipeline for generating the LOX input file from raw sequence reads and genome features of interest is provided in the LOX package.

LOX output is in the form of a tab-delimited text file with one header row. Each row thereafter displays the results for a single gene, including columns with gene ID and gene name, the estimate of expression level for each treatment (the median of the posterior distribution), 95% percent Bayesian credible intervals (the additions and subtractions to make upper and lower bounds) for that estimate, the stationary acceptance rates for the MCMC steps, a Boolean value indicating whether those rates are within an acceptable range (by default, 0.15–0.50; Gelman et al., 1996) and the best log posterior probability. Bayesian P-values for differential expression are also reported regarding all pairs of treatments, and may be used in conjunction with effect sizes and credible intervals to rank genes by their differential expression. Lastly, optional columns can be output that report the methodological effects and the parameter estimates at the peak of maximum likelihood.

4 CONCLUSION

LOX quantifies gene expression levels, Bayesian credible intervals and statistical significance across multiple treatments or samples using MCMC integration. As the cost of diverse high-throughput sequencing methodologies decreases, LOX will provide increasing utility to a burgeoning number of gene expression studies.

Funding: National Institute of General Medical Sciences P01 GM 068087 and National Institutes of Health RR19895.

Conflict of Interest: none declared.