Abstract
Many eukaryotic proteins are disordered under physiological conditions, and fold into ordered structures only on binding to their cellular targets. Such intrinsically disordered proteins (IDPs) often contain a large fraction of charged amino acids. Here, we use single-molecule Förster resonance energy transfer to investigate the influence of charged residues on the dimensions of unfolded and intrinsically disordered proteins. We find that, in contrast to the compact unfolded conformations that have been observed for many proteins at low denaturant concentration, IDPs can exhibit a prominent expansion at low ionic strength that correlates with their net charge. Charge-balanced polypeptides, however, can exhibit an additional collapse at low ionic strength, as predicted by polyampholyte theory from the attraction between opposite charges in the chain. The pronounced effect of charges on the dimensions of unfolded proteins has important implications for the cellular functions of IDPs.
Keywords: polyampholyte, polyelectrolyte, protein folding, unfolded state, single-molecule FRET
A surprisingly large number of proteins contain extended unstructured segments or fold into a well-defined three-dimensional structure only in the presence of their specific ligands or binding partners (1–4). Especially in eukaryotes, such intrinsically disordered or unstructured proteins (IDPs) appear to be involved in a wide range of cellular functions, including transcription, translation, signal transduction, and the regulation of protein assembly (1). Correspondingly, many IDPs are associated with diseases, such as cancer or neurodegenerative disorders (4). In contrast to stably folded proteins, the polymer properties of IDPs are crucial for many of their functions. Long-range interactions of the unstructured chain with binding partners have been suggested to increase their capture radius, leading to an enhancement of binding rates via the “fly-casting” mechanism (5, 6). Conformational disorder has an important role in mediating binding diversity, enabling interactions with multiple targets (2, 7, 8). Repulsive entropic forces of “brush-like” structures can give rise to very long-range interactions, for instance to provide a mechanism for maintaining neurofilament and microtubule spacing (9, 10). Finally, because part of the binding free energy has to be expended for folding of the IDP upon interaction with its target, intrinsic disorder facilitates highly specific binding at moderate affinities, a mechanism that may be essential for regulation and signal transduction (2). All of these aspects depend crucially on chain flexibility and dimensions, which in turn are dictated by the composition of the polypeptide. Establishing a quantitative relation between charge content, hydrophobicity, and chain dimensions is thus a prerequisite for understanding the molecular mechanisms underlying IDP function.
Prevalent characteristics of IDPs are their low sequence complexity, the low proportion of hydrophobic residues, which usually form the core of a folded protein, and their high content of polar and charged amino acids (11). This correlation between disorder and charge content has strongly aided the identification of IDPs from large scale genomic sequence data bases and now provides an ideal opportunity to investigate the role of sequence composition and especially charge interactions for the conformational properties of unfolded proteins. It also allows us to test quantitative descriptions and predictions of polymer theory for the influence of charged amino acids on chain dimensions. Even though the use of the corresponding simplified models would seem ideally suited for developing a better understanding of the properties of IDPs, there have been few, if any, measurements available that would have allowed a quantitative comparison to polymer theory (9).
Here, we use single-molecule Förster resonance energy transfer (FRET), a method that has been applied successfully to obtain long-range distance distributions and dynamics in unfolded proteins (12–14). By means of the spectroscopic separation of folded and unfolded subpopulations (15), single-molecule FRET allows us to distinguish changes in the conformational properties within one of the subpopulations from a change in their relative abundances, which is often difficult in corresponding ensemble experiments. To sample the range of sequence compositions found in natural proteins, as represented by a plot of net charge versus hydrophobicity calculated from the amino acid sequence (11) (Fig. 1), we chose three representative proteins with very different properties: the globular cold shock protein CspTm, which is stably folded even in the absence of ligands (16–18); the N-terminal domain of HIV-1 integrase (IN), which folds only upon binding of Zn2+ ions and is otherwise denatured (19, 20); and human prothymosin α (ProTα), one of the IDPs with the largest fraction of charged amino acids identified so far (11). ProTα does not assume a well-defined folded structure under any known conditions and does not contain regular secondary structure (21), but plays crucial roles in different biological processes including cell proliferation, transcriptional regulation, and apoptosis (22).
Fig. 1.
Mean net charge versus mean hydrophobicity per residue of the globular and intrinsically disordered proteins used in this study. The dotted line indicates the separation between intrinsically disordered and globular proteins observed by Uversky et al. (11). Small circles are based on calculations taking into account the amino acid sequence only. Vertical bars indicate the influence of the dye charges; horizontal bars are an estimate of the uncertainty in the hydrophobicity of the dyes. To estimate this uncertainty, the hydrophobicity of the residues at the position of fluorophore attachment was varied between the value for the most hydrophilic and the most hydrophobic amino acid, and the resulting average hydrophobicities were computed. The large circles illustrate this range of values. For CspTm and IN, where the dyes were positioned close to the termini, the entire sequence was used for calculating charge and hydrophobicity, for the ProTα variants only the interdye segment. Hydrophobicity values were calculated according to Kyte and Doolittle (67). The positions used for FRET labeling are indicated as small spheres in the structural representations of the proteins.
Results
Single-Molecule FRET Experiments.
We labeled all protein variants with a donor (Alexa Fluor 488) and an acceptor (Alexa Fluor 594) fluorophore (Methods and SI Text), and investigated them with confocal single-molecule fluorescence spectroscopy. For IN and CspTm, the labels were positioned close to the termini of the polypeptides (Fig. 1), such that the properties of the entire chain were probed. For ProTα, the N- and C-terminal segments of the polypeptide exhibit very different charge densities and were investigated separately by positioning one chromophore at position 56 and the other either at position 2 (ProTαN) or at position 110 (ProTαC; see Table S1). In this way, the length of all segments probed was similar and resulted in average interdye-distances sufficiently close to the Förster radius of the dye pair to optimize sensitivity and simplify a quantitative comparison. The efficiency of energy transfer between the dyes upon donor excitation was determined from photon bursts originating from individual molecules freely diffusing through the focal spot of the laser beam as E = nA/(nA + nD), where nA and nD are the number of detected acceptor and donor photons, respectively [including corrections (SI Text)]. A transfer efficiency histogram generated from a large number of such events shows distinct maxima corresponding to the subpopulations present in the sample (Fig. 2).
Fig. 2.
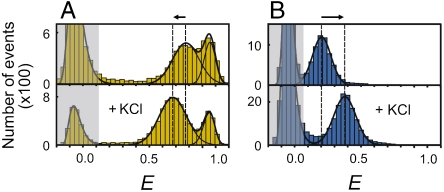
Single-molecule FRET efficiency (E) histograms of (A) CspTm (C-terminally truncated variant), (B) IN, and (C) ProTαC show the GdmCl dependence of the unfolded proteins. The molar GdmCl concentration is indicated in each panel. (A) The peak at E ≈ 0.95 corresponds to folded CspTm, the peak between E ≈ 0.3 and 0.85 to unfolded protein. (B) First panel: Folded IN (E ≈ 0.9) is only populated in the presence of ZnCl2 (100 μM; 0 M GdmCl). Other panels: varying concentrations of GdmCl with 1 mM EDTA. 〈E〉 of the unfolded population ranges between 0.4 and 0.6. (C) ProTαC is unfolded under all conditions. For all proteins, the peaks at E ≈ 0 (shaded) correspond to molecules lacking an active acceptor chromophore (68). The solid lines show fits used to extract the mean transfer efficiencies of the subpopulations (17, 23). The dashed lines indicate the mean transfer efficiencies of the unfolded states at the highest GdmCl concentrations.
Fig. 2 shows examples of FRET efficiency histograms obtained under different solution conditions. For CspTm (Fig. 2A), we used a variant destabilized via a C-terminal truncation of two residues. As a result, the unfolded state is populated in the absence of denaturant, which allows us to determine the unfolded state dimensions of CspTm even under these conditions. The peak at high E corresponds to folded molecules, the peak at intermediate E corresponds to unfolded molecules, and the peak at E ≈ 0 (shaded) originates from molecules with an inactive acceptor. With increasing guanidinium chloride (GdmCl) concentration, the population of folded molecules decreases, and the population of unfolded molecules increases, as expected for a two-state system (15, 23). At the same time, the mean transfer efficiency 〈E〉 of the unfolded state decreases continuously (Fig. 2A), corresponding to the well-studied denaturant-induced expansion of unfolded CspTm (17, 23, 24), a behavior that has now been observed for the unfolded states of many proteins (12). With the ability to separate subpopulations, single-molecule experiments allow such continuous changes in the dimensions of the unfolded state to be clearly distinguished from the contribution of the native state or other populations to the overall signal. In contrast to CspTm, IN (Fig. 2B) is completely unfolded even in the absence of denaturant; i.e., it is in its intrinsically disordered state. Only in the presence of ZnCl2, a folded subpopulation of molecules coexists with unfolded IN. On addition of EDTA, which complexes Zn2+ with high affinity, all molecules unfold. Interestingly, the denaturant dependence of unfolded IN shows a nonmonotonic behavior: starting from 0 M GdmCl, 〈E〉 for unfolded IN first increases slightly up to GdmCl concentrations of about 0.2 M, indicating a collapse of the unfolded state. Only at higher GdmCl concentrations, 〈E〉 starts to decrease due to the denaturant-induced expansion. This effect is even more pronounced for ProTα (Fig. 2C, variant ProTαC), with a drastic increase in 〈E〉 from 0.21 in the absence of GdmCl to 0.43 at 0.8 M GdmCl, followed by the denaturant-induced expansion similar to CspTm and IN at higher GdmCl concentrations. At 0 M denaturant, ProTαC is thus more expanded than at the highest accessible GdmCl concentrations.
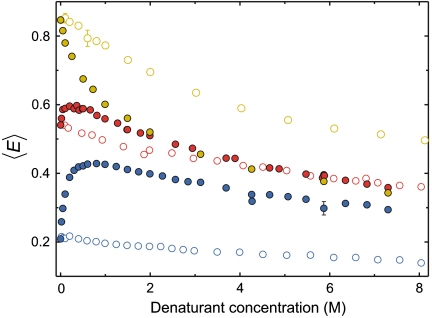
The denaturant dependences of the three proteins are summarized in Fig. 3. It shows the monotonic change in 〈E〉 for unfolded CspTm, corresponding to its continuous expansion with increasing GdmCl concentration, and for the IDPs the remarkable “rollover” of 〈E〉 below approximately 0.5 M GdmCl. The correlation between the amplitude of the rollover and the charge density of the protein strongly suggests that electrostatic repulsion within the polypeptides cause the expansion of the IDPs. In the presence of the ionic denaturant GdmCl, the charges of the amino acid side chains are screened, allowing the polypeptides to compact (25)*. Only at higher concentrations of GdmCl, the denaturant-induced expansion of the chain takes over, and ultimately the transfer efficiencies of the different unfolded proteins converge (Fig. 3), as expected for polypeptides of similar length (26)†. The rollover is absent if the uncharged denaturant urea is used. Moreover, the differences in transfer efficiencies between the proteins in the absence of denaturant are present over the entire range of urea concentrations, indicating that charge-mediated repulsion dominates chain dimensions even at the highest concentrations of urea.
Fig. 3.
Denaturant-dependent collapse and charge-mediated expansion of unfolded proteins. Dependence of the mean transfer efficiencies, 〈E〉, for CspTm (yellow), IN (red), and ProTαC (blue) on the concentration of GdmCl (filled circles) and urea (open circles). The typical uncertainty in transfer efficiency of individual data points is in the range of 0.02. Error bars are shown for conditions where multiple measurements are available.
To facilitate a quantitative analysis of our observations in terms of unfolded state dimensions, we converted the mean transfer efficiencies to a measure of intramolecular distance according to (23)
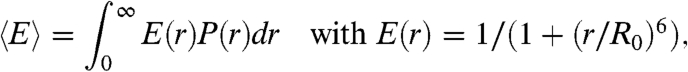 |
[1] |
where r is the distance between donor and acceptor, P(r) is the normalized equilibrium distance distribution, and R0 is the Förster radius (5.4 nm at 0 M denaturant) calculated for the respective solution conditions. Given a measured value of 〈E〉 of the unfolded subpopulation and a suitable model for the distance distribution, the parameters determining P(r) can be calculated numerically. To test the robustness of our results with respect to the functional form of the distance distribution used, we analyzed the data with two different models: the Gaussian chain (12, 17, 23, 27, 28) and a variation of Sanchez theory (28–30), which uses a Flory–Fisk distribution (31) with a solvent-dependent effective interaction within the chain (see SI Text for details). The results from the two types of analysis are very similar (Fig. S1, Fig. S2, Table S2, Table S3, Table S4, and Table S5), suggesting that the chain dimensions derived from the FRET data under our conditions do not strongly depend on the assumptions underlying the individual models. We thus proceed with the dimensions calculated using the simpler model, the Gaussian chain‡.
Fig. 4 shows the resulting values of the radius of gyration, Rg (Eq. S1), as a function of denaturant concentration for all protein variants investigated. Whereas their behavior is similar at GdmCl concentrations above approximately 1 M, the extent of their charge-driven unfolded state expansion at low GdmCl concentration is very different, increasing in amplitude from 8% of the Rg in IN (Fig. 4B) and 14% in ProTαN (Fig. 4C) to 46% in ProTαC (Fig. 4D). The degree of expansion clearly correlates with the net charge of the proteins: CspTm is almost charge-balanced (net charge -2)§; IN shows a slight excess of negative charges (net charge -4), and the two ProTα segments ProTαN (net charge -14) and ProTαC (net charge -27) exhibit a large net charge. This correlation suggests an important role of charge density in the polypeptides for their unfolded state dimensions. To test this hypothesis and to identify a suitable quantitative description of IDPs (32), we applied a polymer physical analysis.
Fig. 4.
Dependence of the apparent radii of gyration (Rg) of the labeled protein segments on the concentration of GdmCl (filled circles) and urea (open circles), with (A) CspTm (yellow), (B) IN (red), (C) ProTαN (cyan), and (D) ProTαC (blue). Fits to a binding model for the urea dependence (Eq. 2, colored dashed lines), and to polyampholyte theory for the GdmCl dependence (Eq. 5, black solid lines) are shown. The two components of Eq. 5, corresponding to the contributions of GdmCl binding and electrostatic repulsion, are indicated as continuous and dashed gray lines, respectively. Note that the fits to Eq. 5 are performed based on thermodynamic activities, but plotted on a concentration scale. The colored squares in (A) and (D) indicate the values of Rg on addition of 1 M KCl (compare to Fig. 5). The gray squares indicate the expected values estimated with Eqs. 4 and 5, assuming the values for K, a, and ρ obtained from the fits of the urea dependencies (Table S4), the value of ν obtained from the fits of the GdmCl dependencies (Table S2), and calculating κ for an ionic strength of 1 M. The remaining difference between experimental and calculated values may be due to the preferential interaction of GdmCl with the polypeptide, leading to a higher local charge density than in the bulk solution and a correspondingly stronger charge shielding than for KCl.
Quantifying Charge Effects on Unfolded State Dimensions.
At least three contributions need to be taken into account to describe our results: (i) the expansion of the polypeptide with increasing denaturant concentration, (ii) the electrostatic interactions between the charges in the chain, and (iii) the screening of these charges by the ionic denaturant GdmCl. To describe chain expansion with increasing denaturant concentration, we use a simple binding model (17, 18, 33) that assumes identical independent binding sites with an effective association constant K
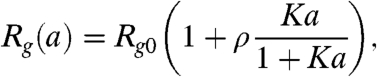 |
[2] |
where Rg0 is the radius of gyration at zero denaturant, a is the thermodynamic activity of denaturant (18, 33), and ρ accounts for the relative change in radius of gyration approached asymptotically at very high denaturant activities. In spite of its simplicity, this model captures the functional form of chain expansion and yields binding constants in agreement with calorimetric measurements (18, 33)¶. Charge screening is treated in terms of Debye–Hückel theory, with the Debye length κ-1 = (8πlBI)-1/2, where I is the ionic strength of the solution and lB is the Bjerrum length, the distance at which the electrostatic energy of the interaction between two elementary charges equals thermal energy, kBT. We obtain lB = e2/(4πε0εrkBT), where e is the elementary charge, ε0 is the permittivity of vacuum, εr is the dielectric constant, kB is Boltzmann’s constant, and T is temperature. To treat the interactions of charges within the chain, we use polyampholyte theory (34), a description that includes both repulsive interactions between charges of the same sign and attractive interactions between charges of opposite sign. Here, we adopt the approach of Higgs and Joanny (35), which can be used to extract Flory-like scaling factors for polyampholytes. This model considers a chain in which monomer n has charge ecn, where cn assumes the value +1 with probability f for the occurrence of a positive charge, -1 with the probability g for the occurrence of a negative charge, and 0 with probability 1 - f - g for the remaining neutral monomers. f and g at our pH of 7.4 were computed using the pKa values of all contributing ionizable groups, including those of the fluorophores (Table S1). The monomers have an excluded volume vb3 (with a segment length b = 0.38 nm, the Cα-Cα distance in a polypeptide, and v≥0), and they interact via screened Coulomb interactions between each pair of monomers m and n, with distances assumed to follow Gaussian chain statistics. Introducing the expansion factor α as the ratio of an effective segment length b1 and the real segment length b, Higgs and Joanny showed that under the condition N1/2κb1 > 1∥ (where N is the number of segments in the chain), electrostatic interactions can be regarded as a contribution to the effective excluded volume ν∗b3. The chain dimensions can then be described using the expression
 |
[3] |
and
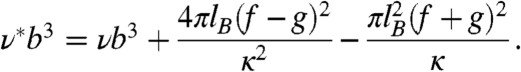 |
[4] |
Here, νb3 is the excluded volume in the uncharged chain. The second term in Eq. 4 accounts for repulsive interactions due to the net charge of the polypeptide, which result in an increase of ν∗b3 as in related formulations of polyelectrolyte theory (36) (see SI Text). The third term leads to a reduction of ν∗b3 through attractive interactions between charges of opposite sign. The polyampholyte model can be combined with the binding model [Eq. 2] to yield
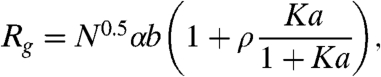 |
[5] |
which can be used to describe the dependence of Rg on GdmCl activity a (Fig. 4). α is determined by Eqs. 3 and 4, such that the only fit parameters are K, ρ, and ν (see SI Text, Table S2, Table S3, Table S4, and Table S5). All other parameters are calculated from the polypeptide sequence and the composition of the solution.
Fits to the GdmCl dependencies of Rg illustrate the strength of this approach (Fig. 4). Polyampholyte theory predicts the rollover in Rg for IN (Fig. 4B) and the ProTα variants (Fig. 4 C and D), both in terms of the functional form and the amplitude of the expansion with good accuracy. Notably, the amplitude does not involve any adjustable fit parameters, but results from the values of f and g, which are computed from the charge composition of the polypeptide sequence. Eq. 5 also captures the monotonic collapse of CspTm (Fig. 4A). Surprisingly, it predicts an additional collapse of unfolded CspTm at low ionic strength caused by the attractive electrostatic interactions between opposite charges in this charge-balanced polyampholyte (34, 35). To illustrate this point, Fig. 4 shows the contributions of the effective binding of GdmCl and of the charge interactions to the changes in Rg as continuous and dashed gray lines, respectively. A charge-induced collapse is consistent with the experimental data, which show a pronounced drop in Rg at the lowest GdmCl concentrations (Fig. 4A), but we tested this hypothesis further. If charge attractions indeed contribute to the collapse of unfolded CspTm, we expect that screening of the charges by adding salt will lead to an expansion of the chain, whereas a collapse is expected for the IDPs. Exactly this behavior is observed experimentally, as Fig. 5 illustrates for ProTαC and CspTm: if 1.0 M potassium chloride is added to screen the charges, 〈E〉 of ProTαC increases, corresponding to a collapse (Fig. 4D), whereas 〈E〉 of unfolded CspTm decreases, indicating an expansion (Fig. 4A)**. We can thus conclude that charge interactions can indeed lead both to an expansion or a collapse of unfolded proteins, depending on the charge balance in the polypeptide.
Fig. 5.
Effect of charge shielding on denatured state dimensions. Transfer efficiency histograms of CspTm (A) and ProTαC (B) in 1.0 M urea in the absence (Upper) and in the presence of 1.0 M KCl (Lower). CspTm expands on addition of KCl, whereas ProTαC collapses, as predicted by polyampholyte theory. For ProTαC, the change in 〈E〉 corresponds to a reduction in Rg from (4.2 ± 0.2) nm without KCl to (2.98 ± 0.09) nm with KCl, close to the value of (2.87 ± 0.09) nm calculated with Eq. 5 from the corresponding reduction in Debye length. For unfolded CspTm, addition of 1.0 M KCl causes an increase in Rg from (1.73 ± 0.05) nm to (1.97 ± 0.05) nm, with a calculated Rg of the charge-shielded unfolded state of (2.15 ± 0.05) nm.
Discussion
The balance of interactions in the unfolded state and their effect on the compactness of the chain is under intense debate, with possible contributions from hydrophobic interactions (37, 38), hydrogen bonding (39, 40), and charge–charge interactions (21, 41–43). Advances in the application of theoretical models and simulations have addressed important aspects; e.g. the influence of solvation and denaturants (27–29, 44–46), temperature (18), and specific interactions (47–49). With the increasing availability of biophysical methods that can provide structural information even on conformationally heterogeneous systems such as unfolded proteins (1, 12, 43, 50–52), we are starting to be able to correlate experimental findings with theoretical models.
Here we used single-molecule FRET to systematically investigate unfolded proteins with different charge composition, and find that charge interactions play a decisive role for unfolded state dimensions. In proteins with high net charge, as prevalent in many IDPs, charge repulsion can lead to a pronounced expansion (43), similar to previous observations in acid-unfolded proteins (25). Even more strikingly, in proteins with a similar number of positive and negative charges, charge attraction can amplify the collapse of the chain, a concept that has been well established in polyampholyte theory, but has eluded experimental investigation in the context of proteins (9). We find that polyampholyte theory offers a remarkably good description of the influence of charged amino acids on chain dimensions and thus provides a means of predicting the dimensions of IDPs and unfolded proteins. As expected for polypeptides with a large net charge, the expansion of ProTα and IN at low ionic strength can also be described by polyelectrolyte theory (36, 53–55) (Table S6); i.e. without taking into account attractive charge interactions (Fig. S3). Even though the net charge of CspTm is close to zero (Table S1), and attractive charge interactions may thus be expected to become dominant, a charge-screened polyelectrolyte in poor solvent could give rise to a collapse behavior similar to what we observe for CspTm (Fig. 4) (36). However, because the addition of a nonchaotropic salt at low denaturant concentration leads to an expansion of unfolded CspTm (Figs. 4A and 5A), attractive charge interactions clearly contribute to its collapse under these conditions. Polyampholyte theory thus appears to be an appropriate generalization of polyelectrolyte theory for describing our results with one simple consistent model. We note, however, that the polyampholyte theory of Higgs and Joanny (35) was developed for polymers in good solvent; i.e., above the theta point. For comparison with the experimentally observed range of values, we estimate the radius of gyration at the theta point from 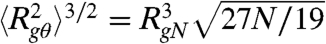 , as suggested by Sanchez (30, 56), where RgN is the radius of gyration of the most compact or folded state. RgN for protein segments of the size investigated here is approximately 1.2 nm, resulting in a radius of gyration of approximately 2.4 nm at the theta point. Only unfolded CspTm in low concentrations of denaturant compacts much below this value of Rg, but it still remains more expanded than the native state. The expansion of collapsed unfolded CspTm on addition of KCl indicates the importance of attractive charge interactions even under these conditions, but it will be interesting to assess the limitations of our analysis, such as the additional role of three-body interactions, effects from the finite size of the polypeptides, and possible correlations between charges within the chain, with more advanced theoretical approaches and molecular simulations (9, 43, 57).
, as suggested by Sanchez (30, 56), where RgN is the radius of gyration of the most compact or folded state. RgN for protein segments of the size investigated here is approximately 1.2 nm, resulting in a radius of gyration of approximately 2.4 nm at the theta point. Only unfolded CspTm in low concentrations of denaturant compacts much below this value of Rg, but it still remains more expanded than the native state. The expansion of collapsed unfolded CspTm on addition of KCl indicates the importance of attractive charge interactions even under these conditions, but it will be interesting to assess the limitations of our analysis, such as the additional role of three-body interactions, effects from the finite size of the polypeptides, and possible correlations between charges within the chain, with more advanced theoretical approaches and molecular simulations (9, 43, 57).
The range of ionic strengths where we observe the expansion of IDPs corresponds to physiologically relevant values, indicating the importance of the effect in a cellular environment. The resulting changes in chain dimensions will affect many of the properties that characterize IDP function, including the capture radii for fly-casting (5, 6), repulsive entropic forces from brush-like structures (9, 10), and the free energy change of folding upon binding (2). From our results, we can estimate the repulsive electrostatic energy that needs to be overcome to compact the chain compared to a neutral polypeptide. At a physiologically relevant ionic strength of 100 mM, polyampholyte theory yields repulsive electrostatic energies†† of (1.4 ± 0.5) kBT and (4.2 ± 0.5) kBT for the two variants of ProTα, a negligible value of (-0.2 ± 0.5) kBT for IN, and an attractive energy of (-2.5 ± 0.5) kBT for CspTm, underlining the critical balance of positive and negative charges that leads to a transition from a pronounced expansion to a charge-mediated compaction of the polypeptides (Fig. S4). Considering the magnitude of the values, the additional energy required to compact and fold IDPs with a large net charge can be a major component that has to be overcompensated by the free energy of binding to their target molecules. The electrostatic energies are in a range sufficient for significantly modulating affinities and dynamics of intracellular interaction partners, thus allowing for high specificity, while at the same time enabling dissociation at a rate that ensures a response of the regulatory system on time scales relevant for cellular processes (2).
Our results also have important implications for the properties of unfolded proteins in general. A large number of experiments have demonstrated a collapse of unfolded proteins at low denaturant concentration (12, 59, 60). However, the interactions responsible for this collapse have been difficult to elucidate. Correspondingly, it has been unclear how collapse is affected by sequence composition, and especially whether IDPs exhibit a similar collapse behavior as the previously investigated globular proteins. Some experiments, theoretical considerations, and simulations have suggested a role of secondary structure formation and hydrogen bonding for collapse (18, 39, 40), even though this is improbable to be the only contribution (45). Recent findings that IDPs and unstructured peptides can form collapsed structures (39, 61, 62) and show a compaction with increasing temperature similar to globular unfolded proteins (18) may be surprising given the lack of hydrophobic side chains and have been taken to indicate that hydrophobic interactions are not predominant in determining unfolded state dimensions. Our results show that charge interactions can play a decisive role. The observation of a charge-driven expansion even for a nearly charge-balanced protein like IN indicates that this behavior will be relevant for a large number of proteins, as recently suggested from results on barstar (42). Investigations of charged IDPs and unfolded states of globular proteins will thus depend critically on the solution conditions, such as pH and salt concentration (21, 25, 63–65).
In summary, whereas our results indicate a denaturant-dependent collapse of IDPs qualitatively similar to that of unfolded globular proteins at high ionic strength, charge interactions can dominate the dimensions of IDPs at low ionic strength. Our findings provide a new opportunity for testing the suitability of polymer physical concepts for describing unfolded state behavior. Interestingly, already a simple polyampholyte theory captures the overall effect of charge interactions on unfolded proteins remarkably well. Together with previous results on the stiffness of uncharged chains (12, 66), this presents a new possibility to predict the effect of the content of charged amino acid on the dimensions of unfolded proteins and IDPs, and to explore the resulting impact on protein stability and interactions. Whereas unfolded proteins have been shown to follow simple scaling laws at high concentrations of GdmCl (26), similar to the behavior expected for homopolymers, sequence composition can obviously have a large effect on chain dimensions under physiological conditions, with important implications for protein dynamics and interactions.
Methods
Preparation and Labeling of Proteins.
Cys residues were introduced by site-directed mutagenesis to provide functional groups for the specific attachment of the dyes Alexa Fluor 488 and 594 essentially as described previously (17, 18, 23). All proteins were purified using a hexahistidine tag. For details, see ref. 18 and SI Text.
Single-Molecule Fluorescence Spectroscopy.
Observations of single-molecule fluorescence were made using a MicroTime 200 confocal microscope (PicoQuant) essentially as described previously (17). Samples were measured with a 20 to 50 pM protein concentration in 50 mM Tris buffer, pH 7.4. 0.001% Tween 20 (Pierce) was included to prevent surface adhesion of the proteins. IN devoid of bound Zn2+ was prepared by adding 1 mM EDTA. To minimize photochemical damage to the chromophores, 200 mM β-mercaptoethanol were included in the samples (18). The Förster radius R0 was corrected for the changes in solution conditions, which were dominated by the change in refractive index with GdmCl, urea, and KCl concentration. All errors given are our estimates of the experimental uncertainty; wherever possible, they represent standard deviations from multiple independent meaurements. For details, see SI Text.
Supplementary Material
Acknowledgments.
We thank A. Vartapetian and A. Evstafieva for a plasmid encoding prothymosin α, R. Craigie for a plasmid encoding the N-terminal domain of HIV integrase and helpful discussion. We thank Robert Best, Dimitrii Makarov, Devarajan Thirumalai, Vladimir Uversky, and Andreas Vitalis for very helpful comments on the manuscript. This work was supported by the Swiss National Science Foundation, the National Center of Competence in Research for Structural Biology, a Starting Researcher Grant of the European Research Council, and a fellowship of the Deutscher Akademische Austauschdienst (V.H.).
Footnotes
The authors declare no conflict of interest.
This article is a PNAS Direct Submission. D.T. is a guest editor invited by the Editorial Board.
See Commentary on page 14519.
This article contains supporting information online at www.pnas.org/lookup/suppl/doi:10.1073/pnas.1001743107/-/DCSupplemental.
*A similar compaction can be achieved by adding other salts (see below).
†The slightly lower transfer efficiency of ProTα at high GdmCl concentrations compared to the other proteins is presumably an excluded volume effect of the large unlabeled segment present in the ProTα chain.
‡Note also that unfolded CspTm was previously shown to be described well with a Gaussian chain model over a broad range of denaturant concentrations (17).
§The numbers given here indicate the net charge at pH 7.4 of the polypeptide segment between the FRET chromophores (Table S1).
¶Other models can be applied to treat the protein-denaturant interactions, but this has no bearing on our conclusions regarding the electrostatically driven expansion and collapse of the chain we are concerned with in this work.
∥The values forN1/2κb1 at the lowest ionic strength of 50 mM used here are 6.8 for ProTαC, 5.5 for ProTαN, 4.1 for IN, and 2.6 for CspTm.
**The experiment is performed at 1.0 M urea to increase the separation of folded and unfolded CspTm in the transfer efficiency histograms.
††Electrostatic energies were calculated according to 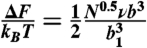 (58).
(58).
References
- 1.Dyson HJ, Wright PE. Intrinsically unstructured proteins and their functions. Nat Rev Mol Cell Biol. 2005;6:197–208. doi: 10.1038/nrm1589. [DOI] [PubMed] [Google Scholar]
- 2.Wright PE, Dyson HJ. Linking folding and binding. Curr Opin Struct Biol. 2009;19:31–38. doi: 10.1016/j.sbi.2008.12.003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Dunker AK, Silman I, Uversky VN, Sussman JL. Function and structure of inherently disordered proteins. Curr Opin Struct Biol. 2008;18:756–764. doi: 10.1016/j.sbi.2008.10.002. [DOI] [PubMed] [Google Scholar]
- 4.Uversky VN, Oldfield CJ, Dunker AK. Intrinsically disordered proteins in human diseases: Introducing the D2 concept. Ann Rev Biophys. 2008;37:215–246. doi: 10.1146/annurev.biophys.37.032807.125924. [DOI] [PubMed] [Google Scholar]
- 5.Shoemaker BA, Portman JJ, Wolynes PG. Speeding molecular recognition by using the folding funnel: The fly-casting mechanism. Proc Natl Acad Sci USA. 2000;97:8868–8873. doi: 10.1073/pnas.160259697. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Turjanski AG, Gutkind JS, Best RB, Hummer G. Binding-induced folding of a natively unstructured transcription factor. PLoS Comput Biol. 2008;4:e1000060. doi: 10.1371/journal.pcbi.1000060. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Kriwacki RW, Hengst L, Tennant L, Reed SI, Wright PE. Structural studies of p21Waf1/Cip1/Sdi1 in the free and Cdk2-bound state: Conformational disorder mediates binding diversity. Proc Natl Acad Sci USA. 1996;93:11504–11509. doi: 10.1073/pnas.93.21.11504. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Oldfield CJ, et al. Flexible nets: Disorder and induced fit in the associations of p53 and 14-3-3 with their partners. BMC Genomics. 2008;9(Suppl 1):S1. doi: 10.1186/1471-2164-9-S1-S1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Bright JN, Woolf TB, Hoh JH. Predicting properties of intrinsically unstructured proteins. Prog Biophys Mol Biol. 2001;76:131–173. doi: 10.1016/s0079-6107(01)00012-8. [DOI] [PubMed] [Google Scholar]
- 10.Brown HG, Hoh JH. Entropic exclusion by neurofilament sidearms: A mechanism for maintaining interfilament spacing. Biochemistry. 1997;36:15035–15040. doi: 10.1021/bi9721748. [DOI] [PubMed] [Google Scholar]
- 11.Uversky VN, Gillespie JR, Fink AL. Why are “natively unfolded” proteins unstructured under physiologic conditions? Proteins. 2000;41:415–427. doi: 10.1002/1097-0134(20001115)41:3<415::aid-prot130>3.0.co;2-7. [DOI] [PubMed] [Google Scholar]
- 12.Schuler B, Eaton WA. Protein folding studied by single-molecule FRET. Curr Opin Struct Biol. 2008;18:16–26. doi: 10.1016/j.sbi.2007.12.003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Haran G. Single-molecule fluorescence spectroscopy of biomolecular folding. J Phys-Condens Mat. 2003;15:R1291–R1317. [Google Scholar]
- 14.Michalet X, Weiss S, Jäger M. Single-molecule fluorescence studies of protein folding and conformational dynamics. Chem Rev. 2006;106:1785–1813. doi: 10.1021/cr0404343. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Deniz AA, et al. Single-molecule protein folding: Diffusion fluorescence resonance energy transfer studies of the denaturation of chymotrypsin inhibitor 2. Proc Natl Acad Sci USA. 2000;97:5179–5184. doi: 10.1073/pnas.090104997. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Nettels D, Gopich IV, Hoffmann A, Schuler B. Ultrafast dynamics of protein collapse from single-molecule photon statistics. Proc Natl Acad Sci USA. 2007;104:2655–2660. doi: 10.1073/pnas.0611093104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Hoffmann A, et al. Mapping protein collapse with single-molecule fluorescence and kinetic synchrotron radiation circular dichroism spectroscopy. Proc Natl Acad Sci USA. 2007;104:105–110. doi: 10.1073/pnas.0604353104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Nettels D, et al. Single molecule spectroscopy of the temperature-induced collapse of unfolded proteins. Proc Natl Acad Sci USA. 2009;106:20740–20745. doi: 10.1073/pnas.0900622106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Cai M, et al. Solution structure of the N-terminal zinc binding domain of HIV-1 integrase. Nat Struct Biol. 1997;4:567–577. doi: 10.1038/nsb0797-567. [DOI] [PubMed] [Google Scholar]
- 20.Zheng R, Jenkins TM, Craigie R. Zinc folds the N-terminal domain of HIV-1 integrase, promotes multimerization, and enhances catalytic activity. Proc Natl Acad Sci USA. 1996;93:13659–13664. doi: 10.1073/pnas.93.24.13659. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Gast K, et al. Prothymosin alpha: a biologically active protein with random coil conformation. Biochemistry. 1995;34:13211–13218. doi: 10.1021/bi00040a037. [DOI] [PubMed] [Google Scholar]
- 22.Pineiro A, Cordero OJ, Nogueira M. Fifteen years of prothymosin alpha: Contradictory past and new horizons. Peptides. 2000;21:1433–1446. doi: 10.1016/s0196-9781(00)00288-6. [DOI] [PubMed] [Google Scholar]
- 23.Schuler B, Lipman EA, Eaton WA. Probing the free-energy surface for protein folding with single-molecule fluorescence spectroscopy. Nature. 2002;419:743–747. doi: 10.1038/nature01060. [DOI] [PubMed] [Google Scholar]
- 24.Magg C, Schmid FX. Rapid collapse precedes the fast two-state folding of the cold shock protein. J Mol Biol. 2004;335:1309–1323. doi: 10.1016/j.jmb.2003.11.050. [DOI] [PubMed] [Google Scholar]
- 25.Uversky VN, Goto Y. Acid denaturation and anion-induced folding of globular proteins: Multitude of equilibium partially folded intermediates. Curr Protein Pept Sc. 2009;10:447–455. doi: 10.2174/138920309789352029. [DOI] [PubMed] [Google Scholar]
- 26.Kohn JE, et al. Random-coil behavior and the dimensions of chemically unfolded proteins. Proc Natl Acad Sci USA. 2004;101:12491–12496. doi: 10.1073/pnas.0403643101. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.O’Brien EP, Morrison G, Brooks BR, Thirumalai D. How accurate are polymer models in the analysis of Förster resonance energy transfer experiments on proteins? J Chem Phys. 2009;130:124903. doi: 10.1063/1.3082151. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Sherman E, Haran G. Coil-globule transition in the denatured state of a small protein. Proc Natl Acad Sci USA. 2006;103:11539–11543. doi: 10.1073/pnas.0601395103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Ziv G, Thirumalai D, Haran G. Collapse transition in proteins. Phys Chem Chem Phys. 2009;11:83–93. doi: 10.1039/b813961j. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Ziv G, Haran G. Protein folding, protein collapse, and Tanford’s transfer model: Lessons from single-molecule FRET. J Am Chem Soc. 2009;131:2942–2947. doi: 10.1021/ja808305u. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Flory PJ, Fisk S. Effect of volume exclusion on dimensions of polymer chains. J Chem Phys. 1966;44:2243–2248. [Google Scholar]
- 32.Bright JN, Woolf TB, Hoh JH. Predicting properties of intrinsically unstructured proteins. Prog Biophys Mol Biol. 2001;76:131–173. doi: 10.1016/s0079-6107(01)00012-8. [DOI] [PubMed] [Google Scholar]
- 33.Makhatadze GI, Privalov PL. Protein interactions with urea and guanidinium chloride. A calorimetric study. J Mol Biol. 1992;226:491–505. doi: 10.1016/0022-2836(92)90963-k. [DOI] [PubMed] [Google Scholar]
- 34.Dobrynin AV, Colby RH, Rubinstein M. Polyampholytes. J Polym Sci Pol Phys. 2004;42:3513–3538. [Google Scholar]
- 35.Higgs PG, Joanny JF. Theory of Polyampholyte Solutions. J Chem Phys. 1991;94:1543–1554. [Google Scholar]
- 36.Ha BY, Thirumalai D. Conformations of a polyelectrolyte chain. Phys Rev A. 1992;46:R3012–R3015. doi: 10.1103/physreva.46.r3012. [DOI] [PubMed] [Google Scholar]
- 37.Hiller S, Wider G, Imbach LL, Wuthrich K. Interactions with hydrophobic clusters in the urea-unfolded membrane protein OmpX. Angew Chem Int Ed Engl. 2008;47:977–981. doi: 10.1002/anie.200703367. [DOI] [PubMed] [Google Scholar]
- 38.Felitsky DJ, Lietzow MA, Dyson HJ, Wright PE. Modeling transient collapsed states of an unfolded protein to provide insights into early folding events. Proc Natl Acad Sci USA. 2008;105:6278–6283. doi: 10.1073/pnas.0710641105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Möglich A, Joder K, Kiefhaber T. End-to-end distance distributions and intrachain diffusion constants in unfolded polypeptide chains indicate intramolecular hydrogen bond formation. Proc Natl Acad Sci USA. 2006;103:12394–12399. doi: 10.1073/pnas.0604748103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Bolen DW, Rose GD. Structure and energetics of the hydrogen-bonded backbone in protein folding. Annu Rev Biochem. 2008;77:339–362. doi: 10.1146/annurev.biochem.77.061306.131357. [DOI] [PubMed] [Google Scholar]
- 41.Zhou HX. A Gaussian-chain model for treating residual charge–charge interactions in the unfolded state of proteins. Proc Natl Acad Sci USA. 2002;99:3569–3574. doi: 10.1073/pnas.052030599. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Hofmann H, Golbik RP, Ott M, Hübner CG, Ulbrich-Hofmann R. Coulomb forces control the density of the collapsed unfolded state of barstar. J Mol Biol. 2008;376:597–605. doi: 10.1016/j.jmb.2007.11.083. [DOI] [PubMed] [Google Scholar]
- 43.Mao AH, Crick SL, Vitalis A, Chicoine CL, Pappu RV. Net charge per residue modulates conformational ensembles of intrinsically disordered proteins. Proc Natl Acad Sci USA. 2010;107:8183–8188. doi: 10.1073/pnas.0911107107. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.O’Brien EP, Ziv G, Haran G, Brooks BR, Thirumalai D. Effects of denaturants and osmolytes on proteins are accurately predicted by the molecular transfer model. Proc Natl Acad Sci USA. 2008;105:13403–13408. doi: 10.1073/pnas.0802113105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Tran HT, Mao A, Pappu RV. Role of backbone-solvent interactions in determining conformational equilibria of intrinsically disordered proteins. J Am Chem Soc. 2008;130:7380–7392. doi: 10.1021/ja710446s. [DOI] [PubMed] [Google Scholar]
- 46.Vitalis A, Wang X, Pappu RV. Quantitative characterization of intrinsic disorder in polyglutamine: Insights from analysis based on polymer theories. Biophys J. 2007;93:1923–1937. doi: 10.1529/biophysj.107.110080. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Kohn JE, Gillespie B, Plaxco KW. Non-sequence-specific interactions can account for the compaction of proteins unfolded under “native” conditions. J Mol Biol. 2009;394:343–350. doi: 10.1016/j.jmb.2009.09.005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Weinkam P, Pletneva EV, Gray HB, Winkler JR, Wolynes PG. Electrostatic effects on funneled landscapes and structural diversity in denatured protein ensembles. Proc Natl Acad Sci USA. 2009;106:1796–1801. doi: 10.1073/pnas.0813120106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.Shoemaker BA, Wolynes PG. Exploring structures in protein folding funnels with free energy functionals: The denatured ensemble. J Mol Biol. 1999;287:657–674. doi: 10.1006/jmbi.1999.2612. [DOI] [PubMed] [Google Scholar]
- 50.Nodet G, et al. Quantitative description of backbone conformational sampling of unfolded proteins at amino acid resolution from NMR residual dipolar couplings. J Am Chem Soc. 2009;131:17908–17918. doi: 10.1021/ja9069024. [DOI] [PubMed] [Google Scholar]
- 51.Millett IS, Doniach S, Plaxco KW. Toward a taxonomy of the denatured state: Small angle scattering studies of unfolded proteins. Adv Protein Chem. 2002;62:241–262. doi: 10.1016/s0065-3233(02)62009-1. [DOI] [PubMed] [Google Scholar]
- 52.Gast K, Modler AJ. Studying protein folding and aggregation by laser light scattering. In: Buchner J, Kiefhaber T, editors. Protein Folding Handbook. Weinheim: Wiley-VCH; 2005. pp. 673–709. [Google Scholar]
- 53.Odijk T. Polyelectrolytes near the Rod Limit. J Polym Sci Pol Phys. 1977;15:477–483. [Google Scholar]
- 54.Skolnick J, Fixman M. Electrostatic persistence length of a wormlike polyelectrolyte. Macromolecules. 1977;10:944–948. [Google Scholar]
- 55.Ha BY, Thirumalai D. Persistence length of flexible polyelectrolyte chains. J Chem Phys. 1999;110:7533–7541. [Google Scholar]
- 56.Sanchez IC. Phase-transition behavior of the isolated polymer-chain. Macromolecules. 1979;12:980–988. [Google Scholar]
- 57.Dobrynin AV, Rubinstein M. Flory theory of a polyampholyte chain. J Phys II France. 1995;5:677–695. [Google Scholar]
- 58.Chan HS, Dill KA. Polymer principles in protein structure and stability. Annu Rev Biophys Biophys Chem. 1991;20:447–490. doi: 10.1146/annurev.bb.20.060191.002311. [DOI] [PubMed] [Google Scholar]
- 59.Uversky VN. Use of fast protein size-exclusion liquid chromatography to study the unfolding of proteins which denature through the molten globule. Biochemistry. 1993;32:13288–13298. doi: 10.1021/bi00211a042. [DOI] [PubMed] [Google Scholar]
- 60.Uversky VN, Ptitsyn OB. “Partly folded” state, a new equilibrium state of protein molecules: Four-state guanidinium chloride-induced unfolding of beta-lactamase at low temperature. Biochemistry. 1994;33:2782–2791. doi: 10.1021/bi00176a006. [DOI] [PubMed] [Google Scholar]
- 61.Crick SL, Jayaraman M, Frieden C, Wetzel R, Pappu RV. Fluorescence correlation spectroscopy shows that monomeric polyglutamine molecules form collapsed structures in aqueous solutions. Proc Natl Acad Sci USA. 2006;103:16764–16769. doi: 10.1073/pnas.0608175103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 62.Mukhopadhyay S, Krishnan R, Lemke EA, Lindquist S, Deniz AA. A natively unfolded yeast prion monomer adopts an ensemble of collapsed and rapidly fluctuating structures. Proc Natl Acad Sci USA. 2007;104:2649–2654. doi: 10.1073/pnas.0611503104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 63.Uversky VN, et al. Natively unfolded human prothymosin alpha adopts partially folded collapsed conformation at acidic pH. Biochemistry. 1999;38:15009–15016. doi: 10.1021/bi990752+. [DOI] [PubMed] [Google Scholar]
- 64.Jacob J, Dothager RS, Thiyagarajan P, Sosnick TR. Fully reduced ribonuclease A does not expand at high denaturant concentration or temperature. J Mol Biol. 2007;367:609–615. doi: 10.1016/j.jmb.2007.01.012. [DOI] [PubMed] [Google Scholar]
- 65.Uversky VN. Intrinsically disordered proteins and their environment: effects of strong denaturants, temperature, pH, counter ions, membranes, binding partners, osmolytes, and macromolecular crowding. Protein J. 2009;28:305–325. doi: 10.1007/s10930-009-9201-4. [DOI] [PubMed] [Google Scholar]
- 66.Zhou HX. Polymer models of protein stability, folding, and interactions. Biochemistry. 2004;43:2141–2154. doi: 10.1021/bi036269n. [DOI] [PubMed] [Google Scholar]
- 67.Kyte J, Doolittle RF. A simple method for displaying the hydropathic character of a protein. J Mol Biol. 1982;157:105–132. doi: 10.1016/0022-2836(82)90515-0. [DOI] [PubMed] [Google Scholar]
- 68.Schuler B, Lipman EA, Steinbach PJ, Kumke M, Eaton WA. Polyproline and the “spectroscopic ruler” revisited with single molecule fluorescence. Proc Natl Acad Sci USA. 2005;102:2754–2759. doi: 10.1073/pnas.0408164102. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.