Ensemble-based Methods for Describing Protein Dynamics

Abstract

Molecular dynamics (MD) simulation is a natural approach for studying protein dynamics, and coupled with the ideas of multiscale modeling, MD proves to be the gold standard in computational biology to investigate mechanistic details related to protein function. In principle, if MD trajectories are long enough, the ensemble of protein conformations generated allow thermodynamic and kinetic properties to be predicted. We know from experiments that proteins exhibit a high degree of fidelity in function, and that empirical kinetic models are successful in describing kinetics, suggesting that the ensemble of conformations cluster into well defined thermodynamic states, which are frequently metastable. The experimental evidence suggest that more efficient computational models that retain only essential properties of the protein can be constructed to faithfully reproduce the relatively few observed thermodynamic states, and perhaps describe transition states if the model is sufficiently detailed. Indeed, there are many so called ensemble-based methods that attempt to generate more complete ensembles than MD can provide by focusing on the most important driving forces through simplified representations of how elements within the protein interact. Although coarse-graining is employed in MD and other approaches, such as in elastic network models, the key distinguishing factor of ensemble-based methods is that they are meant to efficiently generate a large ensemble of conformations without solving explicit equations of motion. This review highlights three types of ensemble-based methods, illustrated by COREX and WSME, FRODA and PRM, and the DCM.

Introduction

The purpose of my review is to discuss ensemble-based methods for computationally studying thermodynamic, kinetic and other intrinsic properties of proteins. These methods can be extended to applications in pharmacology involving protein-ligand and protein-protein interactions. Before I delve into details about methodology, it is important to understand why we should care about generating an ensemble of conformations in the first place. An overarching principle in chemistry is the thermodynamic concept of free energy; used to determine if a chemical reaction will be spontaneous, or if work must be done to drive the reaction. Therefore, change in free energy is the currency that keeps proteins functional. Protein function, on the other hand, often involves a conformational change, perhaps, through a specific mechanism that mediates a change in state.

One possible motivation (and a good one) for generating an ensemble of conformations for a protein is to look for a succession of structural changes that carve out a specific pathway in order to identify “the mechanism” responsible for a particular function. More importantly, a fundamental reason for generating an ensemble of conformations is because the free energy depends upon this ensemble, and, hence, so does the driving forces behind a chemical reaction. In this context, it is not necessary for “the mechanism” to be identified as a specific pathway. The mechanism may be associated with multiple pathways, or no pathway where a population shift in molecular states can be modulated by changes in entropy. Therefore, we must not allow ourselves to focus solely on energy exchange, even though there can be processes where entropy changes are negligible.

There is a possibility, of course, that entropy does not play a critical role in regulating protein function. Perhaps proteins have evolved to perform function as if they are miniaturized machines, driven only by energy exchange through specific conformations. The structure/function paradigm has encapsulated this idea well. However, this would require the products and reactants to always maintain negligible entropy differences independent of environmental conditions. Although I find this reasoning counter intuitive because disorder itself is an important driving force through the second law of thermodynamics, this is indeed a fair question that deserves an answer. A quick counter example comes by pointing to the functional role found in intrinsically disordered proteins [1], where the structure/function paradigm breaks down. More generally, the structure/function paradigm is only an idealization that proves to be very useful as a starting point in the sense that all the methods I will describe utilize known three-dimensional protein structures. However, we must generate conformational ensembles to represent equilibrium fluctuations of these stable structures precisely because entropy generally plays a critical role in governing cooperativity.

Many experimental [2–6] and computational [7,8] studies have been made on protein dynamics to better understand functional mechanisms. From these studies it is found that entropy plays a key mechanistic role for cooperative structural transitions in proteins regarding allosteric events [9]. It has been experimentally shown that entropy can directly modulate cooperativity in ligand binding by shifting the thermodynamic stability of a complex [10]. With entropy and flexibility of a protein modulated by osmolytes and other solvation effects [11], entropic considerations become important for drug therapeutics. Unfortunately, despite a large body of work investigating thermodynamic stability, entropy, molecular rigidity and cooperativity, the relationships between these concepts remain poorly understood [12–14]. To resolve issues related to entropy, one must be able to accurately characterize ensembles of conformations.

To predict observed thermodynamic and kinetic properties of proteins [15,16] requires applying principles of statistical physics to an ensemble of conformations generated using a computationally tractable model. There are many ways to do this. I now motivate my review of ensemble-based methods by noting that Molecular Dynamics (MD) simulation is often used to generate an ensemble of conformations by numerically solving equations of motion, even when explicit time dependence is not of interest. A review of MD methods by Dr. Freddie Salsbury is included in this issue. The connection to ensemble-based methods is that MD simulation relies on the ergodic theorem, which asserts that a time average over an infinitely long time is the same as the ensemble average over all accessible microstates. In the MD approach, the accumulated ensemble of conformations from a given simulation will generally lead to incomplete sampling [17]. It is also worth noting that while MD simulation is often based on energy functions at the atomic level, implicit solvent and/or coarse-grained models are also routinely applied to speed up calculations [18]. More recently, the application of multiscale modeling has shown promise in overcoming sampling problems [19,20], and a review over coarse-grain methods is also included in this issue by Dr. Andrew Rader.

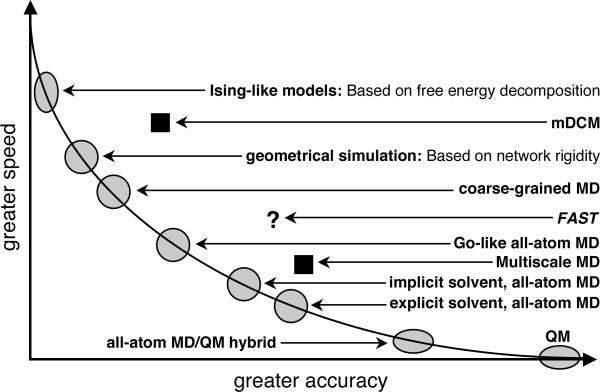
As schematically shown in Fig. 1, tradeoffs must be made between accuracy and speed within computational models. By using simplified models with empirical parameters, ensemble-based methods generate a diverse ensemble of conformations without solving dynamical equations of motion. Ensemble-based methods that rely on the native state topology [18] of known three-dimensional structure tend to reproduce experimental observations with good accuracy [21,22]. In this review, I present three classes of ensemble-based methods including illustrations of specific models within each class, and I discuss similarities and differences in their approximations. The main points of concern are 1) the need for a native protein structure, 2) the importance of solvation effects, 3) identifying the cause and effect of the cooperative nature of protein dynamics, 4) the assumption of additivity in conformational entropy and 5) transferability of empirical parameters. Based on my assessment of the strengths and weakness of the various methods, I outline future directions for a next generation ensemble-based method that I am currently pursuing.

Figure 1.

A schematic speed-accuracy curve where the axes are on a logarithmic scale. The fastest computational methods are based on free energy decomposition where the total free energy of a system is taken as the sum over free energy components. These methods are generally not very accurate because free energies are nonadditive due to conformational entropy. A traditional method to determine conformational entropy requires simulation of the molecular structure. There are many methods to do this that rely on native contacts (Go-like models). Coarse-grained models are also employed to speed calculations, but accuracy is lost in representing interactions. MD simulations are very accurate at the all-atom level using explicit solvent, but they are computationally intensive. Generating ensembles involving quantum mechanical calculations is not feasible. Multi-scale approaches place best on the speed-accuracy curve shown as filled squares. The mDCM (minimal Distance Constraint Model explained below) is an all atom approach based on free energy decomposition, and is a multiscale approach. FAST is based on a new DCM currently being developed, and is expected to perform where the question mark is placed.

Ising-like Models

Originally created to study ferromagnetism as a statistical mechanics problem, the Ising Model is based on discrete spin variables that can be in one of two states (↑ or ↓) representing magnetic moments. The spins are arranged on a lattice, and they interact directly with an external magnetic field and neighboring spins through coupling interactions. The concept of describing the local state of matter with discrete variables that interact with neighbors (coupling) has made the Ising Model a hallmark paradigm to describe phase transitions for all kinds of phenomena. Although details can be quite different, all Ising-like models preserve the spirit of employing a simple representation of microscopic interactions using discrete variables, such as done in the Zimm-Bragg and Lifson-Roig models for the helix-coil transition. The first class of ensemble-based methods I describe is based on decorating a known three-dimensional protein structure with discrete “spin” variables, where for example, spins ↑ or ↓ represent a folded or unfolded part of the protein respectively.

COREX

Developed by Hilser, Freire and co-workers [23]; (i) a residue in the folded state is exposed to solvent in proportion to its solvent accessible surface area (SASA) based on the input structure, and (ii) a residue in the unfolded state is assumed to be fully exposed to solvent. COREX, which is not an acronym, was originally motivated to predict hydrogen-exchange EX2 protection factors that are directly measured. All key formulas can be found in source references [23–25]. A brief description is that all residues are classified as either being polar or non-polar. Two universal formulas are employed for δH_slv(T)and ΔS_slv(T) that describe the transfer of a residue from a non-polar environment (within the core of the protein) to a polar environment (aqueous solution). These functions are expansions about a reference temperature, where the expansion coefficients depend on the SASA of a particular residue in either the folded or unfolded state. These formulas were obtained empirically based on numerous studies in the early nineties by Freire and coworkers as summarized in REF [23]. COREX also includes a conformational entropy change that takes place upon a residue changing state (i.e. flipping its spin).

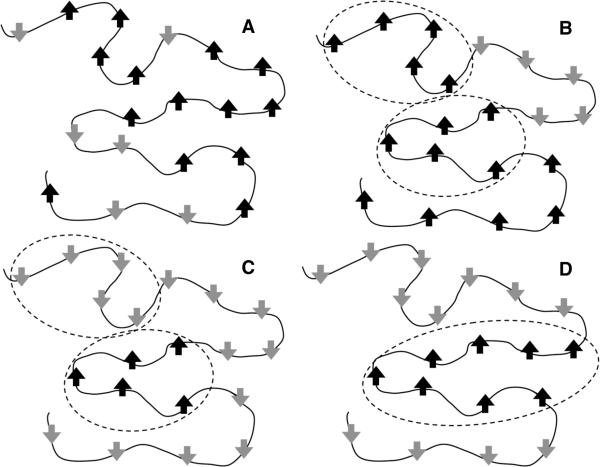
An ensemble that could be generated without enforcing a cooperative mechanism would look like Fig. 2A, where each residue can be either in a folded or unfolded state independent of other residues. If a protein has 100 residues, its ensemble would consist of 2¹⁰⁰ different microstates, making the problem intractable. Therefore, a windowing procedure is used that forces a number of consecutive residues along the backbone to fold or unfolded as a single cooperative unit. Windowing dramatically reduces the ensemble size, as illustrated in Figs. 2B–C. For example, the ensemble for a 100-residue protein using a window size of 10 residues is reduced to 2¹⁰ distinct microstates. COREX employs windowing in a more clever way by adding shifting [23] to increase the size and diversity of the ensemble. It appears the results of COREX are insensitive to a range of window sizes. In recent work, with computers being much faster, COREX uses a window size of 5 residues. These ensembles can be generated in matter of hours on 1 CPU. COREX has been used to characterize the native state ensemble [26] and both heat [27] and cold denatured [28] state ensembles. From these ensembles, the partition function is constructed, and the probability for each microstate is determined.

Figure 2.

A schematic representation of spin variables mapped to a 20-residue protein to highlight cooperative units in Ising-like models. Up and down arrow spins represent residues that are folded and unfolded respectively. (A) An example spin-state without windowing. Since each residue can be folded or unfolded independently, there are 2²⁰ possible spin-states. (B and C) Two example spin-states with a 5-residue windowing scheme. The number of accessible spin-states is reduced to 2⁴. (D) For a single sequence approximation, only one consecutive region can be in a folded state, although its length is not restricted. Higher sequence approximations can also be made.

An important result from COREX has been its ability to characterize allosteric effects in proteins [29] where cooperativity can be described without having to identify a specific pathway. Rather, the collective effect of the generated ensemble of microstates is used, where the energy of a single residue is successively perturbed in turn to change the nature of the ensemble. In this way, all pairwise residue-couplings can be calculated using conditional partition functions, which allows the distal response to be quantified for each perturbed residue location. This approach exemplifies the view of allosterism that perturbations do not necessarily cause conformational distortions that propagate from one active site to another. On the other hand, even if a conformational pathway does exist, it may be difficult to detect (i.e. perhaps using clustering techniques) within an Ising-like type of model. The most important point, however, is that the coupling can still be calculated, regardless of the mechanism, because of the underlying thermodynamic nature of the spin model. COREX is available on a Web server [30] to support these and many more applications.

There are several aspects of COREX worth highlighting. The generated ensemble corresponds to an infinite time-span because all partial unfolding events are fully characterized. By looking at conditional partition functions based on sub-ensembles defined by a specific residue being folded or unfolded, the thermodynamic stability of each residue can be defined, which helps locate regions of the protein more prone to unfold. Interestingly, only 1-body “spin” terms define interactions, which depends on the local geometry for determining the SASA of a residue in its folded state [26]. The approximations of this approach are: No other geometric information beyond the input structure is involved in the calculation (only spin flips are monitored). The solvation parameters depend on whether a residue is a polar or non-polar type, but do not depend on the specific type of residue. In recent versions of COREX, a free parameter is used to scale the conformational entropy term. Because only 1-body terms are used, no interactions between residues (i..e. no “spin-spin” coupling terms) are modeled. This means that without windowing, COREX is equivalent to an inhomogeneous set of paramagnetic spins (in the language of the Ising model analogy), and hence, cooperativity will be non-existent. This suggests that the observed cooperativity derives from sliding windows, wherein each window, all the residues are either folded or unfolded simultaneously causing the model to be cooperative.

In summary, COREX captures essential features of protein stability through solvation effects using a fixed set of parameters across numerous applications. On the other hand, it has not been used to deliver on an early promise of reproducing excess heat capacity curves [24], indicating the cooperative mechanism needs refinement. Hilser argues cooperativity emerges from the SASA differentials, irrespective of the window size. To quantify this, I suggest the sharpness of the excess heat capacity curves be monitored as a function of window size.

WSME

The Wako-Saitô-Muñoz-Eaton model [31] is a sub-class of Ising-like models that differs substantially from COREX in that no attention is given to solvation effects! Rather, focus is placed on the conformational part of free energy. A general WSME model can be written as:

$$G\left(\mathbf{m}\right)=\sum _{i=1}^{N-1}\sum _{j=i+1}^N{\epsilon }_{ij}{\Delta }_{ij}\prod _{k=i}^j{m}_k-RT\sum _{i=1}^N{q}_i(1-m_i)$$ (1)

where G(m) is the free energy for a conformation uniquely labeled by the state vector m, where m= {m_j}, and m_j are the “spins” that can be either 0 or 1 when the j-th residue is unfolded or folded respectively. The model requires all energy couplings, {ε_ij}, for native contacts between the i-th and j-th residues to be specified, where Δ _ij =1 when there is a native contact present in the input structure, otherwise Δ _ij =0. The {q_j} define the gain in conformational entropy that occurs when the j-th residue unfolds, and the term πm_krequires a consecutive number of residues along the backbone to simultaneously fold as a single unit in order for the energy term to contribute, which causes the model to be cooperative. Finally, T is the absolute temperature and R is the ideal gas constant. Remarkably, Eq. (1) can be solved analytically [32]. Nevertheless, it is more common to perform Monte Carlo (MC) sampling. Moreover, Eq. (1) is usually solved within the double or triple sequence approximation that only allows configurations with respectively at most two or three stretches of consecutive folded residues. Both the double and triple sequence approximations reproduce equilibrium and kinetics properties of a diverse set of proteins markedly well [33] using just a few adjustable parameters. A single sequence approximation is shown in Fig. 2D, which also has been used frequently, but is less accurate.

Kinetic properties are obtained using a master equation that takes on the generic for

$$\frac{d{P}_k\left(t\right)}{dt}=\sum _j{T}_{kj}{P}_j\left(t\right)$$ (2)

whereP_k(t)is the probability that the protein is in the k-th microstate at time, t, and T_kj is the rate for the protein to transition from the j-th microstate to the k-th microstate. The master equation can be applied at a very high level of resolution where the indices represent microstates that carefully define the positions of all atoms for each conformation in the ensemble. However, for an Ising-like model, the “microstate” specified by the state vector m, is actually a coarse-grained description of the protein conformation. As such, the generic form given in Eq. (2) is also valid at different scales (both spatial and time scales) such that the indexing can be viewed as “macrostates” of a protein. A macrostate specifies a global property of a protein, regardless of the number of microscopic states that are consistent with its global property. Macrostates are characterized by “order parameters” because they track the folding progress of a protein, for which the total number of native contacts is often used. For example, if there are 1000 native contacts in a protein based on the input structure, and there are 750 native contacts in a macrostate due to partial unfolding events, then the sub-ensemble of all possible state vectors consistent with the macrostate will have the combinatorial number given by (1000!)/(750!×250!) of microstates, as derived from the binomial distribution.

The transition rates are of the form T_kj =Γ_kje^{−(G_k−G_j)/RT} where (G_k−G_j) is the difference in free energy between the macrostates, and the exponential prefactor, Γ_kj, is a fundamental rate related to the microscopic details of how the conformation of a protein dynamically changes. Usually, Γ_kjis assumed to be a global constant, mainly because it is extremely difficult to determine the complete set of {Γ_kj} without a full fledge microscopic theory. Protein kinetics can be described well [33] assuming transitions only take place between nearest neighbor macrostates (i.e. in one dimension, the number of native contacts can increase or decrease by 1) and that there is only a single global prefactor, Γ. Thus, protein kinetics is described by a random walk on the free energy landscape. It has been suggested that a constant prefactor is a good approximation when the master equation is applied to macrostates described by order parameters that slowly change in time, but the rates are too diverse for this approximation to be justified [34] when applied to microstates at high resolution. The success of the WSME approach is in its ability to describe thermodynamics and kinetics for a wide variety of proteins, including the fast folding villin subdomain [35], which has no folding barrier. This body of work suggests the folding process is largely determined by the distribution and strength of native contacts, which is consistent with a funneled energy landscape.

There are several aspects of the WSME model worth highlighting. Interestingly, there are only 2-body energy terms and 1-body conformational entropy terms. In regards to its capabilities in generating ensembles, it has the same conformational advantage over MD simulations that COREX has. The approximations of this approach are: No geometric information beyond the input structure defining contacts is involved in the calculation (only spin flips), which only requires knowing the topology of the native structure. Interactions are considered between residues to allow cooperativity to arise, but the form of the free energy function enforces cooperative units. Non-transferable parameters must be determined for each protein studied in order to fit to experimental data, but this allows for the possibility to study proteins in different types of solvent conditions. Finally, the WSME model does not adequately account for specific residue dependency, solvation effects, and conformational entropies are treated as additive, which is generally not true.

In summary, WSME is a minimal model that captures thermodynamic and kinetic properties of proteins very well, as demonstrated in numerous applications in understanding protein folding. An unfortunate drawback is that there does not seem to be a consensus with respect to model details, and there does not appear to be a convenient public resource for a program to do the calculations.

Explicit pathway generation

The Ising-like models discussed above are extremely fast because they ignore the geometrical aspects of a protein through simplified representations of interactions. Consequently, the ensembles generated by COREX or WSME lack atomic coordinate information. Nevertheless, due to their overall success in describing thermodynamic and kinetic properties, it is clear that native contacts are largely responsible for protein stability and the folding process. This suggests a Go-like strategy of ignoring non-native interactions within a MD simulation (see Fig. 1) will serve as an efficient way to generate ensembles. Although this is the case, this review is limited to ensemble-based methods that are much more efficient in generating ensembles by avoiding propagating equations of motion altogether. The methods discussed here provide explicit pathway generation by taking into account the rigidity and flexibility of native protein structure. By using mechanical information from a graph-rigidity analysis [36], three types of ensemble-based methods have emerged.

FRODA

Developed by Thorpe and co-workers, the strategy of the Framework Rigidity Optimized Dynamic Algorithm [37], referred to as FRODA, is to create a network of distance constraints that is defined by native interactions from an input structure, and explore allowed motions at the atomic level that maintain all imposed distance constraints. The native interactions include covalent bonds, hydrogen bonds (H-bonds) and hydrophobic tethers. Rather then solving complicated equations of motion that enforce distance constraints, the rigid cluster decomposition is determined first [36], and subsequently, each rigid cluster is held together by stiff springs with natural lengths set equal to the distance between pairs of atoms within the input structure. Between atoms from different rigid clusters: Hydrophobic tethers are enforced using distance inequalities, and, a short-range repulsive force prevents atoms (and rigid clusters) from passing through one another. Rigid clusters defined by the input structure are jiggled about without disrupting any distance constraint using MC.

A single MC move consists of two steps. First, all rigid clusters are “jiggled” through a random rotation, translation and deformation. Second, the energy of the system is relaxed so that without clashing, all rigid clusters are maintained within tight distance constraint tolerances throughout the simulation. In this way, only the relative positions of atoms in different rigid clusters change (i.e. in flexible regions), and a trajectory is created after many MC moves. An important feature is that a “momentum” bias is added to the random jiggling by tending to move rigid clusters along the same direction that was previously successful. Computational efficiency is increased by about two orders of magnitude compared to no applied biasing. Samples from this trajectory form an ensemble of conformations that represents the native state ensemble from which principle component analysis (PCA) can be performed to find the collective motions with greatest variance. The FRODA module is included within the FIRST software, which can be freely downloaded from FlexWeb [38].

There are few aspects of FRODA worth highlighting. There are rules that determine if a H-bond or hydrophobic tether exists within the input structure, and how many distance constraints should model an interaction. I find the default settings of FRODA to generally work well. However, many users have expressed concern about the sensitivity of the results to arbitrary settings. Through a recent quantitative assessment (to be published) that compares the PCA modes from FRODA with normal modes from an elastic network, and PCA modes from long MD simulations, we found that FRODA provides robust results that are both consistent with the other methods, and not sensitive to the precise settings. The advantage of FRODA is that it is order of magnitude times faster than MD simulation in probing the native state ensemble (see Fig. 1), and it tracks flexible motions better than elastic network models. However, the approximation of this approach is that once a constraint is defined, it is fixed forever. Although this restriction can be lifted, the current version of FRODA maintains a fixed constraint topology. This method is completely athermal (based solely on mechanics) and does not take into consideration any type of solvation effects. The method is limited to studying only native state ensembles.

I would also like to mention that a different method than FRODA, although similar in spirit, has recently appeared by the same group [39] called Geometric Targeting. Ensembles are generated based on tracing pathways between two known structures. In this new method, H-bond distance constraints are imposed in the form of inequalities, rather than equalities, and there is a mechanism implemented for H-bonds to break and form. This software can be run on a server [40]. Although my familiarity with this method's capabilities is limited, it appears to be a promising approach. For example, the conformations along a pathway can be used as seed positions for umbrella sampling using MD simulation [41] to obtain free energies, allowing one to study kinetics in terms of plausible reaction coordinates.

PRM

Probabilistic roadmap (PRM) is a method commonly used in robotics for motion planning. A roadmap represents a set of conformations and transitions between them as a graph [42]. Similar to the other methods described above, PRM starts with a known input structure, and generates new conformations. Unfortunately, PRM does not solve how to generate ensembles. Different methods must be devised to efficiently explore conformational space, where the dimensionally of this space increases exponentially as more degrees of freedom (DOF) are involved in the protein motion as it unfolds. For WSME models [21], the PRM method was shown to perform much more efficiently than standard MC methods [43]. For geometry based PRM models, Amato and coworkers generate conformations by a MC procedure using internal coordinate methods taken from robotics [44]. In more recent work, their method has been improved by incorporating rigidity concepts, where the probability to rotate dihedral angles within rigid regions is reduced [45], and this method is available on a server [46].

A few aspects of the geometrical PRM are worth highlighting. The employed robotics-based method does not rely on enforcing certain rigid clusters to remain intact. In other words, distance constraints (other than from covalent bonding) are not fixed. Identifying rigid clusters based on a current conformation is used for the purpose to bias which dihedral angles to vary. As such, rigid regions tend to stay rigid, and the effective number of DOF is reduced in a stochastic way. Therefore, this approach allows constraints to break and form in a natural way, and the method is computationally efficient. Effectively, the entire energy landscape can be created, which implies all thermodynamic and kinetic properties of proteins can be predicted. This method is not restricted to native contacts, but requires starting with known protein structure for the exploration to be tractable. The only approximation is the use of a simple energy function, which does not include solvation effects. Also, the exponential prefactors found in a master equation will not be expected to be uniform over the edges within the graph of assessable microstates [34]. Although simplifications are made in the energy function and in constructing the master equation, there does not seem to be any intrinsic disadvantage of the method.

In summary, FRODA, geometric targeting and geometrical PRM are similar to MD simulation in that atomic coordinates are explicitly manipulated. They differ from MD because they employ simplified energy functions, do not solve dynamical equations of motion and invoke network rigidity to reduce the number of DOF involved in larger-scale motions. Taken together, these methods have marked improvements in speed and coverage of the accessible conformational space. Of particular importance, the effective number of DOF depends on the number of crosslinking interactions across the backbone chain(s) as well as the mechanical strength of these crosslinks.

Distance constraint models

The methods described in the previous section that locate flexible and rigid regions within a protein point to a link between conformational entropy and properties of network rigidity. Other compelling evidence was found by showing that the non-additivity measured in double mutant free energy cycles is related to the propagation of rigidity throughout the protein [47]. A Distance Constraint Model (DCM) is an approach that describes protein thermodynamics through an ensemble of accessible constraint topologies determined by covalent bonding and crosslinking interactions that fluctuate, such as H-bonds [48]. Based on a free energy decomposition in terms of specific interactions, energy and entropy contributions are assigned to fluctuating constraints, and a free energy function is defined. Constraints are allowed to break or form by identifying native crosslinks and assigning an Ising “spin” variable to denote whether the constraint is present or not. Under a fixed set of distance constraints, a protein can explore a certain amount of conformational space (i.e. this is what FRODA simulates), which is related to conformational entropy.

The DCM estimates conformational entropy by accounting for a reduction of entropy when a constraint is placed within a flexible region, which indicates that it is an independent constraint. If a constraint is placed within a rigid region, the constraint is redundant, and no entropy cost occurs. In a two-step process, a rigorous lowest upper bound estimate for conformational entropy is made without simulating protein motion (explicit manipulation of atoms). First, a list of all the constraints present within a given network is sorted based on those that can potentially (assuming they are independent) reduce the entropy the most to the least. Second, graph-rigidity algorithms are applied recursively using this preferential sorting to determine if a constraint is independent or redundant. Then a least upper bound estimate for conformational entropy is given as a sum over entropy contributions from independent constraints. In addition, correlated motions and rigid clusters are identified, and total energy is given by the sum over all energy components within the protein. Although loop corrections can be incorporated to improve accuracy, their effect is captured largely through effective parameters, and the remaining error is found to be negligible compared to the dominant effect from the rigid cluster decomposition [49].

mDCM

A minimal DCM (mDCM) was devised by Jacobs and coworkers as a simplified all-atom model to describe protein thermodynamics [50] using the free energy function:

$$G(N_{hb},N_{nt})=U_{hb}\left(N_{hb}\right)-N_{hb}u+N_{nt}v-RT{S}_m(N_{hb},N_{nt})-RT{S}_c(N_{hb},N_{nt}\mid {\delta }_n,{\delta }_d,\gamma )$$ (3)

Free energy is expressed in terms of two order parameters given by the number of native H-bonds, N_hb, and number of native backbone and sidechain torsion angles, N_nt. The total energy for the intramolecular H-bonds is given by U_hb, which is a sum over all H-bonds present in the protein. Meanwhile, there is competition between intramolecular H-bonds and H-bonds that from between the protein and solvent. For example, some intramolecular H-bonds will break so that other H-bonds can form between the protein and solvent, where, u, is the average energy (a negative value) of a solvent H-bond. This term accounts for solvation effects in an effective way. The term N_ntν (ν is negative) accounts for packing, where the more native-like constraints that form in the structure the lower the energy. The S_m term is the mixing entropy associated with the multiplicity of ways N_hb H-bonds and N_nt torsion angles can be arranged in the protein. The S_c term is conformational entropy, estimated as described above, using entropy parameters for various interactions. Respectively, δ_n, δ_d, γ are the entropies assigned to a native torsion, disordered torsion and a entropy scale for H-bonds. H-bond energies and entropies are assigned based on local geometry, where γ is a linear scale factor to facilitate the assumption that greater entropy loss is associated with H-bonds having lower energy. Subsequently, δ_d, γ were fixed as transferable, and {u, ν, δ_n} are free parameters to fit to experimental thermodynamic data, such as excess heat capacity.

There are a few aspects of the mDCM worth highlighting. The Ising-like model employed is at the all-atom level where “spin” variables represent microscopic interactions. Excess heat capacity data is reproduced well with three adjustable parameters and a generic baseline function [51]. The ensemble it produces allows the partition function, thermodynamic quantities and average mechanical properties to be calculated with excellent tradeoff between accuracy and speed (see Fig. 1). The free energy of a protein is directly related to global flexibility (i.e. DOF), and, in general, free energy is expressed in terms of crosslinking constraints. Cooperativity comes about as a consequence (an effect) of explicitly regarding network rigidity as a mechanical interaction that governs enthalpy-entropy mechanisms at a microscopic level. There is no need for a term to enforce cooperative folding units (see Fig. 2). The degree of cooperativity is predicted without using any a priori assumptions. From the ensembles of constraint topologies generated, free energy landscapes, thermodynamic properties, and quantitative stability/flexibility relationships (QSFR) are calculated rapidly, which include mechanical properties. The QSFR predictions have reproduced many disparate biophysical and functional properties of proteins [52–55].

The mDCM was recently applied to study allostery in CheY [56], where the ensemble of conformations that make up the native basin provides quantitative insight into functional mechanisms that include mechanical response (correlated motions) and thermodynamic response (population shifts). The setup of this work is similar to what was done using COREX [29]. Here, a mechanical perturbation was applied at each residue in turn that mimics a localized binding event.

The mDCM is subject to many approximations. It is solved within a mean field approximation combined with MC sampling. Torsion angle interactions are all treated uniformly and no distinction is given to the location of H-bonds as being in the core or on the surface of a protein. Attention to detail is placed only on the intramolecular H-bond network. Free parameters account for solvation effects in an effective way, rendering them as non-transferable. An input structure is required to define native interactions. The mDCM was created to demonstrate proof-of-concept, and many simplifications were made that limit its utility. Consequently, the mDCM has not been made available on a server and is not user friendly.

In summary, despite many approximations that limit the capabilities of the mDCM, overall its QSFR predictions have correlated well with experiments. The most important aspect of the DCM is that the utility of free energy decompositions [57,58] is restored by explicitly accounting for non-additivity in conformational entropy. This key point has been the main focus in a couple of recent papers [59,60] that give an in depth conceptual view of the approach with minimal mathematics.

Future directions

A key element to efficient computational models is to maximize simplicity by taking advantage of the essential physics of a problem. It is safe to say that solvation effects, native contacts and rigidity are essential aspects needed to rapidly generate conformational ensembles that accurately describe protein thermodynamics and kinetics. The mDCM has established proof of concept that total free energies can be calculated rapidly by reconstituting component energy and entropy parts based on a free energy decomposition scheme. Non-additivity effects are taken into account using network rigidity. The general form of a DCM is sufficiently versatile, in that it can incorporate all the essential aspects that ensemble-based methods offer. Moreover, kinetics can be studied with a DCM by employing a master equation approach like done in the WSME models, or following the geometrical PRM approach by interfacing free energy calculations with methods that generate new conformations. The strength of ensemble-based methods is that solvent effects can be modeled using effective fitting parameters, which dramatically increases applicability to studying protein stability in different types of solvent conditions. These issues are being incorporated in a new DCM that I am currently working on. In collaboration with Dennis Livesay, a much more sophisticated DCM that accounts for solvation effects is nearing completion, and is planned to be released as FAST software that will provide a Flexibility And Stability Test on aqueous soluble proteins. It is expected to be located at the question mark on the speed versus accuracy graph shown in Fig. 1.

Conclusions

Ensemble-based methods are under-utilized compared to MD simulations. One reason for this is because MD simulation packages are readily available across the spectrum of finding resources that span from free to commercial software. Another reason is that ensemble-based methods always use specific approximations foreign to most scientists that are not experts in computational biology. Although the generated ensembles are subject to model limitations, ensemble-based methods are important because they provide sound insight into the essential driving forces controlling protein thermodynamics and kinetics, and they outperform MD simulations. These methods are needed because the structure/function paradigm is only an idealization. All the methods described in this review, including MD methods, utilize known three-dimensional protein structures. Taking into account that MD packages come with errors and approximations as well, it can be expected that ensemble-based methods will mature, and acquire a large regular user base.