Tightening of DNA knots by supercoiling facilitates their unknotting by type II DNA topoisomerases

Abstract

Using numerical simulations, we compare properties of knotted DNA molecules that are either torsionally relaxed or supercoiled. We observe that DNA supercoiling tightens knotted portions of DNA molecules and accentuates the difference in curvature between knotted and unknotted regions. The increased curvature of knotted regions is expected to make them preferential substrates of type IIA topoisomerases because various earlier experiments have concluded that type IIA DNA topoisomerases preferentially interact with highly curved DNA regions. The supercoiling-induced tightening of DNA knots observed here shows that torsional tension in DNA may serve to expose DNA knots to the unknotting action of type IIA topoisomerases, and thus explains how these topoisomerases could maintain a low knotting equilibrium in vivo, even for long DNA molecules.

During normal cell growth, various DNA transactions are facilitated by topoisomerase-mediated passage of one DNA segment through another. These strand passages can inadvertently lead to the formation of DNA knots (1–3), which are highly deleterious for living cells if not removed efficiently (4, 5). Type IIA DNA topoisomerases can use the free energy of ATP hydrolysis (6) to decrease the knotting level significantly below the equilibrium value for DNA rings subject to random passages between colliding segments (7). This topoisomerase (topo) IIA ability has been often assumed to be a physiologically relevant mechanism ensuring efficient DNA unknotting and decatenation (7–10), but doubts on this relevance have been raised as well (11). Particularly problematic is the fact that the original study establishing that type IIA DNA topoisomerases actively unknot DNA also revealed that this ability decreases sharply with increasing DNA length. Although based on only two plasmid sizes, that study showed the generality of this length dependence for several topoisomerases (7) and, therefore, active unknotting would be doomed to be ineffective for long DNA molecules, where random passages lead to very frequent knotting (12). While trying to understand why earlier experimental studies predicted ineffectiveness of type IIA DNA topoisomerases in unknotting of long DNA molecules, we recognized that these studies were performed using torsionally relaxed DNA (7), whereas naturally occurring DNA is frequently under torsional tension (13), the best-known examples of this state being negatively supercoiled bacterial plasmids. To investigate the potential effects of torsional constraints on the activity of type IIA topoisomerases, we have performed Brownian dynamics simulations to examine how negative supercoiling affects the structure of knotted DNA molecules and whether DNA supercoiling can cause knotted regions to be recognized specifically and then unknotted by topoisomerases. We observed that DNA supercoiling results in the tightening of knots, which leads directly to an increase in curvature of the knotted regions, in turn rendering these more likely to be bound and unknotted by type IIA topoisomerases.

Results

Brownian dynamics simulations of DNA molecules have proved themselves capable of predicting and/or reproducing the types of behaviors observed using direct-visualization methods. Even situations as complex as DNA stretching in extensional flow fields (14) or the diffusion of knotted regions in stretched DNA molecules (15) have been reproduced reliably by this simulation technique. Here we employ Brownian dynamics simulations to study the properties of negatively supercoiled DNA molecules that form right- or left-handed trefoil knots. To our knowledge, the interplay of supercoiling and knotting has not previously been addressed by Brownian dynamics simulations. Although our DNA model is coarse-grained, it is suitable to observe the phenomena occurring on a length scale that is larger than 30-bp stretches of DNA. In this study, we modeled knotted supercoiled plasmids having 1.5, 3, and 6 kb, where the largest one approaches the 7-kb size of knotted plasmids studied by Rybenkov et al. (7).

Effects of Supercoiling and Knotting on Electrophoretic Mobility.

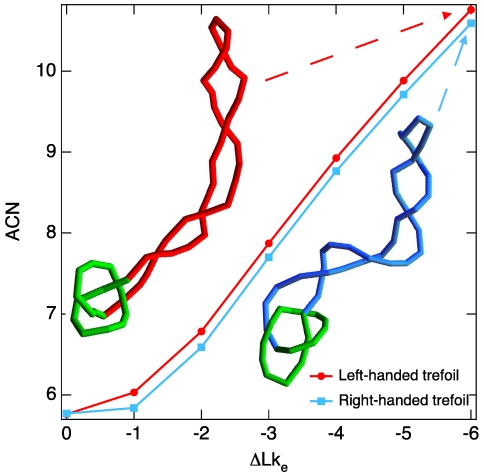
We decided to test first whether our simulations can explain the results of previous experiments showing that negatively supercoiled, left-handed DNA trefoil knots migrate slightly faster during gel electrophoresis than the corresponding negatively supercoiled right-handed trefoils (16). Although a detailed simulation of gel electrophoresis of DNA requires currently unavailable information concerning factors such as gel structure and gel–DNA interactions, a number of experiments and numerical simulations have established that the electrophoretic migration speed of DNA molecules with the same molecular weight increases linearly with their average crossing number (17, 18). By considering equilibrium configurations of the DNA molecules being modeled, we could thus test whether the supercoiled DNA trefoils of the simulation behave in a manner consistent with earlier experimental data. Indeed, we observed (Fig. 1) that, for 1.5-kb molecules, the left-handed forms have higher average crossing numbers, and are therefore expected to migrate more rapidly during gel electrophoresis than the right-handed forms. We explain this difference by the differential absorption of left-handed writhe generated by negative supercoiling by knotted portions of molecules that have positive or negative writhe. The observed correspondence between simulation and experiment for knotted DNA molecules encouraged a deeper investigation of how DNA supercoiling affects the overall structure of the knotted portions of these molecules by Brownian dynamics.

Fig. 1.

Brownian dynamics simulations are consistent with the experimentally observed behavior of supercoiled DNA molecules forming right- or left-handed trefoil knots. Brownian dynamics simulations of 1.5-kb molecules reveal that, at the same level of negative supercoiling, measured by the linking deficit ΔLk_e, DNA molecules forming left-handed trefoil knots adopt configurations with slightly higher average crossing number (ACN) than do molecules forming right-handed trefoil knots [the uncertainty on ACN values (error on the mean) is within the dot size and ranges between 0.006 and 0.014]. Insets show typical configurations obtained in Brownian dynamics simulations of natively supercoiled DNA molecules forming left- and right-handed trefoil knots.

Supercoiling and Knot Size.

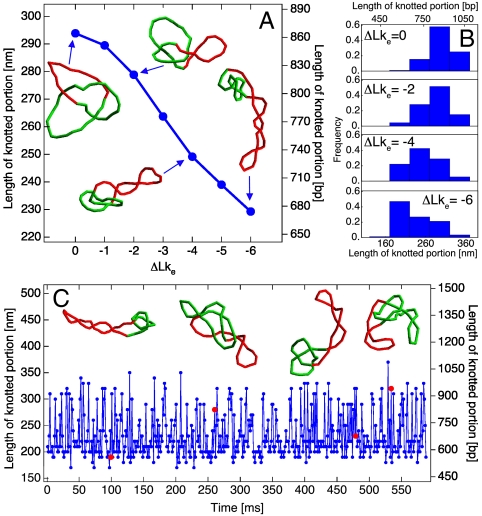
The particular focus of our interest is the size of the knotted domain, which in the case of torsionally relaxed DNA shows a strong correlation with the size of the entire molecule (19). If the tightness of the knotted domains facilitates unknotting, it may explain why only short, torsionally relaxed DNA molecules with relatively tight knotted domains are very efficiently unknotted by type IIA DNA topoisomerases. To measure the size of the knotted domains in individual configurations of simulated DNA molecules, we performed a systematic search for the shortest subchain which, upon closure, still had the same knot type as the original chain (19). Because the size of the knotted domain varies between individual configurations, many independent configurations must be analyzed to estimate the average length of the knotted domain for a given length of DNA molecule and a given level of supercoiling. Fig. 2A shows, for DNA molecules of approximate length 1,500 bp, that the average length of the knotted domain decreases progressively as one introduces supercoiling. For the simulated DNA molecules, the specific linking difference (σ) resulting from an effective linking deficit (20) of ΔLk_e = -6 is σ = -0.043, which is close to the native σ of bacterial plasmids (21). The snapshots in Fig. 2A show configurations with knotted domains whose lengths are typical of the chosen supercoiling levels. Configurations of molecules are determined by two factors: their enthalpy composed of bending, torsional, and electrostatic energy, and their entropy. In the relaxed state (ΔLk_e = 0), it has been shown that entropy weakly localizes knots because it maximizes the number of accessible conformations (22, 23), but knots’ tightening is opposed by enthalpy, which is minimized for delocalized knots (Fig. S1). Therefore, the average conformation is a compromise between these two forces. As the ΔLk_e increases, the contribution of the enthalpy to the free energy of the system also increases and has two minima (see Fig. S1). Moreover, the supercoiled state limits the phase space of the molecule and probably flattens the entropy function. Despite this expectation, we observe a peak in the knot size distribution corresponding to the 220-nm minimum in the enthalpy, which indicates a contribution of the entropy toward the localized conformation of the knot. The peak in the knot size distribution is independent upon the plasmid length as visible in Fig. 3 (plasmid’s lengths of 3 and 6 kb). Although not every configuration has a knotted domain that is tight, such conformations appear frequently during the time evolution of the DNA knots. Fig. 2B shows how the size of the knotted domain fluctuates during its evolution under Brownian dynamics at σ = -0.043. The insets show several uncorrelated configurations where the knotted domains have different lengths.

Fig. 2.

Contour lengths of knotted domains. (A) The average contour lengths of knotted domains decrease with increasing specific linking difference of simulated DNA molecules. Snapshots show configurations at ΔLk_e = 0,-2,-4, and -6 with a knot length corresponding to the peak of the distribution shown in B. (C) The contour length of the knotted domain at ΔLk_e = -6 fluctuates with time during Brownian dynamics simulation, reflecting the temporal evolution of thermally fluctuating DNA molecules. Insets show configurations corresponding to the simulation times indicated by red dots.

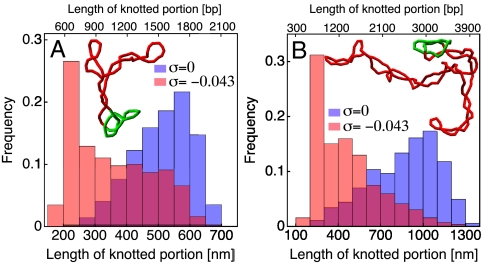
Fig. 3.

Knot tightening by supercoiling also occurs in the case of longer chains of around (A) 3 kb and (B) 6 kb. A clear shift is observed in the distribution of the length of the knotted portion. Interestingly the peak of the distribution is situated in both cases around 220 nm (650 bp), showing that, for the observed molecular lengths, the knot tightening effect is largely independent from the chain size. The snapshots show typical configurations with the localized knotted domain indicated in green.

DNA Bending in Knotted Domains.

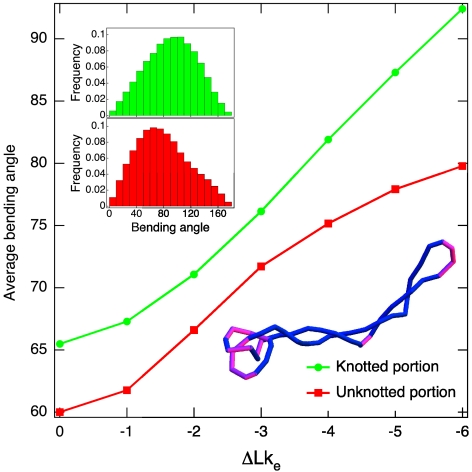
Next we consider which properties of a tightly knotted domain could make it a preferred substrate for binding and unknotting by type IIA topoisomerases. Multiple lines of evidence suggest that type IIA DNA topoisomerases should bind preferentially to DNA regions that are bent: DNA fragments bound by Saccharomyces cerevisiae Topo II were shown to be strongly bent (24); bacterial Topo IV was shown to induce bending in linear and nicked DNA, and was shown to facilitate circularization of short DNA fragments (25); Topo IV has been shown further to bind preferentially to apical loops of supercoiled DNA (25, 26). Taken together, these data suggest that type IIA DNA topoisomerases induce DNA bending, and therefore also bind with higher affinity to prebent regions. Following this idea, we analyzed the average DNA bending angle over a curvilinear distance of 40 nm (118 bp) (the angle between the first and last segments of a four-segment subchain) within the knotted domains and within the remaining portions of supercoiled DNA trefoils. Fig. 4 shows that, as the level of negative supercoiling increases, the knotted portions of the molecule become significantly more bent than the remaining portions, and hence they should indeed be bound preferentially by type IIA DNA topoisomerases. Stronger DNA bending in knotted domains is the natural consequence of the supercoiling-induced tightening of the knotted portions demonstrated in Fig. 2A. Of course, in long plasmids, the total number of strongly bent regions may still be higher in the unknotted than in the knotted chain portions. However, the concentration of bent sites will be higher in the tightly knotted regions, and therefore type IIA DNA topoisomerases should act on these regions more frequently than expected on their share of the plasmid length. In addition, action of type IIA DNA topoisomerases on tightened knotted portions is likely to result in unknotting because of the increased chances that this action involves essential crossings of a knot. We therefore conclude that tightly knotted regions provide ideal substrates for preferential unknotting by DNA topoisomerases.

Fig. 4.

DNA supercoiling accentuates the difference in the average bending angles measured for knotted and unknotted portions of simulated DNA molecules [the uncertainty on the average angular values (error on the mean) is within the dot size and ranges between 0.08 and 0.11]. The inset shows the distribution of bending angles for the knotted and unknotted portions of simulated DNA molecules with a specific linking difference of σ = -0.043. The configuration snapshot, where regions with high bending (> 90°) are shown in pink, illustrates that there are two regions favoring Topo II action: the localized knot and the apical loop.

Fig. 5 presents schematically our proposal of how DNA supercoiling-induced tightening of DNA knots facilitates their efficient unknotting by type IIA DNA topoisomerases. The mechanism presented is relevant primarily for bacterial DNA, which is maintained constantly in supercoiled form. However, transcription- and replication-induced torsional stress is also observed in eukaryotic cells, where it may induce a transient supercoiling in chromatin loops (13).

Fig. 5.

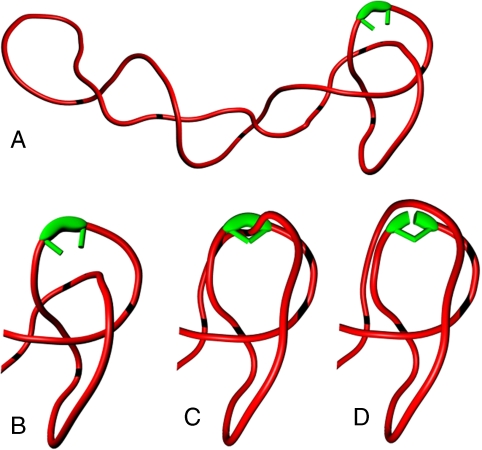
DNA supercoiling-induced tightening of DNA knots facilitates their efficient unknotting by type IIA DNA topoisomerases. (A and B) DNA supercoiling-induced tightening of knotted portions makes these more bent than the remainder of the molecule, which stimulates topoisomerase binding to knotted DNA regions. (C and D) Hooked juxtapositions, believed to be preferential substrates triggering type II topo passages, are encountered frequently in the knotted portions, which favors type II topo action within the knotted domain still further and directs strand-passage reactions toward efficient unknotting.

Discussion

We propose here that DNA supercoiling plays an instrumental role in facilitating DNA unknotting by type IIA topoisomerases. The effect of DNA supercoiling on DNA unknotting by bacterial topoisomerase IV was investigated in 1996 by Ullsperger and Cozzarelli (27), who concluded that supercoiling of knots did not cause an appreciable increase in the rate of their unknotting by Topo IV. However, a closer look at their experimental data reveals that, although the unknotting rate of complex knots with nine crossings appears to be unaffected by supercoiling, there is a clear effect on unknotting of simple knots. Their unknotting was clearly stimulated by DNA supercoiling and this effect was most pronounced in the case of trefoil knots (27). We interpret these results as supporting our proposal. A complex knot with nine crossings imposes by itself a sufficiently high curvature in the region it occupies that supercoiling-induced tightening is not required to increase this curvature still further. By contrast, for simple trefoil knots, the curvature must be increased by supercoiling-induced tightening in order to stimulate Topo IV binding to knotted domains. Results obtained using living bacterial cells also support our proposal: Several studies report that inhibition of DNA gyrase, which is needed for DNA supercoiling, results in a greatly increased frequency of DNA knotting (28, 29). To conclude, our simulations and experimental supporting evidence indicate strongly that supercoiling tightens DNA knots, which leads to their efficient unknotting by type IIA DNA topoisomerases.

Methods

DNA Simulation.

The Brownian dynamics method is based on the model proposed originally by Allison (30) and later refined by several groups (31, 32). The version used in this study is close to that of Vologodskii (15). The DNA chain is modeled as a discrete, worm-like chain of N segments, each of length l₀ = 10 nm (30 bp). A local reference frame is attached to each segment, whose displacement and rotation obeys standard Brownian dynamics equations with the following properties: time increment Δt = 600 ps, diffusion constant D = 0.098 × 10^-9 m²/s, rotational diffusion constant D_rot = 3.3 × 10⁷ s^-1. The force field F used to simulate the properties of DNA is derived from four potentials. (i) A stretching potential E_s = h(l_i - l₀)²/2, where l_i is the current length of the ith segment and 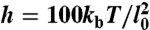is the stretching constant. This potential ensures that the molecule maintains an approximately constant length. (ii) A bending potential 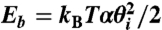, where θ_i is the bending angle between segments i and i + 1, and α is the bending rigidity constant, which is set to α = 4.81 for a DNA molecule with a persistence length of 50 nm. (iii) A torsion potential 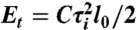, where τ_i is the twist angle between segments i and i + 1, and C is the torsional rigidity constant, which is set to C = 300 × 10^-21 J nm. (iv) An electrostatic Debye–Hückel interaction calculated for n = 5 charges placed on each segment and given by E_e = k_BTH(l_i/n)² exp(-kr_ij)/r_ij, where r_ij is the distance between charges i and j, and H = 6.45 nm^-1 (for a solution of 20 mM NaCl) is a constant calculated by Stigter (33) to mimic a cylinder–cylinder interaction. In total, 10⁹ iterations were performed for each specific linking difference ΔLk_e.

The topological state of the molecule is monitored by measuring its writhe Wr and its twist deviation from the relaxed state ΔTw, which is the sum over all twist angles τ_i, and by definition the sum Wr + ΔTw is an integer. For an unknotted plasmid, the previous sum gives the difference in linking number ΔLk = Wr + ΔTw that describes the deviation from the torsionally relaxed state. This relation is only valid because the writhe of the relaxed unknotted plasmid, the intrinsic Wr₀, is zero. In contrast, a knot has generally a nonzero Wr₀ because of the coiled path it has to follow. In consequence, one has to modify the previous formula to describe the effective difference in linking number ΔLk_e = (Wr - Wr₀) + ΔTw²⁰. When introducing torsional rigidity in the relaxed form of the molecule, the state with minimal elastic energy should have on average Wr = Wr₀ and ΔTw = 0. However, the complication is that Wr₀ for a trefoil is noninteger, which again by definition means that ΔTw ≠ 0. For example, for a trefoil with Wr₀ = 3.4, there will be a minimum difference in twist ΔTw = 0.4. The problem is even worse if one wants to compare the two chiral forms of a knot for which . To be able to compare these two forms, we therefore compensate the noninteger part of Wr₀ by correcting each twist angle τ_i by adding/subtracting 2 × π × 0.4/N to/from it. Starting from such torsionally relaxed but covalently closed DNA molecules, we then decrease the linking number of the molecules progressively to characterize their equilibrium behavior.

Knot Detection.

To detect the knotted region, we adapted a method proposed by Marcone et al. (19) We measure the Alexander polynomial A(s) of subchains of increasing length by starting with subchains of five segments. To close the subchain, three points (p₁, p₂, p₃) are added to each subchain: Points p₁ and p₂ are situated far (1 μm) from the center of mass of the subchain (p_CM), on the lines connecting p_CM to each of the subchain’s ends; p₃ is also far from p_CM (2 μm), equidistant from p₁ and p₂, and in the plane formed by p_CM, p₁, and p₂. If upon closure the subchain indicates the same knotting as the entire molecule, its two ends are pulled away from p_CM by using the Brownian dynamics algorithm. Torsional rigidity is suppressed during pulling to allow for the relaxation of supercoils. Once each end has been pulled away by 100 nm from p_CM, A(s) is recalculated. If it still indicates the correct knotting, the subchain length is considered as the minimal length of the knotted portion. This complex procedure is in particular necessary for long chains, where the closure procedure sometimes passes through supercoiled branches, and indicates a false knotting.

Bending Angles.

The bending angles characterizing the curvature of the knotted and unknotted portions are calculated as the bending between the two end segments of four-segment subchains. This procedure is similar to that used by Vologodskii et al. (25) in their model of the active bending mechanism.