Calmodulin as a Direct Detector of Ca²⁺ Signals

Abstract

Many forms of signal transduction occur when Ca²⁺ enters the cytoplasm of a cell. It has been generally thought that there is a fast buffer that rapidly reduces the free Ca²⁺ level and that it is this buffered level of Ca²⁺ that triggers downstream biochemical processes, notably the activation of calmodulin (CaM) and the resulting activation of CaM-dependent enzymes. Given the importance of these transduction processes, it is critical to understand exactly how Ca²⁺ triggers CaM. We have determined the rate at which Ca²⁺ binds to calmodulin (CaM) and found that Ca²⁺ binds more rapidly than to other Ca²⁺-binding proteins. This property of CaM and its high concentration argue for a new view of signal transduction: CaM directly intercepts incoming Ca²⁺ and sets the free Ca²⁺ levels (i.e., strongly contributes to fast Ca²⁺ buffering) rather than responding to the lower Ca²⁺ level set by other buffers. This property is critical for making CaM an efficient transducer. Our results also suggest a new role for other Ca²⁺ binding proteins (CBPs) in regulating the lifetime of Ca²⁺ bound to CaM, thereby setting the gain of signal transduction.

INTRODUCTION

Given the critical role of CaM in transduction^1,2,3 and Ca²⁺ dynamics⁴, it is essential to understand the kinetics of Ca²⁺ binding to CaM. There are two Ca²⁺-binding sites at the N terminus of CaM and two at the C terminus (N- and C-lobe). These sites have distinct Ca²⁺-binding properties^5,6. Previous work has inferred on-rate constants (k_ons) from measurements of off-rate constants (k_offs) and utilized stopped-flow fluorimetry, a method with a relatively long dead time (> 2 ms) that precludes accurate determination of the fast kinetics of the N lobe^4,7,8. We measured the binding more directly by determining the fall in [Ca²⁺]_free after a rapid (<100 μs) Δ[Ca²⁺]_total produced by flash photolysis of DM-nitrophen (DMn)^9,10,11. We found that the N-lobe of CaM binds Ca²⁺ faster than previously determined for any CBP, and is the first site of cellular Ca²⁺ binding. Furthermore, the cooperativity of Ca²⁺ binding differs significantly between the two lobes giving rise to distinct properties of each lobe. Our findings reveal a highly efficient activation of CaM following a rise in cellular Ca²⁺, possibly resulting in 10–100 times more activated CaM than previously thought.

RESULTS

The Ca²⁺ binding kinetics of CaM

We determined the binding kinetics of CaM in vitro by rapidly (<100 μs) uncaging Ca²⁺ from DMn in the presence of CaM. The uncaged Ca²⁺ is quickly bound by CaM. The [Ca²⁺] dynamics were measured with a fast fluorescent Ca²⁺ indicator (Oregon Green BAPTA 5N, OGB-5N, see methods) also present in the reaction chamber. By analyzing the data with a model that simulates all reactions occurring in the chamber, we derived for the first time the Ca²⁺ binding kinetics of CaM^9,10,11 (see Methods). At a near physiological temperature (35°C) with 47–187 μM CaM present, the decay in [Ca²⁺] had multiple time constants (Fig. 1a). To quantify the binding kinetics, we fitted the data with a two-step binding model of cooperative binding to each lobe¹¹ (see Methods and Supplementary Figs.1–6):

$$[N_T{N}_T]+[{Ca}^{2+}]\underset{k_{\mathit{off}(T),N}}{\overset{2\times k_{on(T),N}}{\rightleftarrows }}[{\mathit{CaN}}_T{N}_R]+[{Ca}^{2+}]\underset{2\times k_{\mathit{off}(R),N}}{\overset{k_{on(R),N}}{\rightleftarrows }}[{\mathit{CaN}}_R{\mathit{CaN}}_R]$$ (eq. 1)

$$[C_T{C}_T]+[{Ca}^{2+}]\underset{k_{\mathit{off}(T),C}}{\overset{2\times k_{on(T),C}}{\rightleftarrows }}[{\mathit{CaC}}_T{C}_R]+[{Ca}^{2+}]\underset{2\times k_{\mathit{off}(R),C}}{\overset{k_{on(R),C}}{\rightleftarrows }}[{\mathit{CaC}}_R{\mathit{CaC}}_R]$$ (eq. 2)

where N_x and C_x represent binding sites on either the N or C lobe; after the first binding, the state changes from T to R, giving rise to cooperativity ¹¹ (see Supplementary Fig. 2). The model had to correctly fit data that were measured over a wide range of experimental conditions. This strongly constrained the fits and assured that accurate kinetics were determined (see Methods). To understand the role of each lobe, we also used CaM mutants that eliminated Ca²⁺ binding to either the N-lobe or the C-lobe.

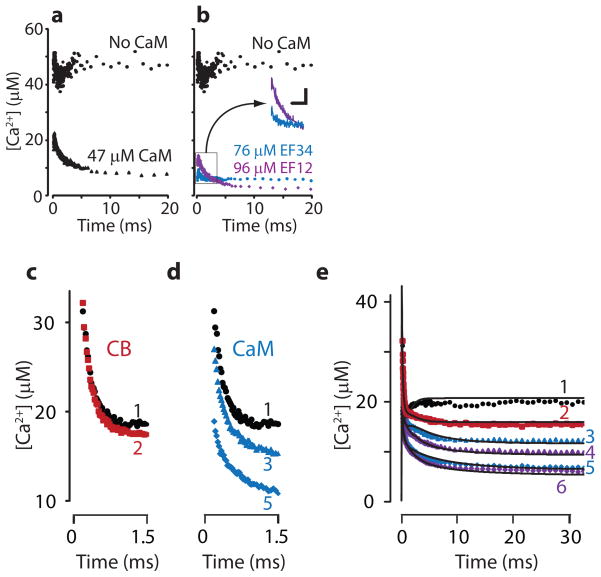
Figure 1. Ca²⁺ buffering by CaM and the different roles of CaM and CB.

a&b) Step in [Ca²⁺]_free as a flash uncages Ca²⁺ bound to DMn (~4.5% of 3.6 mM DMn is uncaged, baseline [Ca²⁺]_free=~500nM (dashed line)¹⁰). a) When CaM is present, the released Ca²⁺ is buffered in at least two phases. Initially, a large part is buffered very rapidly, as indicated by the low [Ca²⁺]_peak. This is followed by a slower decay phase. b) With a CaM mutant in which only the N-lobe binds Ca²⁺ (CaM_EF34), only a fast component is apparent. With a CaM mutant in which only the C-lobe binds Ca²⁺ (CaM_EF12), even a higher concentration produces less initial buffering, but the slow component is evident. Inset shows initial CaM trace at 2× larger scale. c,d, & e) Ca²⁺ transients produced by uncaging 6–7% of 3.6 mM DMn (baseline~300 nM [Ca²⁺]_free). c) When CB (red, trace 2) is added, initial Ca²⁺ dynamics are unchanged compared to control (black, trace 1). d) Addition of CaM increases the fast buffering (adding to the initial rapid reduction caused by DMn alone) (blue, trace 3=13 μM, trace 5=26 μM). e) With CaM present, addition of CB increases the slow reduction (purple, trace 4=34 μM CB+13 μM CaM, trace 6=34 μM CB+26 μM CaM). All data in the mixtures could be closely fit with a mathematical model (solid black lines) using the kinetics of CaM and CB.

The fits (Table 1) reliably describe the data (see Supplementary Figs. 1–6) and are consistent with previous work^5,6 showing that the C-lobe binds Ca²⁺ with higher affinity than the N-lobe (Fig. 1b). Our findings provide two novel insights. First, both lobes show cooperativity, but by different mechanisms. The T-to-R transition strongly increases (~40×) k_on for Ca²⁺ binding to the N-lobe and modestly decreases k_off (~7×). In contrast, k_on of the C-lobe is changed little by the T-to-R transition; cooperativity arises from a ~400× decrease in k_off, consistent with previous experiments^4,7,8. Second, the absolute rate of Ca²⁺ binding to the N-lobe is remarkably fast: the T state has a k_on of 7.7×10⁸ M⁻¹s⁻¹, faster than previous indirect estimates of 2.5–5×10⁸ M⁻¹s^{−1 4,8}. More remarkably, the R state has a k_on of 3.2×10¹⁰ M⁻¹s⁻¹, which greatly exceeds previous indirect estimates^4,7,8 but is within the diffusion limited speed (see Supplementary data 1).

Table 1. Ca²⁺ binding properties of CaM and CB.

CaM measurements were made on wild-type (WT) and Ca²⁺-binding site mutant CaMs (EF3,4 and EF1,2) in which only one lobe is functional. Constants are listed in parentheses and as log values ± S.D. above.

		N terminus		C terminus		CB
		CaMWT (high Kd(app))	CaMEF34	CaMWT (low Kd(app))	CaMEF12
n	conditions	7	4	7	4	10
	traces	94	52	94	51	150
	n (fitsets)	32	26	32	30	30
Kd(T)	log M (μM)	−3.7±0.3 (193)	−3.1±0.6 (641)	−4.6±0.2 (27.8)	−4.1±0.4 (86.9)	−6.4±0.2 (0.393)
Kd(R)	log M (μM)	−6.1±0.3 (0.788)	−6.8±0.6 (0.138)	−6.6±0.3 (0.264)	−6.5±0.3 (0.261)
Kd(app)	log M (μM)	−4.9±0.1 (12.7)	−5.0±0.0 (9.2)	−5.6±0.2 (2.7)	−5.3±0.1 (4.8)
nH		1.9±0.1	2.0±0.0	1.8±0.1	1.9±0.1
kon(T)	log M−1s−1 (M−1s−1)	8.9±0.3 (7.7×108)	8.8±0.4 (7.0×108)	7.9±0.3 (8.4×107)	8.1±0.4 (1.2×108)	7.9±0.1 (7.5×107)
kon(R)	log M−1s−1 (M−1s−1)	10.5±0.6 (3.2×1010)	10.0±0.6 (1.1×1010)	7.4±0.1 (2.5×107)	7.5±0.1 (3.3×107)
koff(T)	log s−1 (s−1)	5.2±0.5 (1.6×105)	5.7±0.7 (5.2×105)	3.4±0.4 (2.6×103)	3.9±0.7 (8.7×103)	1.5±0.2 (29.5)
koff(R)	log M−1s−1 (s−1)	4.3±0.6 (2.2×104)	3.2±0.1 (1.5×103)	1.2±0.3 (6.5)	1.0±0.2 (9.6)

CA1 pyramidal cells have served as a model system for understanding Ca²⁺ dynamics and the role of Ca²⁺ buffers. The major CBP in these cells is calbindin (CB)¹². We measured the properties of CB at 35°C (Table 1 and Supplementary Fig. 4), which were comparable to earlier measurements^9,12 (the small discrepancies can be explained by differences in experimental conditions, see Supplementary data 2). Although CB is generally considered to be a relatively fast Ca²⁺ buffer, it is two orders of magnitude slower than the N-lobe of CaM in the R state.

To understand the implications of these extremely different binding rates, we measured Ca²⁺ dynamics in uncaging experiments with both buffers present. Immediately (<100 μs) after uncaging, Δ[Ca²⁺]_free became bound to CaM (Fig. 1d), well before being bound to CB (Fig. 1c), directly demonstrating that CaM is a faster buffer than CB. Furthermore, the combined action of CaM and CB produced a slower buffering component that was additive when both proteins were present (Fig. 1e). A simple computational model based on the properties of CaM, CB, and DMn (which also acts as a Ca²⁺ buffer) accounts for the Ca²⁺ dynamics in the mixture (Fig. 1e). Although these experiments are done at levels of basal [Ca²⁺]_free higher than the physiological range (this is necessary to keep DMn loaded with Ca²⁺), the resulting model, with a more realistic [Ca²⁺]_free and without DMn, can be used to understand Ca²⁺ dynamics under physiological conditions.

Ca²⁺ buffering by CaM in spines

In dendritic spines of hippocampal CA1 pyramidal cells, Ca²⁺ entry during an action potential (AP) elevates [Ca²⁺]_total by ~50 μM, but the measured rise is only a few μM due to the action of fast buffers^13,14. This buffering action is described by the “buffering capacity” κ (usually measured as the total ΔCa²⁺ that remains undetected by the Ca²⁺ indicator due to fast buffering, relative to the ΔCa²⁺ that is detected by the Ca²⁺ indicator; see Supplementary data 3). We simulated how CaM (100 μM^15,16, see Supplementary data 4) and CB (30 μM¹⁷) affected κ (at [Ca²⁺]_rest= 100 nM). The [Ca²⁺] measured with negligible OGB-1 ([Ca²⁺]_OGB-1) is the [Ca²⁺] as it would be determined with the ‘added buffer’ method^18,19,20. The computed peak [Ca²⁺]_OGB-1 is 2.5 μM during an AP (Fig. 2a), yielding κ=19 (see Supplementary data 5). This buffering capacity is in good agreement with measurements in dendritic spines^13,14. It has been suggested that ATP, which can bind Ca²⁺ when not complexed with Mg²⁺, might also contribute to fast Ca²⁺ buffering²¹. However, our calculations show that in the presence of CaM, addition of ATP (4 mM²¹) increased κ at most by 5%, indicating a minimal contribution of ATP to fast buffering (see Supplementary, data 6). These findings are consistent with CaM being the major fast Ca²⁺ buffer in spines. One property of the fast buffer is that it does not diffuse out of cells¹³. Consistent with this property, much of apo-calmodulin is bound to neurogranin (and is released only on Ca²⁺ binding)^7,22. Moreover, the ability to induce LTP, a phenomenon that depends on CaM, does not rapidly wash out during whole-cell recordings²³, as it would be expected if CaM was freely diffusible.

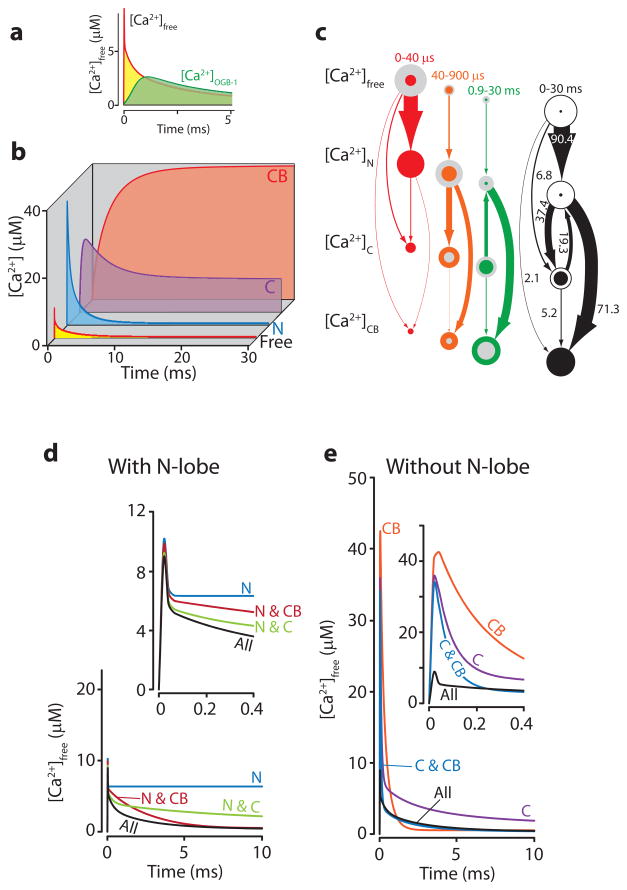
Figure 2. Single-compartment simulations of Ca²⁺ dynamics in a dendritic spine of a hippocampal CA1 pyramidal cell containing 100 μM CaM and 30 μM CB.

At t=0, [Ca²⁺]_total was rapidly (τ=10 μs) increased by 50 μM. a) [Ca²⁺]_free and [Ca²⁺] as it would be measured with 1 yM (10⁻²⁴ M) OGB-1 ([Ca²⁺]_OGB-1). At 20 μs (maximum resolution), [Ca²⁺]_free peaks at 8.8 μM (red line) because most of the Ca²⁺ is immediately bound. The Ca²⁺ detected by experimentally utilized concentrations of OGB-1 (green) is only a fraction of the initial Ca²⁺ signal. b) The Δ[Ca²⁺]_total is distributed between the N-lobe (blue, [Ca²⁺]_N), the C-lobe (purple, [Ca²⁺]_C), CB (red, [Ca²⁺]_CB), and the [Ca²⁺]_free (red line yellow fill). c) Movement of Ca²⁺ through the system. The amount of Ca²⁺ flowing between the four states was calculated for 3 epochs: red, 0–40 μs (peak [Ca²⁺]_N); orange, 40–900 μs (peak [Ca²⁺]_C); green, 0.9–30 ms (end). The [Ca²⁺] in the different states are represented by the area of the circles (grey area=[Ca²⁺]_{start epoch}, colored area=[Ca²⁺]_{end epoch}). Numbers indicate percent of Δ[Ca²⁺]_total. Collapsing of all epochs shows the net fluxes during the whole simulation (black). d & e) Δ[Ca²⁺]_total dynamics of the system when it is simulated without various components (N-lobe/C-lobe/CB). Components present in the simulations are indicated. d) With the N-lobe present, but with either of the other two components missing, the initial fast buffering stays intact (colored traces vs. black traces (no components missing)). e) Without the N-lobe, the initial fast buffering is mostly absent. Whenever CB is present (red in d, blue and orange in e), eventually [Ca²⁺]_free will return to the [Ca²⁺]_final found in the complete model (black). For a more detailed description, see Supplementary figure legend.

Time-dependence of theCa²⁺ distribution

We further analyzed how the different lobes of CaM contribute to fast buffering. Within 40 μs after Ca²⁺ entry, almost 80% of the Δ[Ca²⁺]_total is bound to the N-lobe. Later, this is redistributed to CB and the C-lobe (Figs. 2b, 2c). Consistent with this finding, when CB and/or the C-lobe are taken out of the simulation, the initial fast Ca²⁺ buffering, as indicated by [Ca²⁺]_peak, is only marginally affected (Fig. 3d). In contrast, when the N-lobe is removed (Fig. 3e), the initial fast Ca²⁺ buffering is strongly reduced.

Figure 3. Activation of CaM.

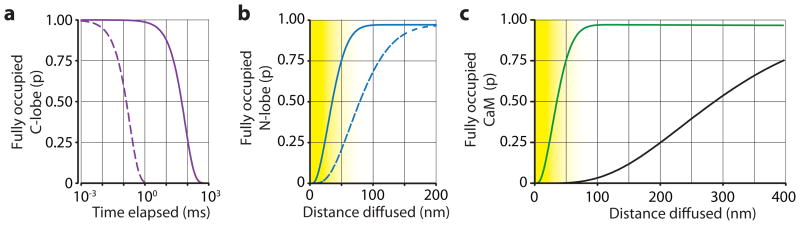
a) The plot shows the probability for a CaM molecule with a fully occupied C-lobe at t=0 to have the C-lobe fully occupied by Ca²⁺ as a function of time in the presence of 100 nM [Ca²⁺] (solid line). It is clear that the C-lobe remains activated with high probability for tens of ms after it binds the second Ca²⁺. In contrast, if the k_off of the C-lobe would not have decreased upon binding the 2^nd Ca²⁺ (dashed line), the lobe would remain activated for less than 1 ms. This indicates that the switch in k_off of the C-lobe is essential for a sustained lifetime of a primed C-lobe. b) The plot shows the probability for a CaM molecule with no Ca²⁺ bound to the N-lobe at t=0 to have the N-lobe fully occupied with Ca²⁺ as it dwells in a nanodomain with 100 μM [Ca²⁺] (D_CaM =50 nm²μs⁻¹, closed line). It is quite likely that the N-lobe will be activated within the size of a nanodomain. However, if the N-lobe would not have increased k_on after binding the 1^st Ca²⁺ (dashed line), the domain size needed for a fully occupied N-lobe would be substantially larger. c) Plot showing the probability for a CaM molecule to become fully occupied by Ca²⁺ as it dwells in a domain with 100 μM [Ca²⁺]. If the molecule has no Ca²⁺ bound at t=0, full activation is unlikely (black line), whereas if the C-lobe is primed (has both binding sites occupied) at t=0, activation within the nanodomain is likely (green line). Yellow areas give approximate size for a nanodomain.

After the initial fast buffering, [Ca²⁺]_free slowly (10–30 ms) falls to 350 nM. This decline is noteworthy because a decay with a similar time course was observed in spines and has been attributed to Ca²⁺ pumps²⁴. Our simulation, however, contains no pumps. Therefore, we further examined the mechanism of the slow Ca²⁺ decrease in the absence of Ca²⁺ pumps. When the N-lobe and/or the C-lobe were removed from the simulation, [Ca²⁺]_final was virtually unchanged. However, if CB was removed, [Ca²⁺]_final was substantially higher (Figs. 3d, 3e). Thus, CB is the main buffer responsible for setting [Ca²⁺]_final. The overall buffering process is determined by sequential binding events in which the Δ[Ca²⁺]_total is initially bound to a fast, low-affinity buffer (>90% to the N-lobe of CaM). Then, Ca²⁺ is transferred to an intermediate state (C-lobe of CaM and CB) followed by a final stage in which a slow and high-affinity CBP, in this case CB, is the major Ca²⁺ buffer (>78% bound, Fig. 2c). Thus, reduction of Ca²⁺ levels can be attributed to the movement of Ca²⁺ from fast low-affinity binding sites to slower high-affinity sites. Other processes such as diffusion and Ca²⁺ pumps will then determine the final aspects of Ca²⁺ dynamics.

DISCUSSION

Activation of CaM

Our data show that the cooperativity of the two CaM lobes arises from quite different mechanisms. These differences lead to a new understanding of how CaM is activated. Measurements indicate that CaM requires Ca²⁺ binding both in the nanodomain of channels and in the bulk solution of the spine head²⁵. In the bulk, a modest elevation of Ca²⁺ (1–10 μM) will be sufficient to cause binding to the relatively high-affinity C-lobe. But, if [Ca²⁺] falls after only one Ca²⁺ binds to the C-lobe, the bound Ca²⁺ will be quickly lost because the extremely fast k_off (2.6×10³ s⁻¹) makes it difficult for this form of CaM to integrate over multiple Ca²⁺ pulses. However, if a second Ca²⁺ binds to the C-lobe, k_off decreases by ~400×, creating a long-lasting primed pool of CaM (~100 ms, Fig. 3a). Further integration can occur when a subsequent Ca²⁺ entry creates a high [Ca²⁺] (100 μM) in the nanodomain; this can load the low-affinity N-lobe of primed CaM (CaM with C-lobe fully occupied, Fig. 3c). A freely diffusing CaM molecule will travel out of the nanodomain within tens of μs. Therefore, a very fast Ca²⁺ binding to the N-lobe is crucial for two Ca²⁺ ions to bind within the nanodomain. Due to the high k_on for the second binding, there is a >90% probability that a second ion binds within 1 μs at 100 μM [Ca²⁺]. Consequently, there is a 75% probability that a totally unoccupied N-lobe gets fully occupied after spending only 12.5 μs in the nanodomain. This time is sufficiently short for a freely diffusing CaM molecule to remain within the nanodomain, since it will travel only ~50 nm in 12.5 μs (D_CaM =50 nm² μs^{−1 26}, Fig. 3b). If k_on did not become elevated due to cooperativity (i.e., it remained at 7.7×10⁸ M⁻¹s⁻¹), CaM would most likely diffuse out of the nanodomain before a second Ca²⁺ binding could occur (Fig. 3b). Thus, the two very different types of cooperativity (primarily increasing k_on for the N-lobe and primarily decreasing k_off for the C-lobe) provide a ‘two-step’ mechanism, one within the bulk solution and one within the nanodomain²⁵, to fully activate CaM (Fig. 3c).

Conclusions

In summary, we find that Ca²⁺ binding to CaM is much faster than to any other major CBP. We show that the high concentration of CaM, together with its fast binding kinetics, can largely account for the rapid Ca²⁺ buffering observed in dendritic spines. It has generally been assumed that free Ca²⁺ is set by an unknown fast buffer and that CaM responds to this modest Ca²⁺ elevation. Our results provide a very different view: CaM itself acts as the fast buffer, directly intercepting Ca²⁺ before it has a chance to be buffered by other CBPs. This results in a highly efficient activation of CaM, possibly resulting in 10–100 times more activated CaM than previously thought (see Supplementary Fig. 8). Our results also have implications for other aspects of Ca²⁺ signaling. The transfer of Ca²⁺ from CaM to CB (or other CBPs) will itself produce a fall in [Ca²⁺]_free, thus contributing to the overall Ca²⁺ dynamics. Previous work tried to explain this fall solely in terms of Ca²⁺ pumping²⁴. A further important implication of our findings relates to the observations that cellular levels of CBPs are strongly affected by activity and disease states^27,28. Our results indicate that such changes in CBPs are effectively gain control mechanisms for transduction that modulates the lifetime of activated CaM.

METHODS

Solutions

All experiments were performed at 35.0±0.1°C in solutions containing 50 mM KCl, 200 mM HEPES, 50–100 μM Oregon Green BAPTA-5N (OGB-5N, Invitrogen/Molecular Probes, Eugene, Oregon) and 3.6–5.6 mM DM-nitrophen (DMn, (4,5-dimethoxi-2-nitrophenyl)-1,2-diaminoethane-N,N,N′,N′-tetrasodium salt, Calbiochem, San Diego, CA). In selected experiments, the solution also contained CB, CaM, or one of the mutants of CaM in which either the Ca²⁺-binding sites on the N-lobe or the C-lobe are unable to bind Ca²⁺ (CaM_EF34 or CaM_EF12, respectively). By adding CaCl₂, the initial [Ca²⁺]_free of each solution was titrated to be between 250 nM and 1.9 μM (measured with the OGB-5N). Solutions (pH=7.30 at 35°C, ionic strength ~130 mM) were always freshly prepared before every experiment.

We used OGB-5N because of its fast kinetics of Ca²⁺ binding and unbinding needed for tracking the expected rapid changes in [Ca²⁺]. The properties of the dye (Invitrogen/Molecular Probes, Eugene, OR, batch lot# 29020W) were determined as previously described¹⁰ (at 35°C, K_d=37.9 μM, k_off=33.2×10³ s⁻¹, k_on=8.8×10⁸ M⁻¹s⁻¹, and F_min/F_max=39.4).

For each group of experiments, we determined the properties of DMn independently^10,11. The observed properties of DMn (K_d=10.0±0.1 nM, k_on= 5.2±0.6×10⁷ M⁻¹s⁻¹, uncaging τ_fast=75±11 μs (67±3%), uncaging τ_slow 1.0±0.1 ms, k_{off(photoproduct)}= 4.6±2.2×10⁵ s⁻¹) were comparable to previously found values^10,11. Also, the [DMn] was determined²⁹ for each solution independently. All chemicals were obtained from Sigma-Aldrich (St. Louis, MO) unless otherwise mentioned. Values are expressed as mean ± S.E.M.

Dynamic Ca²⁺ measurements

To measure the dynamics of Ca²⁺ binding to a protein, we used UV-flash photolysis of DMn as previously described^9,10,11. The setup consists of a ~1 μl chamber mounted on an custom-made inverted epifluorescence microscope with a 505 nm dichroic mirror and 510 LP emission filter (Chroma Technology, Rockingham, VT). On top of the chamber, the polished end of a silica multimode optical fiber (Ø 800 μm, 0.37 NA, Thorlabs, Newton NJ) was mounted to deliver a flash of UV light (5 ns, 355 nm) from a frequency-tripled Nd:YAG laser (Surelite, Continuum, Santa Clara, CA) to photolyze DMn. The power of the UV flash was controlled by the time delay (185–325 μs) of the laser’s pockels cell causing 0.1–8% of the DMn to uncage. To excite the OGB-5N, an argon laser (488 nm, model 95, Lexel, Freemont, CA) was focused through the epifluorescence pathway with a 20x objective (Fluo20, Nikon), forming a small measurement spot directly in front of the uncaging fiber. Fluorescence was measured with a photodiode (PIN-HR008, UDT Sensors, Hawthorne, CA) in the focal plane of the microscope. In spite of using appropriate optical filters and the excitation wavelength of OGB-5N, the high-energy UV flashes still induced brief but large optical transients that saturated the detection system. A custom-built headstage with a fast recovery from overdrive (<10 ns) OP-AMP (OPA699) was used to minimize the duration of the overload (<60μs). Signal were low-pass filtered (50 kHz, 8-pole Bessel, amplifier Model 440, BrownLee, San Jose CA), digitized (200 kHz, PCIO-MIO-16XE-10, National instruments, Austin, TX) and sampled (PC, custom software written in LabView, National Instruments, Austin, TX) for offline analysis. For each flash-evoked transient, a fresh ~1 μl droplet of solution was used.

Calmodulin, CaM_EF12, CaM_EF34, calbindin, and determination of protein concentrations

To identify a specific pair of binding sites to specific properties, we used CaM mutants in which aspartate has been mutated to alanine in the first Ca²⁺ ligand position of either EF hands 1 and 2 (CaM_EF12, C-lobe is mutated) or EF hands 3 and 4 (CaM_EF34, N-lobe is mutated), rendering the mutated EF hand unable to bind Ca²⁺ in the range of the used [Ca²⁺]³⁰. Purified CaM and its mutants were a gift from Dr. John Adelman (Vollum Institute, Portland, OR). Purified CB was a gift from Dr. Ken Baimbridge (University of Britsh Columbia, Vancouver, Canada).

To determine the exact protein concentrations used in the experiments, 10–15 μl from each experimental solution was stored at −80°C for later concentration measurements. The protein concentrations were measured using a detergent-compatible assay based on a folin-phenol reagent (Bio-Rad Hercules, CA) with known bovine serum albumin solutions as standards. CaM concentrations were further validated by optical absorbance measurements (Hewlett-Packard 8453, Palo Alto, CA). Initial tests with solutions containing DMn and OGB-5N revealed that the colorimetric effect of these compounds was negligible at the concentrations present.

Data analysis and modeling

All data were analyzed using MS Excel (Microsoft, Redmond, WA) and the ODE solver Berkeley Madonna 8.0 (BM8, UC Berkeley, Berkeley, CA). To determine the kinetic parameters from the recordings, we used a mathematical model built in BM8 that incorporates all the reactions occurring in the experiments (see Supplementary Fig. 1a). The DMn-uncaging and OGB-5N-signaling parts of this model were used earlier to determine the properties of DMn and calretinin^10,11. This model was adapted to simulate the binding of Ca²⁺ to CaM (see Supplementary Fig. 1b) or CB (see Supplementary Fig. 1c). Spine Ca²⁺ dynamics were modeled using a single-compartment model also built in BM8.

Fitting the Ca²⁺ binding kinetics of CaM and CB

To determine the Ca²⁺ binding kinetics of CaM, at least eight variables (x₁–x_k, for our fits k ≥ 8) need to be fitted leaving too many degrees of freedom to accurately determine all these parameters by fitting single Ca²⁺ transients. We used a procedure¹¹ that simultaneously fits combined sets of uncaging data obtained under varying experimental conditions (Suppl. Fig. 1). This sufficiently constrains the model to yield consistent results. For instance, for wildtype CaM we performed uncaging experiments at seven initial conditions (Suppl. Fig. 2a–g) that varied in the initial free [Ca²⁺] (hence total [Ca²⁺]), total [CaM], total [DMn] and [OGB-5N]. Under each starting condition (a–g), we performed 11 to 16 uncaging experiments (94 totally), each one with a different amount of uncaging (by varying the energy of the UV flash). To constrain the fits, 32 sets (Set₁–Set_n, from here on “sets” always refer to sets randomly picked traces) of 14 randomly selected traces from each initial condition a–g were generated. The 32 sets were randomly chosen with the pre-condition that every trace of a specific starting condition A – G was equally represented across the sets (each trace was picked 4 or 5 times). Each set of traces was fit (Suppl. Fig. 2) with the model and the fit parameters describing the properties of CaM were constrained to be identical for all individual traces within one set. The only parameter that was allowed to vary between traces was the amount of uncaged Ca²⁺. All 32 results for the fitted values were plotted as a (log-)normal cumulative probability distribution (except for n_H, all parameters were log-normally distributed) and fit to determine the average and the standard deviation (Table 1, Suppl. Fig. 3). For CaM_EF12 (51 traces, 4 conditions, 26 random sets), CaM_EF34 (52 traces, 4 conditions, 30 random sets) and CB (150 traces, 4 conditions, 30 random sets) the same procedure was followed (Suppl. Figs. 3 and 4).

For each fitted trace the correlation coefficient (R) was calculated. For all fitted traces, R was >0.85 for more than 90% (R>0.9 >80%, R>0.95 >50%) of the individual curves. Occasionally, one curve within one set could not be fitted very accurately and had a 0.65<R<0.85 which was considered acceptable since the other curves within that set were described with high confidence by the fit.

To further enhance reliability, we actively searched for multiple local minima in the ‘error space’ and tried to determine the validity of the fit results¹¹ by implying multiple fitting rounds for each protein (Suppl. Fig. 5). In the first rounds of fitting all randomly selected fit sets were fit with a wide variety of starting values for each of the parameters. Thus, each set was fit multiple (j) times within groups (from here on, a “group” refers to a group of variables within one fit):

$$\begin{array}{l}\left\{\begin{array}{c}{{}^r\mathit{Group}}_1\\ ⋮\\ {{}^r\mathit{Group}}_j\end{array}\right\}\\ \text{where}{{}^r\mathit{Group}}_j\in \underset{i=1}{\overset{k}{\cup }}{x}_{i,j}\end{array}$$ (eq. 3)

where r indicates a collection of groups that:

• are used as starting values for fit round 1 (r =1),

• are the results of fit round 1 and are used as starting values for fit round 2 (r =2) and

• are the results of fit round 2 (r =3).

In the first round, the fitting routine is set so that variables can easily make large jumps (Suppl. Fig. 5, loose fits). Most fits will find groups of solutions that are comparable for all parameters between the groups (i.e., all variables x_k,1–x_k,i are relatively tightly distributed) which is averaged to one solution group (²Group₁). Most fits will have as the solution a group of values with one or more parameters that are outliers compared to the commonly found fit values (²Group₂ – ²Group_p). All groups (²Group₁ – ²Group_p) are used as starting groups in a second fitting round. In this round all sets are fitted again, but, the fit routine is set so that the parameters only change slowly (Suppl. Fig. 5, stiff fits) so the solutions found will be close to the starting values given. For each group of starting parameters, a collection of groups (one for each fitted data set) will be obtained:

$${\mathit{Collection}}_j\in \underset{i=1}{\overset{n}{\cup }}{{}^3\mathit{Group}}_{j,\text{Set}i}$$ (eq. 4)

A collection consists of multiple groups where all (or most) parameters between the groups are comparable, and can be described by a single group where the parameters x_k are averages from the x_k’s of the multiple groups. Therefore, for each collection j there are k parameters:

$${\overline{x}}_{k,j}=\frac{{\displaystyle \sum _{i=1}^n}{x}_{k,j,\mathit{Seti}}}{n}$$ (eq. 5)

We found that for all the collections of solutions most parameters are tightly distributed (SD<1 or smaller than one order of magnitude). However, thus far, for all but one collection, there is always at least one parameter that has a wide distribution, varying over several orders of magnitude (see¹¹). In these cases, the fits need at least one parameter with a wide distribution to make the fit acceptable. This is an indication that at least one of the other parameters is erroneous, as it forces the system to correct for this error by using a wide distribution of another parameter. Hence, a collection that shows a distribution of several orders of magnitude in one or more parameters was discarded as it must originate from a ‘false’ minimum in error space. For each experiment, we only found one collection for which all parameters have a tight distribution representing the only valid solution. There might be other sets of such solutions that the fitting routine did not encounter at all. However, the wide array of starting values in the first rounds cover the whole range of what is physiologically possible. Therefore, unexplored solution sets have parameters of which at least one parameter will fall outside the physiological range.

Stability of the model

By using the procedure described above, we found that most fits will find very similar solutions for most or all parameters regardless of the initial starting values. From this we conclude that small deviations in the values of these parameters will not cause major changes in the outcome of the model. However, in our model we defined many of the parameters as constants. These parameters — [Ca²⁺]_rest, [protein]_total, rates of (un)binding and uncaging of DMn, rates of (un)binding of the photoproducts of DMn, rates of (un)binding of OGB-5N and the F_ratio of ORB-5N – were determined in independent experiments. We tested if small perturbations of these constants would have a significant influence on the results of our modeling. Two sets of curves of the WT data were randomly picked and were re-fitted with the same model except that each of the above constants was randomly changed by +5%, 0% or −5%. This was repeated 11 times, giving 24 sets of fitted parameters that varied due to the random variations of the constants. We found that the fit results obtained in this manner vary comparably or less than the original fit results of all data (Suppl. Fig 6). Overall, we conclude that small deviations of any of the parameters considered to be constant will not cause any major changes in the outcome of the model, i.e., there are no large non-linear effects in the explored area of the parameter space.