Identifying Molecular Dynamics in Single-Molecule FRET Experiments with Burst Variance Analysis

Abstract

Histograms of single-molecule Förster resonance energy transfer (FRET) efficiency are often used to study the structures of biomolecules and relate these structures to function. Methods like probability distribution analysis analyze FRET histograms to detect heterogeneities in molecular structure, but they cannot determine whether this heterogeneity arises from dynamic processes or from the coexistence of several static structures. To this end, we introduce burst variance analysis (BVA), a method that detects dynamics by comparing the standard deviation of FRET from individual molecules over time to that expected from theory. Both simulations and experiments on DNA hairpins show that BVA can distinguish between static and dynamic sources of heterogeneity in single-molecule FRET histograms and can test models of dynamics against the observed standard deviation information. Using BVA, we analyzed the fingers-closing transition in the Klenow fragment of Escherichia coli DNA polymerase I and identified substantial dynamics in polymerase complexes formed prior to nucleotide incorporation; these dynamics may be important for the fidelity of DNA synthesis. We expect BVA to be broadly applicable to single-molecule FRET studies of molecular structure and to complement approaches such as probability distribution analysis and fluorescence correlation spectroscopy in studying molecular dynamics.

Introduction

Single-molecule Förster resonance energy transfer (FRET) is an important tool for studying the dynamics of biological molecules and has contributed to fields such as protein folding (1,2), nucleic acid structure and dynamics (3,4), and the function of polymerases (5–8). A common method for analyzing single-pair FRET data is through histograms, which report on the distribution of FRET efficiencies and corresponding donor-acceptor distances for a given molecular species (5–7,9,10). Typically, FRET experiments focus on interpreting changes in mean FRET efficiency, which reflect structural changes in the molecules of interest. Besides mean FRET efficiency, the widths and shapes of these distributions also contain information (9,11–18). Broad FRET distributions may indicate the presence of static heterogeneity, dynamic heterogeneity, or a combination of the two. Static heterogeneity is due to the coexistence of multiple species with static but distinct FRET efficiencies in the same sample, whereas dynamic heterogeneity is due to a single molecular species that fluctuates between multiple distinct FRET states. Dynamic heterogeneity is of special interest, since it can report on the relationship between the conformational states of a biomolecule and its mechanism of action (19,20).

Recent methods such as probability distribution analysis (PDA) (13,14,21–23) and proximity ratio histogram analysis (PRH) (12) have helped interpret the widths of FRET distributions. These methods use the experimental distribution of photon counts from either single fluorescence bursts in solution-phase experiments (PRH) or equally sized time windows (PDA), to calculate the shot-noise-limited distribution of FRET values, i.e., the distribution corresponding to a single, static FRET value, broadened only by photon statistics (shot noise). Whereas a shot-noise-limited distribution is consistent with a single donor-acceptor distance and structural homogeneity, additional broadening indicates the presence of heterogeneity. Recent PDA extensions have made it possible to fit models of static or dynamic heterogeneity to these broad distributions (12,14,22,23). However, it is difficult for either PDA or PRH to determine the exact origin of the broadening.

Fluorescence correlation spectroscopy (FCS) methods have been used extensively to identify molecular dynamics (24); however, it is difficult to resolve dynamics on the diffusion timescale with these methods, and they operate at the small-ensemble level, hindering the study of samples with multiple molecular subpopulations or imperfect fluorescent labeling. Although recent FCS-based methods have broadened the range of detectable dynamic timescales (25,26), they require additional experimental controls and are better suited for small-ensemble data. Moreover, although several studies have used correlation-based methods to resolve dynamics in single-molecule subpopulations (27–29), these suffer from the diffusion-timescale insensitivity of ensemble-based correlation methods. There is therefore a need for methods that can detect diffusion-timescale dynamics in single-molecule FRET experiments.

Here, we introduce burst variance analysis (BVA), which directly detects dynamics in single-molecule FRET data by examining how FRET efficiency fluctuates over time in individual molecules. Whereas the standard deviation of FRET for a static molecule is a simple analytical function of its mean FRET, molecules with dynamic fluctuations in FRET are characterized by an increased standard deviation. BVA compares the static and experimentally observed standard deviations, using a strict statistical criterion to determine whether a given sample exhibits dynamic FRET fluctuations. We demonstrate the ability of BVA to distinguish between static and dynamic heterogeneity using simulations and experiments on both static and dynamic DNA standards. We also show that BVA can be used to analyze the shot-noise predictions generated by PDA, providing a second dimension along which to test models of biomolecular dynamics against experimental data. Finally, we apply BVA to study fingers-closing dynamics in the Klenow fragment (KF) of Escherichia coli DNA polymerase I (Pol I). This conformational change precedes nucleotide incorporation and is thought to contribute to the polymerase's impressive fidelity. We found evidence for previously unidentified fingers-closing dynamics in both KF-DNA (binary) and KF-DNA-deoxynucleotide triphosphate (dNTP) (ternary) complexes, which may be functionally important for the fidelity of DNA synthesis.

Materials and Methods

Single-molecule fluorescence

Solution-phase single-molecule fluorescence experiments were performed using alternating laser excitation as described in previous studies (5,30). The excitation powers measured in continuous-wave mode at 532 and 638 nm were 200 μW and 80 μW, respectively, for DNA samples, and 400 μW and 60 μW, respectively, for KF samples. Samples were analyzed at a concentration of 10–50 pM to minimize multimolecule bursts. DNA samples were measured in 400 mM NaCl, 10 mM Tris-HCl, pH 8.0, 1 mM EDTA, and 100 μg/mL BSA; KF samples were measured in 40 mM HEPES-NaOH, pH 7.3, 10 mM MgCl₂, 1 mM DTT, 100 μg/ml BSA, 5% glycerol, and 1 mM β-mercaptoethylamine. Fluorescent labeling and purification of DNA and KF samples is described in the Supporting Material.

Data analysis and simulations

Analysis software was written in MATLAB (The MathWorks, Natick, MA) or C++. Fluorescent bursts were detected as described previously (31) and analyzed to determine the proximity ratio, E^∗, the donor-excitation photon count, N, the burst duration, T, and the donor/acceptor stoichiometry, S. Unless otherwise noted, all data were thresholded using S ≥ 0.45, eliminating acceptor-only fluorescent species from our analysis. BVA was implemented as described (see Theory), and PDA was carried out as described (22). BVA histograms were normalized such that the darkest shade represented the densest point on the histogram; white represented zero density. Simulation software was written in C++ and is described in the Supporting Material.

Results and Discussion

Theory

Proximity ratio

A fluorescence burst contains N donor-excitation photons, each detected in either the donor (D) or acceptor (A) channel. The photons arriving in each channel include contributions from both fluorescence, F_D and F_A, and background, B_D and B_A. Fluorescence due to leakage of donor fluorescence into the acceptor channel, and to direct excitation of the acceptor fluorophores by the donor-excitation laser (32), can also be observed; we include these contributions in the acceptor fluorescence term, F_A. The experimentally observed FRET, or proximity ratio E^∗, therefore includes contributions from background, leakage, and direct excitation and is simply the ratio of photons observed in the acceptor channel to total number of photons observed:

$$E^{\ast }=\frac{F_A+B_A}{F_D+B_D+F_A+B_A}=\frac{F_A+B_A}{N}$$ (1)

The proximity ratio is a standard FRET-based reporter for measuring relative distance changes between two fluorophores (33), and we use it throughout this work.

Probability distribution analysis

In its simplest form, PDA predicts the distribution of observed FRET efficiencies, P(E), when the true FRET efficiency, 〈E〉, is the same for all molecules, and the only source of P(E) broadening is photon statistics (13). For the proximity ratio E^∗, this expected distribution is

$$P\left(E^{\ast }\right)=\sum _{all{F}_A,B_D,B_{A}yielding{E}^{\ast }}P\left(F\right)\times P\left(F_A|\langle E^{\ast }\rangle ,F\right),$$ (2)

where P(F) is the distribution of fluorescence photons per burst, and $\langle E^{\ast }\rangle$ is the mean proximity ratio. Assuming no background, P(F) = P(N), the experimental distribution of photon counts. Moreover, $P\left(F_A|\langle E^{\ast }\rangle ,F\right)$, the distribution of fluorescence photons in the acceptor channel (including leakage and direct excitation), follows a binomial distribution (13):

$$P\left(F_A|\langle E^{\ast }\rangle ,F\right)=\left(\begin{array}{c}F\\ F_A\end{array}\right){\langle E^{\ast }\rangle }^{F_A}{\left(1-\langle E^{\ast }\rangle \right)}^{F-F_A}$$ (3)

The mean FRET, $\langle E^{\ast }\rangle$, is typically a floating parameter, which we fit by minimizing a reduced chi-square objective function, ${\chi }_r^2$ (see Supporting Material). For simplicity, we ignore the contribution of background fluorescence, which is negligible in our experiments (background counts of ≤6 kHz have a negligible effect on FRET histograms under typical experimental conditions (12,22)), though such contributions can be incorporated (Eq. S1, Eq. S2, and Eq. S3) (13).

Extensions of PDA to predict the shot-noise-limited histograms of samples with static or dynamic heterogeneity are presented in Eq. S4, Eq. S5, Eq. S6, Eq. S7, and Eq. S8 in the Supporting Material, and in detail elsewhere (14,22,23). In a previous publication, we developed a method to predict the shot-noise-limited FRET histograms of molecules with kinetic schemes of arbitrary complexity (22). Whereas this method relied on the simplifying assumption of a uniform photon arrival-time distribution, we have since modified the method to incorporate the experimental distribution of arrival times, improving the accuracy of our PDA predictions. We refer to this method as arrival-time PDA (explained in detail in the Supporting Material); the arrival-time-PDA method preserves photon arrival-time information, allowing the PDA prediction itself to be analyzed by BVA for the presence of dynamics. For validation of the arrival-time-PDA method, see Fig. S2 in the Supporting Material.

Burst variance analysis

If the observed FRET distribution is broader than the expected shot-noise distribution, PDA can be used to fit for multiple static components, or multiple interconverting states (12,14,22,23) (also see the Supporting Material); however, it cannot discriminate between these two sources of heterogeneity. In its simplest form, we use BVA to determine whether the observed broadening of the $E^{\ast }$ distribution is due to dynamics.

Whereas PDA examines the heterogeneity in FRET among all molecules in a sample, BVA analyzes the heterogeneity in the FRET of individual molecules over time (Fig. 1). For static heterogeneity, the width of the E^∗ distribution expands beyond shot noise, because different molecules have different originating FRET values; however, the FRET distribution over time for any individual static molecule is consistent with a shot-noise-limited distribution (Fig. 1 A, magenta); in contrast, this single-molecule FRET distribution will be wider than shot noise if the molecule exhibits FRET dynamics (Fig. 1 A, blue). In BVA, we test for dynamics by comparing the expected shot-noise-limited standard deviation for a given mean E^∗, σ_E^∗, against the observed standard deviation, s_E^∗, for individual molecules.

Figure 1.

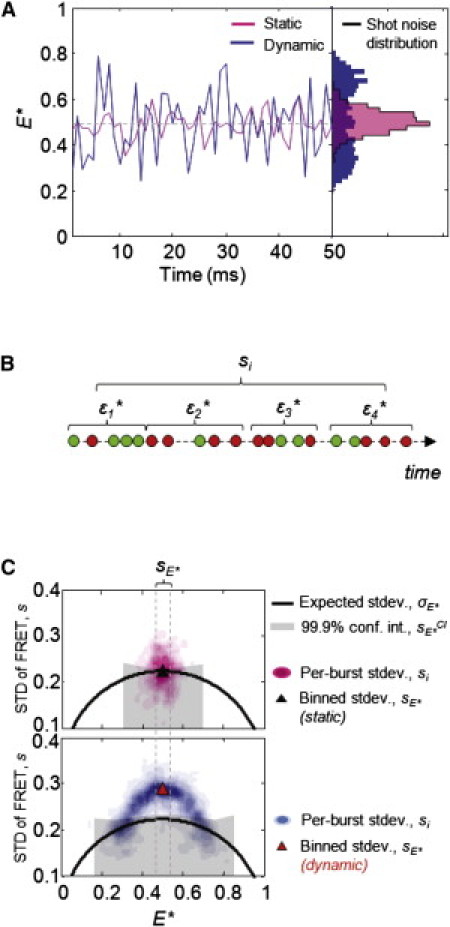
Schematic diagram of the BVA method. (A, left) FRET time traces of simulated single molecules with static (magenta) or dynamic (blue) underlying FRET values. (A, right) FRET fluctuations in the static case are due only to shot noise, and a histogram of these FRET values (magenta) matches the shot-noise prediction (black line), whereas FRET fluctuations in the dynamic case yield histograms wider than the shot-noise prediction (blue). (B) Calculation of the standard deviation of FRET over time for a single molecule, $s_i$. In BVA, M samples of n consecutive photons (M = 4, n = 5 in the diagram) are taken from each burst. The FRET of each n-photon selection (denoted ɛ_j) is calculated, and the standard deviation of FRET, $s_i$, is calculated as the standard deviation of ɛ_j for all M windows (note that there is only a single s_i value per burst). (C) Contour plots of $s_i$ plotted against the proximity ratio, E^∗, for 1000 simulated bursts. The black line indicates the expected standard deviation, ${\sigma }_{E^{\ast }}$, for n photons as a function of E^∗. Whereas bursts with $s_i$ values clustering around ${\sigma }_{E^{\ast }}$ indicate static FRET (upper, magenta), those significantly above ${\sigma }_{E^{\ast }}$ indicate within-burst dynamics (lower, blue). To determine the significance of these apparent dynamics, we select all bursts within a narrow range of E^∗ values (where $L\le E^{\ast }\le U$ and L and U are represented by dashed vertical lines) and calculate the standard deviation of all photon windows belonging to the bursts within it, $s_{E^{\ast }}$ (triangles). We then generate strict confidence intervals, $s_{E^{\ast }}^{CI}$ (gray region): while $s_{E^{\ast }}$ below the confidence interval (upper, black triangle) are consistent with static FRET, $s_{E^{\ast }}$ above the confidence interval (lower, red triangle) are indicative of FRET dynamics.

For a static species, the expected standard deviation due to shot noise, σ_E^∗, depends only on photon statistics. Any set of n consecutive photons will follow a binomial distribution with respect to emission in the donor and acceptor channels. Assuming no background, the expected standard deviation of F_A is that of a binomial, $\sqrt{n{E}^{\ast }\left(1-E^{\ast }\right)}$, with the standard deviation of $E^{\ast }=F_A/n$ being

$${\sigma }_{E^{\ast }}=\sqrt{\frac{E^{\ast }\left(1-E^{\ast }\right)}{n}}.$$ (4)

To calculate the experimental burstwide standard deviation, $s_i$, we segment each burst, i, into M_i consecutive (and nonoverlapping) windows of n photons each (where M_i is the maximum number of windows in burst i; Fig. 1 B), and calculate the standard deviation of all windows within the burst:

$$s_i=\sqrt{\frac{1}{M_i}\sum _{j=1}^{M_i}{\left({\varepsilon }_{ij}-{\mathit{\mu }}_i\right)}^2},\text{where}{\mu }_i=\frac{1}{M_i}\left(\sum _{j=1}^{M_i}{\varepsilon }_{ij}\right),$$ (5)

where ɛ_ij is the proximity ratio of window j in burst i, and μ_i is the mean FRET of all such windows in burst i. In this work, we set n = 5 (rationale and discussion of window size effects is provided in the Supporting Material).

Individual bursts often contain only a few photon windows, resulting in large errors in the calculated s_i. To increase the statistical power of BVA, we segment the E^∗ axis into R bins, each centered on a given value of E^∗ and bearing a width w. For each bin, we calculate the expected standard deviation, s_E^∗, of all windows belonging to bursts in the interval $L\le E^{\ast }<U$, where $L=\left(E^{\ast }-w/2\right)$ and $U=\left(E^{\ast }+w/2\right)$ are lower and upper bounds, respectively, of the bin (Fig. 1 C),

$$s_{E^{\ast }}=\sqrt{\sum _{\underset{L\le E_i^{\ast }<U}{i\text{where}}}\sum _{j=1}^{M_i}\left[\frac{{\left({\varepsilon }_{ij}-\mu \right)}^2}{\sum M_i}\right]},\text{where}\mu =\sum _{\underset{L\le E_i^{\ast }<U}{i\text{where}}}\sum _{j=1}^{M_i}\left(\frac{{\varepsilon }_{ij}}{\sum M_i}\right)$$ (6)

$E_i^{\ast }$ is the proximity ratio of burst i, and μ is the mean FRET of all windows belonging to bursts with $L\le E_i^{\ast }<U$. Unless otherwise indicated, we define R = 20 bins, each with a width of 0.05 along the $E^{\ast }$ axis; for instance, the bin centering on $s_{E^{\ast }=0.5}$ includes windows from all bursts with $0.475\le E_i^{\ast }<0.525$. In this work, we consider s_E^∗ values only from those bins with at least 50 bursts, to ensure that any dynamics detected are representative of the sample. For simplicity, we ignore the contribution of background to BVA; as in PDA, such contributions are usually negligible (see Fig. S3).

We note that, like any method of detecting FRET dynamics, BVA may be sensitive to dynamic changes in fluorophore quantum yield or orientation factor that also give rise to dynamic changes in FRET. It is therefore important to ensure that these artifacts are identified and eliminated with proper controls or else occur on timescales distinct from the dynamics of interest (12,34,35).

Confidence intervals

We calculate upper-limit confidence intervals on ${\sigma }_{E^{\ast }}$ by considering the sampling distribution of standard deviations, P(σ), expected for M windows of n photons. Although this distribution has an approximate analytical solution (see Eq. S9 and accompanying text), we use a computationally expensive, but more precise, Monte Carlo approach to calculate P(σ).To implement the Monte Carlo approach, we simulate the sampling distribution of σ,

$$\sigma =\sqrt{\sum _{\underset{L\le E_i^{\ast }<U}{i\text{where}}}\sum _{j=1}^{M_i}\left[\frac{{\left(\frac{F_A^{ij}}{n}-\mu \right)}^2}{\sum M_i}\right]},\text{where}\mu =\sum _{\underset{L\le E_i^{\ast }<U}{i\text{where}}}\sum _{j=1}^{M_i}\left(\frac{\frac{F_A^{ij}}{n}}{\sum M_i}\right),$$ (7)

and $F_A^{ij}$ are random variables drawn from a binomial distribution with n trials (i.e., the number of photons/window) and E^∗ probability of success. We define the resulting Monte Carlo distribution as $P_{MC}\left(\sigma \right)$.

We use the distribution $P_{MC}\left(\sigma \right)$ to calculate the upper-tail confidence interval on the standard deviation, $s_{E\ast }^{CI}$, and test for dynamics by comparing it to the observed s_E^∗. As we calculate this interval on R = 20 data bins, we employ a Bonferroni correction for multiple hypothesis testing (implementation described in Abidi (36), and in the Supporting Material). Unless otherwise indicated, we set our per-experiment confidence level to $\alpha =.001$; deviations beyond the value of s_E^∗ corresponding to this level should reflect the presence of dynamics.

Simulation results

BVA can distinguish between static and dynamic heterogeneity

We first tested whether BVA can distinguish between static and dynamic heterogeneity as sources of broadening in E^∗ distributions. In addition to a series of single, static FRET species (Fig. S5), we simulated an equimolar mixture of three species with distinct but static FRET efficiencies ($\langle E_1^{\ast }\rangle =0.4$, $\langle E_2^{\ast }\rangle =0.5$, and $\langle E_3^{\ast }\rangle =0.6$) and analyzed it via PDA (Fig. 2 A, upper). As expected, the PDA prediction assuming these static species achieved a good fit to the data (black line; ${\chi }_r^2=1.07$); however, the same data could also be fit well by considering a single species with two dynamically interconverting states. To be specific, we performed a two-parameter fit assuming symmetry about E^∗ = 0.5 and equal forward and backward kinetic rates (red line; $\langle E_1^{\ast }\rangle =0.373\pm 0.003$, $\langle E_2^{\ast }\rangle =0.627\pm 0.003$, $k_{1\to 2}=k_{2\to 1}=883\pm 17{\text{s}}^{-1}$; ${\chi }_r^2=1.19$). The ability of both static and dynamic PDA predictions to account for the observed E^∗ histogram (Fig. 2 A, upper; ${\chi }_r^2<2$) demonstrates the difficulty of resolving static versus dynamic heterogeneity with PDA alone. We then analyzed the static sample with BVA; as expected, all s_E^∗ values fell well within the predicted 99.9% confidence interval (Fig. 2 A, lower, triangles in gray region) correctly suggesting that the observed heterogeneity was due to static, rather than dynamic, sources.

Figure 2.

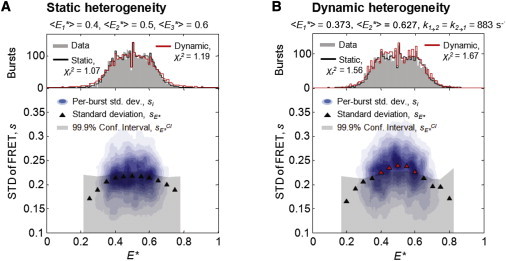
BVA can discriminate between static and dynamic heterogeneity. (A) E^∗ histogram of three simulated, equimolar static species with $\langle E_1^{\ast }\rangle =0.4$, $\langle E_2^{\ast }\rangle =0.5$, and $\langle E_3^{\ast }\rangle =0.6$. PDA predictions (upper) either assuming the presence of the three known static components (black line) or fitting for a two-state dynamic model (red line;$\langle E_1^{\ast }\rangle =0.373\pm 0.003$, $\langle E_2^{\ast }\rangle =0.627\pm 0.003$, $k_{1\to 2}=k_{2\to 1}=883\pm 17{\text{s}}^{-1}$) could adequately account for the observed E^∗ distribution (${\chi }_r^2<2$). BVA of the same sample, however (lower), correctly shows no evidence for dynamics, i.e., all $s_{E^{\ast }}$ fall below the confidence interval (black triangles). (B) E^∗ histogram of a simulated dynamic species fluctuating with the fitted two-state dynamic parameters from A. PDA predictions (upper) are shown for the three-species static model (black line; $\langle E_1^{\ast }\rangle =0.382\pm 0.002$, $\langle E_2^{\ast }\rangle =0.5$ (fixed), $\langle E_3^{\ast }\rangle =0.611\pm 0.001$), and the two-state dynamic model (red line). As in A, either source of heterogeneity could explain the observed E^∗ distribution (${\chi }_r^2<2$). However, BVA (lower) showed clear evidence for dynamics (red triangles; $s_{E^{\ast }}$ of intermediate E^∗ fall above the confidence interval).

We next simulated a simple, two-state dynamic sample (Fig. 2 B) using the FRET values and first-order rate constants from the dynamic PDA prediction in Fig. 2 A ($\langle E_1^{\ast }\rangle =0.373$, $\langle E_2^{\ast }\rangle =0.627$, $k_{1\to 2}=k_{2\to 1}=883{\text{s}}^{\mathrm{-}1}$). Again, PDA predictions assuming either the given two-state dynamic model, or a three-species static model ($\langle E_1^{\ast }\rangle =0.382\pm 0.002$, $\langle E_2^{\ast }\rangle =0.5$ (fixed), $\langle E_3^{\ast }\rangle =0.611\pm 0.001$), could account for the observed E^∗ distribution (Fig. 2 B, upper; ${\chi }_r^2<2$). BVA, however, showed a clear increase in s_E^∗ beyond the confidence interval for intermediate values of E^∗, indicating dynamics (Fig. 2 B, lower, red triangles). Therefore, despite the similarity of E^∗ histograms resulting from static or dynamic heterogeneity, BVA could correctly determine the type of heterogeneity present.

For the dynamic sample, the s_E^∗ values at intermediate E^∗ are above the confidence interval, whereas those nearer to the E^∗ of each individual state are not. This occurs because the diffusion time of the molecules (∼1 ms) is similar to the timescale of dynamics (in our simulations, molecules fluctuate on a timescale of $1/k_{1\to 2}=1/k_{2\to 1}\approx 1.1\text{ms}$); some molecules will therefore sample only one state (e.g., E^∗ ∼ 0.3) during their diffusion through the confocal spot, producing an E^∗ value characteristic of the sampled state, and giving rise to an s_E^∗ value consistent with static behavior. Molecules with an intermediate E^∗ value, however, sample both FRET states, and therefore show an increased s_E^∗.

BVA detects FRET dynamics in a timescale-dependent fashion

Studies on dynamic systems have shown that although FRET histograms broaden in response to dynamics near the diffusion timescale, they appear shot-noise-limited when dynamics are much faster or much slower than diffusion (12). In the former case, molecules interconvert so rapidly that the FRET efficiencies of their states average out, and each burst exhibits an apparently constant (intermediate) FRET efficiency; in the latter, molecules interconvert so slowly that every burst is spent in one state or the other, yielding a shot-noise-limited population corresponding to each state. As BVA detects dynamics through intraburst FRET fluctuations, we expected it to show a timescale dependence similar to that observed when analyzing E^∗ histogram broadening alone.

To test the ability of BVA to detect dynamics on different timescales, we studied the effects of fluctuation timescales on both E^∗ histograms and the s_E^∗ calculated with BVA. We simulated dynamic species fluctuating between two FRET states, $\langle E_1^{\ast }\rangle =0.3$ and $\langle E_2^{\ast }\rangle =0.7$, at timescales on the order of diffusion ($k_{1\to 2}=k_{2\to 1}={10}^3{\text{s}}^{-1}$), or three orders of magnitude above ($k_{1\to 2}=k_{2\to 1}={10}^6{\text{s}}^{-1}$) or below it ($k_{1\to 2}=k_{2\to 1}=1{\text{s}}^{-1}$). As expected, the molecule fluctuating on the diffusion timescale exhibited broadening by PDA, and an increased s_E^∗ (Fig. 3 B). In contrast, molecules fluctuating much slower or faster than the diffusion timescale appeared static by both PDA and BVA (Fig. 3, A and C); thus, at timescales >3 orders of magnitude slower or faster than diffusion, BVA could not detect dynamics.

Figure 3.

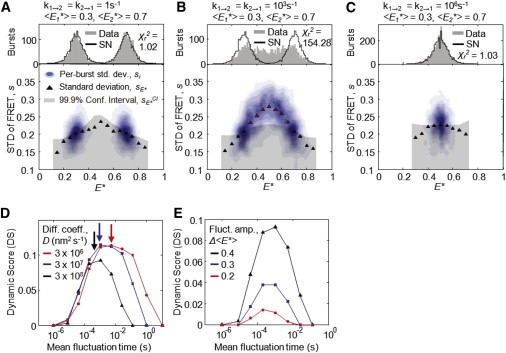
For a simple two-state dynamic species ($\langle E_1^{\ast }\rangle =0.3,\langle E_2^{\ast }\rangle =0.7$), the sensitivity of BVA depends on the timescale of fluctuation. (A–C) PDA plots (upper) and BVA plots (lower) of the effects of fluctuation timescales on E^∗ (upper; PDA plot) and s_E^∗ (lower; determined by BVA). (A) For fluctuation timescales significantly longer than the diffusion time (1 s⁻¹), a dynamic two-state molecule appears as two shot-noise-limited distributions (upper, ${\chi }_r^2=1.02$), with no apparent dynamic component (lower, all s_E^∗ fall below the confidence interval). (B) For fluctuation timescales on the order of the diffusion time (10³ s⁻¹), FRET distributions show significant broadening beyond the shot noise (upper, ${\chi }_r^2>>1$) and evidence for dynamics (lower, s_E^∗ values fall above the confidence interval). (C) For fluctuation timescales significantly faster than the diffusion time (10⁶ s⁻¹), the distribution appears as a single, shot-noise-limited population with a FRET intermediate value between the two states (upper, ${\chi }_r^2=1.03$) and no apparent evidence for dynamics (lower). (D) Plots of the DS over different fluctuation timescales. For molecules with different diffusion coefficients, the DS is maximal near the diffusion time (arrows) in all cases, with greater diffusion times increasing the fluctuation timescale at which sensitivity is greatest. (E) Increasing the amplitude of FRET fluctuation, $\Delta \langle E^{\ast }\rangle$, increases the DS at all fluctuation timescales.

To determine the timescales over which BVA can detect dynamics, we simulated the same two-state fluctuation ($\langle E_1^{\ast }\rangle =0.3,$$\langle E_2^{\ast }\rangle =0.7$) at timescales from ${10}^6{\text{s}}^{-1}$ to ${10}^0{\text{s}}^{-1}$. To quantify our ability to detect dynamics, we calculated a dynamic score (DS), the sum of squared residuals between the observed standard deviation s_E^∗ and the upper-tail confidence interval $s_{E^{\ast }}^{CI}$ for all significant s_E^∗ (i.e., those above the confidence interval):

$$DS=\sqrt{{\sum _{\left(s_{E^{\ast }}-s_{E^{\ast }}^{CI}>0\right)}\left(s_{E^{\ast }}-s_{E^{\ast }}^{CI}\right)}^2}$$ (8)

The DS is a least-squares-like objective function providing an intuitive measure of dynamics: the DS is zero when all s_E^∗ are within the confidence interval and the molecule appears static, and nonzero when there is strong evidence for dynamics (i.e., some s_E^∗ > 0).

Using the same two-state dynamic species ($\langle E_1^{\ast }\rangle =0.3,$$\langle E_2^{\ast }\rangle =0.7$), we calculated the DS over many timescales, and detected dynamics over four orders of magnitude (Fig. 3 D, black line). BVA was most sensitive to FRET fluctuations near the diffusion timescale, regardless of diffusion coefficient ($D=3.0\times {10}^6$, $3.0\times {10}^7$, $3.0\times {10}^8{\text{nm}}^2{\text{s}}^{\mathrm{-}1}$); in all cases, the maximal DS coincided with mean molecular diffusion time (Fig. 3 D, arrow). As diffusion time depends on the dimensions of the confocal spot, we expect features of the experimental setup to affect the sensitivity of BVA to dynamics. We also tested the effects of photon window size, n (Fig. S4), and fluctuation amplitude, $\Delta \langle E^{\ast }\rangle =\left|\langle E_2^{\ast }\rangle -\langle E_1^{\ast }\rangle \right|$ (Fig. 3 E), on the ability of BVA to detect dynamics. Fluctuation amplitude had a large impact, with a doubling of fluctuation amplitude yielding a roughly fourfold increase in DS at the diffusion timescale.

Experimental results

BVA can detect dynamic heterogeneity in DNA samples examined using smFRET

For the experimental validation of BVA, we prepared a series of DNAs modeled after a DNA hairpin standard (Fig. S1). The hairpin is a stem-loop structure that interconverts dynamically between an open and a closed conformation on the timescale of diffusion (Figs. 4 A and Fig. S1 B) (22,37,38). The donor and acceptor fluorophores are on the stem and loop, respectively, such that opening and closing result in large FRET changes.

Figure 4.

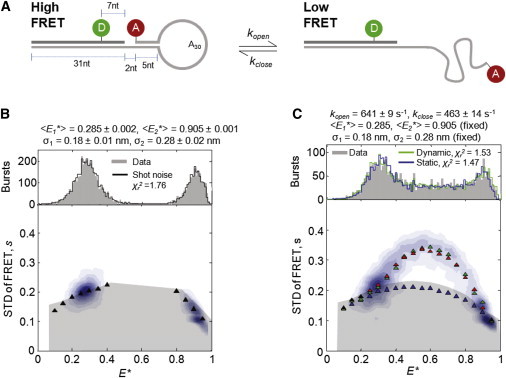
BVA of a dynamic DNA hairpin reveals FRET dynamics. (A) Structure and kinetics of a DNA hairpin. The hairpin is a stem-loop structure, where the stem contains a 31-nucleotide (nt) double-stranded region and the loop contains a stretch of 30 adenines followed by a 5-nt region complementary to a single-stranded portion of the stem. The stem and loop are labeled with donor and acceptor fluorophores (green and red, respectively); in its closed conformation (left; 5-nt region is annealed), the hairpin exhibits high FRET; in its open conformation (right; 5-nt region is melted), it exhibits low FRET. We model the transition between these two states as a simple two-state kinetic system, with first-order kinetic rates $k_{open}$ and $k_{close}$. (B) PDA and BVA of a mixture of two static controls, each of which is designed to mimic either the open or closed conformation of the hairpin. Both distributions show broadening beyond shot noise (Fig. S6) but could be well-fit assuming a Gaussian distribution of FRET efficiencies, with $\langle E_{open}^{\ast }\rangle =0.285\pm 0.002$, ${\sigma }_{open}^r=0.18\pm 0.01\text{nm}$, $\langle E_{closed}^{\ast }\rangle =0.905\pm 0.001$ and ${\sigma }_{closed}^r=0.28\pm 0.02\text{nm}$ (${\chi }_r^2=1.76$, upper). BVA suggests that this heterogeneity is static (lower), or else due to dynamics several orders of magnitude slower than the diffusion timescale (Fig. 3, D and E). (C) PDA and BVA of the dynamic FRET hairpin. The E^∗ histogram could be fit to a two-state dynamic model in which the hairpin fluctuates between the FRET values of the controls at rates $k_{open}=641\pm 9{\text{s}}^{-1}$ and $k_{close}=463\pm 14{\text{s}}^{-1}$ (${\chi }_r^2=1.53$; upper); consistent with this model, BVA shows a dramatic increase in $s_{E^{\ast }}$ at intermediate E^∗ for the experimental data (lower). Furthermore, BVA of the PDA prediction generated an $s_{E^{\ast }}$ profile (green triangles) similar to that of the experimental data (black and red triangles). In contrast, simulations of several static species could accurately reproduce the E^∗ histogram of the dynamic hairpin (upper, blue line,${\chi }_r^2=1.47$); however, BVA analysis of these simulations (blue triangles) produced s_E^∗ values that were clearly static and diverged strongly from the experimental data.

To test whether BVA can distinguish between static and dynamic FRET species, we prepared both a dynamic hairpin and hairpin-like static controls, which remain permanently in either the closed or open conformation (Fig. S1, C and D). We verified that the individual closed and open hairpin conformations are static by testing a mixture of control hairpins (Fig. 4 B); each $E^{\ast }$ distribution was broader than expected from shot noise alone (Fig. S6), and consistent with a Gaussian distribution of $\langle E^{\ast }\rangle$ in the range of 0.15–0.23 nm, as seen previously (12,13,22,34). Such heterogeneity has been attributed to either acceptor dye photophysics, or long-lived states in which fluorophores occupy different positions and/or orientations with respect to the DNA (13,34). Consistent with this proposed quasistatic heterogeneity, BVA analysis showed no evidence for dynamics in either of the two control DNA populations (Fig. 4 B).

We then analyzed the DNA hairpin, which interconverts at the millisecond timescale between the FRET states represented by the two controls, and should yield a large dynamic signal, as we detected previously using a simple form of BVA (31). As expected, BVA revealed a dramatic increase in s_E^∗ at intermediate E^∗ (Fig. 4 C, red triangles); in these bursts, the hairpin switched between the open and closed conformations during its transit through the confocal volume, yielding an intermediate E^∗ and high s_E^∗.

Previously, hairpin dynamics were proposed to occur via a simple two-state kinetic model (22,38,39) wherein the hairpin fluctuates between open and closed conformations with first-order rate constants $k_{close}$ and $k_{open}$ ; we thus tested whether the observed $E^{\ast }$ distribution and s_E^∗ values were consistent with such a model. We first used PDA to fit the data to a two-state dynamic model while fixing the FRET and Gaussian broadening of each state equal to that of the static controls (Fig. 4 C, upper). We obtained best-fit kinetic values of $k_{open}=641\pm 9{\text{s}}^{-1}$ and $k_{close}=463\pm 14{\text{s}}^{-1}$, which yielded a good fit to the data (${\chi }_r^2=1.53$) and an overall reaction time of ${\tau }_R=1/\left(k_{open}+k_{close}\right)=0.91\text{ms}$, consistent with the results of previous correlation-based analyses (${\tau }_R$ of 0.5–1.0 ms) (31,37).

We then used BVA to determine the s_E^∗ of this PDA prediction, and found close agreement between the s_E^∗ of the data and the two-state kinetic model (Fig. 4 C, green triangles); in contrast, the s_E^∗ data could not be explained by a PDA prediction assuming a distribution of static underlying E^∗ values (Fig. 4 C, blue triangles; blue line, upper). This supported earlier PDA-based work suggesting that a two-state dynamic model can account for the dynamics of the hairpin on the timescale of diffusion (25). We note, however, that our best-fit solution exhibits small but systematic deviations in s_E^∗ compared to the data, possibly due to the presence of minor additional states. Indeed, recent work found that a similar hairpin fluctuated with double-exponential kinetics, suggesting an intermediate state between the open and closed forms (40). Overall, our analysis demonstrates that BVA can both detect dynamics in experimental samples and test models of molecular heterogeneity against experimental data.

Dynamics in the Klenow fragment of E. coli DNA Pol I

The bacterial DNA Pol I is an essential component of DNA replication and repair, and it exhibits remarkable fidelity in selecting the correct template-directed nucleotide for addition to a growing DNA chain. Substantial effort has been invested in studying how this fidelity is achieved, with many reports pointing to conformational changes in the polymerase prior to nucleotide incorporation, and especially to a “fingers-closing” transition during which the polymerase forms a tight pocket around both its DNA substrate and an incoming nucleotide, positioning them for catalysis (41,42) (Fig. 5 A).

Figure 5.

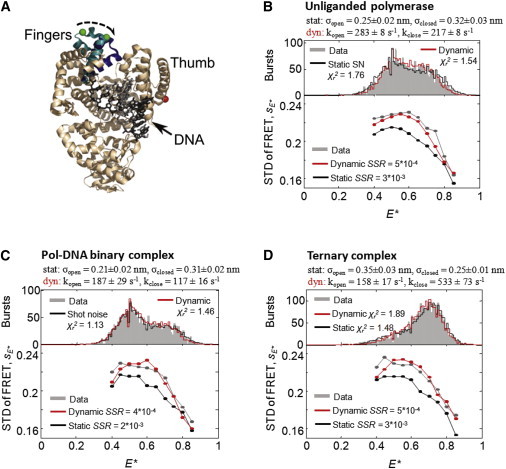
KF and its complexes exhibit conformational dynamics. (A) Superposition of the crystal structures of the Pol-DNA binary complex (PDB 1L3U) and Pol-DNA-dNTP ternary complex (PDB 1LV5) for Bacillus stearothermophilus Pol I (45), a close homolog of E. coli Pol I. The α-carbon backbone of the protein is shown in beige, except for the fingers subdomain, which is shown with fingers open (teal) or closed (dark blue). Green and red spheres indicate the positions of the donor and acceptor fluorophores, respectively, and the arrow indicates the structural change in the fingers subdomain during a fingers-closing transition. (B) Analysis of the unliganded Klenow Fragment (KF) of E. coli Pol I by PDA (upper) and BVA (lower). (Note that BVA analysis shows only s_E^∗ values; for clarity, s_i values are not shown here, but are shown in Fig. S7). The E^∗ histogram was fitted using PDA, assuming either a static two-species model in which KF occupies either the closed or open state, each of which exhibits substantial static E^∗ broadening (black; $\langle E_{open}^{\ast }\rangle =0.5$ (fixed), $\langle E_{closed}^{\ast }\rangle =0.71$ (fixed), ${\sigma }_{open}^r=0.25\pm 0.02\text{nm}$, ${\sigma }_{closed}^r=0.32\pm 0.03\text{nm}$), or a dynamic model in which the two states interconvert dynamically (red; $\langle E_{open}^{\ast }\rangle =0.5$ (fixed), $\langle E_{closed}^{\ast }\rangle =0.71$ (fixed), ${\sigma }_{open}^r={\sigma }_{closed}^r=0.18\text{nm}$ (fixed), $k_{open}=283\pm 8{\text{s}}^{-1}$,$k_{close}=217\pm 8{\text{s}}^{-1}$). Whereas PDA achieved reasonable fits to the data in either scenario (${\chi }_r^2<2$ in both cases), the BVA data strongly favored the dynamic model: the sum of SSRs between the dynamic BVA prediction and experimental data (red) is an order of magnitude lower than the SSR between the static BVA prediction and experimental data (black). The same is true of the Pol-DNA binary complex (C) and the Pol-DNA-dNTP ternary complex (D) supporting the existence of dynamics in all three cases.

Previously, we used single-molecule FRET to monitor the fingers-closing transition in the Klenow Fragment (KF) of E. coli DNA Pol I by labeling it with donor and acceptor fluorophores on the fingers and thumb KF subdomains, respectively (8,25). We showed that fingers-closing and opening occurs dynamically in the absence of a DNA template; this was based on the fact that E^∗ distributions of the unliganded KF were too wide to be accounted for by either one or two shot-noise-limited distributions, and that the unliganded KF appeared dynamic via FCS-based methods and an early form of BVA (8). Recently, we showed that the E^∗ histogram for unliganded KF was consistent with a simple two-state kinetic model using PDA (25), such that unliganded KF appears to fluctuate between its open and closed states on a millisecond timescale, with rates in agreement with the first report of KF dynamics (8).

For the DNA-Pol binary complex and DNA-Pol-dNTP ternary complex, however, the results were less clear: FCS-based methods failed to reveal clear dynamics in these complexes, despite the apparent existence of both open and closed conformations in equilibrium (6,22), and stopped-flow data showing diffusion-timescale fingers-closing during ternary complex formation (43). Moreover, the distributions could be fitted well by either sums of (static) Gaussian distributions (6) or by a PDA-based two-state dynamic model (22). Finally, application of an early form of BVA, which relied on visual comparisons between BVA contour plots of experimental and simulated data, did not clearly identify dynamics, though it lacked the statistical power to do so conclusively (6).

To determine whether the binary and ternary samples are dynamic, we studied them using BVA. In both samples, KF was bound to a nonextensible hairpin DNA with A as the templating nucleotide (Fig. S1 E); in the ternary complex sample, dTTP was added to form the Pol-DNA-dNTP complex (see Materials and Methods).

We first used PDA to test whether the observed E^∗ distributions for each sample could be accounted for with one of two models: a dynamic two-state model or a static two-species model (Fig. 5, B–D). For the dynamic two-state model, we assumed that the polymerase fluctuates between the open and closed complex with first-order rate constants k_close and k_open. In each of the three KF complexes, we fixed the means and Gaussian widths of each state, fit for k_close and k_open, and obtained a good fit to the observed E^∗ distribution (Fig. 5, B–D, upper, red lines; ${\chi }_r^2<2$ in all cases). Furthermore, all fitted k_open and k_close fell in the 100- to 500-s⁻¹ range, consistent with the rate of fingers-closing dynamics expected from previous studies (6,43). We then fit each E^∗ histogram assuming the existence of two static (or slowly interconverting) states, corresponding to the open and closed conformations; as in the dynamic model, we held the mean FRET of each state constant, but fit for the Gaussian widths about these means, ${\sigma }_{open}^r$ and ${\sigma }_{closed}^r$. To avoid introducing new parameters, we fixed the relative occupancy of each state according to the apparent equilibrium from the dynamic fit. As in the dynamic model, this static model achieved a reasonable fit for all three polymerase complexes (Fig. 5, B–D, upper, black lines; ${\chi }_r^2<2$ in all cases). Together, these data suggest that PDA analysis of the observed E^∗ histogram is consistent with both static and dynamic models of polymerase behavior in all three complexes.

We then analyzed each sample and its corresponding PDA predictions with BVA, and compared the resulting s_E^∗ values (Fig. 5, B–D, lower; full contour plots of s_i shown in Fig. S7). The s_E^∗ of the actual data were in qualitative agreement with the s_E^∗ from the dynamic predictions in all cases; in contrast, the s_E^∗ of the static predictions were consistently and substantially lower than the s_E^∗ for either the data or the dynamic prediction. To quantify this difference, we calculated the sum of squared residuals (SSR) between the actual s_E^∗ and those of each prediction, where a smaller SSR indicates a better fit. In all three KF species, the SSR of the dynamic prediction was about an order of magnitude smaller than that of the static prediction (Fig. 5, B–D), suggesting that these wide E^∗ distributions were due to dynamic, rather than static, heterogeneity. To ensure that this result was independent of the model of static heterogeneity employed, we tested a model that includes a third static species with an E^∗ between that of the open and closed complexes; this model, too, did not agree with the data (Fig. S7). We also investigated how the specific timescales used in the dynamic prediction affected their agreement with the experimental data. In addition to finding that predictions using the rates extracted with PDA (100–500 s⁻¹, consistent with fingers-closing dynamics) matched the observed s_E^∗ very well, we found that these rates could be altered by more than an order of magnitude before achieving an SSR comparable to the static prediction (Fig. S8). In conclusion, the full BVA method identified clear dynamics in both the binary and ternary complexes of KF (beyond a strict 99.9% confidence interval) and was able to reproduce the observed standard deviation data accurately using a two-state kinetic model (Fig. 5). These results raise the intriguing possibility that the fingers-closing transition in KF may be dynamic throughout its reaction trajectory, whether DNA-bound or poised for dNTP incorporation.

Conclusions

We introduced BVA, an analytical method that enables the detection of dynamics in single-molecule FRET experiments; it accomplishes this by comparing the standard deviation of FRET from individual molecules over time to that expected from theory. To characterize BVA, we analyzed static DNA molecules, a dynamic DNA hairpin, and the KF of DNA Pol I and its complexes. BVA analysis showed a lack of dynamics in static DNA standards but clear dynamics in a previously characterized dynamic DNA hairpin. We combined BVA with PDA to test specific models of static or dynamic heterogeneity against smFRET data on the DNA hairpin; whereas both static and dynamic sources of heterogeneity could explain the observed E^∗ distribution, only a two-state dynamic model could account for the experimental data when incorporating standard deviation information via BVA.

We used BVA to analyze the conformational dynamics of KF binary and ternary complexes, uncovering millisecond-timescale dynamics not previously detected using a correlation-based approach (6), and suggested (but not conclusively identified) using PDA (21). The presence of dynamics at the millisecond timescale is consistent with recent studies showing that the fingers-closing transition is not rate-limiting for nucleotide addition, supporting a model in which fingers-closing precedes, but does not commit the polymerase to, dNTP incorporation (43,44). Together with our previous results (6), this suggests a model in which fingers-closing, a prechemistry step important for discriminating between matched and mismatched nucleotides, may occur several times prior to successful dNTP incorporation.

Our results illustrate the usefulness of BVA in detecting structural dynamics using single-molecule FRET. Due to its diffusion-timescale sensitivity, BVA complements correlation-based methods, as well as time-resolved smFRET measurements (15), which may have difficulty detecting dynamics near the diffusion timescale. BVA also complements a recent PDA-based method to identify the presence of FRET dynamics (23), both by offering model-free detection of dynamics, and by adding a dimension along which to hypothesis-test specific models of dynamics; the latter is useful in rejecting incorrect models that produce $E^{\ast }$ distributions consistent with experiments, but show poor agreement between predicted and observed BVA data. Since BVA is performed on single-molecule data, it can also be applied to subpopulations of interest, or imperfectly labeled samples, without producing the artifacts inherent to correlation-based methods. BVA should be broadly useful in single-molecule FRET studies of enzyme structures and dynamics, and of protein and nucleic acid folding.