Abstract
Uterine contractions during labor are discretely regulated by rhythmic action potentials (AP) of varying duration and form that serve to determine calcium-dependent force production. We have employed a computational biology approach to develop a fuller understanding of the complexity of excitation-contraction (E-C) coupling of uterine smooth muscle cells (USMC). Our overall aim is to establish a mathematical platform of sufficient biophysical detail to quantitatively describe known uterine E-C coupling parameters and thereby inform future empirical investigations of physiological and pathophysiological mechanisms governing normal and dysfunctional labors. From published and unpublished data we construct mathematical models for fourteen ionic currents of USMCs: 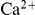 currents (L- and T-type),
currents (L- and T-type),  current, an hyperpolarization-activated current, three voltage-gated
current, an hyperpolarization-activated current, three voltage-gated 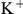 currents, two
currents, two 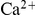 -activated
-activated 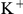 current,
current, 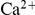 -activated
-activated 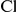 current, non-specific cation current,
current, non-specific cation current, 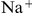 -
-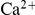 exchanger,
exchanger, 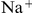 -
-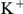 pump and background current. The magnitudes and kinetics of each current system in a spindle shaped single cell with a specified surface area∶volume ratio is described by differential equations, in terms of maximal conductances, electrochemical gradient, voltage-dependent activation/inactivation gating variables and temporal changes in intracellular
pump and background current. The magnitudes and kinetics of each current system in a spindle shaped single cell with a specified surface area∶volume ratio is described by differential equations, in terms of maximal conductances, electrochemical gradient, voltage-dependent activation/inactivation gating variables and temporal changes in intracellular 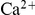 computed from known
computed from known 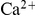 fluxes. These quantifications are validated by the reconstruction of the individual experimental ionic currents obtained under voltage-clamp. Phasic contraction is modeled in relation to the time constant of changing
fluxes. These quantifications are validated by the reconstruction of the individual experimental ionic currents obtained under voltage-clamp. Phasic contraction is modeled in relation to the time constant of changing 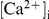 . This integrated model is validated by its reconstruction of the different USMC AP configurations (spikes, plateau and bursts of spikes), the change from bursting to plateau type AP produced by estradiol and of simultaneous experimental recordings of spontaneous AP,
. This integrated model is validated by its reconstruction of the different USMC AP configurations (spikes, plateau and bursts of spikes), the change from bursting to plateau type AP produced by estradiol and of simultaneous experimental recordings of spontaneous AP, 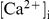 and phasic force. In summary, our advanced mathematical model provides a powerful tool to investigate the physiological ionic mechanisms underlying the genesis of uterine electrical E-C coupling of labor and parturition. This will furnish the evolution of descriptive and predictive quantitative models of myometrial electrogenesis at the whole cell and tissue levels.
and phasic force. In summary, our advanced mathematical model provides a powerful tool to investigate the physiological ionic mechanisms underlying the genesis of uterine electrical E-C coupling of labor and parturition. This will furnish the evolution of descriptive and predictive quantitative models of myometrial electrogenesis at the whole cell and tissue levels.
Introduction
For over 50 years it has been known that uterine smooth muscle (myometrium) generates spontaneous action potentials (APs) [1]–[3]. These precede elevations in intracellular 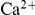 that, in turn, facilitate the actomyosin interactions governing myometrial contractions [4], [5]. The regulation of electrical activity of myometrial cells therefore plays a crucial role in determining the onset, the duration and the strength of uterine contractions during labor. This is essential for a successful conclusion to pregnancy with the safe delivery of the fetus and placenta. Unfortunately, many pregnancies result in complications of labor that compromise the health of the fetus/newborn. Preterm birth, of which activation of uterine contraction is the major cause, occurs in up to
that, in turn, facilitate the actomyosin interactions governing myometrial contractions [4], [5]. The regulation of electrical activity of myometrial cells therefore plays a crucial role in determining the onset, the duration and the strength of uterine contractions during labor. This is essential for a successful conclusion to pregnancy with the safe delivery of the fetus and placenta. Unfortunately, many pregnancies result in complications of labor that compromise the health of the fetus/newborn. Preterm birth, of which activation of uterine contraction is the major cause, occurs in up to 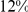 of deliveries and results in a high incidence of mortality and morbidity of the offspring [6]. Prolonged dysfunctional labor at term occurs in
of deliveries and results in a high incidence of mortality and morbidity of the offspring [6]. Prolonged dysfunctional labor at term occurs in 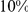 of pregnancies and these patients account for
of pregnancies and these patients account for 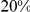 of Cesarean sections [7]. An improved understanding of the physiological complexities of myometrial electrical excitability would assist in the task of developing better targeted therapies for these problematic labors.
of Cesarean sections [7]. An improved understanding of the physiological complexities of myometrial electrical excitability would assist in the task of developing better targeted therapies for these problematic labors.
Modifications of myometrial cell electrophysiological characteristics during pregnancy are evident. The resting membrane potential of myometrial cells becomes progressively more positive towards term [8], gestational-dependent changes in the molecular expressions of ionic channel components occurs [9] and the form of action potentials can change between those of rapid spike-like and tonic plateau-type [10], [11]. Electrophysiological recordings have also identified several classes of individual ionic currents in myometrial cells. It is accepted that the major inward depolarizing current of the AP likely arises from 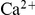 entry via L-type
entry via L-type 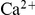 channels [12]. Other myometrial inward currents that have been suggested to be functional, at least in some experimental situations, include those mediated through T-type
channels [12]. Other myometrial inward currents that have been suggested to be functional, at least in some experimental situations, include those mediated through T-type 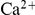 channels [13],
channels [13], 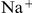 channels [14] or
channels [14] or 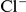 channels [15]. Voltage-dependent outward currents, both those that are sensitive or insensitive to 4-aminopyridine (4-AP), have been identified as have calcium-dependent
channels [15]. Voltage-dependent outward currents, both those that are sensitive or insensitive to 4-aminopyridine (4-AP), have been identified as have calcium-dependent 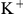 currents [16]–[20]. Molecular expression of genes/proteins of electrogenic ion exchangers, the
currents [16]–[20]. Molecular expression of genes/proteins of electrogenic ion exchangers, the 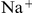 -
-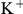 ATPase [21] and the
ATPase [21] and the 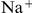 -
-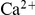 exchangers [22], suggest that these too may have a contribution to make to regulating myometrial membrane potential.
exchangers [22], suggest that these too may have a contribution to make to regulating myometrial membrane potential.
There is increasing awareness of the benefits of developing mathematical descriptions of uterine function [23]–[25] and recent attempts have shown promise regarding the mapping of electrophysiological or contractile data. However, detailed descriptions of the biophysical characteristics of each of the myometrial ionic currents are lacking. In addition, information on how these individual ionic currents are integrated to form the shape and timecourse of APs reflective of those reported for the myometrium is sparse. This severely limits the ability to model simultaneous changes in myometrial membrane potential, 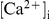 and force that are the essential elements of electrical E-C coupling. It is important to determine each of these circumstances in order to assess fully the likely physiological relevance to AP genesis of any electrophysiological data that has been recorded in isolation and attributed to a particular ion channel subtype. It is also necessary to consider how these electrical events influence E-C coupling parameters leading to the generation of phasic contractions of uterine smooth muscle as this, after all, determines the success of the parturient effort. Therefore, we had three aims to the present work. First, to develop biophysically detailed quantitative (mathematical) descriptions of all known individual ionic currents of uterine smooth muscle cells pertaining to near the end of pregnancy. Second, to compute these, in alliance with descriptions of dynamic
and force that are the essential elements of electrical E-C coupling. It is important to determine each of these circumstances in order to assess fully the likely physiological relevance to AP genesis of any electrophysiological data that has been recorded in isolation and attributed to a particular ion channel subtype. It is also necessary to consider how these electrical events influence E-C coupling parameters leading to the generation of phasic contractions of uterine smooth muscle as this, after all, determines the success of the parturient effort. Therefore, we had three aims to the present work. First, to develop biophysically detailed quantitative (mathematical) descriptions of all known individual ionic currents of uterine smooth muscle cells pertaining to near the end of pregnancy. Second, to compute these, in alliance with descriptions of dynamic 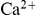 handling parameters, into a mathematical model of myometrial action potential generation. Third, to extend this model to the simulation of concomitant recordings of spontaneous AP,
handling parameters, into a mathematical model of myometrial action potential generation. Third, to extend this model to the simulation of concomitant recordings of spontaneous AP, 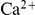 and force in uterine smooth muscle. Moreover, the model is assessed for its ability to simulate published changes in experimental parameters. The development of our quantitative model markedly advances our understanding of the electrophysiological basis of excitation-contraction coupling in uterine smooth muscle. In so doing, it also provides a framework of relevance for exploring the biophysical modeling of individual ionic currents underlying the electrogenic processes in other smooth muscles, tissues and organs.
and force in uterine smooth muscle. Moreover, the model is assessed for its ability to simulate published changes in experimental parameters. The development of our quantitative model markedly advances our understanding of the electrophysiological basis of excitation-contraction coupling in uterine smooth muscle. In so doing, it also provides a framework of relevance for exploring the biophysical modeling of individual ionic currents underlying the electrogenic processes in other smooth muscles, tissues and organs.
Results and Discussion
The general mathematical formulae used for parameter modeling are given in the Methods (equations 1–9). A glossary of symbols used in the modeling equations is given in Tables S1, S2. Detailed formulations of individual model components are given in Appendix S1 (equations 10–105).
L-type Calcium current – 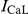
Mathematical descriptions of the biophysical characteristics of this current are given in Appendix S1 (equations 10–19).
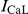 is attributed as the major inward current in myometrial cells [8], [14], [26]–[28].
is attributed as the major inward current in myometrial cells [8], [14], [26]–[28]. 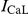 first appears at
first appears at 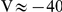 to
to 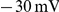 ; the peak of the current-voltage (I–V) relationship arises between
; the peak of the current-voltage (I–V) relationship arises between 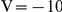 to
to 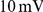 and the reversal potential
and the reversal potential 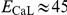 to
to 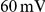 at
at 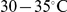 with
with 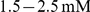
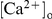 [12], [15], [29], [30]. L-type calcium channels in other cell types have been reported to be permeable to other cations [31] but there is no data specific to myometrial cells. Thus, the Goldman-Hodgkin-Katz formulation commonly used in other muscle cell models is not used here; instead,
[12], [15], [29], [30]. L-type calcium channels in other cell types have been reported to be permeable to other cations [31] but there is no data specific to myometrial cells. Thus, the Goldman-Hodgkin-Katz formulation commonly used in other muscle cell models is not used here; instead, 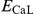 in the model is fixed at
in the model is fixed at 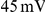 as suggested by experimental data [12], [30], [32].
as suggested by experimental data [12], [30], [32].
Properties of 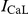 are derived from experimental data at
are derived from experimental data at 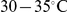 of myometrial cells from late pregnant rat. The equations of
of myometrial cells from late pregnant rat. The equations of 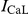 incorporate an activation gating variable (
incorporate an activation gating variable (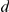 ) and fast (
) and fast (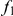 ) and slow (
) and slow (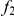 ) inactivation gating variables. Different steady-state values for activation and inactivation at
) inactivation gating variables. Different steady-state values for activation and inactivation at 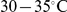 have been reported and representatives of the data range are plotted in Figure 1A–B. This may reflect different
have been reported and representatives of the data range are plotted in Figure 1A–B. This may reflect different 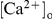 employed between studies or slightly differing residual hormonal influences. Yoshino et al., [33] showed that the half-activation and the I–V relationship were right-shifted by
employed between studies or slightly differing residual hormonal influences. Yoshino et al., [33] showed that the half-activation and the I–V relationship were right-shifted by 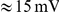 when
when 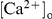 was increased from
was increased from 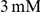 to
to 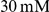 ; the rather rightward steady-state inactivation values from Amedee et al., [29] were recorded from myometrial cells exposed to
; the rather rightward steady-state inactivation values from Amedee et al., [29] were recorded from myometrial cells exposed to 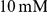
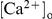 . Yamamoto [30] showed that the
. Yamamoto [30] showed that the 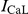 half-inactivation was left-shifted, and the I–V relationship was reduced, in the myometrial cells exposed to estradiol; in rodents, estradiol increases near term. The myometrial cells from late pregnant rats reported by Shmigol et al., [12] exhibit a leftward shift in inactivation and activation curves relative to the other reports possibly reflective of an influence of altered steroidal levels near to term. Alternatively, as the holding potential (
half-inactivation was left-shifted, and the I–V relationship was reduced, in the myometrial cells exposed to estradiol; in rodents, estradiol increases near term. The myometrial cells from late pregnant rats reported by Shmigol et al., [12] exhibit a leftward shift in inactivation and activation curves relative to the other reports possibly reflective of an influence of altered steroidal levels near to term. Alternatively, as the holding potential (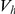 ) in Shmigol et al., [12] was
) in Shmigol et al., [12] was 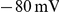 , a tentative explanation could be the additional presence of
, a tentative explanation could be the additional presence of 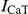 (see below) contributing to this dataset. In the model, we placed the
(see below) contributing to this dataset. In the model, we placed the 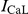 steady-state functions close to the control datasets from Yamamoto [30], which are representative of the steady-state values of
steady-state functions close to the control datasets from Yamamoto [30], which are representative of the steady-state values of 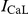 from a collection of other studies that, for clarity of presentation, are not plotted in Figure 1
[14], [33]–[35].
from a collection of other studies that, for clarity of presentation, are not plotted in Figure 1
[14], [33]–[35].
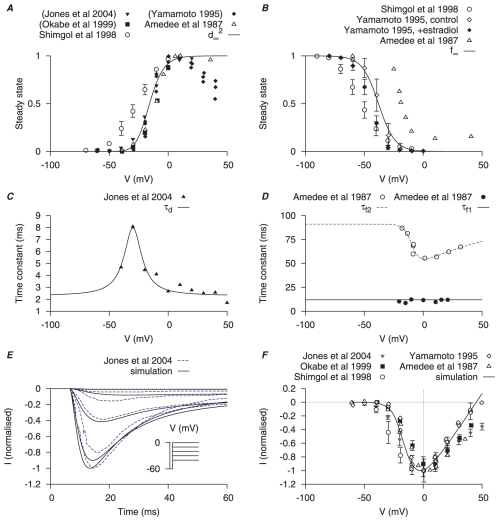
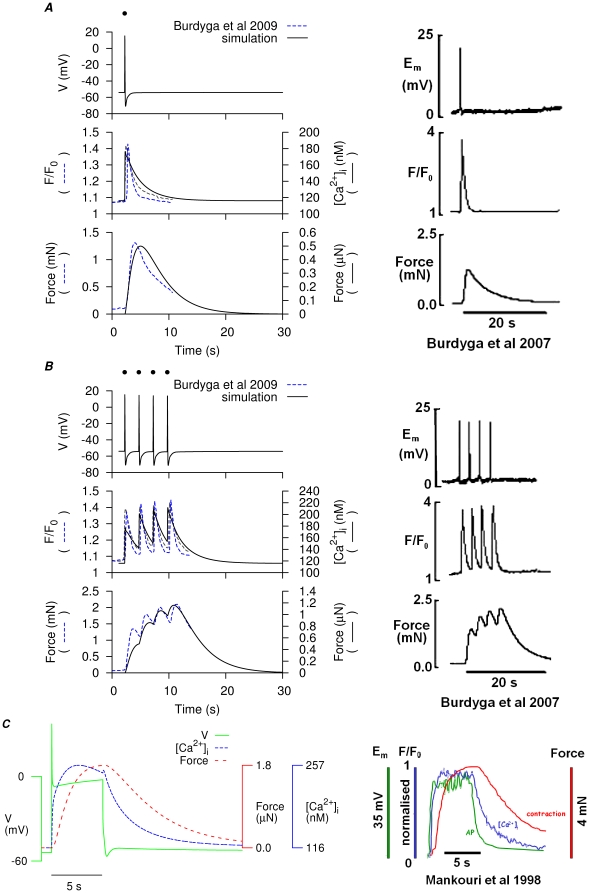
Figure 1. Myometrial 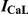 model.
model.
Properties of 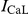 are derived from experimental data of myometrial longitudinal cells from late pregnant rat [12], [15], [29], [30], [32], [35]. A, voltage (V)-dependent activation steady-state (
are derived from experimental data of myometrial longitudinal cells from late pregnant rat [12], [15], [29], [30], [32], [35]. A, voltage (V)-dependent activation steady-state (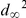 ); experimental data in brackets were extrapolated from current-voltage (I–V) relationships using the function
); experimental data in brackets were extrapolated from current-voltage (I–V) relationships using the function 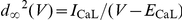 and normalized to the maximum value. B, V-dependent inactivation steady-state (
and normalized to the maximum value. B, V-dependent inactivation steady-state (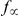 ). C, V-dependent activation time constant (
). C, V-dependent activation time constant (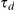 ); extracted by fitting current tracings from Jones et al.
[15]. D, V-independent fast inactivation time constant (
); extracted by fitting current tracings from Jones et al.
[15]. D, V-independent fast inactivation time constant (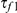 , solid circles) and V-dependent slow inactivation time constant (
, solid circles) and V-dependent slow inactivation time constant (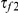 , empty circles). E, simulated voltage-clamp
, empty circles). E, simulated voltage-clamp 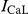 at voltage steps of
at voltage steps of 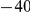 to
to 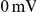 from a holding potential of
from a holding potential of 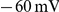 are superimposed on experimental current tracings from Jones et al., [15]; F, simulated peak I–V relationship of
are superimposed on experimental current tracings from Jones et al., [15]; F, simulated peak I–V relationship of 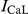 together with different experimental I–V data. In both E and F, all data are normalized to the peak current value at
together with different experimental I–V data. In both E and F, all data are normalized to the peak current value at 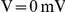 .
.
There is little information available for voltage-dependent activation time constants of myometrial 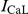 , so we proceeded to extract time constants from published
, so we proceeded to extract time constants from published 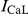 current tracings. Amedee et al., [29] and Jones et al., [15] had reported
current tracings. Amedee et al., [29] and Jones et al., [15] had reported 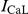 current tracings at
current tracings at 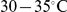 , but in Amedee et al., [29] only at a single voltage step and of poor quality for curve fitting purposes. There are other
, but in Amedee et al., [29] only at a single voltage step and of poor quality for curve fitting purposes. There are other 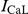 current tracings [14], [33]–[35] at room temperature but we are unaware of published
current tracings [14], [33]–[35] at room temperature but we are unaware of published 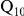 values for myometrial
values for myometrial 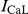 . The experiments of Jones et al., [15], performed at
. The experiments of Jones et al., [15], performed at 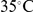 , were designed to study
, were designed to study 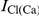 wherein
wherein 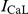 was first activated to enable plasmalemmal
was first activated to enable plasmalemmal 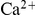 entry that, subsequently, activated a current taken to be
entry that, subsequently, activated a current taken to be 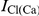 . The initial fast inward current was attributed as
. The initial fast inward current was attributed as 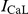 because it was blocked by nifedipine, was permeable to
because it was blocked by nifedipine, was permeable to 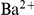 and was increased by the L-type Ca channel agonist Bay K8644. We presumed that activation of
and was increased by the L-type Ca channel agonist Bay K8644. We presumed that activation of 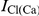 would be slower than
would be slower than 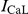 and, thus, voltage-dependent activation time constants for
and, thus, voltage-dependent activation time constants for 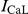 were obtained by fitting the initial few tens of milliseconds of raw data tracings, i.e. prior to peak current at each voltage step being reached, from Jones et al., [15] (Figure 1C). This assumption is backed up by the activation time constants for
were obtained by fitting the initial few tens of milliseconds of raw data tracings, i.e. prior to peak current at each voltage step being reached, from Jones et al., [15] (Figure 1C). This assumption is backed up by the activation time constants for 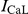 in other smooth muscles being
in other smooth muscles being 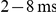 whereas that for
whereas that for 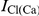 has been estimated at
has been estimated at 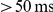 [36]. The two inactivation time constants,
[36]. The two inactivation time constants,  and
and 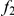 , were taken from Amedee et al., [29] (Figure 1D). The fast inactivation
, were taken from Amedee et al., [29] (Figure 1D). The fast inactivation 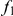 is voltage-independent at
is voltage-independent at 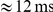 and the slow inactivation is voltage-dependent with a minimum of
and the slow inactivation is voltage-dependent with a minimum of 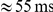 at
at 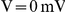 .
.
Simulated time tracings of 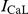 under voltage-clamp conditions and
under voltage-clamp conditions and 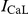 I–V relationships were compared to experimental data in Figure 1E–F. The simulated time tracings closely matched the experimental time data from Jones et al., [15];
I–V relationships were compared to experimental data in Figure 1E–F. The simulated time tracings closely matched the experimental time data from Jones et al., [15]; 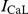 reached its peak in
reached its peak in 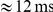 then quickly inactivated. Only the time tracings at voltage steps between
then quickly inactivated. Only the time tracings at voltage steps between 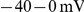 from Jones et al., [15] were used for comparison in order to minimize contamination by
from Jones et al., [15] were used for comparison in order to minimize contamination by 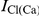 . The simulated I–V relationship further shows that
. The simulated I–V relationship further shows that 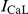 first appears at
first appears at  and peaks at
and peaks at 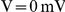 , similar to that seen experimentally [12], [15], [29], [30]. Validation of the model is also evinced by the ability to reproduce the effects of estradiol on the
, similar to that seen experimentally [12], [15], [29], [30]. Validation of the model is also evinced by the ability to reproduce the effects of estradiol on the 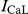 I–V relationships reported by Yamamoto [30]. Herein, the effect on the simulated I–V relationship of experimentally observed estradiol-induced changes in current were examined. The model reproduced the estradiol-mediated leftward shift in inactivation, and the reduction in I–V amplitude, from a
I–V relationships reported by Yamamoto [30]. Herein, the effect on the simulated I–V relationship of experimentally observed estradiol-induced changes in current were examined. The model reproduced the estradiol-mediated leftward shift in inactivation, and the reduction in I–V amplitude, from a 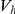 of
of 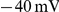 (Figure S1).
(Figure S1).
Peak 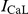 currents in myometrial cells of late pregnant rat have been reported to be
currents in myometrial cells of late pregnant rat have been reported to be 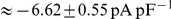 (
(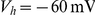 , Jones et al., [15]) and
, Jones et al., [15]) and 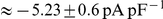 (
(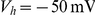 , Okabe et al., [32]) at
, Okabe et al., [32]) at 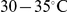 . This gives a maximal conductance (
. This gives a maximal conductance ( ) of
) of 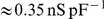 for modeling the ionic current data.
for modeling the ionic current data.
With 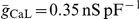 in the later development of the USMC action potential simulations, the rate of rise of an AP was
in the later development of the USMC action potential simulations, the rate of rise of an AP was 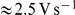 which was less than the reported experimental range of
which was less than the reported experimental range of 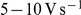 [37]. Thus, it is necessary to set
[37]. Thus, it is necessary to set 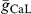 at a higher value at
at a higher value at 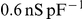 .
.
It is possible that the reported 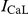 current density may represent the lower limits in late pregnant rat myometrial cells given that (i) the expression of mRNA encoding L-type Ca channel protein subunits increases before labor in rat myometrial cells [38]–[40] and the protein expression of the pore forming
current density may represent the lower limits in late pregnant rat myometrial cells given that (i) the expression of mRNA encoding L-type Ca channel protein subunits increases before labor in rat myometrial cells [38]–[40] and the protein expression of the pore forming 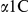 subunit is regulated by ratio of sex hormones [41]; (ii) the
subunit is regulated by ratio of sex hormones [41]; (ii) the 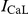 current density may be underestimated by in vitro experimental conditions:
current density may be underestimated by in vitro experimental conditions: 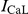 current density in isolated cells diminishes with time [11], [15]. Myometrial
current density in isolated cells diminishes with time [11], [15]. Myometrial 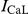 also showed calcium-dependent inactivation [26], [29]. This is described by a Hill equation with
also showed calcium-dependent inactivation [26], [29]. This is described by a Hill equation with 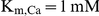 and a Hill coefficient of 4 in the whole USMC cell model.
and a Hill coefficient of 4 in the whole USMC cell model.
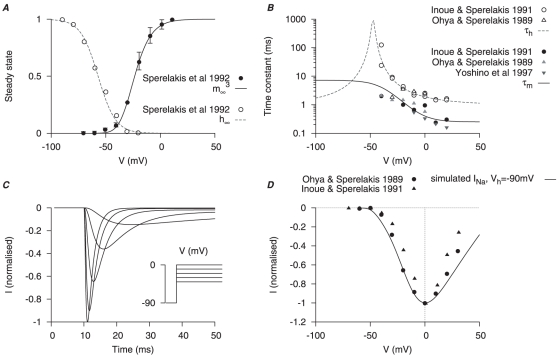
Sodium current – 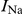
Mathematical descriptions of the biophysical characteristics of this current are given in Appendix S1 (equations 20–27).
Modeling of 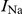 is accomplished using data from myometrial cells of late pregnant rats or humans recorded at room temperature [14], [33], [34], [42].
is accomplished using data from myometrial cells of late pregnant rats or humans recorded at room temperature [14], [33], [34], [42]. 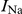 first appears at
first appears at 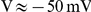 and the peak I–V relationship occurs between
and the peak I–V relationship occurs between 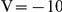 to
to 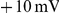 . Raw data current tracings showed that
. Raw data current tracings showed that 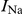 reached its peak of activation within
reached its peak of activation within 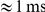 and almost completely inactivated after
and almost completely inactivated after 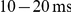 [14], [33], [34], [42].
[14], [33], [34], [42].
The equation for 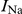 incorporates an activation gating variable (
incorporates an activation gating variable ( ) and an inactivation gating variable (
) and an inactivation gating variable (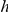 ). Steady-state values for activation and inactivation are shown in Figure 2A. The time constants of activation and inactivation (Figure 2B) were each obtained by fitting the raw data current tracings from the literature [14], [33], [34], [42]. Simulated traces of
). Steady-state values for activation and inactivation are shown in Figure 2A. The time constants of activation and inactivation (Figure 2B) were each obtained by fitting the raw data current tracings from the literature [14], [33], [34], [42]. Simulated traces of 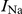 current under voltage-clamp conditions presented in Figure 2C show dynamic profiles similar to the raw data [14], [33], [34], [42]: at voltage steps of
current under voltage-clamp conditions presented in Figure 2C show dynamic profiles similar to the raw data [14], [33], [34], [42]: at voltage steps of 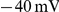 to
to 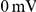 , from a
, from a 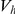 of
of 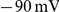 ,
, 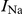 reached its peak in
reached its peak in 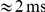 then quickly inactivated within
then quickly inactivated within 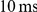 . The reported peak currents for
. The reported peak currents for 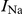 range from
range from 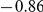 to
to 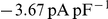 [33], [34], [42], which gives a maximal conductance range
[33], [34], [42], which gives a maximal conductance range 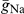 of
of 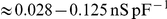 . Simulated I–V relationship of
. Simulated I–V relationship of 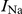 matched to the experimental data as shown in Figure 2D
[14], [34], [42].
matched to the experimental data as shown in Figure 2D
[14], [34], [42].
Figure 2. Myometrial 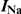 model.
model.
Properties of 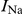 are derived from experimental data of myometrial longitudinal cells [14], [33], [34], [42] from late pregnant rats. A, V-dependent steady-states of activation (
are derived from experimental data of myometrial longitudinal cells [14], [33], [34], [42] from late pregnant rats. A, V-dependent steady-states of activation (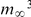 ) and inactivation (
) and inactivation (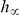 ); B, V-dependent time constants of activation (
); B, V-dependent time constants of activation (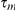 ) and inactivation (
) and inactivation (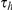 ). In both A and B, solid and empty circles are experimental data for activation and inactivation respectively. C, simulated
). In both A and B, solid and empty circles are experimental data for activation and inactivation respectively. C, simulated 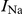 at voltage steps of
at voltage steps of 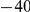 to
to 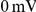 from a
from a 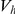 of
of 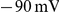 ; D, simulated peak I–V relationship of
; D, simulated peak I–V relationship of 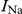 at
at 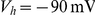 and experimental I–V data. In both C and D, all data are normalized to the peak current value at
and experimental I–V data. In both C and D, all data are normalized to the peak current value at 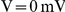 .
.
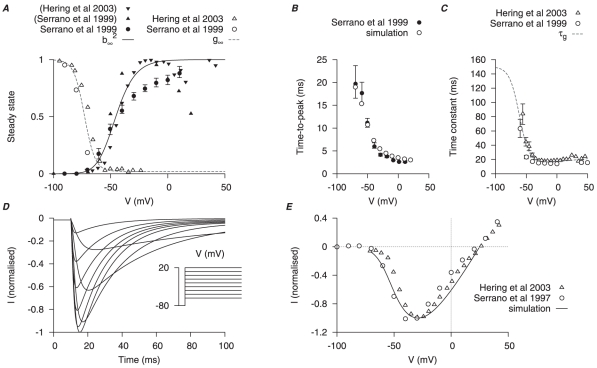
T-type Calcium current – 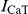
Mathematical description of the biophysical characteristics of this current are given in Appendix S1 (equations 28–34).
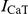 has been reported in human myometrial cells [13], [14], [28], [37], [42]. Moreover: (i) Ohkubo et al., [40] showed that the expressions of mRNA encoding for the
has been reported in human myometrial cells [13], [14], [28], [37], [42]. Moreover: (i) Ohkubo et al., [40] showed that the expressions of mRNA encoding for the 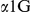 and
and 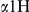 protein subunits of the T-type calcium channel were gestationally regulated in rat myometrial cells; (ii) detailed electrophysiological data of cells expressing rat
protein subunits of the T-type calcium channel were gestationally regulated in rat myometrial cells; (ii) detailed electrophysiological data of cells expressing rat 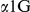 /Cav3.1 are available [43], [44]; and (iii) spontaneous contractions in myometrial tissue strips from late pregnant rats were markedly inhibited by the putative T-type calcium channel blockers mibefradil, NNC 55-0396 (a non-hydrolyzable analogue of mibefradil) and
/Cav3.1 are available [43], [44]; and (iii) spontaneous contractions in myometrial tissue strips from late pregnant rats were markedly inhibited by the putative T-type calcium channel blockers mibefradil, NNC 55-0396 (a non-hydrolyzable analogue of mibefradil) and 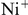 [45], [46]. Therefore, we developed a model of
[45], [46]. Therefore, we developed a model of 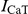 electrophysiological characteristics from the rat
electrophysiological characteristics from the rat 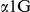 /Cav3.1 clonal expression cell data recorded at room temperature [43], [44] adjusted to the current density of human myometrial cell
/Cav3.1 clonal expression cell data recorded at room temperature [43], [44] adjusted to the current density of human myometrial cell 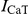 [13], [18], [28]. It is note-worthy that the activation and inactivation steady-state values, and the I–V relationships, are similar between these different datasets.
[13], [18], [28]. It is note-worthy that the activation and inactivation steady-state values, and the I–V relationships, are similar between these different datasets.
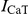 first appears at
first appears at 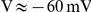 , the peak I–V relationship occurs between
, the peak I–V relationship occurs between 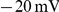 and
and 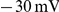 , and published raw data current tracings indicate a fast activation but with inactivation temporal profiles varying between
, and published raw data current tracings indicate a fast activation but with inactivation temporal profiles varying between 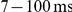 [13], [18], [28], [43], [44], [47, ]
Figure S2. This last may be influenced by the different external divalent cation concentrations used between experimental conditions (Figure S3). The datasets with the fastest inactivation profiles expected of
[13], [18], [28], [43], [44], [47, ]
Figure S2. This last may be influenced by the different external divalent cation concentrations used between experimental conditions (Figure S3). The datasets with the fastest inactivation profiles expected of 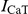 had the highest divalent cation concentrations and, indeed, were those attributed to Serrano et al., [43], Hering et al., [44] and Blanks et al., [13].
had the highest divalent cation concentrations and, indeed, were those attributed to Serrano et al., [43], Hering et al., [44] and Blanks et al., [13].
The equation for 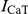 incorporates an activation gating variable (
incorporates an activation gating variable (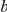 ) and an inactivation gating variable (
) and an inactivation gating variable (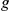 ). Steady-state values for activation and inactivation are shown in Figure 3A. A function is chosen for activation time constants to fit the time-to-peak experimental data (Figure 3B). The time constant of inactivation is shown in Figure 3C. Simulated
). Steady-state values for activation and inactivation are shown in Figure 3A. A function is chosen for activation time constants to fit the time-to-peak experimental data (Figure 3B). The time constant of inactivation is shown in Figure 3C. Simulated 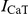 tracings under voltage-clamp conditions and I–V relationships are shown in Figure 3D and Figure 3E respectively and are compared to experimental data from Serrano et al., [43] and Hering et al., [44]. In Figure 3E,
tracings under voltage-clamp conditions and I–V relationships are shown in Figure 3D and Figure 3E respectively and are compared to experimental data from Serrano et al., [43] and Hering et al., [44]. In Figure 3E, 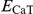 is fixed at
is fixed at 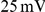 to match the experimental values in Serrano et al., [43] and Hering et al., [44]. The reported peak current for
to match the experimental values in Serrano et al., [43] and Hering et al., [44]. The reported peak current for 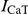 is
is 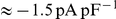 at
at 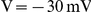 from a
from a 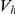 of
of 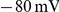 in human myometrial cells [13], which gives a maximal conductance
in human myometrial cells [13], which gives a maximal conductance 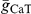 of
of 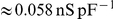 . For incorporation of the
. For incorporation of the 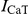 model in the later development of the USMC AP simulations,
model in the later development of the USMC AP simulations, 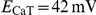 so as to mimic that of Blanks et al., [13].
so as to mimic that of Blanks et al., [13].
Figure 3. Myometrial 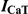 model.
model.
Properties of 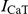 are derived primarily from experimental data of Serrano et al., [43] and Hering et al., [44]. A, V-dependent steady-states of activation (
are derived primarily from experimental data of Serrano et al., [43] and Hering et al., [44]. A, V-dependent steady-states of activation (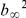 ) and inactivation (
) and inactivation (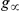 ); experimental data in brackets were extrapolated from the published I–V relationships and normalized to the maximum value. B, superimposed simulated and experimental time-to-peak of
); experimental data in brackets were extrapolated from the published I–V relationships and normalized to the maximum value. B, superimposed simulated and experimental time-to-peak of 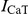 at different V stepped from
at different V stepped from 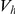 of
of 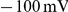 ; a function for the V-dependent activation time constant is chosen so that the simulated time-to-peak (empty circles) matched the experimental data (solid circle). C, V-dependent inactivation time constant (
; a function for the V-dependent activation time constant is chosen so that the simulated time-to-peak (empty circles) matched the experimental data (solid circle). C, V-dependent inactivation time constant (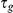 ). D, simulated
). D, simulated 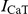 at voltage steps of
at voltage steps of 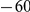 to
to 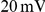 from a
from a 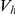 of
of 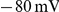 ; E, simulated peak I–V relationship of
; E, simulated peak I–V relationship of 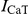 and experimental I–V data. In both D and E, all data are normalized to the peak current value at
and experimental I–V data. In both D and E, all data are normalized to the peak current value at 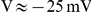 .
.
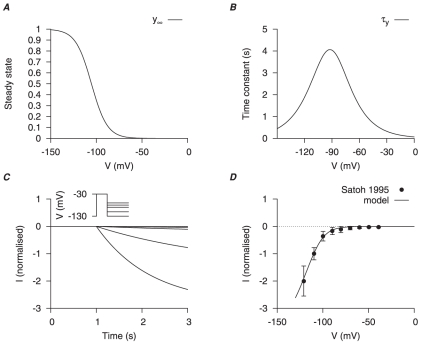
Hyperpolarization-activated current – 
Mathematical description of the biophysical characteristics of this current are given in Appendix S1 (equations 35–39).
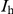 has been reported in myometrial cells of pregnant rats [48], [49]. Activated by hyperpolarization beyond resting membrane potential,
has been reported in myometrial cells of pregnant rats [48], [49]. Activated by hyperpolarization beyond resting membrane potential, 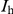 first appears at
first appears at 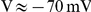 from a
from a 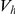 of
of 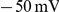 . In the voltage-clamp experiments, activation of
. In the voltage-clamp experiments, activation of 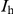 is slow, taking
is slow, taking 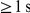 , and it does not inactivate. It is more permeable to
, and it does not inactivate. It is more permeable to 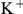 ions than
ions than 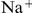 ions, is blocked by
ions, is blocked by 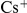 , and has a reversal potential (
, and has a reversal potential (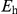 ) of
) of 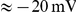 .
.
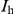 was modeled at room temperature to
was modeled at room temperature to 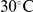 using myometrial cells of pregnant rats [48], [49]. Our model of
using myometrial cells of pregnant rats [48], [49]. Our model of 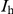 biophysical characteristics was first developed with the data of [49] with an activation gating variable (
biophysical characteristics was first developed with the data of [49] with an activation gating variable (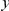 ) and
) and 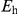 approximated by the Goldman-Hodgkin-Katz (GHK) equation with a permeability ratio
approximated by the Goldman-Hodgkin-Katz (GHK) equation with a permeability ratio  . The half-activation was adjusted and the activation time constant was corrected with the reported
. The half-activation was adjusted and the activation time constant was corrected with the reported 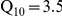 [49] in order to match the experimental I–V relationship of Satoh [48] (Figure 4). The current density was
[49] in order to match the experimental I–V relationship of Satoh [48] (Figure 4). The current density was 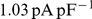 at
at 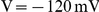 from a
from a 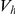 of
of  [48], which gives a maximum conductance of
[48], which gives a maximum conductance of 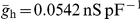 .
.
Figure 4. Myometrial 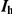 model.
model.
Properties of 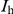 are derived from experimental data of Okabe et al., [49] in rat circular myometrial cells and adjusted to experimental data of longitudinal cells [48]. A, V-dependent activation steady-state (
are derived from experimental data of Okabe et al., [49] in rat circular myometrial cells and adjusted to experimental data of longitudinal cells [48]. A, V-dependent activation steady-state (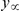 ); B, V-dependent activation time constant (
); B, V-dependent activation time constant (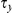 ). C, simulated voltage-clamp
). C, simulated voltage-clamp 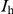 at voltage steps of
at voltage steps of 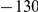 to
to 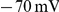 from a holding potential of
from a holding potential of 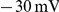 . D, simulated I–V relationship of
. D, simulated I–V relationship of 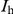 and experimental I–V data Satoh [48]. In both C and D, all data are normalized to the current value at
and experimental I–V data Satoh [48]. In both C and D, all data are normalized to the current value at 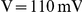 .
.
Potassium Currents
We have considered the electrophysiological data of several major types of potassium currents described from myometrial cells of rat and human myometrium: (two) voltage-gated potassium currents (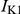 and
and 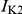 ), A-type transient potassium current (
), A-type transient potassium current (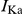 ) and
) and 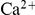 -activated potassium currents (
-activated potassium currents (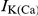 ). The kinetics of individual potassium currents are described in detail below; their current densities are discussed in the later section concerned with total potassium current.
). The kinetics of individual potassium currents are described in detail below; their current densities are discussed in the later section concerned with total potassium current.
Voltage-dependent potassium currents – 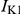 and
and 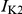
Mathematical descriptions of the biophysical characteristics of these currents are given in Appendix S1 (equations 40–58).
Myometrial potassium currents have been roughly categorized by their inactivation properties and sensitivity to pharmacological blockers of varying channel subtype specificity [17], [19]. At least two different types of potassium currents with rectifying properties were found in myometrial cells of late pregnant rats [17] and humans [19]; their dynamics were very slow compared to other membrane currents in myometrial cells. These potassium currents were separated as C1 and C2 components of the total potassium current in Wang et al., [17] and as 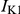 and
and 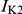 in Knock et al., [19].
in Knock et al., [19].
C1 and 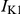 , and C2 and
, and C2 and 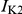 have similar voltage-dependent kinetics. Both C1 and
have similar voltage-dependent kinetics. Both C1 and 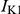 first appear at
first appear at 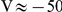 to
to 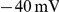 and with half-inactivation (
and with half-inactivation (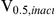 ) between
) between 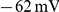 to
to 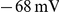 . Both C2 and
. Both C2 and 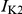 first appear at
first appear at 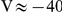 to
to 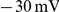 and with
and with 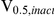 between
between 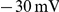 to
to 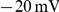 . Wang et al., [17] distinguished between C1 and C2 by their activation thresholds and inactivation properties whereas Knock et al., [19] separated
. Wang et al., [17] distinguished between C1 and C2 by their activation thresholds and inactivation properties whereas Knock et al., [19] separated 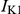 and
and 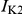 by these properties and current sensitivities to 4-aminopyridine (4-AP) and TEA. As such, we developed mathematical models predominantly based upon the more abundant information of electrophysiological characteristics of human myometrial
by these properties and current sensitivities to 4-aminopyridine (4-AP) and TEA. As such, we developed mathematical models predominantly based upon the more abundant information of electrophysiological characteristics of human myometrial 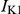 and
and 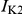 and complemented these with data on rat myometrial C1 and C2 of Wang et al., [17] at room temperature.
and complemented these with data on rat myometrial C1 and C2 of Wang et al., [17] at room temperature.
The equations of 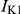 (not to be confused with the myocardial inward rectifying potassium current commonly designated also as
(not to be confused with the myocardial inward rectifying potassium current commonly designated also as 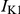 [50]) and
[50]) and 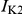 each incorporate three gating variables: an activation gating variable (
each incorporate three gating variables: an activation gating variable (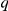 for
for 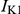 ;
; 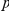 for
for 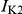 ), a fast inactivation gating variable (
), a fast inactivation gating variable (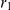 for
for 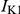 ;
; 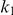 for
for 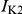 ) and a slow inactivation gating variable (
) and a slow inactivation gating variable (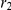 for
for 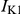 ;
; 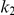 for
for 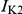 ). The activation and inactivation steady-state values were used as reported from Wang et al., [17] with the assumption that both currents were completely inactivated (Figure 5A, 6A, see below). For
). The activation and inactivation steady-state values were used as reported from Wang et al., [17] with the assumption that both currents were completely inactivated (Figure 5A, 6A, see below). For 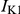 , voltage-dependent steady-state of inactivation (
, voltage-dependent steady-state of inactivation (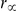 ) is formulated with the reported half-inactivation of
) is formulated with the reported half-inactivation of 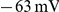 and slope factor of
and slope factor of 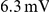 and, for
and, for 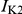 , voltage-dependent steady-state of inactivation (
, voltage-dependent steady-state of inactivation (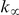 ) is assessed with the reported half-inactivation of
) is assessed with the reported half-inactivation of 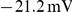 ) and slope factor of
) and slope factor of 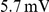 reported by Wang et al., [17].
reported by Wang et al., [17].
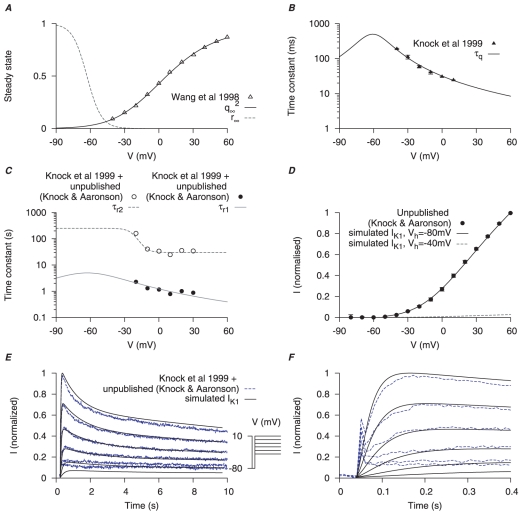
Figure 5. Myometrial 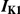 model.
model.
Steady-state properties of 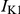 are derived from experimental data of myometrial longitudinal cells in late pregnant rats [17]; the kinetics are from myometrial cells in late pregnant women from Knock et al., [19] and Knock G & Aaronson P (personal communication, including unpublished time tracings - see Figure S4). A, V-dependent steady-states of activation (
are derived from experimental data of myometrial longitudinal cells in late pregnant rats [17]; the kinetics are from myometrial cells in late pregnant women from Knock et al., [19] and Knock G & Aaronson P (personal communication, including unpublished time tracings - see Figure S4). A, V-dependent steady-states of activation (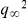 ) and inactivation (
) and inactivation (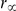 ). B, V-dependent activation time constants (
). B, V-dependent activation time constants (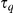 ). C, V-dependent fast (
). C, V-dependent fast (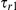 ) and slow (
) and slow (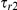 ) inactivation time constants. The experimental fast (solid circles) and slow (empty circles) inactivation time constants were extracted by fitting voltage-clamp time tracings averaged from five cells (1 published and 4 unpublished with the average values labeled as ‘Knock et al 1999+unpublished (Knock & Aaronson)’ in the figure). D, simulated I–V relationship of
) inactivation time constants. The experimental fast (solid circles) and slow (empty circles) inactivation time constants were extracted by fitting voltage-clamp time tracings averaged from five cells (1 published and 4 unpublished with the average values labeled as ‘Knock et al 1999+unpublished (Knock & Aaronson)’ in the figure). D, simulated I–V relationship of 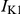 from holding potentials of
from holding potentials of 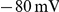 and
and 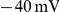 with
with 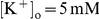 and
and 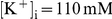 ; all values are normalized to the peak current at
; all values are normalized to the peak current at 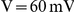 from
from 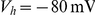 . E, simulated time tracings and averaged raw data of
. E, simulated time tracings and averaged raw data of 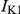 at voltage steps of
at voltage steps of 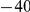 to
to 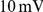 from
from 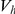 of
of 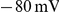 ; both simulated and experimental currents are normalized to the peak current at
; both simulated and experimental currents are normalized to the peak current at 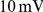 ; F, enlarged E showing activation of
; F, enlarged E showing activation of 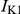 during the first few hundred milli-seconds.
during the first few hundred milli-seconds.
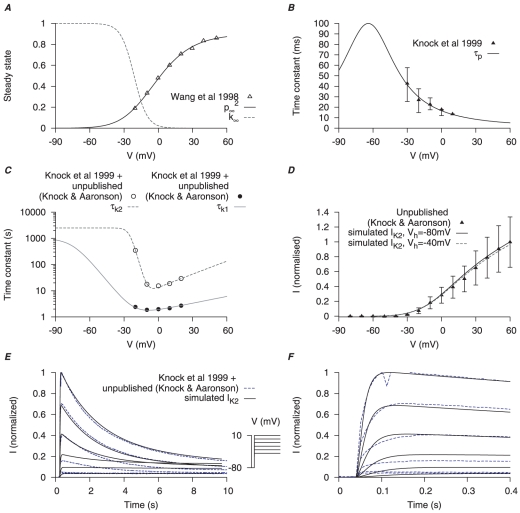
Figure 6. Myometrial 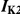 model.
model.
Steady-state properties of 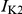 are derived from experimental data of myometrial longitudinal cells in late pregnant rats [17]; the kinetics are extracted from raw data tracings from myometrial cells of late pregnant women from Knock et al., [19] and Knock G & Aaronson P (personal communication, including unpublished time tracings - see Figure S5). A, V-dependent steady-states of activation (
are derived from experimental data of myometrial longitudinal cells in late pregnant rats [17]; the kinetics are extracted from raw data tracings from myometrial cells of late pregnant women from Knock et al., [19] and Knock G & Aaronson P (personal communication, including unpublished time tracings - see Figure S5). A, V-dependent steady-states of activation (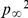 ) and inactivation (
) and inactivation (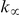 ). B, V-dependent activation time constants (
). B, V-dependent activation time constants (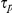 ) C, V-dependent fast (
) C, V-dependent fast (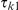 ) and slow (
) and slow (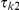 ) inactivation time constants. The experimental fast (solid circles) and slow (empty circles) inactivation time constants were extracted from voltage-clamp time tracings averaged from four cells (1 published and 3 unpublished with the average values labeled as ‘Knock et al 1999+unpublished (Knock & Aaronson)’ in the figure. D, simulated I–V relationship of
) inactivation time constants. The experimental fast (solid circles) and slow (empty circles) inactivation time constants were extracted from voltage-clamp time tracings averaged from four cells (1 published and 3 unpublished with the average values labeled as ‘Knock et al 1999+unpublished (Knock & Aaronson)’ in the figure. D, simulated I–V relationship of 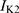 from a holding potential of
from a holding potential of 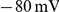 and
and 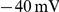 with
with 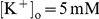 and
and 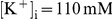 ; all values are normalized to the peak current at
; all values are normalized to the peak current at 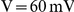 from
from 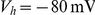 . E, simulated time tracings of
. E, simulated time tracings of 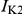 at voltage steps of
at voltage steps of 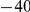 to
to 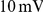 from a holding potential of
from a holding potential of 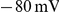 ; both simulated and experimental currents are normalized to the peak current at
; both simulated and experimental currents are normalized to the peak current at 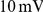 ; F, enlarged E showing activation of
; F, enlarged E showing activation of 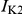 during the first few hundred milli-seconds.
during the first few hundred milli-seconds.
Activation time constants of 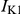 and
and 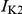 currents were from Knock et al., [19] (Figure 5B, 6B) for
currents were from Knock et al., [19] (Figure 5B, 6B) for 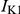 and
and 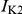 respectively. However, Knock et al., [19] reported the inactivation time constants of
respectively. However, Knock et al., [19] reported the inactivation time constants of 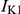 and
and 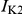 currents elicited at only one voltage step (
currents elicited at only one voltage step (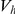 of
of 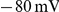 stepped to
stepped to 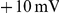 ): inactivation of
): inactivation of 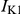 was described as a double exponential and a constant whereas inactivation of
was described as a double exponential and a constant whereas inactivation of 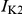 was described as a monoexponential and a constant. Their inclusion of constant values was due to the currents not inactivating during the course of the 10 sec voltage pulse. However, using these values it was impossible to simulate the published raw current tracings of the voltage-clamp protocols for
was described as a monoexponential and a constant. Their inclusion of constant values was due to the currents not inactivating during the course of the 10 sec voltage pulse. However, using these values it was impossible to simulate the published raw current tracings of the voltage-clamp protocols for 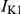 and
and 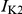 (Figure 4 in Knock et al., [19]). We therefore sought to extract a more complete set of inactivation time constants that encompassed currents elicited at each voltage step of the protocols listed in Knock et al., [19]. This was accomplished by examining the raw data tracings kindly supplied by Drs Greg Knock and Phil Aaronson (Kings College London). The
(Figure 4 in Knock et al., [19]). We therefore sought to extract a more complete set of inactivation time constants that encompassed currents elicited at each voltage step of the protocols listed in Knock et al., [19]. This was accomplished by examining the raw data tracings kindly supplied by Drs Greg Knock and Phil Aaronson (Kings College London). The 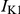 or
or 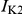 currents in each of these datasets were produced in
currents in each of these datasets were produced in 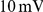 steps between
steps between 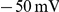 and
and 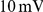 from a
from a 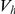 of
of 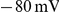 . Averaging the
. Averaging the 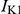 (5 cells, Figure S4) or
(5 cells, Figure S4) or 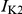 (4 cells, Figure S5) at each step enabled a calculation of the voltage-dependent inactivation time constants (Figure 5C and 6C for
(4 cells, Figure S5) at each step enabled a calculation of the voltage-dependent inactivation time constants (Figure 5C and 6C for 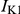 and
and 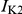 respectively). The inactivations of
respectively). The inactivations of 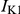 and
and 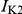 were described by a fast and a slow time constants. Moreover, we removed the need for a constant value used by Knock et al., [19] by assuming that each current was completely inactivated. This, in fact, was reported to be the case by Knock et al., [19] when they extended the experimental voltage pulses beyond 10 seconds. Satisfactory simulation of the published I–V curves and raw current data was now possible. Simulated I–V relationships of
were described by a fast and a slow time constants. Moreover, we removed the need for a constant value used by Knock et al., [19] by assuming that each current was completely inactivated. This, in fact, was reported to be the case by Knock et al., [19] when they extended the experimental voltage pulses beyond 10 seconds. Satisfactory simulation of the published I–V curves and raw current data was now possible. Simulated I–V relationships of 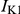 and
and 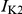 (Figure 5D, 6D) stepping from two different
(Figure 5D, 6D) stepping from two different 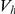 ,
, 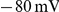 and
and 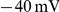 , showed that while
, showed that while 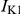 was mostly inactivated with
was mostly inactivated with 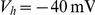 ,
, 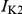 remained available. From the simulated current tracings (Figure 5E, 6E) both
remained available. From the simulated current tracings (Figure 5E, 6E) both 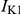 and
and 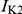 took more than
took more than 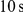 to inactivate but
to inactivate but  was inactivated faster than
was inactivated faster than 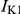 . Current densities of
. Current densities of 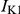 and
and 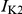 are discussed in the section of total potassium current.
are discussed in the section of total potassium current.
A-type transient potassium current – 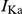
Mathematical descriptions of the biophysical characteristics of this current are given in Appendix S1 (equations 59–65).
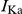 is a 4-AP sensitive, TEA-insensitive potassium current with very fast activation and inactivation kinetics. It is found in myometrial cells of both rat and human [27], [51].
is a 4-AP sensitive, TEA-insensitive potassium current with very fast activation and inactivation kinetics. It is found in myometrial cells of both rat and human [27], [51].
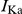 is first evident at
is first evident at 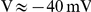 and raw data tracings show
and raw data tracings show 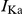 peak activation within
peak activation within 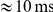 and almost completely inactivated within
and almost completely inactivated within 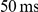 [27], [51]. In human myometrial cells,
[27], [51]. In human myometrial cells, 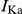 has a half-inactivation of
has a half-inactivation of 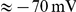 and a slope factor of
and a slope factor of 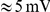 [19], [51]. These characteristics are very similar to the transient potassium current in myometrial cells isolated from immature rats [52] which were inhibited by
[19], [51]. These characteristics are very similar to the transient potassium current in myometrial cells isolated from immature rats [52] which were inhibited by 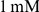 of 4-AP and were measured within
of 4-AP and were measured within 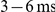 of the voltage step; it has a half-inactivation of
of the voltage step; it has a half-inactivation of 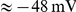 and a slope factor of
and a slope factor of 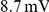 .
.
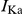 is modeled from data of myometrial cells from pregnant rats and humans recorded at room temperature. The model of
is modeled from data of myometrial cells from pregnant rats and humans recorded at room temperature. The model of 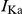 incorporates one activation gating variable (
incorporates one activation gating variable ( ) and an inactivation gating variable (
) and an inactivation gating variable ( ). Steady-state values for activation and inactivation are shown in Figure 7A. Voltage-dependent steady-state of inactivation
). Steady-state values for activation and inactivation are shown in Figure 7A. Voltage-dependent steady-state of inactivation 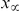 is formulated with the reported half-inactivation of
is formulated with the reported half-inactivation of 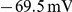 and slope factor of
and slope factor of 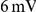 reported by Knock et al., [19]. The activation time constants were chosen to fit the time-to-peak experimental data (Figure 7B). Experimental values of steady-state and time-to-peak are kindly provided by Drs Greg Knock and Phil Aaronson (Kings College London). The inactivation time constants were obtained by fitting the raw data current tracings from Knock et al., [51] and the simulated time tracings showed dynamics similar to the experimental time tracings (Figure 7C). The simulated I–V relationship shows that
reported by Knock et al., [19]. The activation time constants were chosen to fit the time-to-peak experimental data (Figure 7B). Experimental values of steady-state and time-to-peak are kindly provided by Drs Greg Knock and Phil Aaronson (Kings College London). The inactivation time constants were obtained by fitting the raw data current tracings from Knock et al., [51] and the simulated time tracings showed dynamics similar to the experimental time tracings (Figure 7C). The simulated I–V relationship shows that 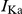 first appears at
first appears at 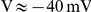 , similar to experimental data [51] (Figure 7D). Current density of
, similar to experimental data [51] (Figure 7D). Current density of 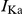 is discussed in the section of total potassium current.
is discussed in the section of total potassium current.
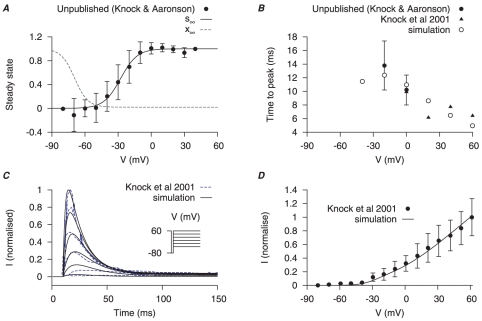
Figure 7. Myometrial  model.
model.
Properties of 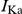 are derived from experimental data of myometrial cells from Knock et al., [19], [51] and Knock G & Aaronson P (unpublished data, personal communication) in late pregnant women. Functions for V-dependent activation and inactivation time constants are chosen so that the simulated time-to-peak, current tracings and I–V relationship matched the experimental data. A, V-dependent steady-states of activation (
are derived from experimental data of myometrial cells from Knock et al., [19], [51] and Knock G & Aaronson P (unpublished data, personal communication) in late pregnant women. Functions for V-dependent activation and inactivation time constants are chosen so that the simulated time-to-peak, current tracings and I–V relationship matched the experimental data. A, V-dependent steady-states of activation (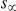 ) and inactivation (
) and inactivation (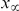 ). B, simulated (empty points) and experimental (solid points) time-to-peak of
). B, simulated (empty points) and experimental (solid points) time-to-peak of 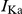 at different V stepped from a
at different V stepped from a 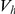 of
of 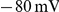 . C, simulated voltage-clamp
. C, simulated voltage-clamp 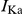 at voltage steps of
at voltage steps of 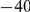 to
to 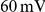 from a holding potential of
from a holding potential of 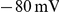 are superimposed on experimental current tracings from Knock et al., [51]; F, simulated peak I–V relationship of
are superimposed on experimental current tracings from Knock et al., [51]; F, simulated peak I–V relationship of 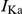 and experimental I–V data. In both E and F, all data are normalized to the peak current value at
and experimental I–V data. In both E and F, all data are normalized to the peak current value at 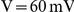 .
.
Calcium-activation potassium current – 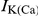
Mathematical descriptions of the biophysical characteristics of this current are given in Appendix S1 (equations 66–78).
Calcium-activated potassium currents (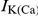 ) have been suggested to play important roles in suppressing the excitability of smooth muscle cells especially those in the vasculature. In myometrial cells
) have been suggested to play important roles in suppressing the excitability of smooth muscle cells especially those in the vasculature. In myometrial cells 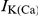 is under complex gestational-mediated regulation: the large conductance
is under complex gestational-mediated regulation: the large conductance 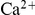 -activated
-activated 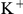 channels (termed
channels (termed 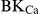 channel) subunit compositions and current density are diminished near to term. As such, although
channel) subunit compositions and current density are diminished near to term. As such, although 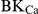 channels have been a focus of much interest in the myometrium [16], [17], [19], [53]–[62], detailed biophysical information on
channels have been a focus of much interest in the myometrium [16], [17], [19], [53]–[62], detailed biophysical information on 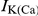 whole cell current is rather restricted.
whole cell current is rather restricted.
When detected in myometrial whole cell recordings, 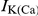 was distinctly noisy and its activation was almost instantaneous [17], [27]. From the reported recordings of
was distinctly noisy and its activation was almost instantaneous [17], [27]. From the reported recordings of 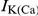 in myometrial cells by Khan et al., [16], [61], [62], Wang et al., [17] and Noble et al., [20] many of the biophysical parameters required to model complete ion current characteristics are absent. Therefore, a biophysical quantification of the
in myometrial cells by Khan et al., [16], [61], [62], Wang et al., [17] and Noble et al., [20] many of the biophysical parameters required to model complete ion current characteristics are absent. Therefore, a biophysical quantification of the 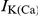 current is developed from experimental whole cell electrophysiological data obtained at room temperature from cloned mammalian smooth muscle
current is developed from experimental whole cell electrophysiological data obtained at room temperature from cloned mammalian smooth muscle  (pore-forming) and
(pore-forming) and 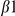 (regulatory) subunits of
(regulatory) subunits of 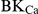 subsequently expressed in Xenopus laevis oocytes [63], [64]. The current densities of
subsequently expressed in Xenopus laevis oocytes [63], [64]. The current densities of 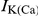 in the model are adjusted to replicate published human myometrial cell data [65], [66].
in the model are adjusted to replicate published human myometrial cell data [65], [66].
We assumed that the transmembrane 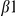 subunits were separately regulated from the pore-forming
subunits were separately regulated from the pore-forming  subunits and, therefore, two subtypes of
subunits and, therefore, two subtypes of 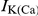 were developed: one where
were developed: one where 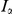 reflects an
reflects an 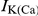 consisting of
consisting of  subunits; another where
subunits; another where 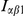 represents an
represents an 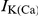 consisting of
consisting of  and
and 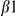 subunits; the total
subunits; the total 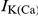 is then taken as the sum of
is then taken as the sum of 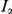 and
and 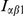 . This also enabled investigation of the effects of changing voltage- and calcium-sensitivities of
. This also enabled investigation of the effects of changing voltage- and calcium-sensitivities of 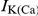 .
.
The conductances of 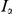 and
and 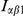 are each modeled by an activation gating variable (
are each modeled by an activation gating variable (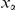 for
for 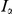 ;
; 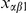 for
for 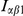 ). The half-activation and the corresponding gating charge were functions of
). The half-activation and the corresponding gating charge were functions of 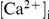 (Figure 8A); the simulated activation steady-states in comparison to the experimental values at different
(Figure 8A); the simulated activation steady-states in comparison to the experimental values at different 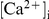 [63], [64] are shown in Figure 8B and the activation time constants in Figure 8C. A ratio of
[63], [64] are shown in Figure 8B and the activation time constants in Figure 8C. A ratio of 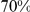
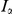 to
to 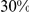
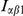 was found to produce the best fit of myometrial cell experimental I–V relationships [65], [66]. Using estimates of resting and peak global
was found to produce the best fit of myometrial cell experimental I–V relationships [65], [66]. Using estimates of resting and peak global 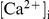 in myometrial cells of
in myometrial cells of 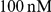 and
and 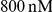 respectively [67], the simulated I–V curves showed that high
respectively [67], the simulated I–V curves showed that high 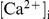 increased
increased 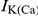 at positive membrane potentials (Figure 8D). Current density of
at positive membrane potentials (Figure 8D). Current density of 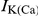 is discussed in the section of total potassium current.
is discussed in the section of total potassium current.
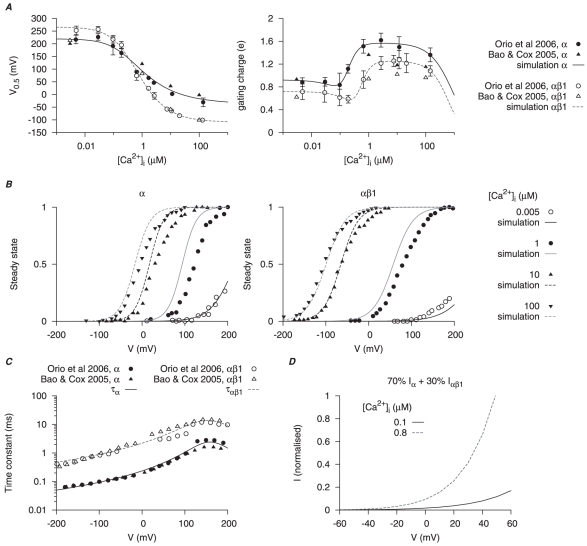
Figure 8. Myometrial 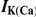 model.
model.
The calcium- (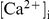 ), voltage- (V) and time-dependent kinetics for the two types of
), voltage- (V) and time-dependent kinetics for the two types of 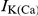 currents,
currents, 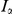 and
and 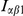 , are developed with experimental data from cloned mammalian myometrial and smooth muscle MaxiK
, are developed with experimental data from cloned mammalian myometrial and smooth muscle MaxiK  and
and 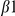 subunits expressed in Xenopus laevis oocytes [63], [64]; the current density and proportion of
subunits expressed in Xenopus laevis oocytes [63], [64]; the current density and proportion of 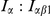 are adjusted with I–V relationships from different mammalian myometrial cells [17], [65], [66]. In A and C, solid and empty circles are experimental data for
are adjusted with I–V relationships from different mammalian myometrial cells [17], [65], [66]. In A and C, solid and empty circles are experimental data for 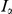 and
and 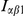 respectively. A,
respectively. A, 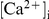 -dependent half-activation (
-dependent half-activation (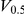 ) and activation gating charge. B, simulated activation steady-states for
) and activation gating charge. B, simulated activation steady-states for 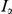 and
and 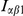 at different
at different 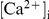 ; solid and empty circles are experimental data from Orio et al., [64] and Bao & Cox [63] respectively. C, V-dependent activation time constants for
; solid and empty circles are experimental data from Orio et al., [64] and Bao & Cox [63] respectively. C, V-dependent activation time constants for 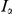 and
and 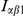 . D, simulated I–V relationships of
. D, simulated I–V relationships of 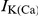 at anticipated myometrial resting and peak
at anticipated myometrial resting and peak 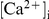 levels, with the proportion of
levels, with the proportion of 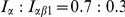 . Both I–V relationships are normalized to
. Both I–V relationships are normalized to 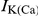 at
at 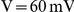 at peak
at peak 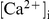 level.
level.
Background potassium current – 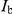
Mathematical description of the biophysical characteristics of this current are given in Appendix S1 (equation 79).
We have described so far the biophysical properties of the major myometrial 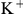 currents for which there is sufficient detailed electrophysiological information (
currents for which there is sufficient detailed electrophysiological information (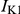 ,
, 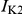 ,
, 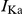 and
and 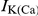 ). Other, less biophysically detailed electrophysiological information, together with evolving molecular and pharmacological data, suggests the possible existence of other myometrial
). Other, less biophysically detailed electrophysiological information, together with evolving molecular and pharmacological data, suggests the possible existence of other myometrial 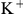 current sub-types including small-conductance
current sub-types including small-conductance 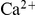 -activated
-activated 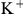 channels (termed
channels (termed 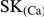 ) and voltage-dependent Kv7 (KCNQ) channels [20], [68]–[71]. Therefore,
) and voltage-dependent Kv7 (KCNQ) channels [20], [68]–[71]. Therefore, 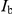 , a linear background potassium current is added and it collectively represents the remaining
, a linear background potassium current is added and it collectively represents the remaining 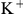 currents.
currents.
Whole cell total potassium current – 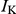
In order to model the whole cell 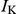 it is necessary to combine the current densities of each of the potassium current components.
it is necessary to combine the current densities of each of the potassium current components.
The current densities of voltage-gated potassium currents (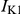 and
and 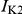 ) reported in myometrial cells show considerable variability. The total voltage-gated potassium current at the voltage step of
) reported in myometrial cells show considerable variability. The total voltage-gated potassium current at the voltage step of 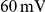 , from
, from 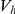 between
between 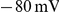 and
and 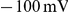 in myometrial cells studied by Knock et al., [19], [51] varied between
in myometrial cells studied by Knock et al., [19], [51] varied between 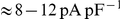 . Interestingly, the majority of human myometrial cells consisted of either
. Interestingly, the majority of human myometrial cells consisted of either 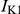 (24/42 cells) or
(24/42 cells) or 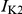 (18/42 cells) as the dominant potassium current [19] with only a very small number of myometrial cells reported to exhibit both
(18/42 cells) as the dominant potassium current [19] with only a very small number of myometrial cells reported to exhibit both 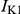 and
and 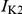 [51]. In contrast, Wang et al., [17] reported a voltage-gated potassium current density of
[51]. In contrast, Wang et al., [17] reported a voltage-gated potassium current density of 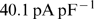 at
at 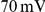 from
from 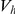 of
of 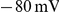 . The potassium current was a mixture of
. The potassium current was a mixture of 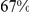 C1 (corresponding to
C1 (corresponding to 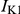 in Knock et al., [19]) and
in Knock et al., [19]) and 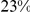 C2 (corresponding to
C2 (corresponding to 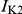 in Knock et al., [19]) and, together, they accounted for almost
in Knock et al., [19]) and, together, they accounted for almost 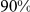 of total potassium current during a
of total potassium current during a 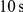 voltage step; the remaining
voltage step; the remaining 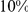 were sustained currents consisting of mostly
were sustained currents consisting of mostly 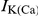 with an activation threshold of
with an activation threshold of 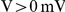 .
.
The reported peak current for 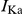 ranges between
ranges between 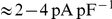 in human myometrial cells [51] and
in human myometrial cells [51] and 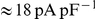 in rat myometrial cells [27] at voltage steps of
in rat myometrial cells [27] at voltage steps of 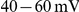 from a
from a 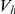 of
of 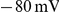 . However, from the raw time tracing [27], [51], the ratio of the peak
. However, from the raw time tracing [27], [51], the ratio of the peak 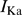 (occurring at
(occurring at 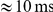 ) with respect to the peak total potassium current (occurring at
) with respect to the peak total potassium current (occurring at 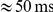 ) was consistent at
) was consistent at 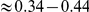 over a range of voltage steps from
over a range of voltage steps from 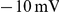 to
to 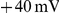 . Therefore, the maximal conductance of
. Therefore, the maximal conductance of 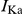 was chosen so that the peak of
was chosen so that the peak of 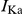 corresponds to
corresponds to 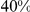 of the peak total potassium current (Figure 9A).
of the peak total potassium current (Figure 9A).
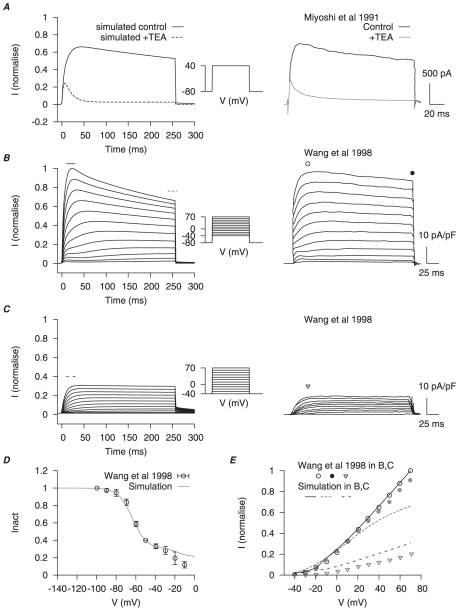
Figure 9. Myometrial total 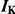 model.
model.
Potassium currents including 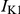 ,
, 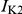 ,
, 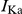 ,
, 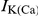 and
and 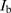 were combined to simulate the whole cell
were combined to simulate the whole cell 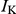 data of Miyoshi et al., [27] and Wang et al., [17]. A, simulated effects of
data of Miyoshi et al., [27] and Wang et al., [17]. A, simulated effects of 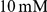 TEA (left), which blocks
TEA (left), which blocks  ,
, 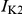 and
and 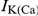 but not
but not 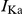 , at a voltage step of
, at a voltage step of 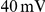 from a holding potential (
from a holding potential (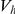 ) of
) of 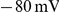 ; corresponding experimental results [27] (right). B, simulated whole cell potassium currents (left) and corresponding experimental results [17] (right) at voltage steps from
; corresponding experimental results [27] (right). B, simulated whole cell potassium currents (left) and corresponding experimental results [17] (right) at voltage steps from 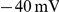 to
to 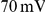 from a
from a 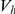 of
of 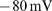 ; and C, from a
; and C, from a 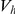 of
of 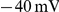 . D, simulated inactivation of whole cell potassium currents with the same two-step protocol in Wang et al., [17]:
. D, simulated inactivation of whole cell potassium currents with the same two-step protocol in Wang et al., [17]: 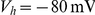 , followed with a
, followed with a 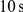 conditional step ranging from
conditional step ranging from 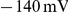 to
to 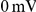 , then a final test step at
, then a final test step at 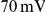 for
for 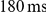 . The peak current during the the test steps is normalized to test step at
. The peak current during the the test steps is normalized to test step at 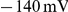 . E, the I–V relationships at peak and at the end of the voltage step in B and C. In B and C, simulated currents are normalized to the peak current at
. E, the I–V relationships at peak and at the end of the voltage step in B and C. In B and C, simulated currents are normalized to the peak current at 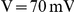 from
from 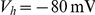 .
.
We have chosen the maximal conductances of 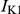 ,
, 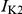 ,
, 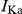 ,
, 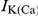 and
and 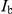 such that, together, the simulated total potassium current under different voltage-clamp protocols fits the profiles of experimental voltage-clamp results in Miyoshi et al., [27] and Wang et al., [17] (Figure 9).
such that, together, the simulated total potassium current under different voltage-clamp protocols fits the profiles of experimental voltage-clamp results in Miyoshi et al., [27] and Wang et al., [17] (Figure 9).
In the later development of the USMC AP simulations, the total potassium current density was scaled to match the experimental data of whole cell potassium current in Okabe et al., [32]; 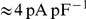 at
at 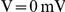 from a
from a 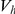 of
of 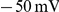 .
.
Other membrane currents
A non-selective cation current (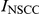 ) and a calcium-activated chloride current (
) and a calcium-activated chloride current (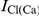 ) have been reported for myometrial cells from late pregnant rats. We also formulated electrogenic currents for the
) have been reported for myometrial cells from late pregnant rats. We also formulated electrogenic currents for the 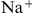 -
- ATPase and
ATPase and 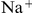 -
-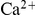 exchangers,
exchangers, 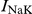 and
and 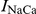 respectively, by extrapolating data from other cell systems.
respectively, by extrapolating data from other cell systems. 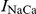 will be discussed with
will be discussed with 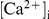 dynamics in a later section.
dynamics in a later section.
Calcium-activated chloride current – 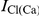
Mathematical descriptions of the biophysical characteristics of this current are given in Appendix S1 (equations 80–86).
The presence of channels permeable to chloride in myometrial cells was first reported by Coleman & Parkington [72]. Subsequently, there have been several reports of calcium-activated chloride current in myometrial cells, albeit the biophysical characteristics have not been as thoroughly explored as in other smooth muscles and tissues [15], [17], [73], [74]. In addition, Clca isoforms 3 and 4, suggested to encode for channel proteins responsible for 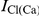 , have been found in the uterus and the induced expression of Clca4 in mammalian cells elicited a calcium-dependent chloride current [75], [76].
, have been found in the uterus and the induced expression of Clca4 in mammalian cells elicited a calcium-dependent chloride current [75], [76].
The only serious single cell electrophysiological assessment of 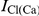 in myometrial cells (rat,
in myometrial cells (rat, 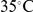 ) is from Jones et al., [15] and therefore, this is the experimental data used for our modeling purposes. They used two different voltage-clamp protocols: a single step voltage-clamp and a two-step voltage-clamp (illustrated in Figures 1 and 2, respectively, of Jones et al., [15]). Both protocols relied on the activation of
) is from Jones et al., [15] and therefore, this is the experimental data used for our modeling purposes. They used two different voltage-clamp protocols: a single step voltage-clamp and a two-step voltage-clamp (illustrated in Figures 1 and 2, respectively, of Jones et al., [15]). Both protocols relied on the activation of 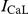 to raise
to raise 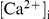 which, in turn, was proposed to activate
which, in turn, was proposed to activate 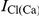 .
. 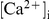 , however, was not clamped in Jones et al., [15] and so, for modeling purposes, it was not possible to determine the steady-state values nor the activation kinetics. However, such information is available from the data of Arreola et al., [77] for
, however, was not clamped in Jones et al., [15] and so, for modeling purposes, it was not possible to determine the steady-state values nor the activation kinetics. However, such information is available from the data of Arreola et al., [77] for 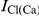 in rat parotid acinar cells whereupon
in rat parotid acinar cells whereupon 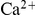 buffers were introduced intracellularly to control
buffers were introduced intracellularly to control 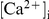 . This enabled the recording and modeling of calcium- and voltage-dependencies of
. This enabled the recording and modeling of calcium- and voltage-dependencies of 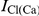 . In addition, the Arreola et al., [77] model could reproduce the calcium- and voltage-dependencies of
. In addition, the Arreola et al., [77] model could reproduce the calcium- and voltage-dependencies of 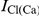 in pulmonary vascular smooth muscle cells [78]. As such, we applied the model of Arreola et al., [77] to simulate the myometrial data of Jones et al., [15]. Utilizing the values for the calcium-dependent time constant of activation from Arreola et al., [77], or even changing them substantially, failed to provide a suitable fit to the Jones et al., [15]
in pulmonary vascular smooth muscle cells [78]. As such, we applied the model of Arreola et al., [77] to simulate the myometrial data of Jones et al., [15]. Utilizing the values for the calcium-dependent time constant of activation from Arreola et al., [77], or even changing them substantially, failed to provide a suitable fit to the Jones et al., [15]
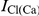 dynamics. If one assumed only a voltage-dependency to the activation time constant then the raw data time tracings of Jones et al., [15] could be fitted by the Arreola et al., [77] model (Figure 10). Thus we include
dynamics. If one assumed only a voltage-dependency to the activation time constant then the raw data time tracings of Jones et al., [15] could be fitted by the Arreola et al., [77] model (Figure 10). Thus we include 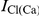 in our later model of USMC AP form with the caveat that the activation kinetics are different from that described in other cells [77], [78].
in our later model of USMC AP form with the caveat that the activation kinetics are different from that described in other cells [77], [78].
Figure 10. Myometrial 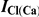 model.
model.
The steady-state of 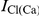 is modified from Arreola et al., [77]. A, steady-state of
is modified from Arreola et al., [77]. A, steady-state of 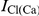 with respect to V in three different
with respect to V in three different 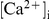 concentrations; B, steady-state of
concentrations; B, steady-state of 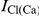 with respect to
with respect to 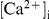 at four different membrane potentials. C, V-dependent activation time constant; the experimental data points are obtained by fitting the tail currents in figure 2 of Jones et al., [15]. D, simulated currents (left) and the corresponding experimental currents in Jones et al., [15] (right) elicited by a single-step voltage-clamp protocol (inset). The peak of the inward currents, the current values at the end of the voltage pulse, and the peak of the tail currents were marked for both simulated current (lines) and experimental current tracings (circles). E, I–V relationships, showing the marked peak at each voltage step in D. F, simulated currents (left) and the corresponding experimental currents in Jones et al., [15] (right) by a two-step voltage-clamp protocol (inset). The peak of the tail currents were marked for both simulated current (lines) and experimental current tracings (circles). G, I–V relationships, showing the marked peaks of the tail currents at each voltage step in F. The simulated currents qualitatively reproduced the experimental current tracings in both voltage-clamp protocols, with almost zero net current at the holding potential and comparable amplitude and rate of decay of the tail currents.
at four different membrane potentials. C, V-dependent activation time constant; the experimental data points are obtained by fitting the tail currents in figure 2 of Jones et al., [15]. D, simulated currents (left) and the corresponding experimental currents in Jones et al., [15] (right) elicited by a single-step voltage-clamp protocol (inset). The peak of the inward currents, the current values at the end of the voltage pulse, and the peak of the tail currents were marked for both simulated current (lines) and experimental current tracings (circles). E, I–V relationships, showing the marked peak at each voltage step in D. F, simulated currents (left) and the corresponding experimental currents in Jones et al., [15] (right) by a two-step voltage-clamp protocol (inset). The peak of the tail currents were marked for both simulated current (lines) and experimental current tracings (circles). G, I–V relationships, showing the marked peaks of the tail currents at each voltage step in F. The simulated currents qualitatively reproduced the experimental current tracings in both voltage-clamp protocols, with almost zero net current at the holding potential and comparable amplitude and rate of decay of the tail currents.
Non-selective cation current – 
Mathematical descriptions of the biophysical characteristics of this current are given in Appendix S1 (equations 87–92).
Miyoshi et al., [79] had identified a non-specific cation current in late pregnant rat myometrial cells. 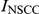 is a linear, time-independent cation current. It is permeable to
is a linear, time-independent cation current. It is permeable to 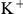 ,
, 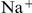 ,
, 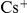 and
and 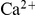 , with relative permeability ratios of
, with relative permeability ratios of 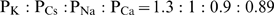 . The conductance of
. The conductance of 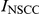 depends on extracellular concentrations of permeable cations and it was inhibited by extracellular
depends on extracellular concentrations of permeable cations and it was inhibited by extracellular 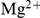 ,
, 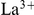 and
and 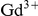 . The reported reversal potential and current density under standard conditions in Miyoshi et al., [79], with
. The reported reversal potential and current density under standard conditions in Miyoshi et al., [79], with 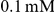
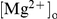 and utilizing a voltage ramp protocol, were, respectively,
and utilizing a voltage ramp protocol, were, respectively, 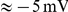 and
and 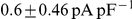 .
.
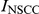 is modeled with data from late pregnant rat myometrial cells recorded at room temperature. The reversal potential of
is modeled with data from late pregnant rat myometrial cells recorded at room temperature. The reversal potential of 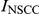 (
(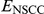 ) is approximated by the Goldman-Hodgkin-Katz (GHK) equation [80] with the reported permeability ratio [79]. Intracellular and extracellular concentrations of
) is approximated by the Goldman-Hodgkin-Katz (GHK) equation [80] with the reported permeability ratio [79]. Intracellular and extracellular concentrations of 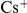 and NMDG with
and NMDG with 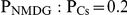 were included in the calculation of
were included in the calculation of  while fitting experimental data in Miyoshi et al., [79]; these parameters for
while fitting experimental data in Miyoshi et al., [79]; these parameters for  and NMDG were excluded in the later development of the USMC whole cell model.
and NMDG were excluded in the later development of the USMC whole cell model.
The conductances of  for different cations from the voltage ramp I–V relationships have a ratio of
for different cations from the voltage ramp I–V relationships have a ratio of 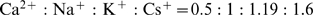 [79]. Similar to
[79]. Similar to 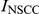 in guinea-pig endocardial endothelial cells [81], conductance of myometrial
in guinea-pig endocardial endothelial cells [81], conductance of myometrial 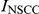 was reduced with decreasing
was reduced with decreasing 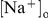 . With reference to Manabe et al., [81], this relationship was described by a Hill equation with a half-saturating concentration of
. With reference to Manabe et al., [81], this relationship was described by a Hill equation with a half-saturating concentration of 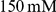 and a Hill coefficient of 2. We have normalized the Hill equation with the
and a Hill coefficient of 2. We have normalized the Hill equation with the 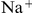 conductance at
conductance at 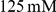
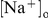 and we assumed the same relationship held for other permeable cations; for
and we assumed the same relationship held for other permeable cations; for 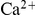 ions, the Hill equation is normalized to the
ions, the Hill equation is normalized to the 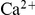 conductance observed at
conductance observed at 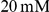
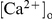 . Inhibition by
. Inhibition by 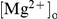 is described by a Hill equation with a half-saturating concentration of
is described by a Hill equation with a half-saturating concentration of 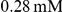 and a Hill coefficient of 1.3 [79].
and a Hill coefficient of 1.3 [79].  is also permeable to other cations ions [79] and, therefore, a small leak component (
is also permeable to other cations ions [79] and, therefore, a small leak component ( ) in its conductance is needed to match the experimental voltage ramp data. Under physiological conditions with
) in its conductance is needed to match the experimental voltage ramp data. Under physiological conditions with 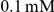
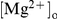 the simulated
the simulated 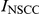 consists of mostly
consists of mostly 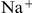 and leak components.
and leak components.
Sodium potassium pump current – 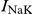
Mathematical descriptions of the biophysical characteristics of this current are given in Appendix S1 (equations 93–96).
Evidence of 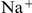 -
-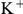 pump activity has been reported in myometrial cells of late pregnant rats [82]–[84] and human [8]. mRNA and protein expression corresponding to
pump activity has been reported in myometrial cells of late pregnant rats [82]–[84] and human [8]. mRNA and protein expression corresponding to  and
and 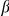 subunits of the
subunits of the 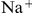 -
-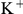 ATPase have been reported in rodent and human myometrium with isoform-specific changes associated with advancing gestation and/or estrogen treatment [21], [84]–[86]. In sodium-rich myometrial tissues of late pregnant rats [82], [83] and human [8], changes of the membrane potential were sensitive to ouabain, the absence of external potassium or intracellular sodium and to low temperature, results that are suggestive of an electrogenic
ATPase have been reported in rodent and human myometrium with isoform-specific changes associated with advancing gestation and/or estrogen treatment [21], [84]–[86]. In sodium-rich myometrial tissues of late pregnant rats [82], [83] and human [8], changes of the membrane potential were sensitive to ouabain, the absence of external potassium or intracellular sodium and to low temperature, results that are suggestive of an electrogenic 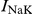 . Despite this molecular and biophysical data supporting a role of the
. Despite this molecular and biophysical data supporting a role of the 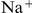 -
-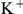 pump in regulating myometrial activity, there is little information about the biophysical properties of
pump in regulating myometrial activity, there is little information about the biophysical properties of 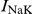 current in myometrial cells. Therefore, we adopted the formulation of an electrogenic
current in myometrial cells. Therefore, we adopted the formulation of an electrogenic 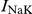 from rodent myocardial cells [87], which was dependent on membrane voltage,
from rodent myocardial cells [87], which was dependent on membrane voltage, 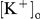 ,
, 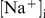 and
and 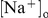 . The parameter values of voltage,
. The parameter values of voltage, 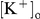 and
and 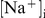 dependencies, as well as current densities, are then fitted with the experimental data from rodent vascular smooth muscle cells [88] at
dependencies, as well as current densities, are then fitted with the experimental data from rodent vascular smooth muscle cells [88] at 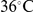 . A
. A 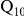 value of 1.87 for
value of 1.87 for 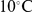 change between
change between  is reported for vascular smooth muscle cells [88]. We assumed the same
is reported for vascular smooth muscle cells [88]. We assumed the same 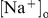 dependency with
dependency with 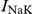 in smooth muscle cells as in the myocardial cells.
in smooth muscle cells as in the myocardial cells.
Calcium fluxes
Mathematical descriptions of the plasmalemmal
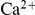 fluxes are given in the
Methods
(
equation 7
) and Appendix S1 (equations 97–103).
fluxes are given in the
Methods
(
equation 7
) and Appendix S1 (equations 97–103).
In myometrial cells from near-term pregnant rats, intracellular 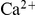 ions are removed from the cytoplasm principally by the plasmalemmal
ions are removed from the cytoplasm principally by the plasmalemmal 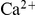 -ATPase (PMCA) and
-ATPase (PMCA) and 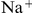 -
-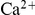 exchanger [12], [67], [89], [90]. From the decay rate constants,
exchanger [12], [67], [89], [90]. From the decay rate constants,  of cytoplasmic
of cytoplasmic 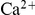 removal was estimated to be via the
removal was estimated to be via the 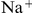 -
-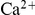 exchanger and sequestration into intracellular stores, and
exchanger and sequestration into intracellular stores, and 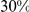 via PMCA when the cell was stimulated by ten short depolarization pulses between
via PMCA when the cell was stimulated by ten short depolarization pulses between 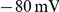 and
and 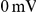 [67].
[67].
We modified a myometrial intracellular calcium model [24] for inclusion in the development of the USMC AP simulations by incorporating time-dependent kinetics from membrane calcium currents. We also modified the formulation of the 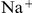 -
-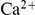 exchanger to overcome its limits in fitting published
exchanger to overcome its limits in fitting published 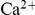 decay tracings. For example, we found that the calcium decay tracings in Shmigol et al., [67] and Shmigol et al., [12] could only be fitted by the procedure described in Bursztyn et al., [24] with
decay tracings. For example, we found that the calcium decay tracings in Shmigol et al., [67] and Shmigol et al., [12] could only be fitted by the procedure described in Bursztyn et al., [24] with 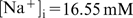 . However, no sodium ions were included in the pipette (intracellular) solution used by Shmigol et al., [67]. The resultant reversal potential of the
. However, no sodium ions were included in the pipette (intracellular) solution used by Shmigol et al., [67]. The resultant reversal potential of the 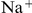 -
-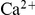 exchanger was predicted at
exchanger was predicted at 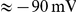 which would mean the
which would mean the 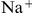 -
-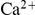 exchanger bringing in extracellular calcium at resting membrane potentials of
exchanger bringing in extracellular calcium at resting membrane potentials of 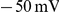 to
to 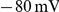 which is incorrect. Our use of the well-described formula of Weber et al., [91] obviated this and enabled us to fit the
which is incorrect. Our use of the well-described formula of Weber et al., [91] obviated this and enabled us to fit the 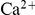 fluxes with the same ionic concentrations used in Shmigol et al., [67] and Shmigol et al., [12]. With
fluxes with the same ionic concentrations used in Shmigol et al., [67] and Shmigol et al., [12]. With 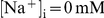 , the resultant reversal potential was in the positive membrane potential range and, thus, the
, the resultant reversal potential was in the positive membrane potential range and, thus, the 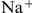 -
-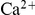 exchanger was predicted to extrude intracellular
exchanger was predicted to extrude intracellular 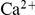 in the physiological range of resting membrane potentials.
in the physiological range of resting membrane potentials.
We have modeled three major plasmalemmal calcium fluxes: the voltage-dependent membrane channels permeable to 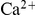 (
(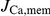 ); the
); the 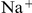 -
-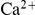 exchanger (
exchanger (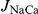 ); and the PMCA (
); and the PMCA (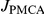 ).
).
The parameters for 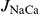 and
and 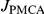 are refitted with experimental results of calcium decay in late pregnant rat myometrial cells recorded at
are refitted with experimental results of calcium decay in late pregnant rat myometrial cells recorded at 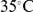 from Shmigol et al., [12], [67]; the modified calcium sub-system is further validated with experimental data (Figure S7A). Details of individual fluxes are described below.
from Shmigol et al., [12], [67]; the modified calcium sub-system is further validated with experimental data (Figure S7A). Details of individual fluxes are described below.
Membrane 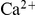 channels –
channels – 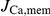
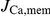 , which includes all the membrane ion channel calcium currents:
, which includes all the membrane ion channel calcium currents: 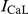 ,
, 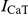 and the calcium component of
and the calcium component of 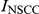 (
(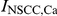 ), was calculated from the total membrane calcium current as described in the Methods (equation 7).
), was calculated from the total membrane calcium current as described in the Methods (equation 7).
Sodium-calcium exchanger – 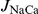
The 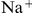 -
-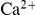 exchanger has been suggested to be involved in calcium translocation in myometrial cells from pregnant rats [12], [67], [89], [90]. However, it is unknown whether the myometrial
exchanger has been suggested to be involved in calcium translocation in myometrial cells from pregnant rats [12], [67], [89], [90]. However, it is unknown whether the myometrial 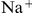 -
-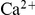 exchanger is electrogenic although the earliest studies of the effects of changing
exchanger is electrogenic although the earliest studies of the effects of changing 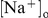 and
and 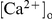 on the rat myometrial cell membrane properties suggested so [92].
on the rat myometrial cell membrane properties suggested so [92].
There are three 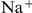 -
-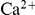 exchanger isoforms (NCX1, NCX2, NCX3) and NCX mRNA and protein has been reported in myometrium [93], [94]. NCX2 is the predominantly expressed isoform in smooth muscle tissues, including the uterus, but its stoichiometry and electrogenicity are unknown. Cloning of NCX2 [95] shows that it shares
exchanger isoforms (NCX1, NCX2, NCX3) and NCX mRNA and protein has been reported in myometrium [93], [94]. NCX2 is the predominantly expressed isoform in smooth muscle tissues, including the uterus, but its stoichiometry and electrogenicity are unknown. Cloning of NCX2 [95] shows that it shares 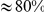 similarity in amino acid sequences with NCX1, the predominant isoform in heart tissues, and they were functionally similar with respect to their I–V relationship and voltage-dependency [96], [97]. Compared to NCX1, NCX2 has a higher dissociation rate (
similarity in amino acid sequences with NCX1, the predominant isoform in heart tissues, and they were functionally similar with respect to their I–V relationship and voltage-dependency [96], [97]. Compared to NCX1, NCX2 has a higher dissociation rate (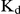 ) for
) for 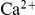 at
at 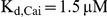 and a lower
and a lower 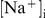 affinity at
affinity at 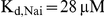 . As the
. As the 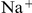 -
-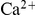 exchangers in cardiac myocytes [98] and aortic smooth muscle cells are electrogenic [99] and the properties of NCX1 and NCX2 isoforms are similar, we presumed the myometrial sodium calcium exchanger would also be electrogenic.
exchangers in cardiac myocytes [98] and aortic smooth muscle cells are electrogenic [99] and the properties of NCX1 and NCX2 isoforms are similar, we presumed the myometrial sodium calcium exchanger would also be electrogenic.
We used an electrogenic 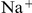 -
-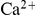 exchanger equation for cardiac cells from Weber et al., [91] that describes current dependencies on membrane potential, intra- and extra-cellular calcium and sodium concentrations and has a stoichiometry of
exchanger equation for cardiac cells from Weber et al., [91] that describes current dependencies on membrane potential, intra- and extra-cellular calcium and sodium concentrations and has a stoichiometry of 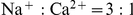 . Dissociation constants for
. Dissociation constants for 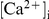 and
and 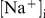 were set as
were set as  and
and 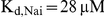 , respectively [22], [95]. Dissociation constants for
, respectively [22], [95]. Dissociation constants for 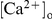 and
and 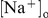 were assumed the same as Weber et al., [91]. The maximum calcium flux via
were assumed the same as Weber et al., [91]. The maximum calcium flux via
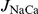 and parameters for
and parameters for 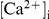 allosteric activation were refitted with experimental results of calcium decay in late pregnant rat myometrial cells [12], [67]. Membrane current from the
allosteric activation were refitted with experimental results of calcium decay in late pregnant rat myometrial cells [12], [67]. Membrane current from the 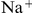 -
-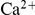 exchanger,
exchanger, 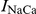 , is converted from the fitted calcium fluxes
, is converted from the fitted calcium fluxes 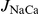 .
.
Plasma membrane 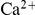 ATPase –
ATPase – 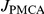
PMCA activity in rat myometrial cells has been characterized in fractionated plasma membranous vesicles with a reported ATP-dependent uptake with half saturation at 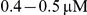
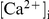 and a Hill coefficient of
and a Hill coefficient of  [22], [100]–[102]. PMCA is described by a Hill equation with a half saturation at
[22], [100]–[102]. PMCA is described by a Hill equation with a half saturation at 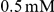
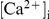 and a Hill coefficient of 2.
and a Hill coefficient of 2.
Cell and tissue modeling: simulations of APs, 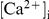 and force
and force
Our ability to integrate the information obtained from the above biophysically detailed models of individual ionic fluxes into simulations of APs and the ensuring changes in  and force at a cellular/tissue level were assessed by the following validations.
and force at a cellular/tissue level were assessed by the following validations.
Model validation 1: simulation of different myometrial action potential configurations
Myometrial cells can produce different forms of APs including those consisting of a single spike, a burst of spikes or a plateau-type. A first task of validation was to assess if integration of our individual ionic current models and 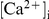 fluxes could simulate these different AP forms.
fluxes could simulate these different AP forms.
We began to assemble a model of AP configuration that incorporated all of the currents and ion fluxes described above. However, under physiological conditions of ionic concentrations [32], this model configuration produced a resting membrane potential (RMP) that was too depolarized (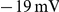 ) and a basal
) and a basal 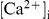 that was too high (
that was too high (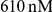 ). Many of the ionic currents described above were found in only a subset of the studied myometrial smooth muscle cells. In particular,
). Many of the ionic currents described above were found in only a subset of the studied myometrial smooth muscle cells. In particular, 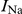 was reported in only 2/30 myometrial cells in Miyoshi et al., [27]. Removing
was reported in only 2/30 myometrial cells in Miyoshi et al., [27]. Removing 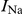 from the model, therefore, produced an RMP of
from the model, therefore, produced an RMP of 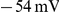 with a resting
with a resting 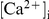 of
of 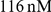 . When some
. When some 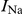 is included (
is included ( ), the USMC model became more excitable with lower voltage threshold (
), the USMC model became more excitable with lower voltage threshold (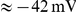 ) and current threshold (
) and current threshold (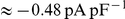 ,
, 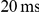 stimulus). The parameters and initial conditions of the USMC model configuration are given in Table S3, S4.
stimulus). The parameters and initial conditions of the USMC model configuration are given in Table S3, S4.
The USMC model is excitable and responds to a brief stimulus with an all-or-none AP. The voltage threshold is 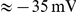 ; the corresponding current threshold is
; the corresponding current threshold is 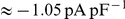 by a
by a 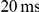 stimulus. The simulated AP usually overshoots
stimulus. The simulated AP usually overshoots 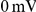 with a maximum rate of rise (dV/dt) up to
with a maximum rate of rise (dV/dt) up to 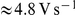 and the AP duration (APD) measured at
and the AP duration (APD) measured at 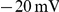 ranges between
ranges between 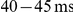 , similar to the experimental values of dV/dt [37] and APD [100] for rodent myometrium.
, similar to the experimental values of dV/dt [37] and APD [100] for rodent myometrium.
The range of AP shapes reported for the pregnant rat myometrium at 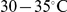 – repetitive spike AP [10], repetitive spike AP upon a depolarized basal membrane potential [101], repetitive spike AP leading to plateau [102] and a plateau-like AP [10] – are reconstructed in Figure 11. The variety of action potential shapes can be produced by this model with small variations in parameter sets and initial conditions. Of the four AP configurations illustrated in Figure 11: a bursting type AP was simulated with a current clamp of
– repetitive spike AP [10], repetitive spike AP upon a depolarized basal membrane potential [101], repetitive spike AP leading to plateau [102] and a plateau-like AP [10] – are reconstructed in Figure 11. The variety of action potential shapes can be produced by this model with small variations in parameter sets and initial conditions. Of the four AP configurations illustrated in Figure 11: a bursting type AP was simulated with a current clamp of 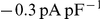 and with the conductance of
and with the conductance of 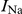 at
at 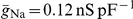 ; a bursting type AP upon a depolarized V was simulated with a current clamp of
; a bursting type AP upon a depolarized V was simulated with a current clamp of 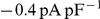 and with a slope factor of
and with a slope factor of 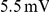 for the
for the 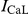 inactivation steady-state; a mixed bursting-plateau type AP was simulated with
inactivation steady-state; a mixed bursting-plateau type AP was simulated with 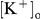 stepped from 6 to
stepped from 6 to 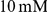 ; a plateau type AP was simulated with a current clamp of
; a plateau type AP was simulated with a current clamp of 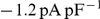 . Thus the integrated model can accommodate a variety of APs seen in uterine in smooth muscle cells.
. Thus the integrated model can accommodate a variety of APs seen in uterine in smooth muscle cells.
Figure 11. Varieties of action potentials.
The USMC model can produce a range of myometrial action potentials (APs) using different initial conditions and parameters values. Four examples are shown (left); all four simulated APs were induced by a 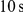 stimulus applied at
stimulus applied at 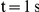 . Representative experimental APs from published recordings [10], [101], [102] are shown for comparison (right). A, bursting type AP with afterpotentials at resting membrane potential (RMP); B, bursting type AP with depolarized afterpotentials; C, a mixed bursting-plateau type AP with initial repetitive spikes that gradually become a flat plateau at
. Representative experimental APs from published recordings [10], [101], [102] are shown for comparison (right). A, bursting type AP with afterpotentials at resting membrane potential (RMP); B, bursting type AP with depolarized afterpotentials; C, a mixed bursting-plateau type AP with initial repetitive spikes that gradually become a flat plateau at 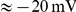 . D, plateau type AP.
. D, plateau type AP.
Model validation 2: simulation of the experimental changes induced by estradiol on myometrial AP and 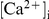 configurations
configurations
The cell model is validated with voltage-clamp and current-clamp experimental data from pregnant rat myometrial cells at 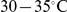 [11], [30], [32], [49] under control conditions and upon exposure to estradiol (Figure 12). Estradiol has been reported to reduce peak
[11], [30], [32], [49] under control conditions and upon exposure to estradiol (Figure 12). Estradiol has been reported to reduce peak 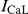 . Estradiol has also been reported to reduce whole cell potassium currents [30], [32], [49] and change the USMC AP configuration from a bursting type AP upon a depolarized V to a plateau type AP [11]. The model was able to simulate this change in AP form by adjusting the appropriate current parameters: left-shifting the half-inactivation of
. Estradiol has also been reported to reduce whole cell potassium currents [30], [32], [49] and change the USMC AP configuration from a bursting type AP upon a depolarized V to a plateau type AP [11]. The model was able to simulate this change in AP form by adjusting the appropriate current parameters: left-shifting the half-inactivation of 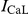 to
to 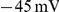 and alters its slope factor to
and alters its slope factor to 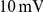 , and reducing total potassium conductance by
, and reducing total potassium conductance by 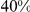 (Figure S1).
(Figure S1).
Figure 12. Simulating estradiol effects on simultaneous recordings of V and 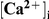 .
.
Action potentials (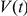 ) and corresponding calcium transients (
) and corresponding calcium transients (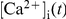 ) during a
) during a 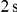 depolarizing current clamp (
depolarizing current clamp (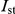 ) under, A, control conditions and, B, the effects of estradiol. In both cases, the initial conditions of the cell model were at their corresponding numerical equilibrium. Action potentials in rat longitudinal myometrial single cells under similar experimental conditions [11], [49] are shown for comparison (insets).
) under, A, control conditions and, B, the effects of estradiol. In both cases, the initial conditions of the cell model were at their corresponding numerical equilibrium. Action potentials in rat longitudinal myometrial single cells under similar experimental conditions [11], [49] are shown for comparison (insets).
Model validation 3: simulation of simultaneous recordings of membrane potential, 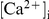 and force
and force
The extraction of the mathematical descriptions for modeling calcium-dependent force changes is denoted in Figure S6 and the resultant equations listed in the Methods ( equations 3 and 8 – 9 ) and Appendix S1 (equations 104–105).
A final step in our validation of the model was to establish if it was able to accommodate the integration of uterine smooth muscle electrical, 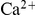 and contractile events necessary for excitation-contraction coupling. In this regard two broad scenarios of E-C coupling were again considered whereupon contractile events arose from either repetitive spike APs or from plateau-type APs. Figure 13 shows the results of simulations of APs,
and contractile events necessary for excitation-contraction coupling. In this regard two broad scenarios of E-C coupling were again considered whereupon contractile events arose from either repetitive spike APs or from plateau-type APs. Figure 13 shows the results of simulations of APs, 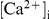 and force compared to published experimental measurements of these variables from rat myometrial tissue at
and force compared to published experimental measurements of these variables from rat myometrial tissue at 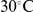 [103], [104]. Of note, we chose to reproduce the repetitive spike AP data with four separate consequent stimuli for two reasons. First, the present USMC model, when induced by a current clamp, exhibited a lower limit for bursting frequency at
[103], [104]. Of note, we chose to reproduce the repetitive spike AP data with four separate consequent stimuli for two reasons. First, the present USMC model, when induced by a current clamp, exhibited a lower limit for bursting frequency at 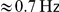 which was faster than that of the experimental recordings. Second, the experimental measurements of relative membrane potential changes from Burdyga et al., [103], [104] were averaged from bundles of myometrial muscle strips. Thus, the low bursting frequency of spikes observed from these data may be a result of the extra electro-potential load from the multicellular environment. Alternatively, one cannot completely rule out the possibility that the four consecutive APs spikes were separate events resulting re-entrant excitation waves.
which was faster than that of the experimental recordings. Second, the experimental measurements of relative membrane potential changes from Burdyga et al., [103], [104] were averaged from bundles of myometrial muscle strips. Thus, the low bursting frequency of spikes observed from these data may be a result of the extra electro-potential load from the multicellular environment. Alternatively, one cannot completely rule out the possibility that the four consecutive APs spikes were separate events resulting re-entrant excitation waves.
Figure 13. Simulation of the simultaneous recordings of myometrial V, 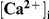 and force development.
and force development.
Simulated APs and corresponding 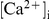 and force (left) compared to experimental simultaneous measurements of membrane potential,
and force (left) compared to experimental simultaneous measurements of membrane potential, 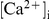 and force in rat myometrial tissue strips. A, simulation of a single spike AP and corresponding
and force in rat myometrial tissue strips. A, simulation of a single spike AP and corresponding 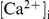 and force induced by a
and force induced by a 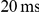 stimulus (dot) at
stimulus (dot) at 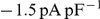 and compared to experimental data [103], [104]. B, four consecutive single spike APs and corresponding
and compared to experimental data [103], [104]. B, four consecutive single spike APs and corresponding 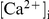 and force modeled by
and force modeled by 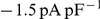 stimuli (dots) of
stimuli (dots) of 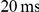 , applied at
, applied at 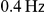 and compared to experimental data [103], [104]. C, superimposed simulated AP,
and compared to experimental data [103], [104]. C, superimposed simulated AP, 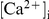 and force development (left), with a
and force development (left), with a  current clamp at
current clamp at 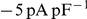 and compared to experimental data [106].
and compared to experimental data [106].
The model could also reproduce several additional published E-C coupling datasets of V(t), 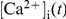 and force recorded from pregnant rats at
and force recorded from pregnant rats at 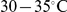 [103]–[106, ].Figures S7, S8
[103]–[106, ].Figures S7, S8
Limitations and Conclusions
Our approach has resulted in a number of advances for our understanding of uterine smooth muscle E-C coupling. The model encompasses the most comprehensive biophysical description of ion channel and exchanger electric currents applied to the myometrium with 14 separate electrogenic components, summarized in Figure 14, used to simulate published myometrial AP forms and their alteration by specific experimental manoeuvres. Using 105 mathematical equations, it is the first model to integrate these electrogenic components with descriptions of 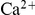 dynamics and phasic force production, the three essential components of electrical E-C coupling, and replicate published myometrial experimental recordings of simultaneous membrane potential,
dynamics and phasic force production, the three essential components of electrical E-C coupling, and replicate published myometrial experimental recordings of simultaneous membrane potential, 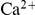 and force.
and force.
Figure 14. Schematic of the electrogenic components considered for the model of myometrial cell electrical excitability.
As with any mathematical model of biological phenomena there are limitations. The 14 electrogenic currents are likely to be an underestimate of the number of ion channel contributors to myometrial AP form. This highlights a lack of sufficient biophysical detail on other currents. In biophysical modeling of cells and tissues, it is often the case that some published electrophysiological information on particular currents is of insufficient detail to furnish biophysical modeling of all its steady-state and dynamic characteristics. Therefore, data from different resources with close cell types, or the same type of cells from different species, are used. This is the same case for the present model. The model is a hybrid containing information primarily from rat myometrium but also from human myometrium and cells expressing smooth muscle ion channel subunits, and this data has been obtained from experiments using different in vitro solutions and at different temperatures. Although this neglects any species-specific quantitative differences in uterine electrogenicity and E-C coupling, it presently is unavoidable. It is also common in biophysical modeling approaches when it is rare that all information is available for one cell type from one species. However, an advantage of the comprehensive assembly of this mathematical model is that it enables identification of gaps in our knowledge of myometrial electrogenesis. This will inform future empirical work in several ways.
First, the putative contribution of many ion channel subtypes to myometrial function has often been extrapolated from molecular data (mRNA or protein) which is incomplete (not all isotypes of channel or exchanger sub-families have been examined) or pharmacological data utilizing compounds of weak specificity (e.g. there are many putative pharmacological blockers/openers 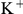 channel sub-family that have not yet been examined on uterine function). In addition, electrophysiological isolation of currents is often lacking. Clearly, identification of the molecular expression patterns of all ion channel and ion exchanger subtypes in myometrial cells of the uterus is essential (e.g. [107]), and marrying such data to precise electrophysiological, pharmacological and simulated profiles (even if initially this is in clonal cells), is required to furnish a complete biophysical characterization of normal uterine function. This should be accomplished for rodent and human myometrium to enable one to move from the present hybrid model to species-specific formulations. Procedures outlined in the development of this mathematical model indicate how this can assist in improving our understanding of uterine E-C coupling.
channel sub-family that have not yet been examined on uterine function). In addition, electrophysiological isolation of currents is often lacking. Clearly, identification of the molecular expression patterns of all ion channel and ion exchanger subtypes in myometrial cells of the uterus is essential (e.g. [107]), and marrying such data to precise electrophysiological, pharmacological and simulated profiles (even if initially this is in clonal cells), is required to furnish a complete biophysical characterization of normal uterine function. This should be accomplished for rodent and human myometrium to enable one to move from the present hybrid model to species-specific formulations. Procedures outlined in the development of this mathematical model indicate how this can assist in improving our understanding of uterine E-C coupling.
Second, from the present information, it is clear that isolated myometrial cells exhibit heterogeneity in ion channel electrophysiology and 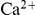 handling characteristics (for example, the proportion of examined cells exhibiting
handling characteristics (for example, the proportion of examined cells exhibiting 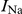 or particular
or particular 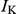 currents). It will be important as one moves forward to consider spatiotemporal aspects of E-C coupling that we establish the implications of this for tissue level electrogenesis [5], [108].
currents). It will be important as one moves forward to consider spatiotemporal aspects of E-C coupling that we establish the implications of this for tissue level electrogenesis [5], [108].
Third, the model serves as a useful tool in the design and assessment of agents that act as putative channel/exchanger blockers or activators. Refinement of the model with continued empirical/theoretical iterations will serve to increase its predictive capacity for use in the in silico assessment of new uterotonic agents especially as species-specific models are developed. For example, if electrophysiological data of sufficient detail for biophysical modeling is known for the actions of a new agonist/antagonist of a particular uterine ion channel then one can develop predictions of the likely action of this drug on uterine E-C coupling for that species. These will serve as hypotheses to be tested in ex vivo or in vivo experimentation. In the longer term, this should bring attendant benefits to developing drugs for the treatment of aberrant uterine activity such as preterm labor, whether experimentally induced in rodents [109] or arising spontaneously in humans, prolonged dysfunctional labor or poorly contracting uterus post-partum.
Methods
Overview
A mathematical model of uterine smooth muscle cell (USMC) function at late pregnancy was developed from the integration of data of individual ionic currents, calcium dynamics and contraction. A glossary of symbols used in the equations is given in Table S1. The USMC model is a system of first-order ordinary differential equations,
| (1) |
| (2) |
| (3) |
where  is the specific membrane capacitance. Eq. 1 describes the electrophysiological activities of myometrial membrane potential (V), which is proportional to the sum of membrane ionic currents (
is the specific membrane capacitance. Eq. 1 describes the electrophysiological activities of myometrial membrane potential (V), which is proportional to the sum of membrane ionic currents (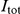 ); Eq. 2 describes the corresponding intracellular calcium (
); Eq. 2 describes the corresponding intracellular calcium (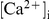 ) dynamics, which is proportional to the sum of calcium fluxes (J). Eq. 3 describes the rate of change of force as a function of
) dynamics, which is proportional to the sum of calcium fluxes (J). Eq. 3 describes the rate of change of force as a function of 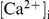 .
.
Electrophysiology
The individual membrane current components that were modeled were (i) four inward currents: L-type and T-type 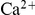 currents (
currents (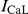 ,
,  ), a fast inward
), a fast inward 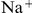 current (
current (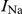 ) and a hyperpolarization-activated current (
) and a hyperpolarization-activated current (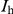 ); (ii) five outward currents: two voltage-gated
); (ii) five outward currents: two voltage-gated 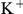 currents (
currents (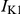 ,
, 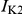 ), an A-type transient
), an A-type transient 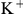 current (
current (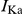 ) and two
) and two 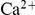 -activated
-activated 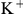 currents (
currents (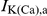 ,
, 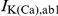 ); (iii) a non-specific cation current (
); (iii) a non-specific cation current (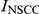 ); (iv) a
); (iv) a 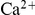 -activated
-activated 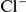 current (
current (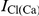 ); (v) a small background potassium current (
); (v) a small background potassium current (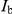 ); and (vi) an electrogenic
); and (vi) an electrogenic 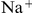 -
-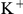 pump (
pump (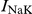 ) and a
) and a 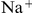 -
-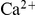 exchanger (
exchanger (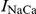 ). Properties of these currents are developed based on published voltage- and current-clamp experimental data of, wherever possible, late pregnant rat myometrial cells and tissues in the literature; where rat myometrial data is not available, but complementary data is available, e.g., from human USMC, or clonal cells expressing rat-derived proteins, then this has been mentioned.
). Properties of these currents are developed based on published voltage- and current-clamp experimental data of, wherever possible, late pregnant rat myometrial cells and tissues in the literature; where rat myometrial data is not available, but complementary data is available, e.g., from human USMC, or clonal cells expressing rat-derived proteins, then this has been mentioned.
Most of the membrane currents were modeled with Hodgkin-Huxley type formulation in the following form:
| (4) |
| (5) |
| (6) |
where  is maximum conductance,
is maximum conductance, 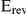 is the reversal potential, R is the universal gas constant, F is the Faraday constant, T is absolute temperature and
is the reversal potential, R is the universal gas constant, F is the Faraday constant, T is absolute temperature and 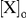 and
and 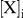 are the extracellular and intracellular ionic concentrations of ion X. The dimensionless gating variable (y) describes the time-dependent activation or inactivation profile of the channel conductance where
are the extracellular and intracellular ionic concentrations of ion X. The dimensionless gating variable (y) describes the time-dependent activation or inactivation profile of the channel conductance where 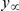 , the steady-state value, and
, the steady-state value, and 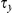 , the time constant, are functions of voltage and/or ionic concentrations. For the electrogenic
, the time constant, are functions of voltage and/or ionic concentrations. For the electrogenic  and
and 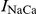 , we adopted the formulations used in the description of cardiac ventricular cells from Nakao & Gadsby [87] and Weber et al., [91] respectively. The nomenclature for the dynamic gating variables of individual membrane currents is listed in Table S2. Experimental data at body temperature, or a reported
, we adopted the formulations used in the description of cardiac ventricular cells from Nakao & Gadsby [87] and Weber et al., [91] respectively. The nomenclature for the dynamic gating variables of individual membrane currents is listed in Table S2. Experimental data at body temperature, or a reported 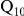 for an individual current, was available for
for an individual current, was available for 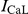 ,
, 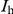 ,
, 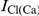 ,
, 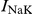 and
and 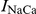 . For other currents, we had to assume the simplest case whereby the dynamics were similar at both room and body temperature.
. For other currents, we had to assume the simplest case whereby the dynamics were similar at both room and body temperature.
Calcium dynamics
Bursztyn et al., [24] modeled 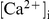 dynamics with three major calcium fluxes in myometrial cells: membrane calcium channels (
dynamics with three major calcium fluxes in myometrial cells: membrane calcium channels (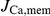 ),
), 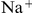 -
-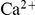 exchanger (
exchanger (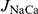 ) and plasma membrane
) and plasma membrane 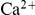 ATPase (
ATPase (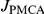 ) assuming
) assuming 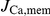 was at its equilibrium, i.e., time-independent. Herein we have included the temporal dynamics of membrane calcium currents in
was at its equilibrium, i.e., time-independent. Herein we have included the temporal dynamics of membrane calcium currents in 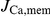 , and adopted the Weber et al., [91] formula for
, and adopted the Weber et al., [91] formula for 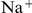 -
-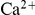 exchanger.
exchanger.
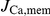 , which includes all the membrane calcium currents:
, which includes all the membrane calcium currents: 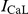 ,
, 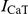 and the calcium component of
and the calcium component of 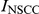 (
(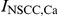 ), was calculated from the total membrane calcium current by
), was calculated from the total membrane calcium current by
| (7) |
where  is the specific membrane capacitance; F is the Faraday constant;
is the specific membrane capacitance; F is the Faraday constant; 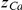 is the valency of
is the valency of 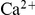 ions;
ions; 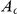 is the cell membrane surface area;
is the cell membrane surface area; 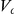 is cell volume; and
is cell volume; and 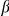 is the proportion of free intracellular
is the proportion of free intracellular 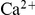 ions.
ions.
The geometry of a uterine smooth muscle cell is assumed to be two cone shapes joined end-to-end at their bases [110]. Reported cell sizes for late pregnant myometrial cells are 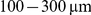 in length with a radius of
in length with a radius of 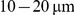 [29], [33]. As these dimensions cover a wide range, we represented the cell geometry with a single parameter,
[29], [33]. As these dimensions cover a wide range, we represented the cell geometry with a single parameter, 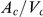 , the surface area to volume ratio. We did not model cytoplasmic
, the surface area to volume ratio. We did not model cytoplasmic 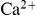 buffering proteins or intracellular calcium stores because such information for myometrial cells is too scant. Instead we assumed simply a tiny fraction of the membrane calcium influx to be free ions and the quantity is represented by the parameter
buffering proteins or intracellular calcium stores because such information for myometrial cells is too scant. Instead we assumed simply a tiny fraction of the membrane calcium influx to be free ions and the quantity is represented by the parameter 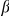 [111].
[111].
Contractile mechanism
Force development during uterine contraction was modeled with a simple first-order ordinary differential equation:
| (8) |
| (9) |
where  is the dimensionless gating variable describing the time-dependent activation profile of force,
is the dimensionless gating variable describing the time-dependent activation profile of force, 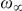 the steady-state value, and
the steady-state value, and 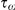 the time constant, are functions of
the time constant, are functions of 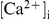 . The force steady-state is described by the
. The force steady-state is described by the 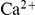 -activated active force relationship from non-pregnant rat myometrium at
-activated active force relationship from non-pregnant rat myometrium at 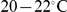 [112]; the time constant function is chosen to reproduce force development in late pregnant myometrial tissues recorded at
[112]; the time constant function is chosen to reproduce force development in late pregnant myometrial tissues recorded at 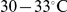 [103], [104] (Figure S6).
[103], [104] (Figure S6).
Model simulations
Action potentials were induced in the whole cell model by applying an external stimulus current ( ), either as brief square pulses for single spike AP or with a current clamp for bursting or plateau AP.
), either as brief square pulses for single spike AP or with a current clamp for bursting or plateau AP.
The initial values of the dynamical variables (V, 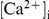 , membrane current gating variables, and
, membrane current gating variables, and 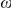 ) are listed in Table S3. The parameter values, which remain constant during simulations, are listed in Table S4. All the equations are given in Appendix S1.
) are listed in Table S3. The parameter values, which remain constant during simulations, are listed in Table S4. All the equations are given in Appendix S1.
Simulations were computed with a fixed time step of 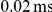 , using XPPAUT [113] with either the fourth-order Runge-Kutta numerical integration method or the Euler Method, in a IBM laptop PC with a Intel(R) Pentium(R) M
, using XPPAUT [113] with either the fourth-order Runge-Kutta numerical integration method or the Euler Method, in a IBM laptop PC with a Intel(R) Pentium(R) M 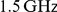 single processor. The Runge-Kutta was the method of choice for developing individual components and short simulations of the whole cell model whereas the Euler method was mainly used for simulations requiring longer integration times. Solutions of the whole USMC model using both integration methods are almost identical.
single processor. The Runge-Kutta was the method of choice for developing individual components and short simulations of the whole cell model whereas the Euler method was mainly used for simulations requiring longer integration times. Solutions of the whole USMC model using both integration methods are almost identical.
A copy of the model source code written in the C programming language is included in Appendix S2.
Annotation of Figures
Within the body of some Figures there are textual annotations that mention the source references for the data plotted in those diagrams. Those references without parenthesis indicate published values that we have reproduced in the diagram. The references mentioned within parentheses reflect data that we have extracted from published raw tracings and refitted as displayed in the figures. Data referred to as ‘unpublished’ is remarked upon in the main text.
Supporting Information
Simulating the effect of estradiol on the inactivation of myometrial 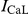 .
.
(PDF)
Different inactivation kinetics of myometrial 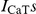 .
.
(PDF)
Divalent ion concentration versus 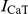 inactivation time constant of rat myometrial
inactivation time constant of rat myometrial 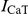 .
.
(PDF)
Experimental current tracings of 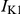 from five cells and an example of extrapolated
from five cells and an example of extrapolated 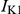 at the voltage step (
at the voltage step (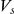 )
) 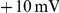 averaged from these five cells.
averaged from these five cells.
(PDF)
Experimental current tracings of 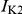 from four cells and an example of extrapolated
from four cells and an example of extrapolated 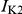 at the voltage step (
at the voltage step (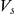 )
) 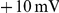 averaged from these four cells.
averaged from these four cells.
(PDF)
Modeling the dynamics of 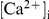 -dependent active force.
-dependent active force.
(PDF)
Modeling simultaneous changes in V and 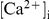 or
or 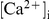 and force development.
and force development.
(PDF)
Modeling force output consequent to spike APs or plateau-like APs.
(PDF)
Definitions of the equation symbols.
(PDF)
Definition of gating variables for individual currents and force, and the corresponding experimental temperature and species.
(PDF)
Initial values of the dynamics variables used in model simulations.
(PDF)
Constant parameter values used in model simulations.
(PDF)
Equations used in the model simulations.
(PDF)
Model source code.
(BZ2)
Acknowledgments
We appreciate the assistance of Drs Phil Aaronson and Greg Knock (King's College London) in providing additional unpublished data to be analysed and reported in this manuscript. We thank Alan Weddell, Business Development Directorate, Newcastle University for advice on source code licensing.
Footnotes
Competing Interests: The authors have declared that no competing interests exist.
Funding: The work described here was supported by grants from MRC (G0900525 and G0902091, www.mrc.ac.uk), BBSRC (BBSRC/B/1678X, www.bbsrc.ac.uk), Tommy's (www.tommys.org) and EU Network of Excellence BioSim (LSHB-CT-2004-005137, http://biosim.fysik.dtu.dk:8080/biosim/). The funders had no role in study design, data collection and analysis, decision to publish, or preparation of the manuscript.
References
- 1.Landa J, West TC. Transmembrane potentials and contractility in the pregnant rat uterus. Am J Physiol. 1956;187:333–337. doi: 10.1152/ajplegacy.1956.187.2.333. [DOI] [PubMed] [Google Scholar]
- 2.Landa JF, West TC, Thiersch JB. Relationships between contraction and membrane electrical activity in the isolated uterus of the pregnant rat. Am J Physiol. 1959;196:905–909. doi: 10.1152/ajplegacy.1959.196.4.905. [DOI] [PubMed] [Google Scholar]
- 3.Csapo IA, Kuriyama HA. Effects of ions and drugs on cell membrane activity and tension in the postpartum rat myometrium. J Physiol. 1963;165:575–592. doi: 10.1113/jphysiol.1963.sp007081. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Garfield RE, Maner WL. Physiology and electrical activity of uterine contractions. Semin Cell Dev Biol. 2007;18:289–295. doi: 10.1016/j.semcdb.2007.05.004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Taggart MJ, Morgan KG. Regulation of the uterine contractile apparatus and cytoskeleton. Semin Cell Dev Biol. 2007;18:296–304. doi: 10.1016/j.semcdb.2007.05.006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Goldenberg RL, Culhane JF, Iams JD, Romero R. Epidemiology and causes of preterm birth. Lancet. 2008;371:75–84. doi: 10.1016/S0140-6736(08)60074-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Bugg GJ, Stanley E, Baker PN, Taggart MJ, Johnston TA. Outcomes of labours augmented with oxytocin. Eur J Obstet Gynecol Reprod Biol. 2006;124:37–41. doi: 10.1016/j.ejogrb.2005.04.015. [DOI] [PubMed] [Google Scholar]
- 8.Parkington HC, Tonta MA, Davies NK, Brennecke SP, Coleman HA. Hyperpolarization and slowing of the rate of contraction in human uterus in pregnancy by prostaglandins E2 and F2α: Involvement of the Na+ pump. J Physiol. 1999;514(Pt 1):229–243. doi: 10.1111/j.1469-7793.1999.229af.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Taggart MJ, Tribe RM. Cellular ionic mechanisms controlling uterine smooth muscle contraction: effects of gestational state. In: Savinneau JP, editor. New Frontiers in Smooth Muscle Biology and Physiology. India: Research Signpost; 2007. pp. 523–549. ISBN: 9788178952956. [Google Scholar]
- 10.Wilde DW, Marshall JM. Effects of tetraethylammonium and 4-aminopyridine on the plateau potential of circular myometrium from the pregnant rat. Biol Reprod. 1988;38:836–845. doi: 10.1095/biolreprod38.4.836. [DOI] [PubMed] [Google Scholar]
- 11.Inoue Y, Okabe K, Soeda H. Augmentation and suppression of action potentials by estradiol in the myometrium of pregnant rat. Can J Physiol Pharmacol. 1999;77:447–453. [PubMed] [Google Scholar]
- 12.Shmigol AV, Eisner DA, Wray S. Properties of voltage-activated [Ca2+]i transients in, single smooth muscle cells isolated from pregnant rat uterus. J Physiol. 1998;511:803–811. doi: 10.1111/j.1469-7793.1998.803bg.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Blanks AM, Zhao ZH, Shmygol A, Bru-Mercier G, Astle S, et al. Characterization of the molecular and electrophysiological properties of the T-type calcium channel in human myometrium. J Physiol. 2007;581:915–926. doi: 10.1113/jphysiol.2007.132126. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Sperelakis N, Inoue Y, Ohya Y. Fast Na+ channels and slow Ca2+ current in smooth muscle from pregnant rat uterus. Mol Cell Biochem. 1992;114:79–89. [PubMed] [Google Scholar]
- 15.Jones K, Shmygol A, Kupittayanant S, Wray S. Electrophysiological characterization and functional importance of calcium-activated chloride channel in rat uterine myocytes. Pflugers Arch. 2004;448:36–43. doi: 10.1007/s00424-003-1224-7. [DOI] [PubMed] [Google Scholar]
- 16.Khan RN, Smith SK, Morrison JJ, Ashford ML. Properties of large-conductance K+ channels in human myometrium during pregnancy and labour. Proc Biol Sci. 1993;251:9–15. doi: 10.1098/rspb.1993.0002. [DOI] [PubMed] [Google Scholar]
- 17.Wang SY, Yoshino M, Sui JL, Wakui M, Kao PN, et al. Potassium currents in freshly dissociated uterine myocytes from nonpregnant and late-pregnant rats. J Gen Physiol. 1998;112:737–756. doi: 10.1085/jgp.112.6.737. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Knock GA, Aaronson PI. Calcium antagonistic properties of the cyclooxygenase-2 inhibitor nimesulide in human myometrial myocytes. Br J Pharmacol. 1999;127:1470–1478. doi: 10.1038/sj.bjp.0702685. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Knock GA, Smirnov SV, Aaronson PI. Voltage-gated K+ currents in freshly isolated myocytes of, the pregnant human myometrium. J Physiol. 1999;518:769–781. doi: 10.1111/j.1469-7793.1999.0769p.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Noble K, Floyd R, Shmygol A, Shmygol A, Mobasheri A, et al. Distribution, expression and functional effects of small conductance Ca-activated potassium (SK) channels in rat myometrium. Cell Calcium. 2010;47:47–54. doi: 10.1016/j.ceca.2009.11.004. [DOI] [PubMed] [Google Scholar]
- 21.Floyd RV, Wray S, Quenby S, Martin-Vasallo P, Mobasheri A. Expression and distribution of Na, K-ATPase isoforms in the human uterus. Reprod Sci. 2010;17:366–376. doi: 10.1177/1933719109355196. [DOI] [PubMed] [Google Scholar]
- 22.Grover AK, Kwan CY, Daniel EE. Na-Ca exchange in rat myometrium membrane vesicles highly enriched in plasma membranes. Am J Physiol. 1981;240:C175–82. doi: 10.1152/ajpcell.1981.240.5.C175. [DOI] [PubMed] [Google Scholar]
- 23.Taggart MJ, Blanks A, Kharche S, Holden A, Wang B, et al. Towards understanding the myometrial physiome: approaches for the construction of a virtual physiological uterus. BMC Pregnancy Childbirth. 2007;7(Suppl 1):S3. doi: 10.1186/1471-2393-7-S1-S3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Bursztyn L, Eytan O, Jaffa AJ, Elad D. Mathematical model of excitation-contraction in a uterine smooth muscle cell. Am J Physiol cell Physiol. 2007;292:1816–1829. doi: 10.1152/ajpcell.00478.2006. [DOI] [PubMed] [Google Scholar]
- 25.Rihana S, Terrien J, Germain G, Marque C. Mathematical modeling of electrical activity of uterine muscle cells. Med Biol Eng Comput. 2009;47:665–675. doi: 10.1007/s11517-009-0433-4. [DOI] [PubMed] [Google Scholar]
- 26.Jmari K, Mironneau C, Mironneau J. Inactivation of calcium channel current in rat uterine smooth muscle: evidence for calcium- and voltage-mediated mechanisms. J Physiol. 1986;380:111–126. doi: 10.1113/jphysiol.1986.sp016275. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Miyoshi H, Urabe T, Fujiwara A. Electrophysiological properties of membrane currents in single myometrial, cells isolated from pregnant rats. Pflugers Arch. 1991;419:386–393. doi: 10.1007/BF00371121. [DOI] [PubMed] [Google Scholar]
- 28.Young RC, Smith LH, McLaren MD. T-type and L-type calcium currents in freshly dispersed human uterine smooth muscle cells. Am J Obstet Gynecol. 1993;169:785–792. doi: 10.1016/0002-9378(93)90006-5. [DOI] [PubMed] [Google Scholar]
- 29.Amedee T, Mironneau C, Mironneau J. The calcium channel current of pregnant rat single myometrial cells, in short-term primary culture. J Physiol. 1987;392:253–272. doi: 10.1113/jphysiol.1987.sp016779. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Yamamoto T. Effects of estrogens on Ca channels in myometrial cells isolated from pregnant rats. Am J Physiol. 1995;268:C64–9. doi: 10.1152/ajpcell.1995.268.1.C64. [DOI] [PubMed] [Google Scholar]
- 31.Mcdonald TF, Pelzer S, Trautwein W, Pelzer DJ. Regulation and modulation of calcium channels in cardiac, skeletal, and smooth muscle cells. Physiol Rev. 1994;74:365–507. doi: 10.1152/physrev.1994.74.2.365. [DOI] [PubMed] [Google Scholar]
- 32.Okabe K, Inoue Y, Soeda H. Estradiol inhibits Ca2+ and K+ channels in smooth muscle cells from pregnant rat myometrium. Eur J Pharmacol. 1999;376:101–108. doi: 10.1016/s0014-2999(99)00353-2. [DOI] [PubMed] [Google Scholar]
- 33.Yoshino M, Wang SY, Kao CY. Sodium and calcium inward currents in freshly dissociated smooth myocytes of rat uterus. J Gen Physiol. 1997;110:565–577. doi: 10.1085/jgp.110.5.565. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Inoue Y, Sperelakis N. Gestational change in Na+ and Ca2+ channel current densities, in rat myometrial smooth muscle cells. Am J Physiol. 1991;260:C658–63. doi: 10.1152/ajpcell.1991.260.3.C658. [DOI] [PubMed] [Google Scholar]
- 35.Kusaka M, Sperelakis N. Inhibition of L-type calcium current by genistein, a tyrosine kinase inhibitor, in pregnant rat myometrial cells. Biochim Biophys Acta. 1995;1240:196–200. doi: 10.1016/0005-2736(95)00191-3. [DOI] [PubMed] [Google Scholar]
- 36.Greenwood IA, Large WA. Analysis of the time course of calcium-activated chloride ‘tail’ currents in rabbit portal vein smooth muscle cells. Pflugers Arch. 1996;432:970–979. doi: 10.1007/s004240050224. [DOI] [PubMed] [Google Scholar]
- 37.Parkington HC, Coleman HA. Excitability in uterine smooth muscle. Front Horm Res. 2001;27:179–200. doi: 10.1159/000061026. [DOI] [PubMed] [Google Scholar]
- 38.Mershon JL, Mikala G, Schwartz A. Changes in the expression of the L-type voltage-dependent calcium channel during pregnancy and parturition in the rat. Biol Reprod. 1994;51:993–1002. doi: 10.1095/biolreprod51.5.993. [DOI] [PubMed] [Google Scholar]
- 39.Tezuka N, Ali M, Chwalisz K, Garfield RE. Changes in transcripts encoding calcium channel subunits of rat myometrium during pregnancy. Am J Physiol. 1995;269:C1008–17. doi: 10.1152/ajpcell.1995.269.4.C1008. [DOI] [PubMed] [Google Scholar]
- 40.Ohkubo T, Kawarabayashi T, Inoue Y, Kitamura K. Differential expression of L- and T-type calcium channels between, longitudinal and circular muscles of the rat myometrium during pregnancy. Gynecol Obstet Invest. 2005;59:80–85. doi: 10.1159/000082333. [DOI] [PubMed] [Google Scholar]
- 41.Helguera G, Olcese R, Song M, Toro L, Stefani E. Tissue-specific regulation of Ca2+ channel protein expression by sex hormones. Biochim Biophys Acta. 2002;1569:59–66. doi: 10.1016/s0304-4165(01)00234-3. [DOI] [PubMed] [Google Scholar]
- 42.Ohya Y, Sperelakis N. Fast Na+ and slow Ca2+ channels in single uterine muscle cells from pregnant rats. Am J Physiol. 1989;257:C408–12. doi: 10.1152/ajpcell.1989.257.2.C408. [DOI] [PubMed] [Google Scholar]
- 43.Serrano JR, Perez-Reyes E, Jones SW. State-dependent inactivation of the alpha1G T-type calcium channel. J Gen Physiol. 1999;114:185–201. doi: 10.1085/jgp.114.2.185. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Hering J, Feltz A, Lambert RC. Slow inactivation of the Cav3.1 isotype of T-type calcium channels. J Physiol. 2003;555:331–344. doi: 10.1113/jphysiol.2003.054361. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Asokan KT, Sarkar SN, Mishra SK, Raviprakash V. Effects of mibefradil on uterine contractility. Eur J Pharmacol. 2002;455:65–71. doi: 10.1016/s0014-2999(02)02487-1. [DOI] [PubMed] [Google Scholar]
- 46.Lee SE, Ahn DS, Lee YH. Role of T-type Ca channels in the spontaneous phasic contraction of pregnant rat uterine smooth muscle. Korean J Physiol Pharmacol. 2009;13:241–249. doi: 10.4196/kjpp.2009.13.3.241. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Inoue Y, Nakao K, Okabe K, Izumi H, Kanda S, et al. Some electrical properties of human pregnant myometrium. Am J Obstet Gynecol. 1990;162:1090–1098. doi: 10.1016/0002-9378(90)91322-4. [DOI] [PubMed] [Google Scholar]
- 48.Satoh H. Identification of a hyperpolarization-activated inward current in uterine smooth muscle cells during pregnancy. Gen Pharmacol. 1995;26:1335–1338. doi: 10.1016/0306-3623(95)00006-m. [DOI] [PubMed] [Google Scholar]
- 49.Okabe K, Inoue Y, Kawarabayashi T, Kajiya H, Okamoto F, et al. Physiological significance of hyperpolarization-activated inward currents (ih) in smooth muscle cells from the circular layers of pregnant rat myometrium. Pflugers Arch. 1999;439:76–85. doi: 10.1007/s004249900140. [DOI] [PubMed] [Google Scholar]
- 50.Shannon TR, Wang F, Puglisi J, Weber C, Bers DM. A mathematical treatment of integrated Ca dynamics within the ventricular myocyte. Biophys J. 2004;87:3351–3371. doi: 10.1529/biophysj.104.047449. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51.Knock GA, Tribe RM, Hassoni AA, Aaronson PI. Modulation of potassium current characteristics in human myometrial smooth muscle by 17beta-estradiol and progesterone. Biol Reprod. 2001;64:1526–1534. doi: 10.1095/biolreprod64.5.1526. [DOI] [PubMed] [Google Scholar]
- 52.Erulkar SD, Rendt J, Nori RD, Ger B. The influence of 17 beta-oestradiol on K+ currents in smooth muscle cells isolated from immature rat uterus. Proc Biol Sci. 1994;256:59–65. doi: 10.1098/rspb.1994.0049. [DOI] [PubMed] [Google Scholar]
- 53.Piedras-Renteria E, Stefani E, Toro L. Potassium currents in freshly dispersed myometrial cells. Am J Physiol. 1991;261:C278–84. doi: 10.1152/ajpcell.1991.261.2.C278. [DOI] [PubMed] [Google Scholar]
- 54.Anwer K, Toro L, Oberti C, Stefani E, Sanborn BM. Ca2+-activated K+ channels in pregnant rat myometrium: modulation by a beta-adrenergic agent. Am J Physiol. 1992;263:C1049–56. doi: 10.1152/ajpcell.1992.263.5.C1049. [DOI] [PubMed] [Google Scholar]
- 55.Anwer K, Oberti C, Perez GJ, Perez-Reyes N, Mcdougall JK, et al. Calcium-activated K+ channels as modulators of human myometrial contractile activity. Am J Physiol. 1993;265:C976–85. doi: 10.1152/ajpcell.1993.265.4.C976. [DOI] [PubMed] [Google Scholar]
- 56.Perez GJ, Toro L, Erulkar SD, Stefani E. Characterization of large-conductance, calcium-activated potassium channels from human myometrium. Am J Obstet Gynecol. 1993;168:652–660. doi: 10.1016/0002-9378(93)90513-i. [DOI] [PubMed] [Google Scholar]
- 57.Song M, Zhu N, Olcese R, Barila B, Toro L, et al. Hormonal control of protein expression and mRNA levels of the MaxiK channel alpha subunit in myometrium. FEBS Lett. 1999;460:427–432. doi: 10.1016/s0014-5793(99)01394-0. [DOI] [PubMed] [Google Scholar]
- 58.Zhou XB, Wang GX, Ruth P, Huneke B, Korth M. BK(Ca) channel activation by membrane-associated cGMP kinase may contribute to uterine quiescence in pregnancy. Am J Physiol Cell Physiol. 2000;279:C1751–9. doi: 10.1152/ajpcell.2000.279.6.C1751. [DOI] [PubMed] [Google Scholar]
- 59.Matharoo-Ball B, Ashford MLJ, Arulkumaran S, Khan RN. Down-regulation of the alpha- and beta-subunits of the calcium-activated potassium channel in human myometrium with parturition. Biol Reprod. 2003;68:2135–2141. doi: 10.1095/biolreprod.102.010454. [DOI] [PubMed] [Google Scholar]
- 60.Curley M, Morrison JJ, Smith TJ. Analysis of maxi-K alpha subunit splice variants in human myometrium. Reprod Biol Endocrinol. 2004;2:67. doi: 10.1186/1477-7827-2-67. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 61.Khan RN, Smith SK, Ashford ML. Contribution of calcium-sensitive potassium channels to NS1619-induced relaxation in human pregnant myometrium. Hum Reprod. 1998;13:208–213. doi: 10.1093/humrep/13.1.208. [DOI] [PubMed] [Google Scholar]
- 62.Khan RN, Matharoo-Ball B, Arulkumaran S, Ashford ML. Potassium channels in the human myometrium. Exp Physiol. 2001;86:255–264. doi: 10.1113/eph8602181. [DOI] [PubMed] [Google Scholar]
- 63.Bao L, Cox DH. Gating and ionic currents reveal how the BK(Ca) channel's Ca2+ sensitivity is enhanced by its beta1 subunit. J Gen Physiol. 2005;12:393–412. doi: 10.1085/jgp.200509346. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 64.Orio P, Torres Y, Rojas P, Carvacho I, Garcia ML, et al. Structural determinants for functional coupling between the beta and alpha subunits in the Ca2+-activated K+ (BK) channel. J Gen Physiol. 2006;127:191–204. doi: 10.1085/jgp.200509370. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 65.Benkusky NA, Fergus DJ, Zucchero TM, England SK. Regulation of the Ca2+-sensitive domains of the maxi-K channel in the mouse myometrium during gestation. J Biol Chem. 2000;275:27712–27719. doi: 10.1074/jbc.M000974200. [DOI] [PubMed] [Google Scholar]
- 66.Zhou XB, Wang GX, Huneke B, Wieland T, Korth M. Pregnancy switches adrenergic signal transduction in rat and human uterine myocytes as probed by BKCa channel activity. J Physiol. 2000;524:339–352. doi: 10.1111/j.1469-7793.2000.t01-1-00339.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 67.Shmigol A, Eisner DA, Wray S. Carboxyeosin decreases the rate of decay of the [Ca2+]i, transient in uterine smooth muscle cells isolated from pregnant rats. Pflugers Arch. 1998;437:158–160. doi: 10.1007/s004240050761. [DOI] [PubMed] [Google Scholar]
- 68.Brown A, Cornwell T, Korniyenko I, Solodushko V, Bond CT, et al. Myometrial expression of small conductance Ca2+-activated K+ channels depresses phasic uterine contraction. Am J Physiol Cell Physiol. 2007;292:C832–C840. doi: 10.1152/ajpcell.00268.2006. [DOI] [PubMed] [Google Scholar]
- 69.Smith RC, McClure MC, Smith MA, Abel PW, Bradley ME. The role of voltage-gated potassium channels in the regulation of mouse uterine contractility. Reprod Biol Endocrinol. 2007;5:41. doi: 10.1186/1477-7827-5-41. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 70.Pierce SL, Kresowik JDK, Lamping KG, England SK. Overexpression of SK3 channels dampens uterine contractility to prevent preterm labor in mice. Biol Reprod. 2008;78:1058–1063. doi: 10.1095/biolreprod.107.066423. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 71.McCallum LA, Pierce SL, England SK, Greenwood IA, Tribe RM. The contribution of Kv7 channels to pregnant mouse and human myometrial contractility. J Cell Mol Med. 2011;15:577–86. doi: 10.1111/j.1582-4934.2010.01021.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 72.Coleman HA, Parkington HC. Single channel Cl− and K+ currents from cells of uterus not treated with enzymes. Pflugers Arch. 1987;410:560–562. doi: 10.1007/BF00586540. [DOI] [PubMed] [Google Scholar]
- 73.Mironneau J, Arnaudeau S, Macrez-Lepretre N, Boittin FX. Ca2+ sparks and Ca2+ waves activate different Ca2+-dependent ion channels in single myocytes from rat portal vein. Cell Calcium. 1996;20:153–160. doi: 10.1016/s0143-4160(96)90104-9. [DOI] [PubMed] [Google Scholar]
- 74.Young RC, Bemis A. Calcium-activated chloride currents prolongs the duration of contractions in pregnant rat myometrial tissue. Reprod Sci. 2009;16:734–739. doi: 10.1177/1933719109334965. [DOI] [PubMed] [Google Scholar]
- 75.Jeong JW, Lee KY, Lydon JP, DeMayo FJ. Steroid hormone regulation of Clca3 expression in the murine uterus. J Endocrinol. 2006;189:473–484. doi: 10.1677/joe.1.06747. [DOI] [PubMed] [Google Scholar]
- 76.Song J, Zhang X, Qi Z, Sun G, Chi S, et al. Cloning and characterization of a calcium-activated chloride channel in rat uterus. Biol Reprod. 2009;80:788–794. doi: 10.1095/biolreprod.108.071258. [DOI] [PubMed] [Google Scholar]
- 77.Arreola J, Melvin JE, Begenisich T. Activation of calcium-dependent chloride channels in rat parotid acinar cells. J Gen Physiol. 1996;108:35–47. doi: 10.1085/jgp.108.1.35. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 78.Angermann JE, Sanguinetti AR, Kenyon JL, Leblanc N, Greenwood IA. Mechanism of the inhibition of Ca2+-activated Cl− currents by phosphorylation in pulmonary arterial smooth muscle cells. J Gen Physiol. 2006;128:73–87. doi: 10.1085/jgp.200609507. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 79.Miyoshi H, Yamaoka K, Garfield RE, Ohama K. Identification of a non-selective cation channel current in myometrial cells isolated from pregnant rats. Pflugers Arch. 2004;447:457–464. doi: 10.1007/s00424-003-1175-z. [DOI] [PubMed] [Google Scholar]
- 80.Chang DC. Dependence of cellular potential on ionic concentrations. data supporting a modification of the constant field equation. Biophys J. 1983;43:149–156. doi: 10.1016/S0006-3495(83)84335-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 81.Manabe K, Takano M, Noma A. Non-selective cation current of guinea-pig endocardial endothelial cells. J Physiol. 1995;487:407–419. doi: 10.1113/jphysiol.1995.sp020889. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 82.Taylor GS, Paton DM, Daniel EE. Evidence for an electrogenic sodium pump in smooth muscle. Life Sci. 1969;8:769–773. doi: 10.1016/0024-3205(69)90268-9. [DOI] [PubMed] [Google Scholar]
- 83.Taylor GS, Paton DM, Daniel EE. Characteristics of electrogenic sodium pumping in rat myometrium. J Gen Physiol. 1970;56:360–375. doi: 10.1085/jgp.56.3.360. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 84.Turi A, Marcsek Z, Mullner N, Kucsera M, Bori Z. The activity of Na+/K+-ATPase and abundance of its mRNA are regulated in rat myometrium during pregnancy. Biochem Biophys Res Commun. 1992;188:1191–1198. doi: 10.1016/0006-291x(92)91357-v. [DOI] [PubMed] [Google Scholar]
- 85.Esplin MS, Fausett MB, Faux DS, Graves SW. Changes in the isoforms of the sodium pump in the placenta and myometrium of women in labor. Am J Obstet Gynecol. 2003;188:759–764. doi: 10.1067/mob.2003.166. [DOI] [PubMed] [Google Scholar]
- 86.Vance CJ, Esplin MS, Hamblin S, Graves SW. Alterations in uterine sodium pump abundance may contribute to the onset and progression of term and preterm labor in mice. Am J Obstet Gynecol. 2006;195:1407–1414. doi: 10.1016/j.ajog.2006.05.009. [DOI] [PubMed] [Google Scholar]
- 87.Nakao M, Gadsby DC. [Na] and [K] dependence of the Na/K pump current-voltage relationship in guinea pig ventricular myocytes. J Gen Physiol. 1989;94:539–565. doi: 10.1085/jgp.94.3.539. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 88.Nakamura Y, Ohya Y, Abe I, Fujishima M. Sodium-potassium pump current in smooth muscle cells from mesenteric resistance arteries of the guinea-pig. J Physiol. 1999;519:203–212. doi: 10.1111/j.1469-7793.1999.0203o.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 89.Taggart MJ, Wray S. Agonist mobilization of sarcoplasmic reticular calcium in smooth muscle: Functional coupling to the plasmalemmal Na+/Ca2+ exchanger? Cell Calcium. 1997;22:333–341. doi: 10.1016/s0143-4160(97)90018-x. [DOI] [PubMed] [Google Scholar]
- 90.Shmigol AV, Eisner DA, Wray S. The role of the sarcoplasmic reticulum as a Ca2+ sink in rat uterine smooth muscle cells. J Physiol. 1999;520 Pt 1:153–163. doi: 10.1111/j.1469-7793.1999.00153.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 91.Weber CR, Ginsburg KS, Philipson KD, Shannon TR, Bers DM. Allosteric regulation of Na/Ca exchange current by cytosolic Ca in intact cardiac myocytes. J Gen Physiol. 2001;117:119–131. doi: 10.1085/jgp.117.2.119. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 92.Abe Y. Effects of changing the ionic environment on passive and active membrane properties of pregnant rat uterus. J Physiol. 1971;214:173–190. doi: 10.1113/jphysiol.1971.sp009426. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 93.Quednau BD, Nicoll DA, Philipson KD. Tissue specificity and alternative splicing of the Na+/Ca2+ exchanger isoforms NCX1, NCX2, and NCX3 in rat. Am J Physiol Cell Physiol. 1997;272:C1250–1261. doi: 10.1152/ajpcell.1997.272.4.C1250. [DOI] [PubMed] [Google Scholar]
- 94.Levitsky DO. Three types of muscles express three sodium-calcium exchanger isoforms. Ann NY Acad Sci. 2007;1099:221–225. doi: 10.1196/annals.1387.063. [DOI] [PubMed] [Google Scholar]
- 95.Li Z, Matsuoka S, Hryshko LV, Nicoll DA, Bersohn MM, et al. Cloning of the NCX2 isoform of the plasma membrane Na+-Ca2+ exchanger. J Biol Chem. 1994;269:17434–17439. [PubMed] [Google Scholar]
- 96.Iwamoto T, Shigekawa M. Differential inhibition of Na+/Ca2+ exchanger isoforms by divalent cations and isothiourea derivative. Am J Physiol. 1998;275:C423–30. doi: 10.1152/ajpcell.1998.275.2.C423. [DOI] [PubMed] [Google Scholar]
- 97.Linck B, Qiu Z, He Z, Tong Q, Hilgemann DW, et al. Functional comparison of the three isoforms of the Na+/Ca2+ exchanger (NCX1, NCX2, NCX3). Am J Physiol. 1998;274:C415–23. doi: 10.1152/ajpcell.1998.274.2.C415. [DOI] [PubMed] [Google Scholar]
- 98.Campbell DL, Giles WR, Robinson K, Shibata EF. Studies of the sodium-calcium exchanger in bull-frog atrial myocytes. J Physiol. 1988;403:317–340. doi: 10.1113/jphysiol.1988.sp017251. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 99.Vigne P, Breittmayer JP, Duval D, Frelin C, Lazdunski M. The Na+/Ca2+ antiporter in aortic smooth muscle cells. J Biol Chem. 1988;263:8078–8083. [PubMed] [Google Scholar]
- 100.Mollard P, Mironneau J, Amedee T, Mironneau C. Electrophysiological characterization of single pregnant rat myometrial cells in short-term primary culture. Am J Physiol. 1986;250:C47–54. doi: 10.1152/ajpcell.1986.250.1.C47. [DOI] [PubMed] [Google Scholar]
- 101.Bengtsson B, Chow EM, Marshall JM. Activity of circular muscle of rat uterus at different times in pregnancy. Am J Physiol. 1984;246:C216–23. doi: 10.1152/ajpcell.1984.246.3.C216. [DOI] [PubMed] [Google Scholar]
- 102.Meisheri KD, Mcneill JH, Marshall JM. Effect of isoproterenol on the isolated pregnant rat myometrium. Eur J Pharmacol. 1979;60:1–6. doi: 10.1016/0014-2999(79)90045-1. [DOI] [PubMed] [Google Scholar]
- 103.Burdyga T, Wray S, Noble K. In situ calcium signaling. no calcium sparks detected in rat myometrium. Ann N Y Acad Sci. 2007;1101:85–96. doi: 10.1196/annals.1389.002. [DOI] [PubMed] [Google Scholar]
- 104.Burdyga T, Borisova L, Burdyga AT, Wray S. Temporal and spatial variations in spontaneous Ca events and mechanical activity in pregnant rat myometrium. Eur J Obstet Gynecol Reprod Biol. 2009;144(Suppl 1):S25–S32. doi: 10.1016/j.ejogrb.2009.02.017. [DOI] [PubMed] [Google Scholar]
- 105.Kawarabayashi T. Electrophysiology of the human myometrium. In: Chard T, Grudzinskas JG, editors. The Uterus. Cambridge, UK: Cambridge University Press, Cambridge Reviews in Human Reproduction, chapter 7; 1994. pp. 148–172. [Google Scholar]
- 106.Mankouri HW, Burdyga T, Taggart MJ, Wray S. Simultaneous measurements of electrical activity, intracellular calcium and contraction in smooth muscle. J Physiol. 1998;509.P:2P–3P. [Google Scholar]
- 107.Zhang J, Taggart M, Thornton S, Shmygol A, Blanks AM. The pregnancy dependent expression profile of the genomic complement of K channels in human myometrial smooth muscle and vasculature. Reprod Sci. 2010;17:78A. [Google Scholar]
- 108.Lammers WJEP, Mirghani H, Stephen B, Dhanasekaran S, Wahab A, et al. Patterns of electrical propagation in the intact pregnant guinea pig uterus. Am J Physiol Regul Integr Comp Physiol. 2008;294:R919–R928. doi: 10.1152/ajpregu.00704.2007. [DOI] [PubMed] [Google Scholar]
- 109.Mitchell BF, Taggart MJ. Are animal models relevant to key aspects of human parturition? Am J Physiol Regul Integr Comp Physiol. 2009;297:R525–R545. doi: 10.1152/ajpregu.00153.2009. [DOI] [PubMed] [Google Scholar]
- 110.Kamishima T, Mccarron JG. Depolarization-evoked increases in cytosolic calcium concentration in isolated smooth muscle cells of rat portal vein. J Physiol. 1996;492(Pt 1):61–74. doi: 10.1113/jphysiol.1996.sp021289. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 111.Standen NB, Stanfield PR. A binding-site model for calcium channel inactivation that depends on calcium entry. Proc R Soc Lond B Biol Sci. 1982;217:101–110. doi: 10.1098/rspb.1982.0097. [DOI] [PubMed] [Google Scholar]
- 112.Crichton CA, Taggart MJ, Wray S, Smith GL. Effects of pH and inorganic phosphate on force production in alpha-toxin-permeabilized isolated rat uterine smooth muscle. J Physiol. 1993;465:629–645. doi: 10.1113/jphysiol.1993.sp019697. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 113.Ermentrout GB. Simulating, analyzing, and animating dynamical systems: a guide to XPPAUT for researchers and students. Philadelphia, US: Society for Industrial and Applied Mathematics; 2002. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Simulating the effect of estradiol on the inactivation of myometrial 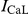 .
.
(PDF)
Different inactivation kinetics of myometrial 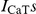 .
.
(PDF)
Divalent ion concentration versus 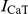 inactivation time constant of rat myometrial
inactivation time constant of rat myometrial 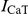 .
.
(PDF)
Experimental current tracings of 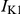 from five cells and an example of extrapolated
from five cells and an example of extrapolated 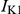 at the voltage step (
at the voltage step (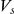 )
) 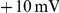 averaged from these five cells.
averaged from these five cells.
(PDF)
Experimental current tracings of  from four cells and an example of extrapolated
from four cells and an example of extrapolated  at the voltage step (
at the voltage step (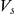 )
) 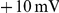 averaged from these four cells.
averaged from these four cells.
(PDF)
Modeling the dynamics of 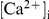 -dependent active force.
-dependent active force.
(PDF)
Modeling simultaneous changes in V and 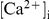 or
or 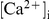 and force development.
and force development.
(PDF)
Modeling force output consequent to spike APs or plateau-like APs.
(PDF)
Definitions of the equation symbols.
(PDF)
Definition of gating variables for individual currents and force, and the corresponding experimental temperature and species.
(PDF)
Initial values of the dynamics variables used in model simulations.
(PDF)
Constant parameter values used in model simulations.
(PDF)
Equations used in the model simulations.
(PDF)
Model source code.
(BZ2)